Comparisons of Inverse Dynamics Formulations in a Spatial Redundantly Actuated Parallel Mechanism Constrained by Two Point Contact Higher Kinematic Pairs
Abstract
1. Introduction
- The inverse dynamics solution of the constrained RAPM has been explored deeply via Newton–Euler’s law, the Lagrangian formulation, and the principle of virtual work, respectively;
- Under the latter two methods, using the dynamics model of the 6RSS PM as the core of the RAPM’s model can considerably alleviate the computational demands;
- The insight into the influence of HKP constraints on the inverse dynamics has been provided clearly in terms of the model structure, the numerical results, and the computational cost.
2. The Robotic Mechanism
3. Kinematics of the Mechanism
3.1. Constrained Motions of the End Effector
3.2. Kinematics of the ith Chain
4. Newton–Euler Formulation
4.1. The End Effector

4.2. The Coupler SiMi
4.3. The Crank GiSi
4.4. The Entire Mechanism
5. Lagrangian Formulation
5.1. Model 1
5.1.1. The End Effector of the RAPM
5.1.2. The ith Chain
5.1.3. The Entire Mechanism
5.2. Model 2
5.2.1. The End Effector of the 6RSS PM
5.2.2. The Entire Mechanism
6. Principle of Virtual Work
6.1. Model 1
6.2. Model 2
7. Numerical Computations and Comparisons
7.1. Newton–Euler’s Approach
7.2. Lagrangian Formulation
7.3. Principle of Virtual Work
7.4. Discussions
7.4.1. Model Structures
7.4.2. Numerical Results
7.4.3. Computational Cost
7.4.4. Influence of HKP Constraints
8. Conclusions
- The robotic mechanism can satisfactorily imitate the chewing motions and forces of human beings. According to the computed actuating torques and constraint forces at spherical joints and HKPs, it is convenient to size actuators, linkages, HKP-related links in the mechanical design;
- Under Newton–Euler’s law, the constraint forces from HKPs onto the end effector is revealed by this law quite well. In comparison, these forces do not appear in the models under the Lagrangian formulation and the principle of virtual work. The model by Newton–Euler’s law under the first objective aim and the four models from the latter two energy methods using the pseudo-inverse solution produce identical numerical results;
- The efficiency of the model from Newton–Euler’s law and the two second models by the energy based methods is quite acceptable, while the first model by the Lagrangian formulation is extremely cumbersome. The two models from the principle of virtual work are the most computationally economic. In the two models by the Lagrangian formulations, the second one is much faster; an identical conclusion is also effective to the two models by the principle of virtual work. The computational cost from both the second models in the latter two methods approximately equals that of the 6RSS PM, mainly because the dynamics model of the 6RSS PM has been used as the core in these two second models;
- By comparing the computational requirements between the RAPM and the 6RSS PM, it is discovered that the HKP constraints greatly raise the complexity of the mechanism.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| {S} | Inertia frame |
| {M} | Frame established at the mass centre OM of the end effector |
| OM | Mass centre of the end effector |
| , and | Euler angles of the end effector |
| GiSi (i = 1, …, 6) | The ith crank |
| SiMi (i = 1, …, 6) | The ith coupler |
| {Ci} | Frame established at the fixed point Gi of the ith crank |
| {Ni} | Frame attached at the mass centre Ei of SiMi |
| Tj (j = L, R) | Left and right condyle ball centres |
| 3 × 1 position vector of OM in {S} | |
| pi (i = 1, …, 6) | Parameters describing the shape of surfaces where condyle ball centres TL and TR slide on |
| X, Y, and Z | Parameters describing translations of the end effector |
| Rotation matrix from {S} to {M} | |
| , and | Rotation matrices about XM, YM, and ZM axes by , and , respectively |
| 6 × 1 vector grouping six motion variables of the end effector | |
| First and second time derivatives of , respectively | |
| qEE | 4 × 1 vector grouping four DOFs of the end effector |
| First and second time derivatives of qEE, respectively | |
| Angular velocity of the end effector | |
| MJ | 6 × 4 Jacobian matrix between XEE and qEE |
| 3 × 3 zero matrix | |
| E3 | 3 × 3 identity matrix |
| 6 × 1 vector containing the displacements of six active joints | |
| and | Length of SiMi and , respectively |
| and | Vectors of in {S} and {M}, respectively |
| 3 × 1 constant position vector of Gi in {S} | |
| and | Rotation matrices from {S} to and at the initial configuration of the mechanism, respectively |
| Rotation matrix about the axis by | |
| and | Euler angles expressing the rotation of the ith coupler |
| 3 × 1 generalized vector specifying the configuration of the ith kinematic chain and its first and second time derivatives | |
| Jacobian matrix of with respect to | |
| Jacobian matrix of with respect to | |
| and | Angular velocity and acceleration of SiMi, respectively |
| and | Translational velocity and acceleration of mass centre Ei of SiMi, respectively |
| Jacobian matrix of with respect to | |
| Constrained forces at the left and right condylar balls, respectively | |
| Constrained forces at | |
| Constrained forces at | |
| g | Gravitational acceleration vector |
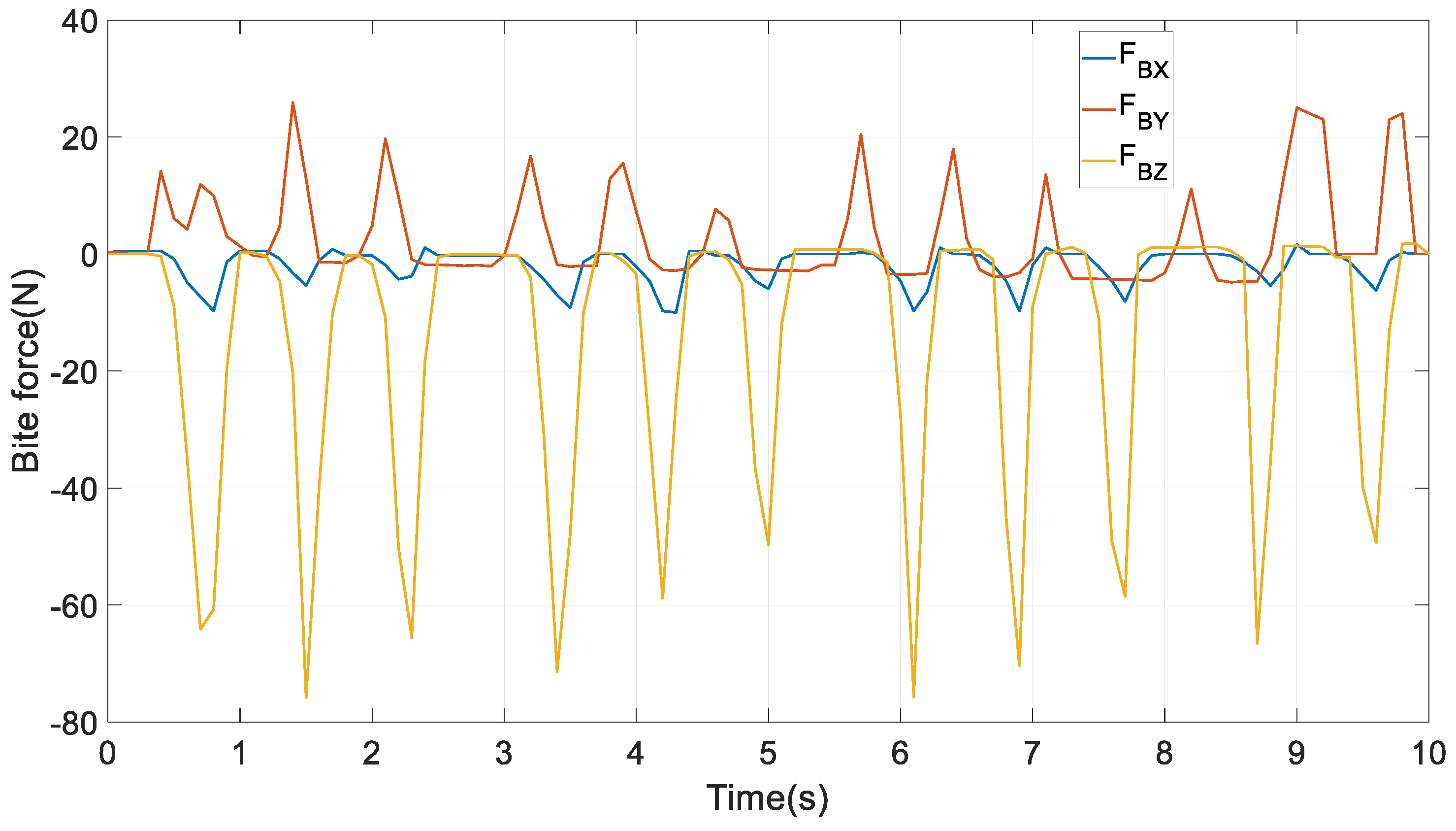
| Bite force on the right molar | |
| Magnitude of the constrained force at two HKPs along ZS axis | |
| mEE and IEE | Mass and inertia matrix of the end effector, respectively |
| and | Mass and the inertia matrix of SiMi with respect to OM and expressed in {S}, respectively |
| Rotational inertia of GiSi | |
| actuating torque provided by the ith actuator | |
| 6 × 1 actuating torque vector by the six actuators | |
| Kinetic energy, potential energy, and Lagrange function of the end effector in Model 1 under the Lagrangian equations | |
| mass matrix, Coriolis and centrifugal force matrix, and gravitational force vector, and the generalised force vector of the end effector, respectively | |
| Kinetic energy and potential energy of the ith coupler | |
| Kinetic energy of the ith crank | |
| Kinetic energy, the potential energy, and the Lagrangian function of the ith chain | |
| , , , | 3 × 3 mass matrix, 3 × 3 Coriolis/centrifugal force matrix, 3 × 1 gravitational force vector, and 3 × 1 generalized force vector of the ith chain, respectively |
| General coordinate vector in Model 1 by the Lagrangian formulation | |
| , , , | Mass matrix, Coriolis and centrifugal force matrix, gravitational force vector, and generalised external force vector free of closed-loop constraints, respectively in Model 1 |
| 18 × 1 constraint equation vector | |
| constraint Jacobian matrix | |
| and | unknown Lagrangian multiplier vectors |
| Jacobian matrix between and | |
| Kinetic energy, potential energy, and Lagrange function of the end effector in Model 2 under the Lagrangian equations | |
| mass matrix, Coriolis and centrifugal force matrix, gravitational force vector, and the generalised force vector of the end effector, respectively, in Model 2 | |
| General coordinate vector in Model 2 by the Lagrangian formulation | |
| , , , | Mass matrix, Coriolis and centrifugal force matrix, gravitational force vector, and generalised external force vector free of closed-loop constraints, respectively, in Model 2 |
| constraint Jacobian matrix | |
| Jacobian matrix between and |
Appendix A
References
- Koolstra, J.H. Dynamics of the human masticatory system. Crit. Rev. Oral Biol. Med. 2002, 13, 366–376. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Xu, W.; Shang, J. Kinematics, stiffness and natural frequency of a redundantly actuated masticatory robot constrained by two point-contact higher kinematic pairs. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamgburg, Germany, 28 September–2 October 2015; pp. 963–970. [Google Scholar]
- Cheng, C.; Xu, W.; Shang, J. Optimal distribution of the actuating torques for a redundantly actuated masticatory robot with two higher kinematic pairs. Nonlinear Dyn. 2014, 79, 1235–1255. [Google Scholar] [CrossRef]
- Xu, W.; Bronlund, J. Mastication Robots: Biological Inspiration to Implementation; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Karmakar, S.; Turner, C.J. A Literature Review on Stewart–Gough Platform Calibrations. J. Mech. Des. 2024, 146, 083302. [Google Scholar] [CrossRef]
- Lin, S.-T.; Huang, S.-Y.; Lan, C.-C.; Chidambaram, M.; Sivaramakrishnan, V. Design and experiment of a new translational parallel manipulator with large payload and high repeatability. Mech. Mach. Theory 2023, 180, 105124. [Google Scholar] [CrossRef]
- Wang, X.; Wu, J.; Zhou, Y. Dynamic Modeling and Performance Evaluation of a 5-DOF Hybrid Robot for Composite Material Machining. Machines 2023, 11, 652. [Google Scholar] [CrossRef]
- Stabile, A.; Yotov, V.V.; Aglietti, G.S.; de Francesco, P.; Richardson, G. Effect of boundary conditions on a high-performance isolation hexapod platform. Mech. Mach. Theory 2022, 177, 105020. [Google Scholar] [CrossRef]
- Ono, T.; Eto, R.; Yamakawa, J.; Murakami, H. Analysis and control of a Stewart platform as base motion compensators—Part I: Kinematics using moving frames. Nonlinear Dyn. 2022, 107, 51–76. [Google Scholar] [CrossRef]
- Cheng, C.; Liao, H. Elastodynamics of a spatial redundantly actuated parallel mechanism constrained by two higher kinematic pairs. Meccanica 2021, 56, 515–533. [Google Scholar] [CrossRef]
- Gosselin, C.; Schreiber, T. Redundancy in Parallel Mechanisms: A Review. Appl. Mech. Rev. 2018, 70, 010802. [Google Scholar] [CrossRef]
- Hufnagel, T.; Muller, A. A Projection Method for the Elimination of Contradicting Decentralized Control Forces in Redundantly Actuated PKM. IEEE Trans. Robot. 2012, 28, 723–728. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, D.; Song, Z.; Guo, H.; Liu, R.; Kou, Z. Workspace analysis and size optimization of planar 3-DOF redundantly actuated parallel mechanism. J. Mech. Sci. Technol. 2024, 38, 957–967. [Google Scholar] [CrossRef]
- Yan, P.; Huang, H.; Li, B.; Zhou, D. A 5-DOF redundantly actuated parallel mechanism for large tilting five-face machining. Mech. Mach. Theory 2022, 172, 104785. [Google Scholar] [CrossRef]
- Jiang, S.; Chi, C.; Fang, H.; Tang, T.; Zhang, J. A minimal-error-model based two-step kinematic calibration methodology for redundantly actuated parallel manipulators: An application to a 3-DOF spindle head. Mech. Mach. Theory 2022, 167, 104532. [Google Scholar] [CrossRef]
- Liu, Z.; Tao, R.; Fan, J.; Wang, Z.; Jing, F.; Tan, M. Kinematics, dynamics, and load distribution analysis of a 4-PPPS redundantly actuated parallel manipulator. Mech. Mach. Theory 2022, 167, 104494. [Google Scholar] [CrossRef]
- Liu, X.; Yao, J.; Li, Q.; Zhao, Y. Coordination dynamics and model-based neural network synchronous controls for redundantly full-actuated parallel manipulator. Mech. Mach. Theory 2022, 160, 104284. [Google Scholar] [CrossRef]
- Mostashiri, N.; Dhupia, J.S.; Verl, A.W.; Xu, W. A Review of Research Aspects of Redundantly Actuated Parallel Robots for Enabling Further Applications. IEEE/ASME Trans. Mechatron. 2018, 23, 1259–1269. [Google Scholar] [CrossRef]
- Wang, L.; Wu, J.; Wang, J. Dynamic formulation of a planar 3-DOF parallel manipulator with actuation redundancy. Robot. Comput. Manuf. 2010, 26, 67–73. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Wang, L.; Liu, X. Dynamic load-carrying capacity of a novel redundantly actuated parallel conveyor. Nonlinear Dyn. 2014, 78, 241–250. [Google Scholar] [CrossRef]
- van der Wijk, V.; Krut, S.; Pierrot, F.; Herder, J.L. Design and experimental evaluation of a dynamically balanced redundant planar 4-RRR parallel manipulator. Int. J. Robot. Res. 2013, 32, 744–759. [Google Scholar] [CrossRef]
- Shang, W.; Cong, S. Robust nonlinear control of a planar 2-DOF parallel manipulator with redundant actuation. Robot. Comput. Manuf. 2014, 30, 597–604. [Google Scholar] [CrossRef]
- Liang, D.; Song, Y.; Sun, T.; Dong, G. Optimum design of a novel redundantly actuated parallel manipulator with multiple actuation modes for high kinematic and dynamic performance. Nonlinear Dyn. 2015, 83, 631–658. [Google Scholar] [CrossRef]
- Lipiński, K. Modeling and control of a redundantly actuated variable mass 3RRR planar manipulator controlled by a model-based feedforward and a model-based-proportional-derivative feedforward–feedback controller. Mechatronics 2016, 37, 42–53. [Google Scholar] [CrossRef]
- Yao, J.; Gu, W.; Feng, Z.; Chen, L.; Xu, Y.; Zhao, Y. Dynamic analysis and driving force optimization of a 5-DOF parallel manipulator with redundant actuation. Robot. Comput. Manuf. 2017, 48, 51–58. [Google Scholar] [CrossRef]
- Lee, G.; Park, S.; Lee, D.; Park, F.C.; Jeong, J.I.; Kim, J. Minimizing Energy Consumption of Parallel Mechanisms via Redundant Actuation. IEEE/ASME Trans. Mechatron. 2015, 20, 2805–2812. [Google Scholar] [CrossRef]
- Liu, S.; Peng, G.; Gao, H. Dynamic modeling and terminal sliding mode control of a 3-DOF redundantly actuated parallel platform. Mechatronics 2019, 60, 26–33. [Google Scholar] [CrossRef]
- Zhou, Z.; Gosselin, C. Simplified inverse dynamic models of parallel robots based on a Lagrangian approach. Meccanica 2024, 59, 657–680. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Wang, L.; Li, T. Dynamics and control of a planar 3-DOF parallel manipulator with actuation redundancy. Mech. Mach. Theory 2009, 44, 835–849. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, F. Dynamic performance comparison of the 8PSS redundant parallel manipulator and its non-redundant counterpart—The 6PSS parallel manipulator. Mech. Mach. Theory 2009, 44, 991–1008. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, B.; Wang, L. A Measure for Evaluation of Maximum Acceleration of Redundant and Nonredundant Parallel Manipulators. J. Mech. Robot. 2016, 8, 021001. [Google Scholar] [CrossRef]
- Fontes, J.V.; da Silva, M.M. On the dynamic performance of parallel kinematic manipulators with actuation and kinematic redundancies. Mech. Mach. Theory 2016, 103, 148–166. [Google Scholar] [CrossRef]
- Wu, J.; Qiu, J.; Ye, H. Torque Optimization Method of a 3-DOF Redundant Parallel Manipulator Based on Actuator Torque Range. J. Mech. Robot. 2022, 15, 021005. [Google Scholar] [CrossRef]
- Mesnard, M.; Coutant, J.C.; Aoun, M.; Morlier, J.; Cid, M.; Caix, P. Relationships between geometry and kinematic characteristics in the temporomandibular joint. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 393–400. [Google Scholar] [CrossRef] [PubMed]
- Siegler, S.; Hayes, R.; Nicolella, D.; Fielding, A. A technique to investigate the three-dimensional kinesiology of the human temporomandibular joint. J. Prosthet. Dent. 1991, 65, 833–839. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Liu, B.; Li, Y.; Liu, Z.; Yang, S.; Wang, Y. Elastodynamic performance of a spatial redundantly actuated parallel mechanism constrained by two point-contact higher kinematic pairs via a model reduction technique. Mech. Mach. Theory 2022, 167, 104570. [Google Scholar] [CrossRef]
- Eskandary, P.K.; Belzile, B.; Angeles, J. Trajectory-Planning and Normalized-Variable Control for Parallel Pick-and-Place Robots. J. Mech. Robot. 2019, 11, 1–14. [Google Scholar] [CrossRef]
- Liang, D.; Song, Y.; Sun, T.; Jin, X. Dynamic modeling and hierarchical compound control of a novel 2-DOF flexible parallel manipulator with multiple actuation modes. Mech. Syst. Signal Process. 2018, 103, 413–439. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, J.; Zou, S.; Zhao, K.; Ma, Z. Trajectory Tracking Control for Delta Parallel Manipulators: A Variable Gain ADRC Approach. IEEE Robot. Autom. Lett. 2022, 7, 7747–7754. [Google Scholar] [CrossRef]
- Tsai, L.-W. Solving the Inverse Dynamics of a Stewart-Gough Manipulator by the Principle of Virtual Work. J. Mech. Des. 1999, 122, 3–9. [Google Scholar] [CrossRef]






| NE | LA1 | LA2 | PVW1 | PVW2 | |
|---|---|---|---|---|---|
| Number of equations | 6 | 4 | 4 | 4 | 4 |
| Number of unknowns | 8 | 6 | 6 | 6 | 6 |
| NE (n = 6) | LA1 | LA2 | PVW1 | PVW2 | ||
|---|---|---|---|---|---|---|
| Number of equations | 6 | 4 | 4 | 4 | 4 | |
| Number of unknowns | 8 | n | n | n | n |
| NE | LA1 | LA2 | PVW1 | PVW2 | |||
|---|---|---|---|---|---|---|---|
| Aim 1 | Aim 2 | ||||||
| F1 (N∙m) | 0.1985 | 0.2727 | 0.2727 | 0.1985 | 0.1985 | 0.1985 | 0.1985 |
| F2 (N) | 7.7028 | 4.1477 × 10−9 | - | ||||
| NE | LA1 | LA2 | PVW1 | PVW2 | |||
|---|---|---|---|---|---|---|---|
| Aim 1 | Aim 2 | ||||||
| Symbolic | 9.720 | 9.720 | 9.720 | 39.054 | 7.731 | 9.923 | 4.311 |
| Numeric | 9.904 | 5.358 | 4.827 | 27.815 | 4.041 | 4.983 | 1.148 |
| Total | 19.624 | 15.078 | 14.547 | 66.869 | 11.772 | 14.906 | 5.459 |
| NE | LA | PVW | |
|---|---|---|---|
| Symbolic | 4.074 | 7.716 | 4.071 |
| Numeric | 1.301 | 4.053 | 1.062 |
| Total | 5.375 | 11.769 | 5.133 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, C.; Yuan, X.; Li, Y.; Liu, J. Comparisons of Inverse Dynamics Formulations in a Spatial Redundantly Actuated Parallel Mechanism Constrained by Two Point Contact Higher Kinematic Pairs. Biomimetics 2024, 9, 564. https://doi.org/10.3390/biomimetics9090564
Cheng C, Yuan X, Li Y, Liu J. Comparisons of Inverse Dynamics Formulations in a Spatial Redundantly Actuated Parallel Mechanism Constrained by Two Point Contact Higher Kinematic Pairs. Biomimetics. 2024; 9(9):564. https://doi.org/10.3390/biomimetics9090564
Chicago/Turabian StyleCheng, Chen, Xiaojing Yuan, Yenan Li, and Jian Liu. 2024. "Comparisons of Inverse Dynamics Formulations in a Spatial Redundantly Actuated Parallel Mechanism Constrained by Two Point Contact Higher Kinematic Pairs" Biomimetics 9, no. 9: 564. https://doi.org/10.3390/biomimetics9090564
APA StyleCheng, C., Yuan, X., Li, Y., & Liu, J. (2024). Comparisons of Inverse Dynamics Formulations in a Spatial Redundantly Actuated Parallel Mechanism Constrained by Two Point Contact Higher Kinematic Pairs. Biomimetics, 9(9), 564. https://doi.org/10.3390/biomimetics9090564





