A Self-Learning Hyper-Heuristic Algorithm Based on a Genetic Algorithm: A Case Study on Prefabricated Modular Cabin Unit Logistics Scheduling in a Cruise Ship Manufacturer
Abstract
1. Introduction
- This paper formulates a multi-objective fuzzy equipment collaborative scheduling model for PMCU logistics, predicated on maximizing the average agreement index of fuzzy due dates and minimizing the maximum fuzzy makespan, thereby addressing inherent uncertainties in cruise shipyard operations.
- A new genetic hyper-heuristic algorithm with a self-learning mechanism (GA-SLHH) is proposed in this paper. In the GA-SLHH framework, low-level heuristics (LLHs) are composed of a set of classical scheduling rules. The high-level strategy (HLS) is composed of a genetic algorithm (GA) and self-learning mechanism. The HLS iteratively optimizes the LLHs, which, in turn, control the solution of the collaborative scheduling model of PMCU logistics.
- The feasibility and applicability of the GA-SLHH proposed in this paper are verified through numerical experiments and enterprise case verification with well-known meta-heuristic algorithms (i.e., GA and PSO), classical scheduling rules, and genetic hyper-heuristic algorithms without a self-learning mechanism (GA-HH).
2. Related Research
3. PMCU Logistics Collaborative Scheduling Problem
3.1. Problem Description
3.2. Environmental Conditions and Constraints
3.2.1. Uncertain Environment
3.2.2. Transport Equipment Constraints
3.3. Assumptions
3.4. Mathematical Model
4. Self-Learning Hyper-Heuristic Algorithm Based on Genetic Algorithm
4.1. Hyper-Heuristic Algorithm Based on Genetic Algorithm (GA-HH)
4.2. Low-Level Heuristics
4.3. High-Level Strategy
- Encoding and decoding
- 2.
- Population initialization
- 3.
- Selection
- 4.
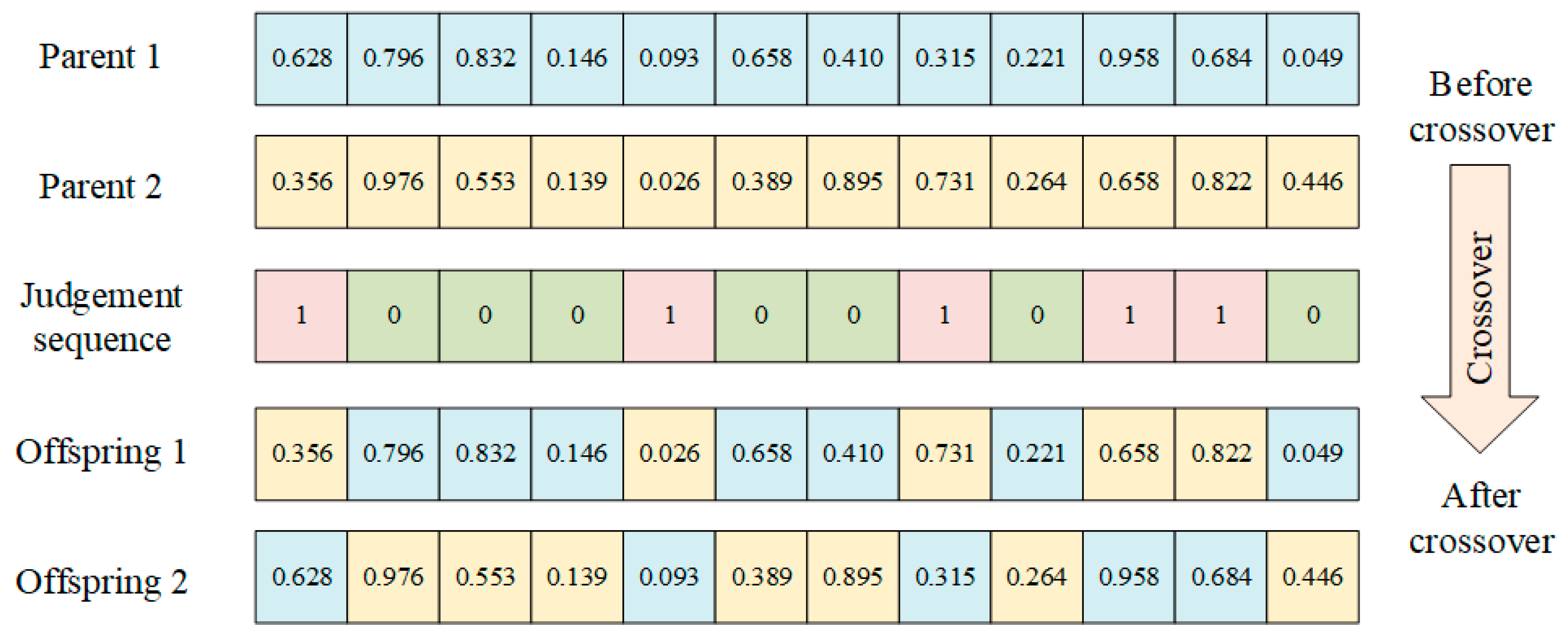
- Crossover
- 5.
- Mutation
- 6.
- Iteration
4.4. Self-Learning Mechanism
4.5. GA-SLHH Flow
| Algorithm 1: GA-SLHH |
| Input: : Maximum number of iterations Output: High-quality feasible scheme Begin ; // Randomly generate an initial population that satisfies a (0,1) uniform distribution ) do do ; // Fitness evaluation based on Equations (1)~(7); endfor do ; individuals; else individuals; endif endfor do ; endif endfor into two sub-populations sub-population I and sub-population II with the same number of individuals; do Convert individuals in sub-population I to LLHs using initial mapping probabilities; Convert individuals in sub-population II to LLHs using self-learning mapping probabilities; endfor ; ; ; endwhile end |
5. Computational Experiments
5.1. Performance Testing
5.2. Case Verification
6. Managerial Implications
7. Conclusions
- This research provides an in-depth analysis of the logistical operations for PMCUs. By characterizing the inherent uncertainties, the bidirectional operations, and the intersection of multiple tasks and equipment types, we have developed a multi-objective mathematical model that reflects the process of PMCU logistics. The two optimization objectives represent the efficiency and plan execution accuracy of PMCU logistics in cruise shipyard, respectively, which have higher practical application significance.
- We propose a novel GA-SLHH to solve the model in this paper. The low-level heuristic is composed of 14 basic dispatching rules. The high-level strategy adopts genetic algorithms and self-learning mechanisms interacting together to drive the low-level heuristics. The self-learning mechanism introduced into the high-level strategy is more suitable for human decision-making characteristics and is more applicable to actual problems in shipyards.
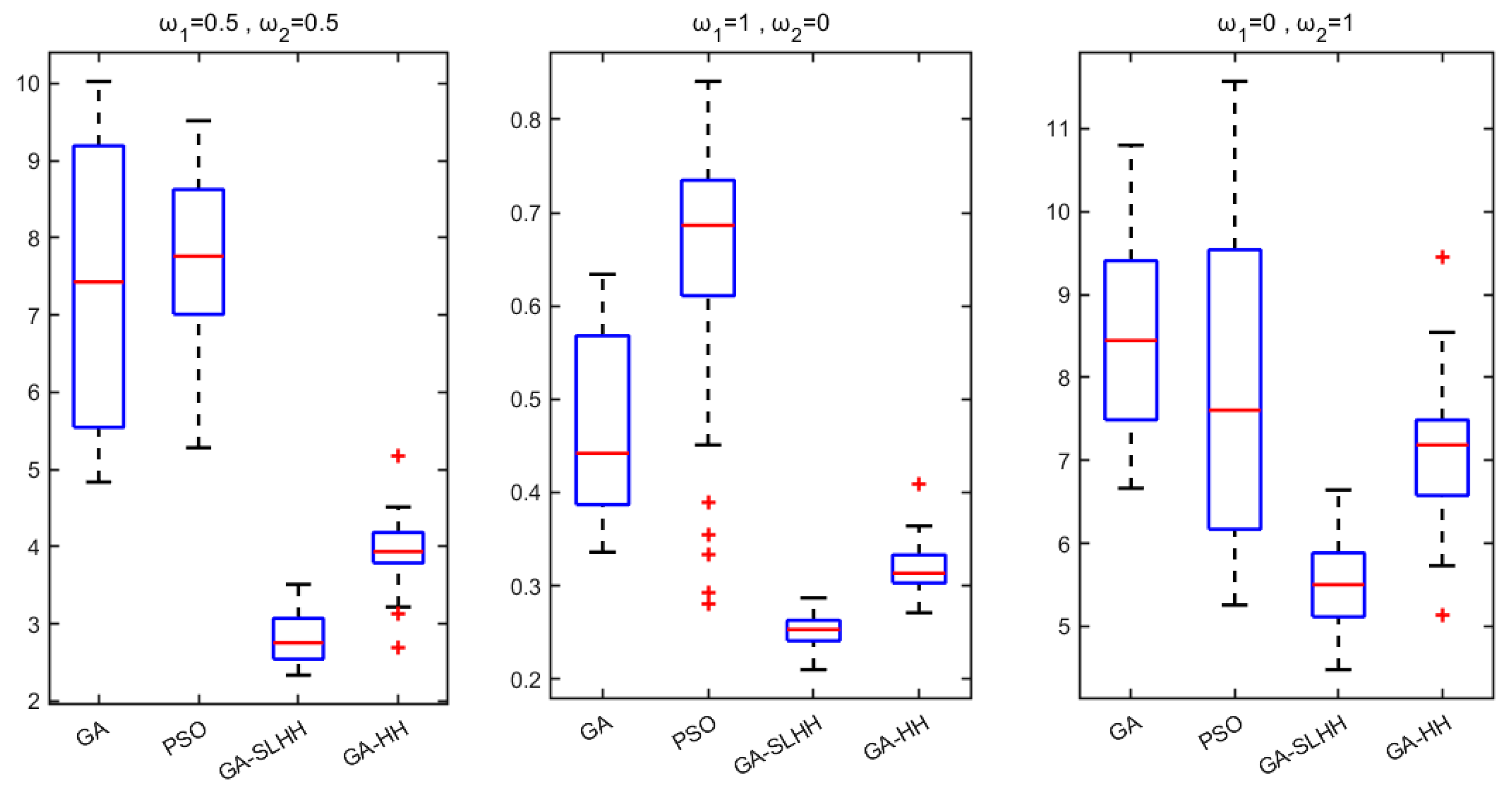
- The performance of the proposed GA-SLHH is validated through performance experiments and an enterprise case. The GA-SLHH shows a superior optimization performance compared to its competitors in the majority of performance experiment instances. In the enterprise case experiments, the GA-SLHH under different optimization weight settings all achieve the best objective function values, showing a better applicability to real-world problems.
- Different from conventional scheduling methods, the GA-SLHH provides cruise shipyards with rational fuzzy scheduling schemes under different circumstances of the project. It is more beneficial for managers to adjust and control the production activities within PMCU logistics under different demands. In a certain application scenario, the scheduling scheme obtained using the methodology of this study can achieve an approximately 37% reduction in time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abualigah, L.; Elaziz, M.A.; Khasawneh, A.M.; Alshinwan, M.; Ibrahim, R.A.; Al-qaness, M.A.A.; Mirjalili, S.; Sumari, P.; Gandomi, A.H. Meta-Heuristic Optimization Algorithms for Solving Real-World Mechanical Engineering Design Problems: A Comprehensive Survey, Applications, Comparative Analysis, and Results. Neural. Comput. Applic. 2022, 34, 4081–4110. [Google Scholar] [CrossRef]
- Van Thieu, N.; Mirjalili, S. MEALPY: An Open-Source Library for Latest Meta-Heuristic Algorithms in Python. J. Syst. Archit. 2023, 139, 102871. [Google Scholar] [CrossRef]
- Bouazza, W. Hyper-Heuristics Applications to Manufacturing Scheduling: Overview and Opportunities. IFAC Pap. 2023, 56, 935–940. [Google Scholar] [CrossRef]
- Drake, J.H.; Kheiri, A.; Özcan, E.; Burke, E.K. Recent Advances in Selection Hyper-Heuristics. Eur. J. Oper. Res. 2020, 285, 405–428. [Google Scholar] [CrossRef]
- Qian, C.; Tang, K.; Zhou, Z.-H. Selection Hyper-Heuristics Can Provably Be Helpful in Evolutionary Multi-Objective Optimization. In Proceedings of the Parallel Problem Solving from Nature—PPSN XIV, Edinburgh, UK, 17–21 September 2016; Handl, J., Hart, E., Lewis, P.R., López-Ibáñez, M., Ochoa, G., Paechter, B., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 835–846. [Google Scholar]
- Dokeroglu, T.; Kucukyilmaz, T.; Talbi, E.-G. Hyper-Heuristics: A Survey and Taxonomy. Comput. Ind. Eng. 2024, 187, 109815. [Google Scholar] [CrossRef]
- Olgun, B.; Koç, Ç.; Altıparmak, F. A Hyper Heuristic for the Green Vehicle Routing Problem with Simultaneous Pickup and Delivery. Comput. Ind. Eng. 2021, 153, 107010. [Google Scholar] [CrossRef]
- Xue, W. Analysis of the application of prefabricated modular cabin unit technology on passenger ship construction. Mech. Electr. Technol. 2019, 4, 74–76. [Google Scholar] [CrossRef]
- Li, Y. Prefabricated modular cabin unit technology and its application prospect in domestic shipbuilding industry. Mar. Technol. 2007, 4, 20–22. [Google Scholar]
- Luo, L.; Liu, C.; Ma, J.; Yu, D.; Chen, T. Application of Prefabricated Modular Cabin Unit. Guangdong Shipbuild. 2021, 40, 53–55+52. [Google Scholar]
- Li, J.; Yan, H.; Yang, B.; Zhou, Q. Improved genetic-harmony search algorithm for solving workshop scheduling problem of marine equipment. Comput. Integr. Manuf. Syst. 2022, 28, 3923–3936. [Google Scholar] [CrossRef]
- Li, J.; Guo, H.; Zhou, Q.; Yang, B. Vehicle Routing and Scheduling Optimization of Ship Steel Distribution Center under Green Shipbuilding Mode. Sustainability 2019, 11, 4248. [Google Scholar] [CrossRef]
- Guo, H.; Wang, J.; Sun, J.; Mao, X. Multi-Objective Green Vehicle Scheduling Problem Considering Time Window and Emission Factors in Ship Block Transportation. Sci. Rep. 2024, 14, 10796. [Google Scholar] [CrossRef]
- Wang, J.; Yin, J.; Khan, R.U.; Wang, S.; Zheng, T. A Study of Inbound Logistics Mode Based on JIT Production in Cruise Ship Construction. Sustainability 2021, 13, 1588. [Google Scholar] [CrossRef]
- Sender, J.; Klink, S.; Flügge, W. Method for Integrated Logistics Planning in Shipbuilding. Procedia CIRP 2020, 88, 122–126. [Google Scholar] [CrossRef]
- Guo, H.; Li, J.; Yang, B.; Mao, X.; Zhou, Q. Green Scheduling Optimization of Ship Plane Block Flow Line Considering Carbon Emission and Noise. Comput. Ind. Eng. 2020, 148, 106680. [Google Scholar] [CrossRef]
- Li, J.; Guo, H. A Hybrid Whale Optimization Algorithm for Plane Block Parallel Blocking Flowline Scheduling Optimization With Deterioration Effect in Lean Shipbuilding. IEEE Access 2021, 9, 131893–131905. [Google Scholar] [CrossRef]
- Zhou, T.; Luo, L.; He, Y.; Fan, Z.; Ji, S. Solving Panel Block Assembly Line Scheduling Problem via a Novel Deep Reinforcement Learning Approach. Appl. Sci. 2023, 13, 8483. [Google Scholar] [CrossRef]
- Wang, C.; Mao, P.; Mao, Y.; Shin, J.G. Research on Scheduling and Optimization under Uncertain Conditions in Panel Block Production Line in Shipbuilding. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 398–408. [Google Scholar] [CrossRef]
- Jingsong, B.; Xiaofeng, H.; Ye, J. A Heuristic Method to Schedule Pipe-Processing Flowshop in a Shipyard. J. Ship Prod. 2007, 23, 210–214. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, C.; Zhang, S.; Shi, J. A Multi-Objective Memetic Algorithm for a Fuzzy Parallel Blocking Flow Shop Scheduling Problem of Panel Block Assembly in Shipbuilding. J. Ship Prod. Des. 2019, 35, 170–181. [Google Scholar] [CrossRef]
- Chen, G.; Wu, X.; Li, J.; Guo, H. Green Vehicle Routing and Scheduling Optimization of Ship Steel Distribution Center Based on Improved Intelligent Water Drop Algorithms. Math. Probl. Eng. 2020, 2020, e9839634. [Google Scholar] [CrossRef]
- Chen, G.; Jiang, Y.; Sheng, X.; Wang, J.; Jia, H. Workstation-Oriented Distribution Optimization of Shipbuilding Materials. MATEC Web Conf. 2019, 272, 01014. [Google Scholar] [CrossRef]
- Liu, J.; Yin, J.; Khan, R.U. Scheduling Management and Optimization Analysis of Intermediate Products Transfer in a Shipyard for Cruise Ships. PLoS ONE 2022, 17, e0265047. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Jiang, Z. Multi-AGVs Scheduling with Vehicle Conflict Consideration in Ship Outfitting Items Warehouse. J. Shanghai Jiaotong Univ. (Sci.) 2022, 29, 492–508. [Google Scholar] [CrossRef]
- Wang, S.; Sun, Y.; Luo, Q.; Li, Z.; Wang, A. A Spatial Scheduling Strategy Based on Evaluation of the Remaining Usable Area for Shipbuilding. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–10 August 2022; pp. 24–29. [Google Scholar]
- Ahn, N.; Kim, S. A Mathematical Formulation and a Heuristic for the Spatial Scheduling of Mega-Blocks in Shipbuilding Industry. J. Ship Prod. Des. 2022, 38, 193–198. [Google Scholar] [CrossRef]
- Wang, T.; Mo, X.; Chen, M.; Hu, X. An Improved Spatial Scheduling Algorithm for Sub-Assembly in Shipbuilding. In Proceedings of the 2023 IEEE 19th International Conference on Automation Science and Engineering (CASE), Auckland, New Zealand, 26–30 August 2023; pp. 1–6. [Google Scholar]
- Mao, X.; Li, J.; Guo, H.; Wu, X. Research on Collaborative Planning and Symmetric Scheduling for Parallel Shipbuilding Projects in the Open Distributed Manufacturing Environment. Symmetry 2020, 12, 161. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, J.; Dong, R.; Zhou, Q.; Yang, B. Optimization of Multi-Execution Modes and Multi-Resource-Constrained Offshore Equipment Project Scheduling Based on a Hybrid Genetic Algorithm. CMES 2022, 134, 1263–1281. [Google Scholar] [CrossRef]
- Rahman, H.F.; Servranckx, T.; Chakrabortty, R.K.; Vanhoucke, M.; El Sawah, S. Manufacturing Project Scheduling Considering Human Factors to Minimize Total Cost and Carbon Footprints. Appl. Soft Comput. 2022, 131, 109764. [Google Scholar] [CrossRef]
- Wu, L.; Jiang, Z.; Li, X. A Stack-Based Retrieval Method for the Steel Plate Yard Retrieval Problem in Shipbuilding. Flex. Serv. Manuf. J. 2023, 36, 343–377. [Google Scholar] [CrossRef]
- Kai, C.; Zuhua, J.; Jianfeng, L.; Bo, S.; Yongwen, H. Shipbuilding Yard Scheduling with Block Inbound Time Window. J. Shanghai Jiaotong Univ. 2016, 50, 1390–1398. [Google Scholar] [CrossRef]
- Chu, L.; Liang, D.; Zhou, Y.; Xu, X.; Zhang, Y.; Ruan, Z.; Xiao, H.; Zuo, S. Co-Scheduling of Quay Cranes and RTGs in the Container Terminal. In Proceedings of the 2022 IEEE International Conference on Smart Internet of Things (SmartIoT), Suzhou, China, 19–21 August 2022; pp. 116–124. [Google Scholar]
- Pu, Y.; Liu, H.; Wang, J.; Hou, Y. Collaborative Scheduling of Port Integrated Energy and Container Logistics Considering Electric and Hydrogen-Powered Transport. IEEE Trans. Smart Grid 2023, 14, 4345–4359. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gao, D.; Pedrycz, W. Solving Multiobjective Fuzzy Job-Shop Scheduling Problem by a Hybrid Adaptive Differential Evolution Algorithm. IEEE Trans. Ind. Inform. 2022, 18, 8519–8528. [Google Scholar] [CrossRef]
- Cengiz Toklu, M. A Fuzzy Multi-Criteria Approach Based on Clarke and Wright Savings Algorithm for Vehicle Routing Problem in Humanitarian Aid Distribution. J. Intell. Manuf. 2023, 34, 2241–2261. [Google Scholar] [CrossRef]
- Afsar, S.; Palacios, J.J.; Puente, J.; Vela, C.R.; González-Rodríguez, I. Multi-Objective Enhanced Memetic Algorithm for Green Job Shop Scheduling with Uncertain Times. Swarm Evol. Comput. 2022, 68, 101016. [Google Scholar] [CrossRef]
- Kong, L.; Ji, M.; Gao, Z. An Exact Algorithm for Scheduling Tandem Quay Crane Operations in Container Terminals. Transp. Res. Part E Logist. Transp. Rev. 2022, 168, 102949. [Google Scholar] [CrossRef]
- Abou Kasm, O.; Diabat, A. The Quay Crane Scheduling Problem with Non-Crossing and Safety Clearance Constraints: An Exact Solution Approach. Comput. Oper. Res. 2019, 107, 189–199. [Google Scholar] [CrossRef]
- Vallada, E.; Belenguer, J.M.; Villa, F.; Alvarez-Valdes, R. Models and Algorithms for a Yard Crane Scheduling Problem in Container Ports. Eur. J. Oper. Res. 2023, 309, 910–924. [Google Scholar] [CrossRef]
- Yang, Y.; Zhong, M.; Dessouky, Y.; Postolache, O. An Integrated Scheduling Method for AGV Routing in Automated Container Terminals. Comput. Ind. Eng. 2018, 126, 482–493. [Google Scholar] [CrossRef]
- Yin, Y.-Q.; Zhong, M.; Wen, X.; Ge, Y.-E. Scheduling Quay Cranes and Shuttle Vehicles Simultaneously with Limited Apron Buffer Capacity. Comput. Oper. Res. 2023, 151, 106096. [Google Scholar] [CrossRef]
- Serrano-Ruiz, J.C.; Mula, J.; Poler, R. Job Shop Smart Manufacturing Scheduling by Deep Reinforcement Learning. J. Ind. Inf. Integr. 2024, 38, 100582. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhuang, Z.; Qin, W.; Fang, H.; Lan, S.; Yang, C.; Tian, Y. A Reinforcement Learning Approach for Integrated Scheduling in Automated Container Terminals. In Proceedings of the 2022 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Kuala Lumpur, Malaysia, 7–10 December 2022; pp. 1182–1186. [Google Scholar]
- Burcin Ozsoydan, F.; Sağir, M. Iterated Greedy Algorithms Enhanced by Hyper-Heuristic Based Learning for Hybrid Flexible Flowshop Scheduling Problem with Sequence Dependent Setup Times: A Case Study at a Manufacturing Plant. Comput. Oper. Res. 2021, 125, 105044. [Google Scholar] [CrossRef]
- Kheiri, A.; Gretsista, A.; Keedwell, E.; Lulli, G.; Epitropakis, M.G.; Burke, E.K. A Hyper-Heuristic Approach Based upon a Hidden Markov Model for the Multi-Stage Nurse Rostering Problem. Comput. Oper. Res. 2021, 130, 105221. [Google Scholar] [CrossRef]
- Zhao, F.; Di, S.; Cao, J.; Tang, J.; Jonrinaldi, A. Novel Cooperative Multi-Stage Hyper-Heuristic for Combination Optimization Problems. Complex Syst. Model. Simul. 2021, 1, 91–108. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, L.; Gao, K. A Genetic Programming Hyper-Heuristic Approach for the Multi-Skill Resource Constrained Project Scheduling Problem. Expert Syst. Appl. 2020, 140, 112915. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Wang, Y.; Zhuang, C. An Improved Genetic Programming Hyper-Heuristic for the Dynamic Flexible Job Shop Scheduling Problem with Reconfigurable Manufacturing Cells. J. Manuf. Syst. 2024, 74, 252–263. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Y.; Zhang, W. Multitask-Oriented Manufacturing Service Composition in an Uncertain Environment Using a Hyper-Heuristic Algorithm. J. Manuf. Syst. 2021, 60, 138–151. [Google Scholar] [CrossRef]
- Song, H.-B.; Lin, J. A Genetic Programming Hyper-Heuristic for the Distributed Assembly Permutation Flow-Shop Scheduling Problem with Sequence Dependent Setup Times. Swarm Evol. Comput. 2021, 60, 100807. [Google Scholar] [CrossRef]
- Lim, K.C.W.; Wong, L.-P.; Chin, J.F. Simulated-Annealing-Based Hyper-Heuristic for Flexible Job-Shop Scheduling. Eng. Optim. 2023, 55, 1635–1651. [Google Scholar] [CrossRef]
- Sugianto, W.C.; Kim, B.S. Iterated Variable Neighborhood Search for Integrated Scheduling of Additive Manufacturing and Multi-Trip Vehicle Routing Problem. Comput. Oper. Res. 2024, 167, 106659. [Google Scholar] [CrossRef]
- Song, H.-B.; Yang, Y.-H.; Lin, J.; Ye, J.-X. An Effective Hyper Heuristic-Based Memetic Algorithm for the Distributed Assembly Permutation Flow-Shop Scheduling Problem. Appl. Soft Comput. 2023, 135, 110022. [Google Scholar] [CrossRef]
- Soleimanian Gharehchopogh, F.; Abdollahzadeh, B.; Arasteh, B. An Improved Farmland Fertility Algorithm with Hyper-Heuristic Approach for Solving Travelling Salesman Problem. Comput. Model. Eng. Sci. 2022, 135, 1–26. [Google Scholar] [CrossRef]
- Li, K.; Liu, T.; Ram Kumar, P.N.; Han, X. A Reinforcement Learning-Based Hyper-Heuristic for AGV Task Assignment and Route Planning in Parts-to-Picker Warehouses. Transp. Res. Part E Logist. Transp. Rev. 2024, 185, 103518. [Google Scholar] [CrossRef]
- Duan, J.; Liu, F.; Zhang, Q.; Qin, J.; Zhou, Y. Genetic Programming Hyper-Heuristic-Based Solution for Dynamic Energy-Efficient Scheduling of Hybrid Flow Shop Scheduling with Machine Breakdowns and Random Job Arrivals. Expert Syst. Appl. 2024, 254, 124375. [Google Scholar] [CrossRef]
- Mahmud, S.; Abbasi, A.; Chakrabortty, R.K.; Ryan, M.J. A Self-Adaptive Hyper-Heuristic Based Multi-Objective Optimisation Approach for Integrated Supply Chain Scheduling Problems. Knowl. Based Syst. 2022, 251, 109190. [Google Scholar] [CrossRef]
- Cui, R.; Han, W.; Su, X.; Zhang, Y.; Guo, F. A Multi-Objective Hyper Heuristic Framework for Integrated Optimization of Carrier-Based Aircraft Flight Deck Operations Scheduling and Resource Configuration. Aerosp. Sci. Technol. 2020, 107, 106346. [Google Scholar] [CrossRef]
- Sakawa, M.; Kubota, R. Fuzzy Programming for Multiobjective Job Shop Scheduling with Fuzzy Processing Time and Fuzzy Duedate through Genetic Algorithms. Eur. J. Oper. Res. 2000, 120, 393–407. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial System; University of Michigan Press: Ann Arbor, MI, USA, 1975; pp. viii–183. [Google Scholar]
- Li, S.; Hu, R.; Qian, B.; Zhang, Z.; Jin, H.-P. Hyper-heuristic genetic algorithm for solving fuzzy flexible job shop scheduling problem. Control Theory Appl. 2020, 37, 316–330. [Google Scholar]
- Dios, M.; Fernandez-Viagas, V.; Framinan, J.M. Efficient Heuristics for the Hybrid Flow Shop Scheduling Problem with Missing Operations. Comput. Ind. Eng. 2018, 115, 88–99. [Google Scholar] [CrossRef]
- Xing, Y.I.N.; Yu, Z.; Qianqian, Z.; Kexin, T. A Study of Integrated Scheduling of Automated Container Terminal Based on DDQN. Traffic Inf. Saf. 2022, 40, 81–91. [Google Scholar] [CrossRef]
- Shao, Z.; Shao, W.; Pi, D. LS-HH: A Learning-Based Selection Hyper-Heuristic for Distributed Heterogeneous Hybrid Blocking Flow-Shop Scheduling. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 111–127. [Google Scholar] [CrossRef]
- Lei, D. A Genetic Algorithm for Flexible Job Shop Scheduling with Fuzzy Processing Time. Int. J. Prod. Res. 2010, 48, 2995–3013. [Google Scholar] [CrossRef]













| Papers | Objectives | Type | Method |
|---|---|---|---|
| Sugianto and Kim [54] | Delivery completion time | Single-objective | Iterated variable neighborhood search with rule-based heuristics |
| Song et al. [55] | Completion time | Single-objective | Hyper-heuristic based memetic algorithm |
| Soleimanian Gharehchopogh et al. [56] | Distance | Single-objective | Improved farmland fertility algorithm with hyper-heuristic |
| Li et al. [57] | Total completion time | Single-objective | Reinforcement learning-based hyper-heuristic |
| Duan et al. [58] | Tardiness, idle energy consumption, and makespan | Multi-objective | Genetic programming hyper-heuristic |
| Mahmud et al. [59] | Cost and sustainability rewards | Multi-objective | Self-adaptive hyper-heuristic |
| Cui et al. [60] | Makespan and resources | Multi-objective | Choice-function-based hyper-heuristic |
| Operations on Fuzzy Time | Rules |
|---|---|
| Ranking | Criterion 1. |
| Criterion 2. | |
| Criterion 3. |
| Assumptions | |
|---|---|
| 1. | All transportation equipment is available at time 0. |
| 2. | The release time of existing transport tasks is not 0. |
| 3. | There are a variety of types of transport tasks to be transported, and the transport stages of each type of task are different. |
| 4. | There is no waiting time for the same transport equipment for adjacent tasks. |
| 5. | The buffer capacity between each stage is unlimited; that is, there is no blocking constraint. |
| 6. | Once the transport task is carried out on transport equipment, no interruption is allowed until the completion of the stage of transport. |
| 7. | The preparation time and return time of the equipment have been considered in task transportation time. |
| 8. | The same equipment can only process one task at a time. |
| Symbols | Meaning |
|---|---|
| Indices | Meaning |
| ; is the total number of transportation tasks in PMCU logistics | |
| ; is the total number of stages in PMCU logistics | |
| ; is the total amount of equipment in PMCU logistics | |
| Parameters | Meaning |
| Large positive number | |
| Variables | Meaning |
| The maximum fuzzy makespan of PMCU logistics | |
| The average fuzzy due date agreement index of PMCU logistics | |
| = 0 |
| No. | Dispatching Rule | Description |
|---|---|---|
| 1 | FIFO | First in, first out |
| 2 | SPT | Shortest processing time |
| 3 | LPT | Longest processing time |
| 4 | LWKR | Least work remaining |
| 5 | MWKR | Most work remaining |
| 6 | SPTswm [64] | Shortest average processing time |
| 7 | LPTswm [64] | Longest average processing time |
| 8 | SDT | Shortest processing time as a percentage of total time |
| 9 | LDT | Longest processing time as a percentage of total time |
| 10 | SDR | Shortest processing time as a percentage of the remaining time |
| 11 | LDR | Longest processing time as a percentage of the remaining time |
| 12 | FRO | Fewest remaining operations |
| 13 | LRO | Most remaining operations |
| 14 | Random | Random selection |
| Step | Description |
|---|---|
| Step 1 | . |
| Step 2 | and the set of equipment. |
| Step 3 | Select the earliest idle equipment from the set of idle equipment. |
| Step 4 | to be processed according to the dispatching rule. |
| Step 5 | . |
| Step 6 | and execute Step 2. Otherwise, execute Step 7. |
| Step 7 | Generate a scheduling scheme. Calculate the fitness corresponding to the current scheduling scheme based on the fitness calculation function and pass it to the HLS. |
| Algorithms | Type | Parameters |
|---|---|---|
| GA | Metaheuristic | |
| PSO | ||
| GA-SLHH | Hyper-heuristic | |
| GA-HH | ||
| FIFO | Dispatching rule | None |
| SPT | ||
| MWKR | ||
| FRO |
| Benchmark Instances | Metaheuristic | Hyper-Heuristic | Dispatching Rule | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GA | PSO | GA-SLHH | GA-HH | FIFO | SPT | MWKR | FRO | ||
| Instance 1 | 1.301 | 1.111 | 0.545 | 0.546 | 0.812 | 0.696 | 2.262 | 0.681 | |
| 48.09 | 49.13 | 36.99 | 37.05 | 40.75 | 35.5 | 53.75 | 41 | ||
| 0.646 | 0.596 | 0.944 | 0.943 | 0.824 | 0.817 | 0.230 | 0.761 | ||
| Instance 2 | 1.175 | 1.261 | 0.640 | 1.069 | 1.039 | 1.001 | 1.967 | 1.206 | |
| 66.90 | 65.51 | 51.28 | 55.39 | 54.75 | 65.75 | 63 | 63.5 | ||
| 0.401 | 0.354 | 0.547 | 0.634 | 0.655 | 0.745 | 0.305 | 0.565 | ||
| Instance 3 | 1.615 | 1.729 | 0.845 | 0.969 | 0.928 | 0.941 | 2.197 | 1.282 | |
| 74.05 | 75.15 | 55.56 | 60.63 | 62 | 67.25 | 68.75 | 68.25 | ||
| 0.413 | 0.383 | 0.642 | 0.768 | 0.838 | 0.828 | 0.272 | 0.638 | ||
| Instance 4 | 1.440 | 1.456 | 0.805 | 0.935 | 0.817 | 0.812 | 2.221 | 0.914 | |
| 60.30 | 61.35 | 46.97 | 50.56 | 47.5 | 50 | 60.5 | 49.75 | ||
| 0.447 | 0.454 | 0.643 | 0.754 | 0.863 | 0.898 | 0.263 | 0.752 | ||
| Case | Number of Tasks | Number of Equipment | Number of Operations per Task | Processing Time of per Operation |
|---|---|---|---|---|
| Case 1 | 4 | 2 | [1, 3] | [1, 5] |
| Case 2 | 4 | 4 | [1, 3] | [1, 5] |
| Case 3 | 6 | 4 | [3, 5] | [2, 7] |
| Case 4 | 6 | 6 | [3, 5] | [2, 7] |
| Case 5 | 8 | 6 | [4, 6] | [5, 9] |
| Case 6 | 10 | 6 | [4, 6] | [6, 13] |
| Case 7 | 10 | 10 | [5, 7] | [7, 20] |
| Case 8 | 10 | 10 | [5, 10] | [5, 25] |
| Case 9 | 15 | 5 | [4, 6] | [1, 10] |
| Case 10 | 15 | 8 | [5, 7] | [10, 15] |
| Case 11 | 15 | 8 | [5, 10] | [1, 10] |
| Case 12 | 20 | 5 | [5, 10] | [5, 13] |
| Case 13 | 20 | 8 | [5, 7] | [5, 13] |
| Case 14 | 20 | 10 | [5, 7] | [10, 30] |
| Case 15 | 30 | 10 | [8, 10] | [10, 30] |
| Case | Metaheuristic | Hyper-Heuristic | Dispatching Rule | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GA | PSO | GA-SLHH | GA-HH | FIFO | SPT | MWKR | FRO | |||||||||
| mean | std. | mean | std. | mean | std. | mean | std. | mean | std. | mean | std. | mean | std. | mean | std. | |
| Case 1 | 0.788 | 0.065 | 0.789 | 0.069 | 0.702 | 0.012 | 0.874 | 0.081 | 1.759 | 0.000 | 1.905 | 0.000 | 4.533 | 0.000 | 1.004 | 0.000 |
| Case 2 | 0.512 | 0.015 | 0.517 | 0.021 | 0.504 | 0.000 | 0.534 | 0.025 | 0.641 | 0.000 | 0.524 | 0.000 | 0.924 | 0.000 | 0.641 | 0.000 |
| Case 3 | 0.932 | 0.066 | 0.924 | 0.113 | 0.908 | 0.042 | 1.089 | 0.084 | 1.192 | 0.000 | 1.081 | 0.000 | 3.054 | 0.000 | 1.287 | 0.000 |
| Case 4 | 0.657 | 0.032 | 0.652 | 0.026 | 0.609 | 0.023 | 0.661 | 0.021 | 0.693 | 0.000 | 0.644 | 0.000 | 0.860 | 0.000 | 0.819 | 0.000 |
| Case 5 | 1.138 | 0.096 | 1.150 | 0.103 | 1.088 | 0.035 | 1.223 | 0.050 | 1.323 | 0.000 | 1.062 | 0.000 | 1.546 | 0.000 | 1.306 | 0.000 |
| Case 6 | 1.567 | 0.146 | 1.608 | 0.205 | 1.560 | 0.049 | 1.774 | 0.098 | 2.071 | 0.000 | 1.537 | 0.000 | 3.522 | 0.000 | 1.982 | 0.000 |
| Case 7 | 1.067 | 0.124 | 1.053 | 0.085 | 1.037 | 0.019 | 1.114 | 0.035 | 1.179 | 0.000 | 1.001 | 0.000 | 1.580 | 0.000 | 1.251 | 0.000 |
| Case 8 | 1.293 | 0.107 | 1.202 | 0.160 | 0.888 | 0.039 | 0.951 | 0.023 | 1.234 | 0.000 | 1.120 | 0.000 | 1.624 | 0.000 | 1.625 | 0.000 |
| Case 9 | 6.784 | 2.343 | 6.717 | 2.174 | 6.277 | 0.582 | 9.829 | 1.741 | 60.737 | 0.000 | 17.732 | 0.000 | 694.691 | 0.000 | 20.927 | 0.000 |
| Case 10 | 3.301 | 0.457 | 3.216 | 0.569 | 2.747 | 0.077 | 3.038 | 0.125 | 3.093 | 0.000 | 2.798 | 0.000 | 6.236 | 0.000 | 3.298 | 0.000 |
| Case 11 | 2.998 | 0.432 | 3.125 | 0.582 | 1.817 | 0.080 | 2.143 | 0.154 | 2.203 | 0.000 | 2.940 | 0.000 | 4.601 | 0.000 | 2.219 | 0.000 |
| Case 12 | 20.983 | 4.017 | 20.864 | 4.154 | 14.122 | 0.662 | 16.734 | 1.077 | 25.720 | 0.000 | 26.400 | 0.000 | 57.592 | 0.000 | 26.205 | 0.000 |
| Case 13 | 8.556 | 1.851 | 9.403 | 2.387 | 5.138 | 0.220 | 5.994 | 0.479 | 11.074 | 0.000 | 11.070 | 0.000 | 24.868 | 0.000 | 9.182 | 0.000 |
| Case 14 | 4.896 | 1.054 | 4.744 | 1.031 | 3.756 | 0.150 | 4.393 | 0.275 | 4.901 | 0.000 | 6.074 | 0.000 | 30.239 | 0.000 | 5.515 | 0.000 |
| Case 15 | 56.615 | 25.364 | 59.560 | 31.099 | 22.422 | 2.206 | 37.503 | 6.097 | 55.684 | 0.000 | 95.365 | 0.000 | 118.121 | 0.000 | 43.898 | 0.000 |
| Task | No. | Assembly Completion Time | Fuzzy due Date | Fuzzy Transportation Time | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Forklift | Delivery Truck | Cabin Lift | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 4 | 1 | 2 | ||||
| Assembled PMCU | 1 | (5,6,7) | (13,15) | (8,12,15) | (10,13,14) | (12,14,15) | - | - | - | - | - | - |
| 2 | (8,9,10) | (17,20) | (10,16,20) | (11,13,15) | (12,13,15) | - | - | - | - | - | - | |
| 3 | (45,46,47) | (53,59) | (15,18,20) | (20,25,27) | (11,16,20) | - | - | - | - | - | - | |
| 4 | (52,56,62) | (60,63) | (16,23,25) | (23,25,27) | (12,15,20) | - | - | - | - | - | - | |
| 5 | (88,90,93) | (110,115) | (14,15,19) | (15,18,20) | (13,16,19) | - | - | - | - | - | - | |
| 6 | (100,106,108) | (120,130) | (17,20,25) | (18,22,28) | (15,18,19) | - | - | - | - | - | - | |
| 7 | (150,158,163) | (176,182) | (15,20,25) | (18,22,24) | (16,18,21) | - | - | - | - | - | - | |
| 8 | (172,180,190) | (191,203) | (16,20,24) | (13,17,20) | (17,22,25) | - | - | - | - | - | - | |
| PMCU awaiting transportation | 1 | - | (63,70) | (5,10,12) | (2,8,10) | (6,12,15) | (40,50,62) | (53,65,73) | (45,53,62) | (43,59,76) | - | (10,15,20) |
| 2 | - | (75,80) | (4,8,15) | (3,7,11) | (2,4,6) | (56,60,68) | (50,58,66) | (40,50,55) | (50,63,76) | - | (12,13,15) | |
| 3 | - | (160,172) | (8,10,12) | (5,7,10) | (7,9,13) | (58,66,73) | (51,60,66) | (43,54,65) | (60,65,76) | - | (10,14,19) | |
| 4 | - | (92,103) | (9,10,12) | (6,8,10) | (10,11,13) | (59,65,70) | (51,60,80) | (56,63,65) | (42,55,63) | - | (13,18,21) | |
| 5 | - | (109,115) | (11,13,15) | (9,12,16) | (5,7,13) | (43,56,69) | (47,54,76) | (35,56,60) | (47,53,66) | (11,12,15) | - | |
| 6 | - | (225,246) | (8,10,13) | (7,11,15) | (8,10,13) | (42,57,63) | (45,54,66) | (38,58,63) | (52,59,63) | (7,12,15) | - | |
| 7 | - | (235,250) | (9,12,18) | (6,9,13) | (5,7,9) | (42,56,63) | (53,59,66) | (59,66,78) | (62,72,79) | (10,13,17) | - | |
| 8 | - | (247,260) | (4,5,10) | (7,10,13) | (11,16,19) | (46,56,63) | (53,59,66) | (59,66,78) | (62,72,79) | (12,15,17) | ||
| Outfitting supplies | 1 | - | (65,75) | - | - | - | - | - | - | - | (43,50,58) | (34,43,46) |
| 2 | - | (70,83) | - | - | - | - | - | - | - | (15,20,31) | (16,18,22) | |
| 3 | - | (110,120) | - | - | - | - | - | - | - | (23,25,28) | (34,39,40) | |
| 4 | - | (110,120) | - | - | - | - | - | - | - | (23,25,28) | (16,20,22) | |
| 5 | - | (156,170) | - | - | - | - | - | - | - | (43,50,58) | (34,43,46) | |
| 6 | - | (164,180) | - | - | - | - | - | - | - | (15,20,31) | (16,18,22) | |
| 7 | - | (180,190) | - | - | - | - | - | - | - | (23,25,28) | (34,39,40) | |
| 8 | - | (176,193) | - | - | - | - | - | - | - | (14,18,21) | (16,20,22) | |
| 9 | - | (208,212) | - | - | - | - | - | - | - | (23,25,28) | (34,39,40) | |
| 10 | - | (245,260) | - | - | - | - | - | - | - | (14,18,21) | (16,20,22) | |
| Algorithms | Type | Weight | |||
|---|---|---|---|---|---|
| GA | Metaheuristic | 7.386 | 4.836 | 10.023 | |
| 0.466 | 0.336 | 0.634 | |||
| 8.567 | 6.664 | 10.796 | |||
| PSO | 7.706 | 5.279 | 9.514 | ||
| 0.634 | 0.281 | 0.841 | |||
| 7.962 | 5.257 | 11.568 | |||
| GA-SLHH | Hyper-heuristic | 2.813 | 2.336 | 3.510 | |
| 0.253 | 0.210 | 0.287 | |||
| 5.528 | 4.479 | 6.645 | |||
| GA-HH | 3.927 | 2.692 | 5.181 | ||
| 0.319 | 0.271 | 0.409 | |||
| 7.102 | 5.137 | 9.444 | |||
| FIFO | Dispatching rule | - | 4.154 | - | |
| - | 0.216 | - | |||
| - | 8.093 | - | |||
| SPT | - | 3.531 | - | ||
| - | 0.313 | - | |||
| - | 6.749 | - | |||
| MWKR | - | 6.587 | - | ||
| - | 0.217 | - | |||
| - | 12.958 | - | |||
| FRO | - | 4.226 | - | ||
| - | 0.418 | - | |||
| - | 8.033 | - |
| Algorithm | Computational Time (Unit: Seconds) | ||
|---|---|---|---|
| GA | 25.869 | 24.617 | 25.249 |
| PSO | 26.429 | 27.052 | 26.888 |
| GA-SLHH | 16.754 | 16.614 | 17.217 |
| GA-HH | 11.659 | 12.112 | 12.597 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Dong, R.; Wu, X.; Huang, W.; Lin, P. A Self-Learning Hyper-Heuristic Algorithm Based on a Genetic Algorithm: A Case Study on Prefabricated Modular Cabin Unit Logistics Scheduling in a Cruise Ship Manufacturer. Biomimetics 2024, 9, 516. https://doi.org/10.3390/biomimetics9090516
Li J, Dong R, Wu X, Huang W, Lin P. A Self-Learning Hyper-Heuristic Algorithm Based on a Genetic Algorithm: A Case Study on Prefabricated Modular Cabin Unit Logistics Scheduling in a Cruise Ship Manufacturer. Biomimetics. 2024; 9(9):516. https://doi.org/10.3390/biomimetics9090516
Chicago/Turabian StyleLi, Jinghua, Ruipu Dong, Xiaoyuan Wu, Wenhao Huang, and Pengfei Lin. 2024. "A Self-Learning Hyper-Heuristic Algorithm Based on a Genetic Algorithm: A Case Study on Prefabricated Modular Cabin Unit Logistics Scheduling in a Cruise Ship Manufacturer" Biomimetics 9, no. 9: 516. https://doi.org/10.3390/biomimetics9090516
APA StyleLi, J., Dong, R., Wu, X., Huang, W., & Lin, P. (2024). A Self-Learning Hyper-Heuristic Algorithm Based on a Genetic Algorithm: A Case Study on Prefabricated Modular Cabin Unit Logistics Scheduling in a Cruise Ship Manufacturer. Biomimetics, 9(9), 516. https://doi.org/10.3390/biomimetics9090516







