The Function of Horn Ridges for Impact Damping
Abstract
1. Introduction
2. Materials and Methods
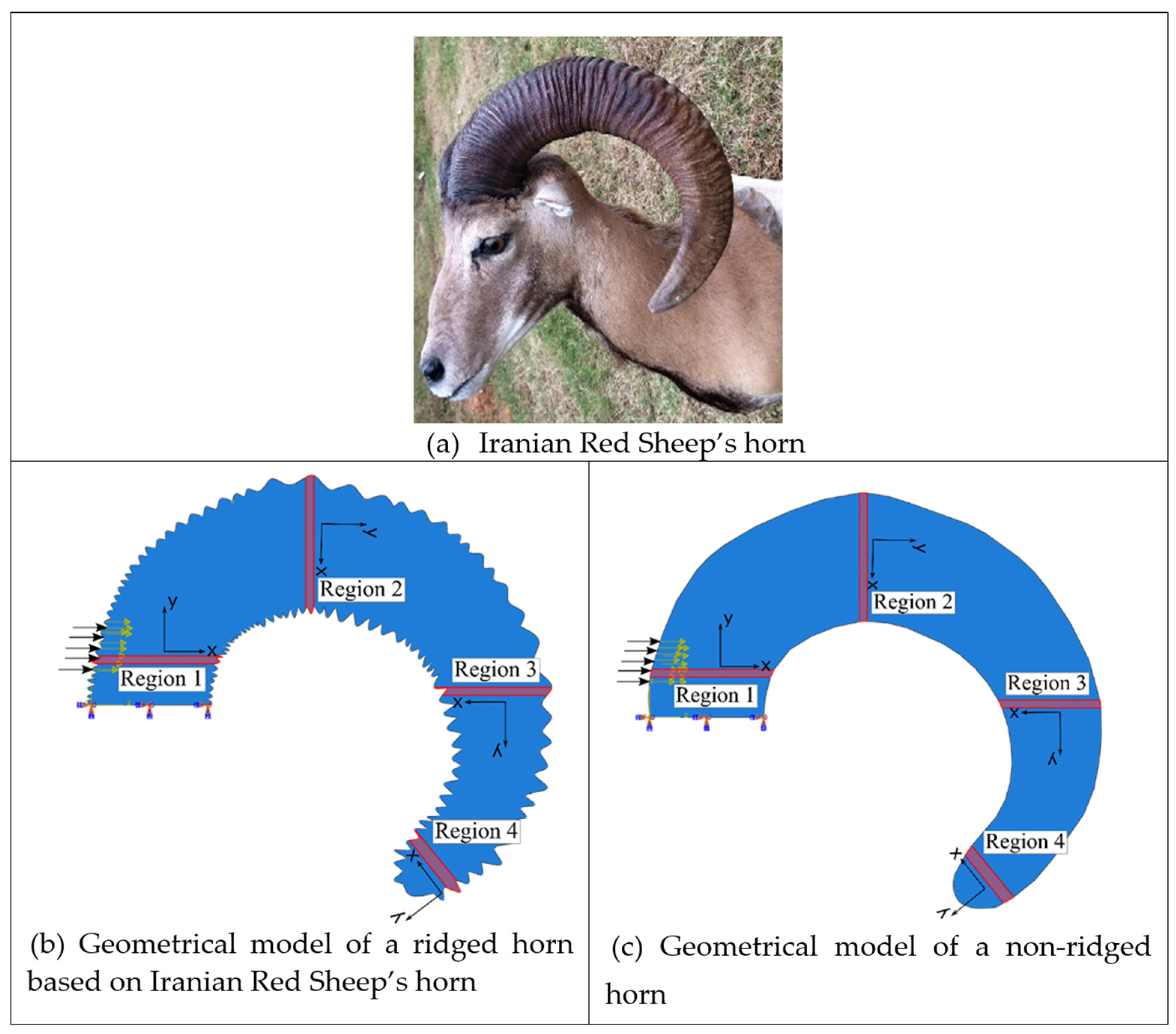
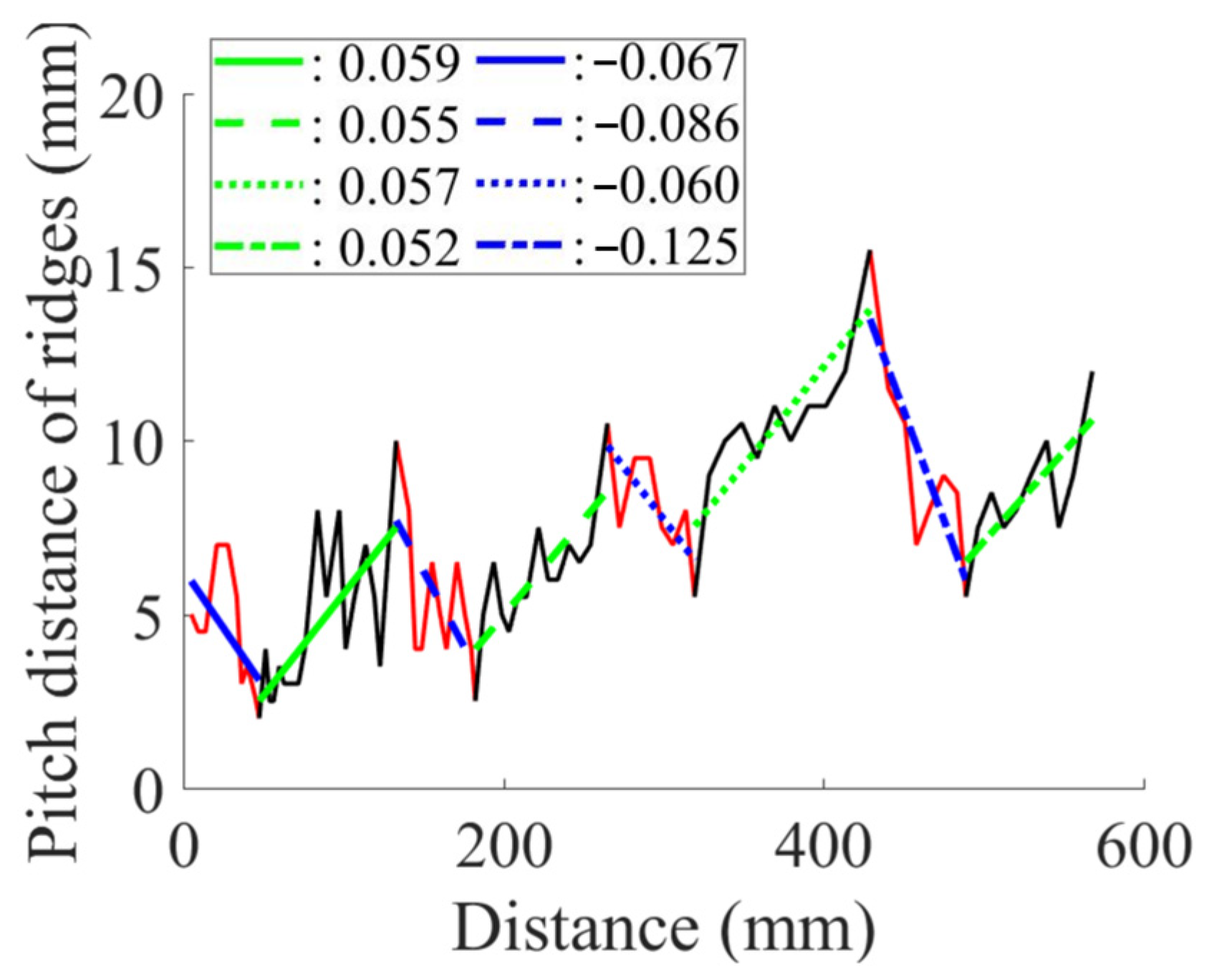
2.1. Measurements of Horn Ridges
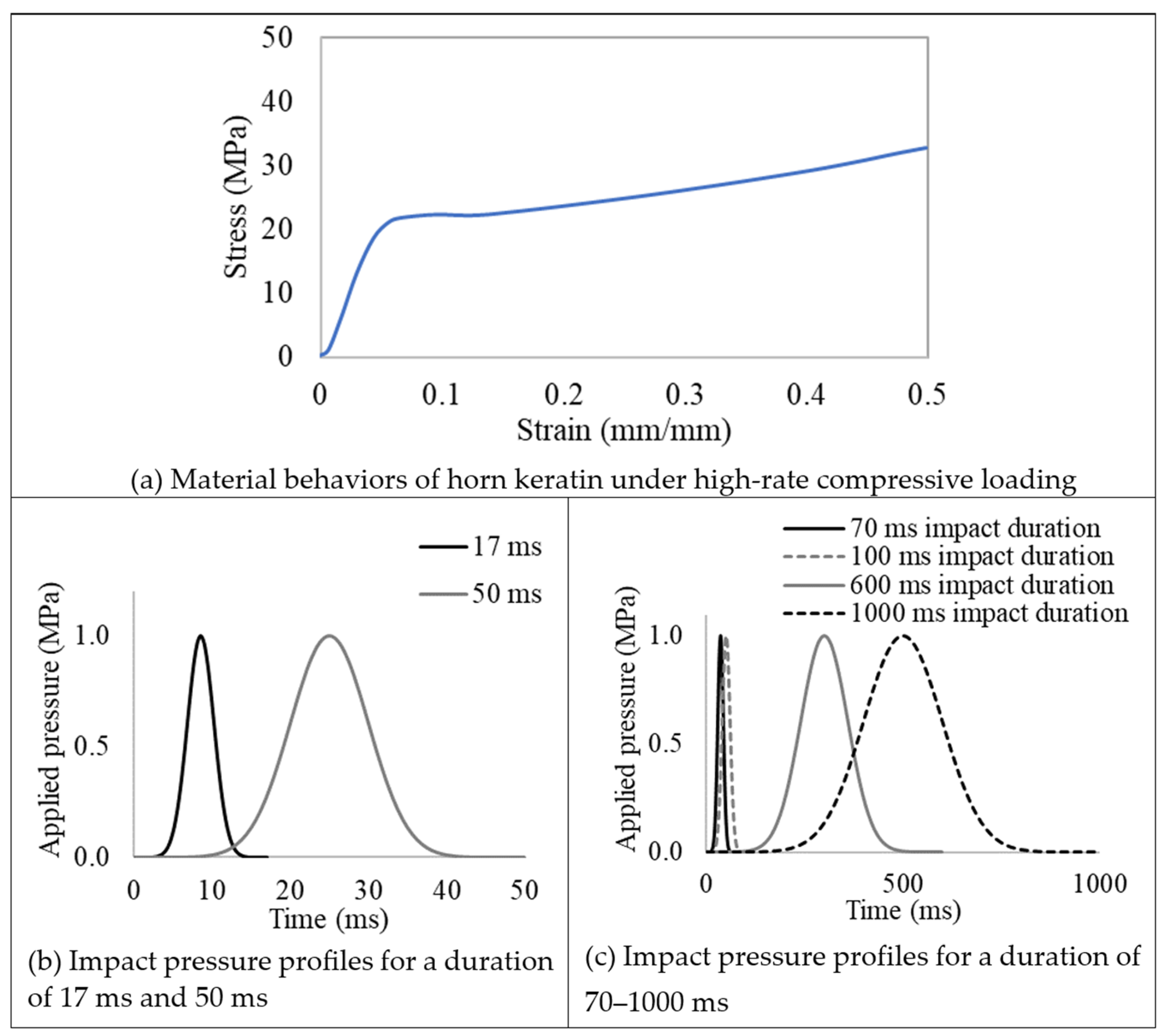
2.2. Simulation Set-Up
3. Results
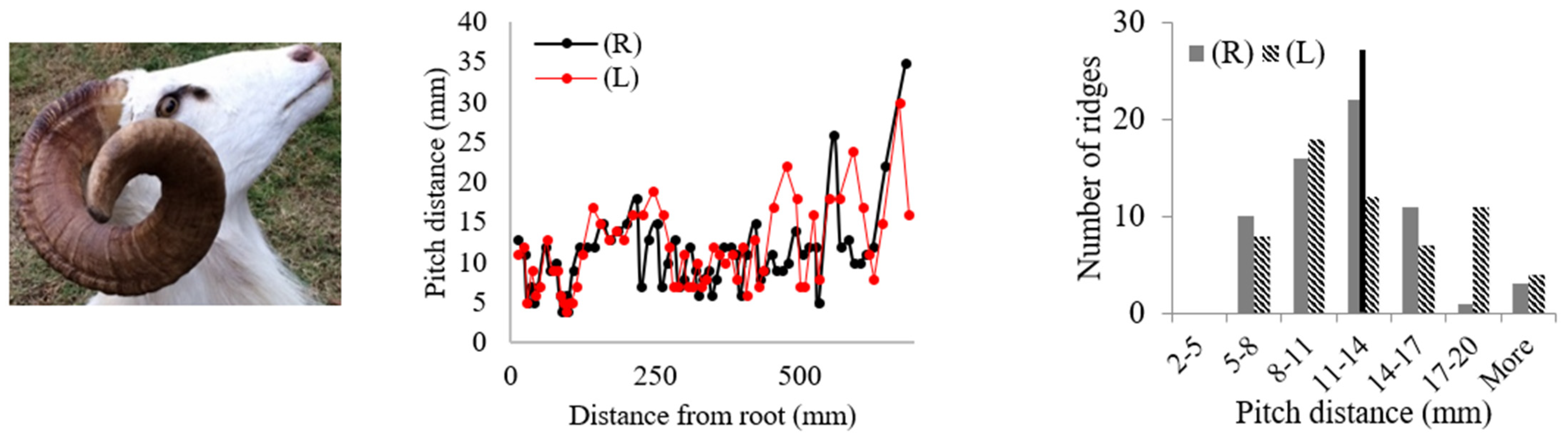
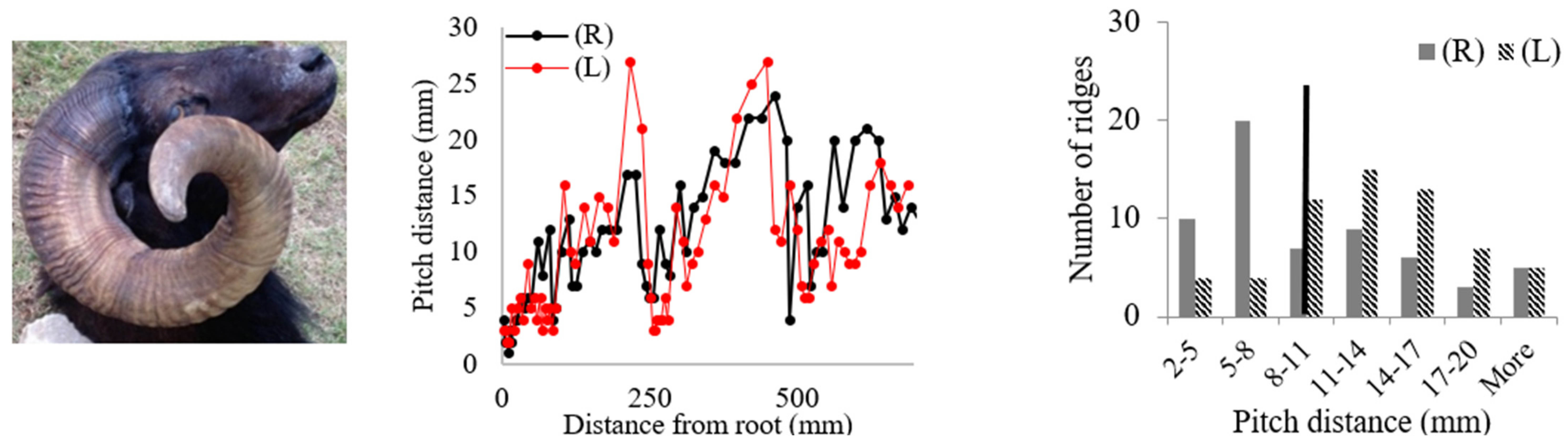
3.1. Geometric Analysis of Horn Ridges
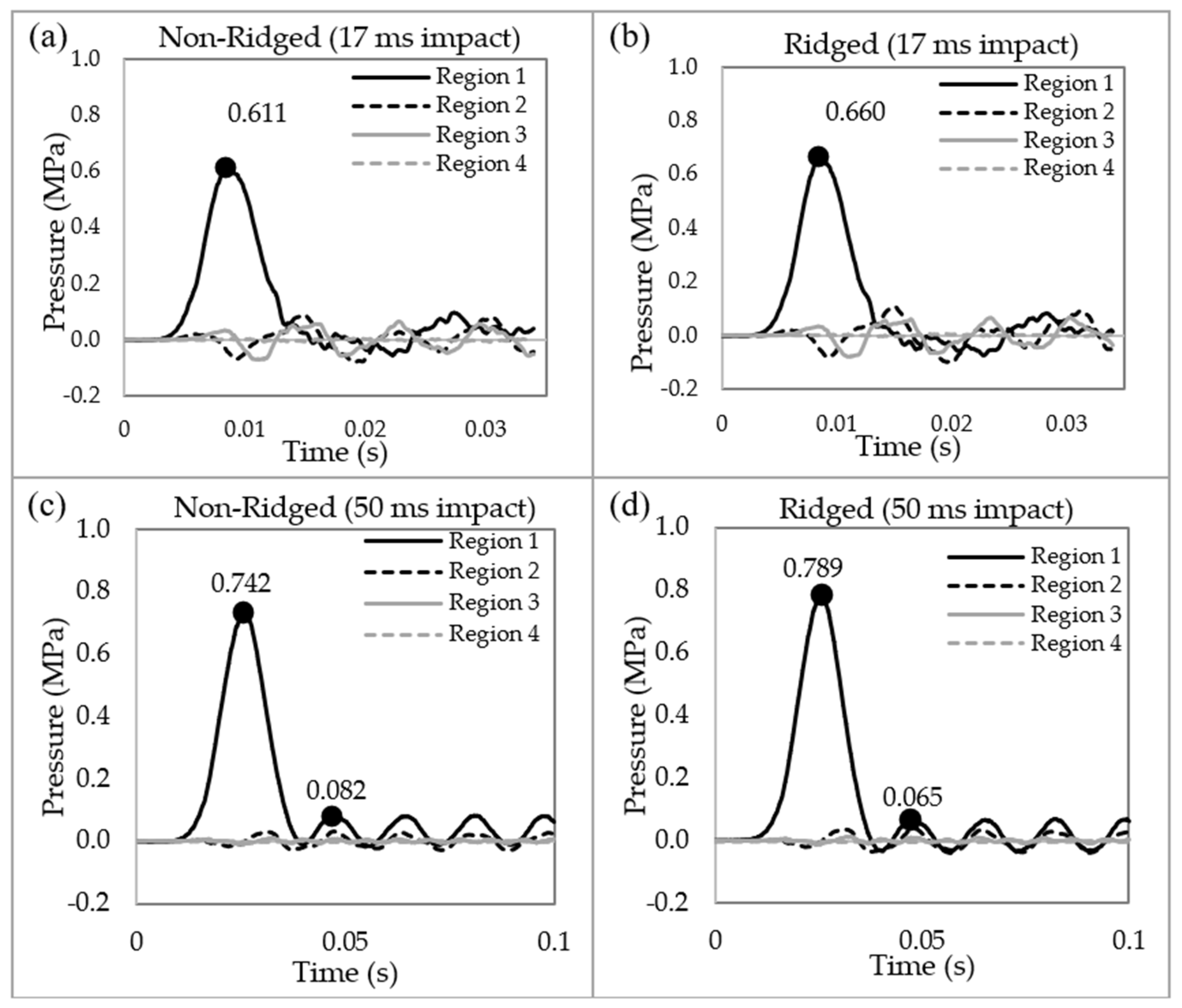
3.2. Impact Simulations on the Ram Horn
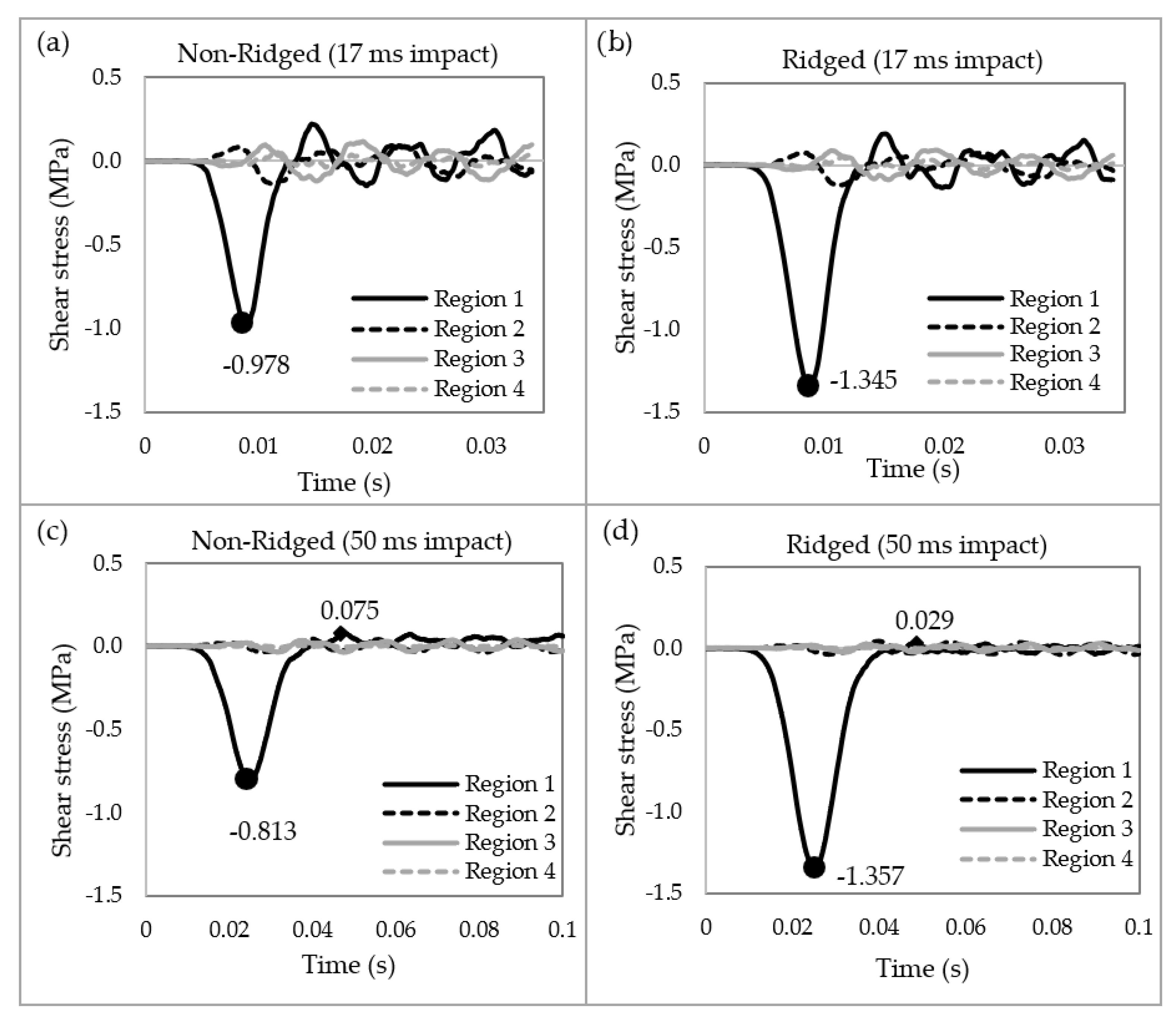
3.2.1. Transferring Longitudinal Waves into Shear Waves
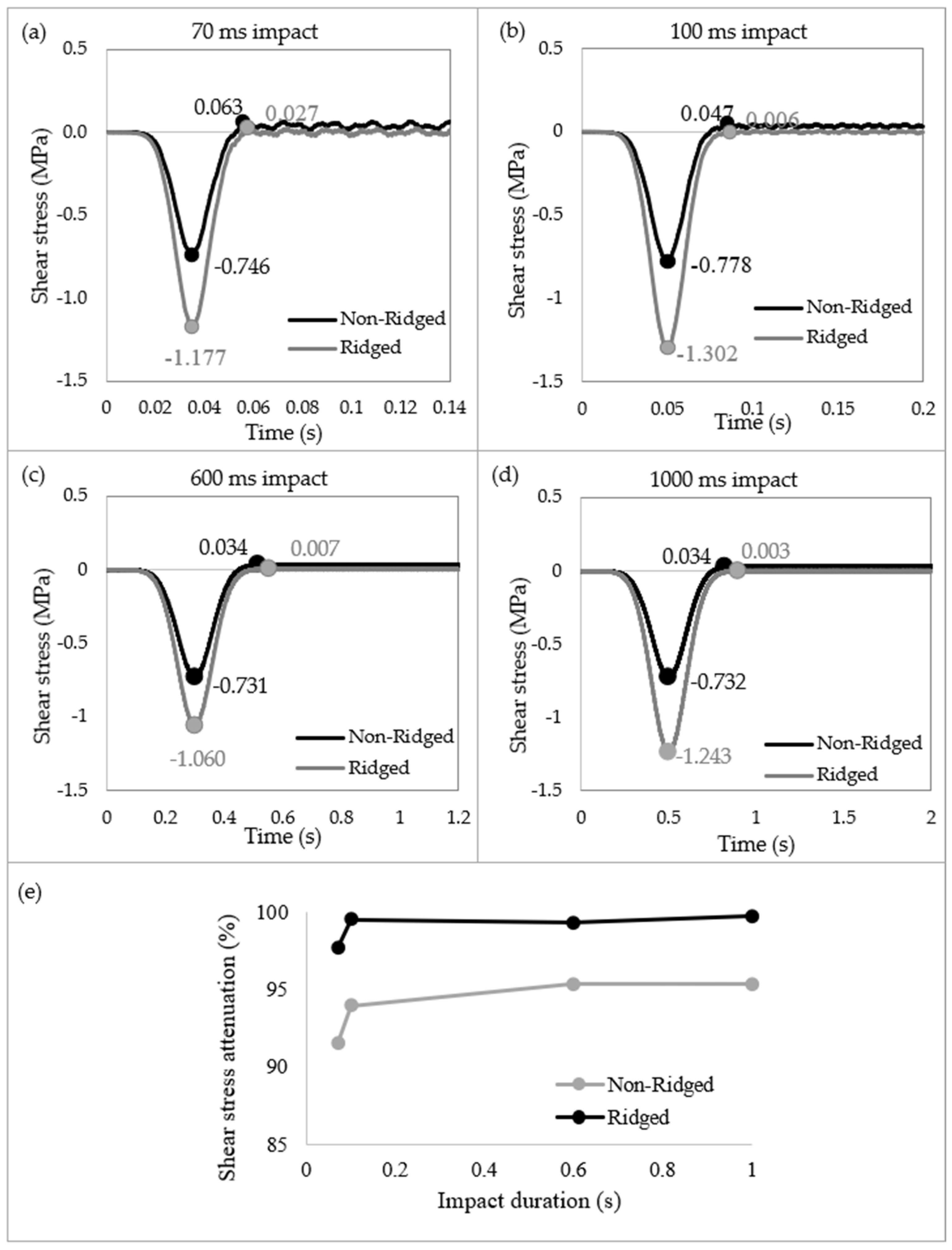
3.2.2. Filtering out Shear Waves
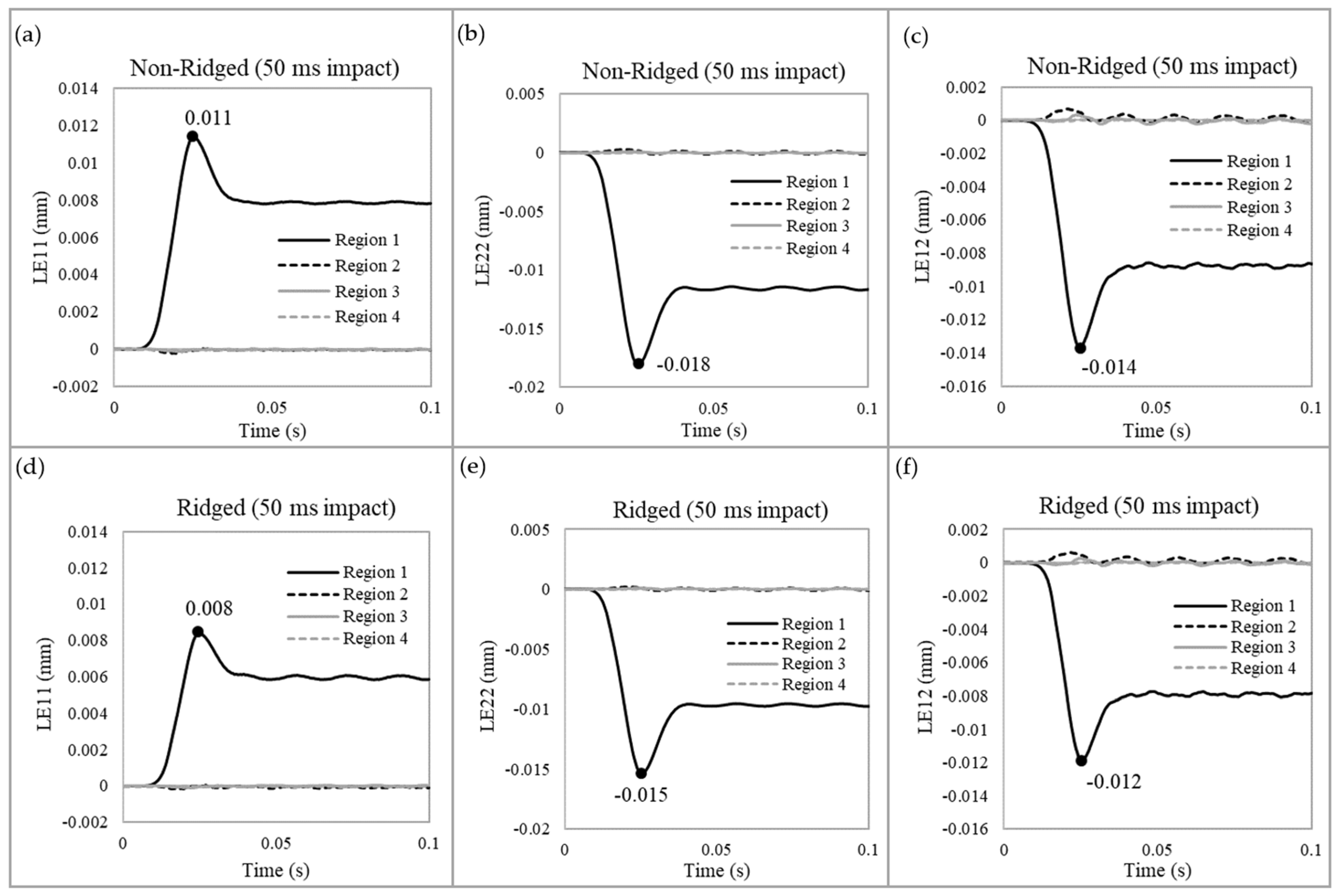
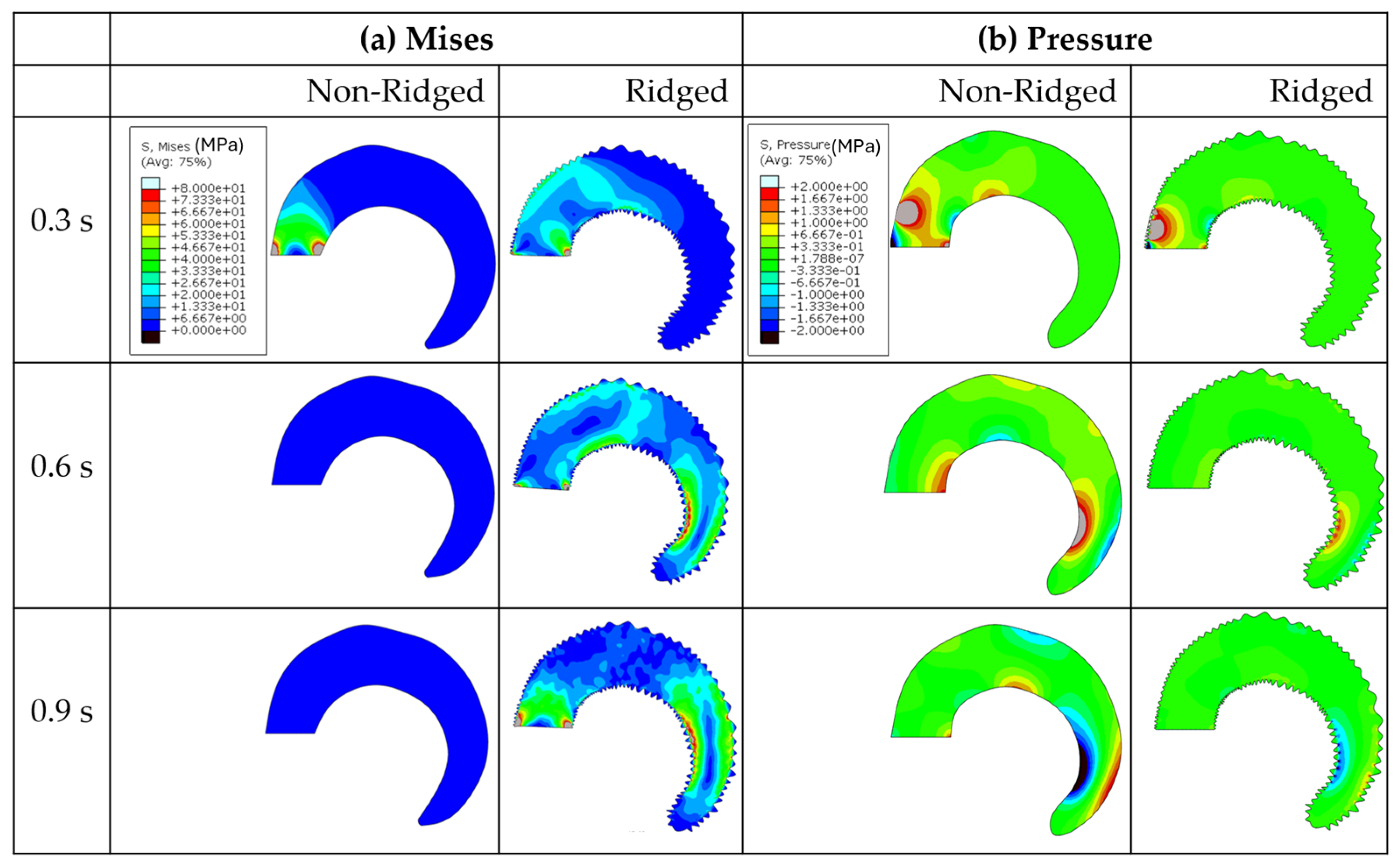
3.2.3. Stabilizing a Structure by Mitigating Excessive Strain
4. Discussion
4.1. Damping Effect
4.2. Shear Filtering
4.3. The Importance of Shear Filtering to Protect a Brain
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, N.; Horstemeyer, M.F.; Rhee, H.; Nabors, B.; Liao, J.; Williams, L.N. Hierarchical multiscale structure–property relationships of the red-bellied woodpecker (Melanerpes carolinus) beak. J. R. Soc. Interface 2014, 11, 20140274. [Google Scholar] [CrossRef] [PubMed]
- Behera, R.P.; Le Ferrand, H. Impact-resistant materials inspired by the mantis shrimp’s dactyl club. Matter 2021, 4, 2831–2849. [Google Scholar] [CrossRef]
- Lee, N.; Berthelson, P.R.; Nguyen, V.; Garrett, M.; Brinda, A.K.; Moser, R.D.; Horstemeyer, M.F.; Rhee, H.; Prabhu, R.K. Microstructure and Nanomechanical Properties of the Exoskeleton of an Ironclad Beetle (Zopherus haldemani). Bioinspir. Biomim. 2021, 16, 036005. [Google Scholar] [CrossRef]
- Huang, W.; Yaraghi, N.A.; Yang, W.; Velazquez-Olivera, A.; Li, Z.; Ritchie, R.O.; Kisailus, D.; Stover, S.M.; McKittrick, J. A natural energy absorbent polymer composite: The equine hoof wall. Acta Biomater. 2019, 90, 267–277. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Taskonak, B.; Mecholsky, J.J., Jr. Measurement of the Energy Absorbed during Nanoscale Deformation of Human Peritubular and Intertubular Dentin. Mater. Sci. Appl. 2022, 13, 144–157. [Google Scholar] [CrossRef]
- Zhang, X.M.; Wang, Y.C.; Su, M.N. Experimental, Numerical and Analytical Study to Develop a Design Method for Bending and Shear Resistances of 3D Printed Beetle Elytron Inspired Sandwich Plate (Beetle Elytron Plate). Thin-Walled Struct. 2023, 183, 110371. [Google Scholar] [CrossRef]
- Zhang, X.M.; Wang, Y.C.; Su, M.N.; Bartolo, P. Elastic–Plastic Buckling Behaviour of Beetle Elytron Plate with Simple, Fixed and Flexible Core Supports. Thin-Walled Struct. 2022, 179, 109534. [Google Scholar] [CrossRef]
- Zhang, X.M.; Wang, Y.C.; Foster, A.S.J.; Su, M.N. Elastic Local Buckling Behaviour of Beetle Elytron Plate. Thin-Walled Struct. 2021, 165, 107922. [Google Scholar] [CrossRef]
- King, A.I.; Yang, K.H.; Zhang, L.; Hardy, W.; Viano, D.C. Is head injury caused by linear or angular acceleration. In Proceedings of the IRCOBI Conference, Lisbon, Portugal, 25–26 September 2003; pp. 1–12. [Google Scholar]
- Faul, M.; Wald, M.M.; Xu, L.; Coronado, V.G. Traumatic Brain Injury in the United States: Emergency Department Visits, Hospitalizations, and Deaths, 2002–2006. 2010. Available online: https://stacks.cdc.gov/view/cdc/5571/cdc_5571_DS1.pdf (accessed on 7 August 2024).
- Daneshvar, D.H.; Nair, E.S.; Baucom, Z.H.; Rasch, A.; Abdolmohammadi, B.; Uretsky, M.; Saltiel, N.; Shah, A.; Jarnagin, J.; Baugh, C.M. Leveraging football accelerometer data to quantify associations between repetitive head impacts and chronic traumatic encephalopathy in males. Nat. Commun. 2023, 14, 3470. [Google Scholar] [CrossRef]
- Lee, N.; Horstemeyer, M.F.; Prabhu, R.; Liao, J.; Rhee, H.; Hammi, Y.; Moser, R.D.; Williams, L.N. The geometric effects of a woodpecker’ s hyoid apparatus for stress wave mitigation. Bioinspir. Biomim. 2016, 11, 066004. [Google Scholar] [CrossRef]
- Lee, N.; Williams, L.N.; Mun, S.; Rhee, H.; Prabhu, R.; Bhattarai, K.R.; Horstemeyer, M.F. Stress wave mitigation at suture interfaces. Biomed. Phys. Eng. Express 2017, 3, 035025. [Google Scholar] [CrossRef]
- Johnson, K.L.; Trim, M.W.; Horstemeyer, M.F.; Lee, N.; Williams, L.N.; Liao, J.; Rhee, H.; Prabhu, R. Geometric effects on stress wave propagation. J. Biomech. Eng. 2014, 136, 021023. [Google Scholar] [CrossRef] [PubMed]
- Drake, A.; Donahue, T.L.H.; Stansloski, M.; Fox, K.; Wheatley, B.B.; Donahue, S.W. Horn and horn core trabecular bone of bighorn sheep rams absorbs impact energy and reduces brain cavity accelerations during high impact ramming of the skull. Acta Biomater. 2016, 44, 41–50. [Google Scholar] [CrossRef] [PubMed]
- Geist, V. Mountain Sheep. A Study in Behavior and Evolution; University of Chicago Press: Chicago, IL, USA, 1971. [Google Scholar]
- Nowak, R.M.; Walker, E.P. Walker’s Mammals of the World; JHU Press: Baltimore, MD, USA, 1999. [Google Scholar]
- Kitchener, A. An analysis of the forces of fighting of the blackbuck (Antilope cervicapra) and the bighorn sheep (Ovis canadensis) and the mechanical design of the horn of bovids. J. Zool. 1988, 214, 1–20. [Google Scholar] [CrossRef]
- Li, B.-W.; Zhao, H.-P.; Feng, X.-Q. Static and dynamic mechanical properties of cattle horns. Mater. Sci. Eng. C 2011, 31, 179–183. [Google Scholar] [CrossRef]
- Maity, P.; Tekalur, S.A. Finite element analysis of ramming in Ovis canadensis. J. Biomech. Eng. 2011, 133, 021009. [Google Scholar] [CrossRef]
- Wheatley, B.B.; Gilmore, E.C.; Fuller, L.H.; Drake, A.M.; Donahue, S.W. How the geometry and mechanics of bighorn sheep horns mitigate the effects of impact and reduce the head injury criterion. Bioinspir. Biomim. 2023, 18, 026005. [Google Scholar] [CrossRef]
- Lundrigan, B. Morphology of horns and fighting behavior in the family Bovidae. J. Mammal. 1996, 77, 462–475. [Google Scholar] [CrossRef]
- Bunnell, F.L. Horn growth and population quality in Dall sheep. J. Wildl. Manag. 1978, 42, 764–775. [Google Scholar] [CrossRef]
- Festa-Bianchet, M.; Coltman, D.W.; Turelli, L.; Jorgenson, J.T. Relative allocation to horn and body growth in bighorn rams varies with resource availability. Behav. Ecol. 2004, 15, 305–312. [Google Scholar] [CrossRef]
- Li, B.W.; Zhao, H.P.; Feng, X.Q.; Guo, W.W.; Shan, S.C. Experimental study on the mechanical properties of the horn sheaths from cattle. J. Exp. Biol. 2010, 213, 479–486. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.L.; Trim, M.W.; Francis, D.K.; Whittington, W.R.; Miller, J.A.; Bennett, C.E.; Horstemeyer, M.F. Moisture; anisotropy, stress state, and strain rate effects on bighorn sheep horn keratin mechanical properties. Acta Biomater. 2017, 48, 300–308. [Google Scholar] [CrossRef] [PubMed]
- Trim, M.W.; Horstemeyer, M.F.; Rhee, H.; El Kadiri, H.; Williams, L.N.; Liao, J.; Walters, K.B.; McKittrick, J.; Park, S.-J. The effects of water and microstructure on the mechanical properties of bighorn sheep (Ovis canadensis) horn keratin. Acta Biomater. 2011, 7, 1228–1240. [Google Scholar] [CrossRef]
- Johnson, K.L.; Trim, M.W.; Mao, Y.; Rhee, H.; Williams, L.N.; Liao, J.; Griggs, J.; Horstemeyer, M.F.; Duan, Y. Finite element analysis of a ram brain during impact under wet and dry horn conditions. J. Mech. Behav. Biomed. Mater. 2021, 119, 104400. [Google Scholar] [CrossRef]
- Gray, G.G.; Simpson, C.D. Weight estimation of barbary sheep from horn length. Wildl. Soc. Bull. 1973–2006 1979, 7, 285–288. [Google Scholar]
- Vasseur, J.O.; Deymier, P.A.; Frantziskonis, G.; Hong, G.; Djafari-Rouhani, B.; Dobrzynski, L. Experimental evidence for the existence of absolute acoustic band gaps in two-dimensional periodic composite media. J. Phys. Condens. Matter. 1998, 10, 6051. [Google Scholar] [CrossRef]
- Valier-Brasier, T.; Potel, C.; Bruneau, M. Shear acoustic waves polarized along the ridged surface of an isotropic solid plate: Mode coupling effects due to the shape profile. J. Appl. Phys. 2010, 108, 074910. [Google Scholar] [CrossRef]
- Valier-Brasier, T.; Potel, C.; Bruneau, M. Modes coupling of shear acoustic waves polarized along a one-dimensional corrugation on the surfaces of an isotropic solid plate. Appl. Phys. Lett. 2008, 93, 164101. [Google Scholar] [CrossRef]
- Raghavan, L.; Phani, A.S. Local resonance bandgaps in periodic media: Theory and experiment. J. Acoust. Soc. Am. 2013, 134, 1950–1959. [Google Scholar] [CrossRef]
- Kundu, T.; Banerjee, S.; Jata, K.V. An experimental investigation of guided wave propagation in corrugated plates showing stop bands and pass bands. J. Acoust. Soc. Am. 2006, 120, 1217–1226. [Google Scholar] [CrossRef]
- Peerless, S.J.; Rewcastle, N.B. Shear injuries of the brain. Can. Med. Assoc. J. 1967, 96, 577–582. [Google Scholar] [PubMed]
- Holbourn, A.H.S. Mechanics of head injuries. Lancet 1943, 242, 438–441. [Google Scholar] [CrossRef]
- Gennarelli, T.A.; Thibault, L.E.; Tomei, G.; Wiser, R.; Graham, D.; Adams, J. Directional dependence of axonal brain injury due to centroidal and non-centroidal acceleration. SAE Trans. 1987, 1355–1359. Available online: https://www.jstor.org/stable/44472897 (accessed on 7 August 2024).
- Margulies, S.S.; Thibault, L.E. A proposed tolerance criterion for diffuse axonal injury in man. J. Biomech. 1992, 25, 917–923. [Google Scholar] [CrossRef] [PubMed]
- Gabler, L.F.; Crandall, J.R.; Panzer, M.B. Development of a metric for predicting brain strain responses using head kinematics. Ann. Biomed. Eng. 2018, 46, 972–985. [Google Scholar] [CrossRef]
- Gabler, L.F.; Crandall, J.R.; Panzer, M.B. Assessment of kinematic brain injury metrics for predicting strain responses in diverse automotive impact conditions. Ann. Biomed. Eng. 2016, 44, 3705–3718. [Google Scholar] [CrossRef]
- Meaney, D.F.; Smith, D.H. Biomechanics of concussion. Clin. Sports Med. 2011, 30, 19–31. [Google Scholar] [CrossRef]

| Sheep | Pitch Distance of Ridges | Distribution of Pitches |
|---|---|---|
| 1. Bighorn Sheep (Ovis canadensis) | ||
 | ||
| 2. Ibex (Capra ibex) | ||
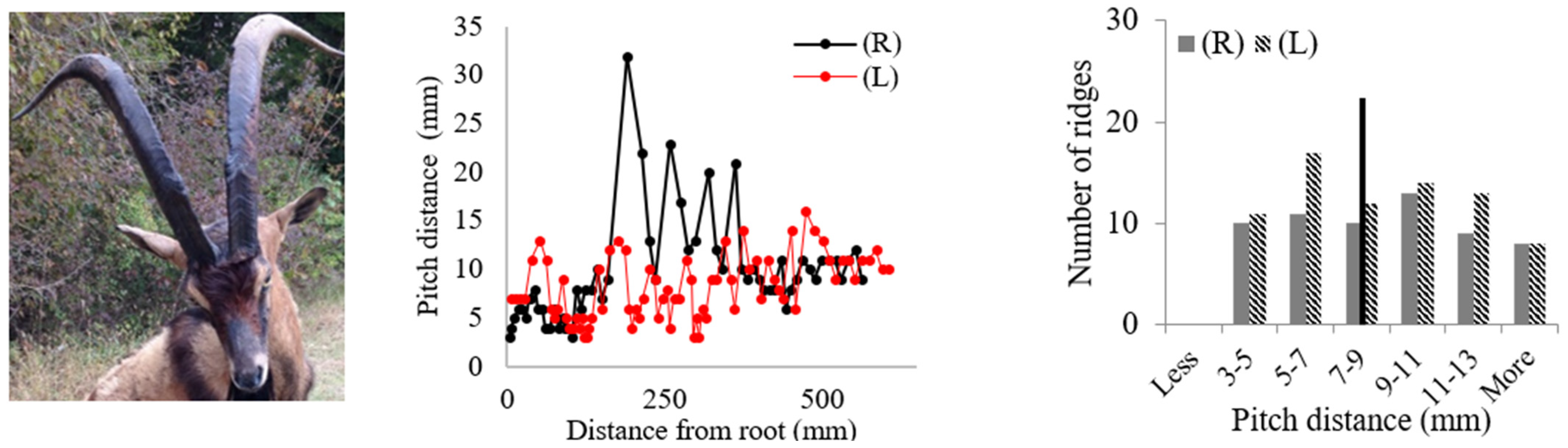 | ||
| 3. Aoudad (Ammotragus lervia) | ||
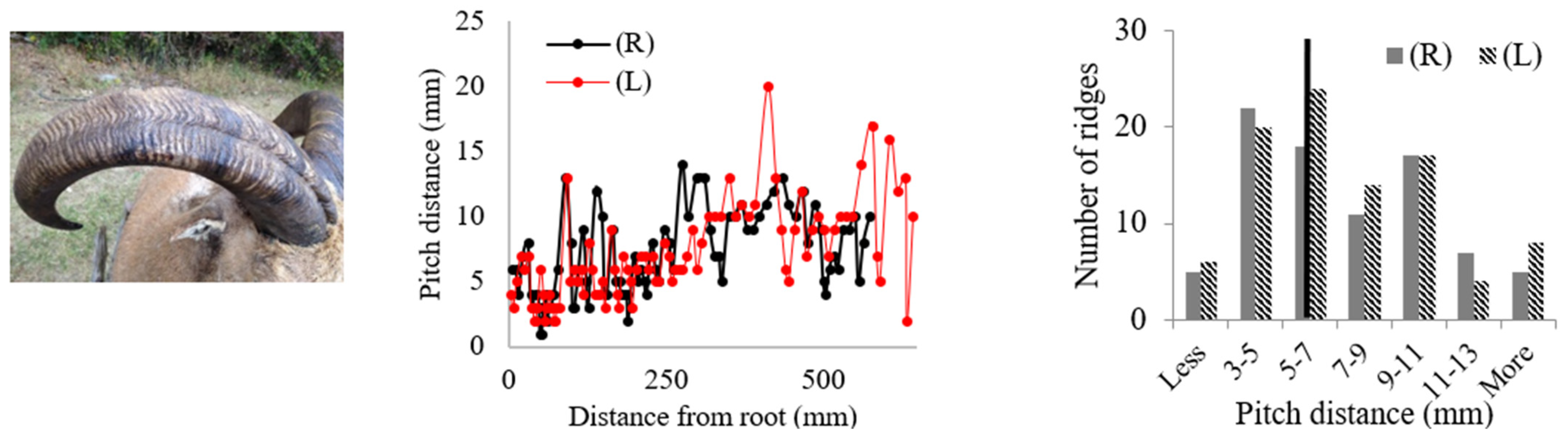 | ||
| 4. Texas Dall (Ovis dalli) | ||
 | ||
| 5. Iranian Red Sheep (Ovis orientalis gmelini) | ||
 | ||
| 6. Black Hawaiian Sheep 1 (Ovis orientalis) | ||
 | ||
| 7. Black Hawaiian Sheep 2 (Ovis orientalis) | ||
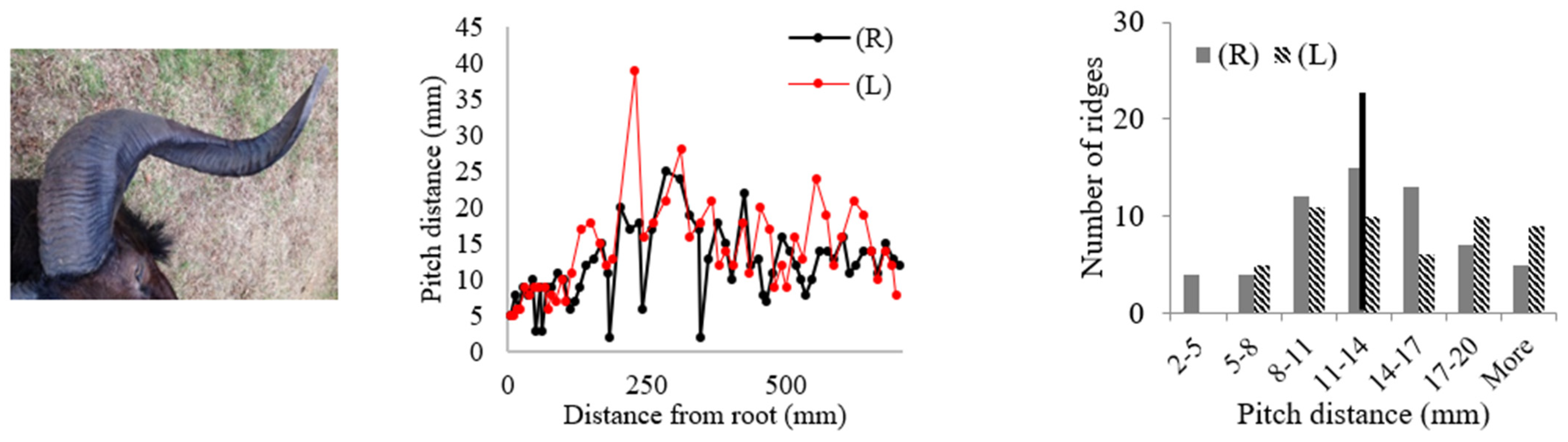 | ||
| 8. Black Hawaiian Sheep 3 (Ovis orientalis) | ||
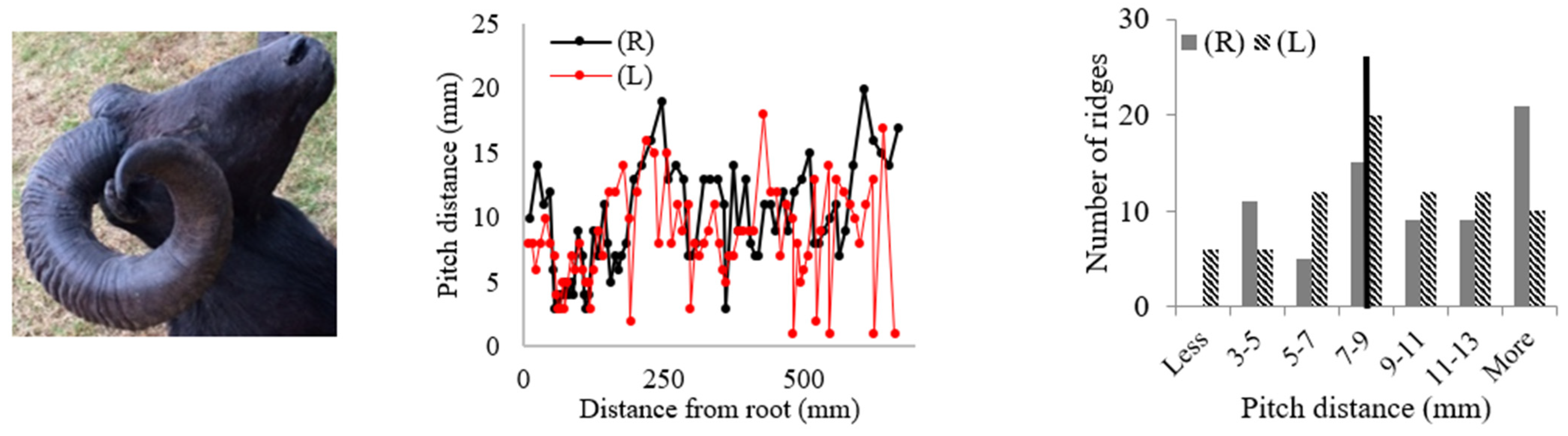 | ||
| Sheep | Average Pitch Distance (mm) | |
|---|---|---|
| 1 | Bighorn Sheep | 9.11 ± 4.16 |
| 2 | Ibex | 8.60 ± 4.32 |
| 3 | Aoudad | 6.84 ± 3.44 |
| 4 | Texas Dall | 11.18 ± 5.10 |
| 5 | Iranian Red Sheep | 7.85 ± 3.53 |
| 6 | Black Hawaiian Sheep 1 | 10.18 ± 5.99 |
| 7 | Black Hawaiian Sheep 2 | 12.65 ± 5.71 |
| 8 | Black Hawaiian Sheep 3 | 8.86 ± 4.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, N.; Mun, S.; Johnson, K.L.; Horstemeyer, M.F. The Function of Horn Ridges for Impact Damping. Biomimetics 2024, 9, 506. https://doi.org/10.3390/biomimetics9080506
Lee N, Mun S, Johnson KL, Horstemeyer MF. The Function of Horn Ridges for Impact Damping. Biomimetics. 2024; 9(8):506. https://doi.org/10.3390/biomimetics9080506
Chicago/Turabian StyleLee, Nayeon, Sungkwang Mun, Kyle L. Johnson, and Mark F. Horstemeyer. 2024. "The Function of Horn Ridges for Impact Damping" Biomimetics 9, no. 8: 506. https://doi.org/10.3390/biomimetics9080506
APA StyleLee, N., Mun, S., Johnson, K. L., & Horstemeyer, M. F. (2024). The Function of Horn Ridges for Impact Damping. Biomimetics, 9(8), 506. https://doi.org/10.3390/biomimetics9080506







