Design and Experimental of the Soil Removal Device for Root-Soil Complex of Gentian Imitating the Percussion of Woodpeckers
Abstract
1. Introduction
2. Materials and Methods
2.1. Characteristics Parameters of the Root-Soil Complex of Gentian
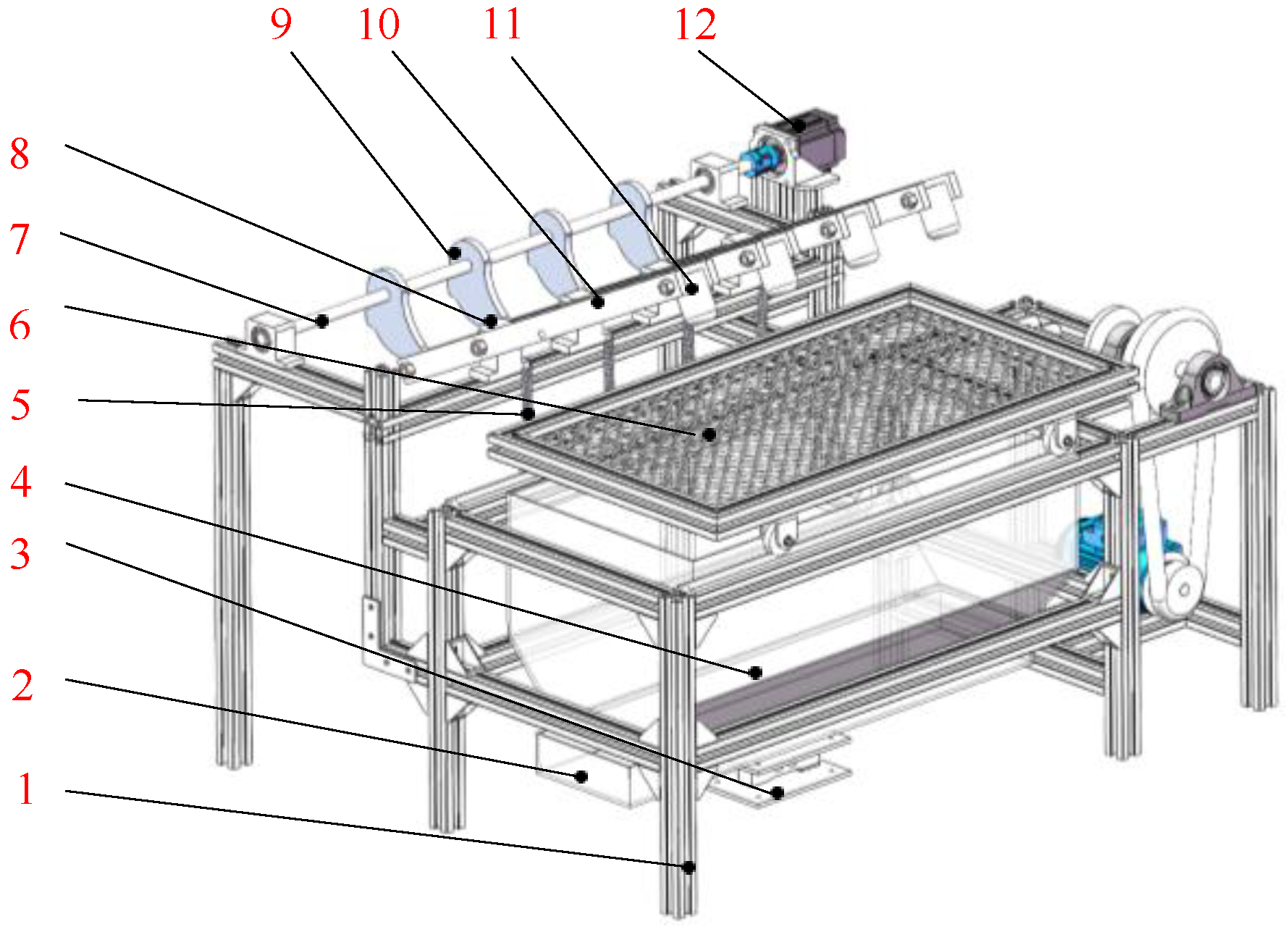
2.2. Machine Structure and Technical Parameters
2.2.1. Machine Structure
2.2.2. Working Principle and Technical Parameters
2.3. Design of the Soil Removal Device for the Root-Soil Complex of Gentian Imitating the Percussion of Woodpeckers
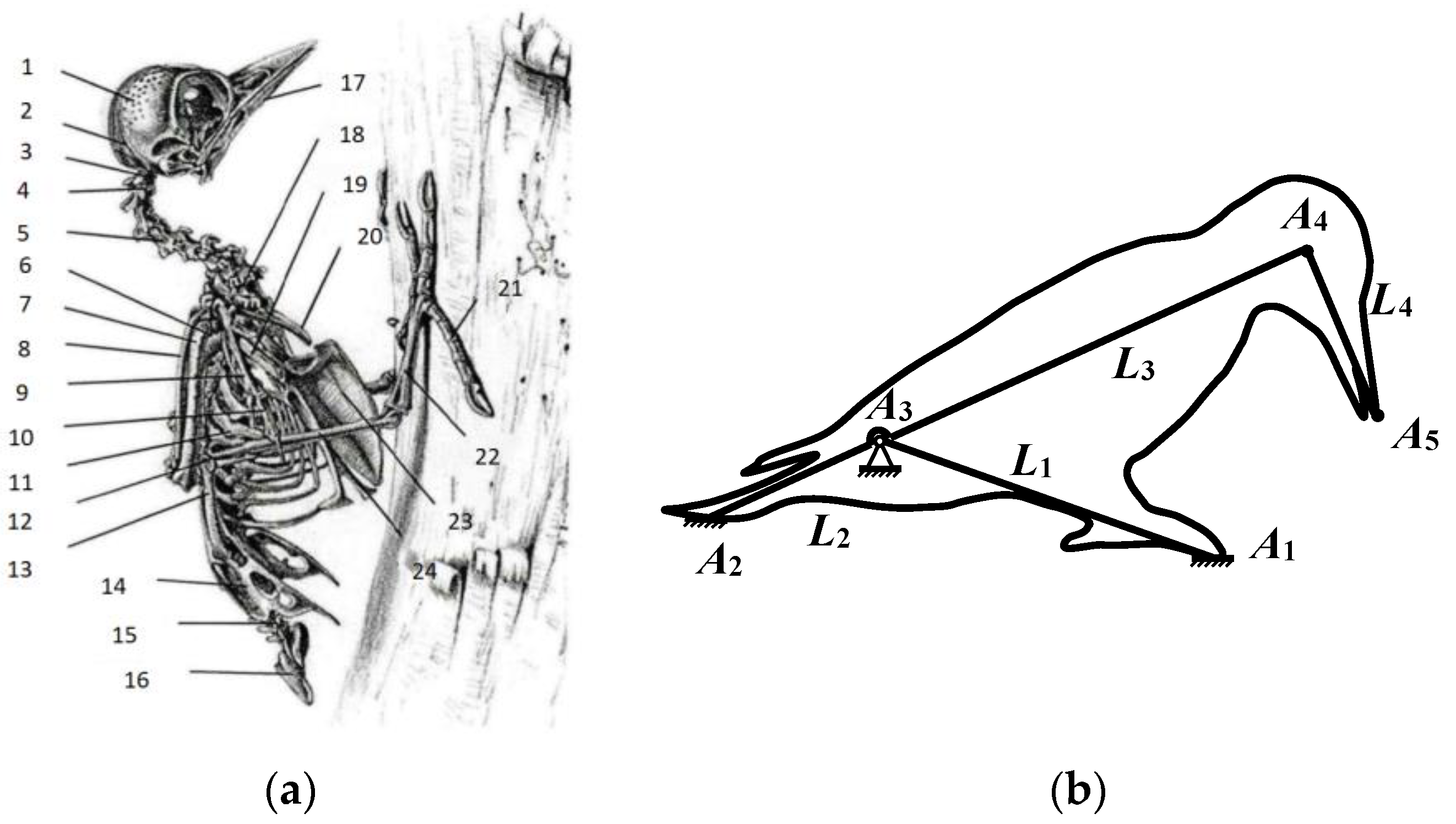
2.3.1. Bionic Principle of Bionic Woodpecker Percussion Mechanism
2.3.2. Simplified Modeling of Woodpecker Percussion Motion
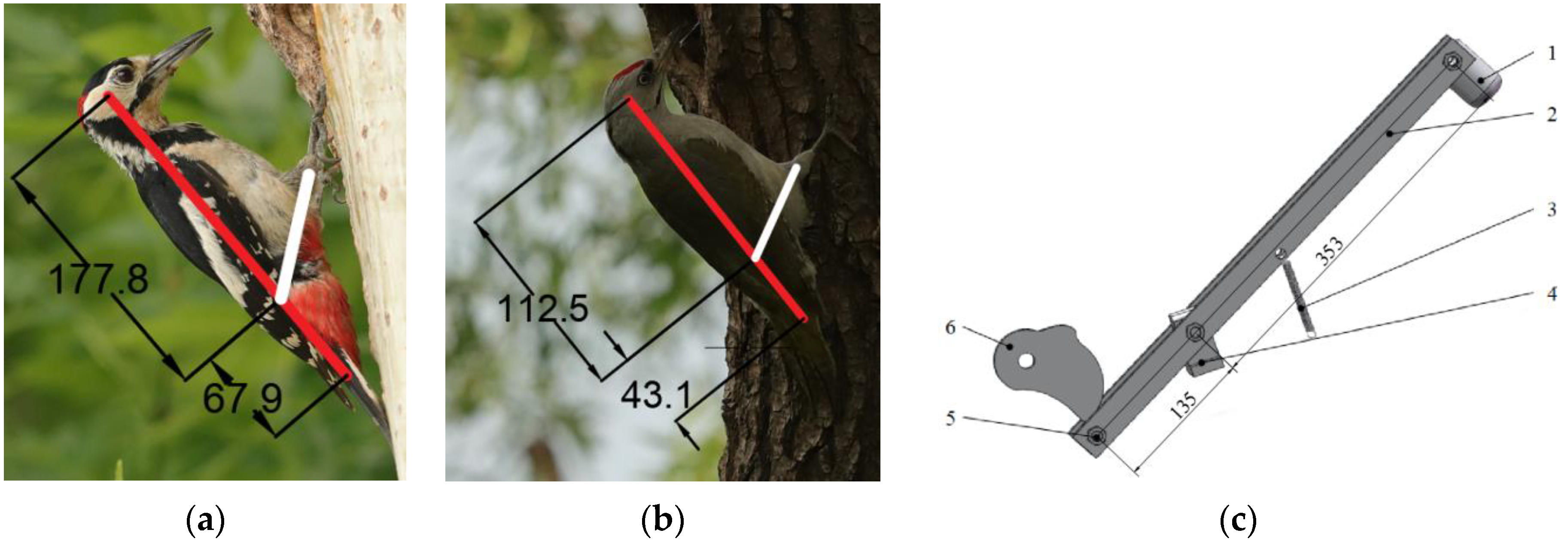
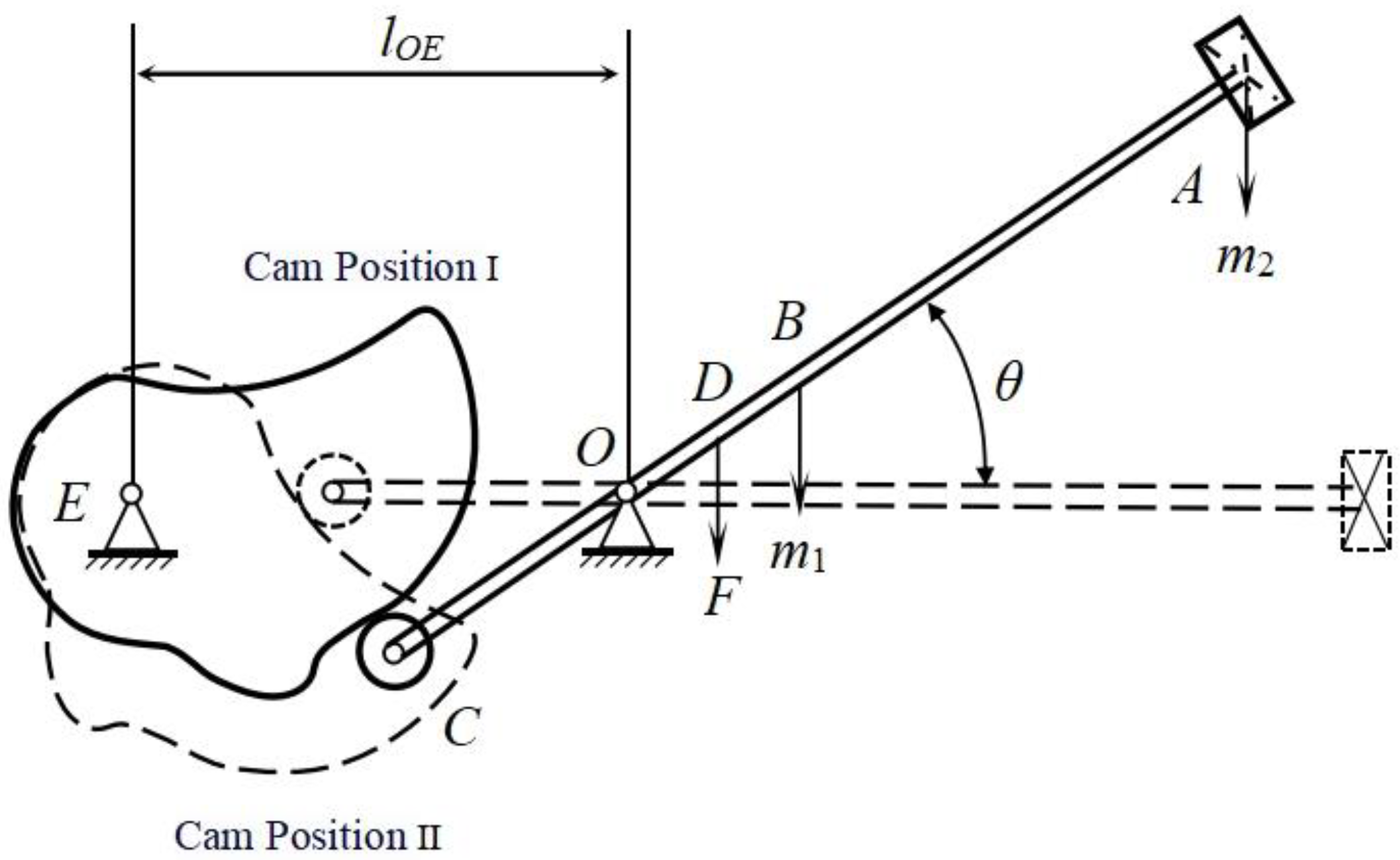
2.3.3. Structure Design of the Bionic Woodpecker Percussion Mechanism
2.3.4. The Parameter Calculation of the Bionic Woodpecker Percussion Mechanism
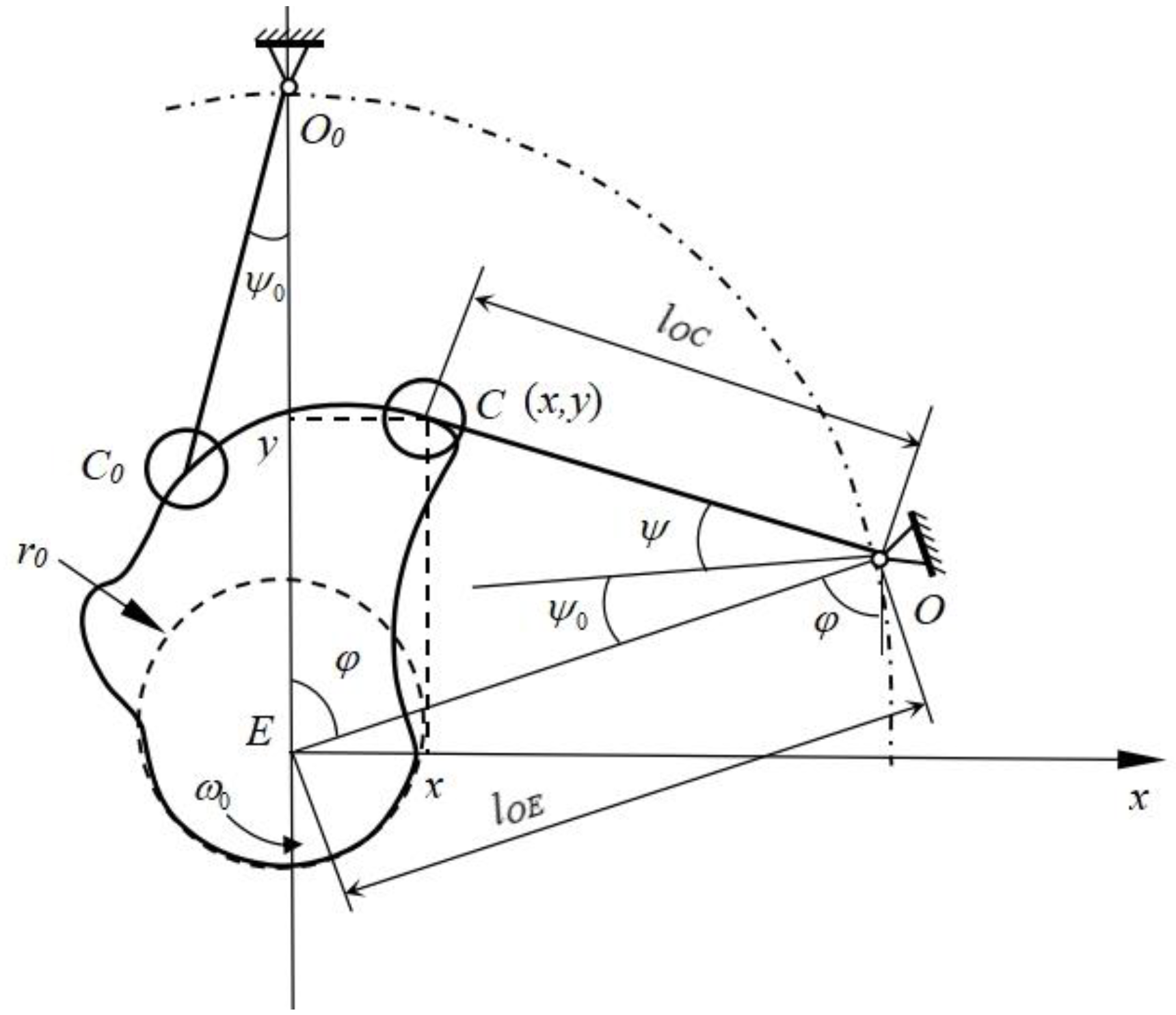
2.3.5. Cam Design of the Bionic Woodpecker Percussion Mechanism
3. Experiment and Results
3.1. Experimental Design
3.1.1. Experimental Materials and Equipment
3.1.2. Experimental Factors
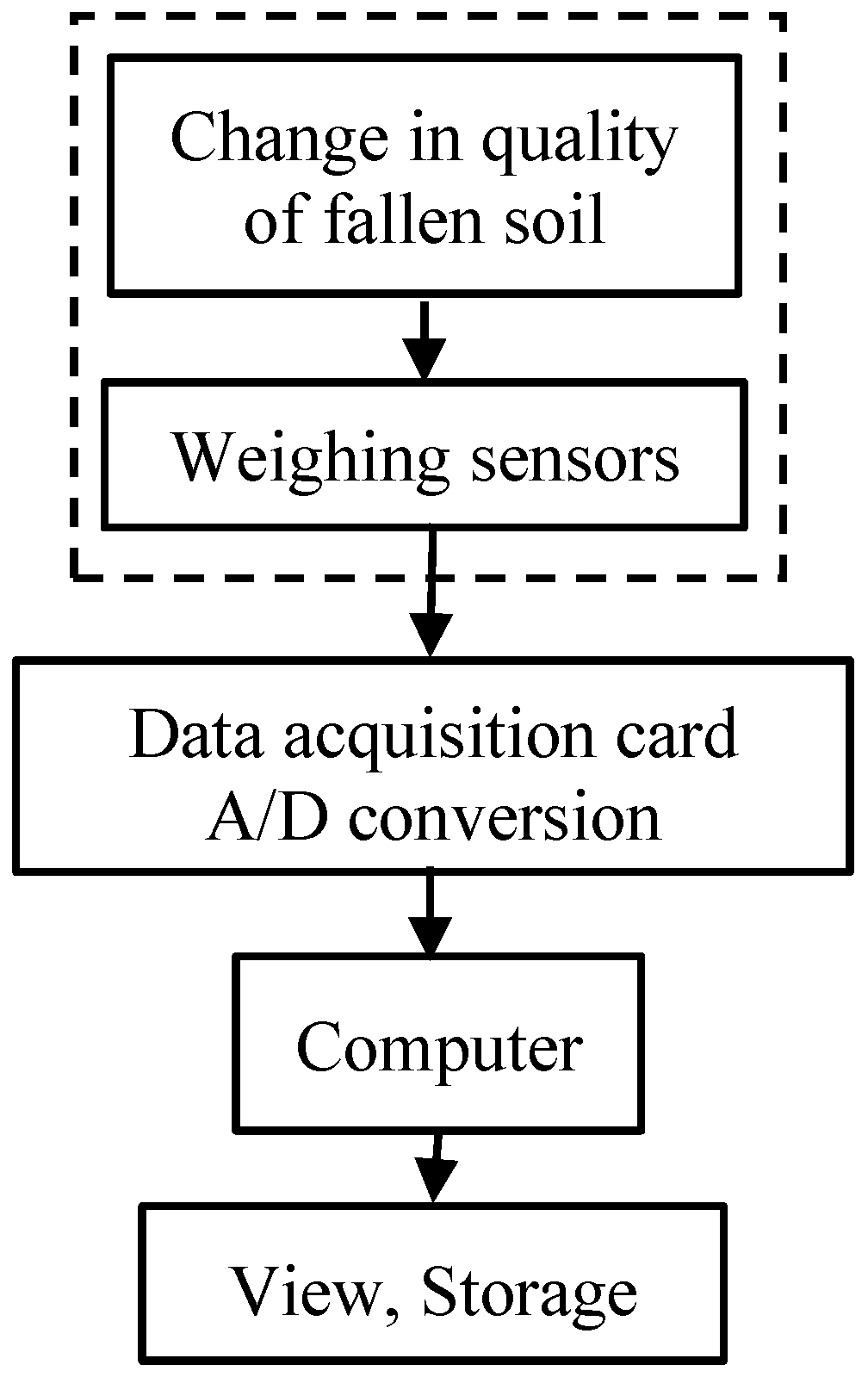
3.1.3. Determination of Experimental Indicators
3.2. Experimental Program and Results
4. Analysis and Discussions
4.1. Regression Modeling and Significant Analysis
- (1)
- Regression analysis and significance experiment of the soil removal rate
- (2)
- Regression analysis and significance experiment of the energy consumption of single hammer percussion
4.2. Effects of Interaction Factors on Response Functions
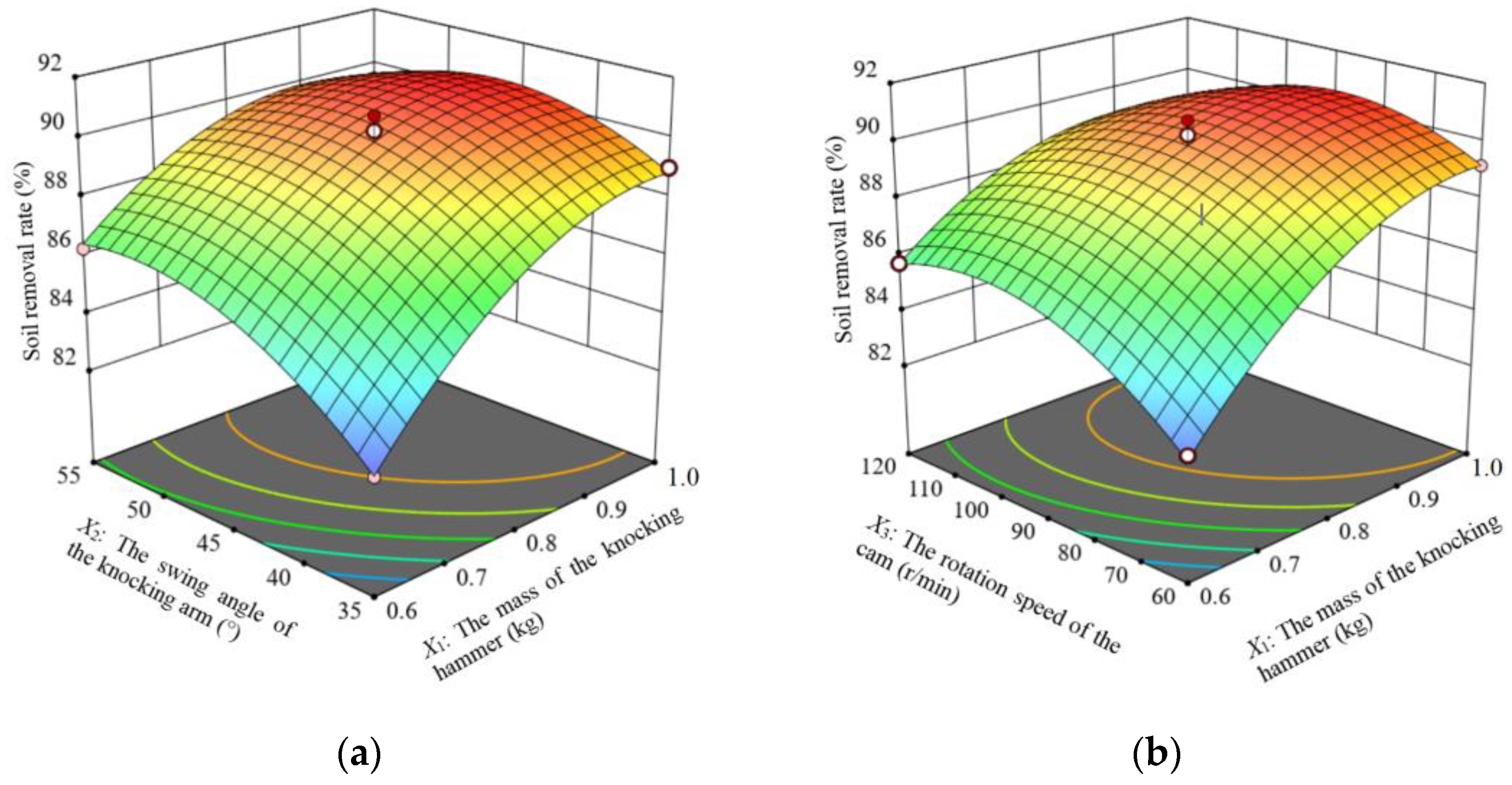
4.2.1. Effects of the Interaction Factors on the Soil Removal Rate
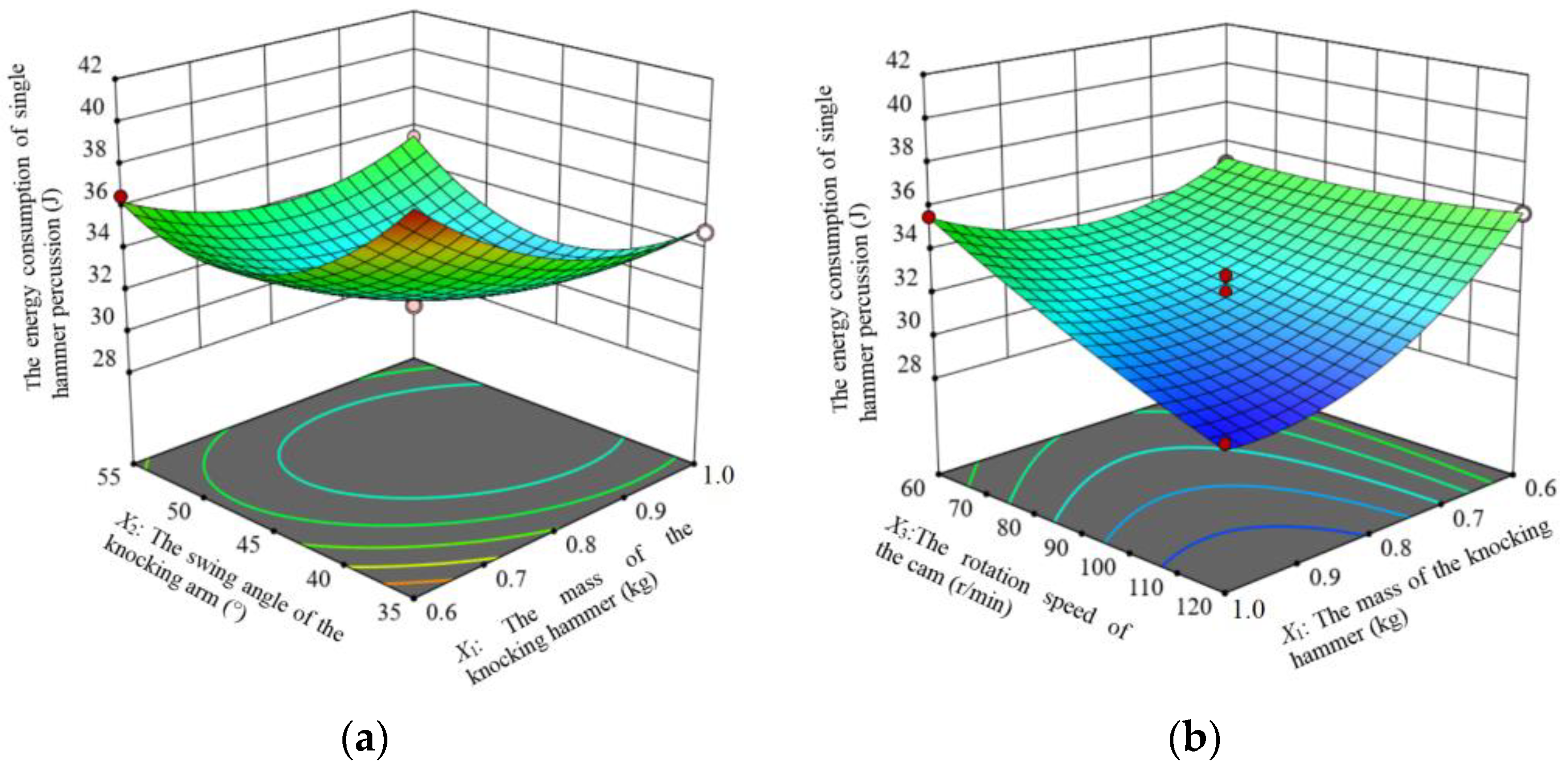
4.2.2. Effects of Interaction Terms on Energy Consumption of the Energy Consumption of Single Hammer Percussion
4.3. Parameter Combination Optimization and Validation
5. Conclusions
- (1)
- A soil removal device for the root-soil complex of Gentian imitating the behavior of woodpeckers striking tree trunks was designed to improve the soil removal rate and reduce power consumption.
- (2)
- A “lever-spring-cam” striking mechanism similar to the percussion motion of woodpeckers was designed based on the analysis of the percussion motion of woodpeckers. According to the physical parameters of woodpeckers, the appropriate length of the bionic striking arm was determined. The theoretical analysis and calculation determined the range of the mass of the striking hammer, the swing angle of the striking arm, and the rotation speed of the cam.
- (3)
- The analysis and the tests on the prototype proved that the soil removal device for the root-soil complex of Gentian imitating the percussion of woodpeckers could improve the soil removal rate and reduce the energy consumption of the single hammer percussion. Through parameter combination optimization experiments, variance analysis, and response surface analysis, the effects of factors were studied. The optimal operating parameter combination was determined as follows: the mass of the striking hammer of 0.9 kg, the swing angle of the striking arm of 47°, and the rotation speed of the cam of 100 r/min. The results of the validation experiment showed that the soil removal rate reached 89.12% and the energy consumption of the single hammer percussion was 31.21 J, which was consistent with the prediction results of the regression model and met the operational requirements of the soil removal device for the root-soil complex of Gentian.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, S.; Sun, W.; Wen, J.; Li, X.; Yang, Z.; Li, L. Diversity of Rhizosphere Bacterial and Function Predicted Analysis in Gentiana scabra Replanting Soil. J. Shenyang Agric. Univ. 2021, 52, 102–108. Available online: https://www.cabidigitallibrary.org/doi/full/10.5555/20220445652 (accessed on 5 August 2024).
- Chen, X.; Ma, X.; Chen, G.; Qi, L.; Wu, T.; Zeng, L. Research on soil-rhizome separating device of deep-rhizome Chinese herbal medicines. Mech. Des. 2015, 32, 65–70. [Google Scholar] [CrossRef]
- Yu, J. The Development and Testing on Hanging Type Harvester of Panax notoginseng; Kunming University of Science and Technology: Kunming, China, 2015. [Google Scholar]
- Cui, Z.; Zhang, Z.; Wang, F.; Cheng, Y.; Yang, H. Kinematic analysis and optimization design of vibration-type device for Panax notoginseng root-soil separation. J. Northwest A F Univ. (Nat. Sci. Ed.) 2018, 46, 146–154. [Google Scholar] [CrossRef]
- Wang, F.; Wen, B.; Xie, X.; Xie, K.; Guo, S.; Zhang, Z. Operation Mechanism Analysis and Parameter Optimization of Conveying and Separating Device of Panax notoginseng Harvester. J. Agric. Mach. 2023, 54, 201–211+259. [Google Scholar] [CrossRef]
- Xue, H. The Whole Machine Design and Simulation Test of Key Components of Panax notoginseng Combined Harvester; Kunming University of Science and Technology: Kunming, China, 2022. [Google Scholar] [CrossRef]
- Song, J.; Qiu, S.; Wang, X. Design and test on 4B-1200 type bulbus Fritillariae ussuriensis medicinal material harvester. J. Agric. Eng. 2015, 31, 34–41. Available online: https://www.ingentaconnect.com/content/tcsae/tcsae/2015/00000031/00000008/art00006# (accessed on 5 August 2024).
- Du, C.; Fang, W.; Han, D.; Chen, X.; Wang, X. Design and Experimental Study of a Biomimetic Pod-Pepper-Picking Drum Based on Multi-Finger Collaboration. Agriculture 2024, 14, 314. [Google Scholar] [CrossRef]
- Yuan, L.; Tang, Z.; Liu, S.; Wang, T.; Zhao, D. Design for Copying Grouser and Bionic Convex Hull Patterns on Track Surfaces of Crawler Combine Harvesters. Agriculture 2024, 14, 1079. [Google Scholar] [CrossRef]
- Lu, Q.; Zhao, J.; Liu, L.; Liu, Z.; Wang, C. Design and Experiment of a Soil-Covering and-Pressing Device for Planters. Agriculture 2024, 14, 1040. [Google Scholar] [CrossRef]
- Chen, D.; Xu, Y.; Song, Y.; Xin, M.; Wu, L.; Kong, A.; Wang, H.; Dai, P.; Yu, H. A Bionic walking wheel for enhanced trafficability in paddy fields with muddy soil. Biomimetics 2024, 9, 68. [Google Scholar] [CrossRef]
- Ding, R.; Cao, C.; Zhan, C.; Lou, S.; Sun, S. Design and experiment of bionic-impact type pecan shell breaker. J. Agric. Eng. 2017, 33, 257–264. [Google Scholar] [CrossRef]
- Zhao, Z. Research on Pecking Mechanism Based on the Motion Mechanism of Woodpecker; Shenyang University of Architecture: Shenyang, China, 2019. [Google Scholar] [CrossRef]
- Sun, H. Research on the Bionic Peck Sampling Mechanism Based on Woodpecker; Northeastern University: Shenyang, China, 2015. [Google Scholar]
- Zhu, Z. The Mechanical Principle of Anti-Shock of Woodpecker Head under Dynamic Impact; Dalian University of Technology: Dalian, China, 2015. [Google Scholar]
- Ni, Y.; Xu, P.; Niu, X.; Wang, L.; Fan, Y. Microstructure of Woodpecker’s Cranial Bone Based on Micro-computed Tomography. Chin. Sci. Life Sci. 2014, 44, 578–583. [Google Scholar] [CrossRef]
- Yan, S. Design and Experiment of Drum Root Soil Separation Device for Codonopsis pilosula Harvest; Shanxi Agricultural University: Jinzhong, China, 2022; Available online: https://link.oversea.cnki.net/doi/10.27285/d.cnki.gsxnu.2022.000449 (accessed on 5 August 2024).
- Xie, K.; Zhang, Z.; Wang, F.; Jiang, S.; Wang, C. Mathematical model construction and verification of soil and Panax notoginseng root adhesion. J. Agric. Eng. 2022, 38, 131–141. [Google Scholar] [CrossRef]
- Li, Z. Design and Experiment of the Control System of Automatic Production Line for Pecan Shell; Anhui Agricultural University: Hefei, China, 2018. [Google Scholar]
- Duan, J.; Chen, B.; Liu, G.; Jin, M.; Xu, X.; Yang, Z.; Fu, H. Mechanical properties and bruise susceptibility of green bananas under repeated impacts. J. Agric. Eng. 2023, 39, 258–266. [Google Scholar] [CrossRef]
- Stark, R.D.; Dodenhoff, D.J.; Johnson, E.V. A Quantitative Analysis of Woodpecker Drumming. Condor 1998, 100, 350–356. [Google Scholar] [CrossRef]
- Vincent, J.F.V.; Sahinkaya, M.N.; O’shea, W. A woodpecker hammer. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2007, 221, 1141–1147. [Google Scholar] [CrossRef]
- May, P.R.A.; Fuster, J.M.; Haber, J.; Hirschman, A. Woodpecker drilling behavior. An endorsement of the rotational theory of impact brain injury. Arch. Neurol. 1979, 36, 370–373. [Google Scholar] [CrossRef]
- Yoon, S.H.; Park, S. A mechanical analysis of woodpecker drumming and its application to shock-absorbing systems. Bioinspiration Biomim. 2011, 6, 016003. [Google Scholar] [CrossRef]
- Collins, M.D. Periodic and transient motions of large woodpeckers. Sci. Rep. 2017, 7, 12551. [Google Scholar] [CrossRef]
- Qian, Z.; Zhang, D. Frictional impact dynamics of flexible manipulator arms. J. Vib. Eng. 2015, 28, 879–886. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Y.; Chen, Y.; Liang, Z.; Liu, L. Impact mechanical characteristics analysis of rice grain. Trans. Chin. Soc. Agric. Mach. 2013, 44, 88–92. [Google Scholar] [CrossRef]
- Wang, F.; Cui, J.; Hu, Z. Analytical design method of swing double rollers follower disc came with variable length of equivalent pendulum rod. J. Mech. Transm. 2014, 28, 73–76. [Google Scholar] [CrossRef]
- Ye, B.; Li, L.; Yu, G.; Liu, A.; Cai, D. Design and test on cam mechanism of seedling pick-up arm for vegetable transplanter for pot seedling. Trans. Chin. Soc. Agric. Eng. 2014, 30, 21–29. [Google Scholar] [CrossRef]



| Parameters | Values/Formal |
|---|---|
| Working method | Bionic percussive |
| Auxiliary power/kW | 0.6 |
| Matching power speed/(r·min−1) | 300 |
| Dimensions (L × W × H)/(mm × mm × mm) | 650 × 565 × 480 |
| Overall quality of the machine/kg | 15.0 |
| Speed range of camshaft/(r·min−1) | 60–120 |
| Quality range of striking hammer/kg | 0.6–1.0 |
| Swing angle range of striking arm/(°) | 35–55 |
| Working efficiency of soil removal device/(kg·h−1) | 40–50 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| The length of striking arm lAC/mm | 488 | The mass of the striking arm m1/kg | 0.3 |
| The length of swing lever lOC/mm | 135 | The mass of the striking hammer m2/kg | 0.6 to 1.0 |
| lOA:lOC | 2.6:1 | The mass of the roller m3/kg | 0.1 |
| Distance from the center of mass of the striking arm to the center of rotation lOB/mm | 109 | The rotation speed of the cam n0/(r/min) | 60 to 120 |
| Coefficient of spring elasticity k/(N/mm) | 0.1 | The swing angle of the striking arm θ/(°) | 35 to 55 |
| Distance from spring to center of rotation lOD/mm | 60 | ω2/(r/min) | 44 to 80 |
| Cam Rotation Angle of Push Transition Segment φα1/(°) | Cam Rotation Angle of Push Segment φα2/(°) | Cam Rotation Angle of Distant Rest Segment φα3/(°) | The Initial Swing Angle of the Striking Arm Ψ0/(°) | The Swing Angle of Push Segment Ψm1/(°) | Centre Distance lOE/mm | Base Circle Radius r0/mm | Roller Radius rg/mm |
|---|---|---|---|---|---|---|---|
| 40 | 75 | 5 | 13 | 27 | 210 | 60 | 15 |
| Level | The Mass of the Striking Hammer X1/kg | The Swing Angle of the Striking Arm X2/° | The Rotation Speed of the Cam X3/r/min |
|---|---|---|---|
| −1 | 0.6 | 35 | 60 |
| 0 | 0.8 | 45 | 90 |
| 1 | 1.0 | 55 | 120 |
| Experiment Number | Factors | Y1 | Y2 | ||
|---|---|---|---|---|---|
| X2 | X3 | ||||
| 1 | 0.6 | 35 | 90 | 82.56 | 40.3532 |
| 2 | 1.0 | 35 | 90 | 89.01 | 34.8355 |
| 3 | 0.6 | 55 | 90 | 86.26 | 36.5526 |
| 4 | 1.0 | 55 | 90 | 89.46 | 35.4932 |
| 5 | 0.6 | 45 | 60 | 82.97 | 34.9398 |
| 6 | 1.0 | 45 | 60 | 89.17 | 35.5581 |
| 7 | 0.6 | 45 | 120 | 85.72 | 35.7339 |
| 8 | 1.0 | 45 | 120 | 88.39 | 29.7395 |
| 9 | 0.8 | 35 | 60 | 85.44 | 37.6093 |
| 10 | 0.8 | 55 | 60 | 86.83 | 35.9547 |
| 11 | 0.8 | 35 | 120 | 85.79 | 34.9341 |
| 12 | 0.8 | 55 | 120 | 89.09 | 32.5484 |
| 13 | 0.8 | 45 | 90 | 90.23 | 31.3066 |
| 14 | 0.8 | 45 | 90 | 89.56 | 32.8719 |
| 15 | 0.8 | 45 | 90 | 90.73 | 31.5675 |
| 16 | 0.8 | 45 | 90 | 89.82 | 32.0893 |
| 17 | 0.8 | 45 | 90 | 88.96 | 31.3066 |
| Source | Square Sum | Degrees of Freedom | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Model | 96.80 | 9 | 10.76 | 38.43 | <0.0001 | ** |
| X1 | 42.87 | 1 | 42.87 | 153.19 | <0.0001 | ** |
| X2 | 9.77 | 1 | 9.77 | 34.90 | 0.0006 | ** |
| X3 | 2.62 | 1 | 2.62 | 9.37 | 0.0183 | * |
| X1X2 | 2.64 | 1 | 2.64 | 9.44 | 0.0180 | * |
| X1X3 | 3.12 | 1 | 3.12 | 11.13 | 0.0125 | * |
| X2X3 | 0.9120 | 1 | 0.9120 | 3.26 | 0.1140 | |
| X12 | 11.20 | 1 | 11.20 | 40.03 | 0.0004 | ** |
| X22 | 8.33 | 1 | 8.33 | 29.75 | 0.0010 | ** |
| X32 | 11.69 | 1 | 11.69 | 41.77 | 0.0003 | ** |
| Residual | 1.96 | 7 | 0.2799 | |||
| Lost Proposal | 0.1637 | 3 | 0.0546 | 0.1216 | 0.9426 | |
| Pure Error | 1.80 | 4 | 0.4489 | |||
| Aggregate | 98.76 | 16 |
| Source | Square Sum | Degrees of Freedom | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Model | 115.55 | 9 | 12.84 | 41.03 | <0.0001 | ** |
| X1 | 17.86 | 1 | 17.86 | 57.08 | 0.0001 | ** |
| X2 | 6.45 | 1 | 6.45 | 20.61 | 0.0027 | ** |
| X3 | 15.42 | 1 | 15.42 | 49.28 | 0.0002 | ** |
| X1X2 | 4.97 | 1 | 4.97 | 15.88 | 0.0053 | ** |
| X1X3 | 10.93 | 1 | 10.93 | 34.94 | 0.0006 | ** |
| X2X3 | 0.1336 | 1 | 0.1336 | 0.4271 | 0.5343 | |
| X12 | 14.50 | 1 | 14.50 | 46.34 | 0.0003 | ** |
| X22 | 41.11 | 1 | 41.11 | 131.38 | < 0.0001 | ** |
| X32 | 0.4013 | 1 | 0.4013 | 1.28 | 0.2947 | |
| Residual | 2.19 | 7 | 0.3129 | |||
| Lost Proposal | 0.4206 | 3 | 0.1402 | 0.3169 | 0.8139 | |
| Pure Error | 1.77 | 4 | 0.4424 | |||
| Aggregate | 117.74 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Du, L.; Xie, Z.; Zhong, W.; Xu, D.; Bian, W.; Jiang, L.; Wang, T.; Wu, L. Design and Experimental of the Soil Removal Device for Root-Soil Complex of Gentian Imitating the Percussion of Woodpeckers. Biomimetics 2024, 9, 479. https://doi.org/10.3390/biomimetics9080479
Cui H, Du L, Xie Z, Zhong W, Xu D, Bian W, Jiang L, Wang T, Wu L. Design and Experimental of the Soil Removal Device for Root-Soil Complex of Gentian Imitating the Percussion of Woodpeckers. Biomimetics. 2024; 9(8):479. https://doi.org/10.3390/biomimetics9080479
Chicago/Turabian StyleCui, Hongguang, Li Du, Zhanqiu Xie, Wei Zhong, Dehui Xu, Weiming Bian, Long Jiang, Tiejun Wang, and Liyan Wu. 2024. "Design and Experimental of the Soil Removal Device for Root-Soil Complex of Gentian Imitating the Percussion of Woodpeckers" Biomimetics 9, no. 8: 479. https://doi.org/10.3390/biomimetics9080479
APA StyleCui, H., Du, L., Xie, Z., Zhong, W., Xu, D., Bian, W., Jiang, L., Wang, T., & Wu, L. (2024). Design and Experimental of the Soil Removal Device for Root-Soil Complex of Gentian Imitating the Percussion of Woodpeckers. Biomimetics, 9(8), 479. https://doi.org/10.3390/biomimetics9080479






