Swifts Form V-Shaped Wings While Dipping in Water to Fine-Tune Balance
Abstract
1. Introduction
2. Materials and Methods
2.1. Image Processing
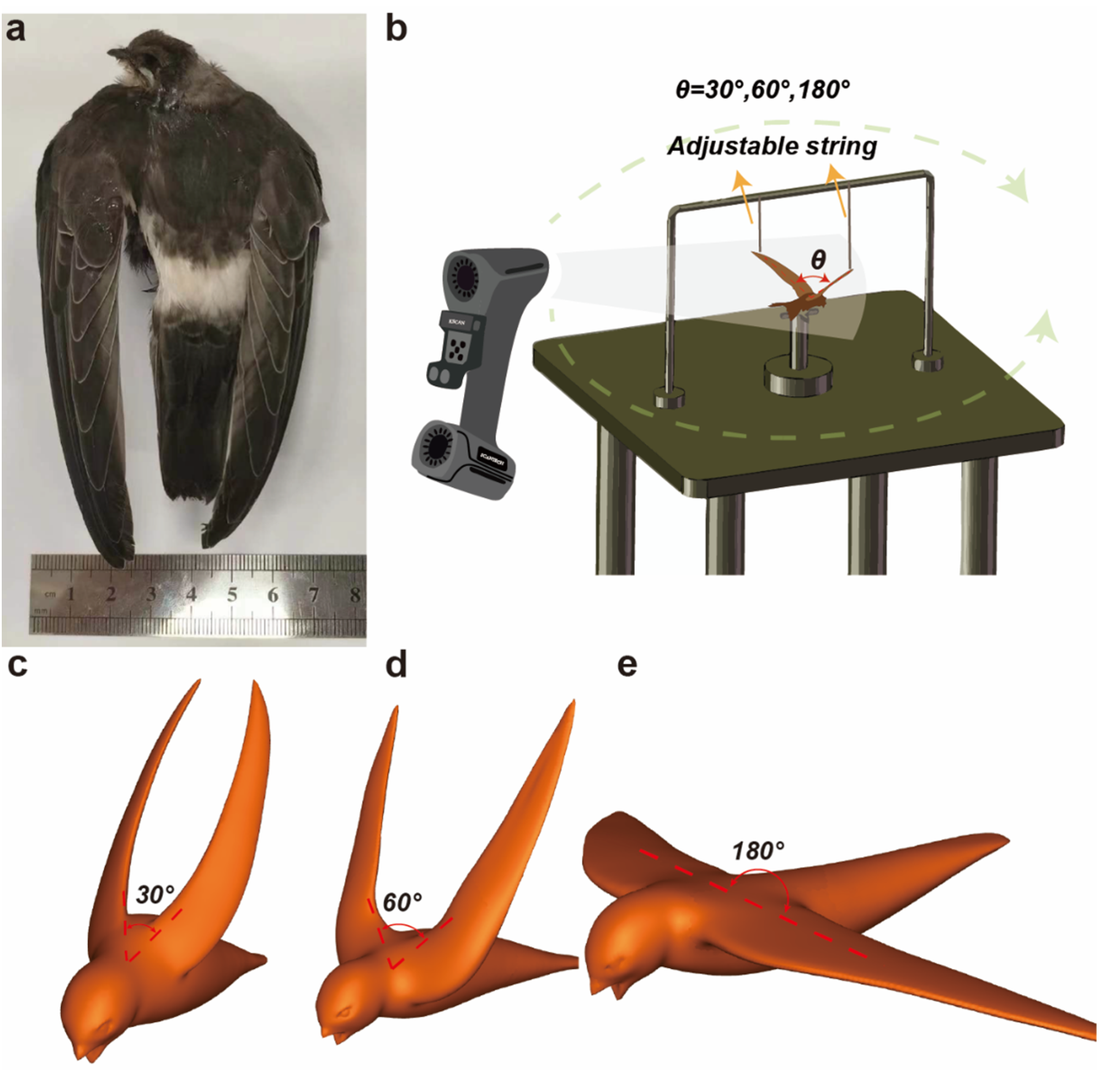
2.2. 3D Scans
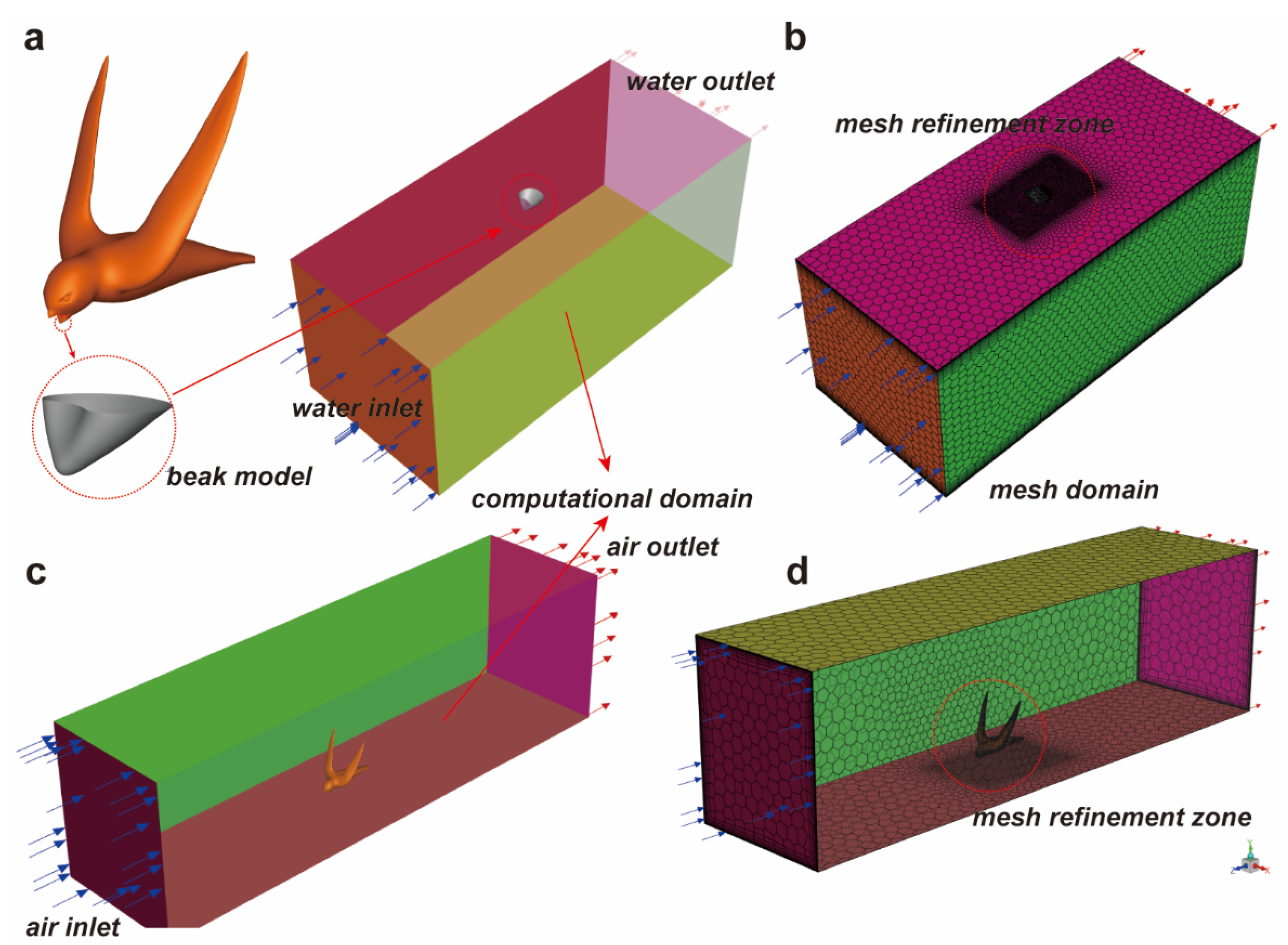
2.3. CFD Simulation
2.4. Computation Settings
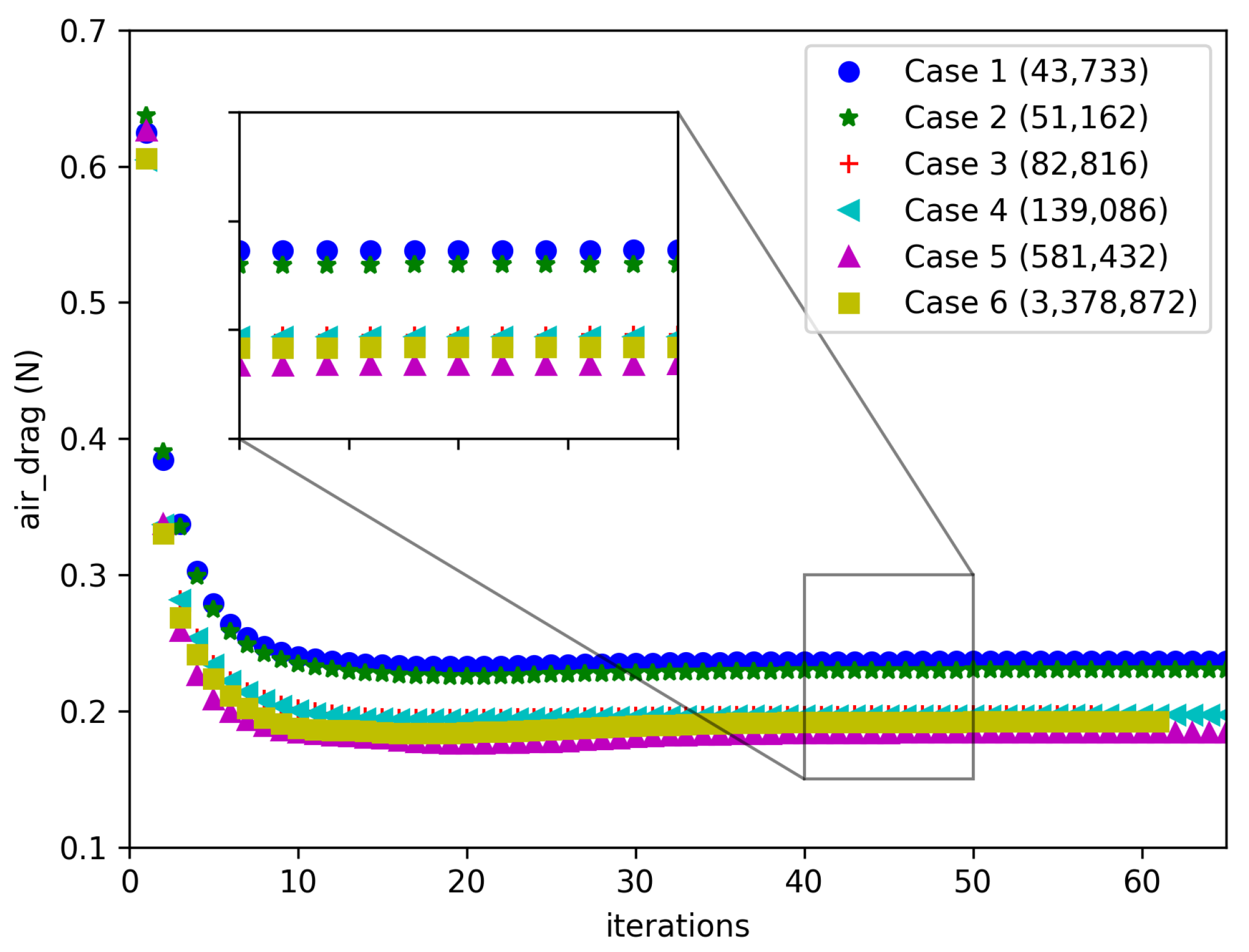
2.5. Mesh Independence
3. Results
3.1. Feeding Behavior
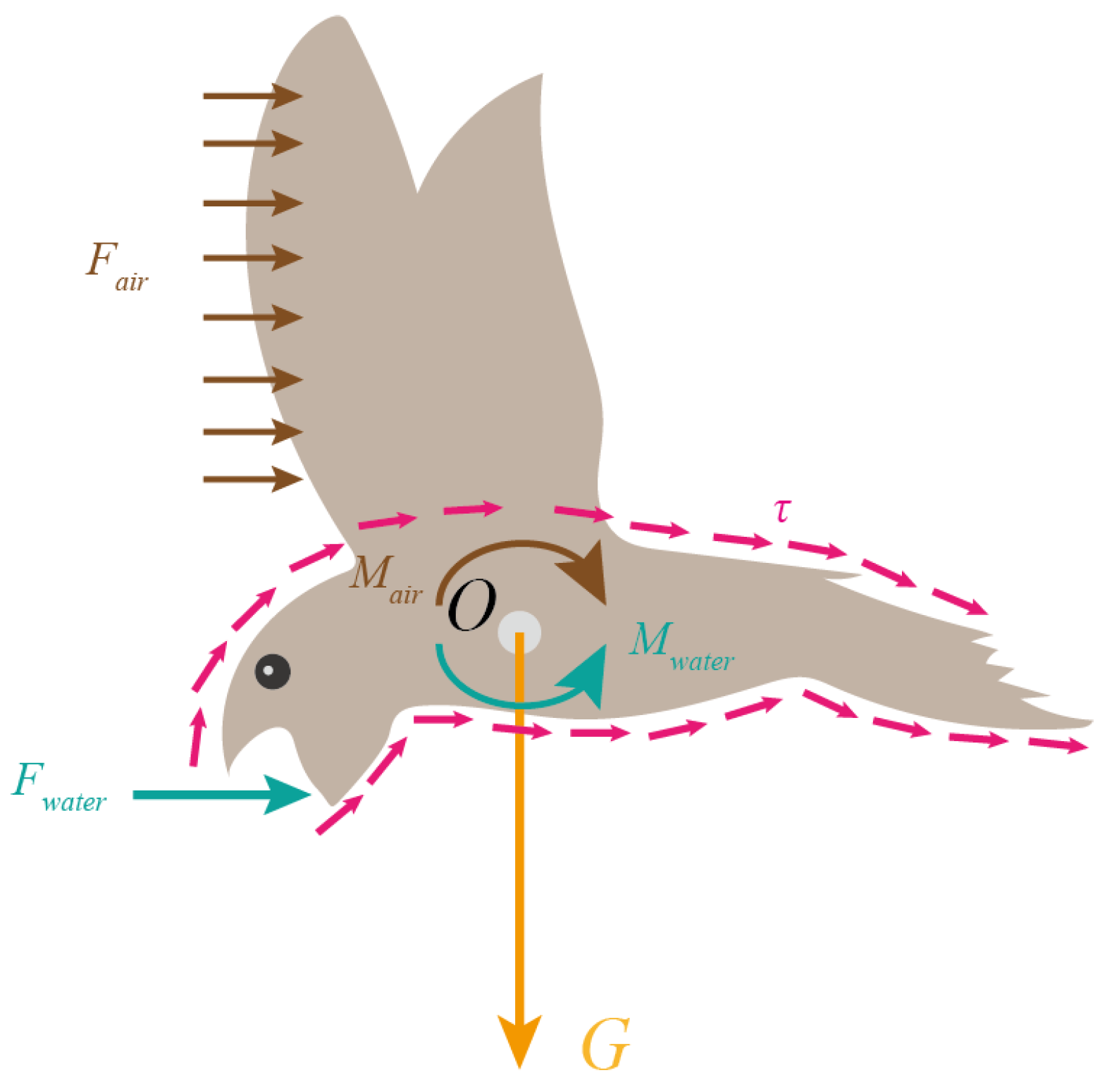
3.2. Force Analysis
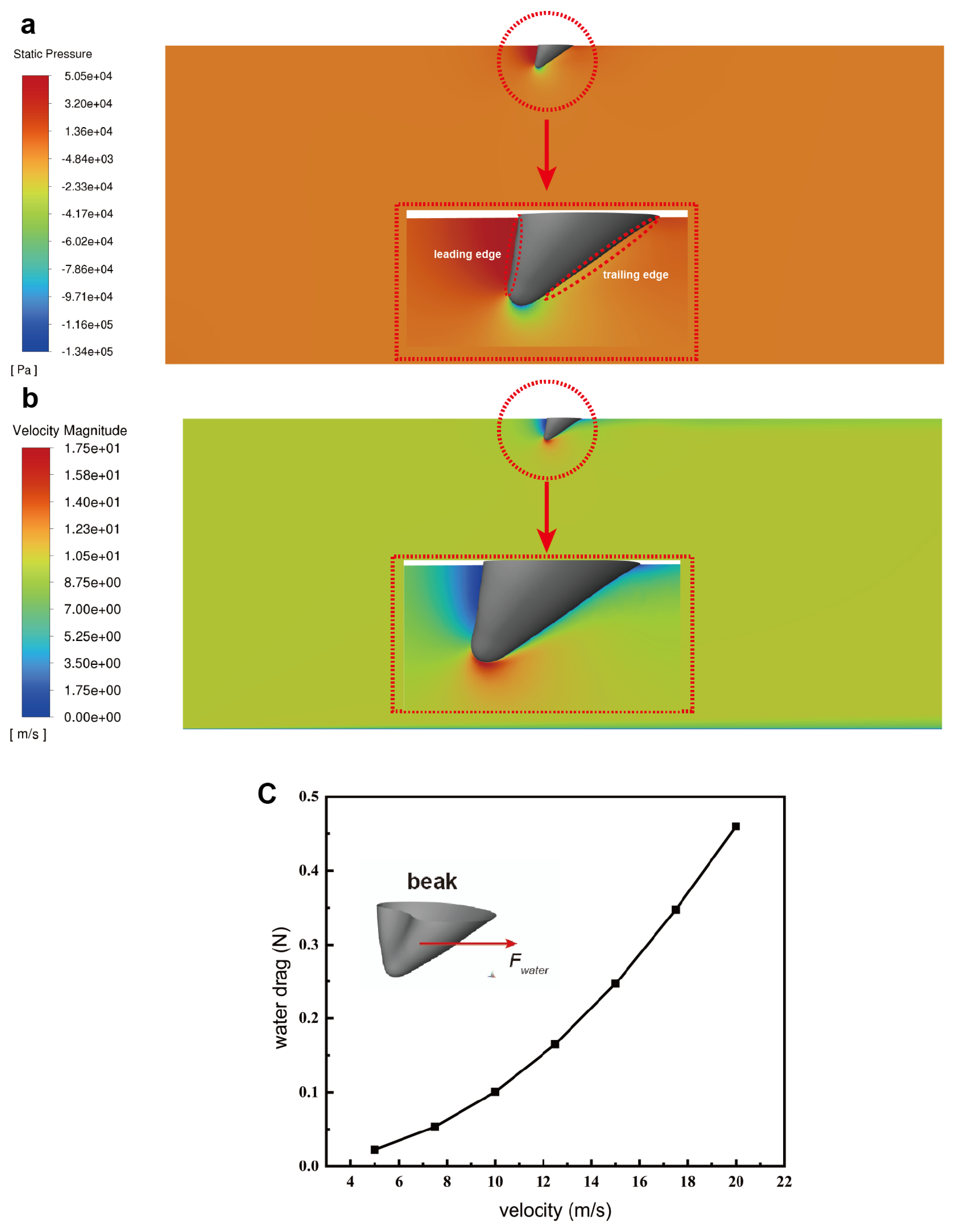
3.3. Water Resistance
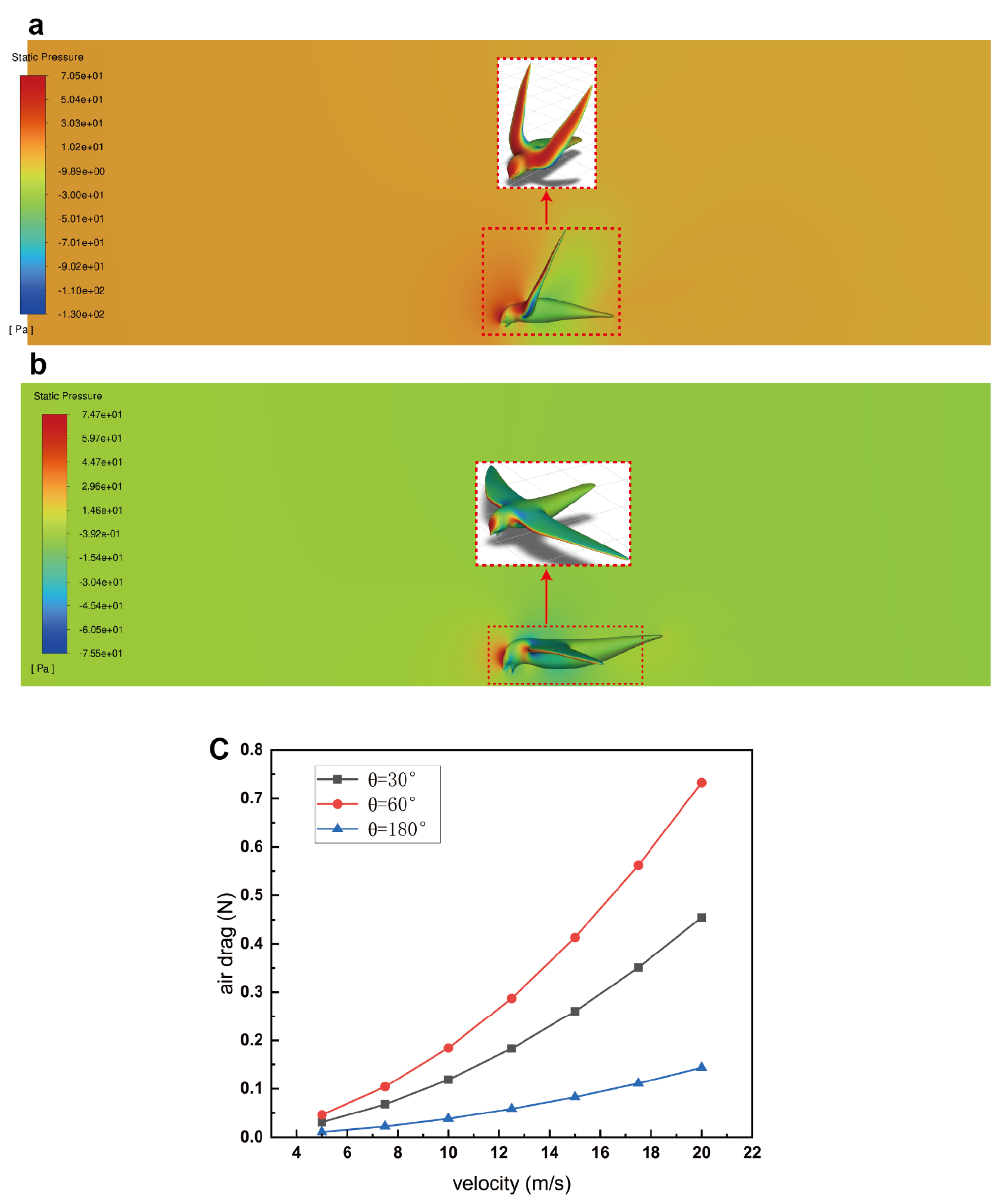
3.4. Air Drag
3.5. Residual Torque
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Lentink, D.; Müller, U.K.; Stamhuis, E.; De Kat, R.; Van Gestel, W.; Veldhuis, L.; Henningsson, P.; Hedenström, A.; Videler, J.J.; Van Leeuwen, J.L. How swifts control their glide performance with morphing wings. Nature 2007, 446, 1082–1085. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Song, B.; Yang, W.; Yang, X.; Xue, D.; Lang, X. A brief review on aerodynamic performance of wingtip slots and research prospect. J. Bionic Eng. 2021, 18, 1255–1279. [Google Scholar] [CrossRef]
- Hedenström, A.; Norevik, G.; Warfvinge, K.; Andersson, A.; Bäckman, J.; Åkesson, S. Annual 10-month aerial life phase in the common swift Apus apus. Curr. Biol. 2016, 26, 3066–3070. [Google Scholar] [CrossRef] [PubMed]
- Alerstam, T.; Hedenström, A.; Åkesson, S. Long-distance migration: Evolution and determinants. Oikos 2003, 103, 247–260. [Google Scholar] [CrossRef]
- Beason, J.P.; Gunn, C.; Potter, K.M.; Sparks, R.A.; Fox, J.W. The Northern Black Swift: Migration path and wintering area revealed. Wilson J. Ornithol. 2012, 124, 1–8. [Google Scholar] [CrossRef]
- Hedenström, A.; Alerstam, T. How fast can birds migrate? J. Avian Biol. 1998, 424–432. [Google Scholar] [CrossRef]
- Ruaux, G.; Monmasson, K.; Hedrick, T.L.; Lumineau, S.; de Margerie, E. Drink safely: Common swifts (Apus apus) dissipate mechanical energy to decrease flight speed before touch-and-go drinking. J. Exp. Biol. 2023, 226, jeb244961. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhao, X.; Wu, L.; Mu, T.; Yu, F.; Kearsley, L.; Liang, X.; Fu, J.; Hou, X.; Peng, P.; et al. A 30,000-km journey by Apus apus pekinensis tracks arid lands between northern China and south-western Africa. Mov. Ecol. 2022, 10, 29. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Peng, X.; Li, J.; Chen, Y. A comparative study on the performance of typical types of bionic groove dry gas seal based on bird wing. J. Bionic Eng. 2016, 13, 324–334. [Google Scholar] [CrossRef]
- Åkesson, S.; Klaassen, R.; Holmgren, J.; Fox, J.W.; Hedenström, A. Migration routes and strategies in a highly aerial migrant, the common swift Apus apus, revealed by light-level geolocators. PLoS ONE 2012, 7, e41195. [Google Scholar] [CrossRef] [PubMed]
- Hedrick, T.L.; Pichot, C.; de Margerie, E. Gliding for a free lunch: Biomechanics of foraging flight in common swifts (Apus apus). J. Exp. Biol. 2018, 221, jeb186270. [Google Scholar] [CrossRef] [PubMed]
- Lentink, D.; De Kat, R. Gliding swifts attain laminar flow over rough wings. PLoS ONE 2014, 9, e99901. [Google Scholar] [CrossRef] [PubMed]
- Azuma, A. The Biokinetics of Flying and Swimming; Springer Science & Business Media: Tokyo, Japan, 2012. [Google Scholar]
- Henningsson, P.; Johansson, L.C.; Hedenström, A. How swift are swifts Apus apus? J. Avian Biol. 2010, 41, 94–98. [Google Scholar] [CrossRef]
- de Margerie, E.; Simonneau, M.; Caudal, J.P.; Houdelier, C.; Lumineau, S. 3D tracking of animals in the field using rotational stereo videography. J. Exp. Biol. 2015, 218, 2496–2504. [Google Scholar] [CrossRef] [PubMed]
- Hedenström, A.; Alerstam, T.; Green, M.; Gudmundsson, G.A. Adaptive variation of airspeed in relation to wind, altitude and climb rate by migrating birds in the Arctic. Behav. Ecol. Sociobiol. 2002, 52, 308–317. [Google Scholar] [CrossRef]
- Alerstam, T.; Lindström, Å. Optimal bird migration: The relative importance of time, energy, and safety. In Bird Migration: Physiology and Ecophysiology; Springer: Berlin/Heidelberg, Germany, 1990; pp. 331–351. [Google Scholar]
- Hedenström, A.; Åkesson, S. Adaptive airspeed adjustment and compensation for wind drift in the common swift: Differences between day and night. Anim. Behav. 2017, 127, 117–123. [Google Scholar] [CrossRef]
- Hedenström, A.; Norevik, G.; Boano, G.; Andersson, A.; Bäckman, J.; Åkesson, S. Flight activity in pallid swifts Apus pallidus during the non-breeding period. J. Avian Biol. 2019, 50. [Google Scholar] [CrossRef]
- Henningsson, P.; Karlsson, H.; Bäckman, J.; Alerstam, T.; Hedenström, A. Flight speeds for different seasons: The case of the swift. Proc. R. Soc. Lond. B 2009, 276, 2395–2401. [Google Scholar]
- Liechti, F.; Witvliet, W.; Weber, R.; Bächler, E. First evidence of a 200-day non-stop flight in a bird. Nat. Commun. 2013, 4, 2554. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, Y.; Liu, Y. Using light-level geolocations to monitor incubation behaviour of a cavity-nesting bird Apus apus pekinensis. Avian Res. 2021, 12, 1–6. [Google Scholar] [CrossRef]
- Raju, A.K.; Sreenath, K. ‘Eastern’ Common Swift Apus apus pekinensis in the Lakshadweep Archipelago, with identification notes on juvenile birds. Indian Birds 2020, 15, 143–144. [Google Scholar]
- Thorup, K. First record of Pallid Swift Apus pallidus in Denmark and of ssp. illyricus in northern Europe. Dan. Ornitol. Foren. Tidsskr. 2001, 95, 169–172. [Google Scholar]
- Ahmed, R.; Adriaens, P. Common, Asian Common and Pallid Swift: Colour nomenclature, moult and identification. Dutch Bird. 2010, 32, 97–105. [Google Scholar]
- Roberts, H.; Campbell, O. Proving the occurrence of Common Swift Apus apus pekinensis in the United Arab Emirates. Sandgrouse 2015, 37, 79–86. [Google Scholar]
- Grieve, A.; Kirwan, G.M. Studies of Socotran birds VII. Forbes-Watson’s Swift Apus berliozi in Arabia—the answer to the mystery of the ‘Dhofar swift’. Bull. Br. Ornithol. Club 2012, 132, 194–206. [Google Scholar]
- Chang, C.y.; Zhang, Z.w.; Chen, X.d. Ultrastructural observation of the feather of Apus pekinensis. J.-Chin. Electron Microsc. Soc. 2003, 22, 496–497. [Google Scholar]
- Beaumont, F.; Murer, S.; Bogard, F.; Polidori, G. Aerodynamic Interaction of Migratory Birds in Gliding Flight. Fluids 2023, 8, 50. [Google Scholar] [CrossRef]
- Song, J.; Cheney, J.A.; Usherwood, J.R.; Bomphrey, R.J. Virtual manipulation of bird tail postures demonstrates drag minimisation when gliding. bioRxiv 2020. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, S.; Peng, Z.; Yang, H.; Liu, H.; Liu, Y.; Wu, J. Swifts Form V-Shaped Wings While Dipping in Water to Fine-Tune Balance. Biomimetics 2024, 9, 457. https://doi.org/10.3390/biomimetics9080457
Cui S, Peng Z, Yang H, Liu H, Liu Y, Wu J. Swifts Form V-Shaped Wings While Dipping in Water to Fine-Tune Balance. Biomimetics. 2024; 9(8):457. https://doi.org/10.3390/biomimetics9080457
Chicago/Turabian StyleCui, Shuangwei, Zhongjun Peng, Hua Yang, Hao Liu, Yang Liu, and Jianing Wu. 2024. "Swifts Form V-Shaped Wings While Dipping in Water to Fine-Tune Balance" Biomimetics 9, no. 8: 457. https://doi.org/10.3390/biomimetics9080457
APA StyleCui, S., Peng, Z., Yang, H., Liu, H., Liu, Y., & Wu, J. (2024). Swifts Form V-Shaped Wings While Dipping in Water to Fine-Tune Balance. Biomimetics, 9(8), 457. https://doi.org/10.3390/biomimetics9080457





