An Improved Football Team Training Algorithm for Global Optimization
Abstract
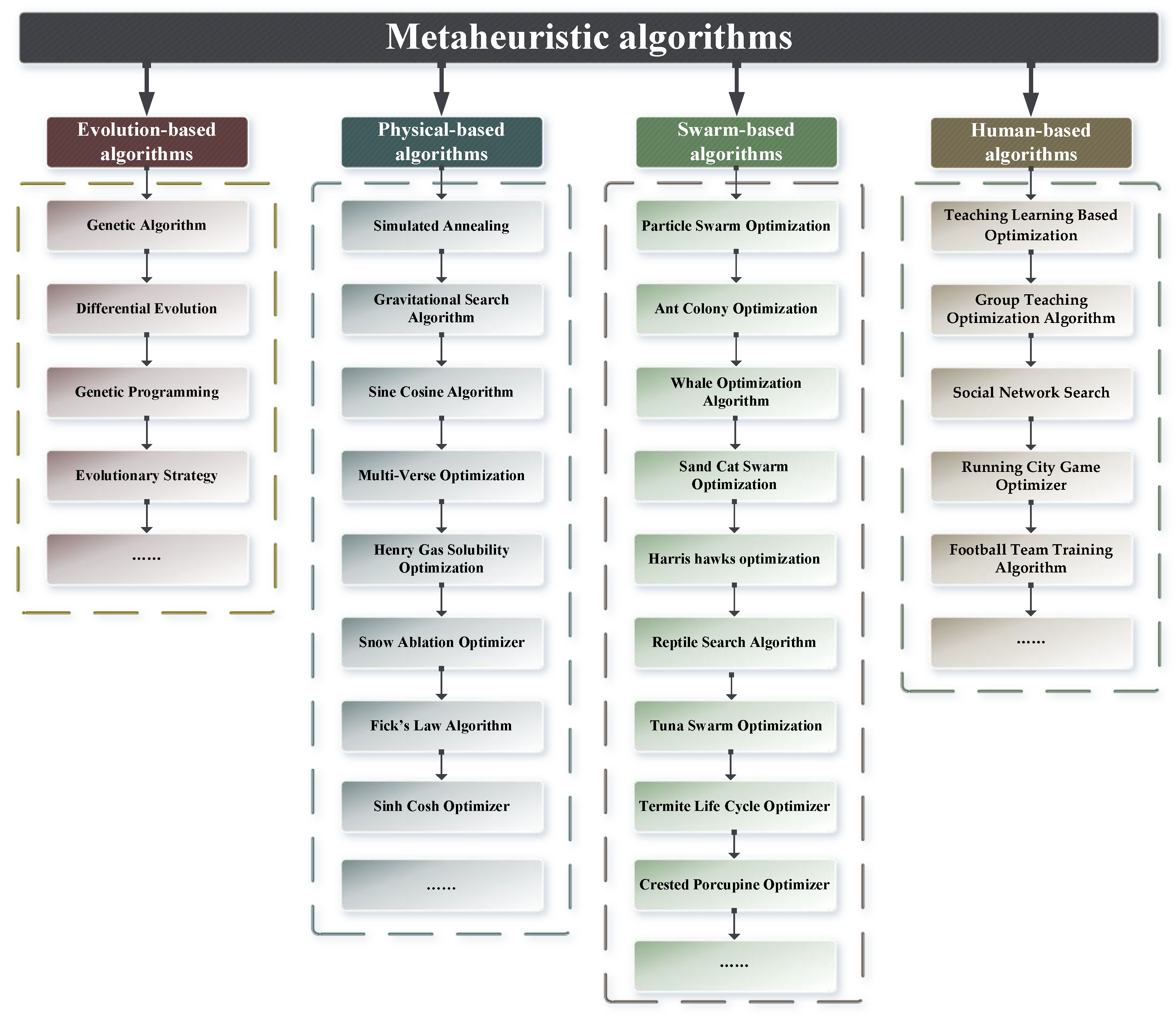
1. Introduction
- This paper presents an FTTA variant based on three strategies, named the IFTTA.
- The introduction of the fitness distance-balanced strategy makes the collective training phase more reasonable and strikes a balance between the exploitation and exploration capabilities of the FTTA.
- In the extra training phase, a non-monopoly search mechanism is integrated to improve the quality of the optimal agent, which effectively prevents the algorithm from falling into the local optimum and improves the overall global optimization performance of the algorithm.
- The population restart mechanism improves the convergence accuracy and population diversity of the algorithm.
- The performance of the IFTTA was compared with seven metaheuristic algorithms including the FTTA in different dimensions (Dim = 10, 30, 50, 100) using the CEC2017 benchmark function. The Wilcoxon rank sum test and the Friedman test were used for the evaluation, thus providing evidence of the efficiency of IFTTA and the validity of the suggested improvements. In addition, the optimal selection of each strategy of the IFTTA is investigated.
- Several engineering-constrained optimization problems confirm the potential of the IFTTA to solve real-world optimization problems.
2. Football Team Training Algorithm (FTTA)
2.1. Initialization Phase
2.2. Collective Training Phase
2.3. Group Training Phase
2.4. Individual Extra Training Phase
3. Proposed IFTTA
3.1. Fitness Distance-Balanced Collective Training Strategy (FTS)
3.2. Non-Monopoly Extra Training Strategy (NTS)
3.3. Population Restart Strategy (PRS)
3.4. Implementation Steps of the IFTTA and Computational Time Complexity
| Algorithm 1 Improved football team training algorithm (IFTTA) |
| 1: Initialization: t = 0, tmax, N. Generate an initial population randomly |
| 2: while (t < tmax) do |
| 3: Calculate the fitness values of each Xi to obtain Xbest and Xworst |
| 4: For i = 1:N |
| 4: Select XFTS using FTS method according to Equation (12) |
| 5: Collective training: update each football player Xi according to Equations (3)–(6) |
| 6: Group training: update each football player Xi according to Equations (7)–(9) |
| 7: Calculate the fitness values of each Xi and Triali |
| 8: End for |
| 9: Find the best player Xbest |
| 10: Individual extra training: update the best player Xbest using NTS method according to Equations (16) and (17) |
| 11: For i = 1:N |
| 12: Update each football player Xi using PRS according to Equation (18) |
| 13: End for |
| 14: Calculate the fitness values of each Xi to obtain Xbest |
| 15: t = t + 1 |
| 14: end while |
4. Numerical Experiments Based on CEC 2017 Test Suite
4.1. Experimental Environment and Parameter Setting
4.2. Test Functions and Performance Metrics
4.3. Determine the Best FTS Method on Test Suite
4.4. Determine the Best NTS Method on Test Suite
4.5. Strategies Effectiveness Analysis
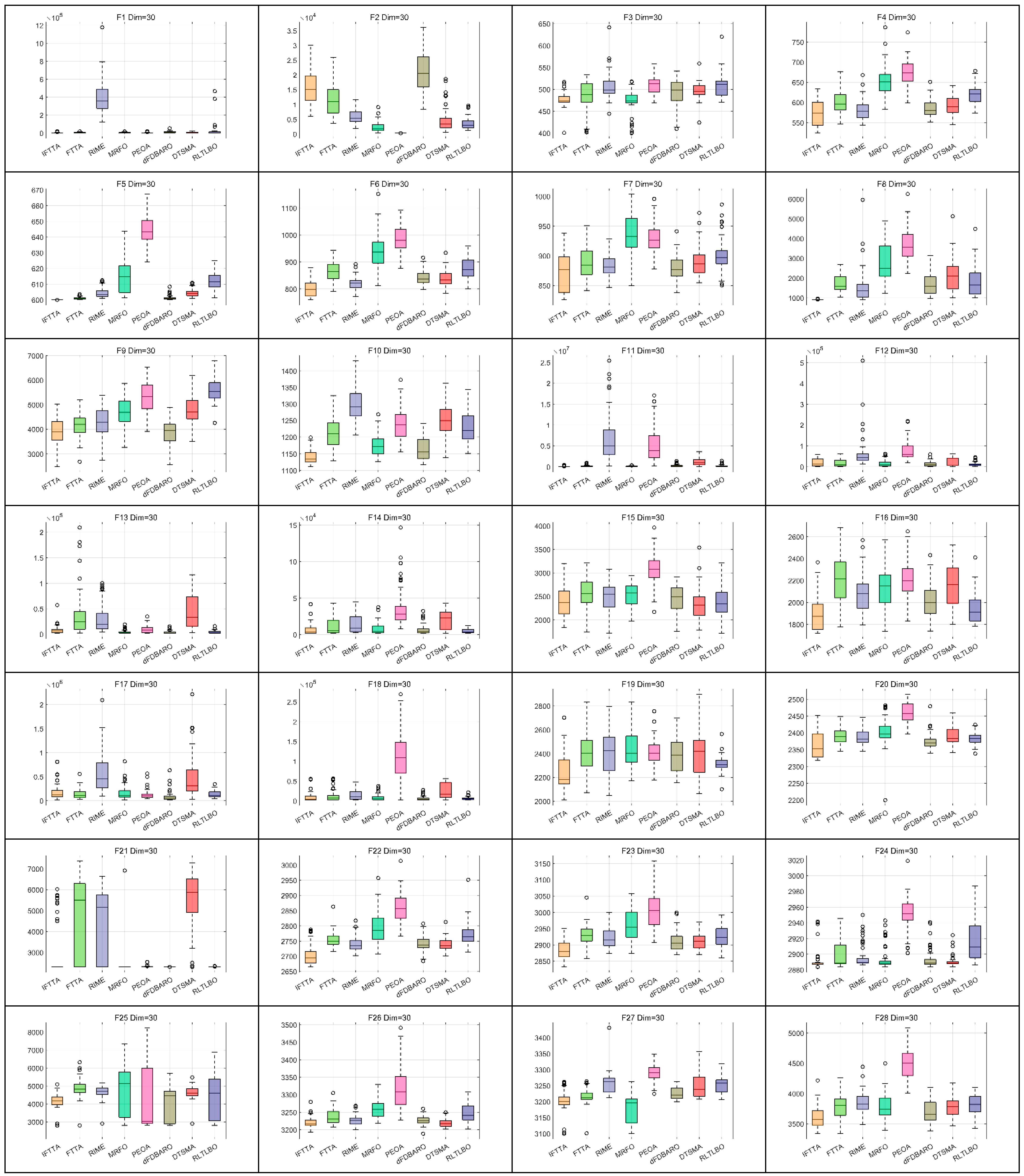
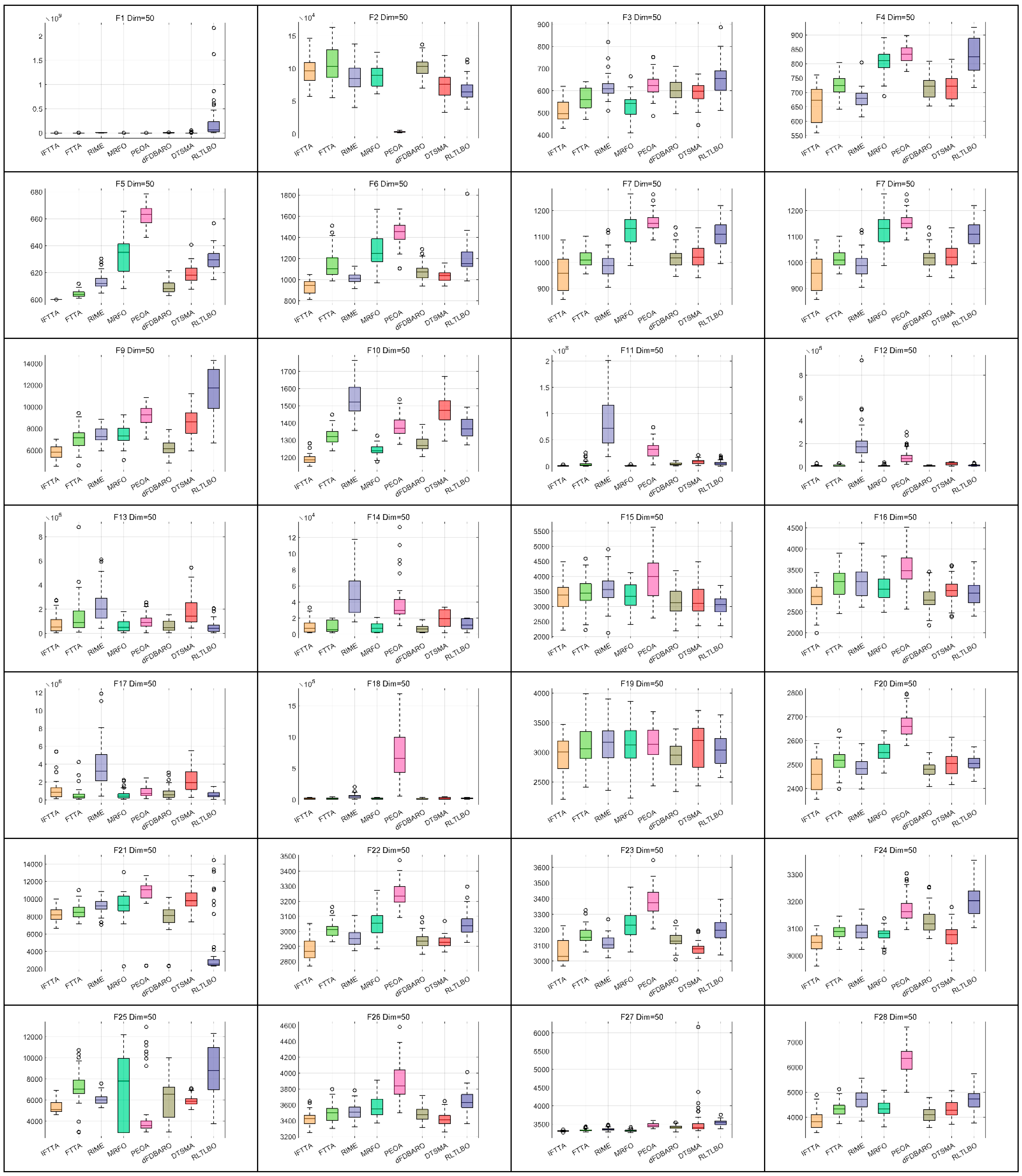
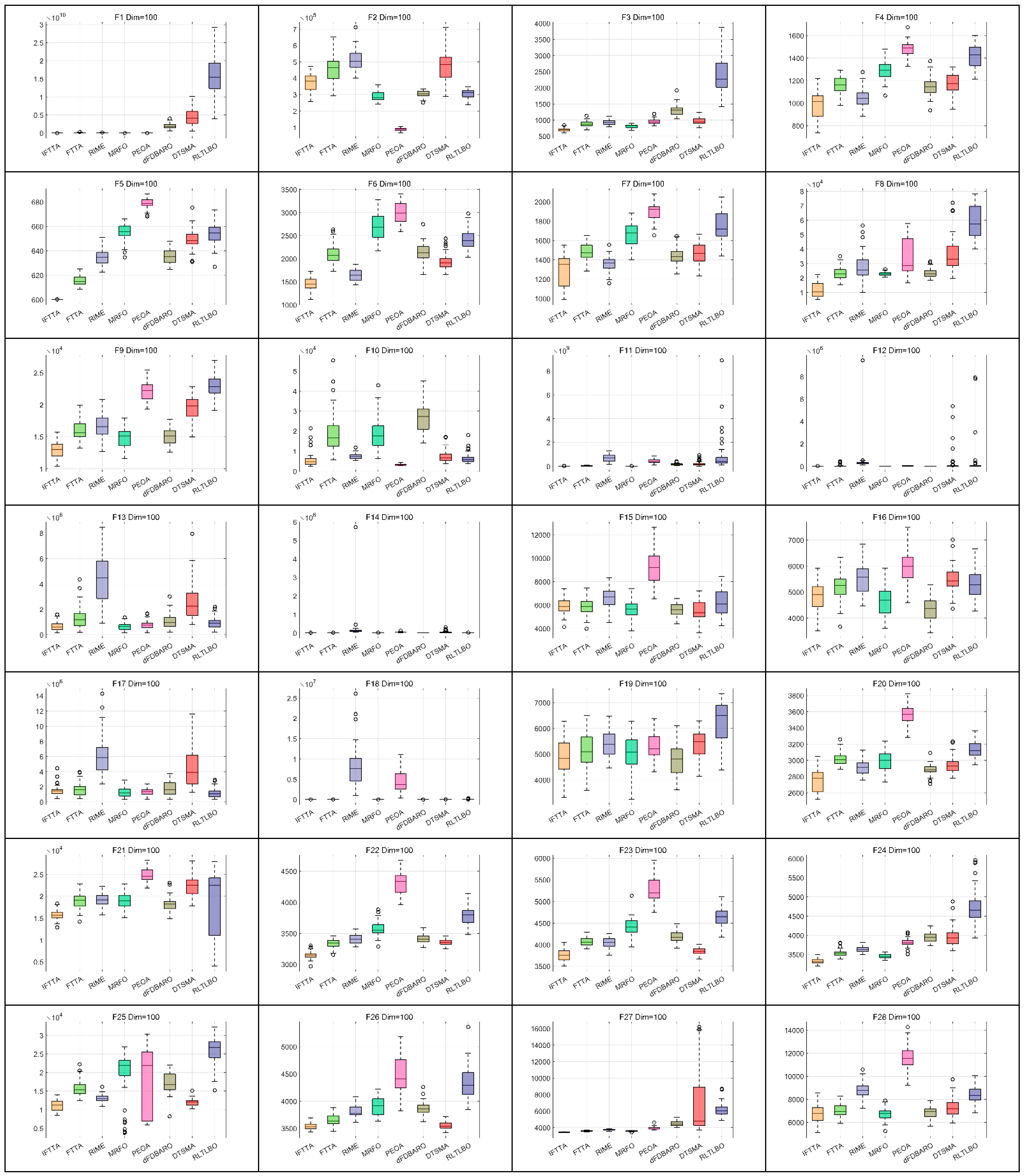
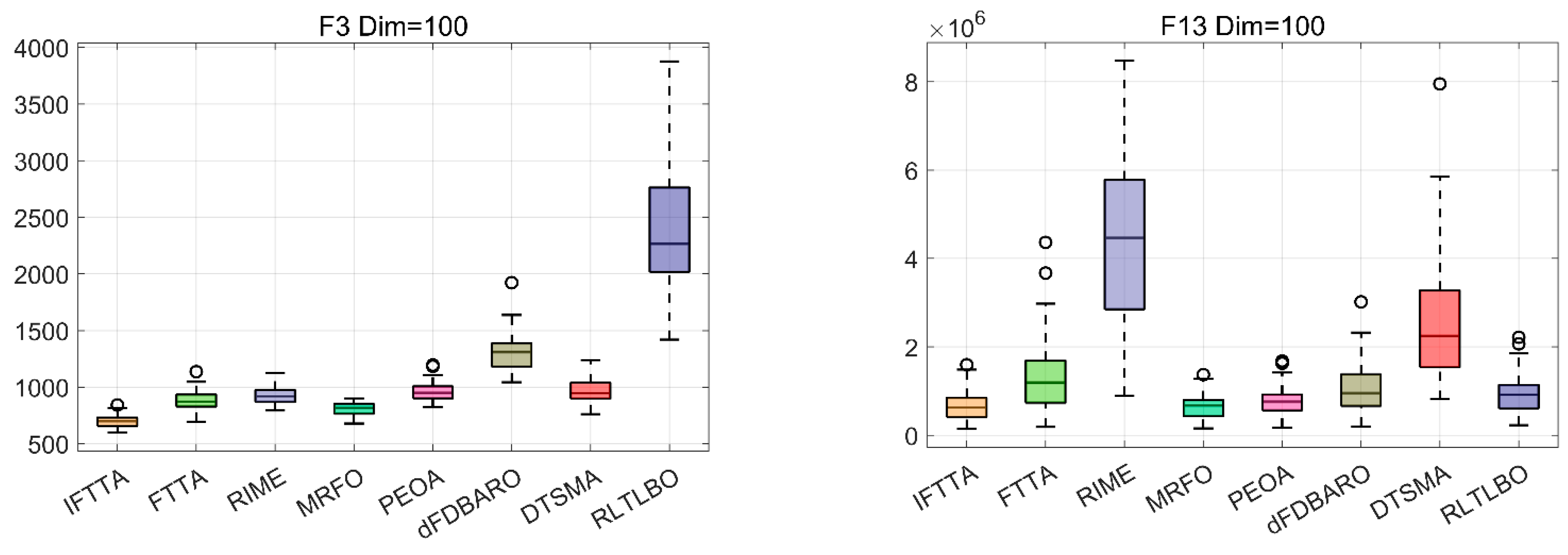
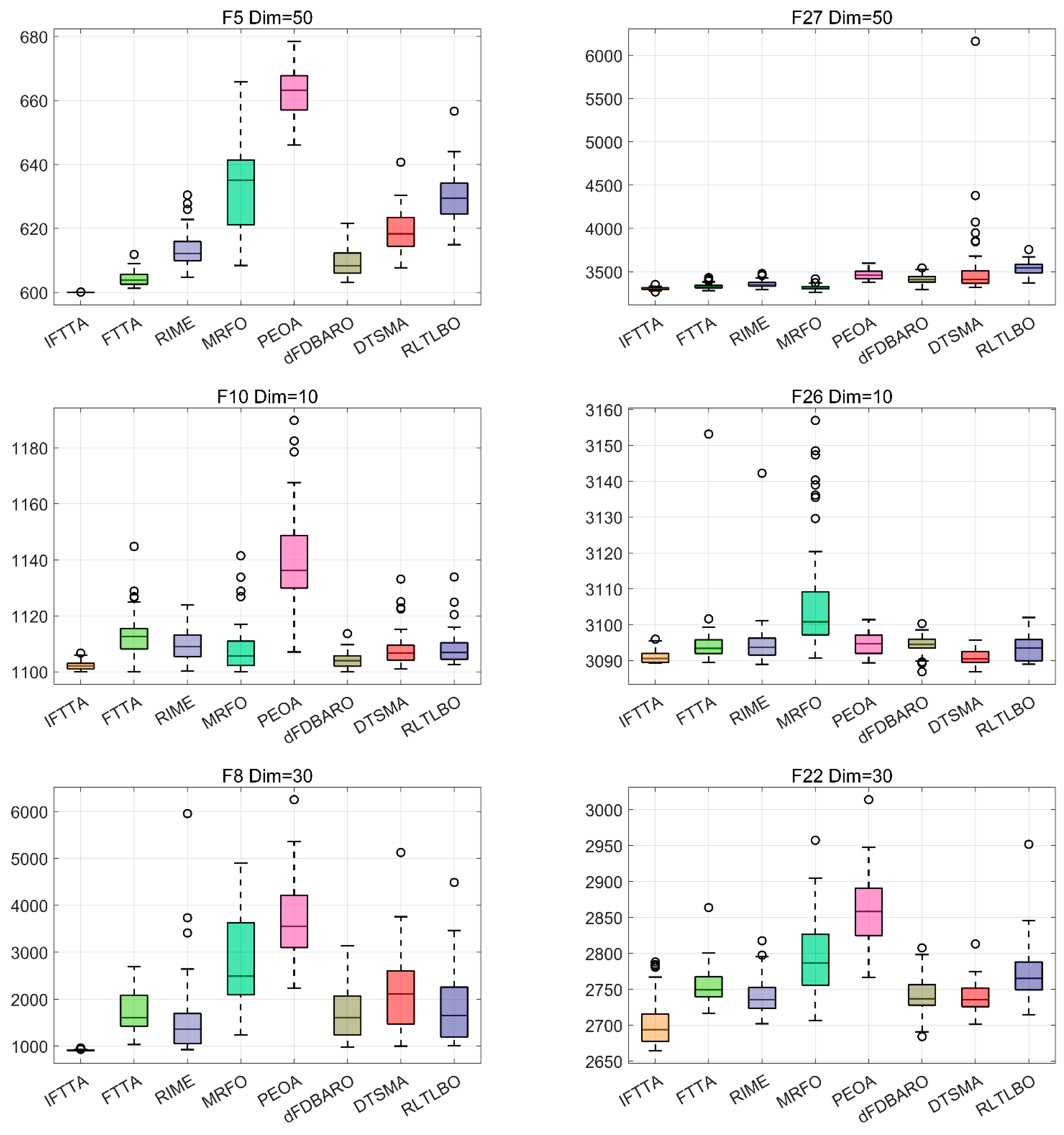
4.6. Comparison with Other Algorithms
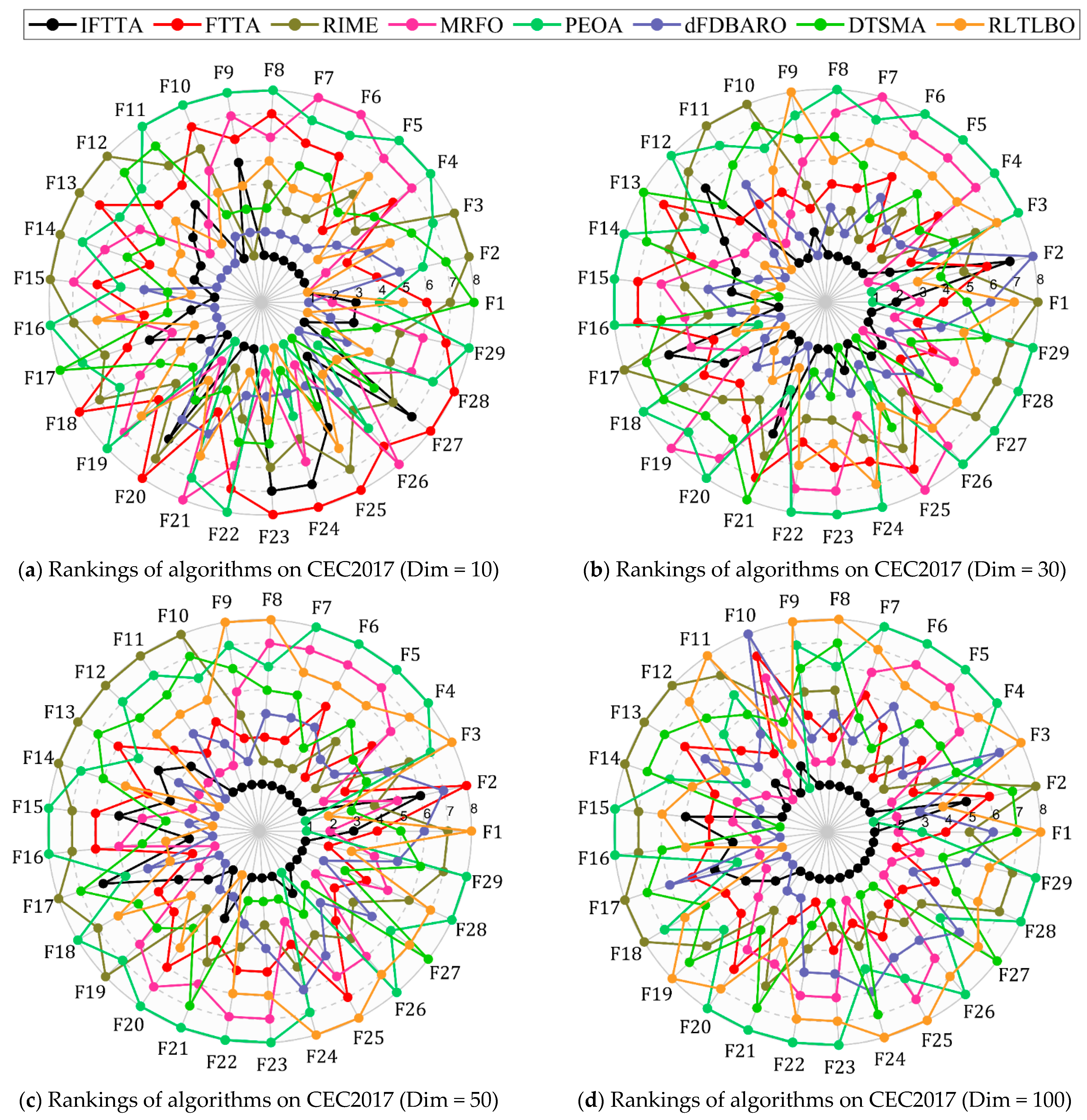
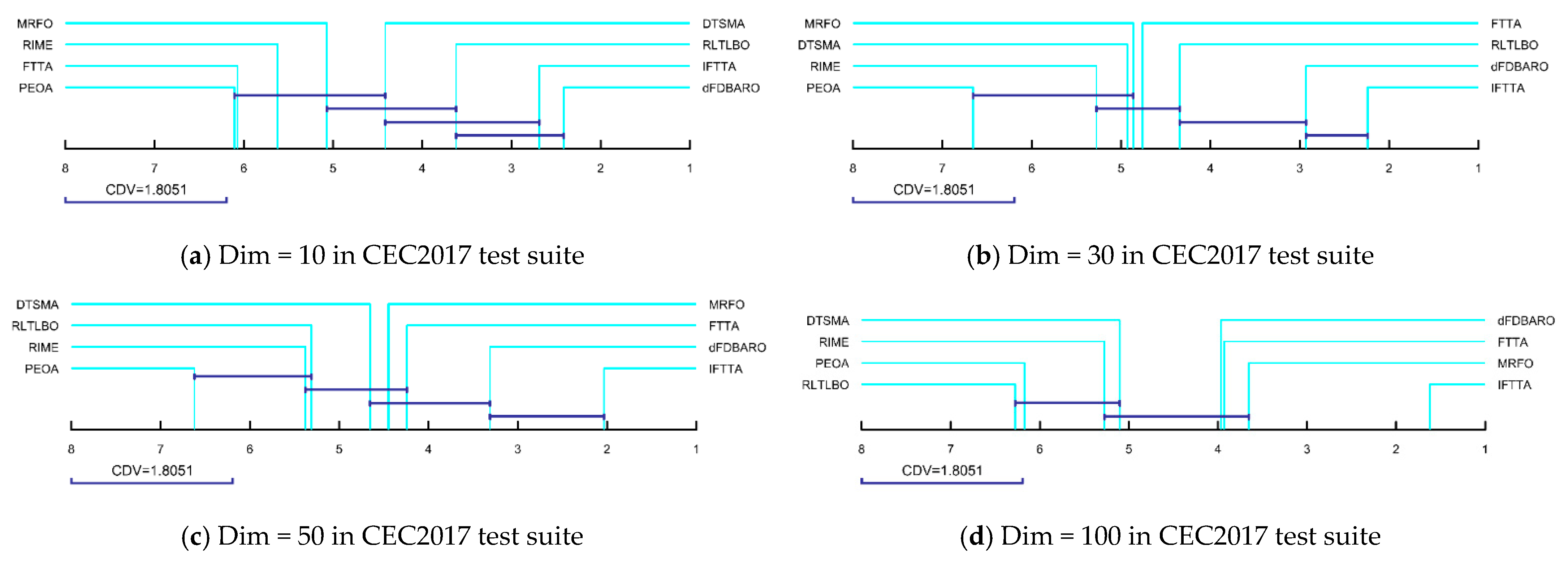
4.6.1. Analysis Using the Wilcoxon Rank Sum Test
- (a)
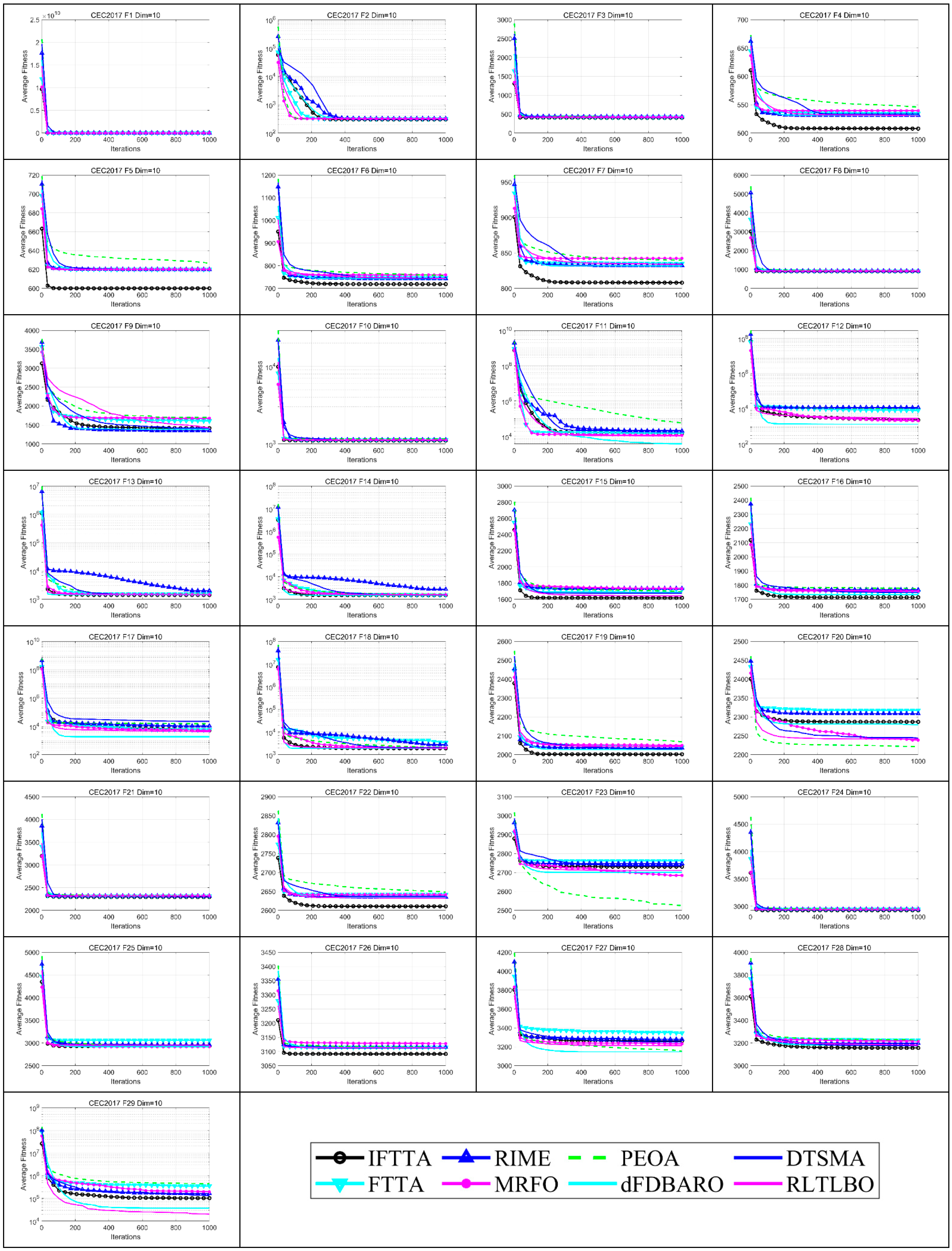
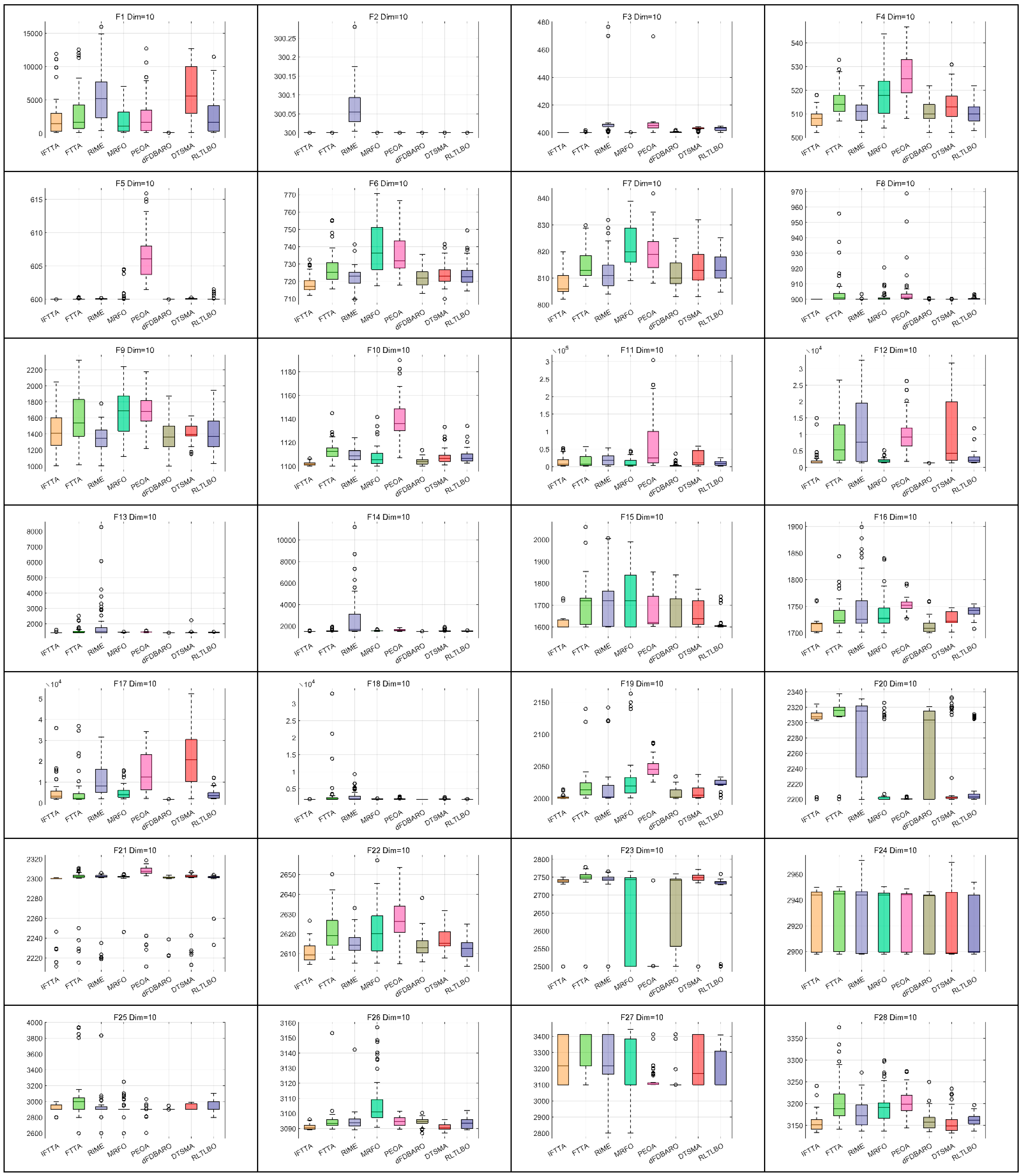
- On Dim = 10, IFTTA outperforms (underperforms) FTTA on 27 (0) benchmark functions, RIME on 24 (3) benchmark functions, MRFO on 18 (3) benchmark functions, PEOA on 23 (2) benchmark functions, dFDBARO on 12 (9) benchmark functions, DTSMA on 20 (4) benchmark functions, and RLTLBO on 18 (3) benchmark functions. It can be concluded that the IFTTA outperforms six comparison algorithms on Dim = 10.
- (b)
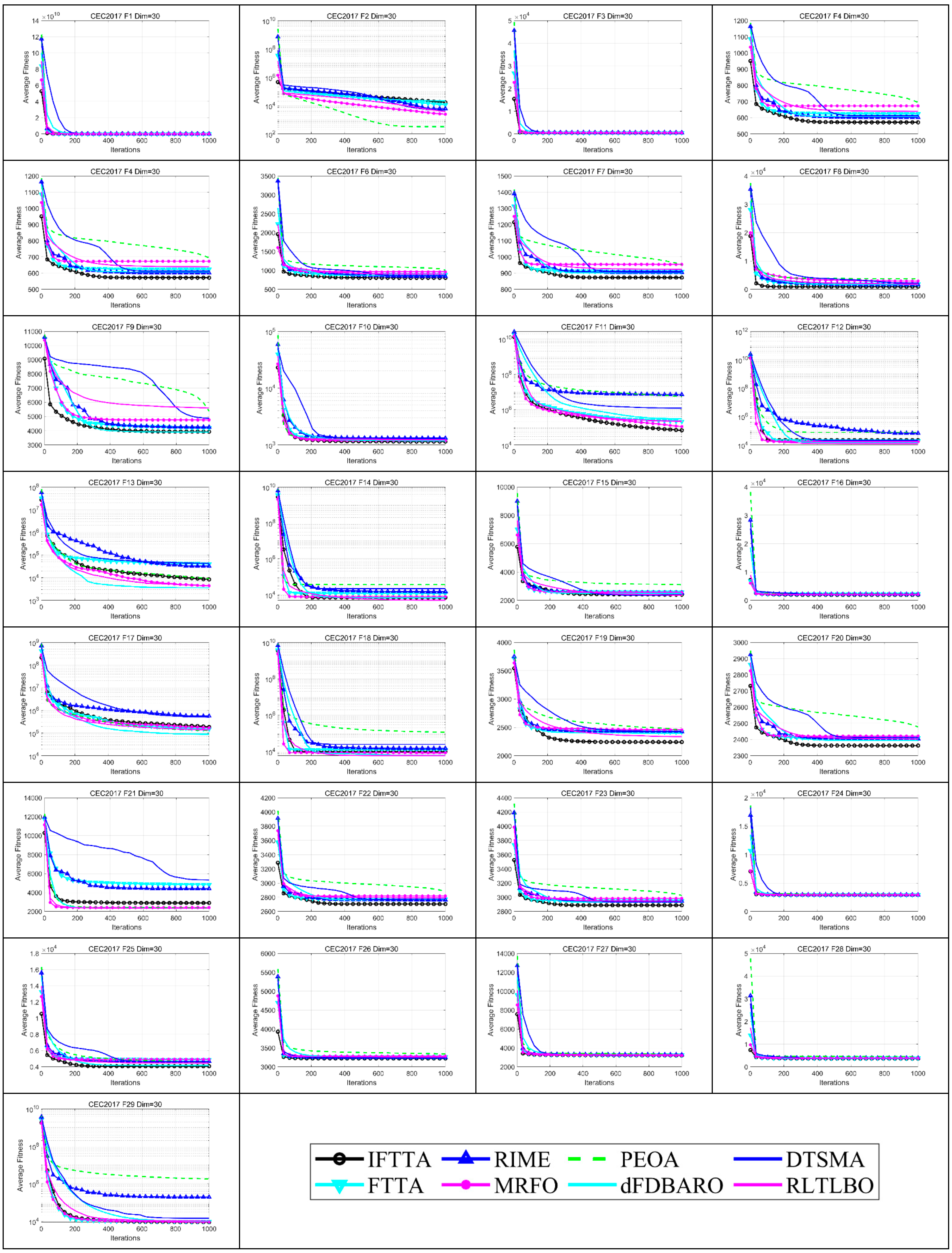
- On Dim = 30, IFTTA outperforms (underperforms) FTTA on 22 (1) benchmark functions, RIME on 25 (1) benchmark functions, MRFO on 17 (3) benchmark functions, PEOA on 23 (4) benchmark functions, dFDBARO on 20 (4) benchmark functions, DTSMA on 23 (2) benchmark functions, and RLTLBO on 18 (3) benchmark functions. It can be concluded that the IFTTA outperforms six comparison algorithms on Dim = 30.
- (c)
- On Dim = 50, IFTTA outperforms (underperforms) FTTA on 22 (1) benchmark functions, RIME on 26 (1) benchmark functions, MRFO on 18 (3) benchmark functions, PEOA on 25 (3) benchmark functions, dFDBARO on 18 (1) benchmark functions, DTSMA on 25 (1) benchmark functions, and RLTLBO on 20 (4) benchmark functions. It can be concluded that the IFTTA outperforms six comparison algorithms on Dim = 50.
- (d)
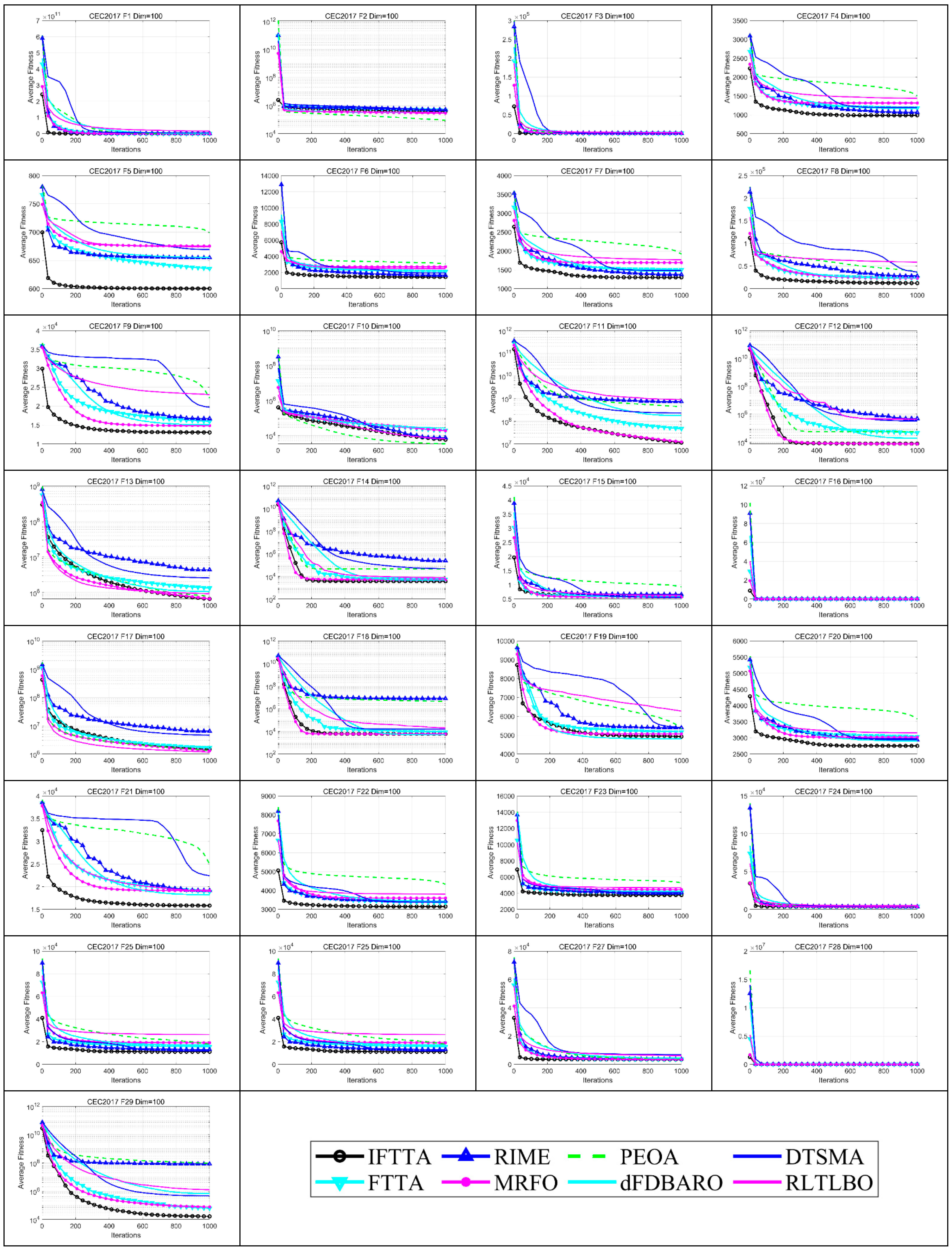
- On Dim = 100, IFTTA outperforms (underperforms) FTTA on 26 (0) benchmark functions, RIME on 28 (0) benchmark functions, MRFO on 20 (1) benchmark functions, PEOA on 25 (2) benchmark functions, dFDBARO on 22 (3) benchmark functions, DTSMA on 27 (1) benchmark functions, and RLTLBO on 26 (2) benchmark functions. It can be concluded that the IFTTA outperforms six comparison algorithms on Dim = 100.
4.6.2. Analysis Using the Friedman Test
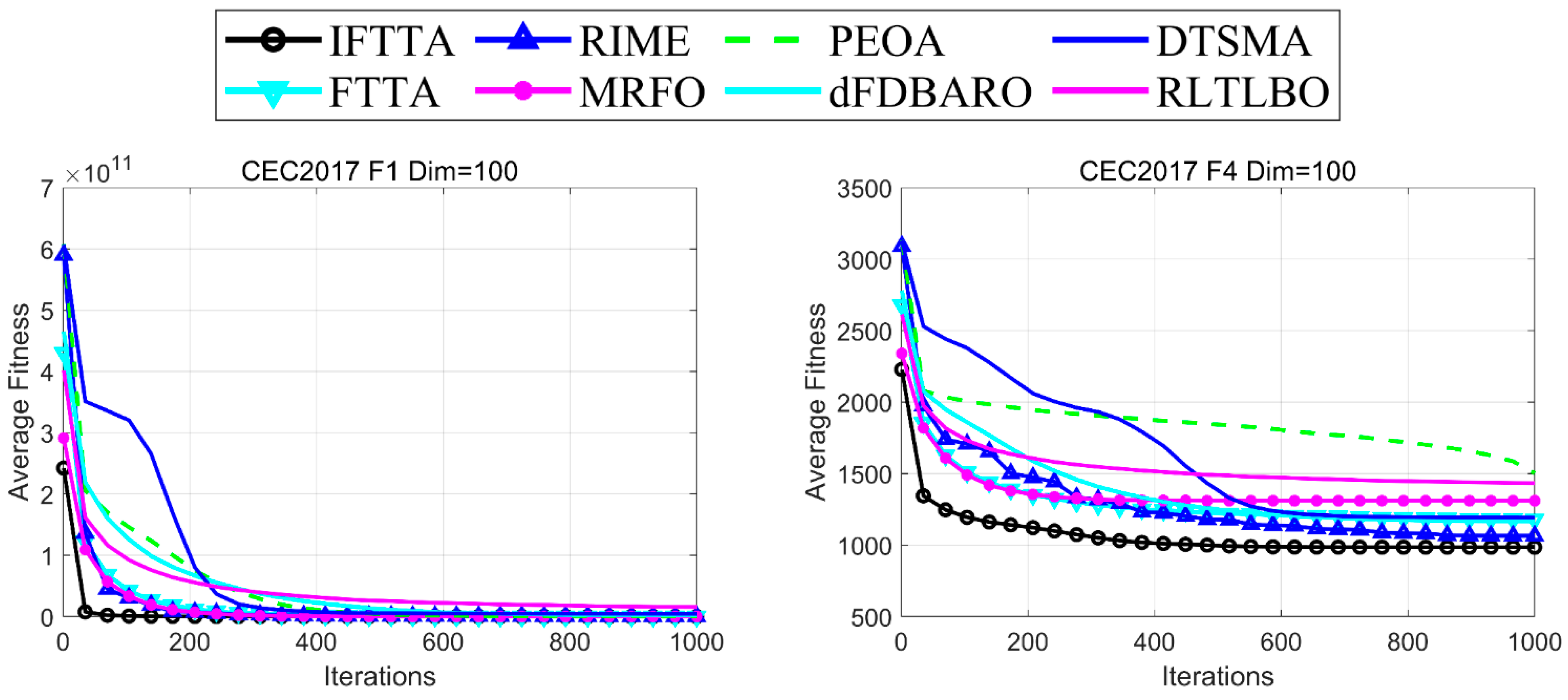
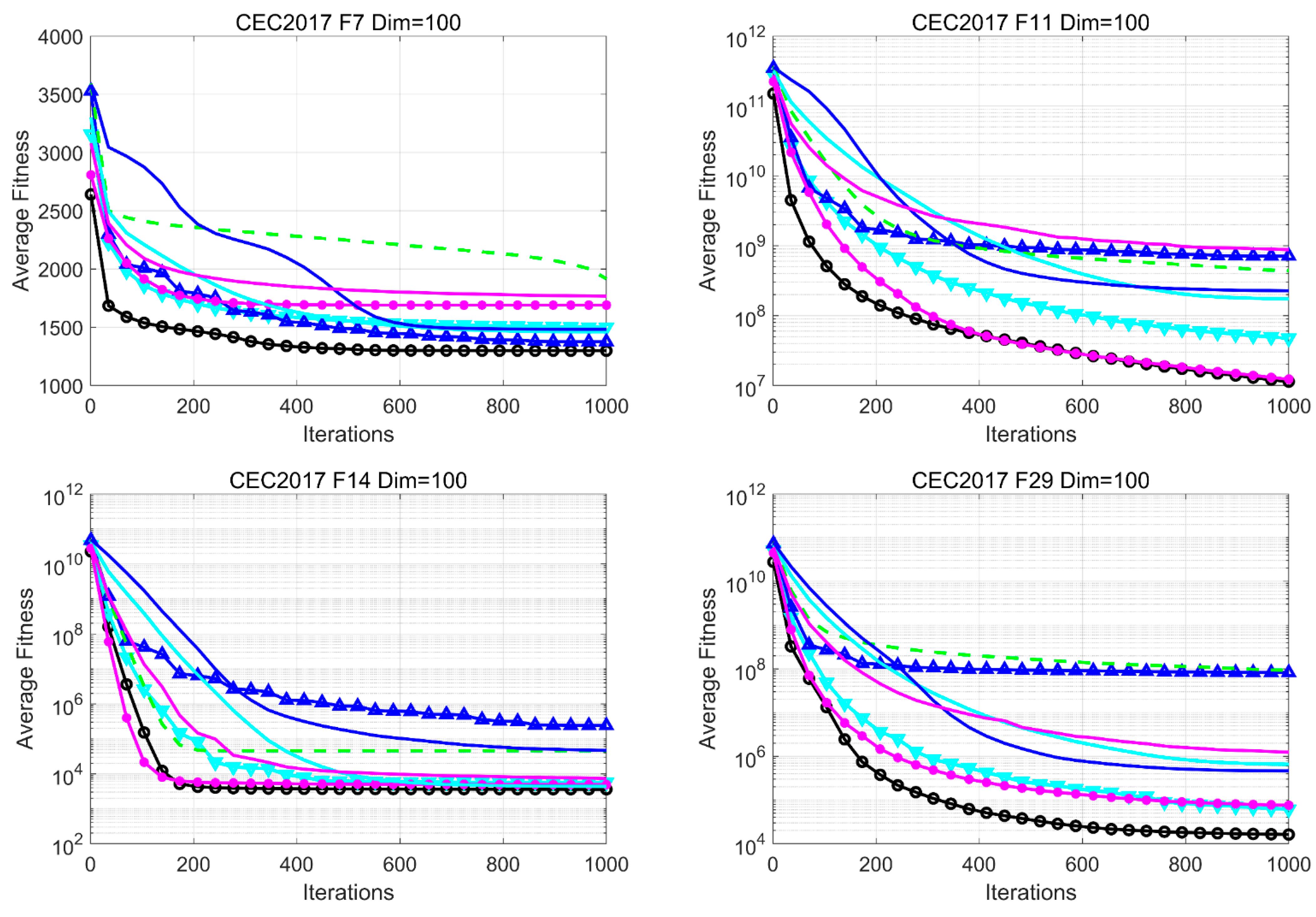
4.6.3. Analysis of Convergence Rate
4.6.4. Analysis of Robustness
5. Engineering-Constrained Optimization Problems
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Function | Index | IFTTA | FTTA | RIME | MRFO | POEA | dFDBARO | DTSMA | RLTLBO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.00 × 102 | 1.00 × 102 | 3.85 × 102 | 1.00 × 102 | 1.01 × 102 | 1.00 × 102 | 1.15 × 102 | 1.00 × 102 |
| Ave | 2.26 × 103 | 2.89 × 103 | 5.76 × 103 | 1.64 × 103 | 2.47 × 103 | 1.00 × 102 | 6.19 × 103 | 2.48 × 103 | |
| Std | 2.76 × 103 | 3.24 × 103 | 4.08 × 103 | 1.61 × 103 | 2.77 × 103 | 5.95 × 10−2 | 4.12 × 103 | 2.83 × 103 | |
| Rank | 3 | 6 | 7 | 2 | 4 | 1 | 8 | 5 | |
| F2 | Best | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 |
| Ave | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | |
| Std | 1.61 × 10−14 | 8.95 × 10−14 | 5.25 × 10−2 | 2.54 × 10−14 | 1.36 × 10−6 | 1.92 × 10−7 | 2.88 × 10−5 | 1.04 × 10−13 | |
| Rank | 1 | 4 | 8 | 1 | 6 | 5 | 7 | 1 | |
| F3 | Best | 4.00 × 102 | 4.00 × 102 | 4.00 × 102 | 4.00 × 102 | 4.00 × 102 | 4.00 × 102 | 4.00 × 102 | 4.00 × 102 |
| Ave | 4.00 × 102 | 4.00 × 102 | 4.08 × 102 | 4.00 × 102 | 4.06 × 102 | 4.00 × 102 | 4.03 × 102 | 4.03 × 102 | |
| Std | 1.44 × 10−2 | 3.54 × 10−1 | 1.35 × 101 | 5.49 × 10−2 | 9.41 × 100 | 3.63 × 10−1 | 7.55 × 10−1 | 1.36 × 100 | |
| Rank | 1 | 3 | 8 | 2 | 7 | 4 | 6 | 5 | |
| F4 | Best | 5.02 × 102 | 5.07 × 102 | 5.02 × 102 | 5.04 × 102 | 5.08 × 102 | 5.02 × 102 | 5.02 × 102 | 5.03 × 102 |
| Ave | 5.08 × 102 | 5.15 × 102 | 5.11 × 102 | 5.19 × 102 | 5.26 × 102 | 5.11 × 102 | 5.13 × 102 | 5.11 × 102 | |
| Std | 3.46 × 100 | 5.78 × 100 | 4.60 × 100 | 8.77 × 100 | 8.98 × 100 | 4.93 × 100 | 5.89 × 100 | 4.59 × 100 | |
| Rank | 1 | 6 | 4 | 7 | 8 | 3 | 5 | 2 | |
| F5 | Best | 6.00 × 102 | 6.00 × 102 | 6.00 × 102 | 6.00 × 102 | 6.01 × 102 | 6.00 × 102 | 6.00 × 102 | 6.00 × 102 |
| Ave | 6.00 × 102 | 6.00 × 102 | 6.00 × 102 | 6.00 × 102 | 6.07 × 102 | 6.00 × 102 | 6.00 × 102 | 6.00 × 102 | |
| Std | 6.34 × 10−5 | 6.43 × 10−2 | 3.62 × 10−2 | 1.02 × 100 | 3.65 × 100 | 1.35 × 10−3 | 5.36 × 10−2 | 3.02 × 10−1 | |
| Rank | 1 | 3 | 5 | 7 | 8 | 2 | 4 | 6 | |
| F6 | Best | 7.12 × 102 | 7.16 × 102 | 7.10 × 102 | 7.18 × 102 | 7.18 × 102 | 7.13 × 102 | 7.10 × 102 | 7.14 × 102 |
| Ave | 7.18 × 102 | 7.27 × 102 | 7.23 × 102 | 7.39 × 102 | 7.36 × 102 | 7.22 × 102 | 7.24 × 102 | 7.24 × 102 | |
| Std | 4.68 × 100 | 9.07 × 100 | 5.70 × 100 | 1.47 × 101 | 1.22 × 101 | 5.56 × 100 | 6.42 × 100 | 6.98 × 100 | |
| Rank | 1 | 6 | 3 | 8 | 7 | 2 | 5 | 4 | |
| F7 | Best | 8.02 × 102 | 8.07 × 102 | 8.04 × 102 | 8.09 × 102 | 8.08 × 102 | 8.03 × 102 | 8.03 × 102 | 8.05 × 102 |
| Ave | 8.08 × 102 | 8.15 × 102 | 8.12 × 102 | 8.22 × 102 | 8.20 × 102 | 8.12 × 102 | 8.15 × 102 | 8.14 × 102 | |
| Std | 4.17 × 100 | 5.68 × 100 | 6.08 × 100 | 8.35 × 100 | 7.72 × 100 | 5.00 × 100 | 6.77 × 100 | 5.05 × 100 | |
| Rank | 1 | 6 | 3 | 8 | 7 | 2 | 5 | 4 | |
| F8 | Best | 9.00 × 102 | 9.00 × 102 | 9.00 × 102 | 9.00 × 102 | 9.00 × 102 | 9.00 × 102 | 9.00 × 102 | 9.00 × 102 |
| Ave | 9.00 × 102 | 9.05 × 102 | 9.00 × 102 | 9.01 × 102 | 9.05 × 102 | 9.00 × 102 | 9.00 × 102 | 9.00 × 102 | |
| Std | 0.00 × 100 | 1.02 × 101 | 4.92 × 10−1 | 3.54 × 100 | 1.22 × 101 | 1.41 × 10−1 | 1.23 × 10−1 | 6.83 × 10−1 | |
| Rank | 1 | 7 | 4 | 6 | 8 | 2 | 3 | 5 | |
| F9 | Best | 1.01 × 103 | 1.02 × 103 | 1.01 × 103 | 1.12 × 103 | 1.22 × 103 | 1.00 × 103 | 1.15 × 103 | 1.03 × 103 |
| Ave | 1.42 × 103 | 1.59 × 103 | 1.33 × 103 | 1.65 × 103 | 1.67 × 103 | 1.37 × 103 | 1.40 × 103 | 1.40 × 103 | |
| Std | 2.29 × 102 | 2.91 × 102 | 1.72 × 102 | 2.79 × 102 | 2.10 × 102 | 2.00 × 102 | 1.13 × 102 | 2.29 × 102 | |
| Rank | 5 | 6 | 1 | 7 | 8 | 2 | 3 | 4 | |
| F10 | Best | 1.10 × 103 | 1.10 × 103 | 1.10 × 103 | 1.10 × 103 | 1.11 × 103 | 1.10 × 103 | 1.10 × 103 | 1.10 × 103 |
| Ave | 1.10 × 103 | 1.11 × 103 | 1.11 × 103 | 1.11 × 103 | 1.14 × 103 | 1.10 × 103 | 1.11 × 103 | 1.11 × 103 | |
| Std | 1.57 × 100 | 8.22 × 100 | 5.63 × 100 | 8.68 × 100 | 1.76 × 101 | 2.89 × 100 | 6.32 × 100 | 5.93 × 100 | |
| Rank | 1 | 7 | 6 | 5 | 8 | 2 | 3 | 4 | |
| F11 | Best | 1.53 × 103 | 1.31 × 103 | 2.00 × 103 | 1.46 × 103 | 4.29 × 103 | 1.20 × 103 | 1.72 × 103 | 1.78 × 103 |
| Ave | 1.51 × 104 | 1.52 × 104 | 2.05 × 104 | 1.16 × 104 | 5.81 × 104 | 3.77 × 103 | 2.19 × 104 | 1.07 × 104 | |
| Std | 1.59 × 104 | 1.50 × 104 | 1.57 × 104 | 1.19 × 104 | 7.11 × 104 | 5.94 × 103 | 2.05 × 104 | 7.16 × 103 | |
| Rank | 4 | 5 | 6 | 3 | 8 | 1 | 7 | 2 | |
| F12 | Best | 1.31 × 103 | 1.31 × 103 | 1.34 × 103 | 1.33 × 103 | 1.86 × 103 | 1.30 × 103 | 1.33 × 103 | 1.32 × 103 |
| Ave | 2.26 × 103 | 7.99 × 103 | 1.14 × 104 | 2.09 × 103 | 9.98 × 103 | 1.31 × 103 | 1.08 × 104 | 2.74 × 103 | |
| Std | 2.53 × 103 | 7.06 × 103 | 1.03 × 104 | 7.02 × 102 | 5.45 × 103 | 4.36 × 100 | 1.11 × 104 | 1.84 × 103 | |
| Rank | 3 | 5 | 8 | 2 | 6 | 1 | 7 | 4 | |
| F13 | Best | 1.40 × 103 | 1.41 × 103 | 1.40 × 103 | 1.43 × 103 | 1.43 × 103 | 1.40 × 103 | 1.40 × 103 | 1.41 × 103 |
| Ave | 1.42 × 103 | 1.53 × 103 | 1.98 × 103 | 1.45 × 103 | 1.46 × 103 | 1.40 × 103 | 1.44 × 103 | 1.43 × 103 | |
| Std | 2.93 × 101 | 2.16 × 102 | 1.26 × 103 | 1.19 × 101 | 2.87 × 101 | 3.03 × 100 | 1.13 × 102 | 1.00 × 101 | |
| Rank | 2 | 7 | 8 | 5 | 6 | 1 | 4 | 3 | |
| F14 | Best | 1.50 × 103 | 1.50 × 103 | 1.50 × 103 | 1.51 × 103 | 1.52 × 103 | 1.50 × 103 | 1.50 × 103 | 1.51 × 103 |
| Ave | 1.51 × 103 | 1.55 × 103 | 2.73 × 103 | 1.56 × 103 | 1.64 × 103 | 1.50 × 103 | 1.55 × 103 | 1.53 × 103 | |
| Std | 1.52 × 101 | 9.08 × 101 | 2.01 × 103 | 3.40 × 101 | 8.05 × 101 | 1.67 × 100 | 9.07 × 101 | 2.00 × 101 | |
| Rank | 2 | 4 | 8 | 6 | 7 | 1 | 5 | 3 | |
| F15 | Best | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 |
| Ave | 1.62 × 103 | 1.70 × 103 | 1.71 × 103 | 1.71 × 103 | 1.67 × 103 | 1.66 × 103 | 1.65 × 103 | 1.62 × 103 | |
| Std | 3.14 × 101 | 9.44 × 101 | 1.20 × 102 | 1.16 × 102 | 8.18 × 101 | 8.48 × 101 | 5.11 × 101 | 4.26 × 101 | |
| Rank | 1 | 6 | 8 | 7 | 5 | 4 | 3 | 2 | |
| F16 | Best | 1.70 × 103 | 1.70 × 103 | 1.70 × 103 | 1.70 × 103 | 1.73 × 103 | 1.70 × 103 | 1.70 × 103 | 1.71 × 103 |
| Ave | 1.71 × 103 | 1.73 × 103 | 1.75 × 103 | 1.74 × 103 | 1.75 × 103 | 1.71 × 103 | 1.73 × 103 | 1.74 × 103 | |
| Std | 1.25 × 101 | 2.79 × 101 | 4.88 × 101 | 3.09 × 101 | 1.32 × 101 | 1.28 × 101 | 1.15 × 101 | 1.00 × 101 | |
| Rank | 2 | 4 | 7 | 5 | 8 | 1 | 3 | 6 | |
| F17 | Best | 1.80 × 103 | 1.81 × 103 | 1.91 × 103 | 1.87 × 103 | 2.15 × 103 | 1.80 × 103 | 2.09 × 103 | 2.01 × 103 |
| Ave | 5.09 × 103 | 5.53 × 103 | 1.05 × 104 | 5.00 × 103 | 1.49 × 104 | 1.80 × 103 | 2.23 × 104 | 4.20 × 103 | |
| Std | 5.63 × 103 | 8.14 × 103 | 7.14 × 103 | 3.35 × 103 | 9.82 × 103 | 1.80 × 100 | 1.37 × 104 | 2.47 × 103 | |
| Rank | 4 | 5 | 6 | 3 | 7 | 1 | 8 | 2 | |
| F18 | Best | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.91 × 103 | 1.91 × 103 | 1.90 × 103 | 1.90 × 103 | 1.91 × 103 |
| Ave | 1.90 × 103 | 3.38 × 103 | 2.73 × 103 | 1.96 × 103 | 2.03 × 103 | 1.90 × 103 | 1.96 × 103 | 1.92 × 103 | |
| Std | 3.10 × 100 | 5.26 × 103 | 1.52 × 103 | 5.66 × 101 | 2.03 × 102 | 6.64 × 10−1 | 1.17 × 102 | 1.25 × 101 | |
| Rank | 2 | 8 | 7 | 5 | 6 | 1 | 4 | 3 | |
| F19 | Best | 2.00 × 103 | 2.00 × 103 | 2.00 × 103 | 2.00 × 103 | 2.03 × 103 | 2.00 × 103 | 2.00 × 103 | 2.00 × 103 |
| Ave | 2.00 × 103 | 2.02 × 103 | 2.02 × 103 | 2.03 × 103 | 2.05 × 103 | 2.01 × 103 | 2.01 × 103 | 2.02 × 103 | |
| Std | 3.09 × 100 | 2.50 × 101 | 3.00 × 101 | 3.79 × 101 | 1.48 × 101 | 8.37 × 100 | 9.95 × 100 | 7.85 × 100 | |
| Rank | 1 | 5 | 4 | 7 | 8 | 2 | 3 | 6 | |
| F20 | Best | 2.20 × 103 | 2.20 × 103 | 2.20 × 103 | 2.20 × 103 | 2.20 × 103 | 2.20 × 103 | 2.20 × 103 | 2.20 × 103 |
| Ave | 2.29 × 103 | 2.30 × 103 | 2.29 × 103 | 2.22 × 103 | 2.20 × 103 | 2.26 × 103 | 2.22 × 103 | 2.22 × 103 | |
| Std | 4.58 × 101 | 4.55 × 101 | 5.18 × 101 | 4.13 × 101 | 8.18 × 10−1 | 5.72 × 101 | 4.60 × 101 | 4.04 × 101 | |
| Rank | 6 | 8 | 7 | 2 | 1 | 5 | 4 | 3 | |
| F21 | Best | 2.21 × 103 | 2.22 × 103 | 2.22 × 103 | 2.25 × 103 | 2.21 × 103 | 2.22 × 103 | 2.21 × 103 | 2.23 × 103 |
| Ave | 2.29 × 103 | 2.30 × 103 | 2.29 × 103 | 2.30 × 103 | 2.30 × 103 | 2.30 × 103 | 2.30 × 103 | 2.30 × 103 | |
| Std | 2.26 × 101 | 2.19 × 101 | 2.39 × 101 | 7.87 × 100 | 2.55 × 101 | 1.76 × 101 | 2.32 × 101 | 1.12 × 101 | |
| Rank | 1 | 4 | 2 | 8 | 7 | 5 | 3 | 6 | |
| F22 | Best | 2.60 × 103 | 2.61 × 103 | 2.61 × 103 | 2.61 × 103 | 2.60 × 103 | 2.61 × 103 | 2.61 × 103 | 2.60 × 103 |
| Ave | 2.61 × 103 | 2.62 × 103 | 2.62 × 103 | 2.62 × 103 | 2.63 × 103 | 2.61 × 103 | 2.62 × 103 | 2.61 × 103 | |
| Std | 5.00 × 100 | 9.45 × 100 | 5.30 × 100 | 1.13 × 101 | 9.78 × 100 | 5.86 × 100 | 5.83 × 100 | 5.29 × 100 | |
| Rank | 1 | 7 | 4 | 6 | 8 | 3 | 5 | 2 | |
| F23 | Best | 2.50 × 103 | 2.50 × 103 | 2.50 × 103 | 2.50 × 103 | 2.50 × 103 | 2.50 × 103 | 2.50 × 103 | 2.50 × 103 |
| Ave | 2.73 × 103 | 2.74 × 103 | 2.73 × 103 | 2.66 × 103 | 2.51 × 103 | 2.68 × 103 | 2.72 × 103 | 2.69 × 103 | |
| Std | 4.72 × 101 | 5.02 × 101 | 6.72 × 101 | 1.18 × 102 | 3.36 × 101 | 1.07 × 102 | 8.71 × 101 | 9.47 × 101 | |
| Rank | 7 | 8 | 6 | 2 | 1 | 3 | 5 | 4 | |
| F24 | Best | 2.90 × 103 | 2.90 × 103 | 2.90 × 103 | 2.90 × 103 | 2.90 × 103 | 2.90 × 103 | 2.90 × 103 | 2.90 × 103 |
| Ave | 2.93 × 103 | 2.93 × 103 | 2.93 × 103 | 2.93 × 103 | 2.92 × 103 | 2.92 × 103 | 2.92 × 103 | 2.92 × 103 | |
| Std | 2.28 × 101 | 2.26 × 101 | 2.48 × 101 | 2.29 × 101 | 2.31 × 101 | 2.31 × 101 | 2.61 × 101 | 2.28 × 101 | |
| Rank | 7 | 8 | 5 | 6 | 4 | 3 | 2 | 1 | |
| F25 | Best | 2.80 × 103 | 2.60 × 103 | 2.60 × 103 | 2.60 × 103 | 2.60 × 103 | 2.90 × 103 | 2.90 × 103 | 2.80 × 103 |
| Ave | 2.93 × 103 | 3.04 × 103 | 2.94 × 103 | 2.90 × 103 | 2.89 × 103 | 2.90 × 103 | 2.93 × 103 | 2.93 × 103 | |
| Std | 4.29 × 101 | 2.70 × 102 | 1.94 × 102 | 1.17 × 102 | 5.33 × 101 | 6.60 × 100 | 3.78 × 101 | 8.10 × 101 | |
| Rank | 5 | 8 | 7 | 2 | 1 | 3 | 4 | 6 | |
| F26 | Best | 3.09 × 103 | 3.09 × 103 | 3.09 × 103 | 3.09 × 103 | 3.09 × 103 | 3.09 × 103 | 3.09 × 103 | 3.09 × 103 |
| Ave | 3.09 × 103 | 3.10 × 103 | 3.09 × 103 | 3.11 × 103 | 3.09 × 103 | 3.09 × 103 | 3.09 × 103 | 3.09 × 103 | |
| Std | 1.90 × 100 | 8.70 × 100 | 7.51 × 100 | 1.65 × 101 | 3.23 × 100 | 2.70 × 100 | 2.12 × 100 | 3.37 × 100 | |
| Rank | 2 | 7 | 5 | 8 | 6 | 4 | 1 | 3 | |
| F27 | Best | 3.10 × 103 | 3.10 × 103 | 2.80 × 103 | 2.80 × 103 | 3.10 × 103 | 3.10 × 103 | 3.10 × 103 | 3.10 × 103 |
| Ave | 3.26 × 103 | 3.33 × 103 | 3.26 × 103 | 3.21 × 103 | 3.13 × 103 | 3.13 × 103 | 3.23 × 103 | 3.19 × 103 | |
| Std | 1.48 × 102 | 1.26 × 102 | 1.48 × 102 | 1.52 × 102 | 7.49 × 101 | 8.34 × 101 | 1.46 × 102 | 1.15 × 102 | |
| Rank | 7 | 8 | 6 | 4 | 2 | 1 | 5 | 3 | |
| F28 | Best | 3.13 × 103 | 3.14 × 103 | 3.14 × 103 | 3.14 × 103 | 3.14 × 103 | 3.14 × 103 | 3.13 × 103 | 3.14 × 103 |
| Ave | 3.16 × 103 | 3.20 × 103 | 3.18 × 103 | 3.20 × 103 | 3.20 × 103 | 3.16 × 103 | 3.16 × 103 | 3.16 × 103 | |
| Std | 2.07 × 101 | 5.19 × 101 | 3.09 × 101 | 3.79 × 101 | 2.86 × 101 | 2.18 × 101 | 2.51 × 101 | 1.23 × 101 | |
| Rank | 1 | 8 | 5 | 6 | 7 | 3 | 2 | 4 | |
| F29 | Best | 3.53 × 103 | 3.60 × 103 | 4.60 × 103 | 3.62 × 103 | 4.94 × 103 | 3.53 × 103 | 3.94 × 103 | 3.80 × 103 |
| Ave | 1.02 × 105 | 3.51 × 105 | 1.63 × 105 | 1.95 × 105 | 4.42 × 105 | 3.69 × 104 | 1.33 × 105 | 2.01 × 104 | |
| Std | 2.65 × 105 | 4.02 × 105 | 3.30 × 105 | 4.19 × 105 | 6.15 × 105 | 1.60 × 105 | 3.10 × 105 | 3.95 × 104 | |
| Rank | 3 | 7 | 5 | 6 | 8 | 2 | 4 | 1 |
| Function | Index | IFTTA | FTTA | RIME | MRFO | POEA | dFDBARO | DTSMA | RLTLBO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.09 × 102 | 1.04 × 102 | 1.21 × 105 | 1.03 × 102 | 1.00 × 102 | 9.94 × 102 | 1.03 × 102 | 1.68 × 102 |
| Ave | 4.20 × 103 | 4.94 × 103 | 3.94 × 105 | 4.85 × 103 | 2.69 × 103 | 1.11 × 104 | 6.58 × 103 | 2.61 × 104 | |
| Std | 4.72 × 103 | 5.44 × 103 | 1.81 × 105 | 5.27 × 103 | 3.65 × 103 | 9.07 × 103 | 7.41 × 103 | 8.31 × 104 | |
| Rank | 2 | 4 | 8 | 3 | 1 | 6 | 5 | 7 | |
| F2 | Best | 5.93 × 103 | 3.55 × 103 | 1.94 × 103 | 4.42 × 102 | 3.00 × 102 | 8.36 × 103 | 5.08 × 102 | 1.25 × 103 |
| Ave | 1.65 × 104 | 1.15 × 104 | 5.94 × 103 | 2.39 × 103 | 3.00 × 102 | 2.12 × 104 | 4.74 × 103 | 3.64 × 103 | |
| Std | 6.64 × 103 | 4.94 × 103 | 2.33 × 103 | 1.75 × 103 | 2.05 × 10−1 | 6.25 × 103 | 4.20 × 103 | 1.97 × 103 | |
| Rank | 7 | 6 | 5 | 2 | 1 | 8 | 4 | 3 | |
| F3 | Best | 4.01 × 102 | 4.02 × 102 | 4.44 × 102 | 4.00 × 102 | 4.69 × 102 | 4.10 × 102 | 4.24 × 102 | 4.71 × 102 |
| Ave | 4.76 × 102 | 4.85 × 102 | 5.07 × 102 | 4.71 × 102 | 5.09 × 102 | 4.94 × 102 | 4.96 × 102 | 5.08 × 102 | |
| Std | 1.60 × 101 | 3.00 × 101 | 2.91 × 101 | 3.09 × 101 | 2.24 × 101 | 2.70 × 101 | 1.92 × 101 | 2.73 × 101 | |
| Rank | 2 | 3 | 6 | 1 | 8 | 4 | 5 | 7 | |
| F4 | Best | 5.24 × 102 | 5.47 × 102 | 5.44 × 102 | 5.83 × 102 | 5.99 × 102 | 5.51 × 102 | 5.45 × 102 | 5.73 × 102 |
| Ave | 5.71 × 102 | 6.03 × 102 | 5.81 × 102 | 6.53 × 102 | 6.74 × 102 | 5.86 × 102 | 5.93 × 102 | 6.19 × 102 | |
| Std | 3.25 × 101 | 3.00 × 101 | 2.52 × 101 | 4.03 × 101 | 3.16 × 101 | 2.16 × 101 | 2.38 × 101 | 2.24 × 101 | |
| Rank | 1 | 5 | 2 | 7 | 8 | 3 | 4 | 6 | |
| F5 | Best | 6.00 × 102 | 6.00 × 102 | 6.01 × 102 | 6.01 × 102 | 6.24 × 102 | 6.00 × 102 | 6.01 × 102 | 6.01 × 102 |
| Ave | 6.00 × 102 | 6.01 × 102 | 6.04 × 102 | 6.15 × 102 | 6.44 × 102 | 6.01 × 102 | 6.05 × 102 | 6.12 × 102 | |
| Std | 6.36 × 10−3 | 7.65 × 10−1 | 2.83 × 100 | 1.09 × 101 | 8.10 × 100 | 1.50 × 100 | 2.50 × 100 | 5.51 × 100 | |
| Rank | 1 | 2 | 4 | 7 | 8 | 3 | 5 | 6 | |
| F6 | Best | 7.59 × 102 | 7.91 × 102 | 7.72 × 102 | 8.13 × 102 | 8.77 × 102 | 7.98 × 102 | 7.85 × 102 | 8.00 × 102 |
| Ave | 8.02 × 102 | 8.67 × 102 | 8.22 × 102 | 9.41 × 102 | 9.84 × 102 | 8.42 × 102 | 8.38 × 102 | 8.77 × 102 | |
| Std | 3.11 × 101 | 3.46 × 101 | 2.46 × 101 | 6.05 × 101 | 5.01 × 101 | 2.70 × 101 | 3.04 × 101 | 4.12 × 101 | |
| Rank | 1 | 5 | 2 | 7 | 8 | 4 | 3 | 6 | |
| F7 | Best | 8.26 × 102 | 8.42 × 102 | 8.47 × 102 | 8.50 × 102 | 8.78 × 102 | 8.38 × 102 | 8.55 × 102 | 8.50 × 102 |
| Ave | 8.72 × 102 | 8.89 × 102 | 8.84 × 102 | 9.34 × 102 | 9.30 × 102 | 8.80 × 102 | 8.90 × 102 | 9.03 × 102 | |
| Std | 3.26 × 101 | 2.57 × 101 | 1.87 × 101 | 3.63 × 101 | 2.49 × 101 | 2.13 × 101 | 2.48 × 101 | 2.77 × 101 | |
| Rank | 1 | 4 | 3 | 8 | 7 | 2 | 5 | 6 | |
| F8 | Best | 9.01 × 102 | 1.03 × 103 | 9.24 × 102 | 1.24 × 103 | 2.23 × 103 | 9.81 × 102 | 1.00 × 103 | 1.01 × 103 |
| Ave | 9.11 × 102 | 1.75 × 103 | 1.58 × 103 | 2.85 × 103 | 3.68 × 103 | 1.66 × 103 | 2.20 × 103 | 1.82 × 103 | |
| Std | 1.06 × 101 | 4.34 × 102 | 8.69 × 102 | 1.03 × 103 | 8.01 × 102 | 5.08 × 102 | 8.99 × 102 | 7.32 × 102 | |
| Rank | 1 | 4 | 2 | 7 | 8 | 3 | 6 | 5 | |
| F9 | Best | 2.47 × 103 | 2.68 × 103 | 2.75 × 103 | 3.25 × 103 | 3.91 × 103 | 2.55 × 103 | 3.50 × 103 | 4.26 × 103 |
| Ave | 3.93 × 103 | 4.17 × 103 | 4.24 × 103 | 4.73 × 103 | 5.34 × 103 | 3.87 × 103 | 4.86 × 103 | 5.57 × 103 | |
| Std | 5.32 × 102 | 4.81 × 102 | 6.50 × 102 | 6.55 × 102 | 6.42 × 102 | 5.48 × 102 | 6.22 × 102 | 5.03 × 102 | |
| Rank | 2 | 3 | 4 | 5 | 7 | 1 | 6 | 8 | |
| F10 | Best | 1.11 × 103 | 1.13 × 103 | 1.21 × 103 | 1.13 × 103 | 1.16 × 103 | 1.12 × 103 | 1.14 × 103 | 1.15 × 103 |
| Ave | 1.14 × 103 | 1.21 × 103 | 1.30 × 103 | 1.17 × 103 | 1.24 × 103 | 1.16 × 103 | 1.25 × 103 | 1.23 × 103 | |
| Std | 2.20 × 101 | 4.54 × 101 | 4.50 × 101 | 3.30 × 101 | 4.83 × 101 | 3.33 × 101 | 5.45 × 101 | 4.80 × 101 | |
| Rank | 1 | 4 | 8 | 3 | 6 | 2 | 7 | 5 | |
| F11 | Best | 1.03 × 104 | 2.09 × 104 | 2.33 × 105 | 1.26 × 104 | 1.99 × 105 | 2.05 × 104 | 5.09 × 104 | 1.35 × 104 |
| Ave | 6.77 × 104 | 2.15 × 105 | 7.03 × 106 | 1.10 × 105 | 5.58 × 106 | 2.98 × 105 | 1.19 × 106 | 2.12 × 105 | |
| Std | 6.58 × 104 | 2.51 × 105 | 5.91 × 106 | 8.50 × 104 | 4.42 × 106 | 2.96 × 105 | 9.36 × 105 | 2.76 × 105 | |
| Rank | 1 | 4 | 8 | 2 | 7 | 5 | 6 | 3 | |
| F12 | Best | 1.39 × 103 | 1.40 × 103 | 1.19 × 104 | 1.38 × 103 | 1.87 × 104 | 1.38 × 103 | 1.46 × 103 | 2.18 × 103 |
| Ave | 2.15 × 104 | 1.94 × 104 | 6.67 × 104 | 1.70 × 104 | 7.69 × 104 | 1.38 × 104 | 2.06 × 104 | 1.23 × 104 | |
| Std | 1.99 × 104 | 1.95 × 104 | 8.09 × 104 | 1.73 × 104 | 4.68 × 104 | 1.29 × 104 | 2.26 × 104 | 9.48 × 103 | |
| Rank | 6 | 4 | 7 | 3 | 8 | 2 | 5 | 1 | |
| F13 | Best | 1.51 × 103 | 2.43 × 103 | 4.55 × 103 | 1.72 × 103 | 1.84 × 103 | 1.46 × 103 | 2.82 × 103 | 1.66 × 103 |
| Ave | 8.29 × 103 | 3.98 × 104 | 3.18 × 104 | 4.38 × 103 | 9.14 × 103 | 3.54 × 103 | 4.28 × 104 | 4.38 × 103 | |
| Std | 8.56 × 103 | 4.72 × 104 | 2.79 × 104 | 3.48 × 103 | 6.85 × 103 | 2.84 × 103 | 3.20 × 104 | 2.89 × 103 | |
| Rank | 4 | 7 | 6 | 3 | 5 | 1 | 8 | 2 | |
| F14 | Best | 1.52 × 103 | 1.55 × 103 | 2.39 × 103 | 1.55 × 103 | 8.20 × 103 | 1.54 × 103 | 1.56 × 103 | 1.70 × 103 |
| Ave | 6.90 × 103 | 1.19 × 104 | 1.48 × 104 | 7.52 × 103 | 3.62 × 104 | 6.62 × 103 | 2.14 × 104 | 4.82 × 103 | |
| Std | 7.68 × 103 | 1.25 × 104 | 1.34 × 104 | 7.82 × 103 | 2.75 × 104 | 6.82 × 103 | 1.44 × 104 | 2.82 × 103 | |
| Rank | 3 | 5 | 6 | 4 | 8 | 2 | 7 | 1 | |
| F15 | Best | 1.84 × 103 | 1.75 × 103 | 1.72 × 103 | 1.97 × 103 | 2.17 × 103 | 1.76 × 103 | 1.78 × 103 | 1.71 × 103 |
| Ave | 2.40 × 103 | 2.57 × 103 | 2.51 × 103 | 2.54 × 103 | 3.08 × 103 | 2.46 × 103 | 2.35 × 103 | 2.35 × 103 | |
| Std | 3.17 × 102 | 3.08 × 102 | 3.06 × 102 | 2.55 × 102 | 3.27 × 102 | 2.74 × 102 | 3.25 × 102 | 2.93 × 102 | |
| Rank | 3 | 7 | 5 | 6 | 8 | 4 | 1 | 2 | |
| F16 | Best | 1.72 × 103 | 1.78 × 103 | 1.80 × 103 | 1.73 × 103 | 1.83 × 103 | 1.74 × 103 | 1.80 × 103 | 1.78 × 103 |
| Ave | 1.90 × 103 | 2.19 × 103 | 2.10 × 103 | 2.13 × 103 | 2.21 × 103 | 2.02 × 103 | 2.15 × 103 | 1.94 × 103 | |
| Std | 1.62 × 102 | 2.20 × 102 | 1.84 × 102 | 2.02 × 102 | 1.82 × 102 | 1.67 × 102 | 2.03 × 102 | 1.28 × 102 | |
| Rank | 1 | 7 | 4 | 5 | 8 | 3 | 6 | 2 | |
| F17 | Best | 1.16 × 104 | 2.70 × 104 | 9.98 × 104 | 2.15 × 104 | 3.89 × 104 | 1.36 × 104 | 3.31 × 104 | 3.73 × 104 |
| Ave | 1.85 × 105 | 1.50 × 105 | 5.60 × 105 | 1.68 × 105 | 1.28 × 105 | 8.87 × 104 | 5.02 × 105 | 1.36 × 105 | |
| Std | 1.73 × 105 | 1.13 × 105 | 4.00 × 105 | 1.54 × 105 | 1.02 × 105 | 1.09 × 105 | 4.57 × 105 | 7.11 × 104 | |
| Rank | 6 | 4 | 8 | 5 | 2 | 1 | 7 | 3 | |
| F18 | Best | 2.04 × 103 | 1.95 × 103 | 2.06 × 103 | 1.92 × 103 | 2.54 × 103 | 1.92 × 103 | 1.93 × 103 | 2.11 × 103 |
| Ave | 9.78 × 103 | 1.25 × 104 | 1.48 × 104 | 8.47 × 103 | 1.14 × 105 | 6.12 × 103 | 2.46 × 104 | 5.84 × 103 | |
| Std | 1.28 × 104 | 1.43 × 104 | 1.29 × 104 | 8.11 × 103 | 6.50 × 104 | 6.13 × 103 | 2.00 × 104 | 3.83 × 103 | |
| Rank | 4 | 5 | 6 | 3 | 8 | 2 | 7 | 1 | |
| F19 | Best | 2.01 × 103 | 2.07 × 103 | 2.05 × 103 | 2.17 × 103 | 2.18 × 103 | 2.16 × 103 | 2.06 × 103 | 2.10 × 103 |
| Ave | 2.24 × 103 | 2.40 × 103 | 2.40 × 103 | 2.44 × 103 | 2.42 × 103 | 2.38 × 103 | 2.41 × 103 | 2.32 × 103 | |
| Std | 1.59 × 102 | 1.71 × 102 | 1.88 × 102 | 1.62 × 102 | 1.07 × 102 | 1.51 × 102 | 1.81 × 102 | 6.52 × 101 | |
| Rank | 1 | 4 | 5 | 8 | 7 | 3 | 6 | 2 | |
| F20 | Best | 2.32 × 103 | 2.35 × 103 | 2.34 × 103 | 2.20 × 103 | 2.40 × 103 | 2.34 × 103 | 2.34 × 103 | 2.34 × 103 |
| Ave | 2.36 × 103 | 2.39 × 103 | 2.38 × 103 | 2.40 × 103 | 2.46 × 103 | 2.37 × 103 | 2.39 × 103 | 2.38 × 103 | |
| Std | 3.94 × 101 | 2.29 × 101 | 2.40 × 101 | 4.28 × 101 | 3.06 × 101 | 2.29 × 101 | 2.86 × 101 | 1.81 × 101 | |
| Rank | 1 | 5 | 4 | 7 | 8 | 2 | 6 | 3 | |
| F21 | Best | 2.30 × 103 | 2.30 × 103 | 2.30 × 103 | 2.30 × 103 | 2.31 × 103 | 2.30 × 103 | 2.30 × 103 | 2.30 × 103 |
| Ave | 2.90 × 103 | 4.81 × 103 | 4.38 × 103 | 2.39 × 103 | 2.33 × 103 | 2.30 × 103 | 5.31 × 103 | 2.31 × 103 | |
| Std | 1.24 × 103 | 1.80 × 103 | 1.69 × 103 | 6.47 × 102 | 5.30 × 101 | 1.48 × 100 | 1.63 × 103 | 8.62 × 100 | |
| Rank | 5 | 7 | 6 | 4 | 3 | 1 | 8 | 2 | |
| F22 | Best | 2.66 × 103 | 2.72 × 103 | 2.70 × 103 | 2.71 × 103 | 2.77 × 103 | 2.68 × 103 | 2.70 × 103 | 2.71 × 103 |
| Ave | 2.70 × 103 | 2.75 × 103 | 2.74 × 103 | 2.80 × 103 | 2.86 × 103 | 2.74 × 103 | 2.74 × 103 | 2.77 × 103 | |
| Std | 3.48 × 101 | 2.59 × 101 | 2.48 × 101 | 5.10 × 101 | 4.72 × 101 | 2.48 × 101 | 2.16 × 101 | 4.01 × 101 | |
| Rank | 1 | 5 | 4 | 7 | 8 | 3 | 2 | 6 | |
| F23 | Best | 2.83 × 103 | 2.86 × 103 | 2.87 × 103 | 2.87 × 103 | 2.91 × 103 | 2.87 × 103 | 2.87 × 103 | 2.86 × 103 |
| Ave | 2.89 × 103 | 2.93 × 103 | 2.92 × 103 | 2.96 × 103 | 3.01 × 103 | 2.91 × 103 | 2.91 × 103 | 2.92 × 103 | |
| Std | 2.93 × 101 | 3.20 × 101 | 2.99 × 101 | 4.91 × 101 | 5.69 × 101 | 3.08 × 101 | 2.50 × 101 | 2.92 × 101 | |
| Rank | 1 | 6 | 4 | 7 | 8 | 2 | 3 | 5 | |
| F24 | Best | 2.88 × 103 | 2.88 × 103 | 2.89 × 103 | 2.88 × 103 | 2.90 × 103 | 2.88 × 103 | 2.88 × 103 | 2.89 × 103 |
| Ave | 2.89 × 103 | 2.90 × 103 | 2.90 × 103 | 2.89 × 103 | 2.95 × 103 | 2.89 × 103 | 2.89 × 103 | 2.92 × 103 | |
| Std | 1.37 × 101 | 1.82 × 101 | 1.48 × 101 | 1.59 × 101 | 2.19 × 101 | 1.31 × 101 | 7.44 × 100 | 2.79 × 101 | |
| Rank | 2 | 6 | 5 | 4 | 8 | 3 | 1 | 7 | |
| F25 | Best | 2.80 × 103 | 2.80 × 103 | 2.90 × 103 | 2.80 × 103 | 2.83 × 103 | 2.80 × 103 | 2.90 × 103 | 2.80 × 103 |
| Ave | 4.08 × 103 | 4.87 × 103 | 4.65 × 103 | 4.90 × 103 | 4.37 × 103 | 4.15 × 103 | 4.63 × 103 | 4.43 × 103 | |
| Std | 5.65 × 102 | 6.02 × 102 | 4.30 × 102 | 1.36 × 103 | 1.71 × 103 | 8.57 × 102 | 3.60 × 102 | 1.32 × 103 | |
| Rank | 1 | 7 | 6 | 8 | 3 | 2 | 5 | 4 | |
| F26 | Best | 3.19 × 103 | 3.21 × 103 | 3.20 × 103 | 3.22 × 103 | 3.23 × 103 | 3.19 × 103 | 3.20 × 103 | 3.20 × 103 |
| Ave | 3.22 × 103 | 3.24 × 103 | 3.23 × 103 | 3.26 × 103 | 3.32 × 103 | 3.23 × 103 | 3.22 × 103 | 3.25 × 103 | |
| Std | 1.54 × 101 | 2.11 × 101 | 1.47 × 101 | 2.61 × 101 | 6.07 × 101 | 1.35 × 101 | 1.19 × 101 | 2.52 × 101 | |
| Rank | 2 | 5 | 4 | 7 | 8 | 3 | 1 | 6 | |
| F27 | Best | 3.10 × 103 | 3.10 × 103 | 3.21 × 103 | 3.10 × 103 | 3.22 × 103 | 3.20 × 103 | 3.21 × 103 | 3.21 × 103 |
| Ave | 3.19 × 103 | 3.22 × 103 | 3.26 × 103 | 3.18 × 103 | 3.29 × 103 | 3.23 × 103 | 3.25 × 103 | 3.25 × 103 | |
| Std | 4.52 × 101 | 2.55 × 101 | 3.46 × 101 | 4.78 × 101 | 2.65 × 101 | 1.94 × 101 | 3.54 × 101 | 2.41 × 101 | |
| Rank | 2 | 3 | 7 | 1 | 8 | 4 | 5 | 6 | |
| F28 | Best | 3.34 × 103 | 3.34 × 103 | 3.49 × 103 | 3.39 × 103 | 4.00 × 103 | 3.38 × 103 | 3.46 × 103 | 3.42 × 103 |
| Ave | 3.59 × 103 | 3.77 × 103 | 3.86 × 103 | 3.78 × 103 | 4.48 × 103 | 3.69 × 103 | 3.77 × 103 | 3.82 × 103 | |
| Std | 1.80 × 102 | 1.80 × 102 | 1.82 × 102 | 2.11 × 102 | 2.69 × 102 | 1.92 × 102 | 1.61 × 102 | 1.60 × 102 | |
| Rank | 1 | 4 | 7 | 5 | 8 | 2 | 3 | 6 | |
| F29 | Best | 5.56 × 103 | 5.47 × 103 | 2.21 × 104 | 5.67 × 103 | 2.10 × 105 | 6.13 × 103 | 5.28 × 103 | 5.56 × 103 |
| Ave | 8.85 × 103 | 9.51 × 103 | 1.94 × 105 | 9.18 × 103 | 1.80 × 106 | 9.81 × 103 | 1.45 × 104 | 1.01 × 104 | |
| Std | 3.25 × 103 | 3.17 × 103 | 1.76 × 105 | 2.72 × 103 | 1.08 × 106 | 2.99 × 103 | 6.75 × 103 | 4.25 × 103 | |
| Rank | 1 | 3 | 7 | 2 | 8 | 4 | 6 | 5 |
| Function | Index | IFTTA | FTTA | RIME | MRFO | POEA | dFDBARO | DTSMA | RLTLBO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.03 × 102 | 3.21 × 103 | 1.71 × 106 | 1.00 × 102 | 1.05 × 102 | 1.14 × 106 | 2.26 × 102 | 3.45 × 106 |
| Ave | 7.41 × 103 | 8.29 × 105 | 4.29 × 106 | 3.85 × 103 | 2.75 × 103 | 4.02 × 106 | 2.91 × 106 | 2.24 × 108 | |
| Std | 8.54 × 103 | 1.63 × 106 | 1.48 × 106 | 4.70 × 103 | 2.75 × 103 | 2.27 × 106 | 8.83 × 106 | 3.99 × 108 | |
| Rank | 3 | 4 | 7 | 2 | 1 | 6 | 5 | 8 | |
| F2 | Best | 5.72 × 104 | 5.55 × 104 | 4.01 × 104 | 6.12 × 104 | 1.05 × 103 | 7.00 × 104 | 3.23 × 104 | 3.80 × 104 |
| Ave | 9.73 × 104 | 1.07 × 105 | 8.56 × 104 | 8.71 × 104 | 2.91 × 103 | 1.02 × 105 | 7.50 × 104 | 6.68 × 104 | |
| Std | 2.10 × 104 | 2.72 × 104 | 2.13 × 104 | 1.54 × 104 | 1.01 × 103 | 1.41 × 104 | 2.01 × 104 | 1.56 × 104 | |
| Rank | 6 | 8 | 4 | 5 | 1 | 7 | 3 | 2 | |
| F3 | Best | 4.29 × 102 | 4.71 × 102 | 5.09 × 102 | 4.09 × 102 | 4.85 × 102 | 4.96 × 102 | 4.44 × 102 | 5.12 × 102 |
| Ave | 5.10 × 102 | 5.61 × 102 | 6.17 × 102 | 5.27 × 102 | 6.23 × 102 | 5.99 × 102 | 5.90 × 102 | 6.52 × 102 | |
| Std | 5.59 × 101 | 5.03 × 101 | 5.00 × 101 | 5.31 × 101 | 5.39 × 101 | 4.74 × 101 | 4.40 × 101 | 7.68 × 101 | |
| Rank | 1 | 3 | 6 | 2 | 7 | 5 | 4 | 8 | |
| F4 | Best | 5.59 × 102 | 6.42 × 102 | 6.16 × 102 | 6.87 × 102 | 7.74 × 102 | 6.53 × 102 | 6.53 × 102 | 7.18 × 102 |
| Ave | 6.60 × 102 | 7.26 × 102 | 6.79 × 102 | 8.07 × 102 | 8.35 × 102 | 7.18 × 102 | 7.22 × 102 | 8.29 × 102 | |
| Std | 6.02 × 101 | 3.33 × 101 | 3.28 × 101 | 4.31 × 101 | 3.21 × 101 | 3.67 × 101 | 4.47 × 101 | 5.97 × 101 | |
| Rank | 1 | 5 | 2 | 6 | 8 | 3 | 4 | 7 | |
| F5 | Best | 6.00 × 102 | 6.01 × 102 | 6.05 × 102 | 6.08 × 102 | 6.46 × 102 | 6.03 × 102 | 6.08 × 102 | 6.15 × 102 |
| Ave | 6.00 × 102 | 6.04 × 102 | 6.13 × 102 | 6.33 × 102 | 6.62 × 102 | 6.09 × 102 | 6.19 × 102 | 6.30 × 102 | |
| Std | 1.90 × 10−2 | 2.17 × 100 | 5.51 × 100 | 1.19 × 101 | 7.45 × 100 | 4.19 × 100 | 6.40 × 100 | 8.09 × 100 | |
| Rank | 1 | 2 | 4 | 7 | 8 | 3 | 5 | 6 | |
| F6 | Best | 8.11 × 102 | 9.90 × 102 | 9.13 × 102 | 9.69 × 102 | 1.11 × 103 | 9.41 × 102 | 9.42 × 102 | 9.88 × 102 |
| Ave | 9.31 × 102 | 1.14 × 103 | 1.01 × 103 | 1.29 × 103 | 1.44 × 103 | 1.07 × 103 | 1.03 × 103 | 1.20 × 103 | |
| Std | 6.78 × 101 | 1.20 × 102 | 4.48 × 101 | 1.70 × 102 | 1.03 × 102 | 7.19 × 101 | 5.04 × 101 | 1.31 × 102 | |
| Rank | 1 | 5 | 2 | 7 | 8 | 4 | 3 | 6 | |
| F7 | Best | 8.57 × 102 | 9.55 × 102 | 9.04 × 102 | 9.89 × 102 | 1.09 × 103 | 9.46 × 102 | 9.42 × 102 | 9.97 × 102 |
| Ave | 9.57 × 102 | 1.01 × 103 | 9.91 × 102 | 1.12 × 103 | 1.15 × 103 | 1.02 × 103 | 1.03 × 103 | 1.11 × 103 | |
| Std | 6.90 × 101 | 3.45 × 101 | 4.48 × 101 | 6.07 × 101 | 3.53 × 101 | 3.85 × 101 | 4.50 × 101 | 5.31 × 101 | |
| Rank | 1 | 3 | 2 | 7 | 8 | 4 | 5 | 6 | |
| F8 | Best | 9.19 × 102 | 2.42 × 103 | 1.69 × 103 | 3.94 × 103 | 6.66 × 103 | 2.69 × 103 | 2.98 × 103 | 3.20 × 103 |
| Ave | 1.20 × 103 | 6.12 × 103 | 5.27 × 103 | 1.03 × 104 | 1.02 × 104 | 6.26 × 103 | 9.30 × 103 | 1.17 × 104 | |
| Std | 3.35 × 102 | 2.20 × 103 | 2.72 × 103 | 2.73 × 103 | 1.61 × 103 | 1.76 × 103 | 4.63 × 103 | 5.17 × 103 | |
| Rank | 1 | 3 | 2 | 7 | 6 | 4 | 5 | 8 | |
| F9 | Best | 4.54 × 103 | 4.62 × 103 | 5.99 × 103 | 5.12 × 103 | 7.04 × 103 | 4.85 × 103 | 5.96 × 103 | 6.66 × 103 |
| Ave | 5.85 × 103 | 7.04 × 103 | 7.39 × 103 | 7.41 × 103 | 9.26 × 103 | 6.23 × 103 | 8.57 × 103 | 1.15 × 104 | |
| Std | 6.05 × 102 | 9.12 × 102 | 7.06 × 102 | 8.47 × 102 | 9.19 × 102 | 6.87 × 102 | 1.25 × 103 | 2.11 × 103 | |
| Rank | 1 | 3 | 4 | 5 | 7 | 2 | 6 | 8 | |
| F10 | Best | 1.15 × 103 | 1.24 × 103 | 1.36 × 103 | 1.18 × 103 | 1.27 × 103 | 1.21 × 103 | 1.29 × 103 | 1.27 × 103 |
| Ave | 1.19 × 103 | 1.32 × 103 | 1.54 × 103 | 1.24 × 103 | 1.38 × 103 | 1.28 × 103 | 1.47 × 103 | 1.37 × 103 | |
| Std | 2.53 × 101 | 4.31 × 101 | 1.00 × 102 | 2.80 × 101 | 6.37 × 101 | 4.04 × 101 | 8.45 × 101 | 5.93 × 101 | |
| Rank | 1 | 4 | 8 | 2 | 6 | 3 | 7 | 5 | |
| F11 | Best | 3.74 × 105 | 5.37 × 105 | 1.88 × 107 | 8.20 × 104 | 3.38 × 106 | 1.08 × 106 | 1.60 × 106 | 9.75 × 105 |
| Ave | 1.36 × 106 | 4.58 × 106 | 8.36 × 107 | 1.38 × 106 | 3.26 × 107 | 5.09 × 106 | 8.80 × 106 | 6.24 × 106 | |
| Std | 9.33 × 105 | 5.14 × 106 | 4.74 × 107 | 9.12 × 105 | 1.59 × 107 | 2.73 × 106 | 4.67 × 106 | 4.39 × 106 | |
| Rank | 1 | 3 | 8 | 2 | 7 | 4 | 6 | 5 | |
| F12 | Best | 1.40 × 103 | 1.63 × 103 | 3.95 × 104 | 1.44 × 103 | 2.16 × 104 | 1.85 × 103 | 2.48 × 103 | 3.57 × 103 |
| Ave | 7.07 × 103 | 8.51 × 103 | 2.02 × 105 | 6.61 × 103 | 8.67 × 104 | 5.57 × 103 | 2.34 × 104 | 9.95 × 103 | |
| Std | 7.02 × 103 | 7.54 × 103 | 1.46 × 105 | 6.54 × 103 | 6.28 × 104 | 4.04 × 103 | 1.25 × 104 | 5.89 × 103 | |
| Rank | 3 | 4 | 8 | 2 | 7 | 1 | 6 | 5 | |
| F13 | Best | 5.54 × 103 | 8.22 × 103 | 3.99 × 104 | 3.47 × 103 | 5.34 × 103 | 2.92 × 103 | 4.42 × 104 | 3.45 × 103 |
| Ave | 7.86 × 104 | 1.36 × 105 | 2.31 × 105 | 5.94 × 104 | 1.02 × 105 | 6.05 × 104 | 1.85 × 105 | 5.02 × 104 | |
| Std | 7.53 × 104 | 1.48 × 105 | 1.36 × 105 | 4.40 × 104 | 5.84 × 104 | 4.16 × 104 | 1.20 × 105 | 4.79 × 104 | |
| Rank | 4 | 6 | 8 | 2 | 5 | 3 | 7 | 1 | |
| F14 | Best | 1.57 × 103 | 1.72 × 103 | 1.52 × 104 | 1.58 × 103 | 1.09 × 104 | 1.70 × 103 | 1.93 × 103 | 1.94 × 103 |
| Ave | 9.28 × 103 | 9.48 × 103 | 4.99 × 104 | 8.59 × 103 | 3.83 × 104 | 6.91 × 103 | 1.97 × 104 | 1.22 × 104 | |
| Std | 7.60 × 103 | 6.79 × 103 | 2.76 × 104 | 6.50 × 103 | 2.40 × 104 | 4.92 × 103 | 1.05 × 104 | 6.44 × 103 | |
| Rank | 3 | 4 | 8 | 2 | 7 | 1 | 6 | 5 | |
| F15 | Best | 2.22 × 103 | 2.22 × 103 | 2.12 × 103 | 2.41 × 103 | 2.61 × 103 | 2.19 × 103 | 2.36 × 103 | 2.36 × 103 |
| Ave | 3.38 × 103 | 3.47 × 103 | 3.56 × 103 | 3.35 × 103 | 3.96 × 103 | 3.16 × 103 | 3.19 × 103 | 3.05 × 103 | |
| Std | 4.99 × 102 | 4.77 × 102 | 4.56 × 102 | 4.34 × 102 | 7.09 × 102 | 4.18 × 102 | 5.08 × 102 | 3.56 × 102 | |
| Rank | 5 | 6 | 7 | 4 | 8 | 2 | 3 | 1 | |
| F16 | Best | 2.00 × 103 | 2.46 × 103 | 2.62 × 103 | 2.49 × 103 | 2.57 × 103 | 2.18 × 103 | 2.37 × 103 | 2.39 × 103 |
| Ave | 2.84 × 103 | 3.20 × 103 | 3.21 × 103 | 3.07 × 103 | 3.53 × 103 | 2.82 × 103 | 3.01 × 103 | 2.94 × 103 | |
| Std | 3.34 × 102 | 3.62 × 102 | 3.65 × 102 | 3.10 × 102 | 3.56 × 102 | 2.70 × 102 | 2.54 × 102 | 3.04 × 102 | |
| Rank | 2 | 6 | 7 | 5 | 8 | 1 | 4 | 3 | |
| F17 | Best | 1.11 × 105 | 4.84 × 104 | 4.18 × 105 | 4.52 × 104 | 1.49 × 105 | 9.99 × 104 | 2.79 × 105 | 6.17 × 104 |
| Ave | 1.05 × 106 | 5.95 × 105 | 3.78 × 106 | 5.55 × 105 | 9.01 × 105 | 7.74 × 105 | 2.26 × 106 | 6.12 × 105 | |
| Std | 9.61 × 105 | 7.18 × 105 | 2.53 × 106 | 4.85 × 105 | 5.38 × 105 | 6.74 × 105 | 1.38 × 106 | 3.79 × 105 | |
| Rank | 6 | 2 | 8 | 1 | 5 | 4 | 7 | 3 | |
| F18 | Best | 1.92 × 103 | 2.15 × 103 | 3.24 × 103 | 1.97 × 103 | 5.32 × 104 | 2.13 × 103 | 2.15 × 103 | 3.06 × 103 |
| Ave | 1.77 × 104 | 1.82 × 104 | 5.51 × 104 | 1.58 × 104 | 6.96 × 105 | 1.49 × 104 | 1.94 × 104 | 2.04 × 104 | |
| Std | 1.08 × 104 | 1.23 × 104 | 4.23 × 104 | 9.42 × 103 | 3.77 × 105 | 8.67 × 103 | 1.69 × 104 | 9.05 × 103 | |
| Rank | 3 | 4 | 7 | 2 | 8 | 1 | 5 | 6 | |
| F19 | Best | 2.20 × 103 | 2.41 × 103 | 2.36 × 103 | 2.23 × 103 | 2.43 × 103 | 2.34 × 103 | 2.44 × 103 | 2.57 × 103 |
| Ave | 2.94 × 103 | 3.11 × 103 | 3.18 × 103 | 3.15 × 103 | 3.16 × 103 | 2.93 × 103 | 3.11 × 103 | 3.04 × 103 | |
| Std | 3.16 × 102 | 3.36 × 102 | 3.48 × 102 | 3.18 × 102 | 2.71 × 102 | 2.42 × 102 | 3.65 × 102 | 2.73 × 102 | |
| Rank | 2 | 4 | 8 | 6 | 7 | 1 | 5 | 3 | |
| F20 | Best | 2.35 × 103 | 2.40 × 103 | 2.40 × 103 | 2.46 × 103 | 2.58 × 103 | 2.41 × 103 | 2.42 × 103 | 2.43 × 103 |
| Ave | 2.46 × 103 | 2.52 × 103 | 2.49 × 103 | 2.55 × 103 | 2.67 × 103 | 2.48 × 103 | 2.50 × 103 | 2.51 × 103 | |
| Std | 7.21 × 101 | 4.59 × 101 | 3.96 × 101 | 4.54 × 101 | 5.32 × 101 | 3.21 × 101 | 4.82 × 101 | 2.96 × 101 | |
| Rank | 1 | 6 | 3 | 7 | 8 | 2 | 4 | 5 | |
| F21 | Best | 6.63 × 103 | 7.18 × 103 | 7.06 × 103 | 2.30 × 103 | 2.33 × 103 | 2.32 × 103 | 7.41 × 103 | 2.34 × 103 |
| Ave | 8.19 × 103 | 8.61 × 103 | 9.21 × 103 | 9.21 × 103 | 1.02 × 104 | 7.48 × 103 | 9.85 × 103 | 4.01 × 103 | |
| Std | 7.47 × 102 | 8.57 × 102 | 7.98 × 102 | 1.75 × 103 | 2.75 × 103 | 2.23 × 103 | 1.07 × 103 | 3.31 × 103 | |
| Rank | 3 | 4 | 5 | 6 | 8 | 2 | 7 | 1 | |
| F22 | Best | 2.77 × 103 | 2.93 × 103 | 2.87 × 103 | 2.88 × 103 | 3.09 × 103 | 2.85 × 103 | 2.86 × 103 | 2.93 × 103 |
| Ave | 2.88 × 103 | 3.01 × 103 | 2.96 × 103 | 3.05 × 103 | 3.25 × 103 | 2.94 × 103 | 2.93 × 103 | 3.05 × 103 | |
| Std | 6.71 × 101 | 5.05 × 101 | 5.66 × 101 | 8.46 × 101 | 8.12 × 101 | 5.13 × 101 | 3.71 × 101 | 7.44 × 101 | |
| Rank | 1 | 5 | 4 | 7 | 8 | 3 | 2 | 6 | |
| F23 | Best | 2.97 × 103 | 3.06 × 103 | 3.02 × 103 | 3.06 × 103 | 3.20 × 103 | 3.01 × 103 | 3.01 × 103 | 3.04 × 103 |
| Ave | 3.06 × 103 | 3.16 × 103 | 3.11 × 103 | 3.24 × 103 | 3.38 × 103 | 3.13 × 103 | 3.08 × 103 | 3.20 × 103 | |
| Std | 7.17 × 101 | 5.89 × 101 | 4.86 × 101 | 9.58 × 101 | 9.26 × 101 | 4.67 × 101 | 3.72 × 101 | 7.84 × 101 | |
| Rank | 1 | 5 | 3 | 7 | 8 | 4 | 2 | 6 | |
| F24 | Best | 2.96 × 103 | 3.02 × 103 | 3.02 × 103 | 3.01 × 103 | 3.10 × 103 | 3.06 × 103 | 2.98 × 103 | 3.10 × 103 |
| Ave | 3.05 × 103 | 3.09 × 103 | 3.09 × 103 | 3.08 × 103 | 3.17 × 103 | 3.13 × 103 | 3.07 × 103 | 3.20 × 103 | |
| Std | 3.43 × 101 | 2.97 × 101 | 3.70 × 101 | 2.57 × 101 | 4.48 × 101 | 4.41 × 101 | 3.81 × 101 | 5.82 × 101 | |
| Rank | 1 | 4 | 5 | 3 | 7 | 6 | 2 | 8 | |
| F25 | Best | 4.62 × 103 | 2.96 × 103 | 5.26 × 103 | 2.90 × 103 | 2.99 × 103 | 2.99 × 103 | 5.11 × 103 | 3.74 × 103 |
| Ave | 5.36 × 103 | 7.30 × 103 | 6.05 × 103 | 6.70 × 103 | 4.58 × 103 | 6.23 × 103 | 5.96 × 103 | 8.70 × 103 | |
| Std | 6.34 × 102 | 1.57 × 103 | 4.77 × 102 | 3.53 × 103 | 2.57 × 103 | 1.93 × 103 | 4.52 × 102 | 2.54 × 103 | |
| Rank | 2 | 7 | 4 | 6 | 1 | 5 | 3 | 8 | |
| F26 | Best | 3.25 × 103 | 3.30 × 103 | 3.32 × 103 | 3.37 × 103 | 3.50 × 103 | 3.32 × 103 | 3.26 × 103 | 3.36 × 103 |
| Ave | 3.42 × 103 | 3.50 × 103 | 3.50 × 103 | 3.59 × 103 | 3.89 × 103 | 3.49 × 103 | 3.43 × 103 | 3.64 × 103 | |
| Std | 8.39 × 101 | 1.09 × 102 | 9.23 × 101 | 1.39 × 102 | 2.39 × 102 | 9.00 × 101 | 8.81 × 101 | 1.33 × 102 | |
| Rank | 1 | 4 | 5 | 6 | 8 | 3 | 2 | 7 | |
| F27 | Best | 3.27 × 103 | 3.28 × 103 | 3.29 × 103 | 3.26 × 103 | 3.38 × 103 | 3.29 × 103 | 3.32 × 103 | 3.37 × 103 |
| Ave | 3.31 × 103 | 3.34 × 103 | 3.36 × 103 | 3.32 × 103 | 3.47 × 103 | 3.41 × 103 | 3.54 × 103 | 3.54 × 103 | |
| Std | 1.59 × 101 | 3.20 × 101 | 4.14 × 101 | 3.00 × 101 | 5.42 × 101 | 5.33 × 101 | 4.28 × 102 | 7.92 × 101 | |
| Rank | 1 | 3 | 4 | 2 | 6 | 5 | 8 | 7 | |
| F28 | Best | 3.38 × 103 | 3.74 × 103 | 3.85 × 103 | 3.62 × 103 | 5.00 × 103 | 3.60 × 103 | 3.72 × 103 | 3.76 × 103 |
| Ave | 3.88 × 103 | 4.33 × 103 | 4.68 × 103 | 4.34 × 103 | 6.31 × 103 | 4.09 × 103 | 4.32 × 103 | 4.70 × 103 | |
| Std | 3.83 × 102 | 2.87 × 102 | 3.49 × 102 | 3.34 × 102 | 5.54 × 102 | 2.93 × 102 | 3.28 × 102 | 4.11 × 102 | |
| Rank | 1 | 4 | 6 | 5 | 8 | 2 | 3 | 7 | |
| F29 | Best | 6.04 × 105 | 6.94 × 105 | 1.09 × 107 | 7.02 × 105 | 3.46 × 107 | 8.17 × 105 | 7.60 × 105 | 5.54 × 105 |
| Ave | 9.33 × 105 | 9.75 × 105 | 2.36 × 107 | 1.07 × 106 | 5.80 × 107 | 1.46 × 106 | 2.10 × 106 | 9.79 × 105 | |
| Std | 2.12 × 105 | 2.14 × 105 | 7.57 × 106 | 2.82 × 105 | 1.56 × 107 | 3.11 × 105 | 8.83 × 105 | 2.87 × 105 | |
| Rank | 1 | 2 | 7 | 4 | 8 | 5 | 6 | 3 |
| Function | Index | IFTTA | FTTA | RIME | MRFO | POEA | dFDBARO | DTSMA | RLTLBO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 7.08 × 103 | 1.72 × 107 | 5.90 × 107 | 1.19 × 105 | 6.59 × 105 | 5.62 × 108 | 5.02 × 108 | 4.01 × 109 |
| Ave | 4.49 × 104 | 8.38 × 107 | 9.86 × 107 | 4.47 × 105 | 2.84 × 106 | 1.97 × 109 | 4.24 × 109 | 1.57 × 1010 | |
| Std | 4.81 × 104 | 6.51 × 107 | 2.03 × 107 | 3.04 × 105 | 3.26 × 106 | 7.43 × 108 | 2.17 × 109 | 5.27 × 109 | |
| Rank | 1 | 4 | 5 | 2 | 3 | 6 | 7 | 8 | |
| F2 | Best | 2.59 × 105 | 2.92 × 105 | 4.00 × 105 | 2.41 × 105 | 6.52 × 104 | 2.51 × 105 | 2.87 × 105 | 2.39 × 105 |
| Ave | 3.76 × 105 | 4.62 × 105 | 5.11 × 105 | 2.86 × 105 | 8.82 × 104 | 3.03 × 105 | 4.73 × 105 | 3.05 × 105 | |
| Std | 5.44 × 104 | 7.92 × 104 | 6.16 × 104 | 2.76 × 104 | 8.83 × 103 | 1.97 × 104 | 8.58 × 104 | 2.56 × 104 | |
| Rank | 5 | 6 | 8 | 2 | 1 | 3 | 7 | 4 | |
| F3 | Best | 5.98 × 102 | 6.94 × 102 | 7.93 × 102 | 6.78 × 102 | 8.21 × 102 | 1.04 × 103 | 7.61 × 102 | 1.42 × 103 |
| Ave | 6.98 × 102 | 8.81 × 102 | 9.28 × 102 | 8.03 × 102 | 9.65 × 102 | 1.31 × 103 | 9.60 × 102 | 2.42 × 103 | |
| Std | 5.14 × 101 | 7.95 × 101 | 8.17 × 101 | 6.04 × 101 | 7.92 × 101 | 1.76 × 102 | 1.08 × 102 | 5.49 × 102 | |
| Rank | 1 | 3 | 4 | 2 | 6 | 7 | 5 | 8 | |
| F4 | Best | 7.35 × 102 | 9.79 × 102 | 8.84 × 102 | 1.07 × 103 | 1.33 × 103 | 9.35 × 102 | 9.46 × 102 | 1.21 × 103 |
| Ave | 9.84 × 102 | 1.16 × 103 | 1.04 × 103 | 1.29 × 103 | 1.48 × 103 | 1.15 × 103 | 1.17 × 103 | 1.41 × 103 | |
| Std | 1.31 × 102 | 7.90 × 101 | 7.85 × 101 | 7.61 × 101 | 6.63 × 101 | 8.31 × 101 | 9.10 × 101 | 1.01 × 102 | |
| Rank | 1 | 4 | 2 | 6 | 8 | 3 | 5 | 7 | |
| F5 | Best | 6.00 × 102 | 6.08 × 102 | 6.22 × 102 | 6.35 × 102 | 6.68 × 102 | 6.25 × 102 | 6.31 × 102 | 6.27 × 102 |
| Ave | 6.00 × 102 | 6.16 × 102 | 6.35 × 102 | 6.55 × 102 | 6.79 × 102 | 6.35 × 102 | 6.49 × 102 | 6.54 × 102 | |
| Std | 4.55 × 10−2 | 4.18 × 100 | 6.20 × 100 | 6.40 × 100 | 4.03 × 100 | 5.91 × 100 | 8.01 × 100 | 8.41 × 100 | |
| Rank | 1 | 2 | 3 | 7 | 8 | 4 | 5 | 6 | |
| F6 | Best | 1.11 × 103 | 1.73 × 103 | 1.43 × 103 | 2.17 × 103 | 2.59 × 103 | 1.66 × 103 | 1.66 × 103 | 2.03 × 103 |
| Ave | 1.43 × 103 | 2.11 × 103 | 1.64 × 103 | 2.68 × 103 | 3.01 × 103 | 2.14 × 103 | 1.92 × 103 | 2.43 × 103 | |
| Std | 1.50 × 102 | 2.02 × 102 | 1.27 × 102 | 3.01 × 102 | 2.24 × 102 | 1.98 × 102 | 1.81 × 102 | 2.26 × 102 | |
| Rank | 1 | 4 | 2 | 7 | 8 | 5 | 3 | 6 | |
| F7 | Best | 9.88 × 102 | 1.28 × 103 | 1.16 × 103 | 1.40 × 103 | 1.65 × 103 | 1.25 × 103 | 1.23 × 103 | 1.44 × 103 |
| Ave | 1.30 × 103 | 1.48 × 103 | 1.36 × 103 | 1.67 × 103 | 1.90 × 103 | 1.44 × 103 | 1.46 × 103 | 1.75 × 103 | |
| Std | 1.47 × 102 | 9.35 × 101 | 8.06 × 101 | 1.26 × 102 | 9.49 × 101 | 8.36 × 101 | 1.05 × 102 | 1.60 × 102 | |
| Rank | 1 | 5 | 2 | 6 | 8 | 3 | 4 | 7 | |
| F8 | Best | 5.00 × 103 | 1.52 × 104 | 9.90 × 103 | 2.05 × 104 | 1.68 × 104 | 1.84 × 104 | 1.98 × 104 | 3.99 × 104 |
| Ave | 1.20 × 104 | 2.33 × 104 | 2.80 × 104 | 2.29 × 104 | 3.50 × 104 | 2.33 × 104 | 3.66 × 104 | 5.86 × 104 | |
| Std | 5.26 × 103 | 4.12 × 103 | 9.27 × 103 | 1.22 × 103 | 1.19 × 104 | 3.02 × 103 | 1.12 × 104 | 1.09 × 104 | |
| Rank | 1 | 3 | 5 | 2 | 6 | 4 | 7 | 8 | |
| F9 | Best | 1.04 × 104 | 1.32 × 104 | 1.27 × 104 | 1.16 × 104 | 1.93 × 104 | 1.27 × 104 | 1.50 × 104 | 1.92 × 104 |
| Ave | 1.30 × 104 | 1.60 × 104 | 1.67 × 104 | 1.48 × 104 | 2.21 × 104 | 1.51 × 104 | 1.96 × 104 | 2.30 × 104 | |
| Std | 1.21 × 103 | 1.53 × 103 | 1.82 × 103 | 1.41 × 103 | 1.38 × 103 | 1.32 × 103 | 1.79 × 103 | 1.78 × 103 | |
| Rank | 1 | 4 | 5 | 2 | 7 | 3 | 6 | 8 | |
| F10 | Best | 2.39 × 103 | 5.59 × 103 | 5.34 × 103 | 6.28 × 103 | 2.71 × 103 | 1.41 × 104 | 3.84 × 103 | 3.69 × 103 |
| Ave | 5.69 × 103 | 1.91 × 104 | 7.41 × 103 | 1.86 × 104 | 3.26 × 103 | 2.72 × 104 | 7.34 × 103 | 6.35 × 103 | |
| Std | 3.62 × 103 | 1.03 × 104 | 1.34 × 103 | 7.74 × 103 | 3.48 × 102 | 7.66 × 103 | 2.95 × 103 | 2.57 × 103 | |
| Rank | 2 | 7 | 5 | 6 | 1 | 8 | 4 | 3 | |
| F11 | Best | 2.35 × 106 | 1.16 × 107 | 1.79 × 108 | 2.96 × 106 | 1.36 × 108 | 6.06 × 107 | 2.03 × 107 | 1.48 × 108 |
| Ave | 1.13 × 107 | 4.73 × 107 | 7.13 × 108 | 1.23 × 107 | 4.40 × 108 | 1.73 × 108 | 2.26 × 108 | 8.77 × 108 | |
| Std | 1.00 × 107 | 2.23 × 107 | 2.99 × 108 | 6.75 × 106 | 1.63 × 108 | 7.33 × 107 | 1.93 × 108 | 1.45 × 109 | |
| Rank | 1 | 3 | 7 | 2 | 6 | 4 | 5 | 8 | |
| F12 | Best | 1.65 × 103 | 4.04 × 103 | 1.29 × 105 | 1.70 × 103 | 2.26 × 104 | 9.39 × 103 | 1.21 × 104 | 1.30 × 104 |
| Ave | 7.70 × 103 | 4.76 × 104 | 4.80 × 105 | 7.42 × 103 | 5.54 × 104 | 1.89 × 104 | 3.30 × 105 | 4.25 × 105 | |
| Std | 7.37 × 103 | 9.48 × 104 | 1.29 × 106 | 5.78 × 103 | 1.94 × 104 | 5.64 × 103 | 1.02 × 106 | 1.58 × 106 | |
| Rank | 2 | 4 | 8 | 1 | 5 | 3 | 6 | 7 | |
| F13 | Best | 1.45 × 105 | 1.86 × 105 | 8.96 × 105 | 1.56 × 105 | 1.73 × 105 | 2.02 × 105 | 8.18 × 105 | 2.29 × 105 |
| Ave | 6.64 × 105 | 1.34 × 106 | 4.38 × 106 | 6.67 × 105 | 7.87 × 105 | 1.07 × 106 | 2.57 × 106 | 9.32 × 105 | |
| Std | 3.33 × 105 | 8.81 × 105 | 1.93 × 106 | 3.02 × 105 | 3.30 × 105 | 5.62 × 105 | 1.36 × 106 | 4.36 × 105 | |
| Rank | 1 | 6 | 8 | 2 | 3 | 5 | 7 | 4 | |
| F14 | Best | 1.63 × 103 | 1.97 × 103 | 4.25 × 104 | 1.75 × 103 | 2.00 × 104 | 2.33 × 103 | 2.74 × 103 | 2.77 × 103 |
| Ave | 3.60 × 103 | 5.64 × 103 | 2.40 × 105 | 4.90 × 103 | 4.55 × 104 | 4.31 × 103 | 4.70 × 104 | 7.23 × 103 | |
| Std | 2.71 × 103 | 3.85 × 103 | 7.85 × 105 | 3.59 × 103 | 1.75 × 104 | 1.73 × 103 | 6.59 × 104 | 3.74 × 103 | |
| Rank | 1 | 4 | 8 | 3 | 6 | 2 | 7 | 5 | |
| F15 | Best | 4.13 × 103 | 3.97 × 103 | 4.51 × 103 | 3.82 × 103 | 6.54 × 103 | 4.41 × 103 | 3.62 × 103 | 4.25 × 103 |
| Ave | 5.90 × 103 | 5.84 × 103 | 6.56 × 103 | 5.65 × 103 | 9.23 × 103 | 5.58 × 103 | 5.56 × 103 | 6.22 × 103 | |
| Std | 7.08 × 102 | 6.79 × 102 | 8.22 × 102 | 7.30 × 102 | 1.49 × 103 | 5.71 × 102 | 7.97 × 102 | 9.91 × 102 | |
| Rank | 5 | 4 | 7 | 3 | 8 | 2 | 1 | 6 | |
| F16 | Best | 3.50 × 103 | 3.67 × 103 | 4.47 × 103 | 3.60 × 103 | 4.58 × 103 | 3.43 × 103 | 4.36 × 103 | 4.28 × 103 |
| Ave | 4.78 × 103 | 5.21 × 103 | 5.50 × 103 | 4.67 × 103 | 5.95 × 103 | 4.36 × 103 | 5.49 × 103 | 5.30 × 103 | |
| Std | 5.59 × 102 | 5.10 × 102 | 5.69 × 102 | 6.00 × 102 | 7.14 × 102 | 4.72 × 102 | 5.26 × 102 | 5.52 × 102 | |
| Rank | 3 | 4 | 7 | 2 | 8 | 1 | 6 | 5 | |
| F17 | Best | 4.74 × 105 | 4.63 × 105 | 2.37 × 106 | 3.86 × 105 | 3.86 × 105 | 3.28 × 105 | 1.28 × 106 | 3.64 × 105 |
| Ave | 1.46 × 106 | 1.65 × 106 | 6.45 × 106 | 1.30 × 106 | 1.33 × 106 | 1.77 × 106 | 4.59 × 106 | 1.14 × 106 | |
| Std | 6.99 × 105 | 8.55 × 105 | 2.79 × 106 | 6.02 × 105 | 4.53 × 105 | 9.32 × 105 | 2.50 × 106 | 6.16 × 105 | |
| Rank | 4 | 5 | 8 | 2 | 3 | 6 | 7 | 1 | |
| F18 | Best | 1.97 × 103 | 2.33 × 103 | 9.88 × 105 | 2.02 × 103 | 3.70 × 105 | 2.17 × 103 | 2.68 × 103 | 2.37 × 103 |
| Ave | 5.93 × 103 | 9.09 × 103 | 8.13 × 106 | 5.76 × 103 | 4.46 × 106 | 5.00 × 103 | 1.56 × 104 | 2.07 × 104 | |
| Std | 4.75 × 103 | 8.26 × 103 | 4.87 × 106 | 4.49 × 103 | 2.58 × 106 | 3.56 × 103 | 1.08 × 104 | 5.03 × 104 | |
| Rank | 3 | 4 | 8 | 2 | 7 | 1 | 5 | 6 | |
| F19 | Best | 3.33 × 103 | 3.60 × 103 | 4.46 × 103 | 3.24 × 103 | 4.32 × 103 | 3.61 × 103 | 4.14 × 103 | 4.38 × 103 |
| Ave | 4.92 × 103 | 5.15 × 103 | 5.37 × 103 | 5.04 × 103 | 5.30 × 103 | 4.78 × 103 | 5.38 × 103 | 6.25 × 103 | |
| Std | 6.72 × 102 | 6.66 × 102 | 5.23 × 102 | 6.67 × 102 | 5.52 × 102 | 5.58 × 102 | 5.97 × 102 | 7.86 × 102 | |
| Rank | 2 | 4 | 6 | 3 | 5 | 1 | 7 | 8 | |
| F20 | Best | 2.52 × 103 | 2.89 × 103 | 2.76 × 103 | 2.73 × 103 | 3.28 × 103 | 2.71 × 103 | 2.78 × 103 | 2.95 × 103 |
| Ave | 2.75 × 103 | 3.02 × 103 | 2.92 × 103 | 3.00 × 103 | 3.56 × 103 | 2.88 × 103 | 2.95 × 103 | 3.13 × 103 | |
| Std | 1.52 × 102 | 8.06 × 101 | 8.81 × 101 | 1.21 × 102 | 1.18 × 102 | 6.64 × 101 | 9.94 × 101 | 1.01 × 102 | |
| Rank | 1 | 6 | 3 | 5 | 8 | 2 | 4 | 7 | |
| F21 | Best | 1.29 × 104 | 1.42 × 104 | 1.58 × 104 | 1.51 × 104 | 2.19 × 104 | 1.49 × 104 | 1.79 × 104 | 4.00 × 103 |
| Ave | 1.58 × 104 | 1.89 × 104 | 1.92 × 104 | 1.91 × 104 | 2.50 × 104 | 1.82 × 104 | 2.24 × 104 | 1.90 × 104 | |
| Std | 1.07 × 103 | 1.70 × 103 | 1.43 × 103 | 1.77 × 103 | 1.50 × 103 | 1.60 × 103 | 2.12 × 103 | 7.74 × 103 | |
| Rank | 1 | 3 | 6 | 5 | 8 | 2 | 7 | 4 | |
| F22 | Best | 2.97 × 103 | 3.16 × 103 | 3.28 × 103 | 3.29 × 103 | 3.96 × 103 | 3.27 × 103 | 3.25 × 103 | 3.48 × 103 |
| Ave | 3.15 × 103 | 3.34 × 103 | 3.41 × 103 | 3.58 × 103 | 4.31 × 103 | 3.41 × 103 | 3.36 × 103 | 3.78 × 103 | |
| Std | 5.99 × 101 | 6.85 × 101 | 7.81 × 101 | 1.13 × 102 | 1.85 × 102 | 7.66 × 101 | 5.14 × 101 | 1.44 × 102 | |
| Rank | 1 | 2 | 4 | 6 | 8 | 5 | 3 | 7 | |
| F23 | Best | 3.50 × 103 | 3.90 × 103 | 3.76 × 103 | 3.95 × 103 | 4.75 × 103 | 3.92 × 103 | 3.67 × 103 | 4.18 × 103 |
| Ave | 3.75 × 103 | 4.07 × 103 | 4.05 × 103 | 4.42 × 103 | 5.25 × 103 | 4.18 × 103 | 3.85 × 103 | 4.65 × 103 | |
| Std | 1.40 × 102 | 9.87 × 101 | 1.14 × 102 | 2.01 × 102 | 2.88 × 102 | 1.10 × 102 | 7.37 × 101 | 1.95 × 102 | |
| Rank | 1 | 4 | 3 | 6 | 8 | 5 | 2 | 7 | |
| F24 | Best | 3.19 × 103 | 3.37 × 103 | 3.49 × 103 | 3.34 × 103 | 3.50 × 103 | 3.72 × 103 | 3.60 × 103 | 3.92 × 103 |
| Ave | 3.31 × 103 | 3.53 × 103 | 3.63 × 103 | 3.45 × 103 | 3.82 × 103 | 3.95 × 103 | 3.97 × 103 | 4.73 × 103 | |
| Std | 6.39 × 101 | 8.80 × 101 | 7.43 × 101 | 5.77 × 101 | 1.01 × 102 | 1.27 × 102 | 2.56 × 102 | 4.56 × 102 | |
| Rank | 1 | 3 | 4 | 2 | 5 | 6 | 7 | 8 | |
| F25 | Best | 8.50 × 103 | 1.24 × 104 | 1.09 × 104 | 3.80 × 103 | 5.85 × 103 | 8.20 × 103 | 1.03 × 104 | 1.52 × 104 |
| Ave | 1.11 × 104 | 1.58 × 104 | 1.31 × 104 | 1.90 × 104 | 1.77 × 104 | 1.72 × 104 | 1.19 × 104 | 2.61 × 104 | |
| Std | 1.45 × 103 | 2.27 × 103 | 9.86 × 102 | 6.93 × 103 | 9.26 × 103 | 2.64 × 103 | 9.59 × 102 | 3.55 × 103 | |
| Rank | 1 | 4 | 3 | 7 | 6 | 5 | 2 | 8 | |
| F26 | Best | 3.43 × 103 | 3.45 × 103 | 3.62 × 103 | 3.63 × 103 | 3.82 × 103 | 3.62 × 103 | 3.42 × 103 | 3.85 × 103 |
| Ave | 3.54 × 103 | 3.65 × 103 | 3.82 × 103 | 3.90 × 103 | 4.46 × 103 | 3.86 × 103 | 3.55 × 103 | 4.33 × 103 | |
| Std | 5.82 × 101 | 1.00 × 102 | 1.12 × 102 | 1.66 × 102 | 3.38 × 102 | 1.29 × 102 | 6.14 × 101 | 3.05 × 102 | |
| Rank | 1 | 3 | 4 | 6 | 8 | 5 | 2 | 7 | |
| F27 | Best | 3.37 × 103 | 3.48 × 103 | 3.56 × 103 | 3.43 × 103 | 3.71 × 103 | 4.01 × 103 | 3.73 × 103 | 4.85 × 103 |
| Ave | 3.43 × 103 | 3.61 × 103 | 3.71 × 103 | 3.57 × 103 | 3.93 × 103 | 4.47 × 103 | 6.87 × 103 | 6.16 × 103 | |
| Std | 3.18 × 101 | 4.91 × 101 | 6.01 × 101 | 4.91 × 101 | 1.62 × 102 | 2.91 × 102 | 3.43 × 103 | 7.75 × 102 | |
| Rank | 1 | 3 | 4 | 2 | 5 | 6 | 8 | 7 | |
| F28 | Best | 5.10 × 103 | 5.92 × 103 | 7.24 × 103 | 5.24 × 103 | 9.23 × 103 | 5.65 × 103 | 5.95 × 103 | 6.83 × 103 |
| Ave | 6.69 × 103 | 7.03 × 103 | 8.80 × 103 | 6.72 × 103 | 1.17 × 104 | 6.84 × 103 | 7.25 × 103 | 8.42 × 103 | |
| Std | 8.13 × 102 | 5.29 × 102 | 6.43 × 102 | 5.24 × 102 | 1.06 × 103 | 5.06 × 102 | 7.61 × 102 | 7.63 × 102 | |
| Rank | 1 | 4 | 7 | 2 | 8 | 3 | 5 | 6 | |
| F29 | Best | 6.40 × 103 | 1.02 × 104 | 1.90 × 107 | 1.75 × 104 | 2.95 × 107 | 1.41 × 105 | 3.19 × 104 | 1.23 × 105 |
| Ave | 1.62 × 104 | 6.15 × 104 | 8.27 × 107 | 7.59 × 104 | 9.36 × 107 | 6.55 × 105 | 4.65 × 105 | 1.24 × 106 | |
| Std | 6.24 × 103 | 5.51 × 104 | 4.31 × 107 | 6.74 × 104 | 4.65 × 107 | 3.74 × 105 | 4.98 × 105 | 2.08 × 106 | |
| Rank | 1 | 2 | 7 | 3 | 8 | 5 | 4 | 6 |

References
- AL Ahmad, A.; Sirjani, R. Optimal placement and sizing of multi-type FACTS devices in power systems using metaheuristic optimisation techniques: An updated review. Ain Shams Eng. J. 2020, 11, 611–628. [Google Scholar] [CrossRef]
- Jin, B.; Cruz, L.; Goncalves, N. Pseudo RGB-D Face Recognition. IEEE Sens. J. 2022, 22, 21780–21794. [Google Scholar] [CrossRef]
- Gao, J.; Wang, H.; Shen, H. Machine Learning Based Workload Prediction in Cloud Computing. In Proceedings of the International Conference on Computer Communications and Networks, ICCCN, Honolulu, HI, USA, 3–6 August 2020. [Google Scholar]
- Zhao, M.; Jha, A.; Liu, Q.; Millis, B.A.; Mahadevan-Jansen, A.; Lu, L.; Landman, B.A.; Tyska, M.J.; Huo, Y. Faster Mean-shift: GPU-accelerated clustering for cosine embedding-based cell segmentation and tracking. Med. Image Anal. 2021, 71, 102048. [Google Scholar] [CrossRef]
- Jin, B.; Cruz, L.; Goncalves, N. Deep Facial Diagnosis: Deep Transfer Learning from Face Recognition to Facial Diagnosis. IEEE Access 2020, 8, 123649–123661. [Google Scholar] [CrossRef]
- Bartz-Beielstein, T.; Zaefferer, M. Model-based methods for continuous and discrete global optimization. Appl. Soft Comput. 2017, 55, 154–167. [Google Scholar] [CrossRef]
- Di Tang, A.; Han, T.; Zhou, H.; Xie, L. An improved equilibrium optimizer with application in unmanned aerial vehicle path planning. Sensors 2021, 21, 1814. [Google Scholar] [CrossRef]
- Abualigah, L.; Elaziz, M.A.; Yousri, D.; Al-qaness, M.A.A.; Ewees, A.A.; Zitar, R.A. Augmented arithmetic optimization algorithm using opposite-based learning and lévy flight distribution for global optimization and data clustering. J. Intell. Manuf. 2022, 34, 3523–3561. [Google Scholar] [CrossRef]
- Ou, Y.; Qin, F.; Zhou, K.-Q.; Yin, P.-F.; Mo, L.-P.; Mohd Zain, A. An Improved Grey Wolf Optimizer with Multi-Strategies Coverage in Wireless Sensor Networks. Symmetry 2024, 16, 286. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Mirjalili, S.; Chakrabortty, R.K.; Ryan, M.J. Solar photovoltaic parameter estimation using an improved equilibrium optimizer. Sol. Energy 2020, 209, 694–708. [Google Scholar] [CrossRef]
- Xie, L.; Han, T.; Zhou, H.; Zhang, Z.-R.; Han, B.; Tang, A. Tuna Swarm Optimization: A Novel Swarm-Based Metaheuristic Algorithm for Global Optimization. Comput. Intell. Neurosci. 2021, 2021, 9210050. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1992. [Google Scholar]
- Sarker, R.A.; Elsayed, S.M.; Ray, T. Differential evolution with dynamic parameters selection for optimization problems. IEEE Trans. Evol. Comput. 2014, 18, 689–707. [Google Scholar] [CrossRef]
- Fogel, D.B. Applying evolutionary programming to selected traveling salesman problems. Cybern. Syst. 1993, 24, 27–36. [Google Scholar] [CrossRef]
- Beyer, H.-G.; Schwefel, H.-P. Evolution strategies—A comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Yang, X. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Frome, UK, 2010; ISBN 9781905986286. [Google Scholar]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Futur. Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Deng, L.; Liu, S. Snow ablation optimizer: A novel metaheuristic technique for numerical optimization and engineering design. Expert Syst. Appl. 2023, 225, 120069. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
- Hashim, F.A.; Mostafa, R.R.; Hussien, A.G.; Mirjalili, S.; Sallam, K.M. Fick’s Law Algorithm: A physical law-based algorithm for numerical optimization. Knowl. Based Syst. 2023, 260, 110146. [Google Scholar] [CrossRef]
- Bai, J.; Li, Y.; Zheng, M.; Khatir, S.; Benaissa, B.; Abualigah, L.; Abdel Wahab, M. A Sinh Cosh optimizer. Knowl. Based Syst. 2023, 282, 111081. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Dorigo, M.; Di Caro, G. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation, CEC 1999, Washington, DC, USA, 6–9 July 1999. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Futur. Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Abualigah, L.; Elaziz, M.A.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Le Minh, H.; Sang-To, T.; Theraulaz, G.; Abdel Wahab, M.; Cuong-Le, T. Termite life cycle optimizer. Expert Syst. Appl. 2023, 213, 119211. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl. Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. CAD Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z. Group teaching optimization algorithm: A novel metaheuristic method for solving global optimization problems. Expert Syst. Appl. 2020, 148, 113246. [Google Scholar] [CrossRef]
- Bayzidi, H.; Talatahari, S.; Saraee, M.; Lamarche, C.P. Social Network Search for Solving Engineering Optimization Problems. Comput. Intell. Neurosci. 2021, 2021, 8548639. [Google Scholar] [CrossRef]
- Ma, B.; Hu, Y.; Lu, P.; Liu, Y. Running city game optimizer: A game-based metaheuristic optimization algorithm for global optimization. J. Comput. Des. Eng. 2023, 10, 65–107. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Tian, Z.; Gai, M. Football team training algorithm: A novel sport-inspired meta-heuristic optimization algorithm for global optimization. Expert Syst. Appl. 2024, 245, 123088. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Aras, S.; Gedikli, E. Fitness-distance balance (FDB): A new selection method for meta-heuristic search algorithms. Knowl. Based Syst. 2020, 190, 105169. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physics-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Trojovský, P. A new human-based metaheuristic algorithm for solving optimization problems based on preschool education. Sci. Rep. 2023, 13, 21472. [Google Scholar] [CrossRef]
- Bakır, H. Dynamic fitness-distance balance-based artificial rabbits optimization algorithm to solve optimal power flow problem. Expert Syst. Appl. 2024, 240, 122460. [Google Scholar] [CrossRef]
- Yin, S.; Luo, Q.; Du, Y.; Zhou, Y. DTSMA: Dominant Swarm with Adaptive T-distribution Mutation-based Slime Mould Algorithm. Math. Biosci. Eng. 2022, 19, 2240–2285. [Google Scholar] [CrossRef]
- Wu, D.; Wang, S.; Liu, Q.; Abualigah, L.; Jia, H. An Improved Teaching-Learning-Based Optimization Algorithm with Reinforcement Learning Strategy for Solving Optimization Problems. Comput. Intell. Neurosci. 2022, 2022, 1535957. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N.; Liang, J.J.; Qu, B.Y. Problem Definitions and Evaluation Criteria for the CEC2017 Special Session and Competition on Single Objective Real-Parameter Numertical Optimization; Tech. Rep.; Nanyang Technological University: Singapore, 2016. [Google Scholar]

| Algorithm | Cauchy | Gaussian | ||
|---|---|---|---|---|
| Equation (16) | Equation (17) | Equation (16) | Equation (17) | |
| FTTA-NTS-1 | × | × | × | √ |
| FTTA-NTS-2 | × | × | √ | × |
| FTTA-NTS-3 | × | √ | × | × |
| FTTA-NTS-4 | √ | × | × | × |
| FTTA-NTS-5 | × | × | √ | √ |
| FTTA-NTS-6 | × | √ | √ | × |
| FTTA-NTS-7 | × | × | √ | √ |
| FTTA-NTS-8 | √ | × | × | √ |
| FTTA-NTS-9 | × | × | × | × |
| Algorithm | Parameter Setting |
|---|---|
| IFTTA | |
| FTTA | |
| RIME [40] | |
| MRFO [41] | |
| PEOA [42] | |
| dFDBARO [43] | |
| DTSMA [44] | |
| RLTLBO [45] |
| Type | ID | CEC2017 Function Name | Rang | Dimension | fmin |
|---|---|---|---|---|---|
| Unimodal | F1 | Shifted and Rotated Bent Cigar Function | [−100, 100] | 10/30/50/100 | 100 |
| F2 | Shifted and Rotated Zakharov Function | [−100, 100] | 10/30/50/100 | 300 | |
| Multimodal | F3 | Shifted and Rotated Rosenbrock’s Function | [−100, 100] | 10/30/50/100 | 400 |
| F4 | Shifted and Rotated Rastrigin’s Function | [−100, 100] | 10/30/50/100 | 500 | |
| F5 | Shifted and Rotated Expanded Scaffer’s F6 Function | [−100, 100] | 10/30/50/100 | 600 | |
| F6 | Shifted and Rotated Lunacek Bi_Rastrigin Function | [−100, 100] | 10/30/50/100 | 700 | |
| F7 | Shifted and Rotated Non-Continuous Rastrigin’s Function | [−100, 100] | 10/30/50/100 | 800 | |
| F8 | Shifted and Rotated Levy Function | [−100, 100] | 10/30/50/100 | 900 | |
| F9 | Shifted and Rotated Schwefel’s Function | [−100, 100] | 10/30/50/100 | 1000 | |
| Hybrid | F10 | Hybrid Function 1 (N = 3) | [−100, 100] | 10/30/50/100 | 1100 |
| F11 | Hybrid Function 2 (N = 3) | [−100, 100] | 10/30/50/100 | 1200 | |
| F12 | Hybrid Function 3 (N = 3) | [−100, 100] | 10/30/50/100 | 1300 | |
| F13 | Hybrid Function 4 (N = 4) | [−100, 100] | 10/30/50/100 | 1400 | |
| F14 | Hybrid Function 5 (N = 4) | [−100, 100] | 10/30/50/100 | 1500 | |
| F15 | Hybrid Function 6 (N = 4) | [−100, 100] | 10/30/50/100 | 1600 | |
| F16 | Hybrid Function 6 (N = 5) | [−100, 100] | 10/30/50/100 | 1700 | |
| F17 | Hybrid Function 6 (N = 5) | [−100, 100] | 10/30/50/100 | 1800 | |
| F18 | Hybrid Function 6 (N = 5) | [−100, 100] | 10/30/50/100 | 1900 | |
| F19 | Hybrid Function 6 (N = 6) | [−100, 100] | 10/30/50/100 | 2000 | |
| Composition | F20 | Composition Function 1 (N = 3) | [−100, 100] | 10/30/50/100 | 2100 |
| F21 | Composition Function 2 (N = 3) | [−100, 100] | 10/30/50/100 | 2200 | |
| F22 | Composition Function 3 (N = 4) | [−100, 100] | 10/30/50/100 | 2300 | |
| F23 | Composition Function 4 (N = 4) | [−100, 100] | 10/30/50/100 | 2400 | |
| F24 | Composition Function 5 (N = 5) | [−100, 100] | 10/30/50/100 | 2500 | |
| F25 | Composition Function 6 (N = 5) | [−100, 100] | 10/30/50/100 | 2600 | |
| F26 | Composition Function 7 (N = 6) | [−100, 100] | 10/30/50/100 | 2700 | |
| F27 | Composition Function 8 (N = 6) | [−100, 100] | 10/30/50/100 | 2800 | |
| F28 | Composition Function 9 (N = 3) | [−100, 100] | 10/30/50/100 | 2900 | |
| F29 | Composition Function 10 (N = 3) | [−100, 100] | 10/30/50/100 | 3000 |
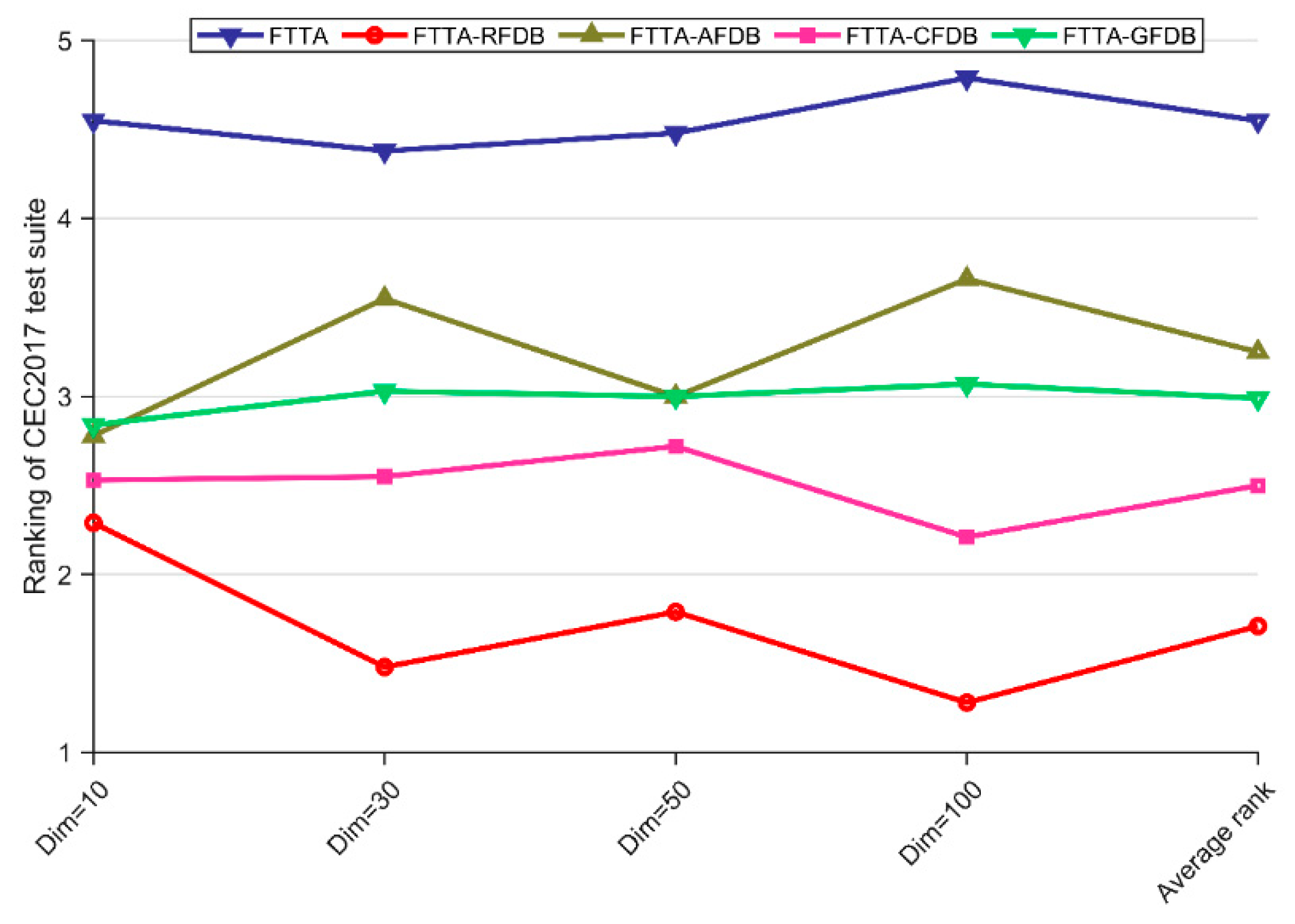
| Test Suite | Dim | FTTA | FTTA-RFDB | FTTA-AFDB | FTTA-CFDB | FTTA-GFDB | Friedman p-Value |
|---|---|---|---|---|---|---|---|
| CEC2017 | 10 | 4.55 | 2.29 | 2.78 | 2.53 | 2.84 | 1.26 × 10−7 |
| 30 | 4.38 | 1.48 | 3.55 | 2.55 | 3.03 | 3.85 × 10−11 | |
| 50 | 4.48 | 1.79 | 3.00 | 2.72 | 3.00 | 9.04 × 10−9 | |
| 100 | 4.79 | 1.28 | 3.66 | 2.21 | 3.07 | 2.34 × 10−17 | |
| Average rank | 4.55 | 1.71 | 3.25 | 2.50 | 2.99 | N/A | |
| vs. FTTA +/=/− | CEC2017 with Dim = 10/30/50/100 | |||
|---|---|---|---|---|
| 10 | 30 | 50 | 100 | |
| FTTA-RFDB | 17/9/3 | 22/6/1 | 21/6/2 | 24/5/0 |
| FTTA-AFDB | 20/8/1 | 16/11/2 | 18/11/0 | 14/15/0 |
| FTTA-CFDB | 20/8/1 | 17/11/1 | 18/10/1 | 24/5/0 |
| FTTA-GFDB | 21/7/1 | 17/10/2 | 19/10/0 | 23/6/0 |
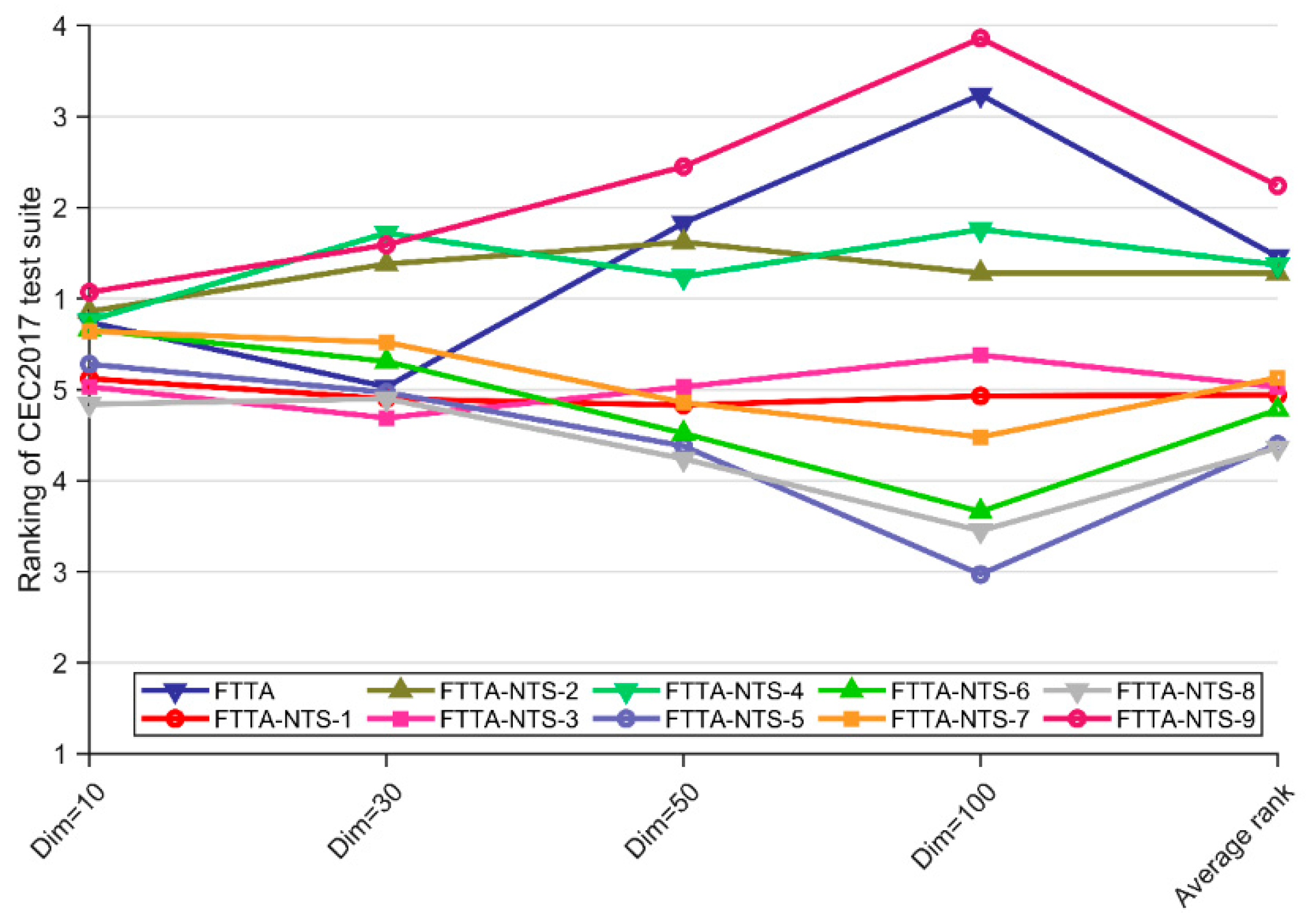
| Test Suite | Dimension | FTTA | FTTA-NTS-1 | FTTA-NTS-2 | FTTA-NTS-3 | FTTA-NTS-4 | FTTA-NTS-5 | FTTA-NTS-6 | FTTA-NTS-7 | FTTA-NTS-8 | FTTA-NTS-9 | Friedman p-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC 2017 | 10 | 5.74 | 5.12 | 5.86 | 5.03 | 5.76 | 5.28 | 5.66 | 5.64 | 4.84 | 6.07 | 8.64 × 10−1 |
| 30 | 5.03 | 4.90 | 6.38 | 4.69 | 6.72 | 4.97 | 5.31 | 5.52 | 4.90 | 6.59 | 4.86 × 10−2 | |
| 50 | 6.83 | 4.83 | 6.62 | 5.03 | 6.24 | 4.38 | 4.52 | 4.86 | 4.24 | 7.45 | 1.28 × 10−5 | |
| 100 | 8.24 | 4.93 | 6.28 | 5.38 | 6.76 | 2.97 | 3.66 | 4.48 | 3.45 | 8.86 | 1.28 × 10−20 | |
| Average rank | 6.46 | 4.94 | 6.28 | 5.03 | 6.37 | 4.40 | 4.78 | 5.13 | 4.36 | 7.24 | N/A | |
| vs. FTTA +/=/− | CEC2017 with Dim = 10/30/50/100 | |||
|---|---|---|---|---|
| 10 | 30 | 50 | 100 | |
| FTTA-NTS-1 | 3/23/3 | 4/17/8 | 11/14/4 | 20/7/2 |
| FTTA-NTS-2 | 4/21/4 | 3/17/9 | 6/20/3 | 17/10/2 |
| FTTA-NTS-3 | 5/21/3 | 5/16/8 | 11/14/4 | 20/7/2 |
| FTTA-NTS-4 | 2/27/0 | 3/16/10 | 8/20/1 | 18/10/1 |
| FTTA-NTS-5 | 3/22/4 | 4/16/9 | 10/16/3 | 22/6/1 |
| FTTA-NTS-6 | 5/22/2 | 3/19/7 | 10/16/3 | 22/6/1 |
| FTTA-NTS-7 | 4/25/0 | 3/16/10 | 10/18/1 | 19/8/2 |
| FTTA-NTS-8 | 4/25/0 | 3/18/8 | 11/17/1 | 19/9/1 |
| FTTA-NTS-9 | 3/24/2 | 4/15/10 | 8/17/4 | 12/14/3 |
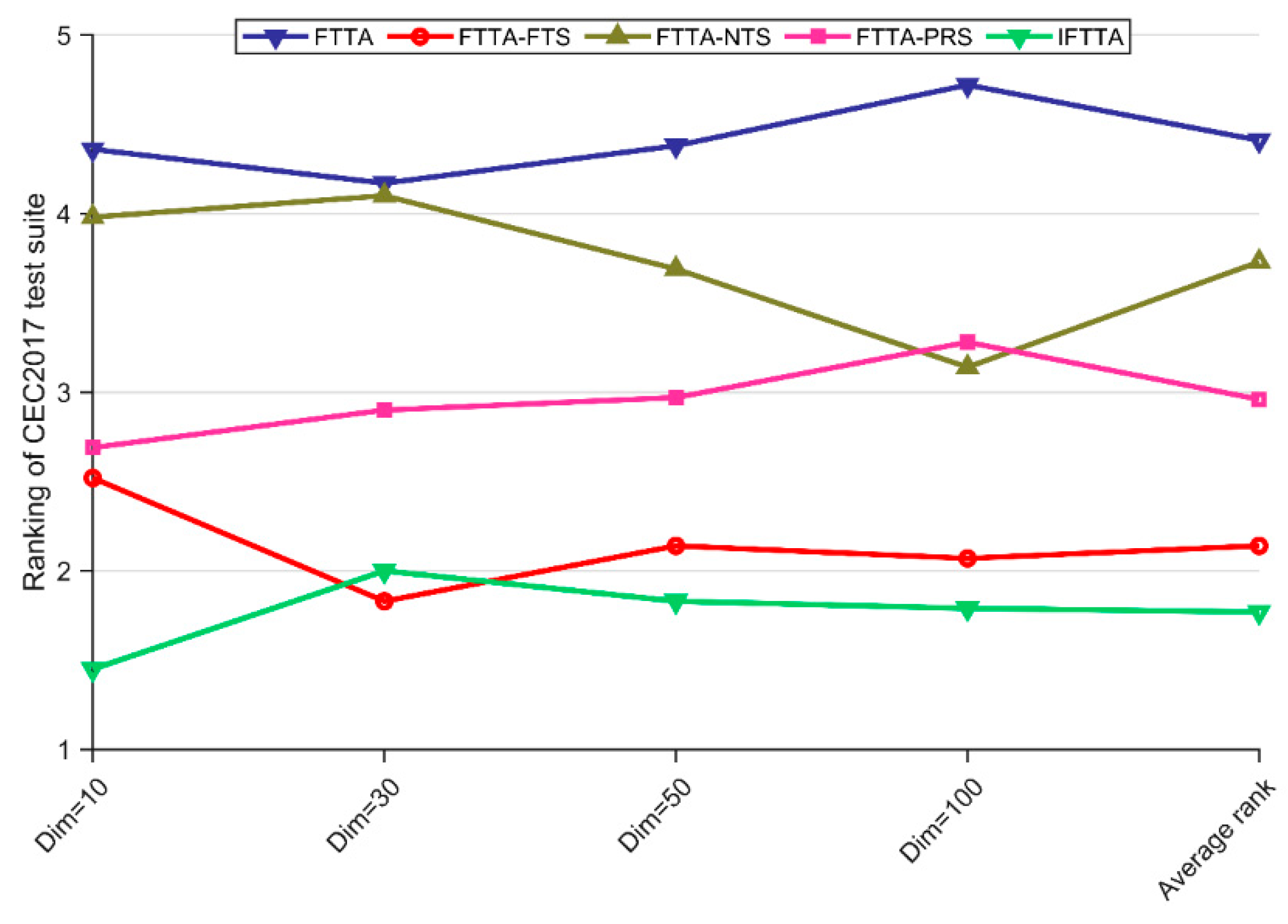
| Test Suite | Dimension | FTTA | FTTA-FTS | FTTA-NTS | FTTA-PRS | IFTTA | Friedman p-Value |
|---|---|---|---|---|---|---|---|
| CEC2017 | 10 | 4.36 | 2.52 | 3.98 | 2.69 | 1.45 | 2.53 × 10−13 |
| 30 | 4.17 | 1.83 | 4.10 | 2.90 | 2.00 | 8.66 × 10−12 | |
| 50 | 4.38 | 2.14 | 3.69 | 2.97 | 1.83 | 1.27 × 10−10 | |
| 100 | 4.72 | 2.07 | 3.14 | 3.28 | 1.79 | 8.49 × 10−13 | |
| Average rank | 4.41 | 2.14 | 3.73 | 2.96 | 1.77 | N/A | |
| vs. FTTA +/=/− | CEC2017 with Dim = 10/30/50/100 | ||||
|---|---|---|---|---|---|
| 10 | 30 | 50 | 100 | Total | |
| FTTA-FTS | 17/9/3 | 22/6/1 | 21/6/2 | 24/5/0 | 84/26/6 |
| FTTA-NTS | 4/25/0 | 3/18/8 | 11/17/1 | 19/9/1 | 37/69/10 |
| FTTA-PRS | 14/14/1 | 9/20/0 | 14/15/0 | 21/8/0 | 58/57/1 |
| IFTTA | 27/2/0 | 22/6/1 | 22/6/1 | 26/3/0 | 87/17/2 |
| +/=/− IFTTA vs. | CEC2017 Test Suite | |||
|---|---|---|---|---|
| Dim = 10 | Dim = 30 | Dim = 50 | Dim = 100 | |
| FTTA | 27/2/0 | 22/6/1 | 22/6/1 | 26/3/0 |
| RIME | 24/2/3 | 25/3/1 | 26/2/1 | 28/1/0 |
| MRFO | 18/8/3 | 17/9/3 | 18/8/3 | 20/8/1 |
| POEA | 23/4/2 | 23/2/4 | 25/1/3 | 25/2/2 |
| dFDBARO | 12/8/9 | 20/5/4 | 18/10/1 | 22/4/3 |
| DTSMA | 20/5/4 | 23/4/2 | 25/3/1 | 27/1/1 |
| RLTLBO | 18/8/3 | 18/8/3 | 20/5/4 | 26/1/2 |
| Test Suite | Dimension | IFTTA | FTTA | RIME | MRFO | POEA | dFDBARO | DTSMA | RLTLBO | Friedman p-Value |
|---|---|---|---|---|---|---|---|---|---|---|
| CEC2017 | 10 | 2.69 | 6.07 | 5.62 | 5.07 | 6.10 | 2.41 | 4.41 | 3.62 | 4.14 × 10−13 |
| 30 | 2.24 | 4.76 | 5.28 | 4.86 | 6.66 | 2.93 | 4.93 | 4.34 | 2.52 × 10−11 | |
| 50 | 2.03 | 4.24 | 5.38 | 4.45 | 6.62 | 3.31 | 4.66 | 5.31 | 1.30 × 10−11 | |
| 100 | 1.62 | 3.93 | 5.28 | 3.66 | 6.17 | 3.97 | 5.10 | 6.28 | 1.45 × 10−14 | |
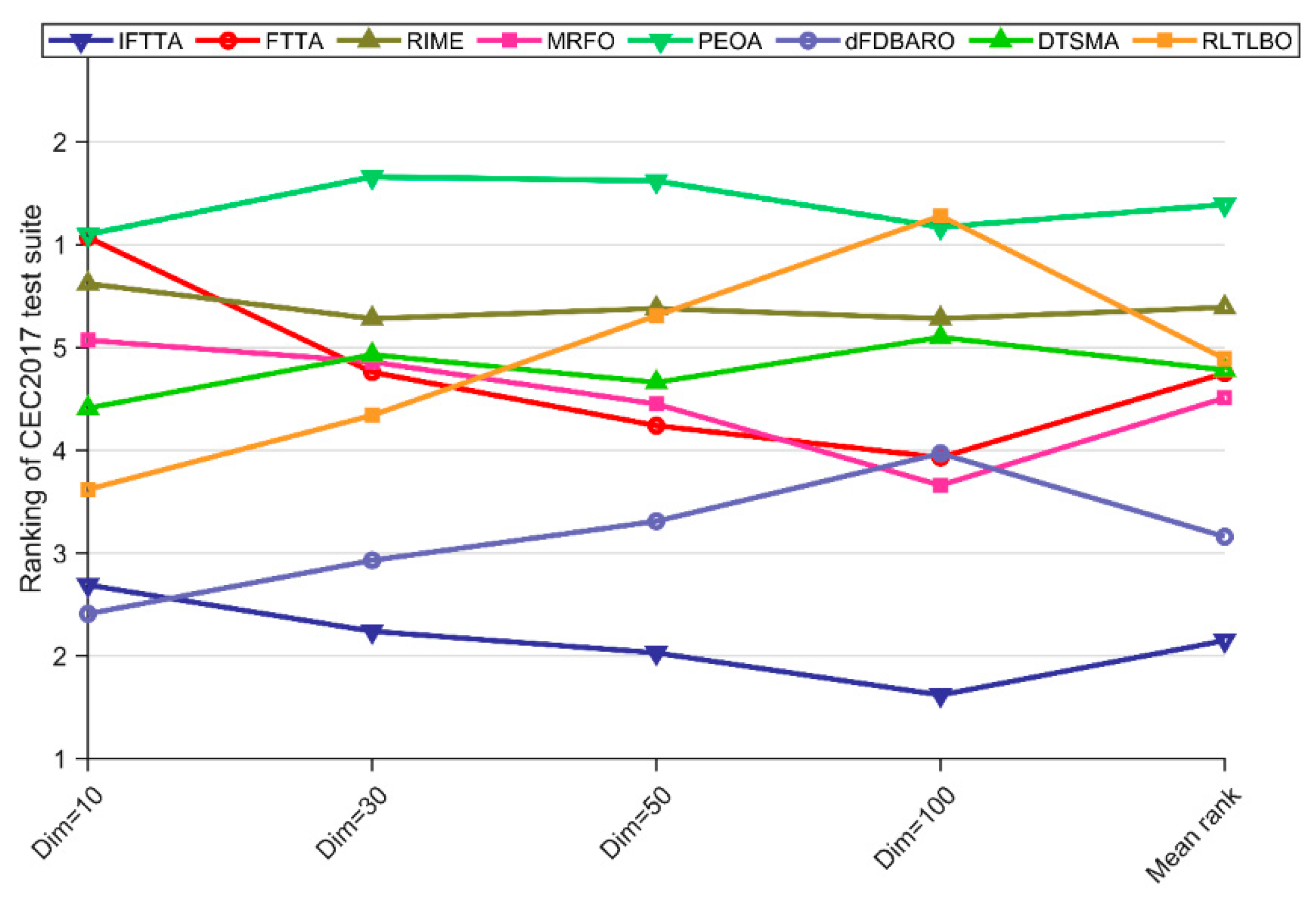
| Mean rank | 2.15 | 4.75 | 5.39 | 4.51 | 6.39 | 3.16 | 4.78 | 4.89 | N/A | |
| Problems | Name | D | g | h |
|---|---|---|---|---|
| EC1 | Welded beam design | 4 | 5 | 0 |
| EC2 | Pressure vessel design | 4 | 4 | 0 |
| EC3 | Tension/compression spring design (case 1) | 3 | 3 | 0 |
| EC4 | Gear train design Problem | 4 | 1 | 1 |
| EC5 | Three-bar truss design problem | 2 | 3 | 0 |
| EC6 | Cantilever beam design | 5 | 1 | 0 |
| EC7 | Weight Minimization of a Speed Reducer | 7 | 11 | 0 |
| No. | Index | IFTTA | FTTA | RIME | MRFO | POEA | dFDBARO | DTSMA | RLTLBO |
|---|---|---|---|---|---|---|---|---|---|
| EC1 | Best | 1.724852 | 1.724852 | 1.743662 | 1.724852 | 1.737015 | 1.724852 | 1.724865 | 1.975659 |
| Ave | 1.724852 | 1.749665 | 2.371319 | 1.724877 | 1.959929 | 1.724855 | 1.732449 | 2.503435 | |
| Std | 1.23 × 10−14 | 0.076744 | 0.525167 | 7.13 × 10−5 | 0.198885 | 7.20 × 10−6 | 0.02822 | 0.227793 | |
| Rank | 1 | 5 | 7 | 3 | 6 | 2 | 4 | 8 | |
| EC2 | Best | 5885.333 | 5885.88 | 6027.581 | 5890.976 | 5888.571 | 5885.356 | 5885.345 | 8007.555 |
| Ave | 5971.134 | 6377.118 | 6777.524 | 5945.544 | 6758.23 | 5891.672 | 18590.68 | 38450.22 | |
| Std | 218.3567 | 492.4652 | 429.8811 | 48.40798 | 447.7315 | 19.1683 | 28752.09 | 47027.59 | |
| Rank | 3 | 4 | 6 | 2 | 5 | 1 | 7 | 8 | |
| EC3 | Best | 0.012665 | 0.012665 | 0.012755 | 0.012668 | 0.012676 | 0.012665 | 0.012665 | 0.012692 |
| Ave | 0.012729 | 0.013076 | 0.016326 | 0.012747 | 0.013396 | 0.012676 | 0.014009 | 2326.591 | |
| Std | 0.000122 | 0.000867 | 0.002004 | 5.44 × 10−5 | 0.00079 | 2.95 × 10−5 | 0.001306 | 8902.235 | |
| Rank | 2 | 4 | 7 | 3 | 5 | 1 | 6 | 8 | |
| EC4 | Best | 2.70 × 10−12 | 1.17 × 10−10 | 2.70 × 10−12 | 2.70 × 10−12 | 2.70 × 10−12 | 2.70 × 10−12 | 2.31 × 10−11 | 1.55 × 10−10 |
| Ave | 7.76 × 10−10 | 6.18 × 10−9 | 1.75 × 10−9 | 1.94 × 10−10 | 3.95 × 10−9 | 6.88 × 10−10 | 7.40 × 10−9 | 2.96 × 10−7 | |
| Std | 8.52 × 10−10 | 8.03 × 10−9 | 3.85 × 10−9 | 5.18 × 10−10 | 5.71 × 10−9 | 1.15 × 10−9 | 1.28 × 10−8 | 6.04 × 10−7 | |
| Rank | 3 | 6 | 4 | 1 | 5 | 2 | 7 | 8 | |
| EC5 | Best | 263.4634 | 263.4634 | 263.4661 | 263.4634 | 263.4634 | 263.4634 | 263.4634 | 263.4634 |
| Ave | 263.4634 | 263.4635 | 264.1753 | 263.4634 | 263.4634 | 263.4634 | 263.4634 | 263.4785 | |
| Std | 3.22 × 10−14 | 0.000472 | 1.533939 | 6.68 × 10−14 | 4.03 × 10−7 | 6.23 × 10−14 | 4.43 × 10−9 | 0.04223 | |
| Rank | 1 | 6 | 8 | 2 | 5 | 2 | 4 | 7 | |
| EC6 | Best | 13.03252 | 13.03259 | 13.04384 | 13.03253 | 13.04794 | 13.03253 | 13.03253 | 13.14157 |
| Ave | 13.03258 | 13.04086 | 13.3142 | 13.03259 | 13.11439 | 13.03291 | 13.03273 | 13.91878 | |
| Std | 6.48 × 10−5 | 0.034553 | 0.262858 | 6.22 × 10−5 | 0.053727 | 0.000553 | 0.000179 | 0.456248 | |
| Rank | 1 | 5 | 7 | 2 | 6 | 4 | 3 | 8 | |
| EC7 | Best | 2919.314 | 2919.314 | 2919.317 | 2919.314 | 2919.315 | 2919.314 | 2919.314 | 2933.098 |
| Ave | 2919.314 | 2919.314 | 2919.401 | 2919.314 | 2921.788 | 2919.336 | 2919.314 | 3097.369 | |
| Std | 2.80 × 10−13 | 3.69 × 10−13 | 0.103366 | 4.35 × 10−10 | 2.986103 | 0.148957 | 5.29 × 10−9 | 102.5708 | |
| Rank | 1 | 1 | 6 | 3 | 7 | 5 | 4 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, J.; Cui, Y.; Rong, M.; Jin, B. An Improved Football Team Training Algorithm for Global Optimization. Biomimetics 2024, 9, 419. https://doi.org/10.3390/biomimetics9070419
Hou J, Cui Y, Rong M, Jin B. An Improved Football Team Training Algorithm for Global Optimization. Biomimetics. 2024; 9(7):419. https://doi.org/10.3390/biomimetics9070419
Chicago/Turabian StyleHou, Jun, Yuemei Cui, Ming Rong, and Bo Jin. 2024. "An Improved Football Team Training Algorithm for Global Optimization" Biomimetics 9, no. 7: 419. https://doi.org/10.3390/biomimetics9070419
APA StyleHou, J., Cui, Y., Rong, M., & Jin, B. (2024). An Improved Football Team Training Algorithm for Global Optimization. Biomimetics, 9(7), 419. https://doi.org/10.3390/biomimetics9070419






