Design of an SMA-Based Actuator for Replicating Normal Gait Patterns in Pediatric Patients with Cerebral Palsy
Abstract
1. Introduction
2. Materials and Methods
2.1. Metrics
2.2. Actuator Computation
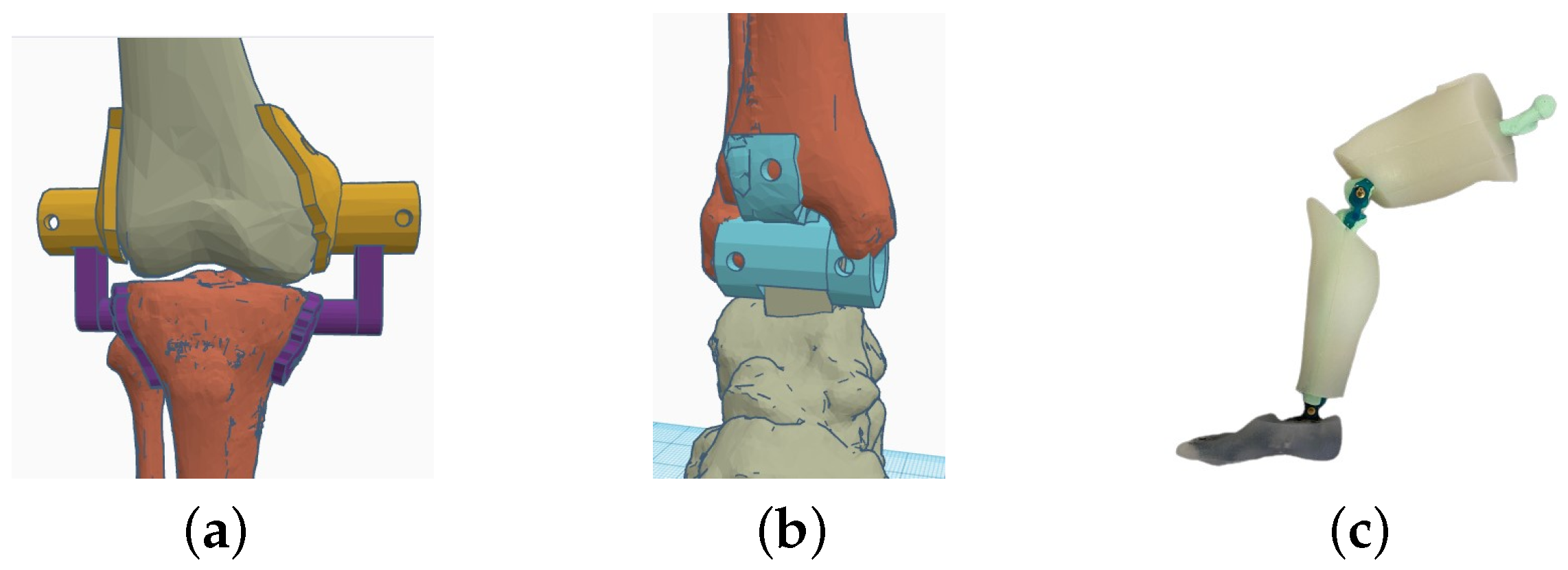
2.3. Exosuit Design
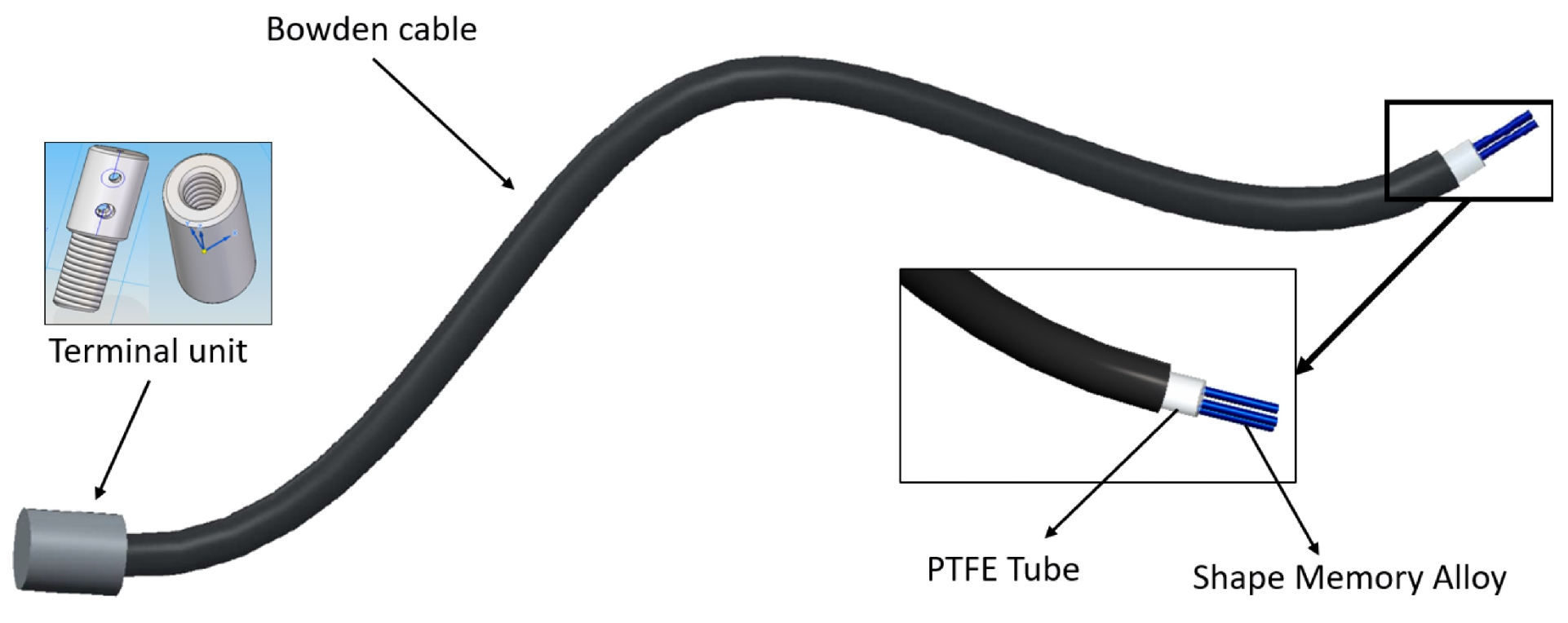
2.4. Hardware
3. Software
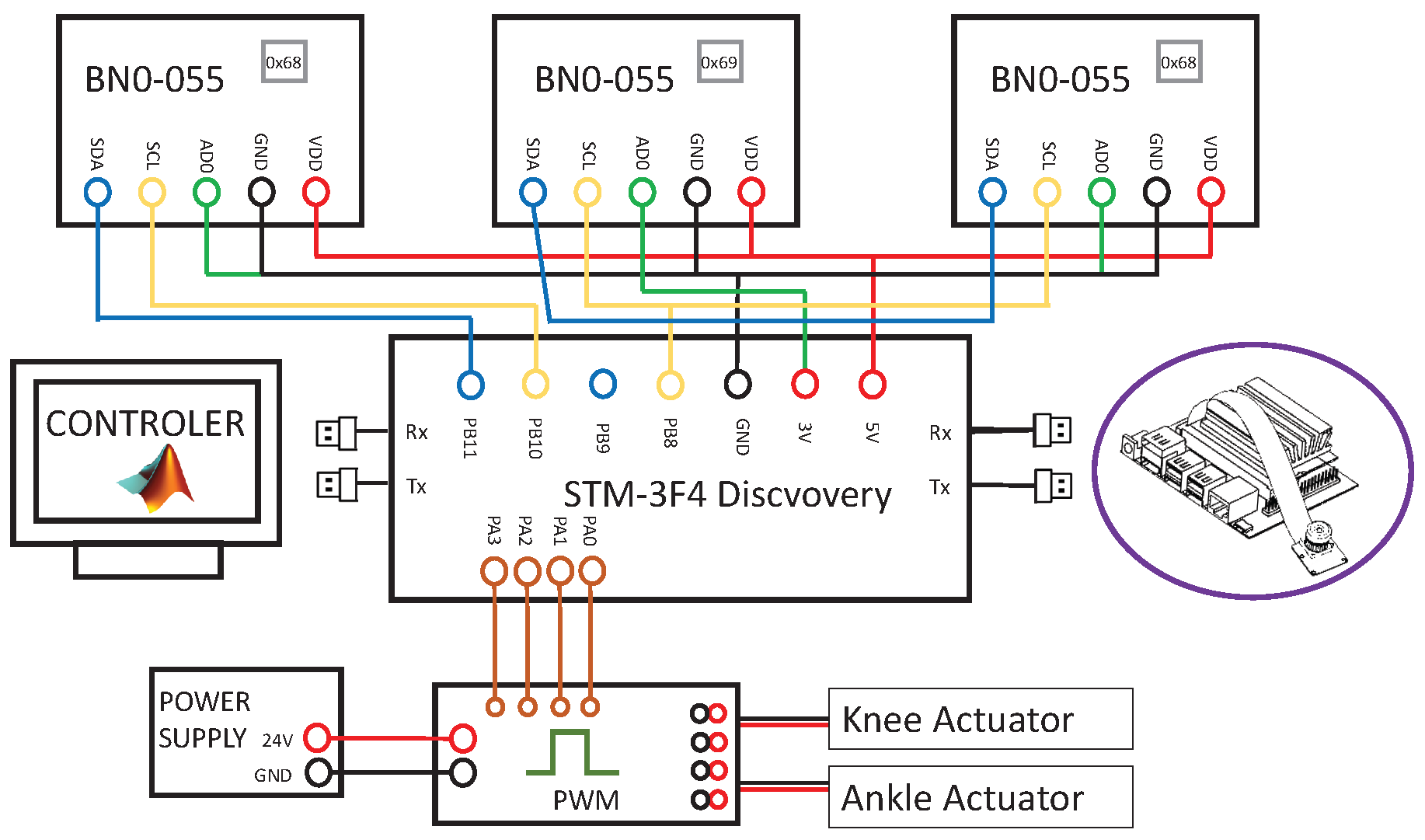
3.1. Inertial Sensors
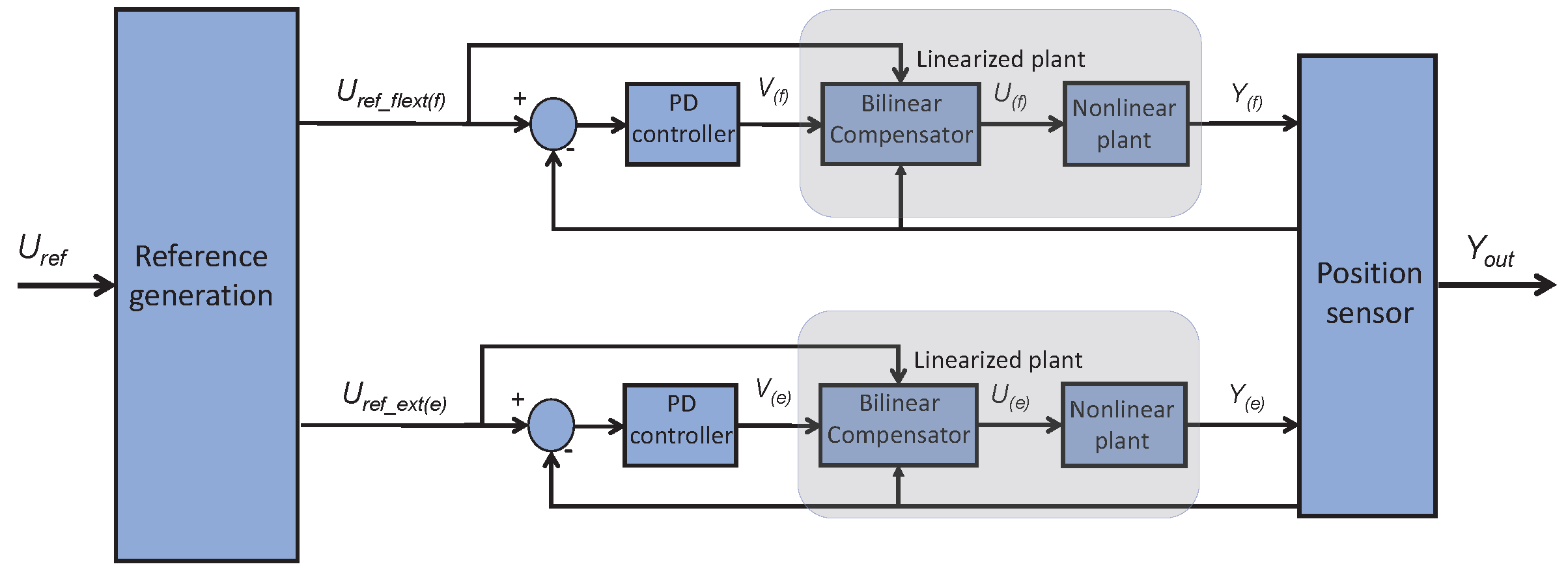
3.2. Control
3.2.1. User Interface
3.2.2. High-Level Controller
3.2.3. Low-Level Controller
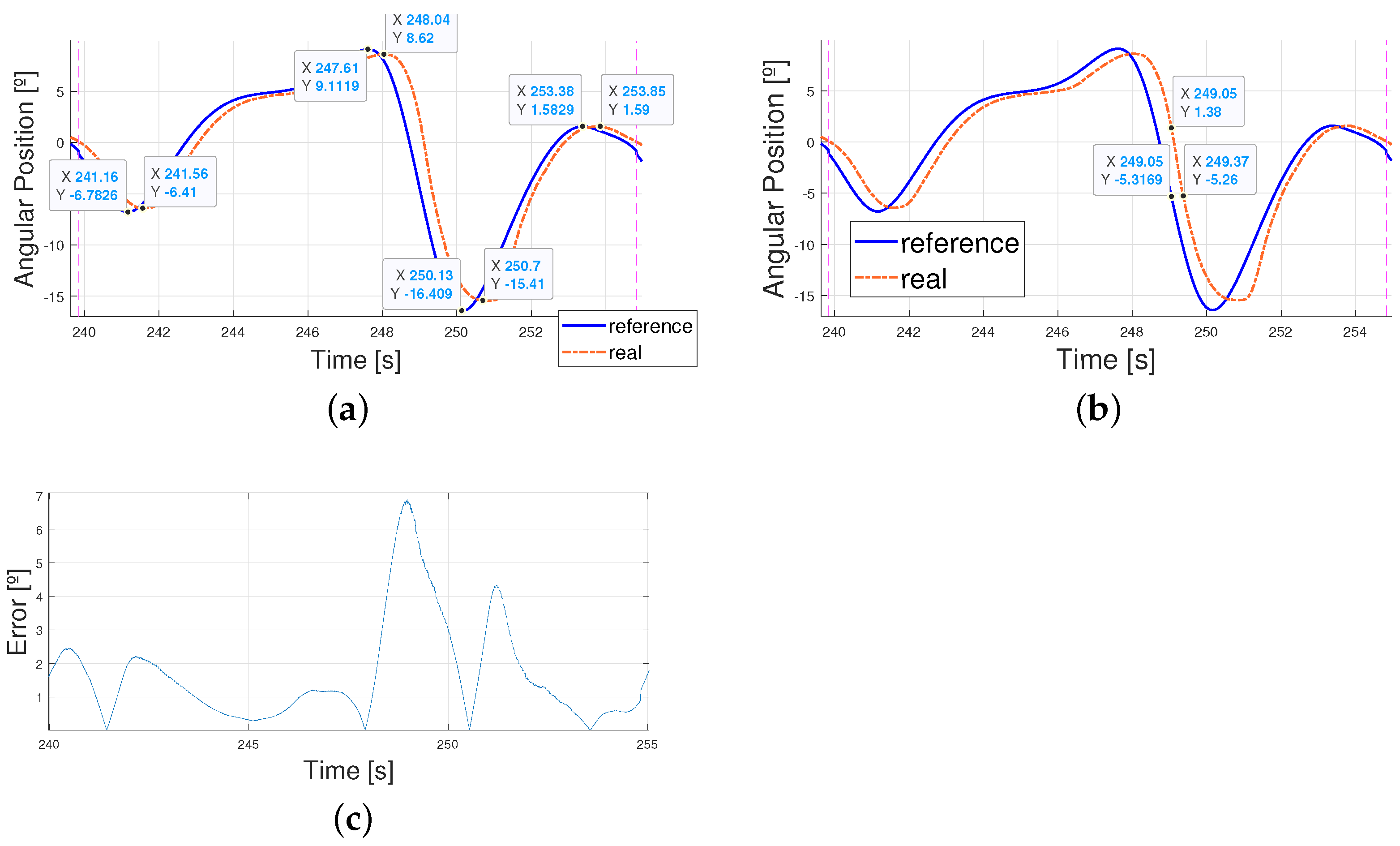
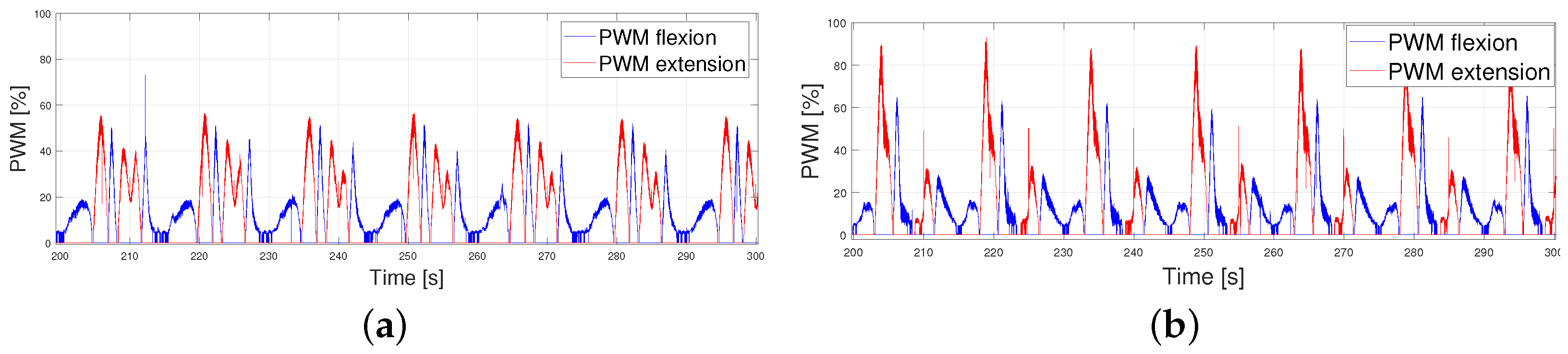
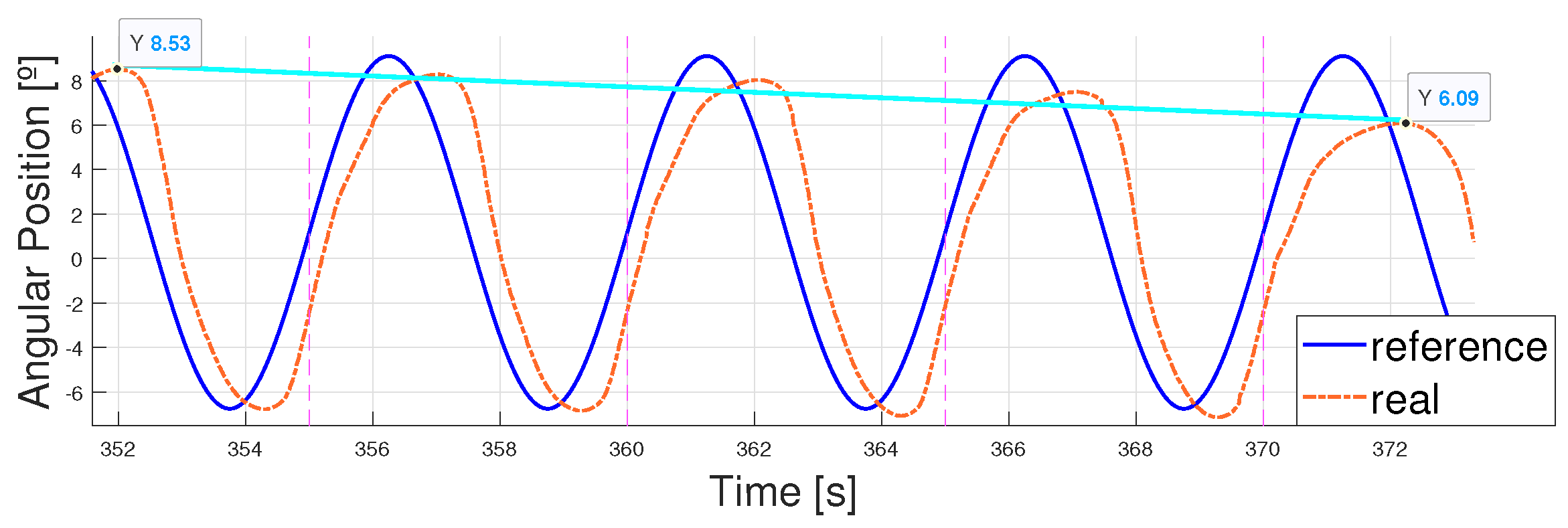
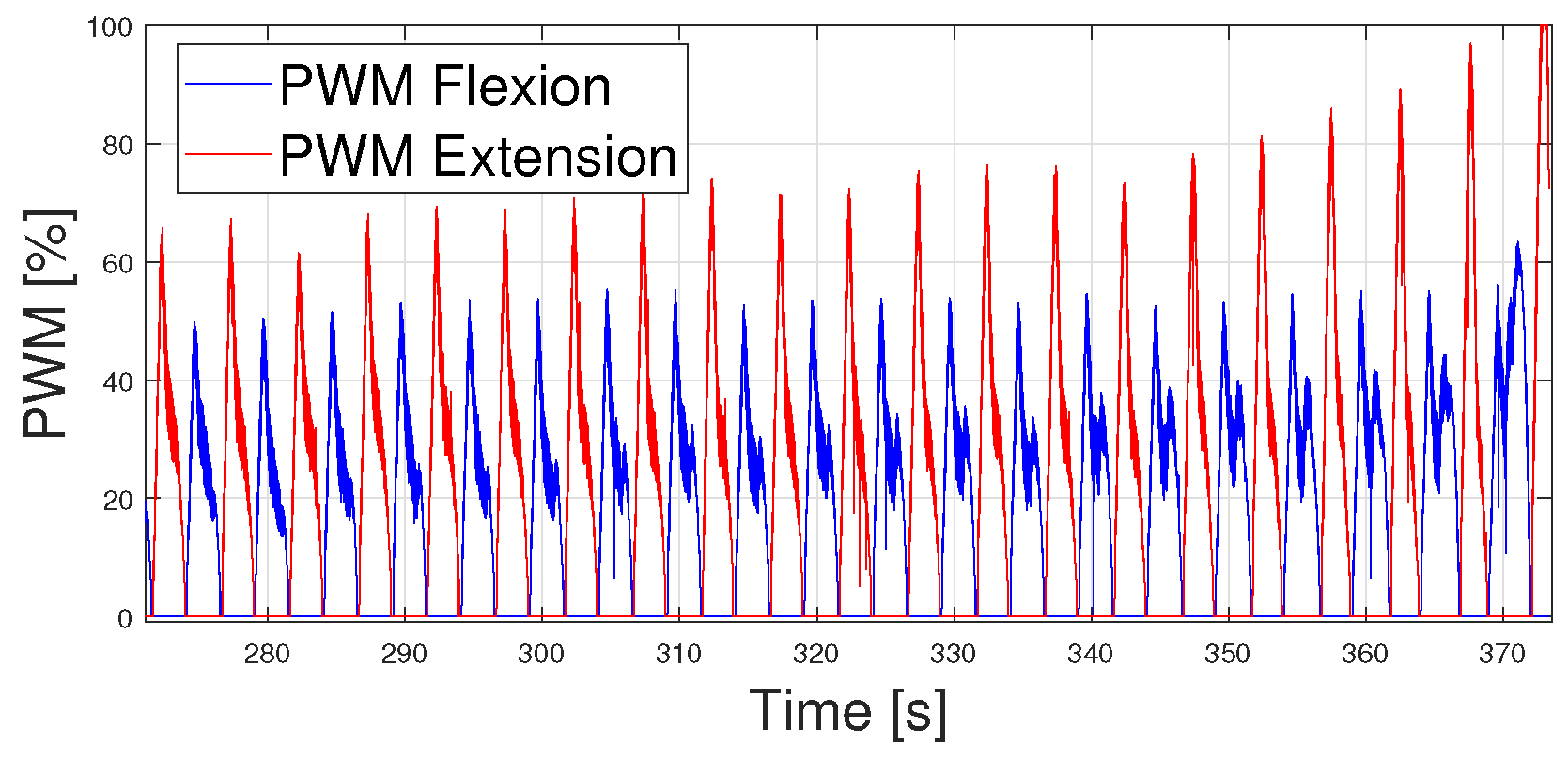
4. Results
- Duration: 10 min. Tests were designed based on the relevant application. As long as the main purpose of this device is to provide a smooth and continuous performance, tests should last for a certain amount of time. The specific selection of 10 min is based on previous tests performed in the research group. In order to be able to compare these results with other devices and tests, the time must be standardized.
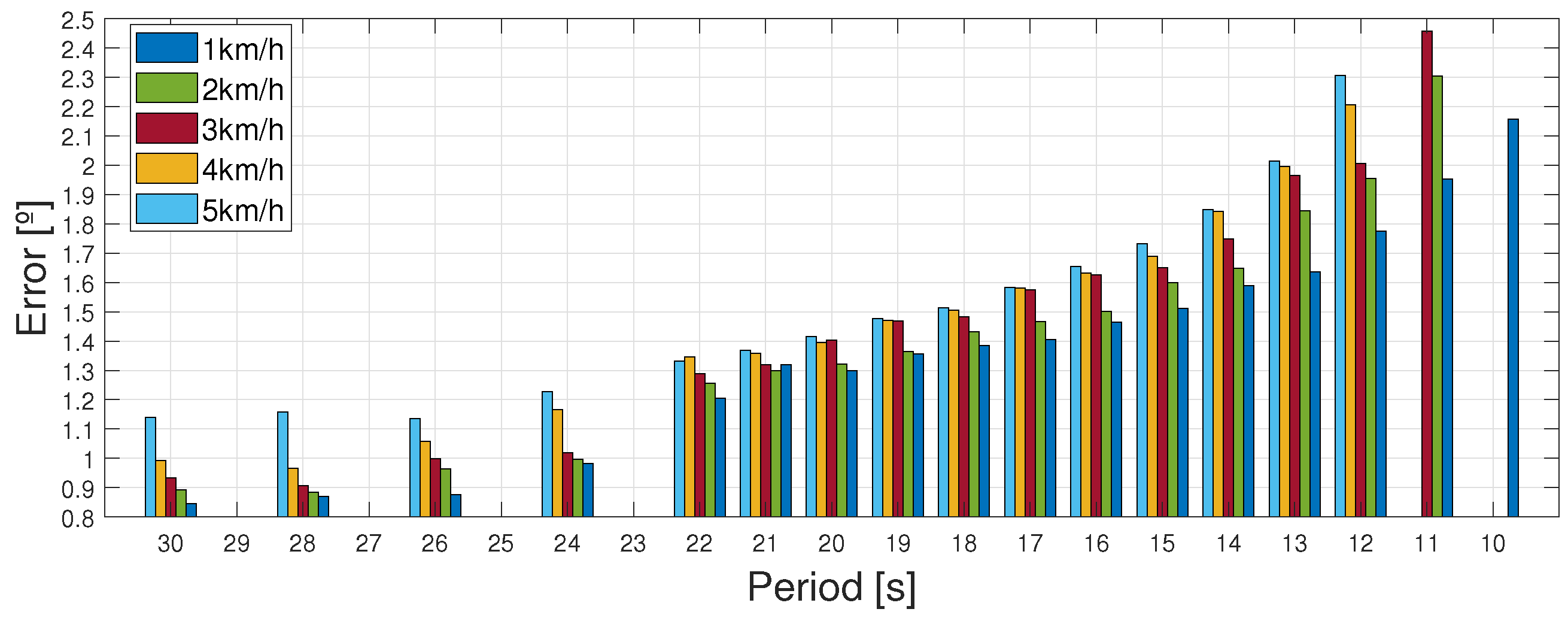
- The error considered was the mean error in absolute terms of the whole cycle, eliminating the first 30 s which were considered variable due to actuator stabilization. This stabilization was set up to 30 s because this was the longest signal period analyzed and it was necessary to ensure that at least one whole period had finished before starting to measure the error.
- The PWM signals generated were also gathered due to the important information provided by them.
- Many patterns were analyzed in these tests. The main idea was to provide a wide range of parameters concerning the frequency of actuation along with the error achieved for each pattern proposed (1–5 km/h patterns). It was crucial to generate a sufficient amount of information that can be used by professionals to select working modes.
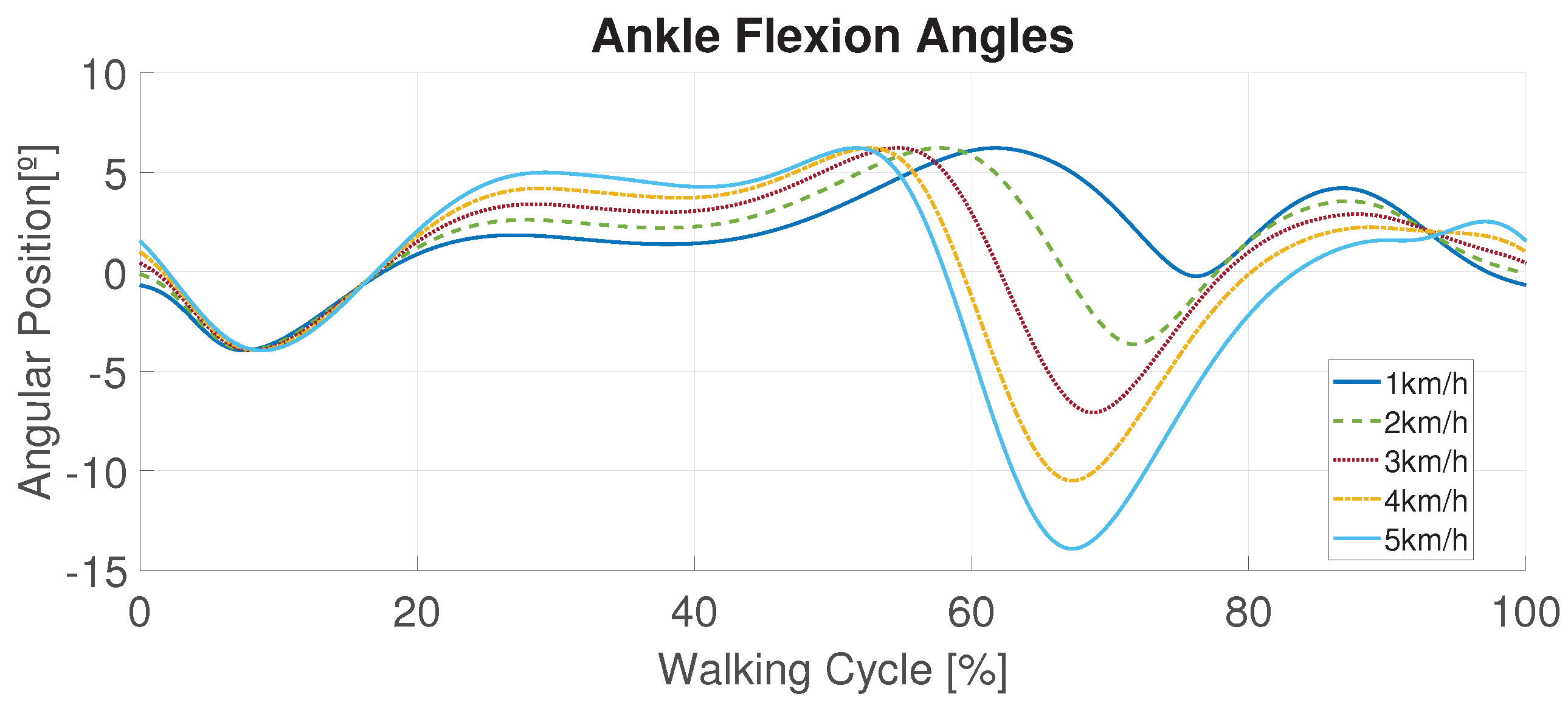
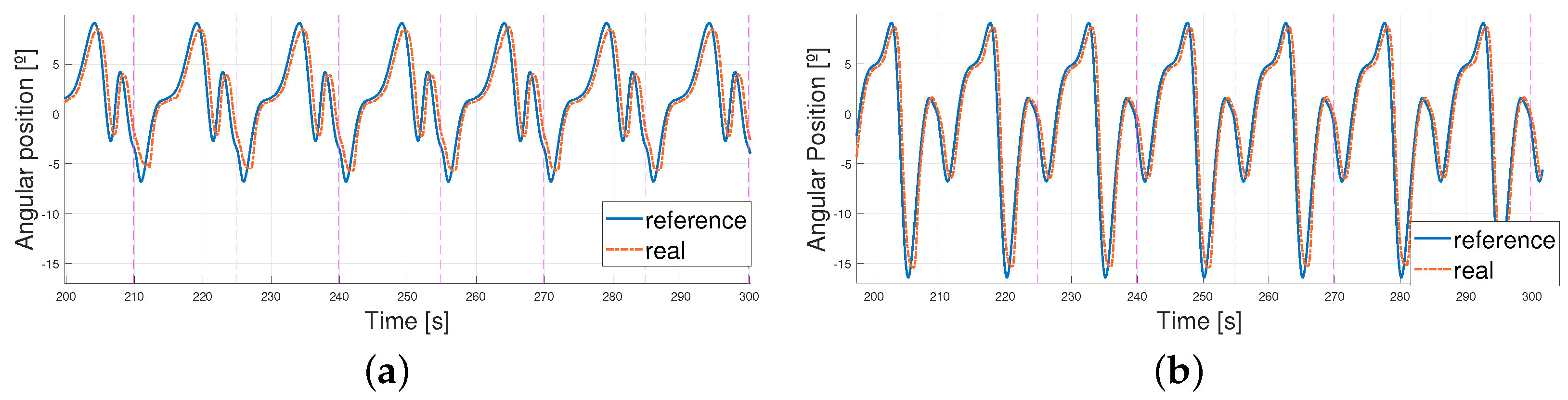
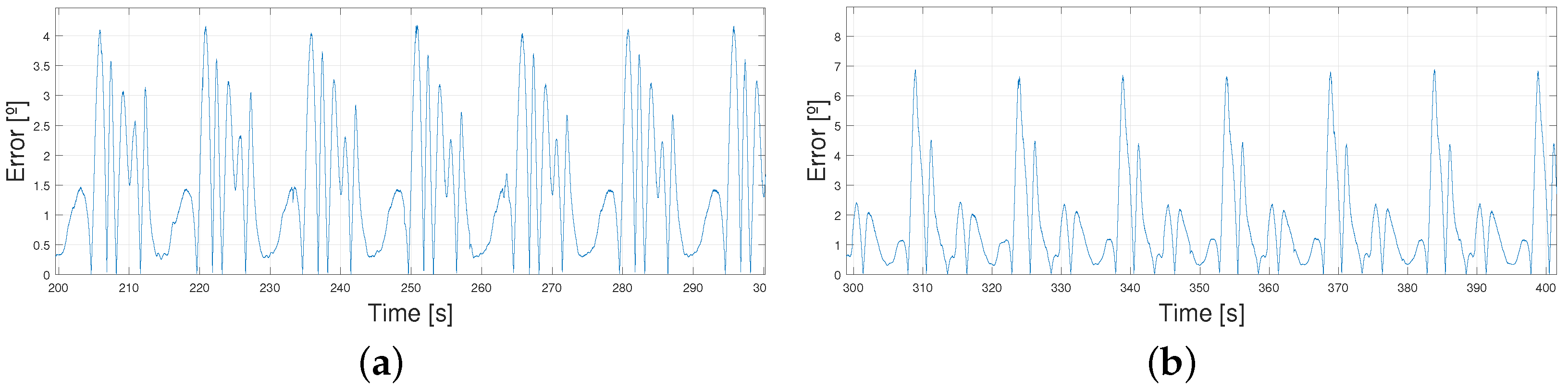
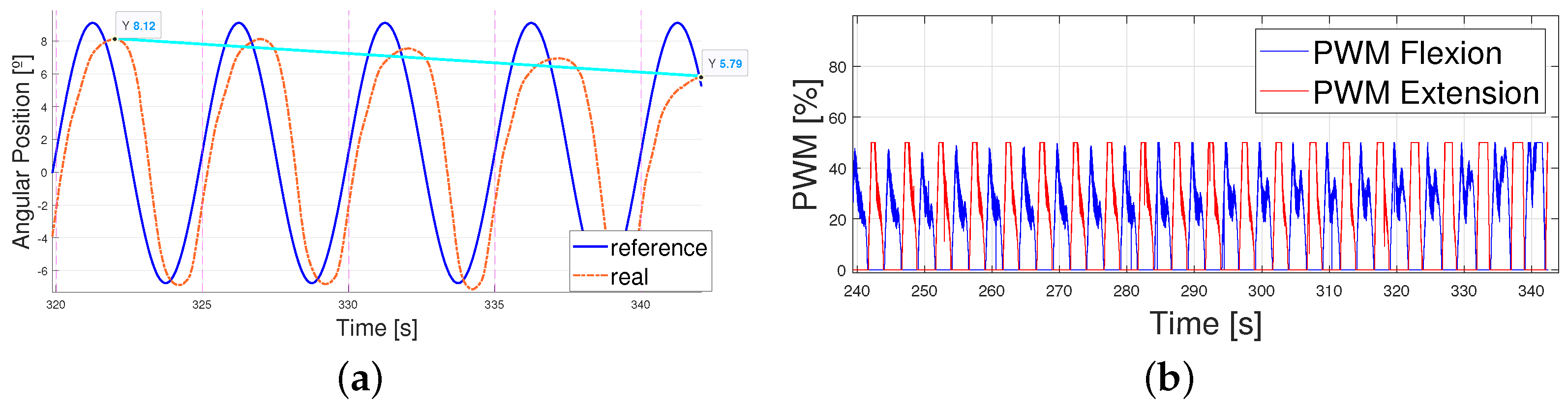
4.1. Following Each Velocity Pattern at Different Periods
4.2. Following a Sinusoidal Pattern
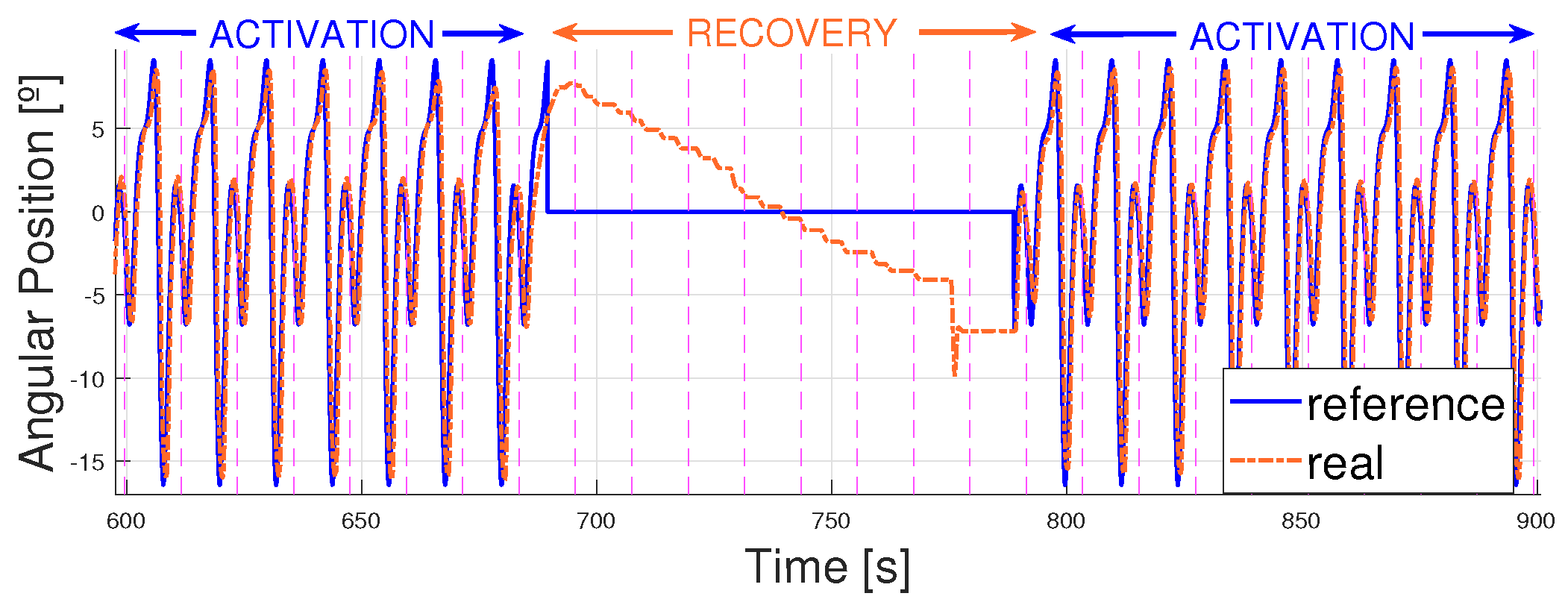
4.3. Working Improvements
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AT | Activation Temperature |
| B-PD | Bilineal PD |
| CAT | Computerize Axial Tomography |
| CP | Ceberal Palsy |
| DICOM | Digital Imaging and Communication in Medicine |
| IMUs | Inertial Measurement Units |
| PLA | Polylactic Acid |
| ROS2 | Robot Operating System 2 |
| SMA | Shape Memory Alloy |
| SMAs | Shape Memory Alloys |
| STL | Standard Triangle Language |
References
- WHO. World Health Statistics; World Health Organization: Geneva, Switzerland, 2023. [Google Scholar]
- Kliegman, R.M.; Marcdante, K.J. Nelson: Pediatría Esencial; Elsevier: Amsterdam, The Netherlands, 2019; Volume 8, pp. 689–690. [Google Scholar]
- Delgado-Oleas, G.; Romero-Sorozabal, P.; Lora-Millan, J.; Gutierrez, A.; Rocon, E. Bioinspired Hierarchical Electronic Architecture for Robotic Locomotion Assistance: Application in Exoskeletons. IEEE Access 2023, 11, 131610–131622. [Google Scholar] [CrossRef]
- Paulson, A. Overview of Four Functional Classification Systems Commonly Used in Cerebral Palsy. Children 2017, 4, 30. [Google Scholar] [CrossRef] [PubMed]
- Palisano, R.; Rosenbaum, P.; Bartlett, D.; Livingston, M.; Walter, S.; Russell, D.; Wood, E.; Galuppi, B. Gross Motor Function Classification System Expanded and Revised. Ref. Dev. Med. Child. Neurol. 2007, 39, 214–223. [Google Scholar] [CrossRef]
- Harvey, R.L. Improving poststroke recovery: Neuroplasticity and task-oriented training. Curr. Treat. Options Cardiovasc. Med. 2009, 11, 251–259. [Google Scholar] [CrossRef] [PubMed]
- Silveira-Moriyama, L. Neuroplasticity and neuromodulation in children. Eur. J. Paediatr. Neurol. 2017, 21, 3. [Google Scholar] [CrossRef]
- Lerner, Z.F.; Damiano, D.L.; Park, H.S.; Gravunder, A.J.; Bulea, T.C. A Robotic Exoskeleton for Treatment of Crouch Gait in Children with Cerebral Palsy: Design and Initial Application. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 650–659. [Google Scholar] [CrossRef] [PubMed]
- Borggraefe, I.; Meyer-Heim, A.; Kumar, A.; Schaefer, J.S.; Berweck, S.; Heinen, F. Improved gait parameters after robotic-assisted locomotor treadmill therapy in a 6-year-old child with cerebral palsy. Mov. Disord. 2008, 23, 280–283. [Google Scholar] [CrossRef]
- Sanz-Merodio, D.; Plaza, A.; Cestari, M.; Sancho-Pérez, J.; García, E. Mechanical description of atlas 2020, a 10-dof paediatric exoskleton. In Proceedings of the 19th International Conference on Climbing and Walking Robots, London, UK, 12–14 September 2016; pp. 12–14. [Google Scholar]
- Morris, L.; Diteesawat, R.S.; Rahman, N.; Turton, A.; Cramp, M.; Rossiter, J. The-state-of-the-art of soft robotics to assist mobility: A review of physiotherapist and patient identified limitations of current lower-limb exoskeletons and the potential soft-robotic solutions. J. Neuroeng. Rehabil. 2023, 20, 18. [Google Scholar] [CrossRef]
- Xiloyannis, M.; Alicea, R.; Georgarakis, A.M.; Haufe, F.L.; Wolf, P.; Masia, L.; Riener, R. Soft Robotic Suits: State of the Art, Core Technologies, and Open Challenges. IEEE Trans. Robot. 2021, 1, 1343–1362. [Google Scholar] [CrossRef]
- Mansilla Navarro, P.; Copaci, D.; Blanco Rojas, D. Design and Control of a Soft Knee Exoskeleton for Pediatric Patients at Early Stages of the Walking Learning Process. Bioengineering 2024, 11, 188. [Google Scholar] [CrossRef]
- Asbeck, A.T.; Dyer, R.J.; Larusson, A.F.; Walsh, C.J. Biologically-inspired soft exosuit. In Proceedings of the 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 24–26 June 2013; pp. 1–8. [Google Scholar]
- Pons, J. Witnessing a wearables transition. Science 2019, 365, 636–637. [Google Scholar] [CrossRef] [PubMed]
- Asbeck, A.; De Rossi, S.M.M.; Galiana, I.; Ding, Y.; Walsh, C.J. Stronger, smarter, softer: Next-generation wearable robots. IEEE Robot. Autom. 2014, 21, 22–33. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, S.; Li, Y.; Chen, X.; Yuan, D.; Liu, M.; Liu, J.; Qin, X.; Cui, H.; Li, B. Biomechanical Design, Modeling and Control of an Ankle-Exosuit System; Springer: Berlin/Heidelberg, Germany, 2023; pp. 489–502. [Google Scholar]
- Siviy, C.; Bae, J.; Baker, L.; Porciuncula, F.; Baker, T.; Ellis, T.D.; Awad, L.N.; Walsh, C.J. Offline assistance optimization of a soft exosuit for augmenting ankle power of stroke survivors during walking. IEEE Robot. Autom. Lett. 2020, 5, 828–835. [Google Scholar] [CrossRef] [PubMed]
- Mohd Jani, J.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Serrano, D.; Copaci, D.S.; Moreno, L.; Blanco, D. SMA based wrist exoskeleton for rehabilitation therapy. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2318–2323. [Google Scholar] [CrossRef]
- Kim, C.; Kim, G.; Lee, Y.; Lee, G.; Han, S.; Kang, D.; Helen, S.; Koh, J.S. Shape memory alloy actuator-embedded smart clothes for ankle assistance. Smart Mater. Struct. 2020, 29, 055003. [Google Scholar] [CrossRef]
- Piao, J.; Kim, M.; Kim, J.; Kim, C.; Han, S.; Back, I.; Koh, J.S.; Koo, S. Development of a comfort suit-type soft-wearable robot with flexible artificial muscles for walking assistance. Sci. Rep. 2023, 14, 4869. [Google Scholar] [CrossRef]
- Głowiński, S.; Błażejewski, A.; Królikowski, T.; Knitter, R. Gait recognition: A challenging task for MEMS signal identification. In Proceedings of the International Conference on Sustainable Design and Manufacturing, Budapest, Hungary, 4–5 July 2019. [Google Scholar]
- Ha, J.H.; Choi, I.H.; Chung, C.Y.; Cho, T.J.; Jung, S.T.; Lee, H.S.; Park, S.S.; Lee, H.Y.; Oh, C.W.; Kim, I.O. Distribution of Lengths of the Normal Femur and Tibia in Korean Children from Three to Sixteen Years of Age. J. Korean Med. Sci. 2003, 18, 715–721. [Google Scholar] [CrossRef] [PubMed]
- Diego-Mas, J.A. Biomecánica—Esfuerzos Estáticos Coplanares; Ergonautas, Universidad Politécnica de Valencia: Valencia, Spain, 2015. [Google Scholar]
- Soto, V.M. Gutiérrez, M. Parámetros Inerciales Para El Modelado Biomecánico Del Cuerpo Humano. Eur. J. Hum. Mov. 2010, 2, 169–189. [Google Scholar]
- Avila-Chaurand, R.; Prado-León, L.R.; González-Munoz, E.L. Dimensiones Antropométricas de Población Latinoamericana; Universidad de Guadalajara: Guadalajara, Mexico, 2007; ISBN -978-970-27-1193-3. [Google Scholar]
- Ortega, A.B.; Bautista, R.F.V.; Vela-Váldes, G.; Marmol, E.Q.; López, G.L. Control of a Virtual Prototype of an Ankle Rehabilitation Machine; Revista Facultad de Ingeniería Universidad de Antioquia: Medellín, Colombia, 2013; pp. 183–196. [Google Scholar]
- Hallemans, A.; De Clercq, D.; Otten, B.; Aerts, P. 3D joint dynamics of walking in toddlers: A cross-sectional study spanning the first rapid development phase of walking. Gait Posture 2005, 22, 107–118. [Google Scholar] [CrossRef]
- Feroca. Platsil Gel Series. 2013. Available online: https://www.feroca.com/documentos/FT_PLATSIL_GEL_SERIES_ES.pdf (accessed on 1 May 2024).
- Ward, S.R.; Lieber, R.L. Density and hydration of fresh and fixed human skeletal muscle. J. Biomech. 2005, 38, 2317–2320. [Google Scholar] [CrossRef]
- Brillat, A. Composición corporal. Manual de Nutrición y Dietética. In Manual de Nutricion y Dietetica; Docta, Universidad Complutense de Madrid: Madrid, Spain, 2018; pp. 1–7. [Google Scholar]
- Sanjuan Cervero, R.; Jiménez Honrado, P.J.; Gil Monzo, E.; Sanchez Rodriguez, R.; Fenollosa Gomez, J. Biomecánica de la rodilla Biomechanics of the knee. Patol. Apar. Locomot. 2005, 3, 189–200. [Google Scholar]
- Richard, D.L.; Adam, M.W.M.; Wayne Vogl, A. Gray. Anatomía Para Estudiantes, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Arias, J.; Copaci, D.; Mansilla, P.; Moreno, L.; Blanco, D. Exo-traje pediátrico actuado con SMA. In Jornadas Robótica Educación Bioingeniería; CEA: Málaga, Spain, 2022. [Google Scholar]
- Copaci, D.S.; Blanco, D.; Martin-Clemente, A.; Moreno, L. Flexible shape memory alloy actuators for soft robotics: Modelling and control. Int. J. Adv. Robot. Syst. 2020, 17, 1729881419886747. [Google Scholar] [CrossRef]
- Copaci, D.; Blanco, D.; Moreno, L.E. Flexible shape-memory alloy-based actuator: Mechanical design optimization according to application. Actuators 2019, 8, 63. [Google Scholar] [CrossRef]
- Dynalloy. Technical Characteristics of Actuator Wires, Dynalloy. In Flexinol-Dynalloy. 2010, pp. 1–12. Available online: https://www.dynalloy.com/pdfs/TCF1140.pdf (accessed on 1 May 2024).
- Gentil, I.A. Podología preventiva: Niños descalzos igual a niños más inteligentes. Rev. Int. Cienc. Podol. 2007, 1, 27–34. [Google Scholar]
- Bosch Sensortec GmbH. BNO055 Data Sheet. 2014, p. 105. Available online: https://cdn-shop.adafruit.com/datasheets/BST_BNO055_DS000_12.pdf (accessed on 1 May 2024).
- Mansilla Navarro, P.; Copaci, D.; Blanco Rojas, D. Desarrollo y validacion de modelos para la estimacion de posiciones angulares en un exotraje a partir de sensores inerciales. In Simposio de Robótica, Bioingeniería y Visión por Computador; CEA: Badajoz, Spain, 2024; pp. 100–106. [Google Scholar]
- Koopman, B.; van Asseldonk, E.H.; Van der Kooij, H. Speed-dependent reference joint trajectory generation for robotic gait support. J. Biomech. 2014, 47, 1447–1458. [Google Scholar] [CrossRef]
- Copaci, D.; Martin, F.; Moreno, L.; Blanco, D. SMA Based Elbow Exoskeleton for Rehabilitation Therapy and Patient Evaluation. IEEE Access 2019, 7, 31473–31484. [Google Scholar] [CrossRef]
- Villoslada, Á.; Escudero, N.; Martín, F.; Flores, A.; Rivera, C.; Collado, M.; Moreno, L. Position control of a shape memory alloy actuator using a four-term bilinear PID controller. Sens. Actuators A Phys. 2015, 236, 257–272. [Google Scholar] [CrossRef]
- Arias Guadalupe, J.; Copaci, D.; Mansilla Navarro, P.; Moreno, L.; Blanco, D. A novel multi-wire SMA-based actuator with high-frequency displacement. Mechatronics 2023, 91, 102957. [Google Scholar] [CrossRef]






| Segment | Length [cm] | Weight [kg] | Diameter [cm] | |||
|---|---|---|---|---|---|---|
| Real | Dummy | Real | Dummy | Real | Dummy | |
| Thigh | 22.5 | 22.8 | 1.55 | 1.43 | 7.5 | 7.3 |
| Shank | 18.8 | 17.8 | 0.65 | 0.61 | 5.0 | 5.1 |
| Foot | 14.4 | 14.2 | 0.23 | 0.25 | 3.0 | 3.0 |
| Movement | Knee | Ankle |
|---|---|---|
| Flexion (∘) | 60 | 5 |
| Extension (∘) | 0 | 15 |
| Joint | Ankle |
|---|---|
| Diameter (mm) | 0.38 |
| Activation Temperature (∘C) | 90 |
| Payload (kg) | 2.25 |
| Current (A) | 2.25 |
| Resistance (Ω/m) | 8.3 |
| Period [s] | Error [∘] | ||||
|---|---|---|---|---|---|
| 9 | - | - | - | - | - |
| 10 | 2.156 | - | - | - | - |
| 11 | 1.953 | 2.305 | 2.457 | - | - |
| 12 | 1.776 | 1.954 | 2.006 | 2.207 | 2.306 |
| 13 | 1.636 | 1.845 | 1.966 | 1.996 | 2.014 |
| 14 | 1.589 | 1.648 | 1.749 | 1.843 | 1.848 |
| 15 | 1.512 | 1.599 | 1.651 | 1.689 | 1.733 |
| 16 | 1.464 | 1.502 | 1.625 | 1.633 | 1.665 |
| 17 | 1.404 | 1.466 | 1.575 | 1.580 | 1.583 |
| 18 | 1.386 | 1.432 | 1.482 | 1.506 | 1.513 |
| 19 | 1.356 | 1.365 | 1.468 | 1.470 | 1.478 |
| 20 | 1.299 | 1.321 | 1.404 | 1.396 | 1.415 |
| 21 | 1.320 | 1.299 | 1.320 | 1.359 | 1.369 |
| 22 | 1.205 | 1.257 | 1.289 | 1.345 | 1.332 |
| 24 | 0.981 | 0.996 | 1.021 | 1.166 | 1.227 |
| 26 | 0.875 | 0.963 | 0.999 | 1.057 | 1.136 |
| 28 | 0.870 | 0.884 | 0.907 | 0.965 | 1.159 |
| 30 | 0.845 | 0.892 | 0.932 | 0.992 | 1.143 |
| Pattern | 1 km/h | 2 km/h | 3 km/h | 4 km/h | 5 km/h |
| Period [s] | Error [∘] | Period [s] | Error [∘] | Period [s] | Error [∘] |
|---|---|---|---|---|---|
| 4 | - | 10 | 1.312 | 17 | 0.795 |
| 5 | 2.499 | 11 | 1.217 | 20 | 0.989 |
| 6 | 2.094 | 12 | 1.149 | 24 | 0.863 |
| 7 | 1.759 | 13 | 1.022 | 26 | 0.896 |
| 8 | 1.589 | 14 | 0.983 | 28 | 0.757 |
| 9 | 1.414 | 15 | 0.832 | 30 | 0.765 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mansilla Navarro, P.; Copaci, D.; Arias, J.; Blanco Rojas, D. Design of an SMA-Based Actuator for Replicating Normal Gait Patterns in Pediatric Patients with Cerebral Palsy. Biomimetics 2024, 9, 376. https://doi.org/10.3390/biomimetics9070376
Mansilla Navarro P, Copaci D, Arias J, Blanco Rojas D. Design of an SMA-Based Actuator for Replicating Normal Gait Patterns in Pediatric Patients with Cerebral Palsy. Biomimetics. 2024; 9(7):376. https://doi.org/10.3390/biomimetics9070376
Chicago/Turabian StyleMansilla Navarro, Paloma, Dorin Copaci, Janeth Arias, and Dolores Blanco Rojas. 2024. "Design of an SMA-Based Actuator for Replicating Normal Gait Patterns in Pediatric Patients with Cerebral Palsy" Biomimetics 9, no. 7: 376. https://doi.org/10.3390/biomimetics9070376
APA StyleMansilla Navarro, P., Copaci, D., Arias, J., & Blanco Rojas, D. (2024). Design of an SMA-Based Actuator for Replicating Normal Gait Patterns in Pediatric Patients with Cerebral Palsy. Biomimetics, 9(7), 376. https://doi.org/10.3390/biomimetics9070376







