An Enhanced Tree-Seed Algorithm for Function Optimization and Production Optimization
Abstract
1. Introduction
- This study introduces an enhanced version of TSA, referred to as WQTSA, which incorporates the water-cycle mechanism and quantum rotation-gate strategy. These mechanisms enhance TSA’s global search capability and facilitate escaping local optima, thereby achieving a balance between search and exploration;
- To evaluate the effectiveness of the proposed WQTSA, it was benchmarked against other state-of-the-art evolutionary algorithms at IEEE CEC 2017. Additionally, this study offers a detailed analysis of how the two improvement mechanisms impact the performance of WQTSA, along with assessing its scalability across various dimensions;
- To assess the performance of the proposed WQTSA in addressing real production challenges, this study employs it to tackle the production optimization problem centered on three-channel reservoirs. Furthermore, the algorithm is compared against other state-of-the-art evolutionary algorithms in resolving this issue. The experimental findings underscore the outstanding optimization capabilities of the proposed algorithm in real-world scenarios.
2. Overview of the Original TSA
| Algorithm 1. Tree-seed algorithm |
|
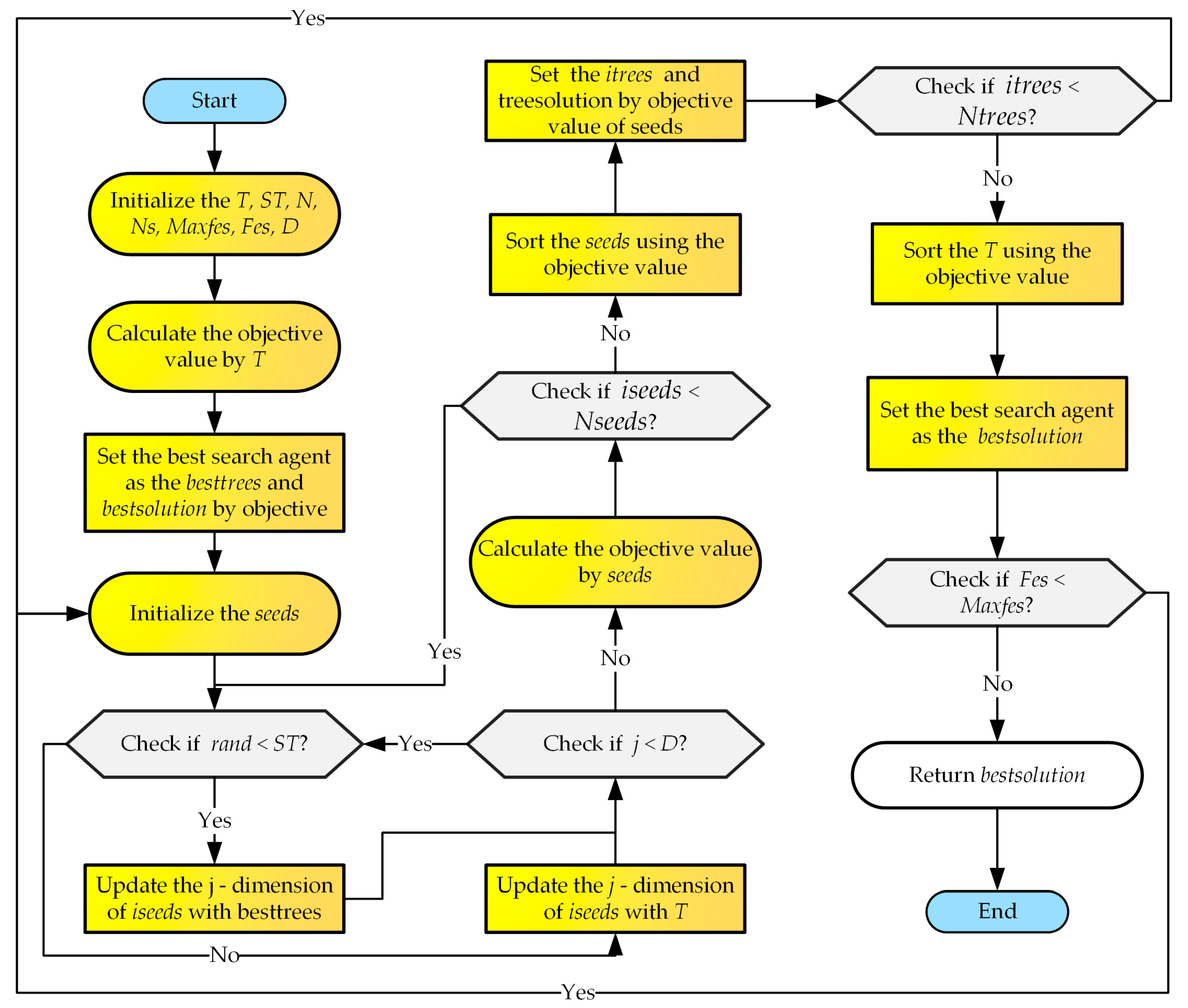
3. The Proposed WQTSA
3.1. The Water-Cycle Mechanism
| Algorithm 2. The water-cycle mechanism |
|
3.2. The Quantum Rotation-Gate Strategy
| Algorithm 3. The quantum rotation-gate strategy |
|
3.3. The Proposed WQTSA
| Algorithm 4. The proposed WQTSA |
|
4. Experimental Results and Analysis
4.1. Experiments on Benchmark Test Functions
4.1.1. Strategy Validation
4.1.2. Scalability Test
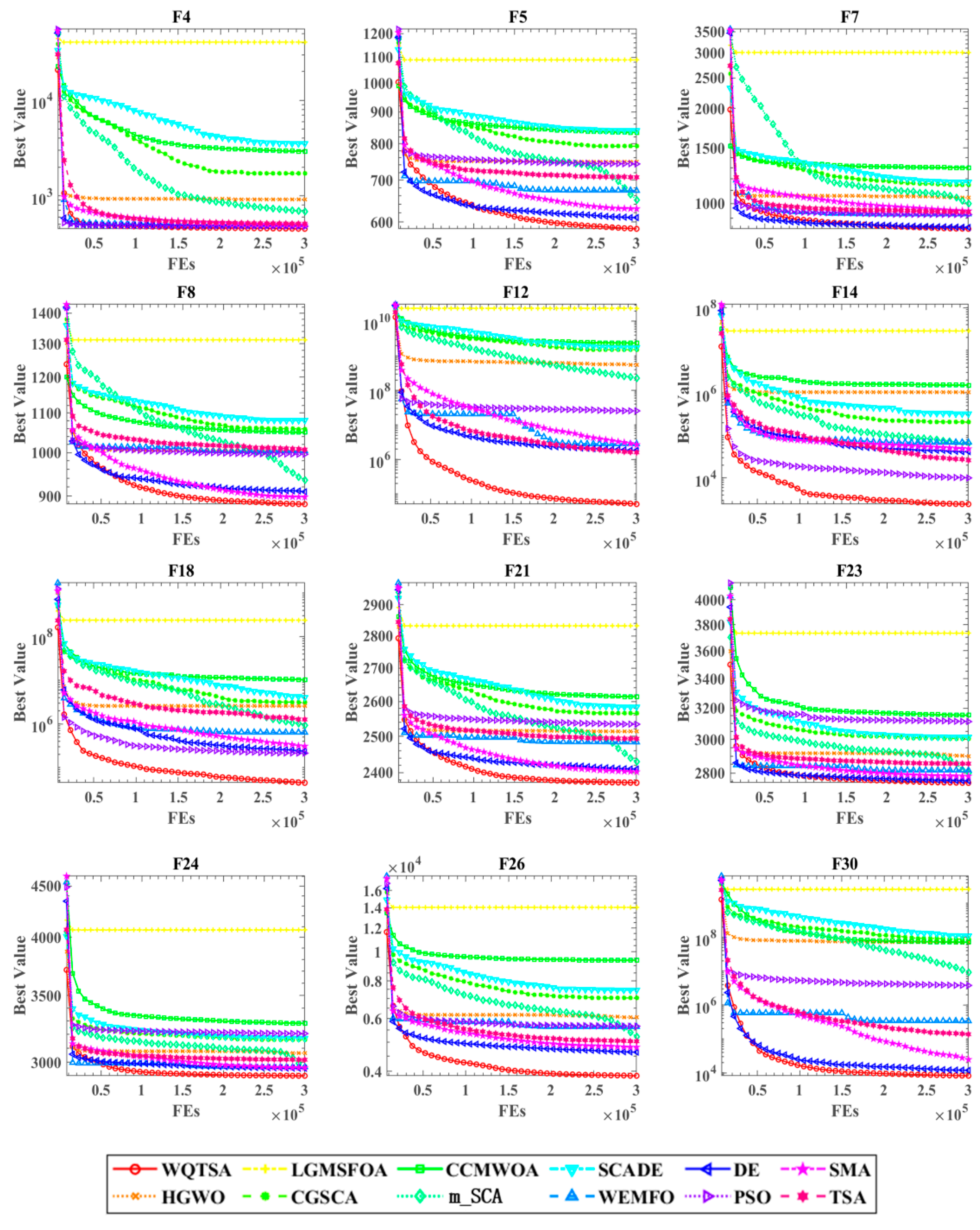
4.1.3. Comparison with Other Algorithms
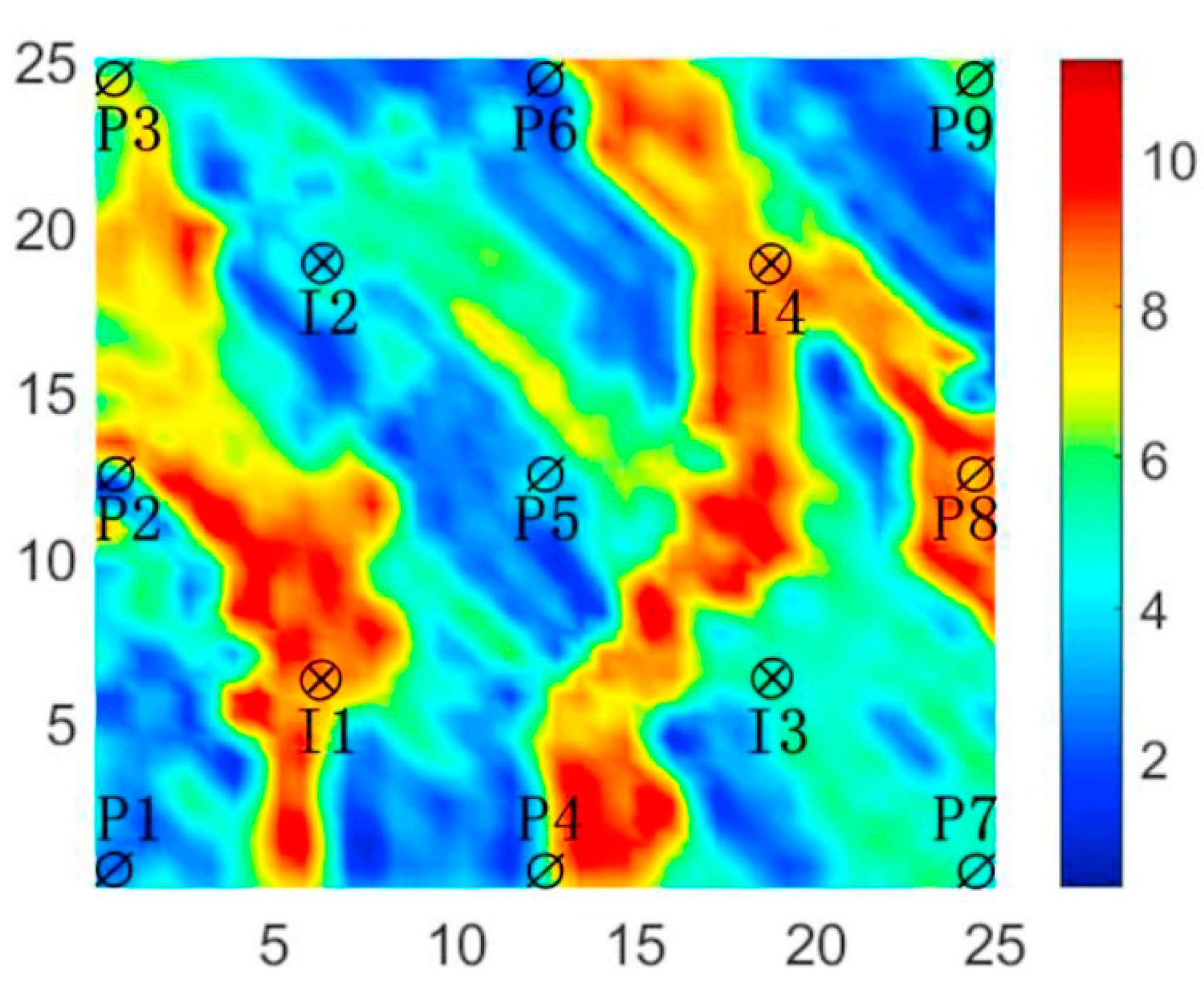
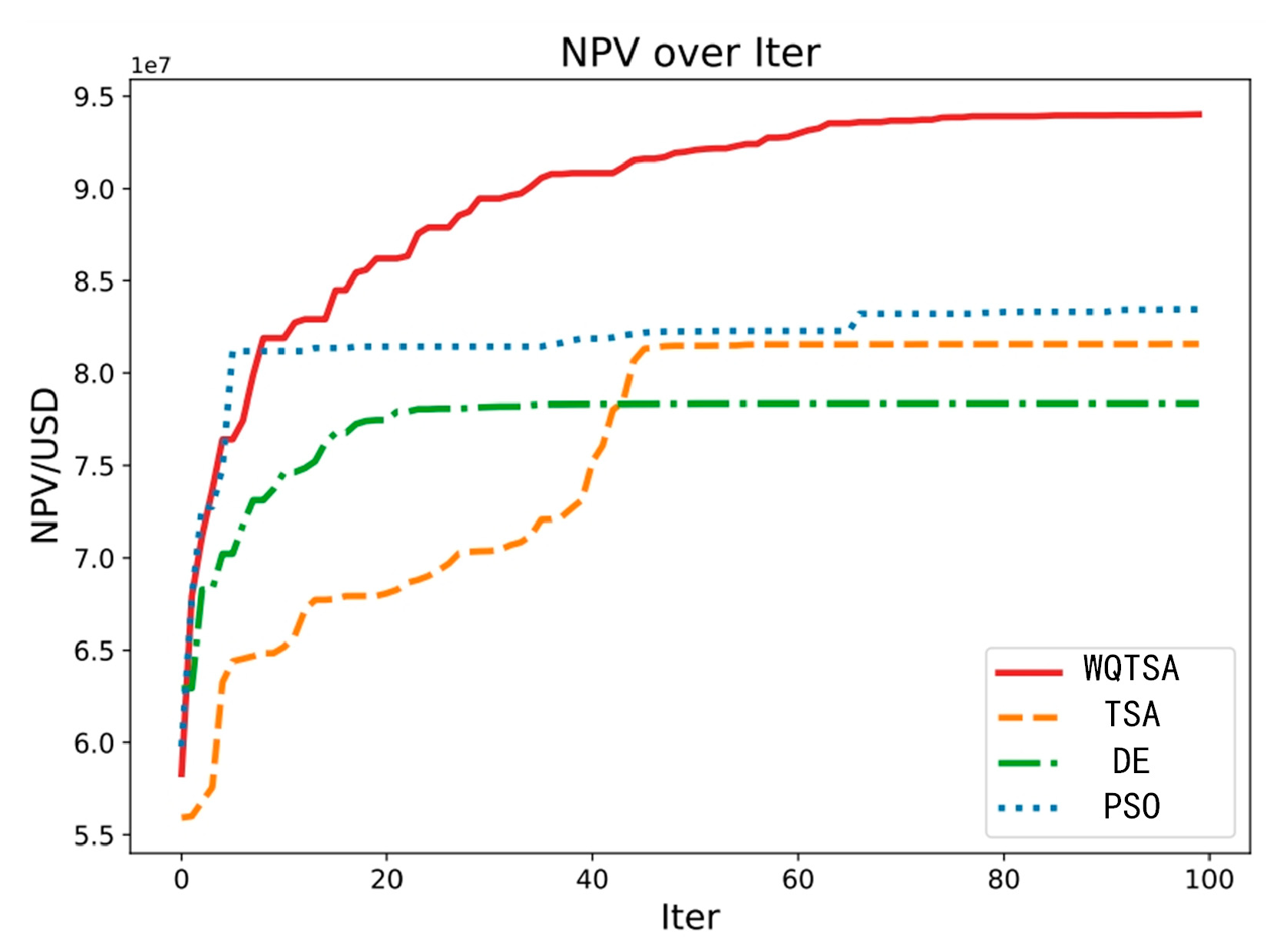
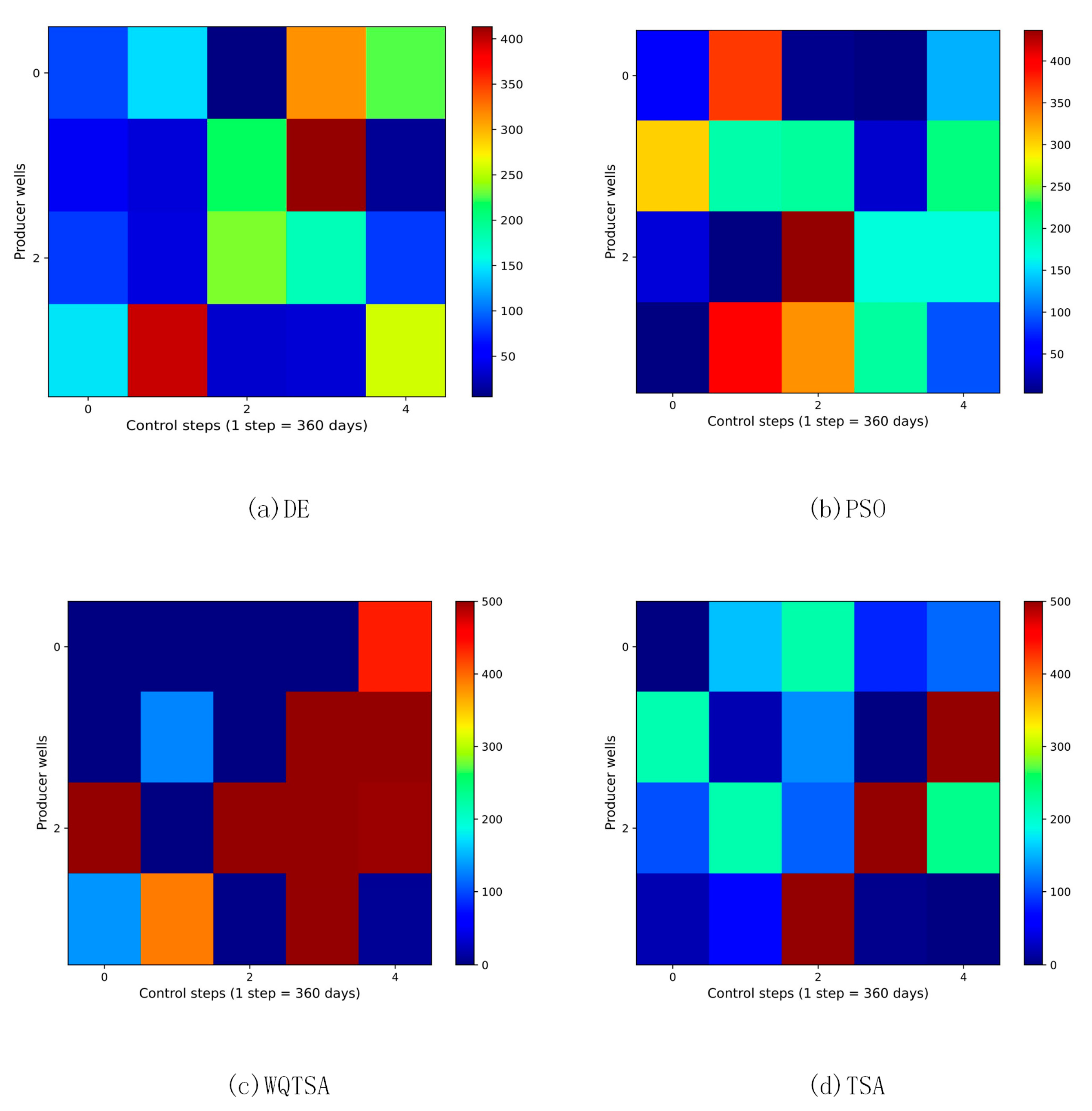
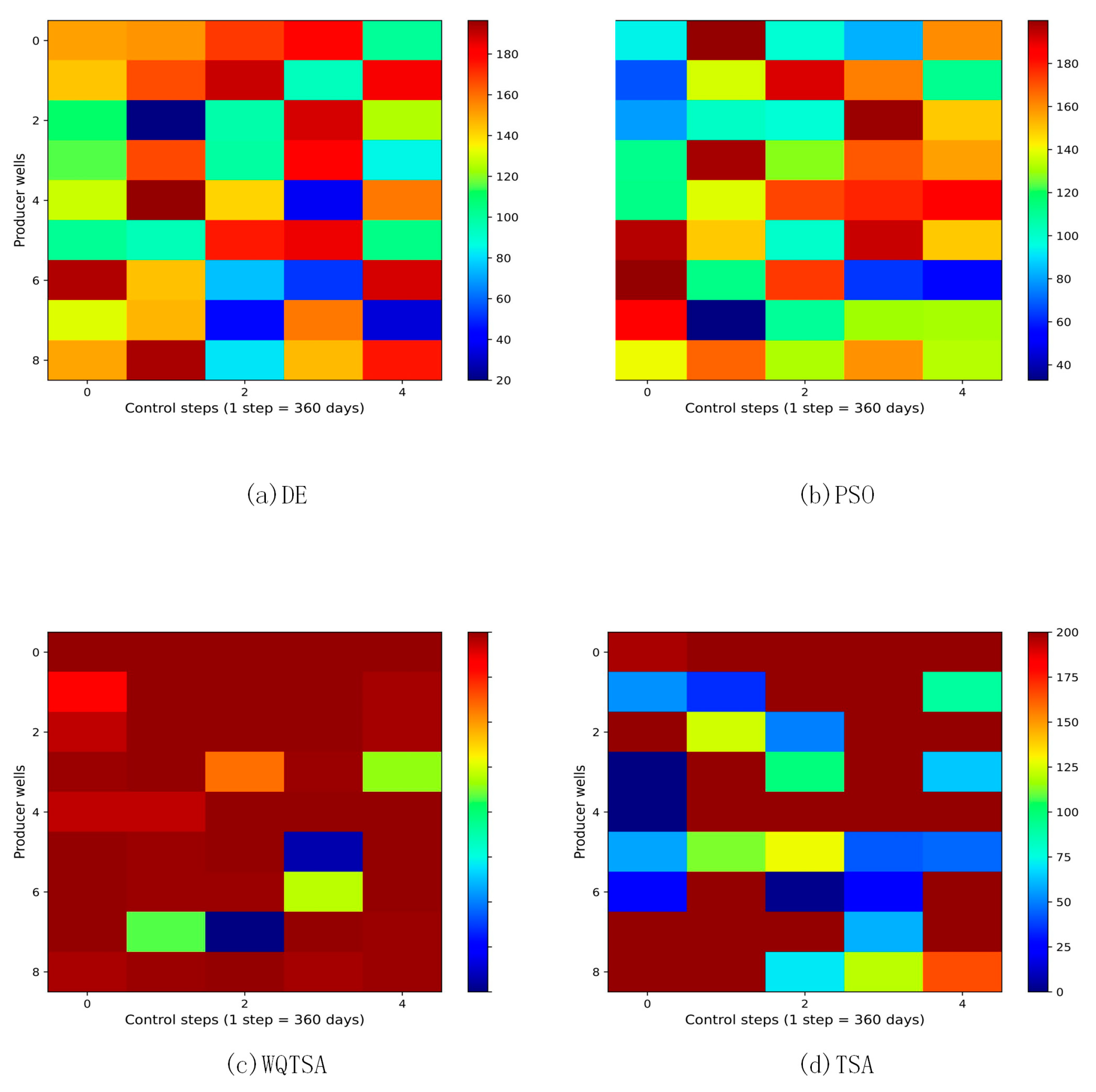
4.2. Application to Oil Reservoir Production
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faris, H.; Ala’M, A.-Z.; Heidari, A.A.; Aljarah, I.; Mafarja, M.; Hassonah, M.A.; Fujita, H. An intelligent system for spam detection and identification of the most relevant features based on evolutionary Random Weight Networks. Inf. Fusion 2019, 48, 67–83. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, J.; Liu, J.; Liu, Y.; Tan, S. A dual distance dominance based evolutionary algorithm with selection-replacement operator for many-objective optimization. Expert Syst. Appl. 2024, 237, 121244. [Google Scholar] [CrossRef]
- Wang, Z.-Z.; Zhang, K.; Chen, G.-D.; Zhang, J.-D.; Wang, W.-D.; Wang, H.-C.; Zhang, L.-M.; Yan, X.; Yao, J. Evolutionary-assisted reinforcement learning for reservoir real-time production optimization under uncertainty. Pet. Sci. 2023, 20, 261–276. [Google Scholar] [CrossRef]
- Zhuang, X.; Wang, W.; Su, Y.; Yan, B.; Li, Y.; Li, L.; Hao, Y. Multi-objective optimization of reservoir development strategy with hybrid artificial intelligence method. Expert Syst. Appl. 2024, 241, 122707. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2007, 1, 28–39. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks—Conference Proceedings, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler’s laws of planetary motion. Knowl. Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl. Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Zhao, Z.; Luo, S. A Crisscross-Strategy-Boosted Water Flow Optimizer for Global Optimization and Oil Reservoir Production. Biomimetics 2024, 9, 20. [Google Scholar] [CrossRef]
- Song, Y.; Cai, X.; Zhou, X.; Zhang, B.; Chen, H.; Li, Y.; Deng, W.; Deng, W. Dynamic hybrid mechanism-based differential evolution algorithm and its application. Expert Syst. Appl. 2023, 213, 118834. [Google Scholar] [CrossRef]
- Li, L.; Liu, L.; Shao, Y.; Zhang, X.; Chen, Y.; Guo, C.; Nian, H. Enhancing Swarm Intelligence for Obstacle Avoidance with Multi-Strategy and Improved Dung Beetle Optimization Algorithm in Mobile Robot Navigation. Electronics 2023, 12, 4462. [Google Scholar] [CrossRef]
- Bian, X.; Zhang, R.; Liu, P.; Xiang, Y.; Wang, S.; Tan, X. Near infrared spectroscopic variable selection by a novel swarm intelligence algorithm for rapid quantification of high order edible blend oil. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 284, 121788. [Google Scholar] [CrossRef]
- Chen, A.; Liao, Y.; Cai, H.; Guo, X.; Zhang, B.; Lin, B.; Zhang, W.; Wei, L.; Tong, Y. Experimental study on 3D source localization in indoor environments with weak airflow based on two bionic swarm intelligence algorithms. Build. Environ. 2023, 230, 110020. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Kiran, M.S. TSA: Tree-seed algorithm for continuous optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]
- Babalik, A.; Cinar, A.C.; Kiran, M.S. A modification of tree-seed algorithm using Deb’s rules for constrained optimization. Appl. Soft Comput. 2018, 63, 289–305. [Google Scholar] [CrossRef]
- Aslan, M.; Beskirli, M.; Kodaz, H.; Kiran, M. An improved tree seed algorithm for optimization problems. Int. J. Mach. Learn Comput. 2018, 8, 20–25. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Korashy, A.; Kamel, S.; Youssef, A.-R.; Jurado, F. Modified water cycle algorithm for optimal direction overcurrent relays coordination. Appl. Soft Comput. 2019, 74, 10–25. [Google Scholar] [CrossRef]
- Osaba, E.; Ser, J.D.; Sadollah, A.; Bilbao, M.N.; Camacho, D. A discrete water cycle algorithm for solving the symmetric and asymmetric traveling salesman problem. Appl. Soft Comput. 2018, 71, 277–290. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Water cycle algorithm for optimal overcurrent relays coordination in electric power systems. Soft Comput. 2019, 23, 12761–12778. [Google Scholar] [CrossRef]
- Elhameed, M.A.; El-Fergany, A.A. Water cycle algorithm-based economic dispatcher for sequential and simultaneous objectives including practical constraints. Appl. Soft Comput. 2017, 58, 145–154. [Google Scholar] [CrossRef]
- Coelho, L.d.S. Gaussian quantum-behaved particle swarm optimization approaches for constrained engineering design problems. Expert Syst. Appl. 2010, 37, 1676–1683. [Google Scholar] [CrossRef]
- Zhu, A.; Xu, C.; Li, Z.; Wu, J.; Liu, Z. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC. J. Syst. Eng. Electron. 2015, 26, 317–328. [Google Scholar] [CrossRef]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, B.K. Single sensor-based MPPT of partially shaded PV system for battery charging by using cauchy and gaussian sine cosine optimization. IEEE Trans. Energy Convers. 2017, 32, 983–992. [Google Scholar] [CrossRef]
- Luo, J.; Chen, H.; Heidari, A.A.; Xu, Y.; Zhang, Q.; Li, C. Multi-strategy boosted mutative whale-inspired optimization approaches. Appl. Math. Model. 2019, 73, 109–123. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. A hybrid self-adaptive sine cosine algorithm with opposition based learning. Expert Syst. Appl. 2019, 119, 210–230. [Google Scholar] [CrossRef]
- Nenavath, H.; Jatoth, R.K. Hybridizing sine cosine algorithm with differential evolution for global optimization and object tracking. Appl. Soft Comput. 2018, 62, 1019–1043. [Google Scholar] [CrossRef]
- Shan, W.; Qiao, Z.; Heidari, A.A.; Chen, H.; Turabieh, H.; Teng, Y. Double adaptive weights for stabilization of moth flame optimizer: Balance analysis, engineering cases, and medical diagnosis. Knowl. Based Syst. 2021, 214, 106728. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, H.; Heidari, A.A.; Zhao, X.; Xu, Y.; Wang, P.; Li, Y.; Li, C. Chaos-induced and Mutation-driven Schemes Boosting Salp Chains-inspired Optimizers. IEEE Access 2019, 7, 31243–31261. [Google Scholar] [CrossRef]

| 0 +1 | 0 −1 | 0 ±1 | 0 0 | ||
| −1 | +1 | 0 | ±1 |
| Population Size | Dimension | Maximum Evaluation |
|---|---|---|
| 30 | 30 | 300,000 |
| Algorithm | Water-Cycle Mechanism | Quantum Rotation-Gate Strategy |
|---|---|---|
| WQTSA | 1 | 1 |
| WTSA | 1 | 0 |
| QTSA | 0 | 1 |
| TSA | 0 | 0 |
| Algorithm | Rank | +/=/− | AVG |
|---|---|---|---|
| WQTSA | 1 | ~ | 1.7511 |
| WTSA | 2 | 2/28/0 | 1.8055 |
| QTSA | 3 | 14/12/4 | 3.1644 |
| TSA | 4 | 16/10/4 | 3.2789 |
| Function | Method | Dim = 50 | Dim = 100 | ||
|---|---|---|---|---|---|
| Avg | Std | Avg | Std | ||
| F1 | WQTSA | 1.4197 × 103 | 1.4471 × 103 | 4.2093 × 103 | 3.1504 × 103 |
| TSA | 2.1062 × 104 | 2.3542 × 104 | 4.7241 × 109 | 1.1577 × 109 | |
| F2 | WQTSA | 3.9106 × 1035 | 1.8553 × 1036 | 6.0307 × 10102 | 3.3017 × 10103 |
| TSA | 5.1592 × 1056 | 1.3834 × 1057 | 1.7191 × 10137 | 7.6164 × 10137 | |
| F3 | WQTSA | 1.8549 × 104 | 8.5976 × 103 | 1.0695 × 105 | 2.8537 × 104 |
| TSA | 1.2177 × 105 | 1.4129 × 104 | 3.6799 × 105 | 2.9832 × 104 | |
| F4 | WQTSA | 5.0997 × 102 | 4.9222 × 10 | 6.5064 × 102 | 3.9680 × 10 |
| TSA | 6.8107 × 102 | 3.6427 × 10 | 2.5319 × 103 | 7.2137 × 102 | |
| F5 | WQTSA | 6.6928 × 102 | 4.4114 × 10 | 9.6846 × 102 | 1.0564 × 102 |
| TSA | 9.3416 × 102 | 1.9242 × 10 | 1.5977 × 103 | 2.7811 × 10 | |
| F6 | WQTSA | 6.0005 × 102 | 2.7953 × 10−2 | 6.1336 × 102 | 7.9760 |
| TSA | 6.0127 × 102 | 3.5299 × 10−1 | 6.2336 × 102 | 2.5496 | |
| F7 | WQTSA | 9.9324 × 102 | 8.0259 × 10 | 1.4958 × 103 | 1.7223 × 102 |
| TSA | 1.2151 × 103 | 2.2312 × 10 | 2.1728 × 103 | 6.0895 × 10 | |
| F8 | WQTSA | 9.7020 × 102 | 5.7475 × 10 | 1.3352 × 103 | 1.2678 × 102 |
| TSA | 1.2382 × 103 | 1.5723 × 10 | 1.9065 × 103 | 3.2687 × 10 | |
| F9 | WQTSA | 1.2881 × 103 | 2.4520 × 102 | 1.5701 × 104 | 5.4030 × 103 |
| TSA | 2.1181 × 103 | 4.1122 × 102 | 2.5347 × 104 | 3.4631 × 103 | |
| F10 | WQTSA | 1.0590 × 104 | 2.3092 × 103 | 2.2647 × 104 | 4.7890 × 103 |
| TSA | 1.4207 × 104 | 3.6583 × 102 | 3.1020 × 104 | 4.1899 × 102 | |
| F11 | WQTSA | 1.2469 × 103 | 4.2471 × 10 | 2.1120 × 103 | 2.6483 × 102 |
| TSA | 1.4328 × 103 | 3.4992 × 10 | 3.9925 × 104 | 6.2341 × 103 | |
| F12 | WQTSA | 6.2668 × 105 | 2.9751 × 105 | 2.2766 × 106 | 8.1725 × 105 |
| TSA | 5.0190 × 107 | 1.8423 × 107 | 9.1039 × 108 | 3.2296 × 108 | |
| F13 | WQTSA | 3.1540 × 103 | 2.9128 × 103 | 4.8837 × 103 | 2.6779 × 103 |
| TSA | 3.4657 × 103 | 2.4187 × 103 | 5.0222 × 103 | 1.7070 × 103 | |
| F14 | WQTSA | 2.0172 × 104 | 2.0150 × 104 | 2.9168 × 105 | 2.5950 × 105 |
| TSA | 2.9488 × 105 | 1.8088 × 105 | 1.1044 × 107 | 2.9593 × 106 | |
| F15 | WQTSA | 9.1881 × 103 | 5.6308 × 103 | 2.7625 × 103 | 9.6328 × 102 |
| TSA | 7.3885 × 103 | 4.0376 × 103 | 2.6287 × 103 | 6.6934 × 102 | |
| F16 | WQTSA | 3.5016 × 103 | 4.0734 × 102 | 6.8120 × 103 | 1.1096 × 103 |
| TSA | 4.7224 × 103 | 2.4342 × 102 | 1.0137 × 104 | 3.0764 × 102 | |
| F17 | WQTSA | 3.0127 × 103 | 3.4188 × 102 | 5.3166 × 103 | 7.3976 × 102 |
| TSA | 3.6998 × 103 | 1.1478 × 102 | 6.9918 × 103 | 2.3810 × 102 | |
| F18 | WQTSA | 1.9738 × 105 | 1.7608 × 105 | 5.9470 × 105 | 3.9607 × 105 |
| TSA | 6.3561 × 106 | 1.9752 × 106 | 2.2474 × 107 | 5.9624 × 106 | |
| F19 | WQTSA | 1.8234 × 104 | 5.6302 × 103 | 3.3909 × 103 | 1.1063 × 103 |
| TSA | 1.4543 × 104 | 4.3221 × 103 | 2.9141 × 103 | 7.7287 × 102 | |
| F20 | WQTSA | 3.1654 × 103 | 2.9736 × 102 | 5.5297 × 103 | 6.5849 × 102 |
| TSA | 3.6917 × 103 | 1.6412 × 102 | 7.0047 × 103 | 1.7127 × 102 | |
| F21 | WQTSA | 2.4701 × 103 | 6.4127 × 10 | 2.8205 × 103 | 1.1717 × 102 |
| TSA | 2.7273 × 103 | 1.1603 × 10 | 3.4304 × 103 | 2.8141 × 10 | |
| F22 | WQTSA | 6.0001 × 103 | 4.8530 × 103 | 2.5513 × 104 | 4.8490 × 103 |
| TSA | 9.7356 × 103 | 5.6897 × 103 | 3.3378 × 104 | 4.4458 × 102 | |
| F23 | WQTSA | 2.9446 × 103 | 5.8987 × 10 | 3.3266 × 103 | 1.6564 × 102 |
| TSA | 3.1744 × 103 | 1.9795 × 10 | 3.9338 × 103 | 1.0051 × 102 | |
| F24 | WQTSA | 3.1068 × 103 | 6.9419 × 10 | 3.9542 × 103 | 1.8350 × 102 |
| TSA | 3.3311 × 103 | 2.1892 × 10 | 4.5084 × 103 | 5.2372 × 10 | |
| F25 | WQTSA | 3.0753 × 103 | 2.4312 × 10 | 3.3198 × 103 | 3.8803 × 10 |
| TSA | 3.1299 × 103 | 2.1999 × 10 | 5.0026 × 103 | 5.8189 × 102 | |
| F26 | WQTSA | 6.2454 × 103 | 9.6312 × 102 | 1.4683 × 104 | 2.7080 × 103 |
| TSA | 8.1255 × 103 | 1.7772 × 102 | 1.8064 × 104 | 4.4427 × 102 | |
| F27 | WQTSA | 3.4545 × 103 | 1.2042 × 102 | 3.6726 × 103 | 1.0113 × 102 |
| TSA | 3.6599 × 103 | 6.2266 × 10 | 4.4969 × 103 | 3.0731 × 102 | |
| F28 | WQTSA | 3.3041 × 103 | 1.6297 × 10 | 3.4165 × 103 | 3.8194 × 10 |
| TSA | 3.3841 × 103 | 3.4199 × 10 | 5.4609 × 103 | 6.6265 × 102 | |
| F29 | WQTSA | 4.3791 × 103 | 3.5064 × 102 | 7.9001 × 103 | 8.6866 × 102 |
| TSA | 5.1581 × 103 | 2.7747 × 102 | 9.9630 × 103 | 3.6747 × 102 | |
| F30 | WQTSA | 1.0761 × 106 | 6.7357 × 105 | 1.8462 × 104 | 1.0874 × 104 |
| TSA | 3.7897 × 106 | 1.3978 × 106 | 1.1488 × 106 | 3.8097 × 105 | |
| Algorithm | Rank | +/=/− | AVG |
|---|---|---|---|
| WQTSA | 1 | ~ | 1.8667 |
| HGWO | 8 | 30/0/0 | 7.9667 |
| LGMSFOA | 12 | 30/0/0 | 12.0000 |
| CGSCA | 9 | 30/0/0 | 8.9000 |
| CCMWOA | 11 | 30/0/0 | 10.2000 |
| m_SCA | 6 | 27/2/1 | 5.5333 |
| SCADE | 10 | 30/0/0 | 10.0333 |
| WEMFO | 5 | 28/1/1 | 5.36667 |
| DE | 2 | 17/8/5 | 2.4333 |
| PSO | 7 | 26/2/2 | 5.6333 |
| SMA | 3 | 25/1/4 | 3.6000 |
| TSA | 4 | 23/1/6 | 4.4007 |
| HGWO | LGMSFOA | CGSCA | CCMWOA | m_SCA | SCADE | |
|---|---|---|---|---|---|---|
| F1 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F2 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F3 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F4 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F5 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F7 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.9209 × 10−6 | 1.7344 × 10−6 |
| F8 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.6394 × 10−5 | 1.7344 × 10−6 |
| F9 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F10 | 2.1827 × 10−2 | 1.7344 × 10−6 | 1.9209 × 10−6 | 7.7122 × 10−4 | 4.3896 × 10−3 | 1.7344 × 10−6 |
| F11 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F12 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F13 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F14 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F15 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F16 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.9209 × 10−6 | 2.3038 × 10−2 | 1.7344 × 10−6 |
| F17 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 7.5213 × 10−2 | 1.7344 × 10−6 |
| F18 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F19 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.9209 × 10−6 | 1.7344 × 10−6 |
| F20 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.1266 × 10−6 | 5.2165 × 10−6 | 4.9498 × 10−2 | 1.7344 × 10−6 |
| F21 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 5.7517 × 10−6 | 1.7344 × 10−6 |
| F22 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F23 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.1265 × 10−5 | 1.7344 × 10−6 |
| F24 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.4936E-05 | 1.7344 × 10−6 |
| F25 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F26 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 6.3391 × 10−6 | 1.7344 × 10−6 |
| F27 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 3.3173 × 10−4 | 1.7344 × 10−6 |
| F28 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F29 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.5846E-03 | 1.7344 × 10−6 |
| F30 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| WEMFO | DE | PSO | SMA | TSA | ||
| F1 | 2.2248 × 10−4 | 6.2884E-01 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7138 × 10−1 | |
| F2 | 2.5637 × 10−2 | 1.7344 × 10−6 | 1.5286 × 10−1 | 4.9080 × 10−1 | 1.7344 × 10−6 | |
| F3 | 2.6033 × 10−6 | 1.7344 × 10−6 | 6.3391 × 10−6 | 5.7517 × 10−6 | 1.7344 × 10−6 | |
| F4 | 1.6394 × 10−5 | 1.3595 × 10−4 | 8.2167 × 10−3 | 2.8434 × 10−5 | 2.6033 × 10−6 | |
| F5 | 3.5152 × 10−6 | 1.3595 × 10−4 | 1.7344 × 10−6 | 3.7243 × 10−5 | 1.7344 × 10−6 | |
| F6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | |
| F7 | 2.3534 × 10−6 | 1.4704 × 10−1 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | |
| F8 | 1.7344 × 10−6 | 6.1564 × 10−4 | 1.7344 × 10−6 | 3.5009 × 10−2 | 1.7344 × 10−6 | |
| F9 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.1561 × 10−1 | |
| F10 | 1.3194 × 10−2 | 4.9080 × 10−1 | 9.0993 × 10−1 | 5.2165 × 10−6 | 1.7344 × 10−6 | |
| F11 | 2.1266 × 10−6 | 1.8519 × 10−2 | 1.7344 × 10−6 | 7.1570 × 10−4 | 3.8822 × 10−6 | |
| F12 | 1.9209 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | |
| F13 | 1.7344 × 10−6 | 1.3601 × 10−5 | 1.7344 × 10−6 | 1.1138 × 10−3 | 4.6528 × 10−1 | |
| F14 | 1.7344 × 10−6 | 1.7344 × 10−6 | 9.3157 × 10−6 | 1.7344 × 10−6 | 3.1817 × 10−6 | |
| F15 | 2.3534 × 10−6 | 3.1123 × 10−5 | 1.7344 × 10−6 | 5.7924 × 10−5 | 4.7162 × 10−2 | |
| F16 | 2.8021 × 10−1 | 1.7344 × 10−6 | 2.4308 × 10−2 | 4.2843 × 10−1 | 1.7344 × 10−6 | |
| F17 | 1.9729 × 10−5 | 8.9443 × 10−4 | 2.6033 × 10−6 | 3.8822 × 10−6 | 1.2866 × 10−3 | |
| F18 | 1.7344 × 10−6 | 1.7344 × 10−6 | 3.1817 × 10−6 | 3.8822 × 10−6 | 1.7344 × 10−6 | |
| F19 | 4.4493 × 10−5 | 1.5658 × 10−2 | 1.7344 × 10−6 | 1.2453 × 10−2 | 8.4508 × 10−1 | |
| F20 | 3.1618 × 10−3 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.7029 × 10−2 | 3.3789 × 10−3 | |
| F21 | 1.7344 × 10−6 | 9.3157 × 10−6 | 1.7344 × 10−6 | 5.3070 × 10−5 | 1.7344 × 10−6 | |
| F22 | 3.1817 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.2888 × 10−1 | |
| F23 | 1.9209 × 10−6 | 7.1903 × 10−2 | 1.9209 × 10−6 | 7.7122 × 10−4 | 1.7344 × 10−6 | |
| F24 | 2.6033 × 10−6 | 5.2165 × 10−6 | 1.7344 × 10−6 | 1.9729 × 10−5 | 1.7344 × 10−6 | |
| F25 | 1.9569 × 10−2 | 2.5364 × 10−1 | 2.7653 × 10−3 | 3.0861 × 10−1 | 2.5364 × 10−1 | |
| F26 | 1.9209 × 10−6 | 1.1973 × 10−3 | 4.5336 × 10−4 | 2.2248 × 10−4 | 2.4118 × 10−4 | |
| F27 | 6.1564 × 10−4 | 2.6033 × 10−6 | 1.1748 × 10−2 | 6.5833 × 10−1 | 9.3157 × 10−6 | |
| F28 | 1.7344 × 10−6 | 4.3896 × 10−3 | 1.7344 × 10−6 | 1.7344 × 10−6 | 9.3157 × 10−6 | |
| F29 | 3.8822 × 10−6 | 3.7243 × 10−5 | 2.1266 × 10−6 | 1.5658 × 10−2 | 1.9729 × 10−5 | |
| F30 | 1.9209 × 10−6 | 4.4493 × 10−5 | 1.7344 × 10−6 | 2.1266 × 10−6 | 1.7344 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Dai, R.; Zhou, G.; Ma, S.; Luo, S. An Enhanced Tree-Seed Algorithm for Function Optimization and Production Optimization. Biomimetics 2024, 9, 334. https://doi.org/10.3390/biomimetics9060334
Zhou Q, Dai R, Zhou G, Ma S, Luo S. An Enhanced Tree-Seed Algorithm for Function Optimization and Production Optimization. Biomimetics. 2024; 9(6):334. https://doi.org/10.3390/biomimetics9060334
Chicago/Turabian StyleZhou, Qingan, Rong Dai, Guoxiao Zhou, Shenghui Ma, and Shunshe Luo. 2024. "An Enhanced Tree-Seed Algorithm for Function Optimization and Production Optimization" Biomimetics 9, no. 6: 334. https://doi.org/10.3390/biomimetics9060334
APA StyleZhou, Q., Dai, R., Zhou, G., Ma, S., & Luo, S. (2024). An Enhanced Tree-Seed Algorithm for Function Optimization and Production Optimization. Biomimetics, 9(6), 334. https://doi.org/10.3390/biomimetics9060334








