Design and Position Control of a Bionic Joint Actuated by Shape Memory Alloy Wires
Abstract
1. Introduction
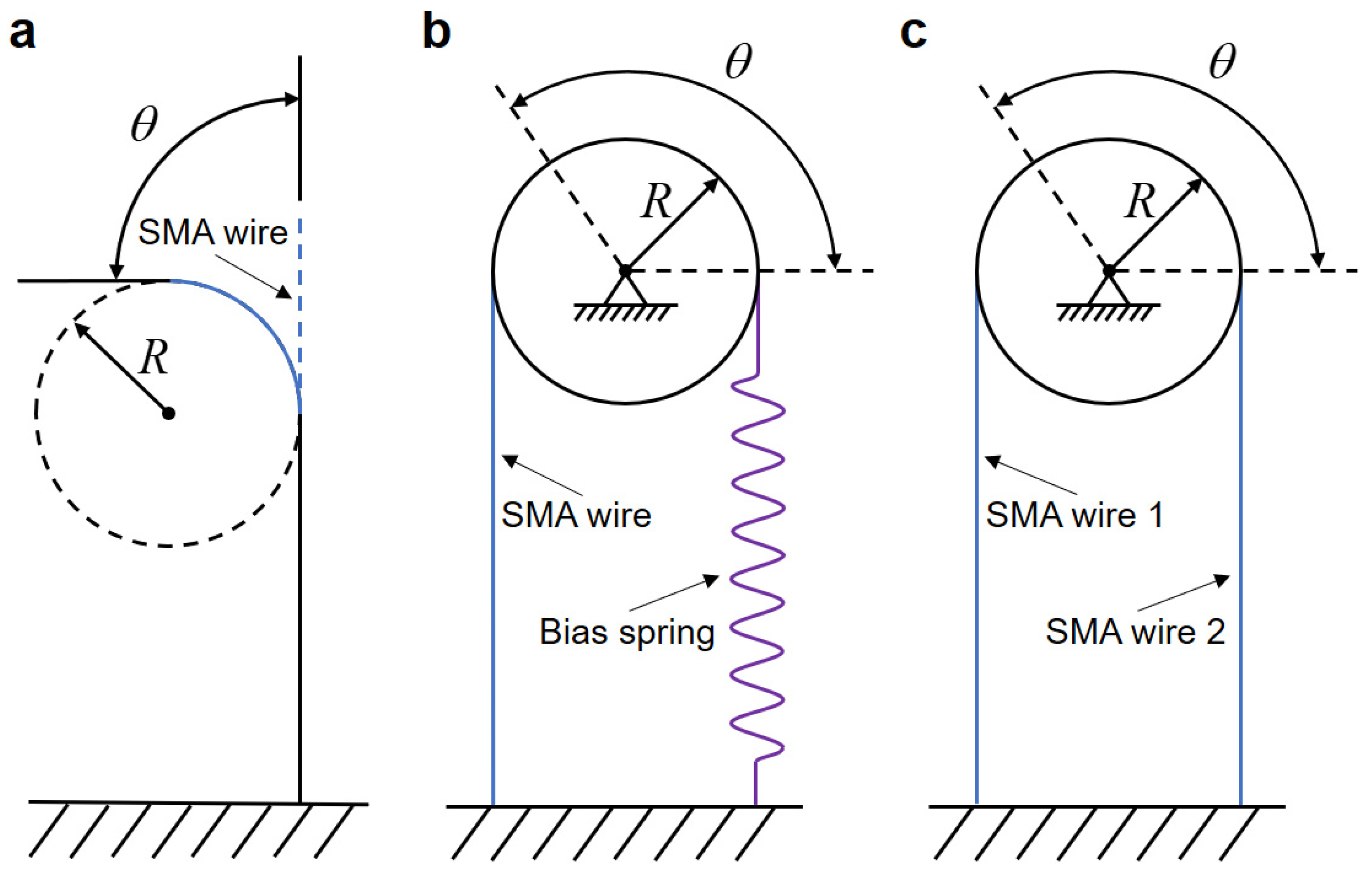
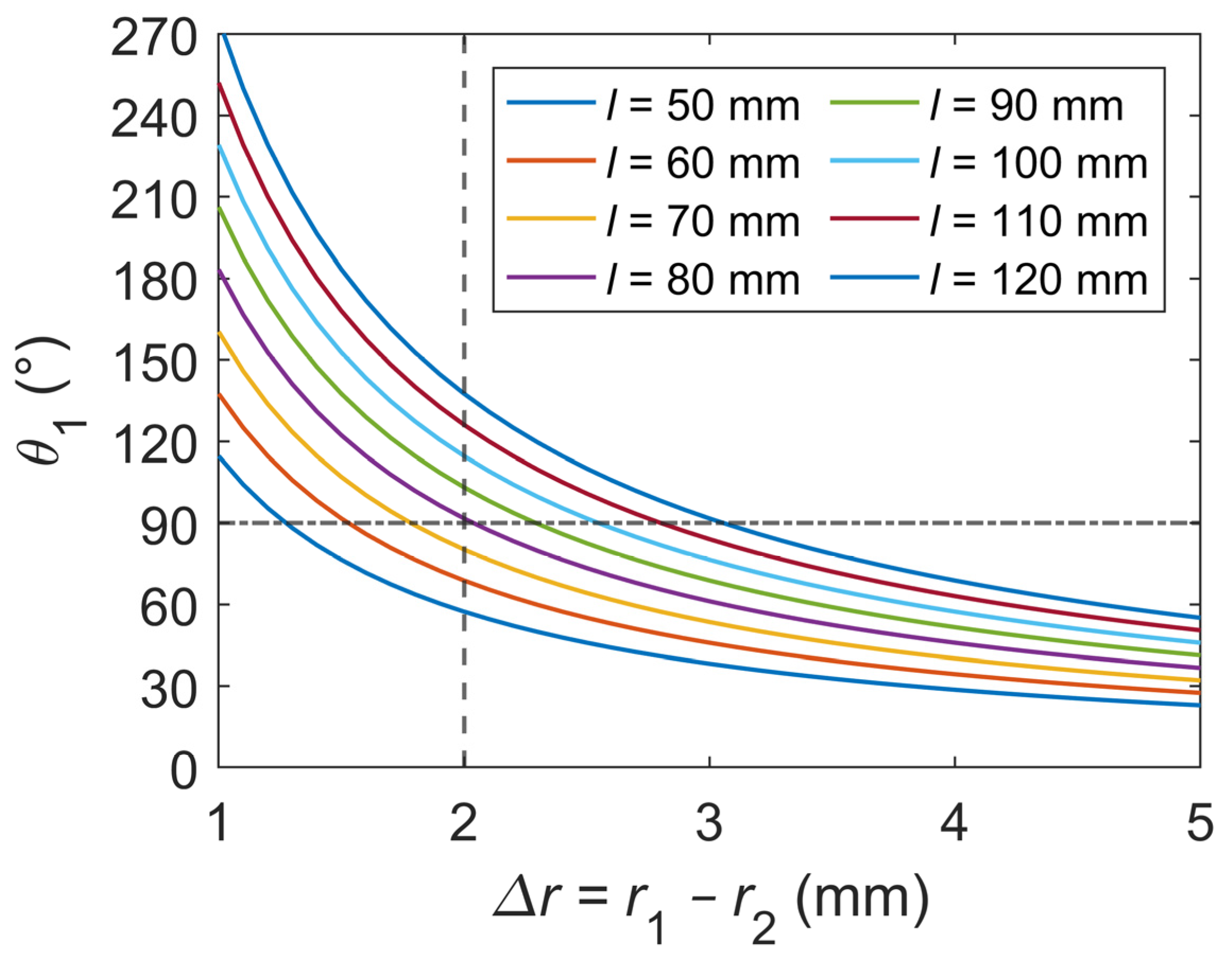
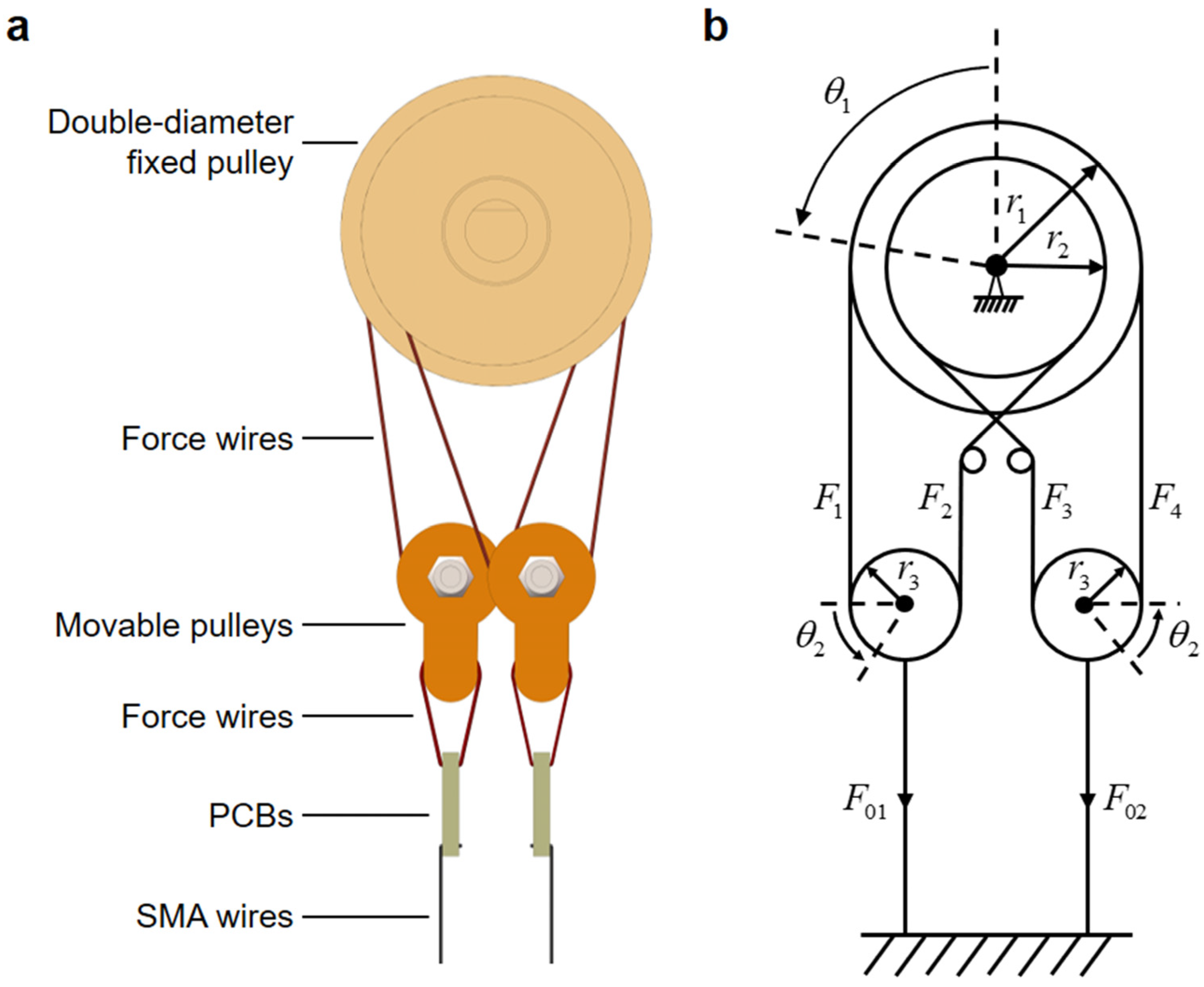
2. Novel Bionic Joint Design
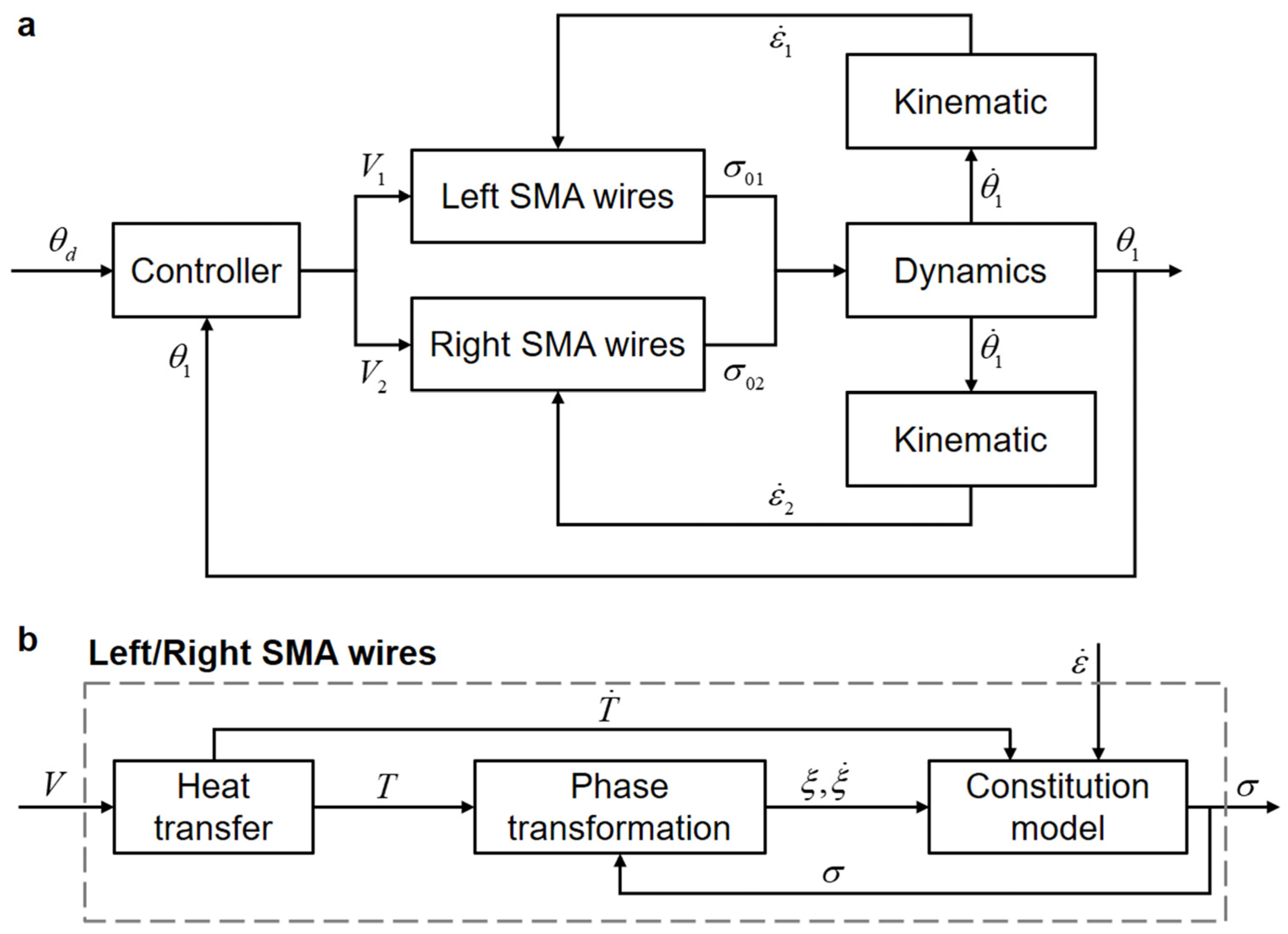
3. Bionic Joint Modeling and Controller Design
3.1. SMA Wire Modeling
3.1.1. Constitutive Model
3.1.2. Phase Transformation Model
3.1.3. Heat Transfer Model
3.2. Bionic Joint Modeling
3.3. PI Controller Design for Position Control
4. Experimental Results
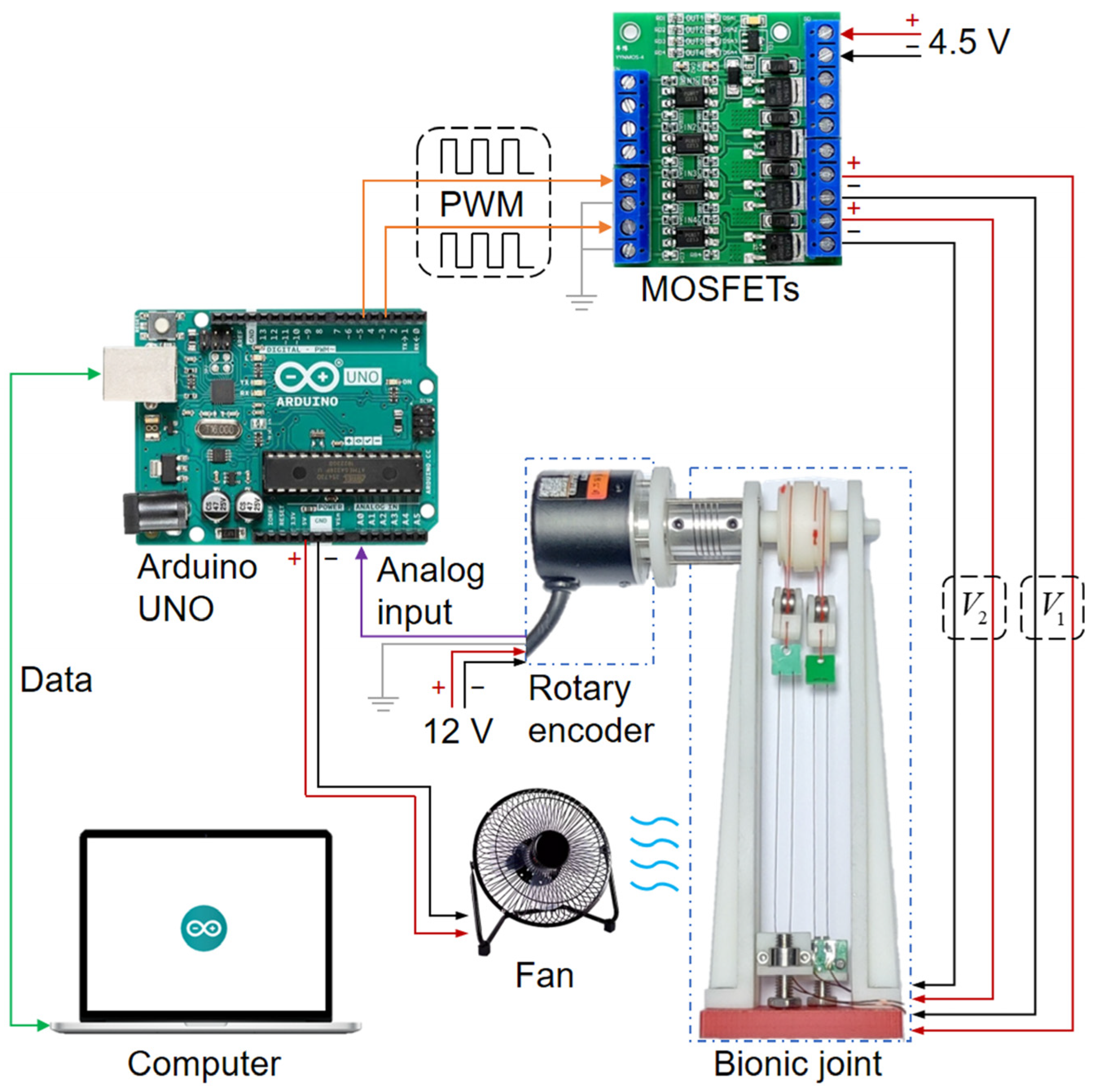
4.1. Experimental Setup
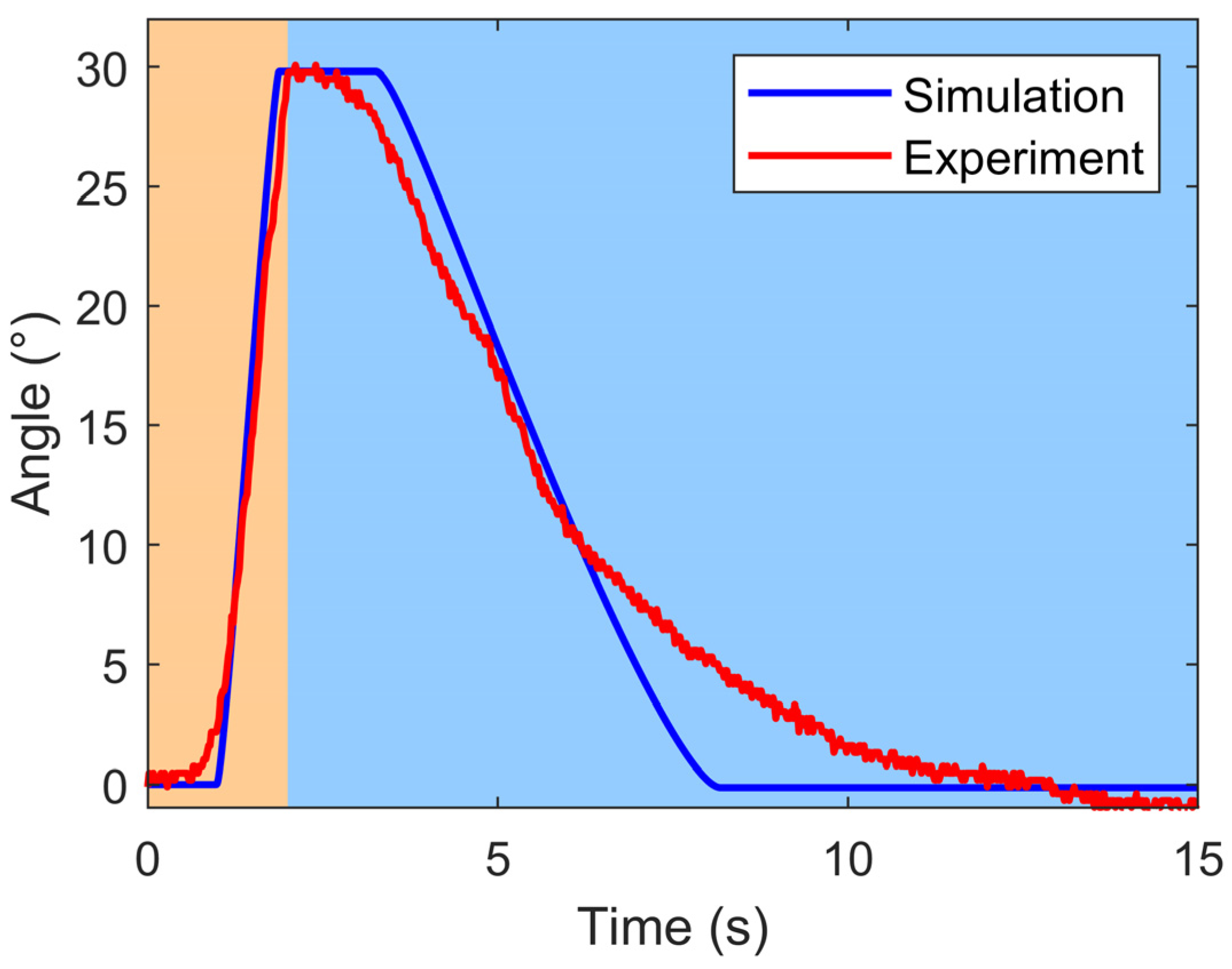
4.2. Open-Loop Simulation and Experiment
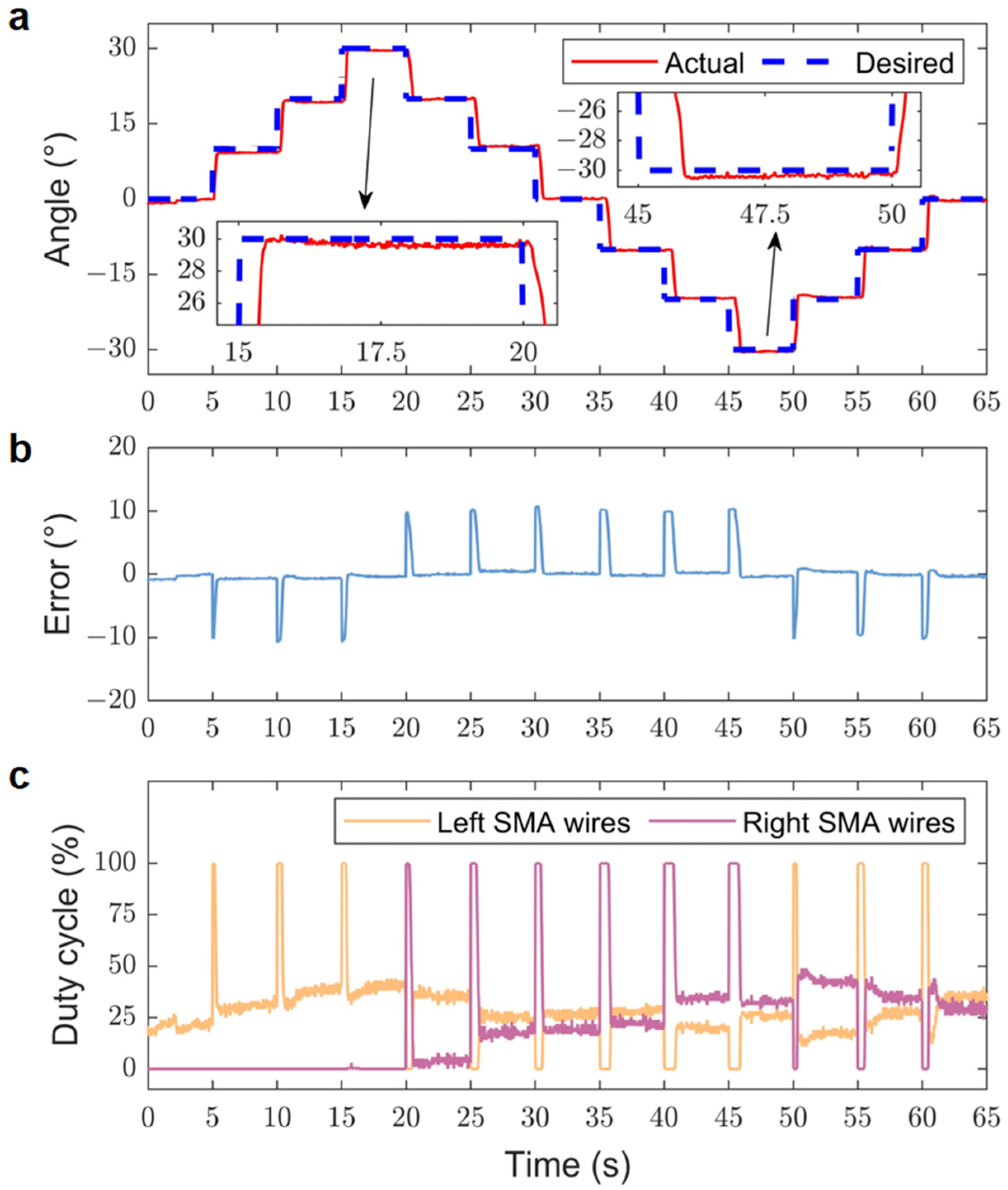
4.3. Position Step Response
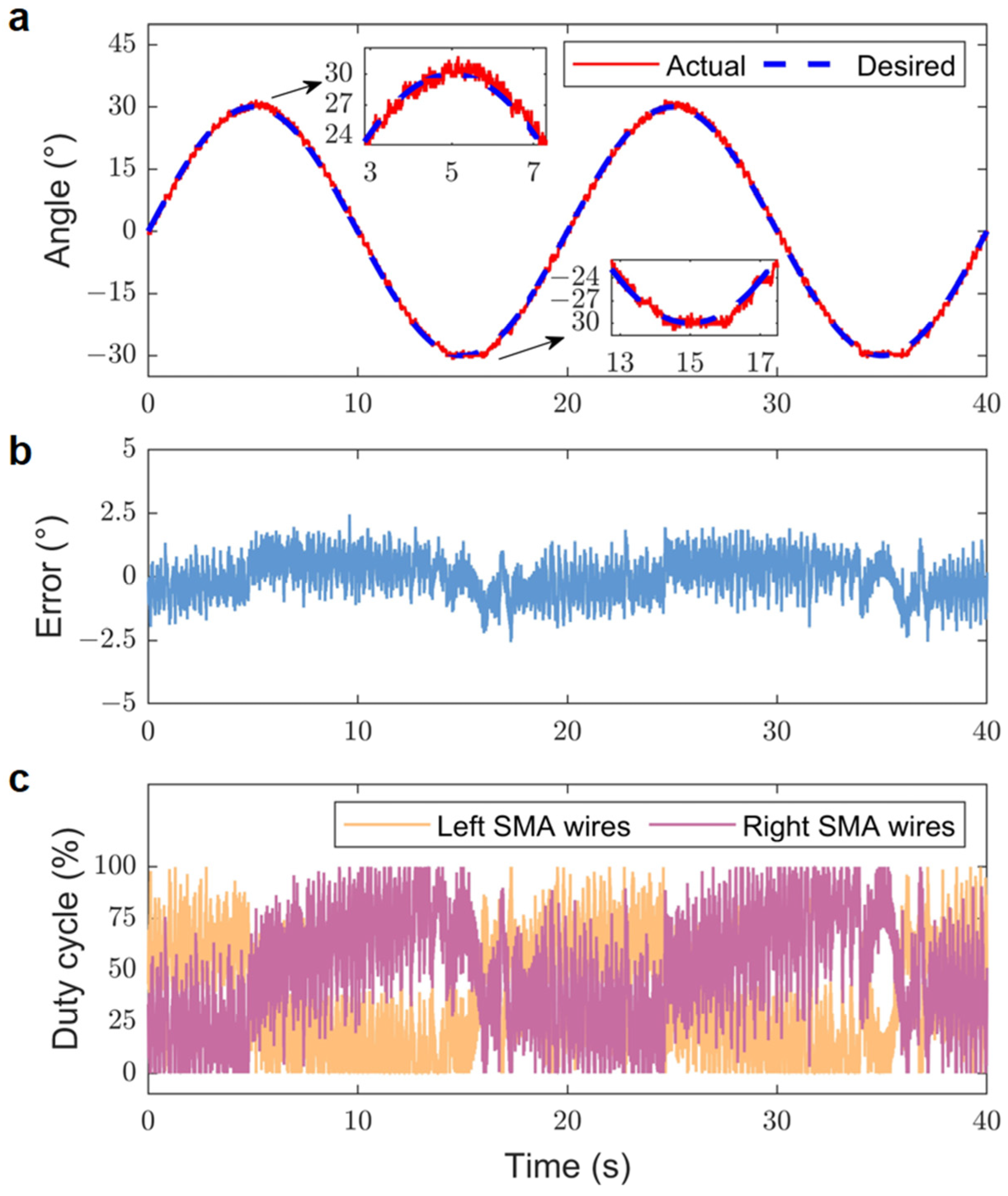
4.4. Position Tracking Response
4.5. Differential SMA Wire-Actuated Bionic Joint Performance Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Chen, P.; Bai, D.; Zhu, X.; Togo, S.; Yokoi, H.; Jiang, Y. Modularization of 2-and 3-DoF Coupled Tendon-Driven Joints. IEEE Trans. Robot. 2021, 37, 905–917. [Google Scholar] [CrossRef]
- Li, H.; Yu, H.; Chen, Y.; Tang, X.; Wang, D.; Meng, Q.; Du, Q. Design of a Minimally Actuated Lower Limb Exoskeleton with Mechanical Joint Coupling. J. Bionic Eng. 2022, 19, 370–389. [Google Scholar] [CrossRef]
- Huang, Z.; Du, C.; Wang, C.; Sun, Q.; Xu, Y.; Shao, L.; Yu, B.; Ma, G.; Kong, X. Bionic Design and Optimization on the Flow Channel of a Legged Robot Joint Hydraulic Drive Unit Based on Additive Manufacturing. Biomimetics 2024, 9, 13. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Jiang, W.; Zhang, Q.; Zhang, W. Design and Simulation of a Seven-Degree-of-Freedom Hydraulic Robot Arm. Actuators 2023, 12, 362. [Google Scholar] [CrossRef]
- Park, D.; Han, J.-B.; Yeu, T.; Cho, S.-G.; Kim, S.; Kim, H.; Lee, Y. Development of an Autonomous Cleaning Robot with a Hydraulic Manipulator Arm for the Cleaning of Niche Areas of a Ship Hull. J. Mar. Sci. Eng. 2023, 11, 973. [Google Scholar] [CrossRef]
- Ma, J.; Chen, D.; Liu, Z.; Wei, J.; Zhang, X.; Zeng, Z.; Jiang, Y. All-Fabric Bi-directional Actuators for Multi-joint Assistance of Upper Limb. J. Bionic Eng. 2023, 20, 2661–2669. [Google Scholar] [CrossRef]
- Mei, D.; Yu, X.; Tang, G.; Liu, S.; Zhao, X.; Zhao, C.; Li, C.; Wang, Y. Blue Hand: A Novel Type of Soft Anthropomorphic Hand Based on Pneumatic Series-Parallel Mechanism. IEEE Robot. Autom. Lett. 2023, 8, 7615–7622. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, Y.; Hu, Y.; Wang, Z.; Li, Y.; Gu, G.; Liu, Y. Adaptive Variable Stiffness Particle Phalange for Robust and Durable Robotic Grasping. Soft Robot. 2020, 7, 743–757. [Google Scholar] [CrossRef] [PubMed]
- Zhang, A.; Wang, L.; Jin, J.; Chen, D.; Liu, R.; Zhao, H. A novel piezoelectric actuated 2-DOF joint for underwater manipulator: Design, simulation, and experimental investigation. Smart Mater. Struct. 2021, 30, 105032. [Google Scholar] [CrossRef]
- Geng, Z.X.; Li, X.N.; Liu, R.X.; Wen, Z.Y.; Wang, B.Q.; Wu, D.W. Development of a stator-rotor integrated piezoelectric actuator for precise joint rotation of the robotic arm. Precis. Eng. 2023, 82, 360–369. [Google Scholar] [CrossRef]
- Sun, H.; Shi, Y.; Wang, Q.; Li, X.; Wang, J. Modeling and Design Optimization of a New Piezoelectric Inchworm Actuator with Screw Clamping Mechanisms. Micromachines 2022, 13, 2038. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Chen, W.; Ma, X.; Deng, J.; Xun, M.; Liu, Y. A low speed piezoelectric actuator with high displacement smoothness and its multi-objective optimized method. Smart Mater. Struct. 2023, 32, 105036. [Google Scholar] [CrossRef]
- Yi, X.; Chakarvarthy, A.; Chen, Z. Cooperative Collision Avoidance Control of Servo/IPMC Driven Robotic Fish With Back-Relaxation Effect. IEEE Robot. Autom. Lett. 2021, 6, 1816–1823. [Google Scholar] [CrossRef]
- Wang, S.; Huang, B.; McCoul, D.; Wang, X.; Zhao, J. Design method of DEMES rotary joint. Smart Mater. Struct. 2020, 29, 035021. [Google Scholar] [CrossRef]
- Jiang, J.; Zhao, Y. Liquid Crystalline Elastomer for Separate or Collective Sensing and Actuation Functions. Small 2023, 19, 2301932. [Google Scholar] [CrossRef] [PubMed]
- Do, P.T.; Le, Q.N.; Luong, Q.V.; Kim, H.-H.; Park, H.-M.; Kim, Y.-J. Tendon-Driven Gripper with Variable Stiffness Joint and Water-Cooled SMA Springs. Actuators 2023, 12, 160. [Google Scholar] [CrossRef]
- Hu, Q.; Huang, H.; Dong, E.; Sun, D. A Bioinspired Composite Finger With Self-Locking Joints. IEEE Robot. Autom. Lett. 2021, 6, 1391–1398. [Google Scholar] [CrossRef]
- Qiu, J.; Ji, A.; Zhu, K.; Han, Q.; Wang, W.; Qi, Q.; Chen, G. A Gecko-Inspired Robot with a Flexible Spine Driven by Shape Memory Alloy Springs. Soft Robot. 2023, 10, 713–723. [Google Scholar] [CrossRef]
- Jia, Z.; Han, G.; Jin, H.; Xu, M.; Dong, E. Design and Force/Angle Independent Control of a Bionic Mechanical Ankle Based on an Artificial Muscle Matrix. Biomimetics 2024, 9, 38. [Google Scholar] [CrossRef]
- Yang, S.Y.; Kim, K.; Seo, S.; Shin, D.; Park, J.H.; Gong, Y.J.; Choi, H.R. Hybrid Antagonistic System With Coiled Shape Memory Alloy and Twisted and Coiled Polymer Actuator for Lightweight Robotic Arm. IEEE Robot. Autom. Lett. 2022, 7, 4496–4503. [Google Scholar] [CrossRef]
- Luong, T.; Kim, K.; Seo, S.; Jeon, J.; Park, C.; Doh, M.; Koo, J.C.; Choi, H.R.; Moon, H. Long Short Term Memory Model Based Position-Stiffness Control of Antagonistically Driven Twisted-Coiled Polymer Actuators Using Model Predictive Control. IEEE Robot. Autom. Lett. 2021, 6, 4141–4148. [Google Scholar] [CrossRef]
- Zhang, J.; Sheng, J.; O’Neill, C.T.; Walsh, C.J.; Wood, R.J.; Ryu, J.H.; Desai, J.P.; Yip, M.C. Robotic Artificial Muscles: Current Progress and Future Perspectives. IEEE Trans. Robot. 2019, 35, 761–781. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Du, H.; Li, G.; Sun, J.; Zhang, Y.; Bai, Y.; Qian, C.; Liang, Y. A review of shape memory alloy artificial muscles in bionic applications. Smart Mater. Struct. 2023, 32, 103001. [Google Scholar] [CrossRef]
- Yuan, H.; Fauroux, J.C.; Chapelle, F.; Balandraud, X. A review of rotary actuators based on shape memory alloys. J. Intell. Mater. Syst. Struct. 2017, 28, 1863–1885. [Google Scholar] [CrossRef]
- Technical Characteristics of Flexinol® Actuator Wires. Available online: https://www.dynalloy.com/pdfs/TCF1140.pdf (accessed on 21 February 2024).
- Baek, H.; Khan, A.M.; Kim, Y. A bidirectional rotating actuator by using a single shape memory alloy wire in a double bend shape. Sens. Actuators A Phys. 2023, 360, 114526. [Google Scholar] [CrossRef]
- Takumi, I.; Sumito, N. SMA micro-hand implemented in small robot for generating gestures. Intell. Serv. Robot. 2021, 14, 399–408. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Pan, Y.; Wee, L.; Yu, H. Design and control of a novel compliant differential shape memory alloy actuator. Sens. Actuators A Phys. 2015, 225, 71–80. [Google Scholar] [CrossRef]
- Britz, R.; Motzki, P.; Seelecke, S. Scalable Bi-Directional SMA-Based Rotational Actuator. Actuators 2019, 8, 60. [Google Scholar] [CrossRef]
- Zhou, H.; Cao, S.; Ma, N. Design and performance analysis of a novel class of SMA-driven rotational mechanisms/joints. Robotica 2022, 40, 3976–3994. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.R.; Aghdam, M.M.; Shakeri, M. A phenomenological SMA model for combined axial-torsional proportional/non-proportional loading conditions. Mater. Sci. Eng. A 2013, 587, 12–26. [Google Scholar] [CrossRef]
- Liang, C.; Rogers, C.A. One-dimensional thermomechanical constitutive relations for shape memory materials. J. Intell. Mater. Syst. Struct. 1997, 8, 285–302. [Google Scholar] [CrossRef]
- Teh, Y.H.; Featherstone, R. An Architecture for Fast and Accurate Control of Shape Memory Alloy Actuators. Int. J. Robot. Res. 2008, 27, 595–611. [Google Scholar] [CrossRef]



| Dimension | Value (Unit) |
|---|---|
| Length, width, and height of the bionic joint | 60 × 60 × 180 mm |
| Large radius of the double-diameter fixed pulley | 13.2 mm |
| Small radius of the double-diameter fixed pulley | 11.2 mm |
| Radius of the V-groove bearing within each movable pulley | 4.2 mm |
| Length, width, and height of PCBs 1 and 3 | 10 × 10 × 1.6 mm |
| Length, width, and height of PCBs 2 and 4 | 17 × 10 × 1.6 mm |
| Length of each SMA wire | 80 mm |
| Diameter of each SMA wire | 0.31 mm |
| Description (Parameters) | Value (Unit) |
|---|---|
| Austenite Young’s modulus () | 78 GPa |
| Martensite Young’s modulus () | 23 GPa |
| Maximum recoverable strain of the SMA wire () | 0.02 |
| Number of parallel SMA wires on each side () | 2 |
| Diameter of the SMA wire () | 0.31 mm |
| Austenite start temperature () | 80 °C |
| Austenite finish temperature () | 98 °C |
| Martensite start temperature () | 78 °C |
| Martensite finish temperature () | 60 °C |
| Austenite stress influence coefficients () | 15 MPa/°C |
| Martensite stress influence coefficient () | 15 MPa/°C |
| Initial martensite volume fraction of the austenite-to-martensite phase transformation () | 0 |
| Initial martensite volume fraction of the martensite-to-austenite phase transformation () | 1 |
| Length of each SMA wire () | 80 mm |
| Density of the SMA wire () | 6450 kg/m3 |
| Specific heat capacity of the SMA wire () | 837 J/(kg·°C) |
| Resistance per unit length of the SMA wire () | 12.2 Ω/m |
| Heat convection constant coefficient () | 80 |
| Heat convection second order coefficient () | 0.001 |
| Ambient temperature () | 20 °C |
| Radius of the large groove on the double-diameter fixed pulley () | 13.2 mm |
| Radius of the small groove on the double-diameter fixed pulley () | 11.2 mm |
| Moment of inertia of the double-diameter fixed pulley () | 1.52 kg·(mm)2 |
| Mass of the movable pulley () | 2.56 g |
| Damping coefficients of SMA wires () | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Jia, Z.; Niu, X.; Dong, E. Design and Position Control of a Bionic Joint Actuated by Shape Memory Alloy Wires. Biomimetics 2024, 9, 210. https://doi.org/10.3390/biomimetics9040210
Zhu Y, Jia Z, Niu X, Dong E. Design and Position Control of a Bionic Joint Actuated by Shape Memory Alloy Wires. Biomimetics. 2024; 9(4):210. https://doi.org/10.3390/biomimetics9040210
Chicago/Turabian StyleZhu, Yida, Zhikun Jia, Xiaojie Niu, and Erbao Dong. 2024. "Design and Position Control of a Bionic Joint Actuated by Shape Memory Alloy Wires" Biomimetics 9, no. 4: 210. https://doi.org/10.3390/biomimetics9040210
APA StyleZhu, Y., Jia, Z., Niu, X., & Dong, E. (2024). Design and Position Control of a Bionic Joint Actuated by Shape Memory Alloy Wires. Biomimetics, 9(4), 210. https://doi.org/10.3390/biomimetics9040210







