Motor Interaction Control Based on Muscle Force Model and Depth Reinforcement Strategy
Abstract
1. Introduction
2. Literature Review
3. Construction of Motor Interaction Control Model Based on Muscle Force Model and Deep Reinforcement Strategy
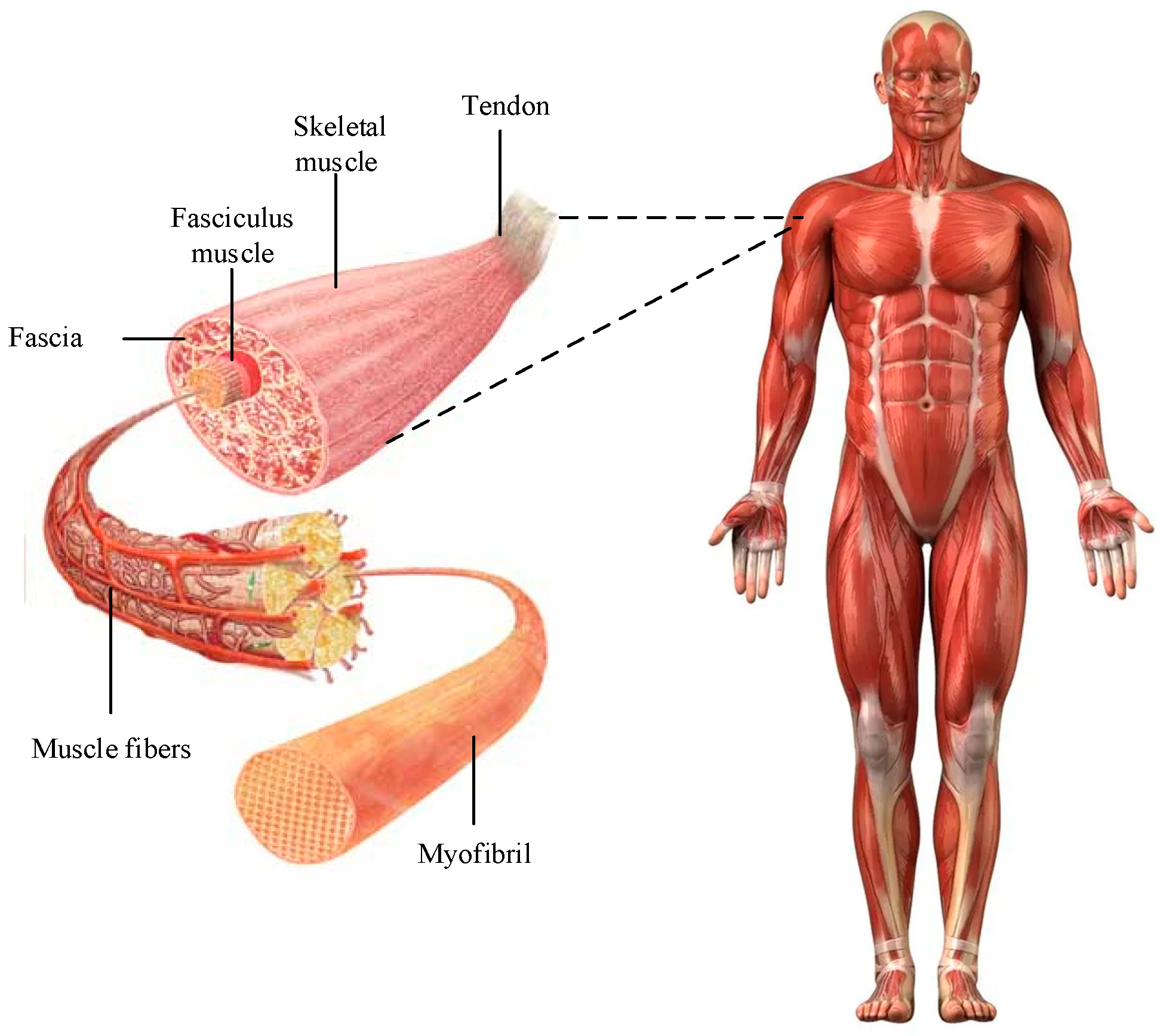
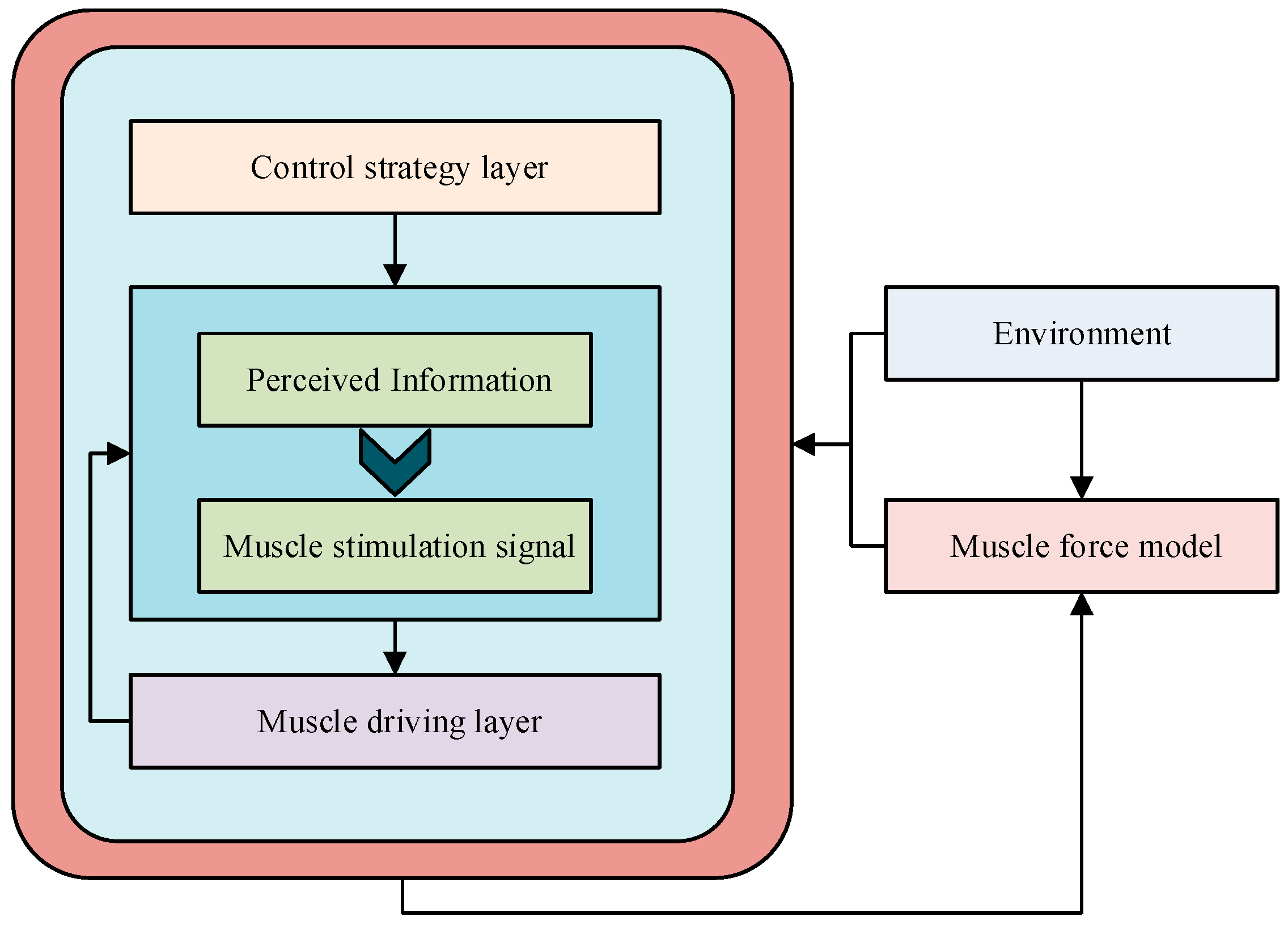
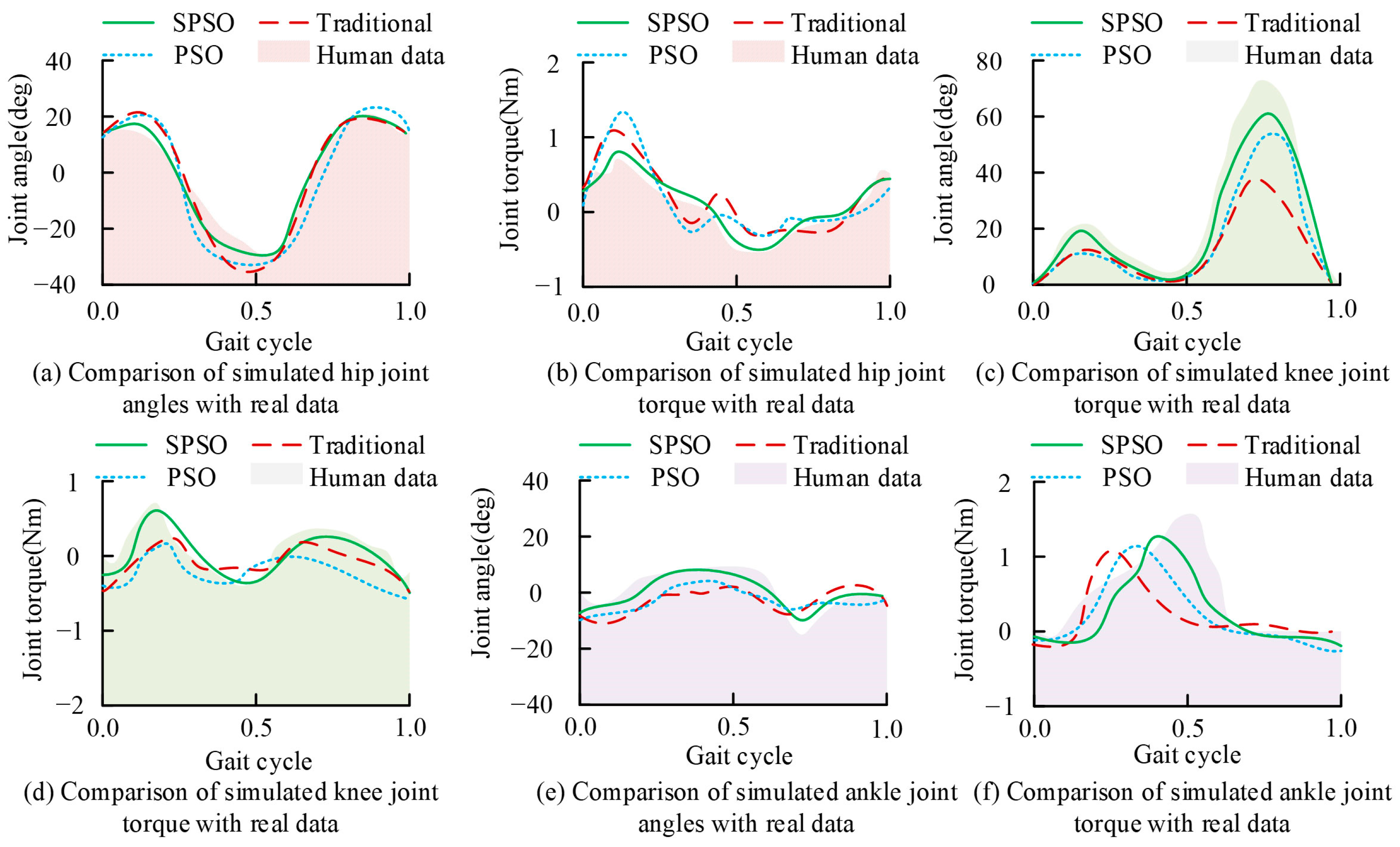
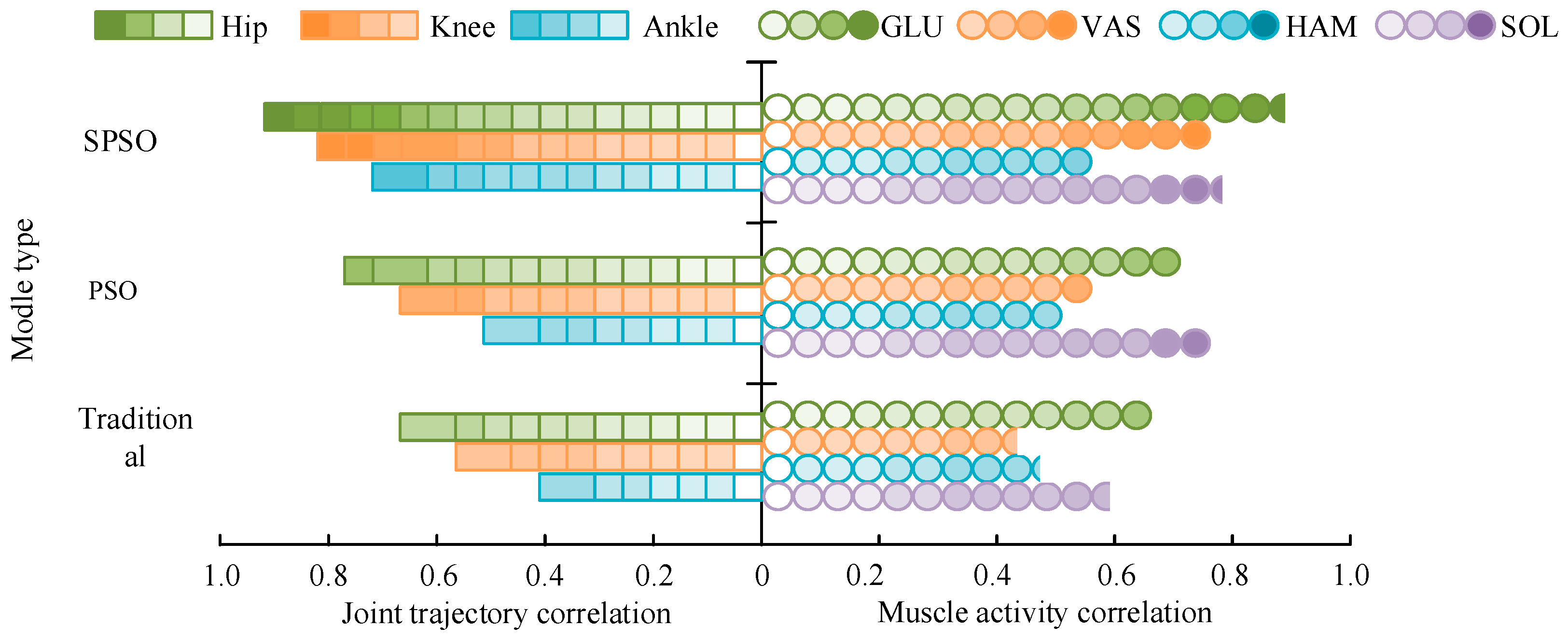
3.1. Human Motion Control Model Based on Muscle Force and Stage Particle Swarm Optimization
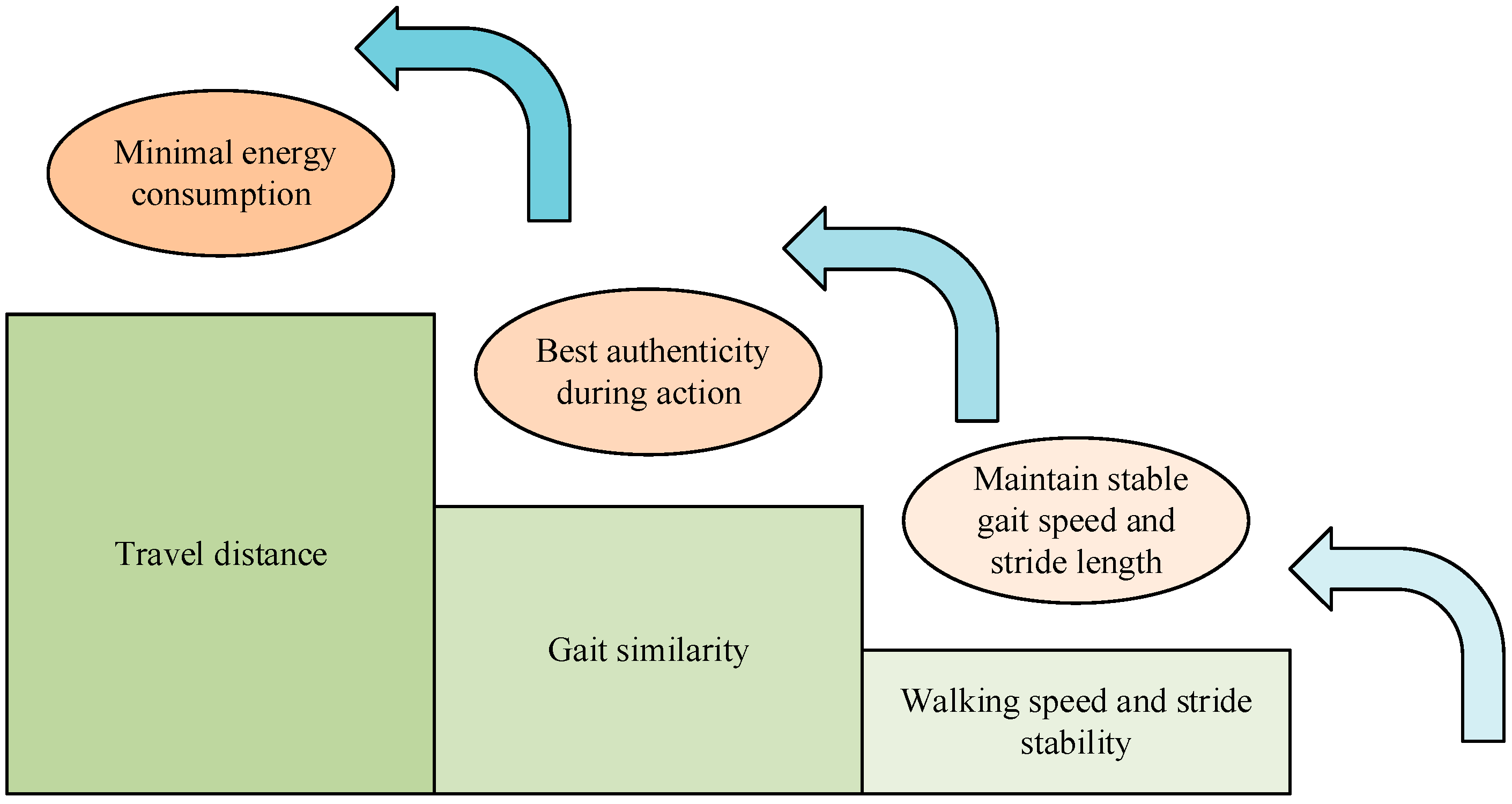
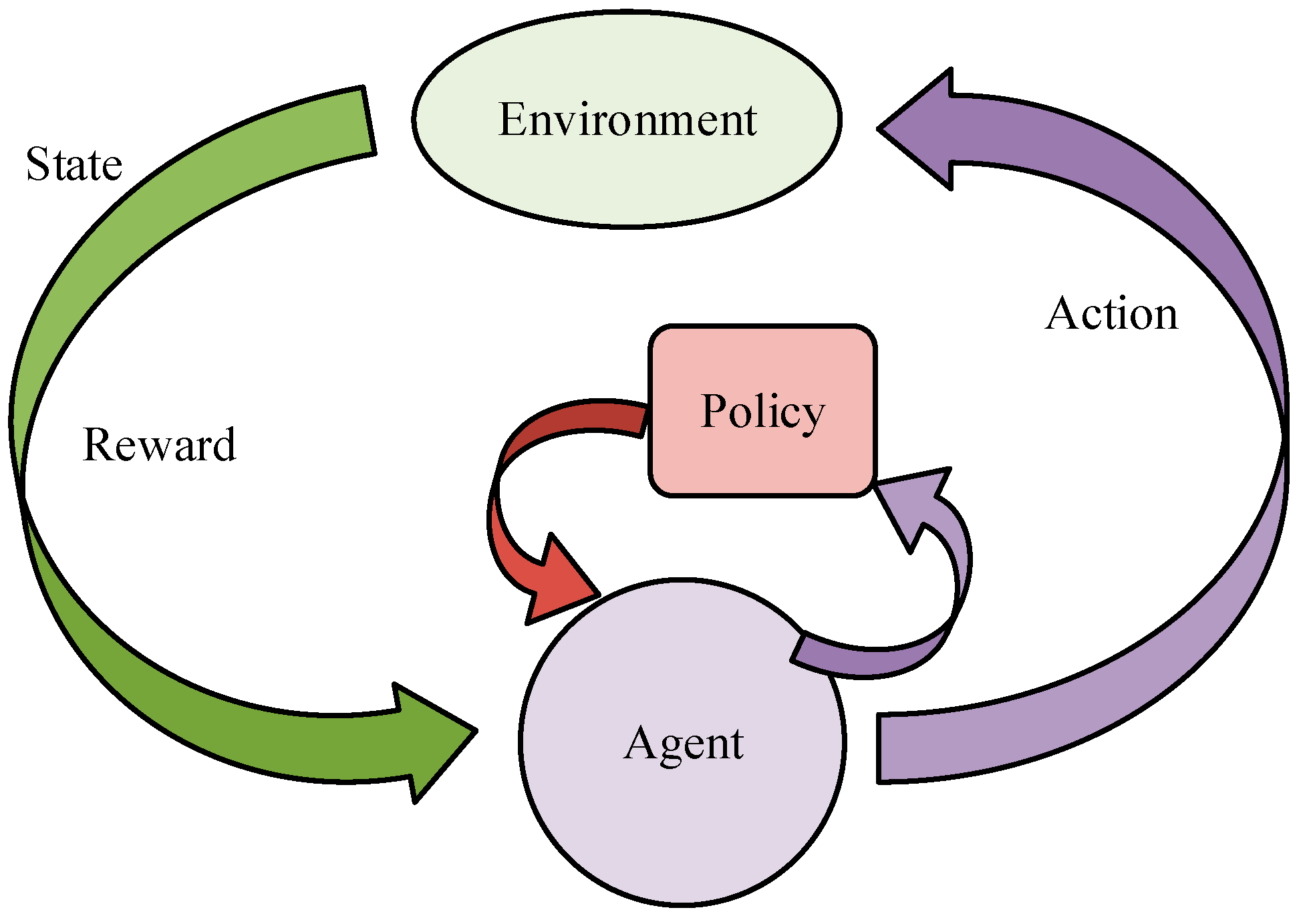
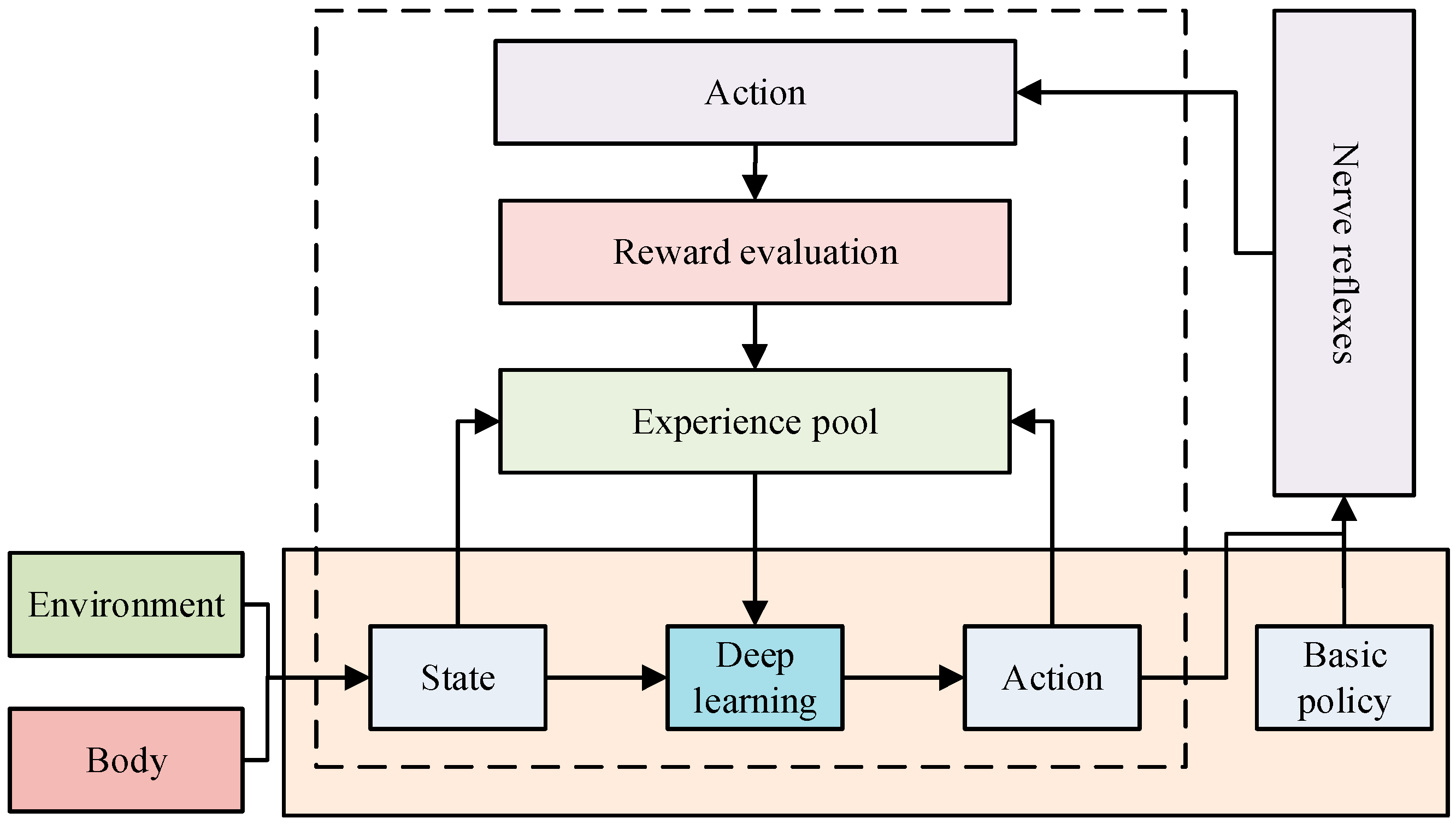
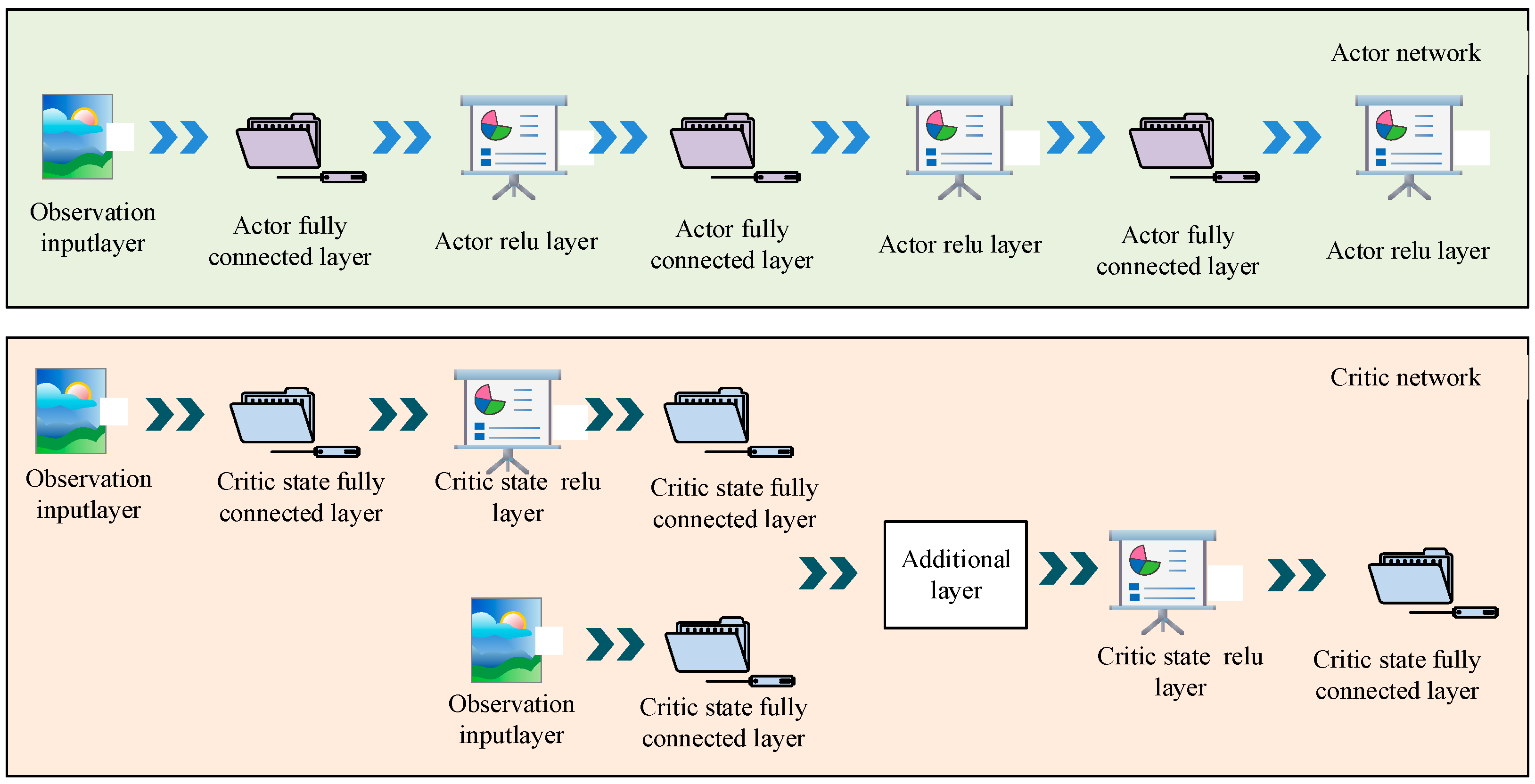
3.2. Enhanced Environment-Oriented Interactive Motion Control Modeling
4. Empirical Experiments on Motor Interaction Control Model Based on Muscle Force Model and Depth Reinforcement Strategy
4.1. Validation of the Effectiveness of the Human Motion Control Model
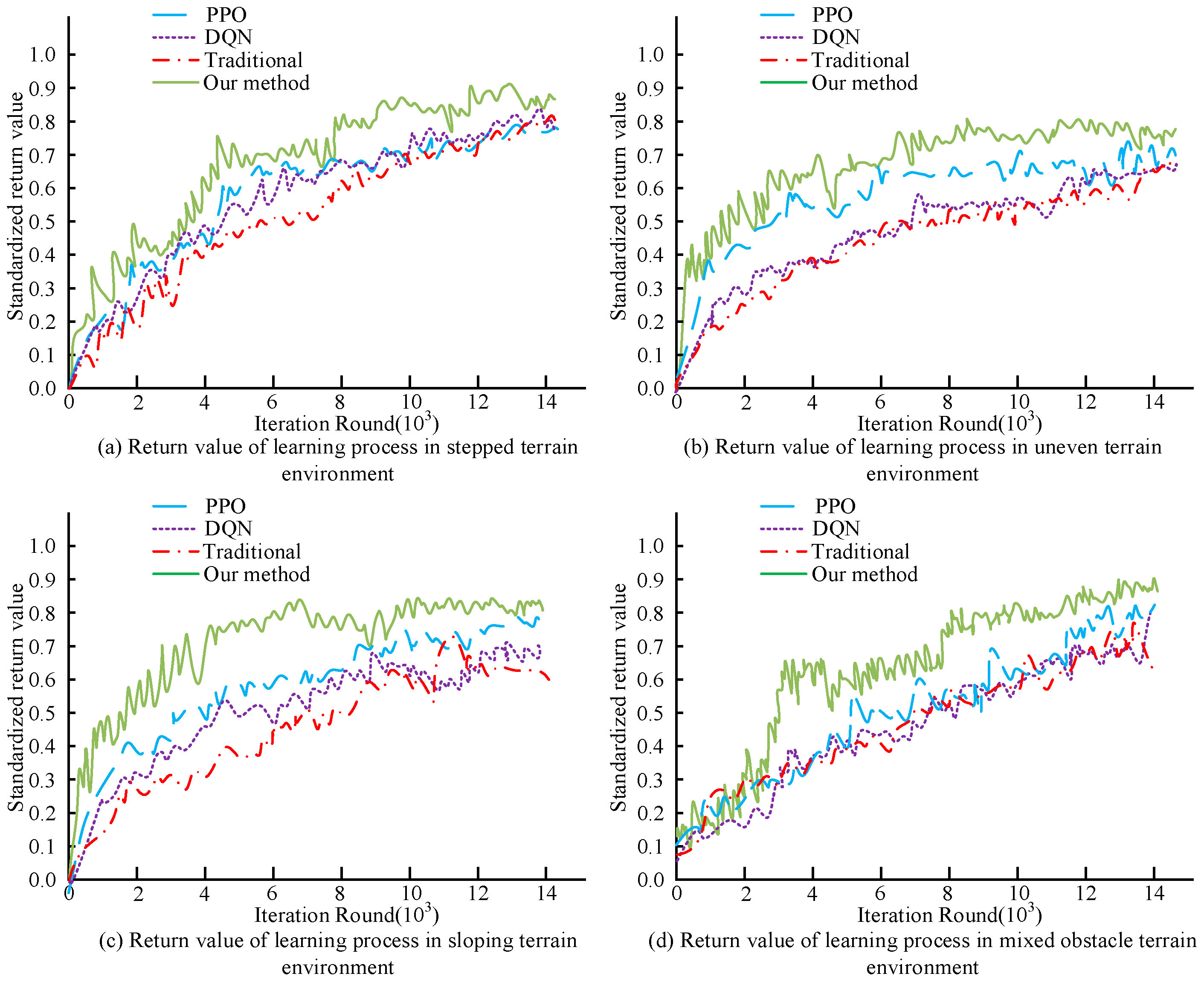
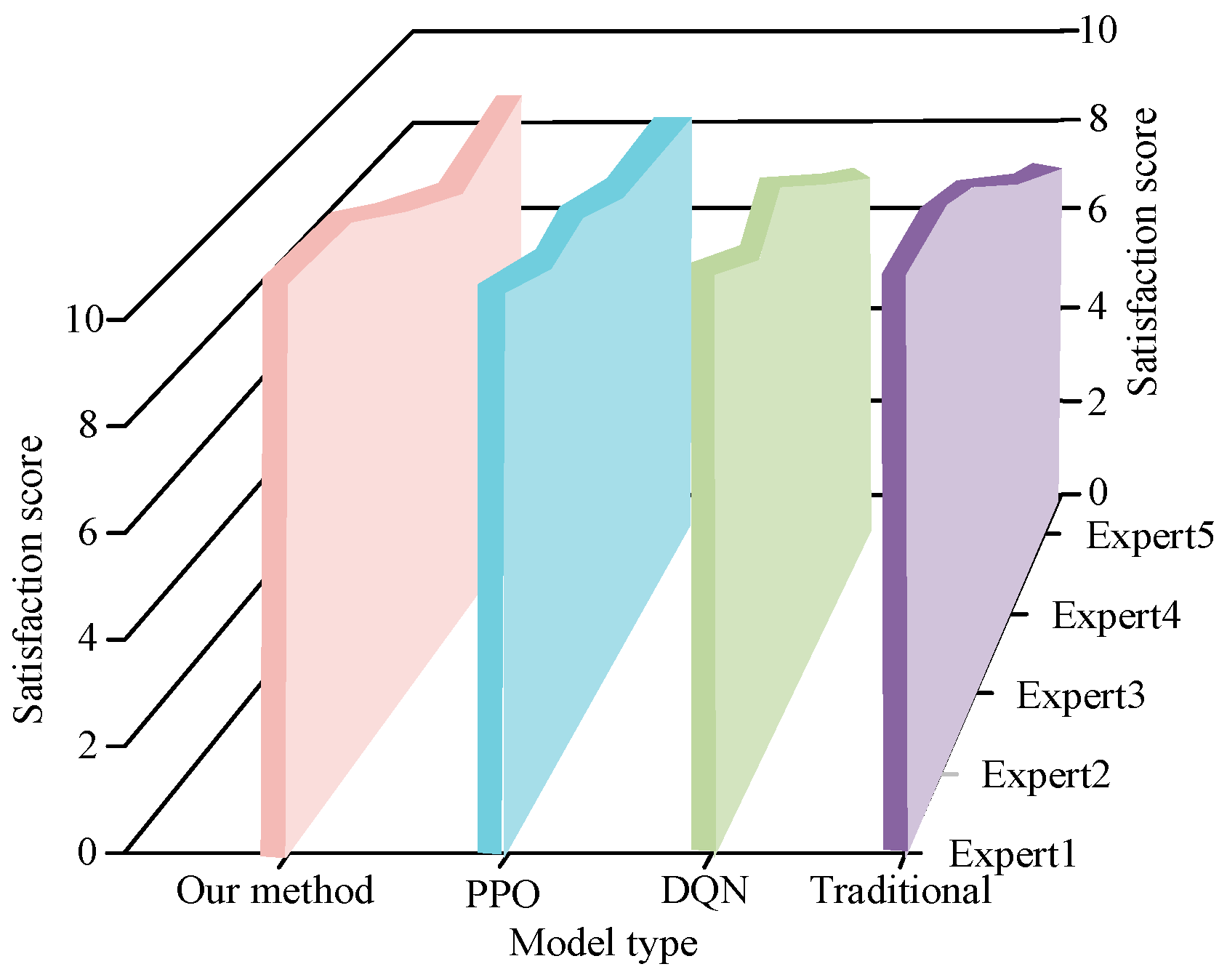
4.2. Enhanced Environment-Oriented Motion Interaction Control Modeling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Dai, Y.; Liu, M.; Chen, Y.; Yi, Z. DeepUWF-plus: Automatic fundus identification and diagnosis system based on ultrawide-field fundus imaging. Appl. Intell. 2021, 51, 7533–7551. [Google Scholar] [CrossRef]
- Luo, S.; Androwis, G.; Adamovich, S.; Nunez, E.; Su, H.; Zhou, X. Robust walking control of a lower limb rehabilitation exoskeleton coupled with a musculoskeletal model via deep reinforcement learning. J. Neuroeng. Rehabil. 2023, 20, 34. [Google Scholar] [CrossRef]
- Malo, P.; Tahvonen, O.; Suominen, A.; Back, P.; Viitasaari, L. Reinforcement learning in optimizing forest management. Can. J. For. Res. 2021, 51, 1393–1409. [Google Scholar] [CrossRef]
- Dorgo, G.; Abonyi, J. Learning and predicting operation strategies by sequence mining and deep learning. Comput. Chem. Eng. 2019, 128, 174–187. [Google Scholar] [CrossRef]
- Anand, A.S.; Gravdahl, J.T.; Abu-Dakka, F.J. Model-based variable impedance learning control for robotic manipulation. Robot. Auton. Syst. 2023, 170, 104531. [Google Scholar] [CrossRef]
- Xue, Y.; Cai, X.; Xu, R.; Liu, H. Wing Kinematics-Based Flight Control Strategy in Insect-Inspired Flight Systems: Deep Reinforcement Learning Gives Solutions and Inspires Controller Design in Flapping MAVs. Biomimetics 2023, 8, 295. [Google Scholar] [CrossRef]
- Qi, B.; Xu, P.; Wu, C. Analysis of the Infiltration and Water Storage Performance of Recycled Brick Mix Aggregates in Sponge City Construction. Water 2023, 15, 363. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Yi, W. Two Time-Scale Caching Placement and User Association in Dynamic Cellular Networks. IEEE Trans. Commun. 2022, 70, 2561–2574. [Google Scholar] [CrossRef]
- Teng, Y.; Cao, Y.; Liu, M. Efficient Blockchain-enabled Large Scale Parked Vehicular Computing with Green Energy Supply. IEEE Trans. Veh. Technol. 2021, 70, 9423–9436. [Google Scholar] [CrossRef]
- Caicedo, J.C.; Roth, J.; Goodman, A.; Becker, T.; Carpenter, A.E. Evaluation of Deep Learning Strategies for Nucleus Segmentation in Fluorescence Images. Cytom. Part A 2019, 95, 952–965. [Google Scholar] [CrossRef]
- Van Sloun, R.J.G.; Solomon, O.; Bruce, M.; Khaing, Z.Z.; Wijkstra, H.; Eldar, Y.C. Super-Resolution Ultrasound Localization Microscopy Through Deep Learning. IEEE Trans. Med. Imaging 2021, 40, 829–839. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; He, H.; Zhao, X.; Wang, Y.; Li, M. Battery health-aware and naturalistic data-driven energy management for hybrid electric bus based on TD3 deep reinforcement learning algorithm. Appl. Energy 2022, 321, 119353. [Google Scholar] [CrossRef]
- Ding, C.; Liang, H.; Lin, N.; Xiong, Z.; Li, Z.; Xu, P. Identification effect of least square fitting method in archives management. Heliyon 2023, 9, e20085. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.; Kim, U.; Kim, J.; Jong, C.; Pak, C. Deep reinforcement learning-based joint optimization of computation offloading and resource allocation in F-RAN. IET Commun. 2023, 17, 549–564. [Google Scholar] [CrossRef]
- Xu, P.; Yuan, Q.; Ji, W.; Zhao, Y.; Yu, R.; Su, Y.; Huo, N. Study on Electrochemical Properties of Carbon Submicron Fibers Loaded with Cobalt-Ferro Alloy and Compounds. Crystals 2023, 13, 282. [Google Scholar] [CrossRef]
- James, J.Q.; Yu, W.; Gu, J. Online vehicle routing with neural combinatorial optimization and deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3806–3817. [Google Scholar]
- Asghari, A.; Sohrabi, M.K.; Yaghmaee, F. Task scheduling, resource provisioning, and load balancing on scientific workflows using parallel SARSA reinforcement learning agents and genetic algorithm. J. Supercomput. 2021, 77, 2800–2828. [Google Scholar] [CrossRef]
- Sreedhar, R.; Varshney, A.; Dhanya, M. Sugarcane crop classification using time series analysis of optical and SAR sentinel images: A deep learning approach. Remote Sens. Lett. 2022, 13, 812–821. [Google Scholar] [CrossRef]
- Hu, X.; Liu, S.; Wang, Y. Deep reinforcement learning-based beam Hopping algorithm in multibeam satellite systems. Commun. IET 2019, 13, 2485–2491. [Google Scholar] [CrossRef]
- Golparvar, A.J.; Yapici, M.K. Graphene Smart Textile-Based Wearable Eye Movement Sensor for Electro-Ocular Control and Interaction with Objects. J. Electrochem. Soc. 2019, 166, 3184–3193. [Google Scholar] [CrossRef]
- Wasaka, T.; Kida, T.; Kakigi, R. Dexterous manual movement facilitates information processing in the primary somatosensory cortex: A magnetoencephalographic study. Eur. J. Neurosci. 2021, 54, 4638–4648. [Google Scholar] [CrossRef] [PubMed]
- Fischer, F.; Bachinski, M.; Klar, M.; Fleig, A.; Müller, J. Reinforcement learning control of a biomechanical model of the upper extremity. Sci. Rep. 2021, 11, 14445. [Google Scholar] [CrossRef]
- Mancisidor, A.; Zubizarreta, A.; Cabanes, I.; Bengoa, P.; Brull, A.; Jung, J.H. Inclusive and seamless control framework for safe robot-mediated therapy for upper limbs rehabilitation. Mechatronics 2019, 58, 70–79. [Google Scholar] [CrossRef]
- Zhuang, Y.; Leng, Y.; Zhou, J.; Song, R.; Li, L.; Su, S.W. Voluntary Control of an Ankle Joint Exoskeleton by Able-Bodied Individuals and Stroke Survivors Using EMG -Based Admittance Control Scheme. IEEE Trans. Biomed. Eng. 2021, 68, 695–705. [Google Scholar] [CrossRef] [PubMed]
- Paz-Alonso Pedro, M.; Navalpotro-Gomez, I.; Boddy, P. Functional inhibitory control dynamics in impulse control disorders in Parkinson’s disease. Mov. Disord. 2020, 35, 316–325. [Google Scholar] [CrossRef]
- Dantas, H.; Warren, D.J.; Wendelken, S. Deep Learning Movement Intent Decoders Trained with Dataset Aggregation for Prosthetic Limb Control. IEEE Trans. Biomed. Eng. 2019, 66, 3192–3203. [Google Scholar] [CrossRef] [PubMed]
- Alireza, H.; Cheikh, M.; Annika, K.; Jari, V. Deep learning for forest inventory and planning: A critical review on the remote sensing approaches so far and prospects for further applications. Forestry 2022, 95, 451–465. [Google Scholar]
- Bom, C.R.; Fraga, B.M.O.; Dias, L.O.; Schubert, P.; Blancovalentin, M.; Furlanetto, C. Developing a victorious strategy to the second strong gravitational lensing data challenge. Mon. Not. R. Astron. Soc. 2022, 515, 5121–5134. [Google Scholar] [CrossRef]
- Gebehart, C.; Schmidt, J.; Ansgar, B. Distributed processing of load and movement feedback in the premotor network controlling an insect leg joint. J. Neurophysiol. 2021, 125, 1800–1813. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Lan, D.; Wang, F.; Shin, I. In-memory computing integrated structure circuit based on nonvolatile flash memory unit. Electronics 2023, 12, 3155. [Google Scholar] [CrossRef]
- Fang, Y.; Luo, B.; Zhao, T. ST-SIGMA: Spatio-temporal semantics and interaction graph aggregation for multi-agent perception and trajectory forecasting. CAAI Trans. Intell. Technol. 2022, 7, 744–757. [Google Scholar] [CrossRef]
- Tang, Y.; Hu, W.; Cao, D. Artificial Intelligence-Aided Minimum Reactive Power Control for the DAB Converter Based on Harmonic Analysis Method. IEEE Trans. Power Electron. 2021, 36, 9704–9710. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Farsizadeh, H.; Tavana, M.R. A Novel Deep Learning Controller for DC/DC Buck-Boost Converters in Wireless Power Transfer Feeding CPLs. IEEE Trans. Ind. Electron. 2020, 68, 6379–6384. [Google Scholar] [CrossRef]
- Nguyen, D.Q.; Vien, N.A.; Dang, V.H. Asynchronous framework with Reptile+ algorithm to meta learn partially observable Markov decision process. Appl. Intell. 2020, 50, 4050–4063. [Google Scholar] [CrossRef]

| Optimized Control Method | Distance Traveled | |||
|---|---|---|---|---|
| Footstep | Slope | Uneven | Admixture | |
| Our method | 409 | 472 | 434 | 423 |
| DQN | 283 | 247 | 207 | 234 |
| PPO | 221 | 204 | 194 | 152 |
| Traditional | 156 | 174 | 143 | 121 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhang, H.; Lee, J.; Xu, P.; Shin, I.; Park, J. Motor Interaction Control Based on Muscle Force Model and Depth Reinforcement Strategy. Biomimetics 2024, 9, 150. https://doi.org/10.3390/biomimetics9030150
Liu H, Zhang H, Lee J, Xu P, Shin I, Park J. Motor Interaction Control Based on Muscle Force Model and Depth Reinforcement Strategy. Biomimetics. 2024; 9(3):150. https://doi.org/10.3390/biomimetics9030150
Chicago/Turabian StyleLiu, Hongyan, Hanwen Zhang, Junghee Lee, Peilong Xu, Incheol Shin, and Jongchul Park. 2024. "Motor Interaction Control Based on Muscle Force Model and Depth Reinforcement Strategy" Biomimetics 9, no. 3: 150. https://doi.org/10.3390/biomimetics9030150
APA StyleLiu, H., Zhang, H., Lee, J., Xu, P., Shin, I., & Park, J. (2024). Motor Interaction Control Based on Muscle Force Model and Depth Reinforcement Strategy. Biomimetics, 9(3), 150. https://doi.org/10.3390/biomimetics9030150







