Path Planning of an Unmanned Aerial Vehicle Based on a Multi-Strategy Improved Pelican Optimization Algorithm
Abstract
1. Introduction
- (1).
- Based on the Pelican Optimization Algorithm (POA), a multi-strategy improved Pelican Optimization Algorithm (IPOA) is proposed. Specifically, by incorporating the iterative chaotic mapping method with refracted reverse learning strategy, nonlinear inertia weight factors, the Levy flight mechanism, and adaptive t-distribution variation, the convergence accuracy and speed of the POA algorithm are enhanced.
- (2).
- Compared with the five intelligent optimization algorithms, the proposed algorithm reduces indicators such as the UAV flight path length, turning cost, iteration count, and distance from obstacles. The meanings of these indicators can be found in Table A2, Appendix A.
2. Related Studies
2.1. UAV Path Planning Based on Traditional Algorithms
2.2. UAV Path Planning Based on Intelligent Optimization Algorithms
3. Problem Model
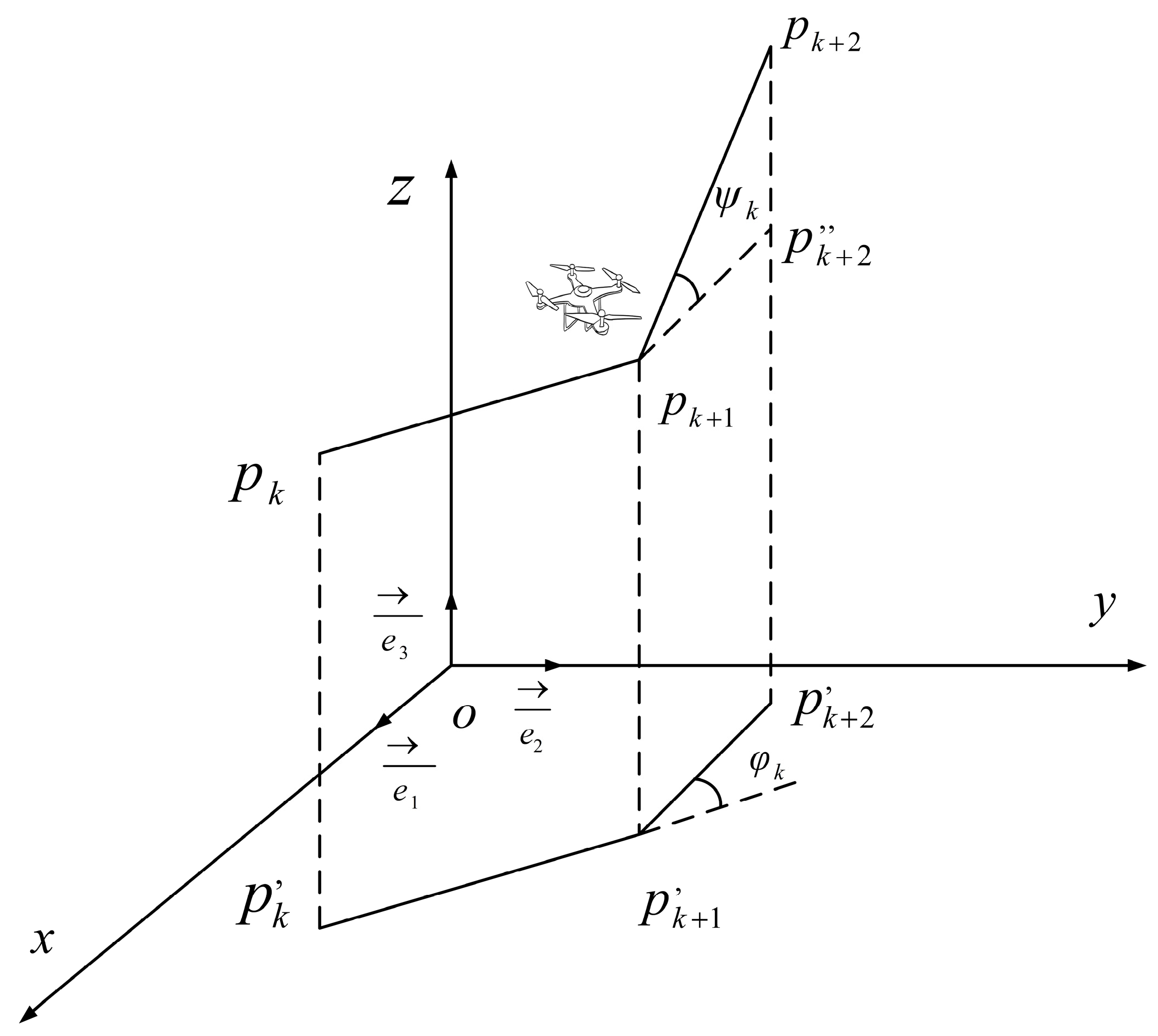
3.1. Three-Dimensional Terrain Model
3.2. Flight Distance Cost
3.3. Turning Angle Cost
3.4. Collision Threat Cost
3.5. Optimize the Target
3.6. Path Smoothing
4. Improved Pelican Optimization Algorithm (IPOA)
4.1. Pelican Optimization Algorithm
4.1.1. Population Initialization
4.1.2. Exploration Phase
4.1.3. Exploitation Phase
4.2. Multi-Strategy Improved Pelican Optimization Algorithm (IPOA)
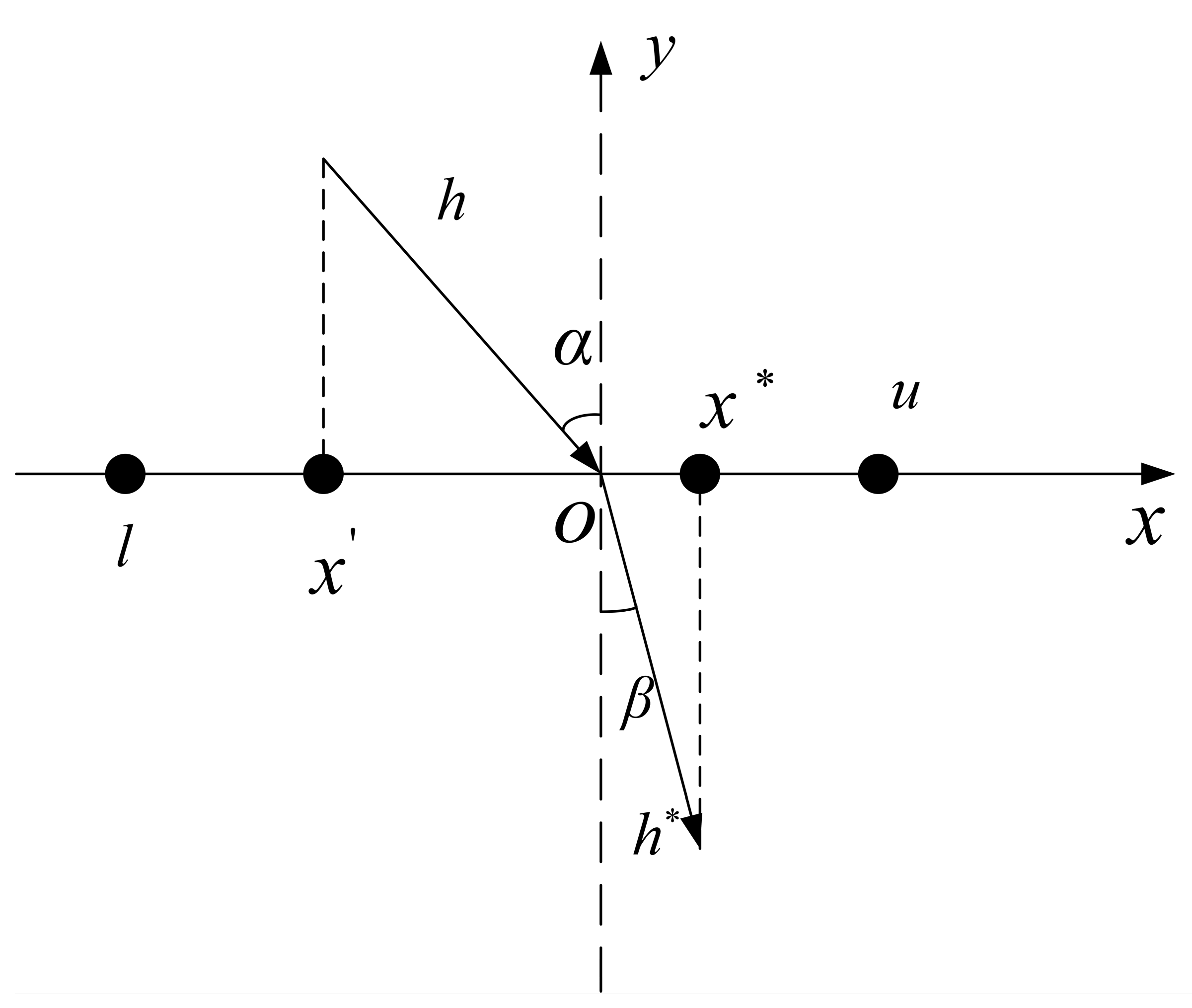
4.2.1. Iterative Chaotic Mapping and Refracted Opposition-Based Learning
- (1).
- Randomly generate candidate positions using iterative chaotic mapping to construct population .
- (2).
- Apply the ROBL to determine the refracted opposition population from population .
- (3).
- Integrate populations and . Sort the combined population in descending order based on individual fitness values and select the top pelican individuals with the highest fitness values to form the initial pelican population.
4.2.2. Nonlinear Inertia Weight Factor
4.2.3. Levy Flight
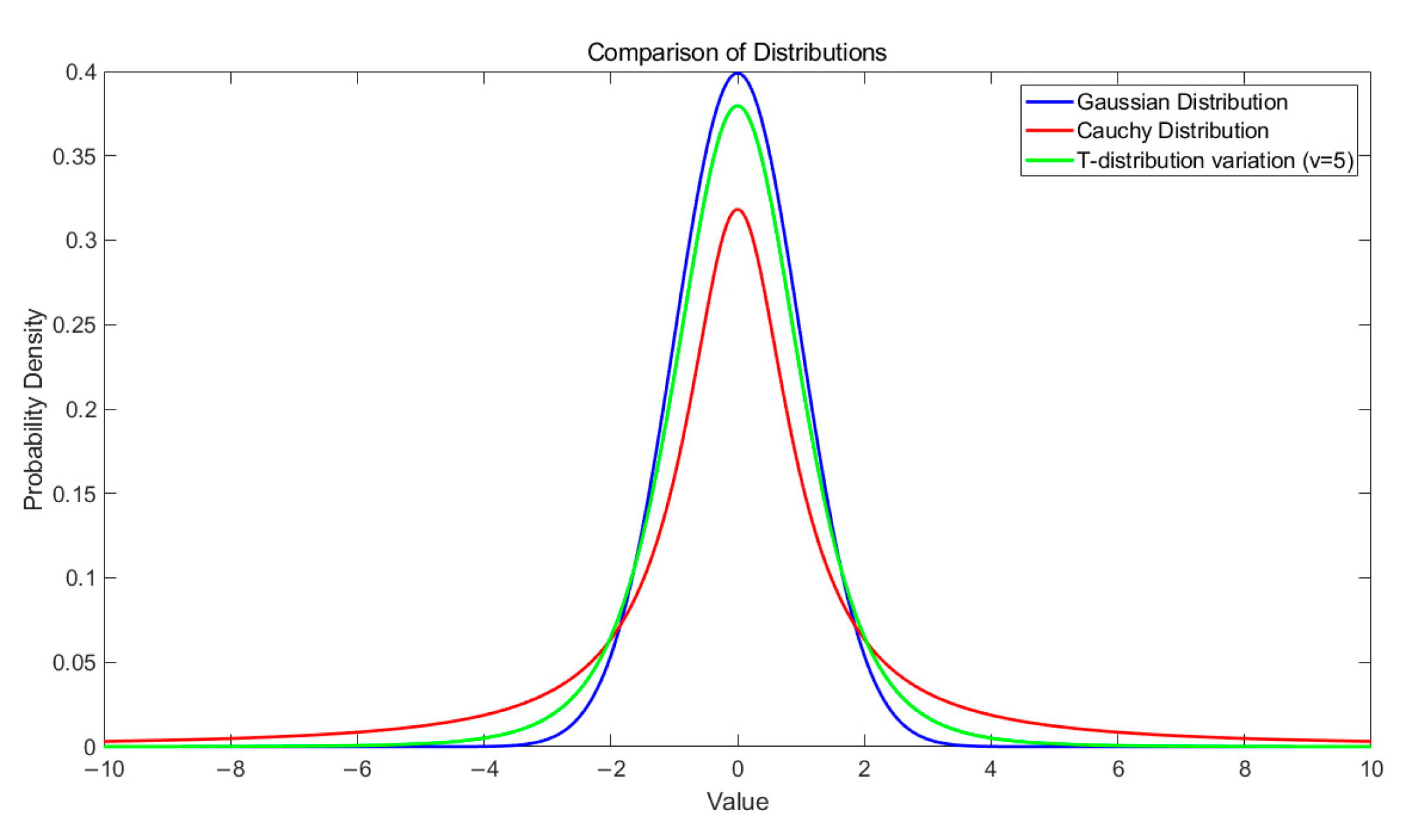
4.2.4. Adaptive t-Distribution Variation
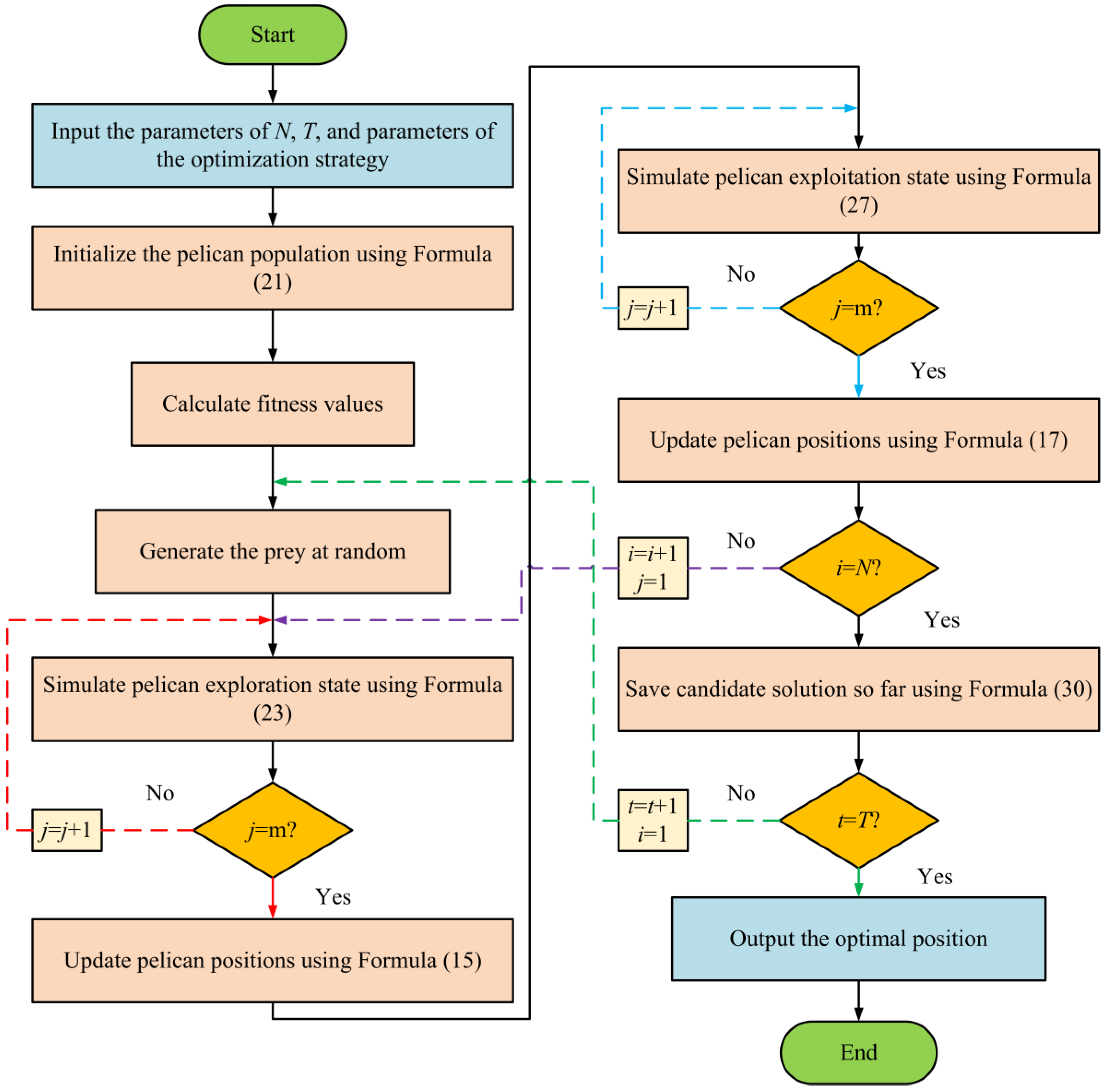
4.3. The Detailed Process of IPOA
| Algorithm 1: Pseudo-code of IPOA | |||
| Input: Maximum number of iterations T, population size N, Improve policy parameters: | |||
| Chaotic mapping constant a, Nonlinear inertia weight factor ω, Levy mechanism | |||
| constant β, degree of freedom v, etc. | |||
| Output: The best location xbest. | |||
| 1 Input various parameters; | |||
| 2 Use Formula (21) to initialize the population; | |||
| 3 Calculating the fitness of the individual by the objective function; | |||
| 4 for t = 1:T do | |||
| 5 | Update the weight factor ω according to Formula (22), Update the degree of freedom v according to Formula (29); | ||
| 6 | Generate the position of the prey at random.; | ||
| 7 | for i = 1:N do | ||
| 8 | Phase 1: Moving towards prey (exploration phase); | ||
| 9 | for j = 1:m do | ||
| 10 | Calculate new status of the j-th dimension using Formula (23); | ||
| 11 | end | ||
| 12 | Update the i-th population member using Formula (15); | ||
| 13 | Phase 2: Winging on the water surface (exploitation phase); | ||
| 14 | for j = 1:m do | ||
| 15 | Calculate new status of the j-th dimension using Formula (27); | ||
| 16 | end | ||
| 17 | Update the i-th population member using Formula (17); | ||
| 18 | end | ||
| 19 | Get the current new location using Formula (30); | ||
| 20 end | |||
| 21 Output best candidate solution obtained. | |||
5. Algorithm Comparison Experiments
5.1. Experimental Design
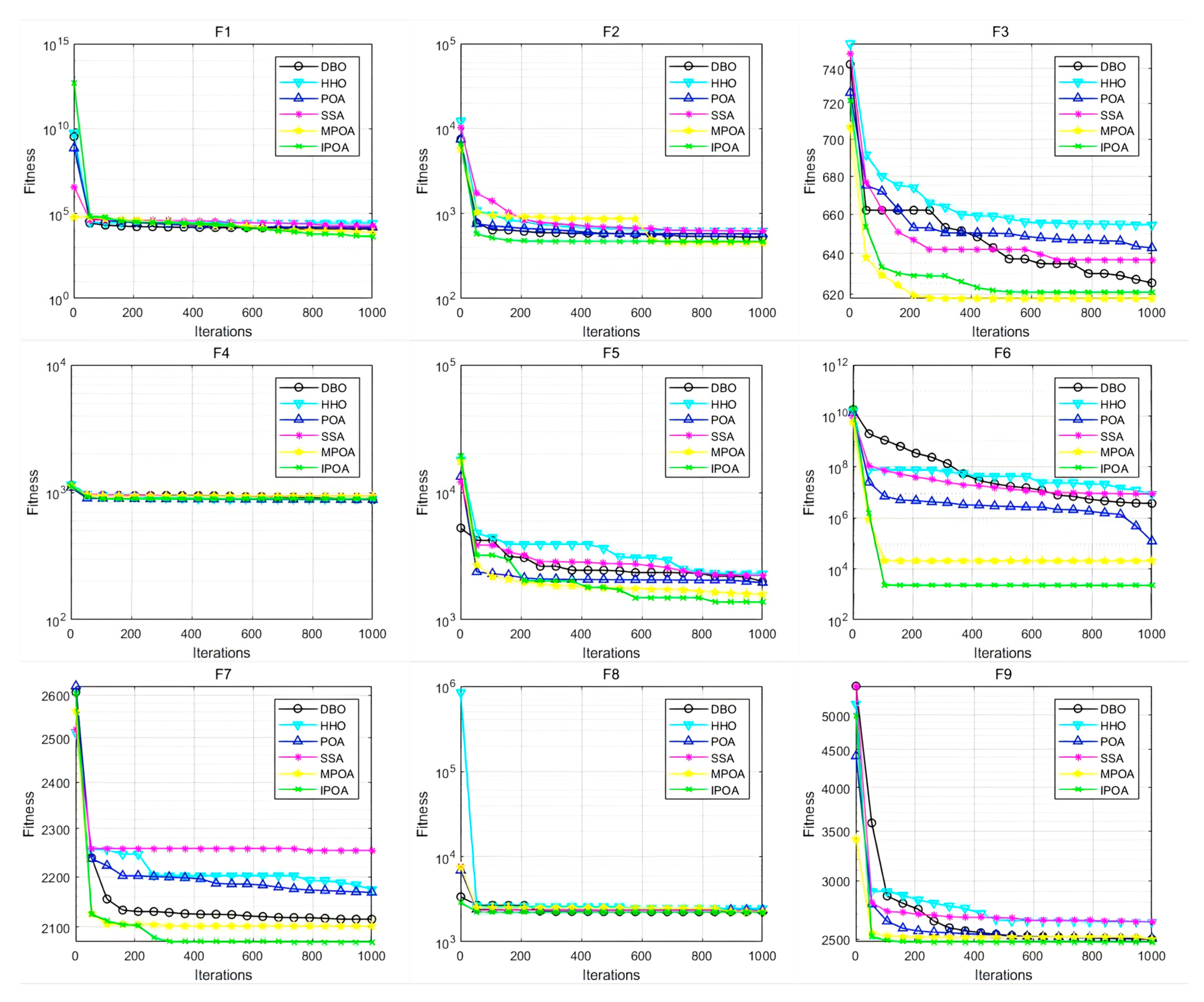
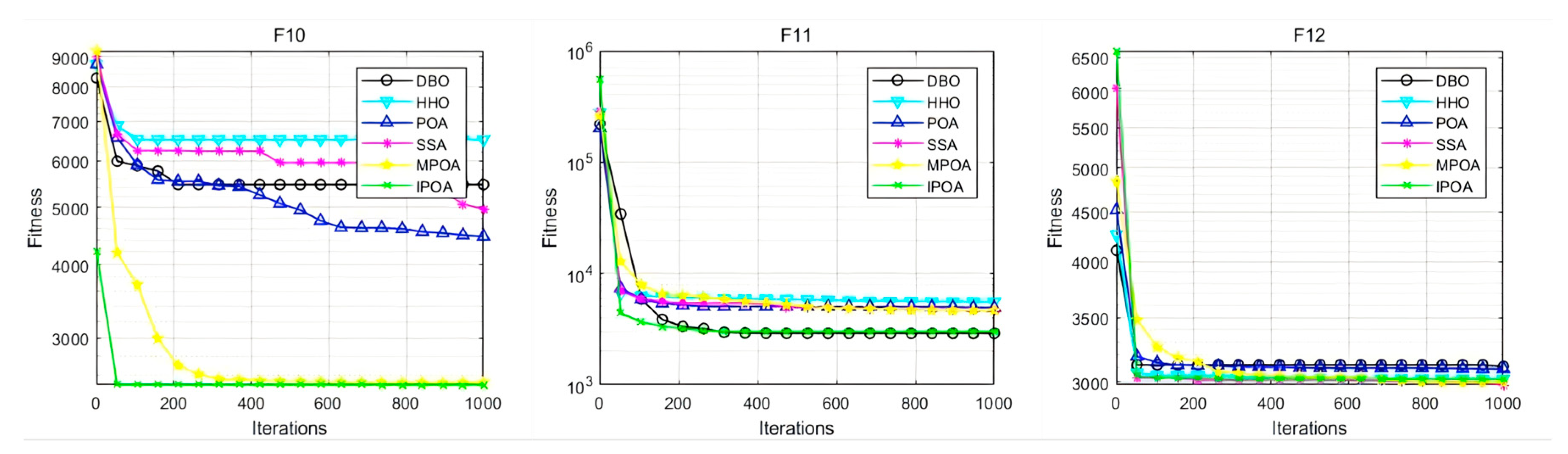
5.2. Comparative Analysis of Algorithms
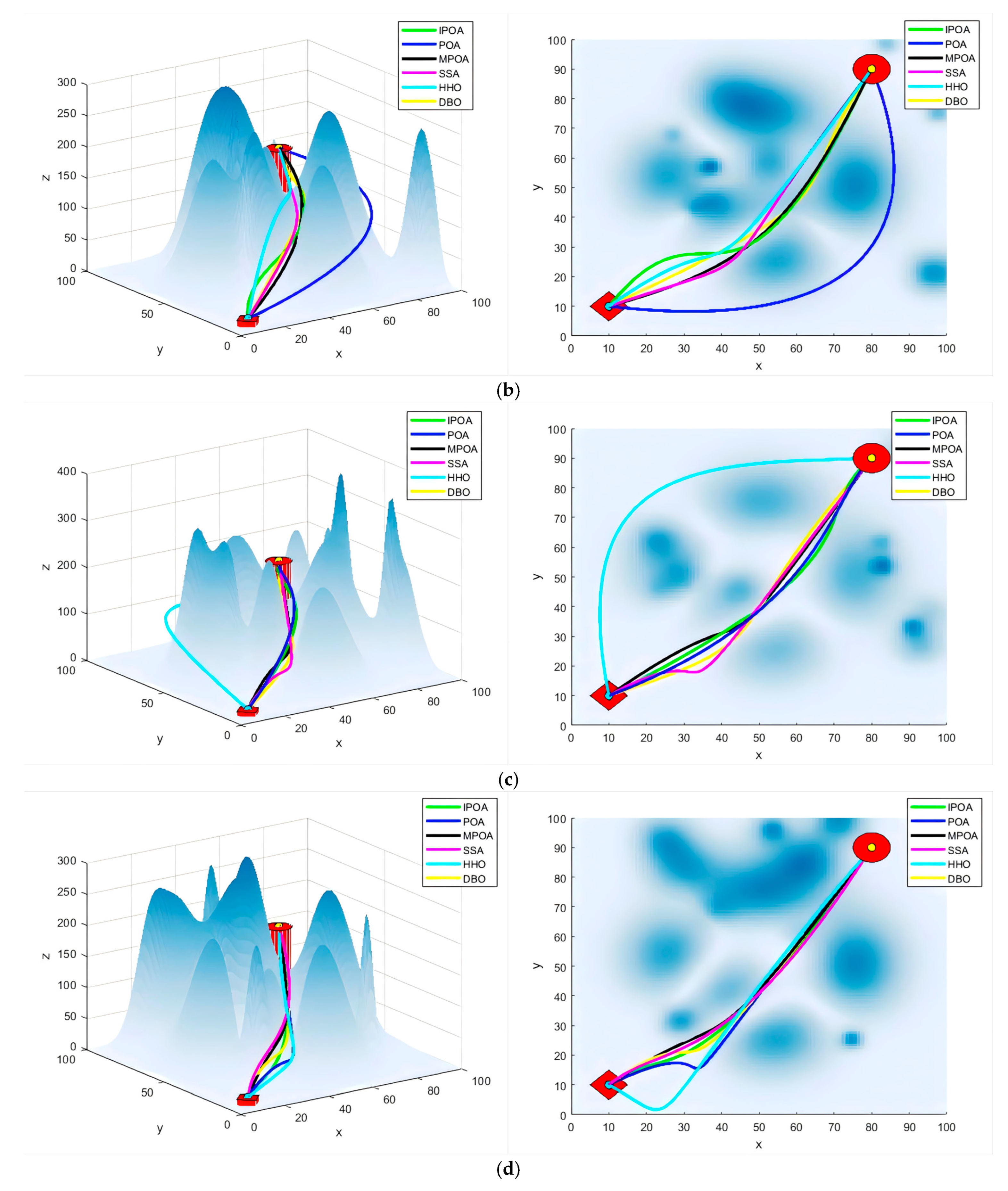
6. UAV Path Planning Experiment
6.1. Simulation Experiment Setup
6.2. Effect of the Cost Function Parameters
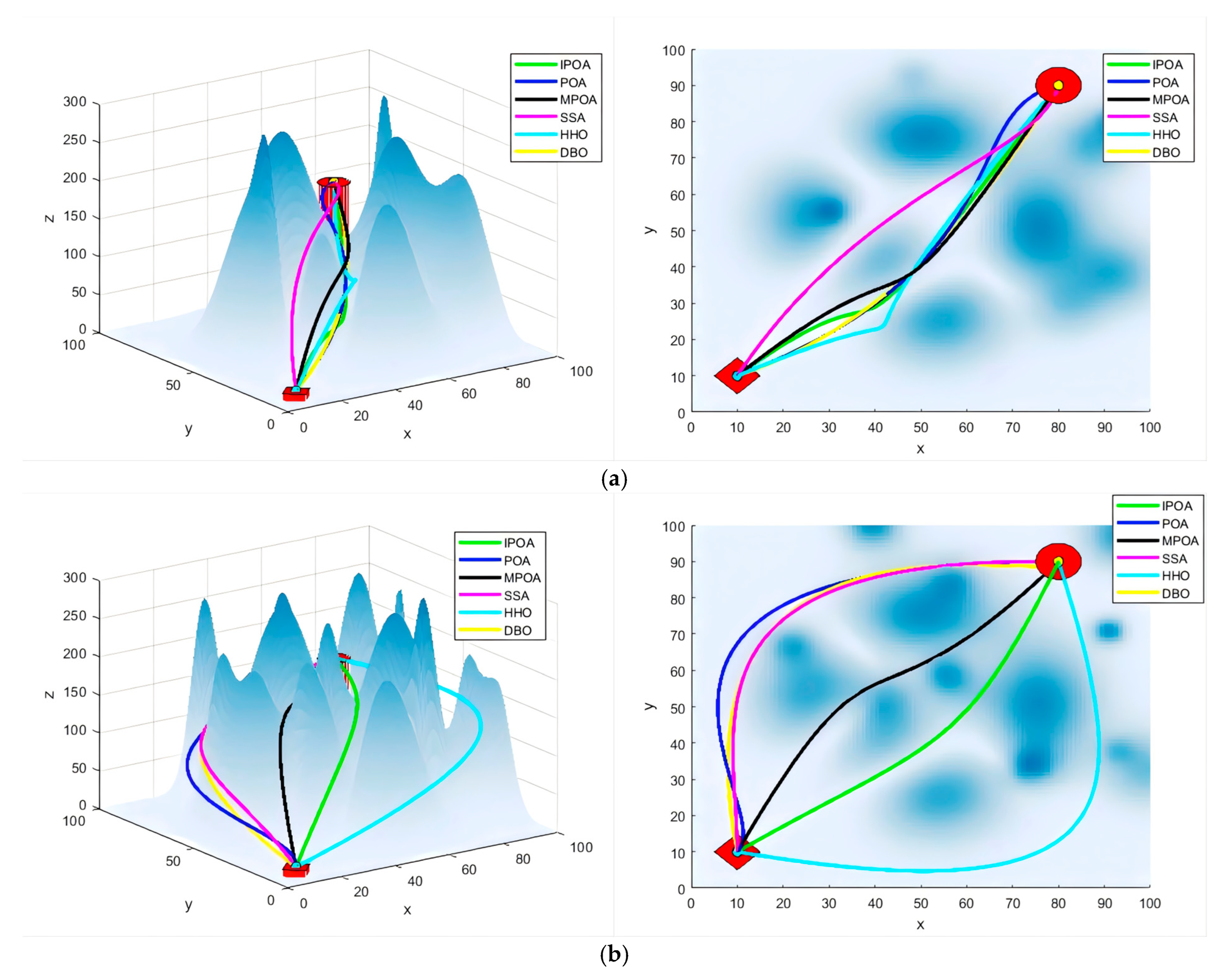
6.3. Random Map Experiment
6.4. Experiment on the Number of Different Obstacles
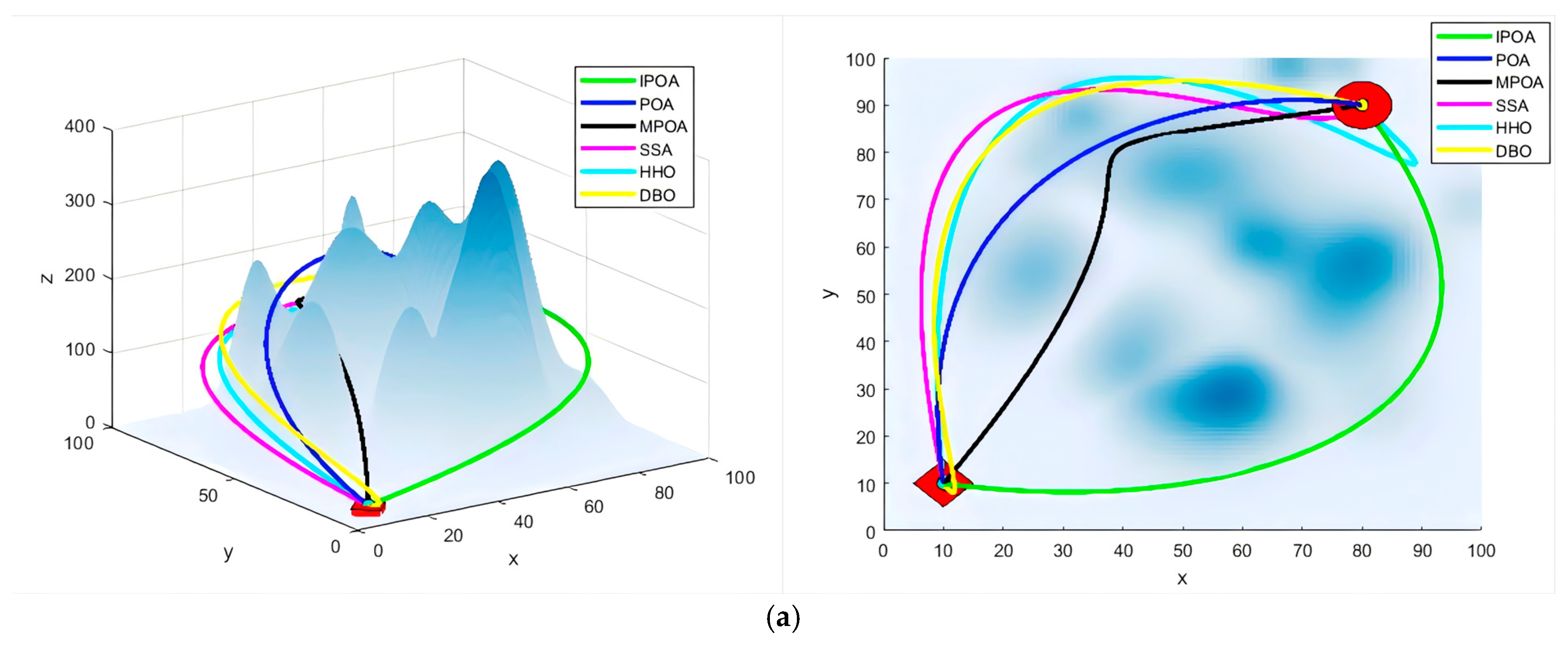
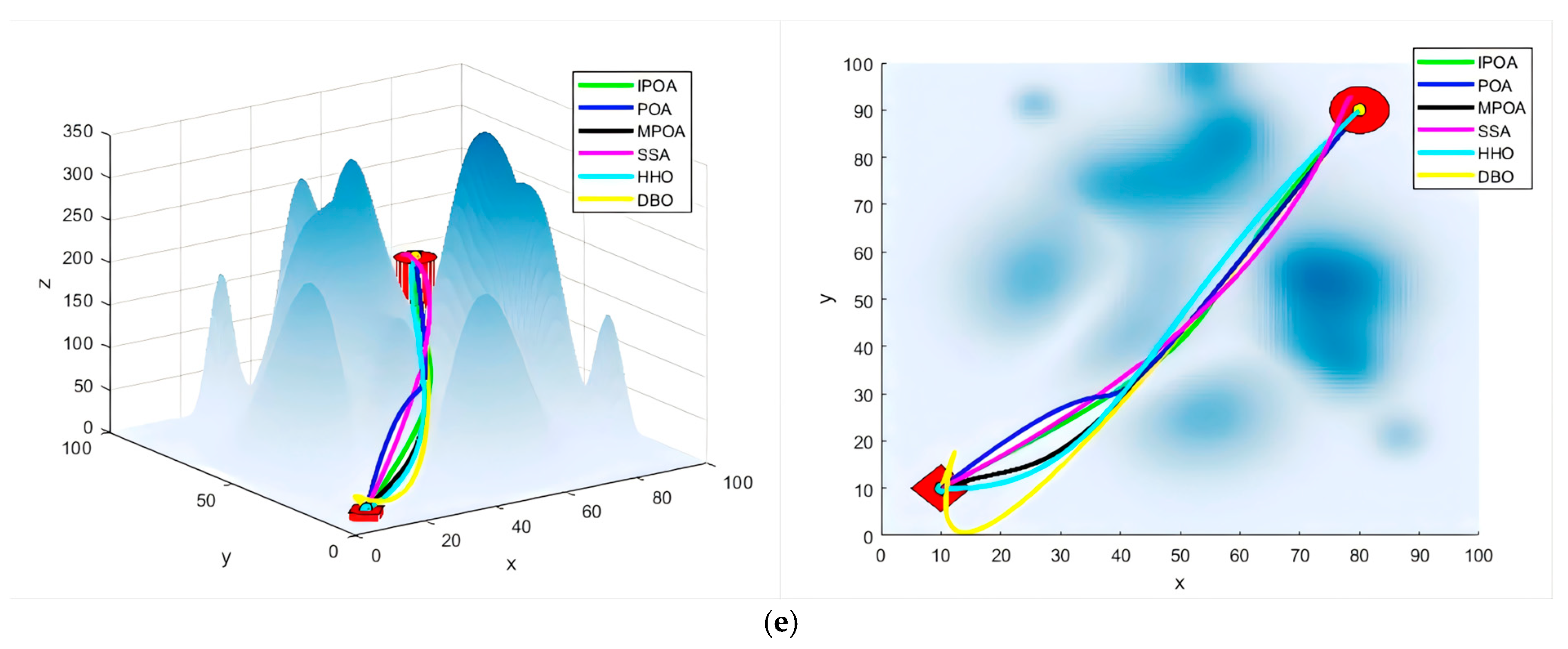
6.5. Simulation Experiment of Real Terrain
6.6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Module Name | Notation | Meaning of Notation |
|---|---|---|
| POA | N | the number of population members |
| m | the dimensionality counter of the problem variables | |
| D | the dimensionality of the problem variables | |
| the lower bounds of the problem variable | ||
| the upper bounds of the problem variable | ||
| I | random integer that can be either 1 or 2 | |
| t | the iteration counter | |
| T | the maximum number of iterations | |
| R | a parameter that can be set between 0 and 1 | |
| Iterative chaotic mapping | a | control parameter |
| ROBL | k | refraction scale factor |
| n | index of refraction | |
| Nonlinear inertia weight factor | nonlinear inertia weight factor | |
| Levy flight | parameter controlling step size | |
| s | the Levy flight path factor | |
| Adaptive t-distribution variation | v | degrees of freedom |
| Evaluation Metrics | Meaning of Notation |
|---|---|
| Best | closest to the global optimum |
| Mean | the average of all results |
| SD | the degree of dispersion of the results |
| Distance | the average path length |
| Iterations | the average number of iterations of the algorithm |
| Turn/° | the average deflection angle difference between two adjacent nodes on the path |
| Dis-obs | the average distance between the current node and the nearest obstacle |
| Time | the average flight time |
References
- Deng, M.; Yang, Q.; Peng, Y. A Real-Time Path Planning Method for Urban Low-Altitude Logistics UAVs. Sensors 2023, 23, 7472. [Google Scholar] [CrossRef] [PubMed]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A Compilation of UAV Applications for Precision Agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Wei, Z.; Zhu, M.; Zhang, N.; Wang, L.; Zou, Y.; Meng, Z.; Wu, H.; Feng, Z. UAV-Assisted Data Collection for Internet of Things: A Survey. IEEE Internet Things J. 2022, 9, 15460–15483. [Google Scholar] [CrossRef]
- Wang, G.; Chen, Y.; An, P.; Hong, H.; Hu, J.; Huang, T. UAV-YOLOv8: A Small-Object-Detection Model Based on Improved YOLOv8 for UAV Aerial Photography Scenarios. Sensors 2023, 23, 7190. [Google Scholar] [CrossRef]
- Li, A.; Hansen, M.; Zou, B. Traffic Management and Resource Allocation for UAV-Based Parcel Delivery in Low-Altitude Urban Space. Transp. Res. Part C Emerg. Technol. 2022, 143, 103808. [Google Scholar] [CrossRef]
- Xiaoning, Z. Analysis of Military Application of UAV Swarm Technology. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 1200–1204. [Google Scholar]
- Mohamed, N.; Al-Jaroodi, J.; Jawhar, I.; Idries, A.; Mohammed, F. Unmanned Aerial Vehicles Applications in Future Smart Cities. Technol. Forecast. Soc. Change 2020, 153, 119293. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Li, R.; Chen, H.; Chu, K. Trajectory Planning for UAV Navigation in Dynamic Environments with Matrix Alignment Dijkstra. Soft Comput. 2022, 26, 12599–12610. [Google Scholar] [CrossRef]
- Li, J.; Liao, C.; Zhang, W.; Fu, H.; Fu, S. UAV Path Planning Model Based on R5DOS Model Improved A-Star Algorithm. Appl. Sci. 2022, 12, 11338. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V. Path Planning for a Solar-Powered UAV Inspecting Mountain Sites for Safety and Rescue. Energies 2021, 14, 1968. [Google Scholar] [CrossRef]
- Khan, A.H.; Cao, X.; Li, S.; Katsikis, V.N.; Liao, L. BAS-ADAM: An ADAM Based Approach to Improve the Performance of Beetle Antennae Search Optimizer. IEEE/CAA J. Autom. Sin. 2020, 7, 461–471. [Google Scholar] [CrossRef]
- Fathy, A.; Alanazi, T.M.; Rezk, H.; Yousri, D. Optimal Energy Management of Micro-Grid Using Sparrow Search Algorithm. Energy Rep. 2022, 8, 758–773. [Google Scholar] [CrossRef]
- Dong, J.; Dou, Z.; Si, S.; Wang, Z.; Liu, L. Optimization of Capacity Configuration of Wind–Solar–Diesel–Storage Using Improved Sparrow Search Algorithm. J. Electr. Eng. Technol. 2022, 17, 1–14. [Google Scholar] [CrossRef]
- Bao, X.; Jia, H.; Lang, C. A Novel Hybrid Harris Hawks Optimization for Color Image Multilevel Thresholding Segmentation. IEEE Access 2019, 7, 76529–76546. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, M.; Hu, Z. Path Planning of Unmanned Aerial Vehicles Based on an Improved Bio-Inspired Tuna Swarm Optimization Algorithm. Biomimetics 2024, 9, 388. [Google Scholar] [CrossRef] [PubMed]
- Jayaweera, H.M.; Hanoun, S. A Dynamic Artificial Potential Field (D-APF) UAV Path Planning Technique for Following Ground Moving Targets. IEEE Access 2020, 8, 192760–192776. [Google Scholar] [CrossRef]
- Diao, Q.; Zhang, J.; Liu, M.; Yang, J. A Disaster Relief UAV Path Planning Based on APF-IRRT* Fusion Algorithm. Drones 2023, 7, 323. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, T.; Feng, O.; Wu, S.; Zhong, G. Research on Public Air Route Network Planning of Urban Low-Altitude Logistics Unmanned Aerial Vehicles. Sustainability 2023, 15, 12021. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Wei, T. Improved A* Algorithm for Obstacle Avoidance Path Planning Strategy of the Blind. Aero Weapon. 2017, 3, 86–92. [Google Scholar]
- Gao, S.; Ai, J.L.; Wang, Z.H. Mixed Population RRT Algorithm for UAV Path Planning. Syst. Eng. Electron. 2020, 1, 101–107. [Google Scholar]
- Hao, G.; Lv, Q.; Huang, Z.; Zhao, H.; Chen, W. UAV Path Planning Based on Improved Artificial Potential Field Method. Aerospace 2023, 10, 562. [Google Scholar] [CrossRef]
- Kong, D.; Miyatake, M. Cooperative Application of Onboard Energy Storage and Stationary Energy Storage in Rail Transit Based on Genetic Algorithm. Energies 2024, 17, 1426. [Google Scholar] [CrossRef]
- Candia, D.A.; Játiva, P.P.; Azurdia Meza, C.; Sánchez, I.; Ijaz, M. Performance Analysis of the Particle Swarm Optimization Algorithm in a VLC System for Localization in Hospital Environments. Appl. Sci. 2024, 14, 2514. [Google Scholar] [CrossRef]
- Tang, K.; Wei, X.-F.; Jiang, Y.-H.; Chen, Z.-W.; Yang, L. An Adaptive Ant Colony Optimization for Solving Large-Scale Traveling Salesman Problem. Mathematics 2023, 11, 4439. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, C.; Pang, Y.; Chen, X.; Pan, Z.; Wang, L.; Fan, D. Temperature Demodulation for an Interferometric Fiber-Optic Sensor Based on Artificial Bee Colony–Long Short-Term Memory. Photonics 2023, 10, 1157. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An Improved Grey Wolf Optimizer for Solving Engineering Problems. Expert. Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Alabool, H.M.; Alarabiat, D.; Abualigah, L.; Heidari, A.A. Harris Hawks Optimization: A Comprehensive Review of Recent Variants and Applications. Neural Comput. Applic 2021, 33, 8939–8980. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V.; Pehlivanoglu, P. An Enhanced Genetic Algorithm for Path Planning of Autonomous UAV in Target Coverage Problems. Appl. Soft Comput. 2021, 112, 107796. [Google Scholar] [CrossRef]
- Ali, Z.A.; Zhangang, H.; Hang, W.B. Cooperative Path Planning of Multiple UAVs by Using Max–Min Ant Colony Optimization along with Cauchy Mutant Operator. Fluct. Noise Lett. 2021, 20, 2150002. [Google Scholar] [CrossRef]
- Lin, S.; Li, F.; Li, X.; Jia, K.; Zhang, X. Improved Artificial Bee Colony Algorithm Based on Multi-Strategy Synthesis for UAV Path Planning. IEEE Access 2022, 10, 119269–119282. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Hu, C. Path Planning with Time Windows for Multiple UAVs Based on Gray Wolf Algorithm. Biomimetics 2022, 7, 225. [Google Scholar] [CrossRef]
- Zhang, R.; Li, S.; Ding, Y.; Qin, X.; Xia, Q. UAV Path Planning Algorithm Based on Improved Harris Hawks Optimization. Sensors 2022, 22, 5232. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat Swarm Optimization: A Nature-Inspired Algorithm to Solve Global Optimization Problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung Beetle Optimizer: A New Meta-Heuristic Algorithm for Global Optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Subtraction-Average-Based Optimizer: A New Swarm-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics 2023, 8, 149. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef]
- Peres, F.; Castelli, M. Combinatorial Optimization Problems and Metaheuristics: Review, Challenges, Design, and Development. Appl. Sci. 2021, 11, 6449. [Google Scholar] [CrossRef]
- Han, X.; Liu, X.; Wu, G.; Song, X.; Cui, L. Research on Additive Manufacturing Path Planning of a Six-Degree-of-Freedom Manipulator. Actuators 2024, 13, 249. [Google Scholar] [CrossRef]
- Varol Altay, E.; Alatas, B. Bird Swarm Algorithms with Chaotic Mapping. Artif. Intell. Rev. 2020, 53, 1373–1414. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-Based Learning: A New Scheme for Machine Intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; Volume 1, pp. 695–701. [Google Scholar]
- Qiao, L.; He, N.; Cui, Y.; Zhu, J.; Xiao, K. Reservoir Porosity Prediction Based on BiLSTM-AM Optimized by Improved Pelican Optimization Algorithm. Energies 2024, 17, 1479. [Google Scholar] [CrossRef]
- Dai, X.; Ke, C.; Quan, Q.; Cai, K.-Y. RFlySim: Automatic Test Platform for UAV Autopilot Systems with FPGA-Based Hardware-in-the-Loop Simulations. Aerosp. Sci. Technol. 2021, 114, 106727. [Google Scholar] [CrossRef]



| Function Type | No. | Functions | |
|---|---|---|---|
| Unimodal function | 300 | Shifted and full Rotated Zakharov Function | |
| Basic functions | 400 | Shifted and full Rotated Rosenbrock Function | |
| 600 | Shifted and full Rotated Expanded Schaffer Function | ||
| 800 | Shifted and full Rotated Non-Continuous Rastrigin Function | ||
| 900 | Shifted and full Rotated Levy Function | ||
| Hybrid functions | 1800 | Hybrid Function (N = 3) | |
| 2000 | Hybrid Function (N = 6) | ||
| 2200 | Hybrid Function (N = 5) | ||
| Composition functions | 2300 | Composition Function (N = 5) | |
| 2400 | Composition Function (N = 4) | ||
| 2600 | Composition Function (N = 5) | ||
| 2700 | Composition Function (N = 6) | ||
| Search range: | |||
| Algorithm | Parameters | Values |
|---|---|---|
| DBO | Deflection coefficient | 0.1 |
| Ball-Rolling dung beetles parameter | 0.1 | |
| Stealing dung beetles parameter | 0.3 | |
| POA | Exploitation phase parameter | 0.2 |
| HHO | Initial energy | |
| Jump strength | (0, 2) | |
| SSA | Safety threshold | 0.6 |
| Proportion of finders | 0.7 | |
| Proportion of vigilante | 0.2 | |
| MPOA | freedom parameter | |
| Proportion of vigilante | 0.2 | |
| IPOA | Exploitation phase parameter | 0.2 |
| Chaotic iterative mapping constant | 0.7 | |
| Levy flight step parameters | 1.5 |
| Functions | Metrics | IPOA | DBO [36] | POA [38] | SSA [34] | MPOA [43] | HHO [27] |
|---|---|---|---|---|---|---|---|
| Best | 6989.62 | 13,293.43 | 14,564.86 | 17,967.23 | 10,699.83 | 19,435.23 | |
| Mean | 8676.68 | 16,612.76 | 17,567.55 | 21,293.43 | 12,879.42 | 24,783.45 | |
| SD | 544.85 | 1649.18 | 1293.82 | 1502.73 | 975.75 | 2182.99 | |
| Ranking | 1 1 1 | 3 3 5 | 4 4 3 | 5 5 4 | 2 2 2 | 6 6 6 | |
| Best | 479.21 | 582.19 | 612.08 | 771.05 | 449.08 | 762.19 | |
| Mean | 522.86 | 673.45 | 698.46 | 820.58 | 489.18 | 872.11 | |
| SD | 33.19 | 66.20 | 55.74 | 34.94 | 31.89 | 65.95 | |
| Ranking | 2 2 2 | 3 3 6 | 4 4 4 | 6 5 3 | 1 1 1 | 5 6 5 | |
| Best | 622.53 | 625.79 | 624.24 | 635.64 | 618.47 | 641.46 | |
| Mean | 625.98 | 634.85 | 635.43 | 646.26 | 626.66 | 658.25 | |
| SD | 3.99 | 6.15 | 7.61 | 9.25 | 7.83 | 13.26 | |
| Ranking | 2 1 1 | 4 3 2 | 3 4 3 | 5 5 5 | 1 2 4 | 6 6 6 | |
| Best | 806.95 | 813.71 | 812.19 | 815.09 | 811.32 | 828.73 | |
| Mean | 822.56 | 825.58 | 821.91 | 825.28 | 823.06 | 844.89 | |
| SD | 5.28 | 9.96 | 6.47 | 4.22 | 6.04 | 9.08 | |
| Ranking | 1 2 3 | 4 5 6 | 3 1 4 | 5 4 1 | 2 3 2 | 6 6 5 | |
| Best | 1943.50 | 2498.45 | 2559.36 | 3285.23 | 2008.52 | 2946.31 | |
| Mean | 2159.24 | 2954.46 | 2856.12 | 3804.16 | 2287.56 | 3214.68 | |
| SD | 149.42 | 296.45 | 193.45 | 256.01 | 180.82 | 369.14 | |
| Ranking | 1 1 1 | 3 4 5 | 4 3 3 | 6 6 4 | 2 2 2 | 5 5 6 | |
| Best | 3347.46 | 8757.56 | 14,549.54 | 12,755.58 | 5489.24 | 16,763.65 | |
| Mean | 8480.64 | 54,207.68 | 66,946.34 | 107,686.45 | 12,657.65 | 226,784.77 | |
| SD | 2365.18 | 42,558.67 | 60,092.98 | 91,572.16 | 5469.12 | 181,273.25 | |
| Ranking | 1 1 1 | 3 3 3 | 5 4 4 | 4 5 5 | 2 2 2 | 6 6 6 | |
| Best | 2009.65 | 2063.38 | 2088.24 | 2099.43 | 2018.23 | 2158.98 | |
| Mean | 2028.55 | 2148.33 | 2122.09 | 2176.61 | 2034.01 | 2176.38 | |
| SD | 13.95 | 67.465 | 28.35 | 52.07 | 18.45 | 14.75 | |
| Ranking | 1 1 1 | 3 4 6 | 4 3 4 | 5 6 5 | 2 2 3 | 6 5 2 | |
| Best | 2207.08 | 2215.71 | 2219.55 | 2225.23 | 2204.25 | 2233.16 | |
| Mean | 2224.47 | 2231.36 | 2230.13 | 2237.66 | 2218.96 | 2266.65 | |
| SD | 9.17 | 15.18 | 8.89 | 10.28 | 8.82 | 29.19 | |
| Ranking | 2 2 3 | 3 4 5 | 4 3 2 | 5 5 4 | 1 1 1 | 6 6 6 | |
| Best | 2526.98 | 2544.43 | 2533.38 | 2535.47 | 2539.18 | 2543.34 | |
| Mean | 2531.12 | 2591.28 | 2552.49 | 2588.45 | 2542.10 | 2579.63 | |
| SD | 2.29 | 28.17 | 18.12 | 38.95 | 0.91 | 19.26 | |
| Ranking | 1 1 2 | 6 6 5 | 3 3 3 | 3 5 6 | 4 2 1 | 5 4 4 | |
| Best | 2501.16 | 2813.10 | 3321.58 | 3049.19 | 2535.88 | 4216.39 | |
| Mean | 2862.44 | 3219.37 | 4044.54 | 4615.24 | 2912.13 | 5891.29 | |
| SD | 203.64 | 285.56 | 363.79 | 625.50 | 212.98 | 598.75 | |
| Ranking | 1 1 1 | 3 3 3 | 5 4 4 | 4 5 6 | 2 2 2 | 6 6 5 | |
| Best | 2942.12 | 2912.46 | 3687.47 | 3572.67 | 3557.19 | 3524.56 | |
| Mean | 3118.91 | 3342.65 | 3916.18 | 4041.52 | 3898.96 | 3619.74 | |
| SD | 109.50 | 252.14 | 189.67 | 244.29 | 177.06 | 178.11 | |
| Ranking | 2 1 1 | 1 2 6 | 6 5 4 | 5 6 5 | 4 4 2 | 3 3 3 | |
| Best | 2938.44 | 2999.95 | 3010.74 | 2946.78 | 2994.06 | 3012.13 | |
| Mean | 2947.18 | 3007.47 | 3029.25 | 2957.64 | 3009.08 | 3028.86 | |
| SD | 5.22 | 6.64 | 10.19 | 12.38 | 10.42 | 18.93 | |
| Ranking | 1 1 1 | 4 3 2 | 5 6 3 | 2 2 5 | 3 4 4 | 6 5 6 |
| Function | DBO [36] | POA [38] | SSA [34] | HHO [27] | MPOA [43] |
|---|---|---|---|---|---|
| 1.4643 × 10−10 | 3.0810 × 10−08 | 3.0198 × 10−11 | 3.0198 × 10−11 | 6.8462 × 10−06 | |
| 0.0415 | 0.0571 | 0.0013 | 0.0002 | 0.6683 | |
| 0.0013 | 1.5422 × 10−07 | 1.6836 × 10−08 | 1.4478 × 10−07 | 4.9364 × 10−04 | |
| 0.0061 | 0.0324 | 0.0463 | 6.9641 × 10−11 | 0.0489 | |
| 0.3415 | 0.2186 | 0.5003 | 0.4801 | 0.7390 | |
| 6.4213 × 10−08 | 0.0004 | 9.9851 × 10−04 | 2.2891 × 10−10 | 3.8936 × 10−05 | |
| 3.1019 × 10−07 | 0.0398 | 2.1341 × 10−07 | 3.7621 × 10−09 | 0.0466 | |
| 4.7173 × 10−05 | 0.3571 | 3.3146 × 10−08 | 6.2251 × 10−10 | 0.8701 | |
| 3.3640 × 10−11 | 3.0815 × 10−09 | 4.7093 × 10−10 | 3.1467 × 10−11 | 4.2914 × 10−08 | |
| 0.5083 | 0.6412 | 0.6721 | 1.9851 × 10−07 | 0.8827 | |
| 1.2375 × 10−06 | 0.1739 | 0.0391 | 5.4226 × 10−09 | 0.2634 | |
| 0.0143 | 0.0188 | 0.0336 | 0.0002 | 0.0296 |
| Weight Combination | Metrics | IPOA | DBO | HHO | POA | MPOA | SSA | |
|---|---|---|---|---|---|---|---|---|
| Experiment 1 | , , = 0.15 | Best | 33.04 | 43.96 | 102.17 | 45.59 | 37.64 | 79.35 |
| Mean | 36.78 | 50.39 | 121.62 | 52.61 | 41.33 | 97.91 | ||
| SD | 2.99 | 3.98 | 16.72 | 4.63 | 3.48 | 14.82 | ||
| Experiment 2 | , , = 0.15 | Best | 36.10 | 47.17 | 116.55 | 43.39 | 38.26 | 76.94 |
| Mean | 41.84 | 55.32 | 132.74 | 52.17 | 43.37 | 92.38 | ||
| SD | 4.15 | 6.24 | 15.57 | 6.61 | 3.96 | 16.67 | ||
| Experiment 3 | , , = 0.7 | Best | 38.41 | 41.09 | 106.65 | 43.66 | 35.02 | 75.28 |
| Mean | 45.25 | 58.63 | 133.87 | 55.81 | 46.77 | 97.96 | ||
| SD | 5.71 | 17.25 | 15.07 | 6.80 | 6.42 | 14.06 |
| Experiment | Metrics | IPOA | DBO | HHO | POA | MPOA | SSA |
|---|---|---|---|---|---|---|---|
| Experiment 1 | Distance | 219.67 | 233.54 | 241.56 | 246.41 | 234.43 | 238.88 |
| Iterations | 72.1 | 79.0 | 89.1 | 87.2 | 70.4 | 77.5 | |
| Turn/° | 52.9 | 43.1 | 44.1 | 51.8 | 48.1 | 48.8 | |
| Dis-obs | 46.1 | 56.4 | 52.0 | 50.9 | 48.4 | 54.5 | |
| Experiment 2 | Distance | 180.39 | 199.24 | 222.45 | 204.76 | 193.63 | 208.65 |
| Iterations | 60.6 | 69.3 | 77.2 | 73.5 | 66.9 | 80.1 | |
| Turn/° | 44.2 | 48.6 | 58.7 | 50.4 | 45.8 | 47.4 | |
| Dis-obs | 49.3 | 51.2 | 42.4 | 47.6 | 49.3 | 58.7 | |
| Experiment 3 | Distance | 187.66 | 200.61 | 208.30 | 201.97 | 195.24 | 200.03 |
| Iterations | 78.7 | 82.6 | 61.1 | 79.2 | 80.8 | 89.4 | |
| Turn/° | 49.9 | 56.7 | 77.1 | 57.2 | 53.1 | 58.1 | |
| Dis-obs | 44.7 | 43.1 | 41.3 | 43.6 | 42.8 | 43.5 | |
| Experiment 4 | Distance | 189.87 | 202.62 | 204.93 | 200.94 | 202.65 | 203.56 |
| Iterations | 86.1 | 95.3 | 99.4 | 101.1 | 90.2 | 95.7 | |
| Turn/° | 46.2 | 46.9 | 61.0 | 43.3 | 49.4 | 53.8 | |
| Dis-obs | 59.7 | 65.2 | 64.8 | 66.9 | 64.1 | 66.4 | |
| Experiment 5 | Distance | 183.46 | 194.73 | 200.65 | 196.48 | 191.63 | 192.42 |
| Iterations | 62.3 | 73.2 | 66.4 | 71.4 | 65.9 | 70.5 | |
| Turn/° | 54.3 | 52.1 | 67.6 | 54.6 | 55.1 | 50.4 | |
| Dis-obs | 42.9 | 43.8 | 48.6 | 44.2 | 41.3 | 46.5 |
| Number of Obstacles | Metrics | IPOA | DBO | HHO | POA | MPOA | SSA |
|---|---|---|---|---|---|---|---|
| 6 | Distance | 184.81 | 192.14 | 198.74 | 198.01 | 191.64 | 199.42 |
| Iterations | 53.0 | 64.3 | 67.9 | 63.1 | 60.4 | 72.5 | |
| Turn/° | 45.3 | 41.6 | 42.1 | 48.3 | 45.4 | 43.8 | |
| Dis-obs | 54.1 | 62.4 | 61.2 | 55.9 | 58.4 | 60.5 | |
| 10 | Distance | 190.96 | 205.37 | 218.33 | 208.79 | 202.24 | 210.23 |
| Iterations | 72.9 | 86.7 | 101.1 | 86.2 | 79.6 | 88.1 | |
| Turn/° | 49.9 | 50.7 | 47.1 | 50.9 | 50.1 | 54.6 | |
| Dis-obs | 41.4 | 43.4 | 41.7 | 42.5 | 42.7 | 45.6 |
| Metrics | IPOA | DBO | HHO | POA | MPOA | SSA |
|---|---|---|---|---|---|---|
| Distance (m) | 286.74 | 318.88 | 342.66 | 313.19 | 298.97 | 322.81 |
| Turn/° | 51.7 | 55.6 | 51.5 | 54.9 | 52.1 | 53.8 |
| Dis-obs (m) | 2.11 | 2.04 | 2.13 | 2.24 | 2.16 | 2.42 |
| Time (s) | 20.23 | 22.77 | 24.16 | 22.32 | 21.12 | 22.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, S.; Dai, J.; Zhao, D. Path Planning of an Unmanned Aerial Vehicle Based on a Multi-Strategy Improved Pelican Optimization Algorithm. Biomimetics 2024, 9, 647. https://doi.org/10.3390/biomimetics9100647
Qiu S, Dai J, Zhao D. Path Planning of an Unmanned Aerial Vehicle Based on a Multi-Strategy Improved Pelican Optimization Algorithm. Biomimetics. 2024; 9(10):647. https://doi.org/10.3390/biomimetics9100647
Chicago/Turabian StyleQiu, Shaoming, Jikun Dai, and Dongsheng Zhao. 2024. "Path Planning of an Unmanned Aerial Vehicle Based on a Multi-Strategy Improved Pelican Optimization Algorithm" Biomimetics 9, no. 10: 647. https://doi.org/10.3390/biomimetics9100647
APA StyleQiu, S., Dai, J., & Zhao, D. (2024). Path Planning of an Unmanned Aerial Vehicle Based on a Multi-Strategy Improved Pelican Optimization Algorithm. Biomimetics, 9(10), 647. https://doi.org/10.3390/biomimetics9100647






