Adaptive Bi-Operator Evolution for Multitasking Optimization Problems
Abstract
1. Introduction
2. Preliminary
2.1. DE
- Mutation
- 2.
- Crossover
- 3.
- Selection
2.2. Simulated Binary Crossover (SBX)
2.3. Evolutionary Multitasking Optimization
2.4. MFEA
| Algorithm 1: MFEA |
| Input: pa, pb: two parent candidates randomly selected from pop. |
| Output: ca, cb: the offspring generated. |
| Begin |
| 1: If τa == τb or rand < rmp: |
| 2: pa and pb crossover and mutate to get ca and cb. |
| 3: If τa == τb: |
| 4: ca imitates pa. cb imitates pb. |
| 5: Else |
| 6: If rand < 0.5: |
| 7: ca imitates pa. cb imitates pb. |
| 8: Else |
| 9: ca imitates pb. cb imitates pa. |
| 10: End If |
| 11: End If |
| 12: Else |
| 13: pa undergoes polynomial mutation to produce offspring ca. |
|
14: pb undergoes polynomial mutation to produce offspring cb. 15: ca imitates pa. cb imitates pb. |
| 16: End If |
| End |
2.5. Related Work
3. BOMTEA
3.1. Motivation
3.2. The Adaptive Bi-Operator Strategy
| Algorithm 2: Adaptive Bi-operator Strategy |
| Input: p: a parent from target task. eopi: Random selection probability of ESOs. |
| Output: c: the offspring generated. |
| Begin |
| 1: If rand < eopi: |
| 2: Generate offspring c using DE/rand/1. |
| 3: Else |
| 4: Generate offspring c using GA. |
| 5: End If |
| End |
3.3. Knowledge Transfer
| Algorithm 3: Knowledge Transfer of GA |
| Input: pa: a parent from target task. pb: a parent randomly selected from source task. |
| Output: c: the offspring generated. |
| Begin |
| 1: pa and pb crossover and mutate to give offspring ca and cb. |
| 2: If rand < 0.5: |
| 3: c = ca |
| 4: Else |
| 5: c = cb |
| 6: End If |
| End |
| Algorithm 4: Knowledge Transfer of DE |
| Input: pt: a parent from target task. popt: the population of target task. pops: the population of source task. |
| Output: c: the offspring generated. |
| Begin |
| 1: Select one individual xr1 from popt randomly and xr1! = pt. |
| 2: Select two individuals xr2, xr3 from pops randomly and xr2! = xr3. |
| 3: According to Formula (1) to generate mutated individual vi. |
| 4: According to Formula (2) to generate offspring c. |
| End |
3.4. Framework
| Algorithm 5: BOMTEA |
| Begin |
|
1: Randomly initialize pop1 and pop2 for two tasks respectively. 2: Evaluate each individual on each optimization task. |
| 3: While FEs < maxFEs: |
| 4: For each individual from pop1 or pop2: |
| 5: Perform Algorithm 2 to allocate ESO. |
|
6: If rand < rmpi: 7: Perform knowledge transfer via Algorithm 3 or 4. |
| 8: Else |
| 9: Generate offspring via ESO. |
| 10: End If |
| 11: End For |
| 12: Select the fittest individuals to form the next pop1 or pop2. |
| 13: Get new eop1 and eop2 via the Formula (7). |
| 14: End While |
| End |
4. Experimental Studies
4.1. Experimental Setup
- SBX and polynomial mutation in MFEA, EMEA, MFEA-AKT, MTGA, RLMFEA and BOMTEA: ηc = 10, ηm = 5.
- DE in EMEA, RLMFEA, BOMTEA: F = 0.5, Cr = 0.6.
- The random mating probability: rmp = 0.3.
- The initial random selection probability of ESO: eop = 0.5.
- Population size: NP = 100 for MFEA, EMEA, MFEA-AKT, MTGA, RLMFEA and BOMTEA.
- Maximum number of fitness evaluations: MaxFEs = 100,000.
- The parameters for which values are not provided are set to the optimal settings specified in the respective papers.
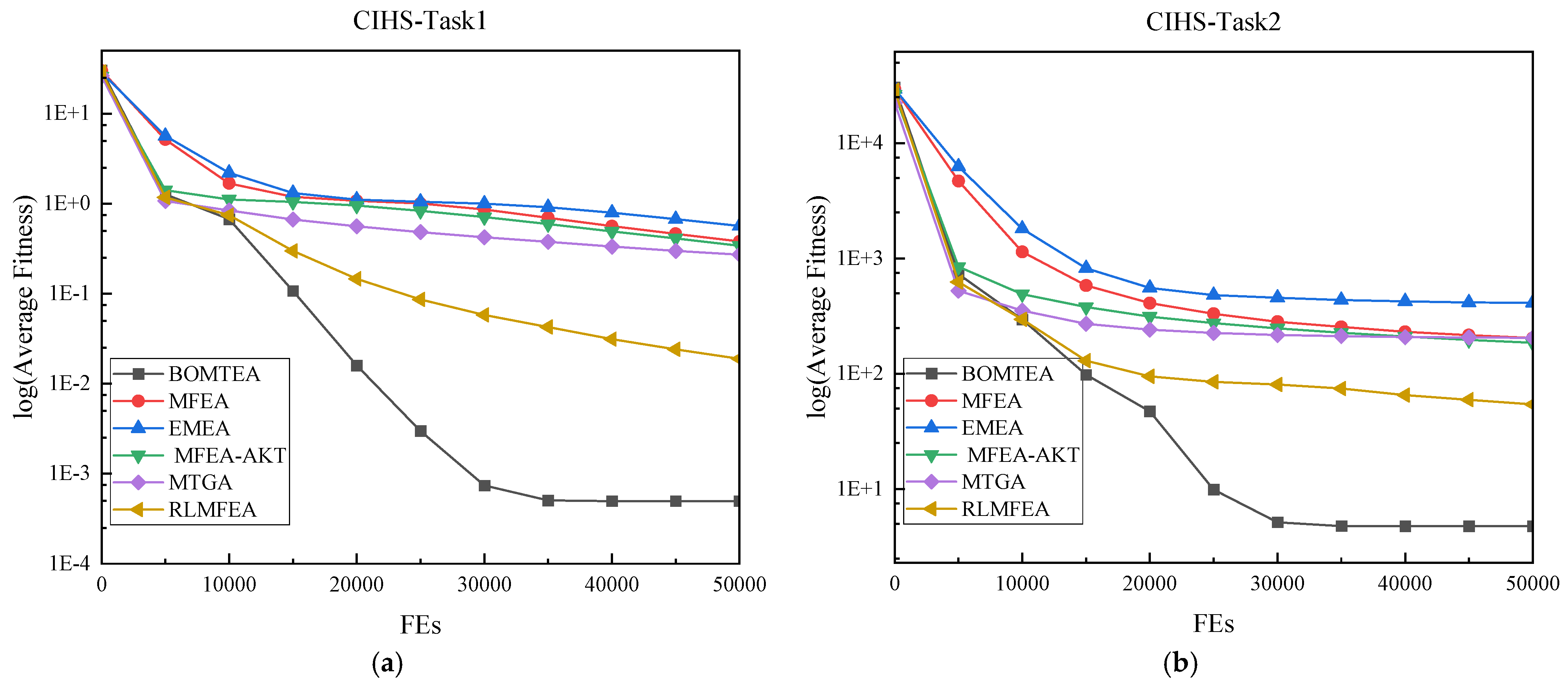
4.2. Experimental Results Comparisons on MTO Benchmarks
4.2.1. CEC17 MTO Benchmarks
4.2.2. CEC22 MTO Benchmarks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bao, X.; Wang, G.; Xu, L.; Wang, Z. Solving the Min-Max Clustered Traveling Salesmen Problem Based on Genetic Algorithm. Biomimetics 2023, 8, 238. [Google Scholar] [CrossRef] [PubMed]
- Poornima, B.S.; Sarris, I.E.; Chandan, K.; Nagaraja, K.V.; Kumar, R.V.; Ben Ahmed, S. Evolutionary Computing for the Radiative–Convective Heat Transfer of a Wetted Wavy Fin Using a Genetic Algorithm-Based Neural Network. Biomimetics 2023, 8, 574. [Google Scholar] [CrossRef] [PubMed]
- Yue, L.; Hu, P.; Zhu, J. Gender-Driven English Speech Emotion Recognition with Genetic Algorithm. Biomimetics 2024, 9, 360. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.-J.; Zhan, Z.-H.; Kwong, S.; Jin, H.; Zhang, J. Adaptive Granularity Learning Distributed Particle Swarm Optimization for Large-Scale Optimization. IEEE Trans. Cybern. 2021, 51, 1175–1188. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, J.; Chen, Y.; Xue, X.; Sun, S. Binary Restructuring Particle Swarm Optimization and Its Application. Biomimetics 2023, 8, 266. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Cao, L.; Chen, Y.; Chen, B.; Yue, Y. Solving Engineering Optimization Problems Based on Multi-Strategy Particle Swarm Optimization Hybrid Dandelion Optimization Algorithm. Biomimetics 2024, 9, 298. [Google Scholar] [CrossRef]
- Zhan, Z.-H.; Wang, Z.-J.; Jin, H.; Zhang, J. Adaptive Distributed Differential Evolution. IEEE Trans. Cybern. 2019, 50, 4633–4647. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, Y.; Meng, K.; Zhu, Z. Otsu Multi-Threshold Image Segmentation Based on Adaptive Double-Mutation Differential Evolution. Biomimetics 2023, 8, 418. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.-J.; Zhan, Z.-H.; Li, Y.; Kwong, S.; Jeon, S.-W.; Zhang, J. Fitness and Distance Based Local Search With Adaptive Differential Evolution for Multimodal Optimization Problems. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 684–699. [Google Scholar] [CrossRef]
- Zhan, Z.-H.; Zhang, J.; Lin, Y.; Li, J.-Y.; Huang, T.; Guo, X.-Q.; Wei, F.-F.; Kwong, S.; Zhang, X.-Y.; You, R. Matrix-Based Evolutionary Computation. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 6, 315–328. [Google Scholar] [CrossRef]
- Zhan, Z.-H.; Li, J.-Y.; Kwong, S.; Zhang, J. Learning-Aided Evolution for Optimization. IEEE Trans. Evol. Comput. 2023, 27, 1794–1808. [Google Scholar] [CrossRef]
- Wang, Z.-J.; Zhan, Z.-H.; Lin, Y.; Yu, W.-J.; Yuan, H.-Q.; Gu, T.-L.; Kwong, S.; Zhang, J. Dual-Strategy Differential Evolution With Affinity Propagation Clustering for Multimodal Optimization Problems. IEEE Trans. Evol. Comput. 2018, 22, 894–908. [Google Scholar] [CrossRef]
- Li, X.; Li, M.; Yu, M.; Fan, Q. Fault Reconfiguration in Distribution Networks Based on Improved Discrete Multimodal Multi-Objective Particle Swarm Optimization Algorithm. Biomimetics 2023, 8, 431. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.-B.; Wang, Z.-J.; Zhang, Y.-H.; Wang, Y.-G.; Kwong, S.; Zhang, J. Wireless Sensor Networks-Based Adaptive Differential Evolution for Multimodal Optimization Problems. Appl. Soft Comput. 2024, 158, 111541. [Google Scholar] [CrossRef]
- Wang, Z.-J.; Yang, Q.; Zhang, Y.-H.; Chen, S.-H.; Wang, Y.-G. Superiority Combination Learning Distributed Particle Swarm Optimization for Large-Scale Optimization. Appl. Soft Comput. 2023, 136, 110101. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Z.-J.; Wang, Y.-G.; Kwong, S.; Zhang, J. Bi-Directional Learning Particle Swarm Optimization for Large-Scale Optimization. Appl. Soft Comput. 2023, 149, 110990. [Google Scholar] [CrossRef]
- Zhan, Z.-H.; Li, J.; Cao, J.; Zhang, J.; Chung, H.S.-H.; Shi, Y.-H. Multiple Populations for Multiple Objectives: A Coevolutionary Technique for Solving Multiobjective Optimization Problems. IEEE Trans. Cybern. 2013, 43, 445–463. [Google Scholar] [CrossRef]
- Han, J.; Watanabe, S. A New Hyper-Heuristic Multi-Objective Optimisation Approach Based on MOEA/D Framework. Biomimetics 2023, 8, 521. [Google Scholar] [CrossRef]
- Gupta, A.; Zhou, L.; Ong, Y.-S.; Chen, Z.; Hou, Y. Half a Dozen Real-World Applications of Evolutionary Multitasking, and More. IEEE Comput. Intell. Mag. 2022, 17, 49–66. [Google Scholar] [CrossRef]
- Azad, A.S.; Islam, M.; Chakraborty, S. A Heuristic Initialized Stochastic Memetic Algorithm for MDPVRP With Interdependent Depot Operations. IEEE Trans. Cybern. 2017, 47, 4302–4315. [Google Scholar] [CrossRef] [PubMed]
- Ponsich, A.; Jaimes, A.L.; Coello, C.A.C. A Survey on Multiobjective Evolutionary Algorithms for the Solution of the Portfolio Optimization Problem and Other Finance and Economics Applications. IEEE Trans. Evol. Comput. 2013, 17, 321–344. [Google Scholar] [CrossRef]
- Xiong, J.; Liu, J.; Chen, Y.; Abbass, H.A. A Knowledge-Based Evolutionary Multiobjective Approach for Stochastic Extended Resource Investment Project Scheduling Problems. IEEE Trans. Evol. Comput. 2014, 18, 742–763. [Google Scholar] [CrossRef]
- McDonnell, J.R.; Reynolds, R.G.; Fogel, D.B. Special Session on Applications of Evolutionary Computation to Biology and Biochemistry. In Evolutionary Programming IV: Proceedings of the Fourth Annual Conference on Evolutionary Programming; MIT Press: Cambridge, MA, USA, 1995; p. 545. ISBN 978-0-262-29092-0. [Google Scholar]
- Chen, Z.-G.; Zhan, Z.-H.; Kwong, S.; Zhang, J. Evolutionary Computation for Intelligent Transportation in Smart Cities: A Survey [Review Article]. IEEE Comput. Intell. Mag. 2022, 17, 83–102. [Google Scholar] [CrossRef]
- Zhan, Z.-H.; Li, J.-Y.; Zhang, J. Evolutionary Deep Learning: A Survey. Neurocomputing 2022, 483, 42–58. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M.; Tan, K.C. Surrogate-Assisted Evolutionary Multitask Genetic Programming for Dynamic Flexible Job Shop Scheduling. IEEE Trans. Evol. Comput. 2021, 25, 651–665. [Google Scholar] [CrossRef]
- Feng, L.; Huang, Y.; Zhou, L.; Zhong, J.; Gupta, A.; Tang, K.; Tan, K.C. Explicit Evolutionary Multitasking for Combinatorial Optimization: A Case Study on Capacitated Vehicle Routing Problem. IEEE Trans. Cybern. 2021, 51, 3143–3156. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, T.; Peng, X. MFEA-IG: A Multi-Task Algorithm for Mobile Agents Path Planning. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Tan, K.C.; Feng, L.; Jiang, M. Evolutionary Transfer Optimization—A New Frontier in Evolutionary Computation Research. IEEE Comput. Intell. Mag. 2021, 16, 22–33. [Google Scholar] [CrossRef]
- Gupta, A.; Ong, Y.-S.; Feng, L. Multifactorial Evolution: Toward Evolutionary Multitasking. IEEE Trans. Evol. Comput. 2016, 20, 343–357. [Google Scholar] [CrossRef]
- Bali, K.K.; Ong, Y.-S.; Gupta, A.; Tan, P.S. Multifactorial Evolutionary Algorithm With Online Transfer Parameter Estimation: MFEA-II. IEEE Trans. Evol. Comput. 2020, 24, 69–83. [Google Scholar] [CrossRef]
- Wu, D.; Tan, X. Multitasking Genetic Algorithm (MTGA) for Fuzzy System Optimization. IEEE Trans. Fuzzy Syst. 2020, 28, 1050–1061. [Google Scholar] [CrossRef]
- Feng, L.; Zhou, W.; Zhou, L.; Jiang, S.W.; Zhong, J.H.; Da, B.S.; Zhu, Z.X.; Wang, Y. An Empirical Study of Multifactorial PSO and Multifactorial DE. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 921–928. [Google Scholar]
- Wang, X.; Kang, Q.; Zhou, M.; Yao, S.; Abusorrah, A. Domain Adaptation Multitask Optimization. IEEE Trans. Cybern. 2023, 53, 4567–4578. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Zhan, Z.-H.; Tan, K.C.; Zhang, J. Block-Level Knowledge Transfer for Evolutionary Multitask Optimization. IEEE Trans. Cybern. 2023, 54, 558–571. [Google Scholar] [CrossRef] [PubMed]
- Da, B.; Ong, Y.-S.; Feng, L.; Qin, A.K.; Gupta, A.; Zhu, Z.; Ting, C.-K.; Tang, K.; Yao, X. Evolutionary Multitasking for Single-Objective Continuous Optimization: Benchmark Problems, Performance Metric, and Baseline Results. arXiv 2017, arXiv:1706.03470. [Google Scholar]
- Feng, L.; Zhou, L.; Zhong, J.; Gupta, A.; Ong, Y.-S.; Tan, K.-C.; Qin, A.K. Evolutionary Multitasking via Explicit Autoencoding. IEEE Trans. Cybern. 2019, 49, 3457–3470. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Wang, L.; Gu, Q. Evolutionary Multitasking via Reinforcement Learning. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 8, 762–775. [Google Scholar] [CrossRef]
- Wen, Y.-W.; Ting, C.-K. Parting Ways and Reallocating Resources in Evolutionary Multitasking. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 2404–2411. [Google Scholar]
- Zhou, L.; Feng, L.; Tan, K.C.; Zhong, J.; Zhu, Z.; Liu, K.; Chen, C. Toward Adaptive Knowledge Transfer in Multifactorial Evolutionary Computation. IEEE Trans. Cybern. 2021, 51, 2563–2576. [Google Scholar] [CrossRef]
- Liaw, R.-T.; Ting, C.-K. Evolutionary Many-Tasking Based on Biocoenosis through Symbiosis: A Framework and Benchmark Problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 2266–2273. [Google Scholar]
- Feng, L. IEEE CEC 2022 Competition on Evolutionary Multitask Optimization. Available online: http://www.bdsc.site/websites/MTO_competition_2021/MTO_Competition_WCCI_2022.html (accessed on 26 July 2024).
- Carrasco, J.; García, S.; Rueda, M.M.; Das, S.; Herrera, F. Recent Trends in the Use of Statistical Tests for Comparing Swarm and Evolutionary Computing Algorithms: Practical Guidelines and a Critical Review. Swarm Evol. Comput. 2020, 54, 100665. [Google Scholar] [CrossRef]
- Qu, B.Y.; Suganthan, P.N.; Das, S. A Distance-Based Locally Informed Particle Swarm Model for Multimodal Optimization. IEEE Trans. Evol. Comput. 2013, 17, 387–402. [Google Scholar] [CrossRef]
- Wang, Z.-J.; Zhou, Y.-R.; Zhang, J. Adaptive Estimation Distribution Distributed Differential Evolution for Multimodal Optimization Problems. IEEE Trans. Cybern. 2022, 52, 6059–6070. [Google Scholar] [CrossRef]
- Wang, Z.-J.; Zhan, Z.-H.; Lin, Y.; Yu, W.-J.; Wang, H.; Kwong, S.; Zhang, J. Automatic Niching Differential Evolution With Contour Prediction Approach for Multimodal Optimization Problems. IEEE Trans. Evol. Comput. 2020, 24, 114–128. [Google Scholar] [CrossRef]
- Binh, H.T.T.; Ngo, S.H. Survivable Flows Routing in Large Scale Network Design Using Genetic Algorithm. In Advances in Computer Science and Its Applications; Jeong, H.Y., Obaidat, M.S., Yen, N.Y., Park, J.J., Eds.; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2014; Volume 279, pp. 345–351. ISBN 978-3-642-41673-6. [Google Scholar]
- Wang, Z.-J.; Zhan, Z.-H.; Yu, W.-J.; Lin, Y.; Zhang, J.; Gu, T.-L.; Zhang, J. Dynamic Group Learning Distributed Particle Swarm Optimization for Large-Scale Optimization and Its Application in Cloud Workflow Scheduling. IEEE Trans. Cybern. 2020, 50, 2715–2729. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.-J.; Jian, J.-R.; Zhan, Z.-H.; Li, Y.; Kwong, S.; Zhang, J. Gene Targeting Differential Evolution: A Simple and Efficient Method for Large-Scale Optimization. IEEE Trans. Evol. Comput. 2023, 27, 964–979. [Google Scholar] [CrossRef]



| Question | BOMTEA | MFEA | EMEA | MFEA-AKT | MTGA | RLMFEA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Task1 | Task2 | Task1 | Task2 | Task1 | Task2 | Task1 | Task2 | Task1 | Task2 | Task1 | Task2 | |
| CIHS | 4.97e−04 | 4.78e+00 | 3.80e−01 (+) | 2.04e+02 (+) | 5.66e−01 (+) | 4.13e+02 (+) | 3.42e−01 (+) | 1.86e+02 (+) | 2.72e−01 (+) | 2.05e+02 (+) | 1.89e−02 (+) | 5.42e+01 (+) |
| CIMS | 3.69e−01 | 1.72e+01 | 5.67e+00 (+) | 2.71e+02 (+) | 3.70e+00 (+) | 4.14e+02 (+) | 5.57e+00 (+) | 2.54e+02 (+) | 3.21e+00(+) | 2.36e+02 (+) | 2.32e+00 (+) | 8.61e+01 (+) |
| CILS | 2.01e+01 | 4.37e+03 | 2.02e+01 (+) | 4.04e+03 (−) | 2.05e+01 (+) | 1.21e+04 (+) | 2.02e+01 (+) | 3.85e+03 (−) | 2.00e+01 (−) | 4.11e+03 (≈) | 2.01e+01 (≈) | 3.24e+03 (−) |
| PIHS | 2.01e+02 | 1.37e−03 | 6.50e+02 (+) | 1.18e+01 (+) | 9.92e+02 (+) | 3.43e−01 (+) | 5.17e+02 (+) | 9.07e+00 (+) | 2.24e+02 (≈) | 3.09e+00 (+) | 2.37e+02 (+) | 2.96e−02 (+) |
| PIMS | 3.48e−01 | 9.15e+01 | 3.85e+00 (+) | 8.16e+02 (+) | 3.63e+00 (+) | 3.19e+02 (+) | 3.02e+00 (+) | 3.74e+02 (+) | 3.28e+00 (+) | 5.14e+02 (+) | 1.54e+00 (+) | 1.35e+02 (+) |
| PILS | 1.42e+00 | 2.13e+00 | 2.00e+01 (+) | 2.16e+01 (+) | 1.78e+01 (+) | 1.71e−01 (−) | 5.41e+00 (+) | 5.81e+00 (+) | 3.06e+00 (+) | 5.72e+00 (+) | 2.68e+00 (+) | 3.21e+00 (+) |
| NIHS | 1.50e+02 | 1.21e+02 | 7.68e+02 (+) | 2.71e+02 (+) | 6.37e+02 (+) | 4.16e+02 (+) | 5.18e+02 (+) | 2.20e+02 (+) | 5.68e+02 (+) | 1.98e+02 (+) | 2.12e+02 (+) | 1.16e+02 (≈) |
| NIMS | 2.80e−03 | 1.61e+01 | 4.17e−01 (+) | 2.73e+01 (+) | 7.31e−01 (+) | 1.20e+01 (−) | 4.13e−01 (+) | 2.42e+01 (+) | 3.79e−01 (+) | 1.54e+01 (≈) | 4.27e−02 (+) | 1.99e+01 (+) |
| NILS | 2.04e+02 | 4.33e+03 | 6.27e+02 (+) | 3.77e+03 (−) | 1.32e+03 (+) | 1.21e+04 (+) | 7.03e+02 (+) | 3.90e+03 (−) | 3.44e+02 (+) | 4.36e+03 (≈) | 2.89e+02 (+) | 3.23e+03 (−) |
| P1 | 6.34e+02 | 6.34e+02 | 6.51e+02 (+) | 6.53e+02 (+) | 6.29e+02 (−) | 6.18e+02 (−) | 6.32e+02 (≈) | 6.32e+02 (−) | 6.18e+02 (−) | 6.19e+02 (−) | 6.30e+02 (−) | 6.32e+02 (≈) |
| P2 | 7.00e+02 | 7.00e+02 | 7.01e+02 (+) | 7.01e+02 (+) | 7.05e+02 (+) | 7.01e+02 (+) | 7.01e+02 (+) | 7.01e+02 (+) | 7.01e+02 (+) | 7.00e+02 (+) | 7.00e+02 (+) | 7.00e+02 (+) |
| P3 | 1.43e+06 | 1.59e+06 | 4.18e+06 (+) | 3.63e+06 (+) | 3.23e+06 (+) | 6.33e+07 (+) | 1.22e+06 (≈) | 1.25e+06 (≈) | 3.06e+06 (+) | 2.84e+06 (+) | 1.60e+06 (≈) | 1.54e+06 (≈) |
| P4 | 1.30e+03 | 1.30e+03 | 1.30e+03 (+) | 1.30e+03 (+) | 1.30e+03 (+) | 1.30e+03 (+) | 1.30e+03 (+) | 1.30e+03 (≈) | 1.30e+03 (−) | 1.30e+03 (−) | 1.30e+03 (≈) | 1.30e+03 (≈) |
| P5 | 1.52e+03 | 1.52e+03 | 1.56e+03 (+) | 1.55e+03 (+) | 1.79e+03 (+) | 1.54e+03 (+) | 1.56e+03 (+) | 1.55e+03 (+) | 1.53e+03 (+) | 1.53e+03 (+) | 1.53e+03 (+) | 1.53e+03 (+) |
| P6 | 1.12e+06 | 7.34e+05 | 1.90e+06 (+) | 1.60e+06 (+) | 1.82e+06 (+) | 2.66e+07 (+) | 1.76e+06 (+) | 1.57e+06 (+) | 1.23e+06 (≈) | 1.20e+06 (+) | 9.38e+05 (≈) | 9.66e+05 (≈) |
| P7 | 3.18e+03 | 3.19e+03 | 3.52e+03 (+) | 3.52e+03 (+) | 3.41e+03 (+) | 4.64e+03 (+) | 3.23e+03 (≈) | 3.41e+03 (+) | 3.08e+03 (≈) | 3.11e+03 (≈) | 3.19e+03 (≈) | 3.20e+03 (≈) |
| P8 | 5.20e+02 | 5.20e+02 | 5.20e+02 (+) | 5.20e+02 (+) | 5.21e+02 (+) | 5.21e+02 (+) | 5.20e+02 (+) | 5.20e+02 (+) | 5.21e+02 (+) | 5.21e+02 (+) | 5.20e+02 (≈) | 5.20e+02 (+) |
| P9 | 7.56e+03 | 1.62e+03 | 8.10e+03 (+) | 1.62e+03 (+) | 8.62e+03 (+) | 1.62e+03 (+) | 7.82e+03 (≈) | 1.62e+03 (+) | 7.96e+03 (+) | 1.62e+03 (−) | 7.87e+03 (≈) | 1.62e+03 (≈) |
| P10 | 3.26e+04 | 2.14e+06 | 2.95e+04 (≈) | 2.63e+06 (≈) | 3.65e+04 (≈) | 2.57e+07 (+) | 2.72e+04 (≈) | 3.11e+06 (+) | 2.05e+04 (−) | 2.14e+06 (≈) | 3.12e+04 (≈) | 2.06e+06 (≈) |
| Number of +/≈/− | 18/1/0 | 16/1/2 | 17/1/1 | 16/0/3 | 14/5/0 | 14/2/3 | 12/3/4 | 11/5/3 | 10/8/1 | 9/8/2 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wang, Z.; Kou, Z. Adaptive Bi-Operator Evolution for Multitasking Optimization Problems. Biomimetics 2024, 9, 604. https://doi.org/10.3390/biomimetics9100604
Wang C, Wang Z, Kou Z. Adaptive Bi-Operator Evolution for Multitasking Optimization Problems. Biomimetics. 2024; 9(10):604. https://doi.org/10.3390/biomimetics9100604
Chicago/Turabian StyleWang, Changlong, Zijia Wang, and Zheng Kou. 2024. "Adaptive Bi-Operator Evolution for Multitasking Optimization Problems" Biomimetics 9, no. 10: 604. https://doi.org/10.3390/biomimetics9100604
APA StyleWang, C., Wang, Z., & Kou, Z. (2024). Adaptive Bi-Operator Evolution for Multitasking Optimization Problems. Biomimetics, 9(10), 604. https://doi.org/10.3390/biomimetics9100604








