Active Vibration Control and Parameter Optimization of Genetic Algorithm for Partially Damped Composites Beams
Abstract
1. Introduction
2. Finite Element Modeling
2.1. Basic Assumptions of the Model
- (1)
- The foundation beam layer and piezoelectric constraint layer can be regarded as the Euler-Bernoulli beam.
- (2)
- The layers are fully bonded without relative displacement.
- (3)
- The material density of each layer is uniform, which conforms to the basic assumption of material mechanics.
- (4)
- The influence of the moment of inertia of each layer is ignored in the analysis.
- (5)
- Regardless of the compression deformation in the Z direction, the transverse displacement (deflection) ω of the three layers is the same.
- (6)
- The viscoelastic damping coefficient is only discussed in viscoelastic linear theory.
- (7)
- The piezoelectric force applied on the damping sandwich beam is uniformly distributed in the element.
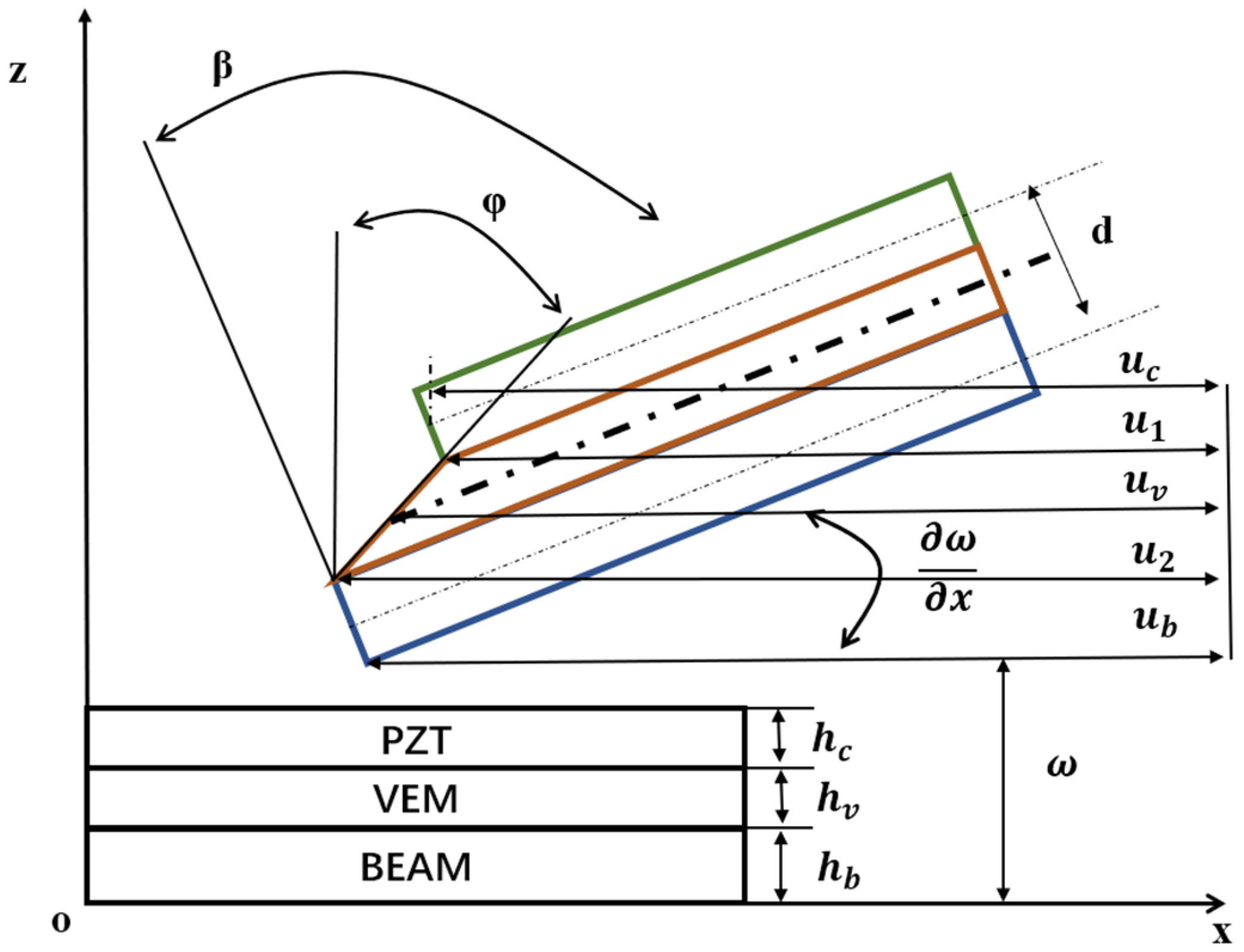
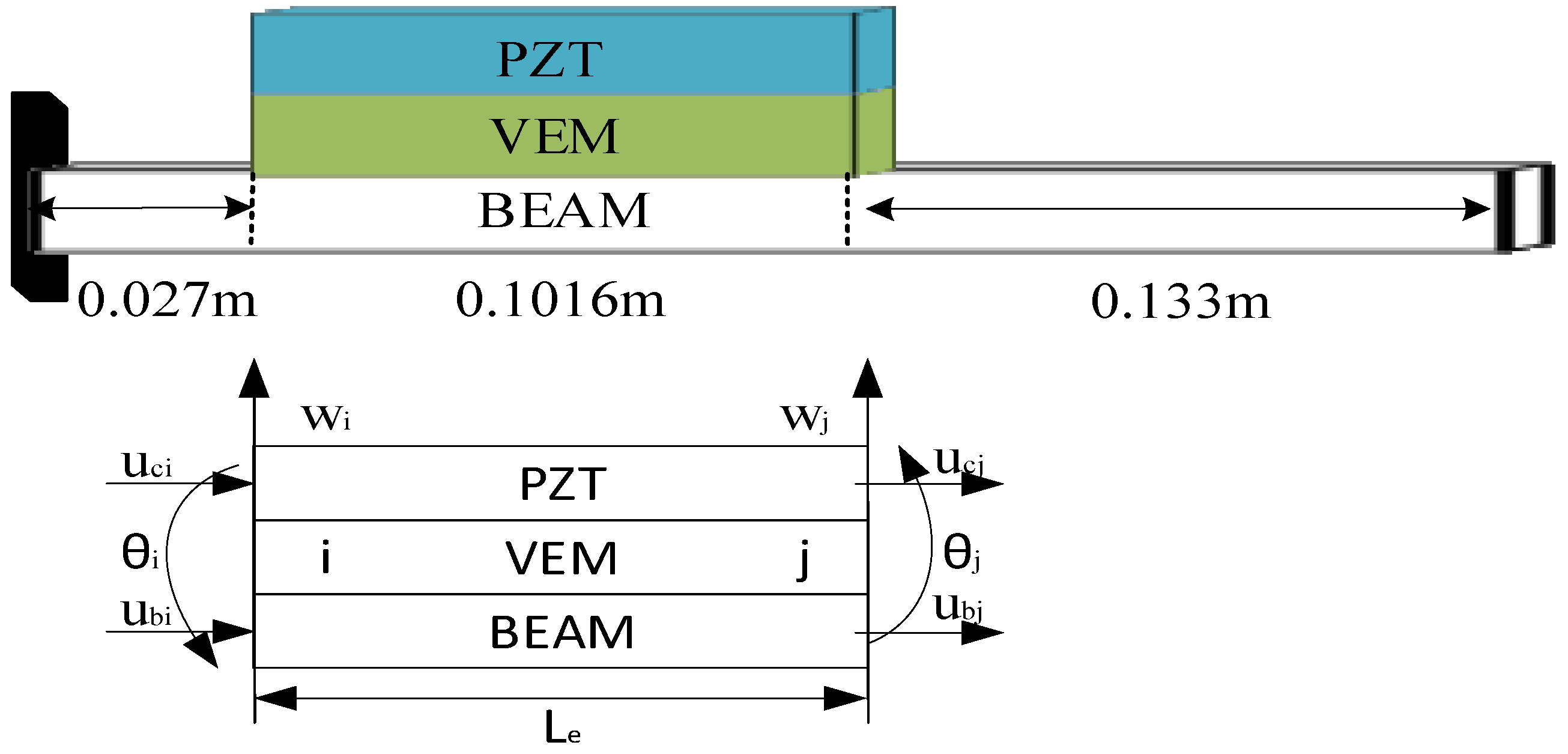
2.2. Geometric Deformation Relationships and Finite Element Elements
2.3. Kinetic Equation
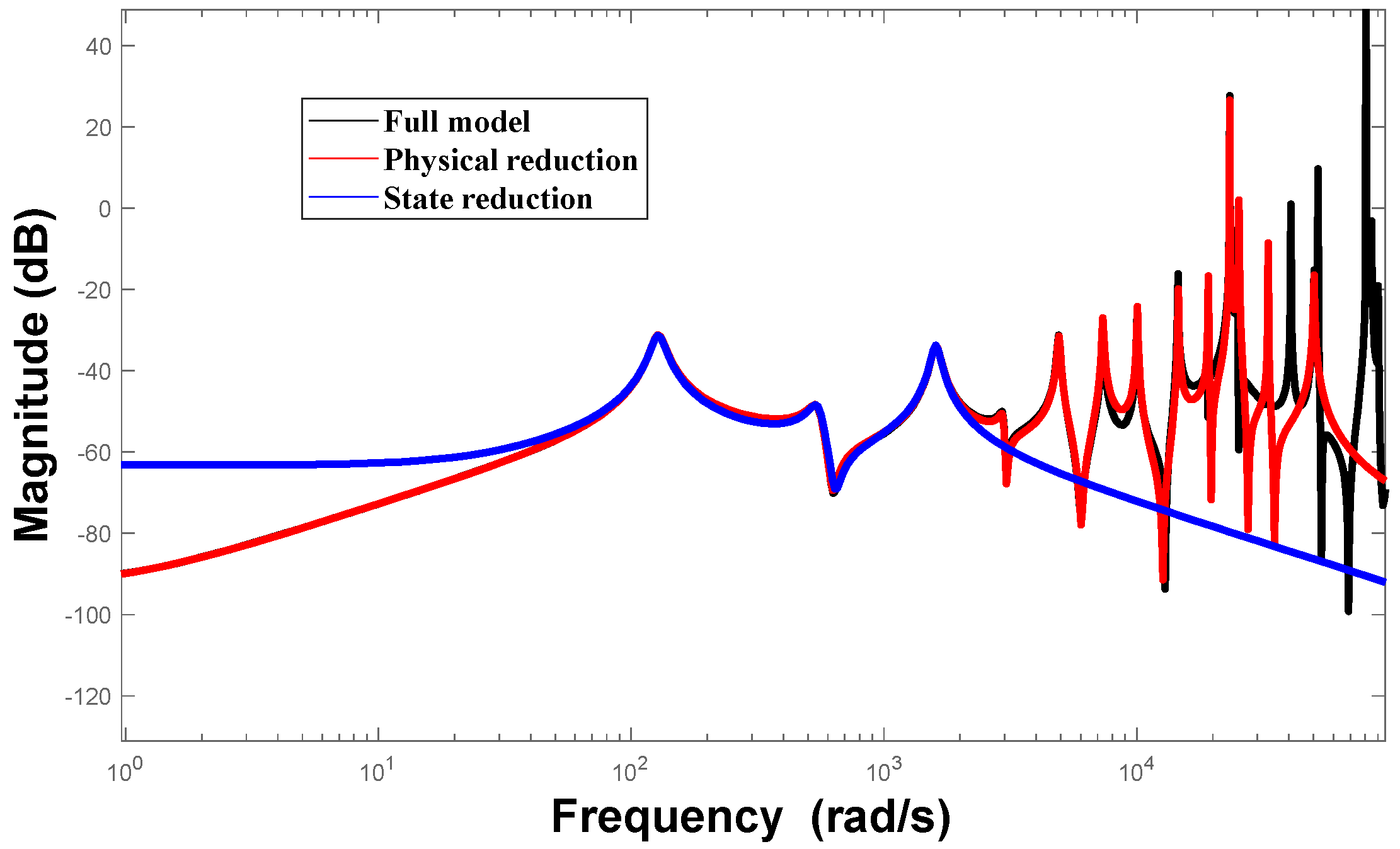
2.4. Model Downgrading
2.4.1. Dynamic Condensation in Physical Space
2.4.2. Modal Decoupling in State Space
3. Active Control
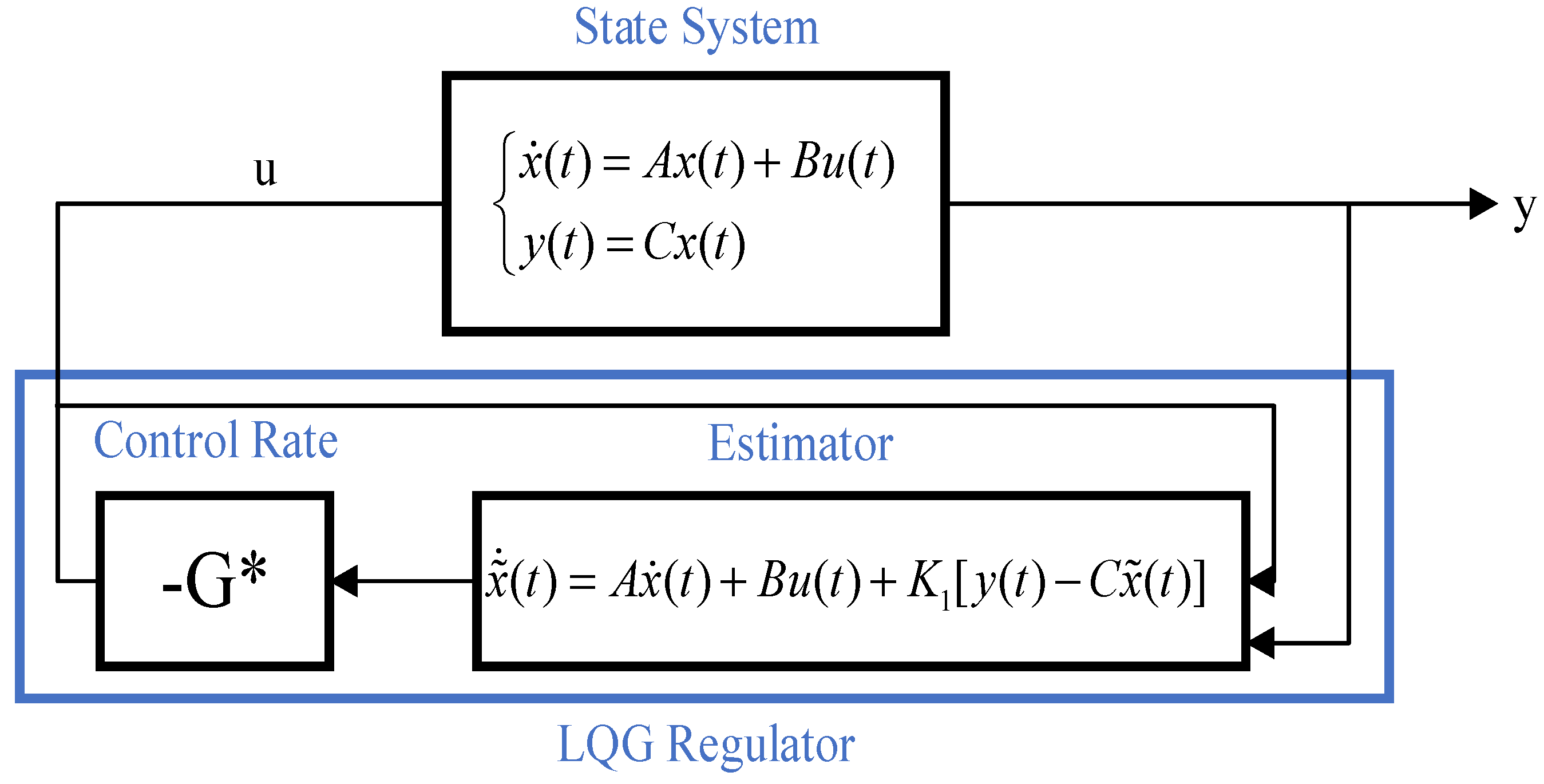
3.1. Linear–Quadratic–Regulator Control
3.2. Kalman Filter and Linear–Quadratic–Gaussian Control
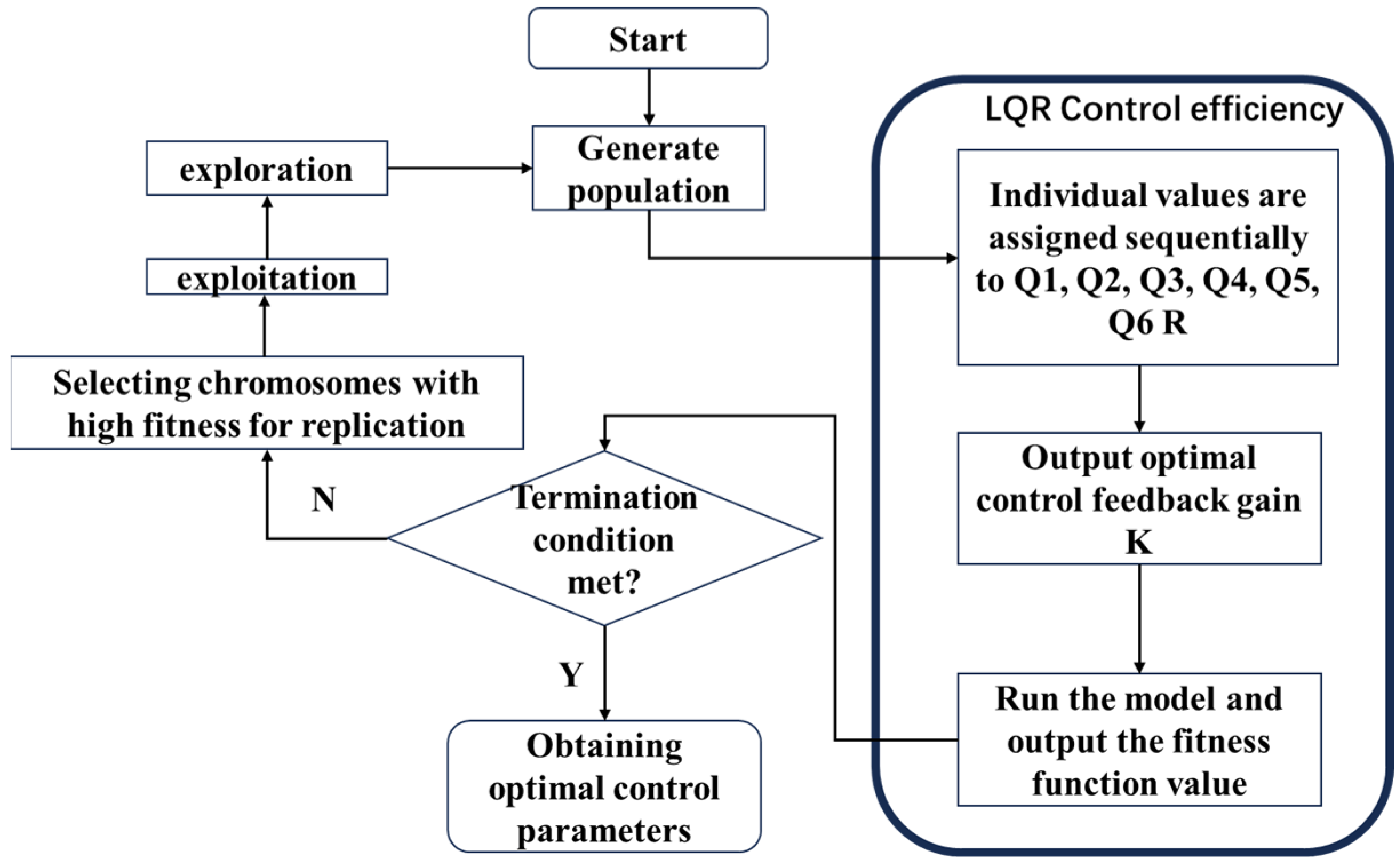
3.3. Genetic Algorithm Optimization Control Parameter Model
4. Numerical Validation and Analysis
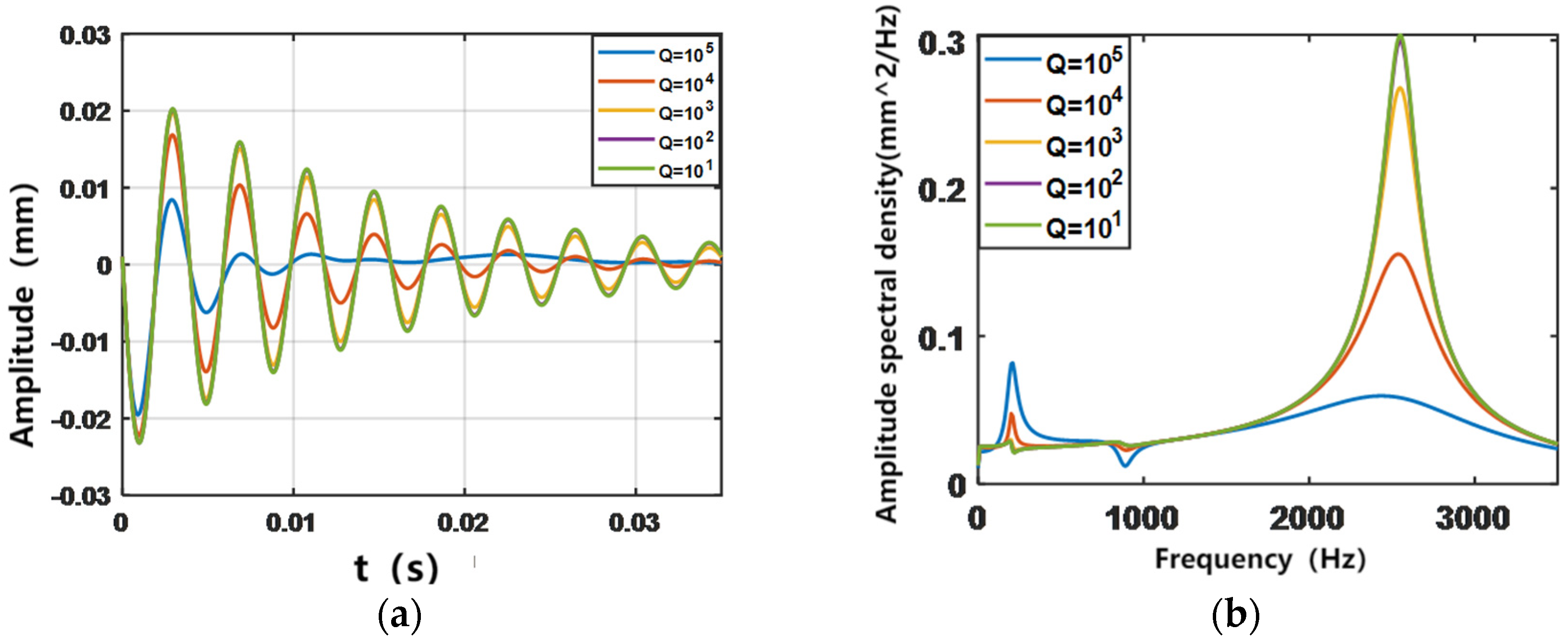
4.1. LQR Parameter Selection
4.2. Model Validation
4.3. Model Reduction
4.4. Vibration Analysis
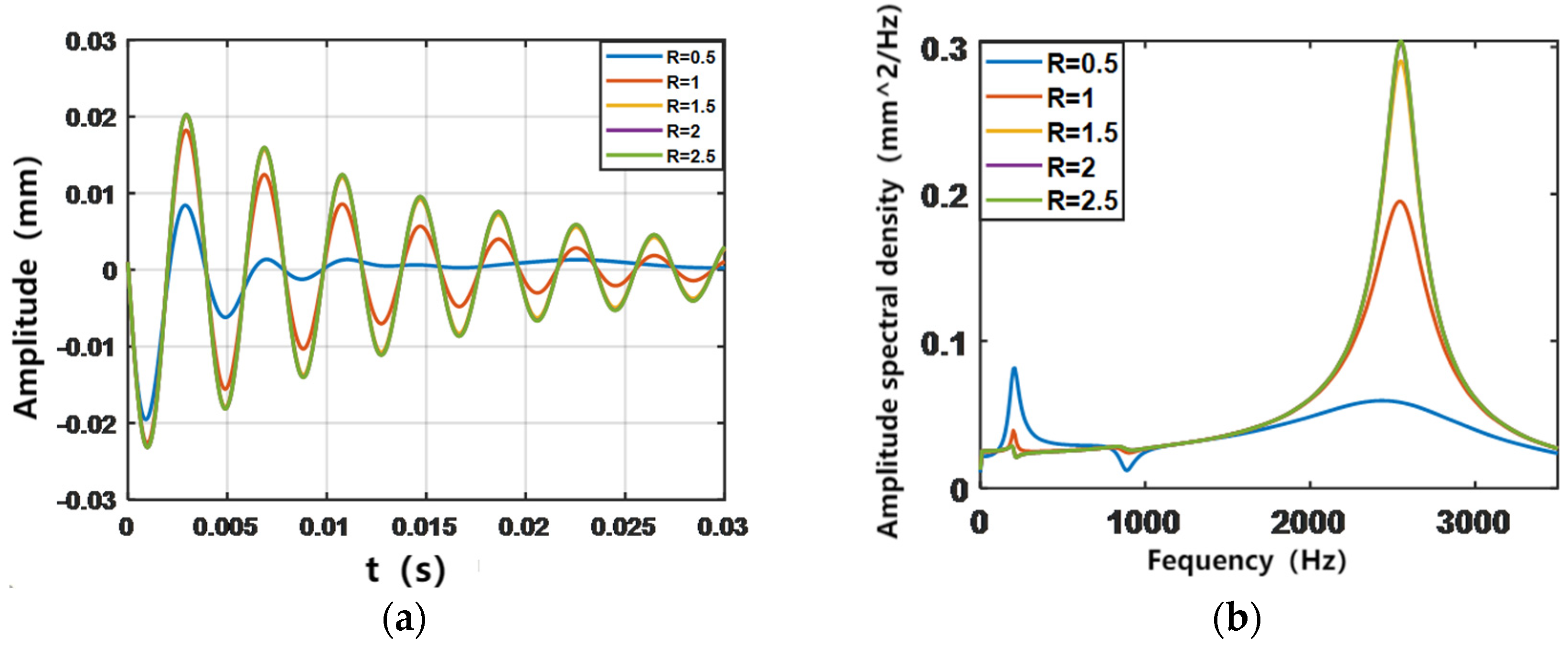
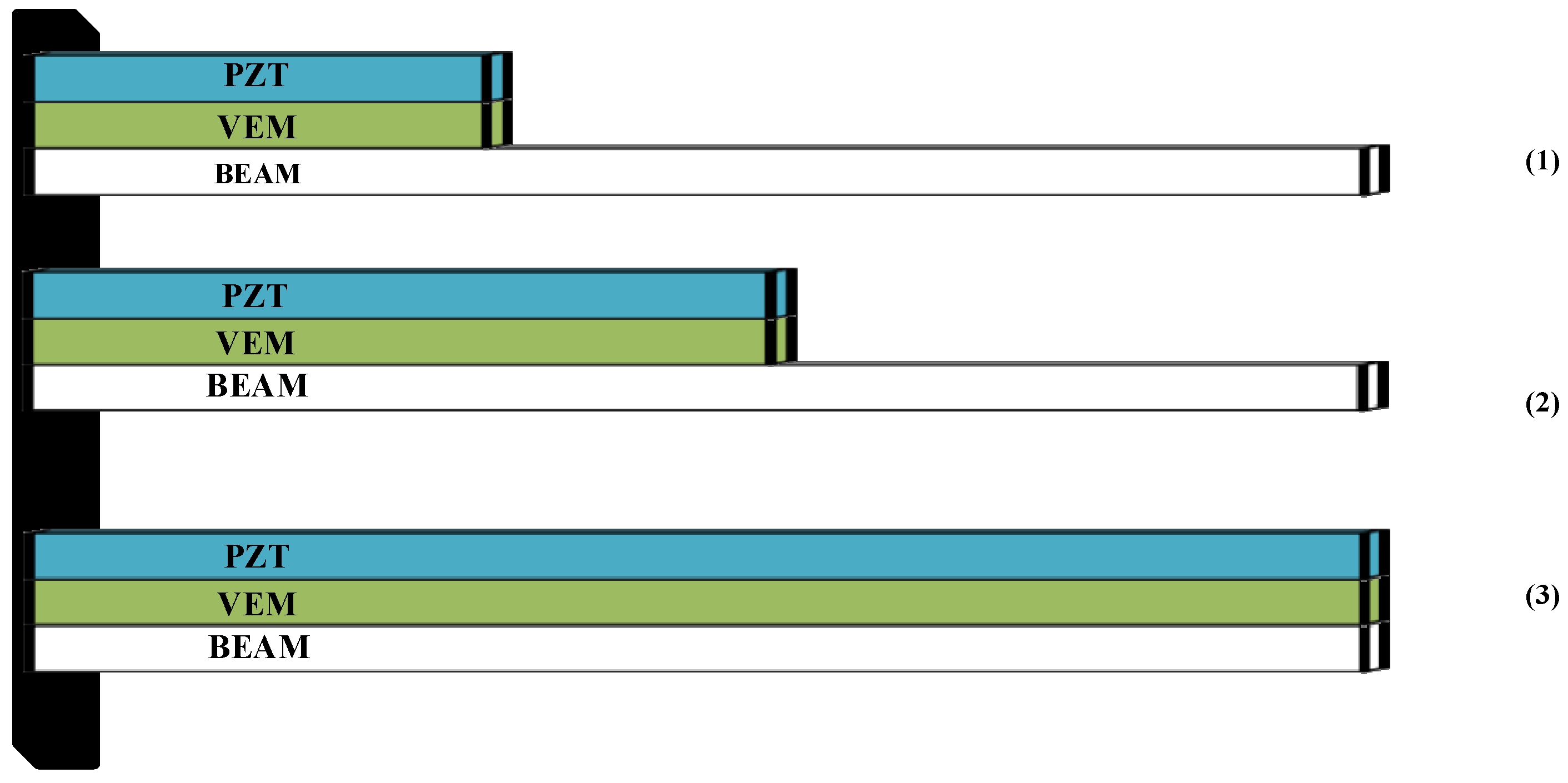
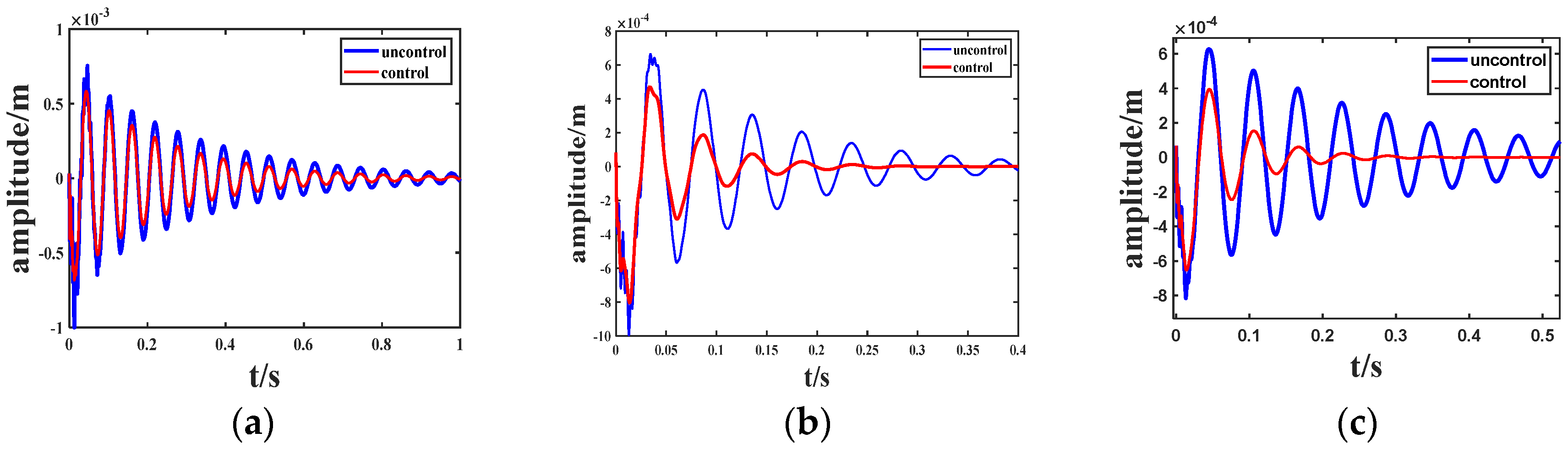
4.4.1. Vibration Analysis with Different Coverage
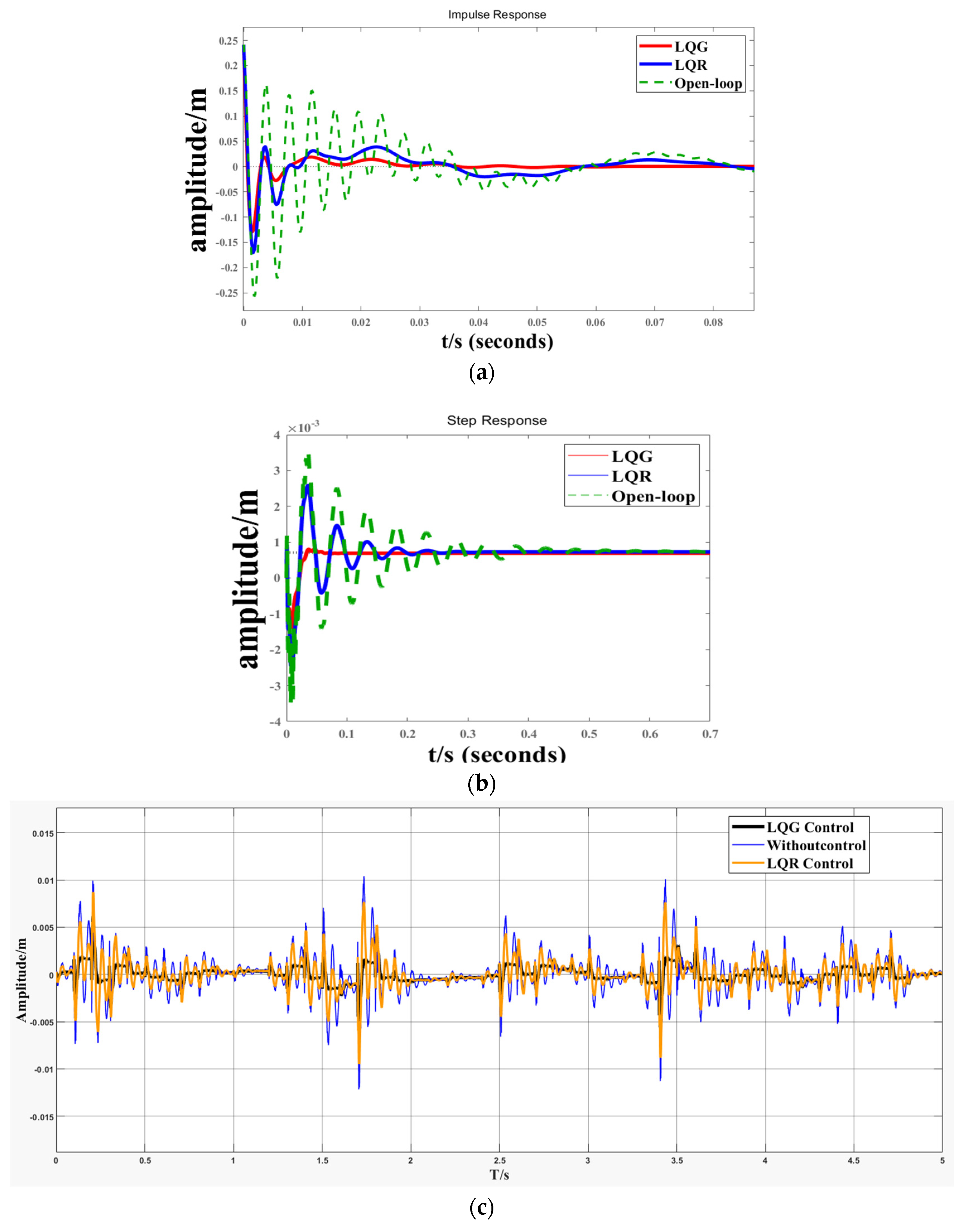
4.4.2. Comparison of LQR and LQG Control Effects
4.5. Genetic Algorithm Optimization of Control Parameters
5. Conclusions
- The combined finite element and GHM model for the cantilever beam demonstrates improved accuracy and reduced degrees of freedom compared to the existing literature. The joint reduction of physical and state spaces proves accurate and effective, particularly in preserving the initial modal characteristics. This reduced-order processing is useful in the aerospace and automotive fields to reduce the computational burden in the design of complex systems while ensuring model accuracy. For instance, the structural vibration control of an aircraft wing or an automobile body can be optimized with the help of this method to ensure high stability and safety even at high speeds.
- Increasing the ACLD patch coverage improves the passive seismic performance of the cantilever beam. However, in active control, full coverage may not always be the optimal choice. When compared to active control, a 4/7 L coverage rate for structure (2) results in a 0.05 s reduction in control time compared to full coverage. In reality, especially in the seismic design of bridges and high-rise buildings, this finding informs the economy of the control system, reducing materials while still achieving the desired control.
- By utilizing the Kalman filter, the LQG controller can significantly reduce noise and interference, leading to improved response speed and accuracy of the control system. Compared to traditional LQR control, the maximum amplitude can be reduced by 31.1%. Additionally, the LQG controller effectively suppresses periodic signals like Gaussian white noise, indicating that linear–quadratic–Gaussian control is more efficient for structures exposed to random excitation environments. However, the effect on single pulse signals is not as noticeable.
- By optimizing the weighted parameters of the controller through the genetic algorithm, the active control effect has significantly improved. The optimized parameters better meet the system’s control requirements and tracking accuracy. Compared to manual parameter tuning methods, genetic algorithms can more quickly find the optimal solution. This is important in areas such as drones and autonomous vehicles, where the requirements for real-time control systems are very high. Genetic Algorithms can quickly find the optimal control parameters to ensure that the system can still maintain stable control accuracy and response speed in complex environments.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, N.; Singh, S.P. Vibration and damping characteristics of beams with active constrained layer treatments under parametric variations. Mater. Des. 2009, 30, 4162–4174. [Google Scholar] [CrossRef]
- Yang, C.; Jin, G.; Liu, Z.; Wang, X.; Miao, X. Vibration and damping analysis of thick sandwich cylindrical shells with a viscoelastic core under arbitrary boundary conditions. Int. J. Mech. Sci. 2015, 92, 162–177. [Google Scholar] [CrossRef]
- Balamurugan, V.; Narayanan, S. Finite element formulation and active vibration control study on beams using smart constrained layer damping (SCLD) treatment. J. Sound Vib. 2002, 249, 227–250. [Google Scholar] [CrossRef]
- Zheng, H.; Tan, X.M.; Cai, C. Damping analysis of beams covered with multiple PCLD patches. Int. J. Mech. Sci. 2006, 48, 1371–1383. [Google Scholar] [CrossRef]
- Guo, Y.; Li, L.; Zhang, D. Dynamic modeling and vibration analysis of rotating beams with active constrained layer damping treatment in temperature field. Compos. Struct. 2019, 226, 111217. [Google Scholar] [CrossRef]
- Jiang, F.; Li, L.; Liao, W.-H.; Zhang, D. Vibration control of a rotating hub-plate with enhanced active constrained layer damping treatment. Aerosp. Sci. Technol. 2021, 118, 107081. [Google Scholar] [CrossRef]
- Xu, K.; Chen, Z.; Sun, W. Optimization of position, size and thickness of viscoelastic damping patch for vibration reduction of a cylindrical shell structure. Compos. Struct. 2021, 276, 114573. [Google Scholar] [CrossRef]
- Baz, A.; Poh, S. Performance of an active control system with piezoelectric actuators. J. Sound Vib. 1988, 126, 327–343. [Google Scholar] [CrossRef]
- Shi, Y.M.; Li, Z.F.; Hua, H.X.; Fu, Z.F.; Liu, T.X. The modelling and vibration control of beams with active constrained layer damping. J. Sound Vib. 2001, 245, 785–800. [Google Scholar] [CrossRef]
- Li, M.; Sun, W.; Liu, Y.; Ma, H. Influence analysis of control signal phase on the vibration reduction effect of active constrained layer damping. Appl. Acoust. 2022, 190, 108658. [Google Scholar] [CrossRef]
- Damanpack, A.R.; Bodaghi, M. A new sandwich element for modeling of partially delaminated sandwich beam structures. Compos. Struct. 2021, 256, 113068. [Google Scholar] [CrossRef]
- Damanpack, A.R.; Bodaghi, M.; Aghdam, M.M.; Shakeri, M. Active control of geometrically non-linear transient response of sandwich beams with a flexible core using piezoelectric patches. Compos. Struct. 2013, 100, 517–531. [Google Scholar] [CrossRef]
- Huang, Z.; Qin, Z.; Chu, F. A comparative study of finite element modeling techniques for dynamic analysis of elastic-viscoelastic-elastic sandwich structures. J. Sandw. Struct. Mater. 2016, 18, 531–551. [Google Scholar] [CrossRef]
- Huang, Z.; Qin, Z.; Chu, F. Damping mechanism of elastic–viscoelastic–elastic sandwich structures. Compos. Struct. 2016, 153, 96–107. [Google Scholar] [CrossRef]
- Gao, Y.S.; Zhang, S.Q.; Zhao, G.Z.; Schmidt, R. Numerical modeling for cantilever sandwich smart structures with partially covered constrained viscoelastic layer. Compos. Struct. 2022, 281, 114981. [Google Scholar] [CrossRef]
- Biglar, M.; Gromada, M.; Stachowicz, F.; Trzepieciński, T. Optimal configuration of piezoelectric sensors and actuators for active vibration control of a plate using a genetic algorithm. Acta Mech. 2015, 226, 3451–3462. [Google Scholar] [CrossRef]
- Huang, Z.; Huang, F.; Wang, X.; Chu, F. Active vibration control of composite cantilever beams. Materials 2022, 16, 95. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Shan, X.; Zhang, L.; Wang, G.; Fan, J. Research on identification and active vibration control of cantilever structure based on NARX neural network. Mech. Syst. Signal Process. 2022, 171, 108872. [Google Scholar] [CrossRef]
- Tian, J.; Guo, Q.; Shi, G. Laminated piezoelectric beam element for dynamic analysis of piezolaminated smart beams and GA-based LQR active vibration control. Compos. Struct. 2020, 252, 112480. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Inman, D.J. Active vibration control of flexible cantilever plates using piezoelectric materials and artificial neural networks. J. Sound Vib. 2016, 363, 33–53. [Google Scholar] [CrossRef]
- Chai, Y.-Y.; Song, Z.-G.; Li, F.-M. Active aerothermoelastic flutter suppression of composite laminated panels with time-dependent boundaries. Compos. Struct. 2017, 179, 61–76. [Google Scholar] [CrossRef]
- Liu, X.; Qin, J.; Zhao, K.; Featherston, C.A.; Kennedy, D.; Jing, Y.; Yang, G. Design optimization of laminated composite structures using artificial neural network and genetic algorithm. Compos. Struct. 2023, 305, 116500. [Google Scholar] [CrossRef]
- Zhang, D.; Zheng, L. Active vibration control of plate partly treated with ACLD using hybrid control. Int. J. Aerosp. Eng. 2014, 2014, 1–12. [Google Scholar] [CrossRef]
- Yaghoobi, S.; Fadali, M.S.; Pekcan, G. Performance-based active controller design for nonlinear structures using modified black hole optimization. J. Vib. Control. 2023, 30, 711–726. [Google Scholar] [CrossRef]
- Abhishek, S.; Chakraborty, S. The effect of an adaptive feedback-control system in the structural vibration control. J. Sound Vib. 2023, 548, 117501. [Google Scholar]
- Li, C.; Shen, L.; Shao, J.; Fang, J. Simulation and experiment of active vibration control based on flexible piezoelectric MFC composed of PZT and PI layer. Polymers 2023, 15, 1819. [Google Scholar] [CrossRef]
- Silva TM, P.; Hameury, C.; Ferrari, G.; Balasubramanian, P.; Franchini, G.; Amabili, M. Particle swarm optimization of a non-collocated MIMO PPF active vibration control of a composite sandwich plate. J. Sound Vib. 2023, 555, 117723. [Google Scholar] [CrossRef]
- Zghal, S.; Bouazizi, M.L.; Bouhaddi, N.; Nasri, R. Model reduction methods for viscoelastic sandwich structures in frequency and time domains. Finite Elem. Anal. Des. 2015, 93, 12–29. [Google Scholar] [CrossRef]
- Huang, Z.; Peng, H.; Wang, X.; Chu, F. Modeling and vibration control of sandwich composite plates. Materials 2023, 16, 896. [Google Scholar] [CrossRef]
- Mohammed, H.A.U.-Q.; Wasmi, H.R. Active vibration control of cantilever beam by using optimal LQR controller. J. Eng. 2018, 24, 1–17. [Google Scholar] [CrossRef]
- Petersen, I.R.; Pota, H.R. Minimax LQG optimal control of a flexible beam. Control Eng. Pract. 2003, 11, 1273–1287. [Google Scholar] [CrossRef]
- Roy, T.; Chakraborty, D. Optimal vibration control of smart fiber reinforced composite shell structures using improved genetic algorithm. J. Sound Vib. 2009, 319, 15–40. [Google Scholar] [CrossRef]


| Parameter | L/m | W/m | THK/m | ρ/kg/m3 | E /Gpa | PR | d31/m/V |
|---|---|---|---|---|---|---|---|
| Base layer | 0.2616 | 0.0127 | 0.002286 | 7600 | 7.4 × | 0.3 | |
| PZT layer | 0.1016 | 0.1027 | 0.000762 | 7600 | 6.67 × | 0.3 | 1.75 × |
| VEM layer | 0.1016 | 0.1027 | 0.00025 | 1250 | 0.3 |
| Modal | Frequency/Hz (Paper) [9] | Frequency/Hz (Present) | Error |
|---|---|---|---|
| 1 mode | 27.90 | 27.83 | 0.25% |
| 2 mode | 150.12 | 147.83 | 1.52% |
| 3 mode | 442.97 | 429.66 | 3.00% |
| 4 mode | 831.76 | 805.08 | 3.21% |
| Natural Frequencies | Structure 1 | Structure 2 | Structure 3 |
|---|---|---|---|
| 1 | 17.02 | 19.85 | 16.37 |
| 2 | 97.45 | 83.23 | 82.52 |
| 3 | 247.04 | 235.25 | 211.43 |
| 4 | 806.16 | 725.19 | 690.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Cheng, Y.; Wang, X.; Wu, N. Active Vibration Control and Parameter Optimization of Genetic Algorithm for Partially Damped Composites Beams. Biomimetics 2024, 9, 584. https://doi.org/10.3390/biomimetics9100584
Huang Z, Cheng Y, Wang X, Wu N. Active Vibration Control and Parameter Optimization of Genetic Algorithm for Partially Damped Composites Beams. Biomimetics. 2024; 9(10):584. https://doi.org/10.3390/biomimetics9100584
Chicago/Turabian StyleHuang, Zhicheng, Yang Cheng, Xingguo Wang, and Nanxing Wu. 2024. "Active Vibration Control and Parameter Optimization of Genetic Algorithm for Partially Damped Composites Beams" Biomimetics 9, no. 10: 584. https://doi.org/10.3390/biomimetics9100584
APA StyleHuang, Z., Cheng, Y., Wang, X., & Wu, N. (2024). Active Vibration Control and Parameter Optimization of Genetic Algorithm for Partially Damped Composites Beams. Biomimetics, 9(10), 584. https://doi.org/10.3390/biomimetics9100584






