Hydrodynamic Simulation and Experiment of a Self-Adaptive Amphibious Robot Driven by Tracks and Bionic Fins
Abstract
1. Introduction
2. Locomotion Principle
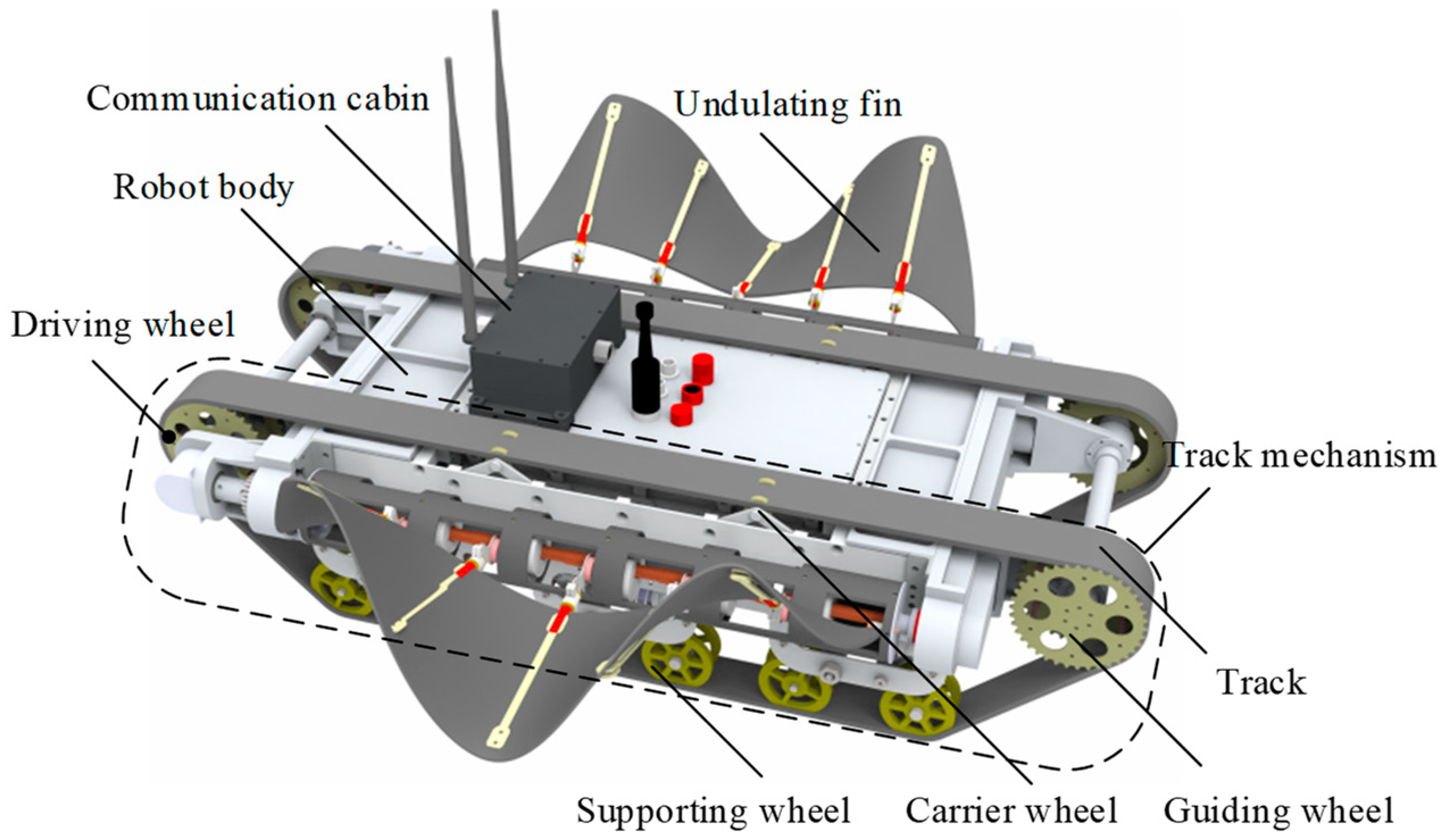
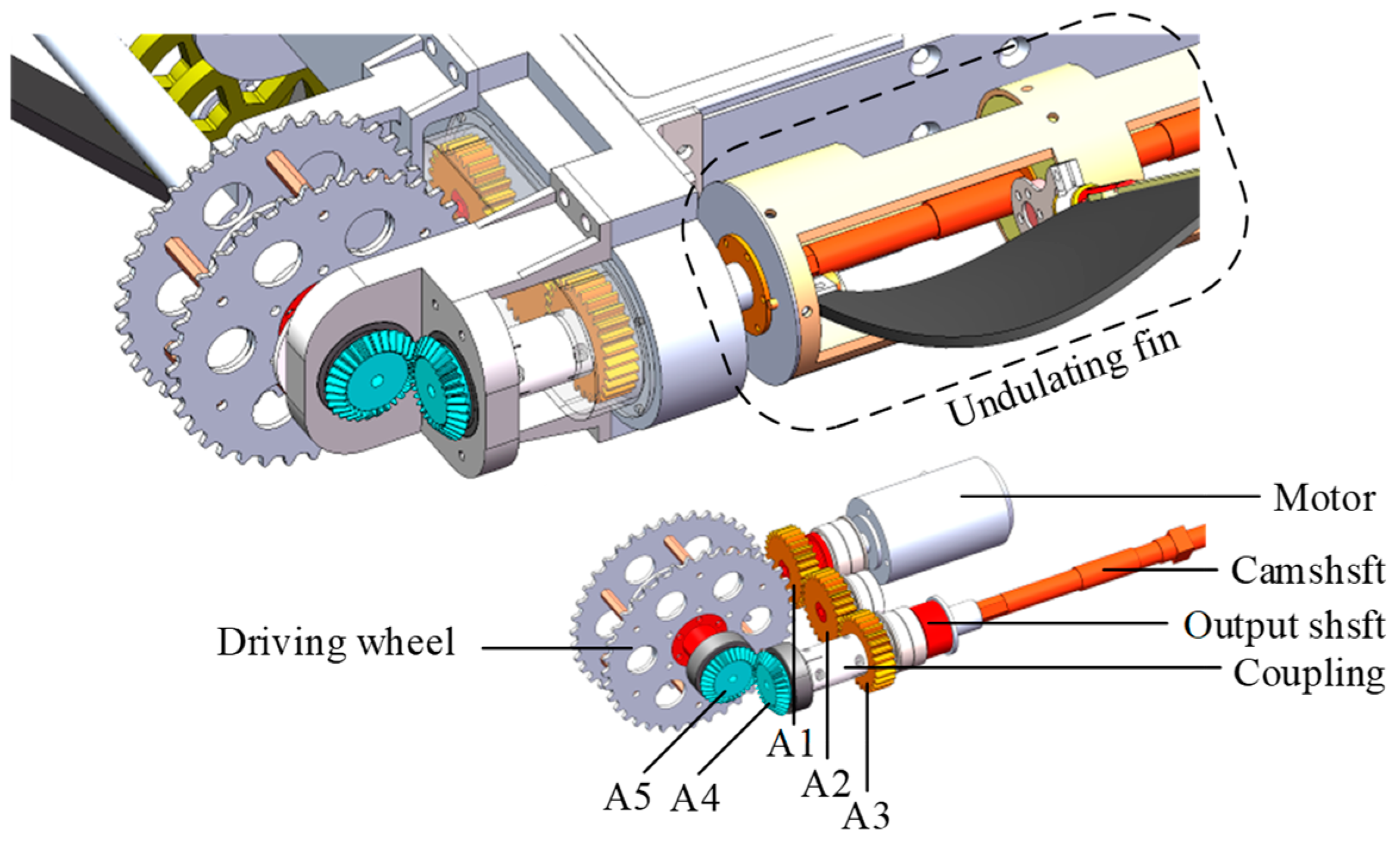
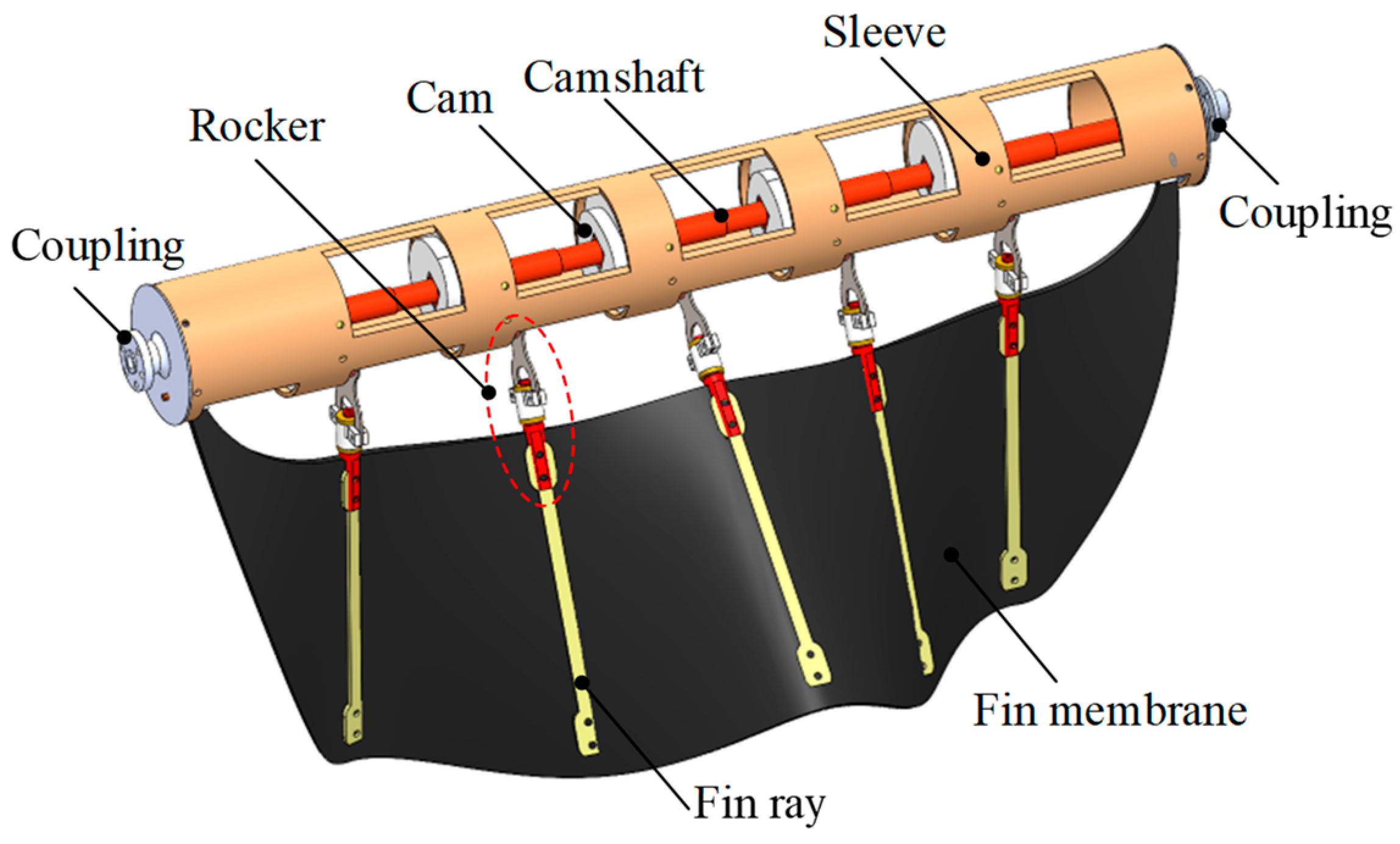
2.1. Robot Structure
2.2. United Operation Mechanism
- Forward movement: When the tracks on both sides rotate clockwise at the same speed (), both tracks offer the same forward speed. Simultaneously, the left and right undulating fins transmit waves to the rear direction with the same frequency (), and the undulating fins generate equal forward propulsion force (). If underwater, the undulating fins propel the robot to move forward; if on the ground, the tracks drive the robot to move forward.
- Backward movement: As shown in Figure 5b, when the tracks on both sides rotate clockwise at the same speed (), the undulating fins transmit waves to the front direction with the same frequency (), and the propulsion force is negative (). The robot moves backwards either underwater or on land.
- Yaw motion: Yaw motion can be achieved by regulating the differential rotation of the tracks in the same direction. For example, when , the robot will turn to the right when moving forward on land. The left propulsive force is greater than that on the right side ( ), and the combined force generates additional yaw torque, causing the robot to turn to the right underwater. Similarly, when , the robot performs forward and left-turning locomotion. Due to symmetry, the robot also adopts the same left and right turn control methods when moving backward.
- Rotation motion: Turning in place is a special case of yaw motion, when the two-side tracks’ speeds are equal but for opposite directions. As shown in Figure 5d, when , there is for undulating fins, so the resultant force is zero. The robot will carry out right-turning motion either on land or underwater. When , the robot will rotate left.
3. Hydrodynamic Simulation
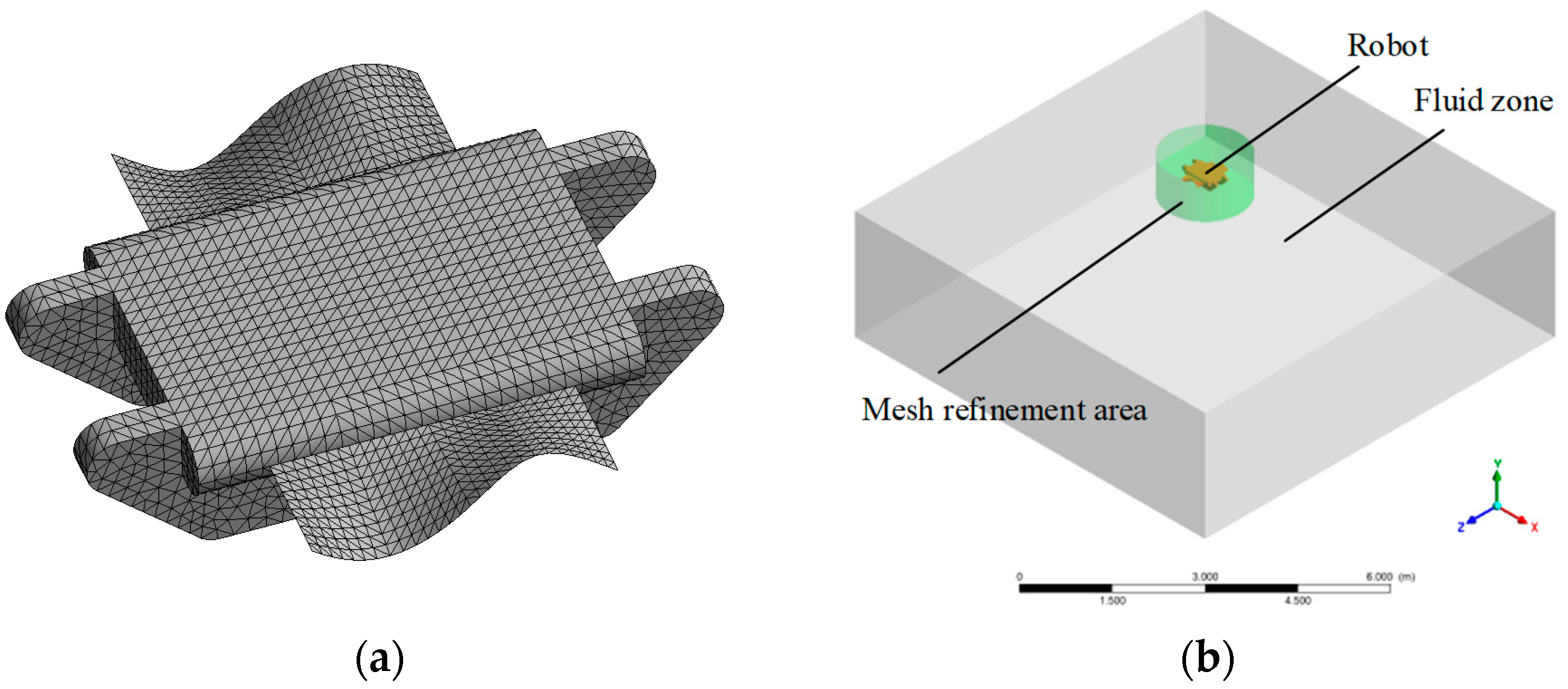
3.1. Simulation Model
3.2. Mathematical Model
3.2.1. Kinematic Model
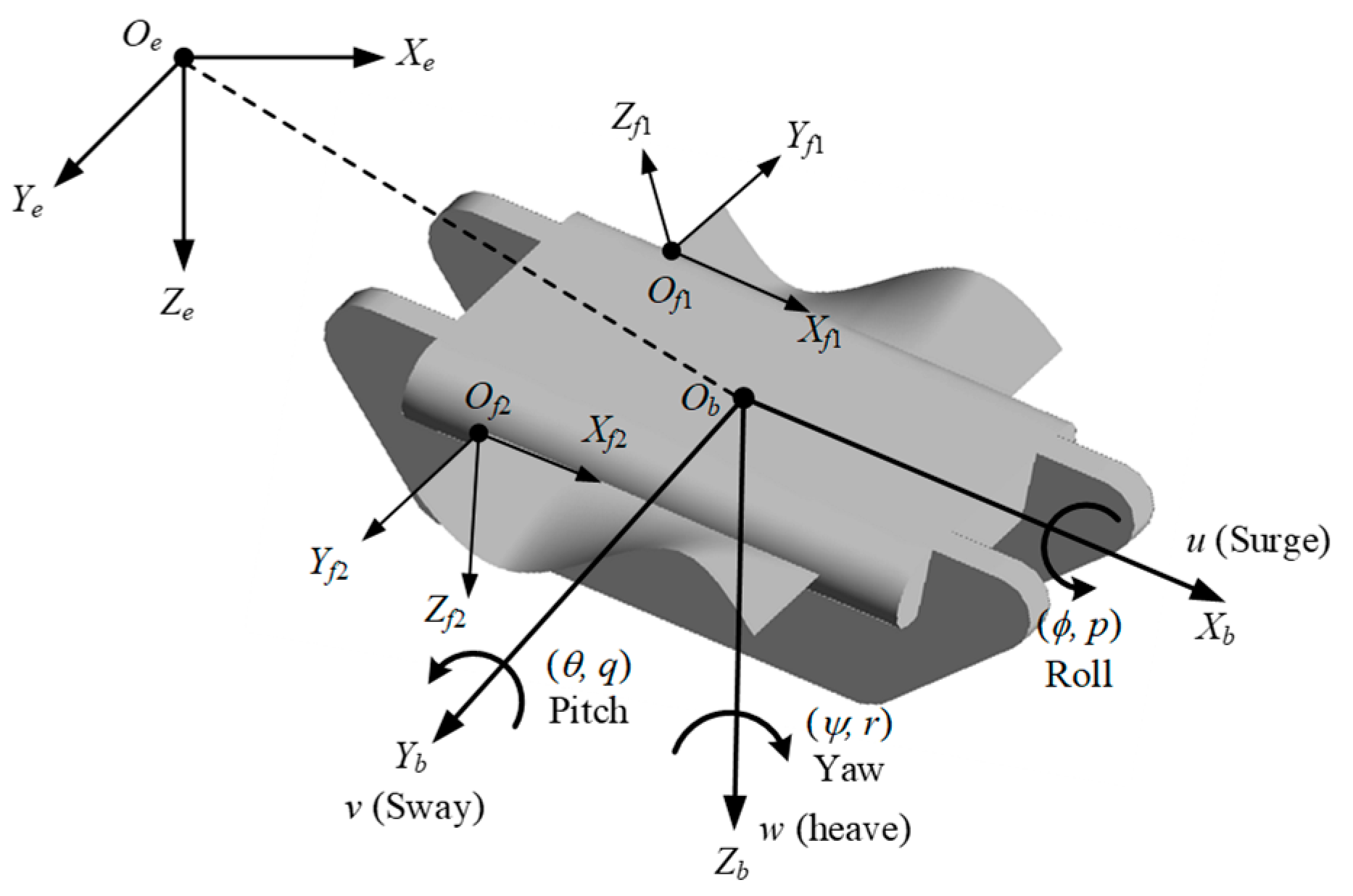
- Global coordinate system, : The origin of coordinate was defined by taking any point within the earth; pointed at any horizontal direction, was vertically downward to the ground, and the direction of was in accordance with the right-hand rule.
- Local coordinate system, : The origin was defined as the mass center of the robot. was along the longitudinal axial direction. pointed straight down the body. was located to the right of the body.
- The fin coordinate system, OfXfYfZf: The origin was located at the base point of the undulating fin. pointed forward along the undulating fin’s base line. was in the symmetrical plane of the undulating fin and pointed outwards. was determined by the right-hand rule. The coordinate systems and were established for the left and right undulating fins, respectively.
3.2.2. Underwater Dynamic Model
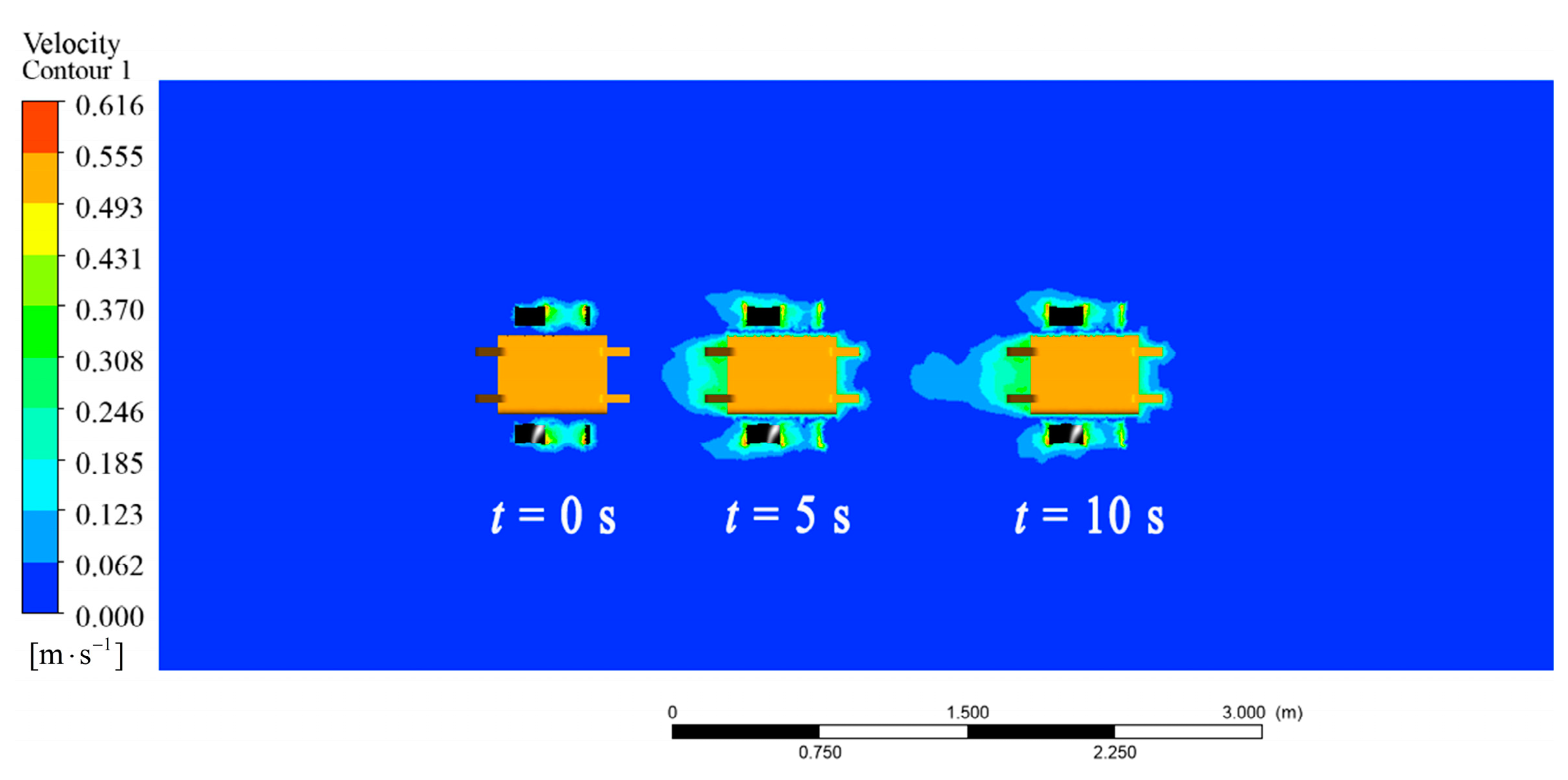
3.3. Simulation Result
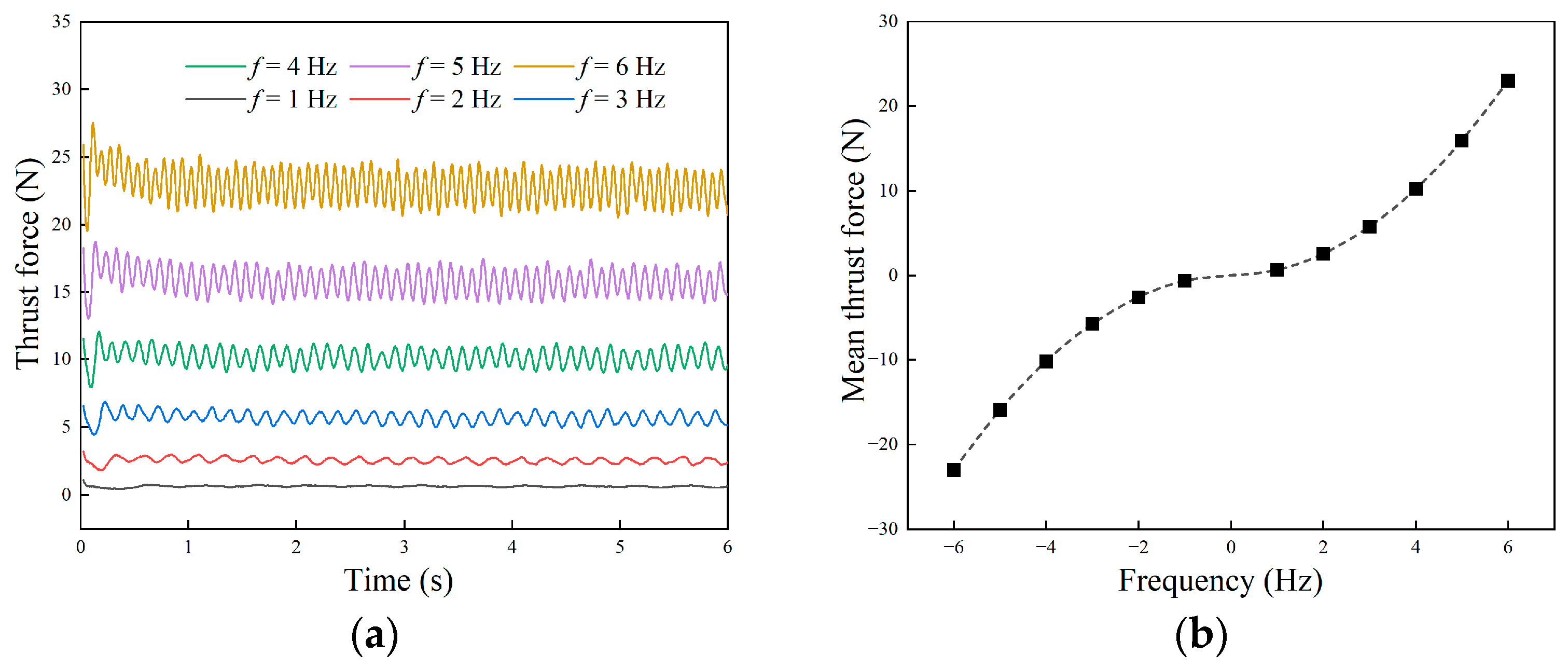
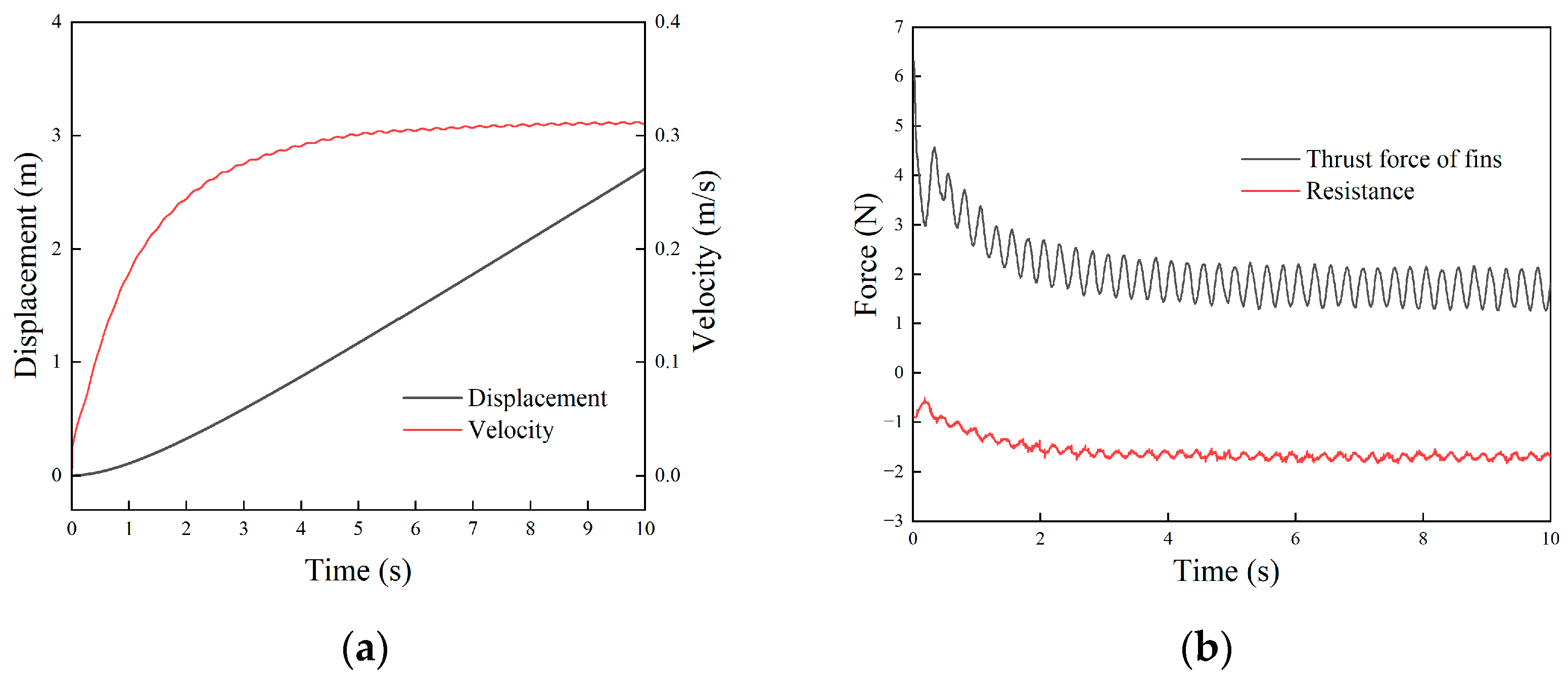
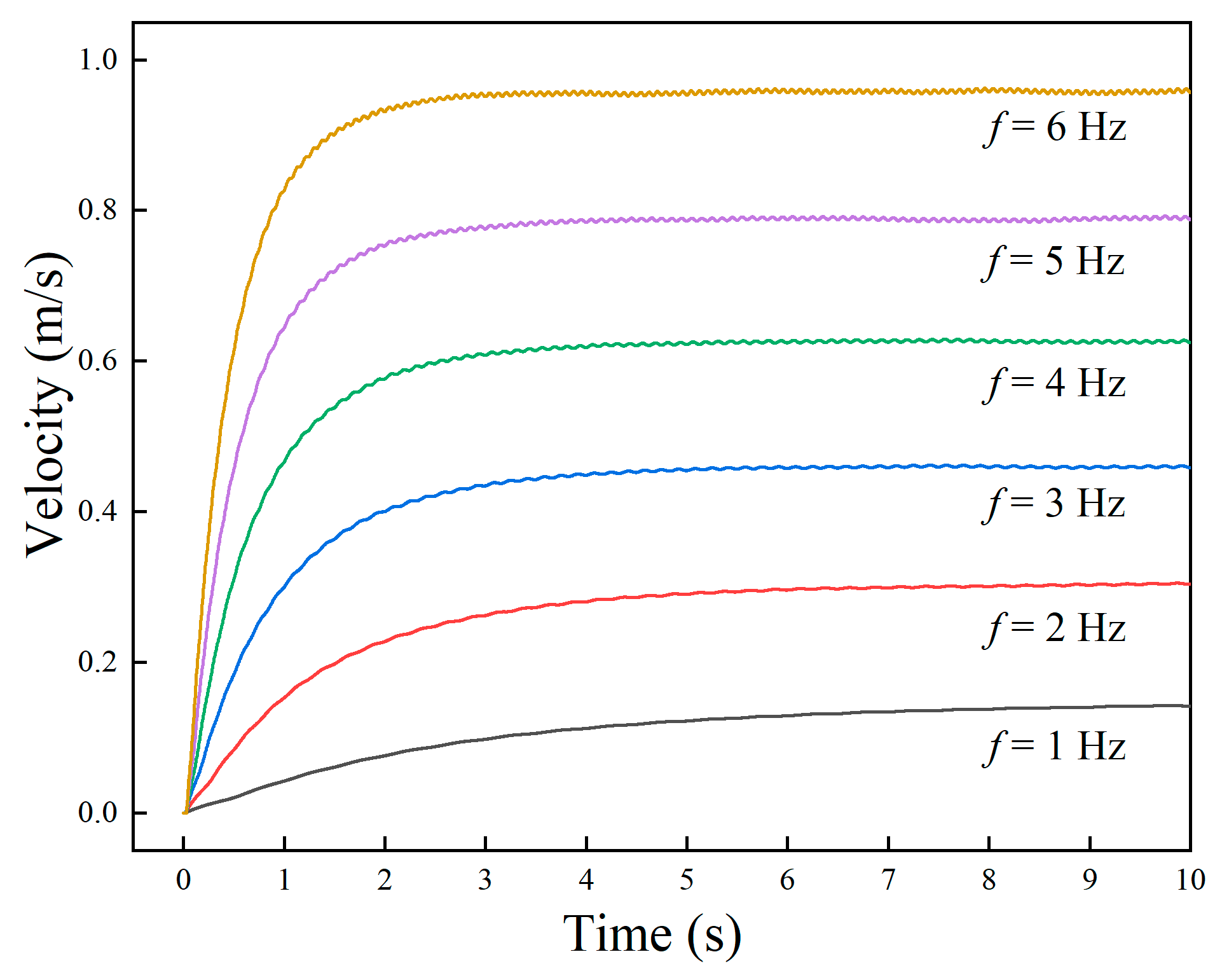
3.3.1. Surge Motion
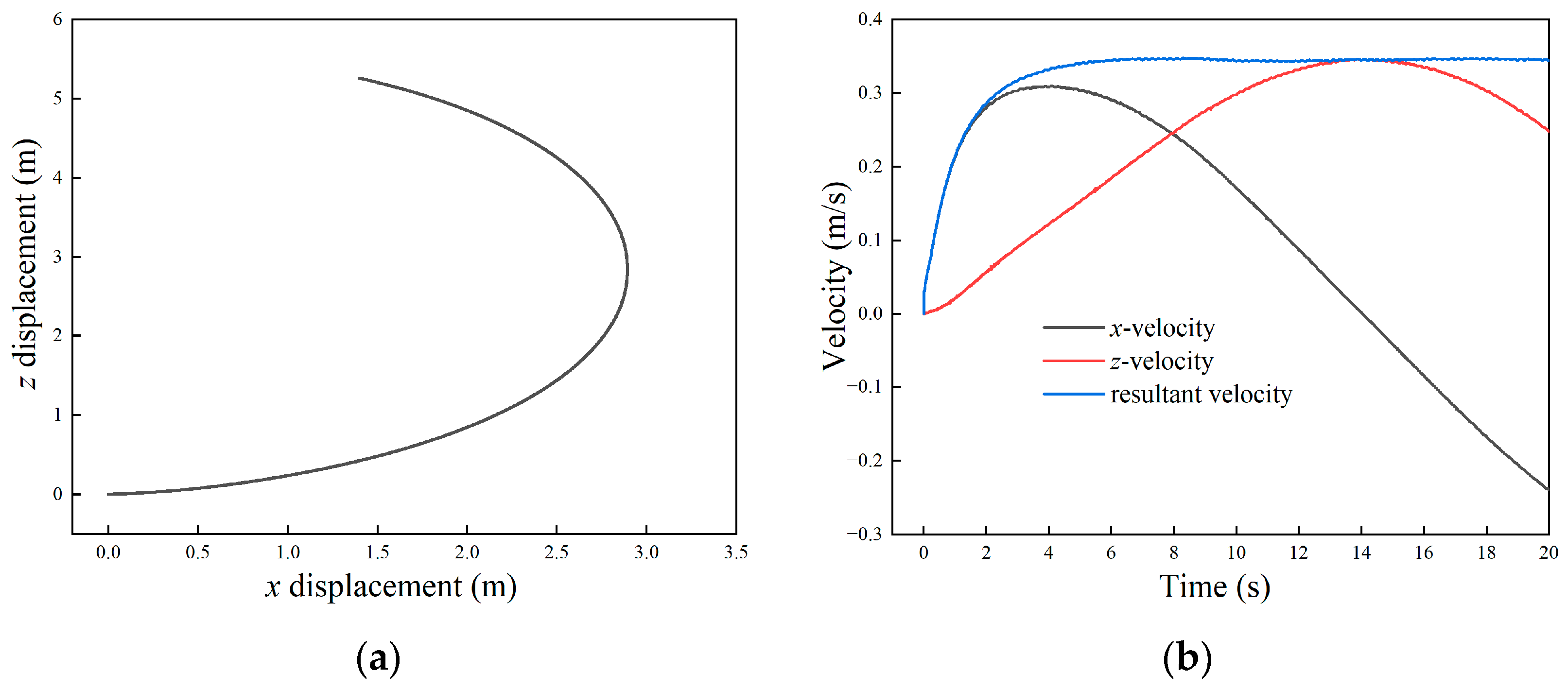
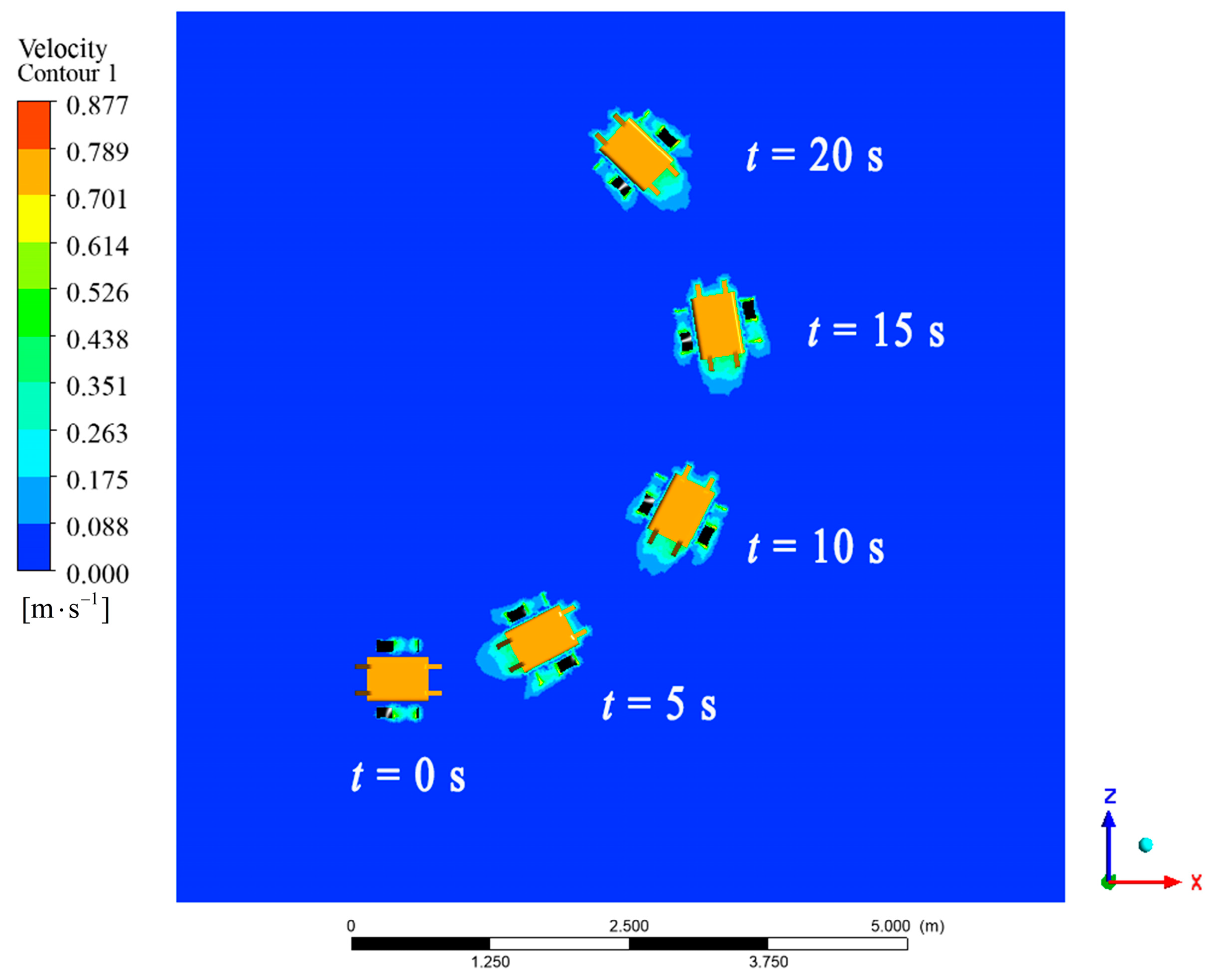
3.3.2. Steering Motion
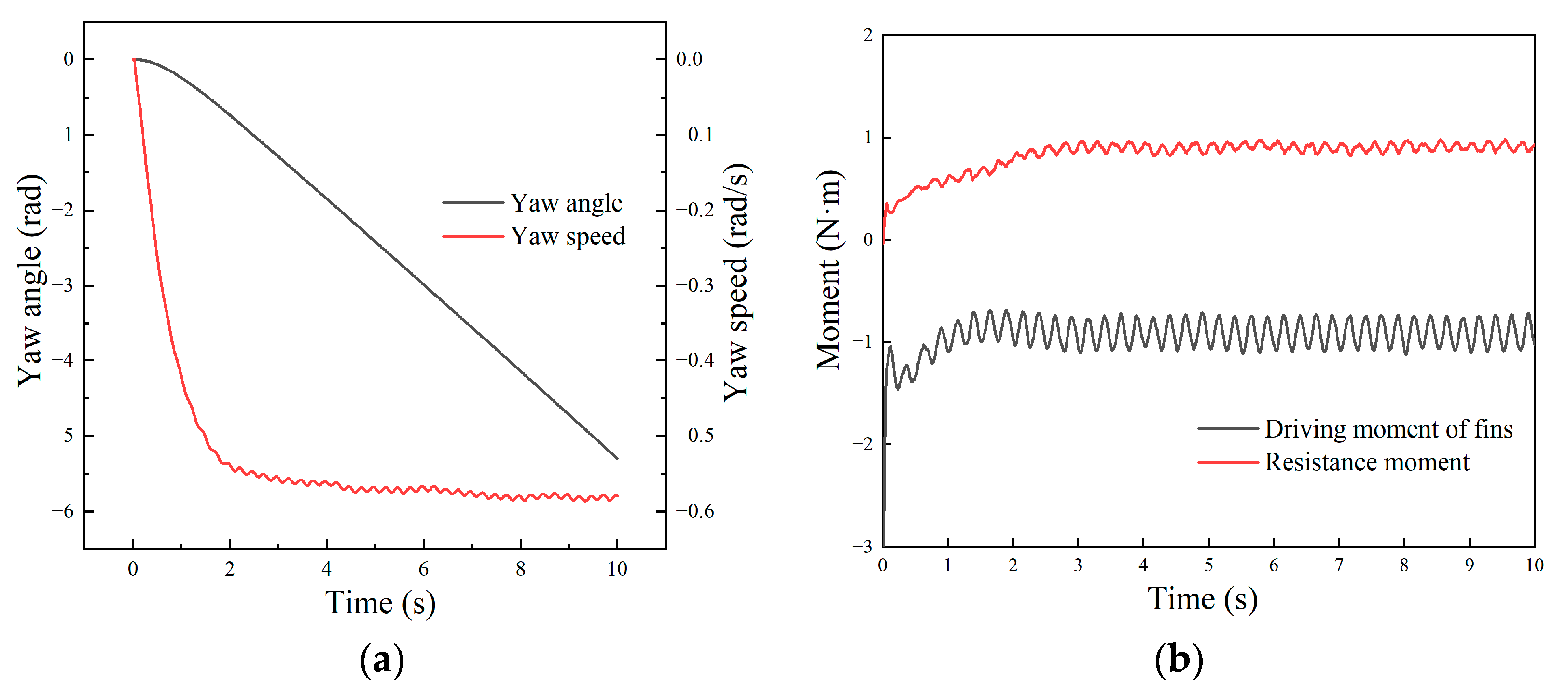
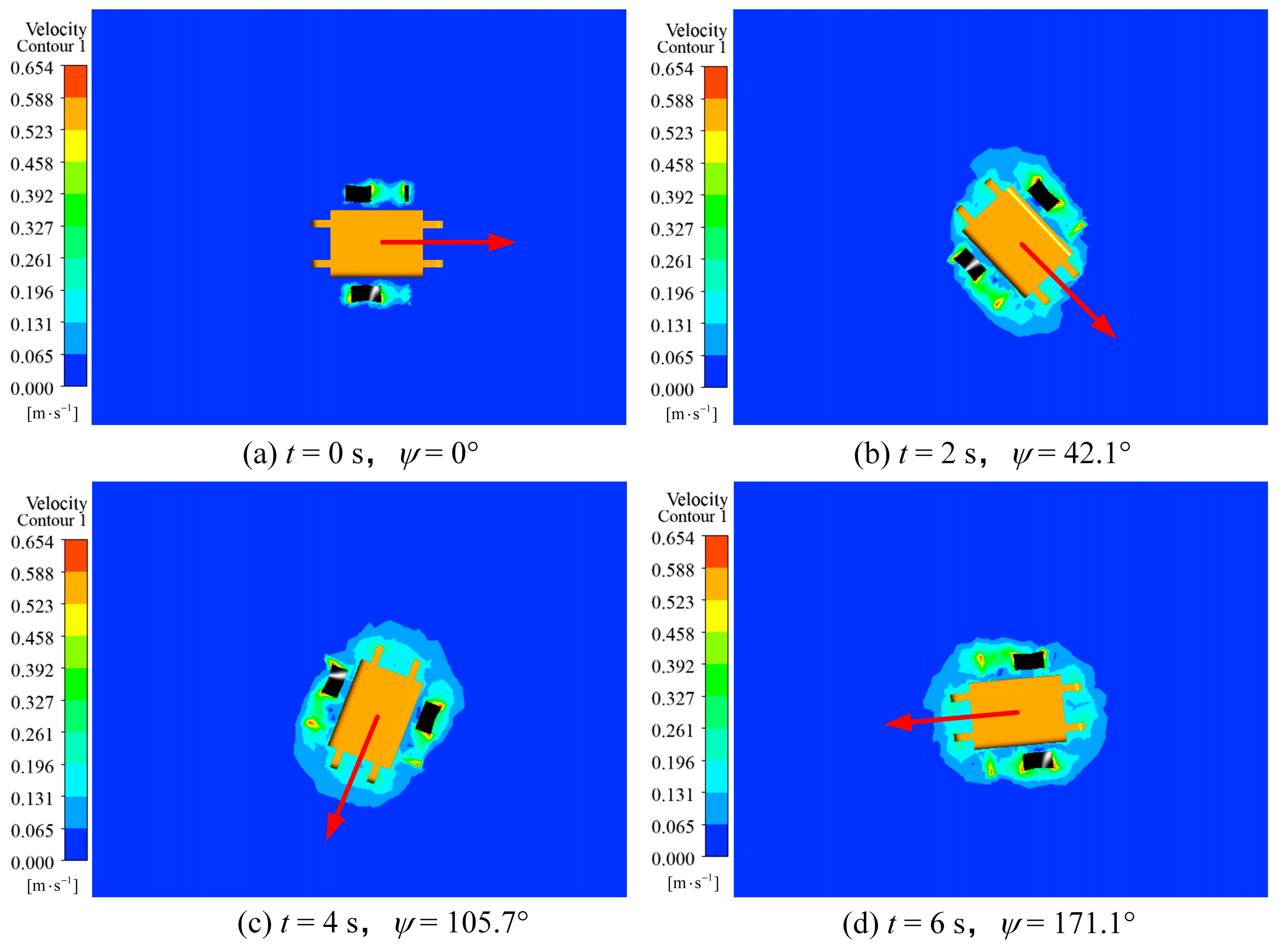
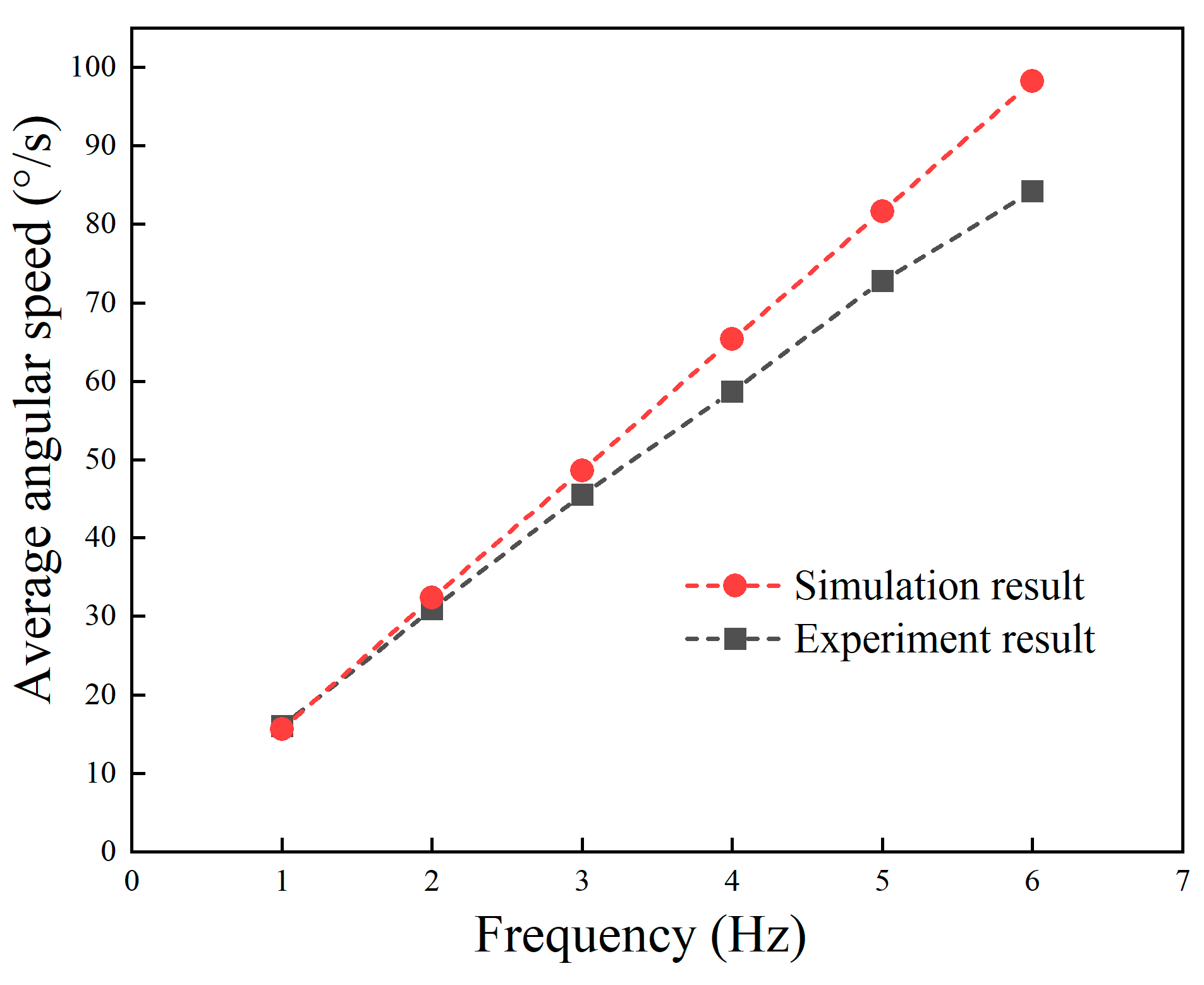
3.3.3. Rotation Motion
4. Experiment Validation
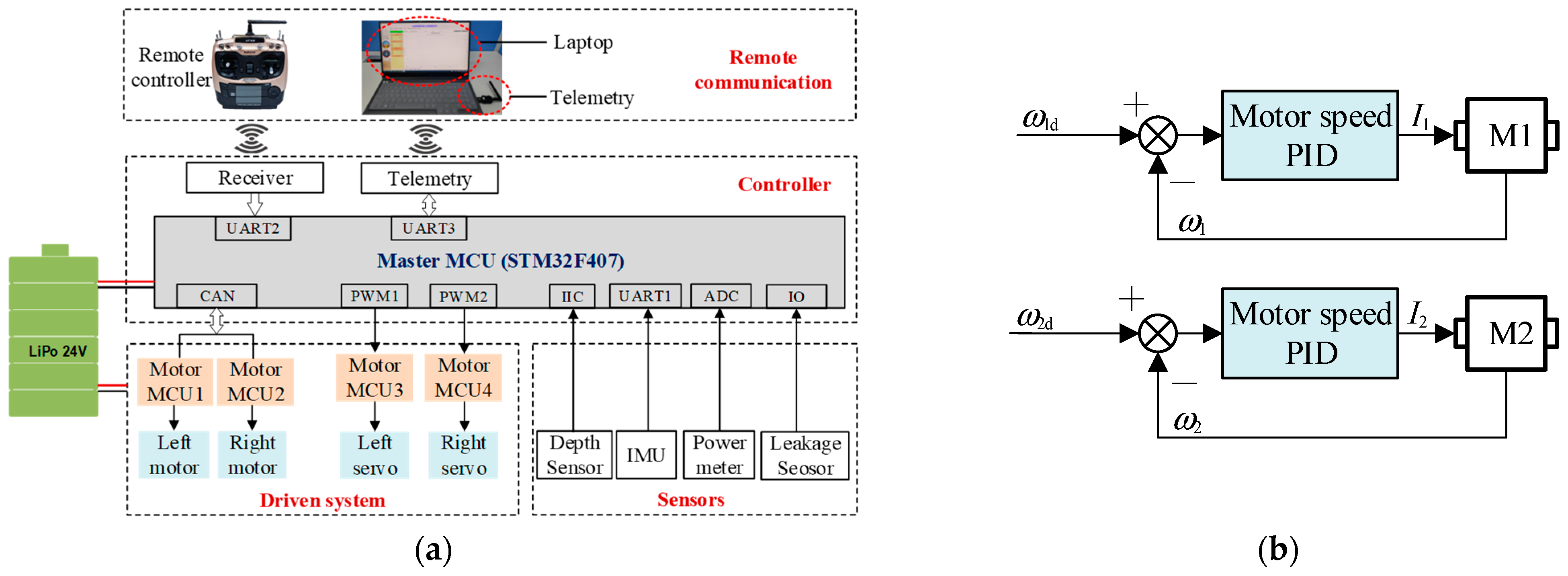
4.1. Robot Prototype
4.2. Underwater Maneuverability
4.2.1. Underwater Linear Motion
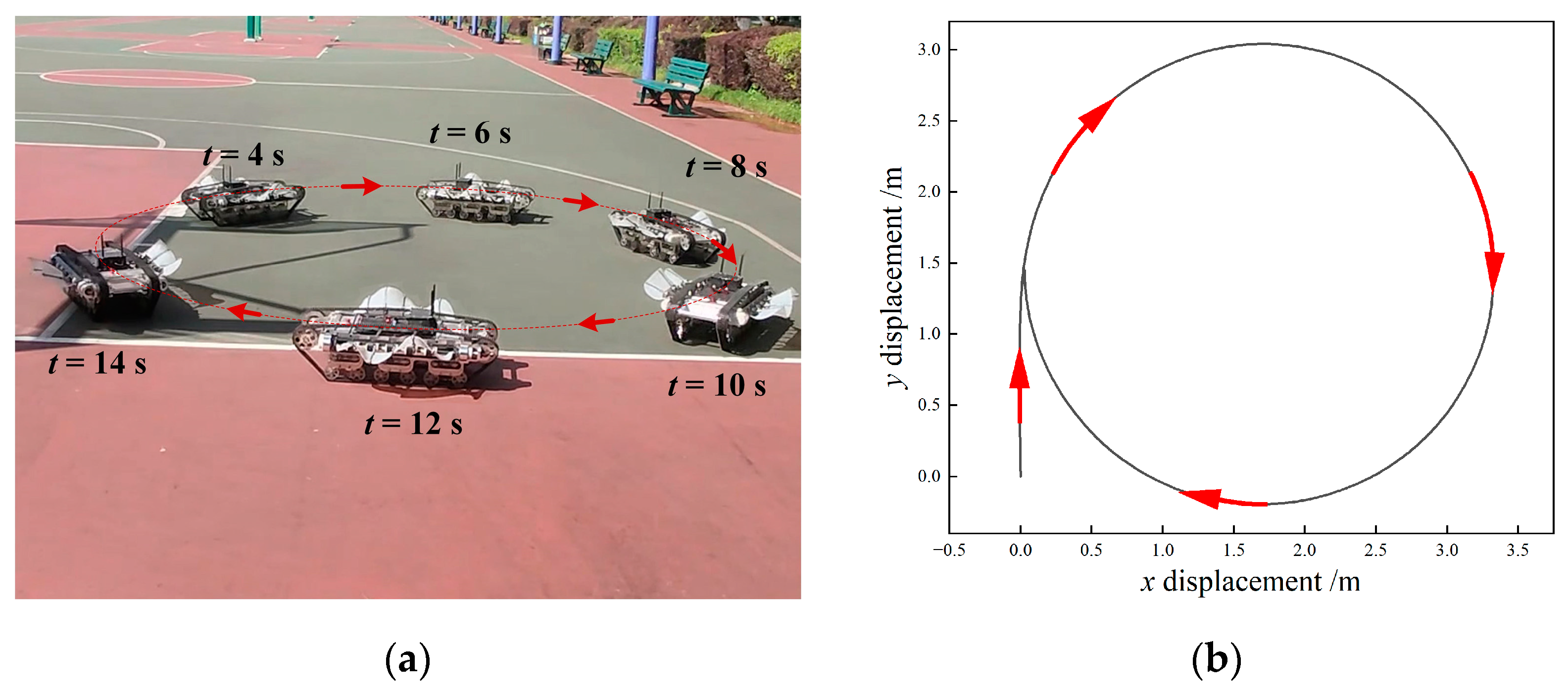
4.2.2. Underwater Steering and Rotation Motion
4.3. Terrestrial Maneuverability
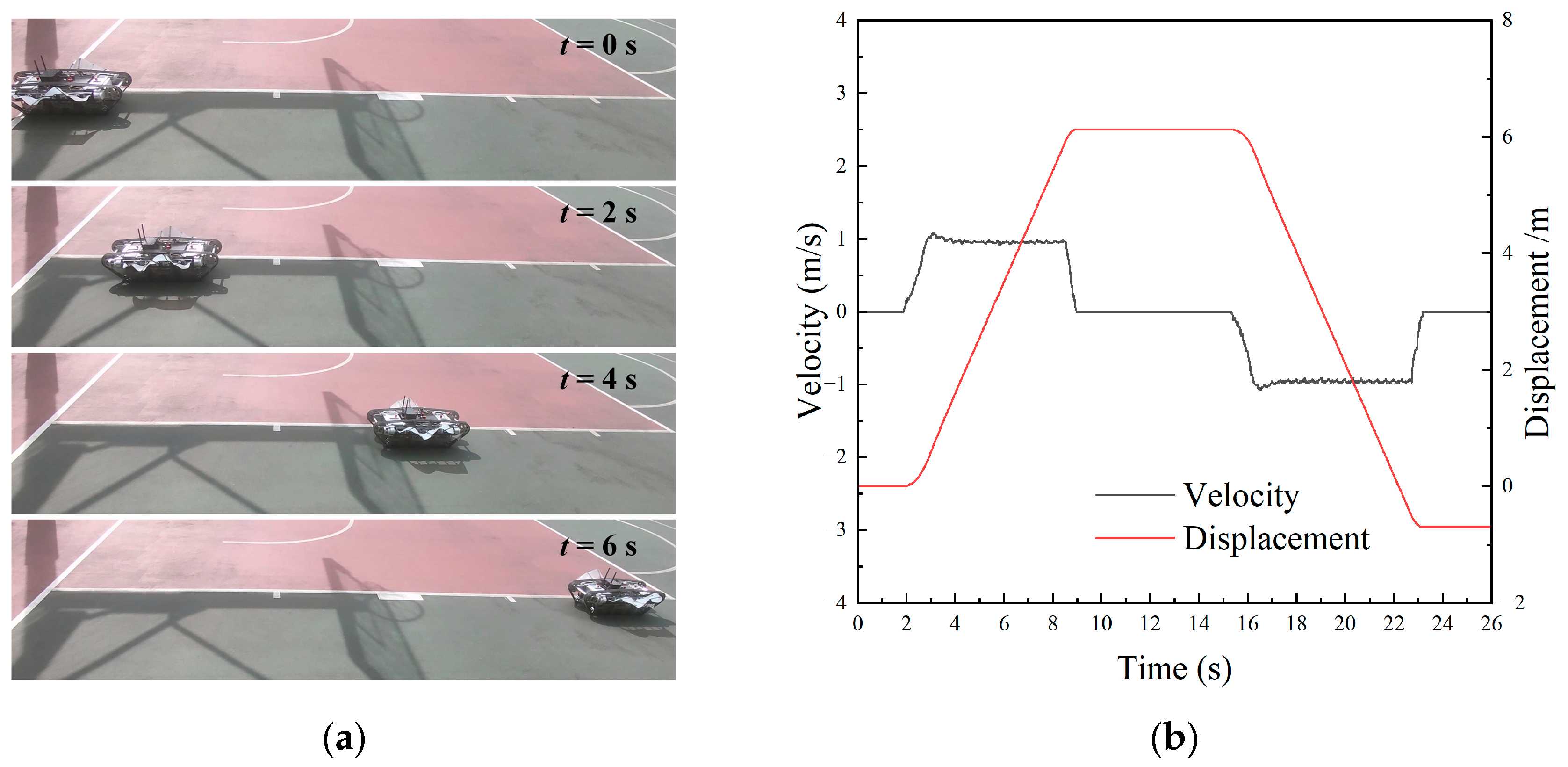
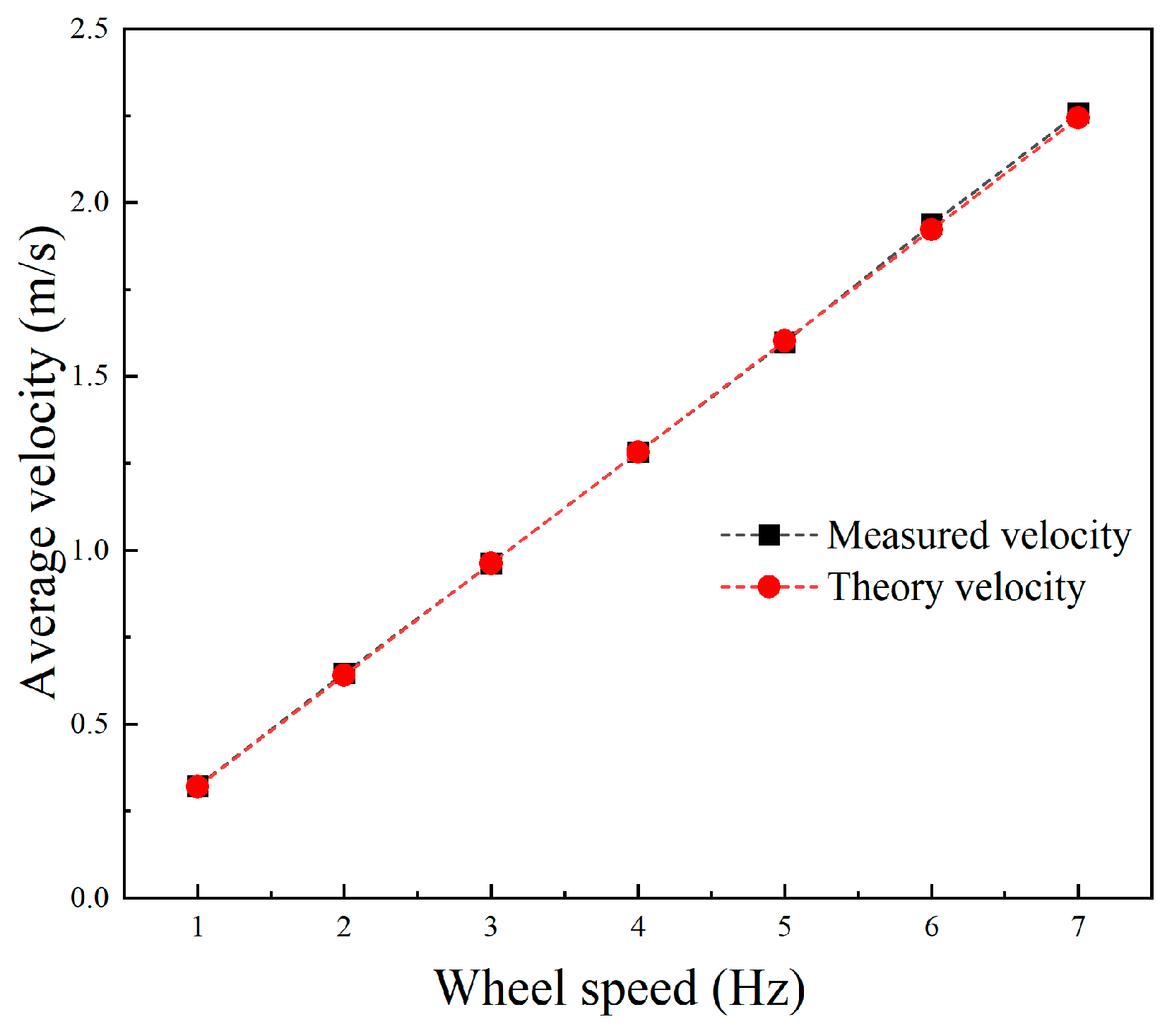
4.3.1. Terrestrial Linear Motion
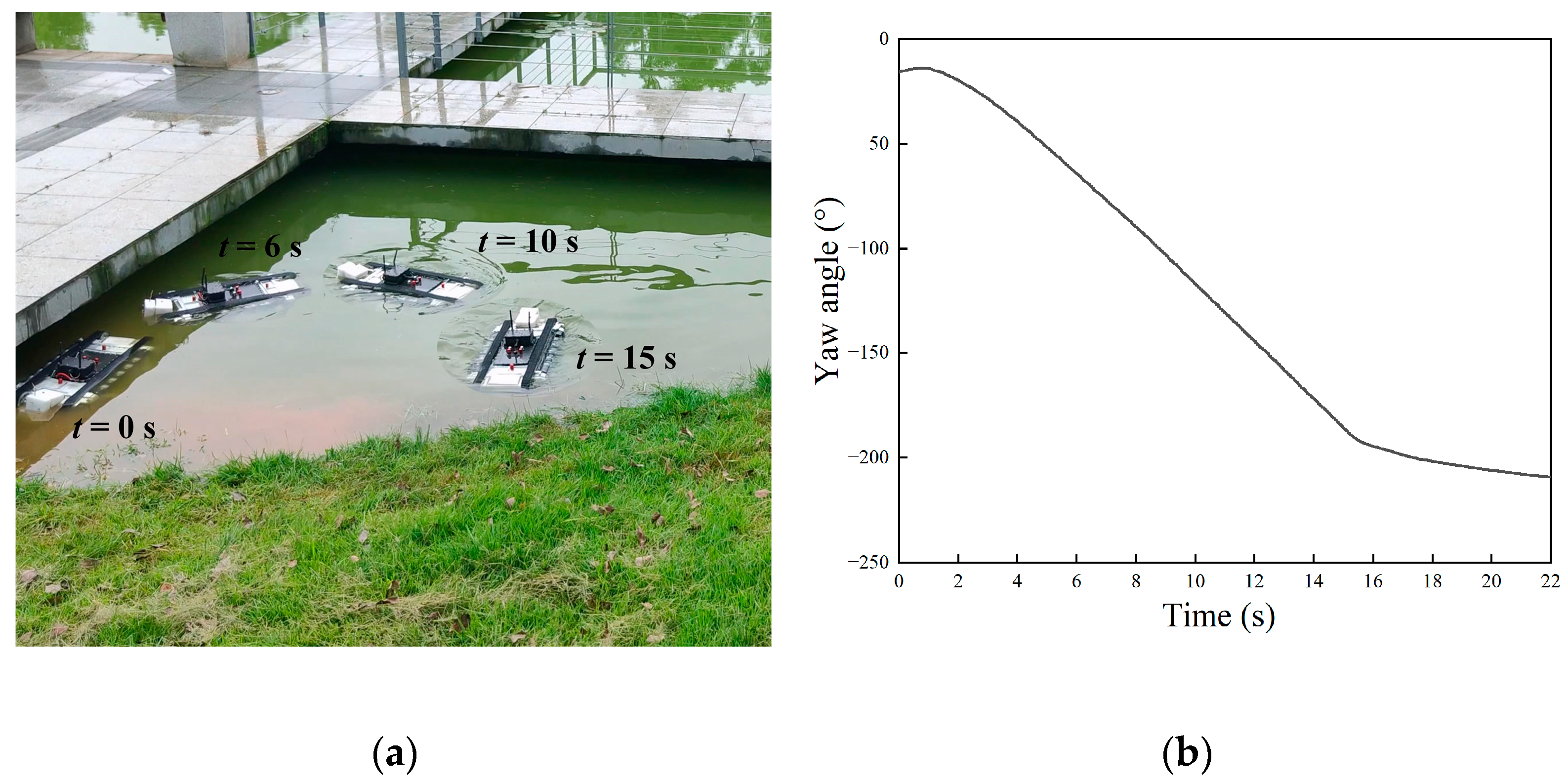
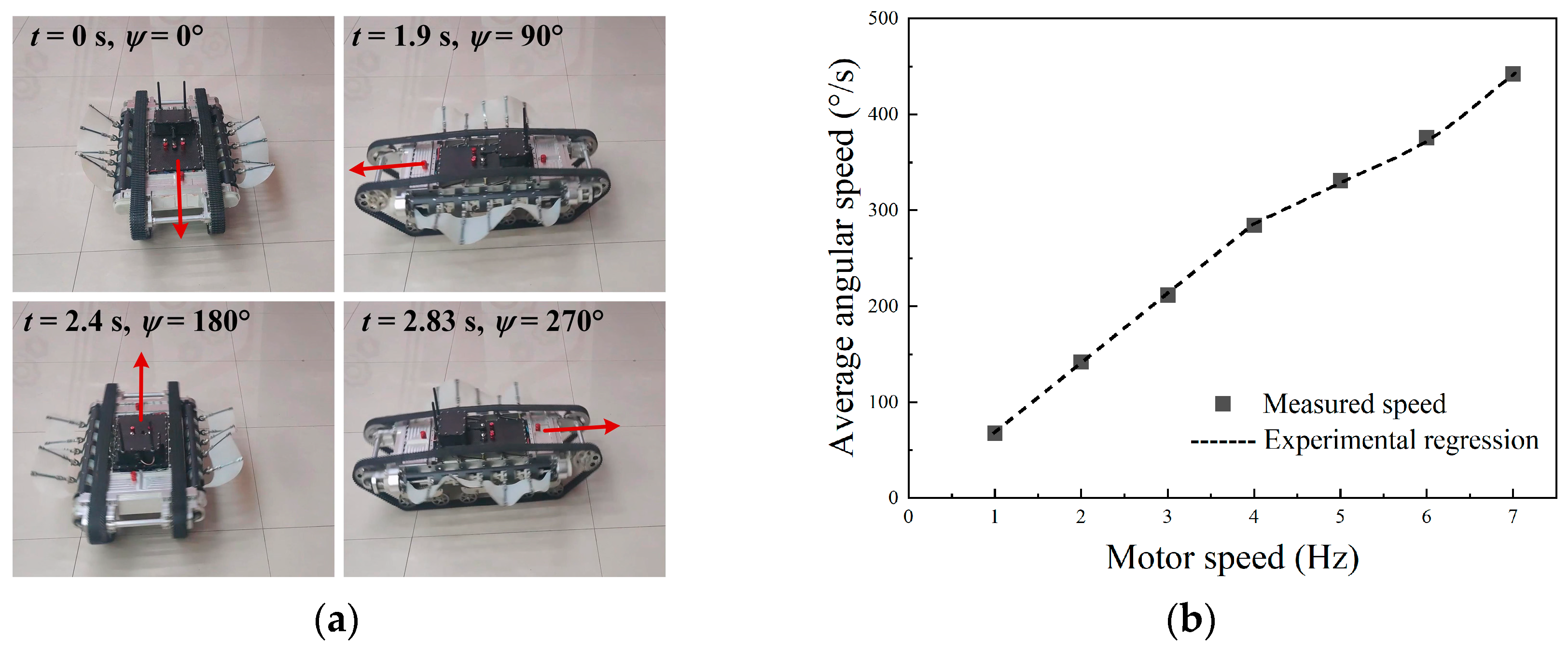
4.3.2. Terrestrial Steering and Rotation Motion
5. Conclusions
- (1)
- A biologically inspired amphibious robot was designed. Through a compound drive mechanism, a pair of bionic undulating fins and a pair of tracks were parallelly equipped on the robot, which were responsible for efficient locomotion underwater and on land, respectively. Sharing a same driving source enabled autonomous switching of the track and the fin, along with a unified motion control strategy both on land and underwater. Therefore, the robot did not need to judge in which kind of environment it was, as the robot’s locomotion and control principles such as forward, backward, and turning were the same in various environments.
- (2)
- Based on the kinematics and dynamics model of the robot as well as the motion equation of the undulating fins, the hydrodynamic and motion performance of the robot under linear motion, steering motion, and in situ rotation motion were simulated using dynamic mesh method. The simulation results showed that the robot could generate vector thrust through the wave-like motion of the undulating fins. Both the linear swimming speed and the turning speed achieved by the robot were proportional to the wave frequency.
- (3)
- The prototype experiment validated the amphibious motion performance of the robot. Using the same motion control strategy, the robot was capable of achieving unified forward and backward, steering, and in-place rotation locomotion both on land and underwater. The maximum linear speed and steering speed on land were 2.26 m/s (2.79 BL/s) and 442°/s, respectively. The maximum linear speed and steering speed underwater were 0.54 m/s (0.67 BL/s) and 84°/s, respectively.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hammond, M.; Cichella, V.; Lamuta, C. Bioinspired Soft Robotics: State of the Art, Challenges, and Future Directions. Curr. Robot. Rep. 2023, 4, 65–80. [Google Scholar] [CrossRef]
- Arena, P.; Bucolo, M.; Buscarino, A.; Fortuna, L.; Frasca, M. Reviewing Bioinspired Technologies for Future Trends: A Complex Systems Point of View. Front. Phys. 2021, 9, 750090. [Google Scholar] [CrossRef]
- Wu, J.; Wu, M.; Chen, W.; Wang, C.; Xie, G. Multi-Modal Soft Amphibious Robots Using Simple Plastic Sheet-Reinforced Thin Pneumatic Actuators. IEEE Trans. Robot. 2024, 40, 1874–1889. [Google Scholar] [CrossRef]
- Guetta, O.; Shachaf, D.; Katz, R.; Zarrouk, D. A Novel Wave-like Crawling Robot Has Excellent Swimming Capabilities. Bioinspir. Biomim. 2023, 18, 026006. [Google Scholar] [CrossRef]
- Yin, Q.; Xia, M.; Luo, Z.; Shang, J. Adaptive Obstacle Climbing and Hydrodynamic Performance Analyses of the Amphibious Robot with Wheels and Flexible Undulating Fins. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 5300–5317. [Google Scholar] [CrossRef]
- Ren, K.; Yu, J. Research Status of Bionic Amphibious Robots: A Review. Ocean Eng. 2021, 227, 108862. [Google Scholar] [CrossRef]
- Bai, X.J.; Shang, J.Z.; Luo, Z.R.; Jiang, T.; Yin, Q. Development of Amphibious Biomimetic Robots. J. Zhejiang Univ.-Sci. A 2022, 23, 157–187. [Google Scholar] [CrossRef]
- Ge, Y.; Gao, F.; Chen, W. A Transformable Wheel-Spoke-Paddle Hybrid Amphibious Robot. Robotica 2024, 42, 701–727. [Google Scholar] [CrossRef]
- Graf, N.M.; Behr, A.M.; Daltorio, K.A. Crab-like Hexapod Feet for Amphibious Walking in Sand and Waves. In Biomimetic and Biohybrid Systems; Springer: Cham, Switzerland, 2019; Volume 11556, pp. 158–170. ISBN 9783030247409. [Google Scholar]
- Marquardt, J.G.; Alvarez, J.; von Ellenrieder, K.D. Characterization and System Identification of an Unmanned Amphibious Tracked Vehicle. IEEE J. Ocean. Eng. 2014, 39, 641–661. [Google Scholar] [CrossRef]
- Yan, Z.; Li, M.; Du, Z.; Yang, X.; Luo, Y.; Chen, X.; Han, B. Study on a Tracked Amphibious Robot Bionic Fairing for Drag Reduction. Ocean Eng. 2023, 267, 113223. [Google Scholar] [CrossRef]
- Shim, H.; Yoo, S.; Kang, H.; Jun, B. Development of Arm and Leg for Seabed Walking Robot CRABSTER200. Ocean Eng. 2016, 116, 55–67. [Google Scholar] [CrossRef]
- Baines, R.; Freeman, S.; Fish, F.; Kramer-Bottiglio, R. Variable Stiffness Morphing Limb for Amphibious Legged Robots Inspired by Chelonian Environmental Adaptations. Bioinspir. Biomim. 2020, 15, 025002. [Google Scholar] [CrossRef] [PubMed]
- Ayers, J. Underwater Walking. Arthropod Locomot. Syst. Biol. Mater. Syst. Robot. 2004, 33, 347–360. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Xu, Y.; Wang, Z.; Tu, J.; Hu, H.; Chen, C.; Xu, Y.; Chai, X.; Zhang, J.; Shi, J. Dynamic Tail Modeling and Motion Analysis of a Beaver-like Robot. Nonlinear Dyn. 2024, 112, 6859–6875. [Google Scholar] [CrossRef]
- Yang, Y.; Geng, Z.; Zhang, J.; Cheng, S.; Fu, M. Design, Modeling and Control of a Novel Amphibious Robot with Dual-Swing-Legs Propulsion Mechanism. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 559–566. [Google Scholar]
- Hirose, S.; Yamada, H. Snake-like Robots [Tutorial]. IEEE Robot. Autom. Mag. 2009, 16, 88–98. [Google Scholar] [CrossRef]
- Thandiackal, R.; Melo, K.; Paez, L.; Herault, J.; Kano, T.; Akiyama, K.; Boyer, F.; Ryczko, D.; Ishiguro, A.; Ijspeert, A.J. Emergence of Robust Self-Organized Undulatory Swimming Based on Local Hydrodynamic Force Sensing. Sci. Robot. 2021, 6, eabf6354. [Google Scholar] [CrossRef]
- Crespi, A.; Ijspeert, A.J. AmphiBot II: An Amphibious Snake Robot That Crawls and Swims Using a Central Pattern Generator. In Proceedings of the 9th International Conference on Climbing and Walking Robots (CLAWAR 2006), Brussels, Belgium, 12–14 September 2006; pp. 19–27. [Google Scholar]
- Yu, S.; Ma, S.; Li, B.; Wang, Y. An Amphibious Snake-like Robot with Terrestrial and Aquatic Gaits. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2960–2961. [Google Scholar]
- Zhang, S.; Zhou, Y.; Xu, M.; Liang, X.; Liu, J.; Yang, J. AmphiHex-I: Locomotory Performance in Amphibious Environments with Specially Designed Transformable Flipper Legs. IEEE/ASME Trans. Mechatron. 2016, 21, 1720–1731. [Google Scholar] [CrossRef]
- Zhong, B.; Zhang, S.; Xu, M.; Zhou, Y.; Fang, T.; Li, W. On a CPG-Based Hexapod Robot: AmphiHex-II with Variable Stiffness Legs. IEEE/ASME Trans. Mechatron. 2018, 23, 542–551. [Google Scholar] [CrossRef]
- Zou, X. Machine Learning-Based Robotic Design: A Case Study on Fin-Based Amphibious Robots. Ph.D. Thesis, The State University of New Jersey, New Brunswick, NJ, USA, 2021. [Google Scholar]
- Baines, R.; Patiballa, S.K.; Booth, J.; Ramirez, L.; Sipple, T.; Garcia, A.; Fish, F.; Kramer-Bottiglio, R. Multi-Environment Robotic Transitions through Adaptive Morphogenesis. Nature 2022, 610, 283–289. [Google Scholar] [CrossRef]
- Wu, M.; Xu, X.; Zhao, Q.; Afridi, W.H.; Hou, N.; Afridi, R.H.; Zheng, X.; Wang, C.; Xie, G. A Fully 3D-Printed Tortoise-Inspired Soft Robot with Terrains-Adaptive and Amphibious Landing Capabilities. Adv. Mater. Technol. 2022, 7, 2200536. [Google Scholar] [CrossRef]
- Xia, M.; Wang, H.; Yin, Q.; Shang, J.; Luo, Z.; Zhu, Q. Design and Mechanics of a Composite Wave-Driven Soft Robotic Fin for Biomimetic Amphibious Robot. J. Bionic Eng. 2023, 20, 934–952. [Google Scholar] [CrossRef]
- Yu, D.; Che, T.; Zhang, H.; Li, Y.; Sun, D.; Wang, Z. Terrestrial Locomotion Stability of Undulating Fin Amphibious Robots: Separated Elastic Fin Rays and Asynchronous Control. Ocean Eng. 2024, 311, 118853. [Google Scholar] [CrossRef]
- Wang, G.; Liu, K.; Ma, X.; Chen, X.; Hu, S.; Tang, Q.; Liu, Z.; Ding, M.; Han, S. Optimal Design and Implementation of an Amphibious Bionic Legged Robot. Ocean Eng. 2023, 272, 113823. [Google Scholar] [CrossRef]
- Dudek, G.; Giguere, P.; Prahacs, C.; Saunderson, S.; Sattar, J.; Torres-Mendez, L.A.; Jenkin, M.; German, A.; Hogue, A.; Ripsman, A.; et al. AQUA: An Amphibious Autonomous Robot. Computer 2007, 40, 46–53. [Google Scholar] [CrossRef]
- Dey, B.B.; Manjanna, S.; Dudek, G. Ninja Legs: Amphibious One Degree of Freedom Robotic Legs. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 5622–5628. [Google Scholar]
- Ma, X.; Wang, G.; Liu, K. Design and Optimization of a Multimode Amphibious Robot with PropellerLeg. IEEE Trans. Robot. 2022, 38, 3807–3820. [Google Scholar] [CrossRef]
- Yu, J.; Ding, R.; Yang, Q.; Tan, M.; Zhang, J. Amphibious Pattern Design of a Robotic Fish with Wheel-Propeller-Fin Mechanisms. J. Field Robot. 2013, 30, 702–716. [Google Scholar] [CrossRef]
- Uddin, M.; Garcia, G.; Curet, O. Underwater Collision Avoidance Using Undulating Elongated Fin Propulsion. Ocean Eng. 2023, 285, 115335. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Zhang, T.; Li, S.; Zeng, Y.; Chen, L.; Hu, Q. Hydrodynamic Performance of a Biomimetic Undulating Fin Robot under Different Water Conditions. Ocean Eng. 2023, 288, 116068. [Google Scholar] [CrossRef]
- Li, Y.; Chen, L.; Wang, Y.; Ren, C. Design and Experimental Evaluation of the Novel Undulatory Propulsors for Biomimetic Underwater Robots. Bioinspir. Biomim. 2021, 16, 056005. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Wei, Q.; Tan, M.; Yu, J. A BioInspired Robot with Undulatory Fins and Its Control Methods. IEEE/ASME Trans. Mechatron. 2022, 22, 206–216. [Google Scholar] [CrossRef]






| Parameter type | Parameters/Unit | Value |
|---|---|---|
| Robot body | Body length, L/m | 0.775 |
| Body width, W/m | 0.404 | |
| Body height, H/m | 0.22 | |
| Undulating fin | Fin length, Lf/m | 0.38 |
| Fin width, h/m | 0.15 | |
| Fin thickness, t/m | 0 | |
| /° | 19.8 | |
| Control parameters | Left fin frequency, f1/Hz | 0–6 |
| Right fin frequency, f2/Hz | 0–6 | |
| Dynamic parameters | Weight, m/kg | 17 |
| Rotational inertia, Jxx/kg·m² | 0.132 | |
| Rotational inertia, Jyy/kg·m² | 0.936 | |
| Rotational inertia, Jzz/kg·m² | 0.863 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, M.; Zhu, Q.; Yin, Q.; Lu, Z.; Zhu, Y.; Luo, Z. Hydrodynamic Simulation and Experiment of a Self-Adaptive Amphibious Robot Driven by Tracks and Bionic Fins. Biomimetics 2024, 9, 580. https://doi.org/10.3390/biomimetics9100580
Xia M, Zhu Q, Yin Q, Lu Z, Zhu Y, Luo Z. Hydrodynamic Simulation and Experiment of a Self-Adaptive Amphibious Robot Driven by Tracks and Bionic Fins. Biomimetics. 2024; 9(10):580. https://doi.org/10.3390/biomimetics9100580
Chicago/Turabian StyleXia, Minghai, Qunwei Zhu, Qian Yin, Zhongyue Lu, Yiming Zhu, and Zirong Luo. 2024. "Hydrodynamic Simulation and Experiment of a Self-Adaptive Amphibious Robot Driven by Tracks and Bionic Fins" Biomimetics 9, no. 10: 580. https://doi.org/10.3390/biomimetics9100580
APA StyleXia, M., Zhu, Q., Yin, Q., Lu, Z., Zhu, Y., & Luo, Z. (2024). Hydrodynamic Simulation and Experiment of a Self-Adaptive Amphibious Robot Driven by Tracks and Bionic Fins. Biomimetics, 9(10), 580. https://doi.org/10.3390/biomimetics9100580







