The Aerodynamic Effect of Biomimetic Pigeon Feathered Wing on a 1-DoF Flapping Mechanism
Abstract
1. Introduction
2. Experimental Setup
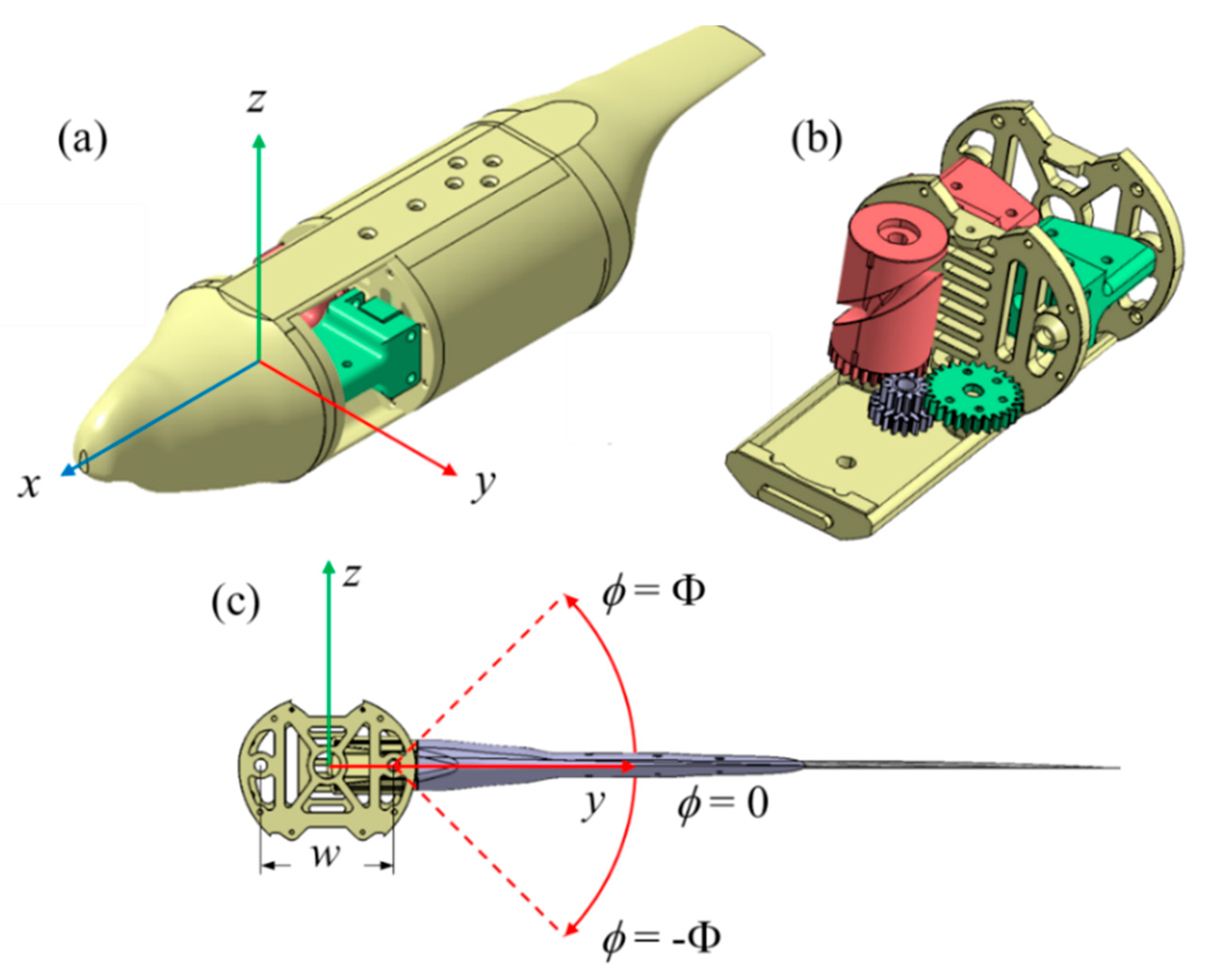
2.1. Flapping Mechanism
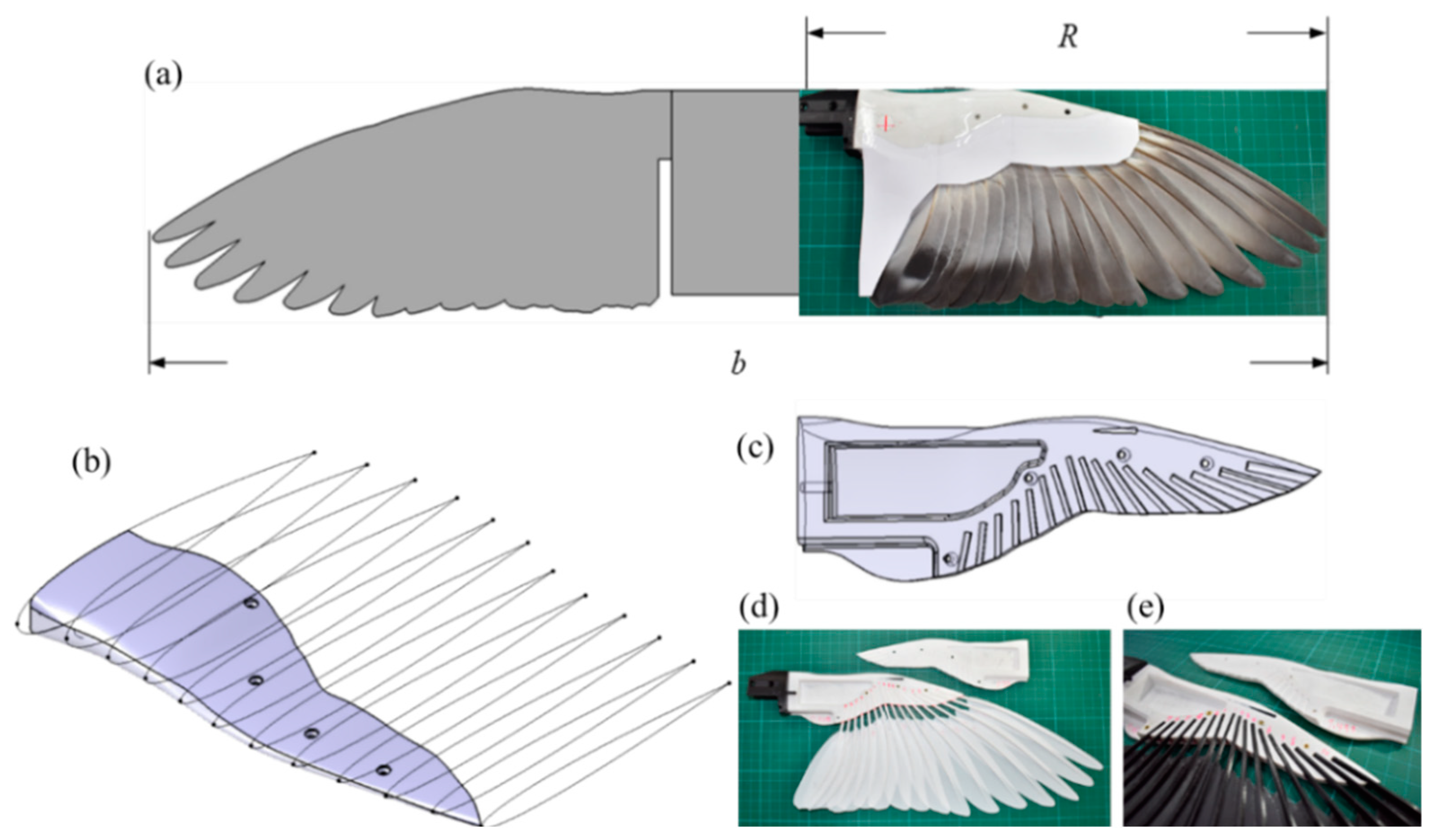
2.2. Feathered Wing Models Design
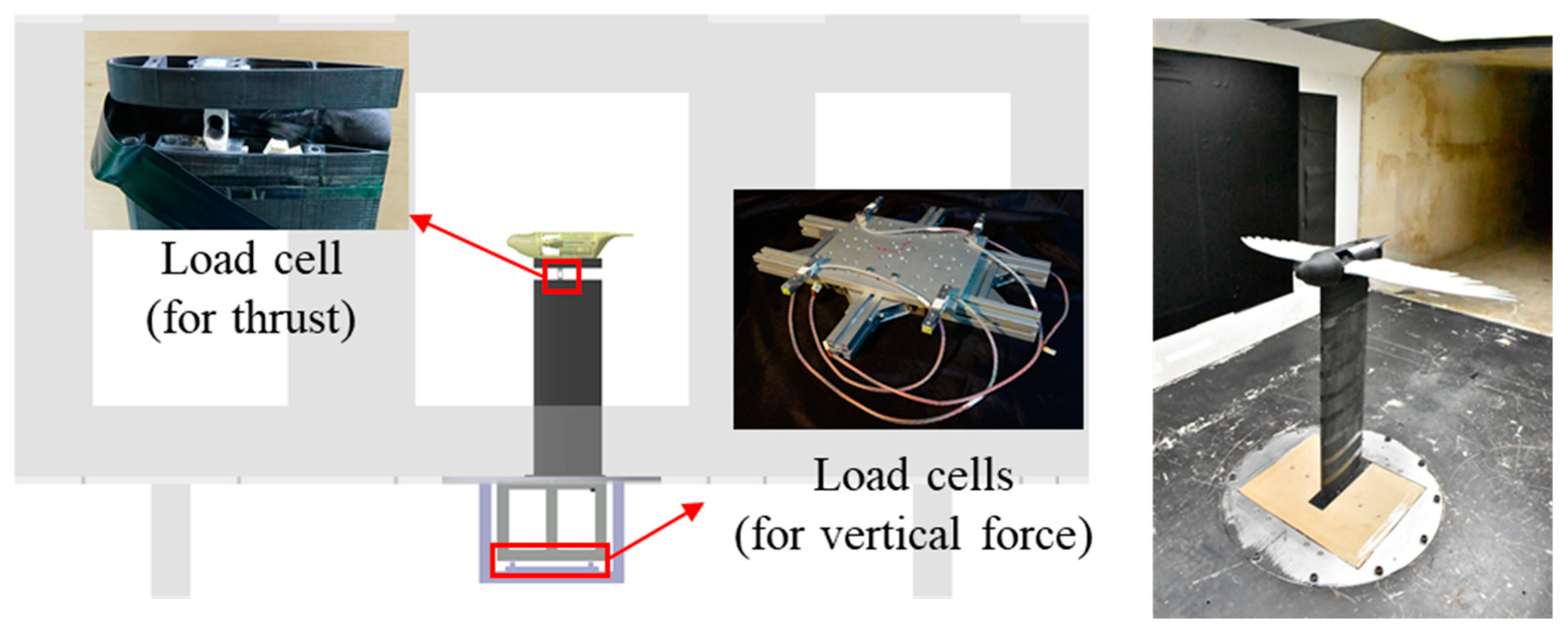
2.3. Experimental Setup
3. Results and Discussion
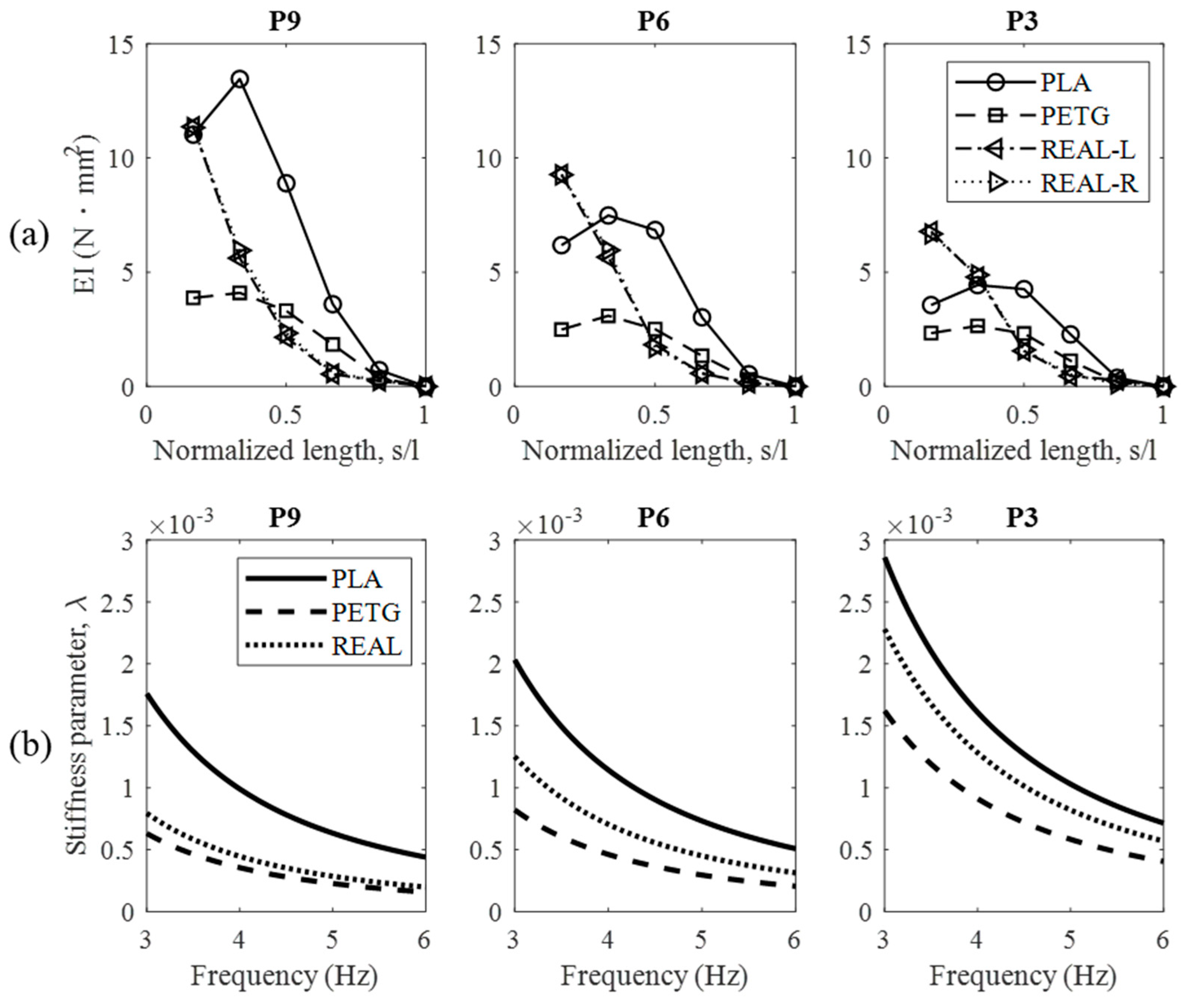
3.1. Stiffeness Distribution of the Feathers
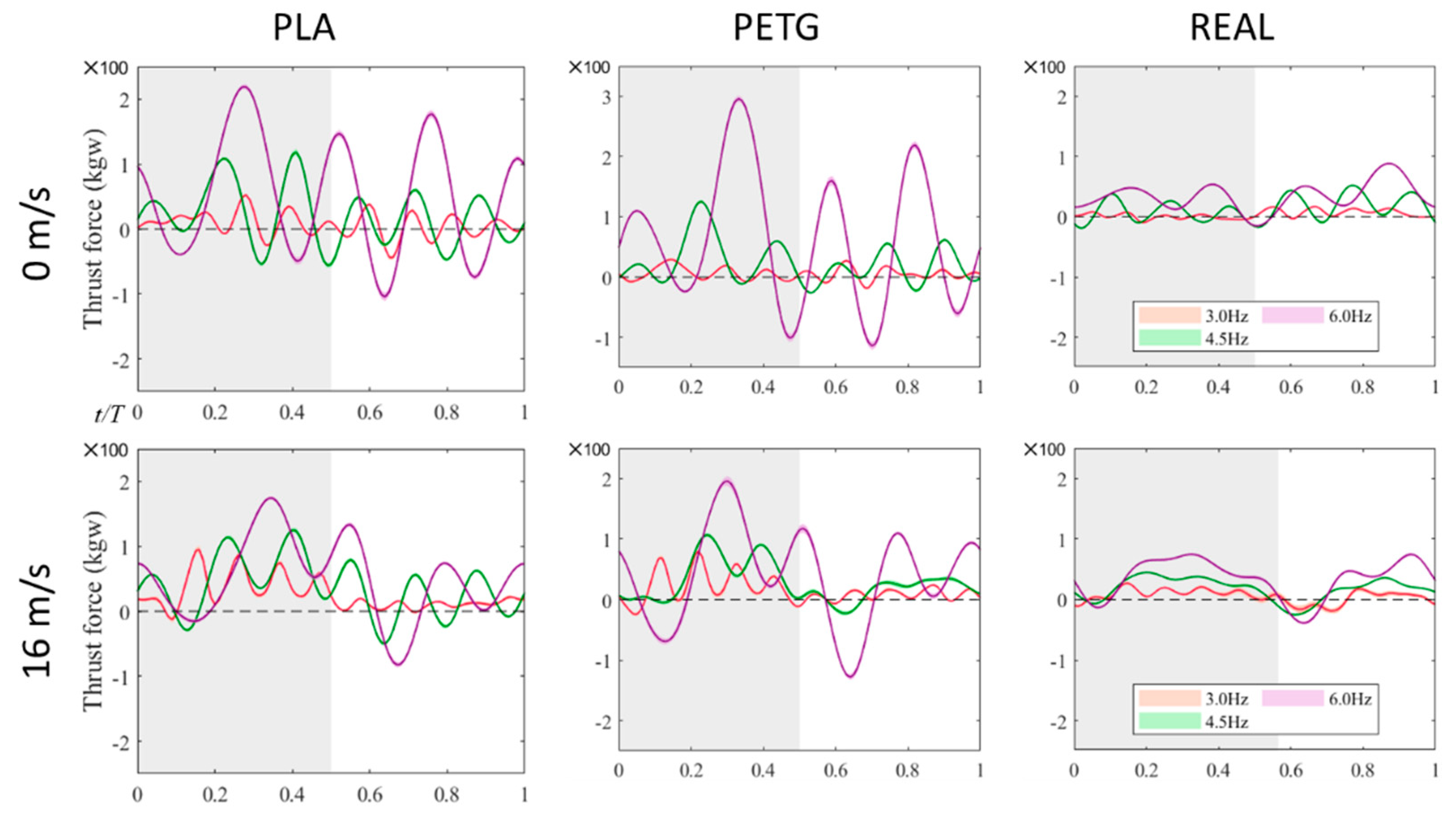
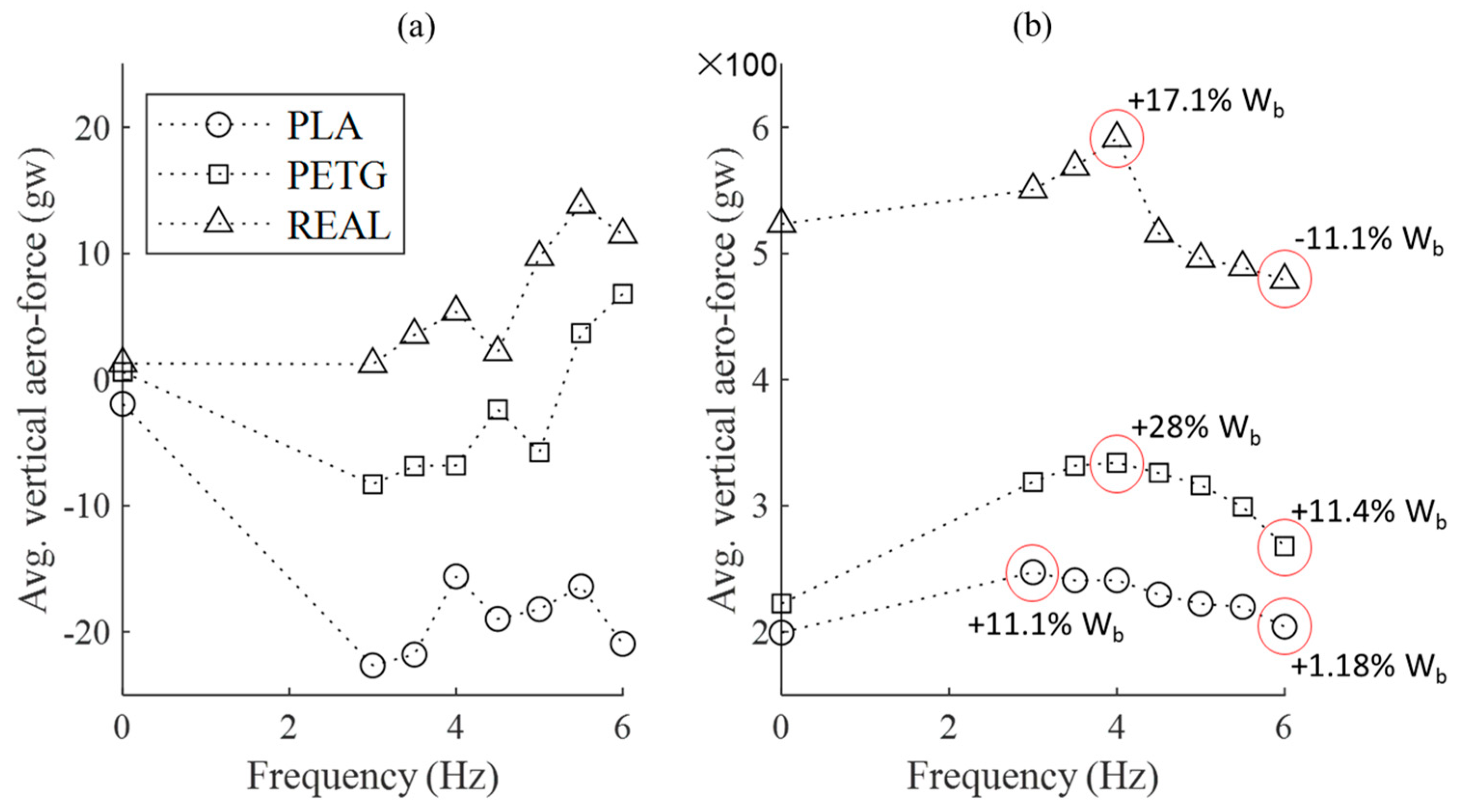
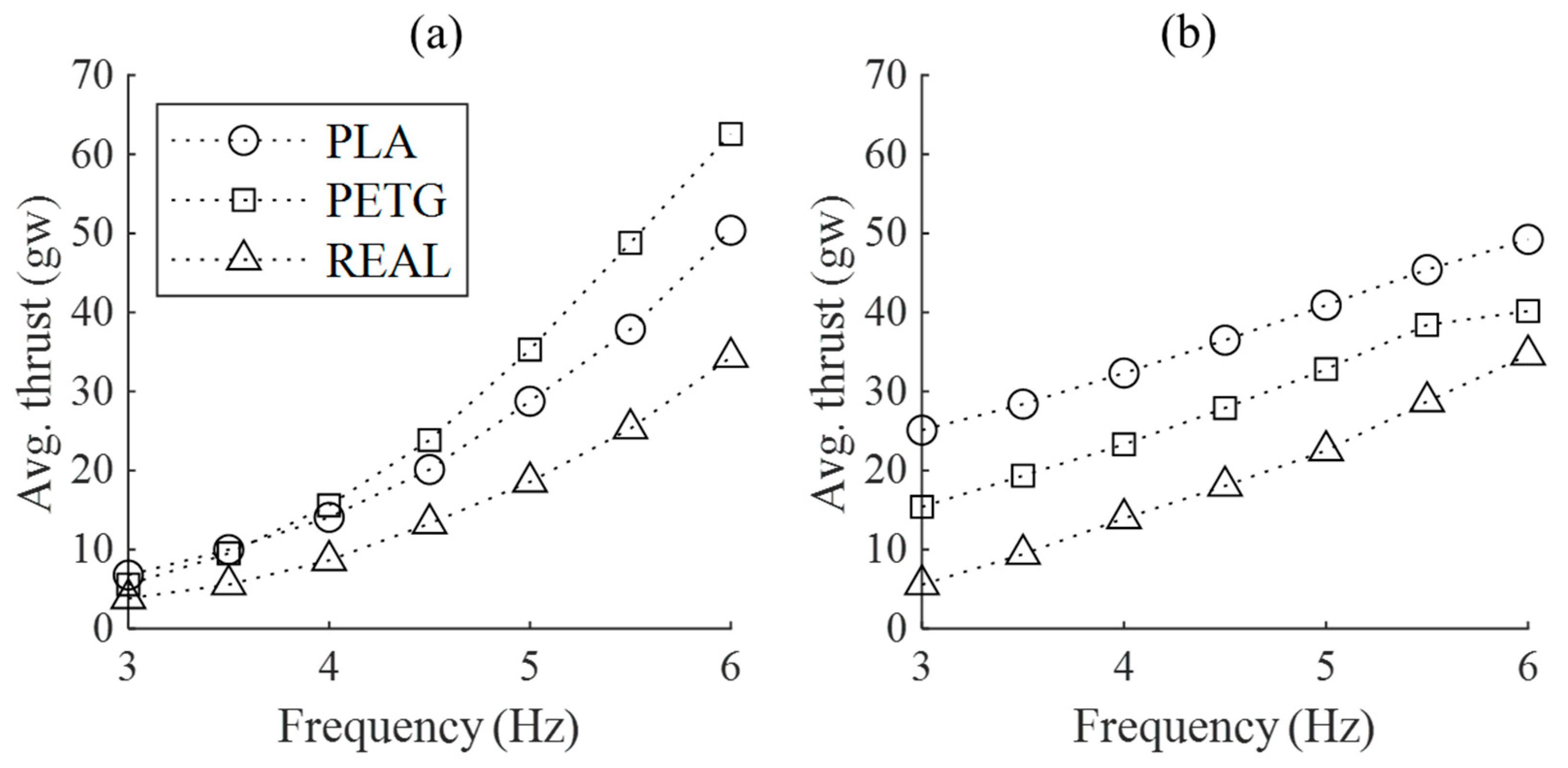
3.2. The Variations in Lift and Thrust
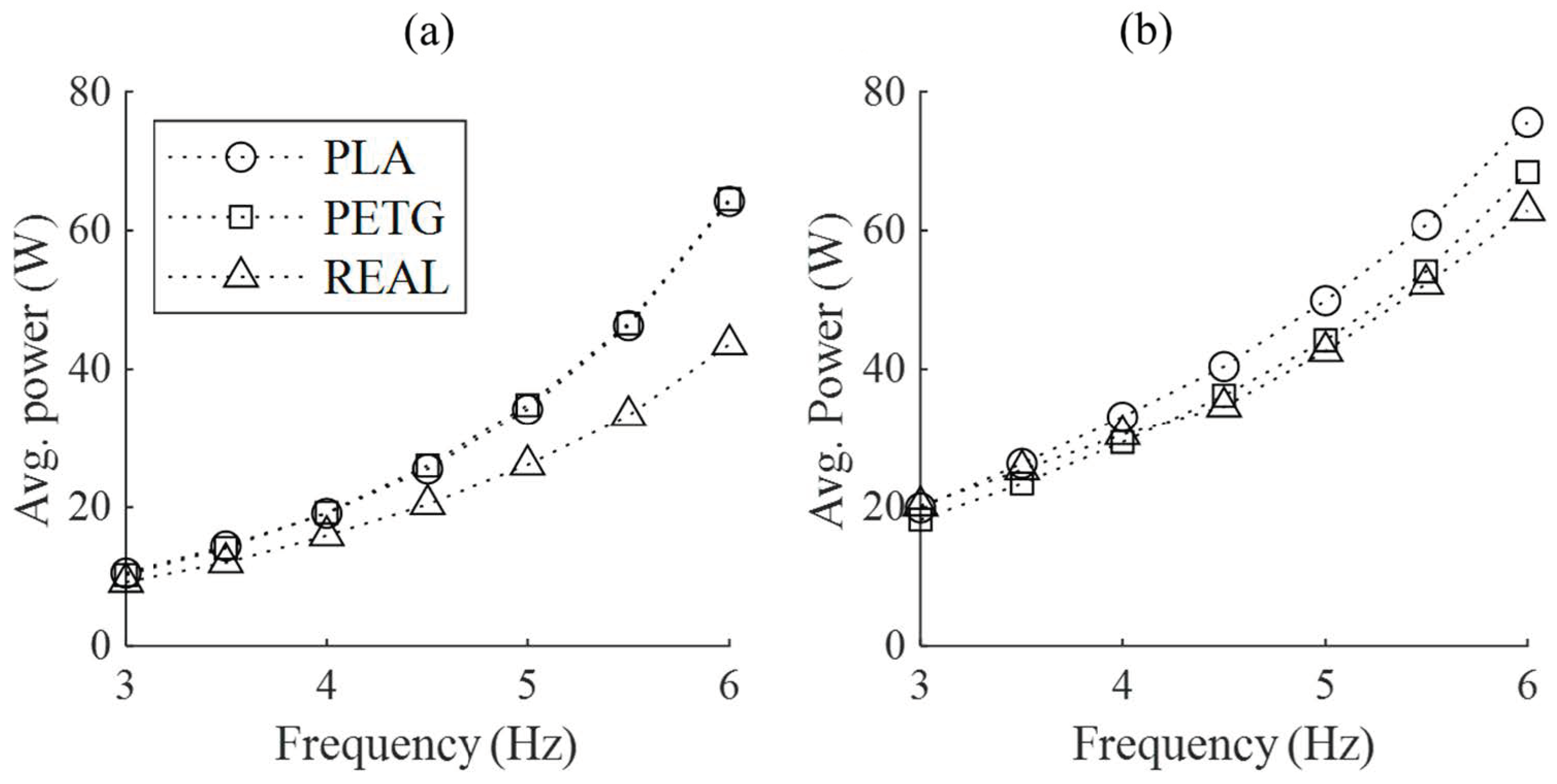
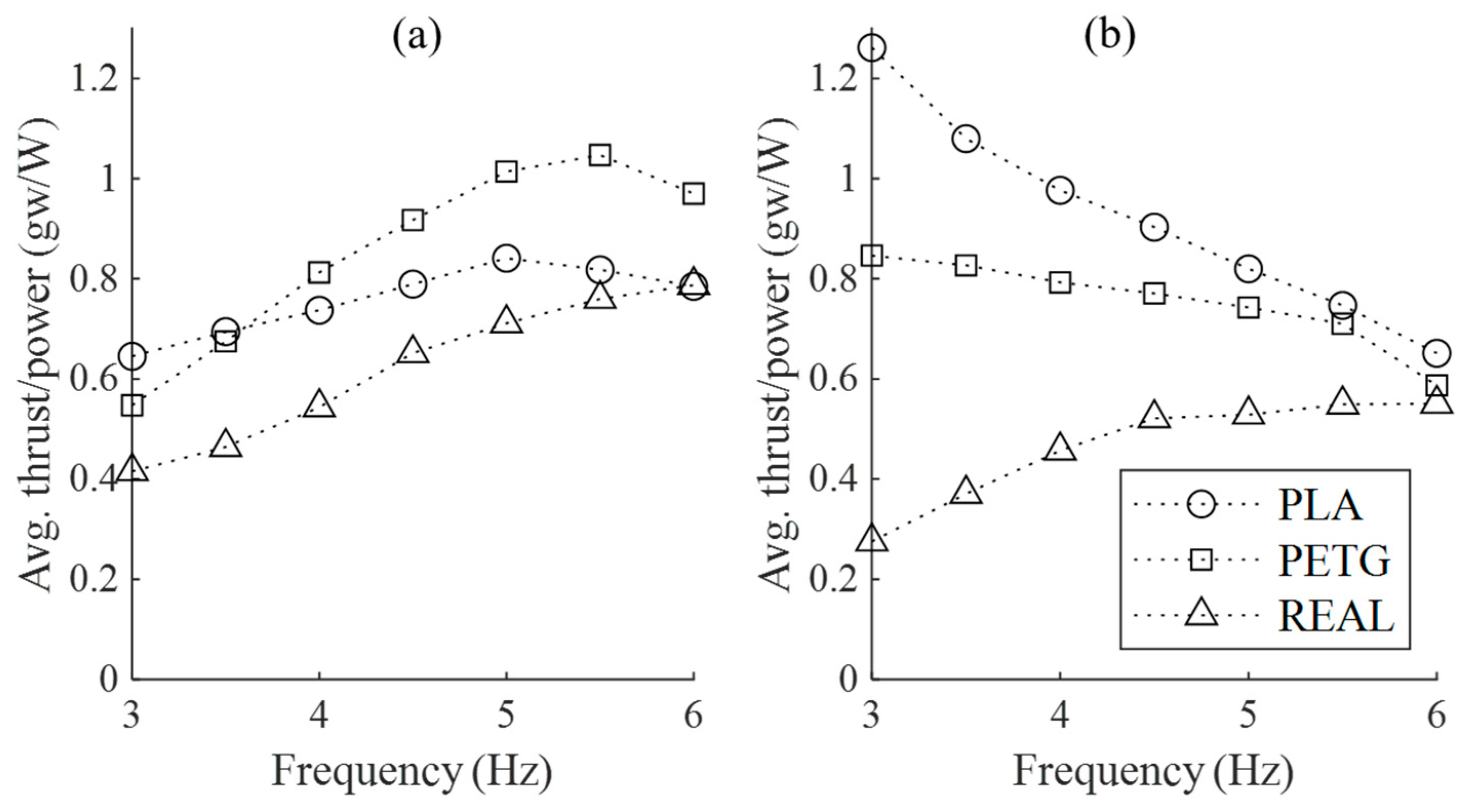
3.3. The Power Consumption of the Flapping Motion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chin, D.D.; Lentink, D. Flapping wing aerodynamics: From insects to vertebrates. J. Exp. Biol. 2016, 219, 920–932. [Google Scholar] [CrossRef] [PubMed]
- Bhar, K.; Chang, B.; Virot, E.; Straker, L.; Kang, H.; Paris, R.; Clanet, C.; Jung, S. How localized force spreads on elastic contour feathers. J. R. Soc. Interface 2019, 16, 20190267. [Google Scholar] [CrossRef] [PubMed]
- Ju, E.; Won, J.; Lee, J.; Choi, B.; Noh, J.; Choi, M.G. Data-driven control of flapping flight. ACM Trans. Graph. 2013, 32, 1–12. [Google Scholar] [CrossRef]
- Tobalske, B.W.; Dial, K.P. Flight kinematics of black-billed magpies and pigeons over a wide range of speeds. J. Exp. Biol. 1996, 199, 263–280. [Google Scholar] [CrossRef] [PubMed]
- Tobalske, B.W. Hovering and intermittent flight in birds. Bioinspir. Biomim. 2010, 5, 045004. [Google Scholar] [CrossRef]
- Muijres, F.T.; Bowlin, M.S.; Johansson, L.C.; Hedenström, A. Vortex wake, downwash distribution, aerodynamic performance and wingbeat kinematics in slow-flying pied flycatchers. J. R. Soc. Interface 2011, 9, 292–303. [Google Scholar] [CrossRef] [PubMed]
- Min, Y.; Zhao, G.; Pan, D.; Shao, X. Aspect Ratio Effects on the Aerodynamic Performance of a Biomimetic Hummingbird Wing in Flapping. Biomimetics 2023, 8, 216. [Google Scholar] [CrossRef] [PubMed]
- Basri, E.I.; Basri, A.A.; Ahmad, K.A. Computational Fluid Dynamics Analysis in Biomimetics Applications: A Review from Aerospace Engineering Perspective. Biomimetics 2023, 8, 319. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, N.; Qu, F. Bio-inspired flapping wing robots with foldable or deformable wings: A review. Bioinspir. Biomim. 2022, 18, 011002. [Google Scholar] [CrossRef]
- Chen, W.-H.; Yeh, S.-I. Aerodynamic effects on an emulated hovering passerine with different wing-folding amplitudes. Bioinspir. Biomim. 2021, 16, 046011. [Google Scholar] [CrossRef]
- Skandalis, D.A.; Segre, P.S.; Bahlman, J.W.; Groom, D.J.; Welch, K.C., Jr.; Witt, C.C.; McGuire, J.A.; Dudley, R.; Lentink, D.; Altshuler, D.L. The biomechanical origin of extreme wing allometry in hummingbirds. Nat. Commun. 2017, 8, 1047. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Song, B. Experimental investigation of aerodynamics of feather-covered flapping wing. Appl. Bion. Biomech. 2017, 2017, 3019640. [Google Scholar] [CrossRef] [PubMed]
- Gordnier, R.E.; Chimakurthi, S.K.; Cesnik, C.E.; Attar, P.J. High-fidelity aeroelastic computations of a flapping wing with spanwise flexibility. J. Fluids Struct. 2013, 40, 86–104. [Google Scholar] [CrossRef]
- Heathcote, S.; Gursul, I. Flexible flapping airfoil propulsion at low Reynolds numbers. AIAA J. 2007, 45, 1066–1079. [Google Scholar] [CrossRef]
- Zakaria, M.Y.; Allen, D.W.; Woolsey, C.A.; Hajj, M.R. Lift and drag of flapping membrane wings at high angles of attack. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Zakaria, M.Y.; Taha, H.E.; Hajj, M.R. Design optimization of flapping ornithopters: The pterosaur replica in forward flight. J. Aircr. 2016, 53, 48–59. [Google Scholar] [CrossRef]
- Mahardika, N.; Nguyen, Q.V.; Park, H.C. A pigeon-inspired design for a biomimetic flapping wing. In Active and Passive Smart Structures and Integrated Systems 2010; SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Tanaka, S.; Asignacion, A.; Nakata, T.; Suzuki, S.; Liu, H. Review of biomimetic approaches for drones. Drones 2022, 6, 320. [Google Scholar] [CrossRef]
- Luan, K.; He, M.; Xu, B.; Wang, P.; Zhou, J.; Hu, B.; Jiang, L.; Liu, H. Spontaneous directional self-cleaning on the feathers of the aquatic bird anser cygnoides domesticus induced by a transient superhydrophilicity. Adv. Funct. Mater. 2021, 31, 2010634. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Chi, Y.-T.; Hung, Y.-H.; Reyes, L.M.C.; Yeh, J.-M. UV-cured electroactive polyurethane acrylate coatings with superhydrophobic surface structure of biomimetic peacock feather for anticorrosion application. Prog. Org. Coat. 2022, 165, 106679. [Google Scholar] [CrossRef]
- Khudiyev, T.; Dogan, T.; Bayindir, M. Biomimicry of multifunctional nanostructures in the neck feathers of mallard (Anas platyrhynchos L.) drakes. Sci. Rep. 2014, 4, 4718. [Google Scholar] [CrossRef]
- Fang, X.; Wen, Y.; Gao, Z.; Gao, K.; Luo, Q.; Peng, H.; Du, R. Review of the Flight Control Method of a Bird-like Flapping-Wing Air Vehicle. Micromachines 2023, 14, 1547. [Google Scholar] [CrossRef]
- Chang, E.; Matloff, L.Y.; Stowers, A.K.; Lentink, D. Soft biohybrid morphing wings with feathers underactuated by wrist and finger motion. Sci. Robot. 2020, 5, eaay1246. [Google Scholar] [CrossRef] [PubMed]
- Matloff, L.Y.; Chang, E.; Feo, T.J.; Jeffries, L.; Stowers, A.K.; Thomson, C.; Lentink, D. How flight feathers stick together to form a continuous morphing wing. Science 2020, 367, 293–297. [Google Scholar] [CrossRef] [PubMed]
- Bachmann, T.W. Anatomical, Morphometrical and Biomechanical Studies of Barn Owls’ and Pigeons’ Wings. Ph.D. Thesis, Publikationsserver der RWTH Aachen University, Aachen, Germany, 2010. [Google Scholar]
- Purslow, P.; Vincent, J. Mechanical properties of primary feathers from the pigeon. J. Exp. Biol. 1978, 72, 251–260. [Google Scholar] [CrossRef]
- Bachmann, T.; Emmerlich, J.; Baumgartner, W.; Schneider, J.M.; Wagner, H. Flexural stiffness of feather shafts: Geometry rules over material properties. J. Exp. Biol. 2012, 215, 405–415. [Google Scholar] [CrossRef] [PubMed]
- Bonser, R.H.; Purslow, P.P. The Young’s modulus of feather keratin. J. Exp. Biol. 1995, 198, 1029–1033. [Google Scholar] [CrossRef]
- Chung, P.-H.; Yeh, S.-I. Aerodynamic effect of an alula-like vortex generator using pressure sensitive paint technique. Front. Phys. 2023, 11, 1127081. [Google Scholar] [CrossRef]
- Huang, J.-K.; Young, W.-B. The mechanical, hygral, and interfacial strength of continuous bamboo fiber reinforced epoxy composites. Compos. Part B Eng. 2019, 166, 272–283. [Google Scholar] [CrossRef]


| Real Pigeon [4] | This Study | |
|---|---|---|
| Wind speed (m/s) | 16 | 0 & 16 |
| Flapping frequency (Hz) | 5.7–6 | 6 |
| Flapping amplitude | ~46.5° | 45° |
| Stroke plane | ~90° | 90° |
| Down stroke percentage | 50% | 50% |
| Wing span (cm) | 62–72 | 73.7 |
| Avg. wing length (cm) | 28–32.5 | 32.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, S.-I.; Hsu, C.-Y. The Aerodynamic Effect of Biomimetic Pigeon Feathered Wing on a 1-DoF Flapping Mechanism. Biomimetics 2024, 9, 36. https://doi.org/10.3390/biomimetics9010036
Yeh S-I, Hsu C-Y. The Aerodynamic Effect of Biomimetic Pigeon Feathered Wing on a 1-DoF Flapping Mechanism. Biomimetics. 2024; 9(1):36. https://doi.org/10.3390/biomimetics9010036
Chicago/Turabian StyleYeh, Szu-I, and Chen-Yu Hsu. 2024. "The Aerodynamic Effect of Biomimetic Pigeon Feathered Wing on a 1-DoF Flapping Mechanism" Biomimetics 9, no. 1: 36. https://doi.org/10.3390/biomimetics9010036
APA StyleYeh, S.-I., & Hsu, C.-Y. (2024). The Aerodynamic Effect of Biomimetic Pigeon Feathered Wing on a 1-DoF Flapping Mechanism. Biomimetics, 9(1), 36. https://doi.org/10.3390/biomimetics9010036





