Vein–Membrane Interaction in Cambering of Flapping Insect Wings
Abstract
:1. Introduction
2. Modeling of Flapping Insect Wings
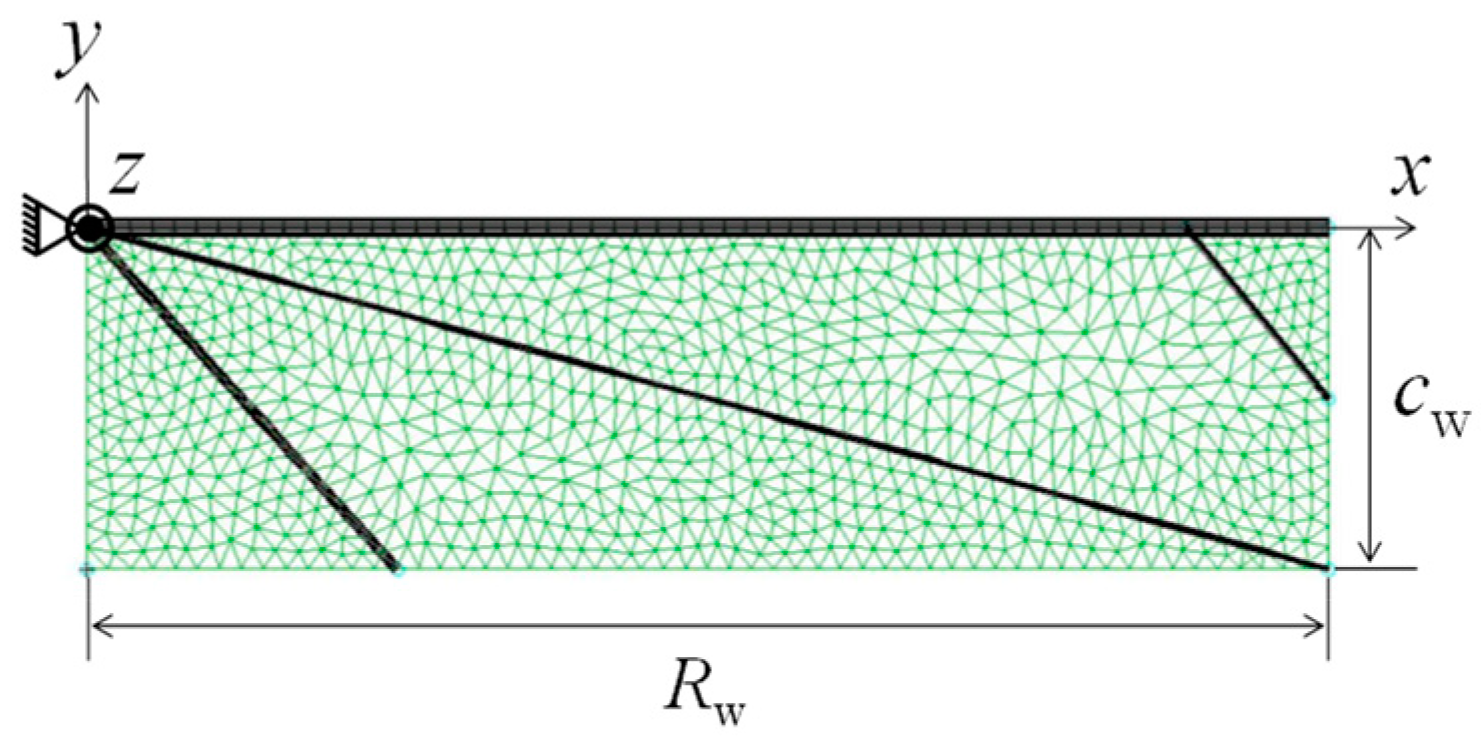
2.1. Shape Simplification Model Using Beam and Shell Structures
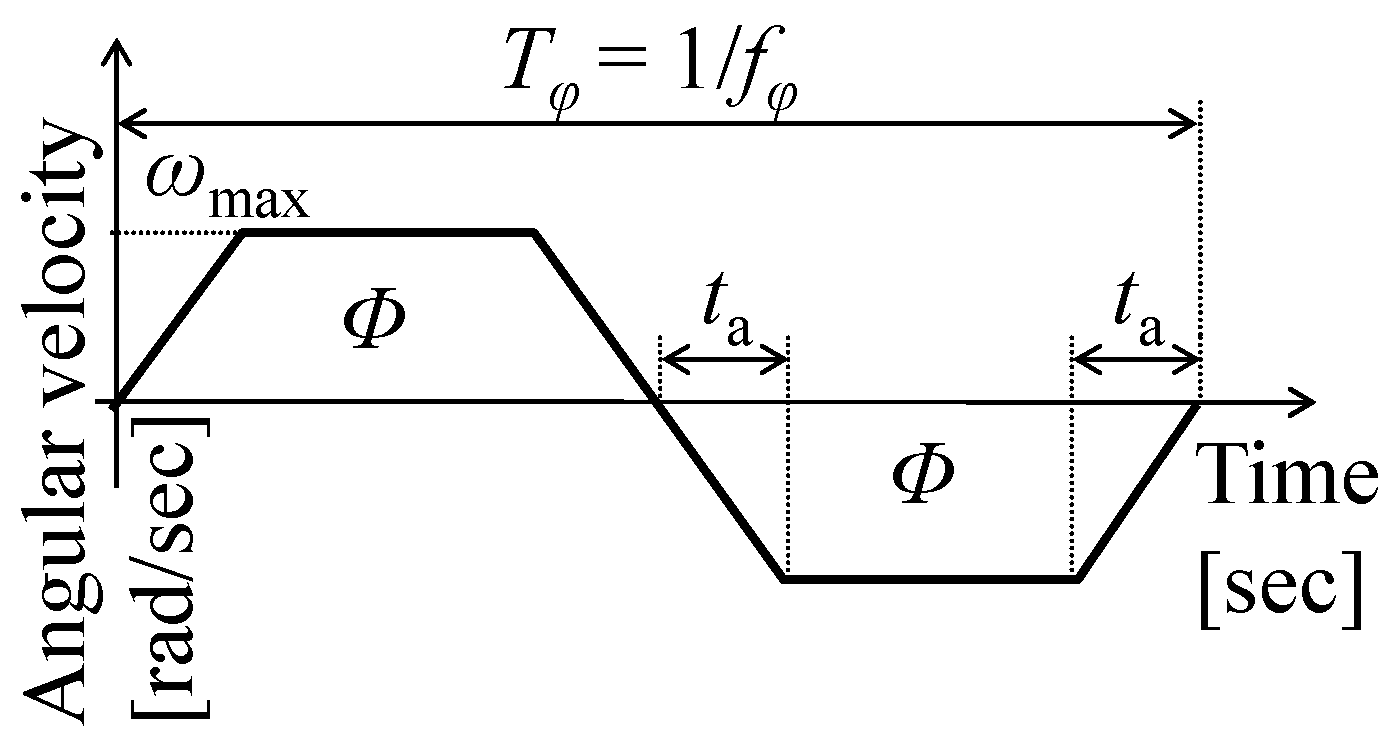
2.2. Quasi-Steady Model of Aerodynamic Forces
3. Monolithic Solution Procedure for Strongly Coupled Beam and Shell Structures with Large Deformations and Large Rotations
3.1. Governing Equations for the Body with Large Displacements and Large Rotations
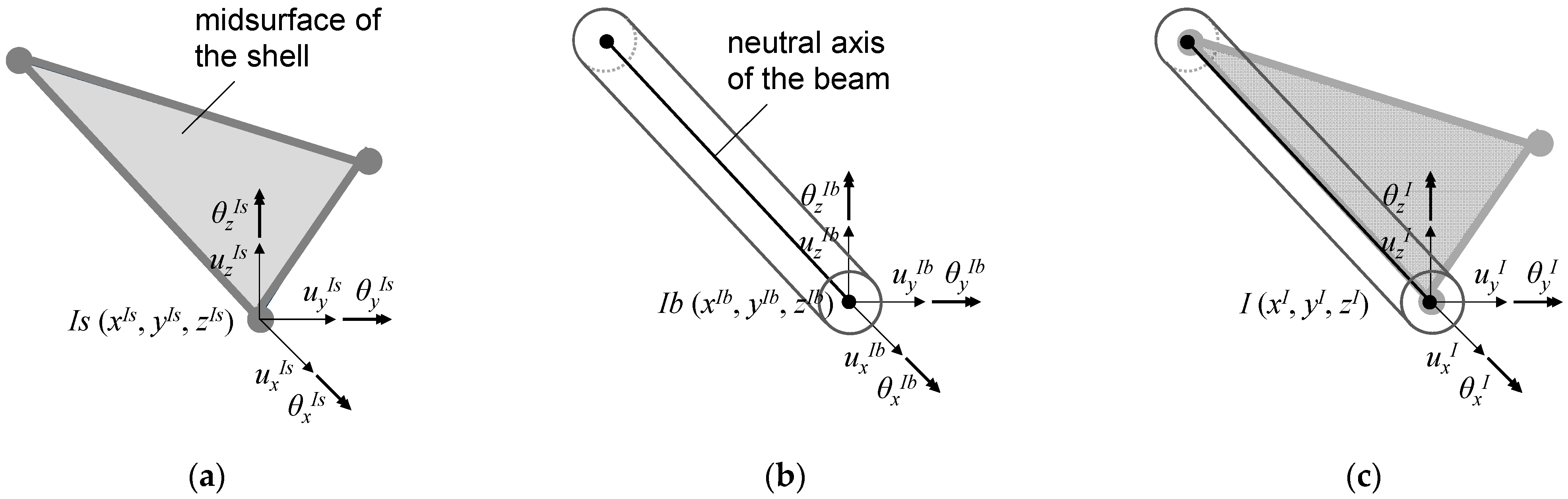
3.2. Compatible Beam and Shell Finite Elements
3.3. Nonlinear Analysis Framework
3.4. Monolithic Solution Procedure for Strongly Coupled Beam and Shell Structures
3.5. Basic Numerical Tests
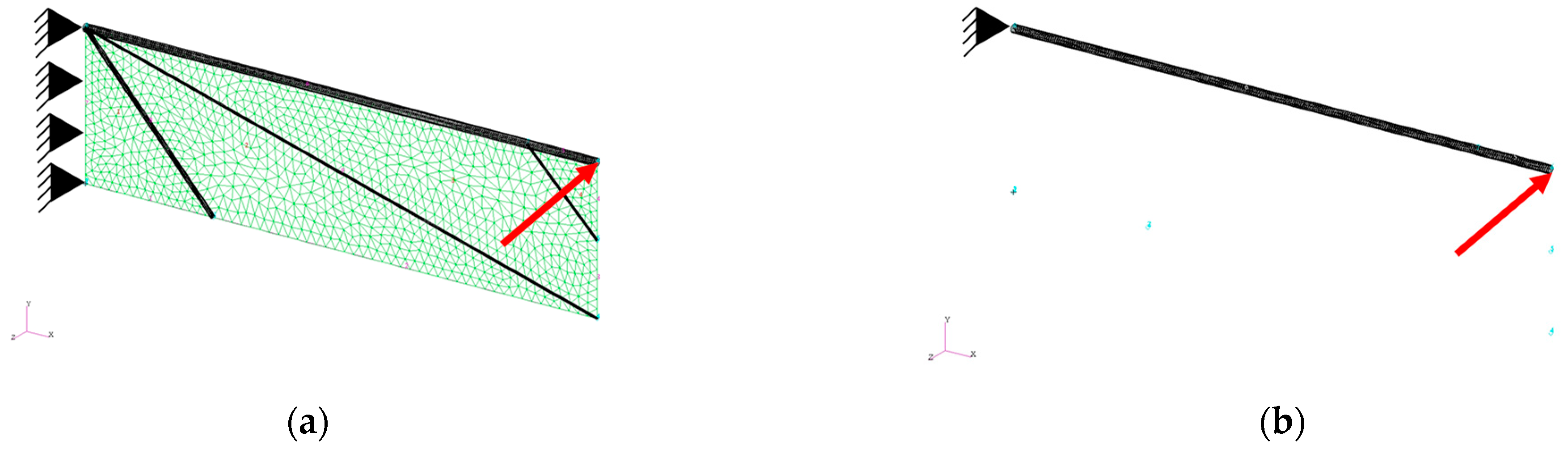
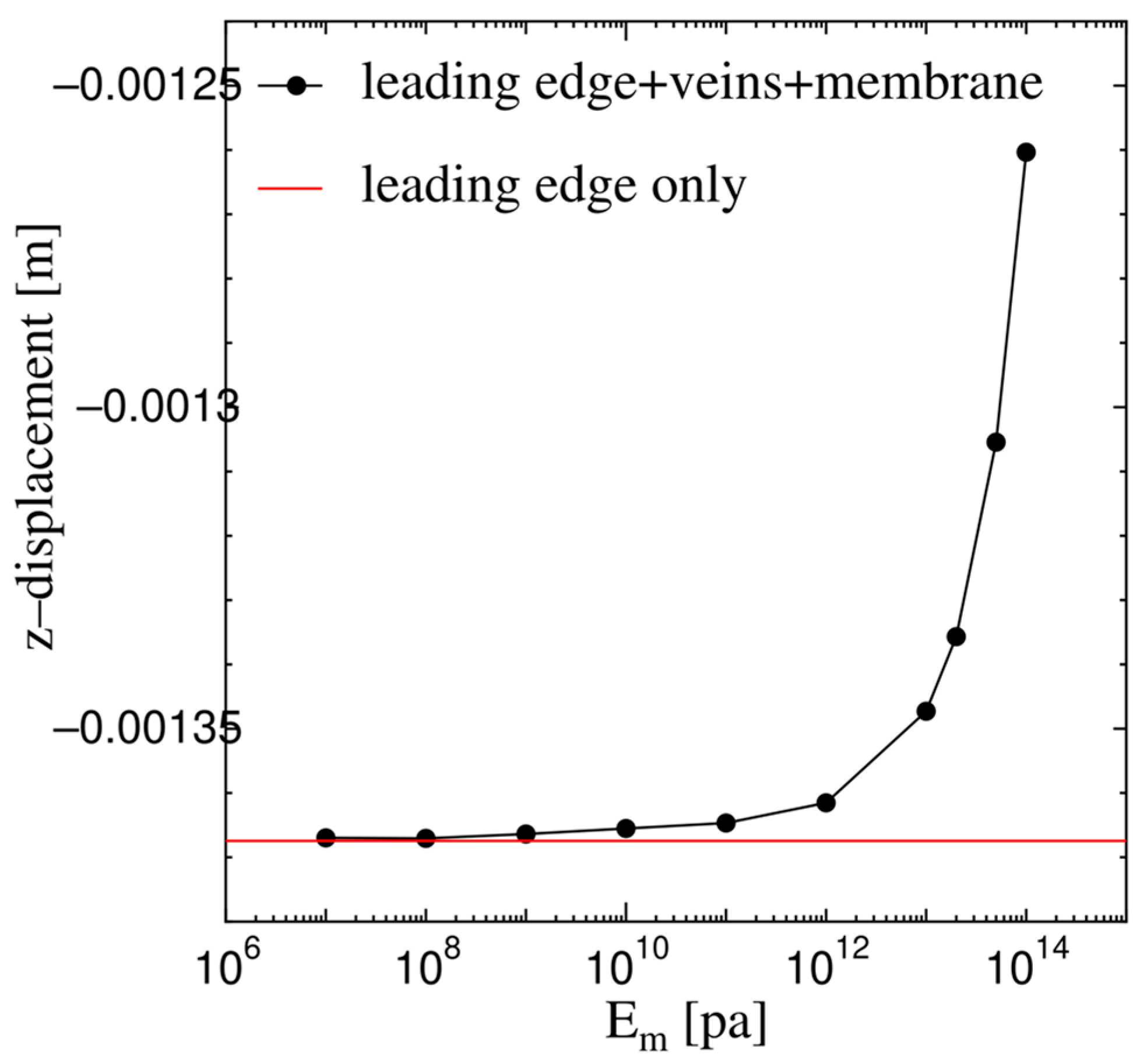
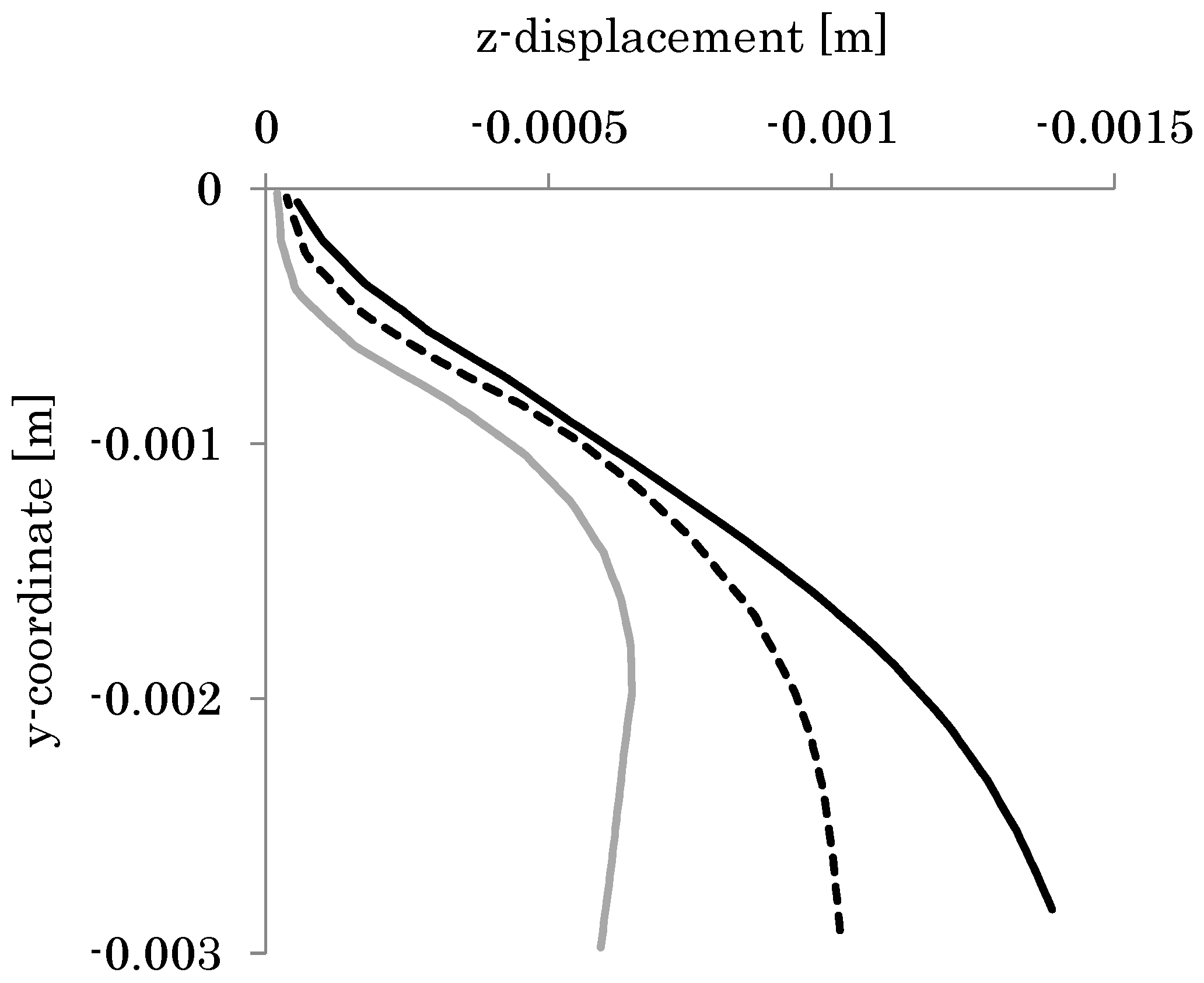
3.5.1. Convergence of the Model Wing
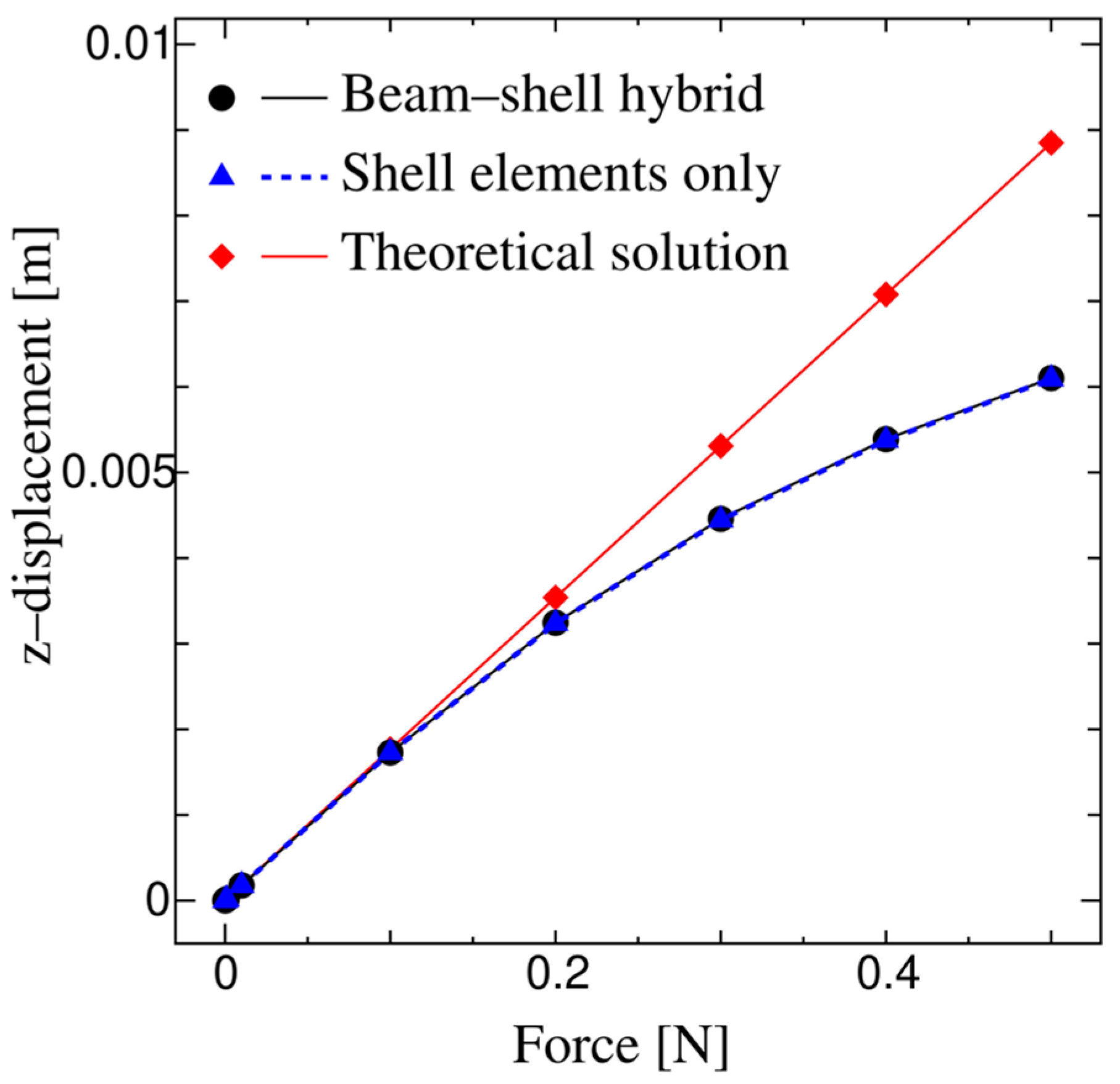
3.5.2. Bending of a Cantilever
4. Setup of Flapping Insect Wing Model
4.1. Shell Structure Representing Wing Membrane
4.2. Beams Representing the Supports from the Veins
4.3. Boundary Conditions
5. Numerical Analysis of Flapping Insect Wing Model
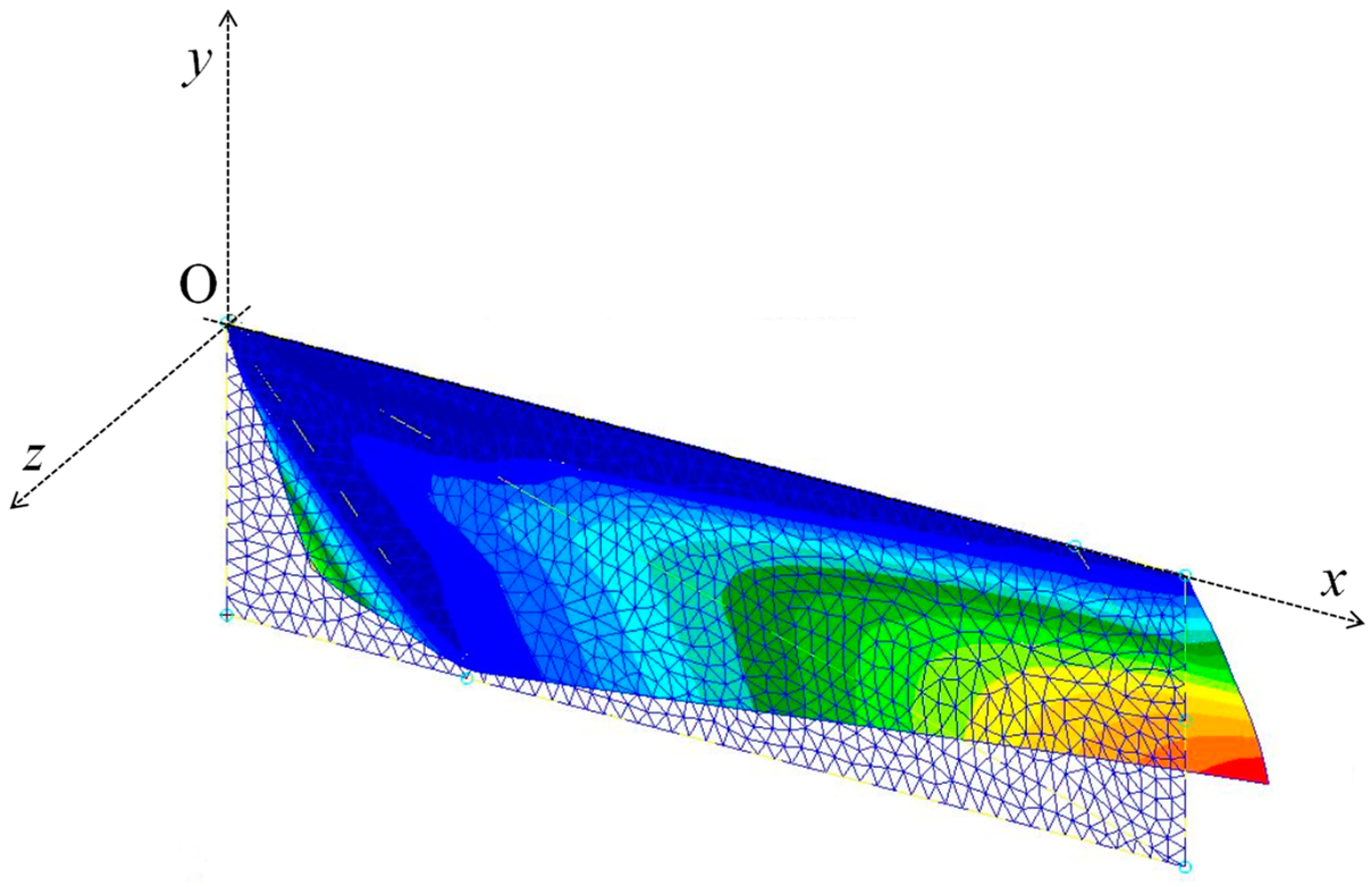
5.1. Basic Validity of the Proposed Model
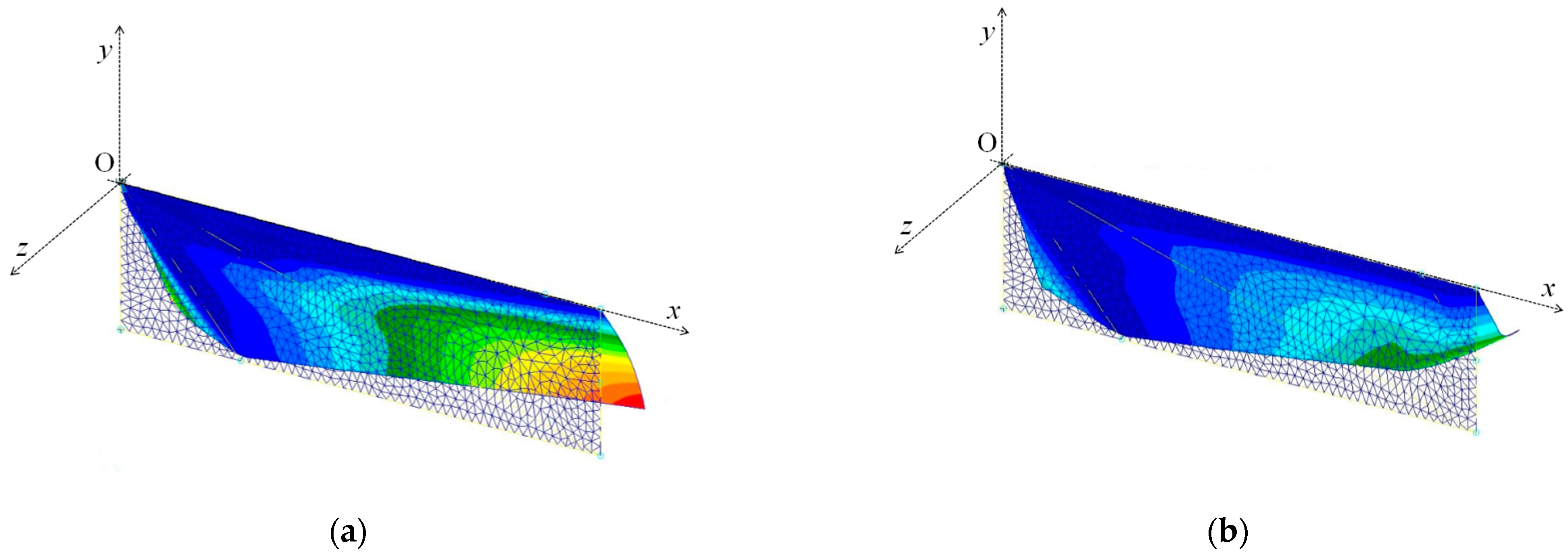
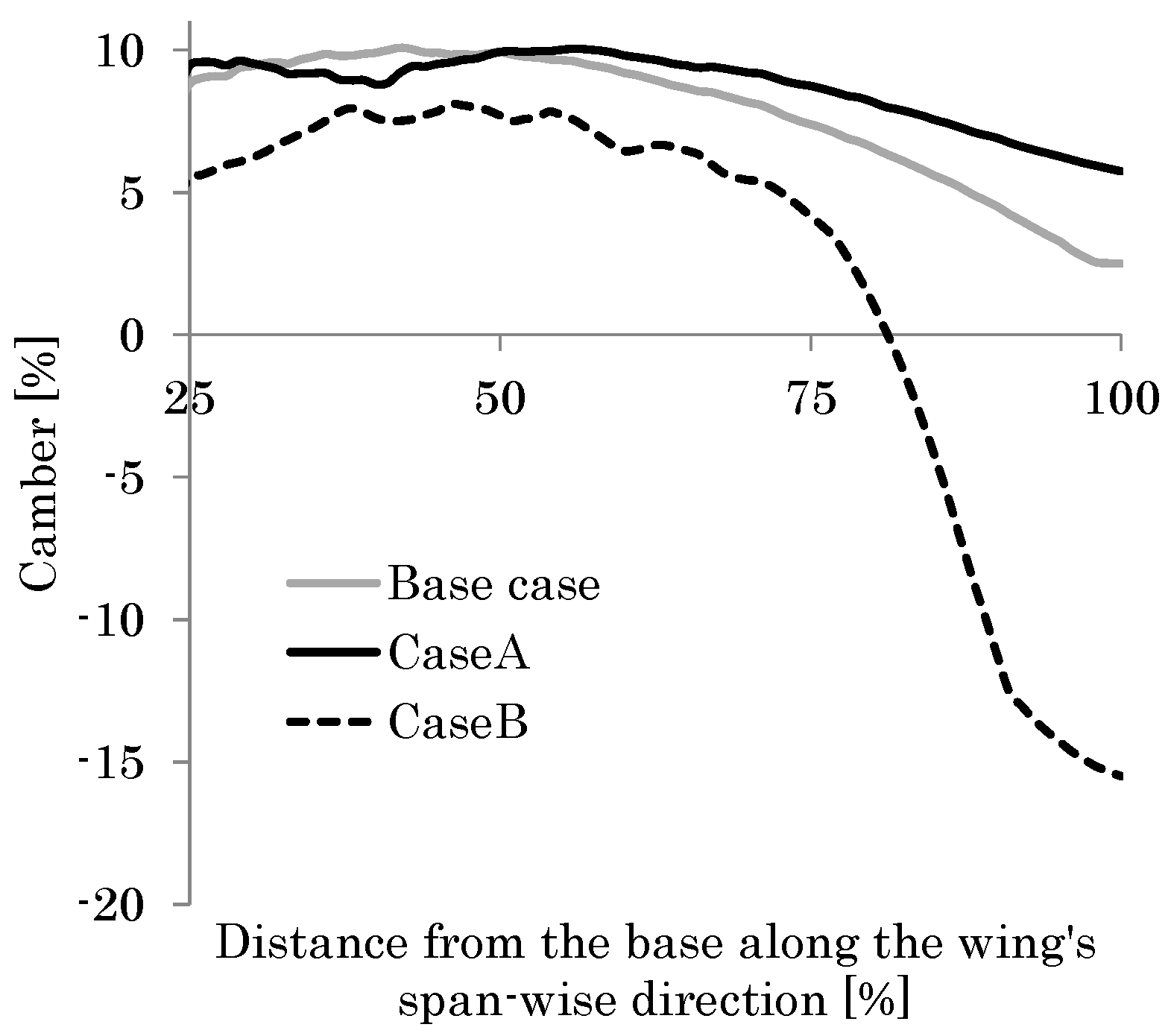
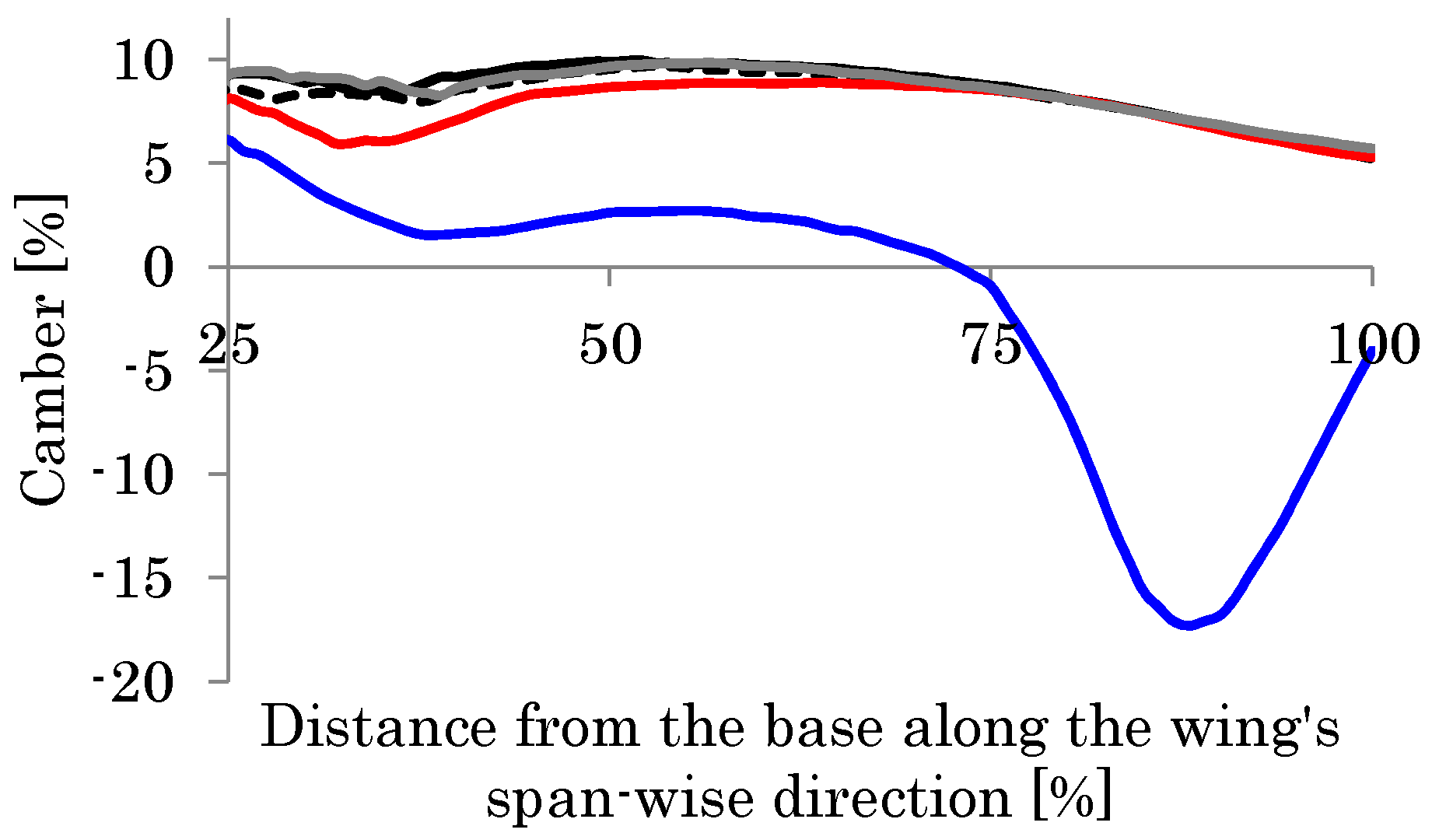
5.2. Effect of Central and Tip Veins
5.3. Effect of Torsional Flexibility of Veins near the Leading Edge
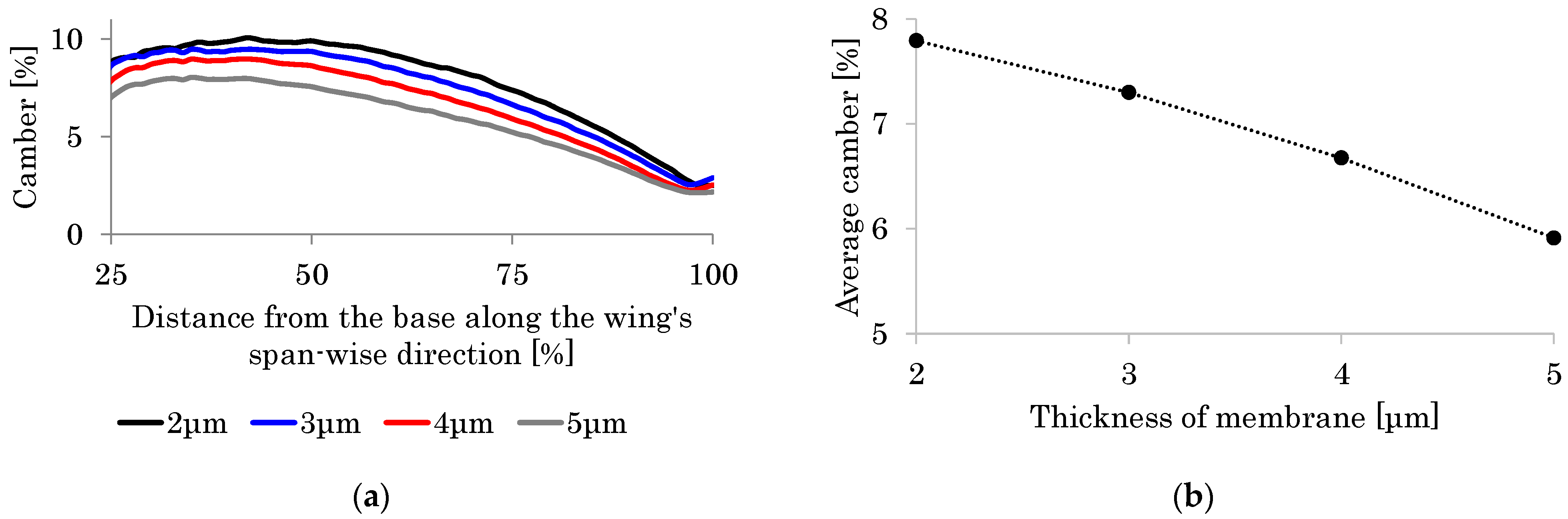
5.4. Effect of the Range of the Central Veins
6. Concluding Remarks
- (a)
- The veins crossing the central domain diagonally transmit the bending moment due to the aerodynamic pressure, such that the bending deformation increases at the middle of the chord along the length. Simultaneously, the central veins increase the bending stiffness of the wing in the vicinity of the trailing edge to restrict the bending deformation in this area. Both of these effects increase the camber effectively.
- (b)
- The veins near the wingtip increase the bending stiffness to restrict the camber in this domain.
- (c)
- The veins near the leading edge increase the initial bending angle of the wing chord in this area as their torsional flexibility increases. This effect increases the camber under the restriction of the bending deformation in the vicinity of the trailing edge given by the veins in the central domain.
- (d)
- The minimum function of the central veins required for cambering the whole wing is that they can form a local camber at the wingtip. In turn, this local camber imposes a deformation on the rest of the wing such that it causes a global camber over the whole wing.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Abbreviations and Symbols
| VMI | vein–membrane interaction |
| Cw | wing chord length |
| Cwm | mean chord length |
| Rw | one wing span length |
| Sw | wing area |
| r2 | nondimensional radius of the second moment of the wing area |
| dv | diameter of the section of the beams representing the intermediate and supplementary supports |
| hm | mean thickness of the wing membrane |
| Vm | total volume of the wing membranes |
| Vv | total volume of the veins |
| Vw | volume of the wing |
| Em | Young’s modulus for the wing membrane |
| Ev | Young’s modulus of the beams representing the intermediate and supplementary supports |
| νm | Poisson’s ratio of the wing membrane |
| νv | Poisson’s ratio of the beams representing the intermediate and supplementary supports |
| ρf | fluid mass density |
| ρw | wing mass density |
| mw | wing weight |
| Gc | bending stiffness along the wing chord |
| Gs | bending stiffness along the wing length |
| Gθ | torsional stiffnesses along the wing length |
| Φ | stroke angle |
| φ | flapping angular displacement |
| θ | feathering angle |
| fφ | flapping frequency |
| Tφ | flapping period or the inverse of fφ |
| ωmax | maximum flapping angular velocity |
| Vmax | maximum flapping speed at each point on the wing surface |
| CD | drag force coefficient |
References
- Azuma, A. The Biokinetics of Flying and Swimming; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2006.
- Brodsky, A.K. The Evolution of Insect Flight; Oxford Science Publication: Oxford, UK, 1994. [Google Scholar]
- Shyy, W.; Kang, C.; Chirarattananon, P.; Ravi, S.; Liu, H. Aerodynamics, sensing and control of insect-scale flapping-wing flight. Proc. R. Soc. A 2016, 472, 20150712. [Google Scholar] [CrossRef]
- Liu, H.; Ravi, S.; Kolomenskiy, D.; Tanaka, H. Biomechanics and biomimetics in insect-inspired flight systems. Philos. Trans. R. Soc. B 2016, 371, 20150390. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, F.-O.; Bartussek, J. Neural control and precision of flight muscle activation in Drosophila. J. Comp. Physiol. A 2017, 203, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, M.H.; Gotz, K.G. Unsteady Aerodynamic Performance of Model Wings at Low Reynolds Numbers. J. Exp. Biol. 1993, 174, 45–64. [Google Scholar] [CrossRef]
- Ellington, C.P.; Van den Berg, C.; Willmott, A.P.; Thomas, L.R. Leading-edge vortices in insect flight. Nature 1996, 384, 626–630. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.-O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef]
- Ellington, C.P. The aerodynamics of hovering insect flight. III. Kinematics. Philos. Trans. R. Soc. Lond. B 1984, 305, 41–78. [Google Scholar]
- Ishihara, D. Role of fluid-structure interaction in generating the characteristic tip path of a flapping flexible wing. Phys. Rev. E 2018, 98, 032411. [Google Scholar] [CrossRef]
- Farisenkov, S.E.; Kolomenskiy, D.; Petrov, P.N.; Engels, T.; Lapina, N.A.; Lehmann, F.-O.; Onishi, R.; Liu, H.; Polilov, A.A. Novel flight style and light wings boost flight performance of tiny beetles. Nature 2021, 602, 96–100. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.-O.; Gotz, K.G. The active control of wing rotation by Drosophila. J. Exp. Biol. 1993, 182, 173–189. [Google Scholar] [CrossRef]
- Beatus, T.; Cohen, I. Wing-pitch modulation in maneuvering fruit flies is explained by an interplay between aerodynamics and a torsional spring. Phys. Rev. E 2015, 92, 022712. [Google Scholar] [CrossRef] [PubMed]
- Ennos, A.R. The importance of torsion in the design of insect wings. J. Exp. Biol. 1988, 140, 137–160. [Google Scholar] [CrossRef]
- Ennos, A.R. The inertial cause of wing rotation in Diptera. J. Exp. Biol. 1988, 140, 161–169. [Google Scholar] [CrossRef]
- Ishihara, D.; Horie, T.; Denda, M. A two-dimensional computational study on the fluid-structure interaction cause of wing pitch changes in dipteran flapping flight. J. Exp. Biol. 2009, 212, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Ishihara, D.; Horie, T. Passive mechanism of pitch recoil in flapping insect wings. Bioinspiratoin Biomim. 2016, 12, 016008. [Google Scholar] [CrossRef] [PubMed]
- Dudley, R. The Biomechanics of Insect Flight; Princeton University Press: Princeton, NJ. USA, 2000. [Google Scholar]
- Wootton, R.J.; Herbert, R.C.; Young, P.G.; Evans, K.E. Approaches to the structural modelling of insect wings. Philos. Trans. R. Soc. Lond. B 2003, 358, 1577–1587. [Google Scholar] [CrossRef] [PubMed]
- Wootton, R.J. The geometry and mechanics of insect wing deformations in flight: A modelling approach. Insects 2020, 11, 446. [Google Scholar] [CrossRef]
- Du, G.; Sun, M. Effects of wing deformation on aerodynamic forces in hovering hoverflies. J. Exp. Biol. 2010, 213, 2273–2283. [Google Scholar] [CrossRef]
- Wang, Q.; Goosen, J.F.L.; van Keulen, F. An efficient fluid–structure interaction model for optimizing twistable flapping wings. J. Fluids Struct. 2017, 73, 82–99. [Google Scholar] [CrossRef]
- Yoon, S.-H.; Cho, H.; Lee, J.; Kim, C.; Shin, S.-J. Effects of camber angle on aerodynamic performance of flapping-wing micro air vehicle. J. Fluids Struct. 2020, 97, 103101. [Google Scholar] [CrossRef]
- Haoyuan, S.; Daochun, L.; Zi, K.; Huadong, L.; Dian, Y.; Jinwu, X. Influence of wing camber on aerodynamic performance of flapping wing rotor. Aerosp. Sci. Technol. 2021, 113, 106732. [Google Scholar]
- Kesel, A.B.; Philippi, U.; Nachtigall, W. Biomechanical aspects of the insect wing: An analysis using the finite element method. Comput. Biol. Med. 1998, 28, 423–437. [Google Scholar] [CrossRef] [PubMed]
- Herbert, R.C.; Young, P.G.; Smith, C.W.; Wootton, R.J.; Evans, K.E. The hind wing of the desert locust (Schistocerca gregaria Forskal) III. A finite element analysis of a deployable structure. J. Exp. Biol. 2000, 203, 2945–2955. [Google Scholar] [CrossRef] [PubMed]
- Combes, S.A.; Daniel, T.L. Flexural stiffness in insect wings I. Scaling and the influence of wing venation. J. Exp. Biol. 2003, 206, 2979–2987. [Google Scholar] [CrossRef] [PubMed]
- Combes, S.A.; Daniel, T.L. Into thin air: Contributions of aerodynamic and inertial-elastic forces to wing bending in the hawkmoth Manduca sexta. J. Exp. Biol. 2003, 206, 2999–3006. [Google Scholar] [CrossRef] [PubMed]
- Mengesha, T.E.; Vallance, R.R.; Barraja, M.; Mittal, R. Parametric structural modeling of insect wings. Bioinspir. Biomim. 2009, 4, 036004. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, J.; Donoughe, S.; Li, K.; Salcedo, M.K.; Rycroft, C.H. A simple developmental model recapitulates complex insect wing venation patterns. Proc. Natl. Acad. Sci. USA 2018, 115, 9905–99102. [Google Scholar] [CrossRef]
- Rees, C.J.C. Form and functions in corrugated insect wings. Nature 1975, 256, 200–203. [Google Scholar] [CrossRef]
- Sunada, S.; Zeng, L.; Kawachi, K. The relationship between dragonfly wing structure and torsional deformation. J. Theor. Biol. 1998, 193, 39–45. [Google Scholar] [CrossRef]
- Tanaka, H.; Wood, R.J. Fabrication of corrugated artificial insect wings using laser micromachined molds. J. Micromech. Microeng. 2010, 20, 075008. [Google Scholar] [CrossRef]
- Wootton, R.J. Functional morphology of insect wings. Annu. Rev. Entomol. 1992, 37, 113–140. [Google Scholar] [CrossRef]
- Wang, X.S.; Li, Y.; Shi, Y.F. Effects of sandwich microstructures on mechanical behaviors of dragonfly wing vein. Compos. Sci. Technol. 2008, 68, 186–192. [Google Scholar] [CrossRef]
- Wootton, R.J. The functional morphology of the wings of Odonata. Adv. Odonatol. 1991, 5, 153–169. [Google Scholar]
- Rajabi, H.; Ghoroubi, N.; Darvizeh, A.; Dirks, J.-H.; Appel, E.; Gorb, S.N. A comparative study of the effects of vein-joints on the mechanical behaviour of insect wings: I. Single joints. Bioinspir. Biomim. 2015, 10, 056003. [Google Scholar] [CrossRef] [PubMed]
- Rajabi, H.; Ghoroubi, N.; Stamm, K.; Appel, E.; Gorb, S.N. Dragonfly wing nodus: A one-way hinge contributing to the asymmetric wing deformation. Acta Biomater. 2017, 60, 330–338. [Google Scholar] [CrossRef] [PubMed]
- Zienkiewicz, O.C.; Talor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Herbert, R.C.; Young, P.G.; Smith, C.W.; Wootton, R.J.; Evans, K.E. The hind wing of the desert locust (Schistocerca gregaria Forskal) I. Functional morphology and mode of operation. J. Exp. Biol. 2000, 203, 2921–2931. [Google Scholar]
- Gorb, S.N. Serial elastic elements in the damselfly wing: Mobile vein joints contain resilin. Naturwissenschaften 1999, 86, 552–555. [Google Scholar] [CrossRef]
- Ma, Y.; Ning, J.G.; Ren, H.L.; Zhang, P.F.; Zhao, H.Y. The function of resilin in honeybee wings. J. Exp. Biol. 2015, 218, 2136–2142. [Google Scholar] [CrossRef]
- Ma, Y.; Ren, H.L.; Rajabi, H.; Zhao, H.; Ning, J.G.; Gorb, S.N. Structure, properties and functions of the forewing-hindwing coupling of honeybees. J. Insect Physiol. 2019, 118, 103936. [Google Scholar] [CrossRef]
- Ennos, A.R. The kinematics and aerodynamics of the free flight of some Diptera. J. Exp. Biol. 1989, 142, 49–85. [Google Scholar] [CrossRef]
- Nakata, T.; Liu, H. A fluid–structure interaction model of insect flight with flexible wings. J. Comput. Phys. 2012, 231, 1822–1847. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- Rugonyi, S.; Bathe, K.J. On finite element analysis of fluid flows fully coupled with structural interactions. Comput. Model. Eng. Sci. 2001, 2, 195–212. [Google Scholar]
- Ishihara, D.; Horie, T. A projection method for the interaction of an incompressible fluid and a structure using new algebraic splitting. Comput. Model. Eng. Sci. 2014, 101, 421–440. [Google Scholar]
- Walker, S.M.; Thomas, A.L.R.; Taylor, G.K. Deformable wing kinematics in free-flying hoverflies. J. R. Soc. Interface 2010, 7, 131–142. [Google Scholar] [CrossRef] [PubMed]
- Wootton, R.J. Support and deformability in insect wings. J. Zool. Lond. 1981, 193, 447–468. [Google Scholar] [CrossRef]
- Weis-Fogh, T. Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production. J. Exp. Biol. 1973, 59, 169–230. [Google Scholar] [CrossRef]
- Sane, S.P. The aerodynamics of insect flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef]
- Whitney, J.P.; Wood, R.J. Aeromechanics of passive rotation in flapping flight. J. Fluid Mech. 2010, 660, 197–220. [Google Scholar] [CrossRef]
- Ishihara, D.; Horie, T.; Niho, T. An experimental and three-dimensional computational study on the aerodynamic contribution to the passive pitching motion of flapping wings in hovering flies. Bioinspir. Biomim. 2014, 9, 046009. [Google Scholar] [CrossRef]
- Ennos, A.R. Inertial and aerodynamic torques on the wings of Diptera in flight. J. Exp. Biol. 1989, 142, 87–95. [Google Scholar] [CrossRef]
- Ellington, C.P. The aerodynamics of hovering insect flight. II. Morphological Parameters. Philos. Trans. R. Soc. Lond. B 1984, 305, 17–40. [Google Scholar]
- Wainwright, S.A.; Biggs, W.D.; Currey, J.D.; Gosline, J.M. Mechanical Design in Organisms; Princeton University Press: Princeton, NJ, USA, 1982. [Google Scholar]
- Tanaka, H.; Whitney, J.P.; Wood, R.J. Effect of flexural and torsional wing flexibility on lift generation in hoverfly flight. Integr. Comp. Biol. 2011, 51, 142–150. [Google Scholar] [CrossRef] [PubMed]
- Dirks, J.-H.; Taylor, D. Veins improve fracture toughness of insect wings. PLoS ONE 2012, 7, e43411. [Google Scholar] [CrossRef] [PubMed]
- Sample, C.S.; Xu, A.K.; Swartz, S.M.; Gibson, L.J. Nanomechanical properties of wing membrane layers in the housecricket (Acheta domesticus Linnaeus). J. Insect Physiol. 2015, 74, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Bao, X.Q.; Bontemps, A.; Gronde, S.; Cattan, E. Design and fabrication of insect-inspired composite wings for MAV application using MEMS technology. J. Micromech. Microeng. 2011, 21, 125020. [Google Scholar] [CrossRef]
- Ma, Y.; Ma, T.; Ning, J.; Gorb, S. Structure and tensile properties of the forewing costal vein of the honeybee Apis mellifera. Soft Matter 2020, 16, 4057–4064. [Google Scholar] [CrossRef] [PubMed]
- Ishihara, D.; Murakami, S.; Ohira, N.; Ueo, J.; Takagi, M.; Urakawa, K.; Horie, T. Polymer Micromachined Transmission for insect-inspired flapping wing nano air vehicles. In Proceedings of the 2020 IEEE 15th International Conference on Nano/Micro Engineered and Molecular System (NEMS), San Diego, CA, USA, 27–30 September 2020; pp. 176–179. [Google Scholar]
- Rashmikant; Ishihara, D.; Suetsugu, R.; Ramegowda, P.C. One-wing polymer micromachined transmission for insect-inspired flapping wing nano air vehicles. Eng. Res. Express 2021, 3, 045006. [Google Scholar] [CrossRef]
- Rashmikant; Suetsugu, R.; Onishi, M.; Ishihara, D. First prototype of polymer micromachined flapping wing nano air vehicle. In Proceedings of the 2023 IEEE 36th International Conference on Micro Electro Mechanical Systems (MEMS), Munich, Germany, 15–19 January 2023; pp. 534–537. [Google Scholar]
- Ishihara, D.; Onishi, M. Computational fluid-structure interaction framework for passive feathering and cambering in flapping insect wings. Int. J. Numer. Methods Fluids. 2021; in printing. [Google Scholar]
- Onishi, M.; Ishihara, D. Partitioned method of insect flapping flight for maneuvering analysis. Comput. Model. Eng. Sci. 2019, 121, 145–175. [Google Scholar] [CrossRef]
- Magome, N.; Morita, N.; Kaneko, S.; Mitsume, N. Higher-continuity s-version of finite element method with B-spline functions. J. Comput. Phys. 2023, 112593. [Google Scholar] [CrossRef]

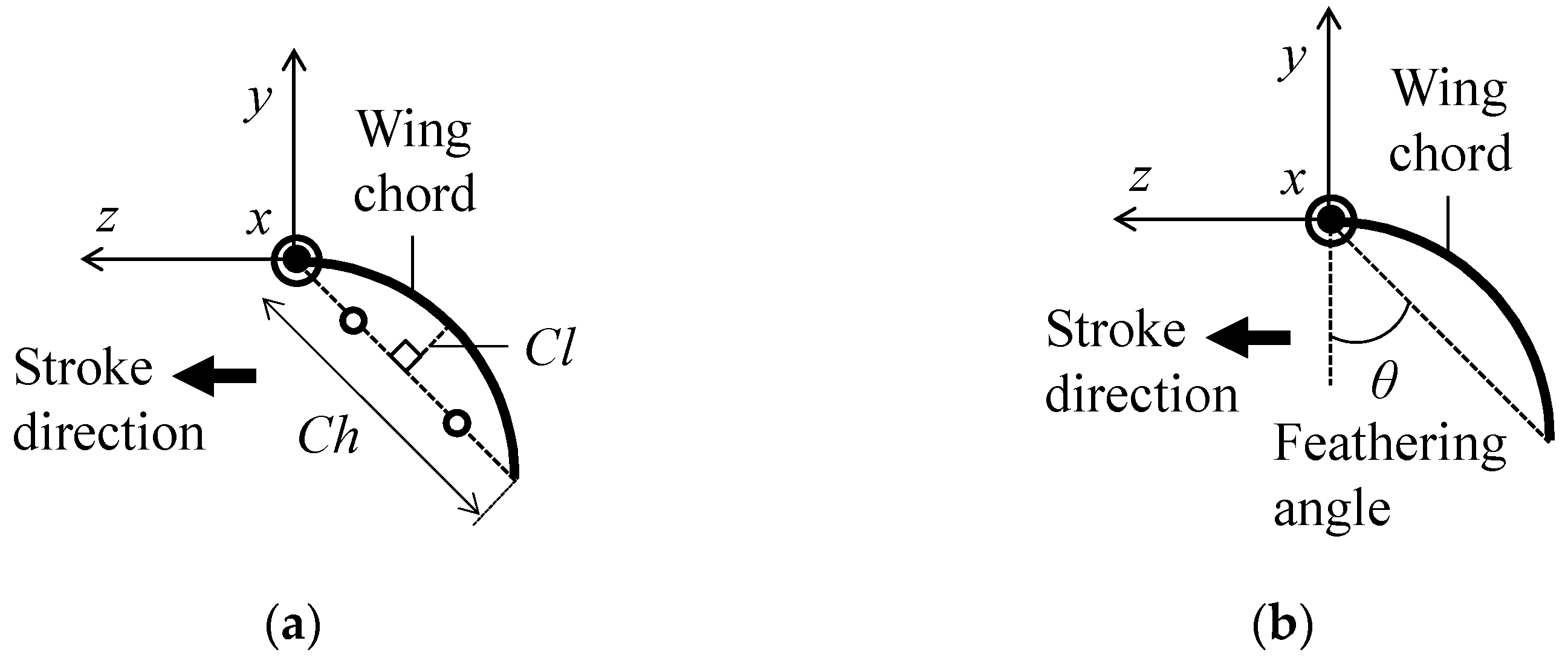


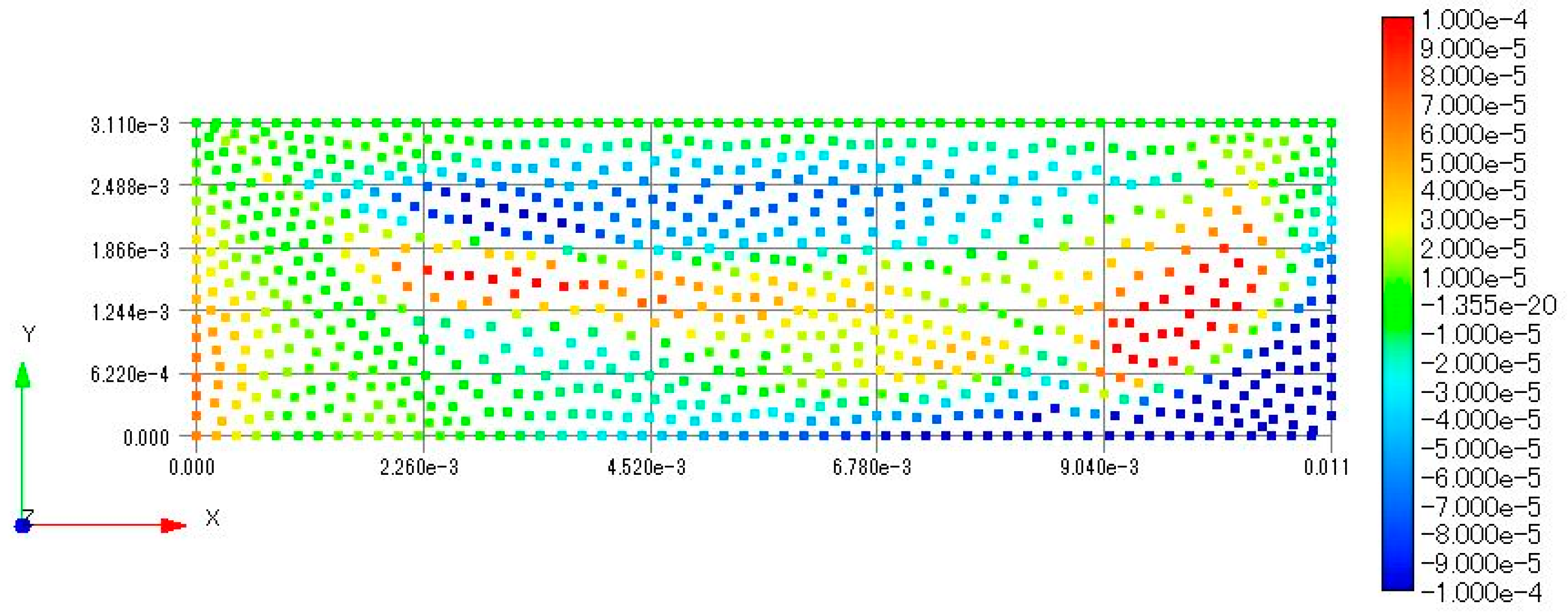
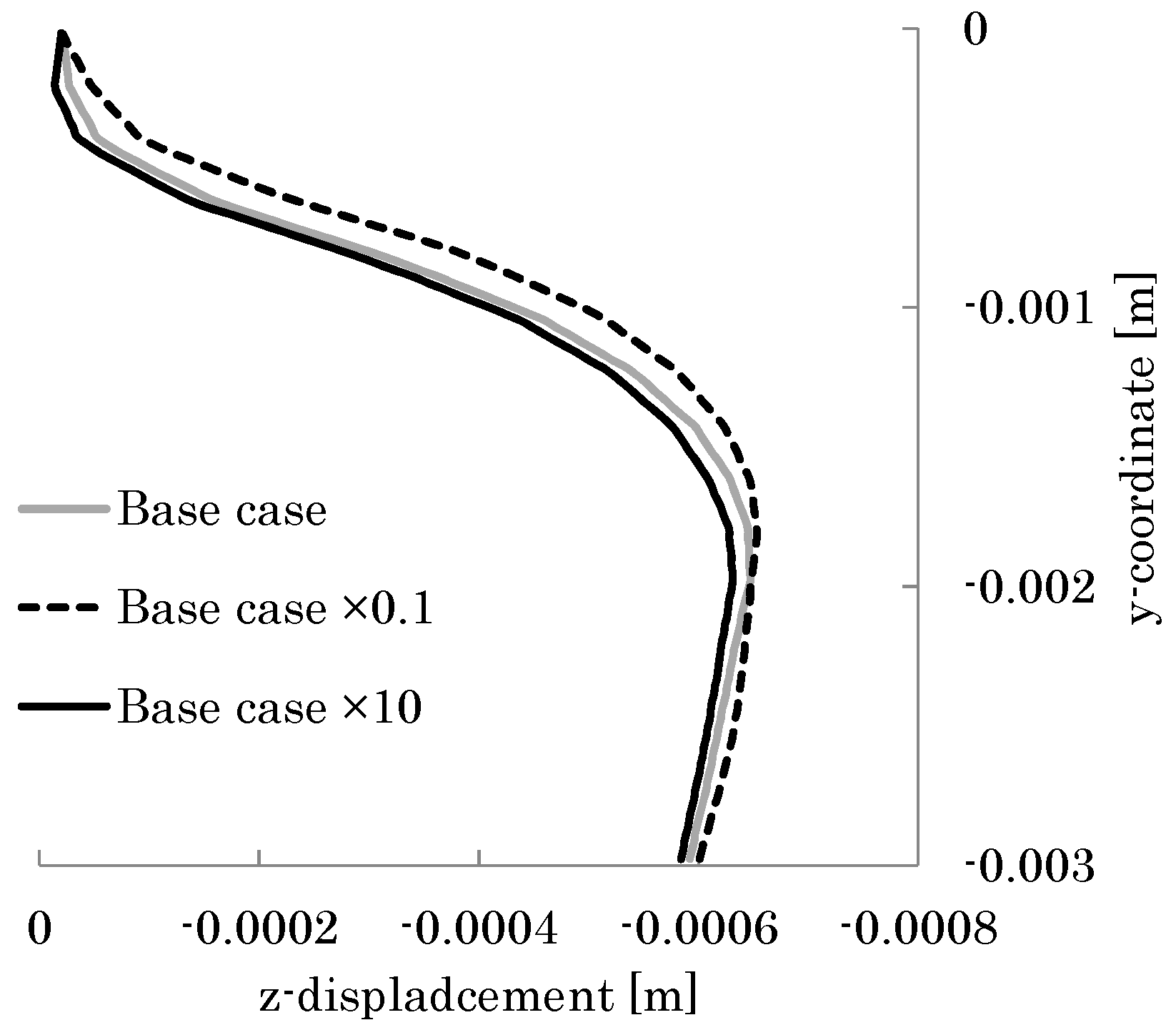



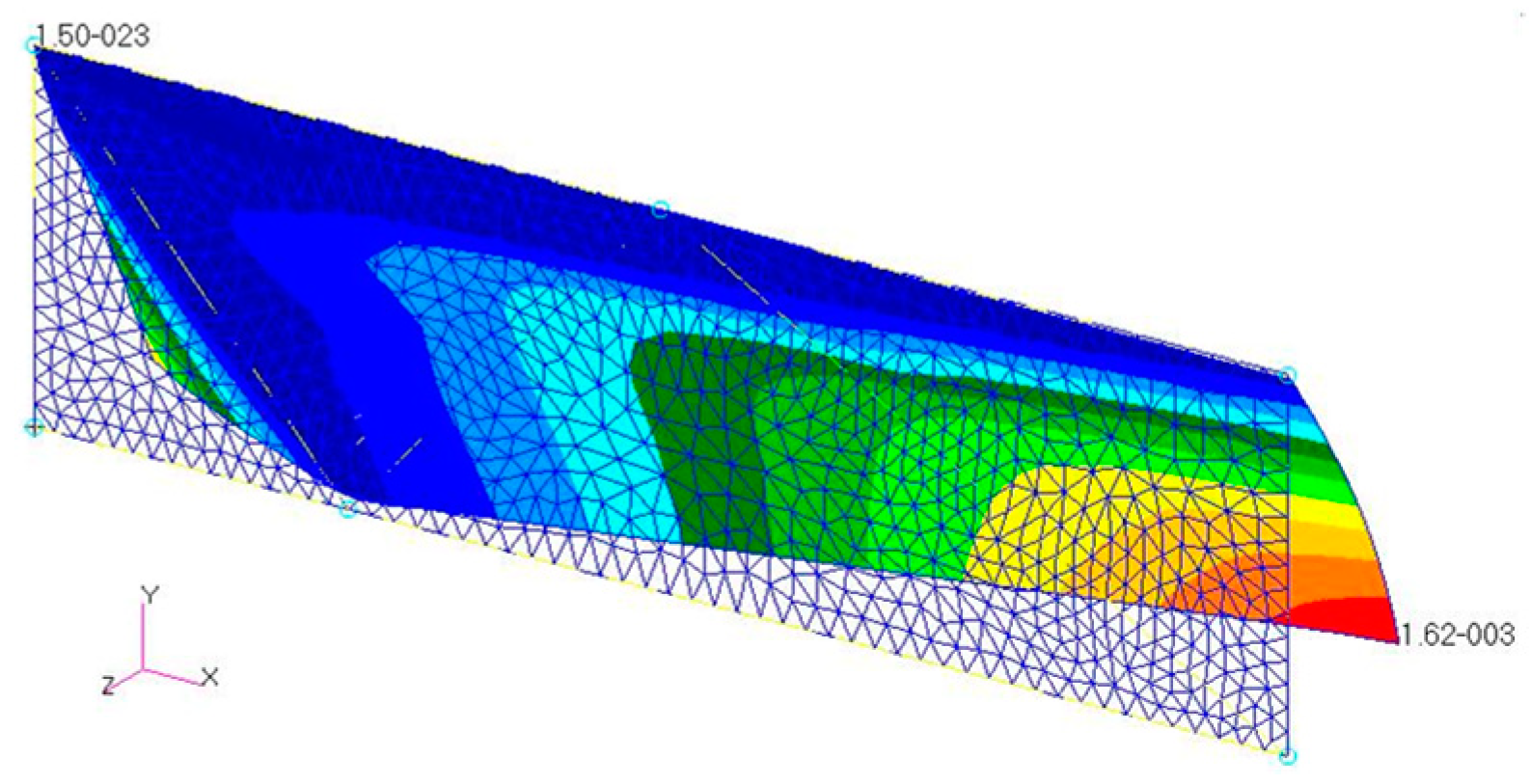
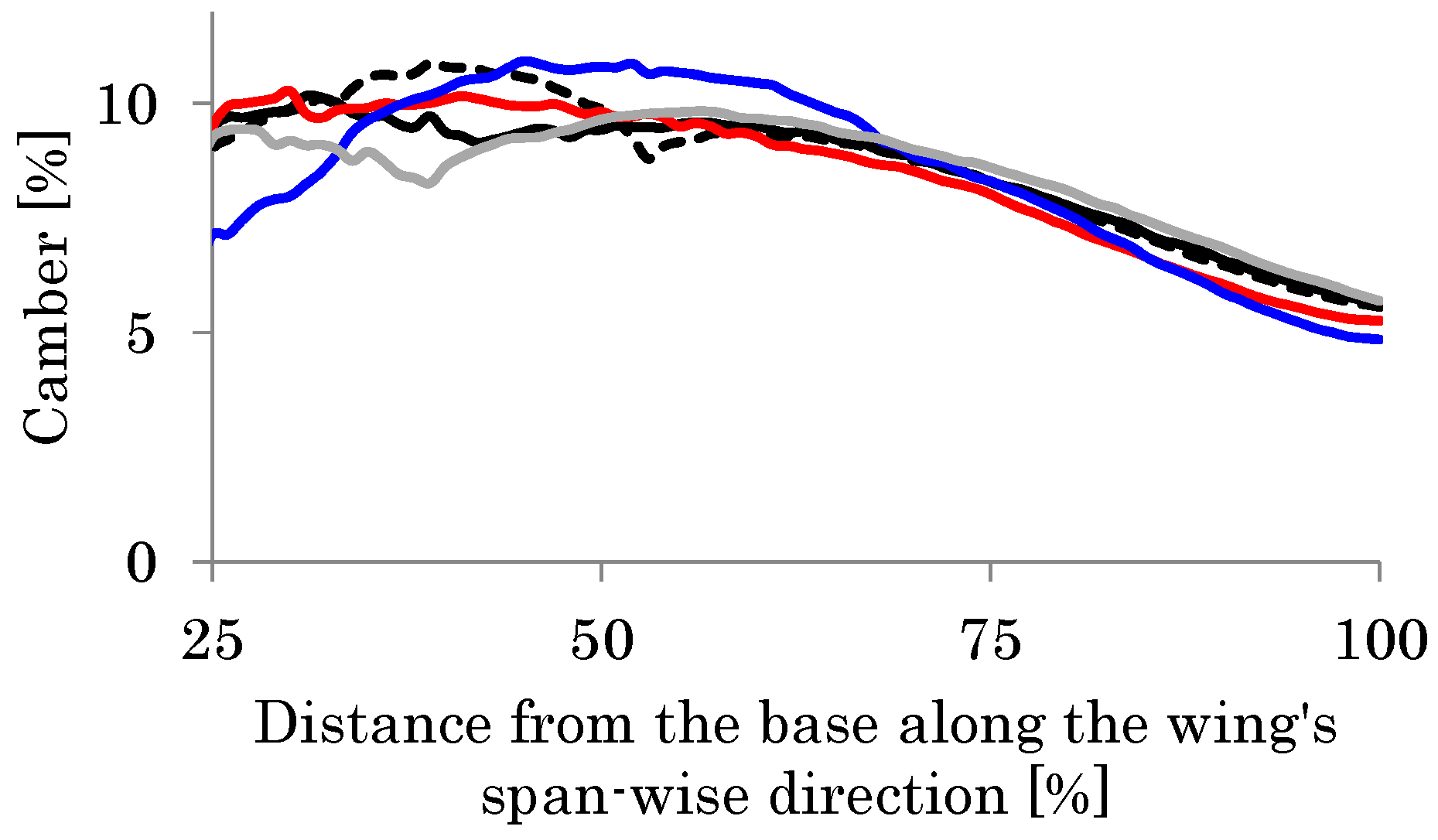

| Properties | Values |
|---|---|
| Wing length [m] | 0.0113 |
| Wing chord length [m] | 0.00311 |
| Young’s modulus of leading edge [GPa] | 100 |
| Diameter of the section of leading edge [μm] | 163 |
| Young’s modulus of root vein [GPa] | 60.0 |
| Diameter of the section of leading edge [μm] | 90.0 |
| Young’s modulus of center and support vein [GPa] | 1.00 |
| Diameter of the section of leading edge [μm] | 48.0 |
| Thickness of wing membrane [μm] | 2.00 |
| Poisson’s ratio | 0.490 |
| Properties | Beam-Shell Hybrid | Beam Only | Shell Only |
|---|---|---|---|
| Length [m] | 0.0113 | ||
| Width [m] | 0.00113 | ||
| Thickness [m] | 0.000113 | ||
| Young’s modulus of beam [GPa] | 100 | 200 | NA |
| Young’s modulus of shell [GPa] | 100 | NA | 200 |
| Poisson’s ratio | 0.0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishihara, D.; Onishi, M.; Sugikawa, K. Vein–Membrane Interaction in Cambering of Flapping Insect Wings. Biomimetics 2023, 8, 571. https://doi.org/10.3390/biomimetics8080571
Ishihara D, Onishi M, Sugikawa K. Vein–Membrane Interaction in Cambering of Flapping Insect Wings. Biomimetics. 2023; 8(8):571. https://doi.org/10.3390/biomimetics8080571
Chicago/Turabian StyleIshihara, Daisuke, Minato Onishi, and Kaede Sugikawa. 2023. "Vein–Membrane Interaction in Cambering of Flapping Insect Wings" Biomimetics 8, no. 8: 571. https://doi.org/10.3390/biomimetics8080571
APA StyleIshihara, D., Onishi, M., & Sugikawa, K. (2023). Vein–Membrane Interaction in Cambering of Flapping Insect Wings. Biomimetics, 8(8), 571. https://doi.org/10.3390/biomimetics8080571






