Bio-Inspired Aquatic Propulsion Mechanism Using Viscoelastic Fin Containing Fiber Composite Shear Thickening Fluid
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fiber Composite Viscoelastic Fin Containing Shear Thickening Fluid
2.1.1. Concept of Bending Speed Dependence of Fin Stiffness
2.1.2. Structure of a Viscoelastic Fin Containing Fiber Composite Shear Thickening Fluid
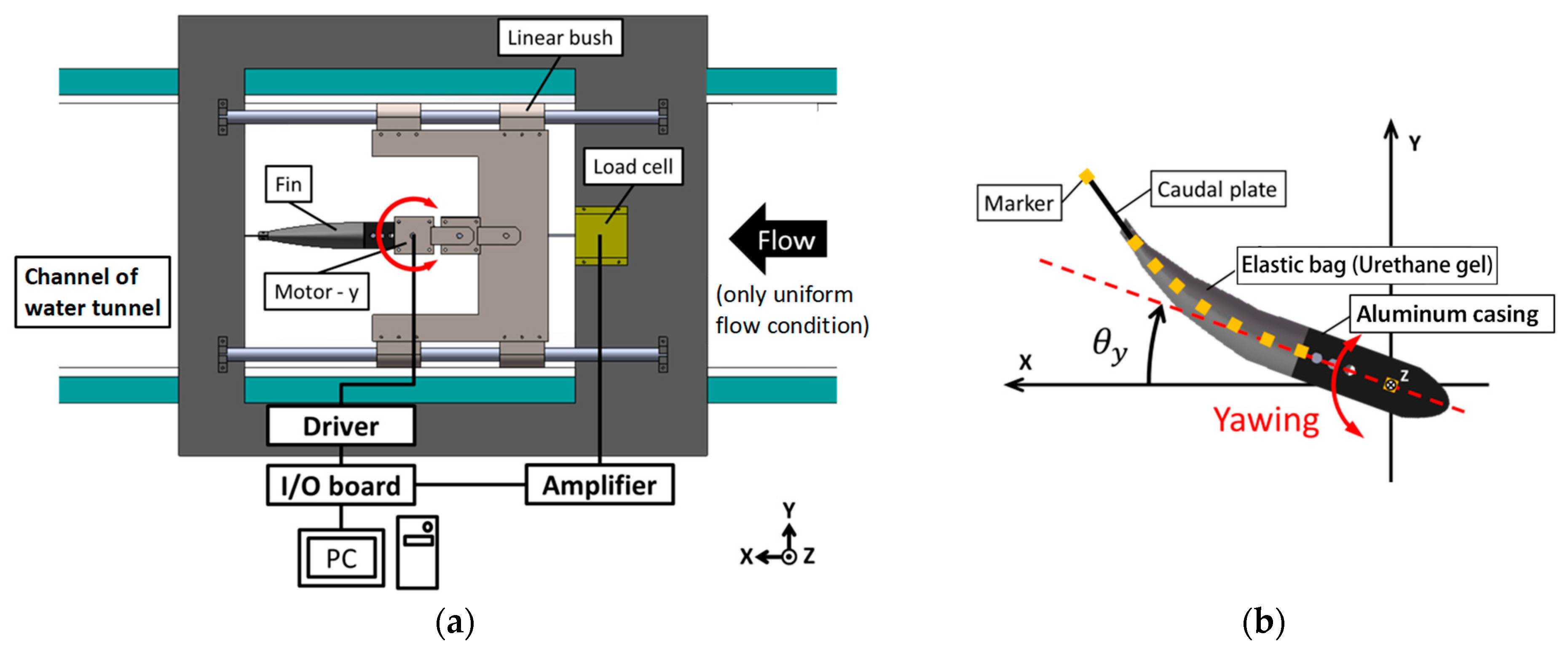
2.2. Experimental Methods to Examine the Bending Resistance of Fins
2.3. Experimental Methods to Examine Propulsion Characteristics
2.3.1. Still Water
2.3.2. Uniform Water Flow
3. Results
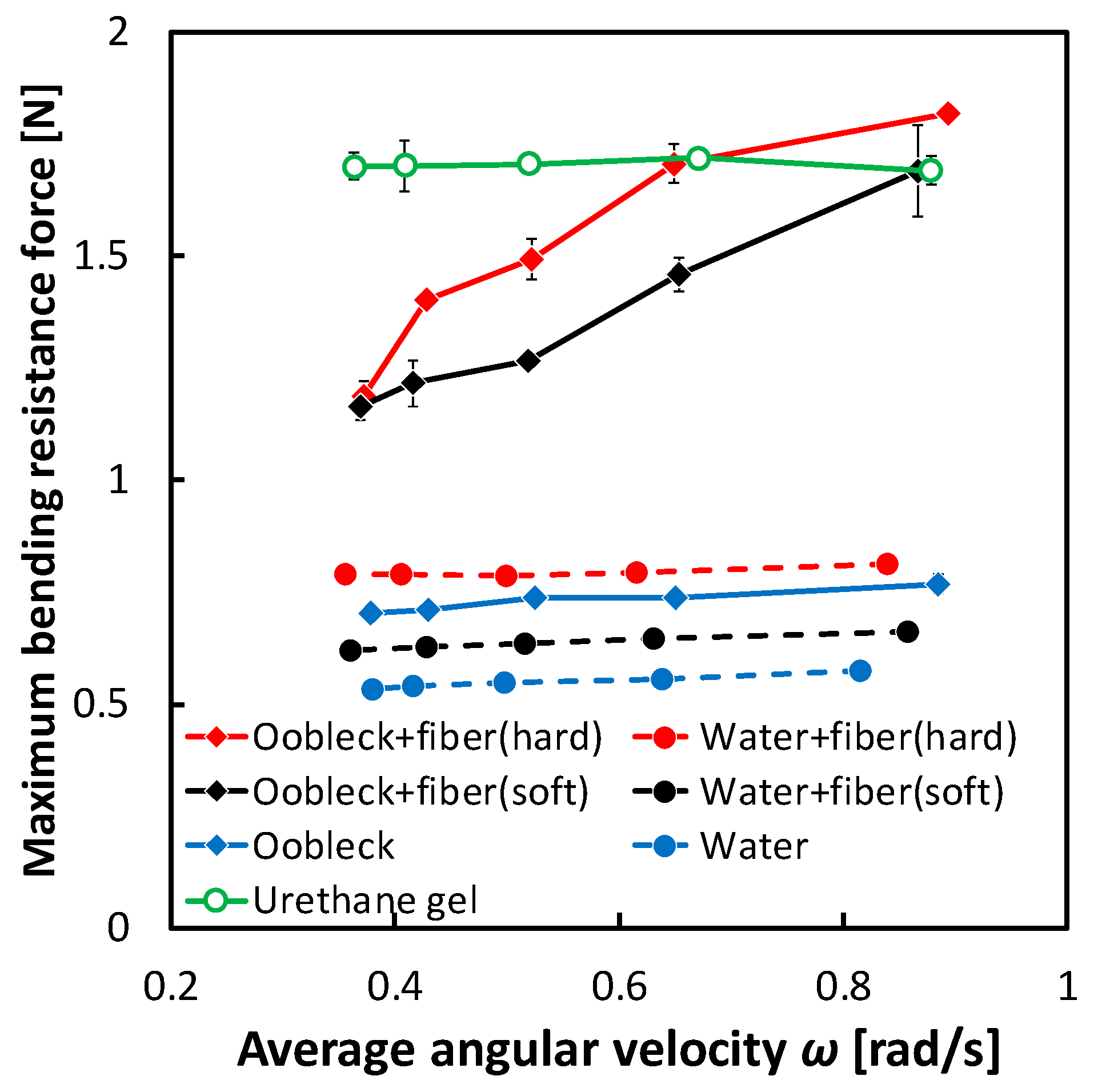
3.1. Bending Resistance Characteristics of Fins
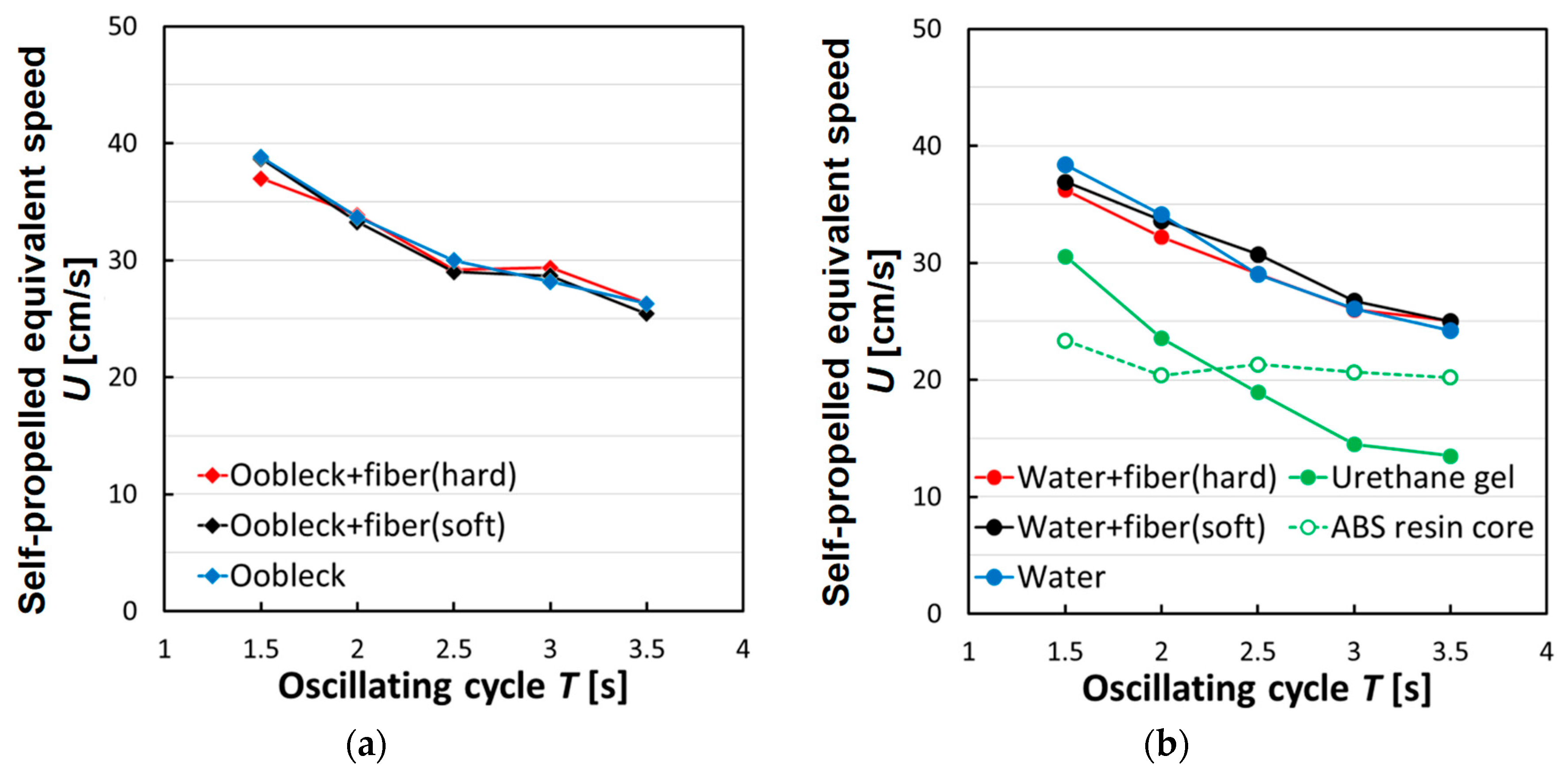
3.2. Propulsion Characteristics in Still Water
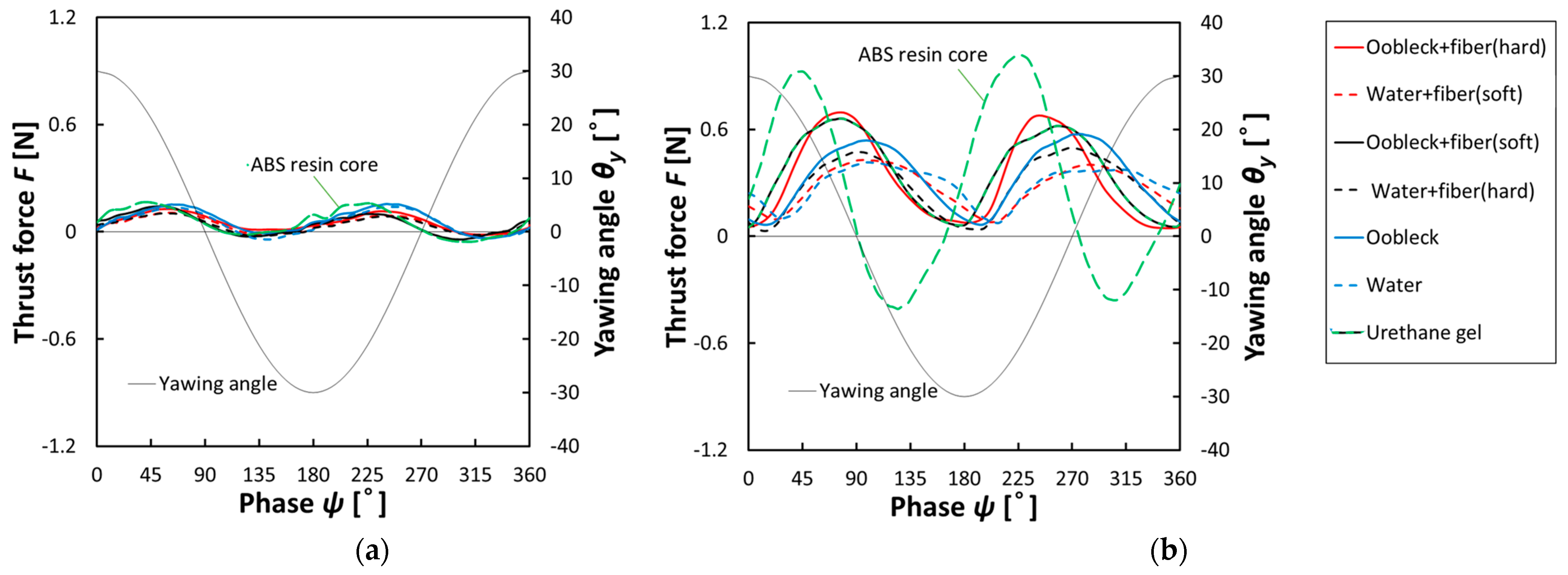
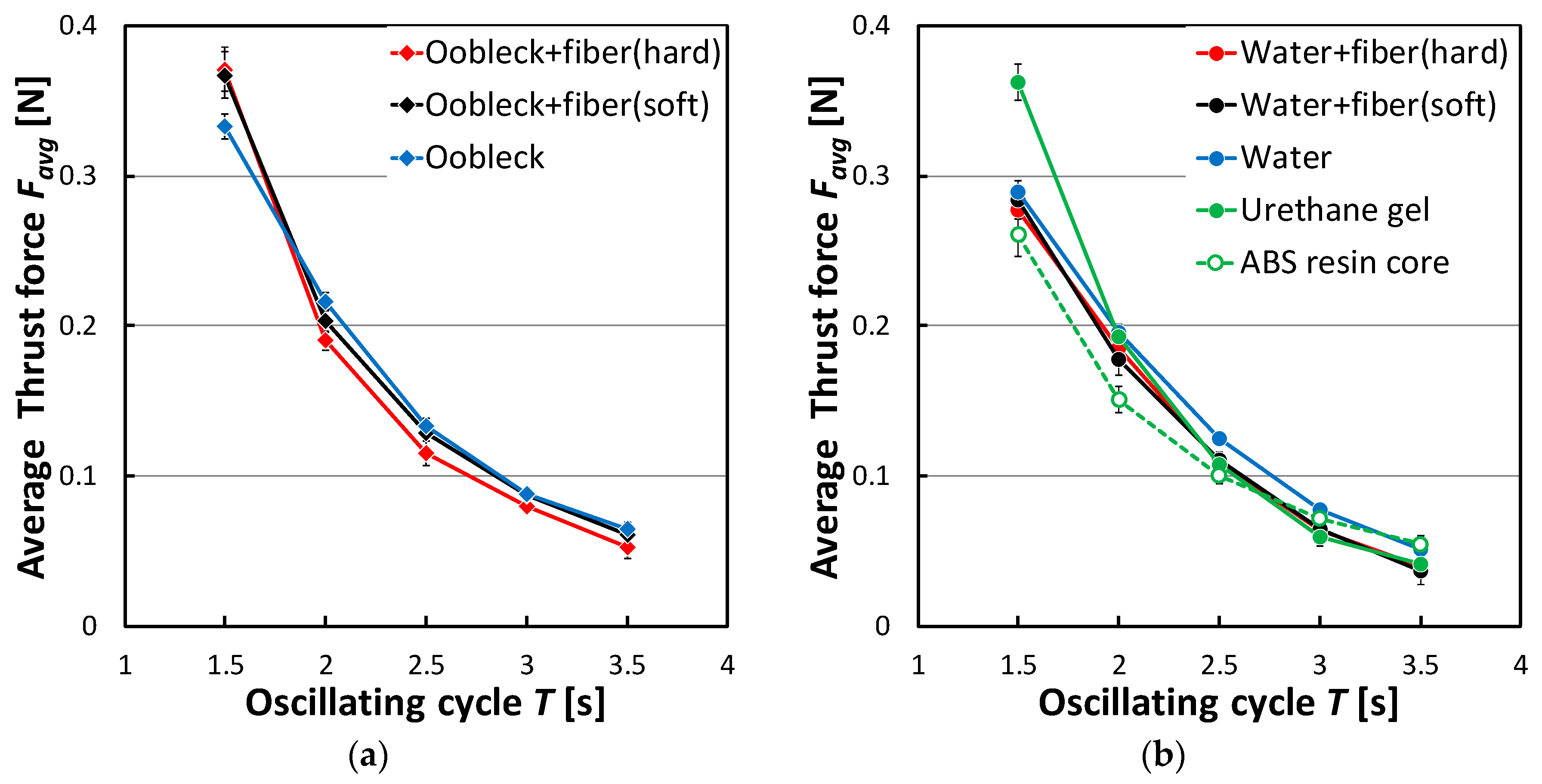
3.2.1. Thrust Force Characteristics
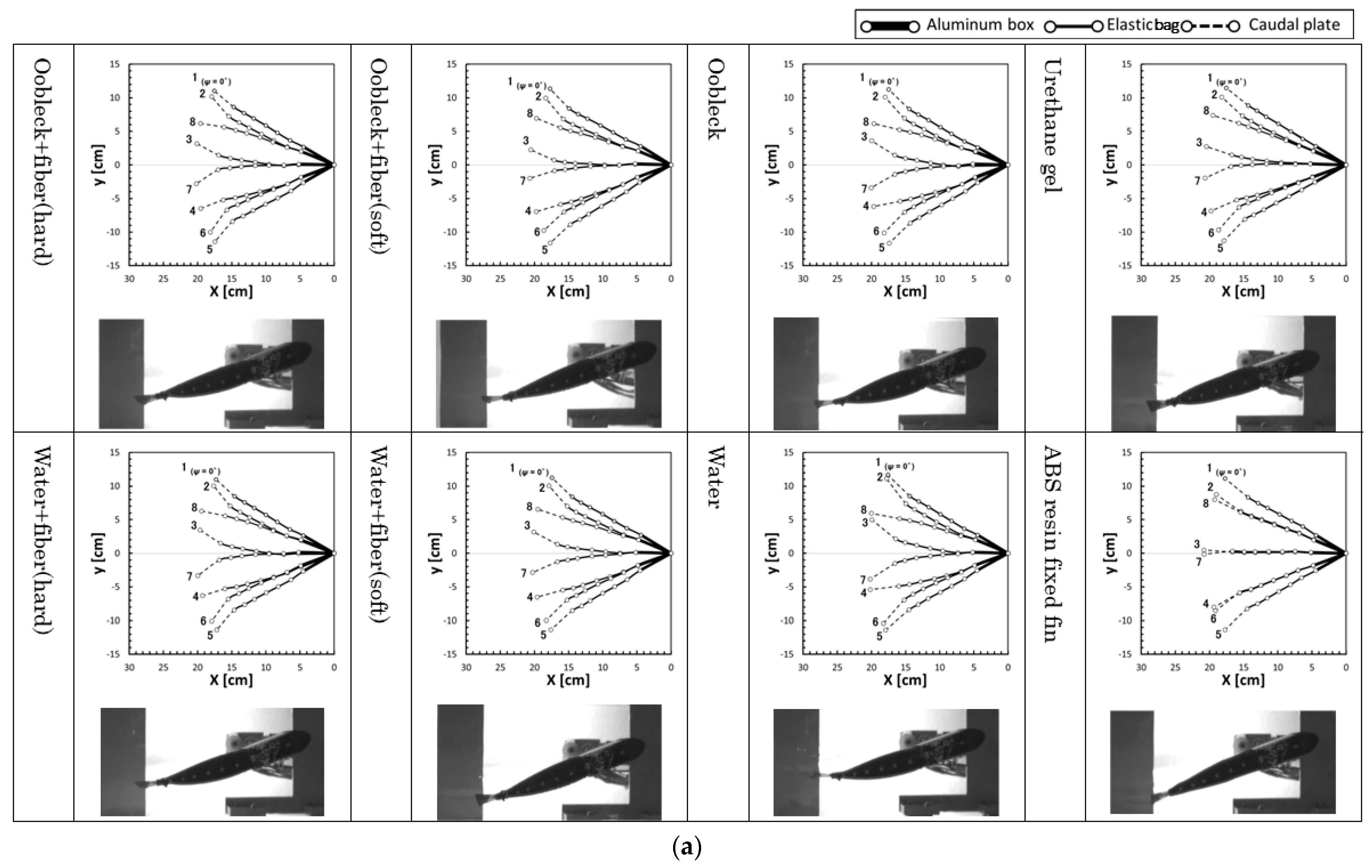
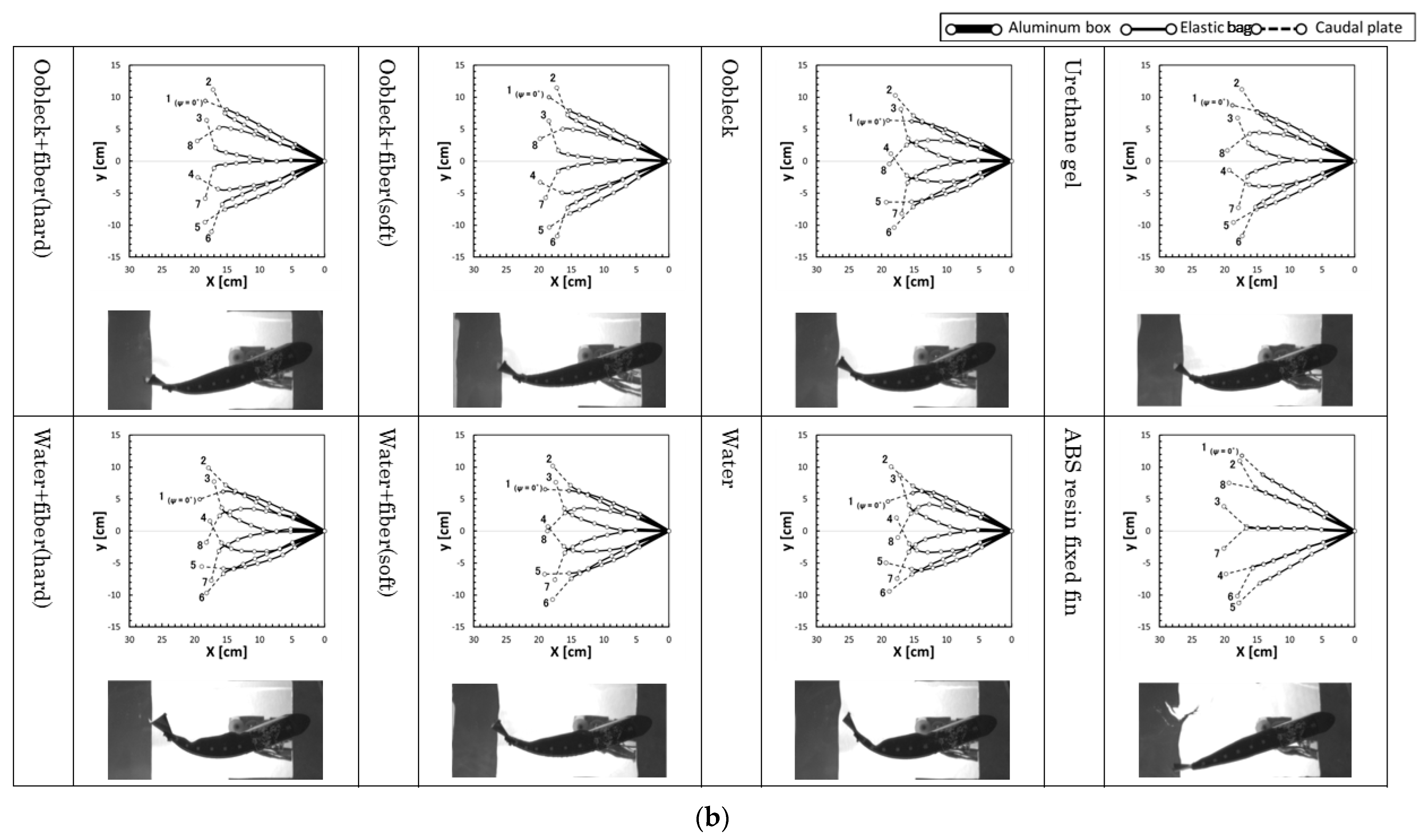
3.2.2. Deformation Behavior
3.3. Propulsion Characteristics in Uniform Water Flow
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Morikawa, H.; Isshiki, N.; Sawada, T.; Motozawa, Y. The Study on a Propulsion System by Fin Stroke-The Development of Fin Ship. J. Mar. Eng. Soc. Jpn. 1983, 18, 393–400. [Google Scholar]
- McGregor, F.; Richardson, A.J.; Armstrong, A.J.; Armstrong, A.O.; Dudgeon, C.L. Rapid wound healing in a reef manta ray masks the extent of vessel strike. PLoS ONE 2019, 14, e0225681. [Google Scholar]
- Nakashima, H.; Tokuo, K.; Ono, K. Experimental Study of a Two-Joint Dolphinlike Propulsion Mechanism (2nd Report, Experiment of Self-Propelled Large Robot). Trans. Jpn. Soc. Mech. Eng. Ser. C 2000, 66, 695–702. [Google Scholar] [CrossRef]
- Watanabe, M.; Muramatsu, K.; Kobayashi, N. Propulsion Performance of an Aquatic Mobile Robot Using Traveling-Wave Motion of a Flexible Fin (Relationship between Propulsion Efficiency and Flow Pattern). Trans. Jpn. Soc. Mech. Eng. Ser. C 2002, 68, 188–196. [Google Scholar] [CrossRef]
- Park, Y.J.; Jeong, U.; Lee, J.; Kwon, S.R.; Kim, H.Y.; Cho, K.J. Kinematic Condition for Maximizing the Thrust of a Robotic Fish Using a Compliant Caudal Fin. IEEE Trans. Robot. 2012, 28, 1216–1227. [Google Scholar] [CrossRef]
- Kobayashi, S.; Nakabayashi, M.; Morikawa, H. Bioinspired Propulsion Mechanism in Fluid Using Fin with Dynamic Variable-Effective-Length Spring. J. Biomech. Sci. Eng. 2006, 1, 280–289. [Google Scholar] [CrossRef]
- Nakabayashi, M.; Kobayashi, R.; Kobayashi, S.; Morikawa, H. Bioinspired Propulsion Mechanism Using a Fin with a Dynamic Variable-Effective-Length Spring -Evaluation of thrust Characteristics and Flow around a Fin in a Uniform Flow. J. Biomech. Sci. Eng. 2009, 4, 82–93. [Google Scholar] [CrossRef]
- Nakabayashi, M.; Soyano, H.; Kobayashi, S.; Morikawa, H. Bio-inspired Aquatic Propulsion Mechanism Using a Fin with a Variable-Effective-Length Spring: Development of a Propulsion Mechanism using the Swaying and Yawing Movements of a Fin. J. Aero Aqua Bio-Mech. 2010, 1, 104–110. [Google Scholar] [CrossRef]
- Kobayashi, S.; Morikawa, H.; Soyano, H.; Nakabayashi, M. Propulsion Mechanism in Fluid Using Variable-Stiffness Fin with Torsional Rectangular Elastic Plates. Int. J. Offshore Polar Eng. 2013, 23, 172–177. [Google Scholar]
- Kobayashi, S.; Sugiyama, K. Bending Speed Dependence Properties of Stiffness of Anisotropic Viscoelastic Fin Containing Fiber Composite Dilatant Fluid. J. Fiber Bioeng. Inform. 2019, 12, 55–62. [Google Scholar] [CrossRef]
- Kamibayashi, M.; Ogura, H.; Otsubo, Y. Shear-thickening flow of nanoparticle suspensions flocculated by polymer bridging. J. Colloid Interface Sci. 2008, 321, 294–301. [Google Scholar] [CrossRef] [PubMed]
- Nishino, Y.; Ito, Y.; Kishida, R.; Kagiyama, Y.; Nemoto, T. Dynamic Viscoelasticity Properties Evaluation of Skin and Making of Dummy Skin for Safety Evaluation. J. Jpn. Soc. Exp. Mech. 2017, 16, 307–314. [Google Scholar]
- Crawford, N.; Popp, L.; Johns, K.; Caire, L.; Peterson, B.; Liberatore, M. Shear thickening of corn starch suspensions: Does concentration matter? J. Colloid Interface Sci. 2013, 396, 83–89. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Ness, C.; Cates, E.; Sun, J.; Cohen, I. Tunable shear thickening in suspensions. Proc. Natl. Acad. Sci. USA 2016, 113, 10774–11077. [Google Scholar] [PubMed]
- Rathee, V.; Miller, J.M.; Blair, D.L.; Urbach, J.S. Structure of propagating high-stress fronts in a shear-thickening suspension. Proc. Natl. Acad. Sci. USA 2022, 119, e2203795119. [Google Scholar] [CrossRef] [PubMed]
- Wei, M.; Lin, K.; Sun, L. Shear thickening fluids and their applications. Mater. Des. 2022, 216, 110570. [Google Scholar]
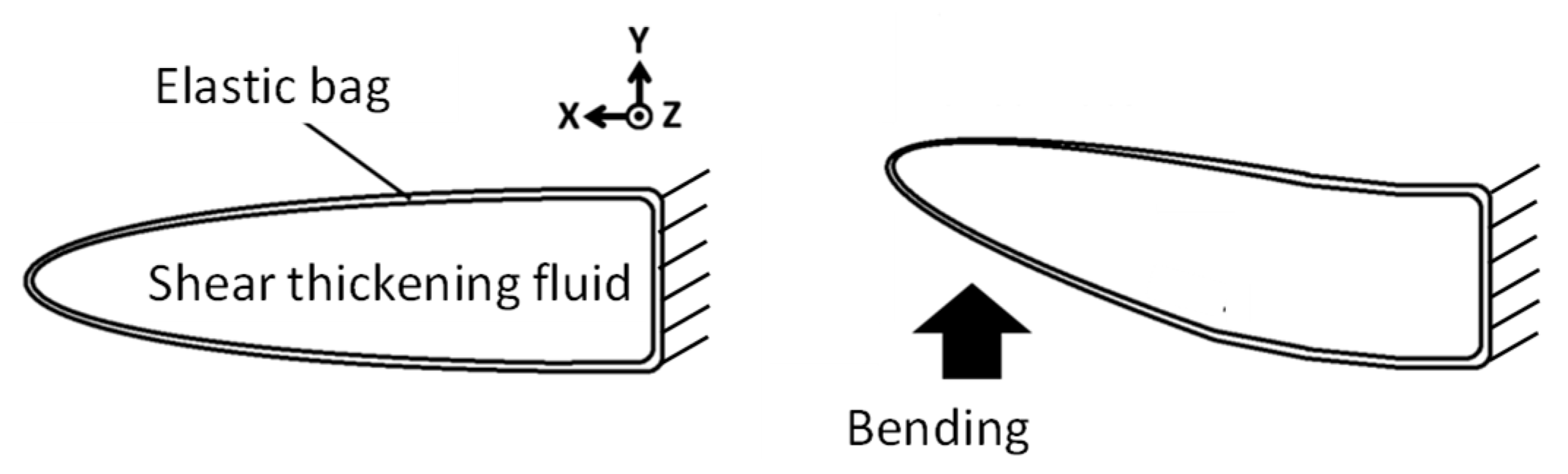
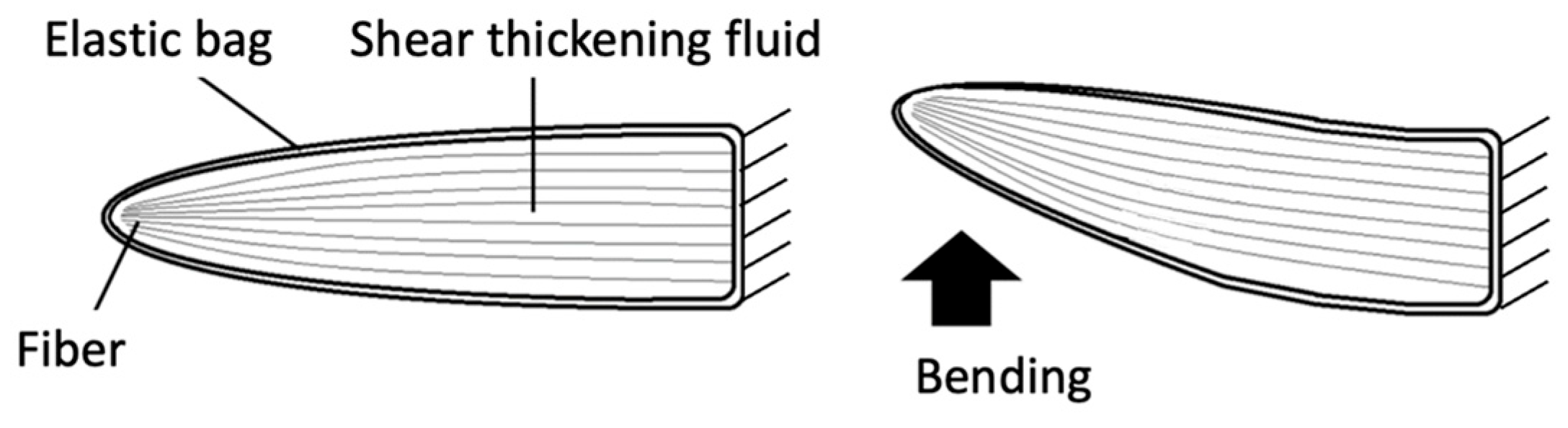

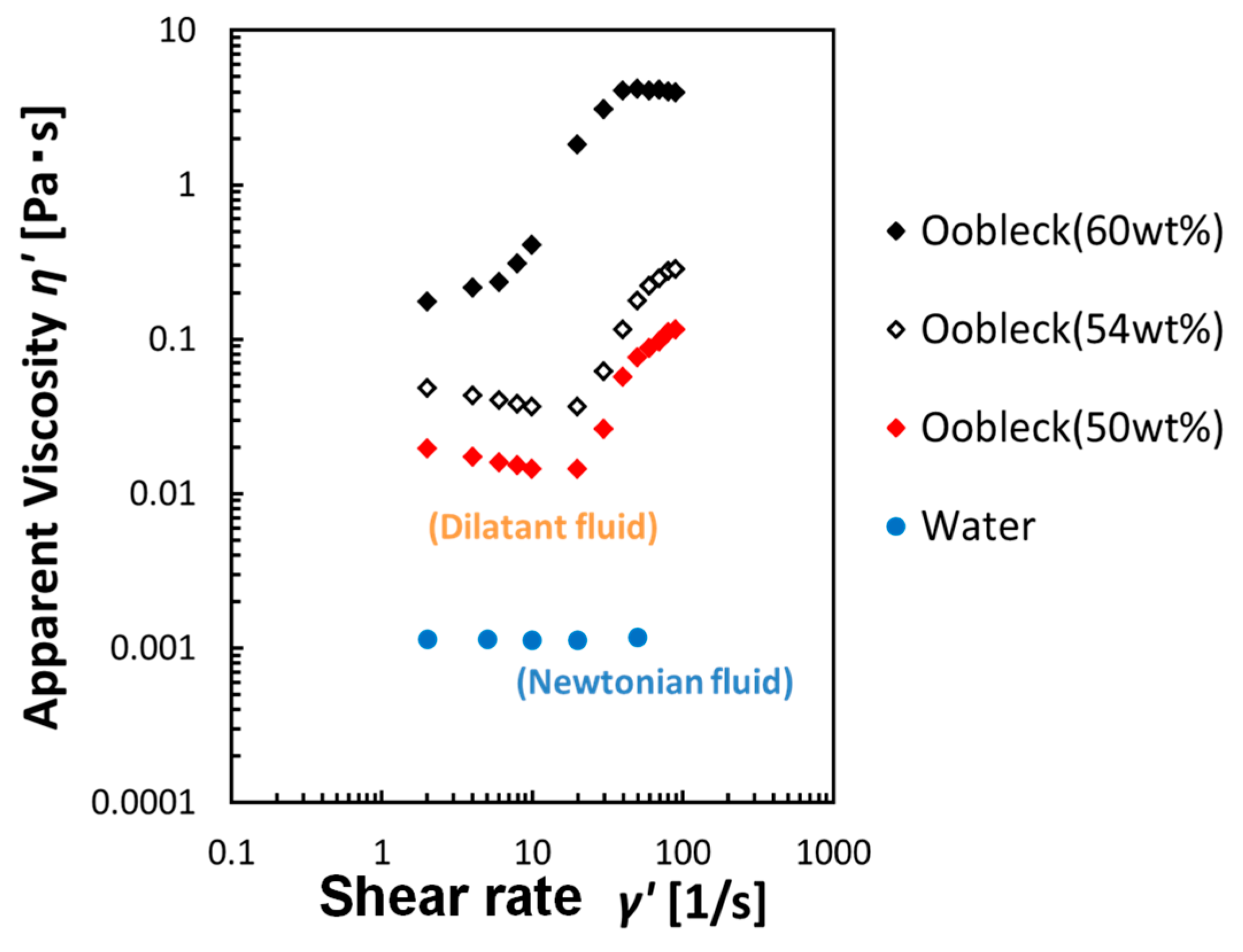
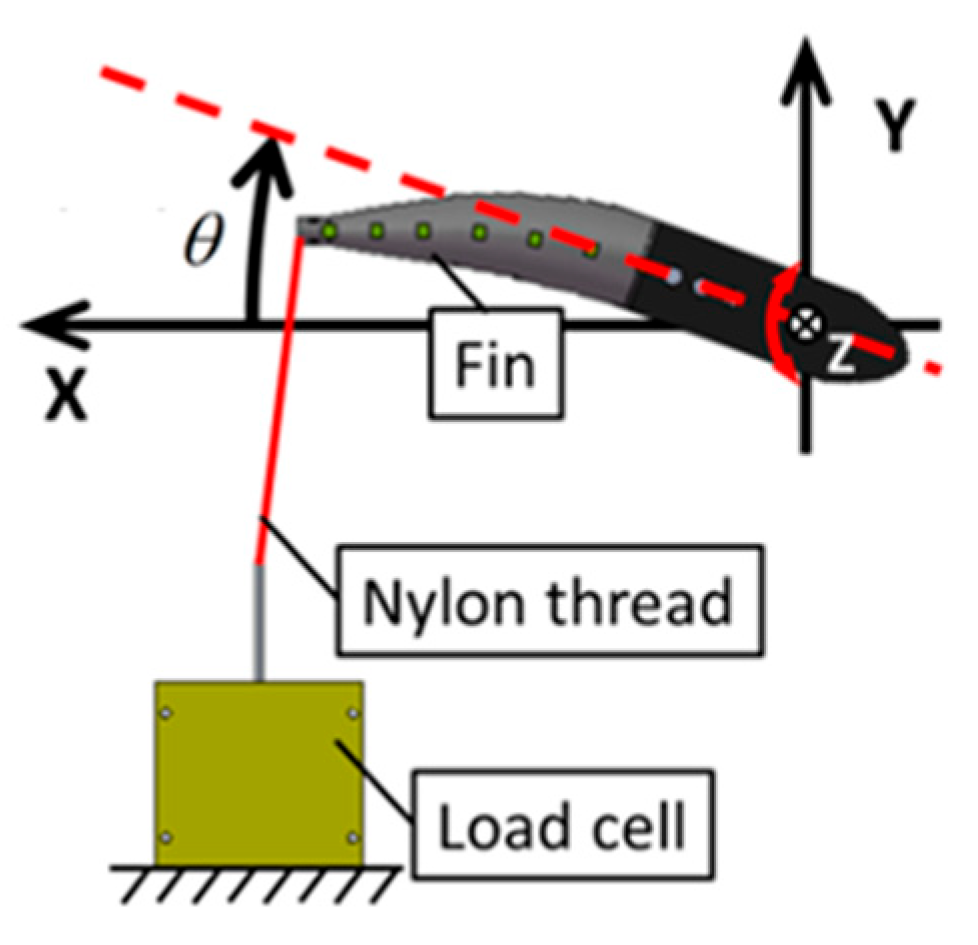
| Horse Hair (Hard) | Horse Hair (Soft) | |
|---|---|---|
| Weight (tex: g/1000 m) | 43.6 | 24.6 |
| Average diameter in wet conditions (μm) | 219 | 162 |
| Resistance of incipient tension (N/tex) | 2.52 | 1.82 |
| Fibered/Unfibered | Contents of the Elastic Bag |
|---|---|
| Fibered * | 60 wt% oobleck (shear thickening fluid) + hard fibers 60 wt% oobleck (shear thickening fluid) + soft fibers Water (Newtonian fluid) + hard fibers Water (Newtonian fluid) + soft fibers |
| Unfibered | 60 wt% oobleck (shear thickening fluid) Water (Newtonian fluid) Urethane gel core (more elastic fin) ABS resin core (rigid fin) |
| Parameter | Range/Value |
|---|---|
| Oscillating cycle T | 1.5–3.0 s |
| Yawing angle θy | +/−30°, Amplitude θy-max = 30° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kobayashi, S.; Sugiyama, K. Bio-Inspired Aquatic Propulsion Mechanism Using Viscoelastic Fin Containing Fiber Composite Shear Thickening Fluid. Biomimetics 2023, 8, 405. https://doi.org/10.3390/biomimetics8050405
Kobayashi S, Sugiyama K. Bio-Inspired Aquatic Propulsion Mechanism Using Viscoelastic Fin Containing Fiber Composite Shear Thickening Fluid. Biomimetics. 2023; 8(5):405. https://doi.org/10.3390/biomimetics8050405
Chicago/Turabian StyleKobayashi, Shunichi, and Kousuke Sugiyama. 2023. "Bio-Inspired Aquatic Propulsion Mechanism Using Viscoelastic Fin Containing Fiber Composite Shear Thickening Fluid" Biomimetics 8, no. 5: 405. https://doi.org/10.3390/biomimetics8050405
APA StyleKobayashi, S., & Sugiyama, K. (2023). Bio-Inspired Aquatic Propulsion Mechanism Using Viscoelastic Fin Containing Fiber Composite Shear Thickening Fluid. Biomimetics, 8(5), 405. https://doi.org/10.3390/biomimetics8050405





