Hybrid Slime Mold and Arithmetic Optimization Algorithm with Random Center Learning and Restart Mutation
Abstract
:1. Introduction
- (1)
- In the exploration and exploitation stage, SMA and AOA should be organically combined to improve the exploration and exploitation capabilities comprehensively;
- (2)
- Innovatively propose a random center strategy, which improves the early convergence speed of the algorithm and effectively maintains a balance between exploration and development while enhancing the diversity of the population;
- (3)
- The introduction of the mutation strategy and restart strategy enhances the ability to solve complex problems while also enhancing the algorithm’s ability to jump out of local optima. By comparing 23 benchmark test functions with different dimensions with the CEC2020 test function, it is proven that the algorithm has significant effectiveness;
- (4)
- Five engineering problems were used simultaneously to verify the feasibility of RCSMAOA on practical engineering problems.
2. Related Works
3. Slime Mold Algorithm
4. Arithmetic Optimization Algorithm
4.1. Mathematical Optimization Acceleration Function
4.2. Exploration Phase
4.3. Exploitation Phase
5. Hybrid Improvement Strategy
5.1. Stochastic Center Learning Strategy (SCLS)
5.2. Mutation Strategy (MS)
5.3. Restart Strategy (RS)
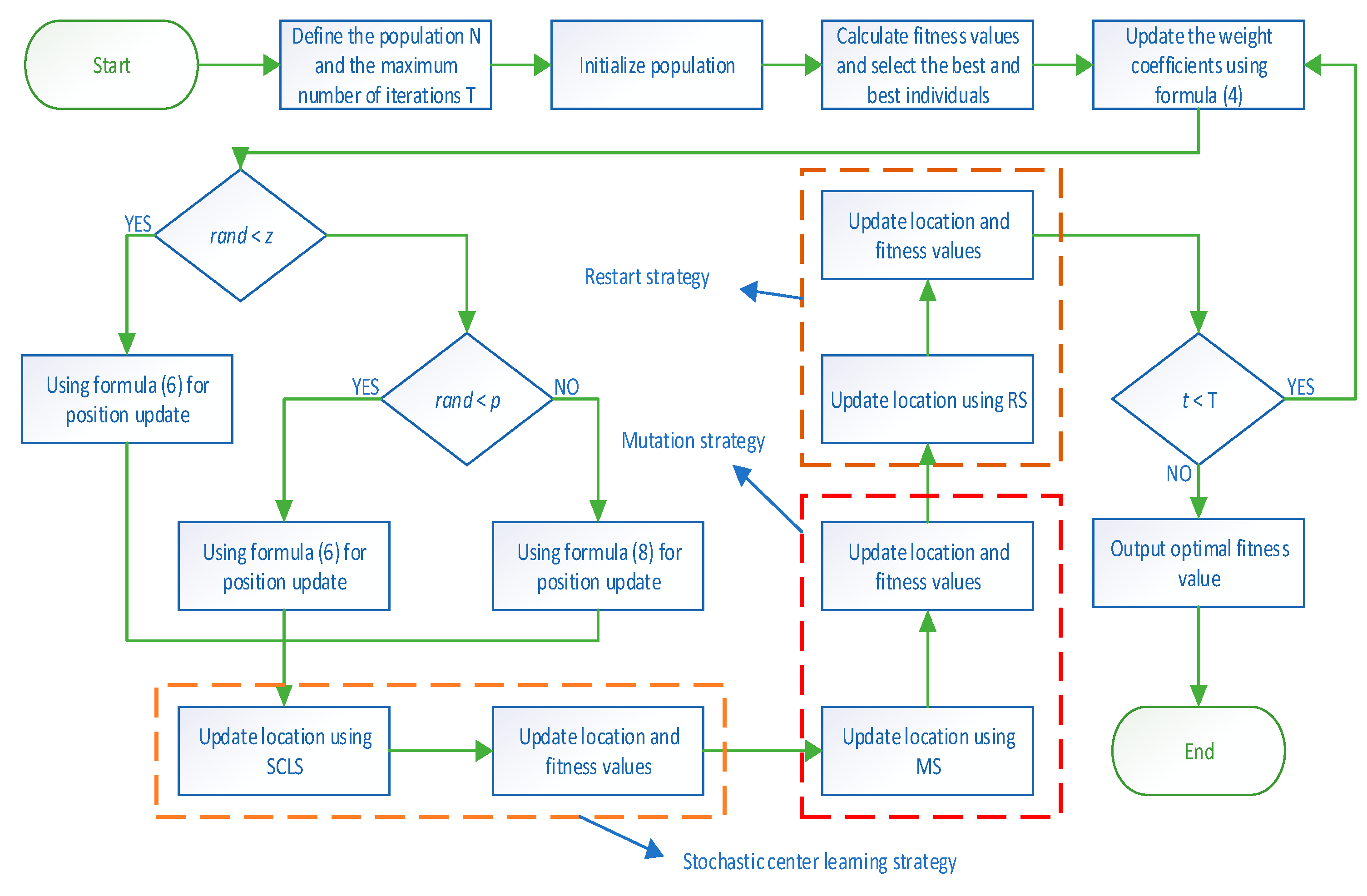
5.4. A Hybrid Optimization Algorithm of Slime Mold and Arithmetic Based on Random Center Learning and Restart Mutation
| Algorithm 1 The pseudocode of the RCLSMAOA |
| Initialization parameters T, Tmax, ub, lb, N, dim, w. |
| Initialize population X according to Equation (1). |
| While T ≤ Tmax |
| Calculate fitness values and select the best individual and optimal location. |
| Update w using Formula (4) |
| For i = 1:N |
| Update the value of parameter a W S using Formulas (2), (4), and (5) |
| If rand < z |
| Update the population position using Formula (6) |
| Else |
| Update vb, vc, and p. |
| If r1 < p |
| Update the population position using Formula (6) |
| Else |
| Update the value of parameter mop using Formula (9) |
| If r2 < 0.5 |
| Update the population position using Formula (8) |
| Else |
| Update the population position using Formula (8) |
| End If |
| End If |
| End If |
| For i = 1:N |
| Update population position using SCLS |
| End For |
| For i = 1:N |
| Update population position using MS |
| End For |
| Update population position using RS |
| Find the current best solution |
| t = t + 1 |
| End While |
| Output the best solution. |
6. Time Complexity Analysis
7. Experimental Part
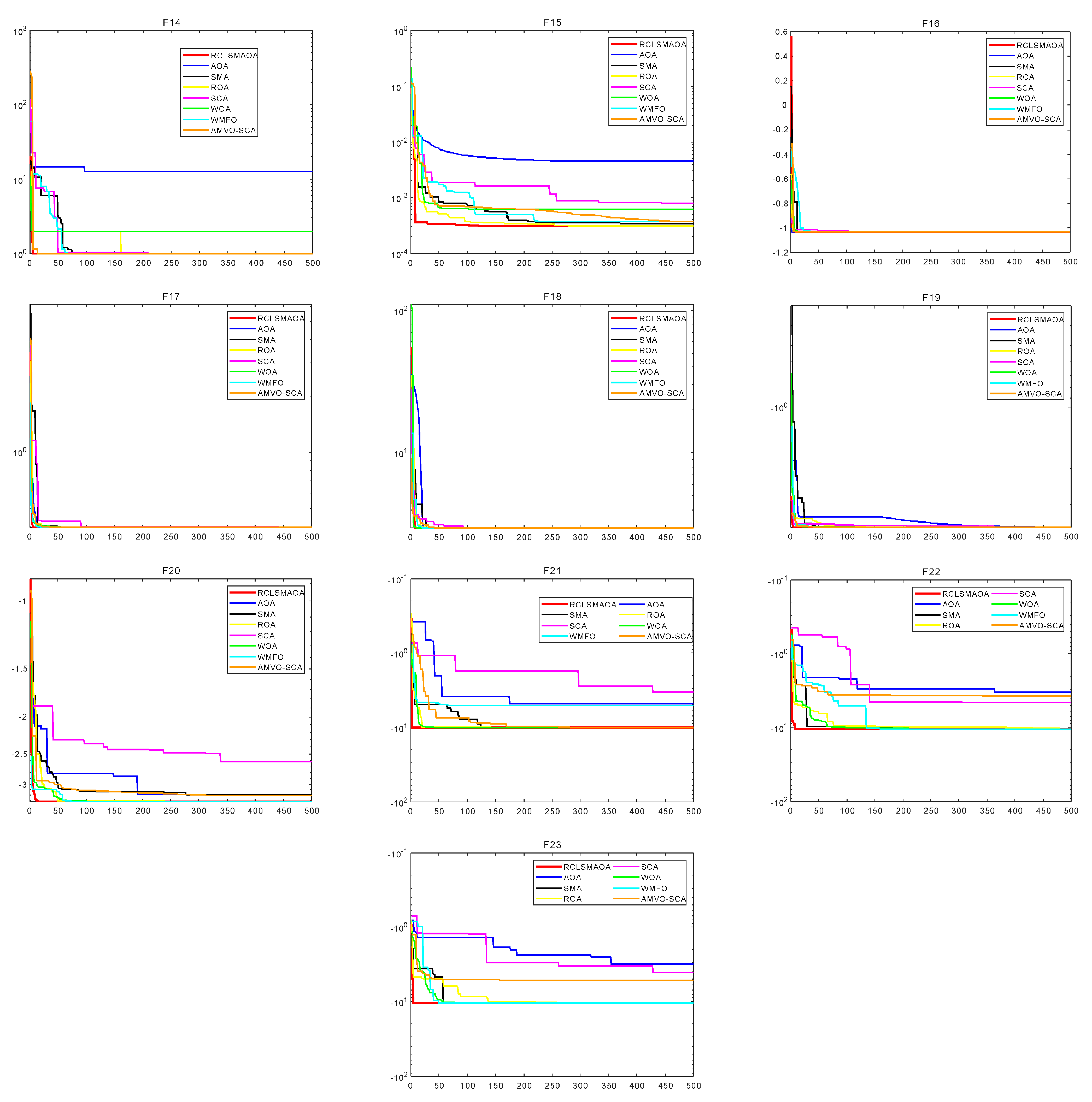
7.1. Experiments on the 23 Standard Benchmark Functions
7.2. Experiments on the CEC2020 Benchmark Function
7.3. Analysis of Wilcoxon Rank Sum Test Results and Friedman Test
8. Engineering Issues
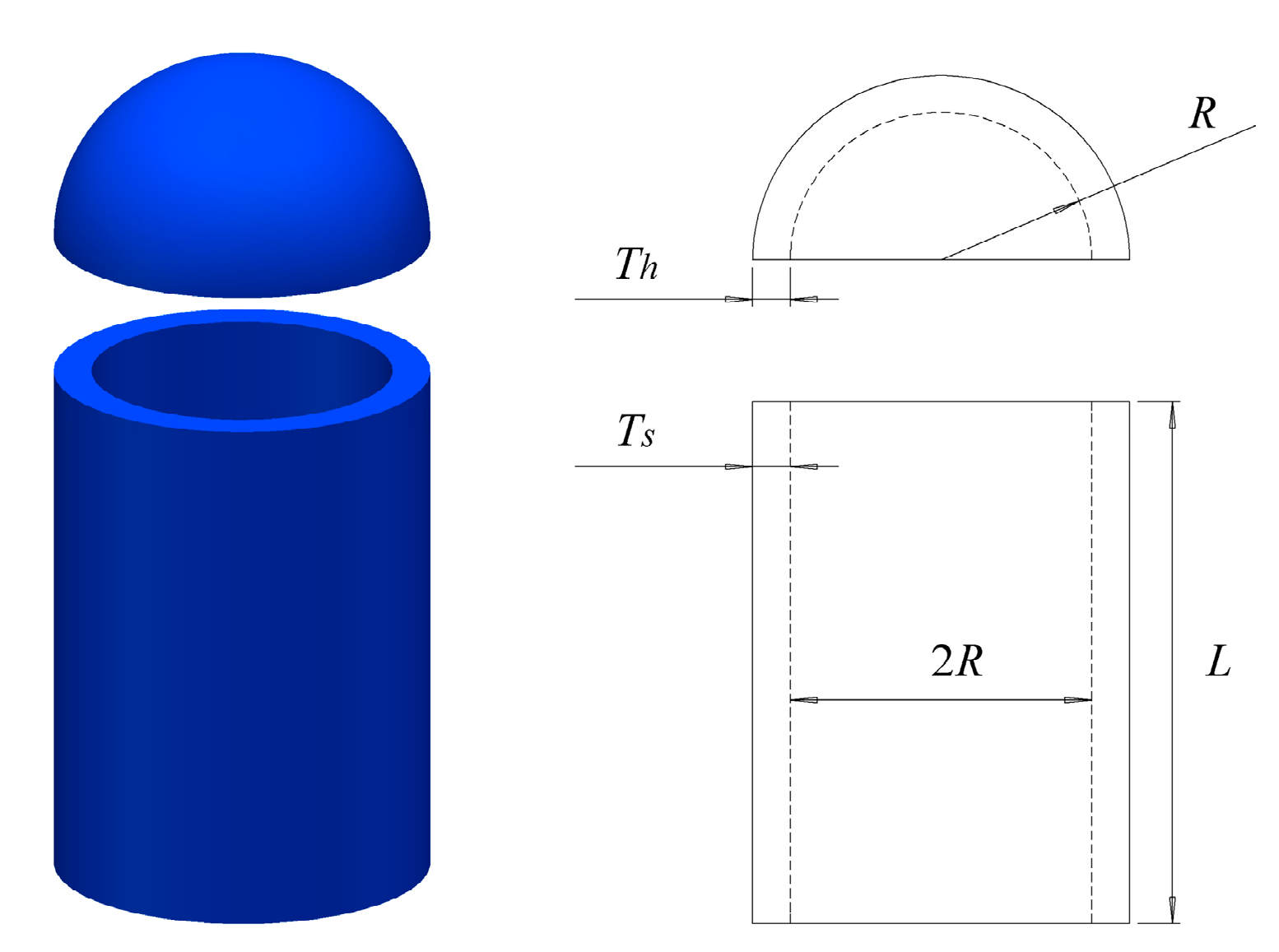
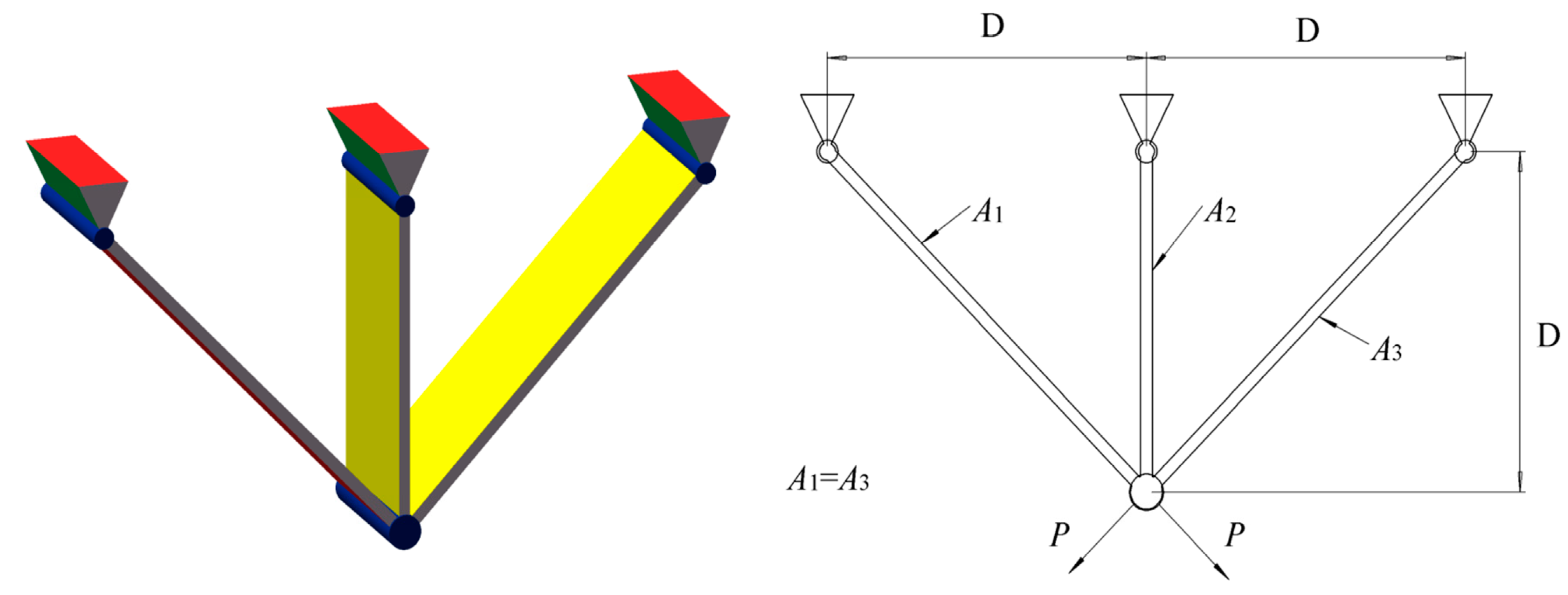
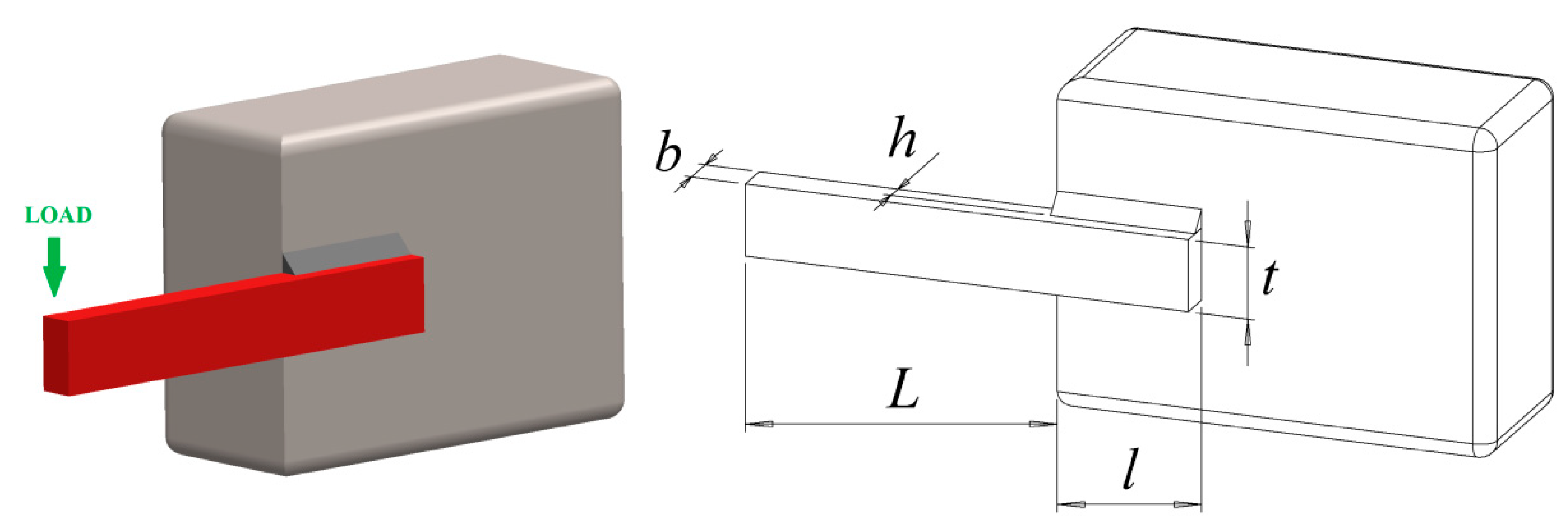
8.1. Pressure Vessel Design Problem
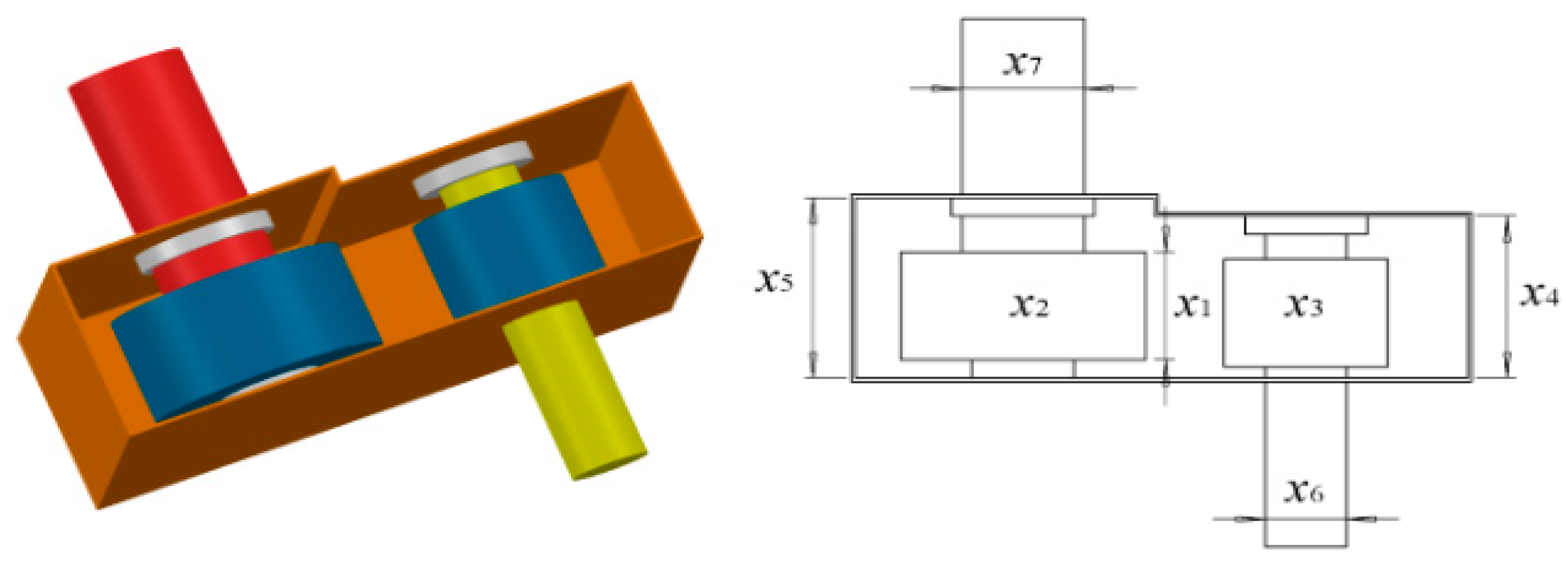
8.2. Speed Reducer Design Problem
8.3. Three-Bar Truss Design Problem
8.4. Welded Beam Design Problem
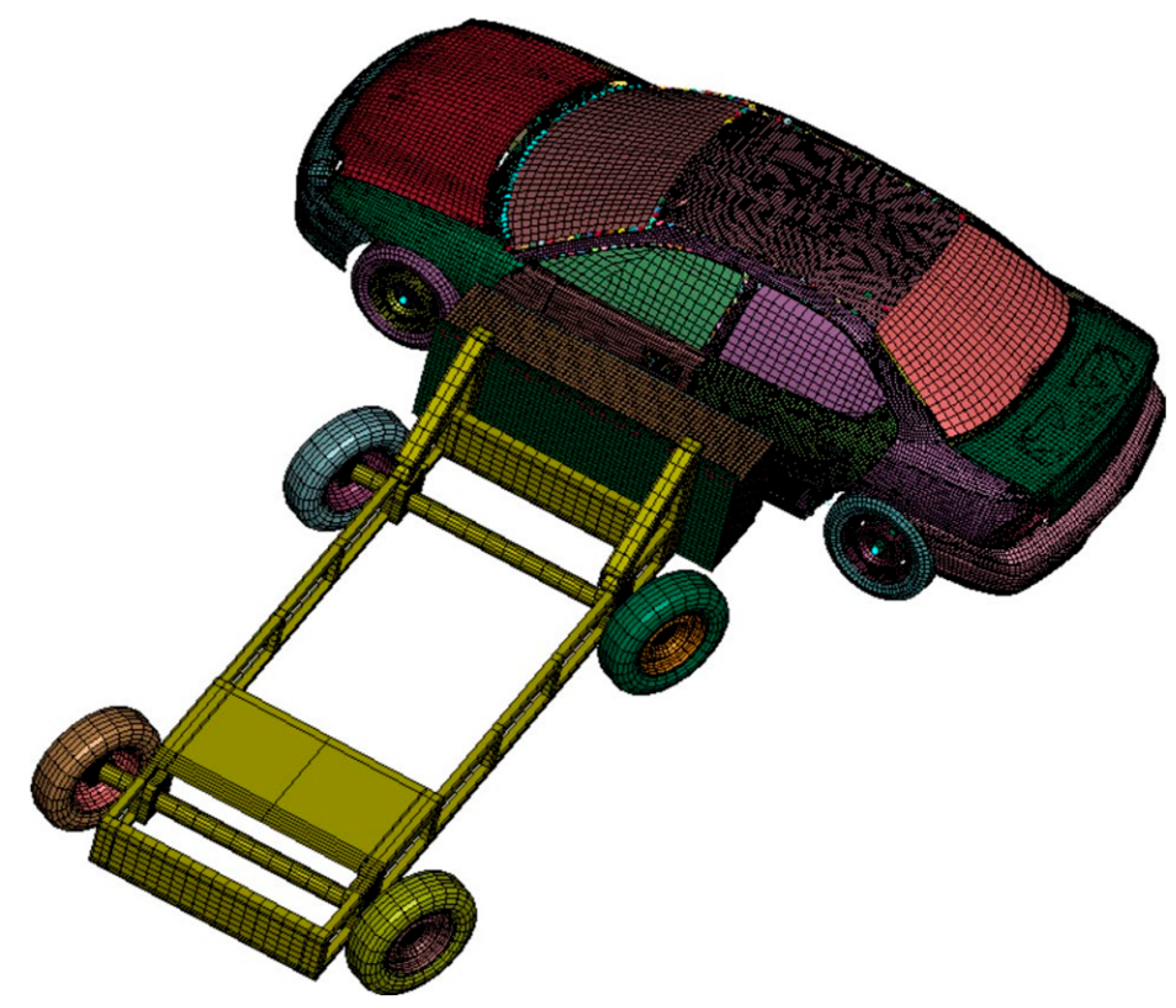
8.5. Car Crashworthiness Design Problem
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pierezan, J.; Coelho, L.D.S. Coyote Optimization Algorithm: A New Metaheuristic for Global Optimization Problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Emperor penguin optimizer: A bio-inspired algorithm for engineering problems. Knowl. Based Syst. 2018, 159, 20–50. [Google Scholar] [CrossRef]
- Malviya, R.; Pratihar, D.K. Tuning of neural networks using particle swarm optimization to model MIG welding process. Swarm Evol. Comput. 2011, 1, 223–235. [Google Scholar] [CrossRef]
- Nanda, S.J.; Panda, G. A survey on nature inspired methaheuristic algorithms for partitional clustering. Swarm Evol. Comput. 2014, 16, 1–18. [Google Scholar] [CrossRef]
- Changdar, C.; Mahapatra, G.; Pal, R.K. An efficient genetic algorithm for multi-objective solid travelling salesman problem under fuzziness. Swarm Evol. Comput. 2014, 15, 27–37. [Google Scholar] [CrossRef]
- Suresh, K.; Kumarappan, N. Hybrid improved binary particle swarm optimization approach for generation maintenance scheduling problem. Swarm Evol. Comput. 2012, 9, 69–89. [Google Scholar] [CrossRef]
- Beyer, H.G.F.; Schwefel, H.P. Evolution strategies-a comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.; Wu, D.; Jia, H.; Wen, C.; Rao, H.; Abualigah, L. An improved multi-strategy beluga whale optimization for global optimization problems. Math. Biosci. Eng. 2023, 20, 13267–13317. [Google Scholar] [CrossRef]
- Wen, C.; Jia, H.; Wu, D.; Rao, H.; Li, S.; Liu, Q.; Abualigah, L. Modified Remora Optimization Algorithm with Multistrategies for Global Optimization Problem. Mathematics 2022, 10, 3604. [Google Scholar] [CrossRef]
- Wu, D.; Rao, H.; Wen, C.; Jia, H.; Liu, Q.; Abualigah, L. Modified Sand Cat Swarm Optimization Algorithm for Solving Constrained Engineering Optimization Problems. Mathematics 2022, 10, 4350. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Elaziz, M.A.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Wang, R.-B.; Wang, W.-F.; Xu, L.; Pan, J.-S.; Chu, S.-C. An Adaptive Parallel Arithmetic Optimization Algorithm for Robot Path Planning. J. Adv. Transp. 2021, 2021, 3606895. [Google Scholar] [CrossRef]
- Khodadadi, N.; Snasel, V.; Mirjalili, S. Dynamic Arithmetic Optimization Algorithm for Truss Optimization Under Natural Frequency Constraints. IEEE Access 2022, 10, 16188–16208. [Google Scholar] [CrossRef]
- Li, X.-D.; Wang, J.-S.; Hao, W.-K.; Zhang, M.; Wang, M. Chaotic arithmetic optimization algorithm. Appl. Intell. 2022, 52, 16718–16757. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Kouadri, R.; Musirin, I.; Slimani, L.; Bouktir, T.; Othman, M. Optimal powerflow control variables using slime mould algorithm forgenerator fuel cost and loss minimization with voltage profileenhancement solution. Int. J. EmergingTrends Eng. Res. 2020, 8, 36–44. [Google Scholar]
- Zhao, J.; Gao, Z.M. The hybridized Harris hawk optimizationand slime mould algorithm. J. Phys. Conf. Ser. 2020, 1682, 012029. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatto, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Banzhaf, W.; Nordin, P.; Keller, R.E.; Francone, F.D. Genetic Programming: An Introduction; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1998; Volume 1. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovská, E.; Trojovský, P. A new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process. Sci. Rep. 2022, 12, 9924. [Google Scholar] [CrossRef]
- Gandomi, A.H. Interior search algorithm (ISA): A novel approach for global optimization. ISA Trans. 2014, 53, 1168–1183. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014. [Google Scholar] [CrossRef]
- Wang, G.G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2018, 10, 151–164. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, H.; Heidari, A.A.; Gandomi, A.H. Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021, 177, 114864. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Tu, J.; Chen, H.; Wang, M.; Gandomi, A.H. The colony predation algorithm. J. Bionic Eng. 2021, 18, 674–710. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Noshadian, S.; Chen, H.; Gandomi, A.H. INFO: An efficient optimization algorithm based on weighted mean of vectors. Expert Syst. Appl. 2022, 195, 116516. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physics-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Zeb, A.; Khan, M.; Khan, N.; Tariq, A.; Ali, L.; Azam, F.; Jaffery, S.H.I. Hybridization of simulated annealing with genetic algorithm for cell formation problem. Int. J. Adv. Manuf. Technol. 2016, 86, 2243–2254. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, R.; Deng, T.; Wang, Y.; Di, W.; Luo, H.; Han, T. Magnetic Anomaly Detection Using Three-Axis Magnetoelectric Sensors Based on the Hybridization of Particle Swarm Optimization and Simulated Annealing Algorithm. IEEE Sensors J. 2021, 22, 3686–3694. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S.; Oliva, D. Hybridizing of Whale and Moth-Flame Optimization Algorithms to Solve Diverse Scales of Optimal Power Flow Problem. Electronics 2022, 11, 831. [Google Scholar] [CrossRef]
- Mohd Tumari, M.Z.; Ahmad, M.A.; Suid, M.H.; Hao, M.R. An Improved Marine Predators Algorithm-Tuned Fractional-Order PID Controller for Automatic Voltage Regulator System. Fractal Fract. 2023, 7, 561. [Google Scholar] [CrossRef]
- Wang, L.; Shi, R.; Dong, J. A Hybridization of Dragonfly Algorithm Optimization and Angle Modulation Mechanism for 0-1 Knapsack Problems. Entropy 2021, 23, 598. [Google Scholar] [CrossRef]
- Devaraj AF, S.; Elhoseny, M.; Dhanasekaran, S.; Lydia, E.L.; Shankar, K. Hybridization of firefly and improved multi-objective particle swarm op-timization algorithm for energy efficient load balancing in cloud computing environments. J. Parallel Distrib. Comput. 2020, 142, 36–45. [Google Scholar] [CrossRef]
- Jui, J.J.; Ahmad, M.A. A hybrid metaheuristic algorithm for identification of continuous-time Hammerstein systems. Appl. Math. Model. 2021, 95, 339–360. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Chen, W.; Heidari, A.A.; Wang, M.; Zhao, X.; Liang, G.; Chen, H.; Zhang, X. Ensemble mutation-driven salp swarm algorithm with restart mechanism: Framework and fundamental analysis. Expert Syst. Appl. 2020, 165, 113897. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Lang, C. Remora optimization algorithm. Expert Syst. Appl. 2021, 185, 115665. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Ozsoydan, F.B. Adaptive firefly algorithm with chaos for mechanical design optimization problems. Appl. Soft Comput. 2015, 36, 152–164. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Czerniak, M.; Zarzycki, H.; Ewald, D. AAO as a new strategy in modeling and simulation of constructional problems optimiza-tion. Simul. Modell. Pract. Theory 2017, 76, 22–33. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Baykasoglu, A.; Akpinar, S. Weighted superposition attraction (WSA): A swarm intelligence algorithm for optimization prob-lems-part2: Constrained optimization. Appl. Softw. Comput. 2015, 37, 396–415. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Rao, H.; Jia, H.; Wu, D.; Wen, C.; Li, S.; Liu, Q.; Abualigah, L. A Modified Group Teaching Optimization Algorithm for Solving Constrained Engineering Optimization Problems. Mathematics 2022, 10, 3765. [Google Scholar] [CrossRef]
- Kaveh, A.; Khayatazad, M. A new meta-heuristic method: Ray Optimization. Comput. Struct. 2012, 112–113, 283–294. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl. Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Wang, S.; Sun, K.; Zhang, W.; Jia, H. Multilevel thresholding using a modified ant lion optimizer with opposition-based learning for color image segmentation. Math. Biosci. Eng. 2021, 18, 3092–3143. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z. Group teaching optimization algorithm: A novel metaheuristic method for solving global optimization problems. Expert Syst. Appl. 2020, 148, 113246. [Google Scholar] [CrossRef]
- Houssein, E.H.; Neggaz, N.; Hosney, M.E.; Hosney, M.E.; Mohamed, W.M.; Hassaballah, M. Enhanced Harris hawks opti-mization with genetic operators for selection chemical descriptors and compounds activities. Neural Comput. Appl. 2021, 33, 13601–13618. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.; Liang, X.; Cai, S.; Xu, M. A Random Opposition-Based Learning Grey Wolf Optimizer. IEEE Access 2019, 7, 113810–113825. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]




| Algorithm | Parameter Settings |
|---|---|
| RCLSMAOA | z = 0.03; µ = 0.499; α = 5 |
| AOA [11] | α = 5; MOP_Max = 1; MOP_Min = 0.2; µ = 0.499 |
| SMA [15] | z = 0.03 |
| ROA [45] | C = 0.1 |
| SCA [46] | a = 2 |
| WOA [47] | |
| WMFO [42] | aϵ[1,2]; b = 1 |
| AMVO-SCA [43] | Wmax = 1; Wmin = 0.2 |
| Fn | Metric | RCLSMAOA | AOA | SMA | ROA | SCA | WOA | WMFO | AMVO-SCA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 0 | 1.77 × 10−163 | 0 | 0 | 2.34 × 10−2 | 2.96 × 10−82 | 3.31 × 10−73 | 5.59 × 10−1 |
| Mean | 0 | 3.59 × 10−22 | 5.24 × 10−306 | 4.33 × 10−306 | 7.04 | 6.68 × 10−72 | 1.49 × 10−54 | 2.15 | |
| Stg | 0 | 1.97 × 10−21 | 0 | 0 | 1.15 × 101 | 3.66 × 10−71 | 5.61 × 10−54 | 8.68 × 10−1 | |
| F2 | Best | 0 | 0 | 2.59 × 10−273 | 2.54 × 10−183 | 4.56 × 10−4 | 4.88 × 10−58 | 3.86 × 10−36 | 2.56 × 10−1 |
| Mean | 0 | 0 | 4.09 × 10−157 | 1.66 × 10−162 | 2.61 × 10−2 | 2.50 × 10−51 | 1.31 × 10−26 | 6.06 × 10−1 | |
| Stg | 0 | 0 | 2.24 × 10−156 | 6.67 × 10−162 | 2.68 × 10−2 | 6.92 × 10−51 | 5.00 × 10−26 | 1.96 × 10−1 | |
| F3 | Best | 0 | 4.73 × 10−117 | 0 | 0 | 1.50 × 103 | 1.03 × 104 | 7.53 × 10−46 | 4.74 × 101 |
| Mean | 0 | 5.09 × 10−3 | 3.79 × 10−275 | 7.70 × 10−280 | 7.07 × 103 | 4.41 × 104 | 3.58 × 101 | 1.18 × 102 | |
| Stg | 0 | 9.36 × 10−3 | 0 | 0 | 4.09 × 103 | 1.49 × 104 | 1.90 × 102 | 4.05 × 101 | |
| F4 | Best | 0 | 1.07 × 10−54 | 3.97 × 10−283 | 1.82 × 10−176 | 2.36 × 101 | 1.91 | 2.11 × 10−30 | 5.16 |
| Mean | 0 | 3.23 × 10−2 | 5.55 × 10−138 | 2.33 × 10−159 | 3.75 × 101 | 4.96 × 101 | 1.17 × 10−10 | 8.09 | |
| Stg | 0 | 1.86 × 10−2 | 3.04 × 10−137 | 1.28 × 10−158 | 7.62 | 2.73 × 101 | 6.20 × 10−10 | 1.97 | |
| F5 | Best | 6.30 × 10−5 | 2.74 × 101 | 4.46 × 10−4 | 2.61 × 101 | 1.12 × 102 | 2.70 × 101 | 0 | 6.04 × 101 |
| Mean | 1.85 × 10−2 | 2.83 × 101 | 5.16 | 2.70 × 101 | 2.84 × 104 | 2.80 × 101 | 1.21 × 101 | 1.37 × 102 | |
| Stg | 2.27 × 10−2 | 3.45 × 10−1 | 9.59 | 5.69 × 10−1 | 5.48 × 104 | 4.53 × 10−1 | 1.40 × 101 | 1.12 × 102 | |
| F6 | Best | 2.61 × 10−7 | 2.73 | 1.35 × 10−5 | 1.37 × 10−2 | 4.98 | 9.36 × 10−2 | 0 | 4.30 |
| Mean | 3.59 × 10−6 | 3.17 | 5.77 × 10−3 | 1.17 × 10−1 | 2.35 × 101 | 4.39 × 10−1 | 0 | 7.05 | |
| Stg | 2.99 × 10−6 | 2.28 × 10−1 | 3.57 × 10−3 | 1.42 × 10−1 | 2.99 × 101 | 2.17 × 10−1 | 0 | 2.60 | |
| F7 | Best | 5.61 × 10−7 | 3.49 × 10−6 | 1.57 × 10−5 | 6.78 × 10−6 | 2.08 × 10−2 | 1.57 × 10−4 | 2.42 × 10−6 | 4.01 × 10−2 |
| Mean | 4.30 × 10−5 | 6.04 × 10−5 | 1.84 × 10−4 | 1.60 × 10−4 | 1.55 × 10−1 | 4.62 × 10−3 | 2.96 × 10−4 | 6.01 × 10−2 | |
| Stg | 4.68 × 10−5 | 5.87 × 10−5 | 1.95 × 10−4 | 1.91 × 10−4 | 2.07 × 10−1 | 9.69 × 10−3 | 2.31 × 10−4 | 1.78 × 10−2 | |
| F8 | Best | −1.26 × 104 | −6.32 × 103 | −1.26 × 104 | −1.26 × 104 | −4.24 × 103 | −1.26 × 104 | −2.37 × 10+22 | −7.24 × 103 |
| Mean | −1.26 × 104 | −5.21 × 103 | −1.26 × 104 | −1.24 × 104 | −3.69 × 103 | −1.05 × 104 | −1.42 × 10+23 | −6.49 × 103 | |
| Stg | 1.22 | 4.71 × 102 | 4.26 × 10−1 | 4.31 × 102 | 2.97 × 102 | 1.76 × 103 | 7.55 × 10+23 | 7.77 × 102 | |
| F9 | Best | 0 | 0 | 0 | 0 | 2.84 × 10−1 | 0 | 0 | 6.28 × 101 |
| Mean | 0 | 0 | 0 | 0 | 4.16 × 101 | 1.89 × 10−15 | 2.65 × 101 | 9.28 × 101 | |
| Stg | 0 | 0 | 0 | 0 | 3.30 × 101 | 1.04 × 10−14 | 3.10 × 101 | 2.26 × 101 | |
| F10 | Best | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 1.04 × 10−1 | 8.88 × 10−16 | 8.88 × 10−16 | 4.46 |
| Mean | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 1.53 × 101 | 3.97 × 10−15 | 1.13 × 10−15 | 6.10 | |
| Stg | 0 | 0 | 0 | 0 | 7.95 | 2.42 × 10−15 | 1.30 × 10−15 | 8.36 × 10−1 | |
| F11 | Best | 0 | 1.39 × 10−2 | 0 | 0 | 3.92 × 10−2 | 0 | 0 | 8.05 × 10−1 |
| Mean | 0 | 1.78 × 10−1 | 0 | 0 | 9.90 × 10−1 | 1.71 × 10−2 | 0 | 9.68 × 10−1 | |
| Stg | 0 | 1.31 × 10−1 | 0 | 0 | 3.80 × 10−1 | 6.81 × 10−2 | 0 | 6.45 × 10−2 | |
| F12 | Best | 5.17 × 10−9 | 4.44 × 10−1 | 2.83 × 10−5 | 2.39 × 10−3 | 2.34 | 3.37 × 10−3 | 1.57 × 10−32 | 7.35 |
| Mean | 8.41 × 10−8 | 5.18 × 10−1 | 5.35 × 10−3 | 9.19 × 10−3 | 6.29 × 104 | 1.97 × 10−2 | 1.04 × 10−1 | 1.11 × 101 | |
| Stg | 8.95 × 10−8 | 4.96 × 10−2 | 6.30 × 10−3 | 4.46 × 10−3 | 2.73 × 105 | 1.41 × 10−2 | 5.68 × 10−1 | 3.00 | |
| F13 | Best | 6.96 × 10−8 | 2.62 | 9.35 × 10−6 | 6.01 × 10−3 | 2.77 | 2.03 × 10−1 | 1.35 × 10−32 | 1.61 × 101 |
| Mean | 7.57 × 10−7 | 2.85 | 4.01 × 10−3 | 2.04 × 10−1 | 1.36 × 105 | 5.37 × 10−1 | 1.80 × 10−27 | 2.91 × 101 | |
| Stg | 9.70 × 10−7 | 8.55 × 10−2 | 3.20 × 10−3 | 1.33 × 10−1 | 3.76 × 105 | 2.60 × 10−1 | 9.89 × 10−27 | 9.91 |
| Fn | Metric | RCLSMAOA | AOA | SMA | ROA | SCA | WOA | WMFO | AMVO-SCA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 0 | 5.96 × 10−1 | 0 | 0 | 2.06 × 105 | 1.70 × 10−76 | 2.80 × 10−68 | 7.37 × 10−1 |
| Mean | 0 | 6.43 × 10−1 | 3.54 × 10−259 | 0 | 2.98 × 105 | 1.75 × 10−69 | 2.15 × 10−52 | 2.32 | |
| Stg | 0 | 5.98 × 10−2 | 0 | 0 | 8.38 × 104 | 3.89 × 10−69 | 1.15 × 10−51 | 1 | |
| F2 | Best | 0 | 2.47 × 10−4 | 9.02 × 10−16 | 1.50 × 10−174 | 9.36 × 101 | 3.38 × 10−51 | 7.99 × 10−37 | 3.51 × 10−1 |
| Mean | 0 | 2.74 × 10−3 | 6.76 × 10−1 | 3.35 × 10−159 | 1.84 × 102 | 6.39 × 10−48 | 7.25 × 10−22 | 6.00 × 10−1 | |
| Stg | 0 | 2.28 × 10−3 | 9.50 × 10−1 | 7.50 × 10−159 | 6.74 × 101 | 1.08 × 10−47 | 3.97 × 10−21 | 1.34 × 10−1 | |
| F3 | Best | 0 | 2.91 × 101 | 0 | 2.49 × 10−291 | 6.53 × 106 | 2.78 × 107 | 3.05 × 10−50 | 3.78 × 101 |
| Mean | 0 | 5.28 × 101 | 4.30 × 10−208 | 2.89 × 10−279 | 8.07 × 106 | 3.90 × 107 | 9.40 | 1.19 × 102 | |
| Stg | 0 | 3.30 × 101 | 0 | 0 | 1.73 × 106 | 8.30 × 106 | 4.41 × 101 | 6.19 × 101 | |
| F4 | Best | 0 | 1.76 × 10−1 | 1.20 × 10−159 | 4.65 × 10−170 | 9.88 × 101 | 5.20 × 101 | 8.09 × 10−32 | 5.36 |
| Mean | 0 | 2.00 × 10−1 | 2.89 × 10−120 | 2.18 × 10−156 | 9.92 × 101 | 7.28 × 101 | 1.03 × 10−10 | 8.33 | |
| Stg | 0 | 4.69 × 10−2 | 6.25 × 10−120 | 4.85 × 10−156 | 2.93 × 10−1 | 2.00 × 101 | 5.64 × 10−10 | 2.02 | |
| F5 | Best | 1.37 × 10−5 | 4.99 × 102 | 3.27 × 101 | 4.94 × 102 | 2.03 × 109 | 4.96 × 102 | 0 | 7.12 × 101 |
| Mean | 7.52 × 10−2 | 4.99 × 102 | 3.70 × 102 | 4.95 × 102 | 2.32 × 109 | 4.97 × 102 | 8.35 | 1.35 × 102 | |
| Stg | 8.06 × 10−2 | 9.93 × 10−2 | 2.03 × 102 | 2.87 × 10−1 | 3.50 × 108 | 4.41 × 10−1 | 1.30 × 101 | 7.25 × 101 | |
| F6 | Best | 1.51 × 10−6 | 1.13 × 102 | 8.25 × 10−1 | 1.38 × 101 | 1.30 × 105 | 2.53 × 101 | 0 | 4.06 |
| Mean | 7.01 × 10−3 | 1.16 × 102 | 5.24 × 101 | 1.98 × 101 | 2.25 × 105 | 3.79 × 101 | 0 | 6.94 | |
| Stg | 9.92 × 10−3 | 1.80 | 4.74 × 101 | 5.45 | 8.80 × 104 | 1.21 × 101 | 0 | 2.07 | |
| F7 | Best | 2.45 × 10−7 | 8.86 × 10−5 | 8.56 × 10−5 | 1.25 × 10−4 | 1.60 × 104 | 1.66 × 10−3 | 3.12 × 10−5 | 3.40 × 10−2 |
| Mean | 2.63 × 10−5 | 1.37 × 10−4 | 7.06 × 10−4 | 3.96 × 10−4 | 1.79 × 104 | 1.21 × 10−2 | 2.90 × 10−4 | 6.14 × 10−2 | |
| Stg | 2.30 × 10−5 | 4.50 × 10−5 | 8.20 × 10−4 | 2.59 × 10−4 | 2.22 × 103 | 1.66 × 10−2 | 2.09 × 10−4 | 1.69 × 10−2 | |
| F8 | Best | −2.09 × 105 | −2.37 × 104 | −2.09 × 105 | −2.09 × 105 | −1.58 × 104 | −2.06 × 105 | −8.54 × 1024 | −7.91 × 103 |
| Mean | −2.09 × 105 | −2.18 × 104 | −2.09 × 105 | −1.99 × 105 | −1.47 × 104 | −1.76 × 105 | −2.85 × 1023 | −6.41 × 103 | |
| Stg | 1.77 × 10−1 | 2.03 × 103 | 2.34 × 102 | 1.55 × 104 | 6.84 × 102 | 4.11 × 104 | 1.56 × 1024 | 6.24 × 102 | |
| F9 | Best | 0 | 0 | 0 | 0 | 5.17 × 102 | 0 | 0 | 5.17 × 101 |
| Mean | 0 | 6.93 × 10−6 | 0 | 0 | 1.42 × 103 | 6.06 × 10−14 | 1.19 × 101 | 9.26 × 101 | |
| Stg | 0 | 6.72 × 10−6 | 0 | 0 | 5.55 × 102 | 3.32 × 10−13 | 2.43 × 101 | 2.28 × 101 | |
| F10 | Best | 8.88 × 10−16 | 7.44 × 10−3 | 8.88 × 10−16 | 8.88 × 10−16 | 8.07 | 8.88 × 10−16 | 8.88 × 10−16 | 5.15 |
| Mean | 8.88 × 10−16 | 8.12 × 10−3 | 8.88 × 10−16 | 8.88 × 10−16 | 1.92 × 101 | 4.32 × 10−15 | 8.88 × 10−16 | 6.14 | |
| Stg | 0 | 3.45 × 10−4 | 0 | 0 | 3.62 | 2.38 × 10−15 | 0 | 6.10 × 10−1 | |
| F11 | Best | 0 | 6.43 × 103 | 0 | 0 | 9.67 × 102 | 0 | 0 | 7.55 × 10−1 |
| Mean | 0 | 1.06 × 104 | 0 | 0 | 2.02 × 103 | 3.70 × 10−18 | 0 | 9.87 × 10−1 | |
| Stg | 0 | 2.97 × 103 | 0 | 0 | 7.53 × 102 | 2.03 × 10−17 | 0 | 6.07 × 10−2 | |
| F12 | Best | 4.18 × 10−13 | 1.06 | 2.34 × 10−5 | 1.43 × 10−2 | 3.40 × 109 | 3.93 × 10−2 | 1.57 × 10−32 | 7.08 |
| Mean | 2.20 × 10−7 | 1.08 | 2.60 × 10−2 | 3.97 × 10−2 | 5.72 × 109 | 1.06 × 10−1 | 1.57 × 10−32 | 1.02 × 101 | |
| Stg | 2.92 × 10−7 | 1.36 × 10−2 | 9.59 × 10−2 | 2.25 × 10−2 | 1.47 × 109 | 5.14 × 10−2 | 5.57 × 10−48 | 2.56 | |
| F13 | Best | 6.02 × 10−11 | 5.01 × 101 | 3.61 × 10−3 | 3.37 | 5.32 × 109 | 8.64 | 1.35 × 10−32 | 1.82 × 101 |
| Mean | 1.79 × 10−3 | 5.02 × 101 | 2.87 | 9.03 | 1.03 × 1010 | 2.00 × 101 | 1.35 × 10−32 | 3.00 × 101 | |
| Stg | 3.77 × 10−3 | 4.33 × 10−2 | 8.97 | 2.72 | 2.39 × 109 | 5.75 | 5.57 × 10−48 | 8.14 |
| Fn | Metric | RCLSMAOA | AOA | SMA | ROA | SCA | WOA | WMFO | AMVO-SCA |
|---|---|---|---|---|---|---|---|---|---|
| F14 | Best | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 |
| Mean | 9.98 × 10−1 | 9.49 | 9.98 × 10−1 | 3.35 | 1.60 | 3.71 | 4.23 | 5.74 | |
| Stg | 0 | 3.63 | 8.61 × 10−13 | 4.01 | 9.23 × 10−1 | 4.02 | 3.92 | 4.34 | |
| F15 | Best | 3.07 × 10−4 | 3.77 × 10−4 | 3.08 × 10−4 | 3.08 × 10−4 | 4.92 × 10−4 | 3.58 × 10−4 | 3.07 × 10−4 | 3.68 × 10−4 |
| Mean | 3.45 × 10−4 | 1.69 × 10−2 | 6.23 × 10−4 | 5.04 × 10−4 | 1.10 × 10−3 | 6.97 × 10−4 | 4.37 × 10−4 | 1.38 × 10−3 | |
| Stg | 9.47 × 10−5 | 3.25 × 10−2 | 3.04 × 10−4 | 3.18 × 10−4 | 3.56 × 10−4 | 4.54 × 10−4 | 2.96 × 10−4 | 1.10 × 10−3 | |
| F16 | Best | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 |
| Mean | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | |
| Stg | 6.78 × 10−16 | 1.34 × 10−7 | 1.59 × 10−9 | 5.27 × 10−8 | 5.73 × 10−5 | 2.87 × 10−9 | 5.80 × 10−10 | 5.27 × 10−3 | |
| F17 | Best | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 |
| Mean | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 4.00 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | |
| Stg | 0 | 1.36 × 10−7 | 2.84 × 10−8 | 1.32 × 10−5 | 1.55 × 10−3 | 5.72 × 10−6 | 1.02 × 10−8 | 7.57 × 10−4 | |
| F18 | Best | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Mean | 3 | 1.34 × 101 | 3 | 3 | 3 | 3 | 3 | 3 | |
| Stg | 2.08 × 10−15 | 2.01 × 101 | 7.57 × 10−11 | 6.18 × 10−5 | 8.12 × 10−5 | 1.05 × 10−2 | 5.99 × 10−6 | 6.46 × 10−13 | |
| F19 | Best | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 |
| Mean | −3.86 | −3.85 | −3.86 | −3.86 | −3.85 | −3.86 | −3.86 | −3.86 | |
| Stg | 2.71 × 10−15 | 5.82 × 10−3 | 1.90 × 10−6 | 2.77 × 10−3 | 6.12 × 10−3 | 1.07 × 10−2 | 3.39 × 10−3 | 1.36 × 10−2 | |
| F20 | Best | −3.32 | −3.16 | −3.32 | −3.32 | −3.13 | −3.32 | −3.32 | −3.32 |
| Mean | −3.29 | −3.02 | −3.24 | −3.21 | −2.87 | −3.20 | −3.13 | −3.01 | |
| Stg | 5.35 × 10−2 | 9.55 × 10−2 | 5.58 × 10−2 | 1.42 × 10−1 | 3.47 × 10−1 | 1.73 × 10−1 | 3.13 × 10−1 | 3.59 × 10−1 | |
| F21 | Best | −1.02 × 101 | −5.16 | −1.02 × 101 | −1.02 × 101 | −5.90 | −1.01 × 101 | −1.02 × 101 | −1.01 × 101 |
| Mean | −1.02 × 101 | −3.62 | −1.02 × 101 | −1.01 × 101 | −2.40 | −7.60 | −5.23 | −4.72 | |
| Stg | 6.96 × 10−15 | 1.06 | 4.55 × 10−4 | 1.58 × 10−2 | 1.86 | 2.81 | 9.31 × 10−1 | 2.63 | |
| F22 | Best | −1.04 × 101 | −7.58 | −1.04 × 101 | −1.04 × 101 | −6.85 | −1.04 × 101 | −1.04 × 101 | −1.04 × 101 |
| Mean | −1.04 × 101 | −4.29 | −1.04 × 101 | −1.04 × 101 | −3.69 | −7.69 | −6.26 | −5.89 | |
| Stg | 1.19 × 10−15 | 1.23 | 2.55 × 10−4 | 1.59 × 10−2 | 1.86 | 3.21 | 2.71 | 3.10 | |
| F23 | Best | −1.05 × 101 | −8.42 | −1.05 × 101 | −1.05 × 101 | −8.38 | −1.05 × 101 | −1.05 × 101 | −1.05 × 101 |
| Mean | −1.05 × 101 | −4.06 | −1.05 × 101 | −1.05 × 101 | −3.86 | −7.34 | −7.29 | −5.23 | |
| Stg | 1.78 × 10−15 | 1.72 | 3.91 × 10−4 | 2.00 × 10−2 | 1.87 | 3.09 | 2.69 | 3.07 |
| CEC | Metric | RCLSMAOA | AOA | SMA | ROA | SCA | WOA | WMFO | AMVO-SCA |
|---|---|---|---|---|---|---|---|---|---|
| CEC_01 | mid | 1.00 × 102 | 2.99 × 109 | 1.05 × 102 | 1.05 × 109 | 4.08 × 108 | 5.00 × 106 | 1.19 × 103 | 3.15 × 103 |
| mean | 1.80 × 103 | 1.02 × 1010 | 7.28 × 103 | 5.69 × 109 | 1.10 × 109 | 7.74 × 107 | 1.57 × 105 | 8.64 × 108 | |
| std | 1.88 × 103 | 4.13 × 109 | 5.00 × 103 | 3.26 × 109 | 5.80 × 108 | 1.13 × 108 | 4.30 × 105 | 1.43 × 109 | |
| CEC_02 | mid | 1.10 × 103 | 1.83 × 103 | 1.34 × 103 | 1.77 × 103 | 1.75 × 103 | 1.63 × 103 | 1.46 × 103 | 1.57 × 103 |
| mean | 1.42 × 103 | 2.22 × 103 | 1.77 × 103 | 2.49 × 103 | 2.54 × 103 | 2.24 × 103 | 1.98 × 103 | 2.00 × 103 | |
| std | 1.33 × 102 | 2.30 × 102 | 2.52 × 102 | 3.17 × 102 | 2.73 × 102 | 3.44 × 102 | 3.62 × 102 | 3.44 × 102 | |
| CEC_03 | mid | 7.11 × 102 | 7.70 × 102 | 7.18 × 102 | 7.71 × 102 | 7.56 × 102 | 7.52 × 102 | 7.22 × 102 | 7.30 × 102 |
| mean | 7.18 × 102 | 7.96 × 102 | 7.32 × 102 | 8.17 × 102 | 7.86 × 102 | 7.97 × 102 | 7.45 × 102 | 7.65 × 102 | |
| std | 2.75 | 1.56 × 101 | 9.63 | 2.46 × 101 | 1.41 × 101 | 2.76 × 101 | 1.59 × 101 | 3.23 × 101 | |
| CEC_04 | mid | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 |
| mean | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | |
| std | 0 | 0 | 0 | 0 | 1.09 | 2.56 × 10−1 | 5.83 × 10−1 | 2.58 | |
| CEC_05 | mid | 1.70 × 103 | 9.15 × 103 | 2.46 × 103 | 4.58 × 103 | 1.23 × 104 | 7.71 × 103 | 6.75 × 103 | 3.67 × 103 |
| mean | 2.91 × 103 | 4.49 × 105 | 2.69 × 104 | 4.77 × 105 | 6.57 × 104 | 2.59 × 105 | 3.36 × 105 | 3.36 × 105 | |
| std | 1.62 × 103 | 3.28 × 105 | 6.82 × 104 | 3.36 × 105 | 6.78 × 104 | 5.10 × 105 | 5.16 × 105 | 3.66 × 105 | |
| CEC_06 | mid | 1.60 × 103 | 1.76 × 103 | 1.61 × 103 | 1.65 × 103 | 1.69 × 103 | 1.65 × 103 | 1.61 × 103 | 1.60 × 103 |
| mean | 1.65 × 103 | 2.15 × 103 | 1.77 × 103 | 1.96 × 103 | 1.86 × 103 | 1.89 × 103 | 1.82 × 103 | 1.86 × 103 | |
| std | 5.85 × 101 | 1.99 × 102 | 1.05 × 102 | 1.52 × 102 | 9.03 × 101 | 1.25 × 102 | 1.39 × 102 | 1.74 × 102 | |
| CEC_07 | mid | 2.10 × 103 | 4.05 × 103 | 2.33 × 103 | 2.98 × 103 | 5.60 × 103 | 8.70 × 103 | 3.43 × 103 | 2.76 × 103 |
| mean | 2.62 × 103 | 1.04 × 106 | 9.48 × 103 | 3.66 × 105 | 1.72 × 104 | 7.75 × 105 | 1.76 × 105 | 5.75 × 105 | |
| std | 7.73 × 102 | 2.14 × 106 | 9.22 × 103 | 1.02 × 106 | 1.06 × 104 | 2.07 × 106 | 3.79 × 105 | 2.97 × 106 | |
| CEC_08 | mid | 2.20 × 103 | 2.59 × 103 | 2.30 × 103 | 2.38 × 103 | 2.33 × 103 | 2.31 × 103 | 2.23 × 103 | 2.30 × 103 |
| mean | 2.30 × 103 | 3.07 × 103 | 2.46 × 103 | 2.71 × 103 | 2.41 × 103 | 2.38 × 103 | 2.40 × 103 | 2.50 × 103 | |
| std | 1.99 × 101 | 3.35 × 102 | 3.69 × 102 | 3.50 × 102 | 4.66 × 101 | 2.92 × 102 | 3.80 × 102 | 3.58 × 102 | |
| CEC_09 | mid | 2.40 × 103 | 2.66 × 103 | 2.50 × 103 | 2.60 × 103 | 2.57 × 103 | 2.57 × 103 | 2.74 × 103 | 2.50 × 103 |
| mean | 2.72 × 103 | 2.88 × 103 | 2.75 × 103 | 2.81 × 103 | 2.79 × 103 | 2.78 × 103 | 2.76 × 103 | 2.76 × 103 | |
| std | 6.67 × 101 | 8.73 × 101 | 3.82 × 101 | 8.55 × 101 | 4.37 × 101 | 5.17 × 101 | 2.41 × 101 | 7.40 × 101 | |
| CEC_10 | mid | 2.90 × 103 | 2.99 × 103 | 2.90 × 103 | 2.97 × 103 | 2.94 × 103 | 2.91 × 103 | 2.90 × 103 | 2.91 × 103 |
| mean | 2.93 × 103 | 3.38 × 103 | 2.95 × 103 | 3.25 × 103 | 2.99 × 103 | 2.98 × 103 | 2.94 × 103 | 2.97 × 103 | |
| std | 2.17 × 101 | 2.89 × 102 | 3.18 × 101 | 2.57 × 102 | 3.12 × 101 | 9.68 × 101 | 2.93 × 101 | 6.47 × 101 |
| F23 | dim | RCLSMAOA vs. AOA | RCLSMAOA vs. SMA | RCLSMAOA vs. ROA | RCLSMAOA vs. SCA | RCLSMAOA vs. WOA | RCLSMAOA vs. WMFO | RCLSMAOA vs. AMVO-SCA |
|---|---|---|---|---|---|---|---|---|
| F1 | 30 | 1.73 × 10−6 | 5.00 × 10−1 | 1 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 |
| 500 | 1.73 × 10−6 | 1.22 × 10−4 | 5.00 × 10−1 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F2 | 30 | 1 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 |
| 500 | 1 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F3 | 30 | 1.73 × 10−6 | 1 | 1.95 × 10−3 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 |
| 500 | 1.73 × 10−6 | 1 | 6.10 × 10−5 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F4 | 30 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 |
| 500 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F5 | 30 | 1.73 × 10−6 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 4.21 × 10−1 | 6.10 × 10−5 |
| 500 | 1.73 × 10−6 | 2.88 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 8.04 × 10−1 | 6.10 × 10−5 | |
| F6 | 30 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 |
| 500 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F7 | 30 | 8.61 × 10−1 | 2.96 × 10−3 | 1.11 × 10−2 | 1.73 × 10−6 | 1.73 × 10−6 | 1.22 × 10−4 | 6.10 × 10−5 |
| 500 | 2.99 × 10−1 | 4.53 × 10−4 | 3.61 × 10−3 | 1.73 × 10−6 | 2.60 × 10−6 | 6.10 × 10−4 | 6.10 × 10−5 | |
| F8 | 30 | 1.73 × 10−6 | 3.16 × 10−2 | 8.13 × 10−1 | 1.73 × 10−6 | 1.92 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 |
| 500 | 1.73 × 10−6 | 1.04 × 10−2 | 4.45 × 10−5 | 1.73 × 10−6 | 2.35 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F9 | 30 | 1 | 1 | 1 | 1.73 × 10−6 | 1 | 3.13 × 10−2 | 6.10 × 10−5 |
| 500 | 1 | 1 | 1 | 1.73 × 10−6 | 2.50 × 10−1 | 7.81 × 10−3 | 6.10 × 10−5 | |
| F10 | 30 | 1 | 1 | 1 | 1.73 × 10−6 | 9.90 × 10−6 | 1 | 6.10 × 10−5 |
| 500 | 1.73 × 10−6 | 1 | 1 | 1.73 × 10−6 | 5.00 × 10−1 | 1 | 6.10 × 10−5 | |
| F11 | 30 | 1.73 × 10−6 | 1 | 1 | 1.73 × 10−6 | 1 | 1 | 6.10 × 10−5 |
| 500 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1 | 6.10 × 10−5 | |
| F12 | 30 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 |
| 500 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F13 | 30 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 |
| 500 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F14 | 2 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 5.00 × 10−1 | 6.10 × 10−5 |
| F15 | 4 | 1.92 × 10−6 | 4.45 × 10−5 | 9.32 × 10−6 | 1.73 × 10−6 | 2.35 × 10−6 | 6.10 × 10−5 | 1.07 × 10−1 |
| F16 | 2 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1 | 6.10 × 10−5 |
| F17 | 2 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1 | 6.10 × 10−5 |
| F18 | 5 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 9.77 × 10−4 | 6.10 × 10−5 |
| F19 | 3 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1 | 6.10 × 10−5 |
| F20 | 6 | 1.73 × 10−6 | 6.32 × 10−5 | 3.52 × 10−6 | 1.73 × 10−6 | 4.53 × 10−4 | 4.03 × 10−3 | 4.21 × 10−1 |
| F21 | 4 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 3.13 × 10−2 | 6.10 × 10−5 |
| F22 | 4 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 7.81 × 10−3 | 6.10 × 10−5 |
| F23 | 4 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 3.13 × 10−2 | 6.10 × 10−5 |
| F23 | dim | RCLSMAOA vs. AOA | RCLSMAOA vs. SMA | RCLSMAOA vs. ROA | RCLSMAOA vs. SCA | RCLSMAOA vs. WOA | RCLSMAOA vs. WMFO | RCLSMAOA vs. AMVO-SCA |
|---|---|---|---|---|---|---|---|---|
| CEC01 | 10 | 1.73 × 10−6 | 6.34 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 4.27 × 10−3 | 6.10 × 10−5 |
| CEC02 | 10 | 1.73 × 10−6 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 3.36 × 10−3 | 3.05 × 10−4 |
| CEC03 | 10 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.22 × 10−4 | 6.10 × 10−5 |
| CEC04 | 10 | 1.73 × 10−6 | 1 | 1 | 1.73 × 10−6 | 1 | 3.13 × 10−2 | 6.10 × 10−5 |
| CEC05 | 10 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.22 × 10−4 | 6.10 × 10−5 |
| CEC06 | 10 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 4.27 × 10−4 | 6.10 × 10−5 |
| CEC07 | 10 | 1.73 × 10−6 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.16 × 10−3 | 2.62 × 10−3 |
| CEC08 | 10 | 1.73 × 10−6 | 2.60 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 6.10 × 10−5 | 6.10 × 10−5 |
| CEC09 | 10 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 8.33 × 10−2 | 8.33 × 10−2 |
| CEC10 | 10 | 1.73 × 10−6 | 1.13 × 10−5 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 2.56 × 10−2 | 3.53 × 10−2 |
| F | RCLSMAOA | AOA | SMA | ROA | SCA | WOA | WMFO | AMVO-SCA |
|---|---|---|---|---|---|---|---|---|
| F1 | 1.933333333 | 4.266666667 | 1.983333333 | 2.083333333 | 7.666666667 | 5.866666667 | 4.866666667 | 7.333333333 |
| F2 | 1.5 | 1.5 | 3.2 | 3.8 | 7 | 5 | 6 | 8 |
| F3 | 1.5 | 4.3 | 1.5 | 3 | 7 | 8 | 4.7 | 6 |
| F4 | 1 | 4.9 | 2.166666667 | 2.833333333 | 7 | 8 | 4.1 | 6 |
| F5 | 1.7 | 5.1 | 2.866666667 | 3.666666667 | 7.966666667 | 5.9 | 1.766666667 | 7.033333333 |
| F6 | 2 | 5.566666667 | 3 | 4 | 7.633333333 | 5.533333333 | 1 | 7.266666667 |
| F7 | 2.333333333 | 1.8 | 3.866666667 | 2.966666667 | 7.533333333 | 6.3 | 4.1 | 7.1 |
| F8 | 3 | 6.8 | 3 | 3 | 8 | 5.4 | 1 | 5.8 |
| F9 | 3.133333333 | 3.133333333 | 3.133333333 | 3.133333333 | 6.866666667 | 3.683333333 | 5.05 | 7.866666667 |
| F10 | 3.116666667 | 3.116666667 | 3.116666667 | 3.116666667 | 7.666666667 | 5.416666667 | 3.116666667 | 7.333333333 |
| F11 | 2.85 | 5.866666667 | 2.85 | 2.85 | 7.3 | 3.9 | 2.85 | 7.533333333 |
| F12 | 2 | 5.733333333 | 3.1 | 3.9 | 7.466666667 | 5.266666667 | 1 | 7.533333333 |
| F13 | 2 | 6 | 3 | 4 | 7.8 | 5 | 1 | 7.2 |
| F14 | 1.416666667 | 6.933333333 | 3 | 4.833333333 | 4.866666667 | 6.733333333 | 1.75 | 6.466666667 |
| F15 | 1.566666667 | 6.166666667 | 4.1 | 2.7 | 5.566666667 | 5.666666667 | 6.266666667 | 3.966666667 |
| F16 | 1.166666667 | 6.6 | 3.8 | 5.733333333 | 7.966666667 | 4.866666667 | 1.833333333 | 4.033333333 |
| F17 | 1.5 | 4.766666667 | 3.6 | 5.866666667 | 7.5 | 7.5 | 1.5 | 3.766666667 |
| F18 | 1.033333333 | 5.1 | 3.066666667 | 6.2 | 6.666666667 | 6.866666667 | 1.966666667 | 5.1 |
| F19 | 1.3 | 6.5 | 3.033333333 | 5 | 6.3 | 7.333333333 | 1.7 | 4.833333333 |
| F20 | 1.3 | 6.4 | 3.833333333 | 4.166666667 | 7.233333333 | 7.266666667 | 2.633333333 | 3.166666667 |
| F21 | 1.033333333 | 6.266666667 | 2.733333333 | 3.833333333 | 7.466666667 | 5.933333333 | 4 | 4.733333333 |
| F22 | 1.116666667 | 6.9 | 3.4 | 4.266666667 | 6.9 | 6.7 | 2.783333333 | 3.933333333 |
| F23 | 1.083333333 | 6.8 | 3.366666667 | 4.266666667 | 6.8 | 6.533333333 | 2.583333333 | 4.566666667 |
| Avg Rank | 1.7644 | 5.5298 | 3.0746 | 3.8789 | 7.1376 | 6.0289 | 2.9376 | 5.9376 |
| Final Rank | 1 | 5 | 3 | 4 | 8 | 7 | 2 | 6 |
| CEC2020 | RCLSMAOA | AOA | SMA | ROA | SCA | WOA | WMFO | AMVO-SCA |
|---|---|---|---|---|---|---|---|---|
| CEC2020_01 | 1.466666667 | 7.6 | 2.133333333 | 5.166666667 | 5.266666667 | 7.366666667 | 2.666666667 | 4.333333333 |
| CEC2020_02 | 1.233333333 | 5.166666667 | 3.066666667 | 4.766666667 | 6.933333333 | 7.566666667 | 3.633333333 | 3.633333333 |
| CEC2020_03 | 1.066666667 | 7 | 2.4 | 4.766666667 | 5.766666667 | 7.633333333 | 2.966666667 | 4.4 |
| CEC2020_04 | 3.383333333 | 3.383333333 | 3.383333333 | 3.383333333 | 5.683333333 | 3.766666667 | 5.083333333 | 7.933333333 |
| CEC2020_05 | 1.133333333 | 7.066666667 | 3.3 | 4.533333333 | 4.466666667 | 5.4 | 5.6 | 4.5 |
| CEC2020_06 | 1.4 | 6.8 | 2.7 | 4.6 | 3.833333333 | 7.1 | 4.466666667 | 5.1 |
| CEC2020_07 | 1.8 | 6.7 | 3.6 | 4.133333333 | 4.333333333 | 7.866666667 | 4.3 | 3.266666667 |
| CEC2020_08 | 1.233333333 | 7.366666667 | 2.8 | 5 | 5.166666667 | 7.133333333 | 3.033333333 | 4.266666667 |
| CEC2020_09 | 1.333333333 | 6.966666667 | 3.033333333 | 4.433333333 | 5.366666667 | 7.033333333 | 3.6 | 4.233333333 |
| CEC2020_10 | 1.8 | 7.566666667 | 2.766666667 | 4.633333333 | 5.066666667 | 7.3 | 3.066666667 | 3.8 |
| Avg Rank | 1.585 | 6.5616 | 2.9183 | 4.5416 | 5.1883 | 6.8166 | 3.8416 | 4.5466 |
| Final Rank | 1 | 7 | 2 | 4 | 6 | 8 | 3 | 5 |
| Algorithm | Optimal Values for Variables | Cost | |||
|---|---|---|---|---|---|
| Ts | Th | R | L | ||
| RCLSMAOA | 0.742433 | 0.370196 | 40.31961 | 200 | 5734.9131 |
| AOA [11] | 0.8303737 | 0.4162057 | 42.75127 | 169.3454 | 6048.7844 |
| SMA [15] | 0.7931 | 0.3932 | 40.6711 | 196.2178 | 5994.1857 |
| WOA [47] | 0.8125 | 0.4375 | 42.0982699 | 176.638998 | 6059.741 |
| GA [21] | 0.8125 | 0.4375 | 42.0974 | 176.6541 | 6059.94634 |
| GWO [48] | 0.8125 | 0.4345 | 42.089181 | 176.758731 | 6051.5639 |
| ACO [49] | 0.8125 | 0.4375 | 42.103624 | 176.572656 | 6059.0888 |
| AO [50] | 1.054 | 0.182806 | 59.6219 | 39.805 | 5949.2258 |
| MVO [51] | 0.8125 | 0.4375 | 42.09074 | 176.7387 | 6060.8066 |
| Algorithm | Optimal Values for Variables | Optimal Weight | ||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | ||
| RCLSMAOA | 3.4975 | 0.7 | 17 | 7.3 | 7.8 | 3.3500 | 5.285 | 2995.437365 |
| AOA [11] | 3.50384 | 0.7 | 17 | 7.3 | 7.72933 | 3.35649 | 5.2867 | 2997.9157 |
| FA [52] | 3.507495 | 0.7001 | 17 | 7.719674 | 8.080854 | 3.351512 | 5.287051 | 3010.137492 |
| RSA [53] | 3.50279 | 0.7 | 17 | 7.30812 | 7.74715 | 3.35067 | 5.28675 | 2996.5157 |
| MFO [54] | 3.497455 | 0.7 | 17 | 7.82775 | 7.712457 | 3.351787 | 5.286352 | 2998.94083 |
| AAO [55] | 3.499 | 0.6999 | 17 | 7.3 | 7.8 | 3.3502 | 5.2872 | 2996.783 |
| HS [56] | 3.520124 | 0.7 | 17 | 8.37 | 7.8 | 3.36697 | 5.288719 | 3029.002 |
| WSA [57] | 3.5 | 0.7 | 17 | 7.3 | 7.8 | 3.350215 | 5.286683 | 2996.348225 |
| CS [58] | 3.5015 | 0.7 | 17 | 7.605 | 7.8181 | 3.352 | 5.2875 | 3000.981 |
| Algorithm | x1 | x2 | Best Weight |
|---|---|---|---|
| RCLSMAOA | 0.78841544 | 0.408113094 | 263.8523464 |
| MVO [51] | 0.788603 | 0.408453 | 263.8958 |
| RSA [53] | 0.78873 | 0.40805 | 263.8928 |
| GOA [59] | 0.788898 | 0.40762 | 263.8959 |
| CS [58] | 0.78867 | 0.40902 | 263.9716 |
| Algorithm | Optimal Values for Variables | Best Weight | |||
|---|---|---|---|---|---|
| h | l | t | b | ||
| RCLSMAOA | 0.20573 | 3.2530 | 9.0366 | 0.20572 | 1.6952 |
| ROA [45] | 0.200077 | 3.365754 | 9.011182 | 0.206893 | 1.706447 |
| MGTOA [60] | 0.205351 | 3.268419 | 9.069875 | 0.205621 | 1.701633939 |
| MVO [51] | 0.205463 | 3.473193 | 9.044502 | 0.205695 | 1.72645 |
| WOA [47] | 0.205396 | 3.484293 | 9.037426 | 0.206276 | 1.730499 |
| MROA [9] | 0.2062185 | 3.254893 | 9.020003 | 0.206489 | 1.699058 |
| RO [61] | 0.203687 | 3.528467 | 9.004233 | 0.207241 | 1.735344 |
| BWO [62] | 0.2059 | 3.2665 | 9.0229 | 0.2064 | 1.6997 |
| Algorithm | RCLSMAOA | ROA [45] | WOA [57] | MALO [63] | GTOA [64] | HHOCM [65] | ROLGWO [66] | MPA [67] |
|---|---|---|---|---|---|---|---|---|
| x1 | 0.5 | 0.5 | 0.8521 | 0.5 | 0.662833 | 0.500164 | 0.501255 | 0.5 |
| x2 | 1.230638152 | 1.22942 | 1.2136 | 1.2281 | 1.217247 | 1.248612 | 1.245551 | 1.22823 |
| x3 | 0.5 | 0.5 | 0.6604 | 0.5 | 0.734238 | 0.659558 | 0.500046 | 0.5 |
| x4 | 1.198406418 | 1.21197 | 1.1156 | 1.2126 | 1.11266 | 1.098515 | 1.180254 | 1.2049 |
| x5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.613197 | 0.757989 | 0.500035 | 0.5 |
| x6 | 1.08390407 | 1.37798 | 1.195 | 1.308 | 0.670197 | 0.767268 | 1.16588 | 1.2393 |
| x7 | 0.5 | 0.50005 | 0.5898 | 0.5 | 0.615694 | 0.500055 | 0.500088 | 0.5 |
| x8 | 0.345067013 | 0.34489 | 0.2711 | 0.3449 | 0.271734 | 0.343105 | 0.344895 | 0.34498 |
| x9 | 0.347988173 | 0.19263 | 0.2769 | 0.2804 | 0.23194 | 0.192032 | 0.299583 | 0.192 |
| x10 | 0.877748111 | 0.62239 | 4.3437 | 0.4242 | 0.174933 | 2.898805 | 3.59508 | 0.44035 |
| x11 | 0.729351464 | - | 2.2352 | 4.6565 | 0.462294 | - | 2.29018 | 1.78504 |
| Best Weight | 23.18907104 | 23.23544 | 25.83657 | 23.2294 | 25.70607 | 24.48358 | 23.22243 | 23.19982 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Wang, Z.; Jia, H.; Zhou, X.; Abualigah, L. Hybrid Slime Mold and Arithmetic Optimization Algorithm with Random Center Learning and Restart Mutation. Biomimetics 2023, 8, 396. https://doi.org/10.3390/biomimetics8050396
Chen H, Wang Z, Jia H, Zhou X, Abualigah L. Hybrid Slime Mold and Arithmetic Optimization Algorithm with Random Center Learning and Restart Mutation. Biomimetics. 2023; 8(5):396. https://doi.org/10.3390/biomimetics8050396
Chicago/Turabian StyleChen, Hongmin, Zhuo Wang, Heming Jia, Xindong Zhou, and Laith Abualigah. 2023. "Hybrid Slime Mold and Arithmetic Optimization Algorithm with Random Center Learning and Restart Mutation" Biomimetics 8, no. 5: 396. https://doi.org/10.3390/biomimetics8050396
APA StyleChen, H., Wang, Z., Jia, H., Zhou, X., & Abualigah, L. (2023). Hybrid Slime Mold and Arithmetic Optimization Algorithm with Random Center Learning and Restart Mutation. Biomimetics, 8(5), 396. https://doi.org/10.3390/biomimetics8050396








