Wing Kinematics-Based Flight Control Strategy in Insect-Inspired Flight Systems: Deep Reinforcement Learning Gives Solutions and Inspires Controller Design in Flapping MAVs
Abstract
1. Introduction
2. Materials and Methods
2.1. Morphological and Kinematic Bumblebee Models
2.2. Aerodynamic and Flight Dynamic Models for Bumblebee Hovering Flight
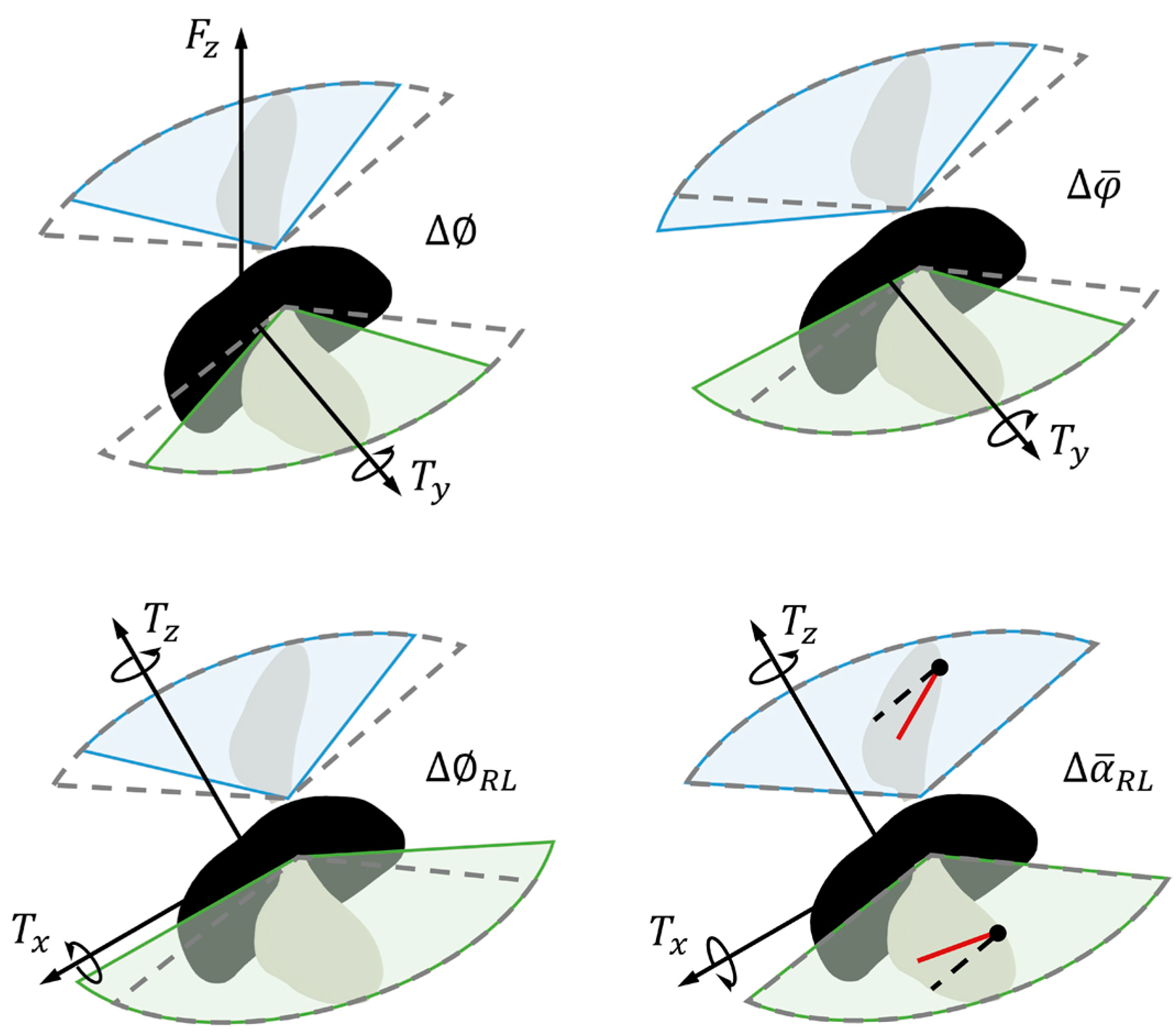
2.3. Wing Kinematics-Based Controller Design
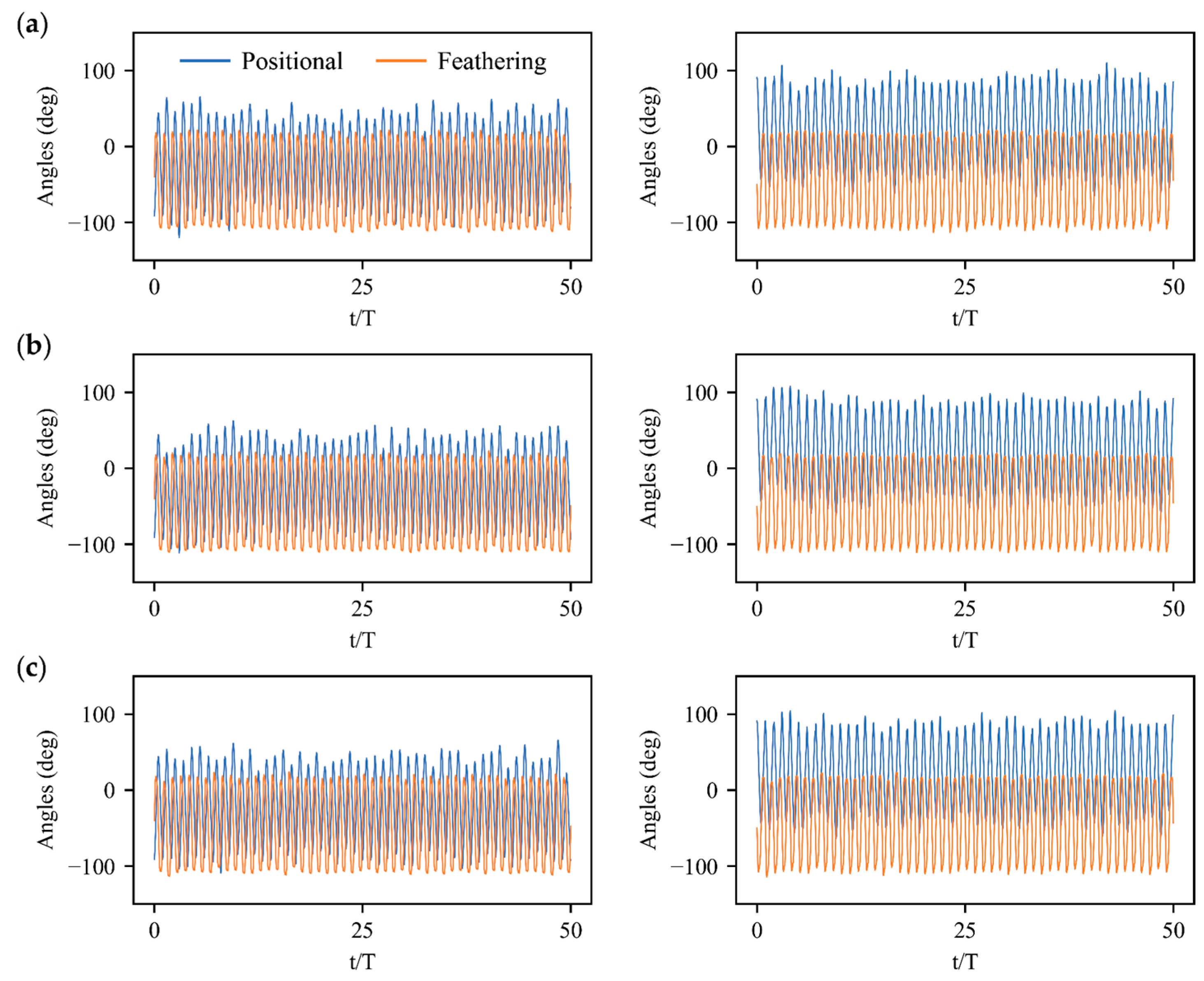
3. Results
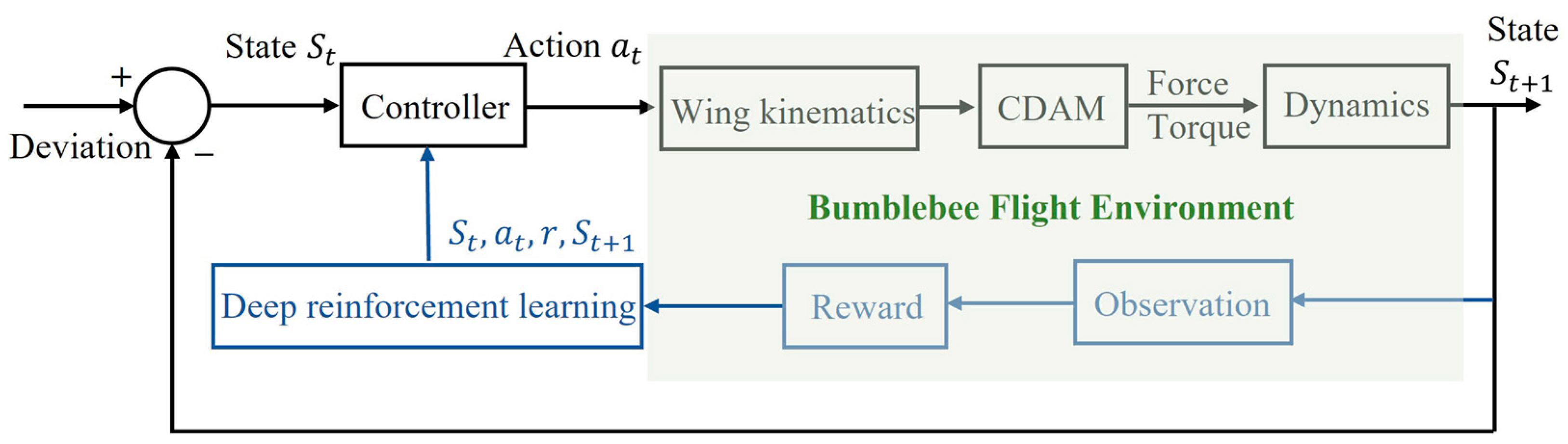
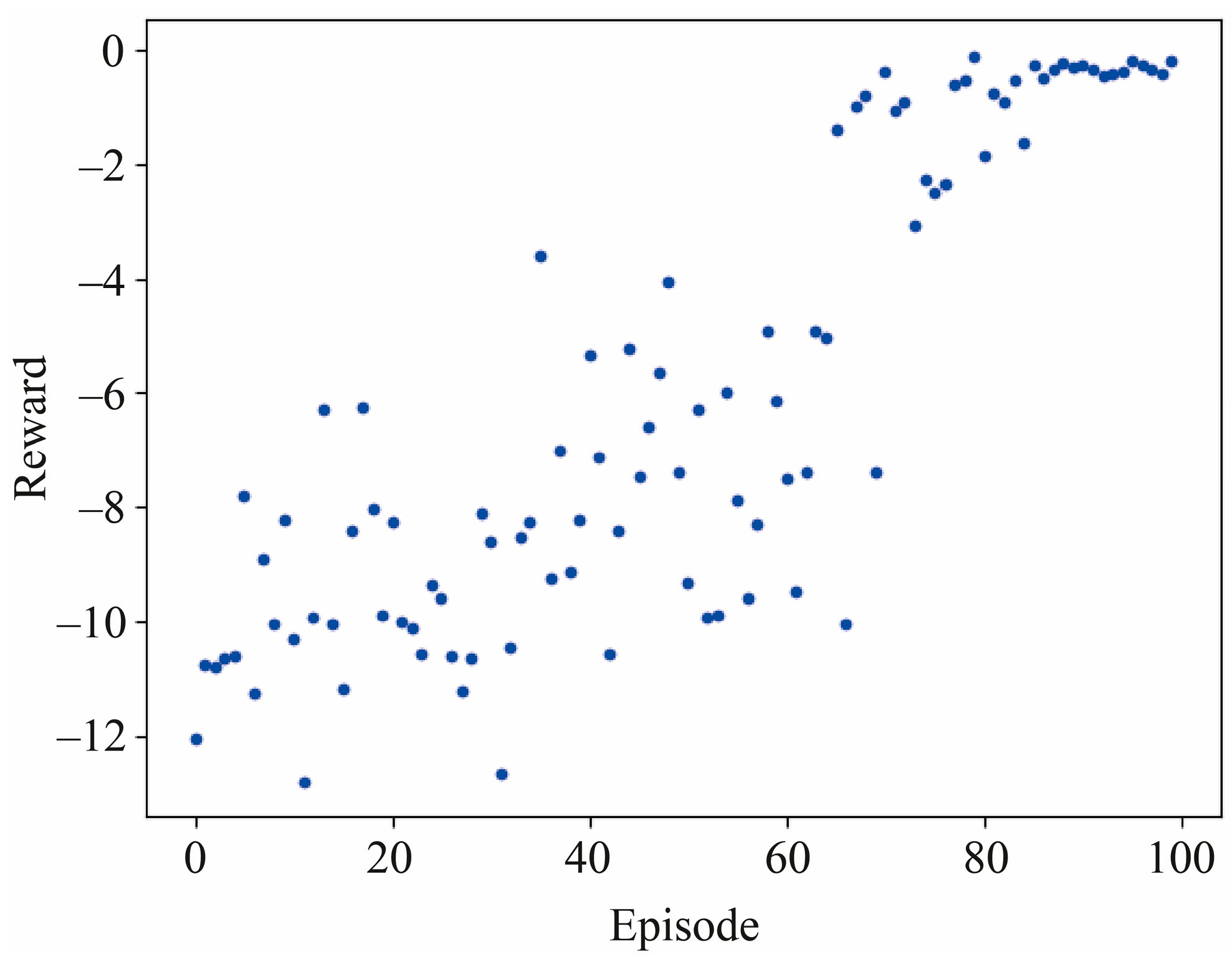
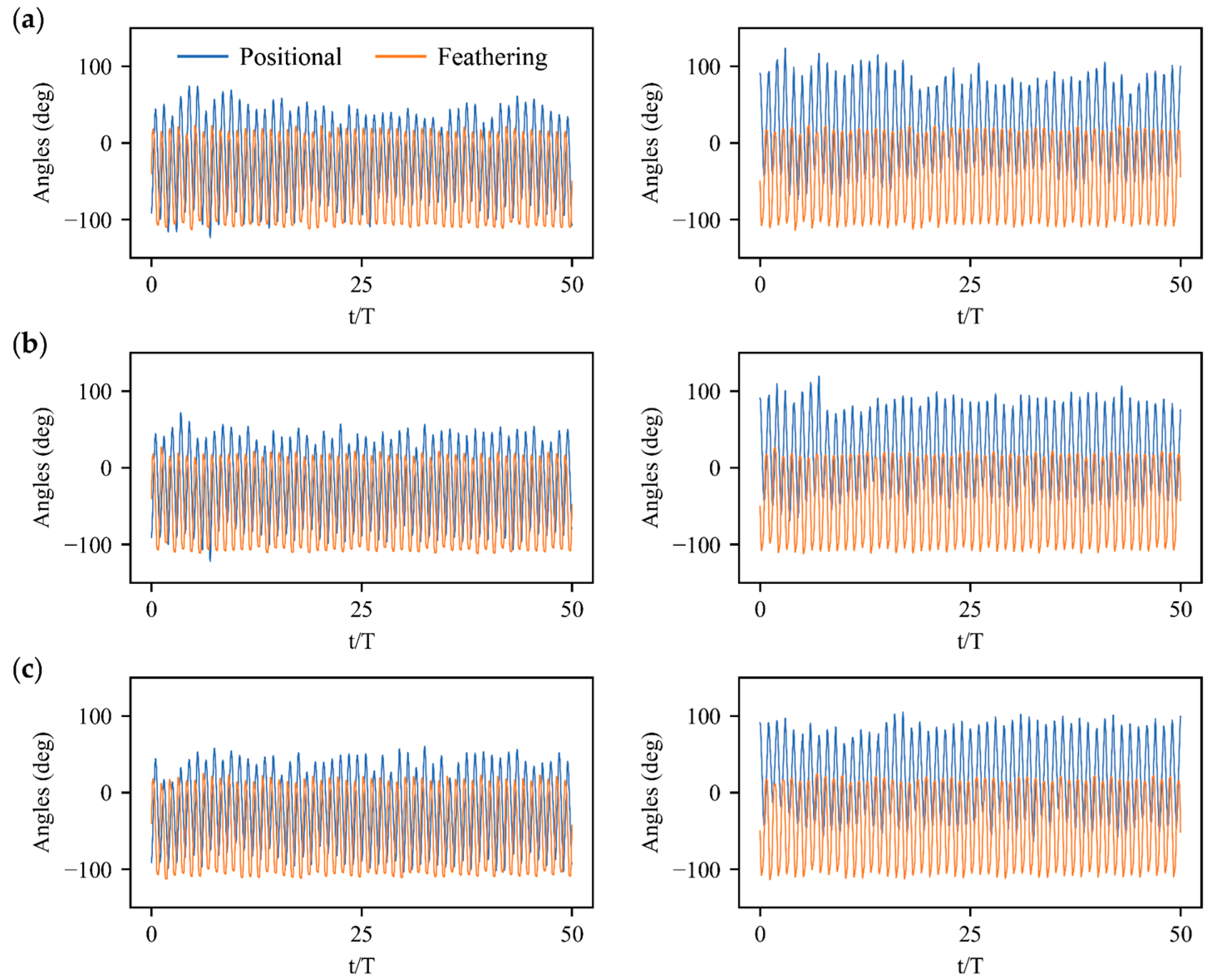
3.1. Deep Reinforcement Learning Policy
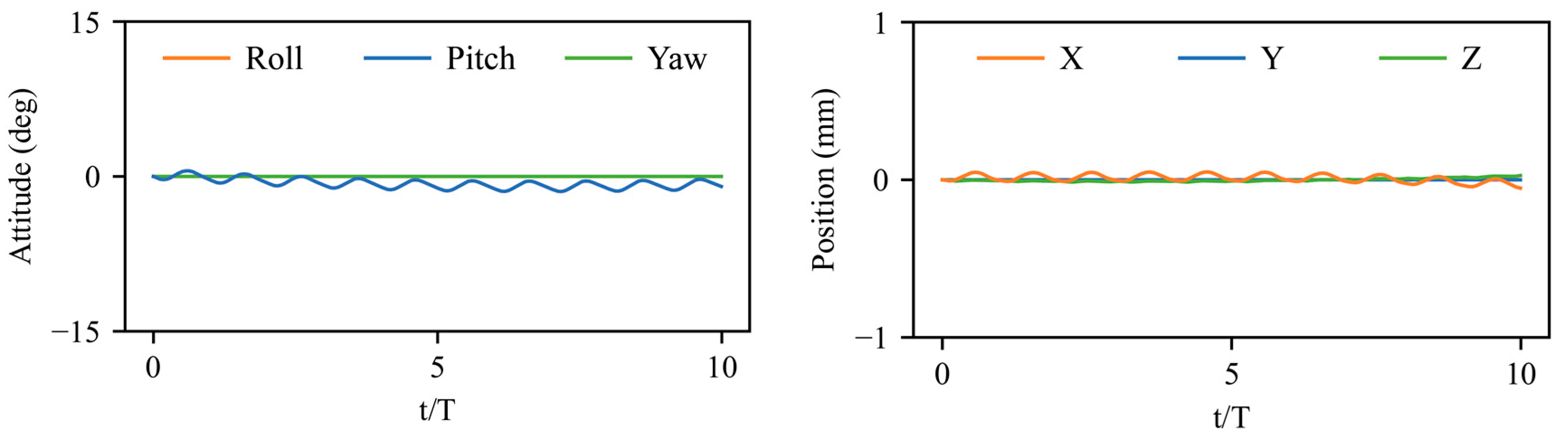
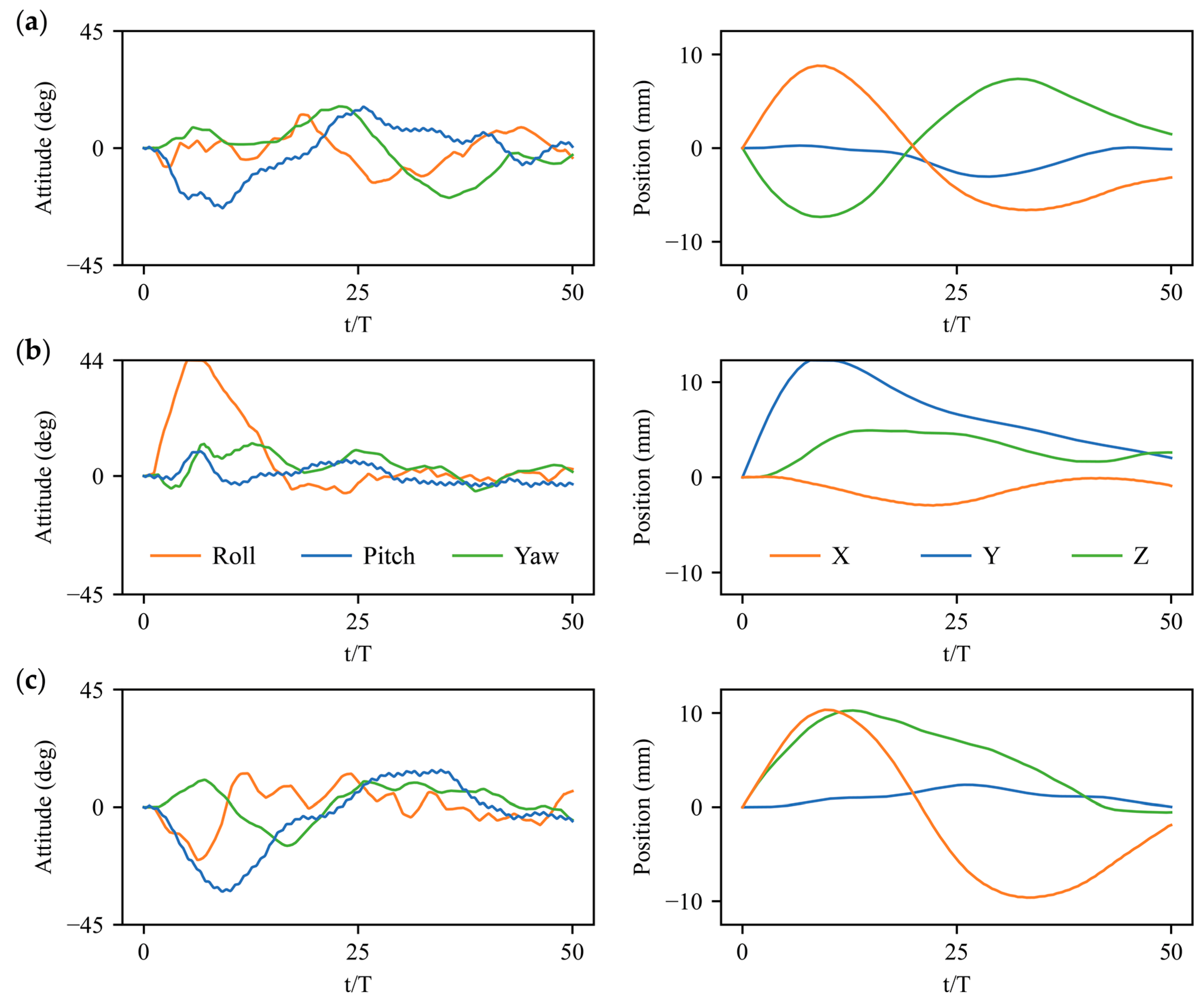
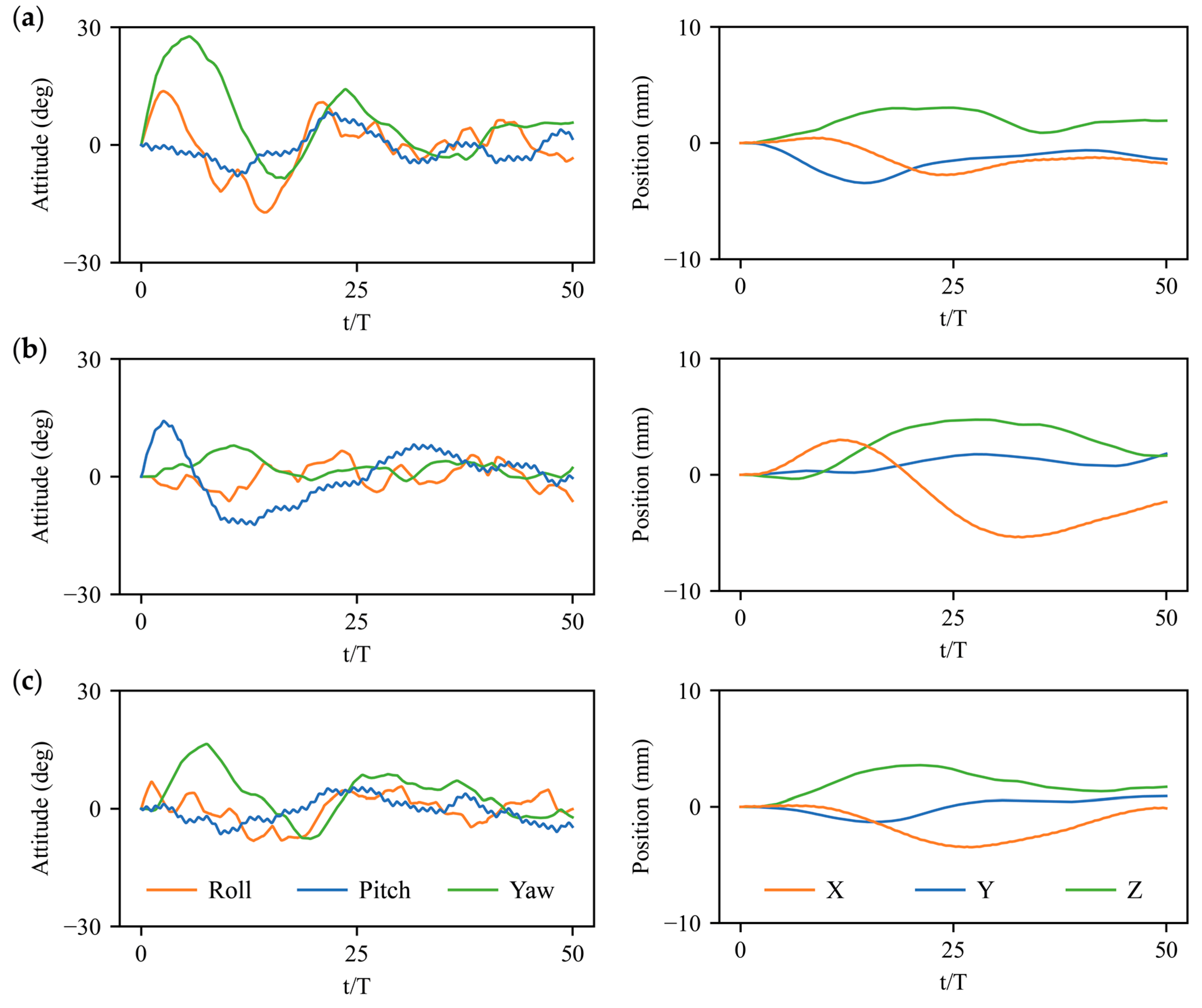
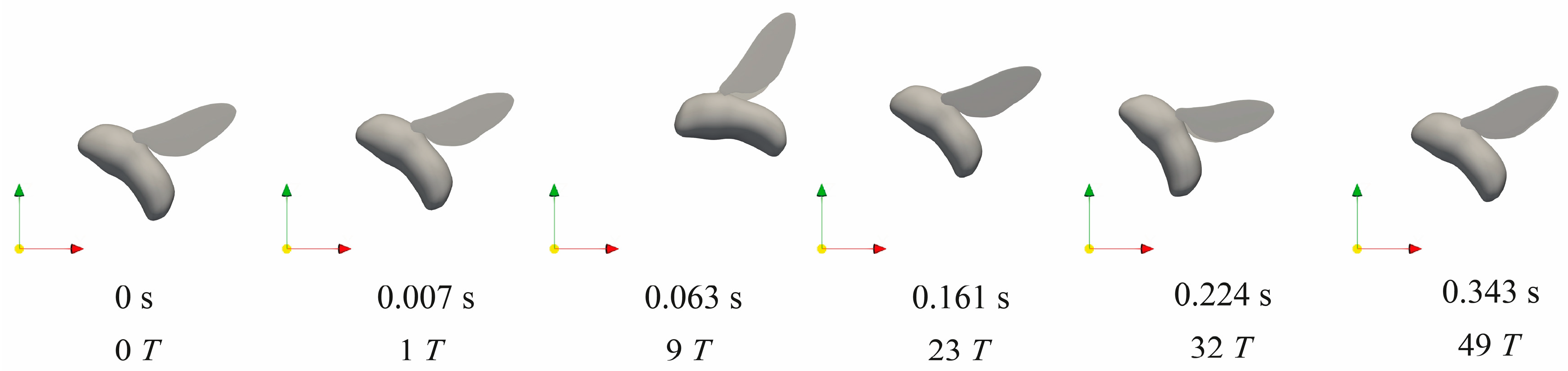
3.2. Stabilization Control under Large Perturbations
3.3. Physical Mechanisms of Control Strategy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ristroph, L.; Bergou, A.J.; Ristroph, G.; Coumes, K.; Berman, G.J.; Guckenheimer, J.; Wang, Z.J.; Cohen, I. Discovering the flight autostabilizer of fruit flies by inducing aerial stumbles. Proc. Natl. Acad. Sci. USA 2010, 107, 4820–4824. [Google Scholar] [CrossRef]
- Beatus, T.; Guckenheimer, J.M.; Cohen, I. Controlling roll perturbations in fruit flies. J. R. Soc. Interface 2015, 12, 20150075. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Deng, X.; Hedrick, T.L. The mechanics and control of pitching manoeuvres in a freely flying hawkmoth (Manduca sexta). J. Exp. Biol. 2011, 214, 4092–4106. [Google Scholar] [CrossRef] [PubMed]
- Liu, H. Simulation-based insect-inspired flight systems. Curr. Opin. Insect Sci. 2020, 42, 105–109. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Ravi, S.; Kolomenskiy, D.; Tanaka, H. Biomechanics and biomimetics in insect-inspired flight systems. Phil. Trans. R. Soc. B 2016, 371, 20150390. [Google Scholar] [CrossRef] [PubMed]
- Gao, N.; Aono, H.; Liu, H. Perturbation analysis of 6DoF flight dynamics and passive dynamic stability of hovering fruit fly Drosophila melanogaster. J. Theor. Biol. 2010, 270, 98–111. [Google Scholar] [CrossRef]
- Sun, M. Insect flight dynamics: Stability and control. Rev. Mod. Phys. 2014, 86, 615–646. [Google Scholar] [CrossRef]
- Dickson, W.B.; Polidoro, P.; Tanner, M.M.; Dickinson, M.H. A linear systems analysis of the yaw dynamics of a dynamically scaled insect model. J. Exp. Biol. 2010, 213, 3047–3061. [Google Scholar] [CrossRef]
- Ristroph, L.; Ristroph, G.; Morozova, S.; Bergou, A.J.; Chang, S.; Guckenheimer, J.; Wang, Z.J.; Cohen, I. Active and passive stabilization of body pitch in insect flight. J. R. Soc. Interface 2013, 10, 20130237. [Google Scholar] [CrossRef]
- Whitehead, S.C.; Beatus, T.; Canale, L.; Cohen, I. Pitch perfect: How fruit flies control their body pitch angle. J. Exp. Biol. 2015, 218, 3508–3519. [Google Scholar] [CrossRef]
- Cai, X.; Kolomenskiy, D.; Nakata, T.; Liu, H. A CFD data-driven aerodynamic model for fast and precise prediction of flapping aerodynamics in various flight velocities. J. Fluid Mech. 2021, 915, A114. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, H. A three-axis PD control model for bumblebee hovering stabilization. J. Bionic Eng. 2018, 15, 494–504. [Google Scholar] [CrossRef]
- Cai, X.; Liu, H. A six-degree-of-freedom proportional-derivative control strategy for bumblebee flight stabilization. J. Biomech. Sci. Eng. 2021, 16, 21–00113. [Google Scholar] [CrossRef]
- Yao, J.; Yeo, K.S. A simplified dynamic model for controlled insect hovering flight and control stability analysis. Bioinspir. Biomim. 2019, 14, 056005. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Yeo, K.S. Forward flight and sideslip manoeuvre of a model hawkmoth. J. Fluid Mech. 2020, 896, A22. [Google Scholar] [CrossRef]
- Hedrick, T.L.; Daniel, T.L. Flight control in the hawkmoth Manduca sexta: The inverse problem of hovering. J. Exp. Biol. 2006, 209, 3114–3130. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Bøhn, E.; Coates, E.M.; Moe, S.; Johansen, T.A. Deep reinforcement learning attitude control of fixed-wing UAVs using proximal policy optimization. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 523–533. [Google Scholar]
- Fei, F.; Tu, Z.; Yang, Y.; Zhang, J.; Deng, X. Flappy hummingbird: An open source dynamic simulation of flapping wing robots and animals. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9223–9229. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.I.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning (ICML), New York City, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. arXiv 2018, arXiv:1802.09477. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. Openai gym. arXiv 2018, arXiv:1606.01540. [Google Scholar]
- Kolomenskiy, D.; Ravi, S.; Xu, R.; Ueyama, K.; Jakobi, T.; Engels, T.; Nakata, T.; Sesterhenn, J.; Schneider, K.; Onishi, R.; et al. The dynamics of passive feathering rotation in hovering flight of bumblebees. J. Fluid Struct. 2019, 91, 102628. [Google Scholar] [CrossRef]
- Gebert, G.; Gallmeier, P.; Evers, J. Equations of motion for flapping flight. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4872. [Google Scholar]
- Sun, M.; Wang, J.; Xiong, Y. Dynamic flight stability of hovering insects. Acta Mech. Sin. 2007, 23, 231–246. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, H.; Sun, J.; Wu, K.; Cai, Z.; Ma, Y.; Wang, Y. Deep reinforcement learning-based end-to-end control for UAV dynamic target tracking. Biomimetics 2022, 7, 197. [Google Scholar] [CrossRef]
- Ravi, S.; Crall, J.D.; Fisher, A.; Combes, S.A. Rolling with the flow: Bumblebees flying in unsteady wakes. J. Exp. Biol. 2013, 216, 4299–4309. [Google Scholar] [CrossRef] [PubMed]
- Jakobi, T.; Kolomenskiy, D.; Ikeda, T.; Watkins, S.; Fisher, A.; Liu, H.; Ravi, S. Bees with attitude: The effects of directed gusts on flight trajectories. Biol. Open 2018, 7, bio034074. [Google Scholar] [CrossRef] [PubMed]
- Lindsay, T.; Sustar, A.; Dickinson, M. The function and organization of the motor system controlling flight maneuvers in flies. Curr. Biol. 2017, 27, 345–358. [Google Scholar] [CrossRef]
- Liang, B.; Sun, M. Nonlinear flight dynamics and stability of hovering model insects. J. R. Soc. Interface 2013, 10, 20130269. [Google Scholar] [CrossRef]

| Horizontal | Lateral | Vertical | |||||||
|---|---|---|---|---|---|---|---|---|---|
| X (mm) | Pitch (°) | Z (mm) | Roll (°) | Y (mm) | Yaw (°) | X (mm) | Pitch (°) | Z (mm) | |
| PD | 16 | 11 | 0 | 23 | 18 | 28 | 15 | 42 | 31 |
| DRL | 9 | 23 | 7 | 45 | 13 | 12 | 10 | 32 | 10 |
| Horizontal | Lateral | Vertical | |||||||
|---|---|---|---|---|---|---|---|---|---|
| X (T) | Pitch (T) | Z (T) | Roll (T) | Y (T) | Yaw (T) | X (T) | Pitch (T) | Z (T) | |
| PD | 50 | 35 | 0 | 31 | 44 | 35 | 19 | 47 | 61 |
| DRL | 20 | 20 | 50 | 16 | 50 | 19 | 42 | 23 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Y.; Cai, X.; Xu, R.; Liu, H. Wing Kinematics-Based Flight Control Strategy in Insect-Inspired Flight Systems: Deep Reinforcement Learning Gives Solutions and Inspires Controller Design in Flapping MAVs. Biomimetics 2023, 8, 295. https://doi.org/10.3390/biomimetics8030295
Xue Y, Cai X, Xu R, Liu H. Wing Kinematics-Based Flight Control Strategy in Insect-Inspired Flight Systems: Deep Reinforcement Learning Gives Solutions and Inspires Controller Design in Flapping MAVs. Biomimetics. 2023; 8(3):295. https://doi.org/10.3390/biomimetics8030295
Chicago/Turabian StyleXue, Yujing, Xuefei Cai, Ru Xu, and Hao Liu. 2023. "Wing Kinematics-Based Flight Control Strategy in Insect-Inspired Flight Systems: Deep Reinforcement Learning Gives Solutions and Inspires Controller Design in Flapping MAVs" Biomimetics 8, no. 3: 295. https://doi.org/10.3390/biomimetics8030295
APA StyleXue, Y., Cai, X., Xu, R., & Liu, H. (2023). Wing Kinematics-Based Flight Control Strategy in Insect-Inspired Flight Systems: Deep Reinforcement Learning Gives Solutions and Inspires Controller Design in Flapping MAVs. Biomimetics, 8(3), 295. https://doi.org/10.3390/biomimetics8030295






