Design of a Bistable Artificial Venus Flytrap Actuated by Low Pressure with Larger Capture Range and Faster Responsiveness
Abstract
1. Introduction
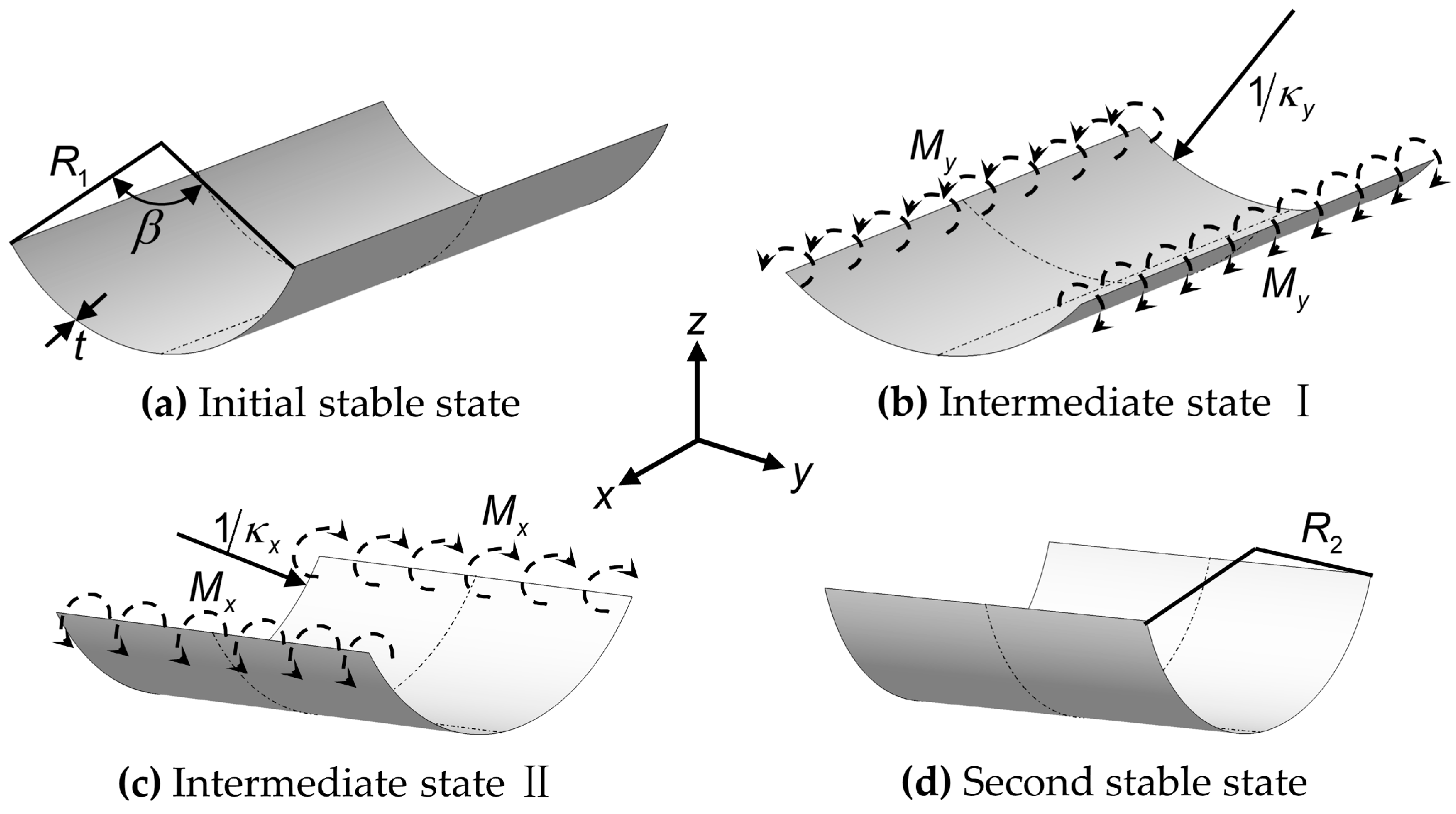
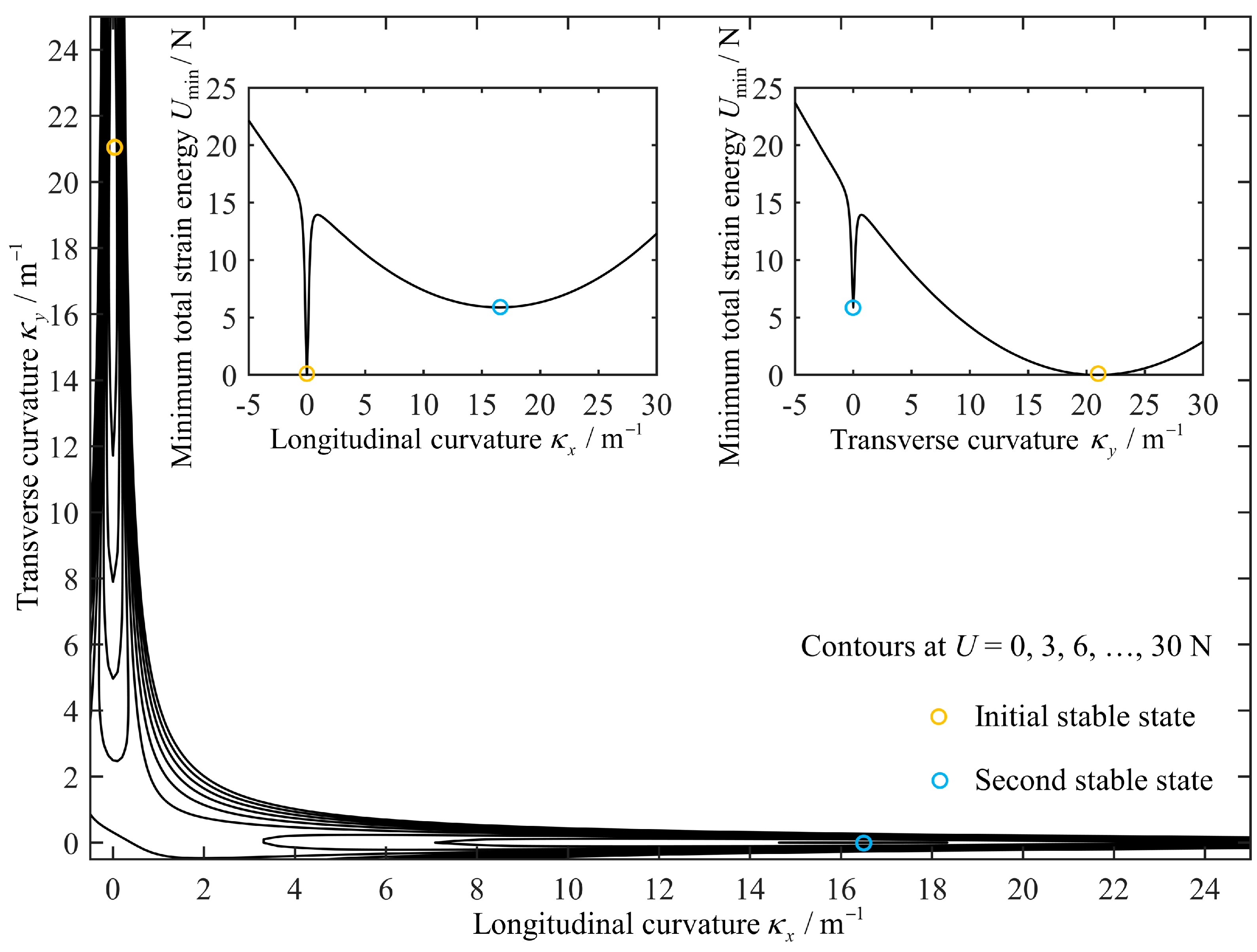
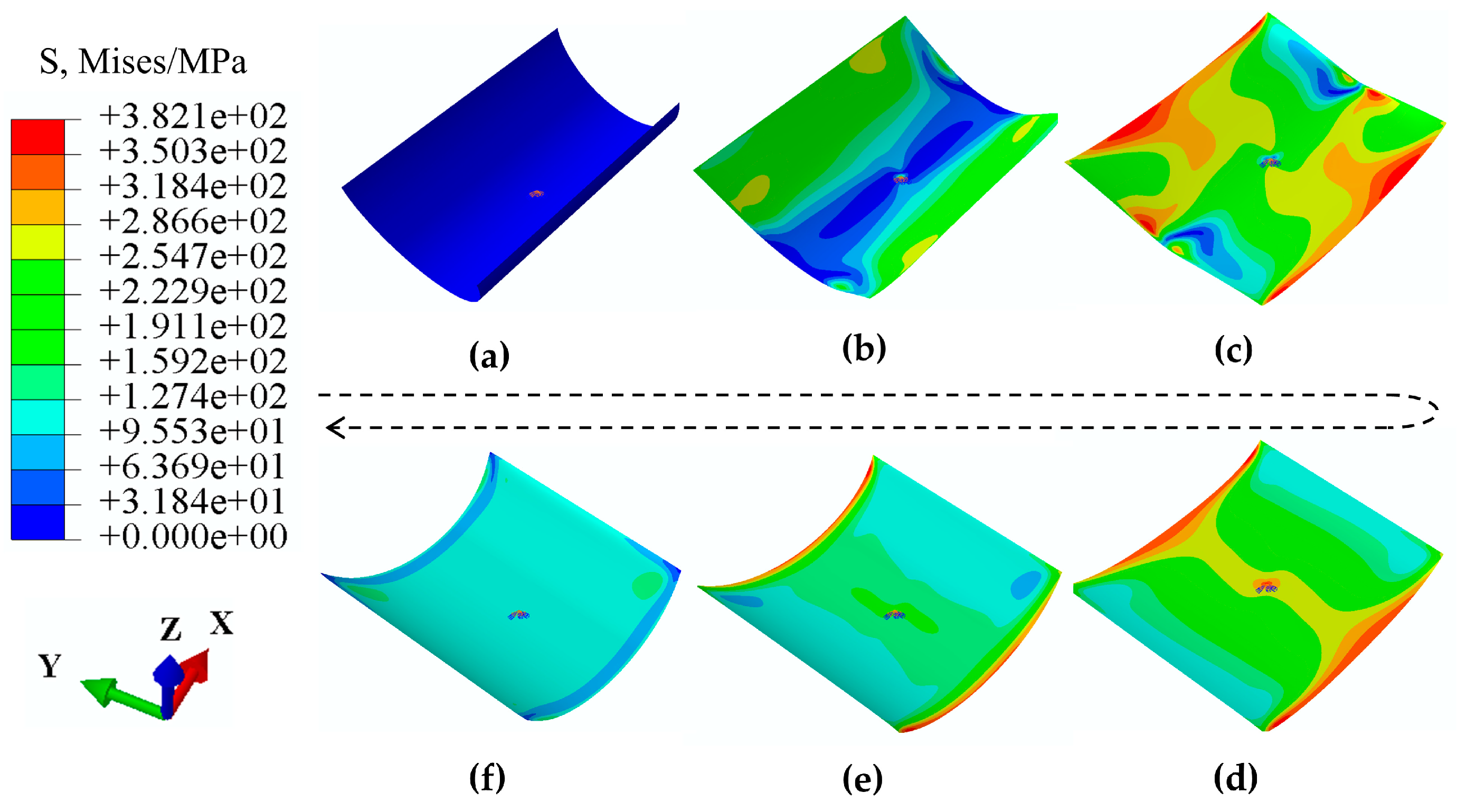
2. Curvature Analysis for the Bistable Antisymmetric Laminated CFRP Structure
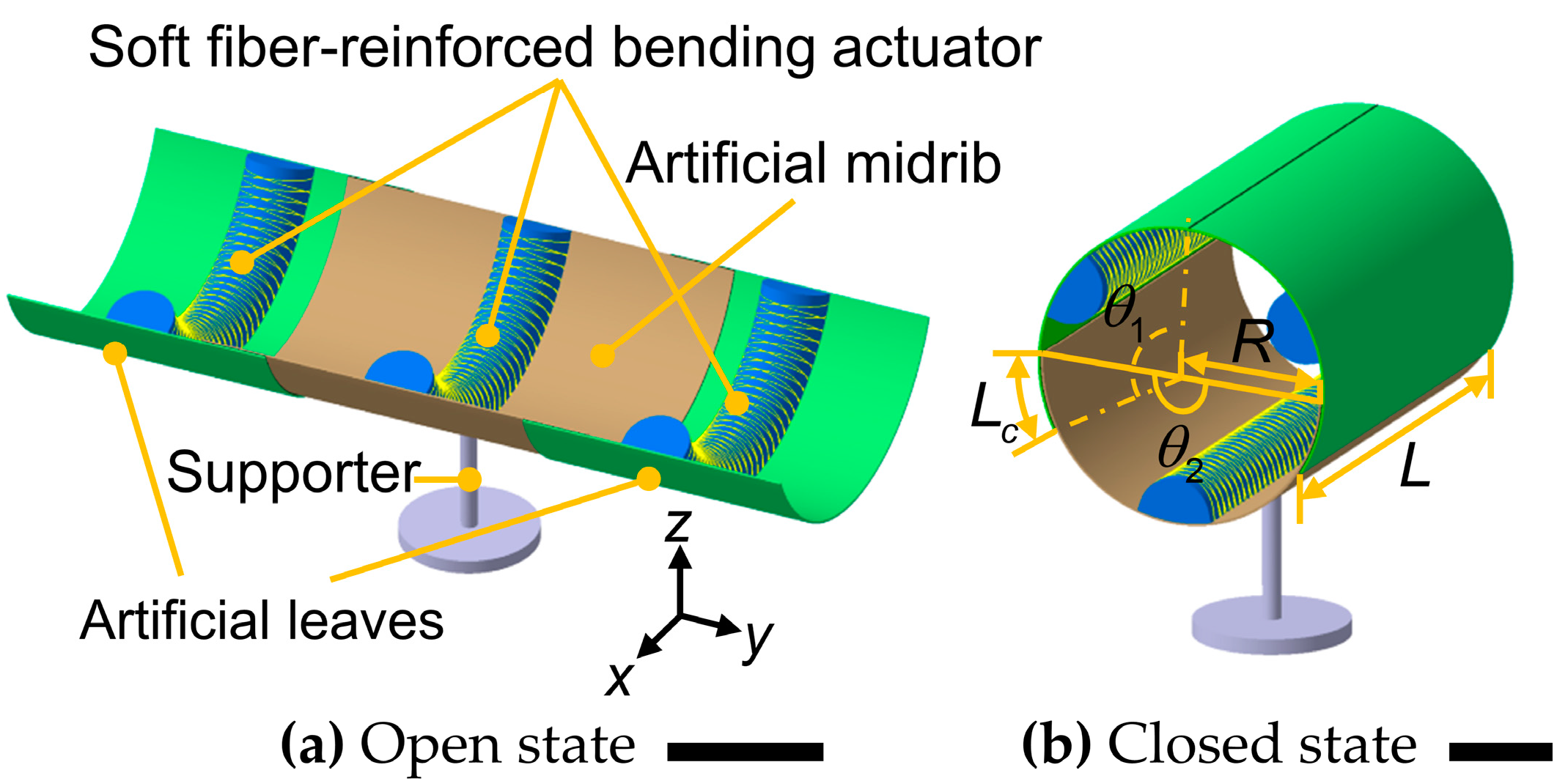
3. Design Concept of the AVFT
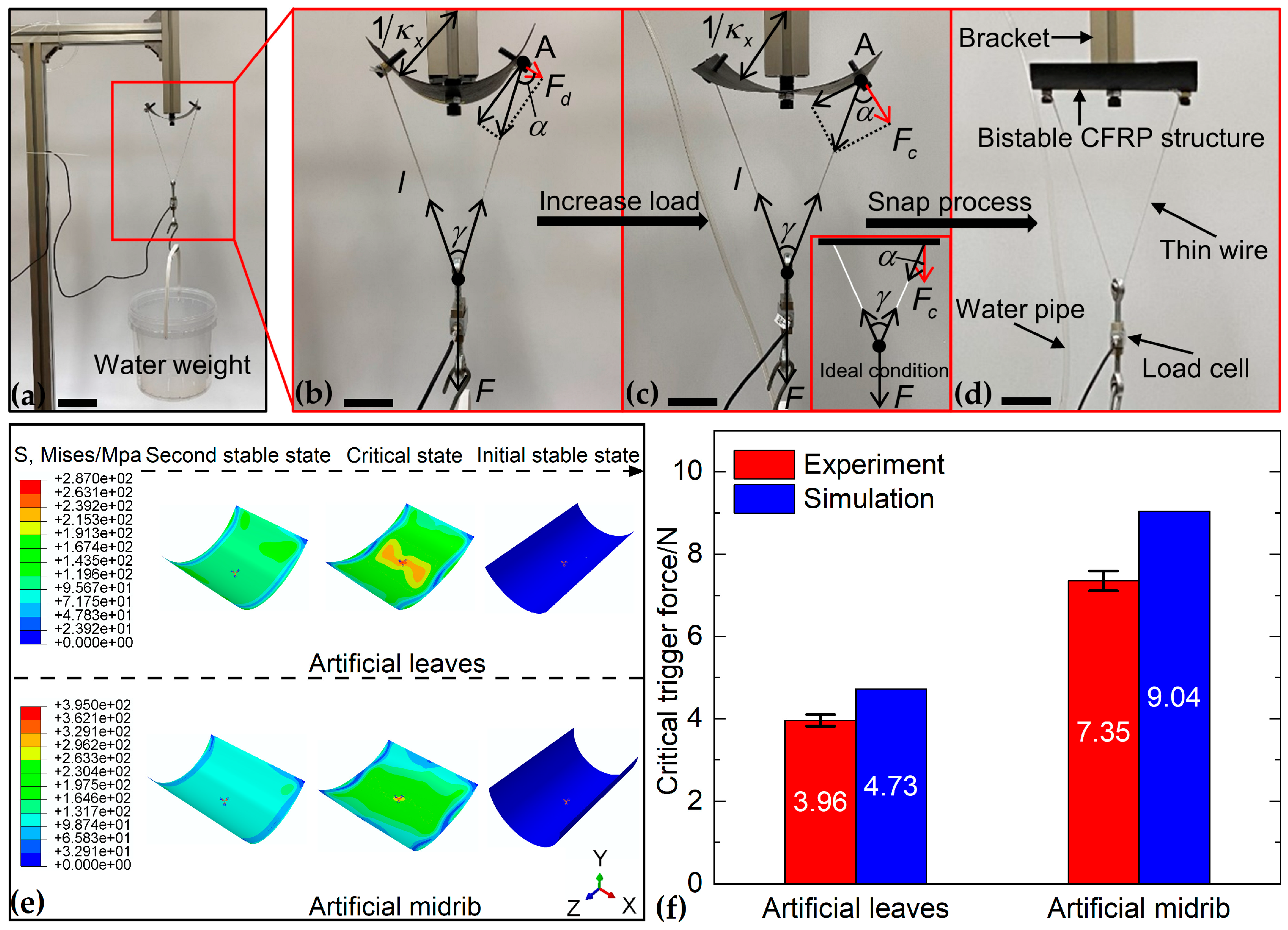
4. Experiment of the Critical Trigger Forces for Artificial Leaves and Artificial Midrib
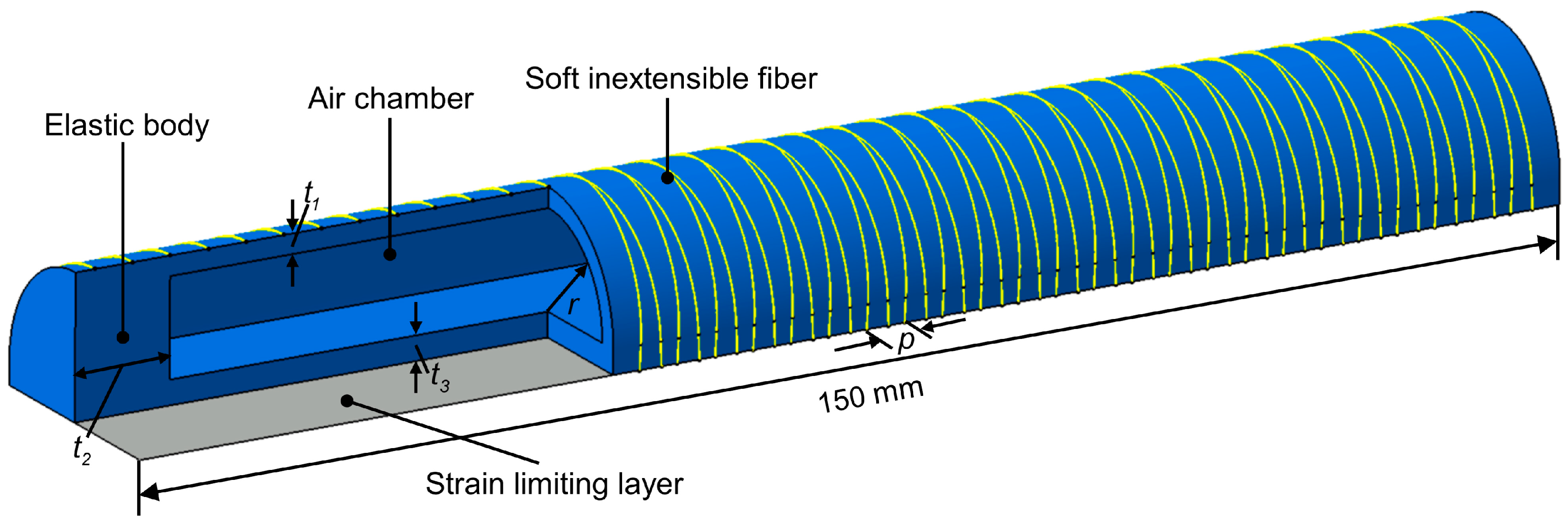
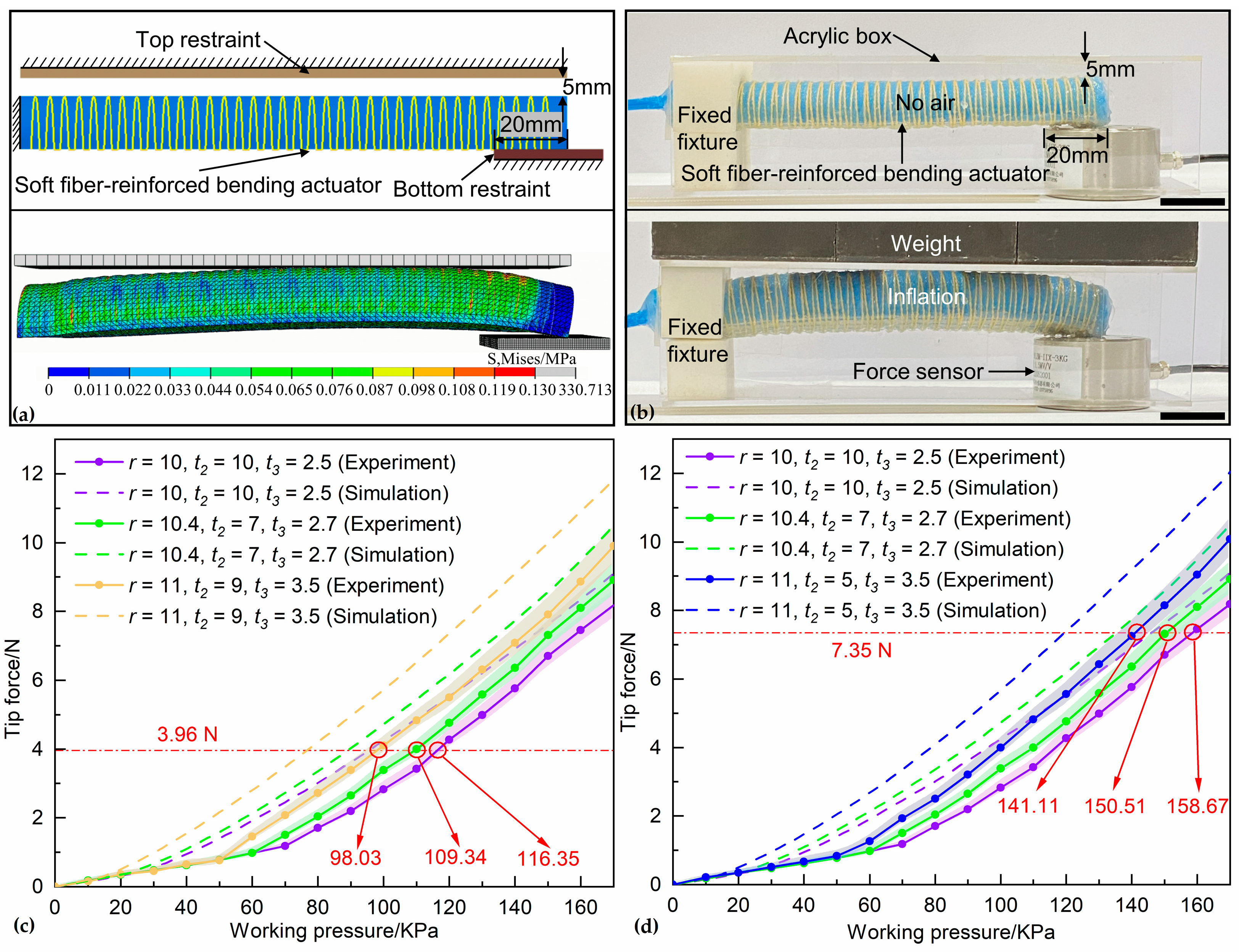
5. Optimization of the Working Pressures for Soft Fiber-Reinforced Bending Actuators
5.1. Optimization Framework and Results
5.2. Experimental Validation
6. Characterization of the AVFT
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Darwin, C.R. Dionaea Muscipula. In Insectivorous Plants; John Murray: London, UK, 1875; p. 286. [Google Scholar]
- Poppinga, S.; Bauer, U.; Speck, T.; Volkov, A.G. Carnivorous Plants: Physiology, Ecology, and Evolution; Oxford University Press: Oxford, UK, 2017. [Google Scholar] [CrossRef]
- Forterre, Y.; Skotheim, J.M.; Dumais, J.; Mahadevan, L. How the Venus flytrap snaps. Nature 2005, 433, 421–425. [Google Scholar] [CrossRef] [PubMed]
- Speck, T.; Cheng, T.; Klimm, F.; Menges, A.; Poppinga, S.; Speck, O.; Tahouni, Y.; Tauber, F.; Thielen, M. Plants as inspiration for material-based sensing and actuation in soft robots and machines. MRS Bull. 2023. [Google Scholar] [CrossRef]
- Esser, F.J.; Auth, P.; Speck, T. Artificial Venus Flytraps: A Research Review and Outlook on Their Importance for Novel Bioinspired Materials Systems. Front. Robot. AI 2020, 7, 75. [Google Scholar] [CrossRef]
- Kim, S.; Koh, J.; Cho, M.; Cho, K. Towards a Bio-mimetic Flytrap Robot Based on a Snap-Through Mechanism. In Proceedings of the 2010 3rd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Tokyo, Japan, 26–29 September 2010; pp. 534–539. [Google Scholar] [CrossRef]
- Kim, S.; Koh, J.; Cho, M.; Cho, K. Design & Analysis a Flytrap Robot using Bi-stable Composite. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 215–220. [Google Scholar] [CrossRef]
- Kim, S.-W.; Koh, J.-S.; Lee, J.-G.; Ryu, J.; Cho, M.; Cho, K.-J. Flytrap-inspired robot using structurally integrated actuation based on bistability and a developable surface. Bioinspir. Biomim. 2014, 9, 036004. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, D.; Wu, H.; Bao, Y.; Chai, G. Non-contact magnetic driving bioinspired Venus flytrap robot based on bistable anti-symmetric CFRP structure. Compos. Struct. 2016, 135, 17–22. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Yu, X.; Chai, H.; Li, Y.; Wu, H.; Jiang, S. Magnetic actuation bionic robotic gripper with bistable morphing structure. Compos. Struct. 2019, 229, 111422. [Google Scholar] [CrossRef]
- Fan, W.; Shan, C.; Guo, H.; Sang, J.; Wang, R.; Zheng, R.; Sui, K.; Nie, Z. Dual-gradient enabled ultrafast biomimetic snapping of hydrogel materials. Sci. Adv. 2019, 5, eaav7174. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Xia, C.; Fang, N.X. First jump of microgel; actuation speed enhancement by elastic instability. Soft Matter 2010, 6, 4342–4345. [Google Scholar] [CrossRef]
- Pal, A.; Goswami, D.; Martinez, R.V. Elastic Energy Storage Enables Rapid and Programmable Actuation in Soft Machines. Adv. Funct. Mater. 2020, 30, 1906603. [Google Scholar] [CrossRef]
- Wani, O.M.; Zeng, H.; Priimagi, A. A light-driven artificial flytrap. Nat. Commun. 2017, 8, 15546. [Google Scholar] [CrossRef]
- Shi, L.; Guo, S.; Kudo, H.; Asaka, K. Development of a Venus flytrap-inspired robotic flytrap. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 551–556. [Google Scholar] [CrossRef]
- Wang, Y.; Gupta, U.; Parulekar, N.; Zhu, J. A soft gripper of fast speed and low energy consumption. Sci. China Technol. Sci. 2018, 62, 31–38. [Google Scholar] [CrossRef]
- Shahinpoor, M. Biomimetic robotic Venus flytrap (Dionaea muscipula Ellis) made with ionic polymer metal composites. Bioinspir. Biomim. 2011, 6, 046004. [Google Scholar] [CrossRef] [PubMed]
- Shahinpoor, M.; Thompson, M.S. The Venus Flytrap as a model for a biomimetic material with built-in sensors and actuators. Mater. Sci. Eng. C 1995, 2, 229–233. [Google Scholar] [CrossRef]
- Lunni, D.; Cianchetti, M.; Filippeschi, C.; Sinibaldi, E.; Mazzolai, B. Plant-Inspired Soft Bistable Structures Based on Hygroscopic Electrospun Nanofibers. Adv. Mater. Interfaces 2020, 7, 1901310. [Google Scholar] [CrossRef]
- Tauber, F.J.; Riechert, L.; Teichmann, J.; Poovathody, N.; Jonas, U.; Schiller, S.; Speck, T. Unit Cell Based Artificial Venus Flytrap. In Biomimetic and Biohybrid Systems; Hunt, A., Vouloutsi, V., Moses, K., Quinn, R., Mura, A., Prescott, T., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 1–12. [Google Scholar] [CrossRef]
- Esser, F.; Scherag, F.D.; Poppinga, S.; Westermeier, A.; Mylo, M.D.; Kampowski, T.; Bold, G.; Rühe, J.; Speck, T. Adaptive Biomimetic Actuator Systems Reacting to Various Stimuli by and Combining Two Biological Snap-Trap Mechanics. In Biomimetic and Biohybrid Systems; Martinez-Hernandez, U., Vouloutsi, V., Mura, A., Mangan, M., Asada, M., Prescott, T.J., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 114–121. [Google Scholar] [CrossRef]
- Tauber, F.J.; Auth, P.; Teichmann, J.; Scherag, F.D.; Speck, T. Novel Motion Sequences in Plant-Inspired Robotics: Combining Inspirations from Snap-Trapping in Two Plant Species into an Artificial Venus Flytrap Demonstrator. Biomimetics 2022, 7, 99. [Google Scholar] [CrossRef] [PubMed]
- Hyer, M.W. Some Observations on the Cured Shape of Thin Unsymmetric Laminates. J. Compos. Mater. 1981, 15, 175–194. [Google Scholar] [CrossRef]
- Hyer, M.W. The Room-Temperature Shapes of Four-Layer Unsymmetric Cross-Ply Laminates. J. Compos. Mater. 1982, 16, 318–340. [Google Scholar] [CrossRef]
- Ryu, J.; Kong, J.-P.; Kim, S.-W.; Koh, J.-S.; Cho, K.-J.; Cho, M. Curvature tailoring of unsymmetric laminates with an initial curvature. J. Compos. Mater. 2012, 47, 3163–3174. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, H.; He, X.; Wu, H.; Bao, Y.; Chai, G. The bistable behaviors of carbon-fiber/epoxy anti-symmetric composite shells. Compos. Part B Eng. 2013, 47, 190–199. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, H.; Ye, G.; Wu, H.; He, X.; Chai, G. Systematic experimental and numerical study of bistable snap processes for anti-symmetric cylindrical shells. Compos. Struct. 2014, 112, 368–377. [Google Scholar] [CrossRef]
- Iqbal, K.; Pellegrino, S.; Daton-Lovett, A. Bi-stable Composite Slit Tubes. In IUTAM-IASS Symposium on Deployable Structures: Theory and Applications; Pellegrino, S., Guest, S.D., Eds.; Springer: Cambridge, UK, 2000; pp. 153–162. [Google Scholar] [CrossRef]
- Dano, M.L.; Hyer, M. Snap-through of unsymmetric fiber-reinforced composite laminates. Int. J. Solids Struct. 2002, 39, 175–198. [Google Scholar] [CrossRef]
- Galletly, D.A.; Guest, S.D. Bistable composite slit tubes. I. A beam model. Int. J. Solids Struct. 2004, 41, 4517–4533. [Google Scholar] [CrossRef]
- Kebadze, E.; Guest, S.; Pellegrino, S. Bistable prestressed shell structures. Int. J. Solids Struct. 2004, 41, 2801–2820. [Google Scholar] [CrossRef]
- Guest, S.; Pellegrino, S. Analytical models for bistable cylindrical shells. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 462, 839–854. [Google Scholar] [CrossRef]
- Zhang, Z.; Ni, X.; Wu, H.; Sun, M.; Bao, G.; Wu, H.; Jiang, S. Pneumatically Actuated Soft Gripper with Bistable Structures. Soft Robot. 2022, 9, 57–71. [Google Scholar] [CrossRef] [PubMed]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft Robotic Grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef]
- Finney, R.H. Finite Element Analysis. In Engineering with Rubber, 3rd ed.; Gent, A.N., Ed.; Hanser: Cincinnati, OH, USA, 2012; pp. 295–343. [Google Scholar] [CrossRef]
- Xavier, M.S.; Tawk, C.D.; Zolfagharian, A.; Pinskier, J.; Howard, D.; Young, T.; Lai, J.; Harrison, S.M.; Yong, Y.K.; Bodaghi, M.; et al. Soft Pneumatic Actuators: A Review of Design, Fabrication, Modeling, Sensing, Control and Applications. IEEE Access 2022, 10, 59442–59485. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Jarrah, H.R.; Dos Santos Xavier, M.; Rolfe, B.; Bodaghi, M. Multimaterial 4D Printing with Tunable Bending Model. Smart Mater. Struct. 2023, 32, 065001. [Google Scholar] [CrossRef]
- Lalegani Dezaki, M.; Bodaghi, M.; Serjouei, A.; Afazov, S.; Zolfagharian, A. Adaptive reversible composite-based shape memory alloy soft actuators. Sens. Actuators A Phys. 2022, 345, 113779. [Google Scholar] [CrossRef]
- Khalid, M.Y.; Arif, Z.U.; Noroozi, R.; Zolfagharian, A.; Bodaghi, M. 4D printing of shape memory polymer composites: A review on fabrication techniques, applications, and future perspectives. J. Manuf. Process. 2022, 81, 759–797. [Google Scholar] [CrossRef]
- Han, M.; Guo, X.; Chen, X.; Liang, C.; Zhao, H.; Zhang, Q.; Bai, W.; Zhang, F.; Wei, H.; Wu, C.; et al. Submillimeter-scale multimaterial terrestrial robots. Sci. Robot. 2022, 7, eabn0602. [Google Scholar] [CrossRef]
- Ji, Z.; Zhao, J.; Song, H.; Xu, S.; Pang, W.; Hu, X.; Zhang, F.; Jin, T.; Shuai, Y.; Lan, Y.; et al. Morphable three-dimensional electronic mesofliers capable of on-demand unfolding. Sci. China Mater. 2022, 65, 2309–2318. [Google Scholar] [CrossRef]
- Dezaki, M.L.; Bodaghi, M. Magnetorheological elastomer-based 4D printed electroactive composite actuators. Sens. Actuators A Phys. 2023, 349, 114063. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Ge, Y.; Zhao, Y.; Jiang, C. Kirigami-Inspired Programmable Soft Magnetoresponsive Actuators with Versatile Morphing Modes. Adv. Sci. 2022, 9, 2203711. [Google Scholar] [CrossRef]
- Pang, W.; Xu, S.; Wu, J.; Bo, R.; Jin, T.; Xiao, Y.; Liu, Z.; Zhang, F.; Cheng, X.; Bai, K.; et al. A soft microrobot with highly deformable 3D actuators for climbing and transitioning complex surfaces. Proc. Natl. Acad. Sci. USA 2022, 119, e2215028119. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Dong, J. Programmable soft electrothermal actuators based on free-form printing of the embedded heater. Soft Matter 2021, 17, 2577–2586. [Google Scholar] [CrossRef]
- Linnebach, P.; Rizzello, G.; Seelecke, S. Design and validation of a dielectric elastomer membrane actuator driven pneumatic pump. Smart Mater. Struct. 2020, 29, 075021. [Google Scholar] [CrossRef]
- Gorissen, B.; Reynaerts, D.; Konishi, S.; Yoshida, K.; Kim, J.-W.; De Volder, M. Elastic Inflatable Actuators for Soft Robotic Applications. Adv. Mater. 2017, 29, 1604977. [Google Scholar] [CrossRef]
- Deimel, R.; Brock, O. A compliant hand based on a novel pneumatic actuator. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 2047–2053. [Google Scholar] [CrossRef]
- Connolly, F.; Polygerinos, P.; Walsh, C.J.; Bertoldi, K. Mechanical Programming of Soft Actuators by Varying Fiber Angle. Soft Robot. 2015, 2, 26–32. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Galloway, K.C.; Wood, R.J.; Walsh, C.J. Soft robotic glove for combined assistance and at-home rehabilitation. Robot. Auton. Syst. 2015, 73, 135–143. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Overvelde, J.T.B.; Galloway, K.C.; Wood, R.J.; Bertoldi, K.; Walsh, C.J. Modeling of Soft Fiber-Reinforced Bending Actuators. IEEE Trans. Robot. 2015, 31, 778–789. [Google Scholar] [CrossRef]
- Connolly, F.; Walsh, C.J.; Bertoldi, K. Automatic design of fiber-reinforced soft actuators for trajectory matching. Proc. Natl. Acad. Sci. USA 2017, 114, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Jeong, O.C.; Konishi, S. All PDMS Pneumatic Microfinger With Bidirectional Motion and Its Application. J. Microelectr. Syst. 2006, 15, 896–903. [Google Scholar] [CrossRef]
- Polygerinos, P.; Lyne, S.; Wang, Z.; Nicolini, L.F.; Mosadegh, B.; Whitesides, G.M.; Walsh, C.J. Towards a soft pneumatic glove for hand rehabilitation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1512–1517. [Google Scholar] [CrossRef]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic Networks for Soft Robotics that Actuate Rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Galloway, K.C.; Becker, K.P.; Phillips, B.T.; Kirby, J.; Licht, S.; Tchernov, D.; Wood, R.J.; Gruber, D.F.; Shen, Z.; Zhong, H.; et al. Soft Robotic Grippers for Biological Sampling on Deep Reefs. Soft Robot. 2016, 3, 23–33. [Google Scholar] [CrossRef] [PubMed]
- Yap, H.K.; Ng, H.Y.; Yeow, C.-H. High-Force Soft Printable Pneumatics for Soft Robotic Applications. Soft Robot. 2016, 3, 144–158. [Google Scholar] [CrossRef]
- Gai, L.; Zong, X. A Fully Soft Bionic Grasping Device with the Properties of Segmental Bending Shape and Automatically Adjusting Grasping Range. J. Bionic Eng. 2022, 19, 1334–1348. [Google Scholar] [CrossRef]
- Xiao, W.; Hu, D.; Chen, W.; Yang, G.; Han, X. Design, Characterization and Optimization of Multi-directional Bending Pneumatic Artificial Muscles. J. Bionic Eng. 2021, 18, 1358–1368. [Google Scholar] [CrossRef]
- Dezaki, M.L.; Bodaghi, M.; Serjouei, A.; Afazov, S.; Zolfagharian, A. Soft Pneumatic Actuators with Controllable Stiffness by Bio-Inspired Lattice Chambers and Fused Deposition Modeling 3D Printing. Adv. Eng. Mater. 2023, 25, 2200797. [Google Scholar] [CrossRef]
- Suzumori, K.; Maeda, T.; Wantabe, H.; Hisada, T. Fiberless flexible microactuator designed by finite-element method. IEEE/ASME Trans. Mechatron. 1997, 2, 281–286. [Google Scholar] [CrossRef]
- Chang, B.C.-M.; Berring, J.; Venkataram, M.; Menon, C.; Parameswaran, M. Bending fluidic actuator for smart structures. Smart Mater. Struct. 2011, 20, 035012. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Mahmud, M.A.P.; Gharaie, S.; Bodaghi, M.; Kouzani, A.Z.; Kaynak, A. 3D/4D-printed bending-type soft pneumatic actuators: Fabrication, modelling, and control. Virtual Phys. Prototyp. 2020, 15, 373–402. [Google Scholar] [CrossRef]
- Marchese, A.D.; Katzschmann, R.; Rus, D.L. A Recipe for Soft Fluidic Elastomer Robots. Soft Robot. 2015, 2, 7–25. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Zhu, W.; Jiang, J.; Xu, Q.; Ke, Y. Computational modelling of postbuckling behavior of composite T-stiffened panels with different bonding methods. Compos. Part B Eng. 2019, 166, 247–256. [Google Scholar] [CrossRef]
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Zhang, Z.; Ni, X.; Gao, W.; Shen, H.; Sun, M.; Guo, G.; Wu, H.; Jiang, S. Pneumatically Controlled Reconfigurable Bistable Bionic Flower for Robotic Gripper. Soft Robot. 2021, 9, 657–668. [Google Scholar] [CrossRef]
- Wang, T.; Ge, L.; Gu, G. Programmable design of soft pneu-net actuators with oblique chambers can generate coupled bending and twisting motions. Sens. Actuators A Phys. 2018, 271, 131–138. [Google Scholar] [CrossRef]
- Van der Velden, A.; Kokan, D. The Synaps Pointer Optimization Engine. In Proceedings of the ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 29 September–2 October 2022; ASME: New York, NY, USA, 2022; Volume 1, pp. 159–165. [Google Scholar] [CrossRef]
- Wang, Z.; Hirai, S. Chamber dimension optimization of a bellow-type soft actuator for food material handling. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 382–387. [Google Scholar] [CrossRef]
- Wang, Z.; Hirai, S. Geometry and Material Optimization of a Soft Pneumatic Gripper for Handling Deformable Object. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 612–617. [Google Scholar] [CrossRef]
- Iqbal, K.; Pellegrino, S. Bi-stable composite shells. In Proceedings of the 41st Structures, Structural Dynamics, and Materials Conference and Exhibit, Atlanta, GA, USA, 3–6 April 2000; pp. 1385–1393. [Google Scholar] [CrossRef]
- Xavier, M.S.; Fleming, A.J.; Yong, Y.K. Finite Element Modeling of Soft Fluidic Actuators: Overview and Recent Developments. Adv. Intell. Syst. 2021, 3, 2000187. [Google Scholar] [CrossRef]


| E1/GPa | E2/GPa | G12/GPa | G13/GPa | G23/GPa | tply/mm | |
|---|---|---|---|---|---|---|
| 145 | 9.5 | 0.3 | 5 | 3.7 | 3.7 | 0.125 |
| Geometric Parameters/mm | No. 1 | No. 2 | No. 3 | No. 4 |
|---|---|---|---|---|
| r = 10 t1 = 2 t2 = 10 t3 = 2.5 p = 4 | r = 10.4 t1 = 1.6 t2 = 7 t3 = 2.7 p = 4 | r = 11 t1 = 1 t2 = 9 t3 = 3.5 p = 4 | r = 11 t1 = 1 t2 = 5 t3 = 3.5 p = 4 | |
| Working pressure/KPa when tip force = 3.96 N | 95.49 | 89.13 | 76.56 | - |
| Working pressure/KPa when tip force = 7.35 N | 146.18 | 135.25 | - | 119.52 |
| The AVFTs Based on Bistable CFRP Structures | Lay-Up | Actuation | Reversibility | Capture Range/° * | Driving Time/s | Snap Time/ms |
|---|---|---|---|---|---|---|
| Kim, S. et al. (2010) [6] | [0°/90°] | SMA | No/manually | ≈90 | null | 80 |
| Kim, S. et al. (2011) [7] | [0°/90°] | SMA | Yes | ≈150 | ≤2.86 | 100 |
| Kim, S. et al. (2014) [8] | [0°/90°] | SMA | Yes | ≈150 | ≥4.4 | ≤100 |
| Zhang, Z. et al. (2016) [9] | [45°/−45°/45/°−45°] | Magnetic | No/manually | ≈150 | 1.32 | 200 |
| Zhang, Z. et al. (2019) [10] | [45°/−45°/45/°−45°] | Magnetic | No/manually | ≈120 | null | 112 |
| Zhang, Z. et al. (2022) [33] | [0°/90°] | Pneumatic | Yes | ≈60 | null | 170 |
| Our AVFT | [45°/−45°/45/°−45°] | Pneumatic | No/manually | 180 | 0.17 | 52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Wang, F.; Lu, Y. Design of a Bistable Artificial Venus Flytrap Actuated by Low Pressure with Larger Capture Range and Faster Responsiveness. Biomimetics 2023, 8, 181. https://doi.org/10.3390/biomimetics8020181
Yang J, Wang F, Lu Y. Design of a Bistable Artificial Venus Flytrap Actuated by Low Pressure with Larger Capture Range and Faster Responsiveness. Biomimetics. 2023; 8(2):181. https://doi.org/10.3390/biomimetics8020181
Chicago/Turabian StyleYang, Junchang, Fenghui Wang, and Yongjun Lu. 2023. "Design of a Bistable Artificial Venus Flytrap Actuated by Low Pressure with Larger Capture Range and Faster Responsiveness" Biomimetics 8, no. 2: 181. https://doi.org/10.3390/biomimetics8020181
APA StyleYang, J., Wang, F., & Lu, Y. (2023). Design of a Bistable Artificial Venus Flytrap Actuated by Low Pressure with Larger Capture Range and Faster Responsiveness. Biomimetics, 8(2), 181. https://doi.org/10.3390/biomimetics8020181







