Abstract
The main advantages of spiking neural networks are the high biological plausibility and their fast response due to spiking behaviour. The response time decreases significantly in the hardware implementation of SNN because the neurons operate in parallel. Compared with the traditional computational neural network, the SNN use a lower number of neurons, which also reduces their cost. Another critical characteristic of SNN is their ability to learn by event association that is determined mainly by postsynaptic mechanisms such as long-term potentiation. However, in some conditions, presynaptic plasticity determined by post-tetanic potentiation occurs due to the fast activation of presynaptic neurons. This violates the Hebbian learning rules that are specific to postsynaptic plasticity. Hebbian learning improves the SNN ability to discriminate the neural paths trained by the temporal association of events, which is the key element of learning in the brain. This paper quantifies the efficiency of Hebbian learning as the ratio between the LTP and PTP effects on the synaptic weights. On the basis of this new idea, this work evaluates for the first time the influence of the number of neurons on the PTP/LTP ratio and consequently on the Hebbian learning efficiency. The evaluation was performed by simulating a neuron model that was successfully tested in control applications. The results show that the firing rate of postsynaptic neurons depends on the number of presynaptic neurons , which increases the effect of LTP on the synaptic potentiation. When activates at a requested rate, the learning efficiency varies in the opposite direction with the number of , reaching its maximum when fewer than two are used. In addition, Hebbian learning is more efficient at lower presynaptic firing rates that are divisors of the target frequency of . This study concluded that, when the electronic neurons additionally model presynaptic plasticity to LTP, the efficiency of Hebbian learning is higher when fewer neurons are used. This result strengthens the observations of our previous research where the SNN with a reduced number of neurons could successfully learn to control the motion of robotic fingers.
1. Introduction
Spiking neural networks (SNNs) benefit from biological plausibility, fast response, high reliability, and low power consumption when implemented in hardware. An SNN operates using spikes that are the effect of neuronal activation that occurs if a given threshold is exceeded and provides the SNN with sensitivity to event occurrence [1,2]. Thus, one of the critical advantages of SNN over traditional convolutional neural networks is the introduction of time in information processing. Another characteristic of SNN is their ability to learn, which is related to time based on the relative occurrence of the events.
1.1. Long-Term Plasticity
The main mechanism that determines learning is the long-term potentiation (LTP) that strengthens the synapses when the presynaptic neuron () activates before the stimulated postsynaptic neuron (). The reversed order of and activation reduces the synaptic weights via long-term depression (LTD) [3]. The amplitude of the synaptic change due to pairs and depends strongly on the temporal difference between the activation of and , respectively [4]. A detailed study of the biological neurons in vitro showed that LTP and LTD windows are asymmetric, making the LTP to dominate the LTD [5], implying that the resultant effect is LTP. Indeed, the essential mechanism of learning in the hippocampus is LTP, as stated in neuroscience [6]. LTP is also the basic element of Hebbian learning that determines the potentiation of the weak synapses if these are paired with strong synapses that activate postsynaptic neurons [7]. This implies that Hebb’s rules are critical for learning in the human brain and they are the foundation for the most biologically plausible supervised SNN learning algorithm [8,9].
1.2. Hebbian Learning in Artificial Systems
Besides the biological importance of Hebbian learning, these rules are used in artificial systems, mainly for training competitive networks [8] and to store memories in Hopfield neural networks [10,11]. Hebb’s rule strengthens neural paths that have temporal correlations between and activation. This implies that each neuron tends to pick out its own cluster of neurons, of which the activation is correlated in time by potentiating the synapses that contribute to the activation of postsynaptic neurons [12,13]. In this case, each neuron competes to respond to a subset of inputs matching the principles of competitive learning [8]. In addition, recent research showed that Hebbian learning is suitable to train SNNs of high biological plausibility to control robotic fingers using external forces mimicking the principles of physical guidance [14]. Here, the effect of the strong synapses that are driven by sensors was associated with the effect of weak synapses driven by a command signal [15].
Supervised learning based on gradient descent is more powerful than Hebbian learning [8] in computational applications. However, these error-correcting learning rules are not suitable for bioinspired SNNs because the explicit adjustment of the synaptic weight is not typically feasible. Therefore, for adaptive systems of high biological plausibility, Hebb’s rules are more suitable to train the synapses unsupervised, as they are trained in the brain.
The repetitive activation of is independent of a activity increase in synaptic efficacy by the presynaptic elements of learning such as post-tetanic potentiation (PTP) [16] that can last from a few seconds to minutes [17]. This synaptic potentiation represents an increase in the quantity of the mediator released from the presynaptic membrane during activation [16,18]. PTP influences the motor learning specific to Purkinje cells that plays a fundamental role in motor control [19]. Taking into account that this type of presynaptic long-term plasticity occurs in the absence of postsynaptic activity, the Hebbian learning mechanisms are altered by PTP [18].
1.3. The Number of Neurons in SNNs
Each neuron is a complex cell comprising multiple interacting parts and small chambers containing molecules, ions, and proteins. The human brain is composed of neurons in the order of connected by about synapses. Creating mathematical and computational models would be an efficient solution towards understanding the functions of the brain, but even if with an exponential increase in computational power, it does not seem achievable in the near future. Even if this could be achieved, the complexity of the resulting simulation maybe as complex as the brain itself. Hence, there is a need for tractable methods for reducing the complexity while preserving the functionality of the neural system. The size effect in SNNs has various approaches. Statistical physics formalism based on the many-body problem was used to derive the fluctuation and correlational effects on finite networks of N neurons as a perturbation expansion of around the mean field limit of [20]. Another method that was used to optimise the size and resilience of the SNN is with empirical analysis using evolutionary algorithms. Thus, smaller networks may be generated by using a multiobjective fitness function incorporating a penalty for the number of neurons evaluating every network in a population [21].
In addition, research on computational neural networks showed that, for classification problems, SNNs use fewer neurons than the second generation of artificial neural networks (ANNs) does [22]. In addition, the hardware implementation of SNNs demonstrated their efficacy in modelling conditional reflex formation [23] or in controlling the contraction of artificial muscles composed of shape memory alloy (SMA). In later applications, SNNs with only a few excitatory and inhibitory neurons have been able to control the force [24,25] and learn the motion [14,15] of anthropomorphic fingers. In addition, using fewer neurons is important in reducing the cost and increasing the reliability of the hardware implementation of SNNs.
Analysing the Hebbian learning efficiency of adaptive SNN provides a useful tool for reducing the size of experimental networks and minimising the simulation time while preserving bioinspired features.
1.4. The Goal and Motivation of the Current Research
The presynaptic long-term plasticity determined by PTP reduces the efficiency of Hebbian learning that is determined by LTP. This mechanism is critical to make the neural network respond to concurrent events by potentiating the untrained synapses when activated with the trained neural paths. Thus, PTP potentiates synapses in the absence of a postsynaptic response, meaning that the causality is broken.
Considering these aspects, the goal of this paper is to determine in which conditions the effect of LTP over PTP is maximised, increasing the efficacy of Hebbian learning. Typically, fewer neurons must fire at a higher rate or have stronger potentiated synapses to activate above the preset rates. Reducing the number of neurons can increase both the firing rate of and the synaptic weights that are necessary to reach the requested frequencies of .
At certain firing rates and synaptic weights, the ratio between the LTP and PTP rates can be higher, implying that associative learning is more efficient. Considering that represents the maximal contribution of LTP and , the effect of PTP to the synaptic weight during the period of training, then there is a maximal ratio: of and . In this work, we consider that the maximal efficiency of Hebbian learning is for , which corresponds to . If a target frequency for the postsynaptic neuron is requested, then a minimal number of untrained presynaptic neurons with weight can be activated to reach . Therefore, the ideal case when LTP is maximal depends on the functions that describe the weight variation by PTP and LTP, and on .
Starting from these ideas, the contribution of this work is twofold: (i) The quantification of Hebbian learning efficiency as the ratio between LTP and PTP; (ii) the evaluation of the influence of the number of neurons on the efficiency of Hebbian learning, focusing on an SNN with reduced number of neurons (fewer than 20 per area).
As presented in Section 1.2 and Section 1.3, there are several comprehensive studies related to Hebbian learning or focused on the influence of variation in the number of neurons on the performance of adaptive SNN. However, there are no studies focused on overlapping these two research directions in systems of high biological plausibility.
The rest of the paper is organised as follows: Section 2 presents the general structure of the neural network and the experimental phases focusing on the proposed neuron model, and on the implementation of PTP and LTP mechanisms. The experimental results along with the details for each measured item are presented in Section 3. The paper ends with Section 4, which discusses the results, focusing on the biological plausibility of the used model, and presents some considerations for future research.
2. Materials and Methods
The SNN is based on a neuronal model of high biological plausibility [14]. Although this electronic neuron was implemented and tested in PCB hardware, the analysis presented in this work was based on spice simulations of the electronic circuit.
2.1. The Model of the Artificial Neuron
An artificial neuron includes a SOMA and one or more synapses. The electronic SOMA models elements related to information processing, such as the temporal integration of incoming stimuli, the detection of the activation threshold, and a refractory period. Electronic synapses model presynaptic elements of learning such as PTP and the postsynaptic plasticity that determines Hebbian learning via long-term potentiation (LTP). In addition, a synapse stores the synaptic weight using a capacitor that can be charged or discharged in real time using cheap circuits [26,27]. Electronic synapses generate excitatory or inhibitory spikes to feed the corresponding .
Figure 1 shows the main elements related to learning that are included by the neuronal schematic that is detailed in Appendix A [14]. The neuron detects the activation threshold using the transistor , and, during activation, generates a spike of variable energy that depends on the synaptic weight . In this work, we refer to as the voltage read in the capacitor , shown in Figure 1. The synapse is potentiated by PTP that is modelled by the discharge of when the neuron activates, and by LTP, which alters the charge in capacitor during the activation of .
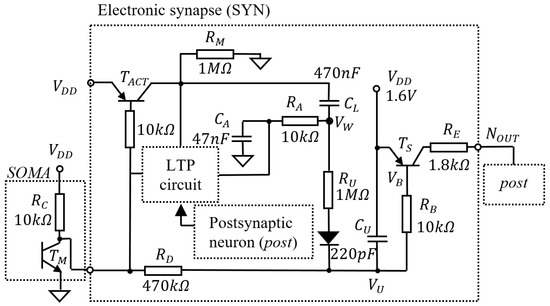
Figure 1.
The main elements of the neuronal schematic that are used to model the mechanisms of learning.
Potential determines the duration of the generated spike at OUT, modelling the effect of synaptic weight on postsynaptic activity. Spike duration is determined by potential because, during SOMA activation, transistor is open as long as (which is proportional with ) is below the emitter-base voltage of . The variation in is given by:
The initial potential is calculated using Equation (2) for cut-off and Equation (3) for saturated regimes of transistor as follows:
In and , and are the forward and emitter base voltages, respectively. Similarly, after SOMA inactivation, is restored to as follows:
where is the initial value of when SOMA inactivates and starts charging.
2.2. Model for PTP and LTP
The activation of the neuron that lasts reverses the polarity of , which is discharged by an amount that is given by:
Equation (5) models the potentiation by PTP of the synapse. For expressing LTP, we should consider the charge variation in when it is discharged using , followed by a reset of the charge in during activation.
During neuronal activation, the potential in the capacitor varies as follows:
where the equivalent capacitance is:
Considering that and represent the variation in potential in and , respectively, we denote the ratio:
Thus, variation in the potential in that represents the temporary potentiation of the synapse is:
During the neuronal idle state after its activation, the resultant variation of the potential in and is:
where is the time window between the moments of the neuronal activation. discharges in until the potentials in both capacitors reach equilibrium. This variation restores the synaptic weight to the value that was before activation of the presynaptic neuron. If the postsynaptic neuron fires during the restoration of the synaptic weight, capacitor is discharged at a significantly higher rate until equilibrium is reached. Taking into account that , the potential variation in during activation is negligible. This implies that the variation in the potential in that models weight variation by LTP is:
decreases according to Equation (8), implying that depends on the time window .
For this neuronal design varies in the opposite direction, with in the range of [0.2 V:1.6 V]. This implies that a lower models higher synaptic potentiation. To simplify the presentation, in this research, we refer to variation in the voltage in that occurs during potentiation.
Therefore, the experiments presented in the following section focus on evaluating how the number of neurons affect learning efficiency.
2.3. The Structure of the SNN
The synaptic configuration includes two presynaptic neural areas, and , which include and neurons, respectively. The included in these neural areas connect to only one , as in Figure 2a. For allowing weight variation by LTP, at the beginning of each experiment, synapses between and were fully potentiated for the activation of , while the weights of synapses driven by were minimal. The SNN included additional neurons and for the evaluation of the potentiation by PTP of , which had the same value as that for . This allowed for us to compare the PTP and LTP effects in similar conditions.
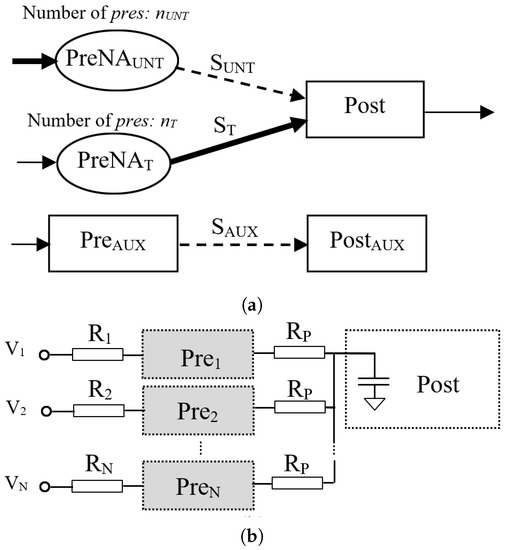
Figure 2.
(a) The structure of the SNN that was used to perform tests; (b) R varied among presynaptic neurons .
As shown in Figure 2b, neurons in each presynaptic area were activated by constant potentials or by pulses, as we detail in the sequel. For modelling the variability in the electronic components, input resistors , , and , shown in Figure 2b, were set in an interval that varied the firing rate of slightly.
The firing rate of the postsynaptic neurons , and the variation in the synaptic weights and due to LTP and PTP, respectively, were determined via measurements on the simulated electronic signals [28,29]. The values of the input voltages for the activation of were set to several values to activate the neurons in the range that was used during our previous experiments [14]. In order to highlight the influence of the number of neurons on the Hebbian learning efficiency, the initial synaptic weights were minimal for extending their variation range.
2.4. Experimental Phases
The experiments started with a preliminary phase in which we determined and for a single spike when took several values, and variation in with the number . Following these preliminary measurements, we evaluated the efficiency of Hebbian learning by calculating the ratio during several phases as follows:
Phase 1. The value of was determined when and in the neural areas and , respectively, varied independently or simultaneously. These results were compared with the effect of PTP when only the neurons in the untrained area were activated. Variation in the synaptic weight included potentiation due to LTP being determined by pair activation and due to PTP that occurred due to action potential.
Typically, the frequency of can be controlled in certain limits by adjusting the firing rate of independent of the number of neurons. In order to simplify the SNN structure during Phases 2 and 3, included one neuron.
Phase 2. Next, we determined the variation in and when synapses in were trained until they were able to activate in the absence of activity.
Phase 3. For the last phase of the experiments, we considered a fixed frequency of the output neuron that matched the firing rate of the output neurons that actuated the robotic junctions in our previous experiments [14]. Thus, the SNN was trained until had reached when stimulated only by independent of . In order to extract the contribution of PTP to the , neuron was activated at the same rate with , and was measured.
For the untrained , we set different frequencies that were not divisible with the firing rate of , mimicking a less favourable scenario of neuronal activation. In this case, the time interval between and activation varied randomly, increasing the diversity of the weight gain per the action potential of . In a favourable scenario, the frequency of is the divisor of the firing rate of , which improves the weight gain via the synchronisation of neuronal activation.
3. Results
The obtained results during the experimental phases mentioned above are presented here.
3.1. Preliminary Phase
In order to asses the influence of the electronics on synaptic potentiation during a single spike, we determined the weight variation by PTP for several values of when activated once. As presented in Figure 3a, PTP decreased as increased. However, long term, this variation was compensated by the number of spikes per time unit that increased at a higher rate with . A similar evaluation was performed for LTP when was activated by trained neurons at after the activation of the untrained . In this case, the influence of LTP presented in Figure 3b was extracted from the measured by the subtraction of the PTP effect shown in Figure 3a.
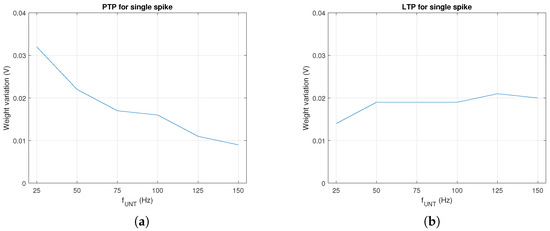
Figure 3.
Weight variation with during a single spike by (a) PTP and (b) LTP for a time window.
Typically, the output frequency of an SNN depends on the number of that stimulate , as shown in Figure 4a. Starting from this observation, we determined after 2 s of training for a different number of in and when and . Figure 4b–d show that depended on the number of following different patterns for the trained and untrained neurons. In addition, the learning rate by LTP increased with the number of , mainly due to higher values of determined by the activation of more .
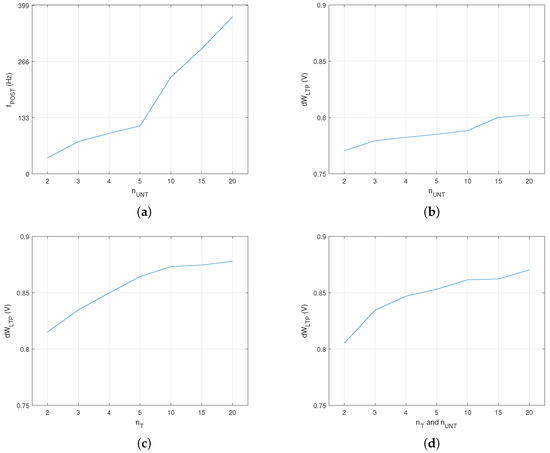
Figure 4.
(a) The frequency of the output neuron. The synaptic weight variation by LTP after 2 s of training for variation in the number of (b) untrained neurons with Hz; (c) trained neurons with Hz; (d) both trained and untrained neurons.
3.2. The Efficiency of Hebbian Learning
Variation in the ratio with the voltage synaptic weight is presented in Figure 5a. This represents the ideal case when LTP is maximal, which was obtained by the activation of the postsynaptic neuron shortly after the untrained . was maximal for a specific weight that was far from the limits of the variation interval.
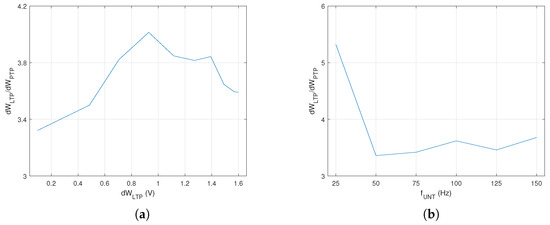
Figure 5.
(a) Variation in the ratio with synaptic weight; (b) the ratio of synaptic weight variation between PTP and LTP after 2 s of training.
Weight variation for different firing rates of was determined for both PTP and LTP when the neurons activated for a fixed period of time . The data plotted in Figure 5b show that variation in the ratio reduced significantly when the frequency of the untrained was above 50 Hz. Thus, taking into account that was almost stable for a single neuron in , for the next experimental phase, we evaluated the influence of the number of neurons on for fixed activation frequency Hz.
In this setup, the SNN was trained until the first activation of by the synapse that was potentiated by LTP. The PTP level for the synapse was determined via the activation of the auxiliary neuron (see SNN structure in Figure 2a) at the same frequency as that of the untrained . In order to determine if had a similar variation for another frequency of the neurons in the , we performed similar measurements for Hz. As presented in Figure 6, the variation in showed that the best learning efficiency was obtained for when Hz and for when Hz. The different number of indicated that influenced the optimal number of neurons for the best learning efficiency when the neural paths were trained until the first activation of by independent of .
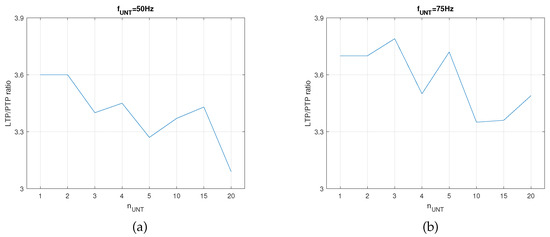
Figure 6.
The ratio of potentiation levels between LTP and PTP when the SNN was trained until first activation of for (a) and (b) .
The next experimental phase evaluated and the duration of the training process when the firing rate of the output neurons reached Hz, while the untrained in the area activated at several firing rates in a set that included divisors of .
The plots in Figure 7a,b show that weight variations and decreased when the number of untrained increased. Typically, is proportional with , implying that the SNN learns faster when more neurons activate . The improved value for was determined by the lower weights that were necessary to activate at the requested firing rate. In order to compare and , we determined the that were potentiated by PTP when the neuron was activated at as the neurons in the area . Figure 8a shows the variation for several firing rates that were not divisors of . In this case, local maximum was for a single neuron per area (). Taking into account that LTP may be more efficient when is a divisor of due to the synchronisation of the neurons, we evaluated the weight variation for 25, 33.3, and 50 Hz. In order to eliminate the variation in PTP with the continuous input voltage of the neurons, the were activated with digital pulses with the same amplitude generated at rate . The results presented in Figure 8b show that the maximal was obtained for neurons. The best learning efficiency was obtained when Hz, and the untrained presynaptic area included two neurons.
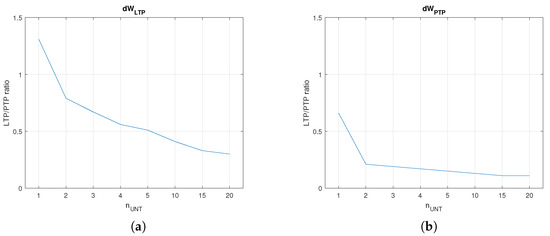
Figure 7.
Learning until Hz when the number of untrained neurons varied. (a) and (b) for Hz.
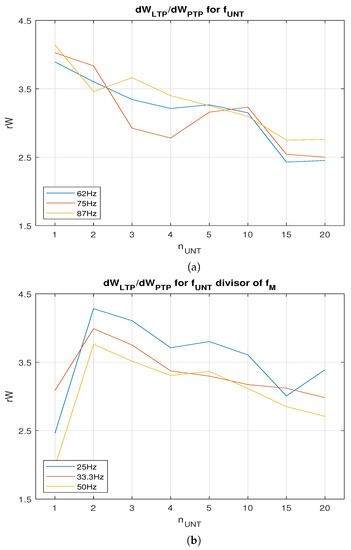
Figure 8.
Variation in ratio with when (a) is not a divisor of and (b) is a divisor of .
Typically, the weight variation with training duration by LTP and PTP varies, following different patterns. The difference between the two functions implies that there is a value for where the ratio between LTP and PTP is maximal. This value corresponds to a synaptic weight obtained by LTP and consequently to a potential . Typically, there is a minimal number of pres firing at a fixed frequency that are able to activate a when the weight is . In our work, the best for neurons corresponded to the potential V in the weight capacitor.
4. Discussion and Conclusions
At the synaptic level, the neural paths in the brain are trained by associative or Hebbian learning that is based on long-term potentiation, which is the postsynaptic element of learning. From a biological point of view, presynaptic long-term plasticity violates Hebbian learning rules that depend on postsynaptic activity. Previous research on SNN showed that the control systems use a reduced number of electronic neurons, while in classification tasks, SNN uses fewer neurons than the traditional CNN does. Starting from these ideas, this work focused on the evaluation of the influence of the number of neurons on the efficiency of Hebbian learning, characterised as the ratio of LTP and PTP effects on the synaptic weights. This ratio increases the effect of LTP and consequently the power of the SNN to discriminate between the neural paths that are trained by associative learning over the paths where only presynaptic plasticity occurs. The simulation results showed that, despite the fact that LTP depends mainly on the frequency of postsynaptic neurons, the number of neurons affect the Hebbian learning efficiency when the must reach a predefined frequency. In this case, the best LTP/PTP ratio was obtained when the frequency of the untrained was the lowest divisor of the target frequency of . The efficiency of Hebbian learning reached a maximum for two and decreased in the opposite direction with the number of . Taking into account that, for a certain number of neurons, the LTP/PTP ratio was better, we could deduce that certain synaptic weights resulted in better Hebbian learning efficiency. Indeed, the position of the maximal inside the variation interval (Figure 8b) matched the variation in the in the ideal case presented in Figure 5a. This implies that the minimal number of neurons that were necessary to activate at the requested firing rate was related to the synaptic weight. In conclusion, previous research showed that electronic SNNs with a reduced number of neurons are trained efficiently by Hebbian learning, while the current research strengthen the idea showing that fewer neurons improve associative learning. This could reduce the cost and improve the reliability of the hardware implementation of SNNs.
Author Contributions
Conceptualisation, M.H.; methodology, G.-I.U. and M.H.; simulation, G.-I.U.; validation, M.H. and A.B.; formal analysis, G.-I.U.; investigation, G.-I.U. and M.H.; data curation, G.-I.U.; writing—original draft preparation, G.-I.U. and M.H.; writing—review and editing, M.H. and A.B.; supervision, M.H.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Doctoral School of TUIASI.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN | Artificial neural network |
| LDT | Long-term depression |
| LTP | Long-term potentiation |
| PCB | Printed circuit board |
| PTP | Post-tetanic potentiation |
| SMA | Shape memory alloy |
| SNN | Spiking neural network |
Appendix A
Figure A1 presents the schematic circuit, including the parametric values, of the electronic neuron that was implemented in PCB hardware [28]. The neuron included one electronic soma (SOMA) and one or more electronic synapses (SYN). The SOMA detects the neuronal activation threshold using transistor and activates the SYNs. The SOMA of the postsynaptic neurons that are stimulated by excitatory or inhibitory synapses includes an integrator of the input activity. When the SOMA activates the connected SYNs, generates pulses at their output , of which the nergy depends on the charge stored in the weight capacitor .
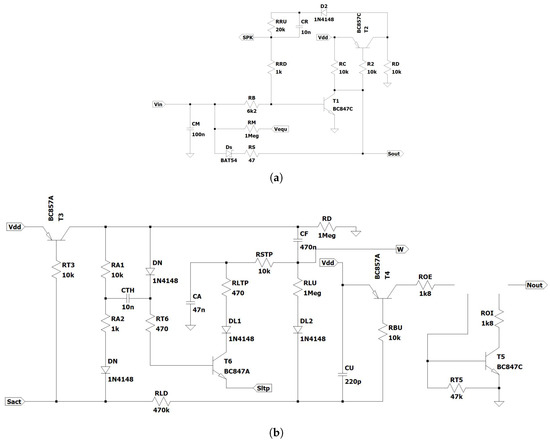
Figure A1.
The schematic of (a) the electronic SOMA and (b) the electronic synapse (SYN).
References
- Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Netw. 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
- Blachowicz, T.; Grzybowski, J.; Steblinski, P.; Ehrmann, A. Neuro-Inspired Signal Processing in Ferromagnetic Nanofibers. Biomimetics 2021, 6, 32. [Google Scholar] [CrossRef] [PubMed]
- Bi, G.Q.; Poo, M.M. Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 1990, 18, 10464–10472. [Google Scholar] [CrossRef] [PubMed]
- Karmarkar, R.; Buonomano, D. A Model of Spike-Timing Dependent Plasticity: One or Two Coincidence Detectors? J. Neurophysiol. 2002, 88, 507–513. [Google Scholar] [CrossRef]
- Sjostrom, P.J.; Turrigiano, G.; Nelson, S. Rate, Timing, and Cooperativity Jointly Determine Cortical Synaptic Plasticity. Neuron 2001, 32, 1149–1164. [Google Scholar] [CrossRef]
- Whitlock, J.R.; Heynen, A.J.; Shuler, M.G.; Bear, M.F. Learning Induces Long-Term Potentiation in the Hippocampus. Science 2006, 313, 1093. [Google Scholar] [CrossRef]
- Barrionuevo, G.; Brown, T.H. Associative long-term potentiation in hippocampal slices. Proc. Natl. Acad. Sci. USA 1983, 80, 7347–7351. [Google Scholar] [CrossRef]
- Mcclelland, J. How far can you go with Hebbian learning, and when does it lead you astray. Atten. Perform. 2006, 21, 33–69. [Google Scholar]
- Gavrilov, A.; Panchenko, K. Methods of Learning for Spiking Neural Networks. A Survey. In Proceedings of the 13th International Scientific-Technical Conference APEIE, Novosibirsk, Russia, 3–6 October 2016. [Google Scholar]
- Alemanno, F.; Aquaro, M.; Kanter, I.; Barra, A.; Agliari, E. Supervised Hebbian Learning. Europhys. Lett. 2022, 141, 11001. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Kempter, R.; Gerstner, W.; van Hemmen, L. Hebbian learning and spiking neurons. Phys. Rev. E 1999, 59, 4498. [Google Scholar] [CrossRef]
- Song, S.; Miller, K.D.; Abbott, L. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 2000, 3, 919–926. [Google Scholar] [CrossRef]
- Hulea, M.; Uleru, G.I.; Caruntu, C.F. Adaptive SNN for anthropomorphic finger control. Sensors 2021, 28, 2730. [Google Scholar] [CrossRef] [PubMed]
- Uleru, G.I.; Hulea, M.; Manta, V.I. Using hebbian learning for training spiking neural networks to control fingers of robotic hands. Int. J. Humanoid Robot. 2022, 2250024. [Google Scholar] [CrossRef]
- Powell, C.M.; Castillo, P.E. 4.36—Presynaptic Mechanisms in Plasticity and Memory. In Learning and Memory: A Comprehensive Reference; Byrne, J.H., Ed.; Academic Press: Cambridge, MA, USA, 2008; pp. 741–769. [Google Scholar]
- Fioravante, D.; Regehr, W.G. Short-term forms of presynaptic plasticity. Curr. Opin. Neurobiol. 2011, 21, 269–274. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Calakos, N. Presynaptic long-term plasticity. Front. Synaptic Neurosci. 2013, 17, 8. [Google Scholar] [CrossRef]
- Kano, M.; Watanabe, M. 4—Cerebellar circuits. In Neural Circuit and Cognitive Development (Second Edition); Rubenstein, J., Rakic, P., Chen, B., Kwan, K.Y., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 79–102. [Google Scholar]
- Buice, M.A.; Chow, C.C. Dynamic Finite Size Effects in Spiking Neural Networks. PLoS Comput. Biol. 2013, 9, 1659–1671. [Google Scholar] [CrossRef]
- Dimovska, M.; Johnston, T.; Schuman, C.; Mitchell, J.; Potok, T. Multi-Objective Optimization for Size and Resilience of Spiking Neural Networks. In Proceedings of the IEEE 10th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 10–12 October 2019; pp. 433–439. [Google Scholar]
- Hussain, I.; Thounaojam, D.M. SpiFoG: An efficient supervised learning algorithm for the network of spiking neurons. Sci. Rep. 2020, 4, 13122. [Google Scholar] [CrossRef]
- Hulea, M.; Barleanu, A. Electronic Neural Network For Modelling The Pavlovian Conditioning. In Proceedings of the International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 19–21 October 2017. [Google Scholar]
- Uleru, G.I.; Hulea, M.; Burlacu, A. Bio-Inspired Control System for Fingers Actuated by Multiple SMA Actuators. Biomimetics 2022, 7, 62. [Google Scholar] [CrossRef]
- Hulea, M.; Uleru, G.I.; Burlacu, A.; Caruntu, C.F. Bioinspired SNN For Robotic Joint Control. In Proceedings of the International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 21–23 May 2020; pp. 1–5. [Google Scholar]
- Hulea, M.; Burlacu, A.; Caruntu, C.F. Intelligent motion planning and control for robotic joints using bio-inspired spiking neural networks. Int. J. Hum. Robot. 2019, 16, 1950012. [Google Scholar] [CrossRef]
- Hulea, M.; Barleanu, A. Refresh Method For The Weights of The Analogue Synapses. In Proceedings of the International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 8–10 October 2020; pp. 102–105. [Google Scholar]
- Hulea, M. Electronic Circuit for Modelling an Artificial Neuron. Patent RO126249 (A2), 29 November 2018. [Google Scholar]
- Hulea, M.; Ghassemlooy, Z.; Rajbhandari, S.; Younus, O.I.; Barleanu, A. Optical Axons for Electro-Optical Neural Networks. Sensors 2020, 20, 6119. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).