Bio-Design, Fabrication and Analysis of a Flexible Valve
Abstract
:1. Introduction
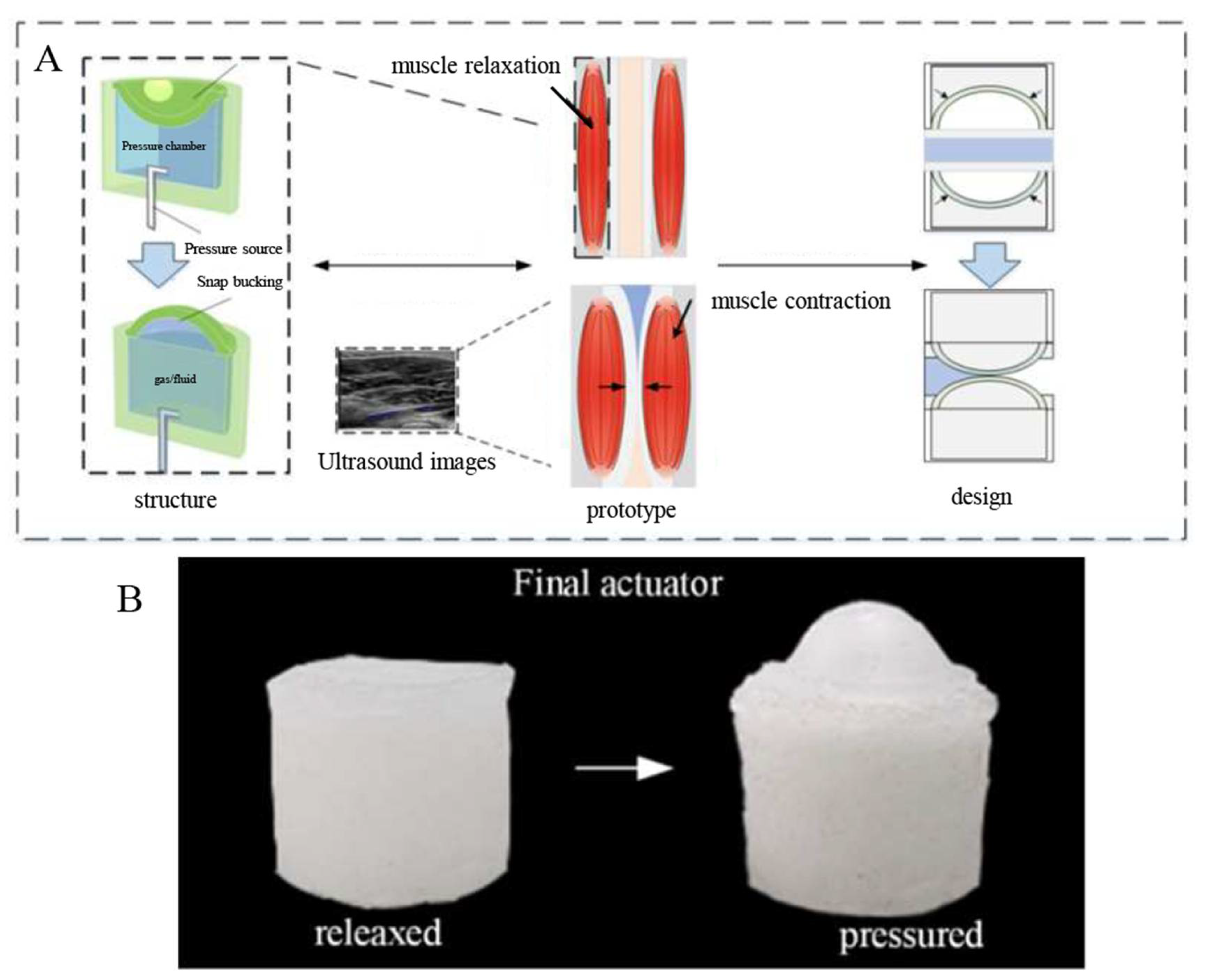
2. Materials and Methods
3. Results
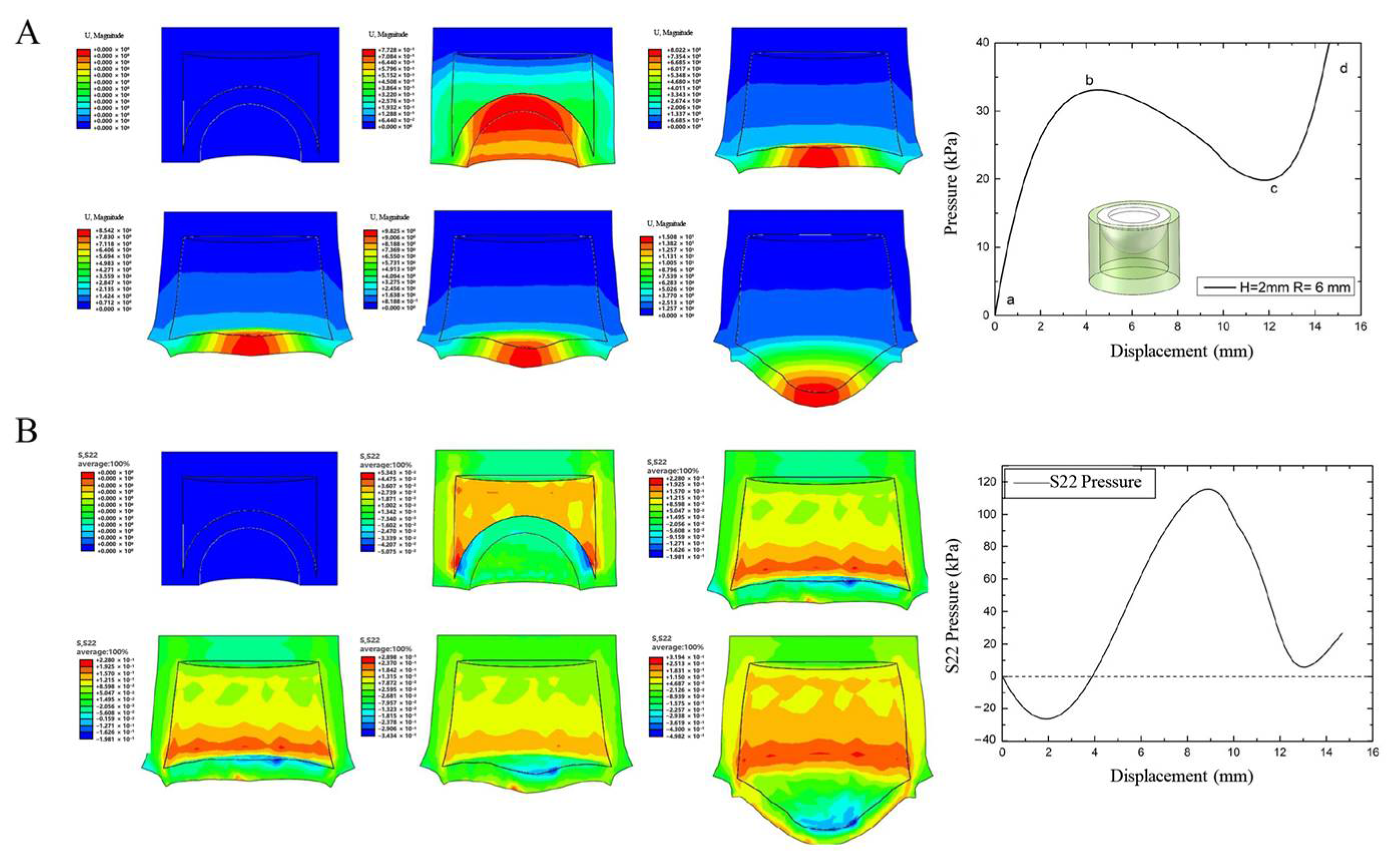
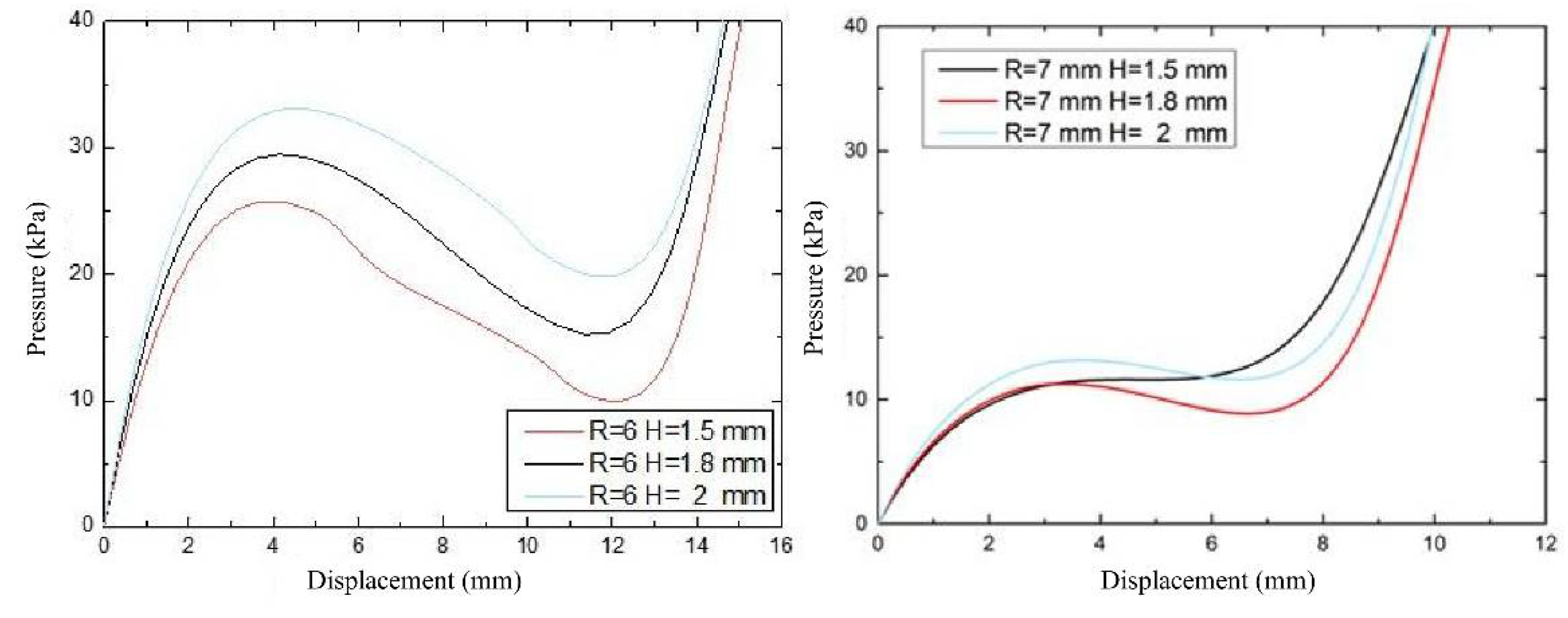
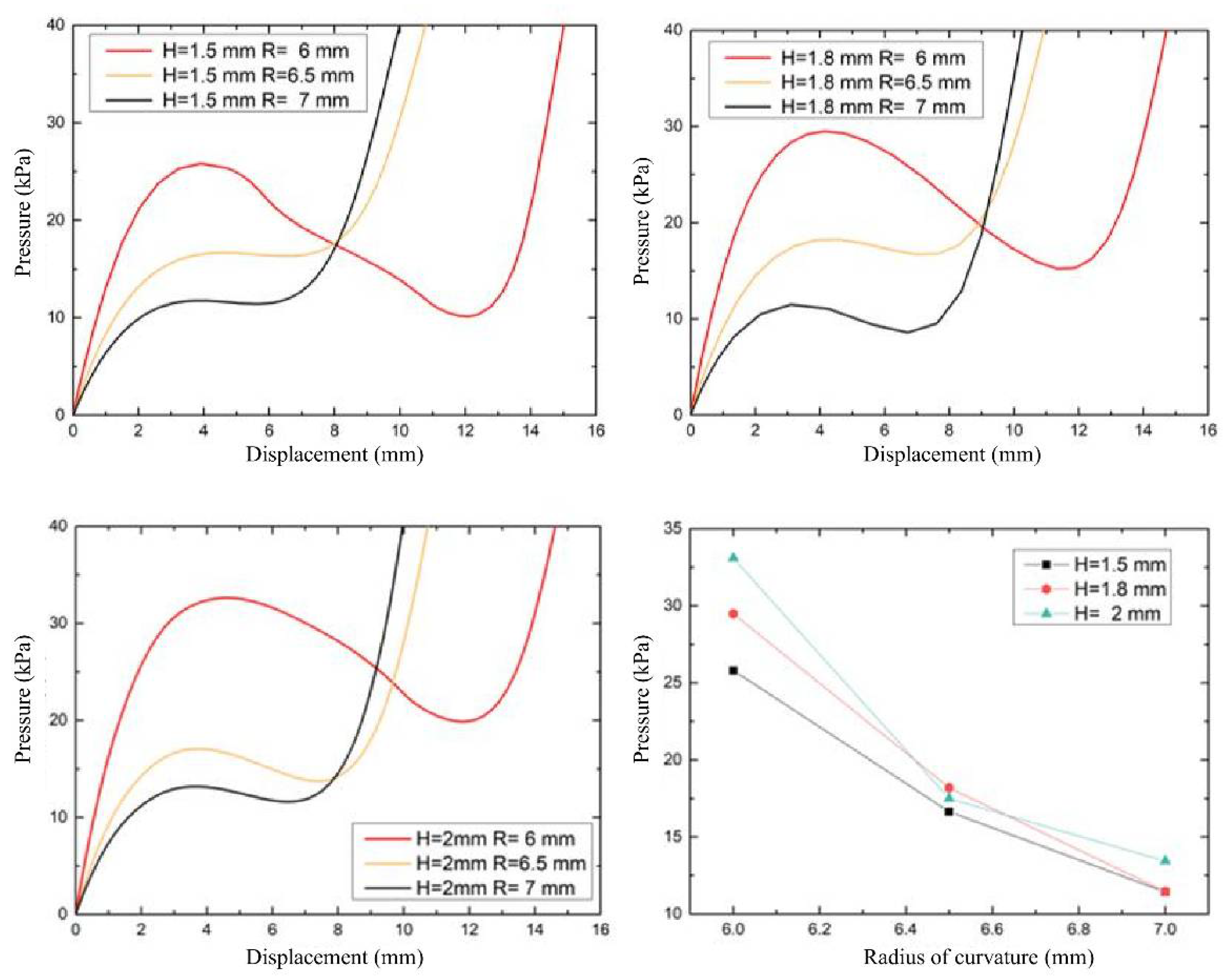
3.1. Simulation and Analysis
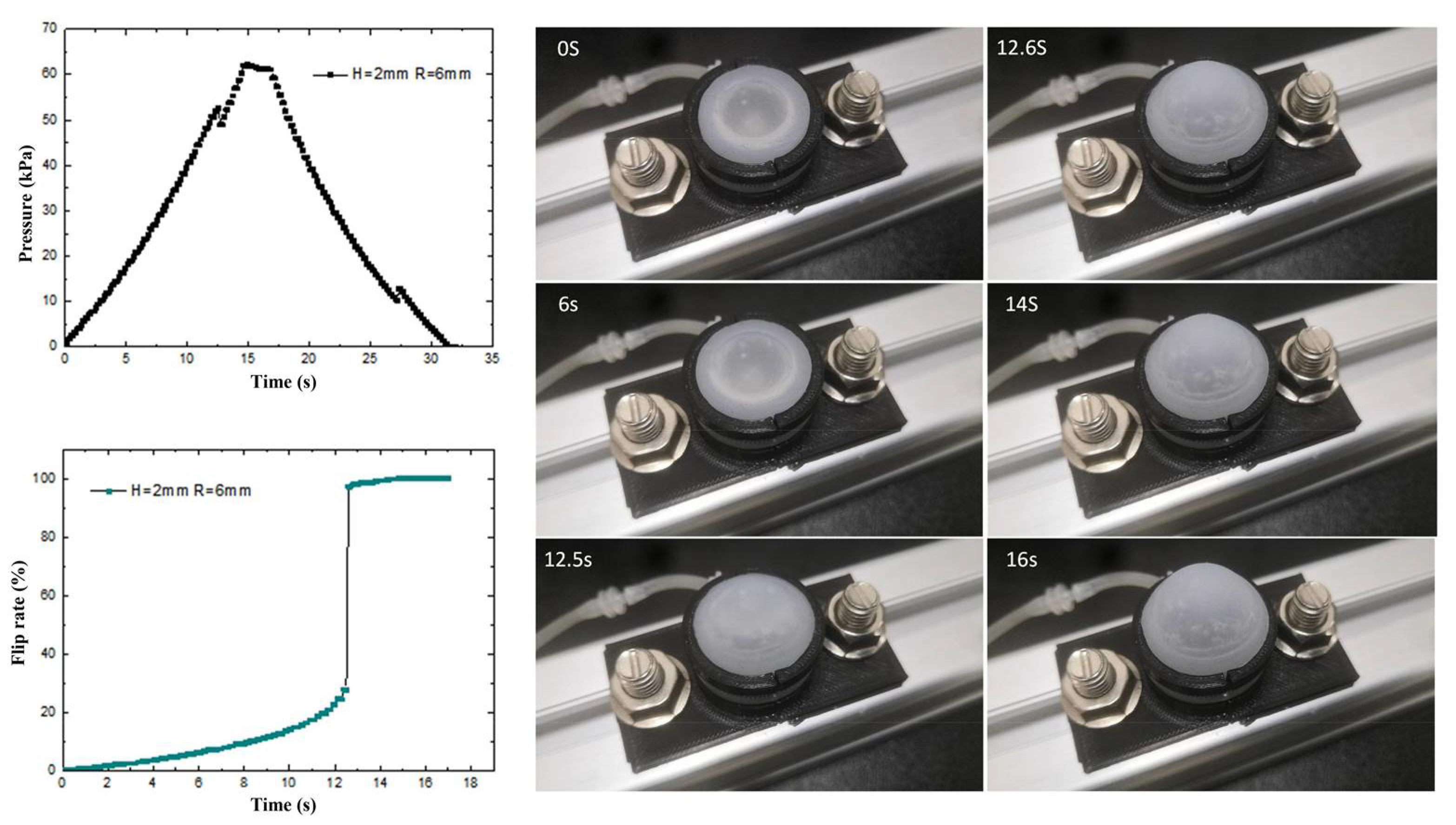
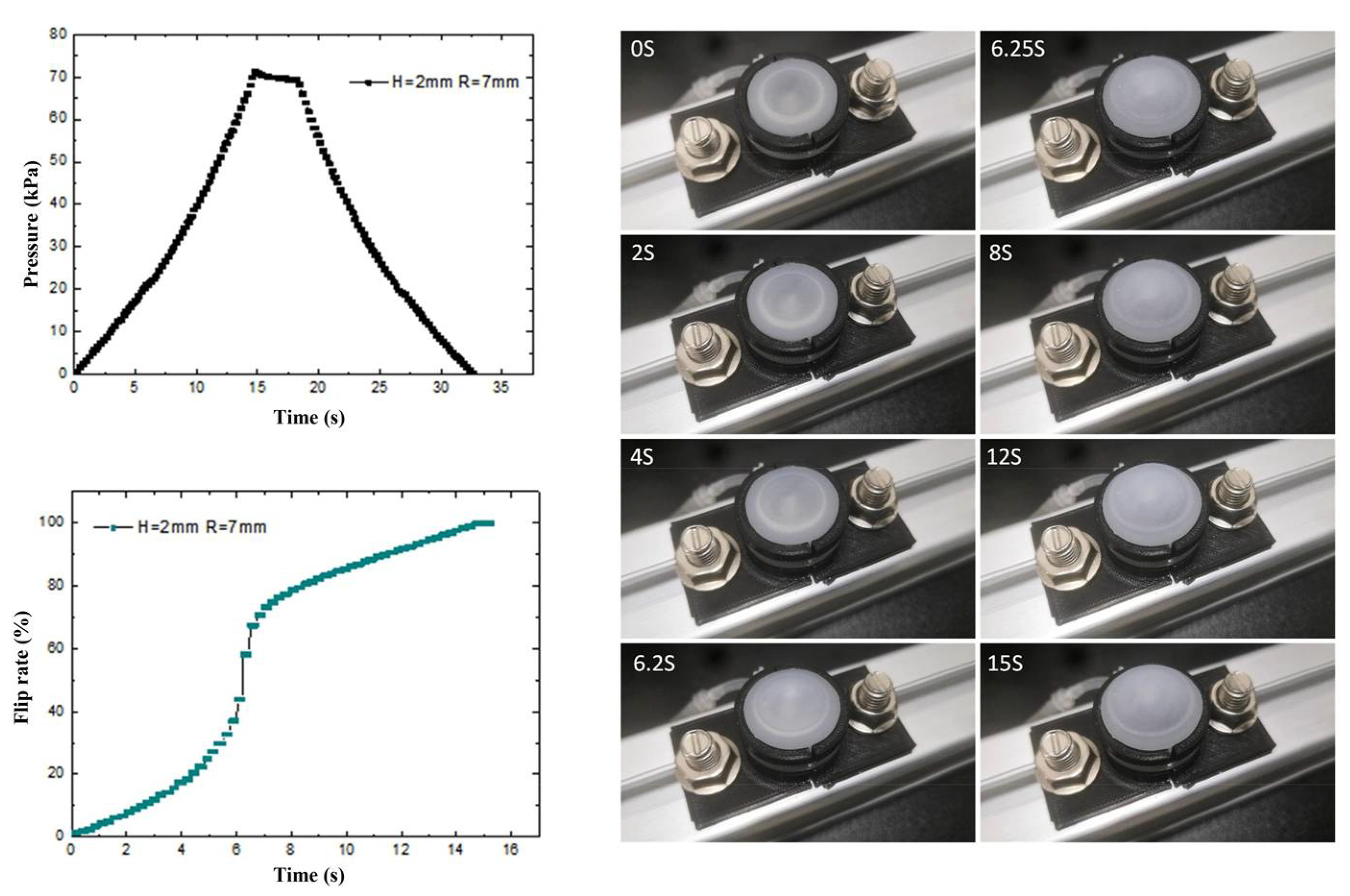
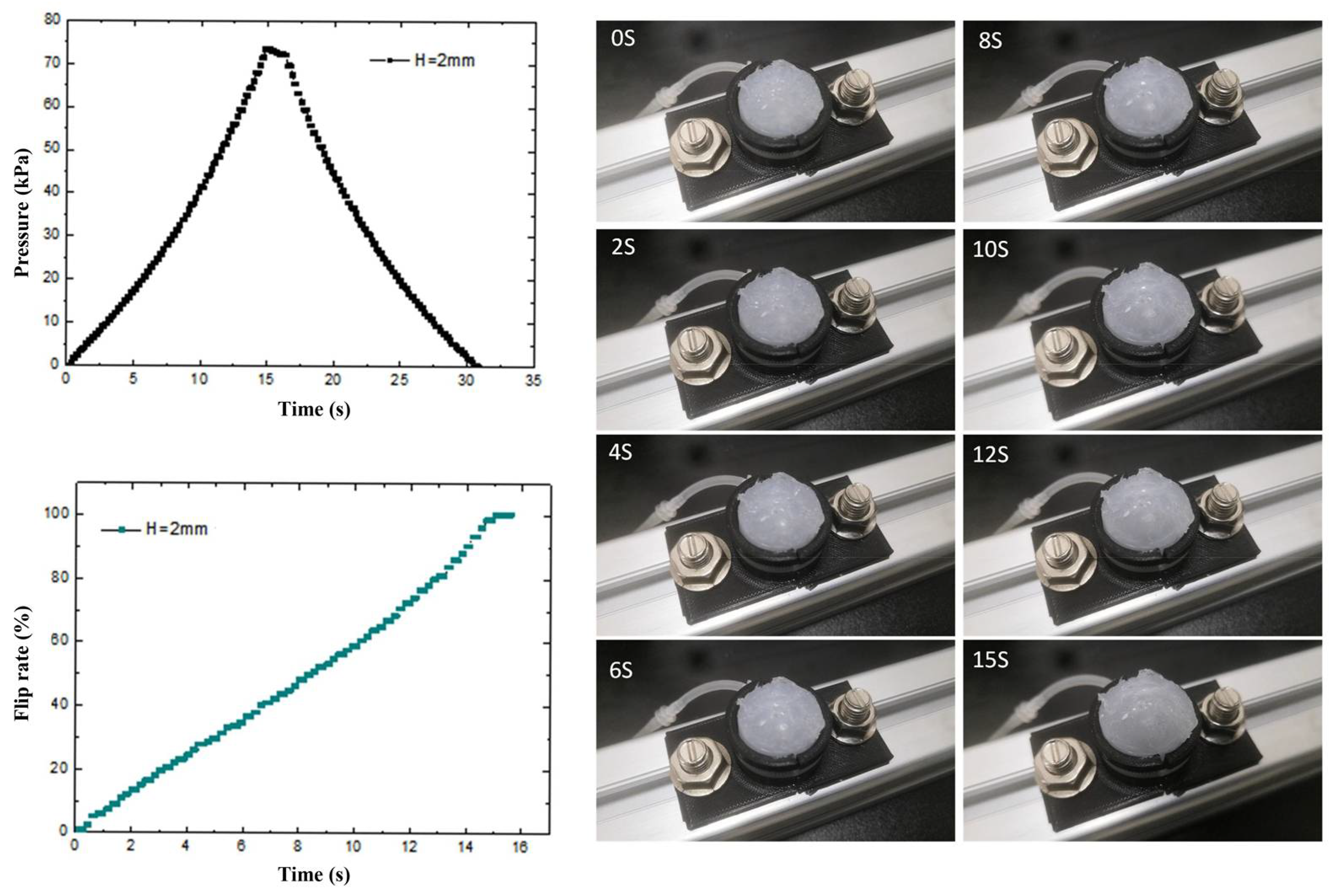
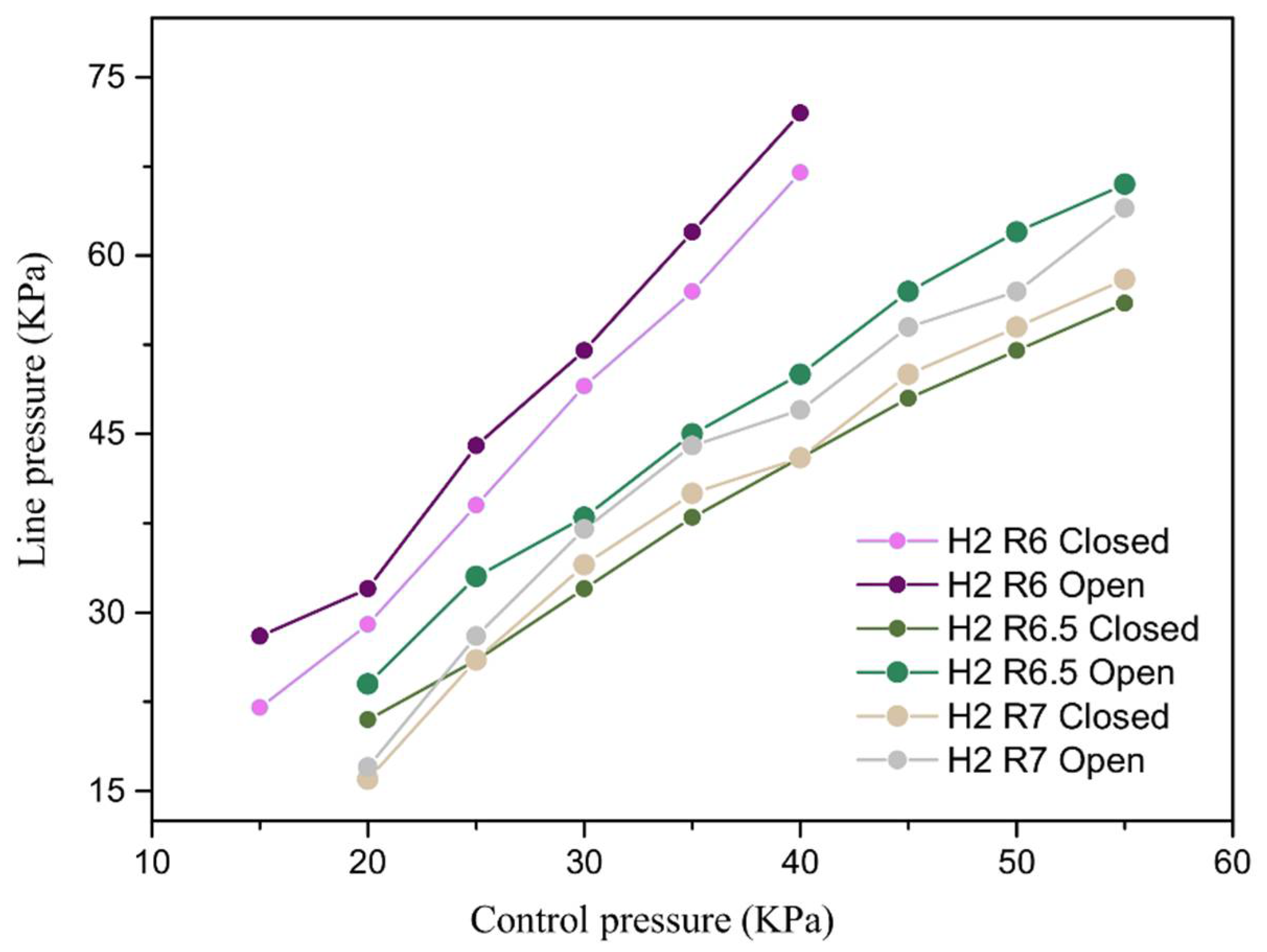
3.2. Experimental Testing and Analysis
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kier, W.M.; Smith, K.K. Tongues, tentacles and trunks: The biomechanics of movement in muscular-hydrostats. Zool. J. Linn. Soc. 2010, 4, 307–324. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Y.; Liu, L.; Leung, Y.S.; Chen, Y.; Guo, Y.; Chai, Y.; Chen, Y. 3D printing of hydroxyapatite/tricalcium phosphate scaffold with hierarchical porous structure for bone regeneration. Bio-Des. Manuf. 2020, 3, 15–29. [Google Scholar] [CrossRef]
- Anderson, E.J.; Grosenbaugh, M.A. Jet flow in steadily swimming adult squid. J. Exp. Biol. 2005, 208, 1125–1146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mcgowan, C.P.; Skinner, J.; Biewener, A.A. Hind limb scaling of kangaroos and wallabies (superfamily Macropodoidea): Implications for hopping performance, safety factor and elastic savings. J. Anat. 2008, 212, 153–163. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.; Goswami, D.; Martinez, R.V. Elastic Energy Storage Enables Rapid and Programmable Actuation in Soft Machines. Adv. Funct. Mater. 2020, 30, 2070002. [Google Scholar] [CrossRef] [Green Version]
- Quinn, T.H.; Baumel, J.J. The digital tendon locking mechanism of the avian foot (Aves). Zoomorphology 1990, 109, 281–293. [Google Scholar] [CrossRef]
- Connolly, F.; Walsh, C.J.; Bertoldi, K. Automatic design of fiber-reinforced soft actuators for trajectory matching. Proc. Natl. Acad. Sci. USA 2017, 114, 51–56. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Bi, Z.; Bian, X.; Ge, A.; He, J.; Li, W.; Shao, H.; Chen, G.; Zhang, X. Study on linear bio-structure print process based on alginate bio-ink in 3D bio-fabrication. Bio-Des. Manuf. 2020, 3, 109–121. [Google Scholar] [CrossRef]
- Shepherd, R.F.; Stokes, A.A.; Freake, J.; Barber, J.; Snyder, P.W.; Mazzeo, A.D.; Cademartiri, L.; Morin, S.A.; Whitesides, G.M. Using Explosions to Power a Soft Robot. Angew. Chem. 2012, 125, 2964–2968. [Google Scholar] [CrossRef]
- Zhang, F.; Qu, K.; Li, X.; Liu, C.; Ortiz, L.S.; Wu, K.; Wang, X.; Huang, N. Gelatin-based hydrogels combined with electrical stimulation to modulate neonatal rat cardiomyocyte beating and promote maturation. Bio-Des. Manuf. 2021, 4, 100–110. [Google Scholar] [CrossRef]
- Tonazzini, A.; Sadeghi, A.; Mazzolai, B. Electrorheological Valves for Flexible Fluidic Actuators. Soft Robot. 2016, 3, 34–41. [Google Scholar] [CrossRef]
- Zatopa, A.; Walker, S.; Menguc, Y. Fully Soft 3D-Printed Electroactive Fluidic Valve for Soft Hydraulic Robots. Soft Robot. 2018, 5, 258–271. [Google Scholar] [CrossRef] [PubMed]
- Gorissen, B.; Melancon, D.; Vasios, N.; Torbati, M.; Bertoldi, K. Inflatable soft jumper inspired by shell snapping. Sci. Robot. 2020, 5, eabb1967. [Google Scholar] [CrossRef] [PubMed]
- Rothemund, P.; Ainla, A.; Belding, L.; Preston, D.J.; Kurihara, S.; Suo, Z.G.; Whitesides, G.M. A soft, bistable valve for autonomous control of soft actuators. Sci. Robot. 2018, 3, eaar7986. [Google Scholar] [CrossRef] [Green Version]
- Kai, L.; Prac, D.; Gmwcd, E.; Zsa, D. Soft kink valves-ScienceDirect. J. Mech. Phys. Solids 2019, 131, 230–239. [Google Scholar]
- Yang, D.; Verma, M.S.; So, J.H.; Mosadegh, B.; Keplinger, C.; Lee, B.; Khashai, F.; Lossner, E.; Suo, Z.; Whitesides, G.M. Buckling Pneumatic Linear Actuators Inspired by Muscle. Adv. Mater. Technol. 2016, 1, 1600055. [Google Scholar] [CrossRef] [Green Version]
- Peretz, O.; Mishra, A.K.; Shepherd, R.F.; Gat, A.D. Underactuated fluidic control of a continuous multistable membrane. Proc. Natl. Acad. Sci. USA 2020, 117, 5217–5221. [Google Scholar] [CrossRef]
- Qiao, C.; Liu, L.; Pasini, D. Bi-Shell Valve for Fast Actuation of Soft Pneumatic Actuators via Shell Snapping Interaction. Adv. Sci. 2021, 8, 2100445. [Google Scholar] [CrossRef]
- Loepfe, M.; Schumacher, C.M.; Burri, C.H.; Stark, W.J. Contrast Agent Incorporation into Silicone Enables Real-Time Flow-Structure Analysis of Mammalian Vein-Inspired Soft Pumps. Adv. Funct. Mater. 2015, 25, 2129–2137. [Google Scholar] [CrossRef]
- Bartlett, N.W.; Tolley, M.T.; Overvelde, J.T.B.; Weaver, J.C.; Mosadegh, B.; Bertoldi, K.; Whitesides, G.M.; Wood, R.J. A 3D-printed, functionally graded soft robot powered by combustion. Science 2015, 349, 161–165. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Xia, C.G.; Fang, N.X. First jump of microgel; actuation speed enhancement by elastic instability. Soft Matter 2010, 6, 4342–4345. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Chi, Y.; Sun, J.; Huang, T.H.; Maghsoudi, O.H.; Spence, A.; Zhao, J.; Su, H.; Yin, J. Leveraging Elastic instabilities for Amplified Performance: Spine-inspired high-speed and high-force soft robots. Sci. Adv. 2020, 6, eaaz6912. [Google Scholar] [CrossRef] [PubMed]
- Preston, D.J.; Jiang, H.J.; Sanchez, V.; Rothemund, P.; Rawson, J.; Nemitz, M.P.; Lee, W.K.; Suo, Z.; Walsh, C.J.; Whitesides, G.M. A soft ring oscillator. Sci. Robot. 2019, 4, eaaw5496. [Google Scholar] [CrossRef] [PubMed]
- Preston, D.J.; Rothemund, P.; Jiang, H.J.; Nemitz, M.P.; Rawson, J.; Suo, Z.; Whitesides, G.M. Digital logic for soft devices. Proc. Natl. Acad. Sci. USA 2019, 116, 7750–7759. [Google Scholar] [CrossRef] [Green Version]
- Luo, K.; Rothemund, P.; Whitesides, G.M.; Suo, Z. Soft kink valves. J. Mech. Phys. Solids 2019, 131, 230–239. [Google Scholar] [CrossRef]
- Su, H.; Qi, W.; Chen, J.; Zhang, D. Fuzzy Approximation-Based Task-Space Control of Robot Manipulators With Remote Center of Motion Constraint. IEEE Trans. Fuzzy Syst. 2022, 30, 1564–1573. [Google Scholar] [CrossRef]
- Qi, W.; Aliverti, A. A Multimodal Wearable System for Continuous and Real-time Breathing Pattern Monitoring During Daily Activity. IEEE J. Biomed. Health Inform. 2020, 24, 2199–2207. [Google Scholar] [CrossRef]
- Qi, W.; Ovur, S.E.; Li, Z.; Marzullo, A.; Song, R. Multi-Sensor Guided Hand Gesture Recognition for a Teleoperated Robot Using a Recurrent Neural Network. IEEE Robot. Autom. Lett. 2021, 6, 6039–6045. [Google Scholar] [CrossRef]
- Qi, W.; Su, H. A Cybertwin based Multimodal Network for ECG Patterns Monitoring using Deep Learning. IEEE Trans. Ind. Inform. 2022, 3, 1–9. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Sun, B.; Xiong, J.; Hu, J.; Liang, Y. Bio-Design, Fabrication and Analysis of a Flexible Valve. Biomimetics 2022, 7, 95. https://doi.org/10.3390/biomimetics7030095
Liu Z, Sun B, Xiong J, Hu J, Liang Y. Bio-Design, Fabrication and Analysis of a Flexible Valve. Biomimetics. 2022; 7(3):95. https://doi.org/10.3390/biomimetics7030095
Chicago/Turabian StyleLiu, Zirui, Bo Sun, Jiawei Xiong, Jianjun Hu, and Yunhong Liang. 2022. "Bio-Design, Fabrication and Analysis of a Flexible Valve" Biomimetics 7, no. 3: 95. https://doi.org/10.3390/biomimetics7030095
APA StyleLiu, Z., Sun, B., Xiong, J., Hu, J., & Liang, Y. (2022). Bio-Design, Fabrication and Analysis of a Flexible Valve. Biomimetics, 7(3), 95. https://doi.org/10.3390/biomimetics7030095






