Thrust Improvement of a Biomimetic Robotic Fish by Using a Deformable Caudal Fin
Abstract
:1. Introduction
2. Materials and Methods
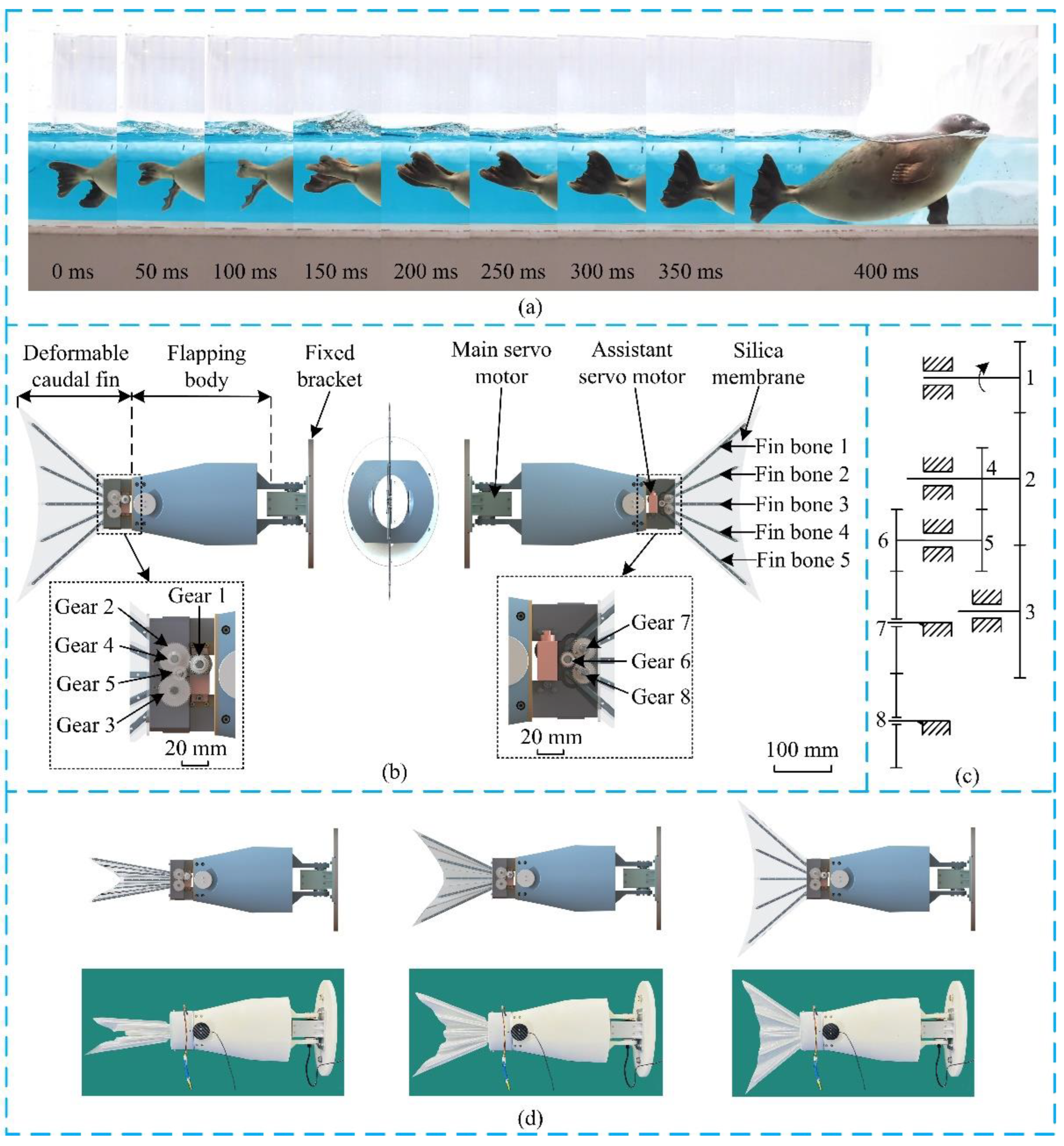
2.1. The Design of the Deformable Caudal Fin
2.2. CPG Control and Deformation Patterns
3. Experiments
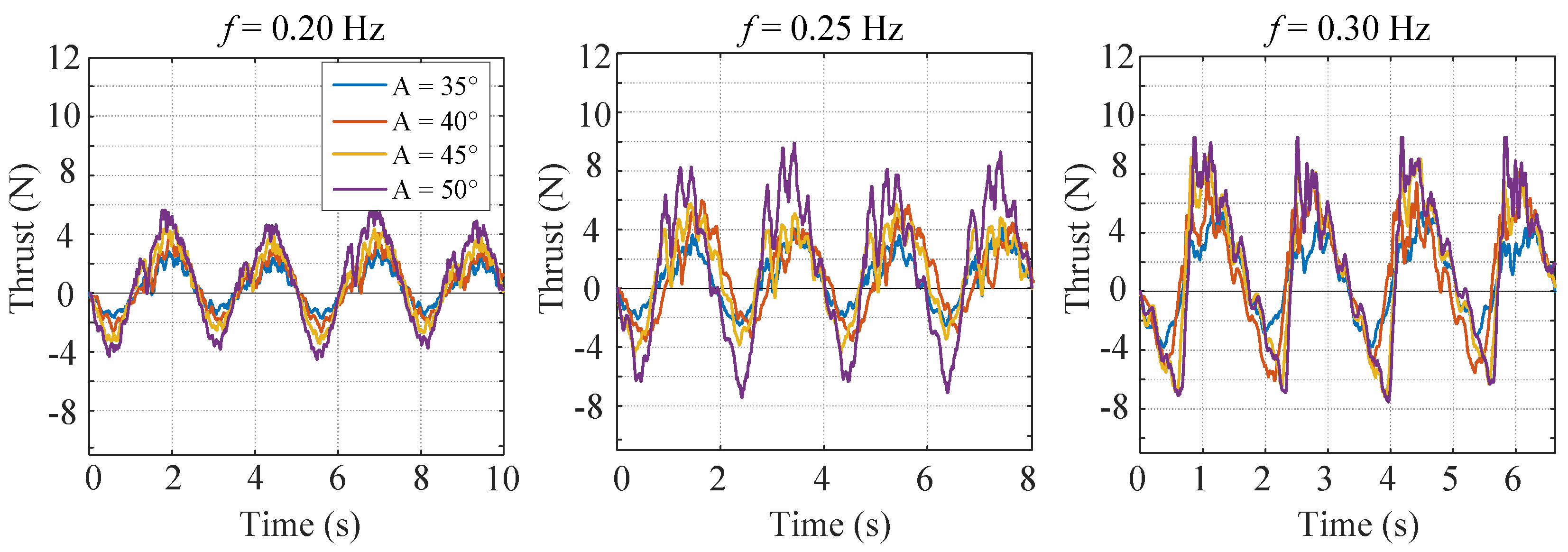
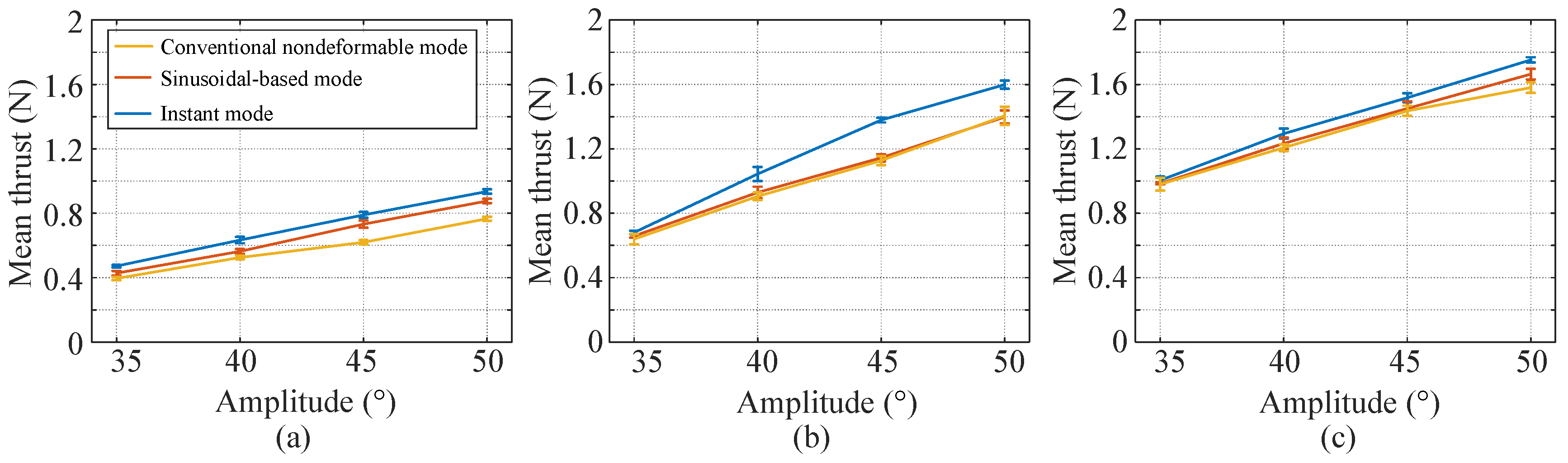
3.1. Conventional Nondeformable Mode
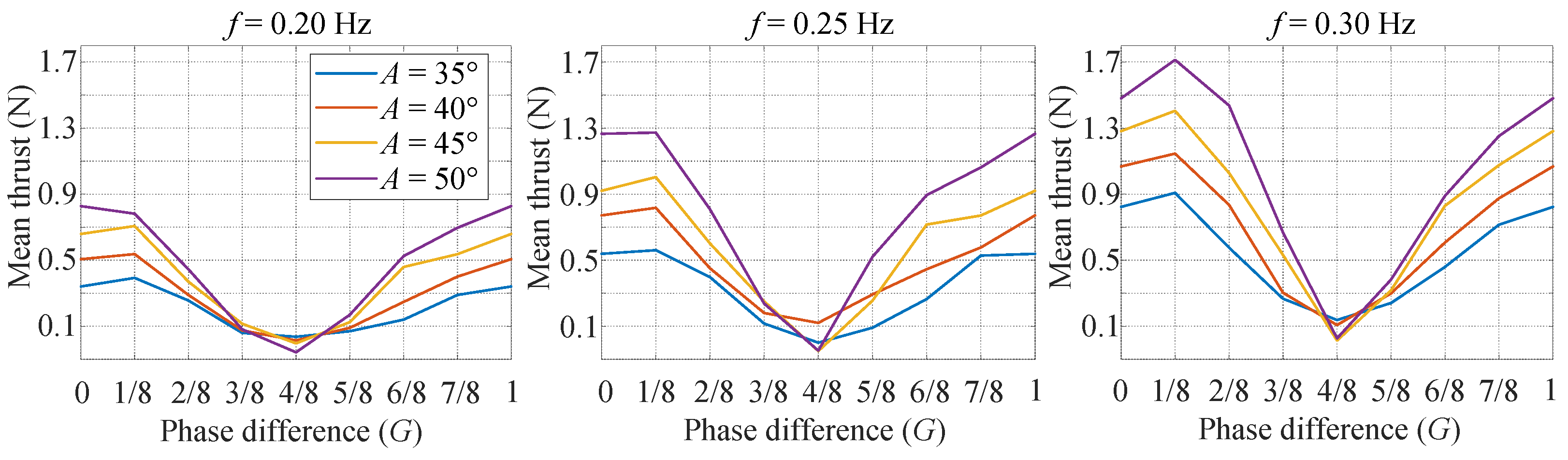
3.2. Sinusoidal-Based Mode
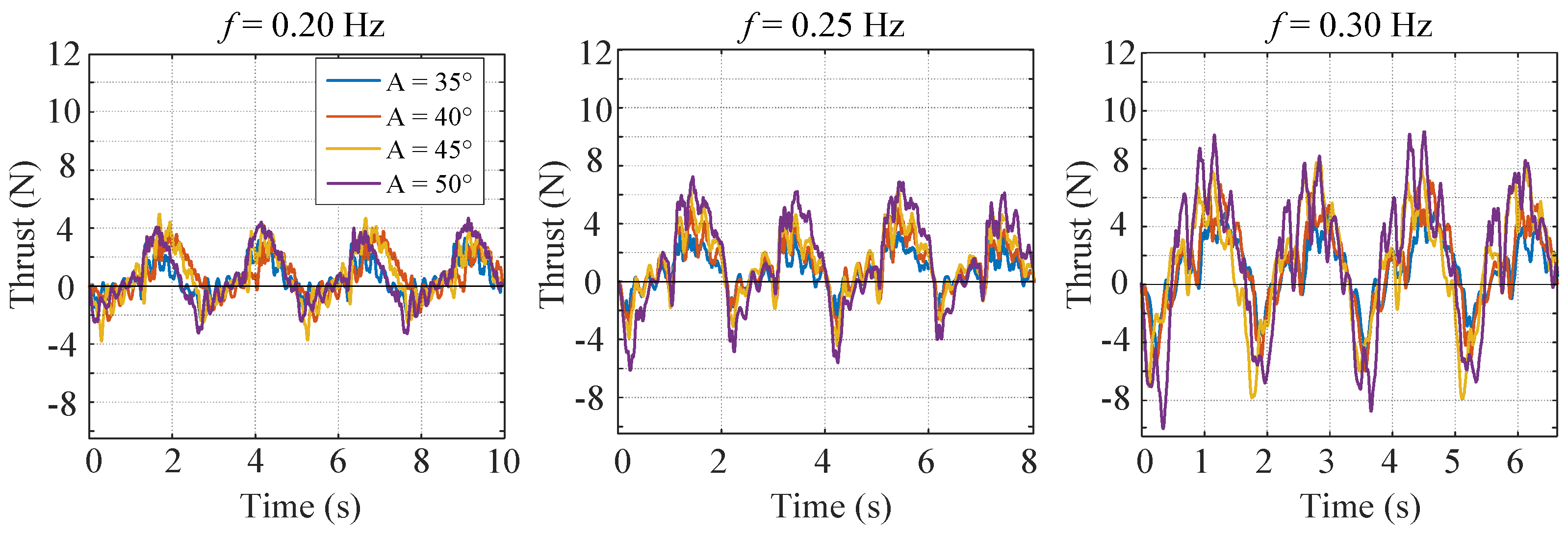
3.3. Instant Mode
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Lindsey, C.C. Form, Function, and Locomotory Habits in Fish. Fish Physiol. 1979, 71, 100. [Google Scholar]
- Webb, P.W. The biology of fish swimming. In Mechanics and Physiology of Animal Swimming; Cambridge University Press: Cambridge, UK, 1994; Volume 4562. [Google Scholar]
- Xie, F.; Li, Z.; Ding, Y.; Zhong, Y.; Du, R. An experimental study on the fish body flapping patterns by using a biomimetic robot fish. IEEE Robot. Autom. Lett. 2020, 5, 64–71. [Google Scholar] [CrossRef]
- Lighthill, M.J. Mathematical Biofluiddynamics; SIAM Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1975. [Google Scholar]
- Lighthill, M.J. Note on the swimming of slender fish. J. Fluid Mech. 1960, 9, 305–317. [Google Scholar] [CrossRef]
- Wolf, Z.; Jusufi, A.; Vogt, D.M.; Lauder, G.V. Fish-like aquatic propulsion studied using a pneumatically-actuated soft-robotic model. Bioinspir. Biomim. 2020, 15, 046008. [Google Scholar] [CrossRef]
- Lucas, K.N.; Thornycroft PJ, M.; Gemmell, B.J.; Colin, S.P.; Costello, J.H.; Lauder, G.V. Effects of non-uniform stiffness on the swimming performance of a passively-flexing, fish-like foil model. Bioinspir. Biomim. 2015, 10, 056019. [Google Scholar] [CrossRef]
- Matta, A.; Pendar, H.; Bayandor, J. A preliminary investigation of caudal fin shape effects on thrust and power of a newly designed robotic tuna. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 58066, p. V01CT21A004. [Google Scholar]
- Matta, A.; Bayandor, J.; Battaglia, F.; Pendar, H. Effects of fish caudal fin sweep angle and kinematics on thrust production during low-speed thunniform swimming. Biol. Open 2019, 8, bio040626. [Google Scholar] [CrossRef]
- Matta, A.; Pendar, H.; Battaglia, F.; Bayandor, J. Impact of caudal fin shape on thrust production of a Thunniform swimmer. J. Bionic Eng. 2020, 17, 254–269. [Google Scholar] [CrossRef]
- Zhang, X.; Su, Y.; Wang, Z. Numerical and experimental studies of influence of the caudal fin shape on the propulsion performance of a flapping caudal fin. J. Hydrodyn. Ser. B 2011, 23, 325–332. [Google Scholar] [CrossRef]
- Lin, X.; Wu, J.; Zhang, T. Effect of torsional spring and shape on the performance of bioinspired caudal fin. Phys. Fluids 2021, 33, 071903. [Google Scholar] [CrossRef]
- Krishnadas, A.; Ravichandran, S.; Rajagopal, P. Analysis of biomimetic caudal fin shapes for optimal propulsive efficiency. Ocean Eng. 2018, 153, 132–142. [Google Scholar] [CrossRef]
- Feilich, K.L.; Lauder, G.V. Passive mechanical models of fish caudal fins: Effects of shape and stiffness on self-propulsion. Bioinspir. Biomim. 2015, 10, 036002. [Google Scholar] [CrossRef]
- Chang, X.; Zhang, L.; He, X. Numerical study of the thunniform mode of fish swimming with different Reynolds number and caudal fin shape. Comput. Fluids 2012, 68, 54–70. [Google Scholar] [CrossRef]
- Low, K.H. Modelling and parametric study of modular undulating fin rays for fish robots. Mech. Mach. Theory 2009, 44, 615–632. [Google Scholar] [CrossRef]
- Lauder, G.V.; Madden, P.G.; Mittal, R.; Dong, H.; Bozkurttas, M. Locomotion with flexible propulsors: I. Experimental analysis of pectoral fin swimming in sunfish. Bioinspir. Biomim. 2006, 1, S25. [Google Scholar] [CrossRef]
- Flammang, B.E.; Lauder, G.V. Caudal fin shape modulation and control during acceleration, braking and backing maneuvers in bluegill sunfish, Lepomis macrochirus. J. Exp. Biol. 2009, 212, 277–286. [Google Scholar] [CrossRef]
- Boute, P.G.; Van Wassenbergh, S.; Stamhuis, E.J. Modulating yaw with an unstable rigid body and a course-stabilizing or steering caudal fin in the yellow boxfish (Ostracion cubicus). R. Soc. Open Sci. 2020, 7, 200129. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, H. Swimming Performance of a Tensegrity Robotic Fish. Soft Robot. 2019, 6, 520–531. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, H. Body stiffness variation of a tensegrity robotic fish using antagonistic stiffness in a kinematically singular configuration. IEEE Trans. Robot. 2021, 37, 1712–1727. [Google Scholar] [CrossRef]
- Park, Y.J.; Huh, T.M.; Park, D.; Cho, K.J. Design of a variable-stiffness flapping mechanism for maximizing the thrust of a bio-inspired underwater robot. Bioinspir. Biomim. 2014, 9, 036002. [Google Scholar] [CrossRef]
- Li, K.; Jiang, H.; Wang, S.; Yu, J. A Soft Robotic Fish with Variable-stiffness Decoupled Mechanisms. J. Bionic Eng. 2018, 15, 599–609. [Google Scholar] [CrossRef]
- Zhong, Q.; Zhu, J.; Fish, F.E.; Kerr, S.J.; Downs, A.M.; Bart-Smith, H.; Quinn, D.B. Tunable stiffness enables fast and efficient swimming in fish-like robots. Sci. Robot. 2021, 6, eabe4088. [Google Scholar] [CrossRef]
- Liu, B.; Wang, L.; Chen, B.Y.; Qin, F.H.; Zhang, S.W. Experimental Research on a Novel Design of Variable Area Caudal Fin. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Frienbach, Switzerland, 2014; Volume 461, pp. 206–212. [Google Scholar]
- Liu, B.; Yang, Y.; Qin, F.; Zhang, S. Performance study on a novel variable area robotic fin. Mechatronics 2015, 32, 59–66. [Google Scholar] [CrossRef]
- Tangorra, J.L.; Esposito, C.J.; Lauder, G.V. Biorobotic fins for investigations of fish locomotion. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 2120–2125. [Google Scholar]
- Tangorra, J.; Phelan, C.; Esposito, C.; Lauder, G. Use of Biorobotic Models of Highly Deformable Fins for Studying the Mechanics and Control of Fin Forces in Fishes. Integr. Comp. Biol. 2011, 51, 176–189. [Google Scholar] [CrossRef]
- Tangorra, J.L.; Mignano, A.P.; Carryon, G.N.; Kahn, J.C. Biologically derived models of the sunfish for experimental investigations of multi-fin swimming. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 580–587. [Google Scholar]
- Yang, Y.; Xia, Y.; Qin, F.; Xu, M.; Li, W.; Zhang, S. Development of a bio-inspired transformable robotic fin. Bioinspir. Biomim. 2016, 11, 056010. [Google Scholar] [CrossRef]
- Tang, Y.; Qin, L.; Li, X.; Chew, C.M.; Zhu, J. A frog-inspired swimming robot based on dielectric elastomer actuators. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 2403–2408. [Google Scholar]
- Pandey, J.; Reddy, N.S.; Ray, R.; Shome, S.N. Biological swimming mechanism analysis and design of robotic frog. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013; pp. 1726–1731. [Google Scholar]
- Liu, A.; Zhao, J.; Li, L.; Xie, G. Micro-force measuring apparatus for robotic fish: Design, implementation and application. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 4938–4943. [Google Scholar] [CrossRef]
- Wen, L.; Wang, T.; Wu, G.; Liang, J. Quantitative thrust efficiency of a self-propulsive robotic fish: Experimental method and hydrodynamic investigation. IEEE/ASME Trans. Mechatron. 2013, 18, 1027–1038. [Google Scholar] [CrossRef]
- Available online: https://www.youtube.com/watch?v=psQoHobrprk (accessed on 13 July 2022).
- Ijspeert, A.J.; Crespi, A.; Ryczko, D.; Cabelguen, J. From swimming to walking with a salamander robot driven by a spinal cord model. Science 2007, 315, 1416–1420. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Crespi, A. Online trajectory generation in an amphibious snake robot using a lamprey-like central pattern generator model. In Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 262–268. [Google Scholar]
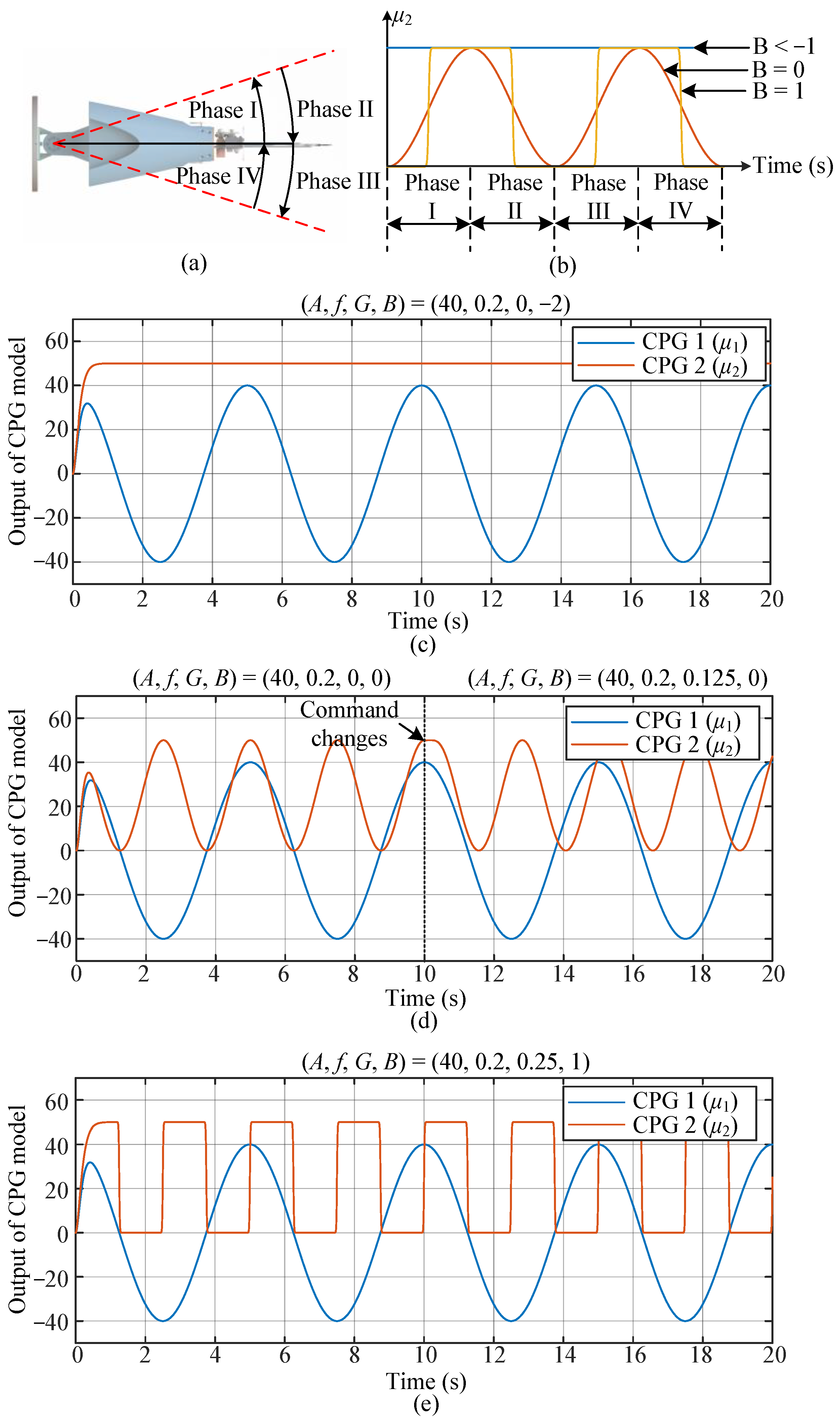


| (A, f, G, B) | Deformation patterns |
| (A, f, 0, −2) | Conventional nondeformable mode |
| (A, f, G, 0) | Sinusoidal-based mode |
| (A, f, 0.25, 25) | Instant mode |
| A | f | G | B |
|---|---|---|---|
| 35°, 40°, 45°, 50° | 0.20 Hz | 0 | −2 |
| 35°, 40°, 45°, 50° | 0.25 Hz | ||
| 35°, 40°, 45°, 50° | 0.30 Hz |
| A | f | G | B |
|---|---|---|---|
| 35°, 40°, 45°, 50° | 0.20 Hz | 0, 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8 | 0 |
| 35°, 40°, 45°, 50° | 0.25 Hz | ||
| 35°, 40°, 45°, 50° | 0.30 Hz |
| A | f | G | B |
|---|---|---|---|
| 35°, 40°, 45°, 50° | 0.20 Hz | 0.25 | 25 |
| 35°, 40°, 45°, 50° | 0.25 Hz | ||
| 35°, 40°, 45°, 50° | 0.30 Hz |
| f | A | |||
|---|---|---|---|---|
| 35° | 40° | 45° | 50° | |
| 0.20 Hz | 8.3% | 7.2% | 18.2% | 14.4% |
| 0.25 Hz | 3.0% | 2.6% | 1.6% | −0.5% |
| 0.30 Hz | 0.5% | 2.2% | 1.0% | 5.3% |
| f | A | |||
|---|---|---|---|---|
| 35° | 40° | 45° | 50° | |
| 0.20 Hz | 19.4% | 20.6% | 27.5% | 22.1% |
| 0.25 Hz | 6.4% | 15.3% | 22.3% | 13.8% |
| 0.30 Hz | 2.4% | 7.2% | 5.7% | 10.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, H.; Dong, B.; Zheng, C.; Li, T.; Zuo, Q.; Xu, Y.; Fang, H.; He, K.; Xie, F. Thrust Improvement of a Biomimetic Robotic Fish by Using a Deformable Caudal Fin. Biomimetics 2022, 7, 113. https://doi.org/10.3390/biomimetics7030113
Shao H, Dong B, Zheng C, Li T, Zuo Q, Xu Y, Fang H, He K, Xie F. Thrust Improvement of a Biomimetic Robotic Fish by Using a Deformable Caudal Fin. Biomimetics. 2022; 7(3):113. https://doi.org/10.3390/biomimetics7030113
Chicago/Turabian StyleShao, Hua, Bingbing Dong, Changzhen Zheng, Te Li, Qiyang Zuo, Yaohui Xu, Haitao Fang, Kai He, and Fengran Xie. 2022. "Thrust Improvement of a Biomimetic Robotic Fish by Using a Deformable Caudal Fin" Biomimetics 7, no. 3: 113. https://doi.org/10.3390/biomimetics7030113
APA StyleShao, H., Dong, B., Zheng, C., Li, T., Zuo, Q., Xu, Y., Fang, H., He, K., & Xie, F. (2022). Thrust Improvement of a Biomimetic Robotic Fish by Using a Deformable Caudal Fin. Biomimetics, 7(3), 113. https://doi.org/10.3390/biomimetics7030113






