Research on the Adhesive Performance of a Biomimetic Goat Hoof Track Shoe Pattern
Abstract
:1. Introduction
2. Materials and Methods
2.1. Bionic Structure Design
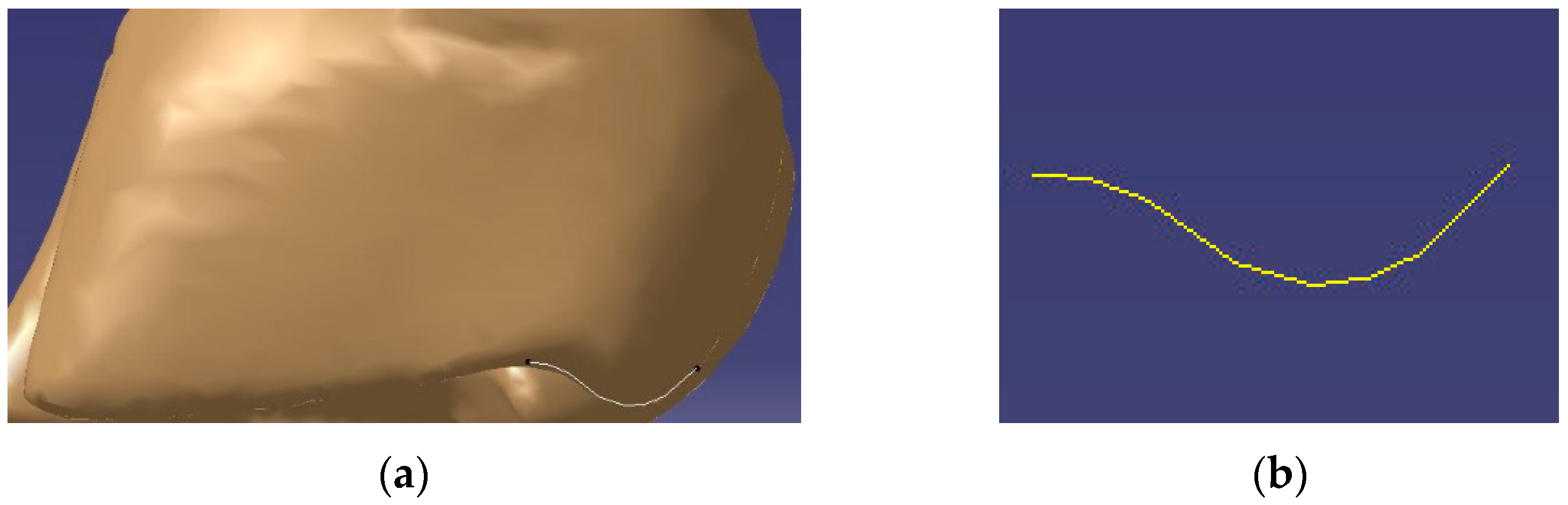
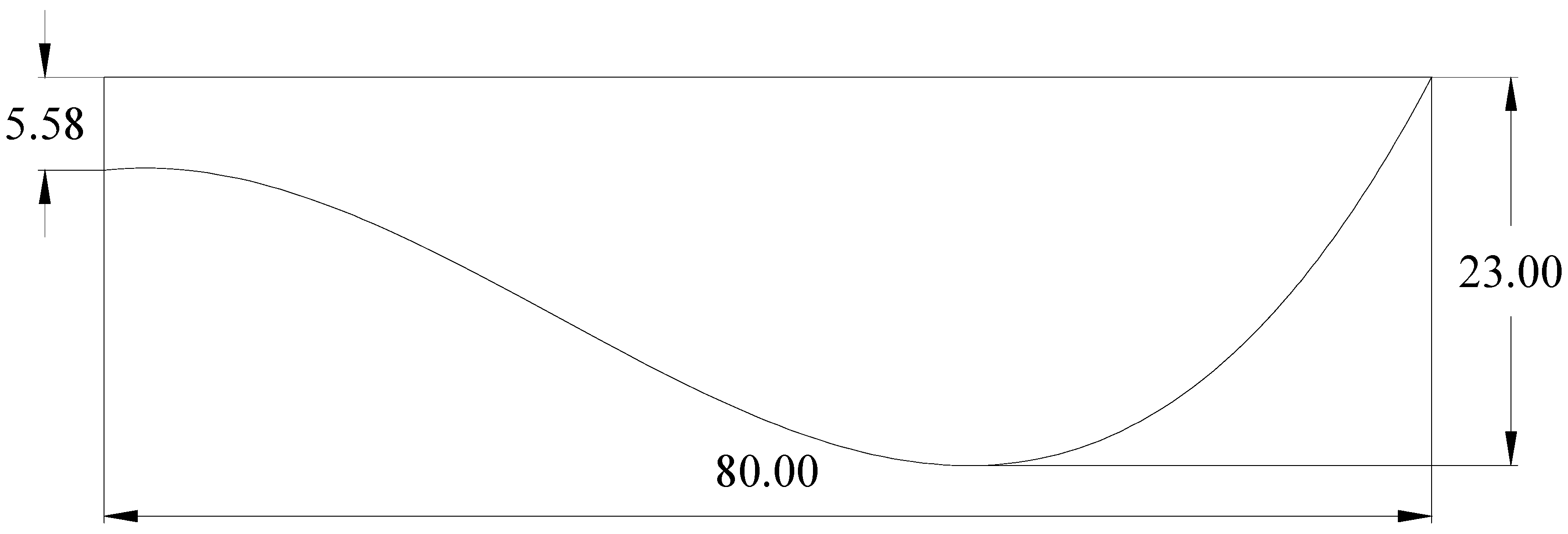
2.1.1. Macro Contour Extraction
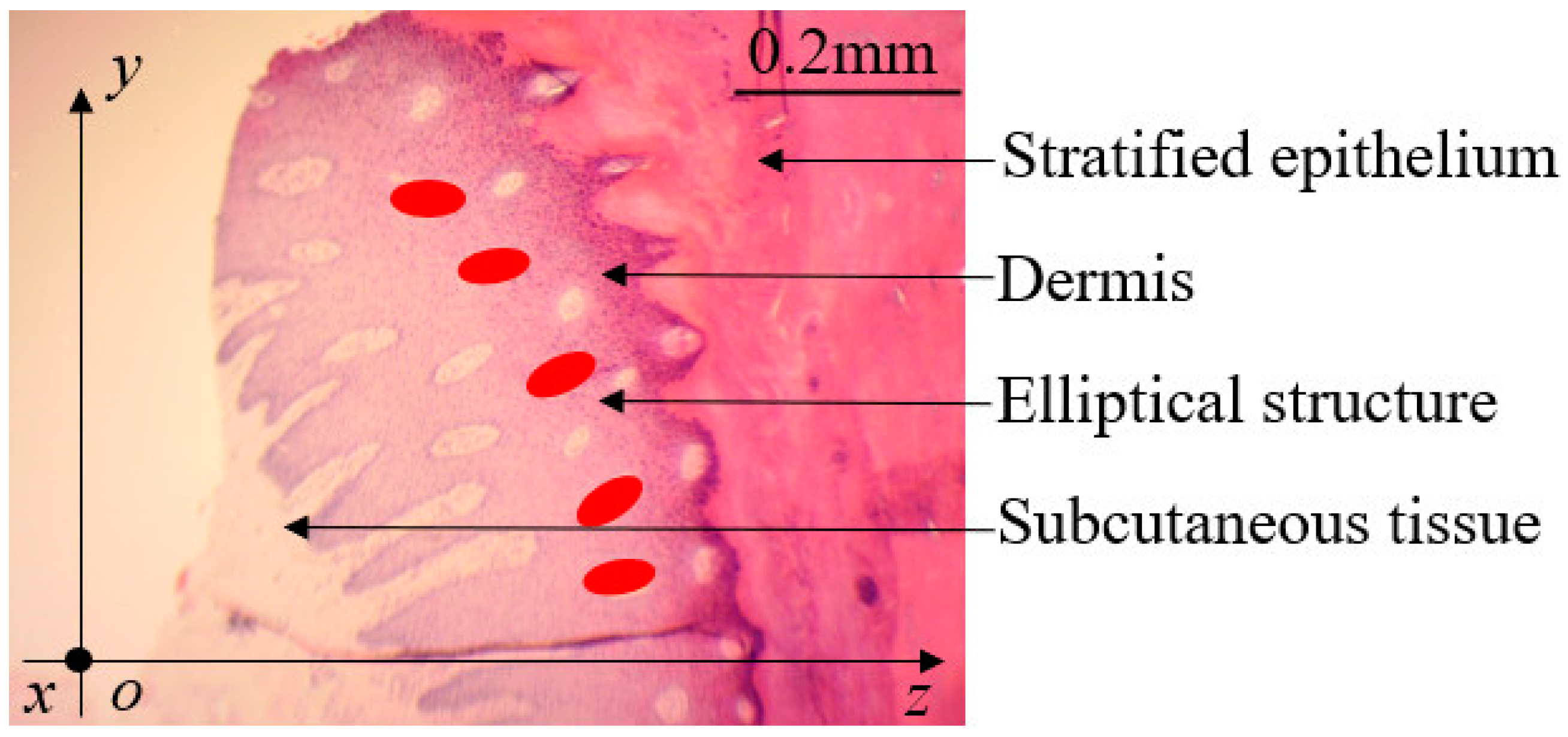
2.1.2. Observation on Tissue Structure of the Goat Hoof Ball
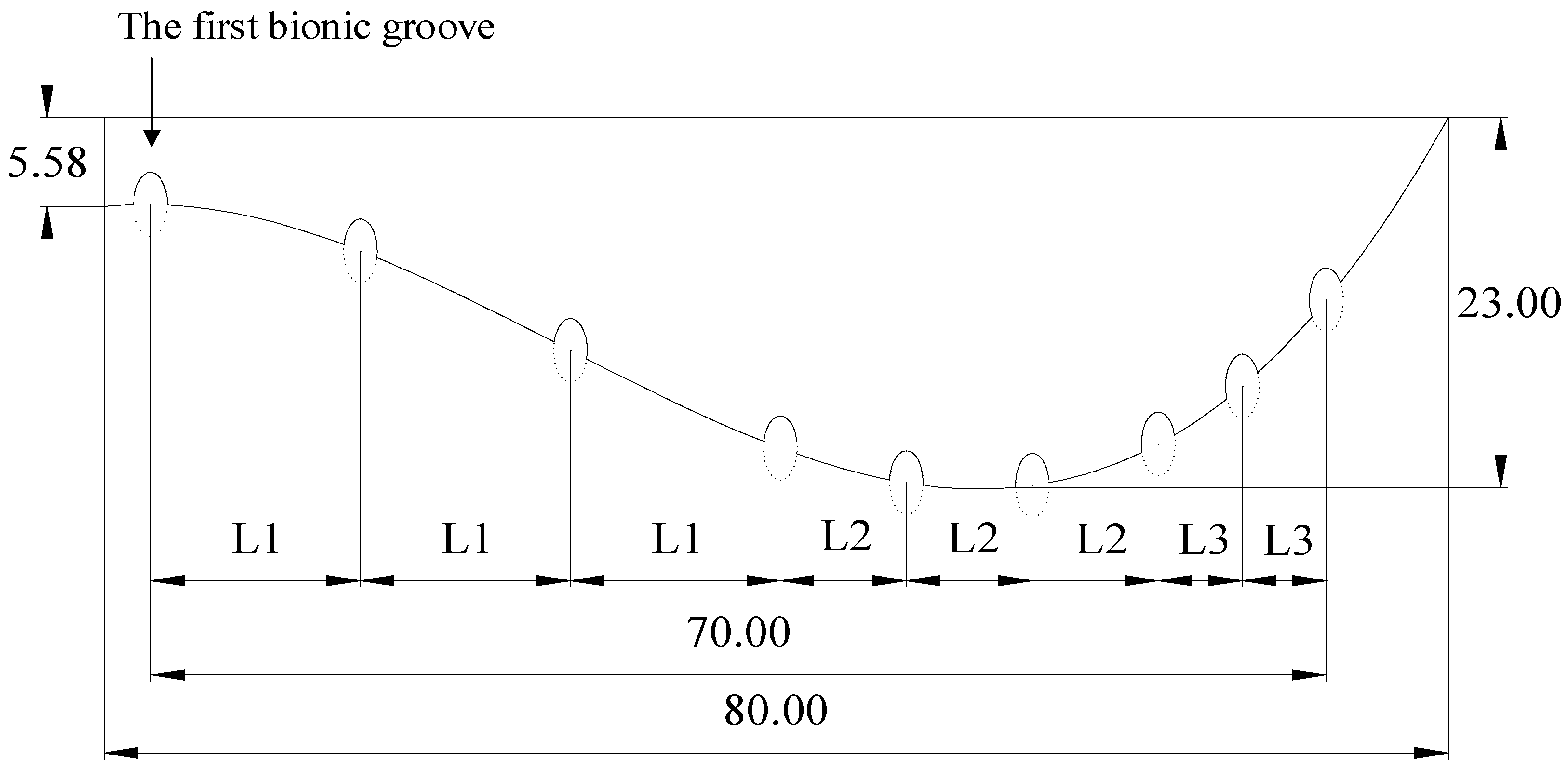
2.1.3. Structure Design of Bionic Track Shoe Pattern
2.1.4. Overall Structure Design of Bionic Track Shoe
2.2. Soil Parameters Measurement
2.2.1. Moisture Content and Density
2.2.2. Poisson’s Ratio
2.2.3. Elastic Modulus
2.3. Soil Repose Angle Test
2.3.1. Measurement Results of Soil Repose Angle
2.3.2. Simulation and Calibration of Soil Parameters
2.4. Contact Model
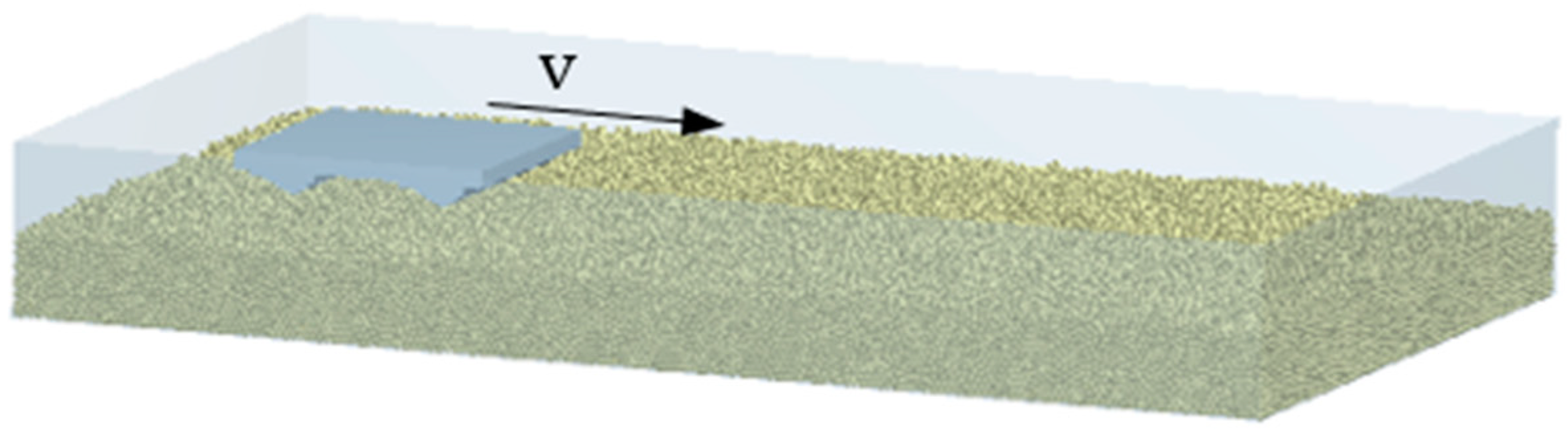
2.5. Establishment of Simulation System
- (1)
- The track plate model was set to fall into the soil particle bed at the speed of 8 mm/s until the track pattern was completely submerged into the particle bed.
- (2)
- After resting for a period of time, the track plate was set to move horizontally at the speed of 8 mm/s.
2.6. Preparation of Track Shoe
2.7. Soil Bin Test
3. Results and Discussion
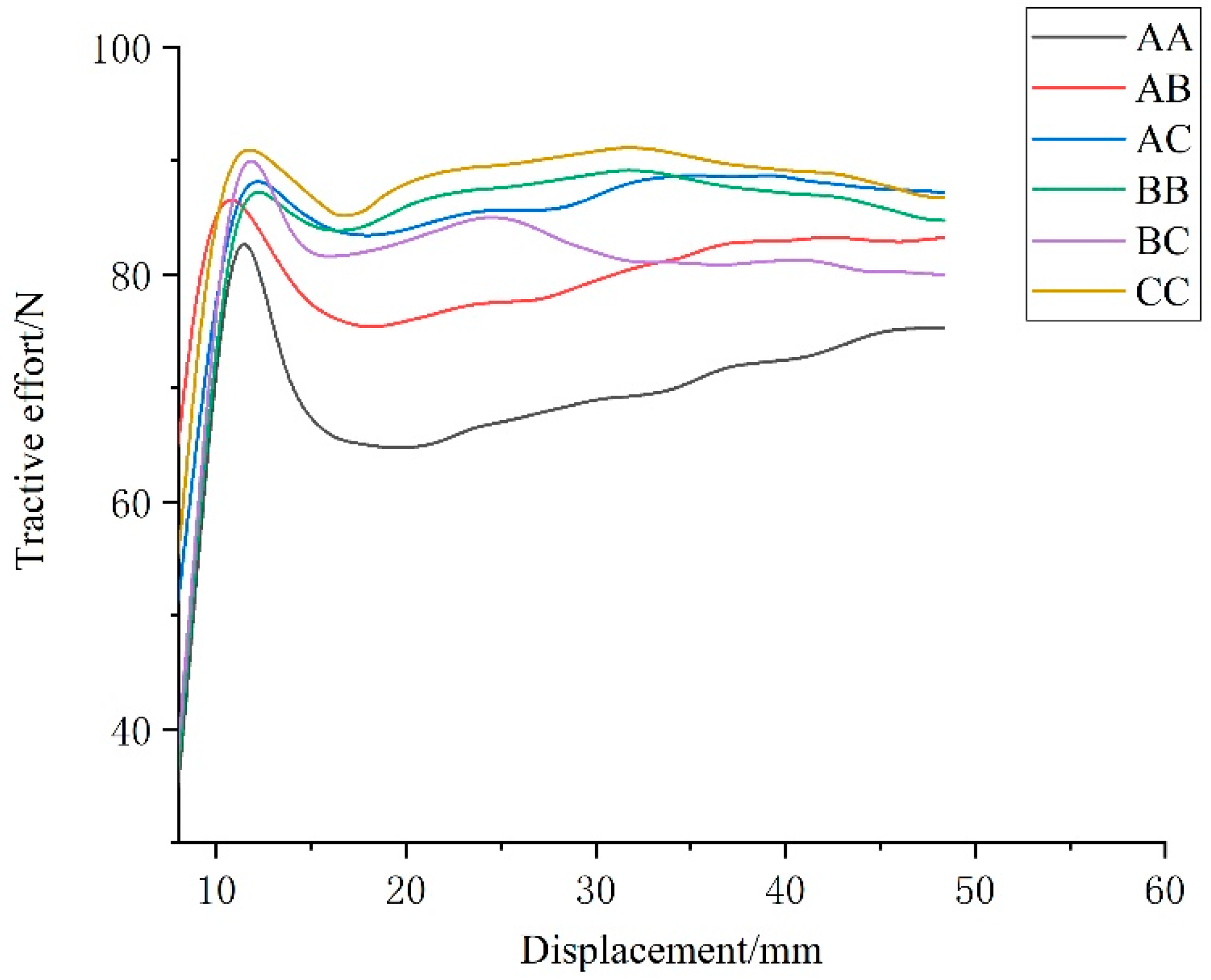
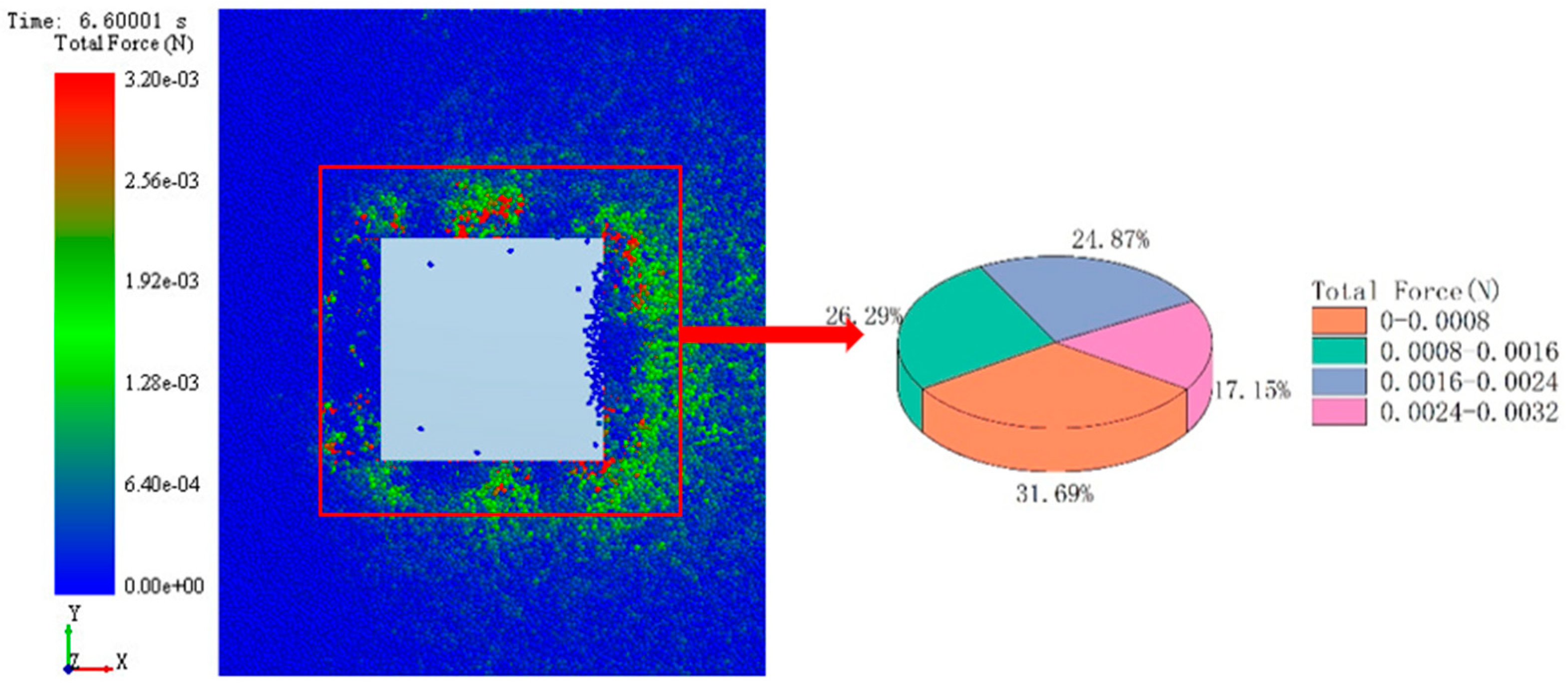
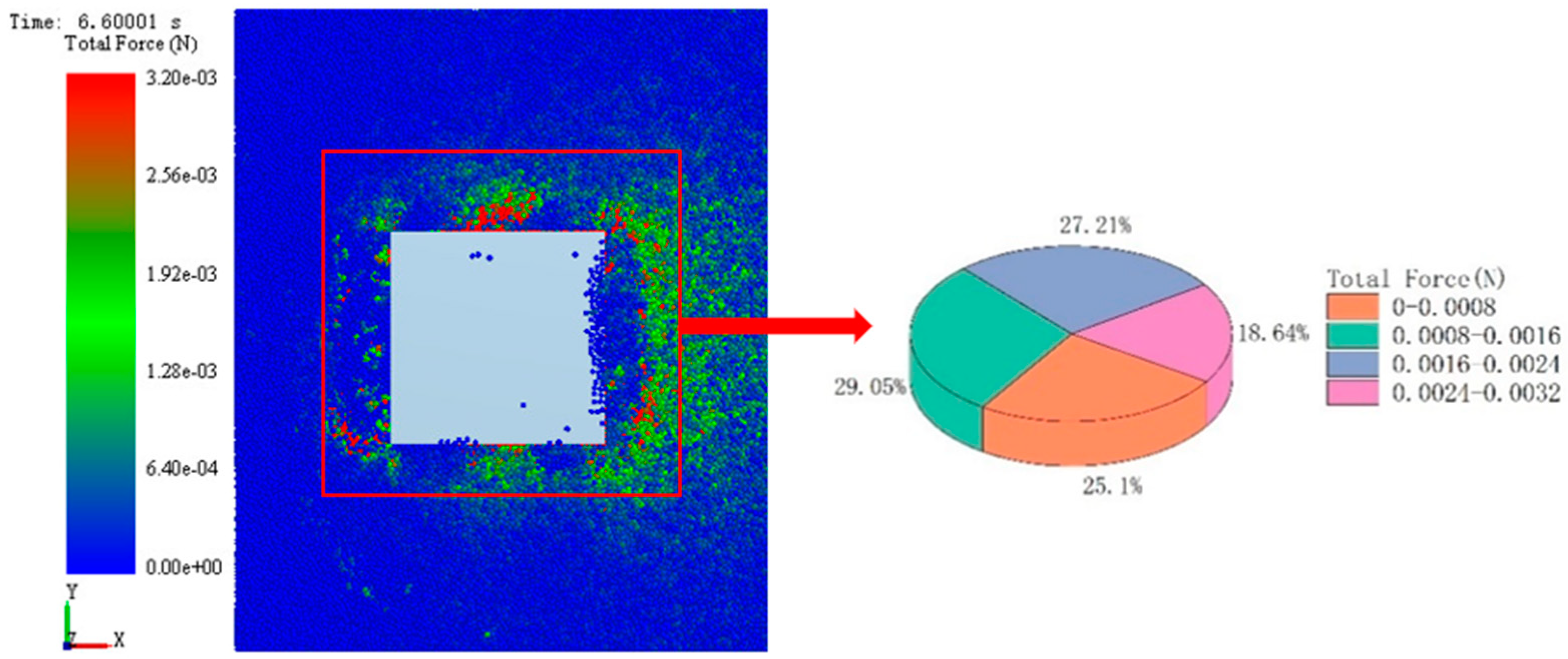
3.1. Numerical Analysis of Simulation Results
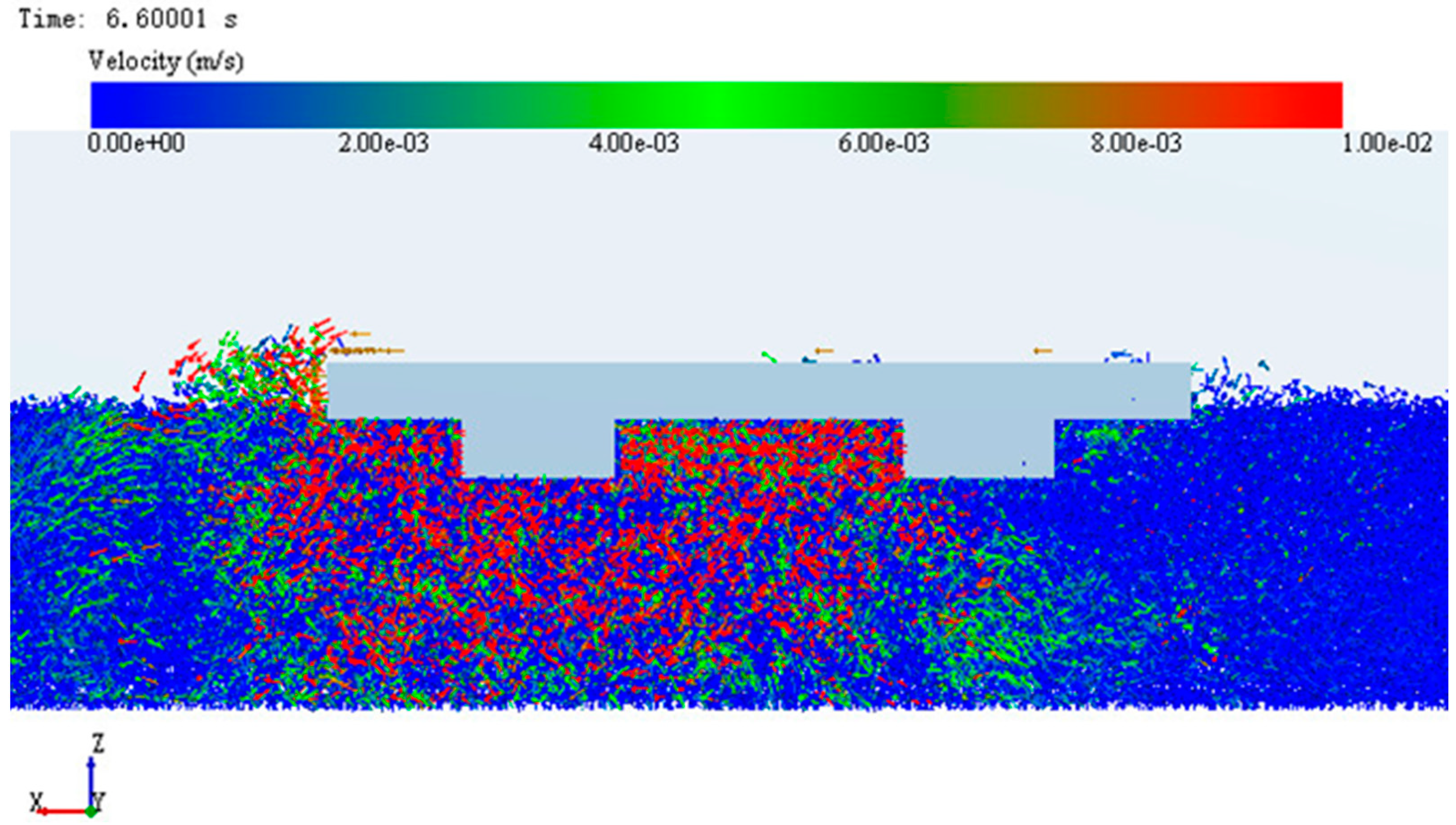
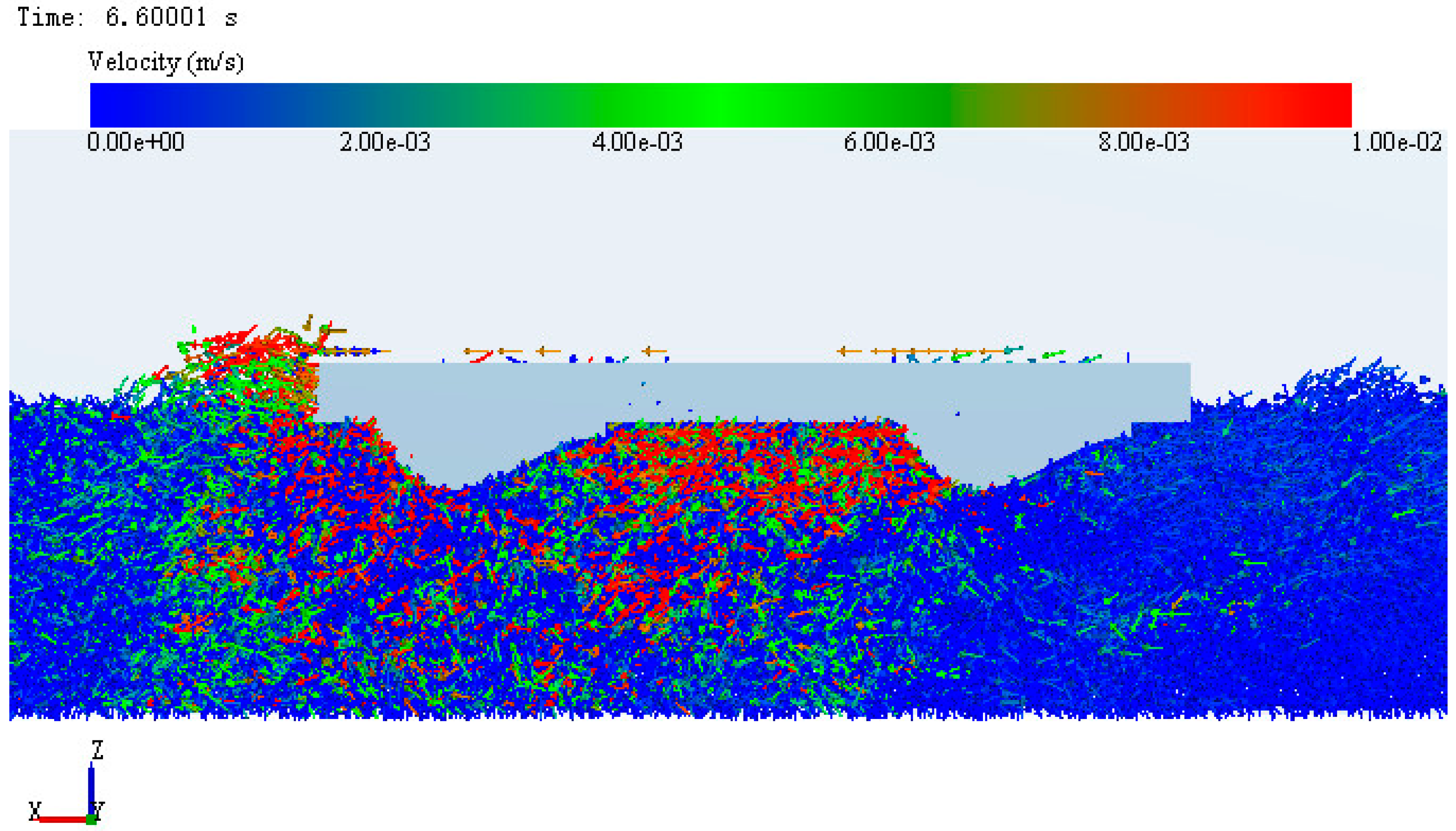
3.2. Microanalysis of Simulation System Based on EDEM
3.3. Comparative Analysis of Simulation and Test Results
4. Discussion
5. Conclusions
- (1)
- The contour curve of the goat hoof ball ridge line was extracted, and its mathematical model was constructed. Combined with the structure of hoof ball, bionic groove was designed, and based on both, the single structure of the goat hoof track pattern was designed.
- (2)
- The soil moisture content, density, Poisson’s ratio, elastic modulus and other parameters were measured. Taking the measured results for the soil stacking angle as the optimization target value, the Box-Behnken optimization method was used to obtain the optimal combination results for the soil contact parameters: recovery coefficient (0.63), static friction coefficient (0.2) and rolling friction coefficient (0.3), and the track shoe–soil simulation system was built.
- (3)
- Compared with the ordinary straight track pattern, the designed mountain-like sheep hoof track pattern has strong adhesion. The EDEM verification experiment showed that the change in the simulation value of the established track shoe-soil model is consistent with the trend of the experimental value, with the maximum error of 10.3%, which proves the reliability of the simulation model, and the adhesion performance of bionic track shoe is improved by 9.1% compared with that of conventional track shoe.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, Y.; Gai, J.T.; Han, Z.D.; Xue, T.Y.; Zeng, G. Study on electric vehicle steering kinematics considered tracks’ skid and slip. Veh. Power Technol. 2017, 1, 6–10. [Google Scholar]
- Fang, Y.; Zhang, Y.N.; Shang, Y.H.; Huang, T.; Yan, M.F. Center-point steering analysis of tracked omni-vehicles based on skid conditions. Mech. Sci. 2021, 12, 511–527. [Google Scholar] [CrossRef]
- Li, J.Z.; Liu, S.J.; Dai, Y. Effect of grouser height on tractive performance of tracked mining vehicle. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2459–2466. [Google Scholar] [CrossRef]
- He, J.; Wu, D.L.; Ma, J.S.; Wang, H.K.; Yang, Y.L. The influence law of grouser shape on soil slide sinkage when tracked vehicle travels on soft road. J. Multi-Body Dyn. 2019, 234, 225–237. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Yang, Z.F.; Liu, S. Research of the micro-crawler tractor adhesion performance-based on orthogonal experiment. J. Agric. Mech. Res. 2013, 35, 190–193,198. [Google Scholar]
- Wu, H.Y.; Chen, X.M.; Liu, S.J.; Gao, Y.Q.; Chen, B.Z. Influence of soft sediment adhered to track on adhesion performance of seabed track vehicle. Trans. Chin. Soc. Agric. Eng. 2010, 26, 140–145. [Google Scholar]
- Du, Y.H.; Gao, J.W.; Jiang, L.H. Numerical analysis on the adhesion property of rigid track on the soft ground with low moisture by discrete element method. Chin. J. Comput. Mech. 2017, 34, 384–389. [Google Scholar]
- Sun, Y.H.; Hao, Y.; Shi, X.F.; Li, H. Analysis of grouser dimension for vehicle mobility performance. J. Ordnance Equip. Eng. 2014, 35, 9–11. [Google Scholar]
- Cai, Q.; Ma, W.B.; Rao, Q.H.; Li, G.X. Optimization design of bionic grousers for the crawled mineral collector based on the deep-sea sediment. Mar. Georesour. Geotechnol. 2020, 38, 48–56. [Google Scholar]
- Ge, J.; Wang, X.L.; Kito, K.; Nakashima, H. Effect of grouser height on tractive performance of single grouser shoe under different moisture contents soil. Int. J. Eng. Technol. 2015, 7, 1414–1423. [Google Scholar]
- Ge, J.; Wang, X.L.; Kito, K. Comparing tractive performance of steel and rubber single grouser shoe under different soil moisture contents. Int. J. Agric. Biol. Eng. 2016, 9, 11–20. [Google Scholar]
- Fu, J.; Li, J.; Tang, X.L.; Wang, R.X.; Chen, Z. Optimization of structure parameters of the grouser shoes for adhesion reduction under black soil. Agriculture 2021, 11, 795. [Google Scholar] [CrossRef]
- Li, Y.; He, D.C.; Si, Q.R.; Meng, X.P. Effect of track shoes structural parameters on traction performance of unmanned underwater tracked bulldozer. Ocean Eng. 2021, 237, 109655. [Google Scholar] [CrossRef]
- Xu, F.; Rao, Q.H.; Ma, W.B. Track shoe structure optimization of deep-sea mining vehicle based on new rheological calculation formulae of sediment. Mech. Based Des. Struct. Mach. 2019, 47, 479–496. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, Y.F.; Teng, S.; Zheng, L.M.; Wang, J.J.; Chen, Z.J. Development of agricultural bionic four-legged robot: Effect of head movement adjustment on the stability of goats. Int. J. Agric. Biol. Eng. 2019, 12, 10–15. [Google Scholar] [CrossRef]
- Zhang, F.; Zheng, L.M.; Wang, W.; Wang, Y.F.; Wang, J.J. Development of agricultural bionic mechanisms: Investigation of the effect of joint angle and pressure on the stability of goats moving on sloping lands. Int. J. Agric. Biol. Eng. 2018, 11, 35–41. [Google Scholar] [CrossRef] [Green Version]
- Abad, S.A.; Sornkarn, N.S.; Nanayakkara, T. The role of morphological computation of the goat hoof in slip reduction. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 5599–5605. [Google Scholar]
- Abad, S.A.; Herzig, N.; Sadati, S.M.H.; Nanayakkara, T. Significance of the compliance of the joints on the dynamic slip resistance of a bioinspired hoof. IEEE Trans. Robot. 2019, 35, 1450–1463. [Google Scholar] [CrossRef] [Green Version]
- Kui, H.L.; Liu, X.Y.; Liu, J.; Liang, W.; Liu, J.; Zhang, S.W.; Qian, Z.H.; Ren, L. The Passive contact stability of blue sheep hoof based on structure, mechanical properties, and surface morphology. Front. Bioeng. Biotechnol. 2020, 8, 1–16. [Google Scholar] [CrossRef]
- Tian, W.J.; Wang, J.Y.; Li, M.; Cong, Q. Design and optimization of vibration reduction structure imitating pore structure in goat capsula ungulae. J. Vib. Eng. 2018, 31, 352–357. [Google Scholar]
- Wang, X.L.; Hu, H.; Wang, Q.J.; Li, H.W.; He, J.; Chen, W.Z. Calibration method of soil contact characteristic parameters based on DEM theory. Trans. Chin. Soc. Agric. Eng. 2017, 48, 78–85. [Google Scholar]
- Wang, Y.X.; Liang, Z.J.; Zhang, D.X.; Cui, T.; Shi, S.; Li, K.H.; Yang, L. Calibration method of contact characteristic parameters for corn seeds based on EDEM. Trans. Chin. Soc. Agric. Eng. 2016, 32, 36–42. [Google Scholar]
- Hao, J.J.; Wei, W.B.; Huang, P.C.; Qin, J.H.; Zhao, J.G. Calibration and experimental verification of discrete element parameters of oil sunflower seeds. Trans. Chin. Soc. Agric. Eng. 2021, 37, 36–44. [Google Scholar]
- Wang, X.L.; Zhong, X.K.; Geng, Y.L.; Wei, Z.C.; Hu, H.; Geng, D.Y.; Zhang, X.C. Construction and parameter calibration of the nonlinear elastoplastic discrete element model for no-tillage soil compaction. Trans. Chin. Soc. Agric. Eng. 2021, 37, 100–107. [Google Scholar]
- Xing, J.J.; Zhang, R.; Wu, P.; Zhang, X.R.; Dong, X.H.; Chen, Y.; Ru, S.F. Parameter calibration of discrete element simulation model for latosol particles in hot areas of Hainan Province. Trans. Chin. Soc. Agric. Eng. 2020, 36, 158–166. [Google Scholar]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1971, 324, 301–313. [Google Scholar]
- Wang, X.Z.; Yue, B.; Gao, X.J.; Zheng, Z.Q.; Zhu, R.X.; Huang, Y.X. Discrete element simulations and experiments of disturbance behavior as affected by mounting height of subsoiler’s wing. Trans. Chin. Soc. Agric. Mach. 2018, 49, 124–136. [Google Scholar]
- Xiong, P.Y.; Yang, Z.; Sun, Z.Q.; Zhang, Q.Q.; Huang, Y.Q.; Zhang, Z.W. Simulation analysis and experiment for three-axis working resistances of rotary blade based on discrete element method. Trans. Chin. Soc. Agric. Eng. 2018, 34, 113–121. [Google Scholar]
- Ding, Q.S.; Ren, J.; Belal, E.A.; Zhao, J.K.; Ge, S.Y.; Li, Y. DEM analysis of subsoiling process in wet clayey paddy soil. Trans. Chin. Soc. Agric. Mach. 2017, 48, 38–48. [Google Scholar]
- Li, B.; Liu, F.Y.; Mu, J.Y.; Chen, J.; Han, W.T. Distinct element method analysis and field experiment of soil resistance applied on the subsoiler. Int. J. Agric. Biol. Eng. 2014, 7, 54–59. [Google Scholar]
- Zheng, K.; He, J.; Li, H.W.; Diao, P.S.; Wang, Q.J.; Zhao, H.B. Research on polyline soil-breaking blade subsoiler based on subsoiling soil model using discrete element method. Trans. Chin. Soc. Agric. Mach. 2016, 47, 60–67. [Google Scholar]






| Category | Code | Length × Width × Height (mm) |
|---|---|---|
| Ordinary I-shaped track shoe pattern | A | 300 × 51 × 23 |
| Biomimetic goat hoof track shoe pattern | B | 300 × 80 × 23 |
| Biomimetic goat hoof treads pattern with grooves | C | 300 × 80 × 23 |
| Number | Combination Scheme | Schematic Diagram |
|---|---|---|
| 1 | AA |  |
| 2 | AB |  |
| 3 | AC |  |
| 4 | BB |  |
| 5 | BC |  |
| 6 | CC |  |
| Code | Factor | ||
|---|---|---|---|
| Recovery Coefficient between Soil and Soil A | Dynamic Friction Coefficient between Soil and Soil B | Static Friction Coefficient between Soil and Soil C | |
| −1 | 0.15 | 0 | 0.20 |
| 0 | 0.45 | 0.10 | 0.26 |
| 1 | 0.75 | 0.20 | 0.32 |
| Number | Factor | Repose Angle/(°) | ||
|---|---|---|---|---|
| A | B | C | ||
| 1 | 0 | −1 | −1 | 23.8 |
| 2 | 1 | 1 | 0 | 24.6 |
| 3 | 0 | 0 | 1 | 24.1 |
| 4 | 0 | 0 | 0 | 29.1 |
| 5 | 0 | 0 | 0 | 28.9 |
| 6 | −1 | 0 | 1 | 6.9 |
| 7 | 0 | −1 | 1 | 24.5 |
| 8 | 0 | 1 | −1 | 29.3 |
| 9 | −1 | −1 | 0 | 7.1 |
| 10 | 0 | 0 | 0 | 24.1 |
| 11 | 0 | 1 | 1 | 24.2 |
| 12 | 1 | 0 | −1 | 25.4 |
| 13 | 0 | 0 | 0 | 25.1 |
| 14 | 1 | −1 | 0 | 24.5 |
| 15 | −1 | 1 | 0 | 7 |
| 16 | −1 | 0 | −1 | 6.7 |
| 17 | 1 | 0 | 1 | 25.4 |
| Variance Source | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| model | 1086.56 | 9 | 120.73 | 26.13 | 0.0001 * |
| A | 651.61 | 1 | 651.61 | 141.03 | <0.0001 ** |
| B | 3.38 | 1 | 3.38 | 0.7316 | 0.4207 |
| C | 2.21 | 1 | 2.21 | 0.4772 | 0.5119 |
| AB | 0.0100 | 1 | 0.0100 | 0.0022 | 0.9642 |
| AC | 0.0100 | 1 | 0.0100 | 0.0022 | 0.9642 |
| BC | 8.41 | 1 | 8.41 | 1.82 | 0.2193 |
| A2 | 413.09 | 1 | 413.09 | 89.41 | <0.0001 ** |
| B2 | 1.30 | 1 | 1.30 | 0.2807 | 0.6126 |
| C2 | 0.2738 | 1 | 0.2738 | 0.0593 | 0.8147 |
| Residual | 32.34 | 7 | 4.62 | ||
| Lack of Fit | 6.63 | 3 | 2.21 | 0.3438 | 0.7965 |
| Pure Error | 25.71 | 4 | 6.43 | ||
| Cor Total | 1118.90 | 16 |
| Material Parameters | Value | Contact Parameter | Value |
|---|---|---|---|
| Soil density (kg/m3) | 1330 | Recovery coefficient between soil and soil | 0.63 |
| Rubber density (kg/m3) | 960 | Dynamic friction coefficient between soil and soil | 0.2 |
| Soil Poisson’s ratio | 0.33 | Static friction coefficient between soil and soil | 0.3 |
| Rubber Poisson’s ratio | 0.45 | Recovery coefficient between soil and rubber | 0.61 |
| Soil elastic modulus (Pa) | 1 × 107 | Dynamic friction coefficient between soil and rubber | 0.23 |
| Elastic modulus of rubber (Pa) | 3448 | Static friction coefficient between soil and rubber | 0.48 |
| Number | Scheme | Mass (Kg) | Adhesive Force (N) | Rate of Increase/% |
|---|---|---|---|---|
| 1 | AA | 7.18 | 83.6 | — |
| 2 | AB | 7.15 | 86.9 | 3.9 |
| 3 | AC | 7.10 | 88.7 | 6.1 |
| 4 | BB | 7.21 | 89.2 | 6.7 |
| 5 | BC | 7.19 | 90.5 | 8.3 |
| 6 | CC | 7.13 | 91.2 | 9.1 |
| Number | Scheme | Result of Simulation/N | Result of Soil Bin Test/N | Error/% |
|---|---|---|---|---|
| 1 | AA | 83.6 | 75.8 | 10.3 |
| 2 | AB | 86.9 | 80.1 | 8.6 |
| 3 | AC | 88.7 | 83.7 | 6.0 |
| 4 | BB | 89.2 | 84.2 | 6.0 |
| 5 | BC | 90.5 | 83.9 | 7.9 |
| 6 | CC | 91.2 | 85.9 | 6.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Zhang, C.; Teng, S.; Cui, X.; Ali, S.; Wang, X. Research on the Adhesive Performance of a Biomimetic Goat Hoof Track Shoe Pattern. Biomimetics 2022, 7, 80. https://doi.org/10.3390/biomimetics7020080
Zhang F, Zhang C, Teng S, Cui X, Ali S, Wang X. Research on the Adhesive Performance of a Biomimetic Goat Hoof Track Shoe Pattern. Biomimetics. 2022; 7(2):80. https://doi.org/10.3390/biomimetics7020080
Chicago/Turabian StyleZhang, Fu, Chaochen Zhang, Shuai Teng, Xiahua Cui, Shaukat Ali, and Xinyue Wang. 2022. "Research on the Adhesive Performance of a Biomimetic Goat Hoof Track Shoe Pattern" Biomimetics 7, no. 2: 80. https://doi.org/10.3390/biomimetics7020080
APA StyleZhang, F., Zhang, C., Teng, S., Cui, X., Ali, S., & Wang, X. (2022). Research on the Adhesive Performance of a Biomimetic Goat Hoof Track Shoe Pattern. Biomimetics, 7(2), 80. https://doi.org/10.3390/biomimetics7020080






