Bone Remodeling Process Based on Hydrostatic and Deviatoric Strain Mechano-Sensing
Abstract
1. Introduction
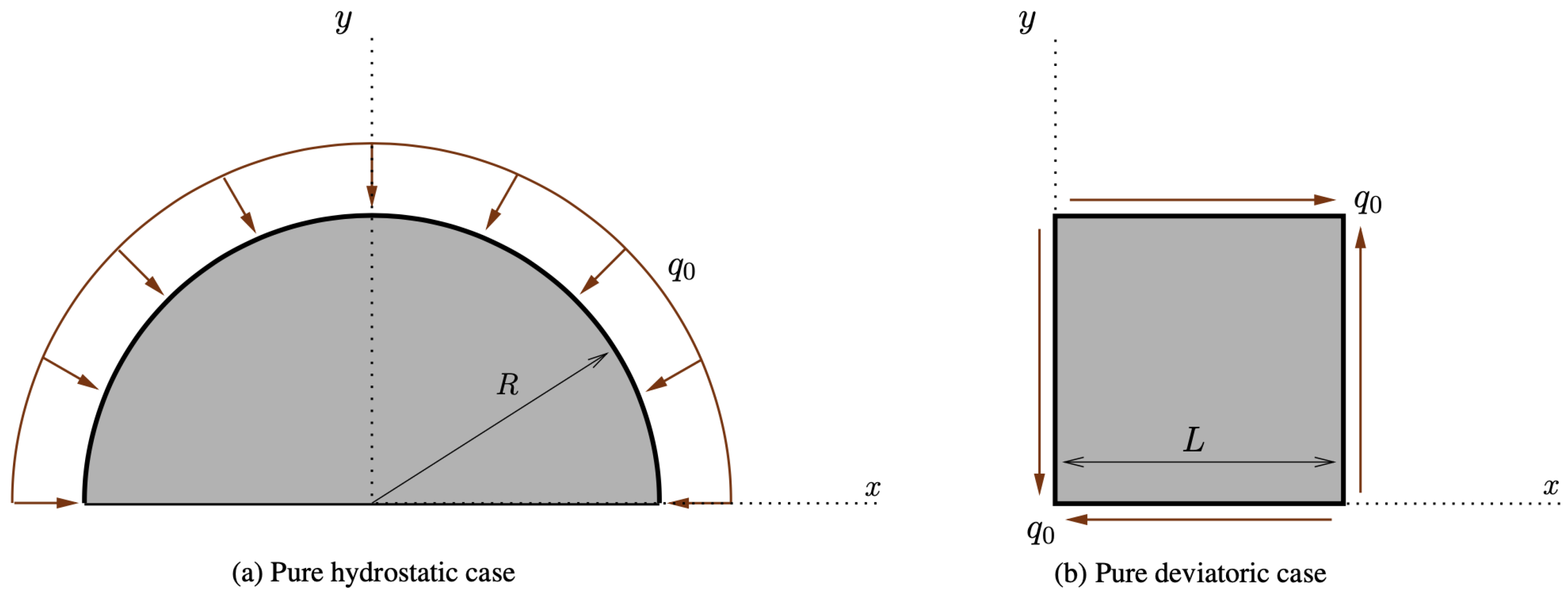
2. Materials and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Turner, C.H. Three rules for bone adaptation to mechanical stimuli. Bone 1998, 23, 399–407. [Google Scholar] [CrossRef]
- Li, M.C.M.; Chow, S.K.H.; Wong, R.M.Y.; Qin, L.; Cheung, W.H. The role of osteocytes-specific molecular mechanism in regulation of mechanotransduction–a systematic review. J. Orthop. Transl. 2021, 29, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, O.D.; Laudier, D.M.; Majeska, R.J.; Sun, H.B.; Schaffler, M.B. Osteocyte apoptosis is required for production of osteoclastogenic signals following bone fatigue in vivo. Bone 2014, 64, 132–137. [Google Scholar] [CrossRef] [PubMed]
- Klein-Nulend, J.; Bakker, A.D.; Bacabac, R.G.; Vatsa, A.; Weinbaum, S. Mechanosensation and transduction in osteocytes. Bone 2013, 54, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Kollmannsberger, P.; Kerschnitzki, M.; Repp, F.; Wagermaier, W.; Weinkamer, R.; Fratzl, P. The small world of osteocytes: Connectomics of the lacuno-canalicular network in bone. New J. Phys. 2017, 19, 073019. [Google Scholar] [CrossRef]
- Heino, T.J.; Hentunen, T.A.; Väänänen, H.K. Conditioned medium from osteocytes stimulates the proliferation of bone marrow mesenchymal stem cells and their differentiation into osteoblasts. Exp. Cell Res. 2004, 294, 458–468. [Google Scholar] [CrossRef]
- Bonewald, L.F. The amazing osteocyte. J. Bone Miner. Res. 2011, 26, 229–238. [Google Scholar] [CrossRef]
- Donahue, H. Gap junctions and biophysical regulation of bone cell differentiation. Bone 2000, 26, 417–422. [Google Scholar] [CrossRef]
- Qin, L.; Liu, W.; Cao, H.; Xiao, G. Molecular mechanosensors in osteocytes. Bone Res. 2020, 8, 1–24. [Google Scholar] [CrossRef]
- Civitelli, R. Cell–cell communication in the osteoblast/osteocyte lineage. Arch. Biochem. Biophys. 2008, 473, 188–192. [Google Scholar] [CrossRef]
- Weinbaum, S.; Cowin, S.C.; Zeng, Y. A model for the excitation of osteocytes by mechanical loading-induced bone fluid shear stresses. J. Biomech. 1994, 27, 339–360. [Google Scholar] [CrossRef]
- Bakker, A.; Klein-Nulend, J.; Burger, E. Shear stress inhibits while disuse promotes osteocyte apoptosis. Biochem. Biophys. Res. Commun. 2004, 320, 1163–1168. [Google Scholar] [CrossRef] [PubMed]
- Riddle, R.C.; Donahue, H.J. From streaming-potentials to shear stress: 25 years of bone cell mechanotransduction. J. Orthop. Res. 2009, 27, 143–149. [Google Scholar] [CrossRef] [PubMed]
- Adachi, T.; Kameo, Y.; Hojo, M. Trabecular bone remodelling simulation considering osteocytic response to fluid-induced shear stress. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 2669–2682. [Google Scholar] [CrossRef]
- Klein-Nulend, J.; Van Der Plas, A.; Semeins, C.M.; Ajubi, N.E.; Erangos, J.A.; Nijweide, P.J.; Burger, E.H. Sensitivity of osteocytes to biomechanical stress in vitro. FASEB J. 1995, 9, 441–445. [Google Scholar] [CrossRef] [PubMed]
- Schaffler, M.B.; Cheung, W.Y.; Majeska, R.; Kennedy, O. Osteocytes: Master orchestrators of bone. Calcif. Tissue Int. 2014, 94, 5–24. [Google Scholar] [CrossRef] [PubMed]
- Hadjidakis, D.J.; Androulakis, I.I. Bone remodeling. Ann. N. Y. Acad. Sci. 2006, 1092, 385–396. [Google Scholar] [CrossRef]
- Raggatt, L.J.; Partridge, N.C. Cellular and molecular mechanisms of bone remodeling. J. Biol. Chem. 2010, 285, 25103–25108. [Google Scholar] [CrossRef]
- Eriksen, E.F. Cellular mechanisms of bone remodeling. Rev. Endocr. Metab. Disord. 2010, 11, 219–227. [Google Scholar] [CrossRef]
- Robling, A.G.; Castillo, A.B.; Turner, C.H. Biomechanical and molecular regulation of bone remodeling. Annu. Rev. Biomed. Eng. 2006, 8, 455–498. [Google Scholar] [CrossRef]
- Wolff, J. Das gesetz der transformation der knochen. Dtsch. Med. Wochenschr. 1893, 19, 1222–1224. [Google Scholar] [CrossRef]
- Wolff, J. The Law of Bone Remodelling; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Pawlikowski, M.; Klasztorny, M.; Skalski, K. Studies on constitutive equation that models bone tissue. Acta Bioeng. Biomech. 2008, 10, 39–47. [Google Scholar] [PubMed]
- George, D.; Allena, R.; Remond, Y. A multiphysics stimulus for continuum mechanics bone remodeling. Math. Mech. Complex Syst. 2018, 6, 307–319. [Google Scholar] [CrossRef]
- George, D.; Allena, R.; Remond, Y. Integrating molecular and cellular kinetics into a coupled continuum mechanobiological stimulus for bone reconstruction. Contin. Mech. Thermodyn. 2019, 31, 725–740. [Google Scholar] [CrossRef]
- George, D.; Allena, R.; Bourzac, C.; Pallu, S.; Bensidhoum, M.; Portier, H.; Rémond, Y. A new comprehensive approach for bone remodeling under medium and high mechanical load based on cellular activity. Math. Mech. Complex Syst. 2020, 8, 287–306. [Google Scholar] [CrossRef]
- Bednarczyk, E.; Lekszycki, T. Evolution of bone tissue based on angiogenesis as a crucial factor: New mathematical attempt. Math. Mech. Solids 2022, 27, 976–988. [Google Scholar] [CrossRef]
- Hernandez-Rodriguez, Y.; Lekszycki, T. Finite memory model of bone healing in analysis of moving interface between mandible tissue and bone substitute material after tooth implant application. Contin. Mech. Thermodyn. 2021, 1–8. [Google Scholar] [CrossRef]
- Hambli, R. Connecting mechanics and bone cell activities in the bone remodeling process: An integrated finite element modeling. Front. Bioeng. Biotechnol. 2014, 2, 6. [Google Scholar] [CrossRef]
- Barkaoui, A.; Kahla, R.B.; Merzouki, T.; Hambli, R. Numerical simulation of apparent density evolution of trabecular bone under fatigue loading: Effect of bone initial properties. J. Mech. Med. Biol. 2019, 19, 1950041. [Google Scholar] [CrossRef]
- Lekszycki, T.; dell’Isola, F. A mixture model with evolving mass densities for describing synthesis and resorption phenomena in bones reconstructed with bio-resorbable materials. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 2012, 92, 426–444. [Google Scholar] [CrossRef]
- Prendergast, P.; Taylor, D. Prediction of bone adaptation using damage accumulation. J. Biomech. 1994, 27, 1067–1076. [Google Scholar] [CrossRef]
- Martínez-Reina, J.; Reina, I.; Domínguez, J.; García-Aznar, J. A bone remodelling model including the effect of damage on the steering of BMUs. J. Mech. Behav. Biomed. Mater. 2014, 32, 99–112. [Google Scholar] [CrossRef] [PubMed]
- Sheidaei, A.; Kazempour, M.; Hasanabadi, A.; Nosouhi, F.; Pithioux, M.; Baniassadi, M.; Rémond, Y.; George, D. Influence of bone microstructure distribution on developed mechanical energy for bone remodeling using a statistical reconstruction method. Math. Mech. Solids 2019, 24, 3027–3041. [Google Scholar] [CrossRef]
- Carter, D.; Van der Meulen, M.; Beaupre, G. Mechanical factors in bone growth and development. Bone 1996, 18, S5–S10. [Google Scholar] [CrossRef]
- Doblaré, M.; Garcıa, J. Anisotropic bone remodelling model based on a continuum damage-repair theory. J. Biomech. 2002, 35, 1–17. [Google Scholar] [CrossRef]
- Hegedus, D.; Cowin, S. Bone remodeling II: Small strain adaptive elasticity. J. Elast. 1976, 6, 337–352. [Google Scholar] [CrossRef]
- Carter, D.; Fyhrie, D.P.; Whalen, R. Trabecular bone density and loading history: Regulation of connective tissue biology by mechanical energy. J. Biomech. 1987, 20, 785–794. [Google Scholar] [CrossRef]
- Carter, D.; Orr, T.; Fyhrie, D.P. Relationships between loading history and femoral cancellous bone architecture. J. Biomech. 1989, 22, 231–244. [Google Scholar] [CrossRef]
- Andreaus, U.; Colloca, M.; Iacoviello, D. Optimal bone density distributions: Numerical analysis of the osteocyte spatial influence in bone remodeling. Comput. Methods Programs Biomed. 2014, 113, 80–91. [Google Scholar] [CrossRef]
- Lu, Y.; Lekszycki, T. New description of gradual substitution of graft by bone tissue including biomechanical and structural effects, nutrients supply and consumption. Contin. Mech. Thermodyn. 2018, 30, 995–1009. [Google Scholar] [CrossRef]
- Giorgio, I.; Andreaus, U.; dell’Isola, F.; Lekszycki, T. Viscous second gradient porous materials for bones reconstructed with bio-resorbable grafts. Extrem. Mech. Lett. 2017, 13, 141–147. [Google Scholar] [CrossRef]
- Andreaus, U.; Colloca, M.; Iacoviello, D. Modeling of trabecular architecture as result of an optimal control procedure. In Biomedical Imaging and Computational Modeling in Biomechanics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 19–37. [Google Scholar]
- Andreaus, U.; Colloca, M.; Iacoviello, D. An optimal control procedure for bone adaptation under mechanical stimulus. Control Eng. Pract. 2012, 20, 575–583. [Google Scholar] [CrossRef]
- Giorgio, I.; Andreaus, U.; Alzahrani, F.; Hayat, T.; Lekszycki, T. On mechanically driven biological stimulus for bone remodeling as a diffusive phenomenon. Biomech. Model. Mechanobiol. 2019, 18, 1639–1663. [Google Scholar] [CrossRef] [PubMed]
- Lekszycki, T. Functional adaptation of bone as an optimal control problem. J. Theor. Appl. Mech. 2005, 43, 555–574. [Google Scholar]
- Reda, H.; Karathanasopoulos, N.; Elnady, K.; Ganghoffer, J.F.; Lakiss, H. The role of anisotropy on the static and wave propagation characteristics of two-dimensional architectured materials under finite strains. Mater. Des. 2018, 147, 134–145. [Google Scholar] [CrossRef]
- Ganghoffer, J.; Reda, H. A variational approach of homogenization of heterogeneous materials towards second gradient continua. Mech. Mater. 2021, 158, 103743. [Google Scholar] [CrossRef]
- Reda, H.; Rahali, Y.; Ganghoffer, J.; Lakiss, H. Wave propagation analysis in 2D nonlinear hexagonal periodic networks based on second order gradient nonlinear constitutive models. Int. J. Non-Linear Mech. 2016, 87, 85–96. [Google Scholar] [CrossRef]
- Massoumi, S.; La Valle, G. Static analysis of 2D micropolar model for describing granular media by considering relative rotations. Mech. Res. Commun. 2022, 119, 103812. [Google Scholar] [CrossRef]
- La Valle, G.; Massoumi, S. A new deformation measure for micropolar plates subjected to in-plane loads. Contin. Mech. Thermodyn. 2022, 34, 243–257. [Google Scholar] [CrossRef]
- Belarbi, M.O.; Li, L.; Houari, M.S.A.; Garg, A.; Chalak, H.D.; Dimitri, R.; Tornabene, F. Nonlocal vibration of functionally graded nanoplates using a layerwise theory. Math. Mech. Solids 2022. [Google Scholar] [CrossRef]
- Karamooz Ravari, M.; Kadkhodaei, M. A computationally efficient modeling approach for predicting mechanical behavior of cellular lattice structures. J. Mater. Eng. Perform. 2015, 24, 245–252. [Google Scholar] [CrossRef]
- Barchiesi, E.; dell’Isola, F.; Bersani, A.M.; Turco, E. Equilibria determination of elastic articulated duoskelion beams in 2D via a Riks-type algorithm. Int. J. Non-Linear Mech. 2021, 128, 103628. [Google Scholar] [CrossRef]
- Cazzani, A.; Stochino, F.; Turco, E. An analytical assessment of finite element and isogeometric analyses of the whole spectrum of Timoshenko beams. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 2016, 96, 1220–1244. [Google Scholar] [CrossRef]
- Turco, E.; Barchiesi, E.; dell’Isola, F. In-plane dynamic buckling of duoskelion beam-like structures: Discrete modeling and numerical results. Math. Mech. Solids 2021. [Google Scholar] [CrossRef]
- Pietraszkiewicz, W.; Eremeyev, V. On natural strain measures of the non-linear micropolar continuum. Int. J. Solids Struct. 2009, 46, 774–787. [Google Scholar] [CrossRef]
- Eremeyev, V.A.; Pietraszkiewicz, W. Material symmetry group and constitutive equations of micropolar anisotropic elastic solids. Math. Mech. Solids 2016, 21, 210–221. [Google Scholar] [CrossRef]
- Misra, A.; Poorsolhjouy, P. Identification of higher-order elastic constants for grain assemblies based upon granular micromechanics. Math. Mech. Complex Syst. 2015, 3, 285–308. [Google Scholar] [CrossRef]
- De Angelo, M.; Placidi, L.; Nejadsadeghi, N.; Misra, A. Non-standard Timoshenko beam model for chiral metamaterial: Identification of stiffness parameters. Mech. Res. Commun. 2020, 103, 103462. [Google Scholar] [CrossRef]
- Abali, B.E.; Müller, W.H.; Eremeyev, V.A. Strain gradient elasticity with geometric nonlinearities and its computational evaluation. Mech. Adv. Mater. Mod. Process. 2015, 1, 1–11. [Google Scholar] [CrossRef]
- Abali, B.E.; Müller, W.H. Theory and computation of higher gradient elasticity theories based on action principles. Arch. Appl. Mech. 2017, 87, 1495–1510. [Google Scholar] [CrossRef]
- Cuomo, M.; dell’Isola, F.; Greco, L.; Rizzi, N. First versus second gradient energies for planar sheets with two families of inextensible fibres: Investigation on deformation boundary layers, discontinuities and geometrical instabilities. Compos. Part B Eng. 2017, 115, 423–448. [Google Scholar] [CrossRef]
- Eugster, S.R.; dell’Isola, F.; Fedele, R.; Seppecher, P. Piola transformations in second-gradient continua. Mech. Res. Commun. 2022, 120, 103836. [Google Scholar] [CrossRef]
- dell’Isola, F.; Eugster, S.R.; Fedele, R.; Seppecher, P. Second-gradient continua: From Lagrangian to Eulerian and back. Math. Mech. Solids 2022. [Google Scholar] [CrossRef]
- Spagnuolo, M.; Franciosi, P.; dell’Isola, F. A Green operator-based elastic modeling for two-phase pantographic-inspired bi-continuous materials. Int. J. Solids Struct. 2020, 188, 282–308. [Google Scholar] [CrossRef]
- Solyaev, Y.; Lurie, S.; Altenbach, H.; dell’Isola, F. On the elastic wedge problem within simplified and incomplete strain gradient elasticity theories. Int. J. Solids Struct. 2022, 239–240, 111433. [Google Scholar] [CrossRef]
- Laudato, M.; Ciallella, A. Perspectives in generalized continua. In Developments and Novel Approaches in Biomechanics and Metamaterials; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–13. [Google Scholar]
- Andreaus, U.; Spagnuolo, M.; Lekszycki, T.; Eugster, S.R. A Ritz approach for the static analysis of planar pantographic structures modeled with nonlinear Euler–Bernoulli beams. Contin. Mech. Thermodyn. 2018, 30, 1103–1123. [Google Scholar] [CrossRef]
- Barchiesi, E.; Eugster, S.R.; dell’Isola, F.; Hild, F. Large in-plane elastic deformations of bi-pantographic fabrics: Asymptotic homogenization and experimental validation. Math. Mech. Solids 2020, 25, 739–767. [Google Scholar] [CrossRef]
- dell’Isola, F.; Andreaus, U.; Placidi, L. At the origins and in the vanguard of peridynamics, non-local and higher-gradient continuum mechanics: An underestimated and still topical contribution of Gabrio Piola. Math. Mech. Solids 2015, 20, 887–928. [Google Scholar] [CrossRef]
- Yang, Z.; Oterkus, E.; Nguyen, C.T.; Oterkus, S. Implementation of peridynamic beam and plate formulations in finite element framework. Contin. Mech. Thermodyn. 2019, 31, 301–315. [Google Scholar] [CrossRef]
- Oterkus, S.; Madenci, E.; Oterkus, E. Fully coupled poroelastic peridynamic formulation for fluid-filled fractures. Eng. Geol. 2017, 225, 19–28. [Google Scholar] [CrossRef]
- Pisano, A.A.; Fuschi, P. Structural symmetry within nonlocal integral elasticity: Theoretical issues and computational strategies. Curved Layer. Struct. 2017, 4, 1–7. [Google Scholar] [CrossRef][Green Version]
- Mullender, M.; Huiskes, R.; Weinans, H. A physiological approach to the simulation of bone remodeling as a self-organizational control process. J. Biomech. 1994, 27, 1389–1394. [Google Scholar] [CrossRef] [PubMed]
- Lekszycki, T. Modelling of bone adaptation based on an optimal response hypothesis. Meccanica 2002, 37, 343–354. [Google Scholar] [CrossRef]
- Andreaus, U.; Giorgio, I.; Madeo, A. Modeling of the interaction between bone tissue and resorbable biomaterial as linear elastic materials with voids. Z. Angew. Math. Phys. 2015, 66, 209–237. [Google Scholar] [CrossRef][Green Version]
- Allena, R.; Cluzel, C. Heterogeneous directions of orthotropy in three-dimensional structures: Finite element description based on diffusion equations. Math. Mech. Complex Syst. 2018, 6, 339–351. [Google Scholar] [CrossRef]
- Cluzel, C.; Allena, R. A general method for the determination of the local orthotropic directions of heterogeneous materials: Application to bone structures using μCT images. Math. Mech. Complex Syst. 2018, 6, 353–367. [Google Scholar] [CrossRef]










| Parameter | Value |
|---|---|
| 18 GPa | |
| 0.3 | |
| D | 0.1 mm |
| 30 GPa | |
| 13.84 GPa | |
| 0.001 N | |
| 0.001 N | |
| ms | |
| ms | |
| ms | |
| ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Branecka, N.; Yildizdag, M.E.; Ciallella, A.; Giorgio, I. Bone Remodeling Process Based on Hydrostatic and Deviatoric Strain Mechano-Sensing. Biomimetics 2022, 7, 59. https://doi.org/10.3390/biomimetics7020059
Branecka N, Yildizdag ME, Ciallella A, Giorgio I. Bone Remodeling Process Based on Hydrostatic and Deviatoric Strain Mechano-Sensing. Biomimetics. 2022; 7(2):59. https://doi.org/10.3390/biomimetics7020059
Chicago/Turabian StyleBranecka, Natalia, Mustafa Erden Yildizdag, Alessandro Ciallella, and Ivan Giorgio. 2022. "Bone Remodeling Process Based on Hydrostatic and Deviatoric Strain Mechano-Sensing" Biomimetics 7, no. 2: 59. https://doi.org/10.3390/biomimetics7020059
APA StyleBranecka, N., Yildizdag, M. E., Ciallella, A., & Giorgio, I. (2022). Bone Remodeling Process Based on Hydrostatic and Deviatoric Strain Mechano-Sensing. Biomimetics, 7(2), 59. https://doi.org/10.3390/biomimetics7020059








