Low-Cost Algorithms for Metabolic Pathway Pairwise Comparison
Abstract
1. Introduction
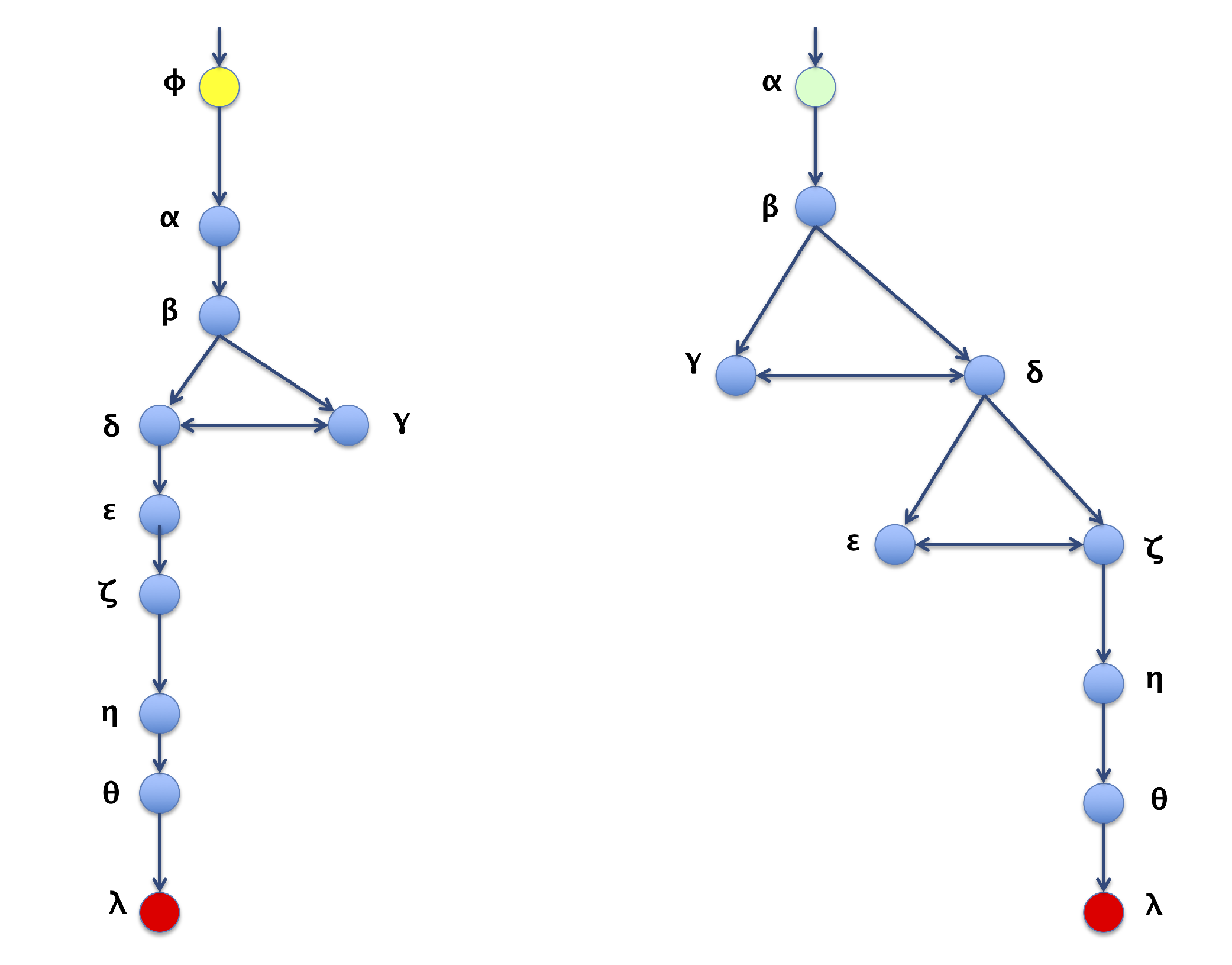
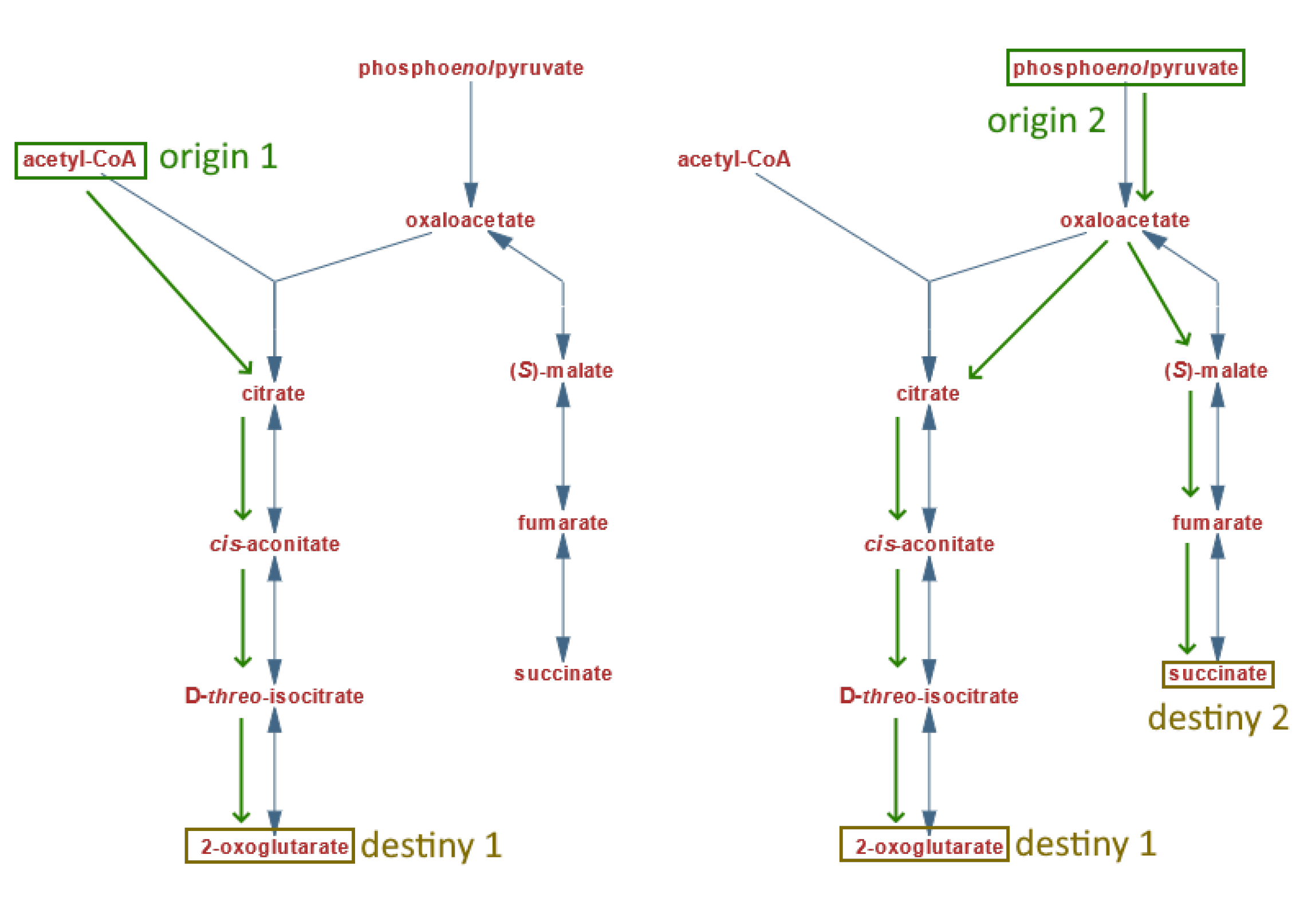
2. Metabolic Pathways and Graphs
- Node label: for any given node in a graph, we refer to “label” as the associated string used to identify each node (which corresponds to the compound or metabolite name of a metabolic pathway represented by said node). Each label is unique within a pathway, meaning that two nodes in the same graph cannot have the same label name.
- Equivalent nodes: any given labeled node present in both graphs being compared, meaning that both pathways involve the use of the same compound described by the associated nodes.
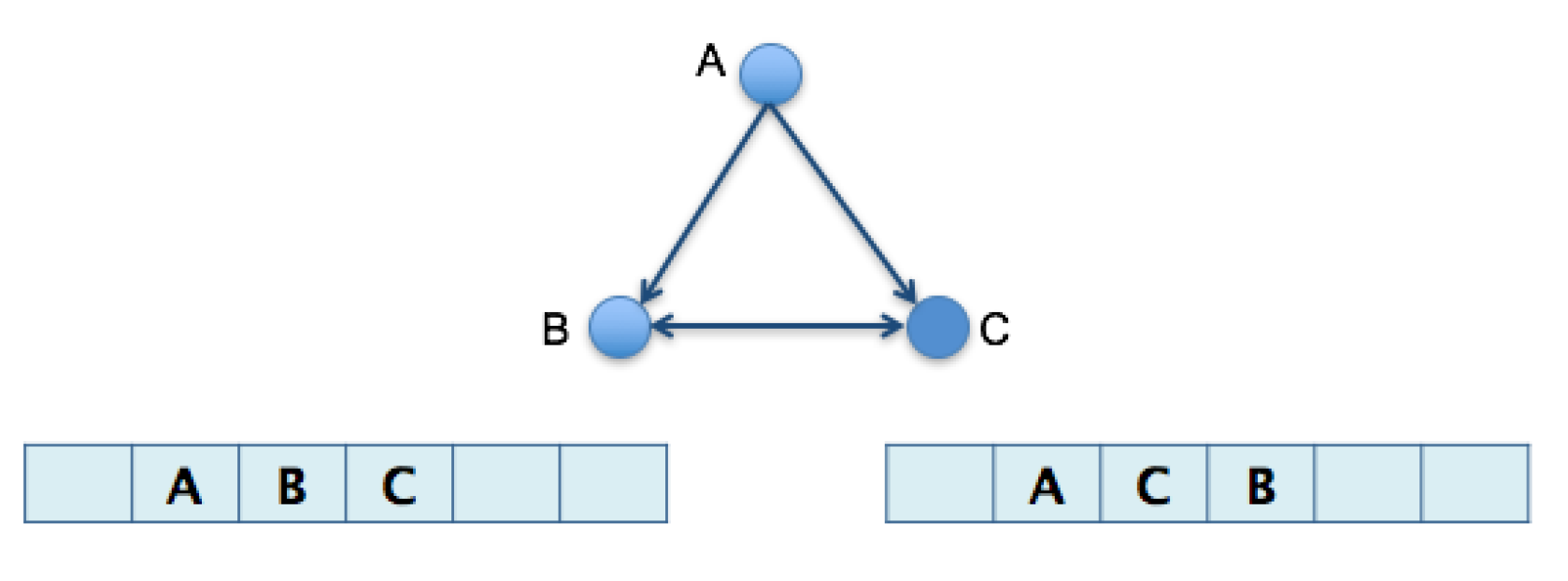
- Analogous order: for two aligned sequences S and T, the elements with analogous order between both sequences are those that conform to the largest possible sub-sequence of both S and T.
3. Algorithms
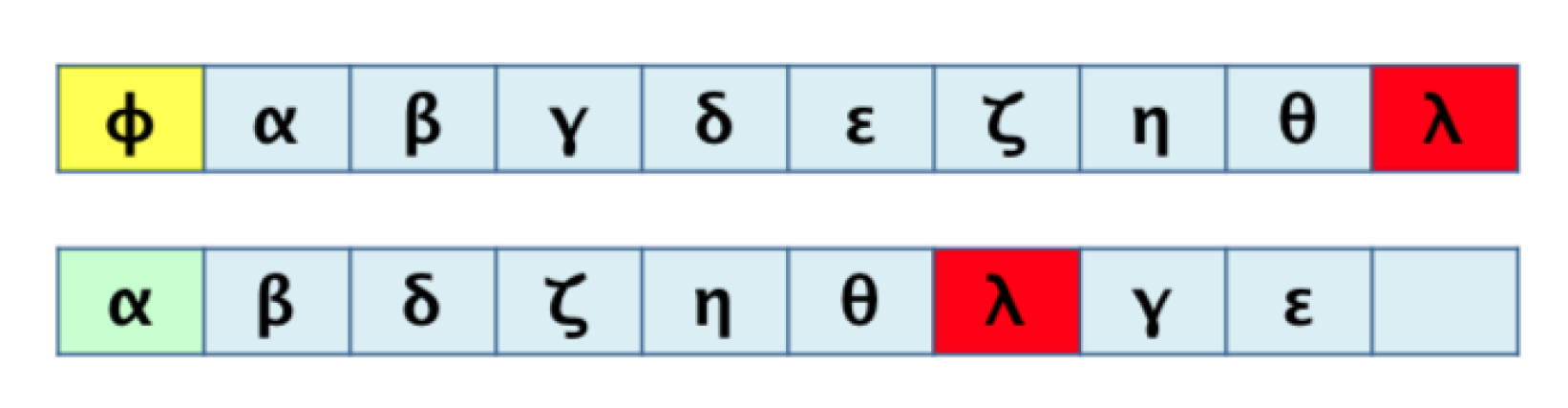
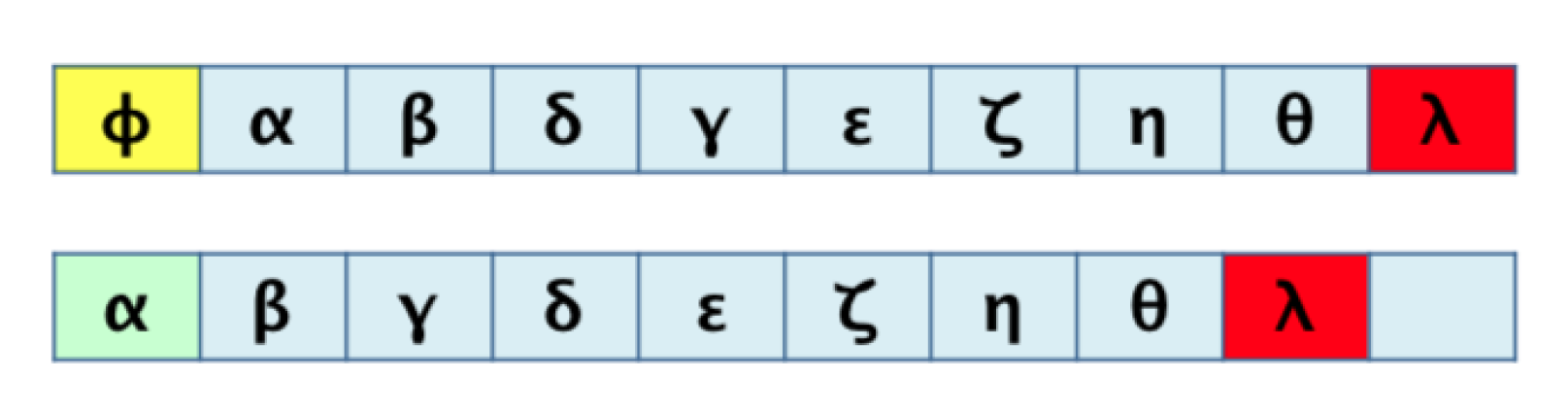
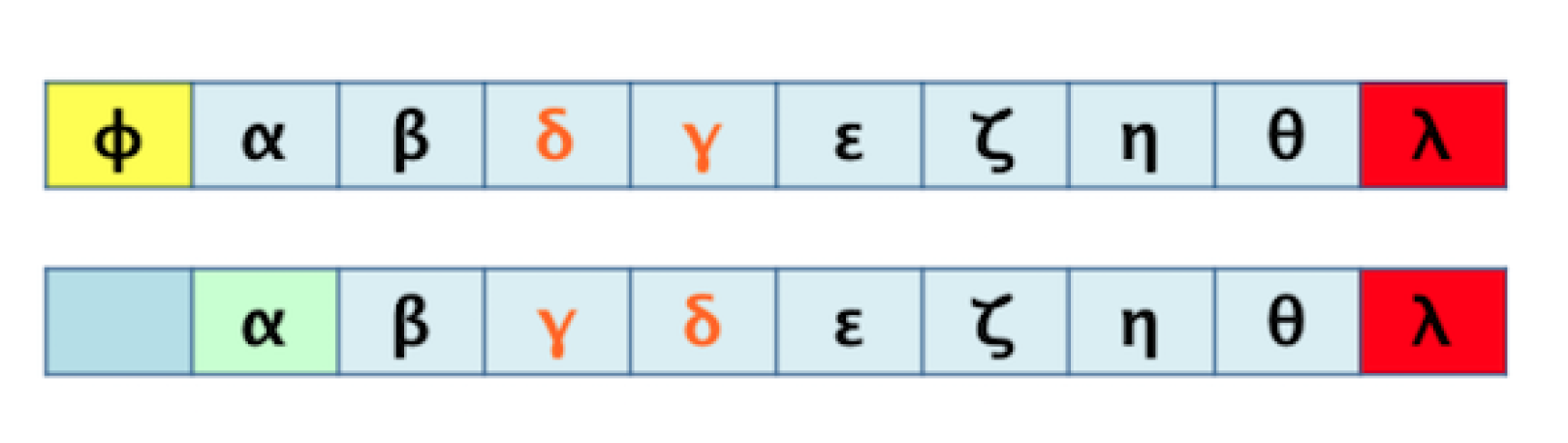
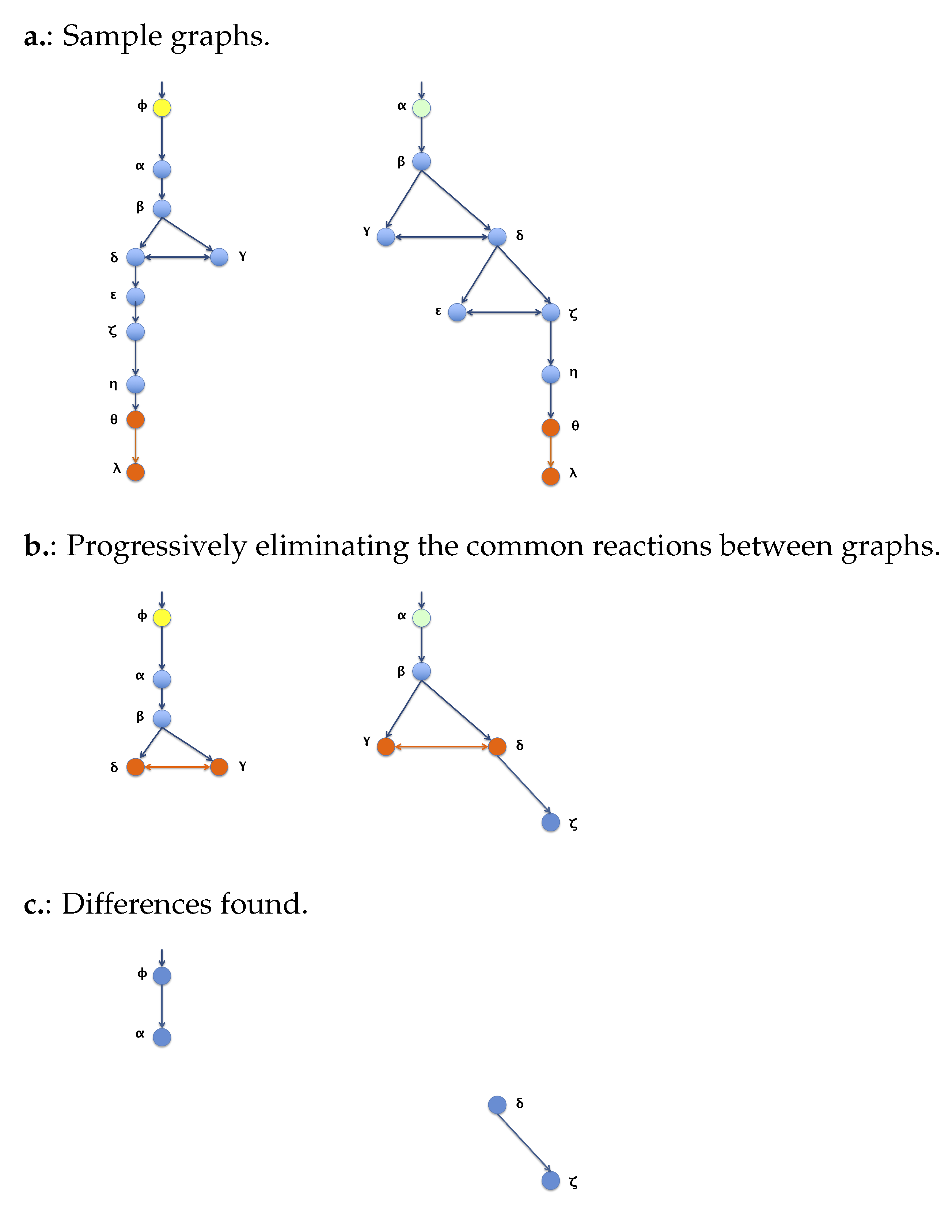
3.1. Algorithm 1: Transformation of the 2D Pathway Graph to a 1D or Linear Structure for Later Alignment and Evaluation
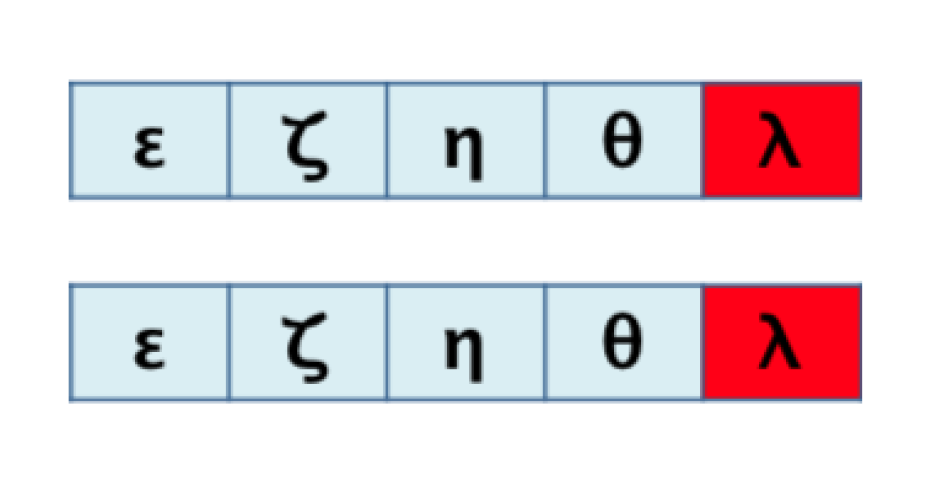
3.2. Algorithm 2: Differentiation by Pairs
4. Materials and Methods
4.1. Factors and Levels
- Size ratio
- (a)
- much difference: x < 0.4, called different
- (b)
- mean difference: 0.4 ≤ x < 0.7, called medium
- (c)
- little difference: x ≥ 0.7, called similar
- Common families
- (a)
- none common families: 0, called none
- (b)
- few common families: 1, 2, 3, called few
- (c)
- several common families: ≥4, called several
4.2. Analysis of Variance: ANOVA
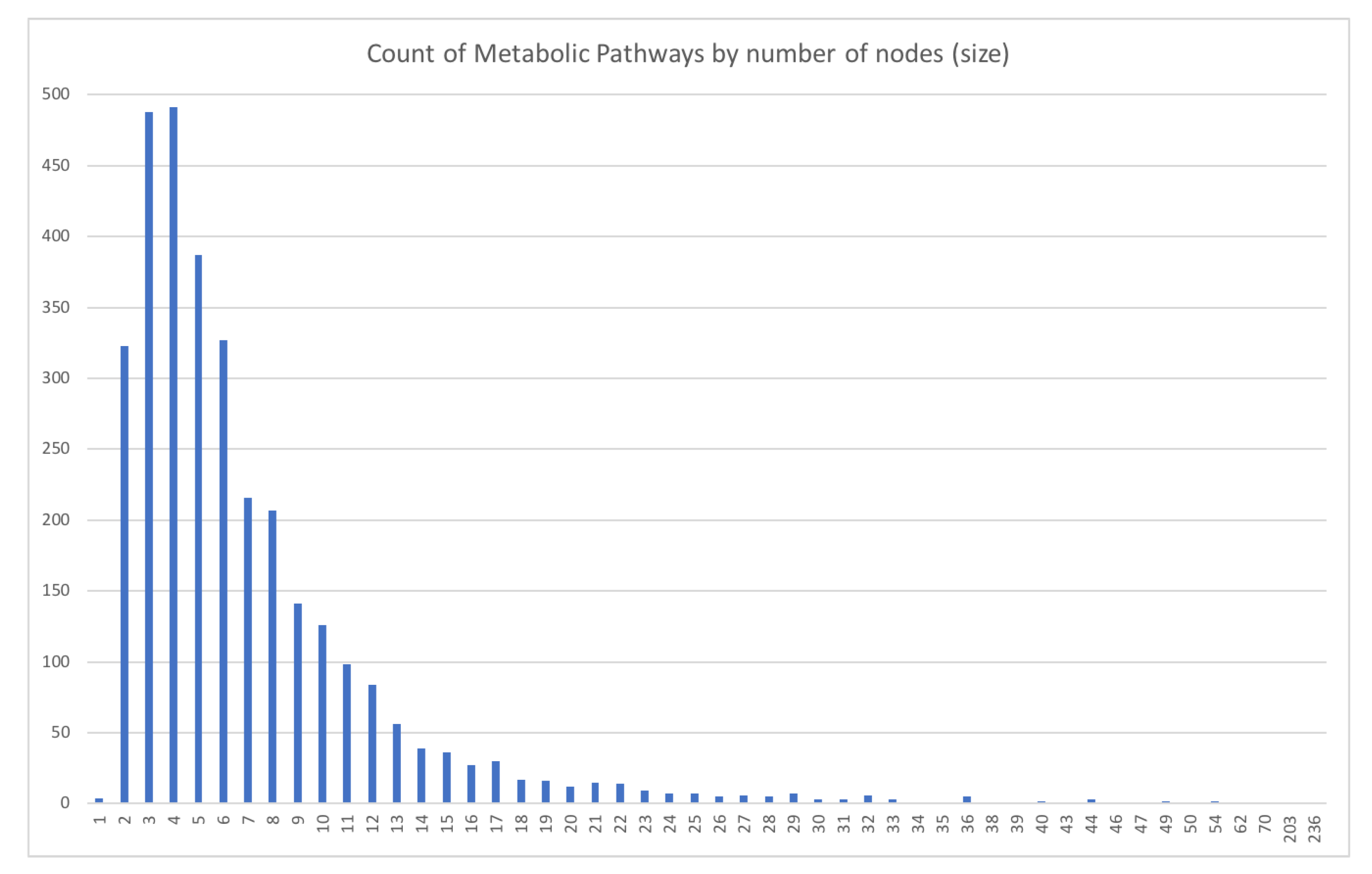
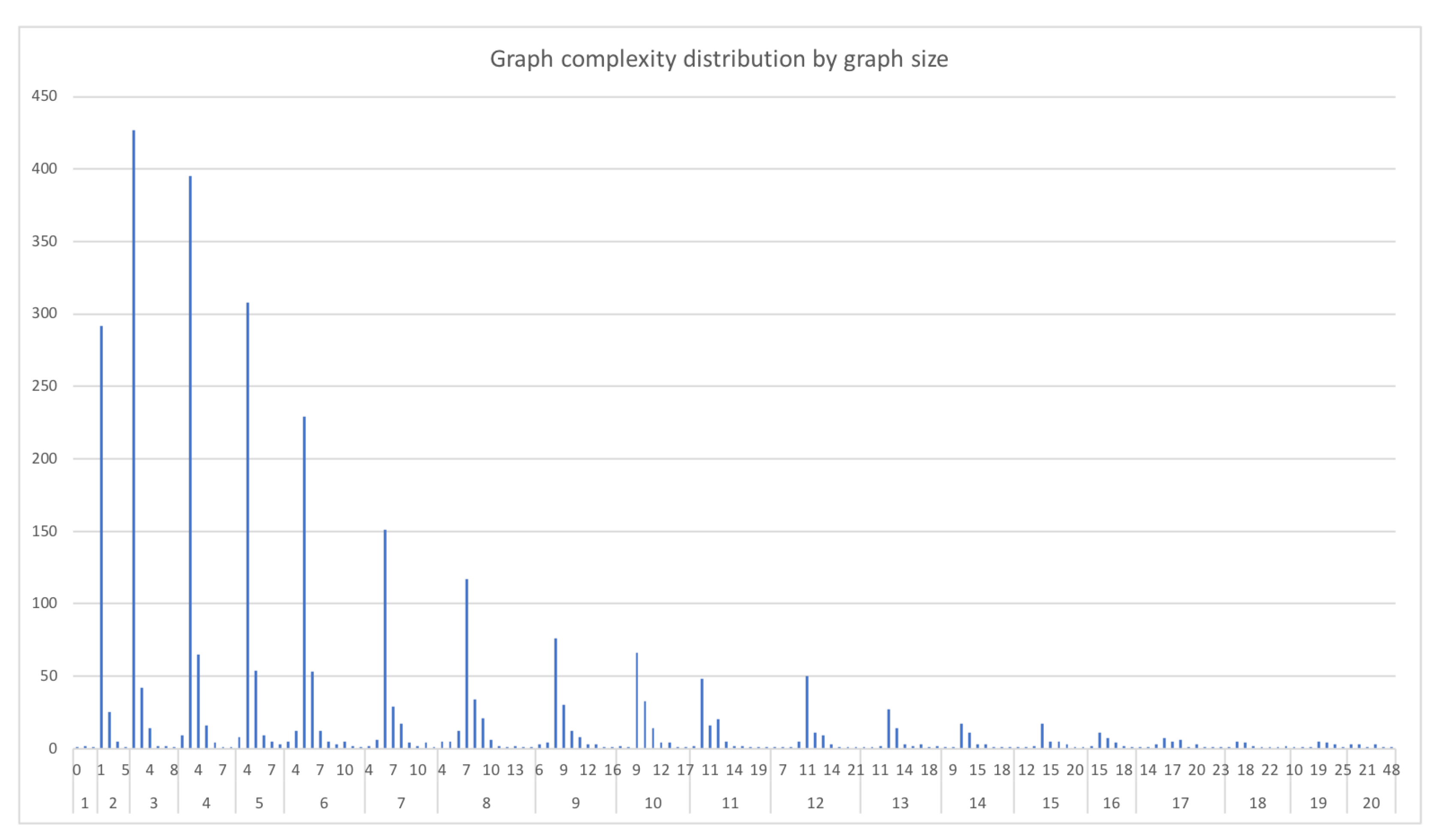
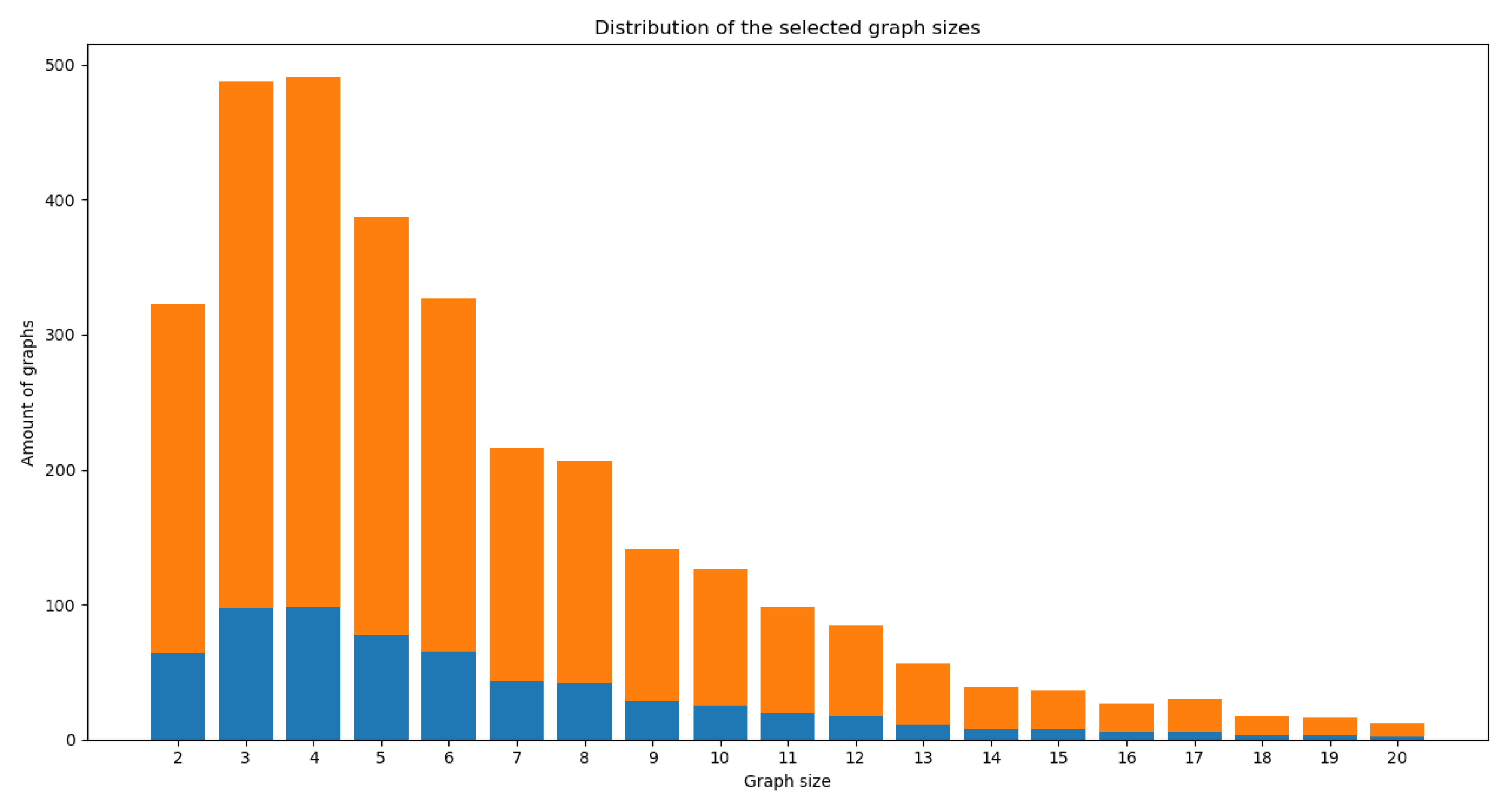
4.3. Obtaining the Data
4.4. Selection of Matching Candidates for the Comparisons
4.5. Graphs vs. Pathways
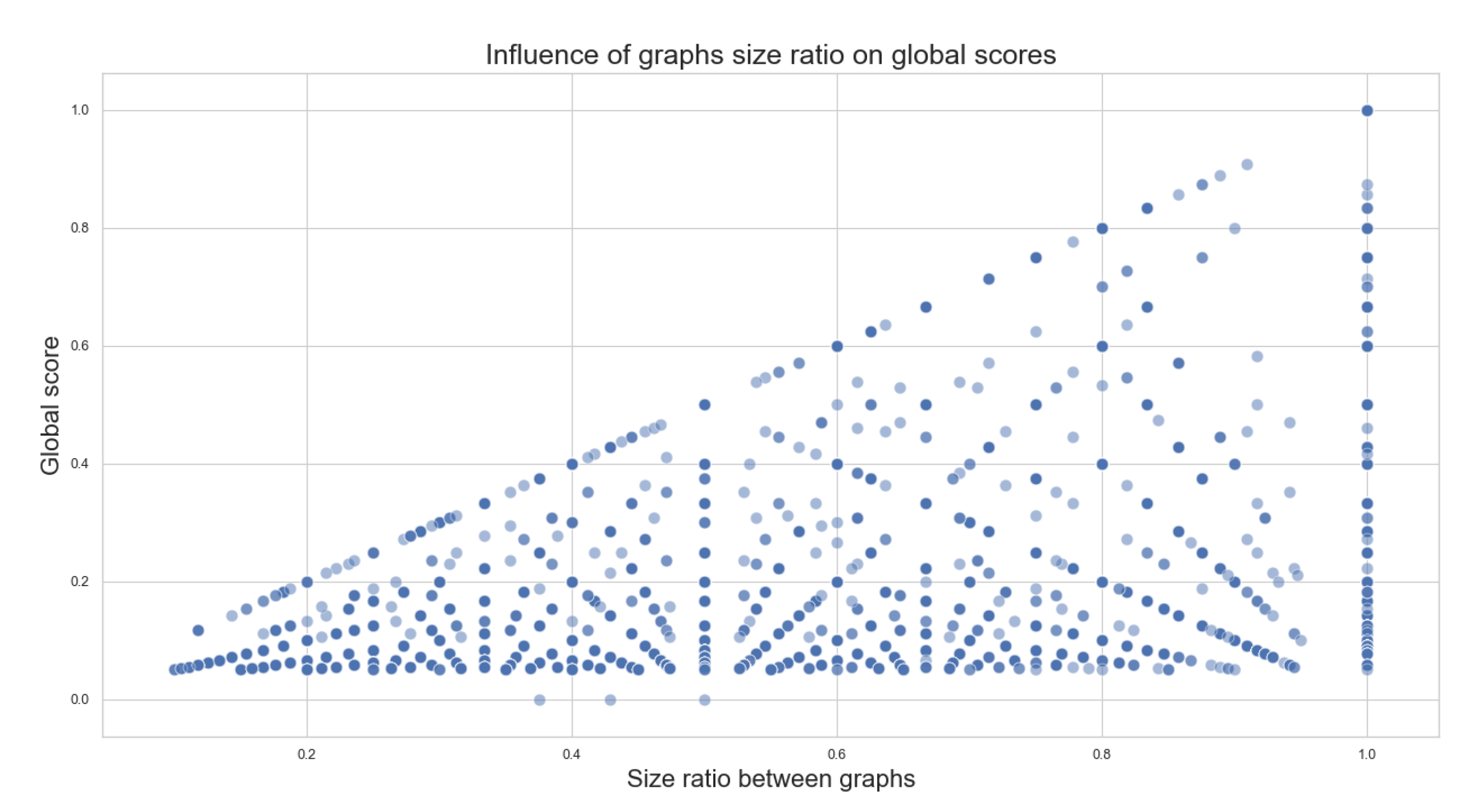
- Size ratio between graphs: for a given graph, we refer to the “size” as the number of nodes described within the graph. The size ratio between graphs consists of dividing the smaller graph’s size (graph with the least amount of nodes) over the bigger graph’s size (graph with the largest number of nodes) to obtain a value between 0 and 1 that represents how different the sizes of the compared graphs are. This value can also be interpreted as how much of the biggest graph’s size can be covered by the smallest graph’s size.
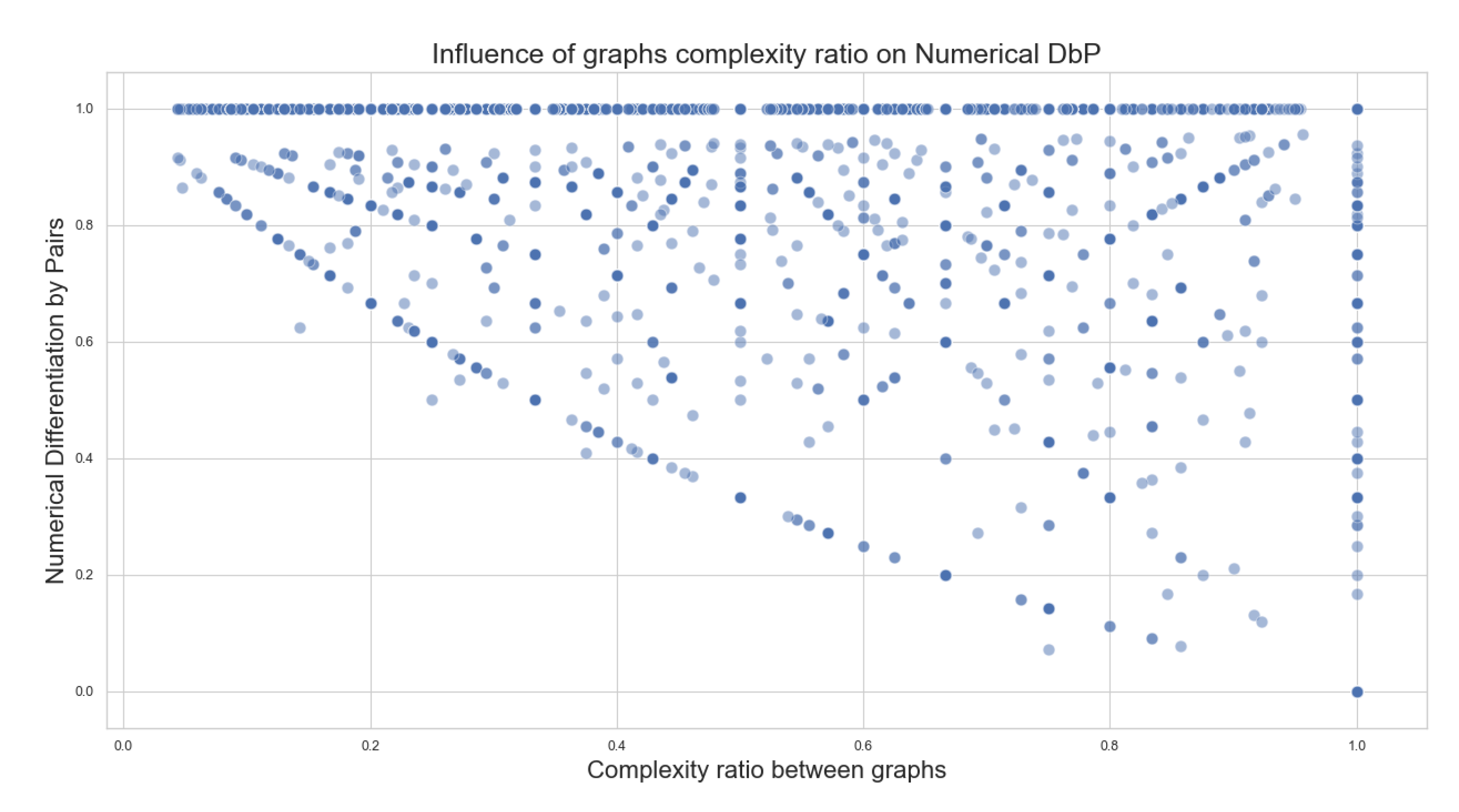
- Complexity ratio between graphs: is the number of edges described within a given graph. The complexity ratio between the graphs consists of dividing the complexity number of the less complex graph (graph with the least amount of edges) over the complexity of the more complex graph (graph with the largest number of edges) to obtain a value between 0 and 1 that represents how different the complexity amounts of the compared graphs are. This value can also be interpreted as how much of the more complex graph can be covered by the less complex graph.
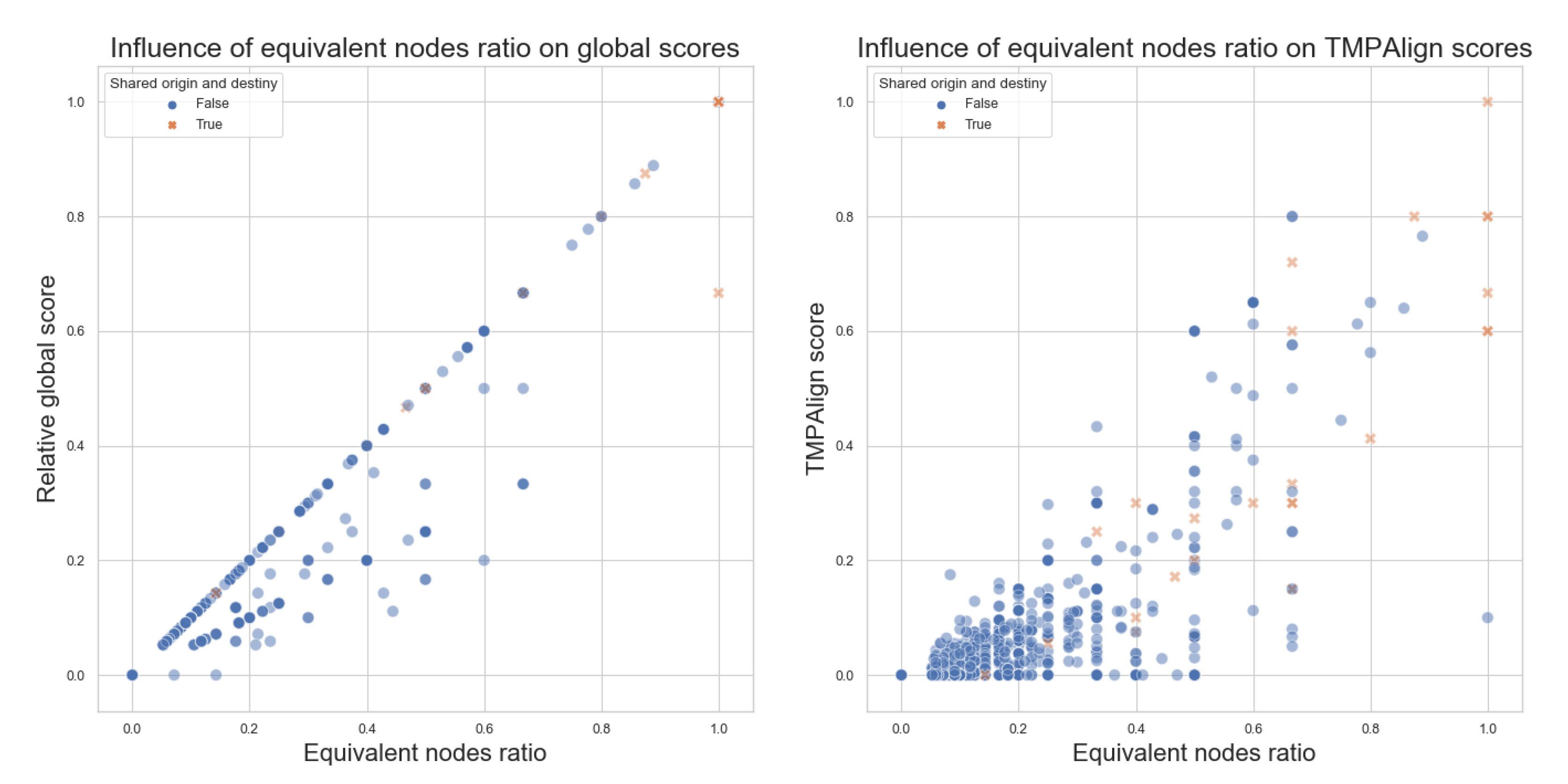
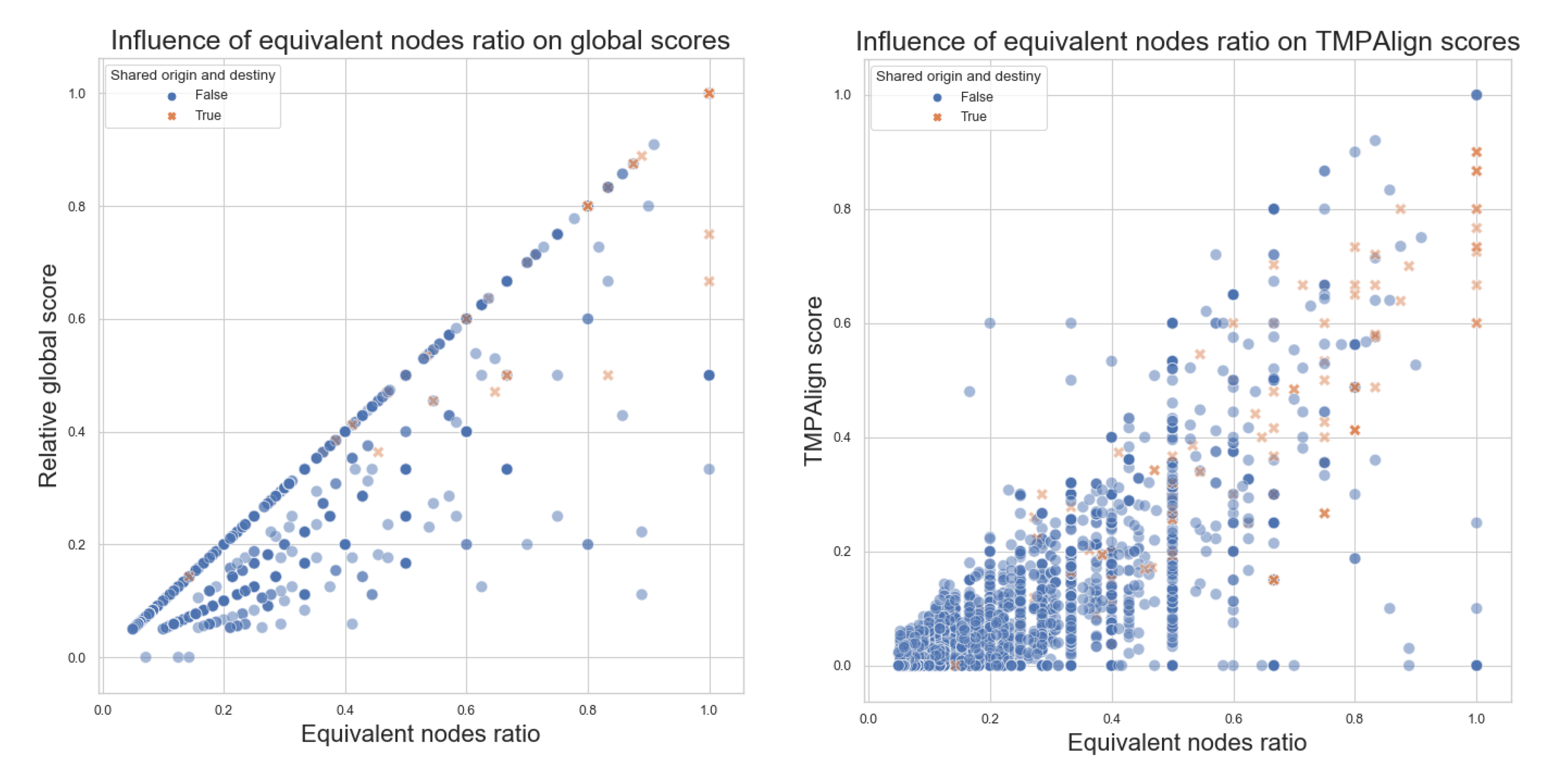
- Equivalent nodes ratio: this is obtained by dividing the number of equivalent nodes over the size of the larger graph. It produces a value between 0 and 1 that can be interpreted as how much percentage of the equivalent-nodes present in the larger graph can also be found within the smaller graphs. Equivalent nodes mean that the same metabolite is present in both graphs.
4.6. Formulas
- Absolute Score: , where S is the score, x is the number of matches, m is the value of a match, y is the number of mismatches, n is the value of a mismatch, z is the number of gaps, g is the value of a gap;
- Relative Global: , where is the relative global score, is the number of matches of the respective global alignment, and S and T are the aligned sequences;
- Relative Local: , where is the relative local score, is the number of matches of the respective local alignment, and S and T are the aligned sequences;
- Relative Semiglobal: , where is the relative semi-global score, is the number of matches of the respective semi-global alignment, and S and T are the aligned sequences.
4.7. Executing Pairwise Comparisons
- Global Score: score generated by the absolute score formula for the optimal global sequence alignment between two traversals (Algorithm 1). The base values used were: match = 1 and mismatch = −1; for gap value, the comparisons were performed using 3 different values: −2, −1 and 0 (explained why later);
- Relative Global Score: value between 0 and 1 obtained from the relative global formula, a percentage value p%, interpreted as “there is a p% similarity between both traversals” or “at least p% elements of the small traversal is present in analogous order on the long traversal”;
- Local Score: score generated by the absolute score formula for the optimal local alignment between two traversals (Algorithm 1). The base values used were: match = 1, mismatch = −1, gap = −2;
- Relative Local Score: value between 0 and 1 obtained from the relative local formula, a percentage value p%, interpreted as “at least p% elements of the small traversal is present in analogous order on the long traversal”;
- Semiglobal Score: Score generated by the absolute score formula for the optimal semi-global alignment between two traversals (Algorithm 1). The base values used were: match = 1, mismatch = −1, gap = −2;
- Relative Semiglobal Score: Value between 0 and 1 obtained from the relative semi-global formula, a percentage value p%, interpreted as “at least p% elements of the small traversal is present in analogous order on the long traversal”;
- Differentiation by Pairs: For each one of the two pathways, a list of distinguished reactions present on the said pathway but absent in the other one was obtained as a result. Each reaction, or edge in the graph, is represented as a string of the form “node_0 -> node_1 ”, meaning a is being transformed into ;
- Numerical Differentiation by Pairs: For a given pairwise comparison between two pathways, consists of the total number of elements of the previous differentiation by pairs results, divided by the sum of complexity of both graphs. This provides a value between 0 and 1 that represents a percentage of the distinguished reactions (edges) constituted between the two graphs that are unique in each graph. The complexity of the graph should be understood as the number of reactions in a single pathway.
5. Results and Discussion
5.1. Former Tests
5.2. Analysis of Algorithms for Pairwise Comparisons
5.3. Experiments
5.4. ANOVA Tests
- Independence of the observations. Each subject should belong to only one group. There is no relationship between the observations in each group. Having repeated measures for the same participants is not allowed;
- No significant outliers in any cell of the design;
- Normality. the data for each design cell should be approximately normally distributed;
- Homogeneity of variances. The variance of the outcome variable should be equal in every cell of the design.
| > |
| # Summary statistics |
| # Compute the mean and the SD (standard deviation) |
| # of the Global score by groups: |
| > doe_selection %>% |
| + group_by(size_ratio, families) %>% |
| + get_summary_stats(global, type = "mean_sd") |
| # A tibble: 9 x 6 |
| size_ratio families variable n mean sd |
| <chr> <fct> <chr> <dbl> <dbl> <dbl> |
| 1 different none global 50 0.095 0.043 |
| 2 different few global 50 0.101 0.048 |
| 3 different several global 50 0.135 0.07 |
| 4 medium none global 50 0.166 0.081 |
| 5 medium few global 50 0.166 0.094 |
| 6 medium several global 50 0.239 0.155 |
| 7 similar none global 50 0.199 0.131 |
| 8 similar few global 50 0.185 0.107 |
| 9 similar several global 50 0.321 0.161 |
| > |
| > |
| # Some common heuristics transformations for non-normal data |
| # include: log for greater skew: |
| # log10(x) for positively skewed data, |
| # log10(max(x+1) - x) for negatively skewed data |
| # Log transformation of the skewed data: |
| > doe_selection$global <- log10 (doe_selection$global) |
| > |
| > |
| # This can be checked using the test of Levene: |
| > doe_selection %>% levene_test (global ~ size_ratio∗families) |
| # A tibble: 1 x 4 |
| df1 df2 statistic p |
| <int> <int> <dbl> <dbl> |
| 1 8 441 3.48 0.000657 |
| > |
- (a)
- ignore this violation, based on your own a priori knowledge of the distributional characteristics of the population being sampled;
- (b)
- relax the assumption of homoscedasticity and run the Welch one-way test, which does not require that assumption [32].
| > |
| # In the R code below, the asterisk represents the interaction |
| # effect and the main effect of each variable |
| # (and all lower-order interactions). |
| > res.aov <- doe_selection %>% |
| + anova_test(global ~ size_ratio ∗ families) |
| Coefficient covariances computed by hccm() |
| > res.aov |
| ANOVA Table (type II tests) |
| Effect DFn DFd F p p<.05 ges |
| 1 size_ratio 2 441 52.229 4.39e-21 ∗ 0.192 |
| 2 families 2 441 27.777 4.35e-12 ∗ 0.112 |
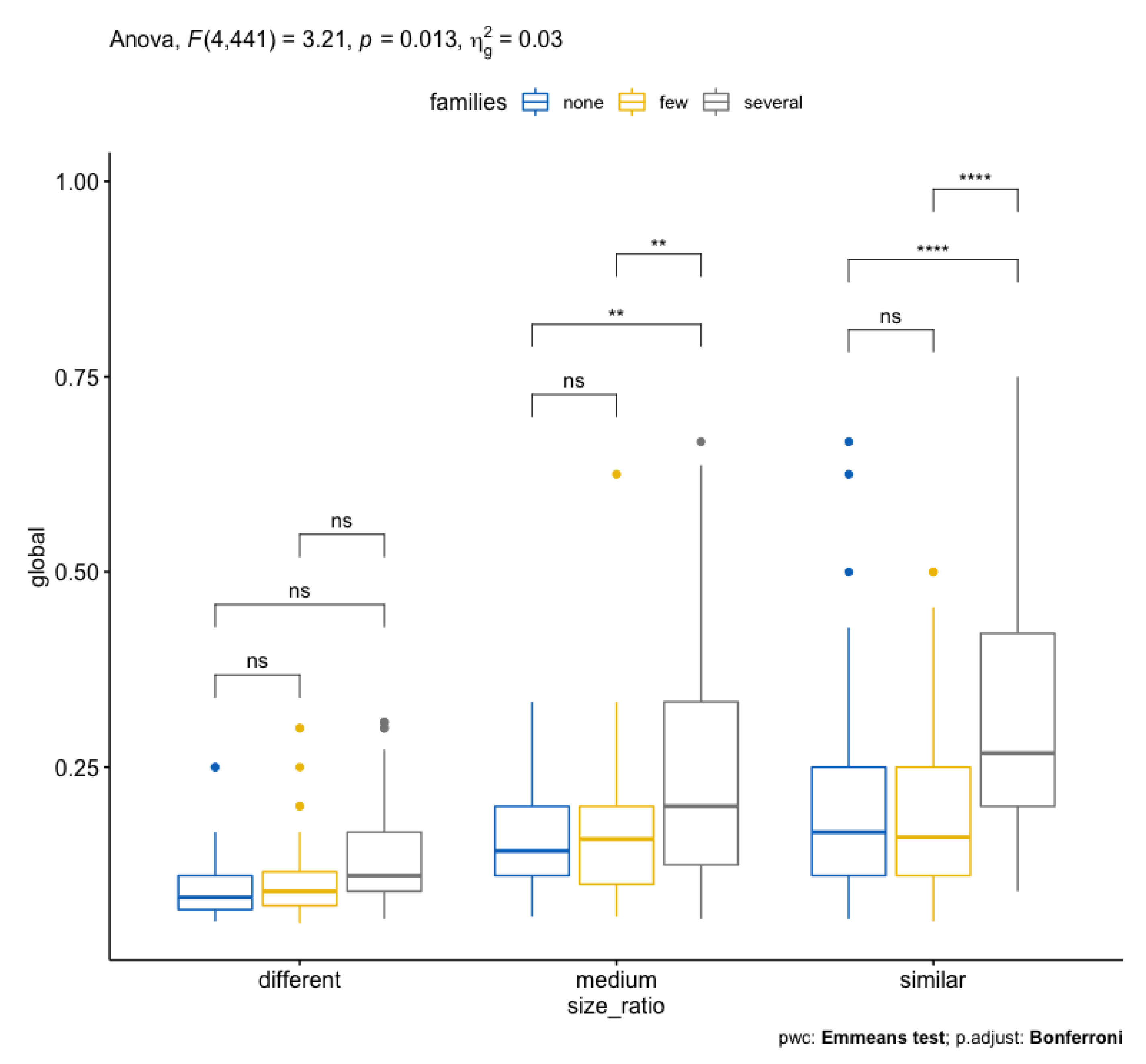
| 3 size_ratio:families 4 441 3.209 1.30e-02 ∗ 0.028 |
| > |
5.5. Tests against Another Algorithm of Reference
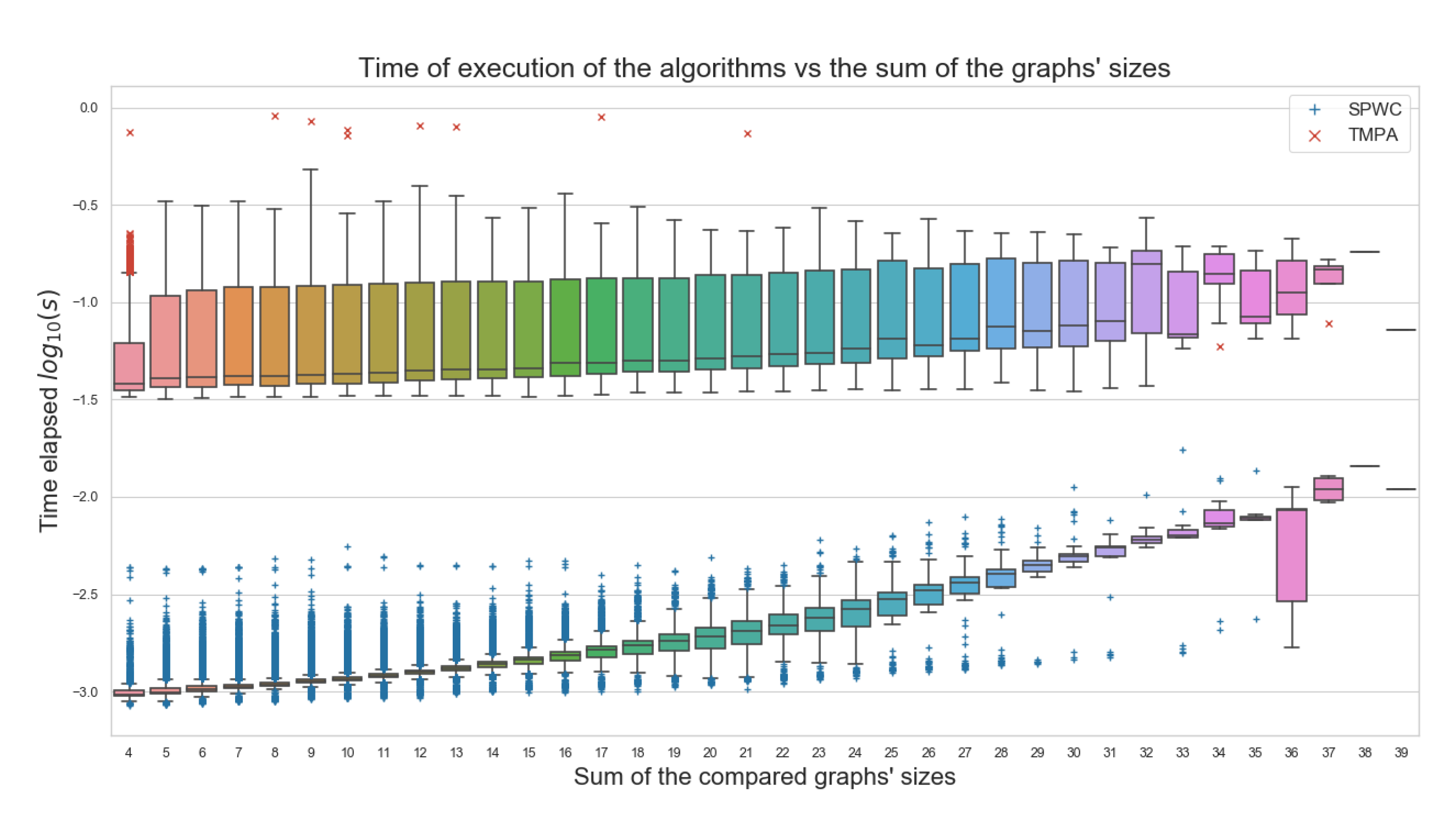
5.6. Timing Evaluations
5.7. Summary
- Data from a real, updated, and important database was used;
- The proposed algorithms execute at least 10 times faster than the external tool used for comparison. One of the main goals for this work;
- Equivalent nodes ratio equals 0, meaning no common elements between the pathways being compared, will always produce a 0 score;
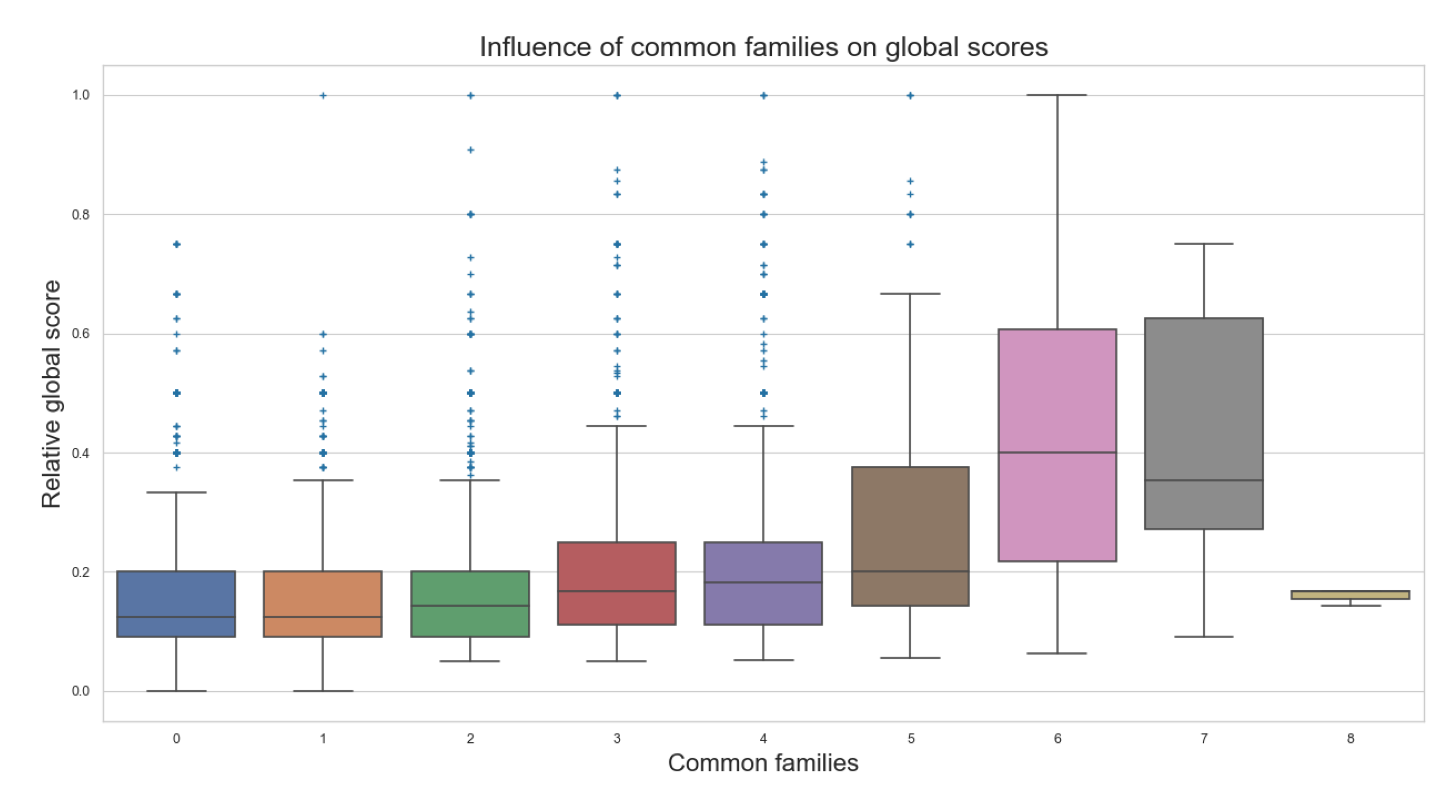
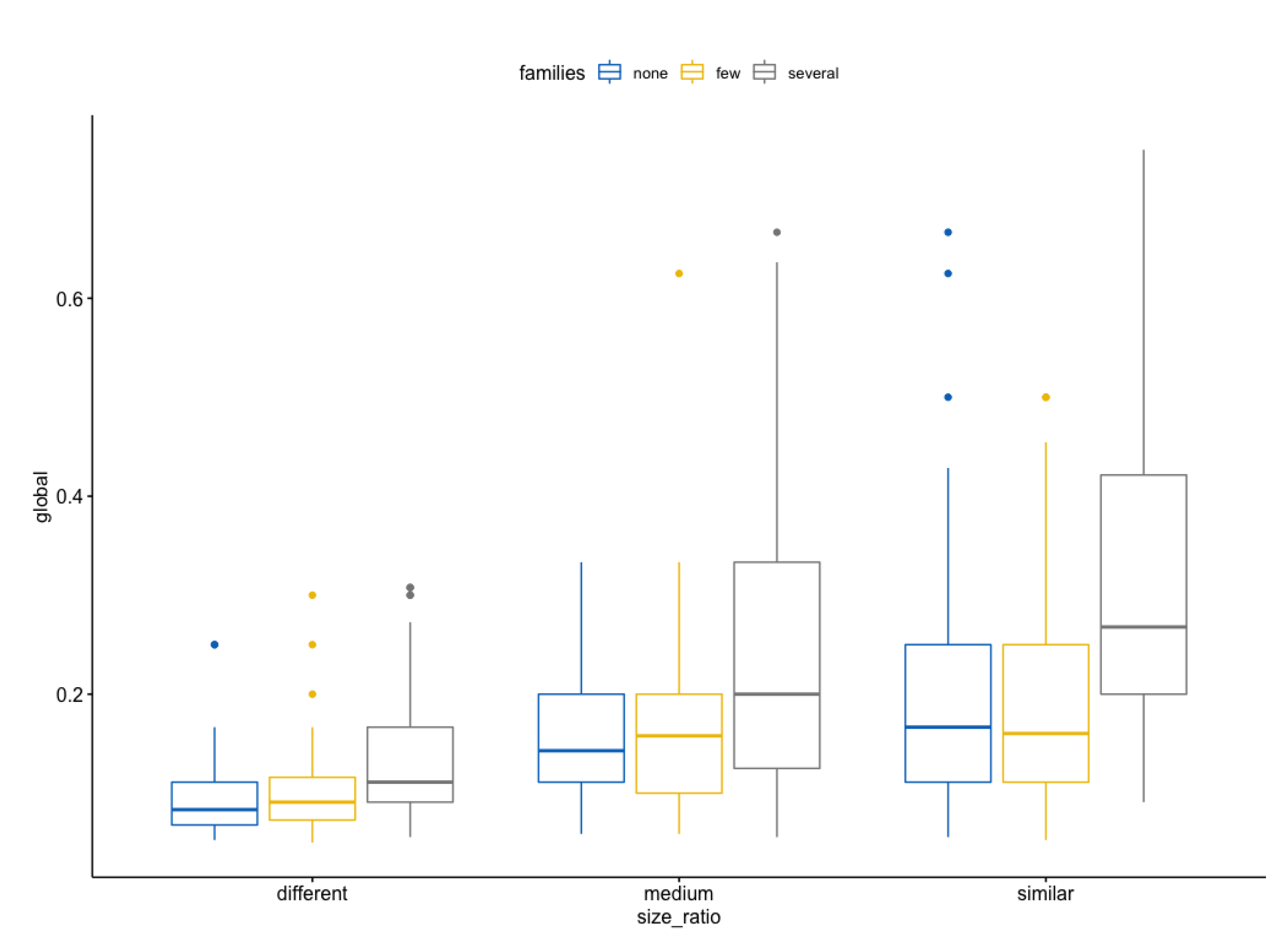
- The more similar the sizes of the metabolic pathways and the more common families between them, the better the scores obtained;
- This is an observation that has biological meaning, with few exceptions;
- As with everything in Biology, there is no rule for 100% of the cases;
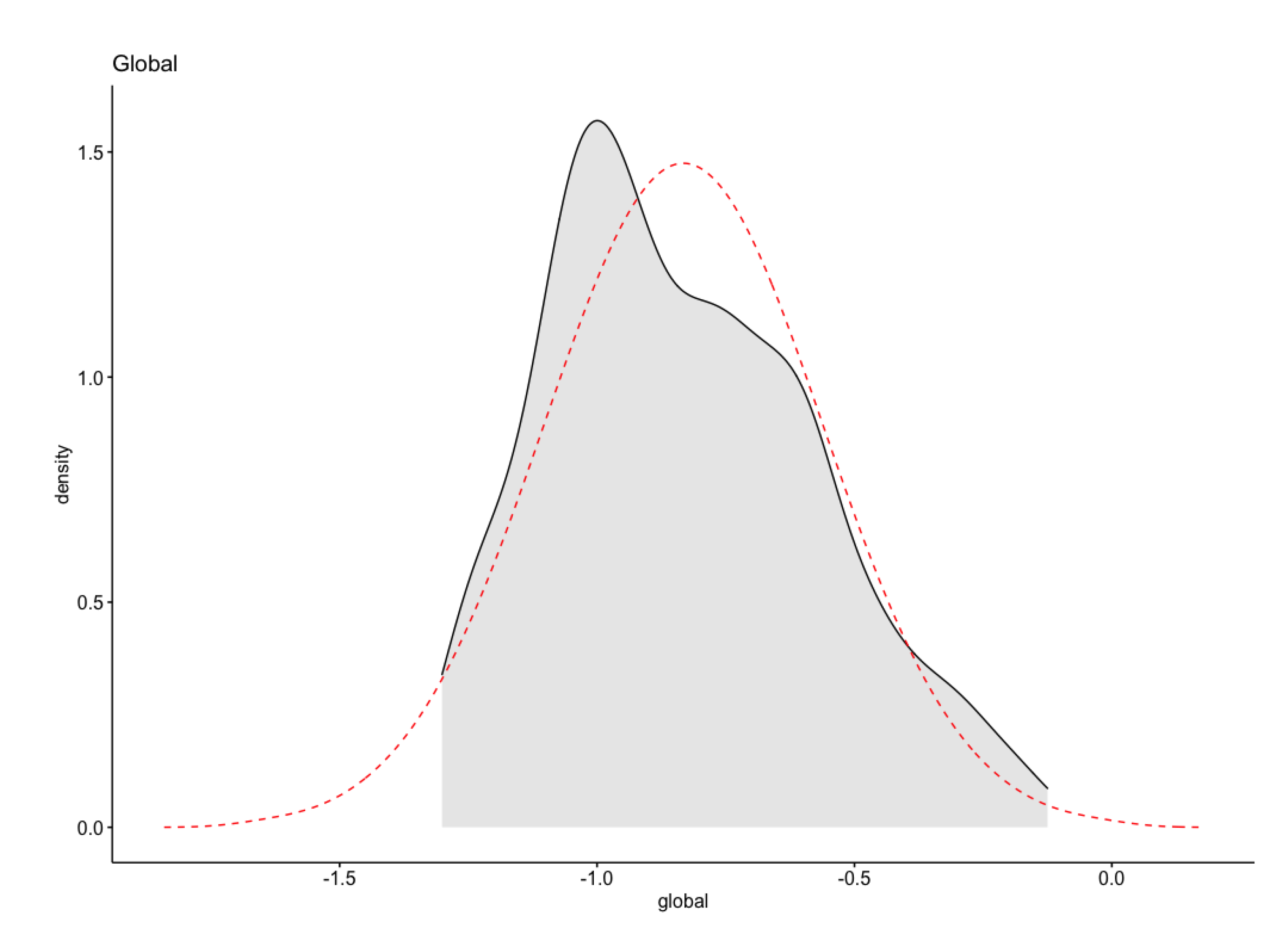
- The data does not follow a normal distribution;
- After a log10 transformation, a normality test shows positively skewed data;
- Homogeneity of variance was not perfectly adjusted;
- The analysis of variance was performed Welch’s ANOVA and Bonferroni correction to the models;
- Thousands of comparisons executed indicated independence in the input data and the resulting scores, but there is significant statistical evidence of the influence of the size ratio and common families;
- Data may have some extreme outliers. It was observed that pairwise compared metabolic pathways with several common families might have a few or none similar elements for comparison, producing lower scores than its counterparts, contradicting some of the general behaviors observed for most of the comparisons;
- Several scientific publications have been produced as a result of this work;
- The algorithms have been applied and extended to real scenarios with data from labs, confirming the biological significance of the proposed algorithms.
6. Conclusions
7. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BFT | Breadth-First Traversal |
| DbP | Differentiation by Pairs |
| DFT | Depth-First Traversal |
References
- Ay, F.; Kellis, M.; Kahveci, T. SubMAP: Aligning metabolic pathways with subnetwork mappings. J. Comput. Biol. 2011, 18, 219–235. [Google Scholar] [CrossRef] [PubMed]
- Abaka, G.; Bıyıkoğlu, T.; Erten, C. CAMPways: Constrained alignment framework for the comparative analysis of a pair of metabolic pathways. Bioinformatics 2013, 29, i145–i153. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Arias-Mendez, E.; Torres-Rojas, F. Alternative low cost algorithms for metabolic pathway comparison. In Proceedings of the 2017 International Conference and Workshop on Bioinspired Intelligence (IWOBI), Funchal, Portugal, 10–12 July 2017; pp. 1–9. [Google Scholar]
- Needleman, S.B.; Wunsch, C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 1970, 48, 443–453. [Google Scholar] [CrossRef]
- Altschul, S.F.; Gish, W.; Miller, W.; Myers, E.W.; Lipman, D.J. Basic local alignment search tool. J. Mol. Biol. 1990, 215, 403–410. [Google Scholar] [CrossRef]
- Clarke, B.L. Stoichiometric network analysis. Cell Biophys. 1988, 12, 237–253. [Google Scholar] [CrossRef]
- Seressiotis, A.; Bailey, J.E. MPS: An artificially intelligent software system for the analysis and synthesis of metabolic pathways. Biotechnol. Bioeng. 1988, 31, 587–602. [Google Scholar] [CrossRef]
- Schuster, R.; Schuster, S. Refined algorithm and computer program for calculating all non–negative fluxes admissible in steady states of biochemical reaction systems with or without some flux rates fixed. Bioinformatics 1993, 9, 79–85. [Google Scholar] [CrossRef]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell; Garland Science: New York, NY, USA, 2007. [Google Scholar]
- Lee, J.M.; Gianchandani, E.P.; Eddy, J.A.; Papin, J.A. Dynamic analysis of integrated signaling, metabolic, and regulatory networks. Plos Comput. Biol. 2008, 4, e1000086. [Google Scholar] [CrossRef]
- Kanehisa, M.; Goto, S.; Sato, Y.; Furumichi, M.; Tanabe, M. KEGG for integration and interpretation of large-scale molecular data sets. Nucleic Acids Res. 2011, 40, D109–D114. [Google Scholar] [CrossRef]
- Caspi, R.; Foerster, H.; Fulcher, C.A.; Kaipa, P.; Krummenacker, M.; Latendresse, M.; Paley, S.; Rhee, S.Y.; Shearer, A.G.; Tissier, C.; et al. The MetaCyc Database of metabolic pathways and enzymes and the BioCyc collection of Pathway/Genome Databases. Nucleic Acids Res. 2007, 36, D623–D631. [Google Scholar] [CrossRef]
- Caspi, R.; Billington, R.; Keseler, I.M.; Kothari, A.; Krummenacker, M.; Midford, P.E.; Ong, W.K.; Paley, S.; Subhraveti, P.; Karp, P.D. The MetaCyc database of metabolic pathways and enzymes-a 2019 update. Nucleic Acids Res. 2020, 48, D445–D453. [Google Scholar] [CrossRef] [PubMed]
- Küffner, R.; Zimmer, R.; Lengauer, T. Pathway analysis in metabolic databases via differential metabolic display (DMD). Bioinformatics 2000, 16, 825–836. [Google Scholar] [CrossRef] [PubMed]
- Mithani, A.; Hein, J.; Preston, G.M. Comparative analysis of metabolic networks provides insight into the evolution of plant pathogenic and nonpathogenic lifestyles in Pseudomonas. Mol. Biol. Evol. 2010, 28, 483–499. [Google Scholar] [CrossRef] [PubMed]
- Heymans, M.; Singh, A.K. Deriving phylogenetic trees from the similarity analysis of metabolic pathways. Bioinformatics 2003, 19, i138–i146. [Google Scholar] [CrossRef] [PubMed]
- Guimerà, R.; Sales-Pardo, M.; Amaral, L.A.N. A network-based method for target selection in metabolic networks. Bioinformatics 2007, 23, 1616–1622. [Google Scholar] [CrossRef]
- Oleksii, K.; Natasa, P. Integrative network alignment reveals large regions of global network similarity in yeast and human. Bioinformatics 2011, 27, 1390–1396. [Google Scholar]
- Pinter, R.Y.; Rokhlenko, O.; Yeger-Lotem, E.; Ziv-Ukelson, M. Alignment of metabolic pathways. Bioinformatics 2005, 21, 3401–3408. [Google Scholar] [CrossRef]
- Tarjan, R. Depth-first search and linear graph algorithms. Siam J. Comput. 1972, 1, 146–160. [Google Scholar] [CrossRef]
- Bundy, A.; Wallen, L. Breadth-first search. In Catalogue of Artificial Intelligence Tools; Springer: Berlin/Heidelberg, Germany, 1984; p. 13. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming, Vol 1: Fundamental Algorithms; Addisson-Wesley: Reading, MA, USA, 1968; p. 634. [Google Scholar]
- Lee, C.Y. An algorithm for path connections and its applications. Ire Trans. Electron. Comput. 1961, EC-10, 346–365. [Google Scholar] [CrossRef]
- Smith, T.F.; Waterman, M.S. Identification of common molecular subsequences. J. Mol. Biol. 1981, 147, 195–197. [Google Scholar] [CrossRef]
- Walpole, R.; Myers, R.; Myers, S. Probability and Statistics for Engineers and Scientists; Pearson Education: New York, NY, USA, 2010. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Alboukadel, K. Comparing Multiple Means in R: ANOVA in R. Available online: https://www.datanovia.com/en/lessons/anova-in-r/ (accessed on 15 May 2021).
- Wittig, U.; De Beuckelaer, A. Analysis and comparison of metabolic pathway databases. Briefings Bioinform. 2001, 2, 126–142. [Google Scholar] [CrossRef] [PubMed]
- Alberich, R.; Llabrés, M.; Sánchez, D.; Simeoni, M.; Tuduri, M. MP-Align: Alignment of metabolic pathways. BMC Syst. Biol. 2014, 8, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Zach. How to Perform Welch’s ANOVA in R (Step-by-Step). 2021. Available online: https://www.statology.org/welchs-anova-in-r/ (accessed on 18 May 2021).
- Frost, J. Benefits of Welch’s ANOVA Compared to the Classic One-Way ANOVA. 2017. Available online: https://statisticsbyjim.com/anova/welchs-anova-compared-to-classic-one-way-anova/ (accessed on 19 May 2021).
- Zach. How to Perform a Bonferroni Correction in R. 2020. Available online: https://www.statology.org/bonferroni-correction-in-r/ (accessed on 18 May 2021).
- Kassambara, A. Transform Data to Normal Distribution in R. 2020. Available online: https://www.datanovia.com/en/lessons/transform-data-to-normal-distribution-in-r/ (accessed on 18 May 2021).

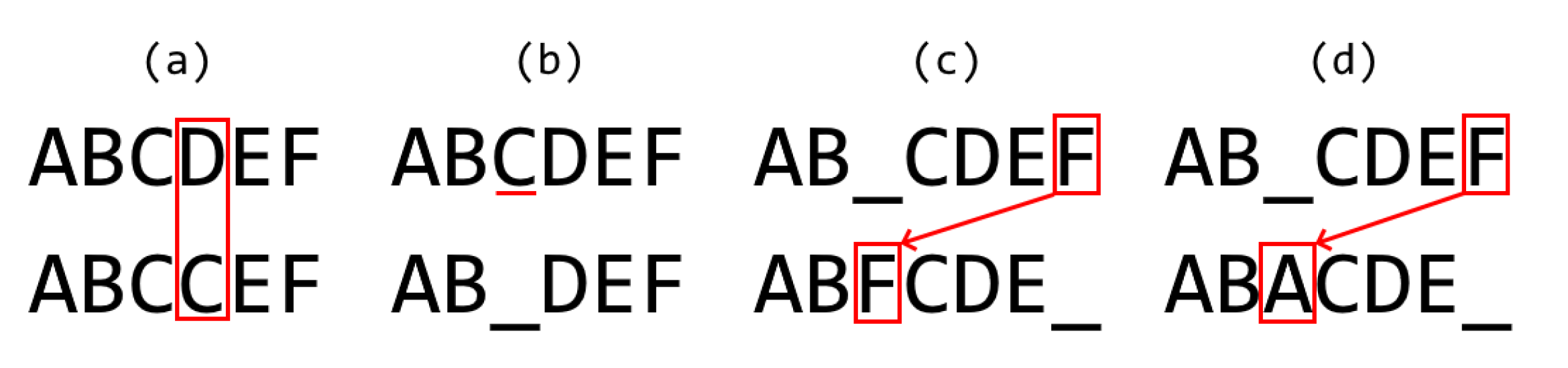
| Factors | ||
|---|---|---|
| Size Ratio | Common Families | |
| Levels | different | none |
| medium | few | |
| similar | several | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arias-Méndez, E.; Barquero-Morera, D.; Torres-Rojas, F.J. Low-Cost Algorithms for Metabolic Pathway Pairwise Comparison. Biomimetics 2022, 7, 27. https://doi.org/10.3390/biomimetics7010027
Arias-Méndez E, Barquero-Morera D, Torres-Rojas FJ. Low-Cost Algorithms for Metabolic Pathway Pairwise Comparison. Biomimetics. 2022; 7(1):27. https://doi.org/10.3390/biomimetics7010027
Chicago/Turabian StyleArias-Méndez, Esteban, Diego Barquero-Morera, and Francisco J. Torres-Rojas. 2022. "Low-Cost Algorithms for Metabolic Pathway Pairwise Comparison" Biomimetics 7, no. 1: 27. https://doi.org/10.3390/biomimetics7010027
APA StyleArias-Méndez, E., Barquero-Morera, D., & Torres-Rojas, F. J. (2022). Low-Cost Algorithms for Metabolic Pathway Pairwise Comparison. Biomimetics, 7(1), 27. https://doi.org/10.3390/biomimetics7010027






