New Aerodynamic Studies of an Adaptive Winglet Application on the Regional Jet CRJ700
Abstract
:1. Introduction
1.1. Literature Review: Aircraft Geometry Improvement
1.2. Paper Objectives
2. Methodology: Adaptive Winglet Analysis
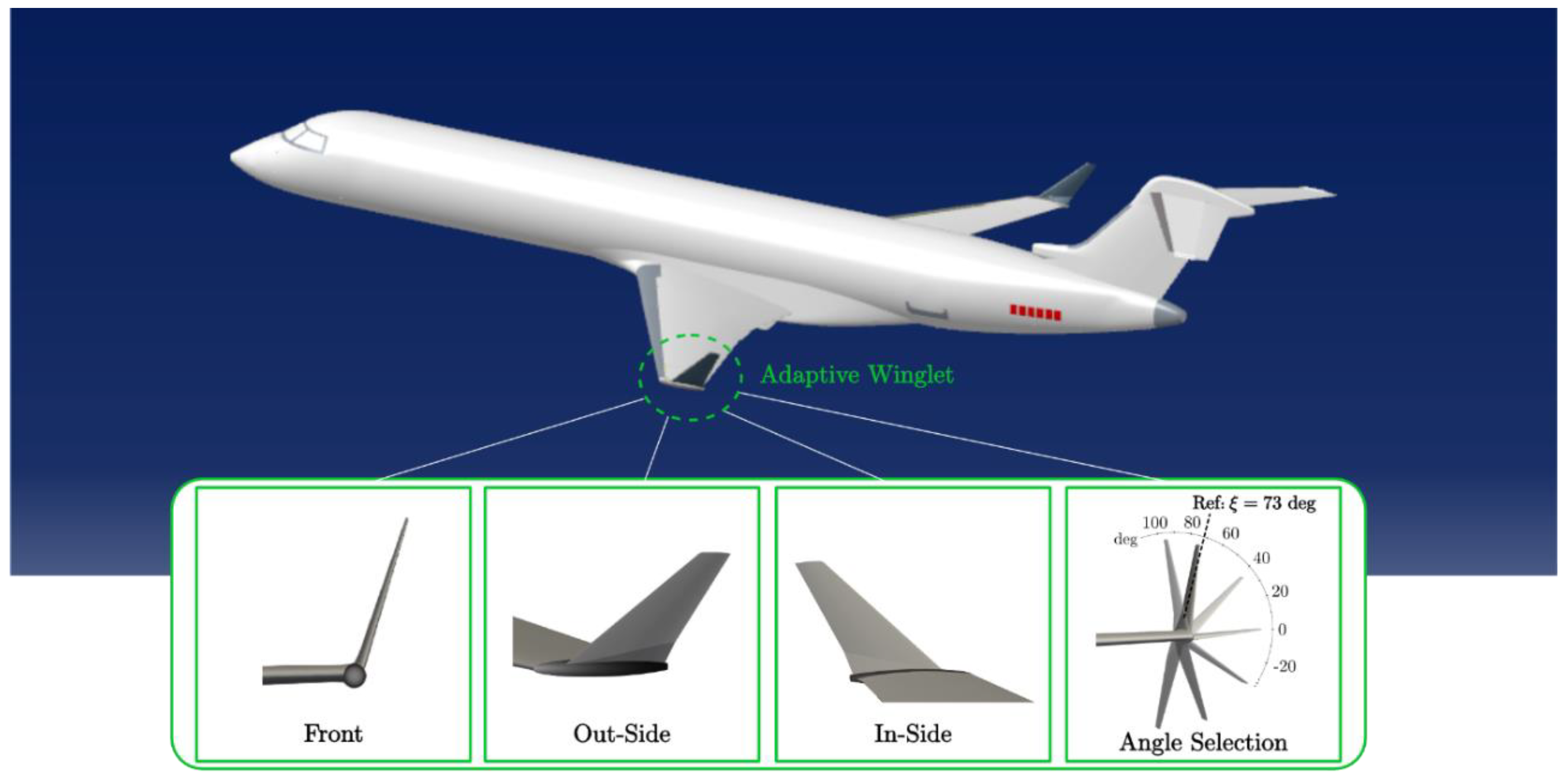
2.1. Adaptive Winglet Design
2.2. Presentation of the Aerodynamic Model
2.2.1. Mesh Design
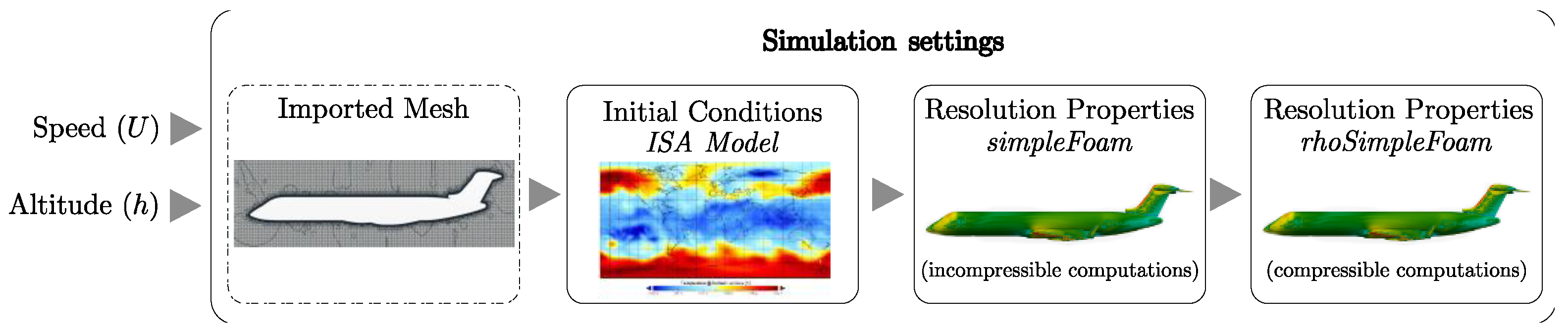
2.2.2. Simulation Settings
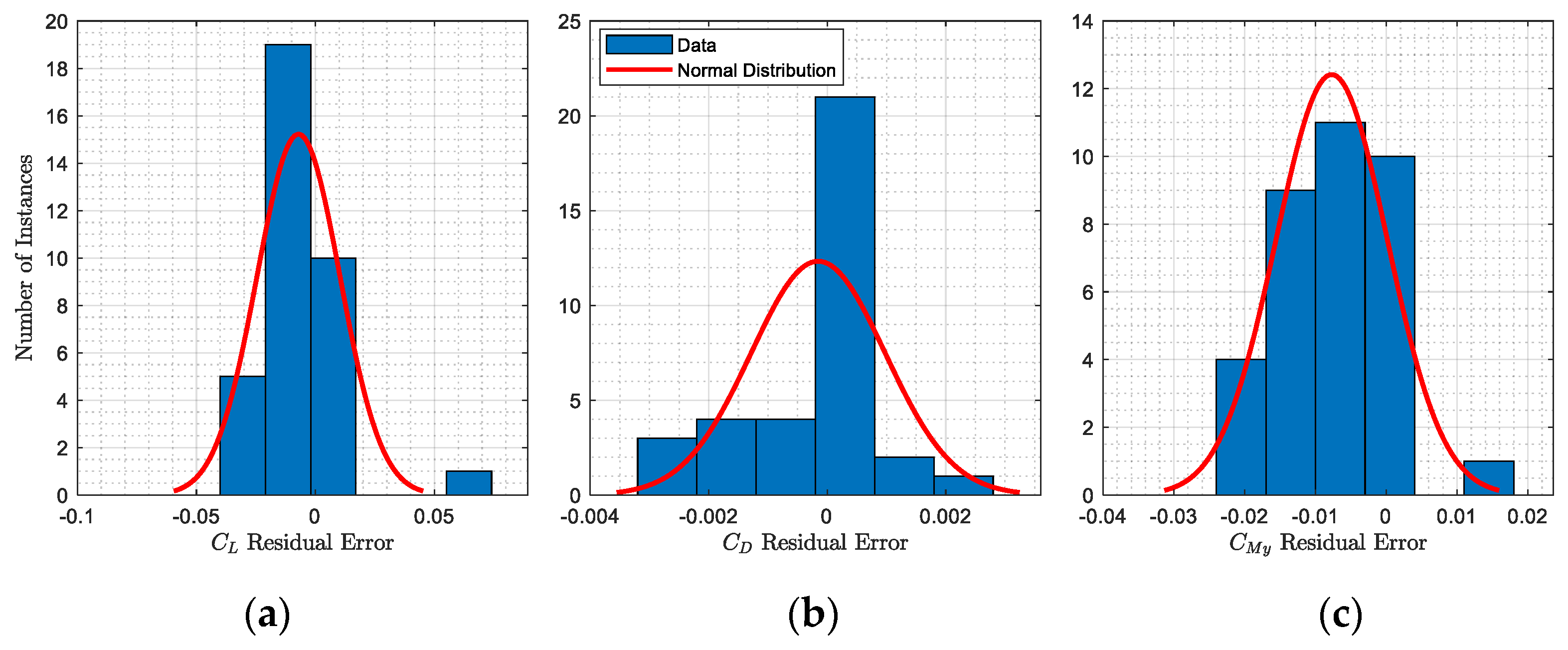
2.2.3. Validation of the CRJ700 Aerodynamic Model
2.3. Comparison of the Original and the Adaptive Winglet Designs of the CRJ700
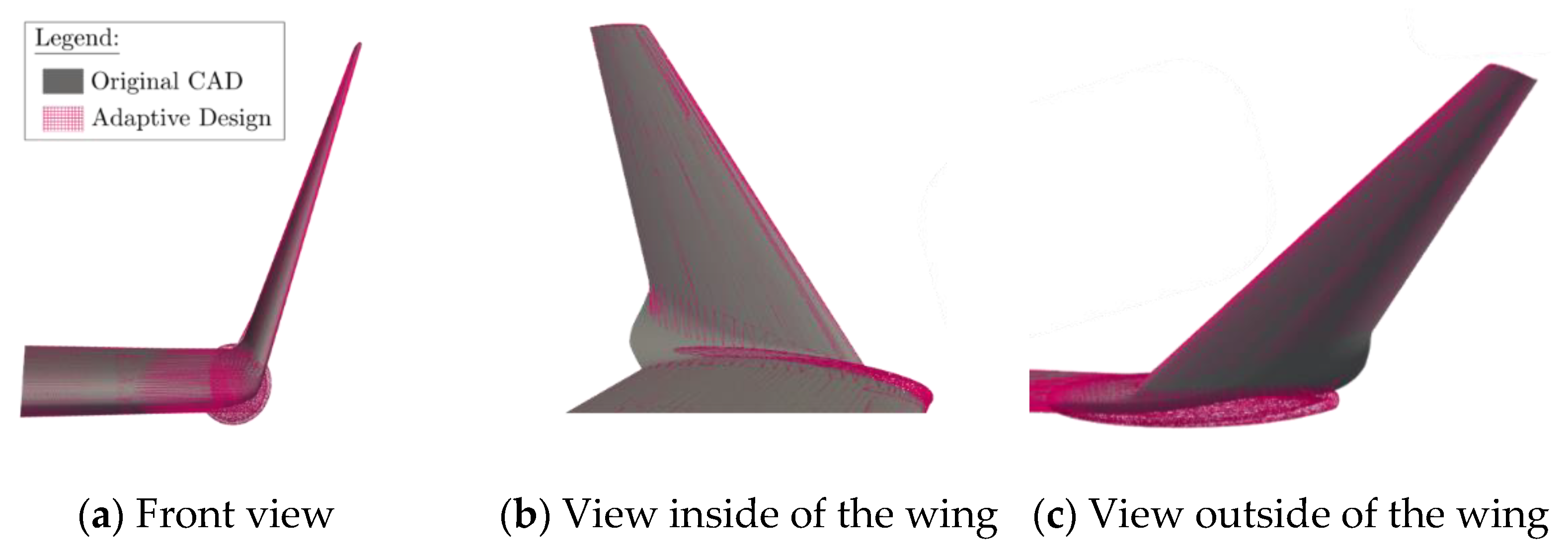
2.3.1. Geometric Comparison
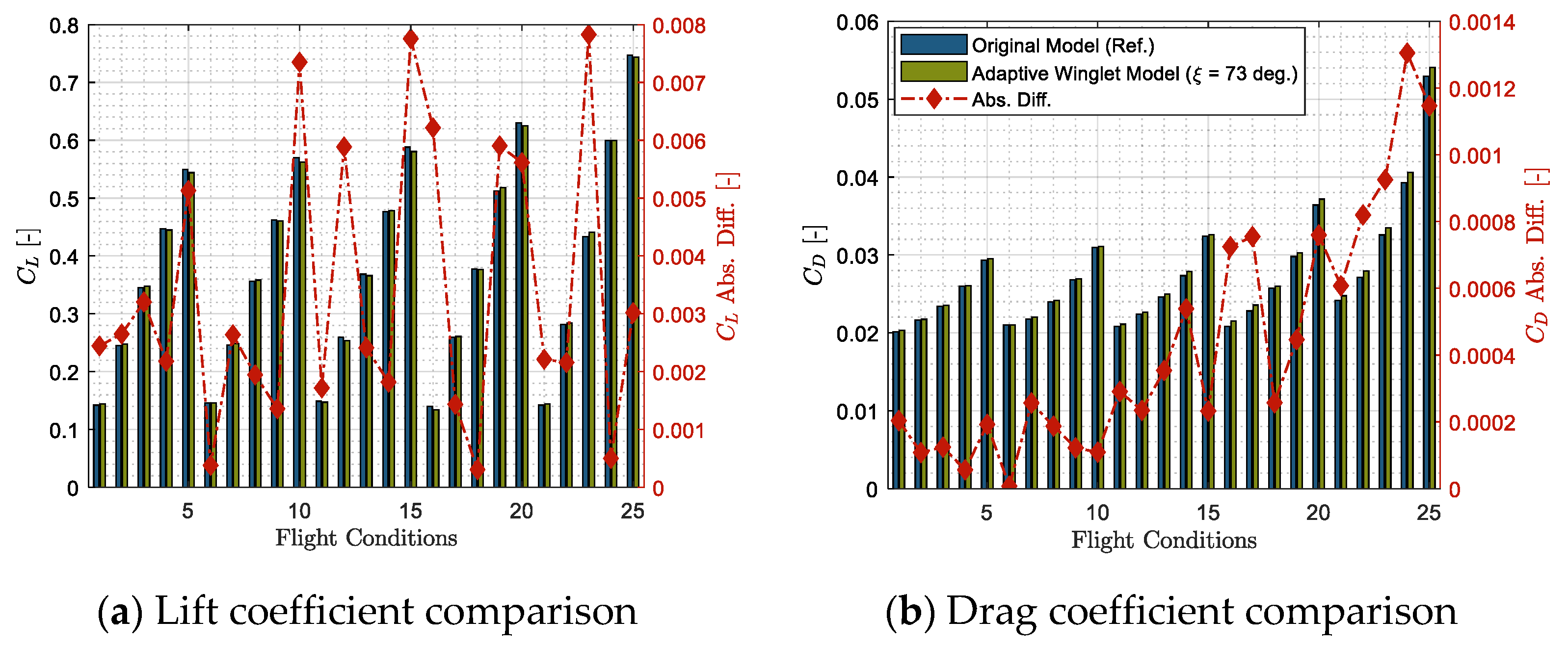
2.3.2. Aerodynamic Comparison
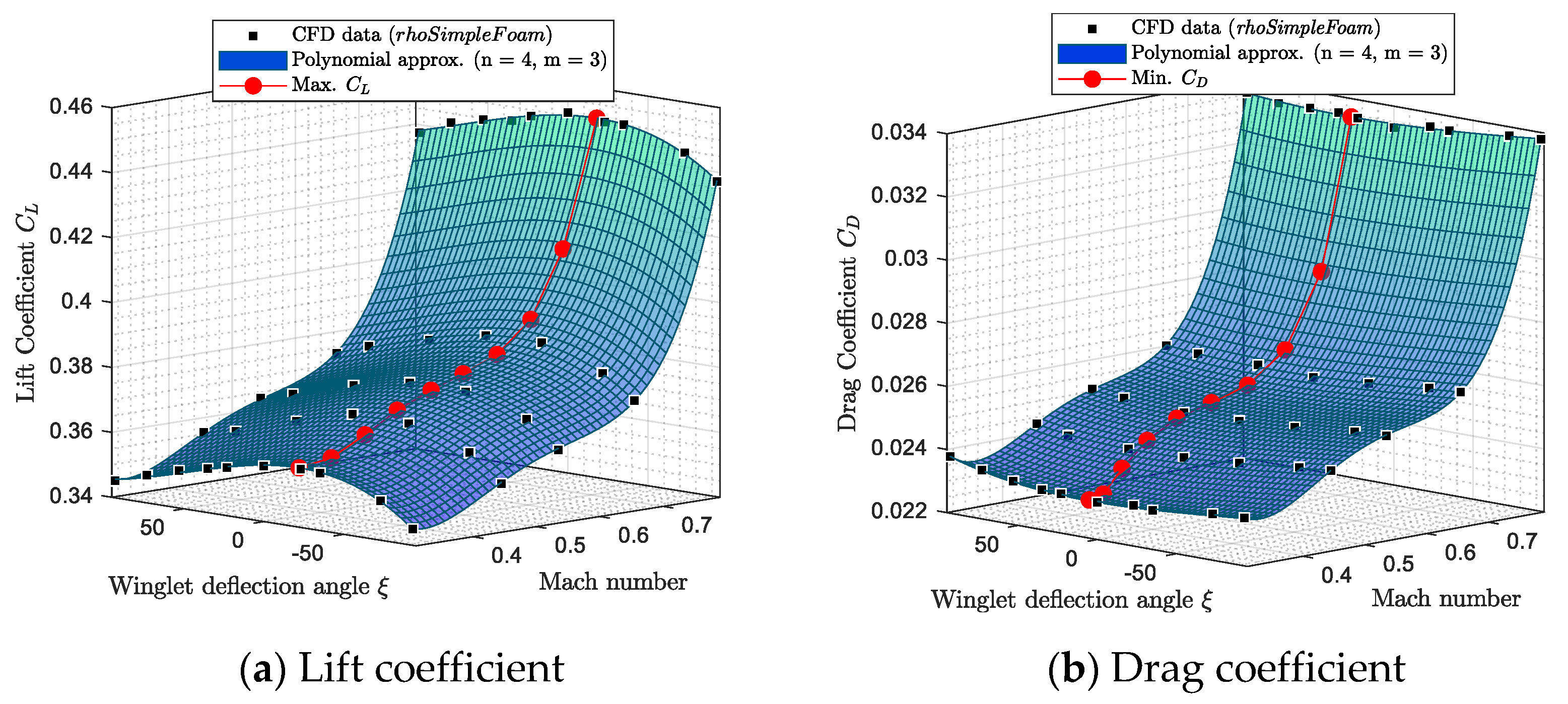
2.4. Aerodynamic Simulations
2.4.1. Aerodynamic Simulations for Specific Winglet Deflection Angles
2.4.2. Continuity Study
3. Results
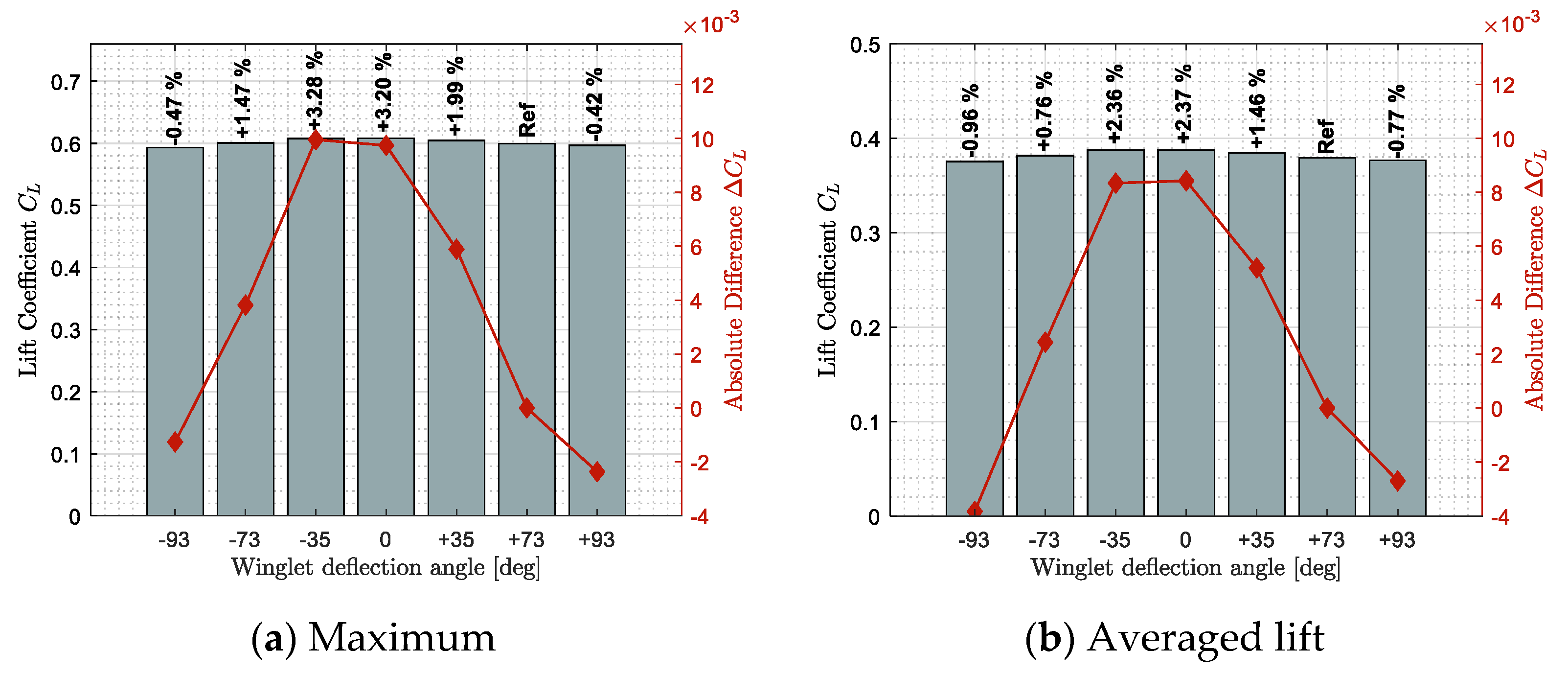
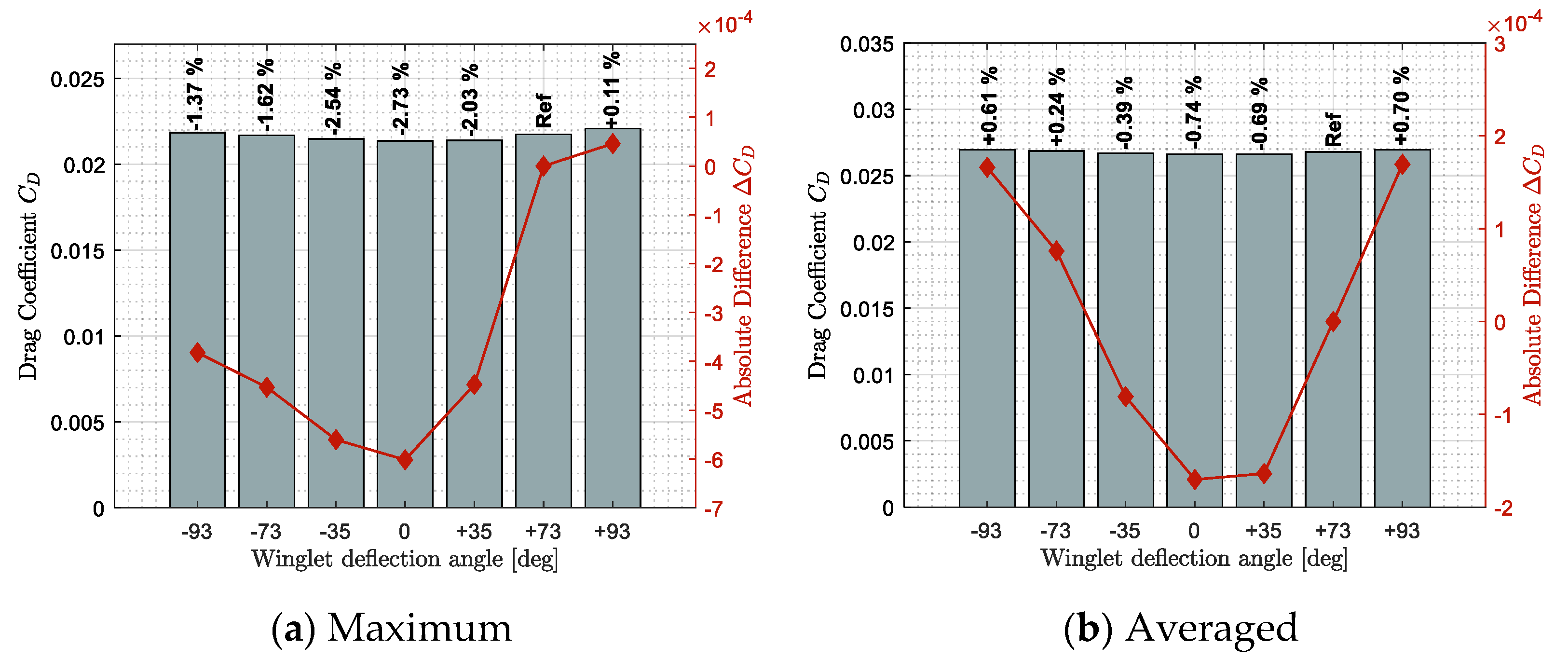
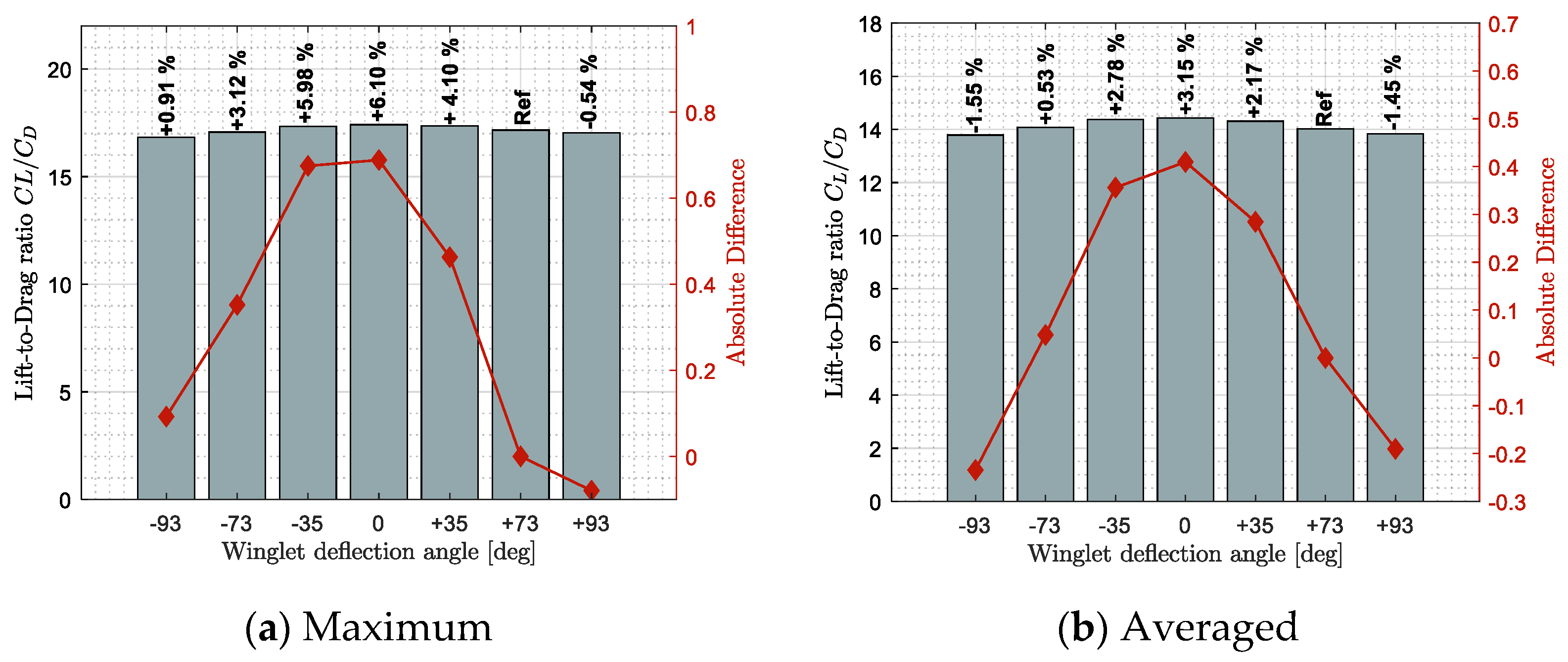
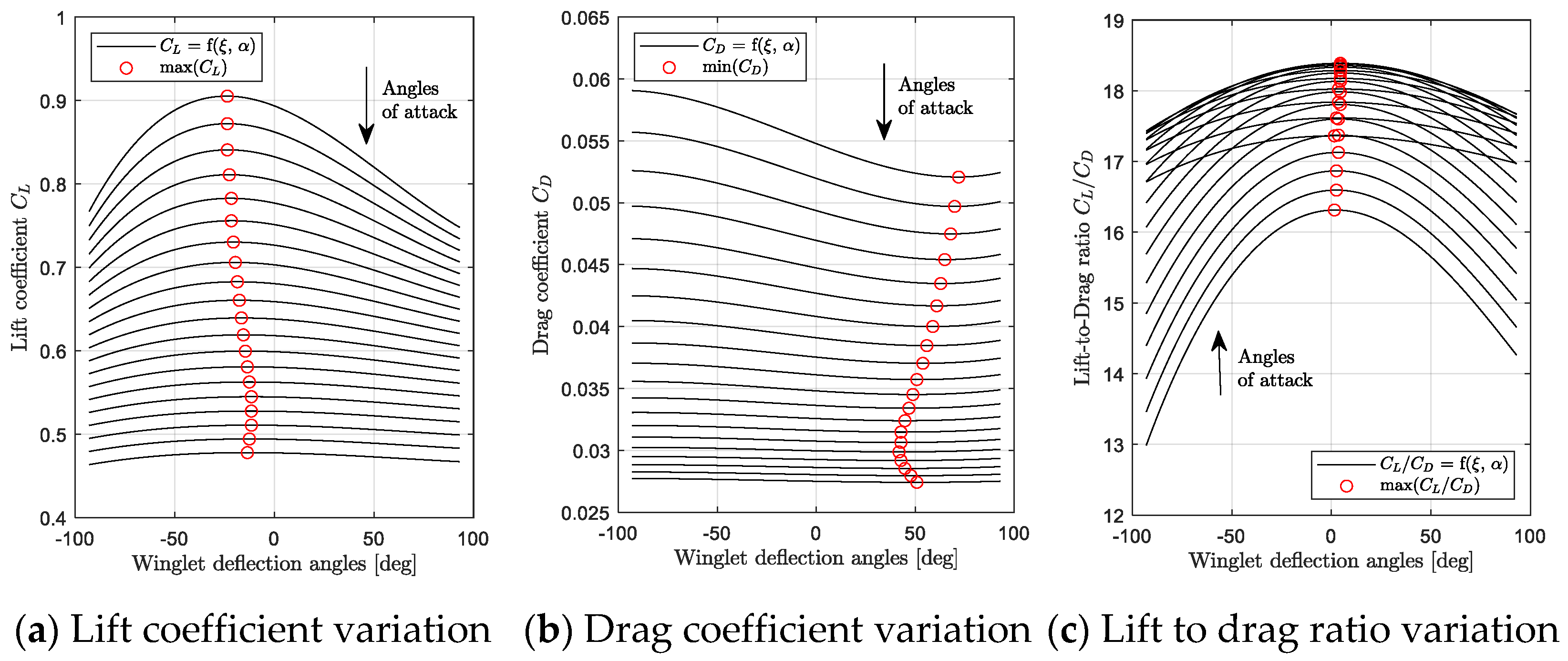
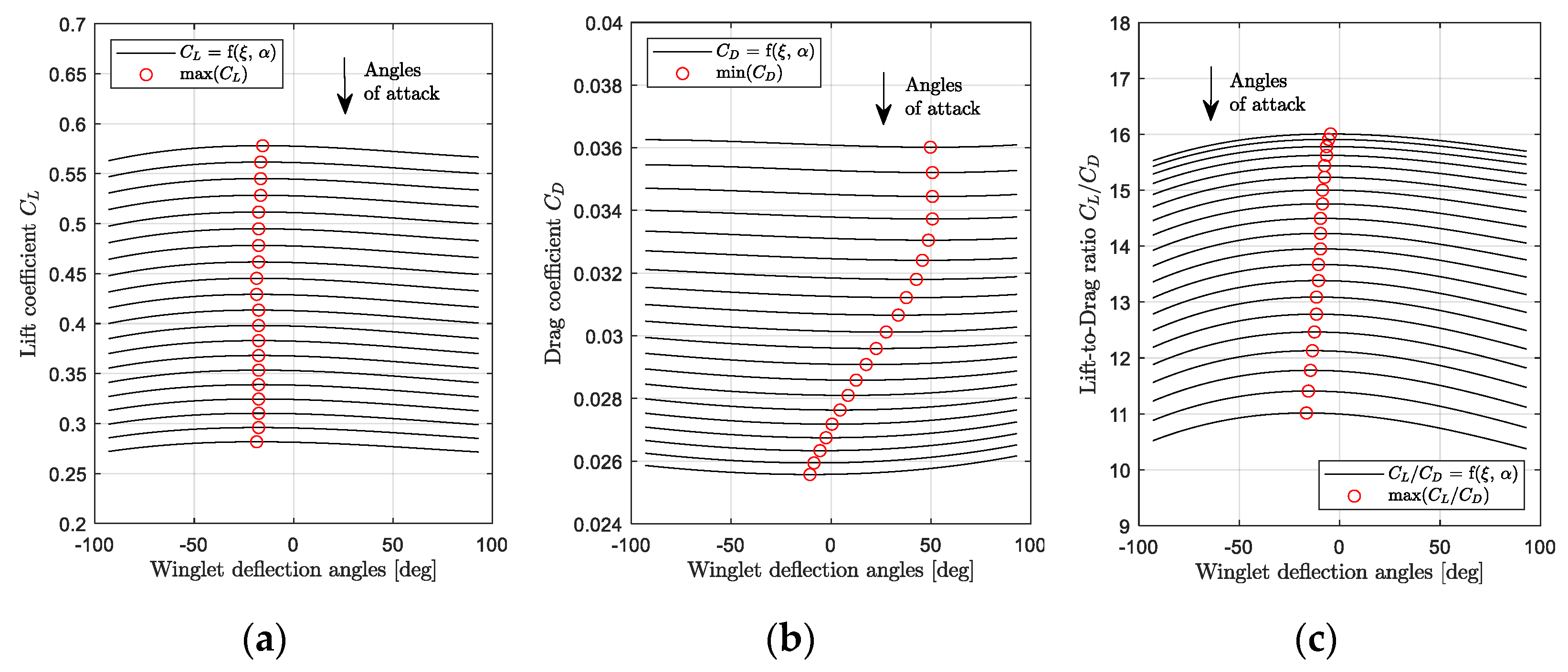
3.1. Aerodynamic Benefits of an Adaptive Winglet
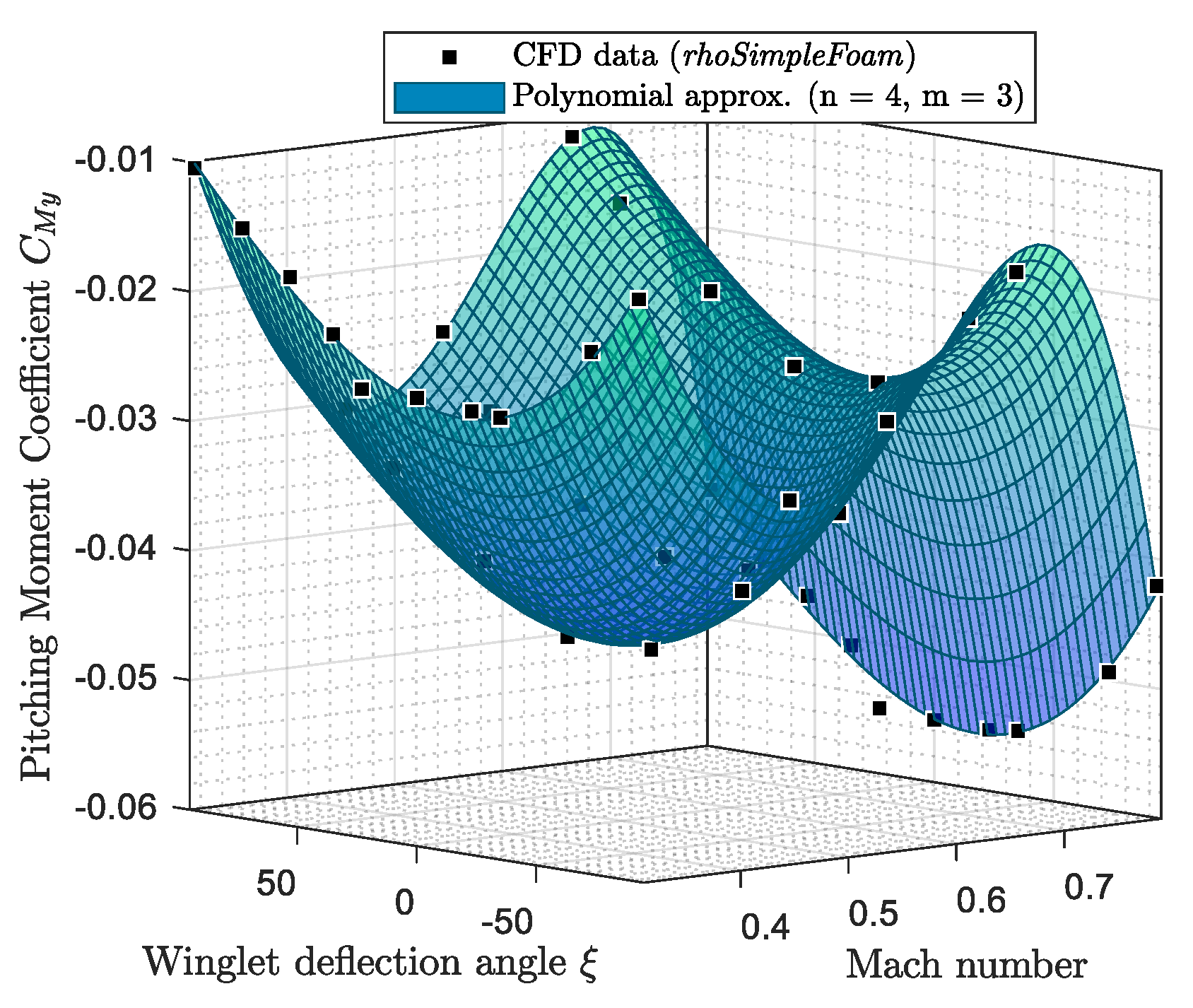
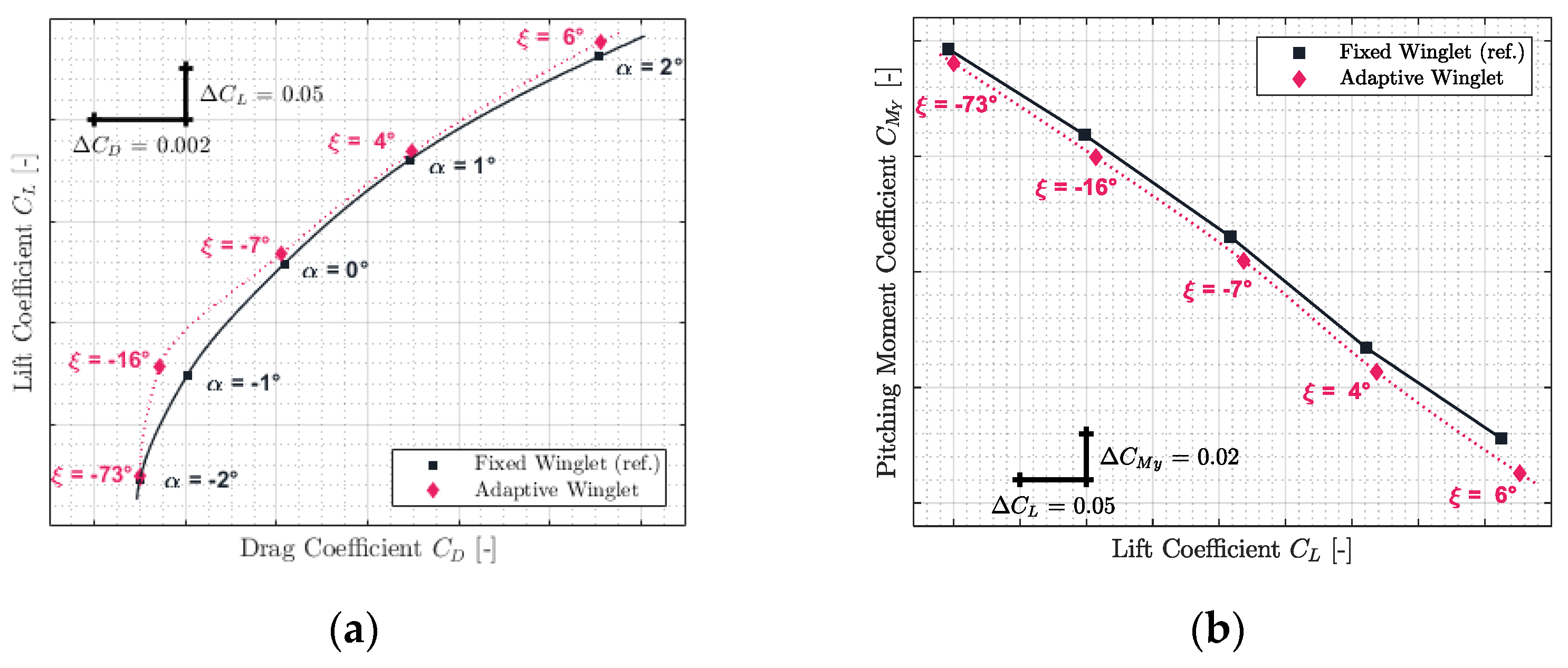
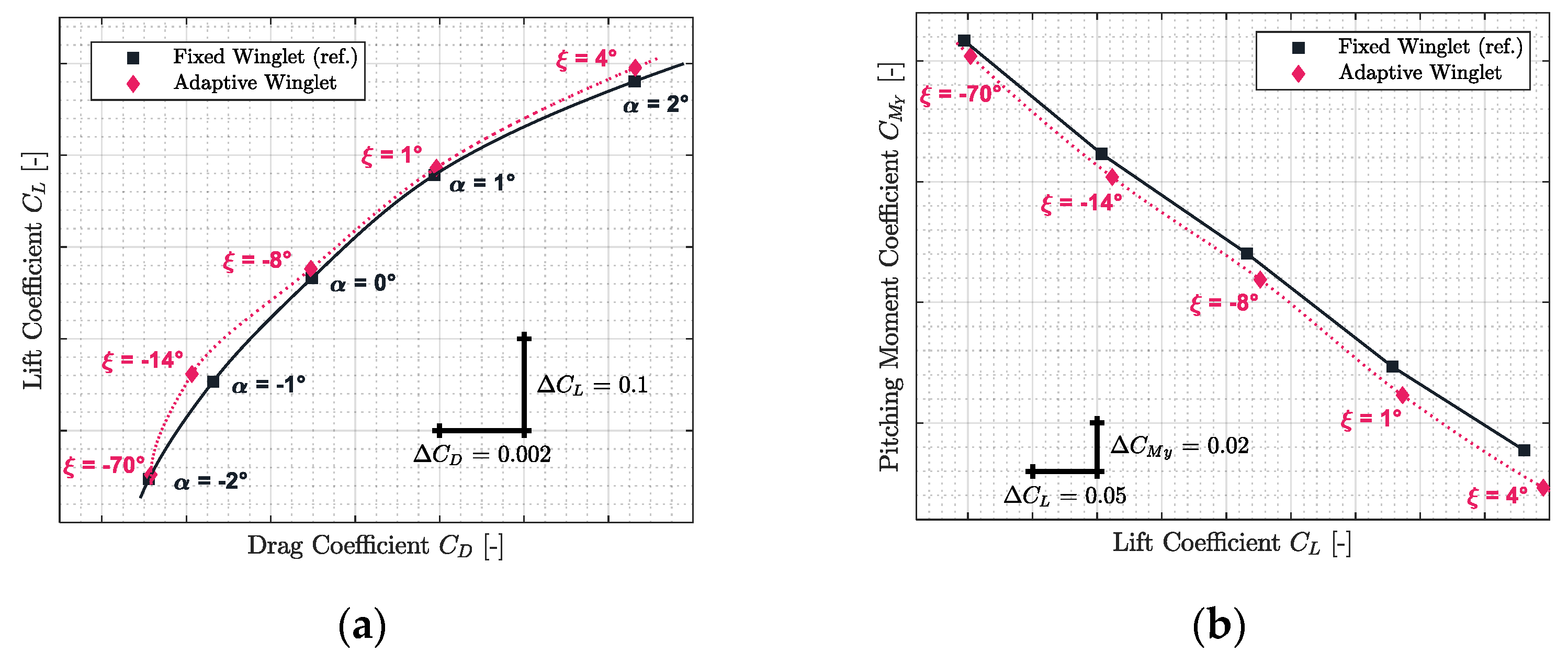
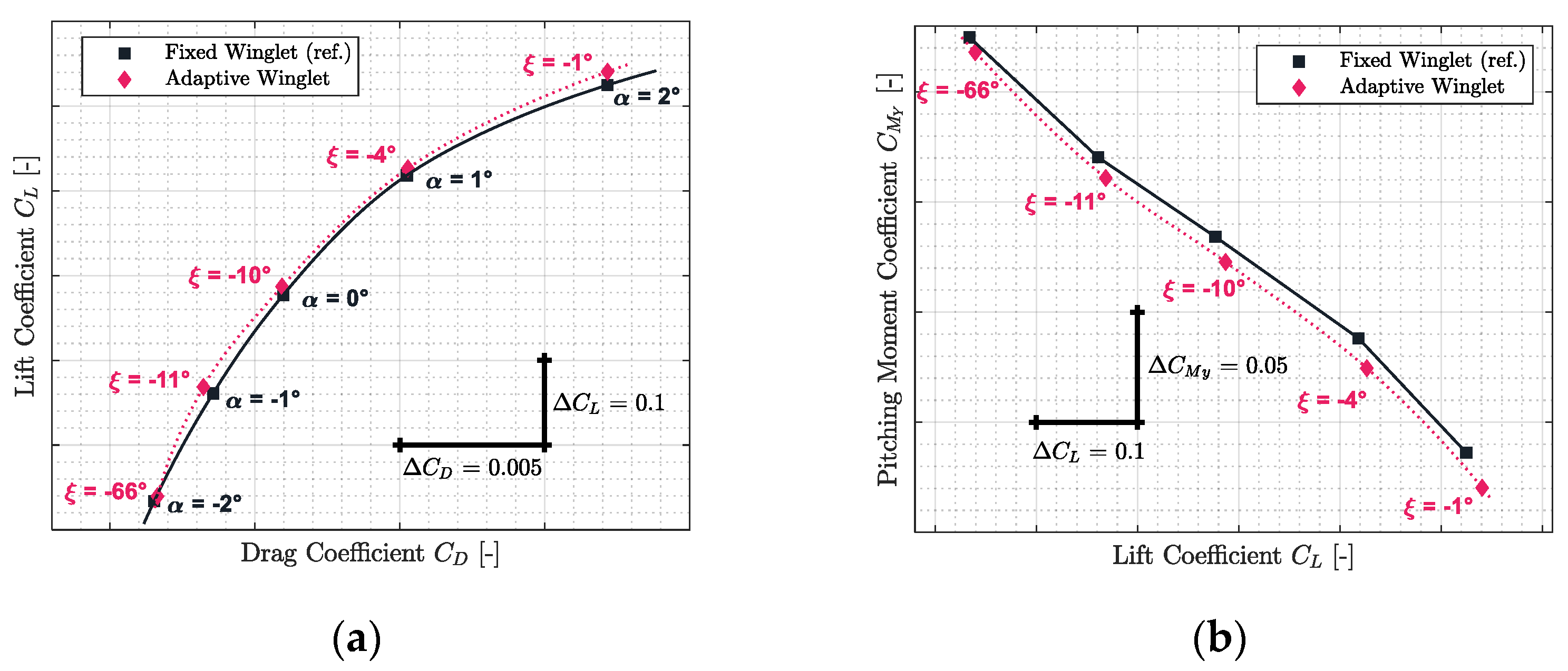
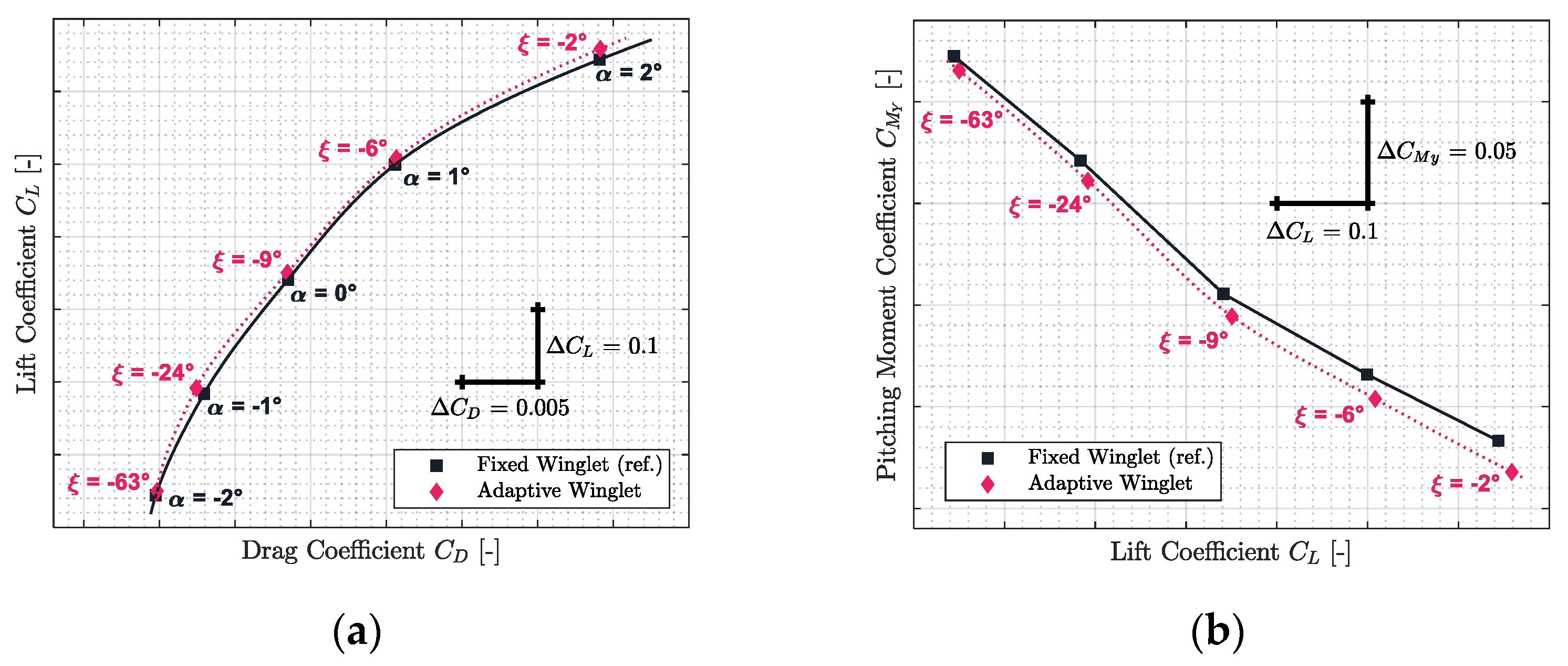
3.2. Comparison of the Characteristics of the CRJ700 Equipped with Fixed versus Adaptive Winglets in Terms of Aerodynamic Polar and Pitching Moment
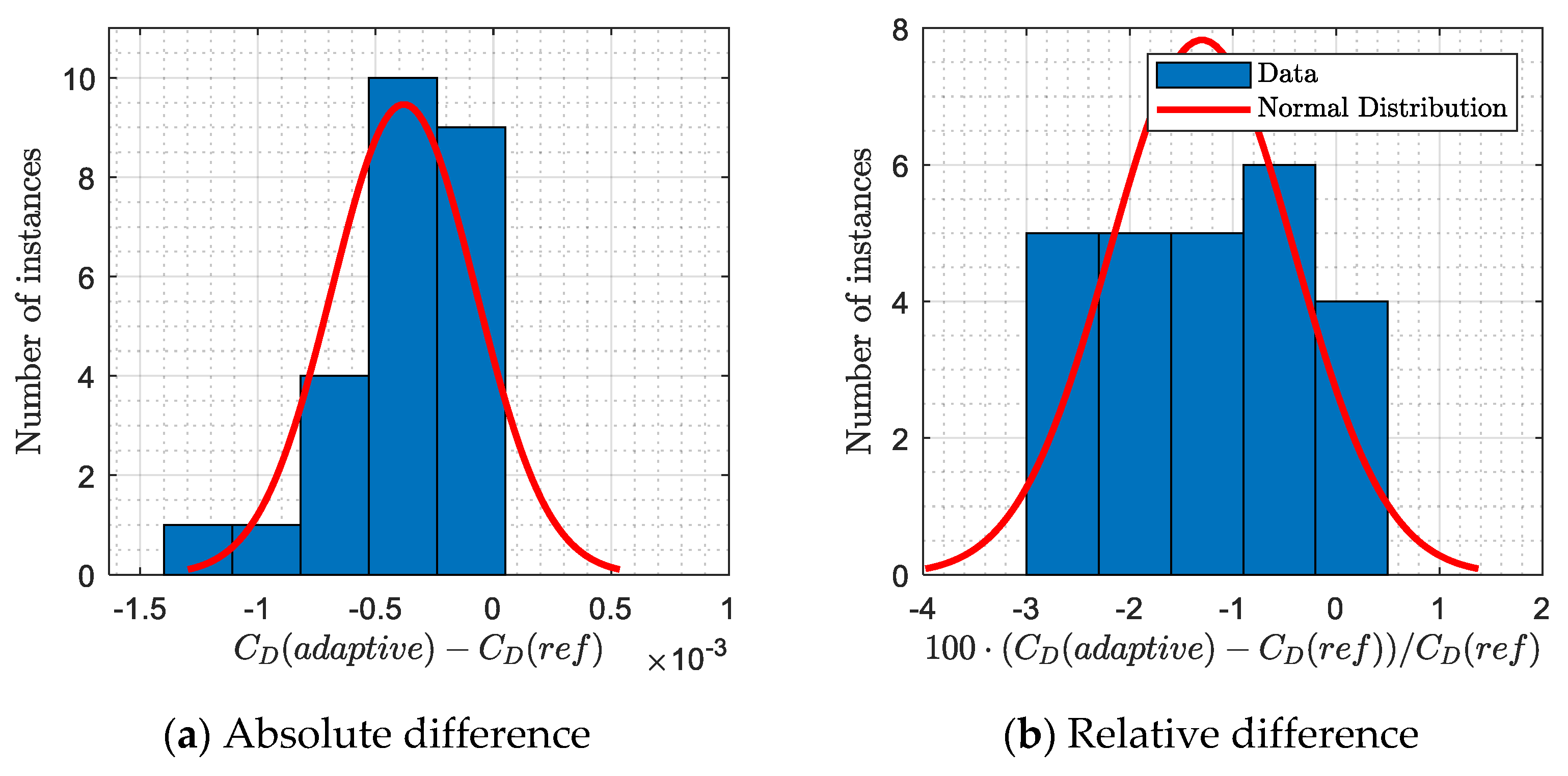
3.3. Drag Improvement Summary
3.4. Evolution of the Winglet Position during a Generic Cruise Profile
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Air Transport Action Group (ATAG). Aviation: Benefits Beyond Borders Report; ATAG: Geneva, Switzerland, 2018; p. 88. [Google Scholar]
- International Air Transport Association (IATA). Industry Statistics Fact. Sheet; IATA: Montreal, QC, Canada, 2019. [Google Scholar]
- ICAO Annex 16-Environmental Protection-Volume IV-Carbon Offsetting and Reduction Scheme for International Aviation (CORSIA). 2020. Available online: https://www.icao.int/environmental-protection/CORSIA/Documents/CORSIA_FAQs_December%202020_final.pdf (accessed on 22 September 2021).
- International Civil Aviation Organization (ICAO). Aviation’s Contribution to Climate Change; ICAO: Montreal, QC, Canada, 2010. [Google Scholar]
- Murrieta-Mendoza, A.; Botez, R.M. Commercial Aircraft Trajectory Optimization to Reduce Flight Costs and Pollution: Metaheuristic Algorithms. In Advances in Visualization and Optimization Techniques for Multidisciplinary Research: Trends in Modelling and Simulations for Engineering Applications; Vucinic, D., Rodrigues Leta, F., Janardhanan, S., Eds.; Springer: Singapore, 2020; pp. 33–62. ISBN 978-9811398063. [Google Scholar]
- Dancila, R.; Botez, R. Vertical flight profile optimization for a cruise segment with RTA constraints. Aeronaut. J. 2019, 123, 970–992. [Google Scholar] [CrossRef]
- Dancila, B.D.; Beulze, B.; Botez, R.M. Flight phase and altitude-dependent geometrical vertical flight plan optimization minimizing the total number of vertical plan segments. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 4825–4838. [Google Scholar] [CrossRef]
- Murrieta-Mendoza, A.; Ternisien, L.; Beuze, B.; Botez, R.M. Aircraft vertical route optimization by beam search and initial search space reduction. J. Aerosp. Inf. Syst. 2018, 15, 157–171. [Google Scholar] [CrossRef]
- Murrieta-Mendoza, A.; Romain, C.; Botez, R.M. Commercial aircraft lateral flight reference trajectory optimization. IFAC-PapersOnLine 2016, 49, 1–6. [Google Scholar] [CrossRef]
- Murrieta-Mendoza, A.; Botez, R.M.; Bunel, A. Four-dimensional aircraft en route optimization algorithm using the artificial bee colony. J. Aerosp. Inf. Syst. 2018, 15, 307–334. [Google Scholar] [CrossRef]
- Ghazi, G.; Gerardin, B.; Gelhaye, M.; Botez, R.M. New adaptive algorithm development for monitoring aircraft performance and improving flight management system predictions. J. Aerosp. Inf. Syst. 2020, 17, 97–112. [Google Scholar] [CrossRef]
- Ghazi, G.; Botez, R.M. Method to calculate cessna citation × aircraft climb and cruise trajectory using an aero-propulsive model. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Denver, CO, USA, 5–9 June 2017; American Institute of Aeronautics and Astronautics: Denver, CO, USA, 2017. [Google Scholar]
- Ghazi, G.; Botez, R.M. Identification and Validation of an Engine Performance Database Model for the Flight Management System. J. Aerosp. Inf. Syst. 2019, 16, 307–326. [Google Scholar] [CrossRef]
- Huvelin, F.; Dequand, S.; Lepage, A.; Liauzun, C. On the validation and use of high-fidelity numerical simulations for gust response analysis. AerospaceLab J. 2018, 6, 1–16. [Google Scholar] [CrossRef]
- Ameduri, S.; Concilio, A. Morphing wings review: Aims, challenges, and current open issues of a technology. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 1, 0954406220944423. [Google Scholar] [CrossRef]
- Dimino, I.; Andreutti, G.; Moens, F.; Fonte, F.; Pecora, R.; Concilio, A. Integrated design of a morphing winglet for active load control and alleviation of turboprop regional aircraft. Appl. Sci. 2021, 11, 2439. [Google Scholar] [CrossRef]
- Amendola, G.; Dimino, I.; Concilio, A.; Pecora, R.; Amoroso, F. A linear guide-based actuation concept for a novel morphing aileron. Aeronaut. J. 2019, 123, 1075–1097. [Google Scholar] [CrossRef]
- Concilio, A.; Dimino, I.; Pecora, R. SARISTU: Adaptive Trailing Edge Device (ATED) design process review. Chin. J. Aeronaut. 2021, 34, 187–210. [Google Scholar] [CrossRef]
- Freestone Aerodynamic Principles of Winglets; Engineering Science Data Unit: London, UK, 1988; ISBN 978 1 86246 050 8.
- The Boeing Company. Operational Efficiency and Environmental Performance. AERO Magazine. 2009. Available online: https://www.boeing.com/commercial/aeromagazine/articles/qtr_03_09/pdfs/AERO_Q309_article01.pdf (accessed on 22 September 2021).
- Hitchens, F. The Encyclopedia of Aerodynamics; Andrews UK Limited: Luton, UK, 2015; ISBN 978-1785383243. [Google Scholar]
- United Airlines. United Airlines Is the First to Fly with New Fuel-Efficient Split Scimitar Winglets, United Airline Worldwide Media Relations. 2014. Available online: https://united.mediaroom.com/2014-02-19-United-Airlines-is-the-First-to-Fly-with-New-Fuel-Efficient-Split-Scimitar-Winglets (accessed on 22 September 2021).
- Heathers, D. New Boeing 777 Raked Wing Tips Improve Fuel Efficiency, Boeing Media Room. 2002. Available online: https://boeing.mediaroom.com/2002-10-01-New-Boeing-777-Raked-Wing-Tips-Improve-Fuel-Efficiency-Good-for-the-Environment (accessed on 22 September 2021).
- John, O. How the 777X’s Folding Wing Tips Work, the Air Current. 2018. Available online: https://theaircurrent.com/technology/how-the-777xs-folding-wing-tips-work/ (accessed on 21 September 2021).
- Boeing: 777X. Available online: https://www.boeing.com/commercial/777x/ (accessed on 10 April 2020).
- Federal Aviation Administration. The Boeing Company Model 777–8 and 777–9 Airplanes Folding Wingtips. Rules and Regulation. Federal Registrer. 2018. Available online: https://www.federalregister.gov/documents/2018/05/18/2018-10576/special-conditions-the-boeing-company-model-777-8-and-777-9-airplanes-folding-wingtips (accessed on 21 September 2021).
- Welcome to the Clean Sky|Clean Sky. Available online: https://www.cleansky.eu/ (accessed on 10 April 2020).
- Control and Alleviation of Loads in Advanced Regional Turbo Fan Configurations (CLARET)-Final Report Summary. Available online: https://cordis.europa.eu/project/id/287078/reporting (accessed on 10 April 2020).
- Cooper, J.E.; Chekkal, I.; Cheung, R.C.M.; Wales, C.; Allen, N.J.; Lawson, S.; Peace, A.J.; Cook, R.; Standen, P.; Hancock, S.D.; et al. Design of a morphing wingtip. J. Aircr. 2015, 52, 1394–1403. [Google Scholar] [CrossRef] [Green Version]
- Healy, F.; Cheung, R.C.; Neofet, T.; Lowenberg, M.H.; Rezgui, D.; Cooper, J.E.; Castrichini, A.; Wilson, T. Folding wingtips for improved roll performance. In Proceedings of the AIAA Scitech 2021 Forum, Online, 11 January 2021; American Institute of Aeronautics and Astronautics: Denver, CO, USA, 2021. [Google Scholar]
- Castrichini, A.; Siddaramaiah, V.H.; Calderon, D.E.; Cooper, J.E.; Wilson, T.; Lemmens, Y. Preliminary investigation of use of flexible folding wing tips for static and dynamic load alleviation. Aeronaut. J. 2017, 121, 73–94. [Google Scholar] [CrossRef] [Green Version]
- Cheung, R.C.M.; Rezgui, D.; Cooper, J.E.; Wilson, T. Testing of a hinged wingtip device for gust loads alleviation. J. Aircr. 2018, 55, 2050–2067. [Google Scholar] [CrossRef]
- Wildschek, A.; Storm, S.; Herring, M.; Drezga, D.; Korian, V.; Roock, O. Design, optimization, testing, verification, and validation of the wingtip active trailing edge. In Smart Intelligent Aircraft Structures (SARISTU); Springer: Cham, Switzerland, 2015; pp. 219–255. ISBN 978-3319224121. [Google Scholar]
- Liauzun, C.; Le Bihan, D.; David, J.-M.; Joly, D.; Paluch, B. Study of morphing winglet concepts aimed at improving load control and the aeroelastic behavior of civil transport aircraft. Aerosp. Lab. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Carossa, G.M.; Ricci, S.; De Gaspari, A.; Liauzun, C.; Dumont, A.; Steinbuch, M. Adaptive Trailing Edge: Specifications, Aerodynamics, and Exploitation. In Smart Intelligent Aircraft Structures (SARISTU); Wölcken, P.C., Papadopoulos, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 143–158. ISBN 978-3319224121. [Google Scholar]
- Amendola, G.; Dimino, I.; Concilio, A.; Andreutti, G.; Pecora, R.; Cascio, M.L. Preliminary design process for an adaptive winglet. Int. J. Mech. Eng. Robot. Res. 2017, 6, 83–92. [Google Scholar] [CrossRef] [Green Version]
- Daniele, E.; De Fenza, A.; Vecchia, P.D. Conceptual adaptive wing-tip design for pollution reductions. J. Intell. Mater. Syst. Struct. 2012, 23, 1197–1212. [Google Scholar] [CrossRef]
- Concilio, A.; Dimino, I.; Lecce, L.; Pecora, R. Morphing Wing Technologies: Large Commercial Aircraft and Civil Helicopters; Butterworth-Heinemann: Oxford, UK, 2018; ISBN 978-0081009642. [Google Scholar]
- Botez, R.M. Morphing wing, UAV and aircraft multidisciplinary studies at the laboratory of applied research in active controls, avionics and aeroservoelasticity LARCASE. AerospaceLab J. 2018, 2, 1–11. [Google Scholar] [CrossRef]
- Tchatchueng Kammegne, M.J.; Botez, R.M.; Grigorie, T.L. A fuel saving way in aerospace engineering based on morphing wing technology–A new multidisciplinary experimental model. Int. J. Contemp. Energy 2016, 11–21. [Google Scholar] [CrossRef]
- Koreanschi, A.; Sugar Gabor, O.; Acotto, J.; Brianchon, G.; Portier, G.; Botez, R.M.; Mamou, M.; Mebarki, Y. Optimization and design of a morphing wing tip aircraft demonstrator for drag reduction at low speed, part I–Aerodynamic optimizations using genetic, bee colony and gradient descent algorithms. Chin. J. Aeronaut. 2017, 30, 149–163. [Google Scholar] [CrossRef]
- Koreanschi, A.; Sugar Gabor, O.; Acotto, J.; Brianchon, G.; Portier, G.; Botez, R.M.; Mamou, M.; Mebarki, Y. Optimization and design of a morphing wing tip aircraft demonstrator for drag reduction at low speeds, part II–Experimental validation using infra-red transition measurements during wind tunnel tests. Chin. J. Aeronaut. 2017, 30, 164–174. [Google Scholar] [CrossRef]
- Koreanschi, A.; Sugar Gabor, O.; Botez, R.M. Drag optimization of a wing equipped with a morphing upper surface. Aeronaut. J. 2016, 120, 473–493. [Google Scholar] [CrossRef]
- Botez, R.M.; Koreanschi, A.; Sugar Gabor, O.; Tondji, Y.; Guezguez, M.; Kammegne, J.T.; Grigorie, T.; Sandu, D.; Mebarki, Y.; Mamou, M.; et al. Numerical and experimental transition results evaluation for a morphing wing and aileron system. Aeronaut. J. 2018, 122, 1–38. [Google Scholar] [CrossRef]
- Sugar Gabor, O. Validation of Morphing Wing Methodologies on an Unmanned Aerial System and a Wind Tunnel Demonstrator. Ph.D. Thesis, École de Technologie Supérieure, Montréal, QC, Canada, 2015. [Google Scholar]
- Segui, M.; Botez, R.M. Cessna Citation X static cruise improvement using morphing wing application on its horizontal tail. In Proceedings of the European Conference for Aeronautics and Space Sciences (EUCASS), Madrid, Spain, 1–4 July 2019. [Google Scholar]
- Segui, M.; Gabor, O.S.; Koreanschi, A.; Botez, R.M. Morphing wing application on hydra technologies UAS-S4. In Proceedings of the 36th IASTED International Conference on Modelling, Identification and Control, Innsbruck, Austria, 20–21 February 2017. [Google Scholar]
- Segui, M.; Bezin, S.; Botez, R.M. Cessna citation X performances improvement by an adaptive winglet during the cruise flight. Int. J. Aerosp. Mech. Eng. 2018, 12, 423–430. [Google Scholar] [CrossRef]
- Segui, M.; Botez, R.M. Cessna Citation X Climb and Cruise Performance Improvement Using Adaptive Winglet. In Proceedings of the Advanced Aircraft Efficiency in a Global Air Transport System 18′ (AEGATS), Toulouse, France, 24 October 2018; Volume 13. [Google Scholar]
- MHI RJ Aviation ULC. CRJ Series; Canada. 2020. Available online: https://mhirj-preview-files.s3-us-west-2.amazonaws.com/mhirj/2020-12/MHIRJ_CRJ700_Factsheet_FR_V1_web.pdf (accessed on 22 September 2021).
- Federal Aviation Administration (FAA). Airplane Simulator Qualification; FAA U.S Department of Transportation: Washington, DC, USA, 1991.
- AIRBUS. Airbus’ “BLADE” Laminar Flow Wing Demonstrator Makes First Flight, Airbus Communication. 2020. Available online: https://www.airbus.com/newsroom/press-releases/en/2017/09/airbus_-_blade_-laminar-flow-wing-demonstrator-makes-first-fligh.html (accessed on 22 September 2021).
- Segui, M.; Roberto, F.A.; Botez, R.M.; Ceruti, A. High fidelity aerodynamic modeling of an aircraft using open foam-application on the CRJ700. Aeronaut. J. 2021. accepted. [Google Scholar]
- OpenCFD Ltd. OpenFoam User-Guide V1912, OpenCFD (ESI Group), Bracknell, England. Available online: https://www.openfoam.com/documentation/guides/latest/doc/ (accessed on 22 September 2021).
- Friedlander, S.; Serre, D. Handbook of Mathematical Fluid Dynamics, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 4, ISBN 978-0444528346. [Google Scholar]
- Yan, X.; Su, X. Linear Regression Analysis Theory and Computing; World Scientific Publishing Co., Pte. Ltd.: Singapore, 2009; ISBN 978-9812834119. [Google Scholar]


| Mesh Quality Parameters | Validated Model (no Pod) | New Model (with Pod) |
|---|---|---|
| Max. non-orthogonality (deg) | 65.060 | 65.020 |
| Max. skewness | 5.0006 | 4.9925 |
| Number of cells (×106) | 11.14 | 11.12 |
| Altitude | Mach Number | Angle of Attack |
|---|---|---|
| 5000 ft | M0.31 | −2 deg to +2 deg |
| 10,000 ft | M0.45 | −2 deg to +2 deg |
| 20,000 ft | M0.54 | −2 deg to +2 deg |
| 25,000 ft | M0.66 | −2 deg to +2 deg |
| 30,000 ft | M0.79 | −2 deg to +2 deg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Segui, M.; Abel, F.R.; Botez, R.M.; Ceruti, A. New Aerodynamic Studies of an Adaptive Winglet Application on the Regional Jet CRJ700. Biomimetics 2021, 6, 54. https://doi.org/10.3390/biomimetics6040054
Segui M, Abel FR, Botez RM, Ceruti A. New Aerodynamic Studies of an Adaptive Winglet Application on the Regional Jet CRJ700. Biomimetics. 2021; 6(4):54. https://doi.org/10.3390/biomimetics6040054
Chicago/Turabian StyleSegui, Marine, Federico R. Abel, Ruxandra M. Botez, and Alessandro Ceruti. 2021. "New Aerodynamic Studies of an Adaptive Winglet Application on the Regional Jet CRJ700" Biomimetics 6, no. 4: 54. https://doi.org/10.3390/biomimetics6040054
APA StyleSegui, M., Abel, F. R., Botez, R. M., & Ceruti, A. (2021). New Aerodynamic Studies of an Adaptive Winglet Application on the Regional Jet CRJ700. Biomimetics, 6(4), 54. https://doi.org/10.3390/biomimetics6040054







