Design of a Carangiform Swimming Robot through a Multiphysics Simulation Environment
Abstract
1. Introduction
2. Materials and Methods
2.1. Tail Kinematics and Optimization Criteria
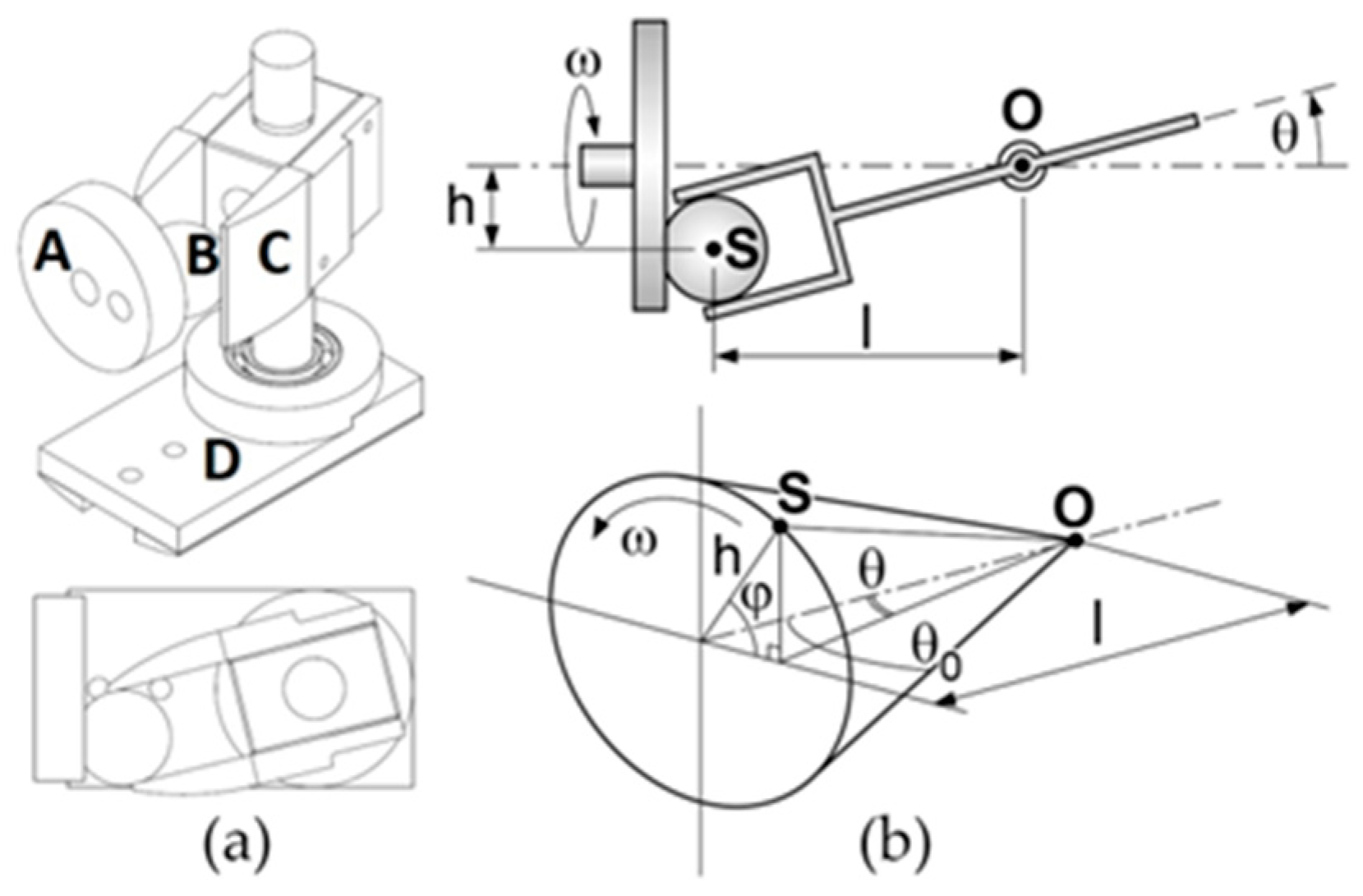
2.2. Elements of the Cam-Joint-Based Transmission System
2.3. Computational Fluid Dynamics Analysis
2.4. Multibody Model
3. Results
3.1. Functional Design of the Transmission System
3.2. Propulsive Performance of the Caudal Fin
3.3. Multibody Analysis
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A

Appendix B

References
- Scaradozzi, D.; Palmieri, G.; Costa, D.; Pinelli, A. BCF swimming locomotion for autonomous underwater robots: A review and a novel solution to improve control and efficiency. Ocean. Eng. 2017, 130, 437–453. [Google Scholar] [CrossRef]
- Salazar, R.; Campos, A.; Fuentes, V.; Abdelkefi, A. A review on the modeling, materials, and actuators of aquatic unmanned vehicles. Ocean. Eng. 2019, 172, 257–285. [Google Scholar] [CrossRef]
- Sfakiotakis, M.; Lane, D.; Davies, J. Review of fish swimming modes for aquatic locomotion. IEEE J. Ocean. Eng. 1999, 24, 237–252. [Google Scholar] [CrossRef]
- Zhao, Z.; Dou, L. Modeling and simulation of the intermittent swimming gait with the muscle-contraction model of pre-strains. Ocean. Eng. 2020, 207, 107391. [Google Scholar] [CrossRef]
- Lighthill, M.J. Note on the swimming of slender fish. J. Fluid Mech. 1960, 9, 305. [Google Scholar] [CrossRef]
- Costa, D.; Palmieri, G.; Palpacelli, M.C.; Callegari, M.; Scaradozzi, D. Design of a bio-inspired underwater vehicle. In Proceedings of the 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016; pp. 1–6. [Google Scholar]
- Koca, G.O.; Bal, C.; Korkmaz, D.; Bingol, M.C.; Ay, M.; Akpolat, Z.H.; Yetkin, S. Three-Dimensional Modeling of a Robotic Fish Based on Real Carp Locomotion. Appl. Sci. 2018, 8, 180. [Google Scholar] [CrossRef]
- Li, L.; Wang, C.; Fan, R.; Xie, G. Exploring the backward swimming ability of a robotic fish. Int. J. Adv. Robot. Syst. 2016, 13. [Google Scholar] [CrossRef]
- Whitesides, G.M. Soft robotics. Angew. Chem. Int. Ed. Engl. 2018, 57, 4258–4273. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Hu, H. Biological inspiration: From carangiform fish to multi-joint robotic fish. J. Bionic Eng. 2010, 7, 35–48. [Google Scholar] [CrossRef]
- Brooks, S.A.; Green, M.A. Experimental Study of Body-Fin Interaction and Vortex Dynamics Generated by a Two Degree-Of-Freedom Fish Model. Biomimetics 2019, 4, 67. [Google Scholar] [CrossRef] [PubMed]
- Costa, D.; Franciolini, M.; Palmieri, G.; Crivellini, A.; Scaradozzi, D. Computational fluid dynamics analysis and design of an ostraciiform swimming robot. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macao, China, 5–8 December 2017. [Google Scholar]
- Wang, J.; Nakata, T.; Liu, H. Development of Mixed Flow Fans with Bio-Inspired Grooves. Biomimetics 2019, 4, 72. [Google Scholar] [CrossRef] [PubMed]
- Amodio, D.; Callegari, M.; Castellini, P.; Crivellini, A.; Palmieri, G.; Palpacelli, M.C.; Paone, N.; Rossi, M.; Sasso, M. Integrating Advanced CAE Tools and Testing Environments for the Design of Complex Mechanical Systems. In The First Outstanding 50 Years of “Università Politecnica delle Marche”; Springer Science and Business Media LLC: Berlin, Germany, 2019; pp. 247–258. [Google Scholar]
- Borazjani, I.; Sotiropoulos, F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes. J. Exp. Boil. 2008, 211, 1541–1558. [Google Scholar] [CrossRef] [PubMed]
- Bassi, F.; Rebay, S. Numerical evaluation of two discontinuous Galerkin methods for the compressible Navier-Stokes equations. Int. J. Numer. Methods Fluids 2002, 40, 197–207. [Google Scholar] [CrossRef]
- Bassi, F.; Botti, L.; Colombo, A.; Crivellini, A.; Franchina, N.; Ghidoni, A. Assessment of a high-order accurate Discontinuous Galerkin method for turbomachinery flows. Int. J. Comput. Fluid Dyn. 2016, 30, 307–328. [Google Scholar] [CrossRef]
- Beaugendre, H.; Morency, F. Penalization of the Spalart–Allmaras turbulence model without and with a wall function: Methodology for a vortex in cell scheme. Comput. Fluids 2018, 170, 313–323. [Google Scholar] [CrossRef]
- Antonelli, G.; Pascal, M. Underwater Robots: Motion and Force Control of Vehicle-Manipulator Systems. Springer Tracts in Advanced Robotics, Vol 2. Appl. Mech. Rev. 2003, 56, B81. [Google Scholar] [CrossRef]
- Fossen, T.I. Marine Control System-Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles; Marine Cybernetics: Trondheim, Norway, 2002. [Google Scholar]
- Fischer, I.S.; Paul, R.N. Kinematic Displacement Analysis of a Double-Cardan-Joint Driveline. J. Mech. Des. 1991, 113, 263–271. [Google Scholar] [CrossRef]
- Hunt, K.H. Constant-Velocity Shaft Couplings: A General Theory. J. Eng. Ind. 1973, 95, 455–464. [Google Scholar] [CrossRef]
- Horton, H.L.; Newell, J.A. Ingenious Mechanisms for Designers and Inventors; Industrial Press Inc.: New York, NY, USA, 1930. [Google Scholar]
- Schouveiler, L.; Hover, F.; Triantafyllou, M. Performance of flapping foil propulsion. J. Fluids Struct. 2005, 20, 949–959. [Google Scholar] [CrossRef]
- Eloy, C. Optimal Strouhal number for swimming animals. J. Fluids Struct. 2012, 30, 205–218. [Google Scholar] [CrossRef]













| 0.5 | [0.8–1.2] |
| A1 | A2 | A3 | Δ1 | Δ2 | Δ3 |
|---|---|---|---|---|---|
| 0.074 | 0.519 | 0.585 | 0 | −0.49 | −1.33 |
| h1 | L1 | δ1 | h2 | L2 | δ2 | h3 | L3 | δ3 |
|---|---|---|---|---|---|---|---|---|
| 4 | 54 | 0 | 11.8 | 26 | −0.57 | 6.3 | 14 | −2.35 |
| Reynolds Number | Propulsive Efficiency % | Thrust Coefficient |
| 1 × 104 | 67.7 | 0.258 |
| 5 × 104 | 68.3 | 0.261 |
| 1 × 105 | 69.5 | 0.263 |
| 5 × 105 | 70.1 | 0.265 |
| 1 × 106 | 70.4 | 0.267 |
| c25% | c75% | B | m | Ixx | Iyy | Izz |
|---|---|---|---|---|---|---|
| 0.080 | 0.060 | 0.168 | 6.147 | 0.143 | 0.012 | 0.139 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, D.; Palmieri, G.; Palpacelli, M.-C.; Scaradozzi, D.; Callegari, M. Design of a Carangiform Swimming Robot through a Multiphysics Simulation Environment. Biomimetics 2020, 5, 46. https://doi.org/10.3390/biomimetics5040046
Costa D, Palmieri G, Palpacelli M-C, Scaradozzi D, Callegari M. Design of a Carangiform Swimming Robot through a Multiphysics Simulation Environment. Biomimetics. 2020; 5(4):46. https://doi.org/10.3390/biomimetics5040046
Chicago/Turabian StyleCosta, Daniele, Giacomo Palmieri, Matteo-Claudio Palpacelli, David Scaradozzi, and Massimo Callegari. 2020. "Design of a Carangiform Swimming Robot through a Multiphysics Simulation Environment" Biomimetics 5, no. 4: 46. https://doi.org/10.3390/biomimetics5040046
APA StyleCosta, D., Palmieri, G., Palpacelli, M.-C., Scaradozzi, D., & Callegari, M. (2020). Design of a Carangiform Swimming Robot through a Multiphysics Simulation Environment. Biomimetics, 5(4), 46. https://doi.org/10.3390/biomimetics5040046