Development of the Third Generation of the Dual-Reciprocating Drill
Abstract
1. Introduction
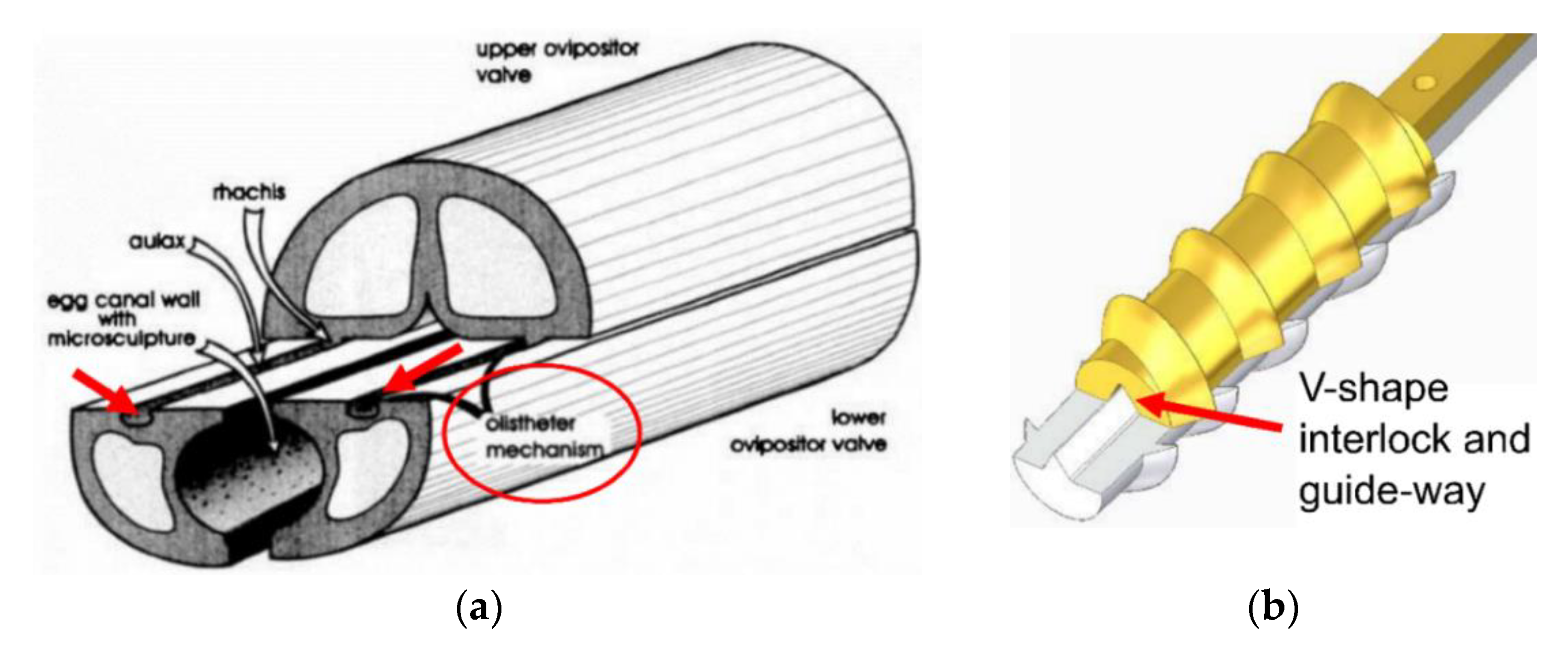
1.1. Evolution of the DRD
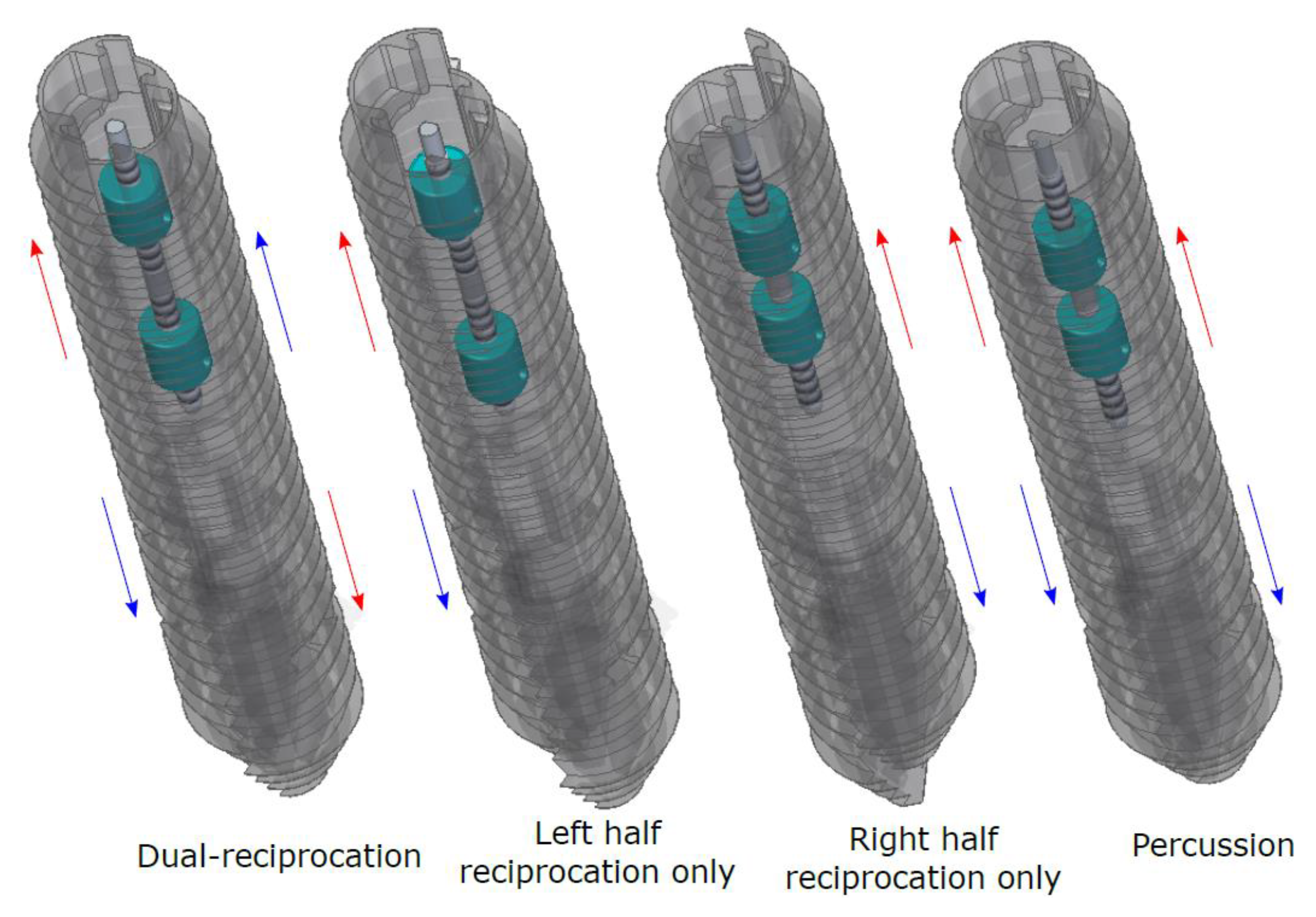
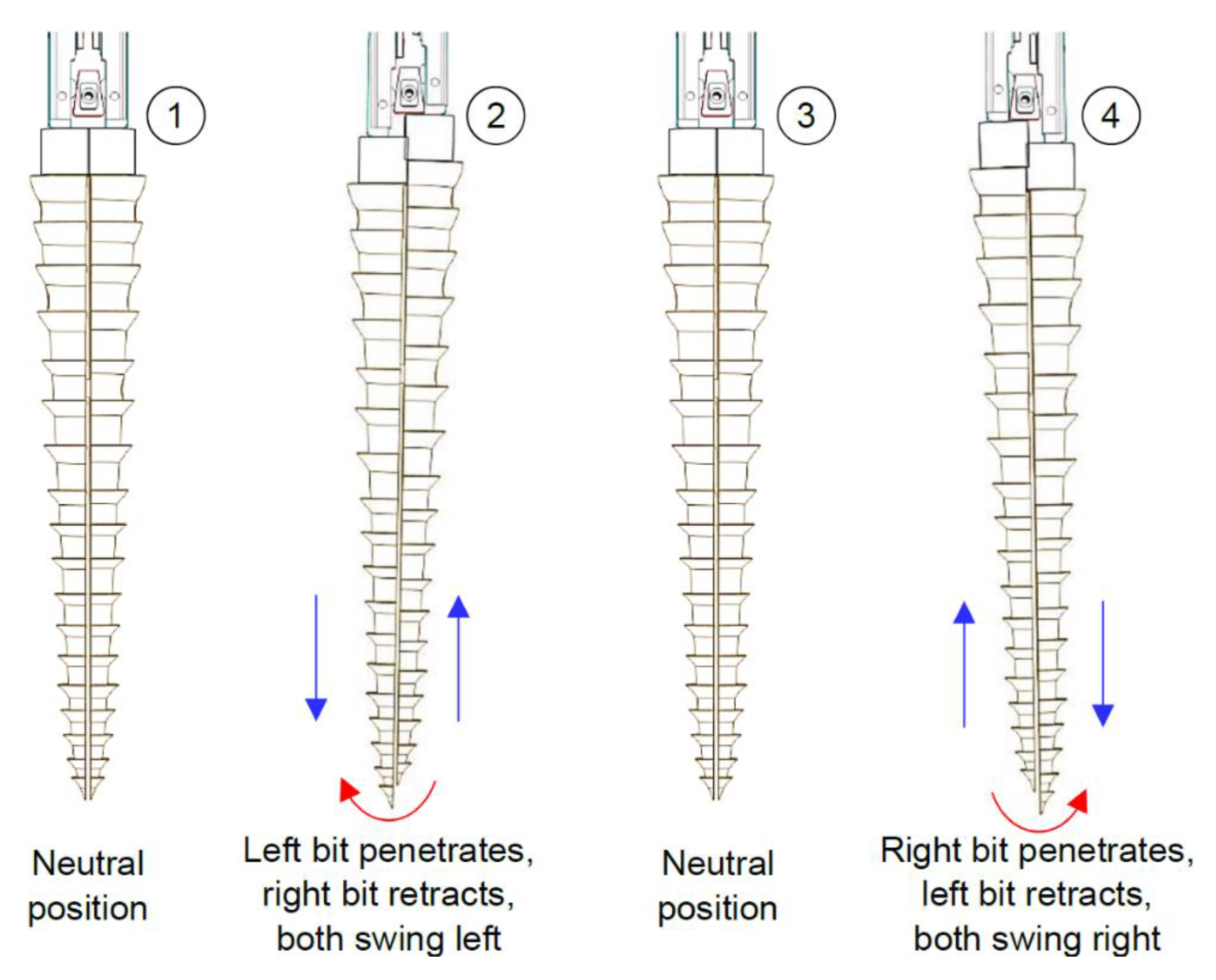
1.1.1. Parameters Defining the DRD Operation
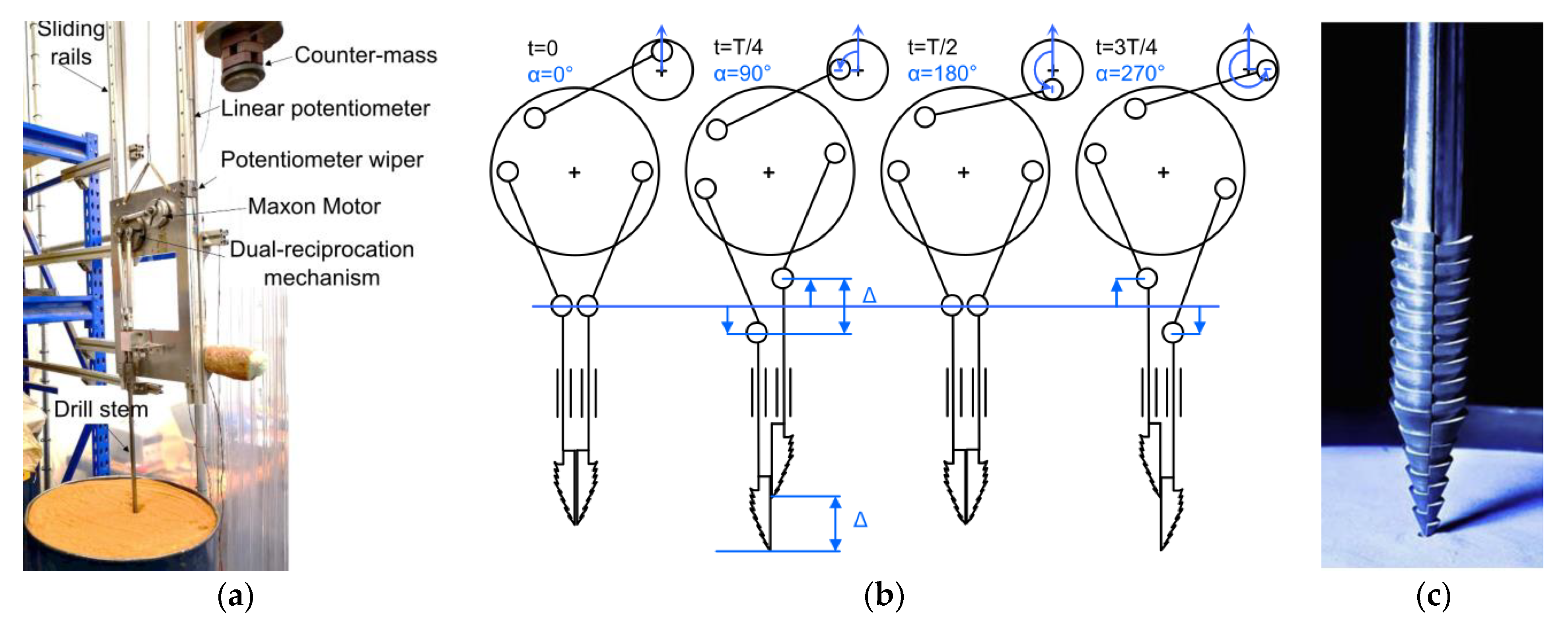
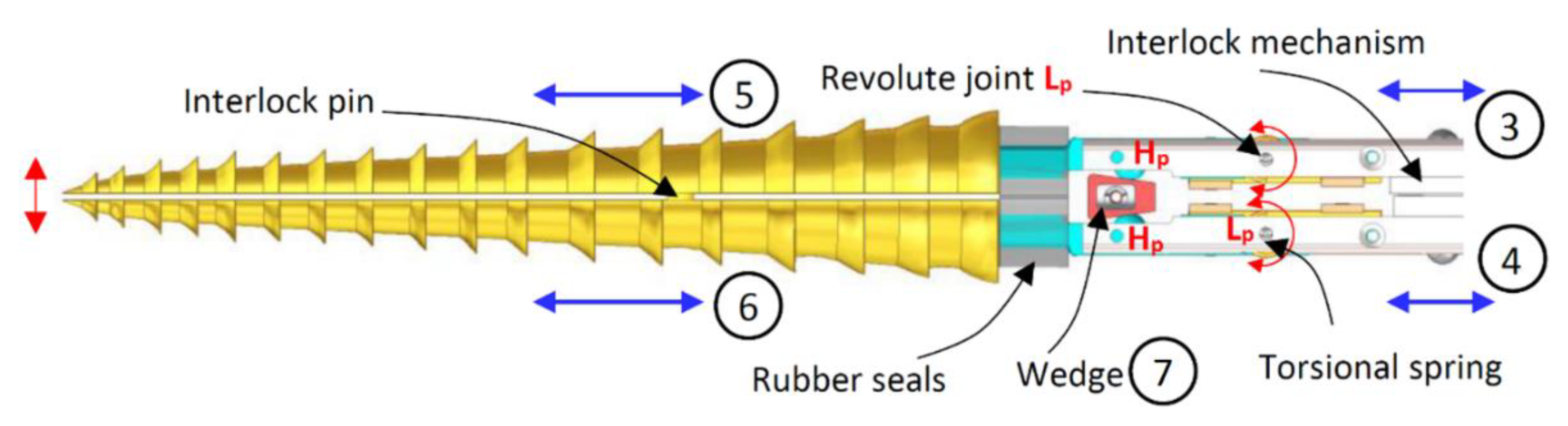
1.1.2. Integrated Actuation Mechanism
2. Methods
2.1. Drill Bit Morphological Design
2.2. Numerical Modelling of the DRD
2.2.1. Overview of the Simulation Techniques Used for Drill/Soil Interactions
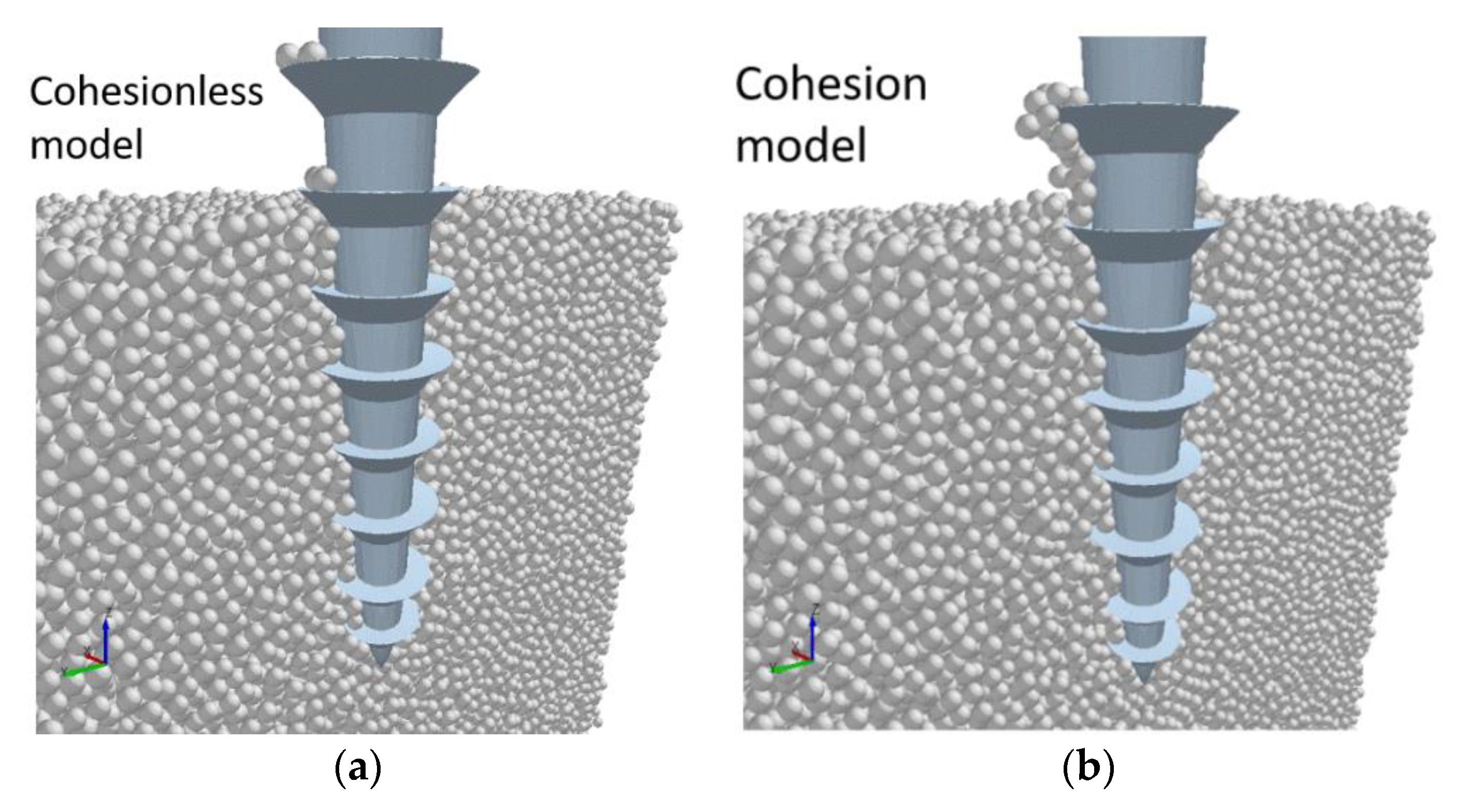
2.2.2. Preliminary Numerical Study
2.3. Development of System Prototypes
3. Results
3.1. Drill Bit Morphological Design
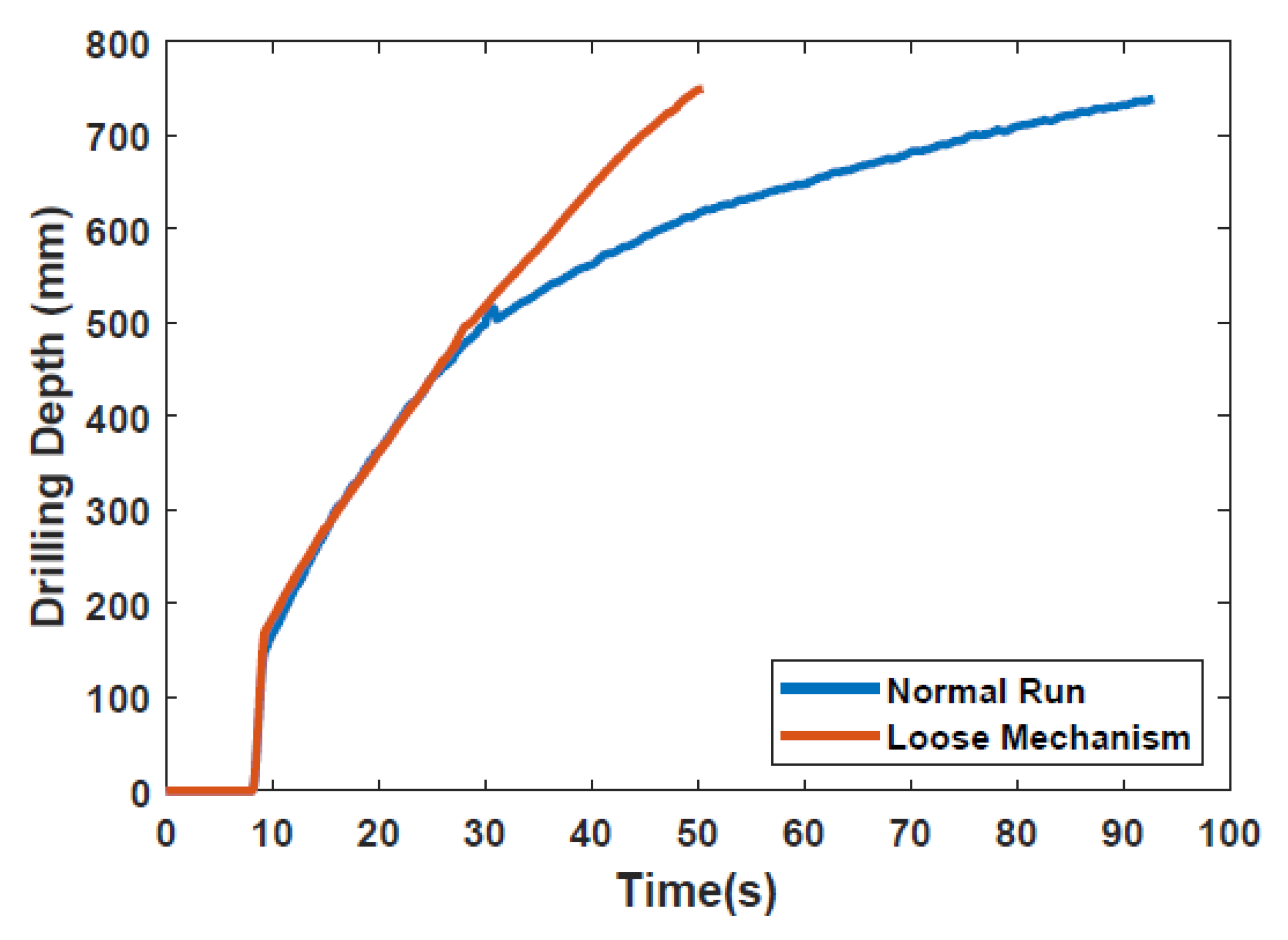
3.2. Numerical Modelling of the DRD with EDEM
4. Discussion
4.1. Development of the Internally Actuated System Prototype
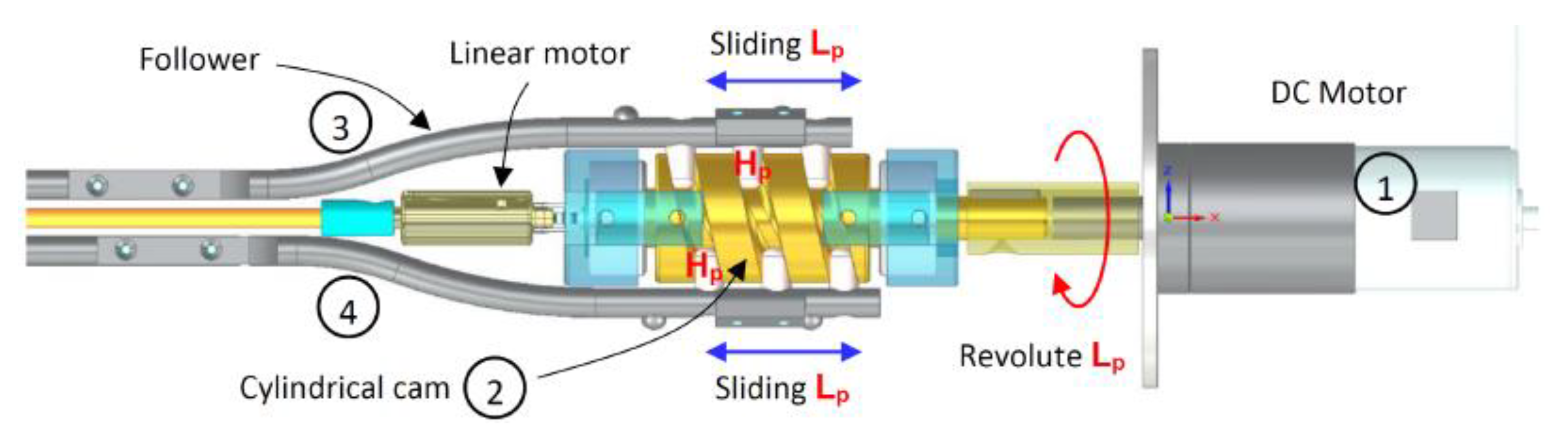
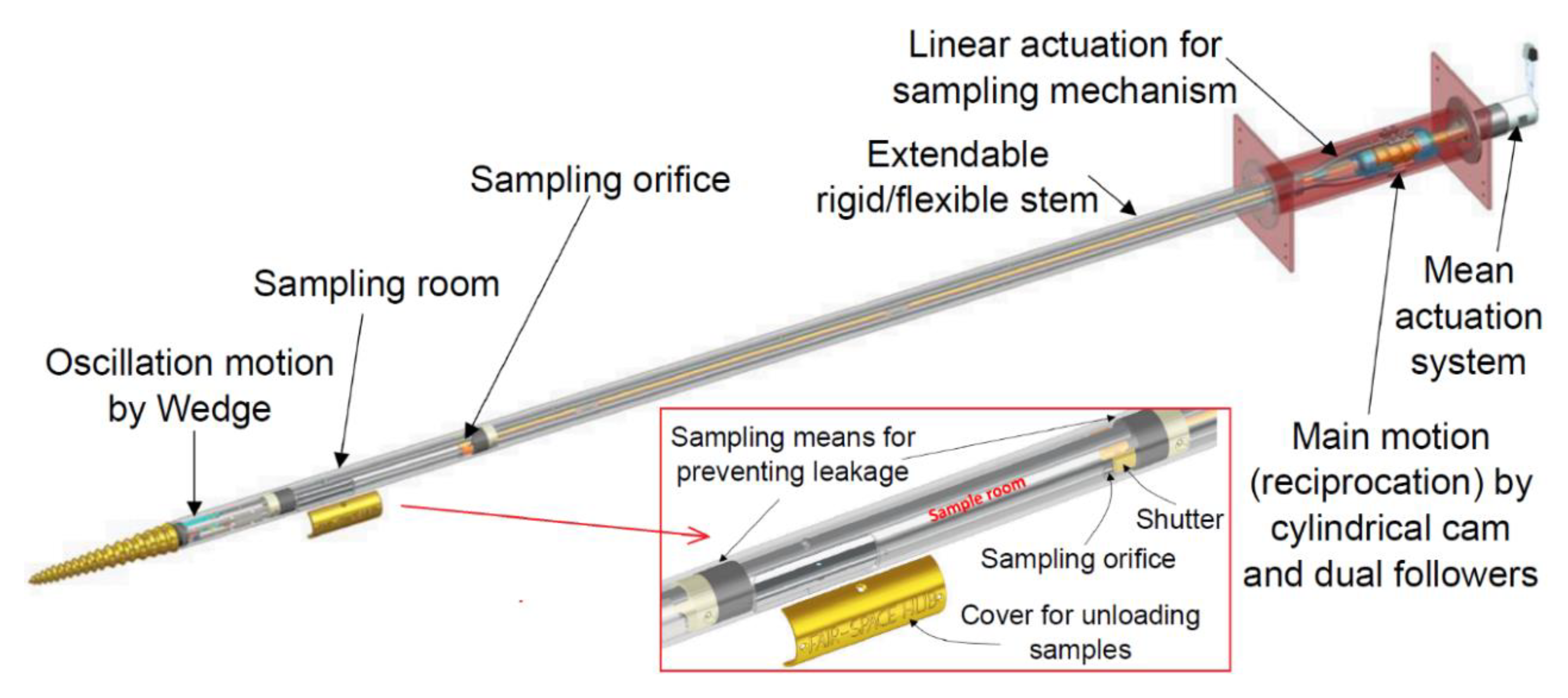
4.2. Development of the Dual Reciprocation Oscillation Drill (DROD) System Prototype
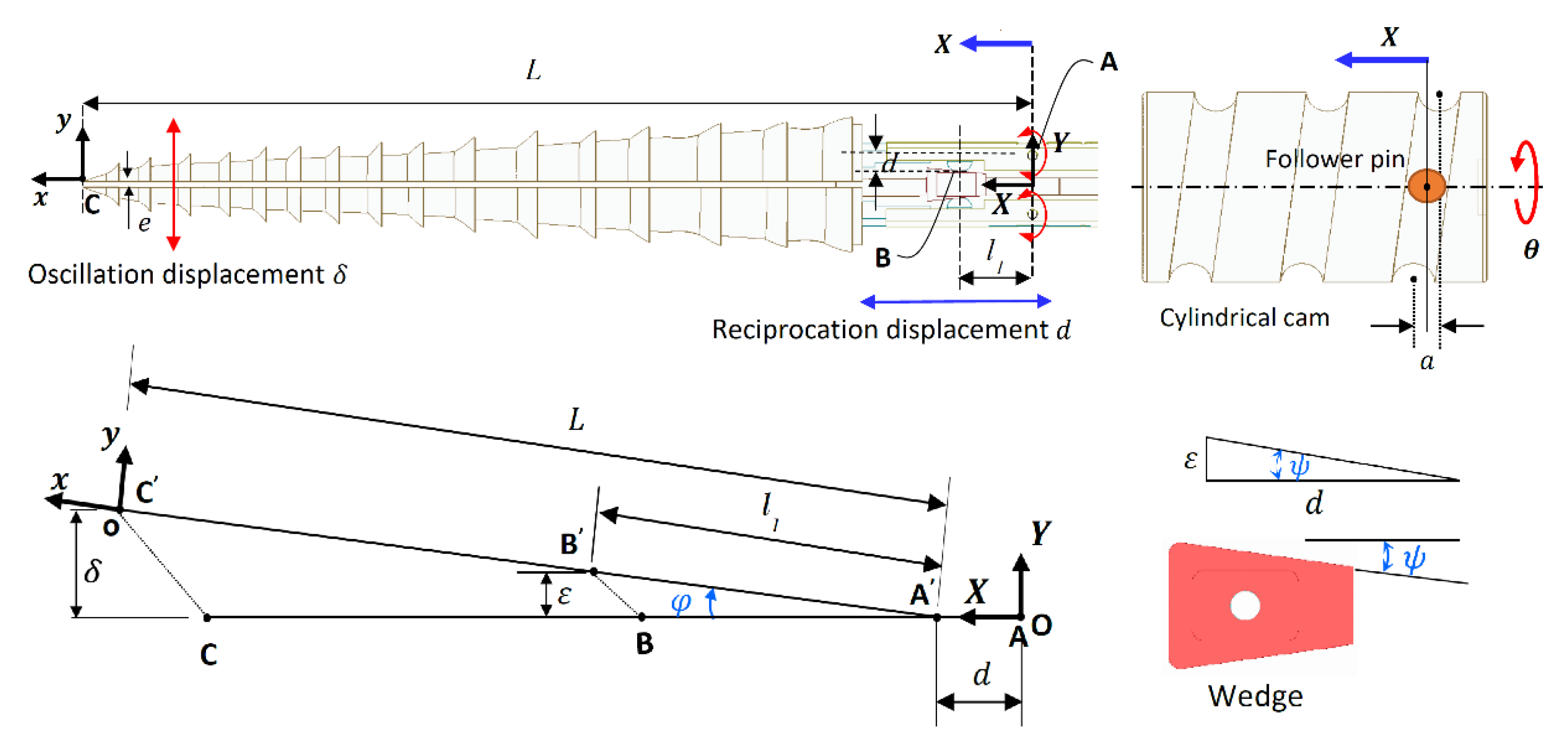
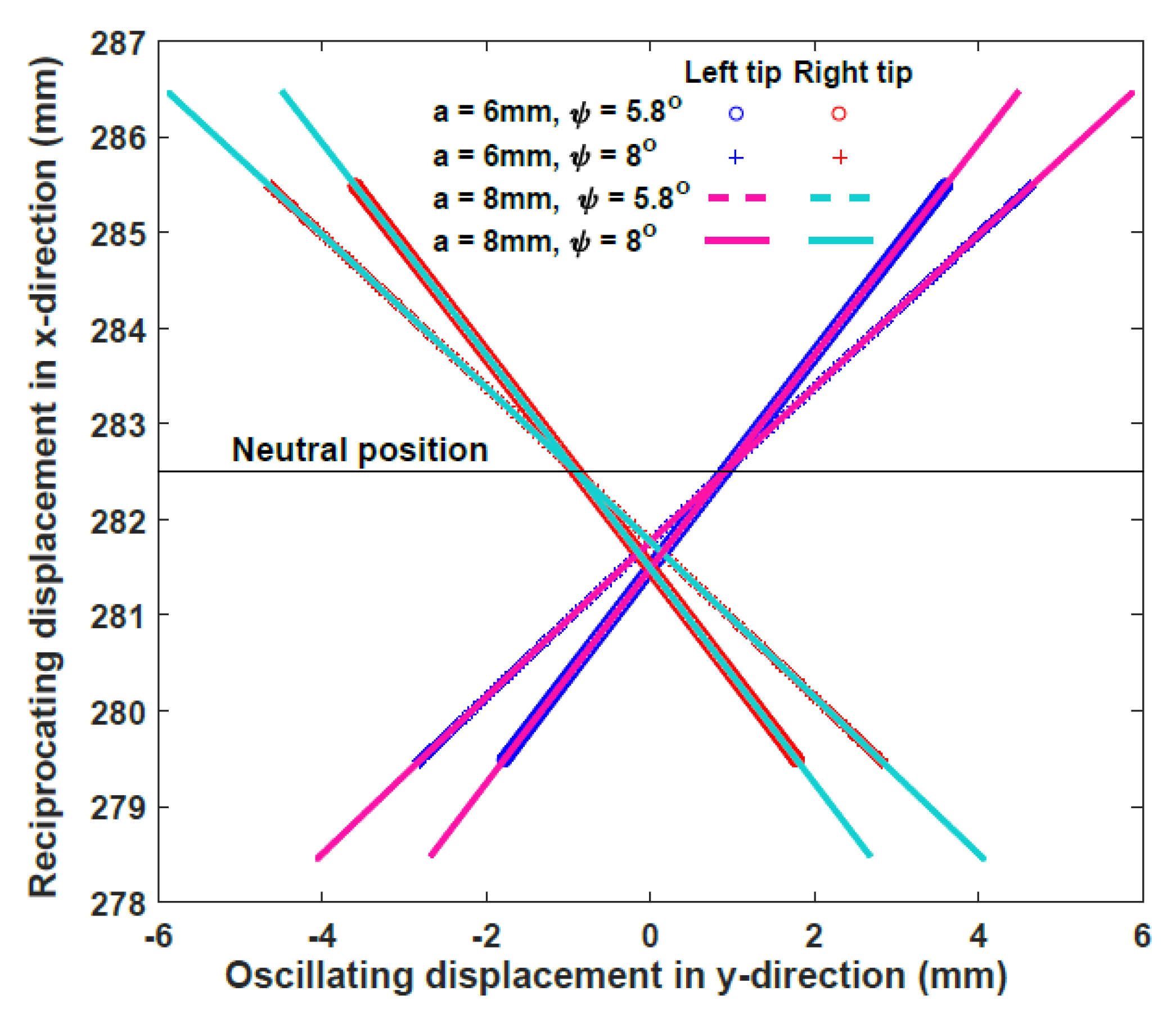
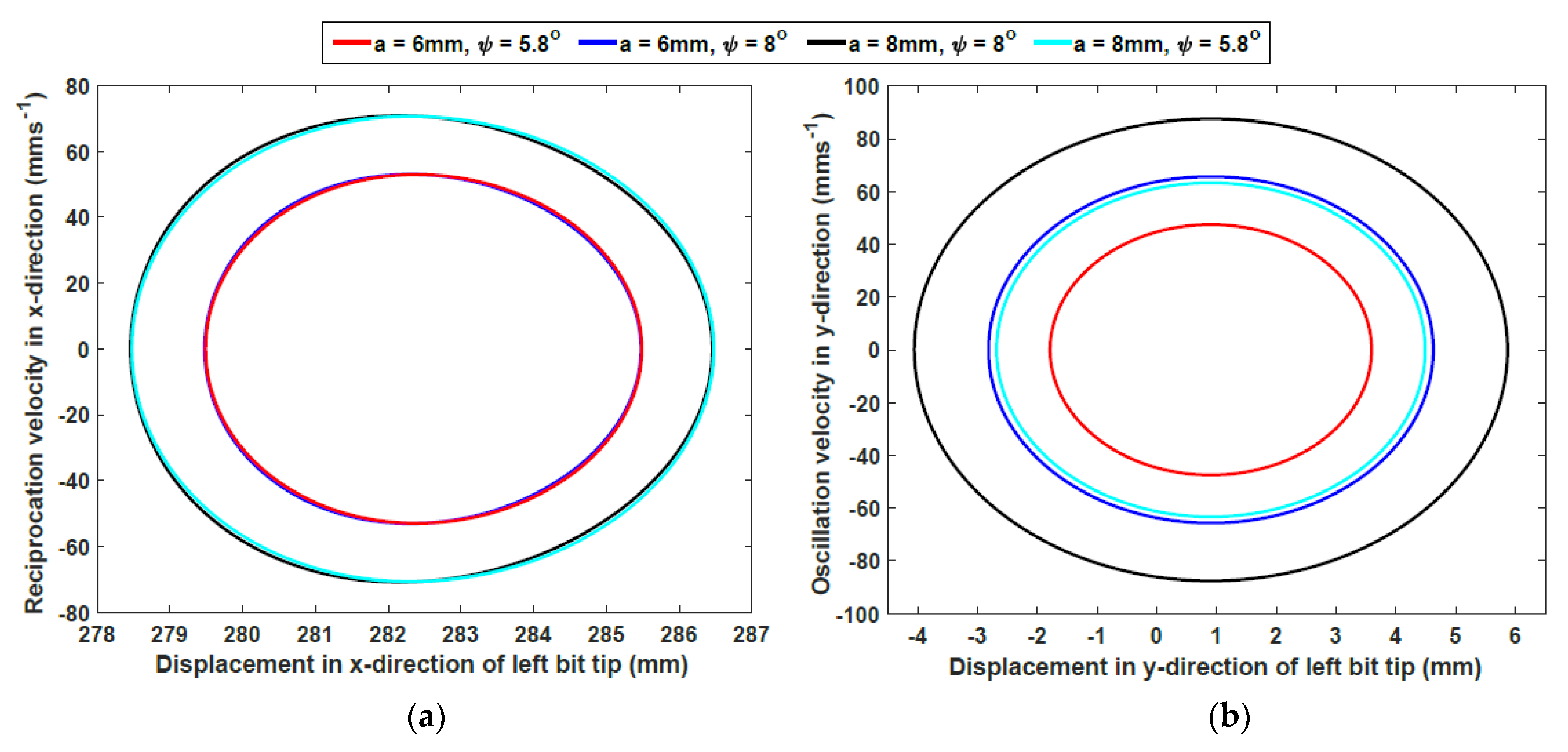
Kinematic Analysis of the DROD
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zacny, K.; Paulsen, G.; Szczesiak, M. Challenges and Methods of Drilling on the Moon and Mars. In Proceedings of the 2011 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011. [Google Scholar]
- Badescu, M.; Kassab, S.; Sherrit, S.; Aldrich, J.; Bao, X.; Bar-Cohen, Y.; Chang, Z. Ultrasonic/Sonic Driller/Corer as a hammer-rotary drill. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical and Aerospace Systems, San Diego, CA, USA, 19 April 2007. [Google Scholar]
- Re, E.; Magnani, P.; Izzo, M.; Rizzi, F.; Senese, S.; del Campo, F.; Finotello, R.; Ferrario, R. ExoMars Multi Rod Drill Development and Testing. In Proceedings of the 10th Workshop on Advanced Space Technologies for Robotics and Automation, Noordwijk, The Netherlands, 11–14 November 2008. [Google Scholar]
- Abbey, W.; Anderson, R.; Beegle, L.; Hurowitz, J.; Williford, K.; Peters, G.; Morookian, J.; Collins, C.; Feldman, J.; Kinnett, R.; et al. A look back: The drilling campaign of the Curiosity rover during the Mars Science Laboratory’s Prime Mission. Icarus 2019, 319, 1–13. [Google Scholar] [CrossRef]
- Richter, L.; Coste, P.; Gromov, V.; Kochan, H.; Nadalini, R.; Ng, T.; Pinna, S.; Richter, H.-E.; Yung, K. Development and testing of subsurface sampling devices for the Beagle 2 lander. Planet. Space Sci. 2002, 50, 903–913. [Google Scholar] [CrossRef]
- Marshall, J.; Hudson, T.; Andrade, J. Experimental Investigation of InSight HP3 Mole Interaction with Martian Regolith Simulant. Space Sci. Rev. 2017, 211, 239–258. [Google Scholar] [CrossRef]
- Verhoeven, C.; Bentum, M.; Monna, G.; Rotteveel, J.; Guo, J. On the origin of satellite swarms. Acta Astronautica 2011, 68, 1392–1395. [Google Scholar] [CrossRef]
- Menon, C.; Broschart, M.; Lan, N. Biomimetics and robotics for space applications: Challenges and emerging technologies. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation—Workshop on Biomimetics Robotics, Rome, Italy, 10–14 April 2007. [Google Scholar]
- Vincent, J.; King, M. The mechanism of drilling by wood wasp ovipositors. Biomim. Plenum Publ. Corp. 1995, 3, 187–201. [Google Scholar]
- Nakajima, K.; Schwarz, O. How to use the Ovipositor Drilling Mechanism of Hymenoptera for Developing a Surgical Instrument in Biomimetic Design. Int. J. Des. Nat. Ecodynamics 2014, 9, 177–189. [Google Scholar] [CrossRef]
- Frasson, L.; Ko, S.; Turner, A.; Parittotokkaporn, T.; Vincent, J.; Rodriguez y Baena, F. STING: A soft-tissue intervention and neuro-surgical guide to access deep brain lesions through curved trajectories. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2009, 224, 775–788. [Google Scholar] [CrossRef]
- Leibinger, A.; Oldfield, M.; Rodriguez y Baena, F. Minimally disruptive needle insertion: A biologically inspired solution. Interface Focus 2016, 6, 20150107. [Google Scholar] [CrossRef]
- Tarabini, M.; Marzaroli, P.; Saggin, B.; Scaccabarozzi, D.; Giberti, H. Position Uncertainty of a System for the Localization of a Reciprocating Drill for Geological Inspections. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Turin, Italy, 22–25 May 2017. [Google Scholar]
- Gao, Y.; Ellery, A.; Sweeting, M.; Vincent, J. Bioinspired Drill for Planetary Sampling: Literature Survey, Conceptual Design, and Feasibility Study. J. Spacecr. Rocket. 2007, 44, 703–709. [Google Scholar] [CrossRef]
- Gao, Y.; Ellery, A.; Jaddou, M.; Vincent, J.; Eckersley, S. Planetary Micro-Penetrator Concept Study with Biomimetic Drill and Sampler Design. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 875–885. [Google Scholar]
- Gouache, T.; Brunskill, C.; Scott, G.; Gao, Y.; Coste, P.; Gourinat, Y. Regolith simulant preparation methods for hardware testing. Planet. Space Sci. 2010, 58, 1977–1984. [Google Scholar] [CrossRef]
- Gouache, T.; Gao, Y.; Coste, P.; Gourinat, Y. First experimental investigation of dual-reciprocating drilling in planetary regoliths: Proposition of penetration mechanics. Planet. Space Sci. 2011, 59, 1529–1541. [Google Scholar] [CrossRef]
- Alkalla, M.; Gao, Y.; Bouton, A. Customizable and Optimized Drill Bits Bio-inspired from Wood-Wasp Ovipositor Morphology for Extraterrestrial Surfaces. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Hong Kong, China, 8–12 July 2019; pp. 430–435. [Google Scholar]
- Pitcher, C.; Gao, Y. Analysis of drill head designs for dual reciprocating drilling technique in planetary regoliths. Adv. Space Res. 2015, 56, 1765–1776. [Google Scholar] [CrossRef]
- Gouache, T.; Gao, Y.; Frame, T.; Coste, P.; Gourinat, Y. Identification of the Forces Between Regolith and a Reciprocating Drill-Head: Perspectives for the Exploration of Martian Regolith. In Proceedings of the 62nd International Astronautical Congress, Cape Town, South Africa, 3–7 October 2011. [Google Scholar]
- Pitcher, C.; Gao, Y. First Implementation of Burrowing Mechanisms in Dual-Reciprocating Drilling Using an Integrated Actuation Mechanism. Adv. Space Res. 2017, 59, 1368–1380. [Google Scholar] [CrossRef][Green Version]
- Gao, Y.; Frame, T.; Pitcher, C. Piercing the Extraterrestrial Subsurface. Integrated Robotic Drill for Planetary Exploration. IEEE Robot. Autom. Mag. 2015, 22, 45–53. [Google Scholar] [CrossRef]
- Rahman, M.; Fitton, M.; Quicke, D. Ovipositor internal microsculpture in the braconidae (insecta, hymenoptera). Zool. Scr. 1998, 27, 319–332. [Google Scholar] [CrossRef]
- Gouache, T.; Patel, N.; Brunskill, C.; Scott, G.; Saaj, C.; Matthews, M.; Cui, L. Soil simulant sourcing for the ExoMars rover testbed. Planet. Space Sci. 2011, 59, 779–787. [Google Scholar] [CrossRef]
- Lai, Z.; Chen, Q. Characterization and discrete element simulation of grading and shape-dependent behavior of JSC-1A Martian regolith simulant. Granul. Matter 2017, 19, 69. [Google Scholar] [CrossRef]
- Jiang, M.; Yin, Z.; Shen, Z. Shear band formation in lunar regolith by discrete element analyses. Granul. Matter 2016, 18, 32. [Google Scholar] [CrossRef]
- Bui, H.; Kobayashi, T.; Fukagawa, R.; Wells, J. Numerical and experimental studies of gravity effect on the mechanism of lunar excavations. J. Terramechanics 2008, 46, 115–124. [Google Scholar] [CrossRef]
- Schafer, C.; Scherrer, S.; Buchwald, R.; Maindl, T.; Speith, R.; Kley, W. Numerical simulations of regolith sampling processes. Planet. Space Sci. 2017, 141, 35–44. [Google Scholar] [CrossRef]
- Gao, X.; Tang, D.; Yue, H.; Jiang, S.; Deng, Z. Influence of friction on sampling disturbance of lunar surface in direct push sampling method based on DEM. Adv. Space Res. 2017, 59, 3036–3044. [Google Scholar] [CrossRef]
- Jiang, M.; Liu, F.; Shen, Z.; Zheng, M. Distinct element simulation of lugged wheel performance under extraterrestrial environmental effect. Acta Astronaut. 2014, 99, 37–51. [Google Scholar] [CrossRef]
- Johnson, J.; Duvoy, P.; Kulchitsky, A.; Creager, C.; Moore, J. Analysis of Mars Exploration Rover wheel mobility processes and the limitations of classical terramechanics models using discrete element method simulations. J. Terramechanics 2017, 73, 61–71. [Google Scholar] [CrossRef]
- Li, W.; Huang, Y.; Cui, Y.; Dong, S.; Wang, J. Trafficability analysis of lunar mare terrain by means of the discrete element method for wheeled rover locomotion. J. Terramechanics 2010, 47, 161–172. [Google Scholar] [CrossRef]
- Cui, J.; Hou, X.; Wen, G.; Liang, Z. DEM thermal simulation of bit and object in drilling of lunar soil simulant. Adv. Space Res. 2018, 62, 967–975. [Google Scholar] [CrossRef]
- Janda, A.; Ooi, J. DEM modeling of cone penetration and unconfined compression in cohesive solids. Powder Technol. 2016, 293, 60–68. [Google Scholar] [CrossRef]
- Li, P.; Jiang, S.; Tang, D.; Xu, B.; Ma, C.; Zhang, H.; Qin, H.; Deng, Z. Design and testing of coring bits on drilling lunar rock simulant. Adv. Space Res. 2017, 59, 1057–1076. [Google Scholar] [CrossRef]
- Gouache, T. Dual Reciprocating Drilling in planetary regoliths: Evolution of a bio-inspired solution. Ph.D. Thesis, University of Surrey, Guildford, UK, July 2011. [Google Scholar]
- Bar-Cohen, Y.; Sherrit, S.; Bao, X.; Badescu, M.; Aldrich, J.; Chang, Z. Ultrasonic/Sonic Driller/Corer (USDC) as a Subsurface Sampler and Sensors Platform for Planetary Exploration Applications. In Proceedings of the 4th International Planetary Probe Workshop, Pasadena, CA, USA, 27–30 June 2006. [Google Scholar]
- Scali, M.; Pusch, T.; Breedveld, P.; Dodou, D. Ovipositor-inspired steerable needle: Design and preliminary experimental evaluation. Bioinspiration Biomim. 2018, 13, 016006. [Google Scholar] [CrossRef]
- Lauder, G.; Tangorra, J. Fish locomotion: Biology and robotics of body and fin-based movements. In Robot Fish; Springer: Berlin/Heidelberg, Germany, 2015; pp. 25–49. [Google Scholar]
- Borazjani, I. The functional role of caudal and anal/dorsal fins during the C-start of a bluegill sunfish. J. Exp. Biol. 2013, 216, 1658–1669. [Google Scholar] [CrossRef]
- Puri, S.; Aegerter-Wilmsen, T.; Jazwinska, A.; Aegerter, C. In vivo quantification of mechanical properties of caudal fins in adult zebra fish. J. Exp. Biol. 2018, 221, 171777. [Google Scholar] [CrossRef] [PubMed]




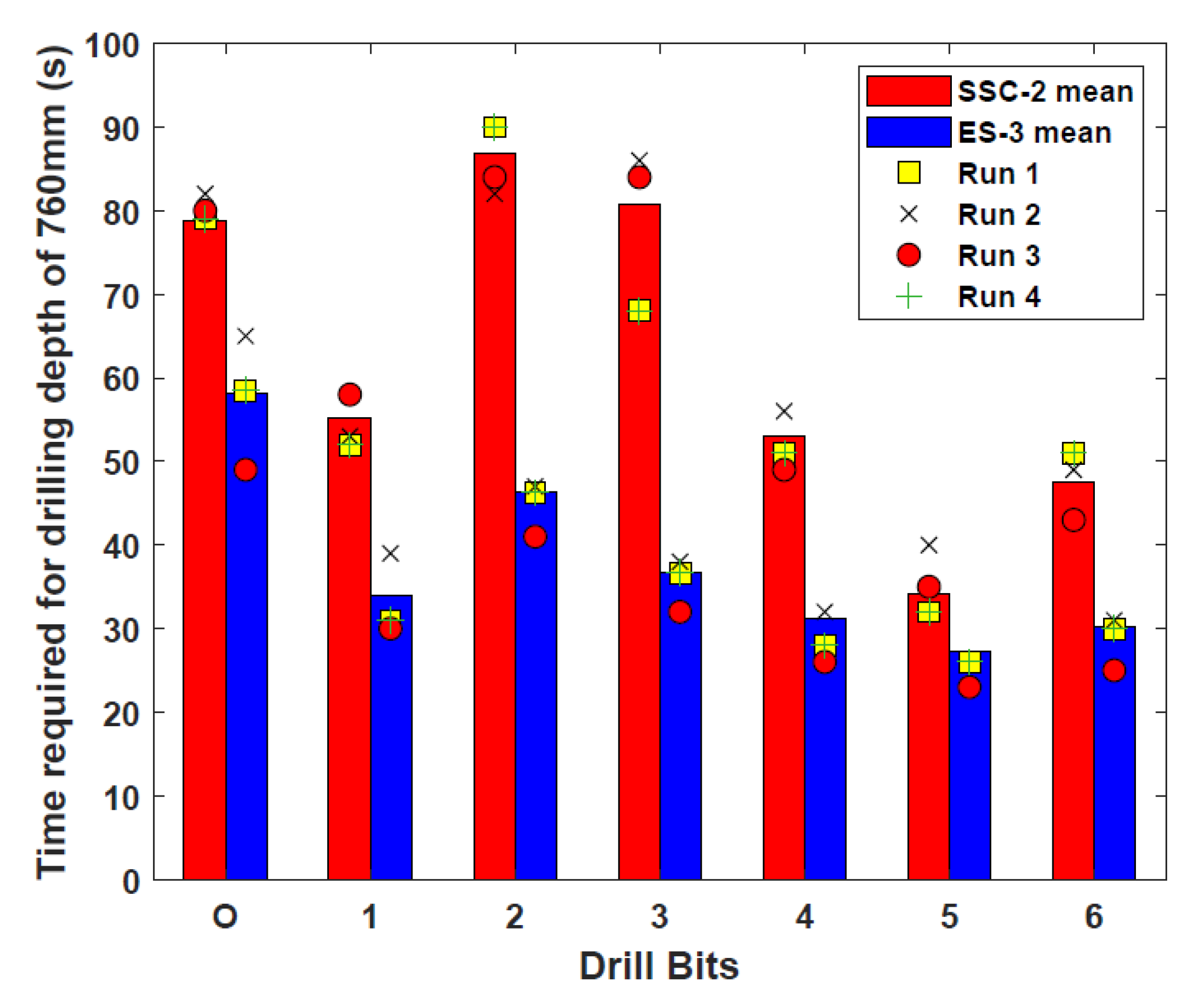




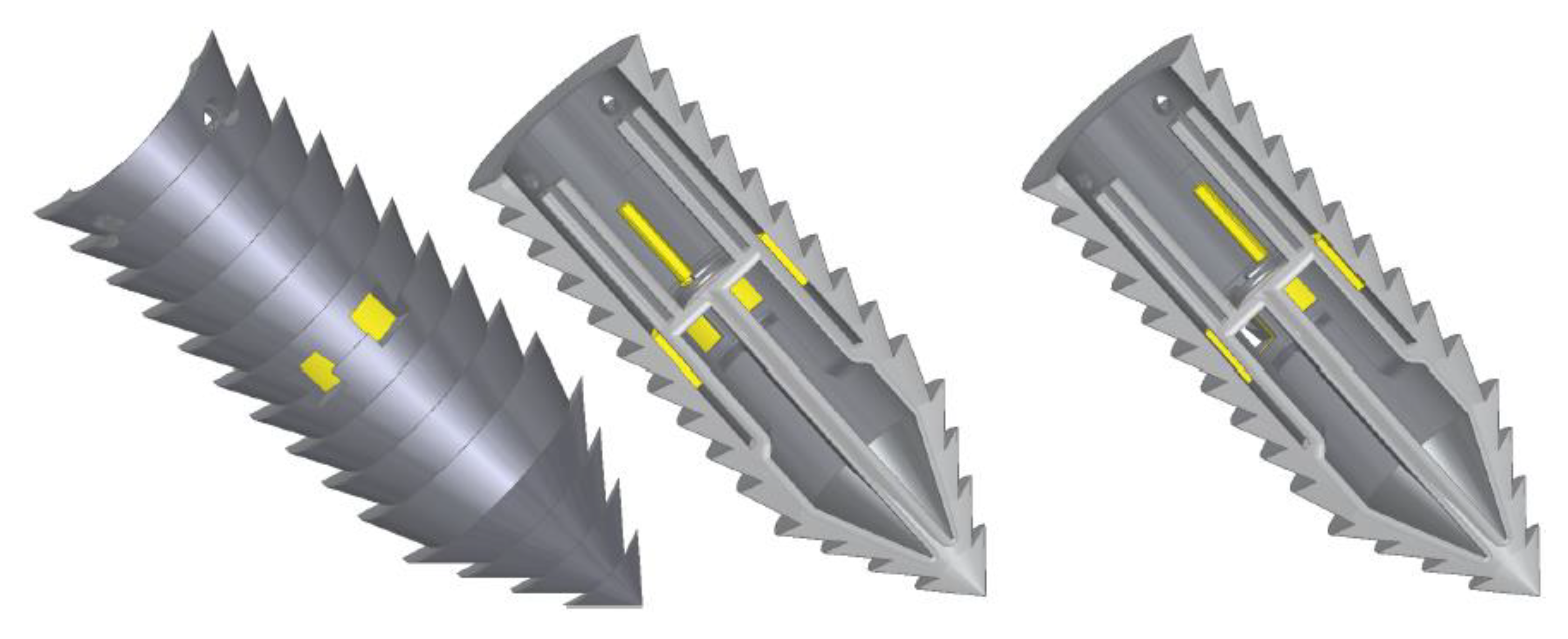
| Drill Bit | Surface Profile | Teeth Angle | Cross-Section Contour | Half Bit Volume ×103 (mm3) |
|---|---|---|---|---|
| O | Cylindrical, conical tip | Straight, H = 0° | Circular | 15.75 |
| 1 | Concave | Straight, H = 0° | Circular | 9.65 |
| 2 | Convex | Straight, H = 0° | Circular | 11.63 |
| 3 | Concave | Helical, Hmax = 20° | Circular | 9.32 |
| 4 | Concave | Straight, H = 0° | Rhombic | 7.891 |
| 5 | Concave | No teeth | Circular | 8.50 |
| 6 | Concave | No teeth | Circular | 15.26 |
| Drill Bit | SSC-2% | ES-3% |
|---|---|---|
| 1 | 29.8 | 41.4 |
| 2 | - | 20.1 |
| 3 | - | 36.8 |
| 4 | 32.7 | 46.1 |
| 5 | 56.5 | 53 |
| 6 | 40.3 | 48 |
| Design Features | Fine Grain Regolith | Coarse Grain Regolith | Potential Icy Regolith |
|---|---|---|---|
| Cylindrical profile | o | – | – – |
| Concave profile | + | + + | + + |
| Convex profile | – – | + | + + |
| Circular cross-section | o | o | o |
| Diamond cross-section | + | + + | + + + |
| Helical teeth | – – | + + | + + + |
| Without teeth | + + + | + | – |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pitcher, C.; Alkalla, M.; Pang, X.; Gao, Y. Development of the Third Generation of the Dual-Reciprocating Drill. Biomimetics 2020, 5, 38. https://doi.org/10.3390/biomimetics5030038
Pitcher C, Alkalla M, Pang X, Gao Y. Development of the Third Generation of the Dual-Reciprocating Drill. Biomimetics. 2020; 5(3):38. https://doi.org/10.3390/biomimetics5030038
Chicago/Turabian StylePitcher, Craig, Mohamed Alkalla, Xavier Pang, and Yang Gao. 2020. "Development of the Third Generation of the Dual-Reciprocating Drill" Biomimetics 5, no. 3: 38. https://doi.org/10.3390/biomimetics5030038
APA StylePitcher, C., Alkalla, M., Pang, X., & Gao, Y. (2020). Development of the Third Generation of the Dual-Reciprocating Drill. Biomimetics, 5(3), 38. https://doi.org/10.3390/biomimetics5030038





