Heart Rate Estimation Using FMCW Radar: A Two-Stage Method Evaluated for In-Vehicle Applications
Abstract
1. Introduction
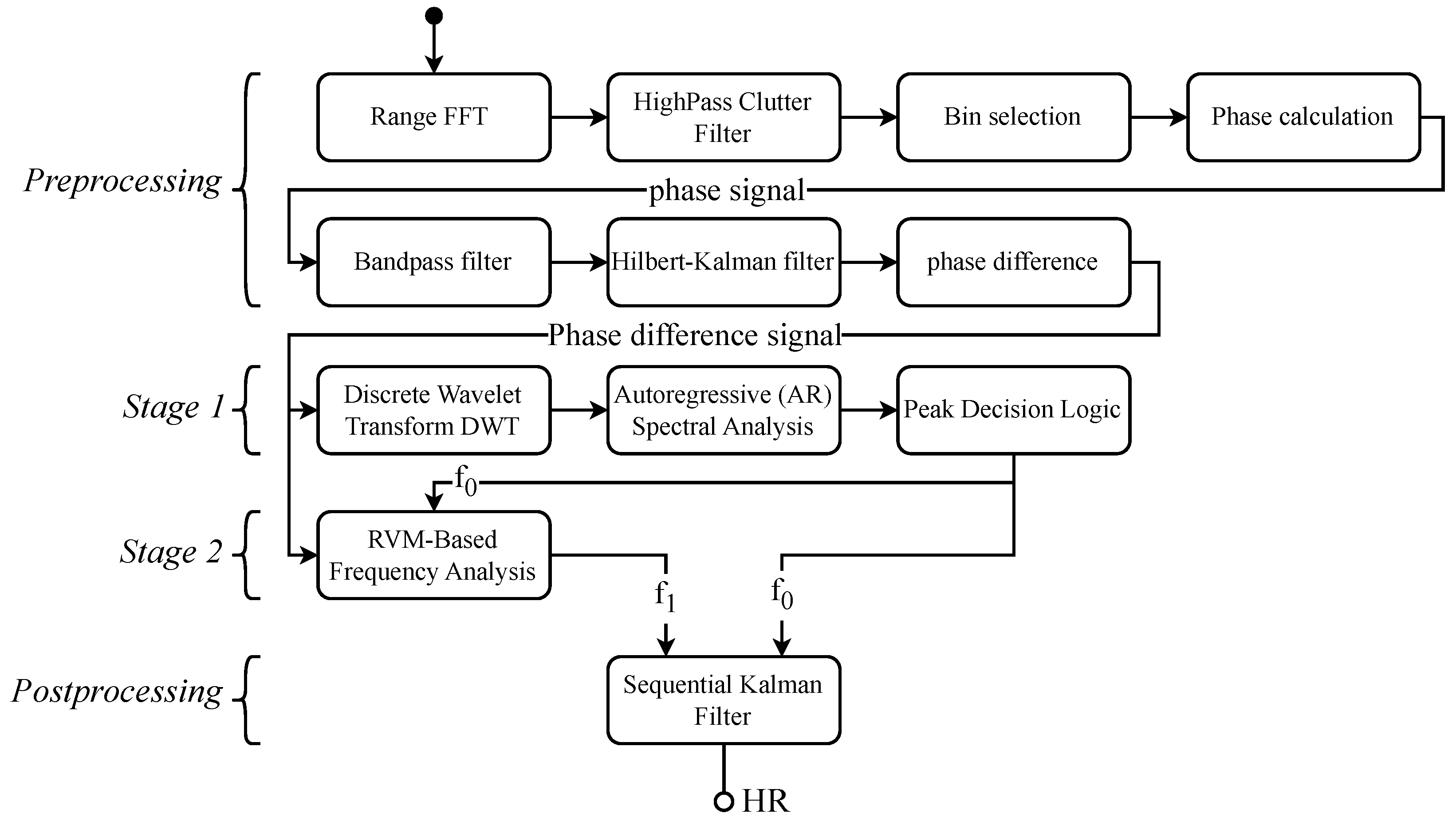
2. Methodology
2.1. Pre-Process
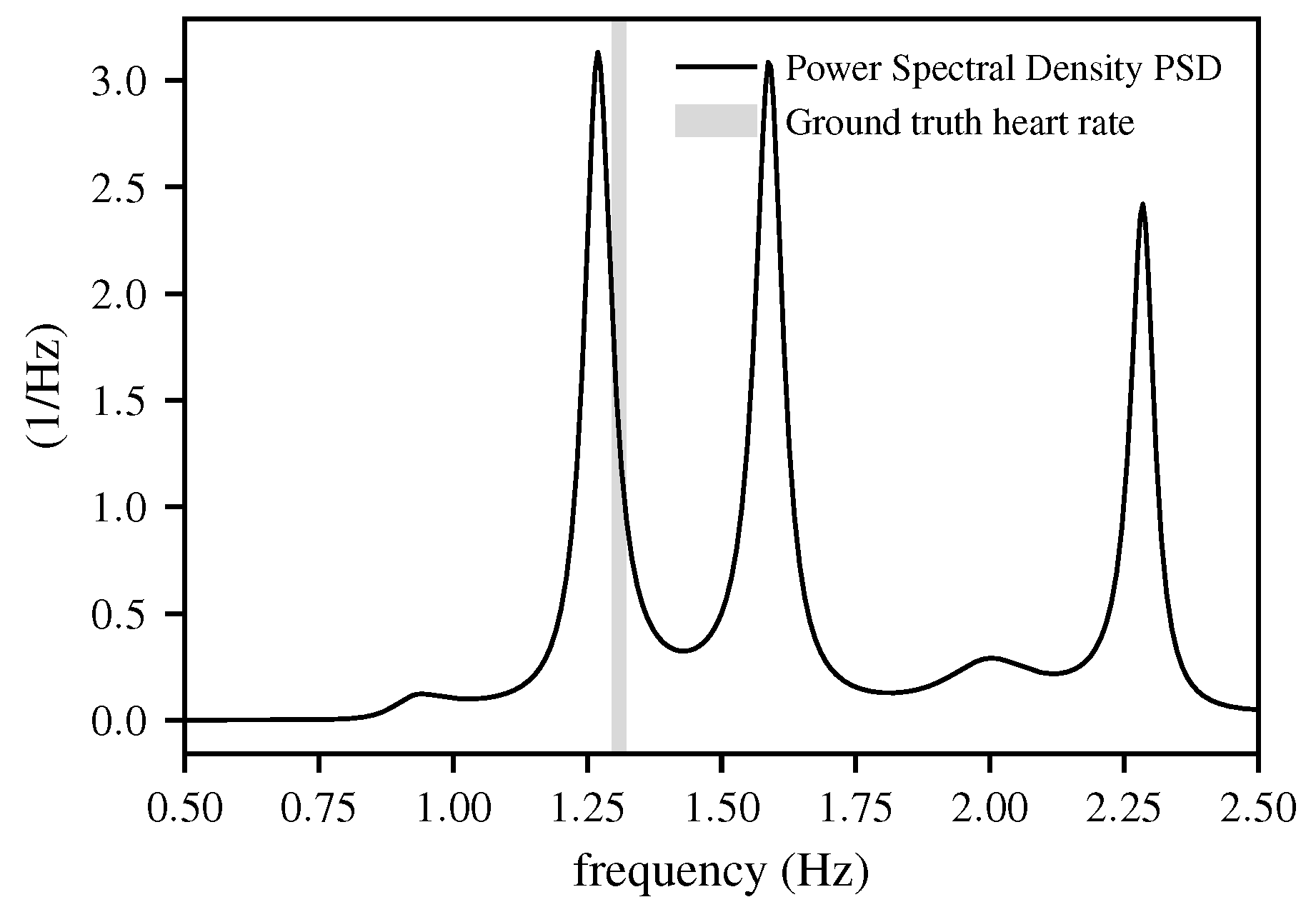
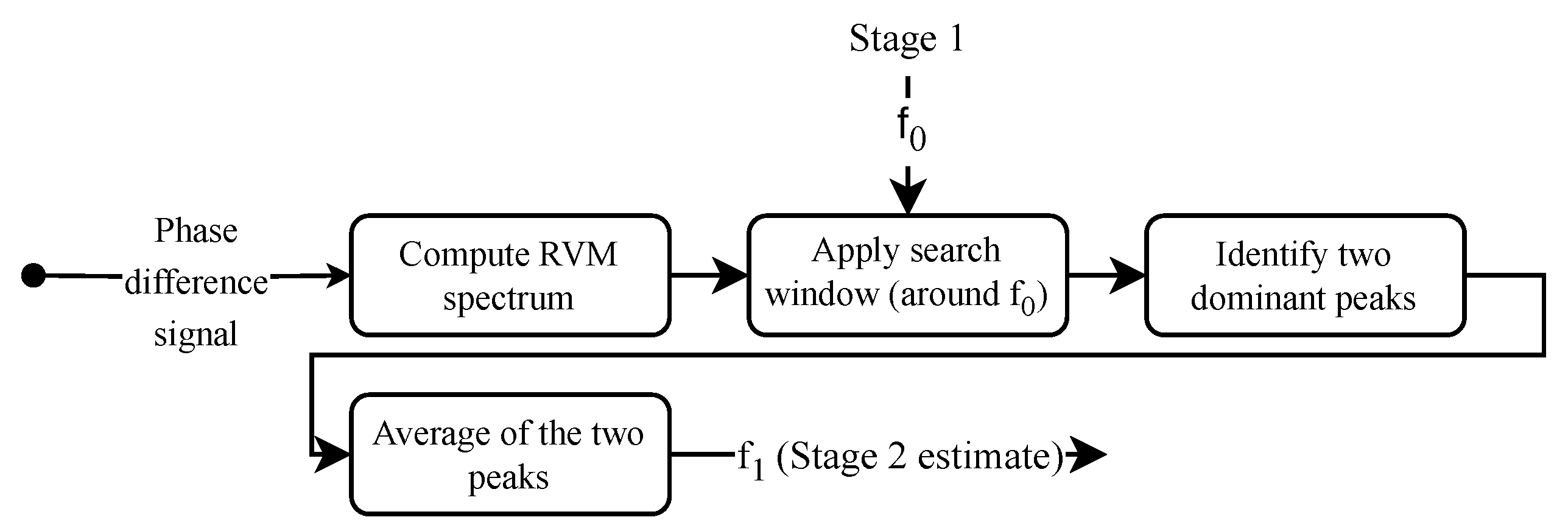
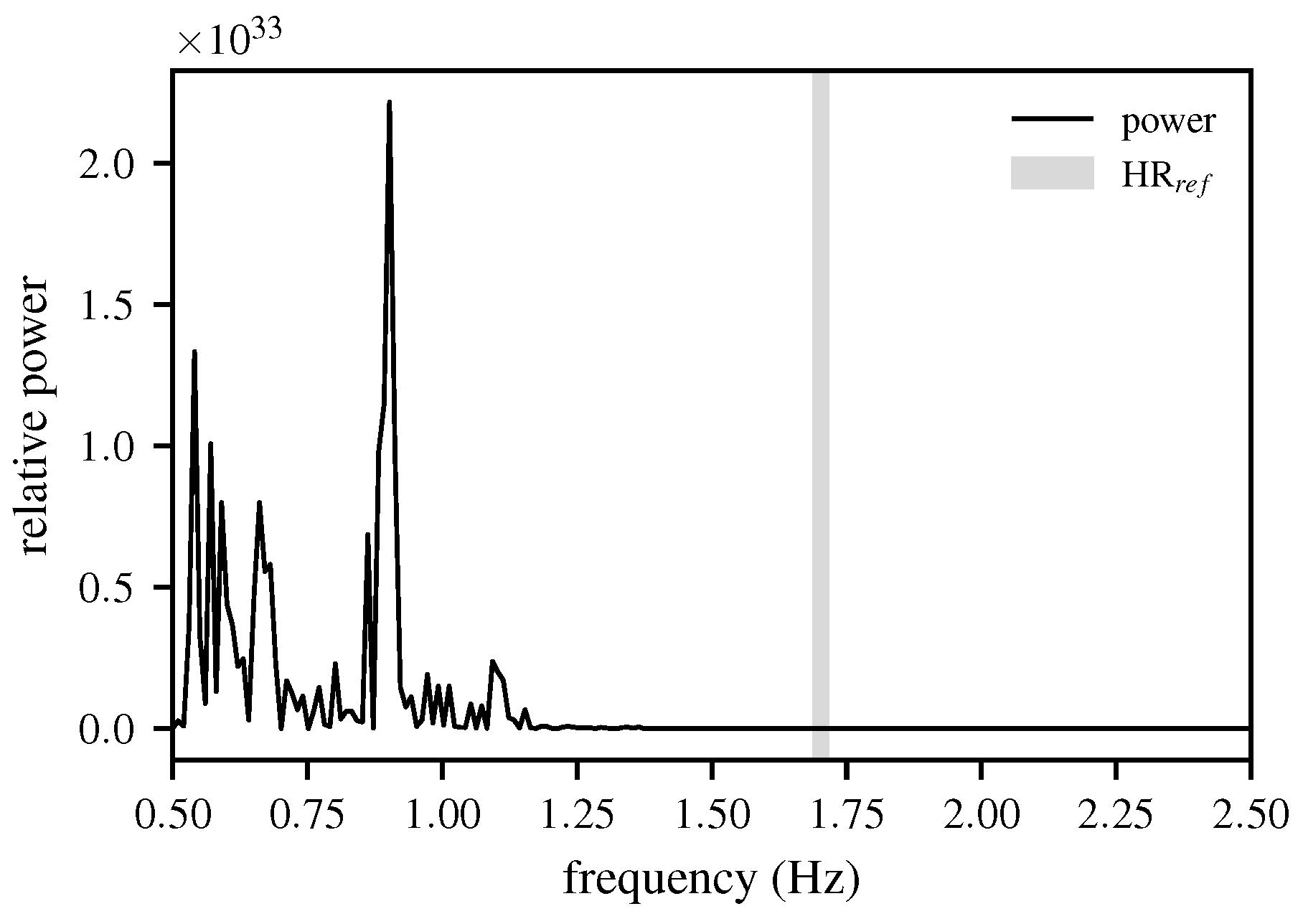
2.2. Stage 1: Coarse Estimation
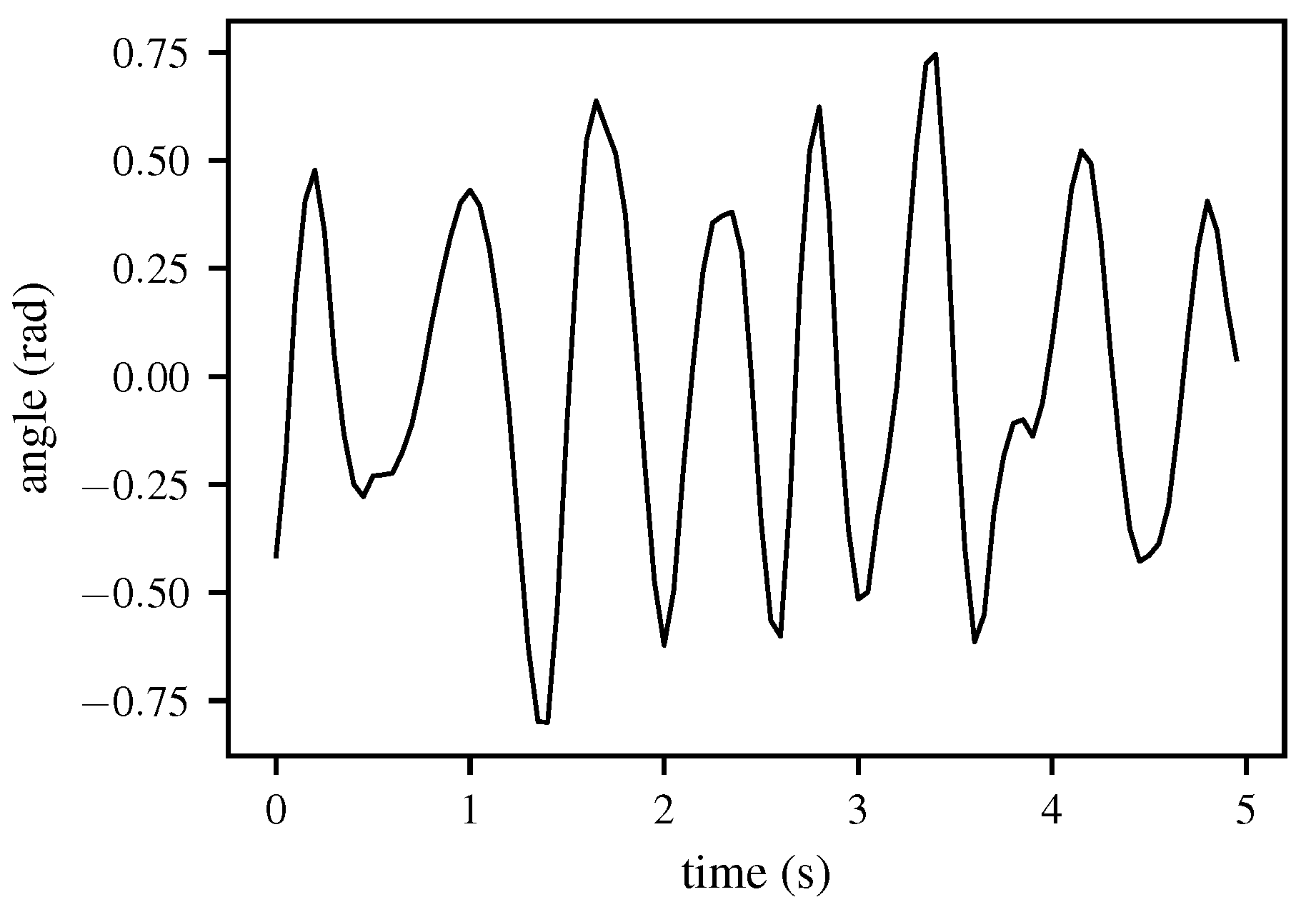
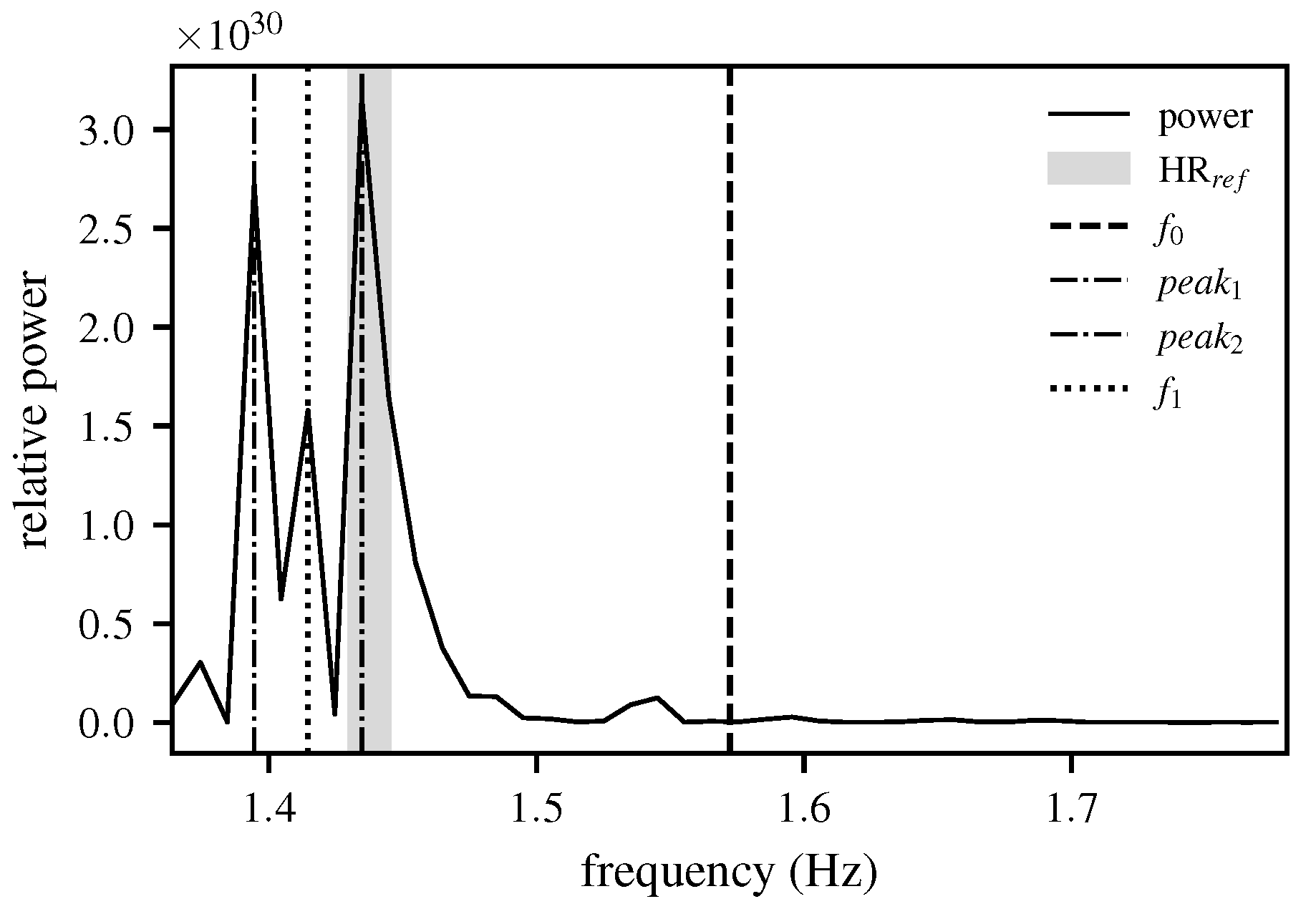
2.3. Stage 2: Fine Estimation
2.4. Post-Processing
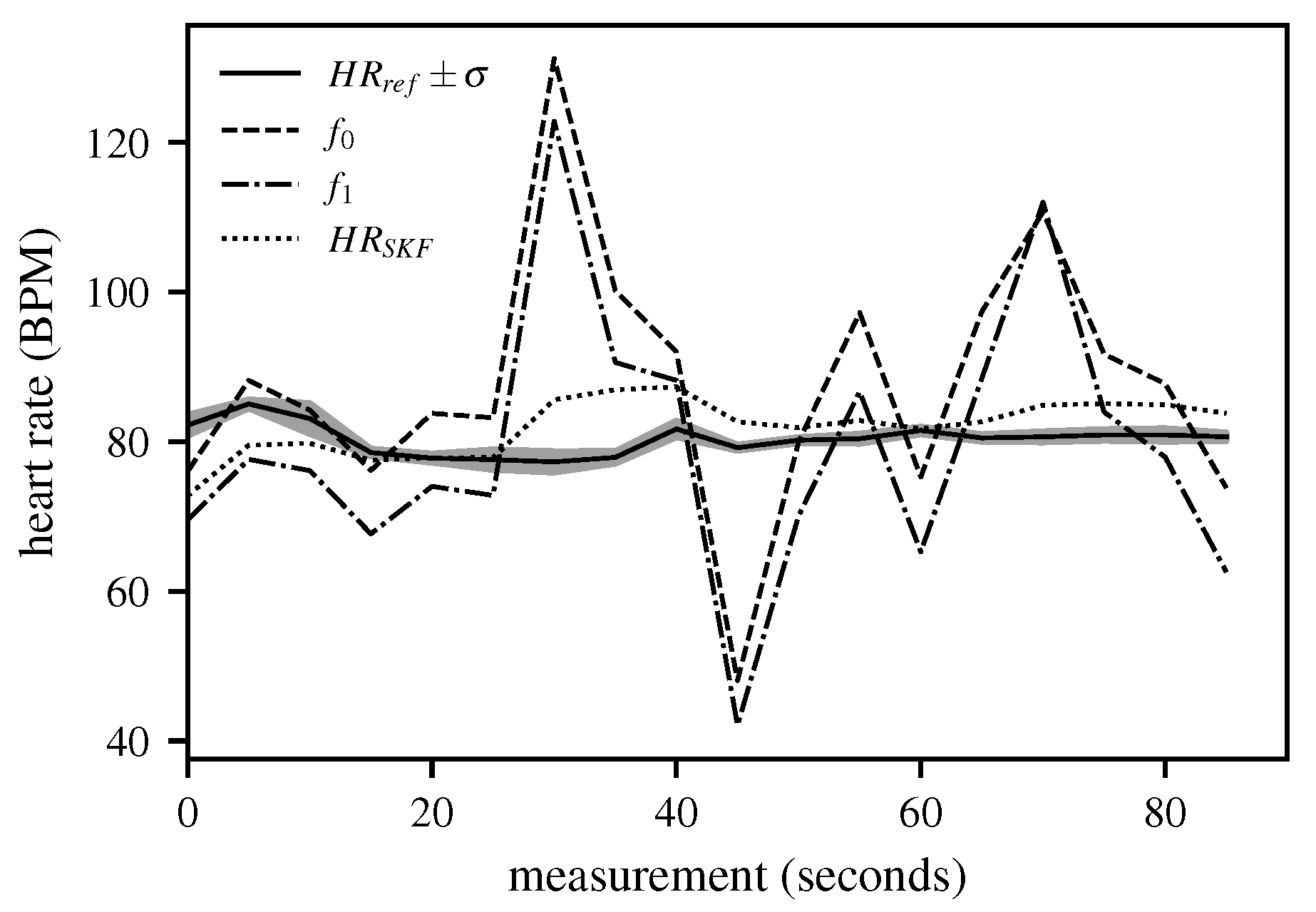
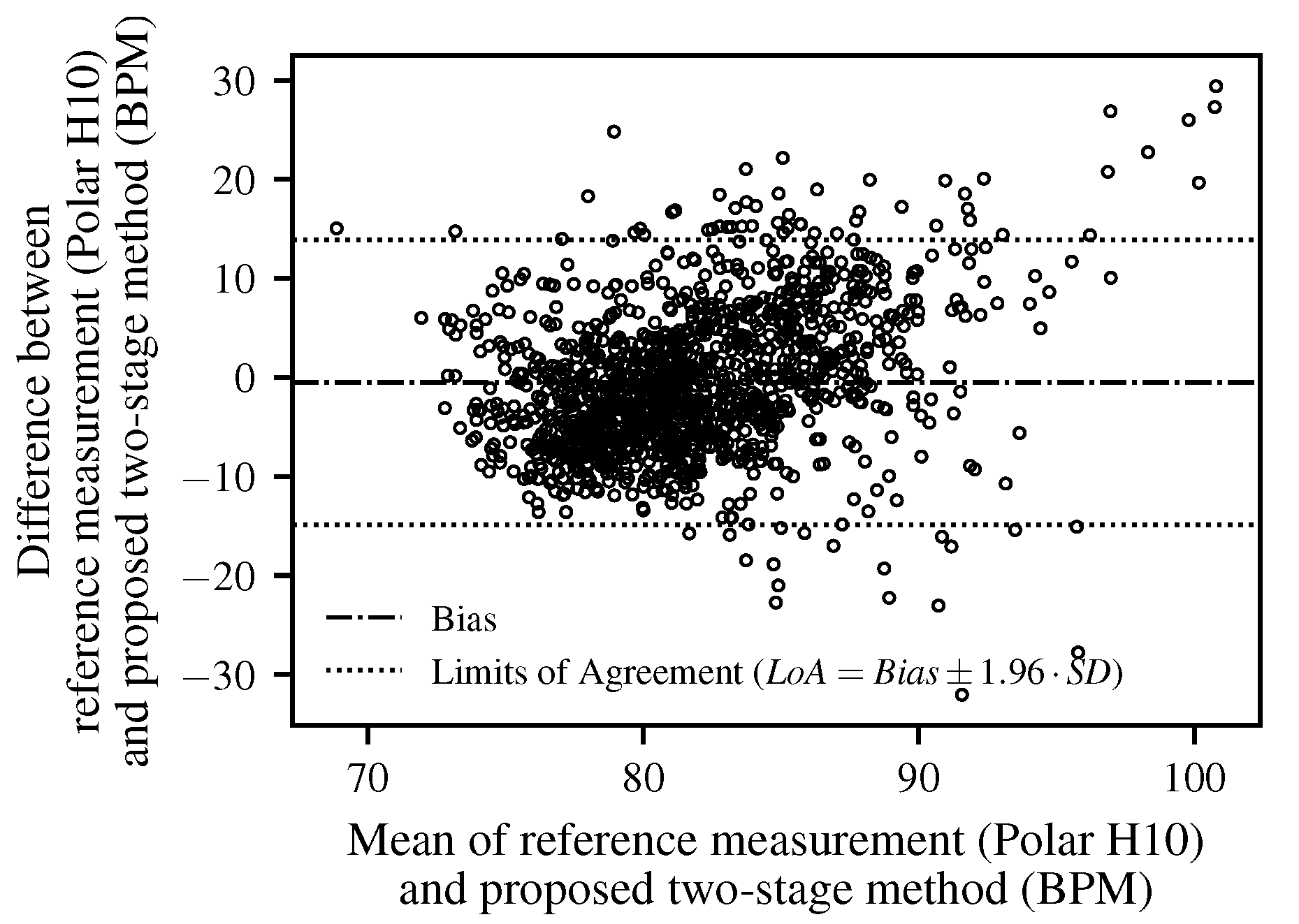
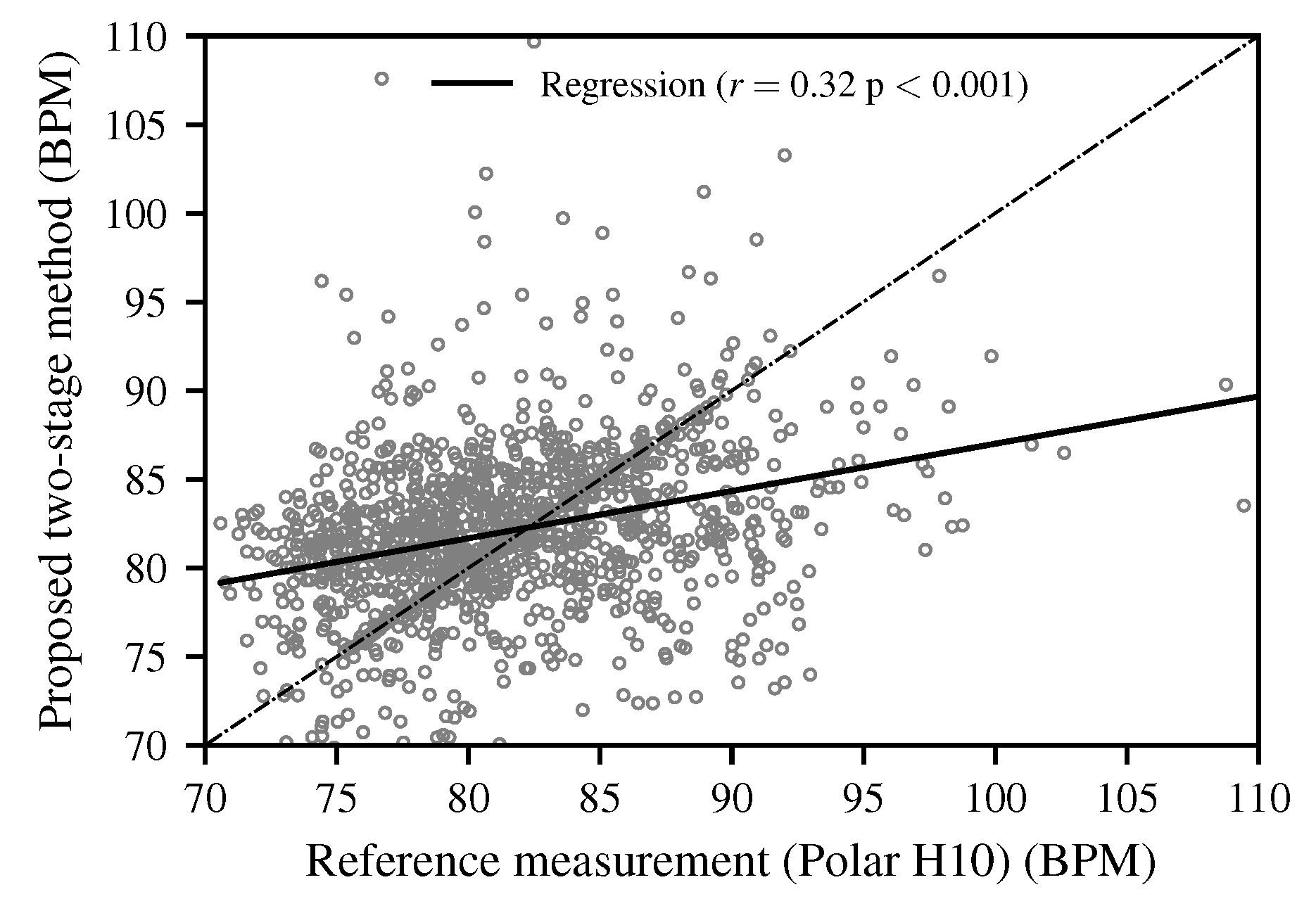
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADASs | advanced driver assistance systems |
| AR | autoregressive |
| BPM | beats per minute |
| DMS | driver monitoring system |
| DWT | discrete wavelet transform |
| FMCW | frequency-modulated continuous wave |
| HR | heart rate |
| HRV | heart rate variability |
| MAE | mean absolute error |
| MRE | mean relative error |
| PSD | power spectral density |
| RVM | relevance vector machine |
| SKF | sequential Kalman filter |
References
- Europäisches Parlament und Rat der Europäischen Union. Verordnung (EU) 2019/2144 des Europäischen Parlaments und des Rates vom 27. November 2019. Volume L 325, pp. 1–40. Available online: https://eur-lex.europa.eu/legal-content/DE/TXT/?uri=CELEX:32019R2144 (accessed on 11 June 2025).
- Thomas, P.; Morris, A.; Talbot, R.; Fagerlind, H. Identifying the causes of road crashes in Europe. Ann. Adv. Automot. Med. 2013, 57, 13–22. [Google Scholar]
- Abdel-Aty, M.; Ding, S. A matched case-control analysis of autonomous vs human-driven vehicle accidents. Nat. Commun. 2024, 15, 4931. [Google Scholar] [CrossRef]
- Möller, T.; Schneiderbauer, T.; Garms, F.; Gläfke, A.; Köster, N.; Stegmüller, S.; Kern, M.; Werner, M.; Bobka, K. The Future of Interior in Automotive. McKinsey Center for Future Mobility. 2021. Available online: https://www.mckinsey.com/capabilities/mckinsey-center-for-future-mobility/our-insights/the-future-of-interior-in-automotive (accessed on 10 July 2025).
- Ryan, J.M.; Howes, L.G. Relations between alcohol consumption, heart rate, and heart rate variability in men. Heart 2002, 88, 641–642. [Google Scholar] [CrossRef]
- Abrams, K.; Cieslowski, K.; Johnson, S.; Krimmel, S.; La Rosa, G.B.D.; Barton, K.; Silverman, P. The effects of alcohol on heartbeat perception: Implications for anxiety. Addict. Behav. 2018, 79, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Brunner, S.; Krewitz, C.; Winter, R.; von Falkenhausen, A.S.; Kern, A.; Brunner, D.; Sinner, M.F. Acute alcohol consumption and arrhythmias in young adults: The MunichBREW II study. Eur. Heart J. 2024, 45, 4938–4949. [Google Scholar] [CrossRef]
- Lu, K.; Dahlman, A.S.; Karlsson, J.; Candefjord, S. Detecting driver fatigue using heart rate variability: A systematic review. Accid. Anal. Prev. 2022, 178, 106830. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.G.; Cheon, E.J.; Bai, D.S.; Lee, Y.H.; Koo, B.H. Stress and heart rate variability: A meta-analysis and review of the literature. Psychiatry Investig. 2018, 15, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.C.; Su, M.I.; Liu, C.W.; Huang, Y.C.; Huang, W.L. Heart rate variability in patients with anxiety disorders: A systematic review and meta-analysis. Psychiatry Clin. Neurosci. 2022, 76, 292–302. [Google Scholar] [CrossRef]
- Warnecke, J.M.; Ganapathy, N.; Koch, E.; Dietzel, A.; Flormann, M.; Henze, R.; Deserno, T.M. Printed and Flexible ECG Electrodes Attached to the Steering Wheel for Continuous Health Monitoring during Driving. Sensors 2022, 22, 4198. [Google Scholar] [CrossRef]
- Choi, Y.J.; Lee, J.Y.; Kong, S.H. Driver ECG Measuring System with a Conductive Fabric-Based Dry Electrode. IEEE Access 2018, 6, 415–427. [Google Scholar] [CrossRef]
- Satti, A.T.; Kim, J.; Yi, E.; Cho, H.y.; Cho, S. Microneedle Array Electrode-Based Wearable EMG System for Detection of Driver Drowsiness through Steering Wheel Grip. Sensors 2021, 21, 5091. [Google Scholar] [CrossRef] [PubMed]
- Babusiak, B.; Hajducik, A.; Medvecky, S.; Lukac, M.; Klarak, J. Design of Smart Steering Wheel for Unobtrusive Health and Drowsiness Monitoring. Sensors 2021, 21, 5285. [Google Scholar] [CrossRef]
- Broto, L.; Okimoto, M. Utilization of low-cost pulse coherent radar for physiological assessment in vehicle interior. In Proceedings of the 38th Simpósio Brasileiro de Telecomunicações e Processamento de Sinais (SBrT), Virtual, 22–25 November 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Singh, D.; Eleonye, T.; Surazynski, L.; Ferdinando, H.; Kumar, A.; Joshi, H.D.; Särestöniemi, M.; Myllylä, T. Preliminary studies on mm-wave radar for vital sign monitoring of driver in vehicular environment. In Nordic Conference on Digital Health and Wireless Solutions; Springer: Cham, Switzerland, 2024; pp. 480–493. [Google Scholar] [CrossRef]
- Ni, C.; Pan, J.; Du, D.; Yang, X.; Shi, C.; Chen, S.; Yang, D.; Liu, S. Accurate heart rate measurement across various body postures using FMCW radar. IEEE Trans. Instrum. Meas. 2024, 73, 1–13. [Google Scholar] [CrossRef]
- Yang, Z.; Bao, Z. Short-time heart rate estimation based on 60-GHz FMCW radar. In Proceedings of the 2023 IEEE MTT-S International Wireless Symposium (IWS), Qingdao, China, 14–17 May 2023; pp. 1–3. [Google Scholar] [CrossRef]
- Jung, D.; Cheon, S.; Kim, D.; Yoon, J.; Kim, B. Short-Time Remote Heart Rate Measurement Based on mmWave FMCW Radar Frame Structure. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 1301–1305. [Google Scholar] [CrossRef]
- Liu, K.; Ding, C.; Zhang, Y. A Coarse-to-Fine Robust Estimation of FMCW Radar Signal for Vital Sign Detection. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Dai, T.K.V.; Oleksak, K.; Kvelashvili, T.; Foroughian, F.; Bauder, C.; Theilmann, P.; Fathy, A.E.; Kilic, O. Enhancement of Remote Vital Sign Monitoring Detection Accuracy Using Multiple-Input Multiple-Output (MIMO) 77 GHz FMCW Radar. IEEE J. Electromagn. RF Microwaves Med. Biol. 2022, 6, 111–122. [Google Scholar] [CrossRef]
- Saluja, J.; Casanova, J.; Lin, J. A Supervised Machine Learning Algorithm for Heart-Rate Detection Using Doppler Motion-Sensing Radar. IEEE J. Electromagn. RF Microwaves Med. Biol. 2020, 4, 45–51. [Google Scholar] [CrossRef]
- Rong, Y.; Dutta, A.; Chiriyath, A.; Bliss, D.W. Motion-Tolerant Non-Contact Heart-Rate Measurements from Radar Sensor Fusion. Sensors 2021, 21, 1774. [Google Scholar] [CrossRef]
- Paterniani, G.; Sgreccia, D.; Davoli, A.; Guerzoni, G.; Di Viesti, P.; Valenti, A.C.; Vitolo, M.; Vitetta, G.M.; Boriani, G. Radar-Based Monitoring of Vital Signs: A Tutorial Overview. Proc. IEEE 2023, 111, 277–317. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, Y.; Ma, Y.; Huang, R.; Qi, A.; Ma, M.; Qi, Y. Enhancing Road Safety: Fast and Accurate Noncontact Driver HRV Detection Based on Huber–Kalman and Autocorrelation Algorithms. Biomimetics 2024, 9, 481. [Google Scholar] [CrossRef]
- Infineon Technologies AG. BGT60TR13C Datasheet V2.4.9; Technischer Bericht; Infineon Technologies AG: München, Germany, 2023. [Google Scholar]
- Zhou, M.; Liu, Y.; Wu, S.; Wang, C.; Chen, Z.; Li, H. A Novel Scheme of High-Precision Heart Rate Detection with a mm-Wave FMCW Radar. IEEE Access 2023, 11, 85118–85136. [Google Scholar] [CrossRef]
- Xiang, M.; Ren, W.; Li, W.; Xue, Z.; Jiang, X. High-Precision Vital Signs Monitoring Method Using a FMCW Millimeter-Wave Sensor. Sensors 2022, 22, 7543. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Guo, S.; Cui, G.; Jiang, M.; Shi, L. An Ingenious Heart Rate Estimation Method in Harmonic Background for FMCW Radar. IEEE Trans. Microw. Theory Tech. 2025, 73, 1235–1247. [Google Scholar] [CrossRef]
- Xu, D.; Yu, W.; Deng, C.; He, Z.S. Non-Contact Detection of Vital Signs Based on Improved Adaptive EEMD Algorithm. Sensors 2022, 22, 6423. [Google Scholar] [CrossRef]
- Yang, Y.; Luo, Y.; Qi, A.; Shi, G.; Miao, M.; Fan, J.; Ma, J.; Qi, Y. Huber Kalman Filter for Wi-Fi Based Vehicle Driver’s Respiration Detection. IEEE Trans. Veh. Technol. 2022, 71, 8933–8943. [Google Scholar] [CrossRef]
- Li, D.; Huang, Y.; Li, H.; Cheng, J.; Zhu, W.; Feng, H. A Novel Approach to Accurate Respiratory Rate and Heart Rate Estimation via FMCW Radar. IEEE Sens. J. 2025, 25, 13937–13945. [Google Scholar] [CrossRef]
- Berenschot, L. Vital Signs Monitoring with an FMCW Radar Sensor. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2022. [Google Scholar]
- Addison, P.S. Wavelet transforms and the ECG: A review. Physiol. Meas. 2005, 26, R155–R199. [Google Scholar] [CrossRef]
- Rao, K.D.; Swamy, M.N.S. Spectral Analysis of Signals. In Digital Signal Processing: Theory and Practice; Springer: Singapore, 2018; pp. 721–751. [Google Scholar] [CrossRef]
- Bos, R.; de Waele, S.; Broersen, P.M.T. Autoregressive spectral estimation by application of the Burg algorithm to irregularly sampled data. IEEE Trans. Instrum. Meas. 2002, 51, 1289–1294. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Zhang, P.; Qi, W.; Deng, Z. Sequential fusion Kalman filter. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 2140–2146. [Google Scholar]
- Chandra Babu, A.; Karri, R.K.; M.S., N. Sensor Data Fusion Using Kalman Filter. In Proceedings of the 2018 International Conference on Design Innovations for 3Cs Compute Communicate Control (ICDI3C), Bangalore, India, 25–28 April 2018; pp. 29–36. [Google Scholar] [CrossRef]
- Raspberry Pi Foundation. Raspberry Pi 5 Product Brief; Technical Report; Raspberry Pi Foundation: Cambridge, UK, 2023; Available online: https://datasheets.raspberrypi.com/rpi5/raspberry-pi-5-product-brief.pdf (accessed on 9 August 2025).
- Polar Electro Oy. Polar H10 Heart Rate Sensor User Manual. 2023. Available online: https://support.polar.com/e_manuals/h10-heart-rate-sensor/polar-h10-user-manual-english/manual.pdf (accessed on 3 June 2025).
- Shcherbina, A.; Mattsson, C.M.; Waggott, D.; Salisbury, H.; Christle, J.W.; Hastie, T.; Wheeler, M.T.; Ashley, E.A. Accuracy in Wrist-Worn, Sensor-Based Measurements of Heart Rate and Energy Expenditure in a Diverse Cohort. J. Pers. Med. 2017, 7, 3. [Google Scholar] [CrossRef]
- Etiwy, M.; Akhrass, Z.; Gillinov, L.; Alashi, A.; Wang, R.; Blackburn, G.; Gillinov, S.M.; Phelan, D.; Gillinov, A.M.; Houghtaling, P.L.; et al. Accuracy of wearable heart rate monitors in cardiac rehabilitation. Cardiovasc. Diagn. Ther. 2019, 9, 262–271. [Google Scholar] [CrossRef]
- Germini, F.; Noronha, N.; Borg Debono, V.; Abraham Philip, B.; Pete, D.; Navarro, T.; Keepanasseril, A.; Parpia, S.; de Wit, K.; Iorio, A. Accuracy and Acceptability of Wrist-Wearable Activity-Tracking Devices: Systematic Review of the Literature. J. Med. Internet Res. 2022, 24, e30791. [Google Scholar] [CrossRef]
- Castro, I.D.; Mercuri, M.; Patel, A.; Puers, R.; Van Hoof, C.; Torfs, T. Physiological Driver Monitoring Using Capacitively Coupled and Radar Sensors. Appl. Sci. 2019, 9, 3994. [Google Scholar] [CrossRef]
- Polar Research and Technology. Polar H10 Heart Rate Sensor System; White Paper; Polar Electro Oy: Kempele, Finland, 2019. [Google Scholar]
- Schaffarczyk, M.; Rogers, B.; Reer, R.; Gronwald, T. Validity of the Polar H10 Sensor for Heart Rate Variability Analysis during Resting State and Incremental Exercise in Recreational Men and Women. Sensors 2022, 22, 6536. [Google Scholar] [CrossRef] [PubMed]
- Amin, O.B.; Mishra, V.; Tapera, T.M.; Volpe, R.; Sathyanarayana, A. Extending Stress Detection Reproducibility to Consumer Wearable Sensors. arXiv 2025, arXiv:2505.05694. [Google Scholar] [CrossRef]
- Huang, X.; Ju, Z.; Zhang, R. Real-Time Heart Rate Detection Method Based on 77 GHz FMCW Radar. Micromachines 2022, 13, 1960. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Ebrahim, M.P.; Hasan, K.; Heydari, F.; Howley, P.; Yuce, M.R. Accurate Heart Rate and Respiration Rate Detection Based on a Higher-Order Harmonics Peak Selection Method Using Radar Non-Contact Sensors. Sensors 2022, 22, 83. [Google Scholar] [CrossRef]
- Ahmed, S.; Park, J.; Cho, S.H. Effects of receiver beamforming for vital sign measurements using FMCW radar at various distances and angles. Sensors 2022, 22, 6877. [Google Scholar] [CrossRef]
- Paddan, G.S.; Griffin, M.J. Evaluation of whole-body vibration in vehicles. J. Sound Vib. 2002, 253, 195–213. [Google Scholar] [CrossRef]
- Apple Inc. MacBook Pro (13-Inch, M2, 2022)—Technical Specifications. 2022. Available online: https://support.apple.com/en-us/111869 (accessed on 5 September 2025).
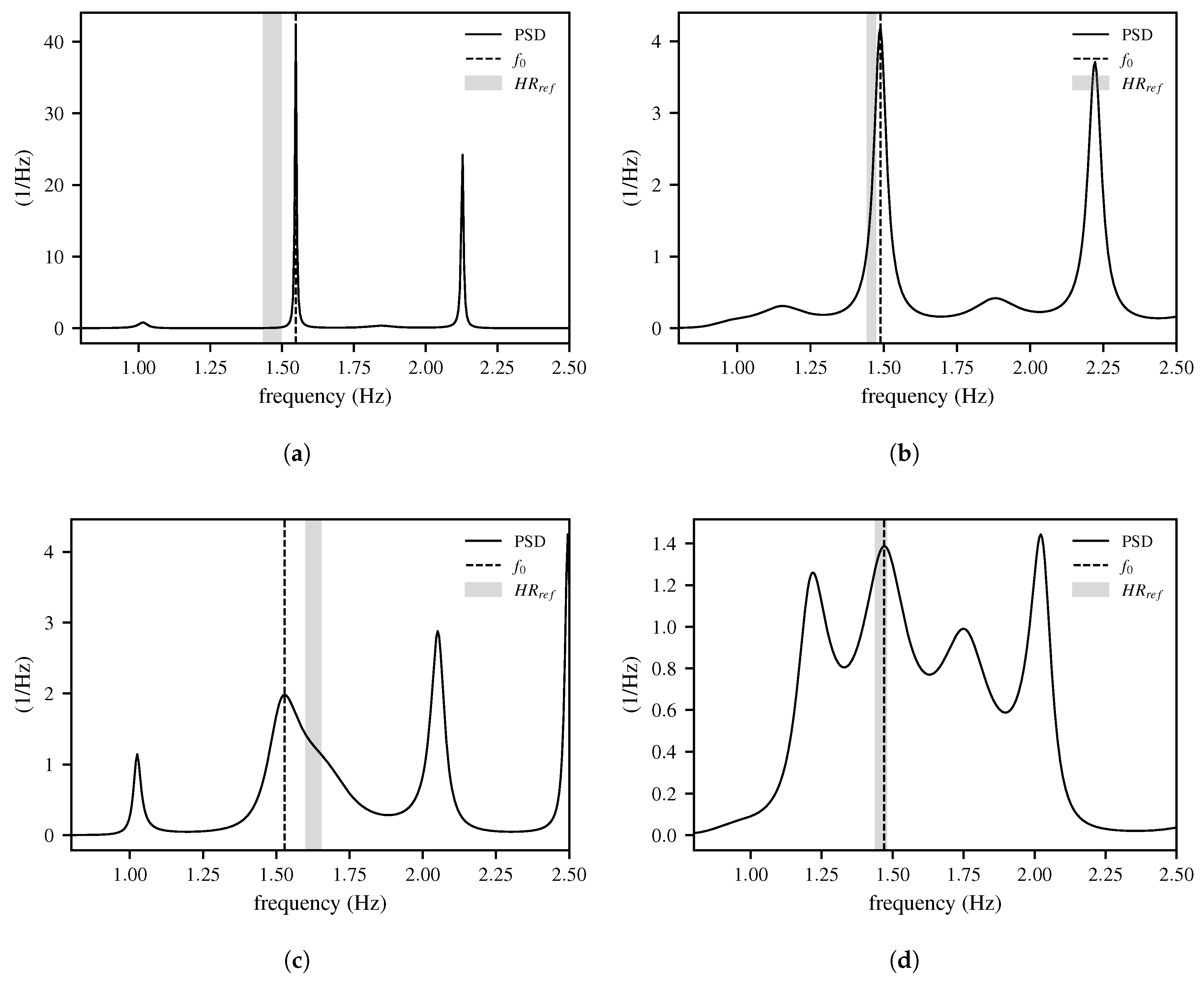
| Number of Peaks Detected (Burg Method) | Match at the Highest Peak [%] | Match Resulting from Logic Application [%] | Proportion of the Entire Test Dataset [%] |
|---|---|---|---|
| 1 | 100.0 | 100.0 | 4.3 |
| 2 | 51.3 | 91.8 (+40.5) | 23.7 |
| 3 | 35.2 | 90.9 (+55.7) | 44.3 |
| 4 | 30.8 | 86.3 (+55.5) | 25.9 |
| >4 | 8.3 | 100 (+91.7) | 1.8 |
| 40.2 | 90.5 | 100.0 |
| Frame Repetition Time | 50 ms |
| Chirp Repetition Time | 0.5 ms |
| Number of Chirps | 1 |
| Start Frequency | 58 GHz |
| End Frequency | 63.5 GHz |
| Sample Rate | 3 MHz |
| Number of Samples | 128 |
| MRE (%) | MAE (bpm) | |||||||
|---|---|---|---|---|---|---|---|---|
| - | SD | Out-of-1-SD | Out-of-2-SD | - | SD | Out-of-1-SD | Out-of-2-SD | |
| Stage 1 | 14.56 | 11.7 | 13.43 | 12.41 | 11.75 | 9.22 | 10.82 | 9.97 |
| Stage 2 | 13.24 | 9.99 | 12.09 | 11.05 | 10.85 | 8.33 | 9.91 | 9.05 |
| Post | ||||||||
| Process | 6.88 | 4.74 | 5.8 | 4.88 | 5.58 | 4.01 | 4.69 | 3.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandstetter, J.; Knoch, E.-M.; Gauterin, F. Heart Rate Estimation Using FMCW Radar: A Two-Stage Method Evaluated for In-Vehicle Applications. Biomimetics 2025, 10, 630. https://doi.org/10.3390/biomimetics10090630
Brandstetter J, Knoch E-M, Gauterin F. Heart Rate Estimation Using FMCW Radar: A Two-Stage Method Evaluated for In-Vehicle Applications. Biomimetics. 2025; 10(9):630. https://doi.org/10.3390/biomimetics10090630
Chicago/Turabian StyleBrandstetter, Jonas, Eva-Maria Knoch, and Frank Gauterin. 2025. "Heart Rate Estimation Using FMCW Radar: A Two-Stage Method Evaluated for In-Vehicle Applications" Biomimetics 10, no. 9: 630. https://doi.org/10.3390/biomimetics10090630
APA StyleBrandstetter, J., Knoch, E.-M., & Gauterin, F. (2025). Heart Rate Estimation Using FMCW Radar: A Two-Stage Method Evaluated for In-Vehicle Applications. Biomimetics, 10(9), 630. https://doi.org/10.3390/biomimetics10090630






