Migratory Bird-Inspired Adaptive Kalman Filtering for Robust Navigation of Autonomous Agricultural Planters in Unstructured Terrains
Abstract
1. Introduction
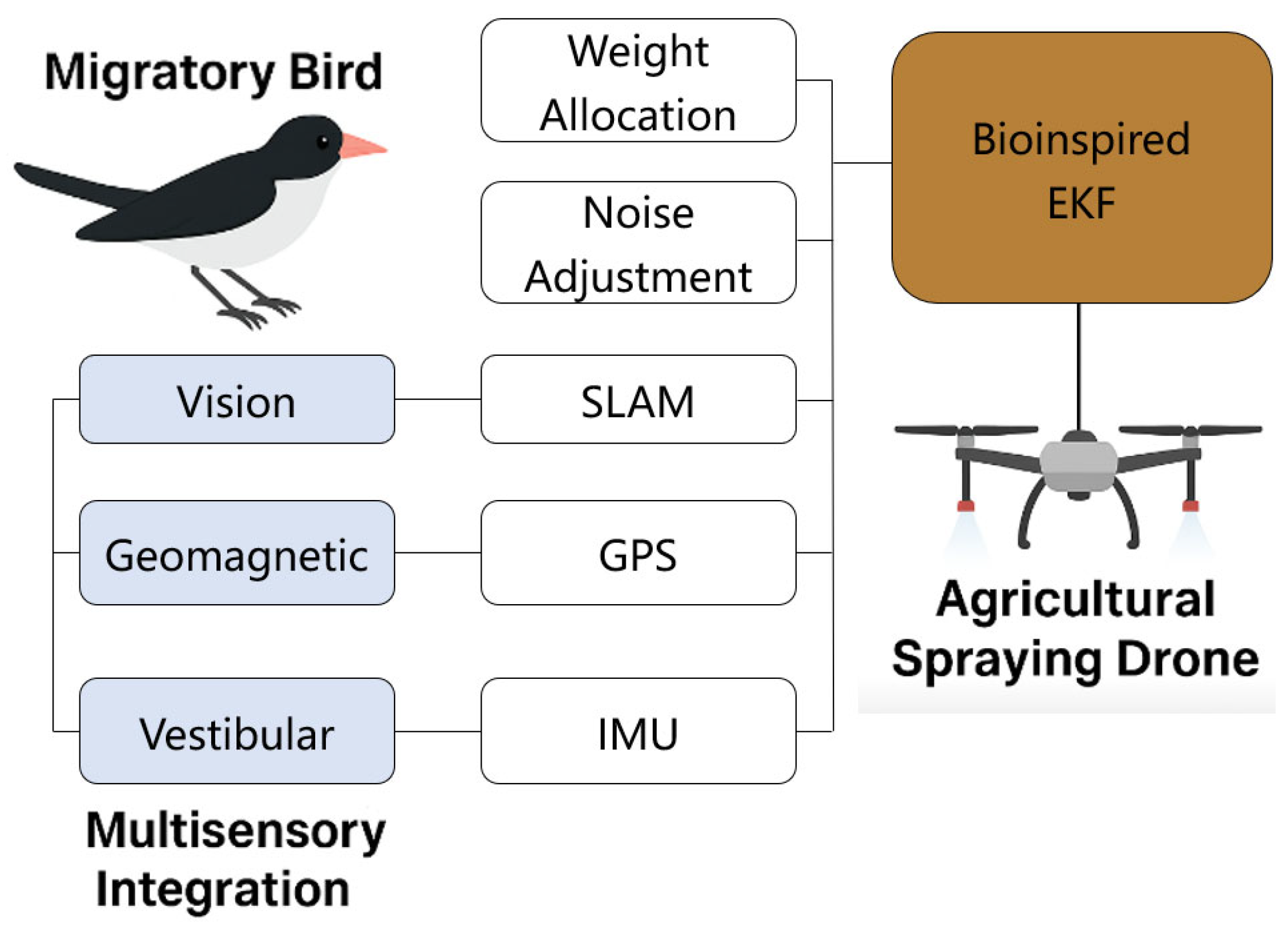
- A mathematical model of the neural navigation mechanism of migratory birds, including a proposed sensory weight mapping formula with structural fusion of state residuals;
- A time-varying fusion and dynamic noise adjustment mechanism, combined with soft switching idea to improve robustness;
- Fusion of deep learning classifiers to realize online environment recognition and parameter self-tuning, breaking through the limitations of traditional EKF that requires manual parameter tuning.
2. System Modeling
2.1. Definition of State Vector
2.2. Nonlinear Dynamic Model
2.3. Measurement Model
3. Biomimetic Extended Kalman Filter (EKF) Algorithm
3.1. Standard Extended Kalman Filter
3.1.1. Prediction Step
3.1.2. Update Steps
3.2. Bio-Inspired Adaptive Mechanisms
3.2.1. Sensor Fusion Weights Adjustment Model
3.2.2. Dynamic Adjustment Model for Noise Covariance
3.2.3. Time-Varying Measurement Noise Estimation
4. Experimental and Simulation Analysis
4.1. Experimental Design
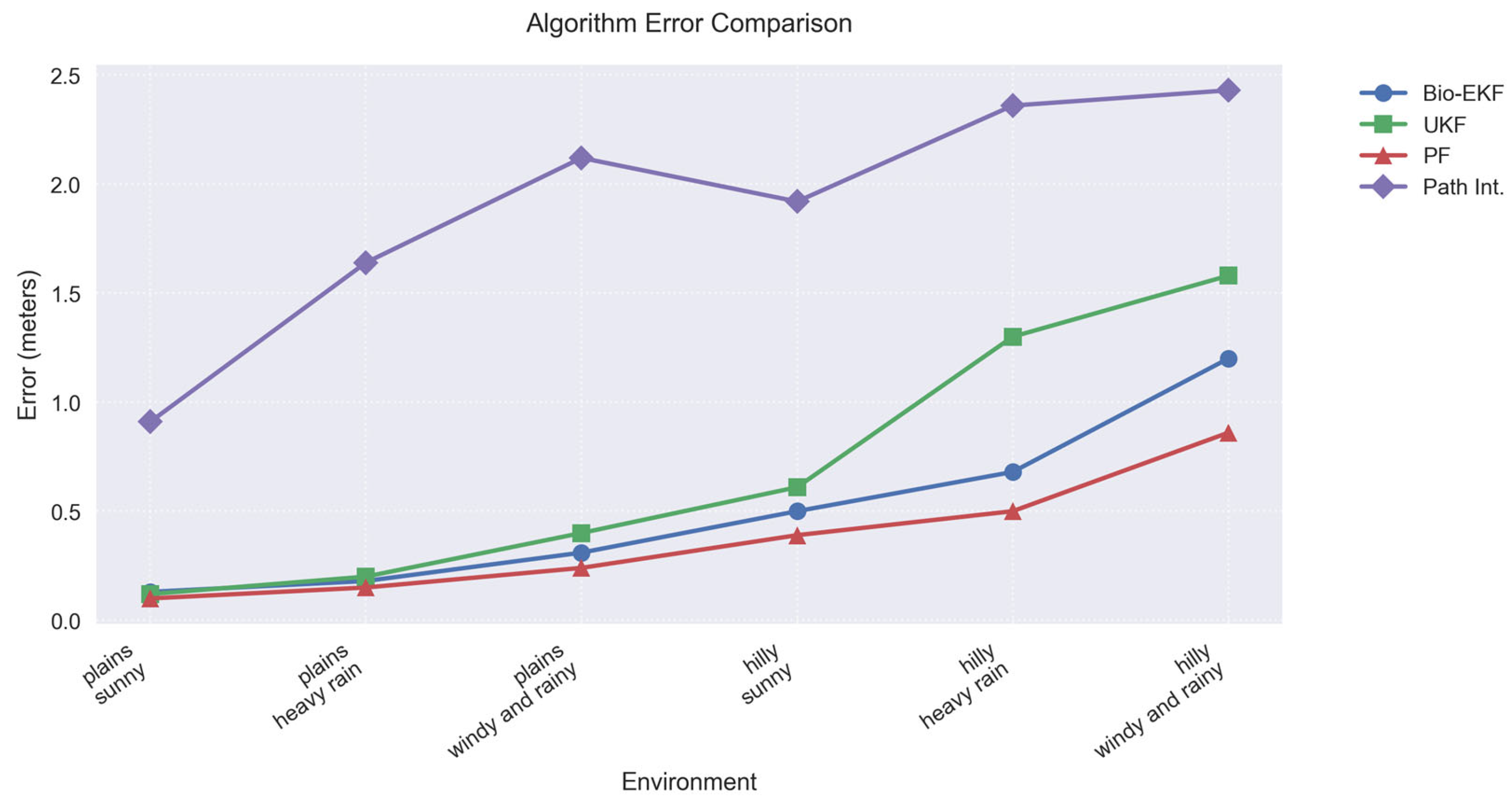
4.2. Simulation Results and Analysis
4.3. Computational Efficiency Evaluation
5. Results
- Forestry monitoring: e.g., fire patrol in mountainous areas, mapping of pest and disease distribution;
- Detection of disaster areas: such as semi-autonomous search and localization of collapsed areas after earthquakes;
- Special terrain transportation robots: such as snow, desert, and other environments in the path estimation.
Author Contributions
Funding
Conflicts of Interest
References
- Kondoyanni, M.; Loukatos, D.; Maraveas, C.; Drosos, C.; Arvanitis, K.G. Bio-Inspired Robots and Structures toward Fostering the Modernization of Agriculture. Biomimetics 2022, 7, 69. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, W. Research Progress on Autonomous Navigation Technology for Multiple Agricultural Scenarios. Comput. Electron. Agric. 2023, 214, 108351. [Google Scholar] [CrossRef]
- Han, X.; Kim, H.J.; Jeon, C.W. GNSS/IMU Integrated Navigation for Agricultural Machinery Based on Fuzzy Adaptive Finite Impulse Response Kalman Filter Algorithm. Comput. Electron. Agric. 2021, 191, 106541. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, G. Application of Updated Sage–Husa Adaptive Kalman Filter in the Navigation of a Translational Sprinkler Irrigation Machine. IFAC-Pap. 2019, 52, 333–338. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W. Autonomous Navigation Method for Agricultural Robots in High-Tunnel Cultivation Environments. Comput. Electron. Agric. 2022, 203, 107107. [Google Scholar] [CrossRef]
- Gonzalez, D.; Ruggiero, V. Development of a Navigation System for Smart Farms. IFAC-Pap. 2018, 51, 1–6. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, Y. Development of an Automatic Navigation System for Following Agricultural Machinery. Comput. Electron. Agric. 2019, 158, 351–360. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y. Design and Experiment of a Field Management Robot and Its Navigation Control System for Agriculture. Agronomy 2024, 14, 654. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R. Comparison of Kalman Filters for Inertial Integrated Navigation. Sensors 2019, 19, 1786. [Google Scholar] [CrossRef]
- Webb, B. Biorobotic Navigation. Robot. Auton. Syst. 2000, 30, 159–177. [Google Scholar] [CrossRef]
- Chahl, J.S.; Mizutani, A. A Biomimetic Radar System for Autonomous Navigation. Sensors 2019, 19, 252. [Google Scholar] [CrossRef]
- Bianchi, G.; Lanzetti, L.; Mariana, D.; Cinquemani, S. Bioinspired Design and Experimental Validation of an Aquatic Snake Robot. Biomimetics 2024, 9, 87. [Google Scholar] [CrossRef]
- He, X.; Li, X.; Wang, X.; Meng, F.; Guan, X.; Jiang, Z.; Yuan, L.; Ba, K.; Ma, G.; Yu, B. Running Gait and Control of Quadruped Robot Based on SLIP Model. Biomimetics 2024, 9, 24. [Google Scholar] [CrossRef]
- Duman, E.; Uysal, M.; Alkaya, A.F. Migrating Birds Optimization: A new metaheuristic approach and its performance on quadratic assignment problem. Inf. Sci. 2012, 217, 65–77. [Google Scholar] [CrossRef]
- Oral, M.; Duman, E. Enhanced migrating birds optimization algorithm for optimization problems in different domains. Ann. Oper. Res. 2024, 351, 455–488. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Li, J. An Improved Migratory Birds Optimization Algorithm for Closed-Loop Supply Chain Network Design under Uncertainty. PLoS ONE 2024, 19, e0306294. [Google Scholar] [CrossRef]
- Pan, Q.K.; Tasgetiren, M.F.; Suganthan, P.N.; Chua, T.J. A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem. Inf. Sci. 2011, 181, 2455–2468. [Google Scholar] [CrossRef]
- Al-Omary, A.; Jafar, A.; Al-Khudairi, O. Migratory birds-inspired navigation system for unmanned aerial vehicles. In Proceedings of the 2017 International Conference on Electrical and Computing Technologies and Applications (ICECTA), Ras Al Khaimah, United Arab Emirates, 21–23 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Q. Review of Bionic Polarized Light Navigation Sensors. Sensors 2023, 23, 5848. [Google Scholar] [CrossRef]
- Mourad, K.; Foppen, R.P. Simulated Experiments Testing Geomagnetic Navigation Strategies During Long-Distance Bird Migration. Mov. Ecol. 2021, 9, 48. [Google Scholar] [CrossRef]
- Guilford, T.; Taylor, G.K. The Navigation of Migratory Birds: Insights from Insect-Inspired Studies. Integr. Comp. Biol. 2014, 54, 683–692. [Google Scholar] [CrossRef]
- Bairlein, F.; Norris, D.R.; Voigt, C.C. New frontiers in bird migration research. Curr. Biol. 2022, 32, R1097–R1107. [Google Scholar] [CrossRef]
- Chernetsov, N. How Migrating Birds Use Quantum Effects to Navigate. Scientific American 2022. Available online: https://www.scientificamerican.com/article/how-migrating-birds-use-quantum-effects-to-navigate/ (accessed on 19 June 2025).
- Mouritsen, H. True navigation in birds: From quantum physics to global migration. J. Zool. 2014, 293, 73–82. [Google Scholar] [CrossRef]
- Guilford, T.; Åkesson, S.; Gagliardo, A.; Holland, R.A.; Mouritsen, H.; Muheim, R.; Wiltschko, R.; Wiltschko, W.; Bingman, V.P. Migratory navigation in birds: New opportunities in an era of fast-developing tracking technology. J. Exp. Biol. 2011, 214, 3705–3712. [Google Scholar] [CrossRef] [PubMed]
- Bingman, V.P.; Cheng, K. The Neural Basis of Long-Distance Navigation in Birds. Annu. Rev. Physiol. 2016, 78, 133–154. [Google Scholar] [CrossRef]
- MacDonald, C.J.; Tonegawa, S. On a Search for a Neurogenomics of Cognitive Processes Supporting Avian Migration and Navigation. Integr. Comp. Biol. 2020, 60, 967–979. [Google Scholar] [CrossRef] [PubMed]
- Hein, C.M.; Zapka, M.; Mouritsen, H. Comparison of Visually Guided Flight in Insects and Birds. Front. Neurosci. 2018, 12, 157. [Google Scholar] [CrossRef]
- Pritchard, D.J.; Healy, S.D. Taking an insect-inspired approach to bird navigation. Learn. Behav. 2018, 46, 7–22. [Google Scholar] [CrossRef]
- Serres, J.R.; Ruffier, F. Towards a Predictive Bio-Inspired Navigation Model. Information 2021, 12, 100. [Google Scholar] [CrossRef]
- Fischer, J.; Kutsch, W. Fast and Robust Bio-inspired Teach and Repeat Navigation. arXiv 2020, arXiv:2010.11326. [Google Scholar] [CrossRef]
- Revach, G.; Shlezinger, N.; Ni, X.; Escoriza, A.L.; Van Sloun, R.J.; Eldar, Y.C. KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics. IEEE Trans. Signal Process. 2022, 70, 1532–1547. [Google Scholar] [CrossRef]
- Harl, N.; Rajagopal, K.; Balakrishnan, S.N. Neural Network Based Modified State Observer for Orbit Uncertainty Estimation. J. Guid. Control. Dyn. 2013, 36, 1194–1209. [Google Scholar] [CrossRef]
- Zhou, X.; Qiao, D.; Li, X. Adaptive Order-Switching Kalman Filter for Orbit Determination Using Deep-Neural-Network-Based Nonlinearity Detection. J. Spacecr. Rocket. 2023, 60, 1724–1741. [Google Scholar] [CrossRef]

| Environmental Combinations | Maximum Adjustment Factor |
|---|---|
| plains + sunny | 0.05 |
| plains + heavy rain | 0.20 |
| plains + windy and rainy | 0.35 |
| hills + sunny | 0.12 |
| hills + heavy rain | 0.35 |
| hills + windy and rainy | 0.50 |
| Environmental Combinations | Title 2 | Title 3 | Title 4 |
|---|---|---|---|
| plains + sunny | 1.0 | 1.0 | 1.0 |
| plains + heavy rain | 3.0 + random perturbation | 1.0 | 1.0 |
| plains + windy and rainy | 3.0 + random perturbation | 4.0 + random perturbation | 2.8 + random perturbation |
| hills + sunny | 5.0 | 1.0 | 3.2 |
| hills + heavy rain | 5.0 × 3.0 | 1.0 | 3.2 × 1.0 |
| hills + windy and rainy | 5.0 × 3.0 | 4.0 + random perturbation | 3.2 × 2.8 |
| Arithmetic | Single-Step Time-Consuming (Milliseconds) |
|---|---|
| Bio-EKF | 0.97 |
| UKF | 1.42 |
| PF | 7.83 |
| Path | 0.71 |
| Arithmetic | MSE (m2) | Width of 95% Confidence Interval (m) |
|---|---|---|
| Bio-EKF | 0.39 | 1.13 |
| UKF | 0.80 | 1.84 |
| PF | 0.20 | 0.98 |
| PATH | 3.86 | 2.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Huang, Y.; Sun, J. Migratory Bird-Inspired Adaptive Kalman Filtering for Robust Navigation of Autonomous Agricultural Planters in Unstructured Terrains. Biomimetics 2025, 10, 543. https://doi.org/10.3390/biomimetics10080543
Zhou Z, Huang Y, Sun J. Migratory Bird-Inspired Adaptive Kalman Filtering for Robust Navigation of Autonomous Agricultural Planters in Unstructured Terrains. Biomimetics. 2025; 10(8):543. https://doi.org/10.3390/biomimetics10080543
Chicago/Turabian StyleZhou, Zijie, Yitao Huang, and Jiyu Sun. 2025. "Migratory Bird-Inspired Adaptive Kalman Filtering for Robust Navigation of Autonomous Agricultural Planters in Unstructured Terrains" Biomimetics 10, no. 8: 543. https://doi.org/10.3390/biomimetics10080543
APA StyleZhou, Z., Huang, Y., & Sun, J. (2025). Migratory Bird-Inspired Adaptive Kalman Filtering for Robust Navigation of Autonomous Agricultural Planters in Unstructured Terrains. Biomimetics, 10(8), 543. https://doi.org/10.3390/biomimetics10080543










