Adaptive Differentiated Parrot Optimization: A Multi-Strategy Enhanced Algorithm for Global Optimization with Wind Power Forecasting Applications
Abstract
1. Introduction
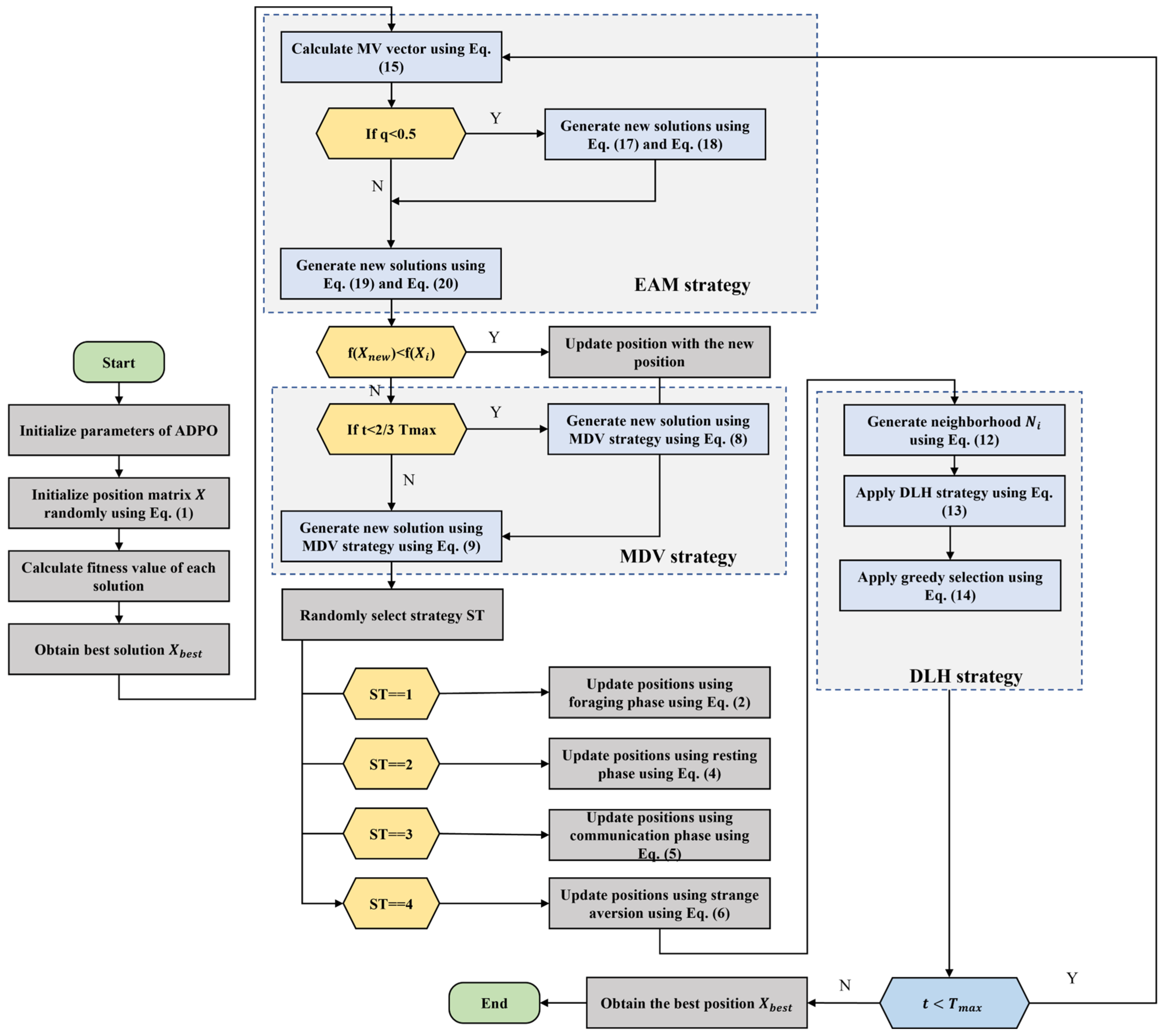
- An excellent improvement of PO, which is known as ADPO, is presented. This variant integrates MDV, DLH, and EAM to address high-dimensional complex optimization problems in a highly efficient manner.
- The DLH strategy enhances the population diversity and boosts the exploration abilities of PO without premature convergence.
- An EAM mechanism is designed to overcome the fixed cooperation with fitness-directed interaction, which enhances balance in intensification and diversification during the optimization process.
- The MDV strategy is used to enhance both the exploration and exploitation ability in diversity loss because of mutation by the dual-phase strategy, which preserves convergence power.
- ADPO is specifically designed to enhance convergence speed and solution accuracy while effectively avoiding local optima through comprehensive diversity preservation mechanisms.
- Thorough numerical tests against the other main intelligent algorithms and robust optimizers on the CEC2017 and CEC2022 test suites have shown that ADPO comports exceptionally well in solving the various optimization problems in multiple dimensions.
- ADPO could be successfully applied to the LSTM neural networks in the wind power forecasting, representing the state-of-the-art results and indicating the feasible applicability in the renewable energy systems.
2. Parrot Optimization Algorithm (PO)
2.1. Phase 1: Population Initialization
2.2. Phase 2: Foraging
2.3. Phase 3: Resting
2.4. Phase 4: Communication
2.5. Phase 5: Strange Aversion
2.6. Phase 6: Termination Condition
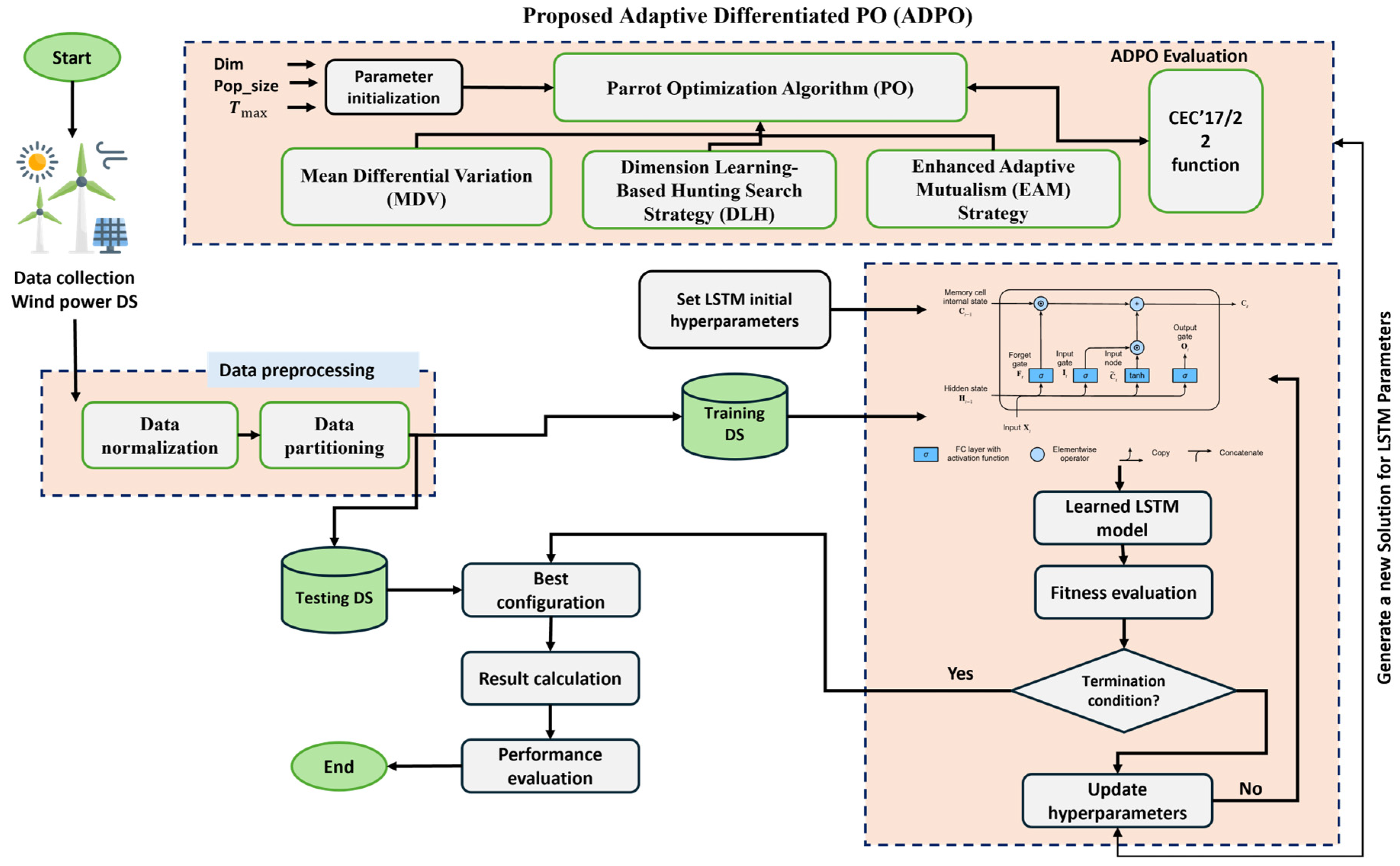
3. Proposed Adaptive Differentiated PO (ADPO)
- Mean Differential Variation (MDV): This overcomes the early loss of diversity by introducing a two-phase mutation mechanism that promotes wide exploration in early iterations and intensifies searching near the best solutions in later stages.
- Dimension Learning-Based Hunting (DLH): This prevents premature convergence by enabling each solution to adaptively learn from dimension-wise neighbors, promoting diversity and enabling coordinated yet independent directional search.
- Enhanced Adaptive Mutualism (EAM): This integrates the rigid mutualism of PO with an adaptive cooperation model that uses fitness-based influence and flexible references to maintain balance between intensification and diversification.
3.1. Mean Differential Variation (MDV)
3.2. Dimension Learning-Based Hunting Search Strategy (DLH)
3.3. Enhanced Adaptive Mutualism (EAM) Strategy
| Algorithm 1: ADPO | |
| Input: Maximum number of iterations , Population size , Number of dimensions , Upper bound . Output: Optimal solution | |
| Initialize the initial population Equation (1) |
| Evaluate the fitness value of each solution |
| Obtain the best solution and its fitness value |
| while do |
| Obtain the best solution and its fitness value |
| for to do |
| Generate new solution using EAM strategy using Equations (17)–(20) |
| if then |
| |
| end if |
| end for |
| for to do |
| Generate new solution using MDV strategy using Equations (8) and (9) |
| end for |
| for to do |
| ST = |
| if then |
| Update the position of solution using Equation (2) |
| Elseif then |
| Update the position of solution using Equation (4) |
| Elseif then |
| Update the position of solution using Equation (5) |
| Elseif then |
| Update the position of solution using Equation (6) |
| end if |
| end for |
| for do |
| Apply DLH strategy for each solution using Equations (11)–(13) |
| Apply greedy selection |
| end for |
| Check if the solution within the defined boundary and calculate fitness values. |
| Update the best solution found |
| end while |
| Return and its fitness value ; |
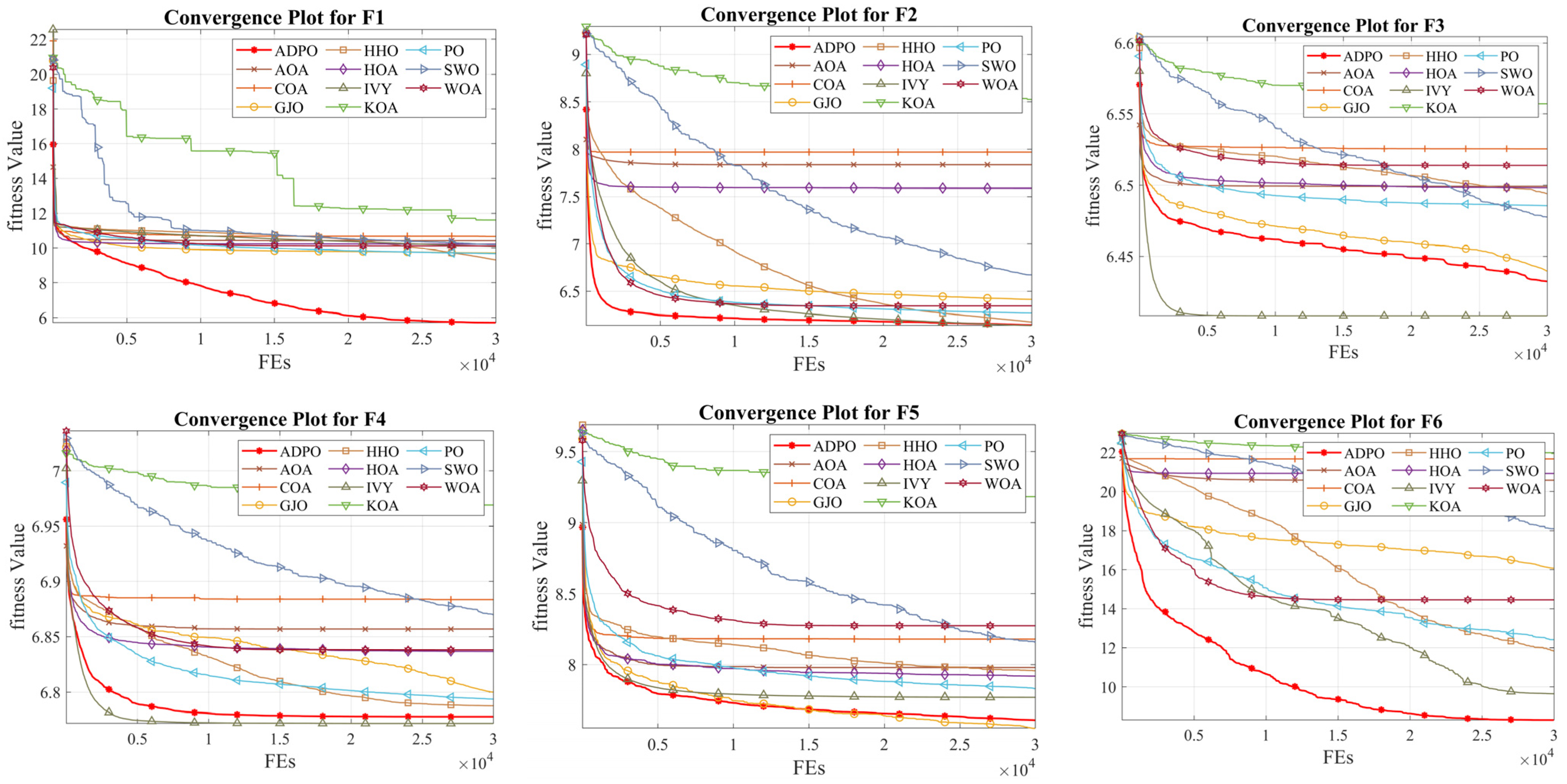
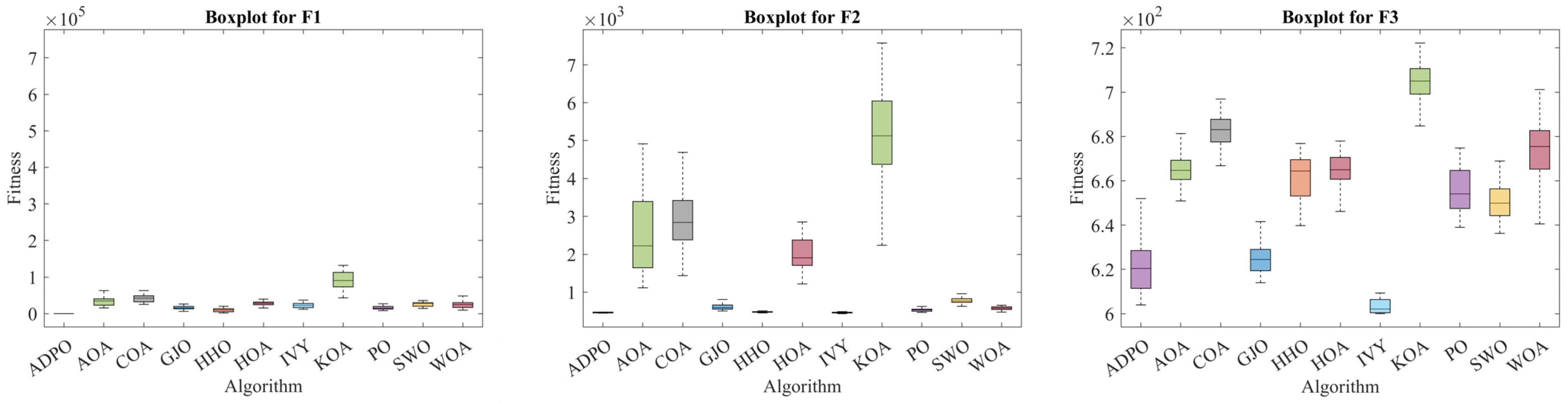
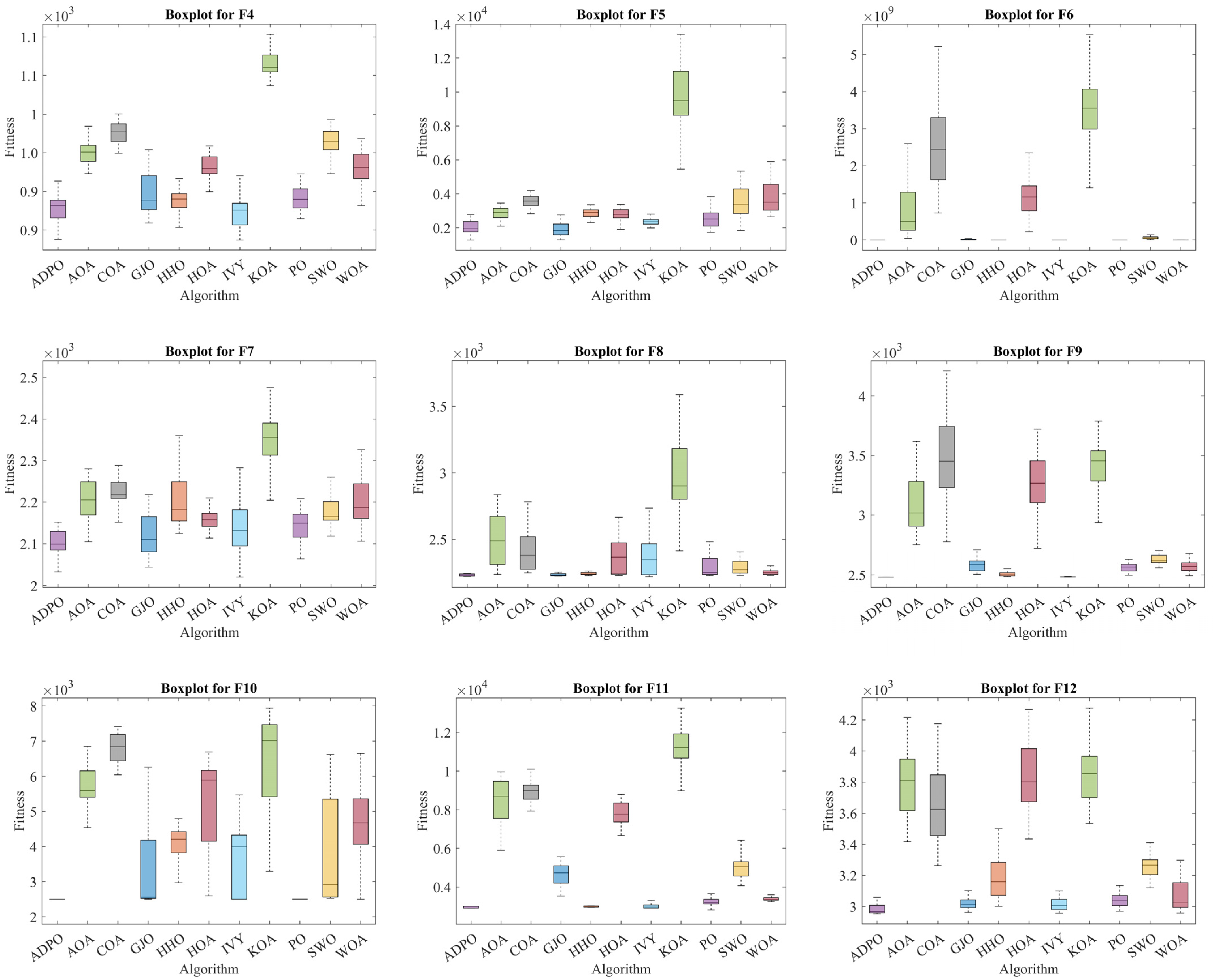
4. Analysis of Global Optimization Performance
4.1. Experimental Configuration and Settings
4.2. Metrics for Evaluating Optimization Performance
- Mean Fitness (AVG): The measure of the quality of solutions typically attained is the average fitness score over different independent runs. This measurement is useful in the evaluation of the correctness and general performance of an algorithm in repetitive usage within the same setup. It is calculated as follows:
- Standard Deviation (SD): SD quantifies the extent of dispersion of the fitness values around the mean, providing information about the consistency and stability of the results produced by the algorithm. Smaller variations show that the optimizer provides consistent results when repeated many times. It can be calculated as follows:
- Friedman Ranking (FR) [40]: This nonparametric statistical test ranks algorithms based on their relative performances across multiple problem instances. A lower average rank suggests superior performance. The final ranking is derived from averaging ranks over all tested functions. The Friedman test statistic is then evaluated using a chi-squared distribution to determine consistency in relative performance across functions.
- Wilcoxon Rank-Sum Test [41]: To establish whether performance differences between ADPO and any competing algorithm are statistically meaningful, the Wilcoxon rank-sum test is utilized. A -value below 0.05 denotes a significant difference. If ADPO achieves better results, it is marked with ; if no clear difference exists, it is annotated with ; and if ADPO underperforms, it is labeled with .
4.3. Ablation Study
- Enhanced Adaptive Mutualism (EAM) strategy analysis: The ablation study reveals that ADPO-EAM emerges as the most impactful individual enhancement, achieving an average rank of 1.75 and securing first place on four functions (F1, F9, F11, F12). This strategy demonstrates exceptional performance on unimodal function F1, with the best average fitness (300.839) and remarkably low standard deviation (0.390), indicating superior exploitation capability and convergence stability. On composition functions F9, F11, and F12, ADPO-EAM consistently outperforms other individual strategies, showcasing its effectiveness in handling complex multimodal landscapes through adaptive fitness-guided cooperation. The substantial improvement over the original PO validates the critical importance of flexible mutualistic interactions in optimization performance.
- Mean Differential Variation (MDV) strategy analysis: ADPO-MDV demonstrates moderate but consistent improvements, with an average rank of 3.25, representing significant enhancement over baseline PO. This strategy shows particular strength in maintaining solution quality across diverse function types, with notable performance on multimodal functions F2–F4, where it consistently ranks third. The dual-phase mutation mechanism effectively balances exploration and exploitation, as evidenced by its reasonable standard deviation values and stable performance across all function categories. However, the strategy shows limitations on more complex hybrid and composition functions, suggesting that while MDV provides valuable diversity preservation, it requires synergistic combination with other mechanisms for optimal performance in challenging optimization landscapes.
- Dimension Learning-Based Hunting (DLH) strategy analysis: ADPO-DLH achieves an average rank of 4.17, showing the most limited individual impact among the three proposed strategies. Interestingly, this strategy demonstrates selective effectiveness, performing competitively on hybrid function F5 (rank 2) while showing poor performance on other function types, particularly unimodal F1, where it ranks fourth. The high standard deviation values observed in several functions (notably F1 and F6) indicate instability in convergence behavior when used in isolation. This pattern suggests that DLH’s dimension-wise learning mechanism requires the stabilizing influence of other strategies to achieve consistent performance, validating its role as a complementary rather than standalone enhancement.
4.4. Results Discussion Using CEC2022
4.5. Results Discussion with Advanced Algorithms Using CEC2017
4.6. Computational Time Analysis
5. Proposed ADPO-LSTM Framework for Wind Power Prediction
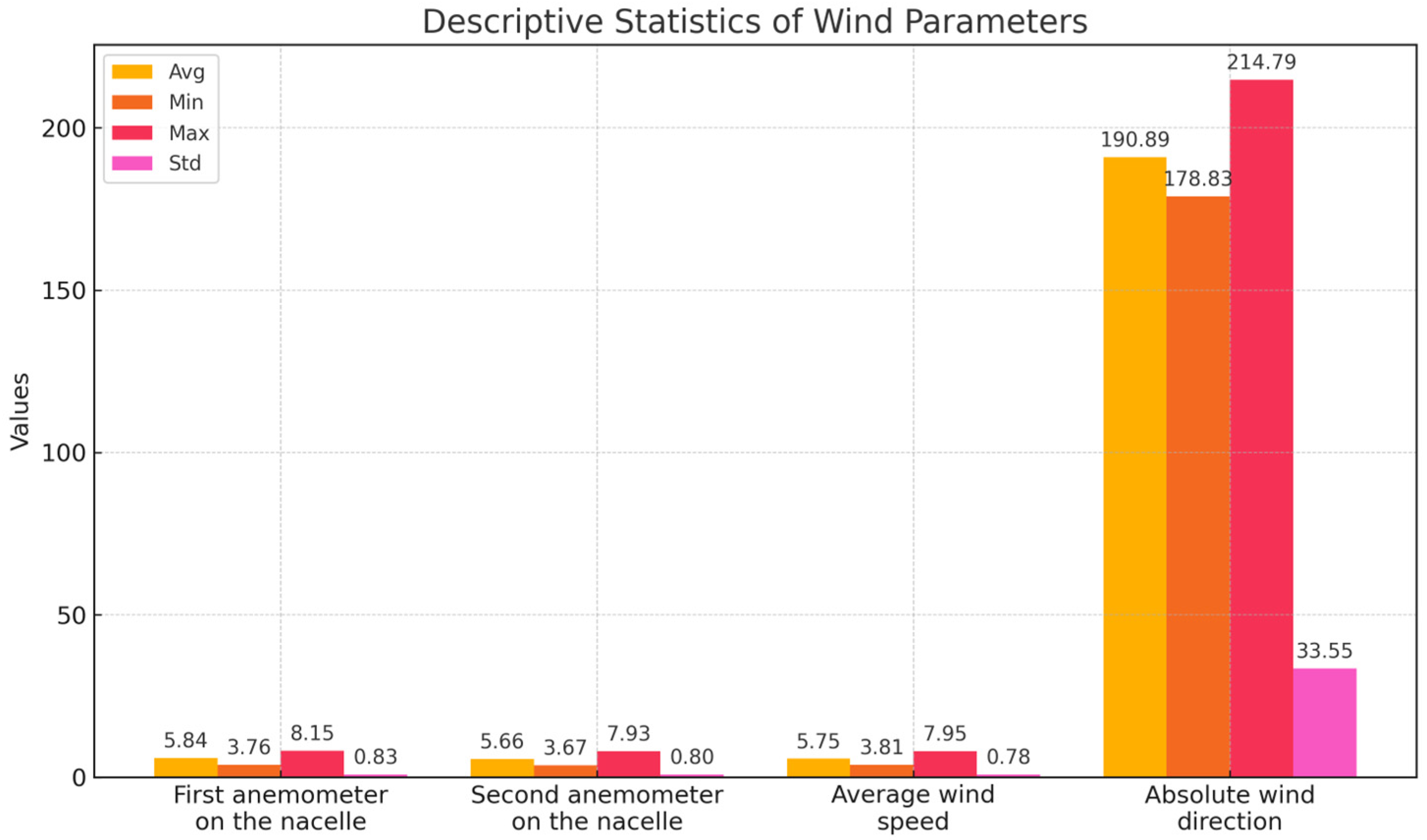
5.1. Dataset Overview
5.2. Preprocessing Workflow
5.3. Optimization-Based LSTM Training Initialization
5.4. Fitness Evaluation
5.5. Testing and Generalization Assessment
5.6. Termination
5.7. Performance Evaluation Metrics
- The Coefficient of Determination (R2) serves as an indicator of the proportion of variability in the actual wind power output that is successfully explained by the model’s predictions. This metric offers insight into the model’s explanatory strength, with values approaching 1 signifying near-perfect alignment between predicted and true outputs. It is calculated as follows:
- The standard deviation of the residuals, or the differences between predicted and actual values, is also known as Root Mean Squared Error (RMSE). It also imposes more punishment on larger errors compared to smaller errors because of its quadratic component, which makes it highly susceptible to outliers and general deviations. RMSE is calculated as follows:
- The Mean Absolute Error (MAE) represents the average absolute deviation between the values obtained and predicted, and does not square the errors. This is a measure of the average magnitude of prediction errors, and it is particularly applicable when every deviation, whether up or down, is equally significant. MAE is defined as
- The Coefficient of Variation (COV) shows the error as a relative value by comparing the RMSE to the mean of the observed wind power values. When converted into a percentage it compares the scale of prediction error to the average level of output as a measure of how relatively stable at various operating levels the prediction is:
5.8. Experimental Results and Performance Evaluation
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nadimi-Shahraki, M.H.; Zamani, H.; Asghari Varzaneh, Z.; Mirjalili, S. A systematic review of the whale optimization algorithm: Theoretical foundation, improvements, and hybridizations. Arch. Comput. Methods Eng. 2023, 30, 4113–4159. [Google Scholar] [CrossRef] [PubMed]
- Ye, M.; Zhou, H.; Yang, H.; Hu, B.; Wang, X. Multi-strategy improved dung beetle optimization algorithm and its applications. Biomimetics 2024, 9, 291. [Google Scholar] [CrossRef]
- Mayer, J. Stochastic Linear Programming Algorithms: A Comparison Based on a Model Management System; Routledge: London, UK, 2022. [Google Scholar]
- Yang, H.; Liu, X.; Song, K. A novel gradient boosting regression tree technique optimized by improved sparrow search algorithm for predicting TBM penetration rate. Arab. J. Geosci. 2022, 15, 461. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, L.; Li, R.; Xu, Y.; Zheng, J. A learning-based dual-population optimization algorithm for hybrid seru system scheduling with assembly. Swarm Evol. Comput. 2025, 94, 101901. [Google Scholar] [CrossRef]
- Howell, T.A.; Le Cleac’h, S.; Singh, S.; Florence, P.; Manchester, Z.; Sindhwani, V. Trajectory optimization with optimization-based dynamics. IEEE Robot. Autom. Lett. 2022, 7, 6750–6757. [Google Scholar] [CrossRef]
- Antonijevic, M.; Zivkovic, M.; Djuric Jovicic, M.; Nikolic, B.; Perisic, J.; Milovanovic, M.; Jovanovic, L.; Abdel-Salam, M.; Bacanin, N. Intrusion detection in metaverse environment internet of things systems by metaheuristics tuned two level framework. Sci. Rep. 2025, 15, 3555. [Google Scholar] [CrossRef]
- Lin, A.; Liao, Y.; Peng, C.; Li, X.; Zhang, X. Elite leader dwarf mongoose optimization algorithm. Sci. Rep. 2025, 15, 20911. [Google Scholar] [CrossRef] [PubMed]
- Tarek, Z.; Alhussan, A.A.; Khafaga, D.S.; El-Kenawy, E.-S.M.; Elshewey, A.M. A snake optimization algorithm-based feature selection framework for rapid detection of cardiovascular disease in its early stages. Biomed. Signal Process. Control 2025, 102, 107417. [Google Scholar] [CrossRef]
- Liang, Z.; Chung, C.Y.; Zhang, W.; Wang, Q.; Lin, W.; Wang, C. Enabling high-efficiency economic dispatch of hybrid AC/DC networked microgrids: Steady-state convex bi-directional converter models. IEEE Trans. Smart Grid 2024, 16, 45–61. [Google Scholar] [CrossRef]
- Benmamoun, Z.; Khlie, K.; Bektemyssova, G.; Dehghani, M.; Gherabi, Y. Bobcat Optimization Algorithm: An effective bio-inspired metaheuristic algorithm for solving supply chain optimization problems. Sci. Rep. 2024, 14, 20099. [Google Scholar] [CrossRef]
- Hamad, R.K.; Rashid, T.A. GOOSE algorithm: A powerful optimization tool for real-world engineering challenges and beyond. Evol. Syst. 2024, 15, 1249–1274. [Google Scholar] [CrossRef]
- Li, X.; Fang, W.; Zhu, S.; Zhang, X. An adaptive binary quantum-behaved particle swarm optimization algorithm for the multidimensional knapsack problem. Swarm Evol. Comput. 2024, 86, 101494. [Google Scholar] [CrossRef]
- Sivanandam, S.; Deepa, S.; Sivanandam, S.; Deepa, S. Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- MIRJALILI, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Xiao, Y.; Cui, H.; Khurma, R.A.; Castillo, P.A. Artificial lemming algorithm: A novel bionic meta-heuristic technique for solving real-world engineering optimization problems. Artif. Intell. Rev. 2025, 58, 84. [Google Scholar] [CrossRef]
- Jia, H.; Abdel-salam, M.; Hu, G. ACIVY: An Enhanced IVY Optimization Algorithm with Adaptive Cross Strategies for Complex Engineering Design and UAV Navigation. Biomimetics 2025, 10, 471. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Cai, L.; Yang, R. Triangulation topology aggregation optimizer: A novel mathematics-based meta-heuristic algorithm for continuous optimization and engineering applications. Expert. Syst. Appl. 2024, 238, 121744. [Google Scholar] [CrossRef]
- Wang, X.; Snášel, V.; Mirjalili, S.; Pan, J.-S.; Kong, L.; Shehadeh, H.A. Artificial Protozoa Optimizer (APO): A novel bio-inspired metaheuristic algorithm for engineering optimization. Knowl.-Based Syst. 2024, 295, 111737. [Google Scholar] [CrossRef]
- Tian, Z.; Gai, M. Football team training algorithm: A novel sport-inspired meta-heuristic optimization algorithm for global optimization. Expert. Syst. Appl. 2024, 245, 123088. [Google Scholar] [CrossRef]
- Taheri, A.; RahimiZadeh, K.; Beheshti, A.; Baumbach, J.; Rao, R.V.; Mirjalili, S.; Gandomi, A.H. Partial reinforcement optimizer: An evolutionary optimization algorithm. Expert. Syst. Appl. 2024, 238, 122070. [Google Scholar] [CrossRef]
- Sowmya, R.; Premkumar, M.; Jangir, P. Newton-Raphson-based optimizer: A new population-based metaheuristic algorithm for continuous optimization problems. Eng. Appl. Artif. Intell. 2024, 128, 107532. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl.—Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Ghasemi, M.; Deriche, M.; Trojovský, P.; Mansor, Z.; Zare, M.; Trojovská, E.; Abualigah, L.; Ezugwu, A.E.; Kadkhoda Mohammadi, S. An efficient bio-inspired algorithm based on humpback whale migration for constrained engineering optimization. Results Eng. 2025, 25, 104215. [Google Scholar] [CrossRef]
- Elhosseny, M.; Abdel-Salam, M.; El-Hasnony, I.M. Adaptive dynamic crayfish algorithm with multi-enhanced strategy for global high-dimensional optimization and real-engineering problems. Sci. Rep. 2025, 15, 10656. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Zou, H.; Wang, K. Improved multi-strategy beluga whale optimization algorithm: A case study for multiple engineering optimization problems. Clust. Comput. 2025, 28, 183. [Google Scholar] [CrossRef]
- Fakhouri, H.N.; Ishtaiwi, A.; Makhadmeh, S.N.; Al-Betar, M.A.; Alkhalaileh, M. Novel hybrid crayfish optimization algorithm and self-adaptive differential evolution for solving complex optimization problems. Symmetry 2024, 16, 927. [Google Scholar] [CrossRef]
- Özcan, A.R.; Mehta, P.; Sait, S.M.; Gürses, D.; Yildiz, A.R. A new neural network–assisted hybrid chaotic hiking optimization algorithm for optimal design of engineering components. Mater. Test. 2025, 67, 1069–1078. [Google Scholar] [CrossRef]
- Xia, H.; Ke, Y.; Liao, R.; Zhang, H. Fractional order dung beetle optimizer with reduction factor for global optimization and industrial engineering optimization problems. Artif. Intell. Rev. 2025, 58, 308. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G.; Ma, L.; Zhu, T.; Wu, X.; Heidari, A.A.; Chen, Y.; Chen, H. Parrot optimizer: Algorithm and applications to medical problems. Comput. Biol. Med. 2024, 172, 108064. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Cai, C.; Li, P.; Tang, C.; Zhao, M.; Zheng, X.; Li, Y.; Zhao, Y.; Liu, C. Hybrid prediction method for solar photovoltaic power generation using normal cloud parrot optimization algorithm integrated with extreme learning machine. Sci. Rep. 2025, 15, 6491. [Google Scholar] [CrossRef]
- Aljaidi, M.; Jangir, P.; Arpita; Agrawal, S.P.; Pandya, S.B.; Parmar, A.; Alkoradees, A.F.; Khishe, M.; Jangid, R. A novel Parrot Optimizer for robust and scalable PEMFC parameter optimization. Sci. Rep. 2025, 15, 11625. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Salam, M.; Alomari, S.A.; Yang, J.; Lee, S.; Saleem, K.; Smerat, A.; Snasel, V.; Abualigah, L. Harnessing dynamic turbulent dynamics in parrot optimization algorithm for complex high-dimensional engineering problems. Comput. Methods Appl. Mech. Eng. 2025, 440, 117908. [Google Scholar] [CrossRef]
- Houssein, E.H.; Emam, M.M.; Alomoush, W.; Samee, N.A.; Jamjoom, M.M.; Zhong, R.; Dhal, K.G. An efficient improved parrot optimizer for bladder cancer classification. Comput. Biol. Med. 2024, 181, 109080. [Google Scholar] [CrossRef]
- Siegel, S.; Castellan, N. The Friedman two-way analysis of variance by ranks. Nonparametric Stat. Behav. Sci. 1988, 174–184. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Hadi, A.A.; Fattouh, A.M.; Jambi, K.M. LSHADE with semi-parameter adaptation hybrid with CMA-ES for solving CEC 2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), San Sebastián, Spain, 5–8 June 2017; pp. 145–152. [Google Scholar]
- Luo, W.; Lin, X.; Li, C.; Yang, S.; Shi, Y. Benchmark functions for CEC 2022 competition on seeking multiple optima in dynamic environments. arXiv 2022, arXiv:2201.00523. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Spider wasp optimizer: A novel meta-heuristic optimization algorithm. Artif. Intell. Rev. 2023, 56, 11675–11738. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert. Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zare, M.; Trojovský, P.; Rao, R.V.; Trojovská, E.; Kandasamy, V. Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm. Knowl.-Based Syst. 2024, 295, 111850. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler’s laws of planetary motion. Knowl.-Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hammad, A.; Emam, M.M.; Ali, A.A. An enhanced Coati Optimization Algorithm for global optimization and feature selection in EEG emotion recognition. Comput. Biol. Med. 2024, 173, 108329. [Google Scholar] [CrossRef]
- Iruthayarajan, M.W.; Baskar, S. Covariance matrix adaptation evolution strategy based design of centralized PID controller. Expert. Syst. Appl. 2010, 37, 5775–5781. [Google Scholar] [CrossRef]
- Long, W.; Cai, S.; Jiao, J.; Xu, M.; Wu, T. A new hybrid algorithm based on grey wolf optimizer and cuckoo search for parameter extraction of solar photovoltaic models. Energy Convers. Manag. 2020, 203, 112243. [Google Scholar] [CrossRef]
- Chen, H.; Yang, C.; Heidari, A.A.; Zhao, X. An efficient double adaptive random spare reinforced whale optimization algorithm. Expert. Syst. Appl. 2020, 154, 113018. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, J.; Du, B.; Wei, G. An enhanced hybrid arithmetic optimization algorithm for engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 394, 114901. [Google Scholar] [CrossRef]
- Khodadadi, N.; Snasel, V.; Mirjalili, S. Dynamic arithmetic optimization algorithm for truss optimization under natural frequency constraints. IEEE Access 2022, 10, 16188–16208. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, A.; Han, Y.; Nan, J.; Li, K. Fast stochastic configuration network based on an improved sparrow search algorithm for fire flame recognition. Knowl.—Based Syst. 2022, 245, 108626. [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Rather, S.A.; Bala, P.S. Hybridization of constriction coefficient based particle swarm optimization and gravitational search algorithm for function optimization. In Proceedings of the International Conference on Advances in Electronics, Electrical & Computational Intelligence (ICAEEC), Malabe, Sri Lanka, 5–6 December 2019. [Google Scholar]
- Abdel-Salam, M.; Chhabra, A.; Braik, M.; Gharehchopogh, F.S.; Bacanin, N. A Halton Enhanced Solution-based Human Evolutionary Algorithm for Complex Optimization and Advanced Feature Selection Problems. Knowl.-Based Syst. 2025, 311, 113062. [Google Scholar] [CrossRef]
- Goh, H.H.; He, R.; Zhang, D.; Liu, H.; Dai, W.; Lim, C.S.; Kurniawan, T.A.; Teo, K.T.K.; Goh, K.C. A multimodal approach to chaotic renewable energy prediction using meteorological and historical information. Appl. Soft Comput. 2022, 118, 108487. [Google Scholar] [CrossRef]
- Askr, H.; Abdel-Salam, M.; Snášel, V.; Hassanien, A.E. A green hydrogen production model from solar powered water electrolyze based on deep chaotic Lévy gazelle optimization. Eng. Sci. Technol. Int. J. 2024, 60, 101874. [Google Scholar] [CrossRef]
- Rashad, M.; Abdellatif, M.S.; Rabie, A.H. An Improved Human Evolutionary Optimization Algorithm for Maximizing Green Hydrogen Generation in Intelligent Energy Management System (IEMS). Results Eng. 2025, 27, 105998. [Google Scholar] [CrossRef]
- Liu, Y.; Li, L.; Liu, J. Short-term wind power output prediction using hybrid-enhanced seagull optimization algorithm and support vector machine: A high-precision method. Int. J. Green. Energy 2024, 21, 2858–2871. [Google Scholar] [CrossRef]
- Yaghoubirad, M.; Azizi, N.; Farajollahi, M.; Ahmadi, A. Deep learning-based multistep ahead wind speed and power generation forecasting using direct method. Energy Convers. Manag. 2023, 281, 116760. [Google Scholar] [CrossRef]
- Ewees, A.A.; Al-qaness, M.A.; Abualigah, L.; Abd Elaziz, M. HBO-LSTM: Optimized long short term memory with heap-based optimizer for wind power forecasting. Energy Convers. Manag. 2022, 268, 116022. [Google Scholar] [CrossRef]
- Al-qaness, M.A.; Ewees, A.A.; Fan, H.; Abualigah, L.; Elsheikh, A.H.; Abd Elaziz, M. Wind power prediction using random vector functional link network with capuchin search algorithm. Ain Shams Eng. J. 2023, 14, 102095. [Google Scholar] [CrossRef]
- Zayed, M.E.; Rehman, S.; Elgendy, I.A.; Al-Shaikhi, A.; Mohandes, M.A.; Irshad, K.; Abdelrazik, A.; Alam, M.A. Benchmarking reinforcement learning and prototyping development of floating solar power system: Experimental study and LSTM modeling combined with brown-bear optimization algorithm. Energy Convers. Manag. 2025, 332, 119696. [Google Scholar] [CrossRef]
- Dagal, I.; Ibrahim, A.-W.; Harrison, A. Leveraging a novel grey wolf algorithm for optimization of photovoltaic-battery energy storage system under partial shading conditions. Comput. Electr. Eng. 2025, 122, 109991. [Google Scholar] [CrossRef]
- Nagarajan, K.; Rajagopalan, A.; Bajaj, M.; Raju, V.; Blazek, V. Enhanced wombat optimization algorithm for multi-objective optimal power flow in renewable energy and electric vehicle integrated systems. Results Eng. 2025, 25, 103671. [Google Scholar] [CrossRef]
- Yu, F.; Guan, J.; Wu, H.; Wang, H.; Ma, B. Multi-population differential evolution approach for feature selection with mutual information ranking. Expert. Syst. Appl. 2025, 260, 125404. [Google Scholar] [CrossRef]
- Abdel-salam, M.; Alomari, S.A.; Almomani, M.H.; Hu, G.; Lee, S.; Saleem, K.; Smerat, A.; Abualigah, L. Quadruple strategy-driven hiking optimization algorithm for low and high-dimensional feature selection and real-world skin cancer classification. Knowl.-Based Syst. 2025, 315, 113286. [Google Scholar] [CrossRef]
- Mostafa, R.R.; Khedr, A.M.; Aghbari, Z.A.; Afyouni, I.; Kamel, I.; Ahmed, N. Medical image segmentation approach based on hybrid adaptive differential evolution and crayfish optimizer. Comput. Biol. Med. 2024, 180, 109011. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; Houssein, E.H.; Emam, M.M.; Samee, N.A.; Jamjoom, M.M.; Hu, G. An adaptive enhanced human memory algorithm for multi-level image segmentation for pathological lung cancer images. Comput. Biol. Med. 2024, 183, 109272. [Google Scholar] [CrossRef]
- Mostafa, R.R.; Vijayan, D.; Khedr, A.M. EGBCR-FANET: Enhanced genghis Khan shark optimizer based Bayesian-driven clustered routing model for FANETs. Veh. Commun. 2025, 54, 100935. [Google Scholar] [CrossRef]
- Mostafa, R.R.; Hashim, F.A.; Khedr, A.M.; AL Aghbari, Z.; Afyouni, I.; Kamel, I.; Ahmed, N. EMGODV-Hop: An efficient range-free-based WSN node localization using an enhanced mountain gazelle optimizer. J. Supercomput. 2025, 81, 140. [Google Scholar] [CrossRef]
- Malti, A.N.; Hakem, M.; Benmammar, B. A new hybrid multi-objective optimization algorithm for task scheduling in cloud systems. Clust. Comput. 2024, 27, 2525–2548. [Google Scholar] [CrossRef]
- Abdel-salam, M.; Hassanien, A.E. Abdel-salam, M.; Hassanien, A.E. A Novel Dynamic Chaotic Golden Jackal Optimization Algorithm for Sensor-Based Human Activity Recognition Using Smartphones for Sustainable Smart Cities. In Artificial Intelligence for Environmental Sustainability and Green Initiatives; Springer: Berlin/Heidelberg, Germany, 2024; pp. 273–296. [Google Scholar]
- Manoharan, H.; Edalatpanah, S. Evolutionary bioinformatics with veiled biological database for health care operations. Comput. Biol. Med. 2025, 184, 109418. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, C.; Yu, H.; Fei, H.; Li, D. Path planning of unmanned vehicles based on adaptive particle swarm optimization algorithm. Comput. Commun. 2024, 216, 112–129. [Google Scholar] [CrossRef]
- Villoth, J.P.; Zivkovic, M.; Zivkovic, T.; Abdel-salam, M.; Hammad, M.; Jovanovic, L.; Simic, V.; Bacanin, N. Two-tier deep and machine learning approach optimized by adaptive multi-population firefly algorithm for software defects prediction. Neurocomputing 2025, 630, 129695. [Google Scholar] [CrossRef]
- Oyelade, O.N.; Aminu, E.F.; Wang, H.; Rafferty, K. An adaptation of hybrid binary optimization algorithms for medical image feature selection in neural network for classification of breast cancer. Neurocomputing 2025, 617, 129018. [Google Scholar] [CrossRef]
- Nirmala, G.; Nayudu, P.P.; Kumar, A.R.; Sagar, R. Automatic cervical cancer classification using adaptive vision transformer encoder with CNN for medical application. Pattern Recognit. 2025, 160, 111201. [Google Scholar] [CrossRef]
- Pashaei, E.; Pashaei, E.; Mirjalili, S. Binary hiking optimization for gene selection: Insights from HNSCC RNA-Seq data. Expert. Syst. Appl. 2025, 268, 126404. [Google Scholar] [CrossRef]
- Yang, J.; Yan, F.; Zhang, J.; Peng, C. Hybrid chaos game and grey wolf optimization algorithms for UAV path planning. Appl. Math. Model. 2025, 142, 115979. [Google Scholar] [CrossRef]
- Yang, J.; Wu, Y.; Yuan, Y.; Xue, H.; Bourouis, S.; Abdel-Salam, M.; Prajapat, S.; Por, L.Y. LLM-AE-MP: Web Attack Detection Using a Large Language Model with Autoencoder and Multilayer Perceptron. Expert. Syst. Appl. 2025, 274, 126982. [Google Scholar] [CrossRef]
- Wang, H.; Chen, S.; Li, M.; Zhu, C.; Wang, Z. Demand-driven charging strategy-based distributed routing optimization under traffic restrictions in internet of electric vehicles. IEEE Internet Things J. 2024, 11, 35917–35927. [Google Scholar] [CrossRef]


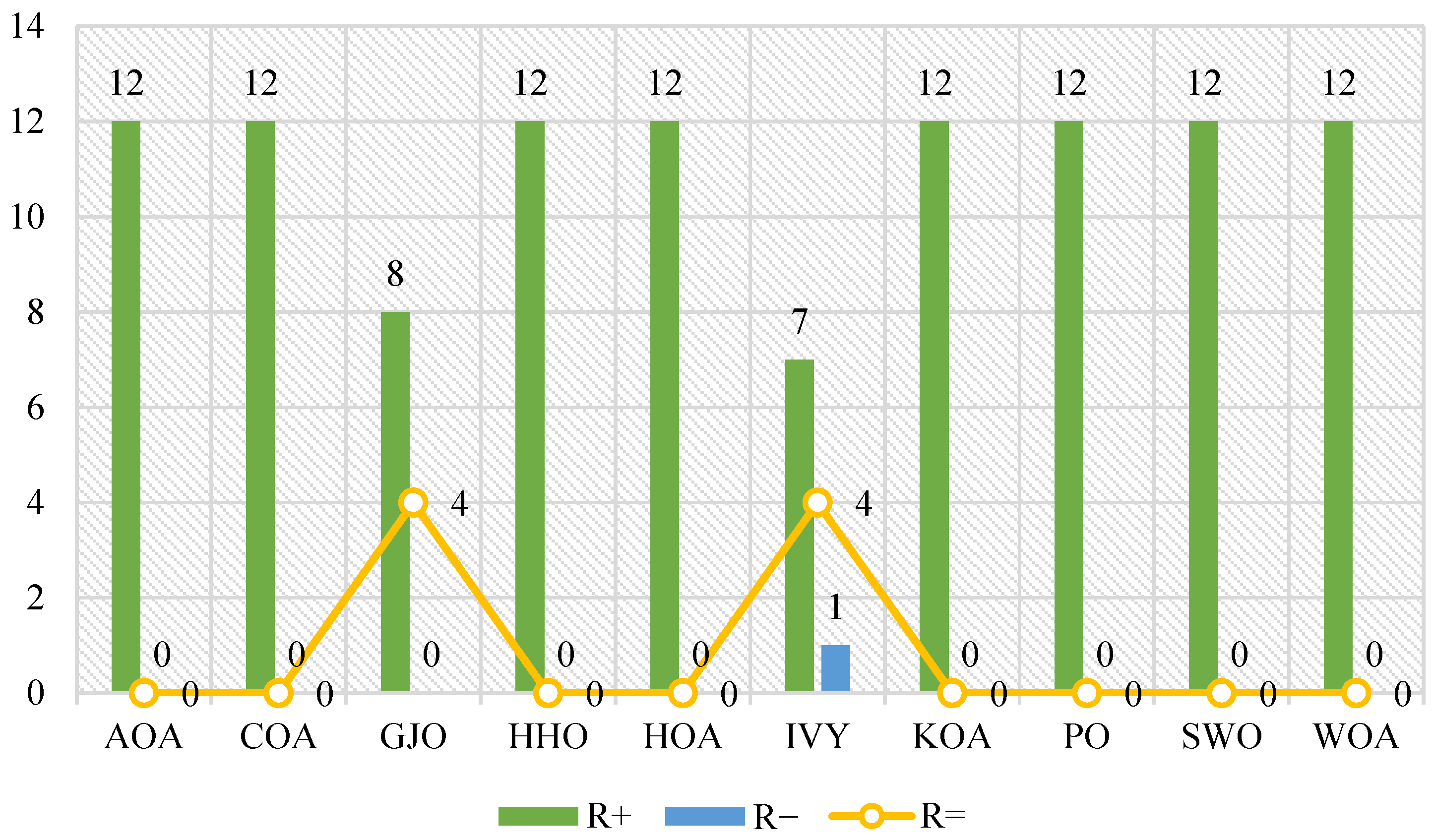
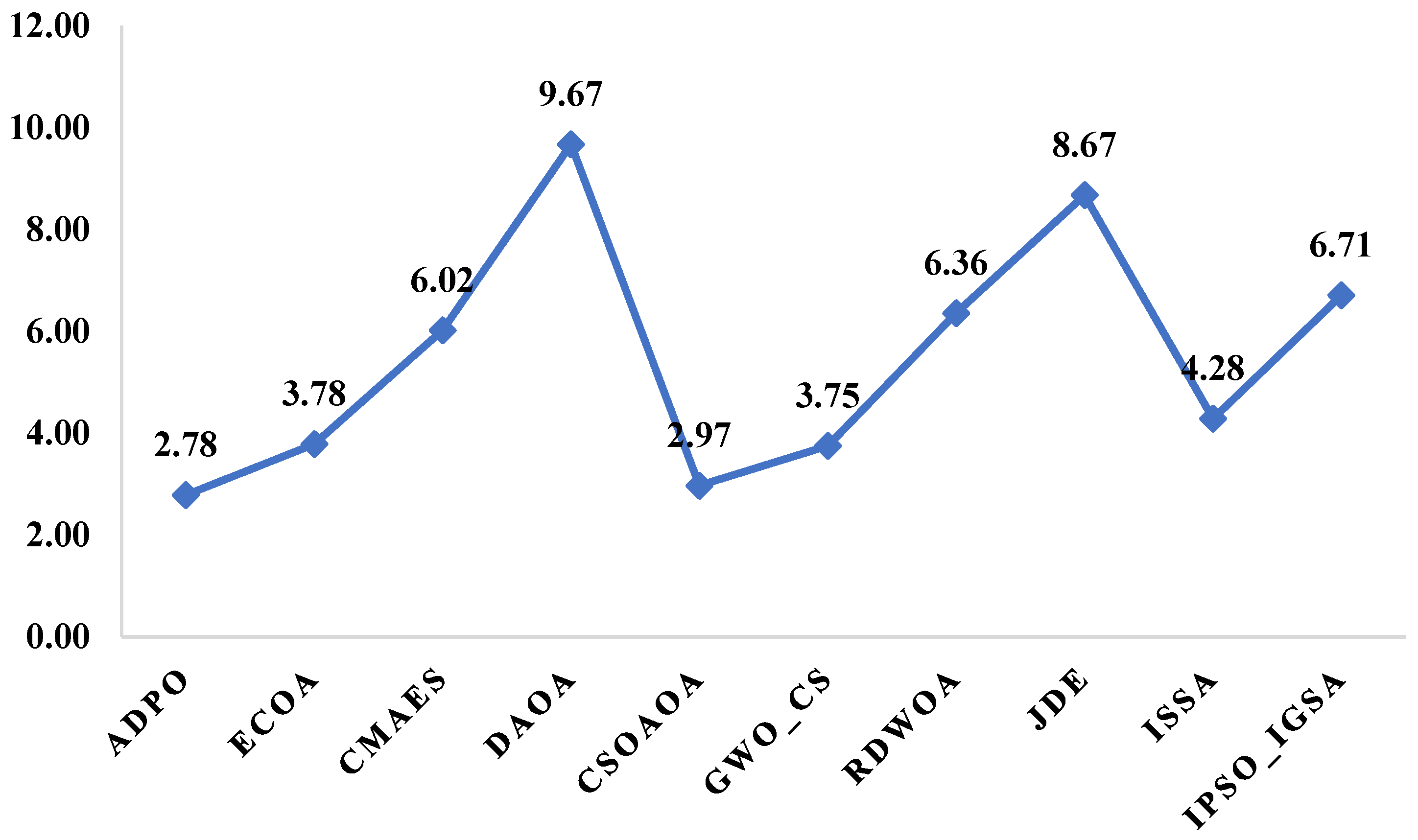
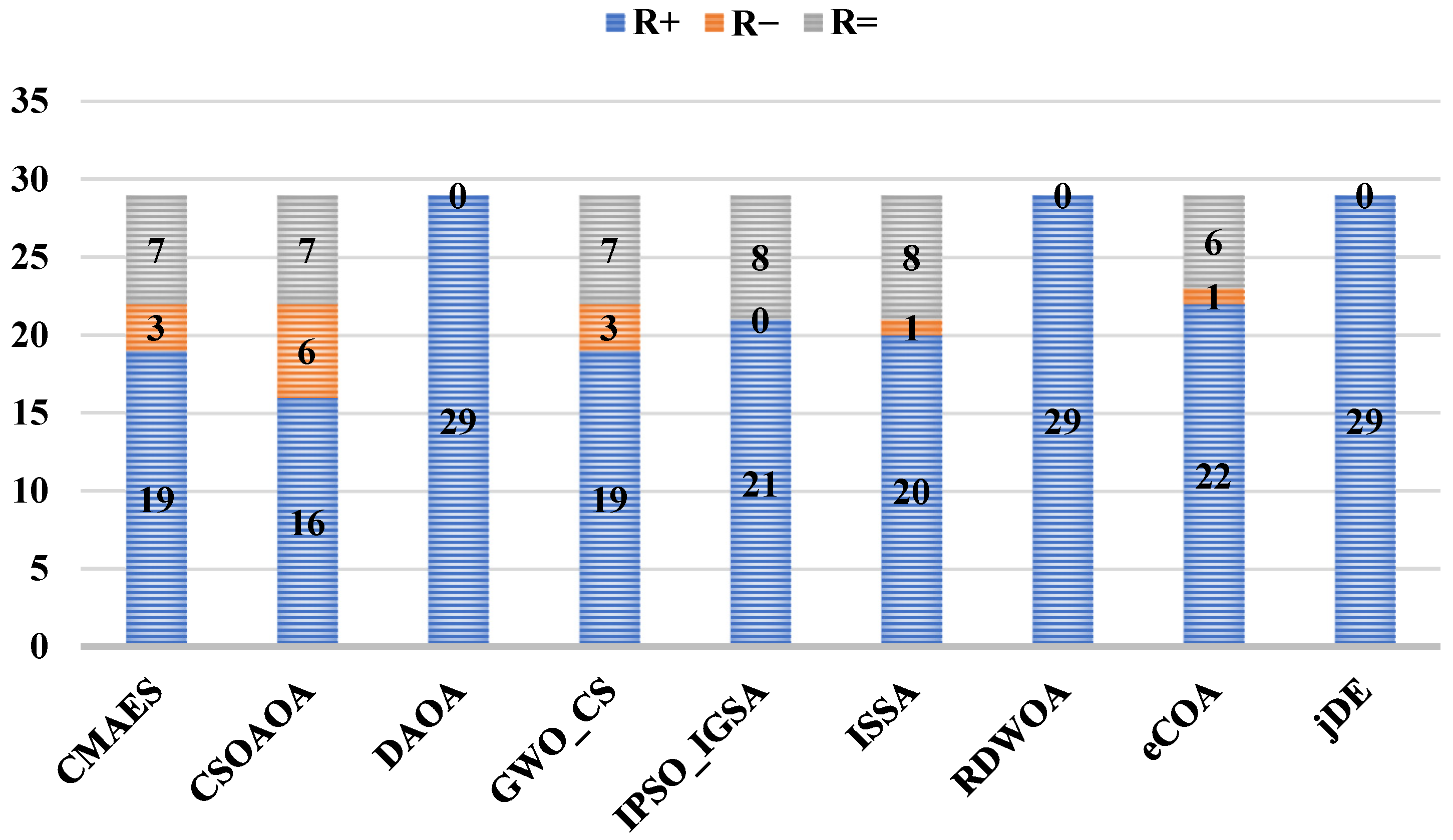
| Algorithm | Parameter Value |
|---|---|
| IVY | |
| HOA | |
| SWO | |
| HHO | changes from −1 to 1 |
| AOA | |
| KOA | |
| GJO | |
| WOA | |
| CMA-ES | σ = 0.5, μ = λ/2 |
| CSOAOA | |
| GWO_CS | |
| RDWOA | |
| jDE | |
| ISSA |
| F | ADPO | ADPO-DLH | ADPO-EAM | ADPO-MDV | PO | |
|---|---|---|---|---|---|---|
| F1 | AVG | 303.862 | 1.66 × 104 | 300.839 | 3185.297 | 1.83 × 104 |
| SD | 2.899 | 3853.111 | 0.390 | 1423.174 | 4152.061 | |
| RAN | 2 | 4 | 1 | 3 | 5 | |
| F2 | AVG | 456.679 | 525.328 | 468.321 | 487.787 | 501.975 |
| SD | 12.155 | 80.608 | 37.535 | 30.722 | 39.841 | |
| RAN | 1 | 5 | 2 | 3 | 4 | |
| F3 | AVG | 618.668 | 650.046 | 623.121 | 649.312 | 657.763 |
| SD | 4.773 | 9.967 | 12.532 | 15.584 | 16.308 | |
| RAN | 1 | 4 | 2 | 3 | 5 | |
| F4 | AVG | 870.459 | 893.445 | 879.201 | 882.195 | 887.711 |
| SD | 18.172 | 18.159 | 11.278 | 17.248 | 16.002 | |
| RAN | 1 | 5 | 2 | 3 | 4 | |
| F5 | AVG | 1793.324 | 1953.369 | 2037.207 | 2395.176 | 2758.038 |
| SD | 386.598 | 165.996 | 492.805 | 392.801 | 361.537 | |
| RAN | 1 | 2 | 3 | 4 | 5 | |
| F6 | AVG | 4812.973 | 9.26 × 105 | 6862.081 | 11428.323 | 2.18 × 105 |
| SD | 3762.032 | 1.39 × 106 | 6587.417 | 7408.561 | 1.75 × 105 | |
| RAN | 1 | 5 | 2 | 3 | 4 | |
| F7 | AVG | 2090.781 | 2143.831 | 2107.010 | 2128.600 | 2132.220 |
| SD | 34.803 | 27.458 | 28.586 | 30.951 | 37.998 | |
| RAN | 1 | 5 | 2 | 3 | 4 | |
| F8 | AVG | 2231.654 | 2288.420 | 2240.885 | 2246.410 | 2277.449 |
| SD | 7.976 | 61.781 | 43.257 | 16.325 | 57.658 | |
| RAN | 1 | 5 | 2 | 3 | 4 | |
| F9 | AVG | 2481.315 | 2575.709 | 2480.978 | 2495.260 | 2594.209 |
| SD | 0.618 | 36.557 | 0.176 | 8.134 | 52.688 | |
| RAN | 2 | 4 | 1 | 3 | 5 | |
| F10 | AVG | 2518.107 | 2559.140 | 2557.694 | 2758.615 | 2622.379 |
| SD | 54.563 | 121.507 | 80.237 | 813.674 | 131.213 | |
| RAN | 1 | 3 | 2 | 5 | 4 | |
| F11 | AVG | 2951.864 | 3223.154 | 2941.356 | 3013.948 | 3231.580 |
| SD | 51.855 | 204.779 | 50.784 | 122.523 | 111.284 | |
| RAN | 2 | 4 | 1 | 3 | 5 | |
| F12 | AVG | 2978.793 | 3030.089 | 2975.518 | 2989.338 | 3040.060 |
| SD | 28.171 | 68.964 | 23.851 | 33.773 | 43.344 | |
| RAN | 2 | 4 | 1 | 3 | 5 | |
| Average rank | 1.33 | 4.17 | 1.75 | 3.25 | 4.50 | |
| Final rank | 1 | 4 | 2 | 3 | 5 | |
| Friedman rank | 1.55 | 4.00 | 1.87 | 3.24 | 4.34 | |
| F | ADPO | PO | IVY | HOA | HHO | AOA | SWO | COA | GJO | WOA | KOA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | AVG | 301.302 | 1.60 × 104 | 2.40 × 104 | 2.77 × 104 | 1.11 × 104 | 3.38 × 104 | 2.70 × 104 | 4.31 × 104 | 1.65 × 104 | 2.48 × 104 | 1.11 × 105 |
| SD | 0.981 | 4.46 × 103 | 1.01 × 104 | 6329.500 | 7244.094 | 1.17 × 104 | 7.67 × 103 | 1.34 × 104 | 5.42 × 103 | 9.44 × 103 | 1.21 × 105 | |
| RAN | 1 | 3 | 5 | 8 | 2 | 9 | 7 | 10 | 4 | 6 | 11 | |
| F2 | AVG | 466.259 | 529.092 | 464.089 | 1975.235 | 481.445 | 2530.853 | 790.688 | 2890.766 | 610.729 | 570.208 | 5045.097 |
| SD | 19.242 | 40.681 | 29.231 | 465.416 | 25.270 | 1023.860 | 106.168 | 796.635 | 78.953 | 54.887 | 1488.769 | |
| RAN | 2 | 4 | 1 | 8 | 3 | 9 | 7 | 10 | 6 | 5 | 11 | |
| F3 | AVG | 621.667 | 655.570 | 606.720 | 663.939 | 661.088 | 664.580 | 650.324 | 682.391 | 626.149 | 674.481 | 704.271 |
| SD | 10.531 | 10.121 | 11.508 | 9.539 | 10.085 | 7.646 | 7.889 | 7.860 | 10.040 | 14.432 | 10.033 | |
| RAN | 2 | 5 | 1 | 7 | 6 | 8 | 4 | 10 | 3 | 9 | 11 | |
| F4 | AVG | 878.170 | 892.127 | 872.859 | 931.436 | 886.788 | 950.451 | 962.916 | 976.083 | 897.802 | 932.687 | 1063.219 |
| SD | 16.148 | 16.820 | 19.693 | 15.451 | 14.546 | 15.147 | 19.739 | 14.435 | 26.177 | 31.132 | 17.626 | |
| RAN | 2 | 4 | 1 | 6 | 3 | 8 | 9 | 10 | 5 | 7 | 11 | |
| F5 | AVG | 2013.369 | 2518.767 | 2368.061 | 2749.518 | 2855.258 | 2920.390 | 3476.263 | 3566.697 | 1900.620 | 3919.915 | 9733.317 |
| SD | 402.268 | 505.119 | 182.276 | 379.229 | 268.721 | 467.652 | 940.511 | 355.377 | 407.825 | 1104.669 | 1941.003 | |
| RAN | 2 | 4 | 3 | 5 | 6 | 7 | 8 | 9 | 1 | 10 | 11 | |
| F6 | AVG | 4028.385 | 2.45 × 105 | 1.56 × 104 | 1.23 × 109 | 1.37 × 105 | 8.68 × 108 | 7.23 × 107 | 2.59 × 109 | 9.56 × 106 | 1.89 × 106 | 3.43 × 109 |
| SD | 3172.272 | 4.90 × 105 | 5.95 × 104 | 7.60 × 108 | 6.95 × 104 | 8.86 × 108 | 6.48 × 107 | 1.15 × 109 | 1.12 × 107 | 6.14 × 106 | 1.12 × 109 | |
| RAN | 1 | 4 | 2 | 9 | 3 | 8 | 7 | 10 | 6 | 5 | 11 | |
| F7 | AVG | 2103.721 | 2143.961 | 2144.343 | 2166.174 | 2205.912 | 2226.781 | 2179.929 | 2222.639 | 2121.605 | 2206.460 | 2356.355 |
| SD | 29.187 | 37.351 | 75.978 | 40.021 | 65.638 | 93.593 | 46.392 | 34.530 | 47.310 | 59.227 | 68.525 | |
| RAN | 1 | 3 | 4 | 5 | 7 | 10 | 6 | 9 | 2 | 8 | 11 | |
| F8 | AVG | 2243.629 | 2297.781 | 2373.706 | 2377.147 | 2255.380 | 2497.090 | 2292.650 | 2432.047 | 2240.629 | 2274.965 | 2983.494 |
| SD | 36.205 | 76.701 | 153.618 | 134.631 | 38.109 | 182.612 | 53.938 | 183.263 | 26.135 | 65.200 | 291.237 | |
| RAN | 2 | 6 | 7 | 8 | 3 | 10 | 5 | 9 | 1 | 4 | 11 | |
| F9 | AVG | 2481.000 | 2564.784 | 2483.255 | 3260.897 | 2508.538 | 3091.623 | 2628.026 | 3477.854 | 2584.904 | 2573.909 | 3402.602 |
| SD | 0.282 | 35.467 | 3.124 | 230.424 | 22.711 | 228.864 | 46.043 | 353.977 | 50.466 | 46.192 | 238.632 | |
| RAN | 1 | 4 | 2 | 9 | 3 | 8 | 7 | 11 | 6 | 5 | 10 | |
| F10 | AVG | 2539.901 | 2778.659 | 3648.251 | 5296.652 | 4088.618 | 5543.269 | 3760.872 | 6381.361 | 3307.365 | 4460.976 | 6499.317 |
| SD | 103.711 | 765.195 | 1006.841 | 1352.603 | 595.663 | 914.065 | 1416.084 | 1214.830 | 1252.848 | 1231.506 | 1325.805 | |
| RAN | 1 | 2 | 4 | 8 | 6 | 9 | 5 | 10 | 3 | 7 | 11 | |
| F11 | AVG | 2935.671 | 3310.221 | 3317.437 | 7820.076 | 3003.779 | 8347.090 | 5050.069 | 8742.492 | 4638.858 | 3384.729 | 1.11 × 104 |
| SD | 138.958 | 487.063 | 1028.409 | 606.779 | 139.075 | 1137.649 | 623.546 | 870.316 | 536.012 | 270.966 | 1390.234 | |
| RAN | 1 | 3 | 4 | 8 | 2 | 9 | 7 | 10 | 6 | 5 | 11 | |
| F12 | AVG | 2991.295 | 3041.325 | 3034.367 | 3846.387 | 3185.708 | 3807.392 | 3261.218 | 3646.558 | 3027.704 | 3086.782 | 3854.341 |
| SD | 51.654 | 41.210 | 91.186 | 210.462 | 137.706 | 236.661 | 71.964 | 231.355 | 57.378 | 137.904 | 189.245 | |
| RAN | 1 | 4 | 3 | 10 | 6 | 9 | 7 | 8 | 2 | 5 | 11 | |
| Average rank | 1.42 | 3.83 | 3.08 | 7.58 | 4.17 | 8.67 | 6.58 | 9.67 | 3.75 | 6.33 | 10.92 | |
| Final rank | 1 | 4 | 2 | 8 | 5 | 9 | 7 | 10 | 3 | 6 | 11 | |
| F | ADPO | PO | IVY | HOA | HHO | AOA | SWO | COA | GJO | WOA | KOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 |
| F2 | 2.48760 × 10−11 | 1.50990 × 10−11 | 6.79720 × 10−8 | 1.84490 × 10−11 | 3.03290 × 10−11 | 2.73100 × 10−6 | 1.50990 × 10−11 | 8.03110 × 10−7 | 4.24240 × 10−9 | 9.28370 × 10−10 | 2.48760 × 10−11 |
| F3 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 4.15730 × 10−3 | 1.50990 × 10−11 | 7.39400 × 10−1 | 1.50990 × 10−11 | 1.67600 × 10−8 | 1.50990 × 10−11 | 1.11360 × 10−9 | 1.50990 × 10−11 |
| F4 | 1.50990 × 10−11 | 1.50990 × 10−11 | 2.78060 × 10−4 | 2.28630 × 10−9 | 1.50990 × 10−11 | 2.01650 × 10−3 | 1.50990 × 10−11 | 7.64580 × 10−6 | 2.03860 × 10−11 | 1.68410 × 10−5 | 1.50990 × 10−11 |
| F5 | 1.50990 × 10−11 | 1.50990 × 10−11 | 2.74700 × 10−11 | 2.35690 × 10−4 | 1.50990 × 10−11 | 1.02330 × 10−1 | 1.50990 × 10−11 | 2.09130 × 10−9 | 1.50990 × 10−11 | 1.07720 × 10−10 | 1.50990 × 10−11 |
| F6 | 1.66920 × 10−11 | 1.50990 × 10−11 | 1.25970 × 10−1 | 2.74700 × 10−11 | 2.25220 × 10−11 | 1.00000 × 10+00 | 1.50990 × 10−11 | 5.46830 × 10−11 | 1.07720 × 10−10 | 2.03860 × 10−11 | 1.66920 × 10−11 |
| F7 | 1.50990 × 10−11 | 1.50990 × 10−11 | 4.94170 × 10−3 | 1.46030 × 10−2 | 2.25220 × 10−11 | 2.17020 × 10−1 | 1.50990 × 10−11 | 4.15730 × 10−3 | 1.50990 × 10−11 | 3.06050 × 10−10 | 1.50990 × 10−11 |
| F8 | 1.46080 × 10−9 | 1.50990 × 10−11 | 2.70710 × 10−1 | 6.43520 × 10−10 | 2.54610 × 10−8 | 2.78060 × 10−4 | 1.50990 × 10−11 | 8.40660 × 10−5 | 6.01160 × 10−9 | 1.84490 × 10−11 | 1.46080 × 10−9 |
| F9 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.66920 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 8.64990 × 10−1 | 1.50990 × 10−11 | 4.49670 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 |
| F10 | 5.86870 × 10−10 | 1.66920 × 10−11 | 2.70710 × 10−1 | 4.87780 × 10−10 | 6.55550 × 10−9 | 5.15730 × 10−3 | 1.50990 × 10−11 | 2.31950 × 10−5 | 7.05490 × 10−10 | 1.43580 × 10−10 | 5.86870 × 10−10 |
| F11 | 6.43520 × 10−10 | 5.86870 × 10−10 | 7.97820 × 10−2 | 8.39880 × 10−4 | 4.42050 × 10−7 | 5.57130 × 10−4 | 1.50990 × 10−11 | 4.14600 × 10−6 | 6.79720 × 10−8 | 1.38630 × 10−5 | 6.43520 × 10−10 |
| F12 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.09790 × 10−7 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 | 1.50990 × 10−11 |
| F | ADPO | eCOA | CMAES | DAOA | CSOAOA | GWO_CS | RDWOA | jDE | ISSA | IPSO_IGSA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | AVG | 2.43 × 106 | 8.08 × 109 | 1.95 × 1010 | 2.62 × 1011 | 2.09 × 108 | 1.42 × 1010 | 2.11 × 1010 | 1.23 × 1011 | 2.27 × 108 | 4.11 × 1010 |
| SD | 2.16 × 106 | 1.24 × 109 | 3.03 × 1010 | 1.46 × 1010 | 7.33 × 107 | 4.30 × 109 | 2.38 × 109 | 7.75 × 1010 | 6.78 × 107 | 1.38 × 1010 | |
| RAN | 1 | 4 | 6 | 10 | 2 | 5 | 7 | 9 | 3 | 8 | |
| F3 | AVG | 2.79 × 104 | 1.29 × 105 | 3.82 × 105 | 5.74 × 107 | 1.17 × 105 | 1.23 × 105 | 1.89 × 105 | 2.88 × 105 | 2.47 × 105 | 1.70 × 105 |
| SD | 8260.825 | 1.21 × 104 | 4.93 × 104 | 1.35 × 108 | 1.18 × 104 | 1.77 × 104 | 1.45 × 104 | 4.19 × 104 | 8.13 × 104 | 1.94 × 104 | |
| RAN | 1 | 4 | 9 | 10 | 2 | 3 | 6 | 8 | 7 | 5 | |
| F4 | AVG | 616.358 | 1465.648 | 8332.552 | 1.30 × 105 | 669.436 | 1496.651 | 4063.559 | 5.20 × 104 | 718.095 | 8698.568 |
| SD | 48.544 | 443.718 | 3064.805 | 2.80 × 104 | 41.225 | 210.031 | 887.200 | 8380.828 | 31.919 | 1866.557 | |
| RAN | 1 | 4 | 7 | 10 | 2 | 5 | 6 | 9 | 3 | 8 | |
| F5 | AVG | 840.354 | 842.542 | 549.891 | 1697.942 | 828.289 | 809.189 | 1043.451 | 1403.854 | 881.798 | 855.080 |
| SD | 63.807 | 54.380 | 3.361 | 91.762 | 34.561 | 23.177 | 28.878 | 43.358 | 26.887 | 106.625 | |
| RAN | 4 | 5 | 1 | 10 | 3 | 2 | 8 | 9 | 7 | 6 | |
| F6 | AVG | 650.472 | 660.316 | 621.711 | 757.645 | 630.582 | 632.558 | 682.780 | 701.936 | 667.615 | 671.656 |
| SD | 7.193 | 9.409 | 33.627 | 8.127 | 15.080 | 7.842 | 8.880 | 22.860 | 2.638 | 19.663 | |
| RAN | 4 | 5 | 1 | 10 | 2 | 3 | 8 | 9 | 6 | 7 | |
| F7 | AVG | 1342.796 | 1421.933 | 956.599 | 6057.349 | 1451.628 | 1180.698 | 1764.588 | 3617.830 | 1673.438 | 1801.288 |
| SD | 142.095 | 192.150 | 155.021 | 466.162 | 162.112 | 96.478 | 112.411 | 1358.797 | 146.308 | 103.252 | |
| RAN | 3 | 4 | 1 | 10 | 5 | 2 | 7 | 9 | 6 | 8 | |
| F8 | AVG | 1161.837 | 1110.964 | 1178.717 | 2017.948 | 1158.436 | 1108.937 | 1321.955 | 1650.974 | 1173.708 | 1169.514 |
| SD | 61.530 | 39.309 | 257.356 | 73.263 | 40.599 | 41.371 | 58.026 | 200.700 | 46.786 | 49.201 | |
| RAN | 4 | 2 | 7 | 10 | 3 | 1 | 8 | 9 | 6 | 5 | |
| F9 | AVG | 1.44 × 104 | 1.30 × 104 | 900.151 | 1.17 × 105 | 1.15 × 104 | 1.51 × 104 | 2.72 × 104 | 6.14 × 104 | 1.56 × 104 | 1.57 × 104 |
| SD | 1699.155 | 563.595 | 0.235 | 1.50 × 104 | 1019.419 | 8516.092 | 2781.981 | 8150.298 | 1433.657 | 6902.928 | |
| RAN | 4 | 3 | 1 | 10 | 2 | 5 | 8 | 9 | 6 | 7 | |
| F10 | AVG | 7718.304 | 8311.301 | 1.50 × 104 | 1.69 × 104 | 6484.701 | 7483.089 | 1.26 × 104 | 1.54 × 104 | 8521.760 | 1.49 × 104 |
| SD | 724.850 | 762.366 | 348.879 | 588.528 | 921.221 | 1289.202 | 1004.835 | 566.957 | 1119.243 | 845.519 | |
| RAN | 3 | 4 | 8 | 10 | 1 | 2 | 6 | 9 | 5 | 7 | |
| F11 | AVG | 1489.778 | 2157.984 | 6.14 × 104 | 1.14 × 105 | 3037.103 | 7629.620 | 5496.289 | 3.83 × 104 | 2492.502 | 1.74 × 104 |
| SD | 83.804 | 322.622 | 2.07 × 104 | 8.49 × 104 | 326.477 | 2509.494 | 1162.624 | 4553.782 | 283.031 | 3825.336 | |
| RAN | 1 | 2 | 9 | 10 | 4 | 6 | 5 | 8 | 3 | 7 | |
| F12 | AVG | 3.26 × 107 | 2.31 × 108 | 2.42 × 1010 | 1.60 × 1011 | 2.66 × 107 | 1.56 × 109 | 4.25 × 109 | 6.21 × 1010 | 4.84 × 107 | 7.34 × 109 |
| SD | 2.00 × 107 | 1.07 × 108 | 4.70 × 109 | 1.58 × 1010 | 2.60 × 107 | 6.91 × 108 | 3.93 × 109 | 1.24 × 1010 | 3.26 × 107 | 2.56 × 109 | |
| RAN | 2 | 4 | 8 | 10 | 1 | 5 | 6 | 9 | 3 | 7 | |
| F13 | AVG | 4.67 × 104 | 1.92 × 105 | 1.14 × 1010 | 9.09 × 1010 | 4.98 × 105 | 8.85 × 107 | 4.06 × 108 | 2.71 × 1010 | 6.71 × 104 | 3.10 × 108 |
| SD | 7.32 × 103 | 3.57 × 105 | 2.70 × 109 | 1.86 × 1010 | 3.71 × 105 | 3.16 × 107 | 2.23 × 108 | 1.64 × 1010 | 2.44 × 104 | 4.35 × 108 | |
| RAN | 1 | 3 | 8 | 10 | 4 | 5 | 7 | 9 | 2 | 6 | |
| F14 | AVG | 2.59 × 105 | 9.18 × 105 | 2.12 × 107 | 3.26 × 108 | 1.67 × 106 | 1.38 × 106 | 6.76 × 106 | 2.27 × 107 | 1.48 × 106 | 8.51 × 106 |
| SD | 1.33 × 105 | 5.70 × 105 | 1.33 × 107 | 2.19 × 108 | 1.10 × 106 | 1.08 × 106 | 5.70 × 106 | 7.78 × 106 | 6.99 × 105 | 8.61 × 106 | |
| RAN | 1 | 2 | 8 | 10 | 5 | 3 | 6 | 9 | 4 | 7 | |
| F15 | AVG | 2.08 × 104 | 2.81 × 104 | 1.38 × 109 | 3.28 × 1010 | 5.33 × 104 | 2.55 × 107 | 7.85 × 107 | 7.45 × 109 | 2.44 × 104 | 5.55 × 107 |
| SD | 6.09 × 103 | 7.25 × 103 | 4.23 × 108 | 1.28 × 1010 | 2.96 × 104 | 3.76 × 107 | 7.93 × 107 | 5.03 × 109 | 1.18 × 104 | 1.15 × 108 | |
| RAN | 1 | 3 | 8 | 10 | 4 | 5 | 7 | 9 | 2 | 6 | |
| F16 | AVG | 4029.422 | 3861.616 | 6539.304 | 1.65 × 104 | 3239.377 | 3395.411 | 5943.220 | 8258.053 | 4081.894 | 4265.301 |
| SD | 367.002 | 322.451 | 523.678 | 3021.001 | 669.226 | 322.737 | 618.996 | 1418.040 | 632.085 | 533.700 | |
| RAN | 4 | 3 | 8 | 10 | 1 | 2 | 7 | 9 | 5 | 6 | |
| F17 | AVG | 3260.336 | 3634.634 | 2665.323 | 520,653.499 | 3297.556 | 3160.881 | 4222.925 | 19,889.934 | 3616.944 | 3787.720 |
| SD | 537.823 | 369.929 | 250.825 | 422,719.420 | 260.826 | 281.760 | 468.911 | 17,601.719 | 429.145 | 532.911 | |
| RAN | 3 | 6 | 1 | 10 | 4 | 2 | 8 | 9 | 5 | 7 | |
| F18 | AVG | 3.48 × 106 | 2.75 × 106 | 1.13 × 108 | 4.64 × 108 | 2.89 × 106 | 9.20 × 106 | 3.00 × 107 | 1.32 × 108 | 5.26 × 106 | 1.16 × 107 |
| SD | 2.16 × 106 | 1.20 × 106 | 2.49 × 107 | 1.41 × 108 | 8.35 × 105 | 7.96 × 106 | 2.46 × 107 | 4.24 × 107 | 5.84 × 106 | 8.37 × 106 | |
| RAN | 3 | 1 | 8 | 10 | 2 | 5 | 7 | 9 | 4 | 6 | |
| F19 | AVG | 4.95 × 104 | 3.96 × 105 | 1.31 × 109 | 1.63 × 1010 | 2.67 × 104 | 6.33 × 106 | 9.78 × 106 | 2.50 × 109 | 3.73 × 104 | 5.50 × 105 |
| SD | 1.96 × 104 | 4.75 × 104 | 7.71 × 108 | 3.63 × 109 | 5.97 × 103 | 1.14 × 107 | 6.49 × 106 | 1.17 × 109 | 1.24 × 104 | 3.68 × 105 | |
| RAN | 3 | 4 | 8 | 10 | 1 | 6 | 7 | 9 | 2 | 5 | |
| F20 | AVG | 3066.824 | 3223.354 | 3755.252 | 5229.949 | 3169.382 | 3079.606 | 3439.724 | 4310.467 | 3547.154 | 3871.279 |
| SD | 222.742 | 312.746 | 244.158 | 279.803 | 428.861 | 130.822 | 108.685 | 353.531 | 213.676 | 214.596 | |
| RAN | 1 | 4 | 7 | 10 | 3 | 2 | 5 | 9 | 6 | 8 | |
| F21 | AVG | 2662.173 | 2636.420 | 2625.002 | 3638.206 | 2650.265 | 2538.095 | 2978.520 | 3212.749 | 2844.101 | 2731.186 |
| SD | 79.079 | 36.434 | 299.277 | 119.440 | 42.254 | 26.879 | 102.297 | 122.748 | 34.360 | 87.016 | |
| RAN | 5 | 3 | 2 | 10 | 4 | 1 | 8 | 9 | 7 | 6 | |
| F22 | AVG | 7956.579 | 1.12 × 104 | 1.68 × 104 | 1.85 × 104 | 8714.231 | 8372.384 | 1.35 × 104 | 1.71 × 104 | 1.07 × 104 | 1.64 × 104 |
| SD | 4437.808 | 842.920 | 189.802 | 1001.036 | 3166.453 | 2254.177 | 736.221 | 373.442 | 490.879 | 399.462 | |
| RAN | 1 | 5 | 8 | 10 | 3 | 2 | 6 | 9 | 4 | 7 | |
| F23 | AVG | 3198.328 | 3174.853 | 3413.438 | 5257.213 | 3043.978 | 3075.586 | 3639.131 | 4205.040 | 3482.904 | 3874.196 |
| SD | 104.785 | 65.958 | 48.089 | 401.928 | 46.192 | 52.803 | 63.119 | 160.957 | 138.772 | 219.283 | |
| RAN | 4 | 3 | 5 | 10 | 1 | 2 | 7 | 9 | 6 | 8 | |
| F24 | AVG | 3446.034 | 3266.602 | 3496.998 | 5962.147 | 3516.754 | 3246.786 | 3716.717 | 4521.426 | 3596.922 | 4138.812 |
| SD | 140.581 | 83.274 | 54.391 | 533.209 | 115.301 | 89.314 | 91.453 | 296.736 | 119.341 | 135.882 | |
| RAN | 3 | 2 | 4 | 10 | 5 | 1 | 7 | 9 | 6 | 8 | |
| F25 | AVG | 3095.805 | 3728.568 | 4054.579 | 5.84 × 104 | 3193.396 | 4070.799 | 5167.651 | 3.04 × 104 | 3212.249 | 7009.422 |
| SD | 28.311 | 192.851 | 1625.322 | 5190.684 | 11.453 | 435.175 | 404.137 | 3538.472 | 46.614 | 1396.288 | |
| RAN | 1 | 4 | 5 | 10 | 2 | 6 | 7 | 9 | 3 | 8 | |
| F26 | AVG | 5827.614 | 1.16 × 104 | 1.12 × 104 | 3.01 × 104 | 8143.500 | 6213.015 | 1.32 × 104 | 2.13 × 104 | 1.05 × 104 | 1.39 × 104 |
| SD | 3845.466 | 924.356 | 70.470 | 3428.947 | 3425.603 | 1555.076 | 785.538 | 1039.129 | 3431.660 | 1758.167 | |
| RAN | 1 | 6 | 5 | 10 | 3 | 2 | 7 | 9 | 4 | 8 | |
| F27 | AVG | 3626.228 | 3866.233 | 3903.322 | 8778.909 | 3606.561 | 3687.598 | 4641.606 | 6086.369 | 3844.967 | 5882.212 |
| SD | 228.514 | 133.222 | 55.881 | 744.725 | 172.600 | 41.701 | 421.257 | 890.516 | 162.791 | 645.253 | |
| RAN | 2 | 5 | 6 | 10 | 1 | 3 | 7 | 9 | 4 | 8 | |
| F28 | AVG | 3357.193 | 4486.564 | 1.00 × 104 | 2.49 × 104 | 3493.394 | 4404.121 | 5969.609 | 1.58 × 104 | 3574.933 | 6795.098 |
| SD | 32.968 | 217.558 | 440.044 | 4179.754 | 57.593 | 303.131 | 330.416 | 1476.058 | 118.711 | 401.804 | |
| RAN | 1 | 5 | 8 | 10 | 2 | 4 | 6 | 9 | 3 | 7 | |
| F29 | AVG | 4581.788 | 6753.843 | 1.33 × 104 | 2.58 × 106 | 4520.731 | 4931.909 | 8368.144 | 1.94 × 104 | 5576.914 | 9624.458 |
| SD | 367.149 | 538.216 | 4948.482 | 1.77 × 106 | 251.205 | 422.919 | 665.707 | 6958.151 | 493.070 | 2865.338 | |
| RAN | 2 | 5 | 8 | 10 | 1 | 3 | 6 | 9 | 4 | 7 | |
| F30 | AVG | 9.03 × 106 | 1.47 × 108 | 2.12 × 109 | 2.43 × 1010 | 1.04 × 106 | 1.76 × 108 | 3.01 × 108 | 2.92 × 109 | 3.76 × 106 | 2.15 × 108 |
| SD | 4.25 × 106 | 1.69 × 107 | 1.01 × 109 | 4.30 × 109 | 1.64 × 105 | 6.86 × 107 | 8.12 × 107 | 1.90 × 109 | 6.31 × 105 | 3.65 × 107 | |
| RAN | 3 | 4 | 8 | 10 | 1 | 5 | 7 | 9 | 2 | 6 | |
| Average rank | 2.34 | 3.76 | 5.97 | 10.00 | 2.55 | 3.38 | 6.79 | 8.93 | 4.41 | 6.86 | |
| Final rank | 1 | 4 | 6 | 10 | 2 | 3 | 7 | 9 | 5 | 8 | |
| F | ADPO | eCOA | CMAES | DAOA | CSOAOA | GWO_CS | RDWOA | jDE | ISSA | IPSO_IGSA |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.93940 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 3.93940 × 10−1 |
| F3 | 1.08230 × 10−11 | 9.92420 × 10−1 | 1.08230 × 10−11 | 6.99130 × 10−1 | 1.08230 × 10−11 | 3.09520 × 10−1 | 1.08230 × 10−11 | 2.40260 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F4 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F5 | 1.08230 × 10−11 | 4.84850 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F6 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.32030 × 10−1 | 1.08230 × 10−11 | 1.00000 × 10+00 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F7 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 2.40260 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F8 | 1.08230 × 10−11 | 1.29870 × 10−9 | 1.08230 × 10−11 | 1.08230 × 10−11 | 3.09520 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F9 | 1.08230 × 10−11 | 9.87010 × 10−1 | 1.08230 × 10−11 | 9.95670 × 10−1 | 5.88740 × 10−1 | 5.88740 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F10 | 9.30740 × 10−9 | 6.99130 × 10−1 | 1.08230 × 10−11 | 6.99130 × 10−1 | 1.32030 × 10−1 | 1.08230 × 10−11 | 7.57580 × 10−11 | 1.32030 × 10−1 | 1.08230 × 10−11 | 9.30740 × 10−9 |
| F11 | 1.08230 × 10−11 | 5.88740 × 10−1 | 1.08230 × 10−11 | 4.84850 × 10−1 | 2.05630 × 10−9 | 1.00000 × 10+00 | 1.29870 × 10−9 | 4.84850 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F12 | 1.08230 × 10−11 | 9.95670 × 10−1 | 1.08230 × 10−11 | 1.29870 × 10−9 | 1.08230 × 10−11 | 2.40260 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F13 | 1.08230 × 10−11 | 9.37230 × 10−1 | 1.08230 × 10−11 | 9.37230 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 2.16450 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F14 | 1.00000 × 10+00 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.00000 × 10+00 | 2.40260 × 10−01 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.00000 × 10+00 |
| F15 | 1.08230 × 10−11 | 1.00000 × 10+00 | 1.08230 × 10−11 | 6.99130 × 10−01 | 1.08230 × 10−11 | 6.99130 × 10−01 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F16 | 2.16450 × 10−11 | 9.97840 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 2.16450 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 2.16450 × 10−11 |
| F17 | 5.88740 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 9.92420 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 2.16450 × 10−11 | 9.87010 × 10−1 | 1.08230 × 10−11 | 5.88740 × 10−1 |
| F18 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 2.16450 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F19 | 2.16450 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 2.05630 × 10−9 | 1.08230 × 10−11 | 4.32900 × 10−11 | 1.08230 × 10−11 | 2.16450 × 10−11 |
| F20 | 6.49350 × 10−9 | 8.18180 × 10−1 | 1.08230 × 10−11 | 3.93940 × 10−1 | 1.08230 × 10−11 | 9.30740 × 10−9 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 6.49350 × 10−9 |
| F21 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F22 | 1.08230 × 10−11 | 5.88740 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F23 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F24 | 1.08230 × 10−11 | 1.00000 × 10+00 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 9.95670 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F25 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 |
| F26 | 1.00000 × 10+00 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.00000 × 10+00 | 1.79650 × 10−1 | 1.08230 × 10−11 | 1.00000 × 10+00 | 1.08230 × 10−11 | 1.00000 × 10+00 |
| F27 | 3.93940 × 10−1 | 9.95670 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 9.30740 × 10−9 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 3.93940 × 10−1 |
| F28 | 1.00000 × 10+00 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 4.32900 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.00000 × 10+00 |
| F29 | 3.93940 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.00000 × 10+00 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 3.93940 × 10−1 |
| F30 | 1.00000 × 10+00 | 1.08230 × 10−11 | 1.08230 × 10−11 | 1.08230 × 10−11 | 9.37230 × 10−1 | 1.08230 × 10−11 | 1.08230 × 10−11 | 6.49350 × 10−9 | 1.08230 × 10−11 | 1.00000 × 10+00 |
| F | ADPO | PO | IVY | HOA | HHO | AOA | SWO | COA | GJO | WOA | KOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 0.90527 | 0.30711 | 1.02636 | 0.13643 | 0.24529 | 0.19685 | 0.00808 | 0.19791 | 0.37429 | 0.10800 | 0.01245 |
| F2 | 0.83592 | 0.33225 | 0.85256 | 0.14001 | 0.24348 | 0.18791 | 0.00458 | 0.18577 | 0.41604 | 0.09141 | 0.00826 |
| F3 | 1.11334 | 0.35110 | 0.83730 | 0.25103 | 0.58962 | 0.27909 | 0.00830 | 0.41503 | 0.42706 | 0.18210 | 0.01042 |
| F4 | 0.95505 | 0.26727 | 0.73182 | 0.15731 | 0.30116 | 0.20894 | 0.00541 | 0.24958 | 0.35999 | 0.11791 | 0.00826 |
| F5 | 1.02721 | 0.28030 | 0.75854 | 0.18023 | 0.37381 | 0.22601 | 0.00623 | 0.27336 | 0.38006 | 0.12129 | 0.00790 |
| F6 | 0.79794 | 0.25164 | 0.85514 | 0.16841 | 0.26711 | 0.20225 | 0.00522 | 0.21654 | 0.34851 | 0.10210 | 0.00808 |
| F7 | 1.31417 | 0.39658 | 0.99009 | 0.34585 | 0.58004 | 0.34228 | 0.01075 | 0.62644 | 0.49630 | 0.24503 | 0.01185 |
| F8 | 1.40221 | 0.53759 | 1.04832 | 0.35390 | 0.60387 | 0.34604 | 0.01059 | 0.60033 | 0.46907 | 0.25624 | 0.01484 |
| F9 | 1.13334 | 0.35283 | 0.82745 | 0.25306 | 0.48302 | 0.30826 | 0.00853 | 0.49496 | 0.43338 | 0.21182 | 0.01091 |
| F10 | 0.99577 | 0.30504 | 0.72540 | 0.20768 | 0.40904 | 0.25597 | 0.00769 | 0.38480 | 0.39198 | 0.17093 | 0.00990 |
| F11 | 1.27403 | 0.39561 | 0.86463 | 0.29485 | 0.57875 | 0.34540 | 0.00983 | 0.58785 | 0.47009 | 0.25866 | 0.01223 |
| F12 | 1.35035 | 0.42902 | 0.87337 | 0.31900 | 0.63377 | 0.37125 | 0.01099 | 0.65977 | 0.50257 | 0.28452 | 0.01371 |
| F | ADPO | eCOA | CMAES | DAOA | CSOAOA | GWO_CS | RDWOA | jDE | ISSA | IPSO_IGSA |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 1.67386 | 1.04293 | 4.24935 | 0.38412 | 1.11464 | 1.95731 | 0.74037 | 1.93376 | 0.50250 | 0.70356 |
| F3 | 1.24174 | 0.78274 | 3.18205 | 0.34024 | 0.68268 | 1.48834 | 0.57144 | 1.59181 | 0.40555 | 0.60406 |
| F4 | 1.27119 | 0.79545 | 3.65005 | 0.36421 | 0.71415 | 1.68225 | 0.61663 | 1.74907 | 0.54113 | 0.69053 |
| F5 | 1.26769 | 0.74569 | 3.25317 | 0.35912 | 0.69168 | 1.48907 | 0.55943 | 1.71071 | 0.43242 | 0.63177 |
| F6 | 1.24742 | 0.76707 | 4.10569 | 0.35237 | 0.70382 | 1.61792 | 0.58115 | 1.63057 | 0.53805 | 0.70901 |
| F7 | 1.91488 | 1.35427 | 3.60396 | 0.64330 | 1.53468 | 2.08135 | 1.59306 | 2.45592 | 1.03826 | 1.03672 |
| F8 | 1.52636 | 0.81190 | 3.90357 | 0.51789 | 0.88587 | 1.77702 | 0.76409 | 1.98049 | 0.65625 | 0.79616 |
| F9 | 1.66943 | 0.80809 | 3.76615 | 0.38082 | 0.76675 | 1.63850 | 0.63280 | 2.10379 | 0.56871 | 0.70744 |
| F10 | 1.37915 | 0.79232 | 3.59767 | 0.38425 | 0.80669 | 1.62632 | 0.66185 | 1.67851 | 0.49674 | 0.65528 |
| F11 | 1.79548 | 1.28484 | 3.87048 | 0.53070 | 1.27787 | 1.95214 | 1.29371 | 2.11562 | 0.80681 | 0.85990 |
| F12 | 1.37442 | 0.93949 | 4.00364 | 0.39737 | 0.80870 | 1.85520 | 0.81436 | 2.94907 | 0.60320 | 0.78276 |
| F13 | 1.71143 | 1.04850 | 3.78872 | 0.49357 | 1.00667 | 1.62320 | 0.75793 | 1.99845 | 0.58631 | 0.73249 |
| F14 | 1.43323 | 0.78878 | 3.40117 | 0.42298 | 0.85382 | 1.74562 | 0.73677 | 1.92145 | 0.55565 | 0.77742 |
| F15 | 1.63211 | 1.06965 | 4.00738 | 0.46520 | 0.94881 | 1.72975 | 0.90415 | 1.93334 | 0.72383 | 0.74677 |
| F16 | 1.28576 | 0.74910 | 3.45059 | 0.39278 | 0.79488 | 1.67217 | 0.71246 | 1.75685 | 0.46508 | 0.66763 |
| F17 | 1.45320 | 0.86406 | 3.79483 | 0.39798 | 0.83967 | 1.56689 | 0.78986 | 1.76792 | 0.55344 | 0.70001 |
| F18 | 1.46303 | 0.96405 | 3.25036 | 0.44445 | 1.02542 | 1.61823 | 0.99470 | 1.87846 | 0.68746 | 0.72306 |
| F19 | 1.33661 | 0.82929 | 3.44134 | 0.40965 | 0.88940 | 1.74197 | 0.65882 | 1.78277 | 0.50382 | 0.66813 |
| F20 | 2.66244 | 1.95475 | 3.91604 | 0.68843 | 1.59952 | 2.00164 | 1.88637 | 2.53899 | 1.29412 | 0.93342 |
| F21 | 1.56125 | 1.15591 | 3.84839 | 0.51652 | 1.22942 | 1.78423 | 1.24303 | 2.07499 | 0.86073 | 0.87118 |
| F22 | 2.76479 | 2.04891 | 4.02151 | 0.77052 | 2.01565 | 2.08038 | 1.97774 | 2.48590 | 1.23581 | 0.94357 |
| F23 | 2.58576 | 2.10752 | 3.85183 | 0.85031 | 2.25358 | 2.09832 | 2.40603 | 2.28780 | 1.40034 | 1.04877 |
| F24 | 2.72834 | 2.28436 | 4.08418 | 0.92072 | 2.32758 | 1.98287 | 2.42022 | 2.46055 | 1.76056 | 1.10898 |
| F25 | 2.67659 | 2.41989 | 3.69647 | 0.81594 | 2.20327 | 2.03049 | 2.32264 | 3.23136 | 1.73430 | 1.03920 |
| F26 | 2.67151 | 2.26036 | 3.73109 | 0.93509 | 2.26509 | 2.01687 | 2.91336 | 2.86992 | 1.91023 | 1.24187 |
| F27 | 3.90093 | 2.87358 | 5.38594 | 1.29246 | 3.48890 | 2.72201 | 4.13461 | 3.70081 | 2.99426 | 2.10145 |
| F28 | 5.33060 | 4.42535 | 6.08019 | 1.73411 | 4.00612 | 3.18132 | 4.94835 | 3.89686 | 3.51751 | 2.25040 |
| F29 | 4.84923 | 3.79245 | 5.73153 | 1.50264 | 4.07170 | 3.53292 | 4.11101 | 3.95262 | 3.62204 | 2.02870 |
| F30 | 4.16924 | 3.24062 | 6.04186 | 1.11887 | 2.95649 | 2.62767 | 3.38150 | 3.58916 | 2.24090 | 1.72986 |
| Algorithm | Parameter Value | Parameter Range |
|---|---|---|
| Number of Hidden Units | [20, 150] | |
| Maximum Epochs | [20, 200] | |
| Optimization Method | 1, 2, 3 for SGDM (1), Adam (2), or RMSProp (3) | |
| Minimum Batch Size | [64, 256] | |
| Learning Rate Drop Factor | [0.1, 0.9] |
| Station A | Station B | |||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | COV | R2 | RMSE | MAE | COV | |
| LSTM | 0.6875 | 0.0024 | 0.0017 | 85.2153 | 0.6385 | 0.0026 | 0.0022 | 115.8742 |
| PO-LSTM | 0.8485 | 0.0014 | 0.0007 | 51.2458 | 0.8475 | 0.0012 | 0.0015 | 60.5874 |
| SCA-LSTM | 0.8425 | 0.0015 | 0.0009 | 53.7894 | 0.8365 | 0.0014 | 0.0016 | 63.2145 |
| WOA-LSTM | 0.8285 | 0.0017 | 0.0011 | 59.8547 | 0.8245 | 0.0016 | 0.0018 | 66.9874 |
| SOA-LSTM | 0.8385 | 0.0015 | 0.0010 | 55.7412 | 0.8325 | 0.0015 | 0.0017 | 64.5789 |
| HHO-LSTM | 0.8515 | 0.0013 | 0.0008 | 50.9685 | 0.8495 | 0.0013 | 0.0014 | 59.8524 |
| ADPO-LSTM | 0.9875 | 0.0002 | 0.0001 | 15.8745 | 0.9851 | 0.0004 | 0.0002 | 23.7412 |
| Station C | Station D | |||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | COV | R2 | RMSE | MAE | COV | |
| LSTM | 0.6185 | 0.0025 | 0.0020 | 101.5874 | 0.6325 | 0.0030 | 0.0022 | 96.8745 |
| PO-LSTM | 0.8125 | 0.0017 | 0.0012 | 63.8745 | 0.8085 | 0.0013 | 0.0012 | 62.7854 |
| SCA-LSTM | 0.8065 | 0.0018 | 0.0013 | 66.2145 | 0.8075 | 0.0015 | 0.0013 | 65.1478 |
| WOA-LSTM | 0.7945 | 0.0020 | 0.0015 | 69.8745 | 0.7975 | 0.0017 | 0.0014 | 68.3654 |
| SOA-LSTM | 0.8025 | 0.0018 | 0.0014 | 67.5896 | 0.8045 | 0.0016 | 0.0013 | 66.9874 |
| HHO-LSTM | 0.8145 | 0.0016 | 0.0011 | 62.1478 | 0.8125 | 0.0014 | 0.0011 | 61.5478 |
| ADPO-LSTM | 0.9758 | 0.0002 | 0.0001 | 25.4578 | 0.9685 | 0.0005 | 0.0003 | 31.2874 |
| Station A | Station B | |||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | COV | R2 | RMSE | MAE | COV | |
| LSTM | 0.6625 | 0.0034 | 0.0026 | 88.7458 | 0.5785 | 0.0037 | 0.0034 | 117.8965 |
| PO-LSTM | 0.8485 | 0.0026 | 0.0019 | 53.7851 | 0.8105 | 0.0020 | 0.0016 | 63.4785 |
| SCA-LSTM | 0.8165 | 0.0027 | 0.0020 | 56.8547 | 0.7945 | 0.0022 | 0.0018 | 65.9874 |
| WOA-LSTM | 0.7945 | 0.0029 | 0.0022 | 61.2458 | 0.7615 | 0.0025 | 0.0020 | 70.3654 |
| SOA-LSTM | 0.8025 | 0.0028 | 0.0021 | 58.9874 | 0.7845 | 0.0023 | 0.0019 | 67.8745 |
| HHO-LSTM | 0.8465 | 0.0025 | 0.0018 | 52.9635 | 0.8125 | 0.0019 | 0.0015 | 62.7854 |
| ADPO-LSTM | 0.9785 | 0.0009 | 0.0008 | 21.5874 | 0.9798 | 0.0010 | 0.0005 | 27.4578 |
| Station C | Station D | |||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | COV | R2 | RMSE | MAE | COV | |
| LSTM | 0.5985 | 0.0037 | 0.0032 | 107.5896 | 0.6105 | 0.0039 | 0.0030 | 102.8745 |
| PO-LSTM | 0.7705 | 0.0021 | 0.0017 | 68.1478 | 0.7695 | 0.0019 | 0.0016 | 68.7854 |
| SCA-LSTM | 0.7345 | 0.0023 | 0.0019 | 71.2587 | 0.7385 | 0.0021 | 0.0017 | 70.1478 |
| WOA-LSTM | 0.7085 | 0.0026 | 0.0021 | 74.8745 | 0.7215 | 0.0024 | 0.0019 | 73.5896 |
| SOA-LSTM | 0.7245 | 0.0024 | 0.0020 | 72.9874 | 0.7325 | 0.0022 | 0.0018 | 71.8745 |
| HHO-LSTM | 0.7725 | 0.0020 | 0.0016 | 67.3654 | 0.7715 | 0.0018 | 0.0015 | 67.9874 |
| ADPO-LSTM | 0.9705 | 0.0008 | 0.0005 | 29.7854 | 0.9615 | 0.0012 | 0.0005 | 32.1478 |
| R2 | RMSE | MAE | COV | |
|---|---|---|---|---|
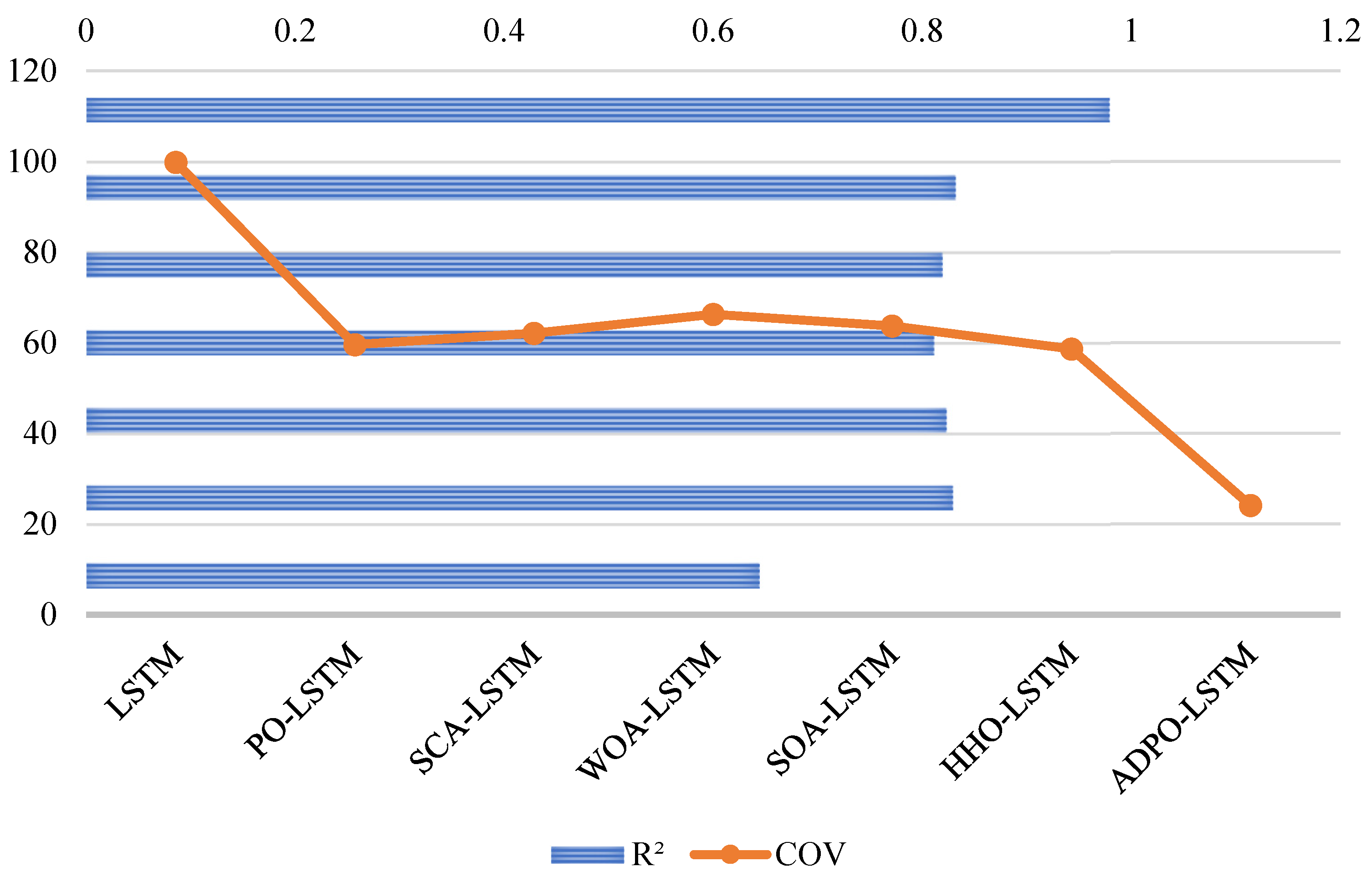
| LSTM | 0.6443 | 0.0026 | 0.0020 | 99.8489 |
| PO-LSTM | 0.8293 | 0.0014 | 0.0012 | 59.6033 |
| SCA-LSTM | 0.8233 | 0.0016 | 0.0013 | 62.0916 |
| WOA-LSTM | 0.8113 | 0.0018 | 0.0015 | 66.2705 |
| SOA-LSTM | 0.8193 | 0.0016 | 0.0014 | 63.7243 |
| HHO-LSTM | 0.8320 | 0.0014 | 0.0011 | 58.6241 |
| ADPO-LSTM | 0.9792 | 0.0003 | 0.0002 | 24.0902 |
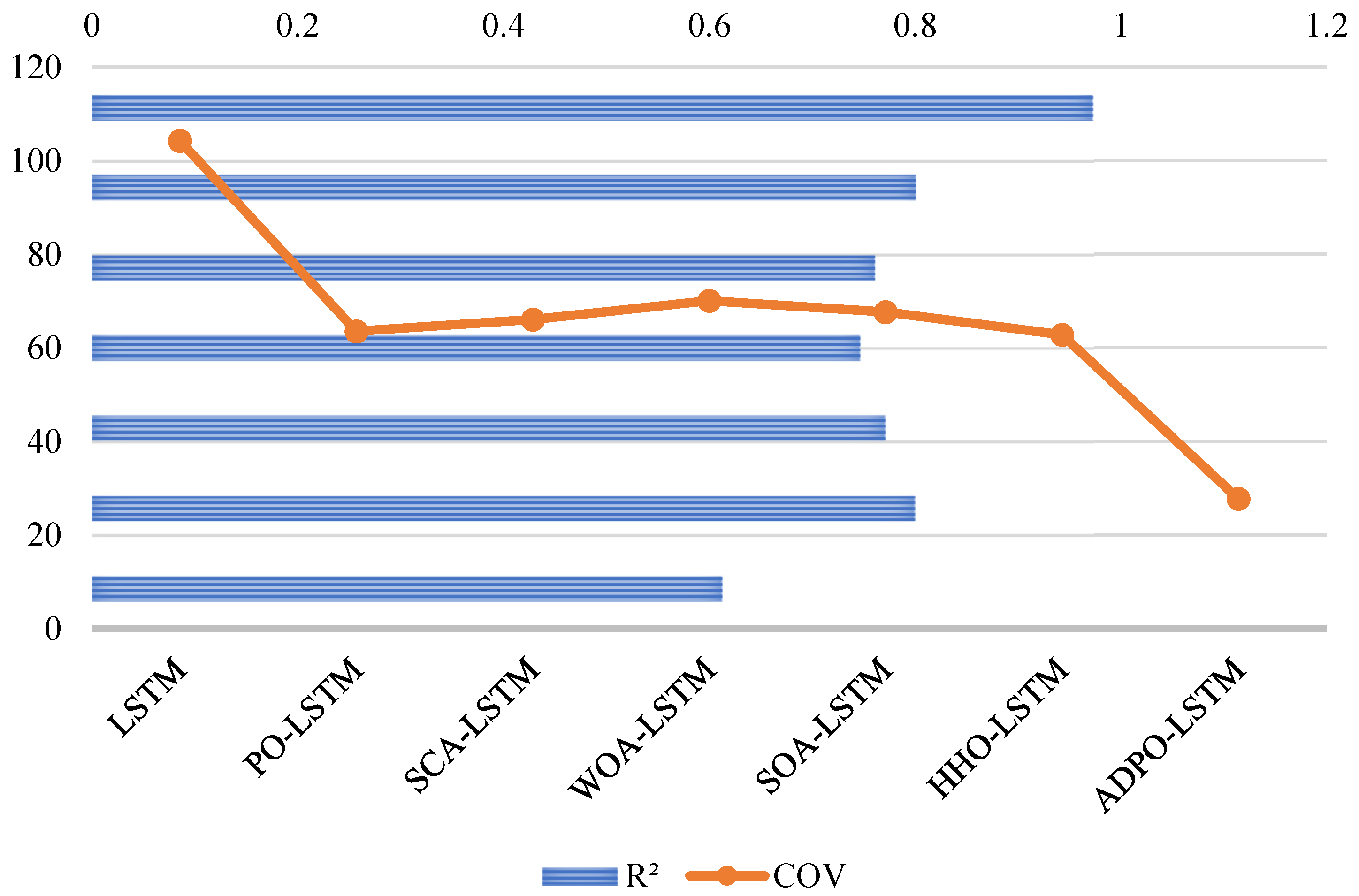
| R2 | RMSE | MAE | COV | |
|---|---|---|---|---|
| LSTM | 0.6125 | 0.0037 | 0.0031 | 104.2516 |
| PO-LSTM | 0.7998 | 0.0022 | 0.0017 | 63.5242 |
| SCA-LSTM | 0.7710 | 0.0023 | 0.0019 | 66.0622 |
| WOA-LSTM | 0.7465 | 0.0026 | 0.0021 | 70.0438 |
| SOA-LSTM | 0.7610 | 0.0024 | 0.0020 | 67.6685 |
| HHO-LSTM | 0.8008 | 0.0021 | 0.0016 | 62.7754 |
| ADPO-LSTM | 0.9726 | 0.0010 | 0.0006 | 27.7271 |
| Station A | Station B | |||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |
| ADPO-LSTM | 0.9785 | 0.0009 | 0.0008 | 0.9798 | 0.0010 | 0.0005 |
| ADPO-Bi-LSTM | 0.8895 | 0.0014 | 0.0013 | 0.8985 | 0.0015 | 0.0013 |
| ADPO-KELM | 0.8625 | 0.0014 | 0.0012 | 0.9125 | 0.0020 | 0.0012 |
| ADPO-ELM | 0.7945 | 0.0021 | 0.0018 | 0.8285 | 0.0019 | 0.0015 |
| ADPO-RF | 0.8075 | 0.0019 | 0.0016 | 0.8495 | 0.0017 | 0.0014 |
| Station C | Station D | |||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |
| ADPO-LSTM | 0.9705 | 0.0008 | 0.0005 | 0.9615 | 0.0012 | 0.0005 |
| ADPO-Bi-LSTM | 0.9205 | 0.0016 | 0.0008 | 0.9185 | 0.0010 | 0.0008 |
| ADPO-KELM | 0.9025 | 0.0021 | 0.0018 | 0.9055 | 0.0011 | 0.0008 |
| ADPO-ELM | 0.8175 | 0.0024 | 0.0020 | 0.8385 | 0.0017 | 0.0014 |
| ADPO-RF | 0.8375 | 0.0022 | 0.0019 | 0.8325 | 0.0016 | 0.0013 |
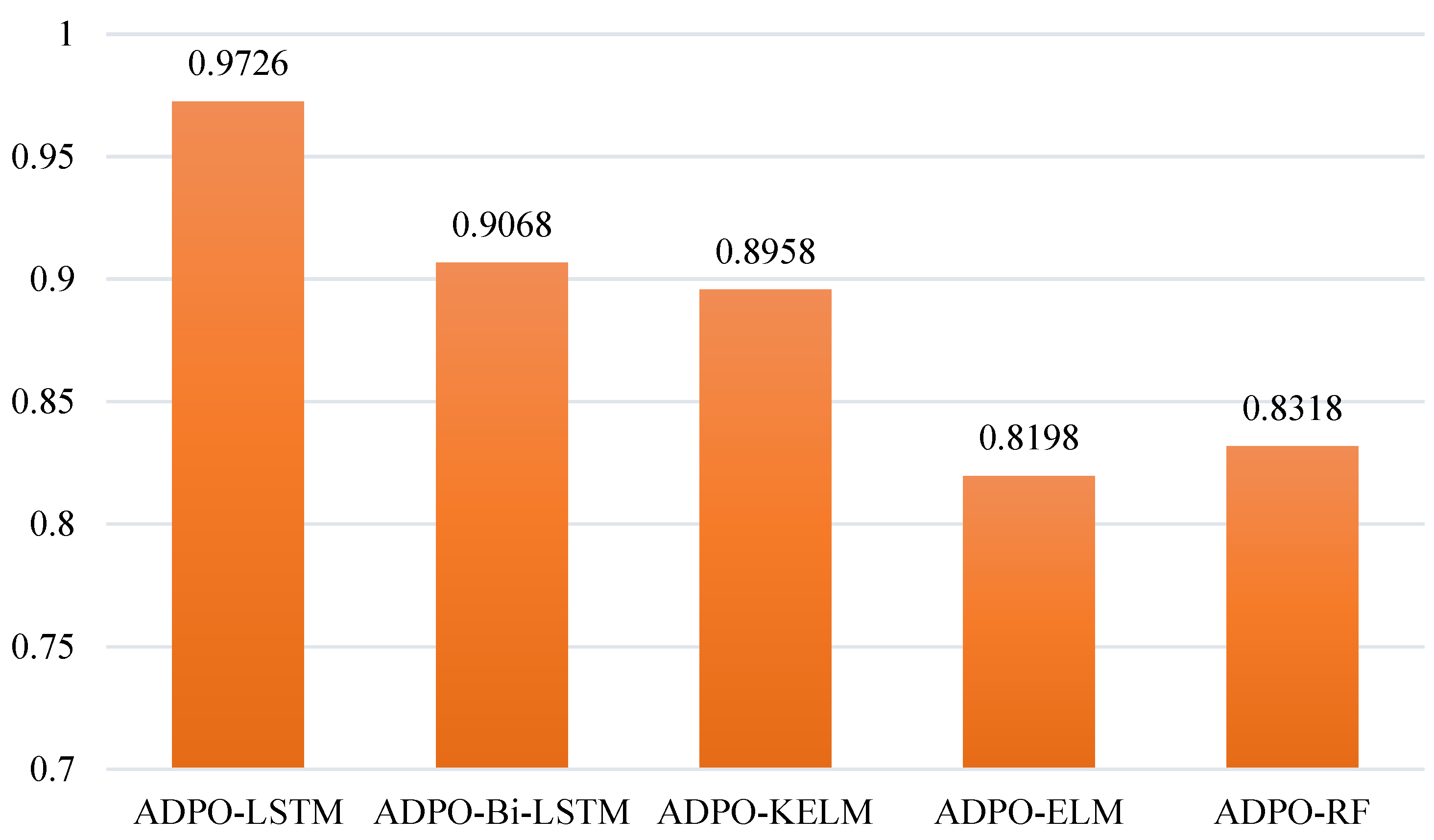
| R2 | RMSE | MAE | |
|---|---|---|---|
| ADPO-LSTM | 0.9726 | 0.0010 | 0.0006 |
| ADPO-Bi-LSTM | 0.9068 | 0.0014 | 0.0011 |
| ADPO-KELM | 0.8958 | 0.0017 | 0.0013 |
| ADPO-ELM | 0.8198 | 0.0020 | 0.0017 |
| ADPO-RF | 0.8318 | 0.0019 | 0.0016 |
| R2 | RMSE | MAE | |
|---|---|---|---|
| LSTM + HBO [67] | 0.9654 | 0.042869 | 0.02998 |
| RVFL + CapSA [68] | 0.9681 | 110.3154 | 64.452775 |
| RVFL + SCA [68] | 0.9562 | 128.4209 | 71.53655 |
| RVFL + GWO [68] | 0.9374 | 154.2171 | 102.3056 |
| ADPO-LSTM (Proposed) | 0.9726 | 0.001010 | 0.00060 |
| Station A | Station B | Station C | Station D | |
|---|---|---|---|---|
| ADPO-LSTM vs. PO-LSTM | 0.0012 | 0.0008 | 0.0015 | 0.0011 |
| ADPO-LSTM vs. SCA-LSTM | 0.0007 | 0.0006 | 0.0009 | 0.0008 |
| ADPO-LSTM vs. WOA-LSTM | 0.0003 | 0.0004 | 0.0005 | 0.0006 |
| ADPO-LSTM vs. SOA-LSTM | 0.0005 | 0.0007 | 0.0008 | 0.0009 |
| ADPO-LSTM vs. HHO-LSTM | 0.0018 | 0.0021 | 0.0019 | 0.0017 |
| ADPO-LSTM vs. LSTM | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, G.; Abdel-salam, M.; Hu, G.; Jia, H. Adaptive Differentiated Parrot Optimization: A Multi-Strategy Enhanced Algorithm for Global Optimization with Wind Power Forecasting Applications. Biomimetics 2025, 10, 542. https://doi.org/10.3390/biomimetics10080542
Lin G, Abdel-salam M, Hu G, Jia H. Adaptive Differentiated Parrot Optimization: A Multi-Strategy Enhanced Algorithm for Global Optimization with Wind Power Forecasting Applications. Biomimetics. 2025; 10(8):542. https://doi.org/10.3390/biomimetics10080542
Chicago/Turabian StyleLin, Guanjun, Mahmoud Abdel-salam, Gang Hu, and Heming Jia. 2025. "Adaptive Differentiated Parrot Optimization: A Multi-Strategy Enhanced Algorithm for Global Optimization with Wind Power Forecasting Applications" Biomimetics 10, no. 8: 542. https://doi.org/10.3390/biomimetics10080542
APA StyleLin, G., Abdel-salam, M., Hu, G., & Jia, H. (2025). Adaptive Differentiated Parrot Optimization: A Multi-Strategy Enhanced Algorithm for Global Optimization with Wind Power Forecasting Applications. Biomimetics, 10(8), 542. https://doi.org/10.3390/biomimetics10080542







