An Enhanced Slime Mould Algorithm Based on Best–Worst Management for Numerical Optimization Problems
Abstract
1. Introduction
- (1)
- The AGM mechanism effectively enhances the exploitation of the SMA and improves its convergence speed while enriching the population diversity.
- (2)
- The BWS enhances the global exploration ability of the algorithm by utilizing the information of the dominant group to guide the population towards high-quality regions, and the introduction of dominant individuals enhances the ability of the SMA to utilize local regions and achieve better convergence to the target solution.
- (3)
- The SRM prevents the population from falling into search stagnation.
- (4)
- The superior performance of the BWSMA is verified by comparing it with eight SMA variants and eight state-of-the-art improved algorithms on the CEC2018 and CEC2022 test sets.
- (5)
- The applicability of the BWSMA is verified in two engineering constrained-optimization problems.
2. Overview of Slime Mould Algorithm
2.1. Population Initialization
2.2. Position Updating
3. Framework of the Proposed BWSMA
3.1. Adaptive Greedy Mechanism
3.2. Best–Worst Management Strategy
3.3. Stagnant Replacement Mechanism
3.4. The Implementation Steps of the BWSMA
| Algorithm 1 Pseudo-code of the BWSMA |
| Begin: |
| //Initialization |
| Initialize z, N, T, lb, ub; |
| Initialize the population by Equation (1) |
| //Main loop |
| While (t < T) do |
| Calculate the fitness of and obtain |
| Calculate the C by Equation (13)//Best–worst management strategy |
| Obtain index by sorting the population according to fitness |
| For i = 1: N do |
| If index(i) < 0.3N then |
| Update the position by Equation (11)//Best–worst management strategy |
| Else if index(i) < 0.7N then |
| Update positions by Equations (3) and (4) |
| Else |
| Update the position by Equation (12)//Best–worst management strategy |
| End if |
| End if |
| End For |
| Select the next population//Adaptive greedy mechanism |
| Calculate the by Equation (10)//Adaptive greedy mechanism |
| For i = 1: N do |
| Update positions by Equation (15)//Stagnant replacement mechanism |
| End for |
| t = t + 1 |
| End While |
| Return: the best fitness and |
4. Experimental Results and Discussion
4.1. Test Functions and Evaluation Metrics
4.2. Comparison with BWSMA-Derived Algorithms
4.3. Comparison with SMA Variant Algorithms
4.4. Comparison with Other Advanced Improved Algorithms
5. Experiments Using Real-World Engineering Problems
5.1. Tension/Compression Spring Design Problem
5.2. Pressure Vessel Design Problem
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Type | ID | Function Names | fmin |
|---|---|---|---|
| Unimodal functions | F1 | Shifted and Rotated Bent Cigar Function | 100 |
| F2 | Shifted and Rotated Zakharov Function | 300 | |
| Multimodal functions | F3 | Shifted and Rotated Rosenbrock Function | 400 |
| F4 | Shifted and Rotated Rastrigin Function | 500 | |
| F5 | Shifted and Rotated Expanded Scaffer Function | 600 | |
| F6 | Shifted and Rotated Lunacek Bi_Rastrigin Function | 700 | |
| F7 | Shifted and Rotated Non-Continuous Rastrigin Function | 800 | |
| F8 | Shifted and Rotated Levy Function | 900 | |
| F9 | Shifted and Rotated Schwefel Function | 1000 | |
| Hybrid functions | F10 | Hybrid Function 1 (N = 3) | 1100 |
| F11 | Hybrid Function 2 (N = 3) | 1200 | |
| F12 | Hybrid Function 3 (N = 3) | 1300 | |
| F13 | Hybrid Function 4 (N = 4) | 1400 | |
| F14 | Hybrid Function 5 (N = 4) | 1500 | |
| F15 | Hybrid Function 6 (N = 4) | 1600 | |
| F16 | Hybrid Function 6 (N = 5) | 1700 | |
| F17 | Hybrid Function 6 (N = 5) | 1800 | |
| F18 | Hybrid Function 6 (N = 5) | 1900 | |
| F19 | Hybrid Function 6 (N = 6) | 2000 | |
| Composition functions | F20 | Composition Function 1 (N = 3) | 2100 |
| F21 | Composition Function 2 (N = 3) | 2200 | |
| F22 | Composition Function 3 (N = 4) | 2300 | |
| F23 | Composition Function 4 (N = 4) | 2400 | |
| F24 | Composition Function 5 (N = 5) | 2500 | |
| F25 | Composition Function 6 (N = 5) | 2600 | |
| F26 | Composition Function 7 (N = 6) | 2700 | |
| F27 | Composition Function 8 (N = 6) | 2800 | |
| F28 | Composition Function 9 (N = 3) | 2900 | |
| F29 | Composition Function 10 (N = 3) | 3000 | |
| Search range: ; dimension: 10/30/50/100 | |||
| Type | ID | Function Names | fmin |
|---|---|---|---|
| Unimodal functions | F1 | Shifted and Fully Rotated Zakharov Function | 300 |
| Basic functions | F2 | Shifted and Fully Rotated Rosenbrock Function | 400 |
| F3 | Shifted and Fully Rotated Expanded Schaffer f6 Function | 600 | |
| F4 | Shifted and Fully Rotated Non-Continuous Rastrigin Function | 800 | |
| F5 | Shifted and Fully Rotated Levy Function | 900 | |
| Hybrid functions | F6 | Hybrid Function 1 (N = 3) | 1800 |
| F7 | Hybrid Function 2 (N = 6) | 2000 | |
| F8 | Hybrid Function 3 (N = 5) | 2200 | |
| Composition functions | F9 | Composition Function 1 (N = 5) | 2300 |
| F10 | Composition Function 2 (N = 4) | 2400 | |
| F11 | Composition Function 3 (N = 5) | 2600 | |
| F12 | Composition Function 4 (N = 6) | 2700 | |
| Search range: ; dimension: 10/20 | |||
| No. | Index | SMA | SMA-AGM | SMA-BWS | SMA-SRM | BWSMA |
|---|---|---|---|---|---|---|
| F1 | Best | 2.9078E+02 | 2.3390E+02 | 1.0245E+02 | 1.2021E+02 | 1.1525E+02 |
| Mean | 7.4836E+03 | 6.3910E+03 | 1.8703E+03 | 6.5469E+03 | 9.2922E+02 | |
| Std | 3.9141E+03 | 4.2793E+03 | 2.2628E+03 | 4.1223E+03 | 7.5662E+02 | |
| Rank | 5 | 3 | 2 | 4 | 1 | |
| F2 | Best | 3.0001E+02 | 3.0000E+02 | 3.0000E+02 | 3.0011E+02 | 3.0000E+02 |
| Mean | 3.0032E+02 | 3.0014E+02 | 3.0000E+02 | 3.0829E+02 | 3.0000E+02 | |
| Std | 1.0550E+00 | 4.8729E−01 | 1.5517E−03 | 2.2793E+01 | 1.6833E−03 | |
| Rank | 4 | 3 | 1 | 5 | 2 | |
| F3 | Best | 4.0003E+02 | 4.0333E+02 | 4.0183E+02 | 4.0161E+02 | 4.0080E+02 |
| Mean | 4.2346E+02 | 4.1423E+02 | 4.0390E+02 | 4.0590E+02 | 4.0420E+02 | |
| Std | 3.2502E+01 | 2.3375E+01 | 9.1994E−01 | 1.3105E+00 | 1.1763E+00 | |
| Rank | 5 | 4 | 1 | 3 | 2 | |
| F4 | Best | 5.0796E+02 | 5.0798E+02 | 5.0199E+02 | 5.0601E+02 | 5.0299E+02 |
| Mean | 5.1866E+02 | 5.1946E+02 | 5.0891E+02 | 5.1451E+02 | 5.0914E+02 | |
| Std | 6.7608E+00 | 6.7990E+00 | 3.7954E+00 | 4.7381E+00 | 3.7821E+00 | |
| Rank | 4 | 5 | 1 | 3 | 2 | |
| F5 | Best | 6.0007E+02 | 6.0006E+02 | 6.0002E+02 | 6.0031E+02 | 6.0000E+02 |
| Mean | 6.0020E+02 | 6.0013E+02 | 6.0007E+02 | 6.0053E+02 | 6.0002E+02 | |
| Std | 9.8348E−02 | 5.2644E−02 | 3.7069E−02 | 1.1395E−01 | 2.4785E−02 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F6 | Best | 7.1335E+02 | 7.1531E+02 | 7.1290E+02 | 7.1495E+02 | 7.1320E+02 |
| Mean | 7.3131E+02 | 7.2762E+02 | 7.2190E+02 | 7.2575E+02 | 7.1869E+02 | |
| Std | 7.0581E+00 | 8.4738E+00 | 5.4214E+00 | 6.9353E+00 | 3.2076E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F7 | Best | 8.0797E+02 | 8.1095E+02 | 8.0398E+02 | 8.0408E+02 | 8.0199E+02 |
| Mean | 8.2081E+02 | 8.1907E+02 | 8.0978E+02 | 8.1294E+02 | 8.0876E+02 | |
| Std | 9.4009E+00 | 6.6306E+00 | 4.8539E+00 | 4.4410E+00 | 3.7990E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F8 | Best | 9.0000E+02 | 9.0000E+02 | 9.0000E+02 | 9.0007E+02 | 9.0000E+02 |
| Mean | 9.0158E+02 | 9.0002E+02 | 9.0000E+02 | 9.0058E+02 | 9.0000E+02 | |
| Std | 8.1711E+00 | 8.3933E−02 | 3.3970E−04 | 8.2944E−01 | 1.6351E−02 | |
| Rank | 5 | 3 | 1 | 4 | 2 | |
| F9 | Best | 1.1536E+03 | 1.1519E+03 | 1.0184E+03 | 1.2391E+03 | 1.0103E+03 |
| Mean | 1.7081E+03 | 1.6321E+03 | 1.5912E+03 | 1.5147E+03 | 1.3616E+03 | |
| Std | 2.6147E+02 | 2.4561E+02 | 2.9097E+02 | 1.6400E+02 | 2.1647E+02 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F10 | Best | 1.1082E+03 | 1.1050E+03 | 1.1012E+03 | 1.1014E+03 | 1.1003E+03 |
| Mean | 1.1856E+03 | 1.1527E+03 | 1.1058E+03 | 1.1162E+03 | 1.1033E+03 | |
| Std | 9.7782E+01 | 8.1399E+01 | 3.3022E+00 | 3.5314E+01 | 1.4183E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F11 | Best | 4.2818E+03 | 6.1369E+03 | 1.4034E+03 | 4.1131E+03 | 1.3188E+03 |
| Mean | 4.2123E+05 | 1.3325E+05 | 2.7181E+03 | 3.1455E+04 | 4.7612E+03 | |
| Std | 4.8182E+05 | 1.7798E+05 | 2.5264E+03 | 2.8147E+04 | 8.4062E+03 | |
| Rank | 5 | 4 | 1 | 3 | 2 | |
| F12 | Best | 1.5841E+03 | 1.4169E+03 | 1.3076E+03 | 1.3290E+03 | 1.3032E+03 |
| Mean | 1.4465E+04 | 1.6476E+04 | 1.3615E+03 | 2.6220E+03 | 1.3120E+03 | |
| Std | 1.3384E+04 | 1.3989E+04 | 5.7105E+01 | 5.6582E+03 | 5.8979E+00 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F13 | Best | 1.4418E+03 | 1.4257E+03 | 1.4011E+03 | 1.4021E+03 | 1.4000E+03 |
| Mean | 2.8325E+03 | 2.1846E+03 | 1.4207E+03 | 1.4262E+03 | 1.4056E+03 | |
| Std | 3.3727E+03 | 1.5898E+03 | 1.0147E+01 | 1.1132E+01 | 8.0927E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F14 | Best | 1.6070E+03 | 1.5256E+03 | 1.5004E+03 | 1.5047E+03 | 1.5002E+03 |
| Mean | 8.8600E+03 | 5.2274E+03 | 1.5105E+03 | 1.5178E+03 | 1.5047E+03 | |
| Std | 8.0006E+03 | 3.5730E+03 | 8.9122E+00 | 1.4698E+01 | 4.8891E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F15 | Best | 1.6019E+03 | 1.6011E+03 | 1.6007E+03 | 1.6006E+03 | 1.6005E+03 |
| Mean | 1.6925E+03 | 1.6652E+03 | 1.6496E+03 | 1.6682E+03 | 1.6129E+03 | |
| Std | 9.0755E+01 | 7.8251E+01 | 6.2346E+01 | 7.9888E+01 | 2.4387E+01 | |
| Rank | 5 | 3 | 2 | 4 | 1 | |
| F16 | Best | 1.7041E+03 | 1.7058E+03 | 1.7013E+03 | 1.7044E+03 | 1.7006E+03 |
| Mean | 1.7650E+03 | 1.7532E+03 | 1.7325E+03 | 1.7385E+03 | 1.7175E+03 | |
| Std | 4.5648E+01 | 3.7474E+01 | 1.8951E+01 | 3.0971E+01 | 1.2925E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F17 | Best | 2.0563E+03 | 2.6257E+03 | 1.8052E+03 | 1.8894E+03 | 1.8004E+03 |
| Mean | 2.7812E+04 | 2.6028E+04 | 1.8495E+03 | 3.0227E+03 | 1.8089E+03 | |
| Std | 1.6829E+04 | 1.6538E+04 | 3.2728E+01 | 3.3024E+03 | 9.1926E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F18 | Best | 1.9841E+03 | 1.9047E+03 | 1.9016E+03 | 1.9046E+03 | 1.9001E+03 |
| Mean | 9.8627E+03 | 1.3235E+04 | 1.9042E+03 | 1.9302E+03 | 1.9014E+03 | |
| Std | 1.1726E+04 | 1.1654E+04 | 1.9151E+00 | 8.1168E+01 | 1.4326E+00 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F19 | Best | 2.0051E+03 | 2.0013E+03 | 2.0052E+03 | 2.0020E+03 | 2.0000E+03 |
| Mean | 2.0412E+03 | 2.0290E+03 | 2.0308E+03 | 2.0216E+03 | 2.0092E+03 | |
| Std | 3.8578E+01 | 2.7652E+01 | 1.7035E+01 | 1.2174E+01 | 1.0646E+01 | |
| Rank | 5 | 3 | 4 | 2 | 1 | |
| F20 | Best | 2.2036E+03 | 2.2035E+03 | 2.2000E+03 | 2.2004E+03 | 2.2000E+03 |
| Mean | 2.3243E+03 | 2.3130E+03 | 2.3025E+03 | 2.3030E+03 | 2.2951E+03 | |
| Std | 3.4698E+01 | 3.7861E+01 | 3.4847E+01 | 3.4904E+01 | 3.7582E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F21 | Best | 2.3003E+03 | 2.3009E+03 | 2.3000E+03 | 2.3006E+03 | 2.3000E+03 |
| Mean | 2.3025E+03 | 2.3025E+03 | 2.3005E+03 | 2.3023E+03 | 2.3001E+03 | |
| Std | 1.0934E+00 | 1.0926E+00 | 5.2637E−01 | 7.6575E−01 | 1.7247E−01 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F22 | Best | 2.6130E+03 | 2.6085E+03 | 2.6057E+03 | 2.6079E+03 | 2.6031E+03 |
| Mean | 2.6250E+03 | 2.6221E+03 | 2.6129E+03 | 2.6156E+03 | 2.6119E+03 | |
| Std | 9.4900E+00 | 1.0863E+01 | 4.7006E+00 | 4.9025E+00 | 5.0350E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F23 | Best | 2.7402E+03 | 2.7380E+03 | 2.7338E+03 | 2.5005E+03 | 2.7317E+03 |
| Mean | 2.7589E+03 | 2.7589E+03 | 2.7419E+03 | 2.7303E+03 | 2.7390E+03 | |
| Std | 1.0265E+01 | 1.1263E+01 | 5.5527E+00 | 6.3099E+01 | 3.9986E+00 | |
| Rank | 4 | 5 | 3 | 1 | 2 | |
| F24 | Best | 2.8978E+03 | 2.8981E+03 | 2.8977E+03 | 2.8988E+03 | 2.8977E+03 |
| Mean | 2.9406E+03 | 2.9416E+03 | 2.9242E+03 | 2.9316E+03 | 2.9273E+03 | |
| Std | 2.9959E+01 | 3.0670E+01 | 2.3225E+01 | 2.1735E+01 | 2.2583E+01 | |
| Rank | 4 | 5 | 1 | 3 | 2 | |
| F25 | Best | 2.9000E+03 | 2.9000E+03 | 2.9000E+03 | 2.8012E+03 | 2.9000E+03 |
| Mean | 3.1154E+03 | 3.1197E+03 | 2.9442E+03 | 2.9292E+03 | 2.9032E+03 | |
| Std | 3.8076E+02 | 3.7496E+02 | 2.1558E+02 | 5.5831E+01 | 1.1957E+01 | |
| Rank | 4 | 5 | 3 | 2 | 1 | |
| F26 | Best | 3.0894E+03 | 3.0890E+03 | 3.0890E+03 | 3.0891E+03 | 3.0890E+03 |
| Mean | 3.0929E+03 | 3.0931E+03 | 3.0913E+03 | 3.0929E+03 | 3.0901E+03 | |
| Std | 2.1748E+00 | 1.1053E+01 | 2.3887E+00 | 1.0979E+01 | 1.6432E+00 | |
| Rank | 3 | 5 | 2 | 4 | 1 | |
| F27 | Best | 3.1683E+03 | 3.1664E+03 | 3.1000E+03 | 3.1006E+03 | 3.1000E+03 |
| Mean | 3.3597E+03 | 3.3624E+03 | 3.2496E+03 | 3.3353E+03 | 3.2457E+03 | |
| Std | 9.0449E+01 | 1.2272E+02 | 1.4723E+02 | 1.4384E+02 | 1.4244E+02 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F28 | Best | 3.1343E+03 | 3.1390E+03 | 3.1340E+03 | 3.1332E+03 | 3.1293E+03 |
| Mean | 3.2208E+03 | 3.2095E+03 | 3.1617E+03 | 3.1590E+03 | 3.1404E+03 | |
| Std | 5.8366E+01 | 6.1415E+01 | 2.2570E+01 | 2.9912E+01 | 1.0094E+01 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F29 | Best | 5.0776E+03 | 5.0063E+03 | 3.4551E+03 | 3.5590E+03 | 3.4600E+03 |
| Mean | 2.6296E+05 | 2.2230E+05 | 3.8716E+05 | 2.5546E+05 | 2.3768E+05 | |
| Std | 5.4917E+05 | 3.9322E+05 | 6.5107E+05 | 4.3565E+05 | 4.4337E+05 | |
| Rank | 4 | 1 | 5 | 3 | 2 |
| No. | Index | SMA | SMA-AGM | SMA-BWS | SMA-SRM | BWSMA |
|---|---|---|---|---|---|---|
| F1 | Best | 6.7439E+04 | 2.2583E+03 | 4.9028E+05 | 8.1515E+06 | 1.0241E+02 |
| Mean | 2.4405E+05 | 1.2736E+04 | 2.6764E+06 | 1.1298E+08 | 3.5430E+03 | |
| Std | 8.1541E+04 | 7.5806E+03 | 2.7402E+06 | 1.7839E+08 | 4.2661E+03 | |
| Rank | 3 | 2 | 4 | 5 | 1 | |
| F2 | Best | 1.0042E+04 | 7.9119E+03 | 7.6985E+03 | 1.5447E+04 | 3.0103E+02 |
| Mean | 3.5881E+04 | 2.5994E+04 | 1.6212E+04 | 2.6238E+04 | 3.5108E+02 | |
| Std | 1.7853E+04 | 1.4161E+04 | 4.9023E+03 | 7.7037E+03 | 6.5321E+01 | |
| Rank | 5 | 3 | 2 | 4 | 1 | |
| F3 | Best | 4.7441E+02 | 4.8884E+02 | 4.7047E+02 | 4.9769E+02 | 4.4193E+02 |
| Mean | 5.1237E+02 | 5.0324E+02 | 5.0524E+02 | 5.4154E+02 | 4.9308E+02 | |
| Std | 2.2657E+01 | 1.4880E+01 | 1.4709E+01 | 3.2096E+01 | 1.6638E+01 | |
| Rank | 4 | 2 | 3 | 5 | 1 | |
| F4 | Best | 5.7881E+02 | 5.6331E+02 | 5.3329E+02 | 5.4712E+02 | 5.2105E+02 |
| Mean | 6.3539E+02 | 6.2221E+02 | 5.5484E+02 | 5.8731E+02 | 5.3446E+02 | |
| Std | 3.3258E+01 | 3.0961E+01 | 1.5583E+01 | 2.4522E+01 | 9.8776E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F5 | Best | 6.0579E+02 | 6.0344E+02 | 6.0233E+02 | 6.0505E+02 | 6.0009E+02 |
| Mean | 6.1431E+02 | 6.0810E+02 | 6.0412E+02 | 6.0824E+02 | 6.0027E+02 | |
| Std | 7.2943E+00 | 3.0892E+00 | 1.2551E+00 | 2.4450E+00 | 7.7242E−02 | |
| Rank | 5 | 3 | 2 | 4 | 1 | |
| F6 | Best | 8.3024E+02 | 7.8920E+02 | 7.7601E+02 | 8.1046E+02 | 7.4556E+02 |
| Mean | 8.8021E+02 | 8.5414E+02 | 8.0362E+02 | 8.5700E+02 | 7.6442E+02 | |
| Std | 3.4858E+01 | 2.7198E+01 | 1.9829E+01 | 2.6410E+01 | 1.0946E+01 | |
| Rank | 5 | 3 | 2 | 4 | 1 | |
| F7 | Best | 8.7241E+02 | 8.7087E+02 | 8.2314E+02 | 8.4859E+02 | 8.1328E+02 |
| Mean | 9.2778E+02 | 9.1591E+02 | 8.5478E+02 | 8.8223E+02 | 8.3911E+02 | |
| Std | 3.2725E+01 | 1.8425E+01 | 2.0200E+01 | 1.7381E+01 | 1.3461E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F8 | Best | 1.9032E+03 | 2.1906E+03 | 9.1052E+02 | 1.2682E+03 | 9.0020E+02 |
| Mean | 4.5906E+03 | 4.6876E+03 | 1.0079E+03 | 1.7800E+03 | 9.0142E+02 | |
| Std | 1.7384E+03 | 1.6363E+03 | 9.6028E+01 | 3.3481E+02 | 1.3383E+00 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F9 | Best | 3.8548E+03 | 2.8270E+03 | 3.3534E+03 | 3.7028E+03 | 3.1575E+03 |
| Mean | 4.8157E+03 | 4.5420E+03 | 4.8611E+03 | 5.2112E+03 | 4.2796E+03 | |
| Std | 6.7942E+02 | 6.5535E+02 | 7.8089E+02 | 7.7753E+02 | 6.4497E+02 | |
| Rank | 3 | 2 | 4 | 5 | 1 | |
| F10 | Best | 1.1741E+03 | 1.1575E+03 | 1.1791E+03 | 1.2160E+03 | 1.1099E+03 |
| Mean | 1.2840E+03 | 1.2960E+03 | 1.2540E+03 | 1.3077E+03 | 1.1536E+03 | |
| Std | 5.4767E+01 | 7.2220E+01 | 3.7576E+01 | 5.4904E+01 | 3.6894E+01 | |
| Rank | 3 | 4 | 2 | 5 | 1 | |
| F11 | Best | 4.0758E+05 | 7.5587E+05 | 2.5154E+05 | 5.7373E+05 | 8.5647E+03 |
| Mean | 5.5961E+06 | 4.5173E+06 | 1.5020E+06 | 6.9770E+06 | 3.0646E+04 | |
| Std | 4.0940E+06 | 2.2622E+06 | 9.5901E+05 | 6.6525E+06 | 2.4784E+04 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F12 | Best | 1.6956E+04 | 7.7280E+03 | 2.5008E+04 | 6.0632E+03 | 1.7429E+03 |
| Mean | 7.0258E+04 | 3.3481E+04 | 8.7179E+04 | 3.4719E+04 | 3.1906E+03 | |
| Std | 4.3349E+04 | 2.5973E+04 | 3.7536E+04 | 2.6800E+04 | 9.1225E+02 | |
| Rank | 4 | 2 | 5 | 3 | 1 | |
| F13 | Best | 1.4183E+04 | 1.0933E+04 | 1.6185E+03 | 1.7703E+03 | 1.4351E+03 |
| Mean | 2.5014E+05 | 2.2363E+05 | 1.8672E+03 | 3.2151E+03 | 1.4590E+03 | |
| Std | 2.4023E+05 | 3.0665E+05 | 1.7197E+02 | 2.3679E+03 | 1.5078E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F14 | Best | 3.0093E+03 | 1.8594E+03 | 1.1059E+04 | 1.7432E+03 | 1.5974E+03 |
| Mean | 2.1864E+04 | 2.1082E+04 | 2.3565E+04 | 1.9586E+04 | 1.7426E+03 | |
| Std | 1.5677E+04 | 1.4954E+04 | 8.3826E+03 | 1.3128E+04 | 1.0656E+02 | |
| Rank | 4 | 3 | 5 | 2 | 1 | |
| F15 | Best | 1.9580E+03 | 2.0555E+03 | 1.7183E+03 | 1.9136E+03 | 1.6057E+03 |
| Mean | 2.6839E+03 | 2.7636E+03 | 2.3378E+03 | 2.4408E+03 | 2.0826E+03 | |
| Std | 3.6369E+02 | 3.4355E+02 | 2.5910E+02 | 3.0942E+02 | 2.6252E+02 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F16 | Best | 1.9746E+03 | 1.8326E+03 | 1.8112E+03 | 1.8375E+03 | 1.7596E+03 |
| Mean | 2.3855E+03 | 2.4637E+03 | 1.9918E+03 | 2.0960E+03 | 1.8777E+03 | |
| Std | 2.5220E+02 | 2.4793E+02 | 1.5646E+02 | 1.6796E+02 | 1.0153E+02 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F17 | Best | 3.2769E+05 | 2.8243E+05 | 1.8212E+04 | 3.6418E+04 | 1.8850E+03 |
| Mean | 3.3322E+06 | 3.7023E+06 | 4.2271E+04 | 1.1091E+05 | 1.9892E+03 | |
| Std | 3.1667E+06 | 4.0584E+06 | 1.5571E+04 | 5.5042E+04 | 6.9781E+01 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F18 | Best | 2.1864E+03 | 1.9710E+03 | 4.0974E+03 | 2.3077E+03 | 1.9250E+03 |
| Mean | 2.5775E+04 | 2.7607E+04 | 1.4770E+04 | 1.8624E+04 | 1.9746E+03 | |
| Std | 2.0354E+04 | 2.1064E+04 | 1.1098E+04 | 1.6668E+04 | 3.3756E+01 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F19 | Best | 2.1610E+03 | 2.1569E+03 | 2.0953E+03 | 2.1121E+03 | 2.0303E+03 |
| Mean | 2.5883E+03 | 2.5468E+03 | 2.3834E+03 | 2.4202E+03 | 2.1999E+03 | |
| Std | 2.1724E+02 | 1.9929E+02 | 2.0607E+02 | 2.0190E+02 | 1.3211E+02 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F20 | Best | 2.3699E+03 | 2.3803E+03 | 2.3295E+03 | 2.3467E+03 | 2.3225E+03 |
| Mean | 2.4379E+03 | 2.4263E+03 | 2.3488E+03 | 2.3858E+03 | 2.3367E+03 | |
| Std | 3.4957E+01 | 3.5131E+01 | 1.5744E+01 | 1.7120E+01 | 1.1600E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F21 | Best | 2.3108E+03 | 2.3032E+03 | 2.3125E+03 | 2.3339E+03 | 2.3003E+03 |
| Mean | 5.8679E+03 | 5.8762E+03 | 4.4677E+03 | 3.4421E+03 | 4.1865E+03 | |
| Std | 1.2259E+03 | 1.2585E+03 | 2.0297E+03 | 1.7667E+03 | 1.6751E+03 | |
| Rank | 4 | 5 | 3 | 1 | 2 | |
| F22 | Best | 2.6957E+03 | 2.7103E+03 | 2.6748E+03 | 2.6895E+03 | 2.6735E+03 |
| Mean | 2.7660E+03 | 2.7685E+03 | 2.7095E+03 | 2.7309E+03 | 2.6919E+03 | |
| Std | 2.9491E+01 | 2.8247E+01 | 1.8177E+01 | 1.9791E+01 | 1.0484E+01 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F23 | Best | 2.8912E+03 | 2.8694E+03 | 2.8479E+03 | 2.8718E+03 | 2.8324E+03 |
| Mean | 2.9398E+03 | 2.9336E+03 | 2.8774E+03 | 2.9033E+03 | 2.8571E+03 | |
| Std | 3.1492E+01 | 3.1571E+01 | 1.7062E+01 | 1.8967E+01 | 1.4884E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F24 | Best | 2.8847E+03 | 2.8879E+03 | 2.8881E+03 | 2.8919E+03 | 2.8870E+03 |
| Mean | 2.8982E+03 | 2.9016E+03 | 2.8999E+03 | 2.9293E+03 | 2.8907E+03 | |
| Std | 1.5124E+01 | 1.6760E+01 | 1.1381E+01 | 2.2353E+01 | 1.0557E+01 | |
| Rank | 2 | 4 | 3 | 5 | 1 | |
| F25 | Best | 2.9036E+03 | 2.9013E+03 | 2.9778E+03 | 4.2425E+03 | 2.9014E+03 |
| Mean | 4.9419E+03 | 4.9095E+03 | 4.1956E+03 | 4.7110E+03 | 3.9298E+03 | |
| Std | 7.0619E+02 | 7.6065E+02 | 4.2475E+02 | 2.2883E+02 | 2.3423E+02 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F26 | Best | 3.1938E+03 | 3.2003E+03 | 3.2034E+03 | 3.1976E+03 | 3.1903E+03 |
| Mean | 3.2339E+03 | 3.2289E+03 | 3.2294E+03 | 3.2333E+03 | 3.2092E+03 | |
| Std | 2.0646E+01 | 1.5779E+01 | 1.4262E+01 | 1.7641E+01 | 1.1246E+01 | |
| Rank | 5 | 2 | 3 | 4 | 1 | |
| F27 | Best | 3.2140E+03 | 3.2174E+03 | 3.2142E+03 | 3.2339E+03 | 3.1515E+03 |
| Mean | 3.2620E+03 | 3.2594E+03 | 3.2581E+03 | 3.3855E+03 | 3.2208E+03 | |
| Std | 3.4961E+01 | 2.7856E+01 | 2.3479E+01 | 3.4102E+02 | 2.4966E+01 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F28 | Best | 3.5903E+03 | 3.4780E+03 | 3.3788E+03 | 3.4418E+03 | 3.3168E+03 |
| Mean | 4.0404E+03 | 3.9055E+03 | 3.7829E+03 | 3.7757E+03 | 3.4787E+03 | |
| Std | 2.5825E+02 | 2.7004E+02 | 2.0724E+02 | 1.8634E+02 | 1.1094E+02 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F29 | Best | 3.6004E+04 | 8.4586E+03 | 1.7874E+04 | 1.2280E+04 | 6.5387E+03 |
| Mean | 1.0546E+05 | 2.8231E+04 | 8.7860E+04 | 1.0773E+05 | 9.2945E+03 | |
| Std | 1.0724E+05 | 1.6547E+04 | 7.2305E+04 | 1.0449E+05 | 1.9576E+03 | |
| Rank | 4 | 2 | 3 | 5 | 1 |
| No. | Index | SMA | SMA-AGM | SMA-BWS | SMA-SRM | BWSMA |
|---|---|---|---|---|---|---|
| F1 | Best | 8.2183E+06 | 2.8479E+05 | 5.9760E+05 | 1.1623E+07 | 2.2080E+04 |
| Mean | 1.2856E+07 | 7.2394E+05 | 4.4184E+06 | 7.7525E+07 | 2.7179E+05 | |
| Std | 4.6592E+06 | 2.9207E+05 | 2.7647E+06 | 8.9826E+07 | 5.6314E+05 | |
| Rank | 4 | 2 | 3 | 5 | 1 | |
| F2 | Best | 1.2020E+05 | 7.0953E+04 | 1.5401E+04 | 2.0020E+04 | 5.1564E+03 |
| Mean | 1.8519E+05 | 1.4168E+05 | 3.1745E+04 | 3.2316E+04 | 1.0326E+04 | |
| Std | 7.5353E+04 | 5.4006E+04 | 9.5936E+03 | 9.1631E+03 | 3.8925E+03 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F3 | Best | 4.6962E+02 | 5.0681E+02 | 5.4087E+02 | 4.8423E+02 | 5.0326E+02 |
| Mean | 6.0014E+02 | 6.1961E+02 | 6.0212E+02 | 6.1931E+02 | 5.5899E+02 | |
| Std | 5.6401E+01 | 5.9190E+01 | 2.9190E+01 | 4.7603E+01 | 4.3939E+01 | |
| Rank | 2 | 5 | 3 | 4 | 1 | |
| F4 | Best | 7.3706E+02 | 7.0206E+02 | 5.4738E+02 | 6.2767E+02 | 5.4801E+02 |
| Mean | 7.8933E+02 | 7.7741E+02 | 5.8949E+02 | 6.6198E+02 | 5.7606E+02 | |
| Std | 3.4825E+01 | 5.0289E+01 | 2.6423E+01 | 2.2716E+01 | 1.7387E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F5 | Best | 6.2216E+02 | 6.1673E+02 | 6.0303E+02 | 6.0772E+02 | 6.0112E+02 |
| Mean | 6.4172E+02 | 6.3936E+02 | 6.0518E+02 | 6.1033E+02 | 6.0182E+02 | |
| Std | 1.5086E+01 | 1.3841E+01 | 1.4292E+00 | 2.3668E+00 | 5.9044E−01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F6 | Best | 9.7074E+02 | 9.6898E+02 | 8.1512E+02 | 8.9816E+02 | 7.9464E+02 |
| Mean | 1.0838E+03 | 1.0650E+03 | 8.5568E+02 | 9.6941E+02 | 8.3589E+02 | |
| Std | 6.2668E+01 | 4.9898E+01 | 2.0298E+01 | 4.7288E+01 | 1.8005E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F7 | Best | 1.0177E+03 | 9.8811E+02 | 8.7311E+02 | 9.0091E+02 | 8.5654E+02 |
| Mean | 1.1196E+03 | 1.0552E+03 | 8.9317E+02 | 9.5757E+02 | 8.8566E+02 | |
| Std | 6.1274E+01 | 4.2631E+01 | 1.3360E+01 | 3.5032E+01 | 1.7938E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F8 | Best | 9.6214E+03 | 8.5137E+03 | 9.4608E+02 | 1.2156E+03 | 9.1860E+02 |
| Mean | 1.7114E+04 | 1.5143E+04 | 1.1975E+03 | 2.4407E+03 | 1.0031E+03 | |
| Std | 4.5611E+03 | 3.5521E+03 | 1.9382E+02 | 6.4226E+02 | 7.9316E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F9 | Best | 5.5925E+03 | 6.0820E+03 | 5.5637E+03 | 7.5996E+03 | 5.4488E+03 |
| Mean | 8.0296E+03 | 7.3215E+03 | 7.9025E+03 | 9.0716E+03 | 6.7879E+03 | |
| Std | 1.2121E+03 | 6.9510E+02 | 1.1477E+03 | 9.9591E+02 | 9.5459E+02 | |
| Rank | 4 | 2 | 3 | 5 | 1 | |
| F10 | Best | 1.3516E+03 | 1.3371E+03 | 1.2537E+03 | 1.3450E+03 | 1.1790E+03 |
| Mean | 1.4461E+03 | 1.4262E+03 | 1.3369E+03 | 1.4497E+03 | 1.2767E+03 | |
| Std | 4.8539E+01 | 8.2728E+01 | 4.5767E+01 | 4.5519E+01 | 5.1713E+01 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F11 | Best | 8.2005E+06 | 7.6849E+06 | 2.6098E+06 | 3.1245E+06 | 1.7229E+05 |
| Mean | 3.7223E+07 | 3.1027E+07 | 5.6827E+06 | 2.6682E+07 | 1.4553E+06 | |
| Std | 2.6893E+07 | 1.7743E+07 | 2.8291E+06 | 2.6057E+07 | 1.6432E+06 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F12 | Best | 4.6341E+04 | 2.2802E+04 | 1.8597E+04 | 4.7165E+03 | 9.5964E+03 |
| Mean | 1.5881E+05 | 5.9807E+04 | 5.3175E+04 | 2.5774E+04 | 2.0906E+04 | |
| Std | 9.3827E+04 | 2.2093E+04 | 2.6815E+04 | 1.5847E+04 | 5.8453E+03 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F13 | Best | 1.5568E+05 | 1.3038E+05 | 2.0134E+03 | 1.8294E+03 | 1.5925E+03 |
| Mean | 1.0541E+06 | 6.6633E+05 | 2.2200E+03 | 2.7247E+03 | 1.6316E+03 | |
| Std | 7.8127E+05 | 4.3652E+05 | 1.6232E+02 | 5.3196E+02 | 4.5953E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F14 | Best | 7.9972E+03 | 5.8670E+03 | 1.0982E+04 | 1.8788E+03 | 2.3777E+03 |
| Mean | 4.0842E+04 | 2.2011E+04 | 2.2232E+04 | 2.1569E+04 | 3.0764E+03 | |
| Std | 2.6657E+04 | 1.0955E+04 | 8.8148E+03 | 1.3590E+04 | 4.9527E+02 | |
| Rank | 5 | 3 | 4 | 2 | 1 | |
| F15 | Best | 2.9519E+03 | 3.0565E+03 | 2.3151E+03 | 2.5691E+03 | 2.1960E+03 |
| Mean | 3.7503E+03 | 3.6921E+03 | 2.9145E+03 | 2.9431E+03 | 2.8367E+03 | |
| Std | 4.2168E+02 | 4.7714E+02 | 3.1752E+02 | 2.2359E+02 | 3.6862E+02 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F16 | Best | 2.8413E+03 | 2.9096E+03 | 2.1692E+03 | 2.2362E+03 | 2.3598E+03 |
| Mean | 3.3775E+03 | 3.3524E+03 | 2.6178E+03 | 2.8262E+03 | 2.6411E+03 | |
| Std | 3.3740E+02 | 3.1984E+02 | 2.9819E+02 | 2.1980E+02 | 1.6929E+02 | |
| Rank | 5 | 4 | 1 | 3 | 2 | |
| F17 | Best | 3.5370E+05 | 1.4022E+06 | 1.9531E+04 | 4.1169E+04 | 2.5336E+03 |
| Mean | 8.5300E+06 | 6.1442E+06 | 3.8483E+04 | 7.9007E+04 | 4.7529E+03 | |
| Std | 7.0700E+06 | 3.8511E+06 | 1.2048E+04 | 2.1625E+04 | 2.4743E+03 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F18 | Best | 5.1009E+03 | 2.6364E+03 | 2.9996E+03 | 2.2017E+03 | 2.0305E+03 |
| Mean | 1.9546E+04 | 1.1189E+04 | 1.2251E+04 | 1.1914E+04 | 2.3563E+03 | |
| Std | 1.6310E+04 | 1.2189E+04 | 9.5490E+03 | 1.1647E+04 | 5.1207E+02 | |
| Rank | 5 | 2 | 4 | 3 | 1 | |
| F19 | Best | 2.6298E+03 | 2.6451E+03 | 2.1832E+03 | 2.5961E+03 | 2.2358E+03 |
| Mean | 3.2557E+03 | 3.3260E+03 | 2.8912E+03 | 3.0051E+03 | 2.6872E+03 | |
| Std | 3.7625E+02 | 3.0929E+02 | 3.3499E+02 | 2.5498E+02 | 3.3124E+02 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F20 | Best | 2.4890E+03 | 2.5074E+03 | 2.3384E+03 | 2.4002E+03 | 2.3525E+03 |
| Mean | 2.5799E+03 | 2.5613E+03 | 2.3761E+03 | 2.4459E+03 | 2.3787E+03 | |
| Std | 5.5410E+01 | 5.9196E+01 | 2.0881E+01 | 2.1252E+01 | 1.8977E+01 | |
| Rank | 5 | 4 | 1 | 3 | 2 | |
| F21 | Best | 7.1981E+03 | 7.3031E+03 | 7.1930E+03 | 8.7972E+03 | 6.6908E+03 |
| Mean | 9.2642E+03 | 8.9452E+03 | 9.1413E+03 | 1.0288E+04 | 8.3897E+03 | |
| Std | 9.5940E+02 | 1.1444E+03 | 1.1486E+03 | 6.8626E+02 | 1.1551E+03 | |
| Rank | 4 | 2 | 3 | 5 | 1 | |
| F22 | Best | 2.9641E+03 | 2.9102E+03 | 2.7806E+03 | 2.8353E+03 | 2.7757E+03 |
| Mean | 3.0372E+03 | 3.0222E+03 | 2.8229E+03 | 2.8882E+03 | 2.8072E+03 | |
| Std | 5.8050E+01 | 7.1554E+01 | 2.5725E+01 | 3.3025E+01 | 1.7922E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F23 | Best | 3.0653E+03 | 3.0887E+03 | 2.9609E+03 | 2.9849E+03 | 2.9318E+03 |
| Mean | 3.1665E+03 | 3.1582E+03 | 2.9776E+03 | 3.0289E+03 | 2.9672E+03 | |
| Std | 5.6220E+01 | 8.2456E+01 | 1.7550E+01 | 2.2846E+01 | 2.0565E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F24 | Best | 3.0647E+03 | 3.0100E+03 | 3.0291E+03 | 3.0625E+03 | 2.9855E+03 |
| Mean | 3.1140E+03 | 3.0660E+03 | 3.0507E+03 | 3.1225E+03 | 3.0392E+03 | |
| Std | 3.2669E+01 | 3.5213E+01 | 1.8340E+01 | 5.2224E+01 | 2.4640E+01 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F25 | Best | 2.9544E+03 | 3.2925E+03 | 4.0930E+03 | 4.6883E+03 | 4.2395E+03 |
| Mean | 5.7661E+03 | 6.2563E+03 | 4.5688E+03 | 5.2760E+03 | 4.5684E+03 | |
| Std | 2.3239E+03 | 1.2044E+03 | 2.2997E+02 | 3.5387E+02 | 2.6927E+02 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F26 | Best | 3.3376E+03 | 3.3883E+03 | 3.2843E+03 | 3.3181E+03 | 3.2423E+03 |
| Mean | 3.5268E+03 | 3.4819E+03 | 3.3522E+03 | 3.4269E+03 | 3.3114E+03 | |
| Std | 1.1761E+02 | 7.2070E+01 | 5.6175E+01 | 6.7091E+01 | 6.3983E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F27 | Best | 3.3225E+03 | 3.3053E+03 | 3.2628E+03 | 3.3349E+03 | 3.2625E+03 |
| Mean | 3.3769E+03 | 3.3716E+03 | 3.3194E+03 | 3.5799E+03 | 3.2966E+03 | |
| Std | 4.6650E+01 | 5.3085E+01 | 3.6726E+01 | 2.5394E+02 | 2.4399E+01 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F28 | Best | 4.5063E+03 | 4.0633E+03 | 3.4389E+03 | 3.5108E+03 | 3.6198E+03 |
| Mean | 5.0444E+03 | 4.8017E+03 | 4.1870E+03 | 4.1645E+03 | 3.9003E+03 | |
| Std | 3.0683E+02 | 4.0681E+02 | 3.2938E+02 | 2.8621E+02 | 1.8966E+02 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F29 | Best | 5.2654E+06 | 1.4821E+06 | 2.1609E+06 | 1.1233E+06 | 1.5738E+06 |
| Mean | 9.3141E+06 | 3.2614E+06 | 3.7768E+06 | 4.0330E+06 | 2.2526E+06 | |
| Std | 3.0736E+06 | 1.2900E+06 | 1.3681E+06 | 2.7910E+06 | 4.1165E+05 | |
| Rank | 5 | 2 | 3 | 4 | 1 |
| No. | Index | SMA | SMA-AGM | SMA-BWS | SMA-SRM | BWSMA |
|---|---|---|---|---|---|---|
| F1 | Best | 2.9335E+08 | 6.1175E+07 | 3.3174E+08 | 2.7694E+09 | 7.0450E+07 |
| Mean | 6.1449E+08 | 1.0262E+08 | 7.4634E+08 | 6.7584E+09 | 1.9438E+08 | |
| Std | 1.4285E+08 | 3.3841E+07 | 2.7285E+08 | 3.3645E+09 | 5.6174E+07 | |
| Rank | 3 | 1 | 4 | 5 | 2 | |
| F2 | Best | 3.6324E+05 | 2.9355E+05 | 2.6784E+05 | 1.7191E+05 | 1.3985E+05 |
| Mean | 9.3939E+05 | 6.9383E+05 | 3.0176E+05 | 2.2057E+05 | 1.5957E+05 | |
| Std | 2.4631E+05 | 3.3450E+05 | 2.6071E+04 | 2.5909E+04 | 1.8424E+04 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F3 | Best | 9.2617E+02 | 7.5527E+02 | 8.4046E+02 | 1.0052E+03 | 7.6371E+02 |
| Mean | 1.0117E+03 | 8.7867E+02 | 9.7985E+02 | 1.2733E+03 | 8.5964E+02 | |
| Std | 5.9868E+01 | 5.7837E+01 | 7.6284E+01 | 1.5521E+02 | 5.7241E+01 | |
| Rank | 4 | 2 | 3 | 5 | 1 | |
| F4 | Best | 1.2153E+03 | 1.1507E+03 | 7.7038E+02 | 9.4583E+02 | 7.2204E+02 |
| Mean | 1.3500E+03 | 1.2694E+03 | 8.7054E+02 | 1.0297E+03 | 8.0471E+02 | |
| Std | 1.0779E+02 | 6.9625E+01 | 5.1830E+01 | 5.0712E+01 | 3.7713E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F5 | Best | 6.4928E+02 | 6.4046E+02 | 6.2356E+02 | 6.2225E+02 | 6.1293E+02 |
| Mean | 6.6278E+02 | 6.5564E+02 | 6.2800E+02 | 6.3251E+02 | 6.1802E+02 | |
| Std | 6.4471E+00 | 7.6191E+00 | 2.5103E+00 | 5.0945E+00 | 3.4028E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F6 | Best | 1.9039E+03 | 1.8034E+03 | 1.3258E+03 | 1.5294E+03 | 1.2112E+03 |
| Mean | 2.1697E+03 | 2.0658E+03 | 1.5129E+03 | 1.7287E+03 | 1.3253E+03 | |
| Std | 1.8561E+02 | 1.9328E+02 | 8.0094E+01 | 1.0803E+02 | 6.2628E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F7 | Best | 1.5448E+03 | 1.4227E+03 | 1.1313E+03 | 1.2214E+03 | 1.0353E+03 |
| Mean | 1.6851E+03 | 1.5787E+03 | 1.1874E+03 | 1.3127E+03 | 1.0991E+03 | |
| Std | 8.2218E+01 | 9.9907E+01 | 4.0329E+01 | 6.8417E+01 | 3.7806E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F8 | Best | 3.3315E+04 | 2.7073E+04 | 5.9457E+03 | 9.0112E+03 | 3.8381E+03 |
| Mean | 3.9850E+04 | 3.4222E+04 | 8.2614E+03 | 2.2512E+04 | 6.0605E+03 | |
| Std | 4.0371E+03 | 4.9529E+03 | 1.3150E+03 | 7.7692E+03 | 2.0907E+03 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F9 | Best | 1.5562E+04 | 1.3387E+04 | 1.5699E+04 | 1.6224E+04 | 1.5098E+04 |
| Mean | 1.8444E+04 | 1.6680E+04 | 1.8014E+04 | 2.0501E+04 | 1.6738E+04 | |
| Std | 1.4215E+03 | 1.9066E+03 | 1.8078E+03 | 2.6631E+03 | 1.3312E+03 | |
| Rank | 4 | 1 | 3 | 5 | 2 | |
| F10 | Best | 1.3188E+04 | 1.6800E+04 | 1.0084E+04 | 3.8439E+03 | 3.2800E+03 |
| Mean | 3.5506E+04 | 3.1681E+04 | 1.5490E+04 | 6.4362E+03 | 4.4914E+03 | |
| Std | 1.5518E+04 | 1.4828E+04 | 2.2524E+03 | 2.1344E+03 | 8.8862E+02 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F11 | Best | 1.6072E+08 | 7.3803E+07 | 9.0859E+07 | 2.1048E+08 | 4.1783E+07 |
| Mean | 3.9468E+08 | 2.1963E+08 | 1.9447E+08 | 6.7318E+08 | 9.9655E+07 | |
| Std | 1.5571E+08 | 1.0086E+08 | 7.0554E+07 | 3.7604E+08 | 4.1968E+07 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F12 | Best | 1.3116E+05 | 4.5573E+04 | 6.5328E+04 | 2.5624E+04 | 4.3968E+04 |
| Mean | 3.1379E+06 | 5.3748E+05 | 1.4098E+05 | 6.7967E+04 | 6.2741E+04 | |
| Std | 1.0416E+07 | 1.1832E+06 | 5.8255E+04 | 6.1766E+04 | 1.0634E+04 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F13 | Best | 2.3864E+06 | 1.6864E+06 | 1.3525E+05 | 6.0192E+04 | 6.6748E+03 |
| Mean | 5.0827E+06 | 5.3299E+06 | 3.2445E+05 | 3.3047E+05 | 2.6564E+04 | |
| Std | 2.8888E+06 | 4.1994E+06 | 1.0532E+05 | 1.7111E+05 | 2.4931E+04 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F14 | Best | 6.0233E+04 | 3.5023E+04 | 5.0827E+04 | 4.9362E+03 | 1.0864E+04 |
| Mean | 7.9729E+05 | 3.9549E+05 | 9.0593E+04 | 8.0804E+04 | 2.4456E+04 | |
| Std | 2.0219E+06 | 6.3747E+05 | 3.0032E+04 | 2.4914E+05 | 9.9346E+03 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F15 | Best | 4.9391E+03 | 5.0057E+03 | 4.4450E+03 | 4.1776E+03 | 4.5656E+03 |
| Mean | 6.6359E+03 | 5.9270E+03 | 5.6523E+03 | 5.9308E+03 | 5.4122E+03 | |
| Std | 8.6079E+02 | 5.4788E+02 | 5.1037E+02 | 8.4544E+02 | 5.0119E+02 | |
| Rank | 5 | 3 | 2 | 4 | 1 | |
| F16 | Best | 4.3427E+03 | 4.7909E+03 | 4.2258E+03 | 3.7957E+03 | 3.4256E+03 |
| Mean | 5.6436E+03 | 5.7837E+03 | 4.8933E+03 | 4.6775E+03 | 4.4578E+03 | |
| Std | 6.3468E+02 | 6.0216E+02 | 4.0687E+02 | 4.1494E+02 | 5.1992E+02 | |
| Rank | 4 | 5 | 3 | 2 | 1 | |
| F17 | Best | 4.8225E+06 | 3.2832E+06 | 3.2128E+05 | 3.1771E+05 | 3.9945E+04 |
| Mean | 1.0047E+07 | 1.2209E+07 | 5.3833E+05 | 7.5870E+05 | 8.4975E+04 | |
| Std | 5.1570E+06 | 4.2439E+06 | 1.4655E+05 | 3.5742E+05 | 2.2609E+04 | |
| Rank | 4 | 5 | 2 | 3 | 1 | |
| F18 | Best | 1.4745E+05 | 1.8794E+04 | 2.7676E+04 | 4.5420E+03 | 6.1620E+03 |
| Mean | 5.1427E+05 | 5.7059E+04 | 1.5172E+05 | 4.5762E+04 | 5.1381E+04 | |
| Std | 3.4018E+05 | 6.9333E+04 | 8.4132E+04 | 8.6485E+04 | 6.8858E+04 | |
| Rank | 5 | 3 | 4 | 1 | 2 | |
| F19 | Best | 4.7325E+03 | 4.7012E+03 | 4.0084E+03 | 3.5119E+03 | 4.0953E+03 |
| Mean | 5.6316E+03 | 5.6474E+03 | 5.0096E+03 | 4.7446E+03 | 4.7803E+03 | |
| Std | 6.0655E+02 | 4.3625E+02 | 5.7107E+02 | 5.9582E+02 | 4.4110E+02 | |
| Rank | 4 | 5 | 3 | 1 | 2 | |
| F20 | Best | 3.0111E+03 | 3.0150E+03 | 2.6000E+03 | 2.7235E+03 | 2.5563E+03 |
| Mean | 3.1982E+03 | 3.1252E+03 | 2.7139E+03 | 2.8302E+03 | 2.6131E+03 | |
| Std | 1.3199E+02 | 9.1378E+01 | 5.6976E+01 | 4.9585E+01 | 4.5271E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F21 | Best | 1.8213E+04 | 1.6996E+04 | 1.7409E+04 | 1.8614E+04 | 1.7145E+04 |
| Mean | 2.1446E+04 | 1.9405E+04 | 2.0236E+04 | 2.2924E+04 | 1.9601E+04 | |
| Std | 1.6005E+03 | 1.1228E+03 | 1.9280E+03 | 2.6962E+03 | 1.4572E+03 | |
| Rank | 4 | 1 | 3 | 5 | 2 | |
| F22 | Best | 3.4530E+03 | 3.2757E+03 | 3.1496E+03 | 3.1483E+03 | 3.0796E+03 |
| Mean | 3.5663E+03 | 3.4255E+03 | 3.2539E+03 | 3.2321E+03 | 3.1696E+03 | |
| Std | 7.4896E+01 | 7.9695E+01 | 6.3334E+01 | 5.6727E+01 | 4.1180E+01 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F23 | Best | 4.0054E+03 | 3.8992E+03 | 3.6334E+03 | 3.6694E+03 | 3.5192E+03 |
| Mean | 4.2415E+03 | 4.0220E+03 | 3.7328E+03 | 3.7755E+03 | 3.6361E+03 | |
| Std | 1.5605E+02 | 8.1787E+01 | 5.0837E+01 | 6.4949E+01 | 4.7330E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F24 | Best | 3.5860E+03 | 3.4276E+03 | 3.6184E+03 | 3.8896E+03 | 3.4140E+03 |
| Mean | 3.6867E+03 | 3.5996E+03 | 3.7191E+03 | 4.1964E+03 | 3.5716E+03 | |
| Std | 8.0200E+01 | 9.1593E+01 | 7.2304E+01 | 2.7611E+02 | 7.2742E+01 | |
| Rank | 3 | 2 | 4 | 5 | 1 | |
| F25 | Best | 5.4651E+03 | 1.1827E+04 | 9.2849E+03 | 9.8766E+03 | 8.8280E+03 |
| Mean | 1.4782E+04 | 1.3894E+04 | 1.0594E+04 | 1.1010E+04 | 9.4549E+03 | |
| Std | 2.9616E+03 | 1.2148E+03 | 5.9529E+02 | 6.7521E+02 | 4.7181E+02 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F26 | Best | 3.5984E+03 | 3.4979E+03 | 3.5013E+03 | 3.4836E+03 | 3.4289E+03 |
| Mean | 3.7580E+03 | 3.6221E+03 | 3.6150E+03 | 3.5923E+03 | 3.5420E+03 | |
| Std | 8.4152E+01 | 6.8361E+01 | 7.9835E+01 | 8.0731E+01 | 5.5613E+01 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F27 | Best | 3.6185E+03 | 3.5844E+03 | 3.6672E+03 | 4.0497E+03 | 3.5928E+03 |
| Mean | 3.7325E+03 | 3.6287E+03 | 3.8290E+03 | 4.6433E+03 | 3.6984E+03 | |
| Std | 7.4455E+01 | 3.6295E+01 | 1.5112E+02 | 5.0183E+02 | 7.5370E+01 | |
| Rank | 3 | 1 | 4 | 5 | 2 | |
| F28 | Best | 6.9713E+03 | 6.2396E+03 | 6.4695E+03 | 5.8348E+03 | 5.5167E+03 |
| Mean | 8.1562E+03 | 7.4903E+03 | 7.3101E+03 | 6.8188E+03 | 6.6386E+03 | |
| Std | 6.8176E+02 | 8.2938E+02 | 6.8984E+02 | 4.4825E+02 | 6.6864E+02 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F29 | Best | 2.9704E+06 | 6.6771E+05 | 2.2302E+06 | 1.3346E+06 | 3.3834E+05 |
| Mean | 1.1563E+07 | 2.5856E+06 | 5.4763E+06 | 6.7743E+06 | 1.1179E+06 | |
| Std | 5.1551E+06 | 1.3197E+06 | 2.9529E+06 | 4.7646E+06 | 7.1226E+05 | |
| Rank | 5 | 2 | 3 | 4 | 1 |
| No. | Index | SMA | SMA-AGM | SMA-BWS | SMA-SRM | BWSMA |
|---|---|---|---|---|---|---|
| F1 | Best | 3.0000E+02 | 3.0000E+02 | 3.0000E+02 | 3.0006E+02 | 3.0000E+02 |
| Mean | 3.0006E+02 | 3.0001E+02 | 3.0000E+02 | 3.0136E+02 | 3.0000E+02 | |
| Std | 6.7015E−02 | 1.7061E−02 | 5.3818E−04 | 1.3789E+00 | 1.3704E−03 | |
| Rank | 4 | 3 | 1 | 5 | 2 | |
| F2 | Best | 4.0026E+02 | 4.0628E+02 | 4.0001E+02 | 4.0028E+02 | 4.0002E+02 |
| Mean | 4.1030E+02 | 4.1272E+02 | 4.0721E+02 | 4.0716E+02 | 4.0649E+02 | |
| Std | 1.5297E+01 | 1.7776E+01 | 2.6036E+00 | 2.0174E+00 | 2.8829E+00 | |
| Rank | 4 | 5 | 3 | 2 | 1 | |
| F3 | Best | 6.0009E+02 | 6.0008E+02 | 6.0003E+02 | 6.0024E+02 | 6.0000E+02 |
| Mean | 6.0032E+02 | 6.0016E+02 | 6.0009E+02 | 6.0050E+02 | 6.0002E+02 | |
| Std | 4.0248E−01 | 5.2959E−02 | 2.5504E−02 | 1.1786E−01 | 1.9725E−02 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F4 | Best | 8.1294E+02 | 8.1194E+02 | 8.0199E+02 | 8.0506E+02 | 8.0298E+02 |
| Mean | 8.3131E+02 | 8.2963E+02 | 8.0945E+02 | 8.1519E+02 | 8.0813E+02 | |
| Std | 1.3203E+01 | 1.0735E+01 | 5.1254E+00 | 6.8395E+00 | 3.4574E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F5 | Best | 9.0001E+02 | 9.0000E+02 | 9.0000E+02 | 9.0008E+02 | 9.0000E+02 |
| Mean | 9.4552E+02 | 9.1954E+02 | 9.0003E+02 | 9.0104E+02 | 9.0001E+02 | |
| Std | 1.2699E+02 | 5.5046E+01 | 1.1542E−01 | 1.6423E+00 | 2.2714E−02 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F6 | Best | 1.8662E+03 | 1.9092E+03 | 1.8058E+03 | 1.8814E+03 | 1.8002E+03 |
| Mean | 4.6717E+03 | 4.6491E+03 | 1.8529E+03 | 3.4391E+03 | 1.8130E+03 | |
| Std | 1.9392E+03 | 2.0367E+03 | 3.1883E+01 | 2.0096E+03 | 1.1076E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F7 | Best | 2.0011E+03 | 2.0020E+03 | 2.0017E+03 | 2.0073E+03 | 2.0000E+03 |
| Mean | 2.0197E+03 | 2.0198E+03 | 2.0224E+03 | 2.0215E+03 | 2.0163E+03 | |
| Std | 5.7652E+00 | 4.7928E+00 | 9.0545E+00 | 3.5909E+00 | 8.6227E+00 | |
| Rank | 2 | 3 | 5 | 4 | 1 | |
| F8 | Best | 2.2203E+03 | 2.2201E+03 | 2.2015E+03 | 2.2017E+03 | 2.2002E+03 |
| Mean | 2.2213E+03 | 2.2213E+03 | 2.2204E+03 | 2.2193E+03 | 2.2138E+03 | |
| Std | 8.2023E−01 | 9.3656E−01 | 5.6025E+00 | 7.1824E+00 | 9.4827E+00 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F9 | Best | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 |
| Mean | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 | |
| Std | 1.7370E−03 | 7.2037E−04 | 5.6549E−04 | 1.3252E−02 | 1.1269E−04 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F10 | Best | 2.5002E+03 | 2.5003E+03 | 2.5002E+03 | 2.5004E+03 | 2.5002E+03 |
| Mean | 2.5228E+03 | 2.5495E+03 | 2.5225E+03 | 2.5270E+03 | 2.5225E+03 | |
| Std | 5.1515E+01 | 6.1680E+01 | 4.5112E+01 | 4.8908E+01 | 4.5283E+01 | |
| Rank | 3 | 5 | 2 | 4 | 1 | |
| F11 | Best | 2.6001E+03 | 2.6000E+03 | 2.6000E+03 | 2.6006E+03 | 2.6000E+03 |
| Mean | 2.7716E+03 | 2.7302E+03 | 2.7101E+03 | 2.6985E+03 | 2.7400E+03 | |
| Std | 1.8946E+02 | 1.4058E+02 | 1.3610E+02 | 1.6760E+02 | 1.5222E+02 | |
| Rank | 5 | 3 | 2 | 1 | 4 | |
| F12 | Best | 2.8597E+03 | 2.8596E+03 | 2.8594E+03 | 2.8614E+03 | 2.8594E+03 |
| Mean | 2.8633E+03 | 2.8628E+03 | 2.8634E+03 | 2.8624E+03 | 2.8631E+03 | |
| Std | 1.3500E+00 | 1.2611E+00 | 1.6675E+00 | 1.0167E+00 | 1.5168E+00 | |
| Rank | 4 | 2 | 5 | 1 | 3 |
| No. | Index | SMA | SMA-AGM | SMA-BWS | SMA-SRM | BWSMA |
|---|---|---|---|---|---|---|
| F1 | Best | 3.6330E+02 | 3.2140E+02 | 3.3457E+02 | 7.0865E+02 | 3.0007E+02 |
| Mean | 2.4384E+03 | 1.5993E+03 | 6.6314E+02 | 1.9003E+03 | 3.0044E+02 | |
| Std | 1.7939E+03 | 1.5122E+03 | 3.1066E+02 | 1.1377E+03 | 2.9651E−01 | |
| Rank | 5 | 3 | 2 | 4 | 1 | |
| F2 | Best | 4.0651E+02 | 4.4494E+02 | 4.0614E+02 | 4.4543E+02 | 4.4490E+02 |
| Mean | 4.6788E+02 | 4.5922E+02 | 4.4851E+02 | 4.5697E+02 | 4.5129E+02 | |
| Std | 4.1839E+01 | 2.1495E+01 | 1.1992E+01 | 2.1808E+01 | 7.9738E+00 | |
| Rank | 5 | 4 | 1 | 3 | 2 | |
| F3 | Best | 6.0080E+02 | 6.0062E+02 | 6.0073E+02 | 6.0159E+02 | 6.0004E+02 |
| Mean | 6.0477E+02 | 6.0186E+02 | 6.0108E+02 | 6.0265E+02 | 6.0012E+02 | |
| Std | 4.1965E+00 | 1.2873E+00 | 2.7204E−01 | 8.8362E−01 | 4.7548E−02 | |
| Rank | 5 | 3 | 2 | 4 | 1 | |
| F4 | Best | 8.2696E+02 | 8.4387E+02 | 8.1111E+02 | 8.1434E+02 | 8.0996E+02 |
| Mean | 8.8920E+02 | 8.8459E+02 | 8.2343E+02 | 8.4273E+02 | 8.1862E+02 | |
| Std | 3.2891E+01 | 2.3304E+01 | 8.5538E+00 | 1.5012E+01 | 7.9788E+00 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F5 | Best | 1.0131E+03 | 1.0384E+03 | 9.0018E+02 | 9.1043E+02 | 9.0000E+02 |
| Mean | 1.9123E+03 | 1.8509E+03 | 9.0585E+02 | 1.0188E+03 | 9.0010E+02 | |
| Std | 7.1176E+02 | 7.1082E+02 | 4.8808E+00 | 9.5581E+01 | 1.1172E−01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F6 | Best | 2.0474E+03 | 2.0387E+03 | 3.7582E+03 | 2.0255E+03 | 1.8632E+03 |
| Mean | 1.9453E+04 | 1.8429E+04 | 1.1103E+04 | 1.7173E+04 | 1.9348E+03 | |
| Std | 7.1187E+03 | 8.4444E+03 | 4.2549E+03 | 7.9368E+03 | 6.9540E+01 | |
| Rank | 5 | 4 | 2 | 3 | 1 | |
| F7 | Best | 2.0264E+03 | 2.0256E+03 | 2.0269E+03 | 2.0277E+03 | 2.0024E+03 |
| Mean | 2.0870E+03 | 2.0836E+03 | 2.0529E+03 | 2.0519E+03 | 2.0253E+03 | |
| Std | 4.4533E+01 | 3.1829E+01 | 1.7438E+01 | 2.7550E+01 | 7.2348E+00 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F8 | Best | 2.2237E+03 | 2.2215E+03 | 2.2235E+03 | 2.2235E+03 | 2.2082E+03 |
| Mean | 2.2691E+03 | 2.2550E+03 | 2.2318E+03 | 2.2262E+03 | 2.2223E+03 | |
| Std | 4.9492E+01 | 4.9085E+01 | 2.1404E+01 | 1.4406E+00 | 2.9836E+00 | |
| Rank | 5 | 4 | 3 | 2 | 1 | |
| F9 | Best | 2.4808E+03 | 2.4808E+03 | 2.4808E+03 | 2.4810E+03 | 2.4808E+03 |
| Mean | 2.4815E+03 | 2.4812E+03 | 2.4809E+03 | 2.4824E+03 | 2.4808E+03 | |
| Std | 9.8731E−01 | 4.9868E−01 | 6.4140E−02 | 1.6644E+00 | 1.3075E−02 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F10 | Best | 2.5006E+03 | 2.5007E+03 | 2.5004E+03 | 2.5006E+03 | 2.5003E+03 |
| Mean | 3.0343E+03 | 2.9643E+03 | 3.4922E+03 | 3.2711E+03 | 2.8591E+03 | |
| Std | 3.7503E+02 | 2.5676E+02 | 9.2910E+02 | 5.7995E+02 | 3.7931E+02 | |
| Rank | 3 | 2 | 5 | 4 | 1 | |
| F11 | Best | 2.6056E+03 | 2.6016E+03 | 2.9023E+03 | 2.6857E+03 | 2.9001E+03 |
| Mean | 2.9821E+03 | 2.9170E+03 | 2.9093E+03 | 3.1823E+03 | 2.9007E+03 | |
| Std | 1.9050E+02 | 1.2221E+02 | 3.9249E+00 | 3.0207E+02 | 3.6095E−01 | |
| Rank | 4 | 3 | 2 | 5 | 1 | |
| F12 | Best | 2.9383E+03 | 2.9377E+03 | 2.9361E+03 | 2.9401E+03 | 2.9320E+03 |
| Mean | 2.9526E+03 | 2.9495E+03 | 2.9476E+03 | 2.9504E+03 | 2.9413E+03 | |
| Std | 1.5183E+01 | 1.5834E+01 | 9.6213E+00 | 1.0136E+01 | 7.2332E+00 | |
| Rank | 5 | 3 | 2 | 4 | 1 |
| No. | Index | BWSMA | PSMADE | MSSMA | ESMA | LSMA | AOSMA | EOSMA | ISMA | DTSMA |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.1525E+02 | 1.0000E+02 | 1.0480E+02 | 3.3766E+02 | 1.0106E+02 | 2.2654E+02 | 1.0409E+05 | 1.0047E+02 | 1.5864E+02 |
| Mean | 9.2922E+02 | 1.1348E+03 | 5.2064E+03 | 5.9063E+03 | 6.0436E+03 | 5.9570E+03 | 6.8593E+05 | 2.5497E+03 | 5.0336E+03 | |
| Std | 7.5662E+02 | 2.9113E+03 | 3.7387E+03 | 4.2704E+03 | 4.4007E+03 | 4.5631E+03 | 7.4809E+05 | 2.4183E+03 | 3.7765E+03 | |
| Rank | 1 | 2 | 5 | 6 | 8 | 7 | 9 | 3 | 4 | |
| F2 | Best | 3.0000E+02 | 3.0000E+02 | 3.0001E+02 | 3.0001E+02 | 3.0000E+02 | 3.0010E+02 | 1.3481E+03 | 3.0313E+02 | 3.0000E+02 |
| Mean | 3.0000E+02 | 4.4092E+02 | 3.0185E+02 | 3.1096E+02 | 3.0044E+02 | 3.4406E+02 | 3.3211E+03 | 3.1842E+02 | 3.1303E+02 | |
| Std | 1.6833E−03 | 5.0798E+02 | 5.5960E+00 | 2.6013E+01 | 1.0952E+00 | 6.4518E+01 | 1.3413E+03 | 1.7765E+01 | 2.6402E+01 | |
| Rank | 1 | 8 | 3 | 4 | 2 | 7 | 9 | 6 | 5 | |
| F3 | Best | 4.0080E+02 | 4.0000E+02 | 4.0040E+02 | 4.0379E+02 | 4.0398E+02 | 4.0270E+02 | 4.0522E+02 | 4.0017E+02 | 4.0036E+02 |
| Mean | 4.0420E+02 | 4.0949E+02 | 4.1175E+02 | 4.1372E+02 | 4.1135E+02 | 4.1470E+02 | 4.0707E+02 | 4.1593E+02 | 4.1412E+02 | |
| Std | 1.1763E+00 | 2.2113E+01 | 1.7780E+01 | 2.1449E+01 | 1.6796E+01 | 2.1458E+01 | 7.3466E−01 | 2.5399E+01 | 2.2843E+01 | |
| Rank | 1 | 3 | 5 | 6 | 4 | 8 | 2 | 9 | 7 | |
| F4 | Best | 5.0299E+02 | 5.0497E+02 | 5.0882E+02 | 5.0796E+02 | 5.0597E+02 | 5.0703E+02 | 5.0713E+02 | 5.0995E+02 | 5.0597E+02 |
| Mean | 5.0914E+02 | 5.2020E+02 | 5.2191E+02 | 5.2122E+02 | 5.2149E+02 | 5.3625E+02 | 5.1654E+02 | 5.2747E+02 | 5.1784E+02 | |
| Std | 3.7821E+00 | 8.3928E+00 | 8.3356E+00 | 7.2438E+00 | 9.8673E+00 | 1.9161E+01 | 4.9419E+00 | 1.1378E+01 | 6.2010E+00 | |
| Rank | 1 | 4 | 7 | 5 | 6 | 9 | 2 | 8 | 3 | |
| F5 | Best | 6.0000E+02 | 6.0026E+02 | 6.0005E+02 | 6.0003E+02 | 6.0002E+02 | 6.0025E+02 | 6.0006E+02 | 6.0072E+02 | 6.0001E+02 |
| Mean | 6.0002E+02 | 6.0052E+02 | 6.0062E+02 | 6.0014E+02 | 6.0048E+02 | 6.0911E+02 | 6.0044E+02 | 6.0696E+02 | 6.0022E+02 | |
| Std | 2.4785E−02 | 2.7202E−01 | 8.6464E−01 | 9.7639E−02 | 7.3214E−01 | 7.3403E+00 | 3.1397E−01 | 6.0355E+00 | 1.6123E−01 | |
| Rank | 1 | 6 | 7 | 2 | 5 | 9 | 4 | 8 | 3 | |
| F6 | Best | 7.1320E+02 | 7.1506E+02 | 7.1362E+02 | 7.1326E+02 | 7.1541E+02 | 7.2759E+02 | 7.2306E+02 | 7.2427E+02 | 7.1041E+02 |
| Mean | 7.1869E+02 | 7.3256E+02 | 7.4629E+02 | 7.3046E+02 | 7.2834E+02 | 7.5537E+02 | 7.3222E+02 | 7.5322E+02 | 7.2609E+02 | |
| Std | 3.2076E+00 | 1.1198E+01 | 1.4137E+01 | 1.1355E+01 | 8.6943E+00 | 2.3183E+01 | 7.4905E+00 | 1.6527E+01 | 7.1927E+00 | |
| Rank | 1 | 6 | 7 | 4 | 3 | 9 | 5 | 8 | 2 | |
| F7 | Best | 8.0199E+02 | 8.0995E+02 | 8.1194E+02 | 8.0995E+02 | 8.0597E+02 | 8.1194E+02 | 8.0580E+02 | 8.1194E+02 | 8.0597E+02 |
| Mean | 8.0876E+02 | 8.2044E+02 | 8.2443E+02 | 8.2086E+02 | 8.2371E+02 | 8.2979E+02 | 8.1481E+02 | 8.2412E+02 | 8.1625E+02 | |
| Std | 3.7990E+00 | 7.0319E+00 | 6.6665E+00 | 8.3917E+00 | 1.0377E+01 | 1.1545E+01 | 5.1266E+00 | 6.6350E+00 | 6.3880E+00 | |
| Rank | 1 | 4 | 8 | 5 | 6 | 9 | 2 | 7 | 3 | |
| F8 | Best | 9.0000E+02 | 9.0000E+02 | 9.0000E+02 | 9.0000E+02 | 9.0000E+02 | 9.0540E+02 | 9.0003E+02 | 9.0046E+02 | 9.0000E+02 |
| Mean | 9.0000E+02 | 9.0442E+02 | 9.5771E+02 | 9.0567E+02 | 9.0754E+02 | 1.1309E+03 | 9.0114E+02 | 9.7620E+02 | 9.0093E+02 | |
| Std | 1.6351E−02 | 7.0758E+00 | 1.0014E+02 | 1.7355E+01 | 2.2059E+01 | 2.0473E+02 | 9.6746E−01 | 1.1078E+02 | 1.6285E+00 | |
| Rank | 1 | 4 | 7 | 5 | 6 | 9 | 3 | 8 | 2 | |
| F9 | Best | 1.0103E+03 | 1.1389E+03 | 1.1451E+03 | 1.1465E+03 | 1.2050E+03 | 1.1431E+03 | 1.4580E+03 | 1.1286E+03 | 1.3532E+03 |
| Mean | 1.3616E+03 | 1.6731E+03 | 1.6486E+03 | 1.6792E+03 | 1.6947E+03 | 1.9624E+03 | 2.0234E+03 | 1.9231E+03 | 1.5548E+03 | |
| Std | 2.1647E+02 | 2.9115E+02 | 2.8148E+02 | 3.4063E+02 | 2.5951E+02 | 3.6337E+02 | 2.6822E+02 | 3.1313E+02 | 1.7767E+02 | |
| Rank | 1 | 4 | 3 | 5 | 6 | 8 | 9 | 7 | 2 | |
| F10 | Best | 1.1003E+03 | 1.1030E+03 | 1.1018E+03 | 1.1024E+03 | 1.1030E+03 | 1.1114E+03 | 1.1054E+03 | 1.1065E+03 | 1.1027E+03 |
| Mean | 1.1033E+03 | 1.1299E+03 | 1.1141E+03 | 1.1629E+03 | 1.2100E+03 | 1.1842E+03 | 1.1161E+03 | 1.1556E+03 | 1.1116E+03 | |
| Std | 1.4183E+00 | 6.2013E+01 | 6.7529E+00 | 9.1142E+01 | 1.0595E+02 | 8.7463E+01 | 1.0388E+01 | 6.5645E+01 | 6.6829E+00 | |
| Rank | 1 | 5 | 3 | 7 | 9 | 8 | 4 | 6 | 2 | |
| F11 | Best | 1.3188E+03 | 1.2002E+03 | 8.4906E+03 | 7.7630E+03 | 4.8931E+04 | 5.3783E+03 | 4.7938E+04 | 2.2102E+04 | 3.1000E+03 |
| Mean | 4.7612E+03 | 5.5029E+04 | 1.1003E+06 | 6.4135E+05 | 1.8834E+06 | 1.8176E+06 | 5.2268E+05 | 1.5507E+06 | 4.8607E+04 | |
| Std | 8.4062E+03 | 2.2660E+05 | 1.3296E+06 | 5.8337E+05 | 1.7870E+06 | 2.0472E+06 | 6.2716E+05 | 1.5903E+06 | 5.9313E+04 | |
| Rank | 1 | 3 | 6 | 5 | 9 | 8 | 4 | 7 | 2 | |
| F12 | Best | 1.3032E+03 | 1.3032E+03 | 1.3407E+03 | 1.3118E+03 | 2.3084E+03 | 2.8489E+03 | 2.1155E+03 | 2.2187E+03 | 1.6455E+03 |
| Mean | 1.3120E+03 | 3.3078E+03 | 7.5088E+03 | 1.0260E+04 | 1.6716E+04 | 1.8833E+04 | 4.5519E+03 | 2.0517E+04 | 1.1988E+04 | |
| Std | 5.8979E+00 | 5.0804E+03 | 8.4492E+03 | 1.0485E+04 | 1.4565E+04 | 1.3517E+04 | 1.9597E+03 | 1.2549E+04 | 1.2255E+04 | |
| Rank | 1 | 2 | 4 | 5 | 7 | 8 | 3 | 9 | 6 | |
| F13 | Best | 1.4000E+03 | 1.4237E+03 | 1.4091E+03 | 1.4153E+03 | 1.4653E+03 | 1.4711E+03 | 1.4740E+03 | 1.4426E+03 | 1.4121E+03 |
| Mean | 1.4056E+03 | 1.6827E+03 | 1.4652E+03 | 6.6774E+03 | 2.2495E+03 | 3.4047E+03 | 1.5324E+03 | 1.9548E+03 | 2.2008E+03 | |
| Std | 8.0927E+00 | 5.3475E+02 | 4.1237E+01 | 7.5946E+03 | 1.2199E+03 | 4.0271E+03 | 4.2084E+01 | 7.4434E+02 | 1.3103E+03 | |
| Rank | 1 | 4 | 2 | 9 | 7 | 8 | 3 | 5 | 6 | |
| F14 | Best | 1.5002E+03 | 1.5031E+03 | 1.5138E+03 | 1.5318E+03 | 1.7105E+03 | 1.6591E+03 | 1.6815E+03 | 1.6146E+03 | 1.5096E+03 |
| Mean | 1.5047E+03 | 1.8723E+03 | 1.6978E+03 | 5.9587E+03 | 5.8695E+03 | 4.9736E+03 | 2.2277E+03 | 3.4941E+03 | 2.2402E+03 | |
| Std | 4.8891E+00 | 9.7124E+02 | 5.3544E+02 | 5.3195E+03 | 5.0393E+03 | 3.8093E+03 | 4.6001E+02 | 2.6984E+03 | 1.1201E+03 | |
| Rank | 1 | 3 | 2 | 9 | 8 | 7 | 4 | 6 | 5 | |
| F15 | Best | 1.6005E+03 | 1.6011E+03 | 1.6006E+03 | 1.6007E+03 | 1.6123E+03 | 1.6034E+03 | 1.6083E+03 | 1.6047E+03 | 1.6017E+03 |
| Mean | 1.6129E+03 | 1.6967E+03 | 1.7250E+03 | 1.7499E+03 | 1.6889E+03 | 1.7948E+03 | 1.6561E+03 | 1.7609E+03 | 1.6655E+03 | |
| Std | 2.4387E+01 | 1.0537E+02 | 1.0414E+02 | 1.2356E+02 | 9.3393E+01 | 1.3418E+02 | 6.3066E+01 | 1.0103E+02 | 8.1236E+01 | |
| Rank | 1 | 5 | 6 | 7 | 4 | 9 | 2 | 8 | 3 | |
| F16 | Best | 1.7006E+03 | 1.7030E+03 | 1.7226E+03 | 1.7054E+03 | 1.7335E+03 | 1.7266E+03 | 1.7316E+03 | 1.7300E+03 | 1.7016E+03 |
| Mean | 1.7175E+03 | 1.7430E+03 | 1.7686E+03 | 1.7579E+03 | 1.7926E+03 | 1.7851E+03 | 1.7557E+03 | 1.7633E+03 | 1.7366E+03 | |
| Std | 1.2925E+01 | 2.7849E+01 | 4.3245E+01 | 4.7442E+01 | 4.6760E+01 | 4.0134E+01 | 1.3308E+01 | 2.3608E+01 | 2.4100E+01 | |
| Rank | 1 | 3 | 7 | 5 | 9 | 8 | 4 | 6 | 2 | |
| F17 | Best | 1.8004E+03 | 1.8214E+03 | 3.0761E+03 | 2.1102E+03 | 6.7235E+03 | 2.3857E+03 | 3.8406E+03 | 4.8596E+03 | 8.2724E+03 |
| Mean | 1.8089E+03 | 7.0401E+03 | 2.6025E+04 | 3.0814E+04 | 2.7917E+04 | 2.9458E+04 | 1.4321E+04 | 2.1373E+04 | 2.9249E+04 | |
| Std | 9.1926E+00 | 9.9823E+03 | 1.6023E+04 | 1.9249E+04 | 1.3963E+04 | 1.3557E+04 | 7.2371E+03 | 1.4615E+04 | 1.2063E+04 | |
| Rank | 1 | 2 | 5 | 9 | 6 | 8 | 3 | 4 | 7 | |
| F18 | Best | 1.9001E+03 | 1.9012E+03 | 1.9027E+03 | 1.9338E+03 | 1.9978E+03 | 1.9730E+03 | 1.9492E+03 | 2.0143E+03 | 1.9039E+03 |
| Mean | 1.9014E+03 | 3.9873E+03 | 4.2267E+03 | 1.2969E+04 | 1.6045E+04 | 1.0622E+04 | 2.8139E+03 | 4.9575E+03 | 8.9580E+03 | |
| Std | 1.4326E+00 | 5.5127E+03 | 4.3312E+03 | 1.2647E+04 | 9.5582E+03 | 9.9016E+03 | 1.1243E+03 | 4.5816E+03 | 7.0951E+03 | |
| Rank | 1 | 3 | 4 | 8 | 9 | 7 | 2 | 5 | 6 | |
| F19 | Best | 2.0000E+03 | 2.0050E+03 | 2.0053E+03 | 2.0050E+03 | 2.0225E+03 | 2.0377E+03 | 2.0230E+03 | 2.0245E+03 | 2.0004E+03 |
| Mean | 2.0092E+03 | 2.0320E+03 | 2.0623E+03 | 2.0359E+03 | 2.0638E+03 | 2.1121E+03 | 2.0425E+03 | 2.1104E+03 | 2.0160E+03 | |
| Std | 1.0646E+01 | 1.7704E+01 | 4.9253E+01 | 2.5263E+01 | 3.8850E+01 | 5.4830E+01 | 1.2920E+01 | 6.4250E+01 | 1.2499E+01 | |
| Rank | 1 | 3 | 6 | 4 | 7 | 9 | 5 | 8 | 2 | |
| F20 | Best | 2.2000E+03 | 2.2000E+03 | 2.2004E+03 | 2.2027E+03 | 2.2012E+03 | 2.2025E+03 | 2.2031E+03 | 2.2005E+03 | 2.2007E+03 |
| Mean | 2.2951E+03 | 2.3170E+03 | 2.3197E+03 | 2.3076E+03 | 2.3039E+03 | 2.3261E+03 | 2.2735E+03 | 2.2067E+03 | 2.2564E+03 | |
| Std | 3.7582E+01 | 3.3580E+01 | 3.3733E+01 | 4.7849E+01 | 5.2178E+01 | 4.3407E+01 | 5.1597E+01 | 2.2037E+01 | 5.7330E+01 | |
| Rank | 4 | 7 | 8 | 6 | 5 | 9 | 3 | 1 | 2 | |
| F21 | Best | 2.3000E+03 | 2.3008E+03 | 2.3012E+03 | 2.3000E+03 | 2.2402E+03 | 2.3013E+03 | 2.2511E+03 | 2.2403E+03 | 2.3010E+03 |
| Mean | 2.3001E+03 | 2.3025E+03 | 2.3632E+03 | 2.3022E+03 | 2.3732E+03 | 2.3411E+03 | 2.3016E+03 | 2.2993E+03 | 2.3031E+03 | |
| Std | 1.7247E−01 | 1.2737E+00 | 2.0125E+02 | 1.3134E+00 | 2.7993E+02 | 2.0183E+02 | 9.6576E+00 | 1.5901E+01 | 1.3148E+00 | |
| Rank | 2 | 5 | 8 | 4 | 9 | 7 | 3 | 1 | 6 | |
| F22 | Best | 2.6031E+03 | 2.6085E+03 | 2.6105E+03 | 2.6097E+03 | 2.6140E+03 | 2.6135E+03 | 2.6069E+03 | 2.6139E+03 | 2.6101E+03 |
| Mean | 2.6119E+03 | 2.6204E+03 | 2.6240E+03 | 2.6231E+03 | 2.6242E+03 | 2.6306E+03 | 2.6164E+03 | 2.6292E+03 | 2.6200E+03 | |
| Std | 5.0350E+00 | 7.4125E+00 | 9.4657E+00 | 6.9834E+00 | 6.6024E+00 | 1.1225E+01 | 4.5414E+00 | 8.4811E+00 | 6.8633E+00 | |
| Rank | 1 | 4 | 6 | 5 | 7 | 9 | 2 | 8 | 3 | |
| F23 | Best | 2.7317E+03 | 2.5004E+03 | 2.7414E+03 | 2.7398E+03 | 2.5001E+03 | 2.5009E+03 | 2.5214E+03 | 2.5000E+03 | 2.5014E+03 |
| Mean | 2.7390E+03 | 2.7448E+03 | 2.7587E+03 | 2.7607E+03 | 2.7465E+03 | 2.7480E+03 | 2.6901E+03 | 2.6462E+03 | 2.7431E+03 | |
| Std | 3.9986E+00 | 4.7343E+01 | 1.0029E+01 | 1.4095E+01 | 4.7579E+01 | 6.8380E+01 | 8.4535E+01 | 1.2759E+02 | 4.6720E+01 | |
| Rank | 3 | 5 | 8 | 9 | 6 | 7 | 2 | 1 | 4 | |
| F24 | Best | 2.8977E+03 | 2.8985E+03 | 2.8980E+03 | 2.8984E+03 | 2.8978E+03 | 2.8991E+03 | 2.8990E+03 | 2.8988E+03 | 2.8978E+03 |
| Mean | 2.9273E+03 | 2.9245E+03 | 2.9413E+03 | 2.9401E+03 | 2.9368E+03 | 2.9467E+03 | 2.9278E+03 | 2.9350E+03 | 2.9274E+03 | |
| Std | 2.2583E+01 | 2.4741E+01 | 3.6399E+01 | 3.3668E+01 | 2.9531E+01 | 4.2640E+01 | 2.0356E+01 | 2.1839E+01 | 2.4010E+01 | |
| Rank | 2 | 1 | 8 | 7 | 6 | 9 | 4 | 5 | 3 | |
| F25 | Best | 2.9000E+03 | 2.9000E+03 | 2.8002E+03 | 2.9000E+03 | 2.9000E+03 | 2.8000E+03 | 2.8335E+03 | 2.6001E+03 | 2.9000E+03 |
| Mean | 2.9032E+03 | 3.0291E+03 | 3.0941E+03 | 3.2396E+03 | 3.1279E+03 | 3.1002E+03 | 2.9229E+03 | 2.9457E+03 | 2.9501E+03 | |
| Std | 1.1957E+01 | 1.9114E+02 | 3.5240E+02 | 4.3707E+02 | 3.7141E+02 | 3.7626E+02 | 2.6615E+01 | 1.2609E+02 | 4.4351E+01 | |
| Rank | 1 | 5 | 6 | 9 | 8 | 7 | 2 | 3 | 4 | |
| F26 | Best | 3.0890E+03 | 3.0784E+03 | 3.0890E+03 | 3.0880E+03 | 3.0890E+03 | 3.0898E+03 | 3.0908E+03 | 3.0893E+03 | 3.0890E+03 |
| Mean | 3.0901E+03 | 3.0908E+03 | 3.1007E+03 | 3.0944E+03 | 3.0918E+03 | 3.0956E+03 | 3.0957E+03 | 3.0944E+03 | 3.0969E+03 | |
| Std | 1.6432E+00 | 3.4881E+00 | 2.0273E+01 | 1.2550E+01 | 2.6843E+00 | 3.4264E+00 | 1.9211E+00 | 3.6044E+00 | 1.7267E+01 | |
| Rank | 1 | 2 | 9 | 4 | 3 | 6 | 7 | 5 | 8 | |
| F27 | Best | 3.1000E+03 | 3.1000E+03 | 3.1025E+03 | 3.1004E+03 | 3.1691E+03 | 3.1643E+03 | 3.1145E+03 | 3.1000E+03 | 3.1000E+03 |
| Mean | 3.2457E+03 | 3.2560E+03 | 3.3223E+03 | 3.3436E+03 | 3.3713E+03 | 3.3618E+03 | 3.1883E+03 | 3.2349E+03 | 3.2842E+03 | |
| Std | 1.4244E+02 | 7.9209E+01 | 1.2023E+02 | 1.5655E+02 | 1.7861E+02 | 8.8264E+01 | 4.5353E+01 | 1.1212E+02 | 1.2119E+02 | |
| Rank | 3 | 4 | 6 | 7 | 9 | 8 | 1 | 2 | 5 | |
| F28 | Best | 3.1293E+03 | 3.1342E+03 | 3.1411E+03 | 3.1372E+03 | 3.1396E+03 | 3.1388E+03 | 3.1482E+03 | 3.1505E+03 | 3.1327E+03 |
| Mean | 3.1404E+03 | 3.1842E+03 | 3.2297E+03 | 3.2365E+03 | 3.2307E+03 | 3.2582E+03 | 3.1920E+03 | 3.2229E+03 | 3.1909E+03 | |
| Std | 1.0094E+01 | 5.0117E+01 | 6.4164E+01 | 7.4800E+01 | 6.5920E+01 | 8.6973E+01 | 2.1988E+01 | 5.0169E+01 | 5.1204E+01 | |
| Rank | 1 | 2 | 6 | 8 | 7 | 9 | 4 | 5 | 3 | |
| F29 | Best | 3.4600E+03 | 3.2667E+03 | 5.7074E+03 | 5.0654E+03 | 8.2037E+03 | 3.9065E+03 | 6.5876E+03 | 1.2329E+04 | 5.2648E+03 |
| Mean | 2.3768E+05 | 5.6184E+04 | 6.4584E+05 | 3.7430E+05 | 1.6850E+05 | 5.4212E+05 | 2.1454E+05 | 5.4490E+05 | 3.8659E+05 | |
| Std | 4.4337E+05 | 1.3969E+05 | 5.2116E+05 | 4.5765E+05 | 3.6875E+05 | 6.4624E+05 | 3.8785E+05 | 5.7543E+05 | 5.4219E+05 | |
| Rank | 4 | 1 | 9 | 5 | 2 | 7 | 3 | 8 | 6 |
| No. | Index | BWSMA | PSMADE | MSSMA | ESMA | LSMA | AOSMA | EOSMA | ISMA | DTSMA |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.0241E+02 | 1.0000E+02 | 1.7291E+02 | 3.7327E+03 | 1.0320E+04 | 1.2304E+05 | 3.5973E+08 | 1.2542E+05 | 5.7404E+03 |
| Mean | 3.5430E+03 | 1.4118E+07 | 1.2998E+05 | 1.6695E+04 | 5.0382E+04 | 3.1874E+06 | 1.2881E+09 | 1.3853E+06 | 4.5185E+07 | |
| Std | 4.2661E+03 | 3.7591E+07 | 4.7172E+05 | 8.5435E+03 | 2.8901E+04 | 5.5201E+06 | 5.3013E+08 | 1.3097E+06 | 8.7864E+07 | |
| Rank | 1 | 7 | 4 | 2 | 3 | 6 | 9 | 5 | 8 | |
| F2 | Best | 3.0103E+02 | 3.0000E+02 | 2.8664E+04 | 2.3037E+04 | 3.3479E+04 | 4.4410E+04 | 4.8077E+04 | 3.0546E+04 | 2.4655E+04 |
| Mean | 3.5108E+02 | 4.8235E+04 | 4.3406E+04 | 5.0769E+04 | 5.7363E+04 | 6.8079E+04 | 9.1421E+04 | 4.4395E+04 | 5.2740E+04 | |
| Std | 6.5321E+01 | 6.1524E+04 | 7.8098E+03 | 1.4251E+04 | 1.5002E+04 | 1.3491E+04 | 1.9067E+04 | 6.8378E+03 | 1.7852E+04 | |
| Rank | 1 | 4 | 2 | 5 | 7 | 8 | 9 | 3 | 6 | |
| F3 | Best | 4.4193E+02 | 4.0000E+02 | 4.5994E+02 | 4.6514E+02 | 4.5151E+02 | 4.9948E+02 | 5.5809E+02 | 4.9150E+02 | 4.6726E+02 |
| Mean | 4.9308E+02 | 4.5967E+02 | 5.1794E+02 | 5.0221E+02 | 5.1506E+02 | 5.5624E+02 | 6.4188E+02 | 5.3694E+02 | 5.1650E+02 | |
| Std | 1.6638E+01 | 7.4924E+01 | 3.6029E+01 | 1.6206E+01 | 3.3691E+01 | 4.7844E+01 | 4.8388E+01 | 3.0625E+01 | 2.2938E+01 | |
| Rank | 2 | 1 | 6 | 3 | 4 | 8 | 9 | 7 | 5 | |
| F4 | Best | 5.2105E+02 | 5.7263E+02 | 5.9859E+02 | 5.6560E+02 | 5.8556E+02 | 6.2068E+02 | 6.1724E+02 | 6.4157E+02 | 5.5880E+02 |
| Mean | 5.3446E+02 | 6.4223E+02 | 6.7198E+02 | 6.2131E+02 | 6.3729E+02 | 7.1174E+02 | 6.7363E+02 | 7.1666E+02 | 6.0262E+02 | |
| Std | 9.8776E+00 | 6.3477E+01 | 4.0051E+01 | 2.9501E+01 | 3.4407E+01 | 5.1709E+01 | 2.3317E+01 | 3.5392E+01 | 2.4976E+01 | |
| Rank | 1 | 5 | 6 | 3 | 4 | 8 | 7 | 9 | 2 | |
| F5 | Best | 6.0009E+02 | 6.0791E+02 | 6.1292E+02 | 6.0294E+02 | 6.0794E+02 | 6.3444E+02 | 6.0773E+02 | 6.3228E+02 | 6.0467E+02 |
| Mean | 6.0027E+02 | 6.2241E+02 | 6.2577E+02 | 6.0798E+02 | 6.2798E+02 | 6.5342E+02 | 6.1455E+02 | 6.5279E+02 | 6.1451E+02 | |
| Std | 7.7242E−02 | 1.1111E+01 | 8.8767E+00 | 4.9515E+00 | 9.8583E+00 | 9.7114E+00 | 3.4375E+00 | 9.1784E+00 | 5.0759E+00 | |
| Rank | 1 | 5 | 6 | 2 | 7 | 9 | 4 | 8 | 3 | |
| F6 | Best | 7.4556E+02 | 8.2562E+02 | 8.7381E+02 | 8.2215E+02 | 8.1802E+02 | 9.2856E+02 | 8.9876E+02 | 8.8149E+02 | 8.0496E+02 |
| Mean | 7.6442E+02 | 9.3173E+02 | 9.9274E+02 | 8.6649E+02 | 8.7752E+02 | 1.0956E+03 | 9.4882E+02 | 1.0810E+03 | 8.8302E+02 | |
| Std | 1.0946E+01 | 5.5169E+01 | 7.8436E+01 | 3.1701E+01 | 4.2533E+01 | 9.4316E+01 | 2.8888E+01 | 9.1748E+01 | 3.7495E+01 | |
| Rank | 1 | 5 | 7 | 2 | 3 | 9 | 6 | 8 | 4 | |
| F7 | Best | 8.1328E+02 | 8.6169E+02 | 8.8482E+02 | 8.6285E+02 | 8.6865E+02 | 9.2066E+02 | 9.2705E+02 | 8.9276E+02 | 8.7115E+02 |
| Mean | 8.3911E+02 | 9.3280E+02 | 9.6105E+02 | 9.2403E+02 | 9.2335E+02 | 9.8956E+02 | 9.6043E+02 | 9.5771E+02 | 9.1814E+02 | |
| Std | 1.3461E+01 | 3.8781E+01 | 3.8919E+01 | 2.8858E+01 | 2.9913E+01 | 3.4721E+01 | 1.8896E+01 | 3.3429E+01 | 2.3699E+01 | |
| Rank | 1 | 5 | 8 | 4 | 3 | 9 | 7 | 6 | 2 | |
| F8 | Best | 9.0020E+02 | 1.6277E+03 | 2.5918E+03 | 1.2613E+03 | 2.1267E+03 | 3.6763E+03 | 1.1939E+03 | 2.7916E+03 | 1.3675E+03 |
| Mean | 9.0142E+02 | 4.2393E+03 | 4.1371E+03 | 3.4255E+03 | 4.4393E+03 | 5.9129E+03 | 1.9597E+03 | 5.0284E+03 | 3.5924E+03 | |
| Std | 1.3383E+00 | 2.3427E+03 | 8.3651E+02 | 1.3889E+03 | 1.5165E+03 | 1.2604E+03 | 8.0695E+02 | 1.2445E+03 | 1.2773E+03 | |
| Rank | 1 | 6 | 5 | 3 | 7 | 9 | 2 | 8 | 4 | |
| F9 | Best | 3.1575E+03 | 3.8546E+03 | 3.3938E+03 | 3.3154E+03 | 3.5730E+03 | 4.3268E+03 | 7.1904E+03 | 4.0389E+03 | 3.8054E+03 |
| Mean | 4.2796E+03 | 5.4032E+03 | 4.5987E+03 | 4.6209E+03 | 5.0531E+03 | 5.5795E+03 | 8.1447E+03 | 5.2110E+03 | 5.4042E+03 | |
| Std | 6.4497E+02 | 7.7695E+02 | 6.5881E+02 | 7.5897E+02 | 5.6597E+02 | 8.6252E+02 | 5.2737E+02 | 5.9170E+02 | 8.5662E+02 | |
| Rank | 1 | 6 | 2 | 3 | 4 | 8 | 9 | 5 | 7 | |
| F10 | Best | 1.1099E+03 | 1.1796E+03 | 1.1773E+03 | 1.1493E+03 | 1.2155E+03 | 1.2433E+03 | 1.4725E+03 | 1.2276E+03 | 1.1713E+03 |
| Mean | 1.1536E+03 | 1.4494E+03 | 1.2612E+03 | 1.2524E+03 | 1.3757E+03 | 1.4130E+03 | 2.2375E+03 | 1.3180E+03 | 1.3519E+03 | |
| Std | 3.6894E+01 | 2.7676E+02 | 4.8352E+01 | 5.5387E+01 | 7.5120E+01 | 1.0104E+02 | 3.8970E+02 | 6.0377E+01 | 7.6869E+01 | |
| Rank | 1 | 8 | 3 | 2 | 6 | 7 | 9 | 4 | 5 | |
| F11 | Best | 8.5647E+03 | 1.9807E+03 | 8.4931E+05 | 7.2331E+04 | 8.3585E+05 | 3.4579E+06 | 2.5360E+06 | 2.7654E+06 | 2.7002E+05 |
| Mean | 3.0646E+04 | 3.6501E+06 | 4.9991E+06 | 3.8483E+06 | 1.7322E+07 | 2.1958E+07 | 2.7577E+07 | 2.3192E+07 | 5.3178E+06 | |
| Std | 2.4784E+04 | 1.1853E+07 | 3.0312E+06 | 2.3742E+06 | 1.6666E+07 | 1.9430E+07 | 2.1720E+07 | 1.7543E+07 | 6.0905E+06 | |
| Rank | 1 | 2 | 4 | 3 | 6 | 7 | 9 | 8 | 5 | |
| F12 | Best | 1.7429E+03 | 2.6599E+03 | 5.0559E+03 | 2.6558E+03 | 6.5428E+04 | 4.9793E+04 | 1.0877E+05 | 1.9101E+04 | 4.7654E+03 |
| Mean | 3.1906E+03 | 8.1774E+04 | 3.2921E+04 | 2.9090E+04 | 2.8900E+05 | 3.3489E+05 | 6.3503E+05 | 1.8810E+05 | 3.4571E+04 | |
| Std | 9.1225E+02 | 3.1742E+05 | 2.9239E+04 | 3.1265E+04 | 1.6906E+05 | 2.9559E+05 | 7.0519E+05 | 1.2780E+05 | 2.9324E+04 | |
| Rank | 1 | 5 | 3 | 2 | 7 | 8 | 9 | 6 | 4 | |
| F13 | Best | 1.4351E+03 | 1.5261E+03 | 2.2473E+03 | 2.4087E+04 | 3.7078E+04 | 2.2516E+04 | 3.8881E+03 | 7.2448E+03 | 7.9603E+03 |
| Mean | 1.4590E+03 | 5.9915E+04 | 2.4842E+05 | 5.3696E+05 | 1.5930E+05 | 6.6267E+05 | 6.1935E+04 | 1.6982E+05 | 8.4231E+04 | |
| Std | 1.5078E+01 | 1.5248E+05 | 2.5042E+05 | 7.7928E+05 | 1.1421E+05 | 8.3978E+05 | 4.6318E+04 | 1.8260E+05 | 8.5102E+04 | |
| Rank | 1 | 2 | 7 | 8 | 5 | 9 | 3 | 6 | 4 | |
| F14 | Best | 1.5974E+03 | 1.8174E+03 | 1.8245E+03 | 2.4421E+03 | 2.7453E+04 | 1.5066E+04 | 1.4090E+04 | 8.1183E+03 | 1.7036E+03 |
| Mean | 1.7426E+03 | 1.6312E+04 | 1.2053E+04 | 1.7751E+04 | 1.2018E+05 | 8.9923E+04 | 1.0210E+05 | 6.2507E+04 | 1.4969E+04 | |
| Std | 1.0656E+02 | 1.4071E+04 | 1.2954E+04 | 1.4528E+04 | 6.2277E+04 | 4.2838E+04 | 1.3378E+05 | 4.7386E+04 | 1.4640E+04 | |
| Rank | 1 | 4 | 2 | 5 | 9 | 7 | 8 | 6 | 3 | |
| F15 | Best | 1.6057E+03 | 2.1962E+03 | 2.0153E+03 | 2.1159E+03 | 2.1554E+03 | 2.2986E+03 | 2.2915E+03 | 2.2115E+03 | 1.7616E+03 |
| Mean | 2.0826E+03 | 2.7379E+03 | 2.8356E+03 | 2.7355E+03 | 2.8494E+03 | 3.1349E+03 | 2.9765E+03 | 3.2118E+03 | 2.4722E+03 | |
| Std | 2.6252E+02 | 3.4771E+02 | 3.1194E+02 | 3.2624E+02 | 3.8787E+02 | 4.0943E+02 | 3.0070E+02 | 3.6609E+02 | 4.0025E+02 | |
| Rank | 1 | 4 | 5 | 3 | 6 | 8 | 7 | 9 | 2 | |
| F16 | Best | 1.7596E+03 | 1.8194E+03 | 1.7941E+03 | 2.0875E+03 | 1.8798E+03 | 2.1020E+03 | 1.9196E+03 | 2.0644E+03 | 1.8731E+03 |
| Mean | 1.8777E+03 | 2.2901E+03 | 2.4482E+03 | 2.4729E+03 | 2.3369E+03 | 2.6026E+03 | 2.0996E+03 | 2.4454E+03 | 2.2179E+03 | |
| Std | 1.0153E+02 | 2.6634E+02 | 2.9442E+02 | 1.9341E+02 | 2.2396E+02 | 2.9935E+02 | 1.2709E+02 | 2.3559E+02 | 1.7630E+02 | |
| Rank | 1 | 4 | 7 | 8 | 5 | 9 | 2 | 6 | 3 | |
| F17 | Best | 1.8850E+03 | 6.5967E+03 | 3.1736E+05 | 2.6581E+05 | 3.9312E+05 | 2.8630E+05 | 3.3235E+05 | 6.7536E+04 | 1.8968E+05 |
| Mean | 1.9892E+03 | 2.4335E+06 | 3.4410E+06 | 3.3765E+06 | 3.2823E+06 | 4.0981E+06 | 1.2317E+06 | 1.7889E+06 | 2.2733E+06 | |
| Std | 6.9781E+01 | 5.5680E+06 | 4.3506E+06 | 3.0887E+06 | 3.1294E+06 | 4.2853E+06 | 8.9160E+05 | 1.9863E+06 | 2.2462E+06 | |
| Rank | 1 | 5 | 8 | 7 | 6 | 9 | 2 | 3 | 4 | |
| F18 | Best | 1.9250E+03 | 2.1552E+03 | 1.9932E+03 | 2.0785E+03 | 2.4984E+04 | 8.1859E+03 | 1.4645E+04 | 2.9067E+04 | 2.1916E+03 |
| Mean | 1.9746E+03 | 2.6974E+04 | 1.1809E+04 | 2.1619E+04 | 2.8949E+05 | 1.0086E+05 | 2.5905E+05 | 4.9970E+05 | 2.2184E+04 | |
| Std | 3.3756E+01 | 2.1763E+04 | 1.4207E+04 | 2.2347E+04 | 1.4936E+05 | 1.0037E+05 | 2.8063E+05 | 4.2058E+05 | 1.9196E+04 | |
| Rank | 1 | 5 | 2 | 3 | 8 | 6 | 7 | 9 | 4 | |
| F19 | Best | 2.0303E+03 | 2.2112E+03 | 2.1115E+03 | 2.1977E+03 | 2.3453E+03 | 2.4294E+03 | 2.2385E+03 | 2.2954E+03 | 2.1049E+03 |
| Mean | 2.1999E+03 | 2.5440E+03 | 2.4647E+03 | 2.5567E+03 | 2.7181E+03 | 2.7463E+03 | 2.5622E+03 | 2.5784E+03 | 2.3865E+03 | |
| Std | 1.3211E+02 | 2.2853E+02 | 2.0716E+02 | 2.5932E+02 | 1.9639E+02 | 1.4144E+02 | 1.8271E+02 | 1.7645E+02 | 1.9170E+02 | |
| Rank | 1 | 4 | 3 | 5 | 8 | 9 | 6 | 7 | 2 | |
| F20 | Best | 2.3225E+03 | 2.3640E+03 | 2.3980E+03 | 2.3699E+03 | 2.3606E+03 | 2.4222E+03 | 2.4234E+03 | 2.3930E+03 | 2.3727E+03 |
| Mean | 2.3367E+03 | 2.4514E+03 | 2.4622E+03 | 2.4239E+03 | 2.4290E+03 | 2.5139E+03 | 2.4608E+03 | 2.4813E+03 | 2.4145E+03 | |
| Std | 1.1600E+01 | 6.9749E+01 | 4.5525E+01 | 3.2081E+01 | 3.4988E+01 | 5.0959E+01 | 1.7872E+01 | 4.2456E+01 | 3.1120E+01 | |
| Rank | 1 | 5 | 7 | 3 | 4 | 9 | 6 | 8 | 2 | |
| F21 | Best | 2.3003E+03 | 2.3000E+03 | 2.3038E+03 | 2.3025E+03 | 2.3063E+03 | 2.3083E+03 | 2.4109E+03 | 2.3130E+03 | 2.3146E+03 |
| Mean | 4.1865E+03 | 5.9580E+03 | 5.0575E+03 | 5.6692E+03 | 6.3206E+03 | 6.7003E+03 | 2.8344E+03 | 2.4912E+03 | 6.0817E+03 | |
| Std | 1.6751E+03 | 1.6452E+03 | 1.8966E+03 | 1.0780E+03 | 1.5673E+03 | 1.3190E+03 | 1.2660E+03 | 8.9335E+02 | 1.7492E+03 | |
| Rank | 3 | 6 | 4 | 5 | 8 | 9 | 2 | 1 | 7 | |
| F22 | Best | 2.6735E+03 | 2.7140E+03 | 2.7212E+03 | 2.7163E+03 | 2.7145E+03 | 2.7902E+03 | 2.7633E+03 | 2.7835E+03 | 2.7045E+03 |
| Mean | 2.6919E+03 | 2.7709E+03 | 2.7931E+03 | 2.7648E+03 | 2.7682E+03 | 2.8755E+03 | 2.8118E+03 | 2.8748E+03 | 2.7585E+03 | |
| Std | 1.0484E+01 | 4.6940E+01 | 3.8668E+01 | 2.3102E+01 | 2.7202E+01 | 6.4277E+01 | 2.5633E+01 | 6.4406E+01 | 2.8925E+01 | |
| Rank | 1 | 5 | 6 | 3 | 4 | 9 | 7 | 8 | 2 | |
| F23 | Best | 2.8324E+03 | 2.8691E+03 | 2.9088E+03 | 2.8752E+03 | 2.8681E+03 | 2.9288E+03 | 2.9489E+03 | 2.9202E+03 | 2.8973E+03 |
| Mean | 2.8571E+03 | 2.9401E+03 | 2.9753E+03 | 2.9444E+03 | 2.9328E+03 | 3.0065E+03 | 2.9861E+03 | 3.0176E+03 | 2.9193E+03 | |
| Std | 1.4884E+01 | 6.4039E+01 | 4.4717E+01 | 3.8130E+01 | 3.2989E+01 | 5.2661E+01 | 2.1654E+01 | 5.6275E+01 | 1.5390E+01 | |
| Rank | 1 | 4 | 6 | 5 | 3 | 8 | 7 | 9 | 2 | |
| F24 | Best | 2.8870E+03 | 2.8760E+03 | 2.8852E+03 | 2.8840E+03 | 2.8920E+03 | 2.9007E+03 | 2.9622E+03 | 2.9091E+03 | 2.8848E+03 |
| Mean | 2.8907E+03 | 2.9097E+03 | 2.9185E+03 | 2.8960E+03 | 2.9229E+03 | 2.9484E+03 | 3.0280E+03 | 2.9506E+03 | 2.9243E+03 | |
| Std | 1.0557E+01 | 3.4297E+01 | 2.8471E+01 | 1.0110E+01 | 2.1556E+01 | 2.8941E+01 | 3.9173E+01 | 2.7926E+01 | 2.9201E+01 | |
| Rank | 1 | 3 | 4 | 2 | 5 | 7 | 9 | 8 | 6 | |
| F25 | Best | 2.9014E+03 | 4.4571E+03 | 3.3839E+03 | 2.9019E+03 | 2.9175E+03 | 2.8931E+03 | 3.7856E+03 | 2.8275E+03 | 4.4050E+03 |
| Mean | 3.9298E+03 | 5.3702E+03 | 5.3353E+03 | 4.8042E+03 | 5.0892E+03 | 6.0703E+03 | 5.2000E+03 | 4.5094E+03 | 4.8686E+03 | |
| Std | 2.3423E+02 | 7.8087E+02 | 6.9976E+02 | 7.1782E+02 | 4.9934E+02 | 1.0926E+03 | 6.2731E+02 | 1.6966E+03 | 2.4936E+02 | |
| Rank | 1 | 8 | 7 | 3 | 5 | 9 | 6 | 2 | 4 | |
| F26 | Best | 3.1903E+03 | 3.1699E+03 | 3.2141E+03 | 3.2131E+03 | 3.2073E+03 | 3.2227E+03 | 3.2498E+03 | 3.2204E+03 | 3.2024E+03 |
| Mean | 3.2092E+03 | 3.2029E+03 | 3.2400E+03 | 3.2319E+03 | 3.2373E+03 | 3.2563E+03 | 3.2923E+03 | 3.2731E+03 | 3.2257E+03 | |
| Std | 1.1246E+01 | 2.5796E+01 | 1.7800E+01 | 1.3820E+01 | 1.8337E+01 | 1.8603E+01 | 2.1097E+01 | 4.1984E+01 | 1.6433E+01 | |
| Rank | 2 | 1 | 6 | 4 | 5 | 7 | 9 | 8 | 3 | |
| F27 | Best | 3.1515E+03 | 3.1000E+03 | 3.2243E+03 | 3.2149E+03 | 3.2374E+03 | 3.2482E+03 | 3.3422E+03 | 3.2359E+03 | 3.2179E+03 |
| Mean | 3.2208E+03 | 3.2945E+03 | 3.2798E+03 | 3.2797E+03 | 3.3135E+03 | 3.3366E+03 | 3.4381E+03 | 3.3154E+03 | 3.3196E+03 | |
| Std | 2.4966E+01 | 1.6891E+02 | 3.6831E+01 | 5.3500E+01 | 5.7544E+01 | 6.6068E+01 | 5.9463E+01 | 3.6098E+01 | 9.5669E+01 | |
| Rank | 1 | 4 | 3 | 2 | 5 | 8 | 9 | 6 | 7 | |
| F28 | Best | 3.3168E+03 | 3.5729E+03 | 3.6311E+03 | 3.6183E+03 | 3.7617E+03 | 3.7044E+03 | 3.7077E+03 | 3.6549E+03 | 3.5798E+03 |
| Mean | 3.4787E+03 | 4.1508E+03 | 4.1094E+03 | 4.0179E+03 | 4.2156E+03 | 4.4999E+03 | 4.0290E+03 | 4.3329E+03 | 3.9628E+03 | |
| Std | 1.1094E+02 | 3.2398E+02 | 2.2662E+02 | 2.0908E+02 | 2.8726E+02 | 4.5512E+02 | 2.0377E+02 | 2.9657E+02 | 1.9952E+02 | |
| Rank | 1 | 6 | 5 | 3 | 7 | 9 | 4 | 8 | 2 | |
| F29 | Best | 6.5387E+03 | 3.5199E+03 | 1.0919E+04 | 9.4444E+03 | 1.6955E+05 | 2.0461E+05 | 5.1950E+05 | 4.9837E+05 | 7.7834E+03 |
| Mean | 9.2945E+03 | 4.5718E+04 | 3.1062E+04 | 2.7255E+04 | 2.2564E+06 | 1.8785E+06 | 2.9361E+06 | 4.5101E+06 | 4.7543E+04 | |
| Std | 1.9576E+03 | 7.1343E+04 | 2.0563E+04 | 2.1276E+04 | 1.5693E+06 | 2.1123E+06 | 1.6713E+06 | 3.4826E+06 | 6.4662E+04 | |
| Rank | 1 | 4 | 3 | 2 | 7 | 6 | 8 | 9 | 5 |
| No. | Index | BWSMA | PSMADE | MSSMA | ESMA | LSMA | AOSMA | EOSMA | ISMA | DTSMA |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 2.2772E+04 | 1.0000E+02 | 6.4899E+05 | 9.7295E+05 | 3.9392E+06 | 9.5649E+07 | 5.6239E+09 | 5.7046E+07 | 3.4340E+07 |
| Mean | 2.8243E+05 | 6.1813E+08 | 4.5348E+08 | 2.4241E+06 | 1.9712E+07 | 3.6576E+08 | 9.6131E+09 | 2.1697E+08 | 1.6302E+09 | |
| Std | 3.9156E+05 | 1.3707E+09 | 6.8866E+08 | 1.1989E+06 | 1.3938E+07 | 2.2345E+08 | 2.4211E+09 | 1.3587E+08 | 1.5894E+09 | |
| Rank | 1 | 7 | 6 | 2 | 3 | 5 | 9 | 4 | 8 | |
| F2 | Best | 4.8335E+03 | 3.0000E+02 | 8.7522E+04 | 1.0773E+05 | 1.3557E+05 | 1.4008E+05 | 1.3961E+05 | 1.0639E+05 | 1.0150E+05 |
| Mean | 1.2313E+04 | 2.1724E+04 | 1.2955E+05 | 1.9671E+05 | 2.1779E+05 | 2.4652E+05 | 2.1285E+05 | 1.4603E+05 | 1.8305E+05 | |
| Std | 5.5277E+03 | 7.1891E+04 | 2.7665E+04 | 8.3683E+04 | 6.2447E+04 | 6.5210E+04 | 4.3165E+04 | 2.7059E+04 | 3.9778E+04 | |
| Rank | 1 | 2 | 3 | 6 | 8 | 9 | 7 | 4 | 5 | |
| F3 | Best | 4.7970E+02 | 4.0000E+02 | 5.3376E+02 | 5.1636E+02 | 5.8210E+02 | 6.4686E+02 | 1.1197E+03 | 5.9973E+02 | 5.9039E+02 |
| Mean | 5.6915E+02 | 5.8963E+02 | 6.9837E+02 | 6.3937E+02 | 6.8473E+02 | 8.1523E+02 | 1.6784E+03 | 7.4700E+02 | 7.0552E+02 | |
| Std | 4.6928E+01 | 3.2269E+02 | 9.5195E+01 | 8.2290E+01 | 8.0461E+01 | 1.0539E+02 | 3.3899E+02 | 9.5846E+01 | 9.0605E+01 | |
| Rank | 1 | 2 | 5 | 3 | 4 | 8 | 9 | 7 | 6 | |
| F4 | Best | 5.4801E+02 | 6.9568E+02 | 7.1428E+02 | 6.7726E+02 | 7.0535E+02 | 7.7916E+02 | 8.1320E+02 | 7.7826E+02 | 6.8301E+02 |
| Mean | 5.7665E+02 | 8.6683E+02 | 8.4565E+02 | 7.7474E+02 | 8.2337E+02 | 8.8183E+02 | 8.8336E+02 | 8.6257E+02 | 7.8430E+02 | |
| Std | 1.8467E+01 | 8.2701E+01 | 5.1042E+01 | 4.9038E+01 | 5.8738E+01 | 4.5495E+01 | 3.9031E+01 | 4.5313E+01 | 4.5274E+01 | |
| Rank | 1 | 7 | 5 | 2 | 4 | 8 | 9 | 6 | 3 | |
| F5 | Best | 6.0118E+02 | 6.3126E+02 | 6.3528E+02 | 6.1203E+02 | 6.2703E+02 | 6.4602E+02 | 6.1869E+02 | 6.5129E+02 | 6.1841E+02 |
| Mean | 6.0176E+02 | 6.5209E+02 | 6.5763E+02 | 6.3189E+02 | 6.5783E+02 | 6.6525E+02 | 6.2796E+02 | 6.6608E+02 | 6.3405E+02 | |
| Std | 4.0912E−01 | 1.2810E+01 | 7.0569E+00 | 1.3147E+01 | 1.3764E+01 | 9.6085E+00 | 4.5632E+00 | 5.9429E+00 | 8.6927E+00 | |
| Rank | 1 | 5 | 6 | 3 | 7 | 8 | 2 | 9 | 4 | |
| F6 | Best | 8.1345E+02 | 1.0202E+03 | 1.1952E+03 | 9.8396E+02 | 1.0587E+03 | 1.4611E+03 | 1.1407E+03 | 1.2768E+03 | 1.0032E+03 |
| Mean | 8.3261E+02 | 1.3281E+03 | 1.3932E+03 | 1.0710E+03 | 1.1928E+03 | 1.6114E+03 | 1.2732E+03 | 1.5255E+03 | 1.1562E+03 | |
| Std | 1.3712E+01 | 1.9399E+02 | 1.2780E+02 | 5.8507E+01 | 6.9656E+01 | 9.0108E+01 | 5.0025E+01 | 1.2564E+02 | 7.8902E+01 | |
| Rank | 1 | 6 | 7 | 2 | 4 | 9 | 5 | 8 | 3 | |
| F7 | Best | 8.5389E+02 | 9.8108E+02 | 9.6875E+02 | 9.7108E+02 | 9.8655E+02 | 1.0898E+03 | 1.1298E+03 | 1.1131E+03 | 9.9292E+02 |
| Mean | 8.8293E+02 | 1.1569E+03 | 1.0984E+03 | 1.0608E+03 | 1.0799E+03 | 1.1762E+03 | 1.1809E+03 | 1.1857E+03 | 1.0817E+03 | |
| Std | 1.6990E+01 | 1.2745E+02 | 5.5483E+01 | 4.2841E+01 | 4.7072E+01 | 4.0532E+01 | 3.6644E+01 | 4.8019E+01 | 5.4665E+01 | |
| Rank | 1 | 6 | 5 | 2 | 3 | 7 | 8 | 9 | 4 | |
| F8 | Best | 9.1646E+02 | 7.3420E+03 | 9.8470E+03 | 6.7604E+03 | 5.7581E+03 | 1.1029E+04 | 4.8197E+03 | 9.2286E+03 | 4.5803E+03 |
| Mean | 9.8237E+02 | 1.2779E+04 | 1.3742E+04 | 1.3700E+04 | 1.5300E+04 | 1.7266E+04 | 8.6381E+03 | 1.5002E+04 | 1.5044E+04 | |
| Std | 6.5657E+01 | 4.2815E+03 | 2.3205E+03 | 3.4261E+03 | 4.6562E+03 | 3.5880E+03 | 2.5935E+03 | 2.8783E+03 | 6.4447E+03 | |
| Rank | 1 | 3 | 5 | 4 | 8 | 9 | 2 | 6 | 7 | |
| F9 | Best | 5.4030E+03 | 7.6646E+03 | 5.8646E+03 | 5.3024E+03 | 6.9870E+03 | 7.4566E+03 | 1.2738E+04 | 7.0330E+03 | 7.6102E+03 |
| Mean | 7.0530E+03 | 9.0861E+03 | 7.7637E+03 | 7.7454E+03 | 9.2959E+03 | 9.1503E+03 | 1.4042E+04 | 9.3203E+03 | 1.0048E+04 | |
| Std | 8.3965E+02 | 8.0896E+02 | 8.3191E+02 | 1.0840E+03 | 9.4611E+02 | 9.5531E+02 | 6.9658E+02 | 1.1188E+03 | 1.3253E+03 | |
| Rank | 1 | 4 | 3 | 2 | 6 | 5 | 9 | 7 | 8 | |
| F10 | Best | 1.1788E+03 | 1.2681E+03 | 1.3106E+03 | 1.2641E+03 | 1.5093E+03 | 1.5648E+03 | 3.9085E+03 | 1.6562E+03 | 1.3758E+03 |
| Mean | 1.2613E+03 | 1.5997E+03 | 1.6696E+03 | 1.6011E+03 | 1.7681E+03 | 1.9905E+03 | 7.6993E+03 | 2.3330E+03 | 1.7888E+03 | |
| Std | 4.9045E+01 | 7.2125E+02 | 5.4318E+02 | 3.6943E+02 | 1.5322E+02 | 2.8048E+02 | 2.3595E+03 | 4.2746E+02 | 6.0474E+02 | |
| Rank | 1 | 2 | 4 | 3 | 5 | 7 | 9 | 8 | 6 | |
| F11 | Best | 2.6165E+05 | 4.8274E+03 | 5.6123E+06 | 4.9412E+06 | 3.1661E+07 | 1.4728E+07 | 2.3931E+08 | 1.1518E+07 | 7.1583E+06 |
| Mean | 1.5527E+06 | 2.9104E+07 | 2.4402E+07 | 3.1679E+07 | 1.3788E+08 | 1.8082E+08 | 4.8420E+08 | 1.5218E+08 | 5.9298E+07 | |
| Std | 9.5160E+05 | 6.6964E+07 | 1.2898E+07 | 1.7887E+07 | 6.2919E+07 | 1.0877E+08 | 2.1731E+08 | 1.0985E+08 | 4.3923E+07 | |
| Rank | 1 | 3 | 2 | 4 | 6 | 8 | 9 | 7 | 5 | |
| F12 | Best | 9.5964E+03 | 3.1327E+03 | 6.3253E+03 | 2.0611E+04 | 9.1026E+04 | 8.9658E+04 | 2.7505E+06 | 4.7423E+04 | 1.6261E+04 |
| Mean | 2.2395E+04 | 4.3151E+04 | 2.9145E+04 | 5.0479E+04 | 3.4285E+05 | 3.2943E+05 | 1.7669E+07 | 2.3177E+05 | 9.3725E+04 | |
| Std | 7.7615E+03 | 9.6662E+04 | 1.8915E+04 | 1.5178E+04 | 1.7265E+05 | 2.0768E+05 | 1.3889E+07 | 2.4851E+05 | 5.6176E+04 | |
| Rank | 1 | 3 | 2 | 4 | 8 | 7 | 9 | 6 | 5 | |
| F13 | Best | 1.5033E+03 | 2.0889E+03 | 1.9077E+05 | 2.3245E+05 | 4.1731E+04 | 1.1731E+05 | 3.9002E+04 | 9.8721E+04 | 6.2884E+04 |
| Mean | 1.6526E+03 | 2.9368E+05 | 1.6980E+06 | 1.6337E+06 | 7.4726E+05 | 1.9352E+06 | 5.5138E+05 | 9.9456E+05 | 6.2524E+05 | |
| Std | 7.8456E+01 | 5.4349E+05 | 1.7153E+06 | 1.3047E+06 | 4.9908E+05 | 2.0747E+06 | 4.4313E+05 | 7.8930E+05 | 3.9331E+05 | |
| Rank | 1 | 2 | 8 | 7 | 5 | 9 | 3 | 6 | 4 | |
| F14 | Best | 2.5115E+03 | 1.9923E+03 | 2.4372E+03 | 3.0474E+03 | 4.4306E+04 | 5.2545E+04 | 7.9464E+04 | 9.0954E+03 | 3.7593E+03 |
| Mean | 3.1552E+03 | 2.3014E+04 | 1.6238E+04 | 1.8430E+04 | 1.9472E+05 | 1.7005E+05 | 4.4899E+05 | 7.3543E+04 | 2.5794E+04 | |
| Std | 6.6451E+02 | 2.8203E+04 | 9.0873E+03 | 1.0653E+04 | 1.2988E+05 | 8.2724E+04 | 4.8514E+05 | 9.6703E+04 | 1.2565E+04 | |
| Rank | 1 | 4 | 2 | 3 | 8 | 7 | 9 | 6 | 5 | |
| F15 | Best | 1.7799E+03 | 2.2160E+03 | 2.8406E+03 | 2.6805E+03 | 2.5063E+03 | 3.2678E+03 | 3.2432E+03 | 3.1045E+03 | 2.5820E+03 |
| Mean | 2.8279E+03 | 3.8730E+03 | 3.7318E+03 | 3.5517E+03 | 3.9490E+03 | 4.2687E+03 | 3.9910E+03 | 4.2396E+03 | 3.5876E+03 | |
| Std | 4.5854E+02 | 6.1011E+02 | 4.6396E+02 | 4.3651E+02 | 5.1307E+02 | 5.0142E+02 | 3.4916E+02 | 5.6080E+02 | 4.3924E+02 | |
| Rank | 1 | 5 | 4 | 2 | 6 | 9 | 7 | 8 | 3 | |
| F16 | Best | 2.1039E+03 | 3.0801E+03 | 2.9636E+03 | 2.6659E+03 | 3.1485E+03 | 3.1694E+03 | 2.7991E+03 | 2.9940E+03 | 2.7311E+03 |
| Mean | 2.5797E+03 | 3.7260E+03 | 3.4508E+03 | 3.3790E+03 | 3.7855E+03 | 3.9485E+03 | 3.5078E+03 | 3.6257E+03 | 3.3087E+03 | |
| Std | 2.5402E+02 | 4.3092E+02 | 2.6435E+02 | 3.2551E+02 | 3.6903E+02 | 3.9901E+02 | 2.8821E+02 | 3.3162E+02 | 3.1031E+02 | |
| Rank | 1 | 7 | 4 | 3 | 8 | 9 | 5 | 6 | 2 | |
| F17 | Best | 2.4931E+03 | 5.7230E+03 | 5.0978E+05 | 6.3527E+05 | 5.5984E+05 | 9.3466E+05 | 1.5501E+06 | 1.1075E+06 | 5.7002E+05 |
| Mean | 6.6545E+03 | 1.4355E+06 | 7.1096E+06 | 5.8980E+06 | 7.1864E+06 | 8.5324E+06 | 6.1690E+06 | 5.7511E+06 | 5.8071E+06 | |
| Std | 5.3557E+03 | 3.2474E+06 | 6.0555E+06 | 3.8228E+06 | 5.4004E+06 | 6.0432E+06 | 3.5232E+06 | 6.9422E+06 | 3.9372E+06 | |
| Rank | 1 | 2 | 7 | 5 | 8 | 9 | 6 | 3 | 4 | |
| F18 | Best | 1.9961E+03 | 2.2001E+03 | 2.2033E+03 | 2.5872E+03 | 1.7702E+05 | 2.1330E+05 | 1.3118E+04 | 3.3468E+05 | 2.2445E+03 |
| Mean | 2.4372E+03 | 1.5373E+04 | 2.4267E+04 | 1.9118E+04 | 1.4870E+06 | 9.0219E+05 | 6.5246E+05 | 2.5440E+06 | 1.9678E+04 | |
| Std | 7.1108E+02 | 1.5870E+04 | 1.5578E+04 | 1.5900E+04 | 8.5286E+05 | 6.7015E+05 | 4.9698E+05 | 1.8325E+06 | 1.7534E+04 | |
| Rank | 1 | 2 | 5 | 3 | 8 | 7 | 6 | 9 | 4 | |
| F19 | Best | 2.1923E+03 | 2.3610E+03 | 2.5608E+03 | 2.3493E+03 | 2.7197E+03 | 2.5954E+03 | 2.9493E+03 | 2.7084E+03 | 2.4565E+03 |
| Mean | 2.7642E+03 | 3.4931E+03 | 3.2342E+03 | 3.1603E+03 | 3.5204E+03 | 3.6650E+03 | 3.5330E+03 | 3.2753E+03 | 3.2692E+03 | |
| Std | 3.0558E+02 | 3.8923E+02 | 3.2802E+02 | 3.4727E+02 | 3.2343E+02 | 3.4552E+02 | 2.7198E+02 | 2.7457E+02 | 2.9840E+02 | |
| Rank | 1 | 6 | 3 | 2 | 7 | 9 | 8 | 5 | 4 | |
| F20 | Best | 2.3525E+03 | 2.4628E+03 | 2.5003E+03 | 2.4647E+03 | 2.4897E+03 | 2.6142E+03 | 2.5620E+03 | 2.5834E+03 | 2.4656E+03 |
| Mean | 2.3792E+03 | 2.7182E+03 | 2.6108E+03 | 2.5588E+03 | 2.5829E+03 | 2.7551E+03 | 2.6545E+03 | 2.7188E+03 | 2.5445E+03 | |
| Std | 1.5952E+01 | 1.7438E+02 | 6.5267E+01 | 5.4364E+01 | 5.5821E+01 | 7.1946E+01 | 3.6505E+01 | 7.4931E+01 | 4.2963E+01 | |
| Rank | 1 | 7 | 5 | 3 | 4 | 9 | 6 | 8 | 2 | |
| F21 | Best | 5.8954E+03 | 7.9284E+03 | 2.3225E+03 | 7.6005E+03 | 8.0607E+03 | 8.4443E+03 | 1.3962E+04 | 2.5834E+03 | 1.0015E+04 |
| Mean | 8.2923E+03 | 1.0139E+04 | 9.2732E+03 | 9.3368E+03 | 1.0376E+04 | 1.0890E+04 | 1.5541E+04 | 1.0491E+04 | 1.1635E+04 | |
| Std | 9.2514E+02 | 7.8962E+02 | 1.6194E+03 | 9.3280E+02 | 1.2507E+03 | 1.1995E+03 | 7.1557E+02 | 2.2906E+03 | 1.1931E+03 | |
| Rank | 1 | 4 | 2 | 3 | 5 | 7 | 9 | 6 | 8 | |
| F22 | Best | 2.7643E+03 | 2.9340E+03 | 2.9430E+03 | 2.9190E+03 | 2.9364E+03 | 3.0835E+03 | 3.0353E+03 | 3.0611E+03 | 2.9154E+03 |
| Mean | 2.8093E+03 | 3.1147E+03 | 3.0742E+03 | 3.0007E+03 | 3.0245E+03 | 3.2612E+03 | 3.1254E+03 | 3.2536E+03 | 2.9857E+03 | |
| Std | 2.3901E+01 | 1.6809E+02 | 6.0556E+01 | 4.8584E+01 | 4.6460E+01 | 1.2045E+02 | 3.2962E+01 | 9.9453E+01 | 4.4996E+01 | |
| Rank | 1 | 6 | 5 | 3 | 4 | 9 | 7 | 8 | 2 | |
| F23 | Best | 2.9373E+03 | 3.0184E+03 | 3.0966E+03 | 3.0755E+03 | 3.0720E+03 | 3.2100E+03 | 3.1916E+03 | 3.1287E+03 | 3.0444E+03 |
| Mean | 2.9723E+03 | 3.1773E+03 | 3.2383E+03 | 3.1713E+03 | 3.1390E+03 | 3.3821E+03 | 3.2632E+03 | 3.3169E+03 | 3.1376E+03 | |
| Std | 1.6964E+01 | 1.0223E+02 | 6.3556E+01 | 6.2760E+01 | 4.6589E+01 | 9.4779E+01 | 3.7262E+01 | 9.9917E+01 | 5.2025E+01 | |
| Rank | 1 | 5 | 6 | 4 | 3 | 9 | 7 | 8 | 2 | |
| F24 | Best | 2.9855E+03 | 2.9312E+03 | 3.0572E+03 | 3.0519E+03 | 3.0675E+03 | 3.1051E+03 | 3.5453E+03 | 3.1440E+03 | 3.1005E+03 |
| Mean | 3.0412E+03 | 2.9676E+03 | 3.2137E+03 | 3.1071E+03 | 3.1506E+03 | 3.2843E+03 | 4.1380E+03 | 3.2235E+03 | 3.2335E+03 | |
| Std | 2.2587E+01 | 1.2279E+02 | 9.6798E+01 | 3.6783E+01 | 4.0343E+01 | 6.7984E+01 | 3.7539E+02 | 5.8671E+01 | 1.1355E+02 | |
| Rank | 2 | 1 | 5 | 3 | 4 | 8 | 9 | 6 | 7 | |
| F25 | Best | 4.1717E+03 | 6.0278E+03 | 3.8480E+03 | 2.9401E+03 | 3.3680E+03 | 4.5733E+03 | 6.5525E+03 | 4.0205E+03 | 5.2928E+03 |
| Mean | 4.5449E+03 | 8.0511E+03 | 8.2157E+03 | 6.1177E+03 | 6.1024E+03 | 9.7460E+03 | 7.8129E+03 | 7.5498E+03 | 6.4015E+03 | |
| Std | 2.3611E+02 | 1.5523E+03 | 2.1005E+03 | 1.8223E+03 | 2.0601E+03 | 1.5762E+03 | 5.7347E+02 | 3.2412E+03 | 4.5993E+02 | |
| Rank | 1 | 7 | 8 | 3 | 2 | 9 | 6 | 5 | 4 | |
| F26 | Best | 3.2264E+03 | 3.2000E+03 | 3.4081E+03 | 3.3502E+03 | 3.3825E+03 | 3.3675E+03 | 3.6584E+03 | 3.5170E+03 | 3.3002E+03 |
| Mean | 3.3094E+03 | 3.2497E+03 | 3.6312E+03 | 3.4914E+03 | 3.5325E+03 | 3.7199E+03 | 3.8608E+03 | 3.7184E+03 | 3.5019E+03 | |
| Std | 3.8880E+01 | 1.3086E+02 | 1.2887E+02 | 9.5240E+01 | 1.0043E+02 | 1.6699E+02 | 1.1246E+02 | 1.6586E+02 | 8.4692E+01 | |
| Rank | 2 | 1 | 6 | 3 | 5 | 8 | 9 | 7 | 4 | |
| F27 | Best | 3.2632E+03 | 3.3000E+03 | 3.3887E+03 | 3.3090E+03 | 3.3401E+03 | 3.5230E+03 | 4.2240E+03 | 3.4343E+03 | 3.6218E+03 |
| Mean | 3.3027E+03 | 3.6494E+03 | 3.7291E+03 | 3.4022E+03 | 3.7394E+03 | 3.9086E+03 | 4.7918E+03 | 3.6985E+03 | 4.5933E+03 | |
| Std | 3.1206E+01 | 9.2299E+02 | 5.6153E+02 | 8.2011E+01 | 4.4994E+02 | 5.0080E+02 | 3.3160E+02 | 1.2370E+02 | 5.4456E+02 | |
| Rank | 1 | 3 | 5 | 2 | 6 | 7 | 9 | 4 | 8 | |
| F28 | Best | 3.3828E+03 | 4.0942E+03 | 3.6990E+03 | 3.7354E+03 | 4.4689E+03 | 4.8256E+03 | 4.5305E+03 | 4.8457E+03 | 3.8868E+03 |
| Mean | 3.8790E+03 | 5.4609E+03 | 4.7477E+03 | 4.6392E+03 | 5.5211E+03 | 6.3663E+03 | 5.0799E+03 | 6.3122E+03 | 4.8225E+03 | |
| Std | 2.2118E+02 | 8.6846E+02 | 3.9770E+02 | 4.1482E+02 | 5.1188E+02 | 6.8571E+02 | 3.0028E+02 | 6.7974E+02 | 5.2890E+02 | |
| Rank | 1 | 6 | 3 | 2 | 7 | 9 | 5 | 8 | 4 | |
| F29 | Best | 1.0807E+06 | 3.7388E+03 | 1.1910E+06 | 1.6414E+06 | 2.6098E+07 | 1.5959E+07 | 4.0173E+07 | 2.8447E+07 | 4.1697E+06 |
| Mean | 2.5866E+06 | 4.2287E+06 | 2.8195E+06 | 2.9428E+06 | 5.0468E+07 | 6.5650E+07 | 9.1566E+07 | 1.0305E+08 | 1.2572E+07 | |
| Std | 9.6265E+05 | 9.1032E+06 | 1.1761E+06 | 7.7206E+05 | 1.9286E+07 | 2.3721E+07 | 2.5710E+07 | 4.1232E+07 | 5.1729E+06 | |
| Rank | 1 | 4 | 2 | 3 | 6 | 7 | 8 | 9 | 5 |
| No. | Index | BWSMA | PSMADE | MSSMA | ESMA | LSMA | AOSMA | EOSMA | ISMA | DTSMA |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.0265E+08 | 1.0000E+02 | 1.0273E+10 | 1.5980E+08 | 1.3914E+09 | 5.7963E+09 | 6.0312E+10 | 5.0720E+09 | 1.9181E+10 |
| Mean | 2.8491E+08 | 2.0209E+09 | 2.8975E+10 | 2.2008E+08 | 4.5267E+09 | 1.3254E+10 | 8.7886E+10 | 1.0330E+10 | 3.8529E+10 | |
| Std | 1.7408E+08 | 1.1069E+10 | 1.1025E+10 | 3.5040E+07 | 1.5496E+09 | 3.7959E+09 | 1.3888E+10 | 2.8149E+09 | 1.2755E+10 | |
| Rank | 2 | 3 | 7 | 1 | 4 | 6 | 9 | 5 | 8 | |
| F2 | Best | 1.3769E+05 | 6.5811E+02 | 2.4868E+05 | 3.1837E+05 | 3.2539E+05 | 3.3116E+05 | 3.6328E+05 | 2.9425E+05 | 4.4900E+05 |
| Mean | 1.6598E+05 | 6.2645E+04 | 3.1088E+05 | 9.5370E+05 | 7.9412E+05 | 5.9109E+05 | 5.4570E+05 | 3.4426E+05 | 7.4169E+05 | |
| Std | 2.2104E+04 | 2.0461E+05 | 5.8454E+04 | 2.7790E+05 | 3.4020E+05 | 3.1668E+05 | 1.0958E+05 | 2.8032E+04 | 1.3130E+05 | |
| Rank | 2 | 1 | 3 | 9 | 8 | 6 | 5 | 4 | 7 | |
| F3 | Best | 6.9066E+02 | 4.0000E+02 | 1.1313E+03 | 7.1488E+02 | 1.0305E+03 | 1.5504E+03 | 8.0323E+03 | 1.3348E+03 | 1.3791E+03 |
| Mean | 8.3589E+02 | 6.8358E+02 | 1.9135E+03 | 9.2868E+02 | 1.4377E+03 | 2.5573E+03 | 1.0049E+04 | 2.0374E+03 | 2.3361E+03 | |
| Std | 6.2124E+01 | 1.1038E+03 | 6.5387E+02 | 9.6152E+01 | 1.9733E+02 | 4.7336E+02 | 1.3399E+03 | 4.3262E+02 | 6.8833E+02 | |
| Rank | 2 | 1 | 5 | 3 | 4 | 8 | 9 | 6 | 7 | |
| F4 | Best | 7.2204E+02 | 1.2034E+03 | 1.2513E+03 | 1.0907E+03 | 1.2478E+03 | 1.3443E+03 | 1.4119E+03 | 1.2258E+03 | 1.1609E+03 |
| Mean | 8.0340E+02 | 1.3592E+03 | 1.3776E+03 | 1.2785E+03 | 1.4234E+03 | 1.4986E+03 | 1.5635E+03 | 1.4727E+03 | 1.3270E+03 | |
| Std | 3.9544E+01 | 1.5183E+02 | 7.0398E+01 | 1.0696E+02 | 8.2376E+01 | 6.0082E+01 | 6.5691E+01 | 7.2246E+01 | 1.0034E+02 | |
| Rank | 1 | 4 | 5 | 2 | 6 | 8 | 9 | 7 | 3 | |
| F5 | Best | 6.1384E+02 | 6.4660E+02 | 6.5098E+02 | 6.4089E+02 | 6.5884E+02 | 6.6770E+02 | 6.4678E+02 | 6.6969E+02 | 6.5472E+02 |
| Mean | 6.1915E+02 | 6.6098E+02 | 6.6499E+02 | 6.5353E+02 | 6.7448E+02 | 6.7724E+02 | 6.5588E+02 | 6.7855E+02 | 6.6524E+02 | |
| Std | 3.2956E+00 | 7.6064E+00 | 4.2144E+00 | 6.6013E+00 | 5.6399E+00 | 5.3401E+00 | 5.3264E+00 | 5.2588E+00 | 6.7805E+00 | |
| Rank | 1 | 4 | 5 | 2 | 7 | 8 | 3 | 9 | 6 | |
| F6 | Best | 1.2112E+03 | 2.1898E+03 | 2.5445E+03 | 1.7037E+03 | 1.9892E+03 | 2.6188E+03 | 2.4914E+03 | 2.5839E+03 | 2.1128E+03 |
| Mean | 1.3225E+03 | 2.9305E+03 | 2.8889E+03 | 2.0733E+03 | 2.4867E+03 | 3.1360E+03 | 2.6646E+03 | 3.1600E+03 | 2.4525E+03 | |
| Std | 6.0837E+01 | 3.9502E+02 | 1.8954E+02 | 1.6539E+02 | 2.6303E+02 | 1.9145E+02 | 1.2601E+02 | 2.1020E+02 | 2.0140E+02 | |
| Rank | 1 | 7 | 6 | 2 | 4 | 8 | 5 | 9 | 3 | |
| F7 | Best | 1.0303E+03 | 1.4547E+03 | 1.5244E+03 | 1.3885E+03 | 1.5666E+03 | 1.7462E+03 | 1.7250E+03 | 1.7466E+03 | 1.3715E+03 |
| Mean | 1.1138E+03 | 1.7599E+03 | 1.7277E+03 | 1.6059E+03 | 1.7476E+03 | 1.9288E+03 | 1.8680E+03 | 1.8976E+03 | 1.6628E+03 | |
| Std | 4.4101E+01 | 2.2933E+02 | 9.5766E+01 | 1.2007E+02 | 1.0755E+02 | 8.8628E+01 | 7.1663E+01 | 6.5942E+01 | 1.1775E+02 | |
| Rank | 1 | 6 | 4 | 2 | 5 | 9 | 7 | 8 | 3 | |
| F8 | Best | 3.3200E+03 | 1.7656E+04 | 2.3437E+04 | 2.2879E+04 | 2.9949E+04 | 2.7167E+04 | 3.3780E+04 | 2.7446E+04 | 3.0431E+04 |
| Mean | 5.6313E+03 | 2.5263E+04 | 2.9508E+04 | 3.3904E+04 | 3.5627E+04 | 3.6056E+04 | 4.5519E+04 | 3.7223E+04 | 5.0494E+04 | |
| Std | 1.9177E+03 | 6.3680E+03 | 4.1699E+03 | 4.5039E+03 | 3.7481E+03 | 6.9673E+03 | 7.0502E+03 | 4.6684E+03 | 1.2132E+04 | |
| Rank | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 7 | 9 | |
| F9 | Best | 1.4404E+04 | 1.4789E+04 | 1.3664E+04 | 1.3776E+04 | 1.7255E+04 | 1.4275E+04 | 2.9286E+04 | 1.6856E+04 | 1.8778E+04 |
| Mean | 1.7008E+04 | 1.7120E+04 | 1.5993E+04 | 1.6928E+04 | 2.0754E+04 | 1.9953E+04 | 3.0990E+04 | 2.0679E+04 | 2.3748E+04 | |
| Std | 1.6548E+03 | 1.6567E+03 | 1.2731E+03 | 1.5835E+03 | 1.8778E+03 | 2.0016E+03 | 8.1299E+02 | 1.6560E+03 | 2.5491E+03 | |
| Rank | 3 | 4 | 1 | 2 | 7 | 5 | 9 | 6 | 8 | |
| F10 | Best | 3.2800E+03 | 2.3545E+03 | 1.9234E+04 | 1.9824E+04 | 3.6450E+04 | 4.5393E+04 | 1.1277E+05 | 3.5420E+04 | 1.8560E+04 |
| Mean | 4.5120E+03 | 1.2215E+04 | 4.6116E+04 | 6.2465E+04 | 7.3751E+04 | 1.3203E+05 | 1.5850E+05 | 9.0541E+04 | 7.2622E+04 | |
| Std | 8.6733E+02 | 3.1913E+04 | 1.3927E+04 | 3.1548E+04 | 1.8775E+04 | 4.3091E+04 | 2.6668E+04 | 2.8683E+04 | 2.7561E+04 | |
| Rank | 1 | 2 | 3 | 4 | 6 | 8 | 9 | 7 | 5 | |
| F11 | Best | 4.3706E+07 | 1.5220E+04 | 1.0893E+08 | 7.9872E+07 | 3.3278E+08 | 3.9815E+08 | 6.6482E+09 | 5.9159E+08 | 4.9303E+08 |
| Mean | 9.5046E+07 | 1.5894E+08 | 6.4656E+08 | 2.5477E+08 | 9.2137E+08 | 1.5528E+09 | 1.1253E+10 | 1.2719E+09 | 1.7100E+09 | |
| Std | 3.5906E+07 | 8.6647E+08 | 8.7260E+08 | 8.8376E+07 | 3.7032E+08 | 6.6314E+08 | 2.8981E+09 | 5.2978E+08 | 9.5708E+08 | |
| Rank | 1 | 2 | 4 | 3 | 5 | 7 | 9 | 6 | 8 | |
| F12 | Best | 3.2287E+04 | 7.3629E+03 | 2.3195E+04 | 4.5849E+04 | 8.7732E+04 | 1.9407E+05 | 7.2208E+07 | 1.4726E+05 | 7.9464E+04 |
| Mean | 6.1914E+04 | 5.3463E+05 | 2.5788E+05 | 2.5030E+06 | 5.7856E+06 | 5.3851E+06 | 4.6223E+08 | 6.0345E+05 | 1.5233E+07 | |
| Std | 1.5329E+04 | 2.8460E+06 | 7.9590E+05 | 6.3380E+06 | 1.4225E+07 | 2.2779E+07 | 2.5845E+08 | 4.2061E+05 | 2.3430E+07 | |
| Rank | 1 | 3 | 2 | 5 | 7 | 6 | 9 | 4 | 8 | |
| F13 | Best | 6.3099E+03 | 2.0865E+03 | 1.0861E+06 | 1.6450E+06 | 9.1892E+05 | 1.3205E+06 | 3.2904E+06 | 2.7567E+06 | 8.4568E+05 |
| Mean | 2.1032E+04 | 3.7529E+05 | 4.4620E+06 | 5.1977E+06 | 6.8331E+06 | 7.1228E+06 | 1.0192E+07 | 5.3935E+06 | 5.9499E+06 | |
| Std | 1.2511E+04 | 1.0311E+06 | 2.1301E+06 | 3.0286E+06 | 3.2925E+06 | 3.6973E+06 | 5.2513E+06 | 2.0616E+06 | 3.6656E+06 | |
| Rank | 1 | 2 | 3 | 4 | 7 | 8 | 9 | 5 | 6 | |
| F14 | Best | 8.1804E+03 | 1.7682E+03 | 5.9453E+03 | 1.1694E+04 | 3.6463E+04 | 5.7567E+04 | 8.4992E+06 | 2.8868E+04 | 3.7769E+04 |
| Mean | 2.6324E+04 | 2.2146E+05 | 6.6900E+04 | 7.9369E+05 | 1.6305E+06 | 7.6887E+05 | 2.8000E+07 | 5.1332E+05 | 3.6294E+05 | |
| Std | 1.1801E+04 | 1.1548E+06 | 1.9317E+05 | 1.6329E+06 | 2.4890E+06 | 3.4224E+06 | 1.4665E+07 | 2.4034E+06 | 1.4097E+06 | |
| Rank | 1 | 3 | 2 | 7 | 8 | 6 | 9 | 5 | 4 | |
| F15 | Best | 4.0879E+03 | 5.2223E+03 | 4.7470E+03 | 4.5316E+03 | 6.2277E+03 | 6.8853E+03 | 7.9990E+03 | 6.9859E+03 | 4.6261E+03 |
| Mean | 4.9977E+03 | 6.1325E+03 | 6.3646E+03 | 6.2083E+03 | 7.4944E+03 | 8.5775E+03 | 8.9878E+03 | 8.9101E+03 | 6.4175E+03 | |
| Std | 7.4905E+02 | 6.5246E+02 | 7.6658E+02 | 7.3010E+02 | 7.9277E+02 | 8.5704E+02 | 5.5377E+02 | 1.3104E+03 | 8.4104E+02 | |
| Rank | 1 | 2 | 4 | 3 | 6 | 7 | 9 | 8 | 5 | |
| F16 | Best | 3.4256E+03 | 4.7067E+03 | 5.0189E+03 | 4.6056E+03 | 5.4948E+03 | 6.0705E+03 | 5.6278E+03 | 5.3169E+03 | 4.5023E+03 |
| Mean | 4.6606E+03 | 6.5558E+03 | 6.1219E+03 | 5.5962E+03 | 6.4246E+03 | 7.4520E+03 | 6.4340E+03 | 6.4170E+03 | 5.8027E+03 | |
| Std | 5.0956E+02 | 9.5349E+02 | 5.8425E+02 | 6.1499E+02 | 6.0518E+02 | 7.4471E+02 | 4.6567E+02 | 5.7613E+02 | 6.5486E+02 | |
| Rank | 1 | 8 | 4 | 2 | 6 | 9 | 7 | 5 | 3 | |
| F17 | Best | 4.7477E+04 | 1.5871E+04 | 1.8163E+06 | 3.0645E+06 | 2.4824E+06 | 1.8904E+06 | 3.6818E+06 | 2.1546E+06 | 1.3697E+06 |
| Mean | 1.1397E+05 | 4.0302E+05 | 8.7971E+06 | 1.1373E+07 | 1.1956E+07 | 1.2483E+07 | 1.3980E+07 | 6.8897E+06 | 9.0052E+06 | |
| Std | 2.9092E+04 | 1.2995E+06 | 6.1019E+06 | 5.9041E+06 | 6.4682E+06 | 6.3501E+06 | 7.2678E+06 | 4.2311E+06 | 6.1256E+06 | |
| Rank | 1 | 2 | 4 | 6 | 7 | 8 | 9 | 3 | 5 | |
| F18 | Best | 5.5765E+03 | 2.9290E+03 | 3.8233E+03 | 8.7634E+03 | 5.0790E+06 | 2.7242E+06 | 1.3736E+07 | 1.6232E+06 | 6.3781E+04 |
| Mean | 3.4841E+04 | 1.6243E+05 | 2.0678E+04 | 1.1120E+05 | 1.4690E+07 | 1.4412E+07 | 4.4835E+07 | 1.5173E+07 | 1.9102E+06 | |
| Std | 5.1133E+04 | 8.0569E+05 | 1.3779E+04 | 1.7466E+05 | 5.4649E+06 | 6.9257E+06 | 2.2778E+07 | 9.3678E+06 | 3.6679E+06 | |
| Rank | 2 | 4 | 1 | 3 | 7 | 6 | 9 | 8 | 5 | |
| F19 | Best | 3.5877E+03 | 4.3344E+03 | 4.2840E+03 | 4.3189E+03 | 5.0748E+03 | 4.3897E+03 | 6.2242E+03 | 4.6176E+03 | 4.8461E+03 |
| Mean | 4.7847E+03 | 5.7490E+03 | 5.3724E+03 | 5.4802E+03 | 5.9994E+03 | 6.0352E+03 | 7.1144E+03 | 5.6219E+03 | 5.9657E+03 | |
| Std | 5.5316E+02 | 6.8522E+02 | 5.0957E+02 | 5.8964E+02 | 6.6859E+02 | 5.8573E+02 | 3.9074E+02 | 4.8114E+02 | 6.3589E+02 | |
| Rank | 1 | 5 | 2 | 3 | 7 | 8 | 9 | 4 | 6 | |
| F20 | Best | 2.5332E+03 | 2.8945E+03 | 2.9976E+03 | 3.0009E+03 | 3.0305E+03 | 3.3541E+03 | 3.2557E+03 | 3.3003E+03 | 2.9346E+03 |
| Mean | 2.6101E+03 | 3.2775E+03 | 3.2069E+03 | 3.1535E+03 | 3.2390E+03 | 3.6939E+03 | 3.3702E+03 | 3.6660E+03 | 3.1476E+03 | |
| Std | 4.1714E+01 | 2.9818E+02 | 1.0983E+02 | 1.1098E+02 | 1.4544E+02 | 1.7412E+02 | 7.0034E+01 | 2.2008E+02 | 1.0797E+02 | |
| Rank | 1 | 6 | 4 | 3 | 5 | 9 | 7 | 8 | 2 | |
| F21 | Best | 1.6957E+04 | 1.5881E+04 | 1.7543E+04 | 1.6381E+04 | 1.9203E+04 | 1.8058E+04 | 3.1234E+04 | 2.0840E+04 | 2.0508E+04 |
| Mean | 1.9600E+04 | 1.8953E+04 | 1.9742E+04 | 1.9304E+04 | 2.2661E+04 | 2.2189E+04 | 3.3638E+04 | 2.4358E+04 | 2.5564E+04 | |
| Std | 1.7835E+03 | 1.6938E+03 | 1.3845E+03 | 1.3837E+03 | 1.6355E+03 | 1.6066E+03 | 1.1045E+03 | 1.9306E+03 | 2.7386E+03 | |
| Rank | 3 | 1 | 4 | 2 | 6 | 5 | 9 | 7 | 8 | |
| F22 | Best | 3.0796E+03 | 3.4184E+03 | 3.3219E+03 | 3.2563E+03 | 3.3552E+03 | 3.8151E+03 | 3.8254E+03 | 3.6516E+03 | 3.3939E+03 |
| Mean | 3.1773E+03 | 3.7474E+03 | 3.5402E+03 | 3.4040E+03 | 3.5996E+03 | 4.0840E+03 | 4.0013E+03 | 4.1253E+03 | 3.5173E+03 | |
| Std | 4.9991E+01 | 3.0734E+02 | 9.1065E+01 | 8.9650E+01 | 1.2057E+02 | 1.8547E+02 | 8.7463E+01 | 1.9708E+02 | 1.1281E+02 | |
| Rank | 1 | 6 | 4 | 2 | 5 | 8 | 7 | 9 | 3 | |
| F23 | Best | 3.5310E+03 | 4.0138E+03 | 3.9474E+03 | 3.7837E+03 | 3.8917E+03 | 4.3896E+03 | 4.4619E+03 | 4.3582E+03 | 3.7723E+03 |
| Mean | 3.6141E+03 | 4.4434E+03 | 4.3264E+03 | 4.0578E+03 | 4.1328E+03 | 4.8687E+03 | 4.7062E+03 | 4.8274E+03 | 4.0445E+03 | |
| Std | 4.8296E+01 | 3.0220E+02 | 1.7642E+02 | 1.4371E+02 | 1.5046E+02 | 2.0576E+02 | 1.3066E+02 | 2.8974E+02 | 1.5119E+02 | |
| Rank | 1 | 6 | 5 | 3 | 4 | 9 | 7 | 8 | 2 | |
| F24 | Best | 3.4140E+03 | 3.1342E+03 | 4.0962E+03 | 3.4387E+03 | 3.9387E+03 | 4.3573E+03 | 8.0506E+03 | 4.2950E+03 | 5.1241E+03 |
| Mean | 3.5994E+03 | 3.3619E+03 | 4.5878E+03 | 3.6223E+03 | 4.3451E+03 | 4.8973E+03 | 9.5649E+03 | 4.6657E+03 | 5.9846E+03 | |
| Std | 7.7347E+01 | 7.5070E+02 | 3.5875E+02 | 8.5393E+01 | 1.8920E+02 | 3.0510E+02 | 1.0302E+03 | 2.3573E+02 | 7.0328E+02 | |
| Rank | 2 | 1 | 5 | 3 | 4 | 7 | 9 | 6 | 8 | |
| F25 | Best | 7.9404E+03 | 1.2056E+04 | 1.6024E+04 | 5.0144E+03 | 1.3366E+04 | 1.7083E+04 | 1.6903E+04 | 8.2631E+03 | 1.1857E+04 |
| Mean | 9.3106E+03 | 1.8961E+04 | 1.9438E+04 | 1.4145E+04 | 1.6818E+04 | 2.3963E+04 | 2.2209E+04 | 2.2351E+04 | 1.4484E+04 | |
| Std | 5.2458E+02 | 3.5047E+03 | 2.4147E+03 | 2.8477E+03 | 2.0762E+03 | 3.8437E+03 | 2.6574E+03 | 5.0108E+03 | 1.3520E+03 | |
| Rank | 1 | 5 | 6 | 2 | 4 | 9 | 7 | 8 | 3 | |
| F26 | Best | 3.4009E+03 | 3.2000E+03 | 3.5941E+03 | 3.4927E+03 | 3.6195E+03 | 3.8200E+03 | 4.4311E+03 | 3.6766E+03 | 3.5763E+03 |
| Mean | 3.5339E+03 | 3.3148E+03 | 3.7556E+03 | 3.6478E+03 | 3.8269E+03 | 4.2150E+03 | 4.7317E+03 | 4.0241E+03 | 3.7398E+03 | |
| Std | 5.6082E+01 | 2.2273E+02 | 1.0393E+02 | 7.8908E+01 | 1.1259E+02 | 2.2145E+02 | 2.1257E+02 | 2.5743E+02 | 1.1569E+02 | |
| Rank | 2 | 1 | 5 | 3 | 6 | 8 | 9 | 7 | 4 | |
| F27 | Best | 3.5590E+03 | 3.2325E+03 | 3.9333E+03 | 3.5705E+03 | 4.0311E+03 | 4.4549E+03 | 9.4426E+03 | 4.3866E+03 | 5.9944E+03 |
| Mean | 3.6806E+03 | 3.4971E+03 | 4.3474E+03 | 3.7210E+03 | 4.6672E+03 | 5.5903E+03 | 1.2459E+04 | 5.2687E+03 | 1.0331E+04 | |
| Std | 9.5163E+01 | 1.0766E+03 | 2.7440E+02 | 1.1732E+02 | 3.9560E+02 | 5.5962E+02 | 1.3068E+03 | 4.4948E+02 | 2.8753E+03 | |
| Rank | 2 | 1 | 4 | 3 | 5 | 7 | 9 | 6 | 8 | |
| F28 | Best | 5.5167E+03 | 6.5066E+03 | 6.9109E+03 | 6.4502E+03 | 8.6281E+03 | 9.4831E+03 | 9.6880E+03 | 9.0513E+03 | 7.1650E+03 |
| Mean | 6.6937E+03 | 9.2483E+03 | 8.0587E+03 | 7.4525E+03 | 1.0005E+04 | 1.1937E+04 | 1.0410E+04 | 1.0798E+04 | 8.8109E+03 | |
| Std | 6.2841E+02 | 1.5798E+03 | 6.3647E+02 | 5.0935E+02 | 8.4343E+02 | 1.2488E+03 | 5.5799E+02 | 9.9748E+02 | 8.0167E+02 | |
| Rank | 1 | 5 | 3 | 2 | 6 | 9 | 7 | 8 | 4 | |
| F29 | Best | 3.2499E+05 | 3.9667E+03 | 4.4536E+05 | 5.5091E+05 | 4.0327E+07 | 4.3498E+07 | 1.1863E+08 | 8.4034E+07 | 5.3455E+06 |
| Mean | 1.1447E+06 | 9.8737E+05 | 2.9147E+06 | 1.7574E+06 | 1.4516E+08 | 1.9708E+08 | 3.0956E+08 | 2.7029E+08 | 4.0235E+07 | |
| Std | 5.1175E+05 | 5.3558E+06 | 2.7549E+06 | 9.2568E+05 | 7.1101E+07 | 1.1442E+08 | 1.0674E+08 | 1.6778E+08 | 2.8711E+07 | |
| Rank | 2 | 1 | 4 | 3 | 6 | 7 | 9 | 8 | 5 |
| No. | Index | BWSMA | NMPA | BEESO | FDBARO | WOSSA | PHISAO | ESLPSO | EPSCA | IGWO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 3.0000E+02 | 3.0965E+02 | 1.1153E+03 | 6.9410E+02 | 3.0251E+02 | 3.4055E+02 | 3.0003E+02 | 3.0000E+02 | 3.0040E+02 |
| Mean | 3.0000E+02 | 3.5010E+02 | 2.4124E+03 | 2.6451E+03 | 5.6494E+02 | 1.2333E+03 | 3.2768E+02 | 3.0000E+02 | 3.0608E+02 | |
| Std | 1.3704E−03 | 3.6816E+01 | 8.9681E+02 | 1.2847E+03 | 4.6474E+02 | 1.0829E+03 | 5.3229E+01 | 3.6367E−13 | 7.1490E+00 | |
| Rank | 2 | 5 | 8 | 9 | 6 | 7 | 4 | 1 | 3 | |
| F2 | Best | 4.0002E+02 | 4.0048E+02 | 4.0505E+02 | 4.0084E+02 | 4.0003E+02 | 4.0003E+02 | 4.0005E+02 | 4.0000E+02 | 4.0004E+02 |
| Mean | 4.0649E+02 | 4.0597E+02 | 4.0788E+02 | 4.0713E+02 | 4.1378E+02 | 4.1382E+02 | 4.0867E+02 | 4.0590E+02 | 4.0425E+02 | |
| Std | 2.8829E+00 | 4.0267E+00 | 1.1353E+00 | 5.3986E+00 | 2.1786E+01 | 1.8793E+01 | 7.2028E+00 | 2.9487E+00 | 3.0498E+00 | |
| Rank | 4 | 3 | 6 | 5 | 8 | 9 | 7 | 2 | 1 | |
| F3 | Best | 6.0000E+02 | 6.0135E+02 | 6.0002E+02 | 6.0055E+02 | 6.0000E+02 | 6.0000E+02 | 6.0000E+02 | 6.0000E+02 | 6.0009E+02 |
| Mean | 6.0002E+02 | 6.0440E+02 | 6.0009E+02 | 6.0140E+02 | 6.0425E+02 | 6.0001E+02 | 6.0000E+02 | 6.0019E+02 | 6.0021E+02 | |
| Std | 1.9725E−02 | 2.3891E+00 | 6.2868E−02 | 5.9746E−01 | 5.9267E+00 | 3.9089E−02 | 7.1738E−05 | 5.9383E−01 | 6.2669E−02 | |
| Rank | 3 | 9 | 4 | 7 | 8 | 2 | 1 | 5 | 6 | |
| F4 | Best | 8.0298E+02 | 8.0657E+02 | 8.1322E+02 | 8.0767E+02 | 8.0995E+02 | 8.0099E+02 | 8.0597E+02 | 8.0497E+02 | 8.0300E+02 |
| Mean | 8.0813E+02 | 8.2033E+02 | 8.2786E+02 | 8.1619E+02 | 8.2355E+02 | 8.0468E+02 | 8.2902E+02 | 8.1721E+02 | 8.1151E+02 | |
| Std | 3.4574E+00 | 6.0268E+00 | 6.4061E+00 | 5.0854E+00 | 7.9996E+00 | 2.4532E+00 | 8.9915E+00 | 1.0183E+01 | 7.3784E+00 | |
| Rank | 2 | 6 | 8 | 4 | 7 | 1 | 9 | 5 | 3 | |
| F5 | Best | 9.0000E+02 | 9.0160E+02 | 9.0000E+02 | 9.0035E+02 | 9.0018E+02 | 9.0000E+02 | 9.0000E+02 | 9.0000E+02 | 9.0000E+02 |
| Mean | 9.0001E+02 | 9.2421E+02 | 9.0015E+02 | 9.0395E+02 | 1.2470E+03 | 9.0011E+02 | 9.0002E+02 | 9.1037E+02 | 9.0004E+02 | |
| Std | 2.2714E−02 | 1.7375E+01 | 2.2947E−01 | 4.7900E+00 | 2.4488E+02 | 2.8510E−01 | 8.2948E−02 | 1.7032E+01 | 3.1145E−02 | |
| Rank | 1 | 8 | 5 | 6 | 9 | 4 | 2 | 7 | 3 | |
| F6 | Best | 1.8002E+03 | 2.2677E+03 | 1.9239E+03 | 1.9669E+03 | 1.9373E+03 | 1.8279E+03 | 1.8258E+03 | 1.8018E+03 | 2.5279E+03 |
| Mean | 1.8130E+03 | 4.7254E+03 | 5.5868E+03 | 3.8589E+03 | 3.8391E+03 | 3.5875E+03 | 2.4158E+03 | 1.8374E+03 | 5.6507E+03 | |
| Std | 1.1076E+01 | 1.9140E+03 | 2.2316E+03 | 1.6484E+03 | 1.9209E+03 | 1.4286E+03 | 1.0026E+03 | 2.1735E+01 | 2.0008E+03 | |
| Rank | 1 | 7 | 8 | 6 | 5 | 4 | 3 | 2 | 9 | |
| F7 | Best | 2.0000E+03 | 2.0077E+03 | 2.0040E+03 | 2.0040E+03 | 2.0020E+03 | 2.0000E+03 | 2.0041E+03 | 2.0010E+03 | 2.0005E+03 |
| Mean | 2.0163E+03 | 2.0264E+03 | 2.0193E+03 | 2.0199E+03 | 2.0285E+03 | 2.0125E+03 | 2.0212E+03 | 2.0218E+03 | 2.0225E+03 | |
| Std | 8.6227E+00 | 7.6143E+00 | 6.0034E+00 | 6.1569E+00 | 2.4754E+01 | 1.1892E+01 | 6.1163E+00 | 6.5941E+00 | 9.7098E+00 | |
| Rank | 2 | 8 | 3 | 4 | 9 | 1 | 5 | 6 | 7 | |
| F8 | Best | 2.2002E+03 | 2.2080E+03 | 2.2051E+03 | 2.2063E+03 | 2.2121E+03 | 2.2071E+03 | 2.2108E+03 | 2.2191E+03 | 2.2058E+03 |
| Mean | 2.2138E+03 | 2.2233E+03 | 2.2246E+03 | 2.2203E+03 | 2.2345E+03 | 2.2209E+03 | 2.2248E+03 | 2.2222E+03 | 2.2249E+03 | |
| Std | 9.4827E+00 | 5.8835E+00 | 5.3873E+00 | 5.3409E+00 | 3.6571E+01 | 2.8473E+00 | 5.3055E+00 | 1.4329E+00 | 6.5047E+00 | |
| Rank | 1 | 5 | 6 | 2 | 9 | 3 | 7 | 4 | 8 | |
| F9 | Best | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 | 2.5297E+03 | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 |
| Mean | 2.5293E+03 | 2.5298E+03 | 2.5293E+03 | 2.5323E+03 | 2.5293E+03 | 2.5293E+03 | 2.5293E+03 | 2.5295E+03 | 2.5293E+03 | |
| Std | 1.1269E−04 | 6.5754E−01 | 5.0892E−05 | 2.2155E+00 | 1.8882E−13 | 1.0924E−03 | 1.2057E−11 | 8.9043E−01 | 1.0193E−02 | |
| Rank | 4 | 8 | 3 | 9 | 1 | 5 | 2 | 7 | 6 | |
| F10 | Best | 2.5002E+03 | 2.5005E+03 | 2.4162E+03 | 2.5004E+03 | 2.5003E+03 | 2.5004E+03 | 2.5003E+03 | 2.5003E+03 | 2.5002E+03 |
| Mean | 2.5225E+03 | 2.5007E+03 | 2.5061E+03 | 2.5045E+03 | 2.5831E+03 | 2.5223E+03 | 2.5384E+03 | 2.5471E+03 | 2.5291E+03 | |
| Std | 4.5283E+01 | 1.8549E−01 | 3.3035E+01 | 2.1513E+01 | 1.1410E+02 | 4.4533E+01 | 5.4936E+01 | 5.8024E+01 | 4.8532E+01 | |
| Rank | 5 | 1 | 3 | 2 | 9 | 4 | 7 | 8 | 6 | |
| F11 | Best | 2.6000E+03 | 2.6129E+03 | 2.6156E+03 | 2.6269E+03 | 2.6000E+03 | 2.6000E+03 | 2.6000E+03 | 2.6000E+03 | 2.6011E+03 |
| Mean | 2.7400E+03 | 2.6891E+03 | 2.8666E+03 | 2.6882E+03 | 2.8350E+03 | 2.7460E+03 | 2.8850E+03 | 2.8541E+03 | 2.7923E+03 | |
| Std | 1.5222E+02 | 6.1054E+01 | 9.5766E+01 | 3.7680E+01 | 1.2257E+02 | 1.0695E+02 | 6.0354E+01 | 1.0875E+02 | 1.4748E+02 | |
| Rank | 3 | 2 | 8 | 1 | 6 | 4 | 9 | 7 | 5 | |
| F12 | Best | 2.8594E+03 | 2.8598E+03 | 2.8614E+03 | 2.8650E+03 | 2.8614E+03 | 2.8626E+03 | 2.8595E+03 | 2.8587E+03 | 2.8587E+03 |
| Mean | 2.8631E+03 | 2.8639E+03 | 2.8630E+03 | 2.8671E+03 | 2.8652E+03 | 2.8657E+03 | 2.8634E+03 | 2.8636E+03 | 2.8615E+03 | |
| Std | 1.5168E+00 | 1.3249E+00 | 1.1777E+00 | 1.4621E+00 | 2.0772E+00 | 3.4210E+00 | 1.3576E+00 | 1.7798E+00 | 1.7010E+00 | |
| Rank | 3 | 6 | 2 | 9 | 7 | 8 | 4 | 5 | 1 |
| No. | Index | BWSMA | NMPA | BEESO | FDBARO | WOSSA | PHISAO | ESLPSO | EPSCA | IGWO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 3.0007E+02 | 1.8039E+03 | 1.3673E+04 | 9.0961E+03 | 5.3098E+03 | 3.6985E+03 | 2.6539E+03 | 3.0000E+02 | 4.7049E+02 |
| Mean | 3.0044E+02 | 4.6668E+03 | 2.2083E+04 | 2.4648E+04 | 2.0495E+04 | 1.6363E+04 | 8.3584E+03 | 3.0000E+02 | 1.2235E+03 | |
| Std | 2.9651E−01 | 1.7709E+03 | 5.2385E+03 | 8.2944E+03 | 9.5228E+03 | 7.2825E+03 | 3.8480E+03 | 2.8731E−04 | 8.5465E+02 | |
| Rank | 2 | 4 | 8 | 9 | 7 | 6 | 5 | 1 | 3 | |
| F2 | Best | 4.4490E+02 | 4.5496E+02 | 4.4379E+02 | 4.6732E+02 | 4.2950E+02 | 4.4915E+02 | 4.2809E+02 | 4.4570E+02 | 4.4551E+02 |
| Mean | 4.5129E+02 | 4.9243E+02 | 4.5352E+02 | 4.9723E+02 | 4.5679E+02 | 4.6030E+02 | 4.5307E+02 | 4.5280E+02 | 4.5206E+02 | |
| Std | 7.9738E+00 | 3.3924E+01 | 1.0620E+01 | 1.8108E+01 | 1.9035E+01 | 1.4497E+01 | 1.2623E+01 | 2.9438E+00 | 7.4437E+00 | |
| Rank | 1 | 8 | 5 | 9 | 6 | 7 | 4 | 3 | 2 | |
| F3 | Best | 6.0004E+02 | 6.1486E+02 | 6.0031E+02 | 6.0713E+02 | 6.1253E+02 | 6.0001E+02 | 6.0001E+02 | 6.0060E+02 | 6.0049E+02 |
| Mean | 6.0012E+02 | 6.2573E+02 | 6.0069E+02 | 6.1146E+02 | 6.3642E+02 | 6.0017E+02 | 6.0004E+02 | 6.0505E+02 | 6.0087E+02 | |
| Std | 4.7548E−02 | 5.9748E+00 | 2.5291E−01 | 3.3456E+00 | 1.4684E+01 | 1.3581E−01 | 9.8757E−02 | 4.2466E+00 | 2.9917E−01 | |
| Rank | 2 | 8 | 4 | 7 | 9 | 3 | 1 | 6 | 5 | |
| F4 | Best | 8.0996E+02 | 8.5589E+02 | 8.5224E+02 | 8.4776E+02 | 8.4179E+02 | 8.0201E+02 | 8.1758E+02 | 8.1293E+02 | 8.1892E+02 |
| Mean | 8.1862E+02 | 8.7798E+02 | 9.0549E+02 | 8.8757E+02 | 8.7558E+02 | 8.1355E+02 | 8.8026E+02 | 8.4285E+02 | 8.6294E+02 | |
| Std | 7.9788E+00 | 1.6972E+01 | 1.6344E+01 | 1.8908E+01 | 1.4255E+01 | 7.4343E+00 | 3.3000E+01 | 2.0627E+01 | 3.3746E+01 | |
| Rank | 2 | 6 | 9 | 8 | 5 | 1 | 7 | 3 | 4 | |
| F5 | Best | 9.0000E+02 | 1.0454E+03 | 9.0138E+02 | 9.4548E+02 | 1.3818E+03 | 9.0019E+02 | 9.0000E+02 | 9.1031E+02 | 9.0048E+02 |
| Mean | 9.0010E+02 | 1.5154E+03 | 9.1601E+02 | 1.2747E+03 | 2.2076E+03 | 9.0433E+02 | 9.0149E+02 | 9.9821E+02 | 9.0330E+02 | |
| Std | 1.1172E−01 | 2.9033E+02 | 1.3881E+01 | 1.9099E+02 | 3.2760E+02 | 5.2224E+00 | 2.6049E+00 | 9.0140E+01 | 4.0960E+00 | |
| Rank | 1 | 8 | 5 | 7 | 9 | 4 | 2 | 6 | 3 | |
| F6 | Best | 1.8632E+03 | 4.6781E+04 | 3.4373E+03 | 9.2970E+04 | 2.0311E+03 | 1.8916E+03 | 2.1741E+03 | 1.8383E+03 | 5.5286E+03 |
| Mean | 1.9348E+03 | 2.7734E+05 | 3.6287E+04 | 6.5703E+05 | 4.7017E+03 | 4.1236E+03 | 6.6227E+03 | 1.9371E+03 | 2.6349E+04 | |
| Std | 6.9540E+01 | 1.8390E+05 | 3.6673E+04 | 4.8947E+05 | 2.8453E+03 | 1.6139E+03 | 4.4147E+03 | 6.2737E+01 | 2.2103E+04 | |
| Rank | 1 | 8 | 7 | 9 | 4 | 3 | 5 | 2 | 6 | |
| F7 | Best | 2.0024E+03 | 2.0476E+03 | 2.0407E+03 | 2.0416E+03 | 2.0493E+03 | 2.0271E+03 | 2.0361E+03 | 2.0337E+03 | 2.0250E+03 |
| Mean | 2.0253E+03 | 2.0835E+03 | 2.0715E+03 | 2.0735E+03 | 2.1554E+03 | 2.0455E+03 | 2.0731E+03 | 2.1053E+03 | 2.0394E+03 | |
| Std | 7.2348E+00 | 2.3341E+01 | 2.1550E+01 | 2.0006E+01 | 9.0132E+01 | 1.6314E+01 | 2.1476E+01 | 4.6183E+01 | 1.5171E+01 | |
| Rank | 1 | 7 | 4 | 6 | 9 | 3 | 5 | 8 | 2 | |
| F8 | Best | 2.2082E+03 | 2.2265E+03 | 2.2318E+03 | 2.2275E+03 | 2.2213E+03 | 2.2215E+03 | 2.2290E+03 | 2.2209E+03 | 2.2251E+03 |
| Mean | 2.2223E+03 | 2.2366E+03 | 2.2440E+03 | 2.2322E+03 | 2.2663E+03 | 2.2237E+03 | 2.2384E+03 | 2.2501E+03 | 2.2321E+03 | |
| Std | 2.9836E+00 | 7.7123E+00 | 8.2011E+00 | 4.2814E+00 | 5.8295E+01 | 1.5108E+00 | 6.0786E+00 | 5.7527E+01 | 4.0645E+00 | |
| Rank | 1 | 5 | 7 | 4 | 9 | 2 | 6 | 8 | 3 | |
| F9 | Best | 2.4808E+03 | 2.4835E+03 | 2.4808E+03 | 2.4855E+03 | 2.4808E+03 | 2.4808E+03 | 2.4808E+03 | 2.4809E+03 | 2.4809E+03 |
| Mean | 2.4808E+03 | 2.4890E+03 | 2.4812E+03 | 2.4986E+03 | 2.4808E+03 | 2.4823E+03 | 2.4808E+03 | 2.4853E+03 | 2.4812E+03 | |
| Std | 1.3075E−02 | 5.7888E+00 | 2.9200E−01 | 7.7565E+00 | 2.1844E−02 | 4.0684E+00 | 1.6510E−01 | 5.1455E+00 | 1.8047E−01 | |
| Rank | 1 | 8 | 5 | 9 | 2 | 6 | 3 | 7 | 4 | |
| F10 | Best | 2.5003E+03 | 2.5006E+03 | 2.5008E+03 | 2.5007E+03 | 2.5009E+03 | 2.5004E+03 | 2.5006E+03 | 2.5006E+03 | 2.5004E+03 |
| Mean | 2.8591E+03 | 2.5097E+03 | 2.6640E+03 | 2.7481E+03 | 3.6943E+03 | 2.6542E+03 | 3.5838E+03 | 3.8779E+03 | 2.7523E+03 | |
| Std | 3.7931E+02 | 3.9295E+01 | 1.6176E+02 | 5.0183E+02 | 7.4353E+02 | 2.8251E+02 | 1.7920E+03 | 9.8056E+02 | 7.7621E+02 | |
| Rank | 6 | 1 | 3 | 4 | 8 | 2 | 7 | 9 | 5 | |
| F11 | Best | 2.9001E+03 | 3.0921E+03 | 3.1382E+03 | 3.4002E+03 | 2.6001E+03 | 2.9029E+03 | 2.9001E+03 | 2.9000E+03 | 2.9262E+03 |
| Mean | 2.9007E+03 | 3.5457E+03 | 3.3026E+03 | 3.7754E+03 | 2.9059E+03 | 2.9347E+03 | 2.9005E+03 | 2.9000E+03 | 2.9484E+03 | |
| Std | 3.6095E−01 | 2.1732E+02 | 1.0598E+02 | 2.6842E+02 | 1.1442E+02 | 5.0484E+01 | 2.2818E−01 | 5.0191E−10 | 1.4977E+01 | |
| Rank | 3 | 8 | 7 | 9 | 4 | 5 | 2 | 1 | 6 | |
| F12 | Best | 2.9320E+03 | 2.9526E+03 | 2.9411E+03 | 2.9755E+03 | 2.9431E+03 | 2.9417E+03 | 2.9326E+03 | 2.9393E+03 | 2.9325E+03 |
| Mean | 2.9413E+03 | 2.9770E+03 | 2.9494E+03 | 3.0062E+03 | 2.9811E+03 | 2.9514E+03 | 2.9490E+03 | 2.9581E+03 | 2.9416E+03 | |
| Std | 7.2332E+00 | 2.0969E+01 | 8.2173E+00 | 1.6236E+01 | 3.9831E+01 | 7.5426E+00 | 1.3392E+01 | 1.2415E+01 | 5.5385E+00 | |
| Rank | 1 | 7 | 4 | 9 | 8 | 5 | 3 | 6 | 2 |
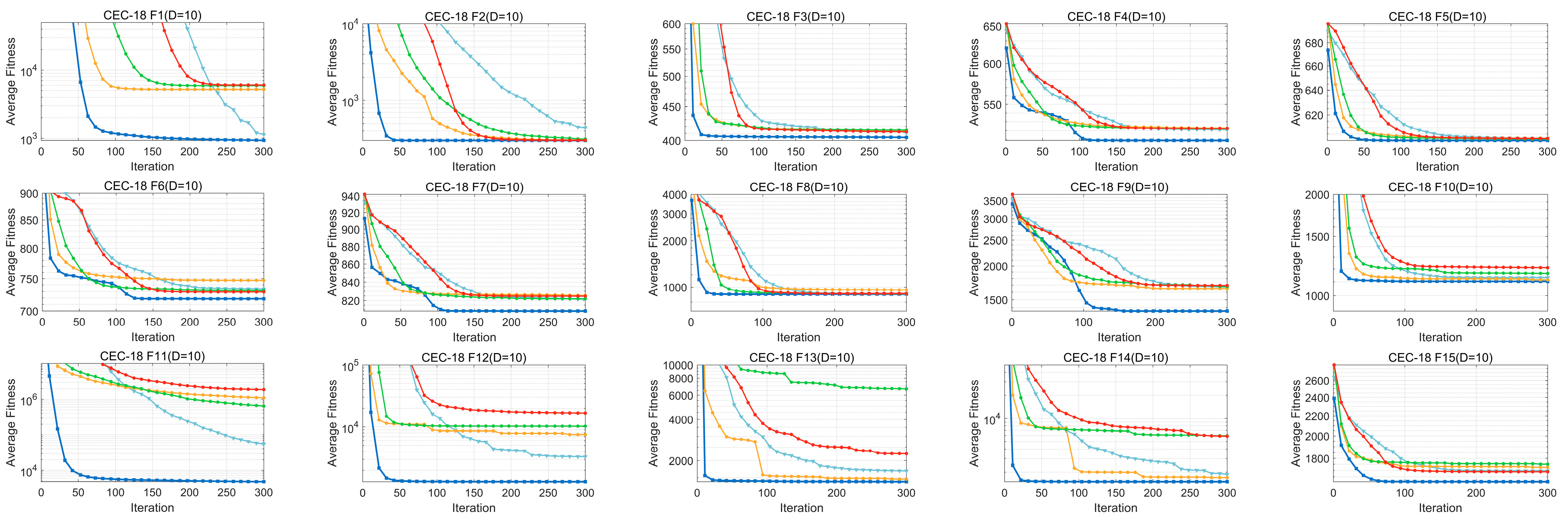


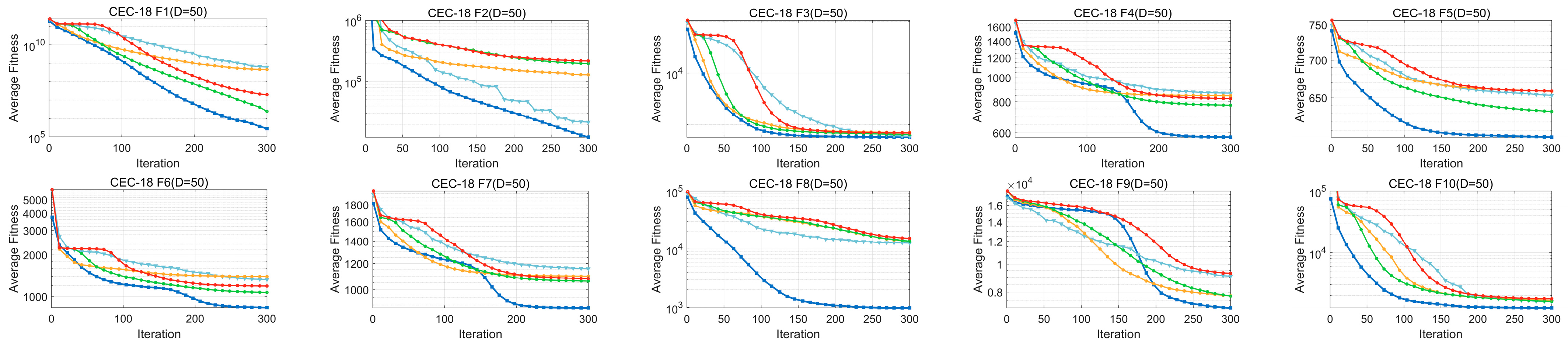
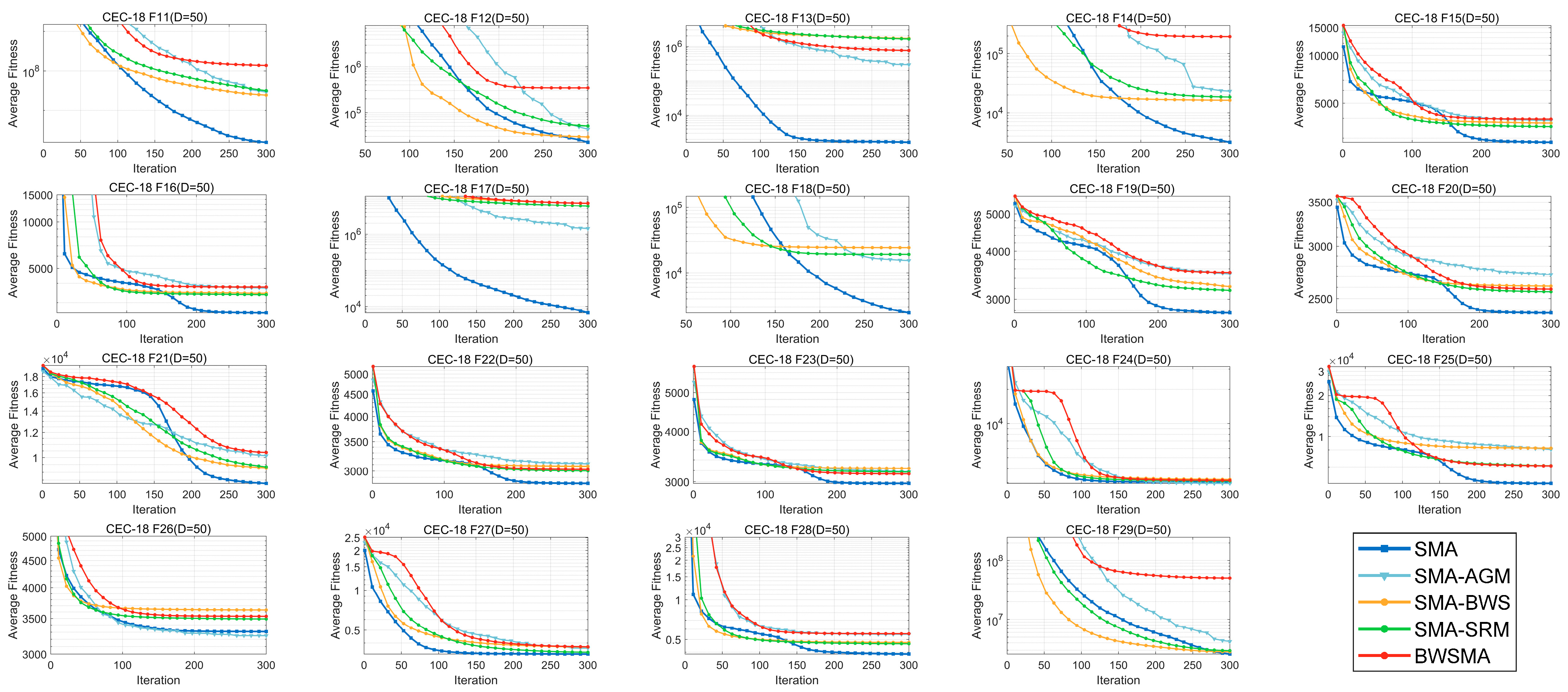

References
- Xie, L.; Han, T.; Zhou, H.; Zhang, Z.-R.; Han, B.; Tang, A. Tuna Swarm Optimization: A Novel Swarm-Based Metaheuristic Algorithm for Global Optimization. Comput. Intell. Neurosci. 2021, 2021, 210050. [Google Scholar] [CrossRef]
- Tang, A.; Zhou, H.; Han, T.; Xie, L. A Chaos Sparrow Search Algorithm with Logarithmic Spiral and Adaptive Step for Engineering Problems. Comput. Model. Eng. Sci. 2021, 130, 331–364. [Google Scholar] [CrossRef]
- Lehmann, T.H. Mathematical Modelling as a Vehicle for Eliciting Algorithmic Thinking. Educ. Stud. Math. 2024, 115, 151–176. [Google Scholar] [CrossRef]
- Droste, S.; Jansen, T.; Wegener, I. Upper and Lower Bounds for Randomized Search Heuristics in Black-Box Optimization. Theory Comput. Syst. 2006, 9, 525–544. [Google Scholar] [CrossRef]
- Tang, A.-D.; Han, T.; Zhou, H.; Xie, L. An Improved Equilibrium Optimizer with Application in Unmanned Aerial Vehicle Path Planning. Sensors 2021, 21, 1814. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Han, T.; Tang, S.; Huang, C.; Zhou, H.; Wang, Y. An Improved Differential Evolution by Hybridizing with Estimation-of-Distribution Algorithm. Inf. Sci. 2023, 619, 439–456. [Google Scholar] [CrossRef]
- Hernández, D.S.; García-Muñoz, J.A.; Gutiérrez, A.I.B. Evaluation of Metaheuristic Optimization Algorithms Applied to Path Planning. Int. J. Adv. Robot. Syst. 2024, 21, 1–10. [Google Scholar] [CrossRef]
- Qiao, L.; Liu, K.; Xue, Y.; Tang, W.; Salehnia, T. A Multi-Level Thresholding Image Segmentation Method Using Hybrid Arithmetic Optimization and Harris Hawks Optimizer Algorithms. Expert Syst. Appl. 2024, 241, 122316. [Google Scholar] [CrossRef]
- Kumar Sahoo, S.; Houssein, E.H.; Premkumar, M.; Kumar Saha, A.; Emam, M.M. Self-Adaptive Moth Flame Optimizer Combined with Crossover Operator and Fibonacci Search Strategy for COVID-19 CT Image Segmentation. Expert Syst. Appl. 2023, 227, 120367. [Google Scholar] [CrossRef]
- Abualigah, L.; Habash, M.; Hanandeh, E.S.; Hussein, A.M.A.; Al Shinwan, M.; Zitar, R.A.; Jia, H. Improved Reptile Search Algorithm by Salp Swarm Algorithm for Medical Image Segmentation. J. Bionic Eng. 2023, 20, 1766–1790. [Google Scholar] [CrossRef]
- Nair, A.T.; Arivazhagan, M. Industrial Activated Sludge Model Identification Using Hyperparameter-Tuned Metaheuristics. SWARM Evol. Comput. 2024, 91, 101733. [Google Scholar] [CrossRef]
- Al Bannoud, M.; da Silva, C.A.M.; Martins, T.D. Applications of Metaheuristic Optimization Algorithms in Model Predictive Control for Chemical Engineering Processes: A Systematic Review. Annu. Rev. Control 2024, 58, 100973. [Google Scholar] [CrossRef]
- Mumtahina, U.; Alahakoon, S.; Wolfs, P. Hyperparameter Tuning of Load-Forecasting Models Using Metaheuristic Optimization Algorithms-A Systematic Review. Mathematics 2024, 12, 3353. [Google Scholar] [CrossRef]
- Wu, D.; Jia, H.; Abualigah, L.; Xing, Z.; Zheng, R.; Wang, H.; Altalhi, M. Enhance Teaching-Learning-Based Optimization for Tsallis-Entropy-Based Feature Selection Classification Approach. Processes 2022, 10, 360. [Google Scholar] [CrossRef]
- Jia, H.M.; Zhou, X.L.; Zhang, J.R.; Mirjalili, S. Superb Fairy-Wren Optimization Algorithm: A Novel Metaheuristic Algorithm for Solving Feature Selection Problems. Clust. Comput. J. Netw. Softw. Tools Appl. 2025, 28, 246. [Google Scholar] [CrossRef]
- Banati, H.; Sharma, R.; Yadav, A. Binary Peacock Algorithm: A Novel Metaheuristic Approach for Feature Selection. J. Classif. 2024, 41, 216–244. [Google Scholar] [CrossRef]
- Barua, S.; Merabet, A.; Al-Durra, A.; El-Fouly, T.; El-Saadany, E.F. Levy Arithmetic Optimization for Energy Management of Solar Wind Microgrid with Multiple Diesel Generators for Off-Grid Communities. Appl. Energy 2024, 371, 123736. [Google Scholar] [CrossRef]
- Khezri, E.; Rezaeipanah, A.; Hassanzadeh, H.; Majidpour, J. Towards Load Frequency Management in Thermal Power Systems Using an Improved Open-Source Development Model Algorithm. Evol. Intell. 2025, 18, 9. [Google Scholar] [CrossRef]
- Akbulut, L.; Tasdelen, K.; Çosgun, A. Review of Metaheuristic Algorithms for Energy Efficiency, Demand Side Management and Cost Estimation. Rocz. Ochr. Sr. 2025, 27, 341–353. [Google Scholar] [CrossRef]
- Ding, W.; Sun, Y.; Ren, L.; Ju, H.; Feng, Z.; Li, M. Multiple Lesions Detection of Fundus Images Based on Convolution Neural Network Algorithm with Improved SFLA. IEEE Access 2020, 8, 97618–97631. [Google Scholar] [CrossRef]
- Myriam, H.; Abdelhamid, A.A.; El-Kenawy, E.S.M.; Ibrahim, A.; Eid, M.M.; Jamjoom, M.M.; Khafaga, D.S. Advanced Meta-Heuristic Algorithm Based on Particle Swarm and Al-Biruni Earth Radius Optimization Methods for Oral Cancer Detection. IEEE Access 2023, 11, 23681–23700. [Google Scholar] [CrossRef]
- Nanda, S.J.; Gulati, I.; Chauhan, R.; Modi, R.; Dhaked, U. A K-Means-Galactic Swarm Optimization-Based Clustering Algorithm with Otsu’s Entropy for Brain Tumor Detection. Appl. Artif. Intell. 2019, 33, 152–170. [Google Scholar] [CrossRef]
- Xu, M.; Zhou, J.; Zhu, P. An Electronic Nose System for the Monitoring of Water Cane Shoots Quality with Swarm Clustering Algorithm. J. Food Saf. 2021, 41, e12860. [Google Scholar] [CrossRef]
- Irshad, R.R.; Alattab, A.A.; Alsaiari, O.A.S.; Sohail, S.S.; Aziz, A.; Madsen, D.Ø.; Alalayah, K.M. An Optimization-Linked Intelligent Security Algorithm for Smart Healthcare Organizations. Healthcare 2023, 11, 580. [Google Scholar] [CrossRef]
- Belardi, V.G.; Trupiano, S.; Fanelli, P.; Vivio, F. Overall Elastic Characterization of Equivalent FE Models for Aluminum Foams through Computational Homogenization Approach and Genetic Algorithm Optimization. Eur. J. Mech. A/Solids 2024, 103, 105189. [Google Scholar] [CrossRef]
- Peng, Y.; Li, T.; Hou, L.; Wang, K.; Xie, G.; Zhang, H. Bio-Inspired Cellular Thin-Walled Structures under Impact Loading: Modeling and Multi-Stage Cooperative Optimization Algorithm. Mech. Adv. Mater. Struct. 2024, 31, 4737–4754. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Opara, K.R.; Arabas, J. Differential Evolution: A Survey of Theoretical Analyses. Swarm Evol. Comput. 2019, 44, 546–558. [Google Scholar] [CrossRef]
- Ahvanooey, M.T.; Li, Q.; Wu, M.; Wang, S. A Survey of Genetic Programming and Its Applications. KSII Trans. Internet Inf. Syst. 2019, 13, 1765–1794. [Google Scholar] [CrossRef]
- Beyer, H.-G.; Beyer, H.-G.; Schwefel, H.-P.; Schwefel, H.-P. Evolution Strategies—A Comprehensive Introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Q.K. Alpha Evolution: An Efficient Evolutionary Algorithm with Evolution Path Adaptation and Matrix Generation. Eng. Appl. Artif. Intell. 2024, 137, 109202. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Saari, M.M.; Daniyal, H.; Mirjalili, S. Evolutionary Mating Algorithm. Neural Comput. Appl. 2023, 35, 487–516. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Wei, Z.; Huang, C.; Wang, X.; Han, T.; Li, Y. Nuclear Reaction Optimization: A Novel and Powerful Physics-Based Algorithm for Global Optimization. IEEE Access 2019, 7, 66084–66109. [Google Scholar] [CrossRef]
- Braik, M.; Al-Hiary, H.; Alzoubi, H.; Hammouri, A.; Al-Betar, M.A.; Awadallah, M.A. Tornado Optimizer with Coriolis Force: A Novel Bio-Inspired Meta-Heuristic Algorithm for Solving Engineering Problems. Artif. Intell. Rev. 2025, 58, 123. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H. Polar Lights Optimizer: Algorithm and Applications in Image Segmentation and Feature Selection. Neurocomputing 2024, 607, 128427. [Google Scholar] [CrossRef]
- Sowmya, R.; Premkumar, M.; Jangir, P. Newton-Raphson-Based Optimizer: A New Population-Based Metaheuristic Algorithm for Continuous Optimization Problems. Eng. Appl. Artif. Intell. 2024, 128, 107532. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Sallam, K.M.; Chakrabortty, R.K. Light Spectrum Optimizer: A Novel Physics-Inspired Metaheuristic Optimization Algorithm. Mathematics 2022, 10, 3466. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Cymerys, K.; Oszust, M. Attraction–Repulsion Optimization Algorithm for Global Optimization Problems. Swarm Evol. Comput. 2024, 84, 101459. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry Gas Solubility Optimization: A Novel Physics-Based Algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Kundu, R.; Chattopadhyay, S.; Nag, S.; Navarro, M.A.; Oliva, D. Prism Refraction Search: A Novel Physics-Based Metaheuristic Algorithm. J. Supercomput. 2024, 80, 10746–10795. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: A Novel Method for Constrained Mechanical Design Optimization Problems. CAD Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Ni, L.; Ping, Y.; Yao, N.; Jiao, J.; Wang, G. Literature Research Optimizer: A New Human-Based Metaheuristic Algorithm for Optimization Problems. Arab. J. Sci. Eng. 2024, 49, 12817–12865. [Google Scholar] [CrossRef]
- Trojovský, P. A New Human-Based Metaheuristic Algorithm for Solving Optimization Problems Based on Preschool Education. Sci. Rep. 2023, 13, 21472. [Google Scholar] [CrossRef]
- Das, B.; Mukherjee, V.; Das, D. Student Psychology Based Optimization Algorithm: A New Population Based Optimization Algorithm for Solving Optimization Problems. Adv. Eng. Softw. 2020, 146, 102804. [Google Scholar] [CrossRef]
- Wu, X.; Li, S.B.; Jiang, X.H.; Zhou, Y.Q. Information Acquisition Optimizer: A New Efficient Algorithm for Solving Numerical and Constrained Engineering Optimization Problems. J. Supercomput. 2024, 80, 25736–25791. [Google Scholar] [CrossRef]
- Tian, Z.; Gai, M. Football Team Training Algorithm: A Novel Sport-Inspired Meta-Heuristic Optimization Algorithm for Global Optimization. Expert Syst. Appl. 2024, 245, 123088. [Google Scholar] [CrossRef]
- Soundhara Raja Pandian, R.; Christopher Columbus, C. Rider Optimization Algorithm Based Optimal Cloud Server Selection in E-Learning. Comput. Syst. Sci. Eng. 2023, 44, 1749–1762. [Google Scholar] [CrossRef]
- Ouyang, K.; Fu, S.; Chen, Y.; Cai, Q.; Heidari, A.A.; Chen, H. Escape: An Optimization Method Based on Crowd Evacuation Behaviors. Artif. Intell. Rev. 2024, 58, 19. [Google Scholar] [CrossRef]
- Javed, S.T.; Zafar, K.; Younas, I. Kids Learning Optimizer: Social Evolution and Cognitive Learning-Based Optimization Algorithm. Neural Comput. Appl. 2024, 36, 17417–17465. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, S.; Zhou, C.; Yan, S.; Xue, J. Human Memory Optimization Algorithm: A Memory-Inspired Optimizer for Global Optimization Problems. Expert Syst. Appl. 2024, 237, 121597. [Google Scholar] [CrossRef]
- Huang, W.; Xu, J. Particle Swarm Optimization. In Springer Tracts in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Abasi, A.K.; Makhadmeh, S.N.; Al-Betar, M.A.; Alomari, O.A.; Awadallah, M.A.; Alyasseri, Z.A.A.; Doush, I.A.; Elnagar, A.; Alkhammash, E.H.; Hadjouni, M. Lemurs Optimizer: A New Metaheuristic Algorithm for Global Optimization. Appl. Sci. 2022, 12, 10057. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Tian, A.Q.; Liu, F.F.; Lv, H.X. Snow Geese Algorithm: A Novel Migration-Inspired Meta-Heuristic Algorithm for Constrained Engineering Optimization Problems. Appl. Math. Model. 2024, 126, 327–347. [Google Scholar] [CrossRef]
- Bai, J.F.; Nguyen-Xuan, H.; Atroshchenko, E.; Kosec, G.; Wang, L.H.; Wahab, M.A. Blood-Sucking Leech Optimizer. Adv. Eng. Softw. 2024, 195, 103696. [Google Scholar] [CrossRef]
- Zhang, H.B.; San, H.J.; Chen, J.P.; Sun, H.J.; Ding, L.; Wu, X.M. Black Eagle Optimizer: A Metaheuristic Optimization Method for Solving Engineering Optimization Problems. Clust. Comput. J. Netw. Softw. Tools Appl. 2024, 27, 12361–12393. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Awadallah, M.A.; Braik, M.S.; Makhadmeh, S.; Doush, I.A. Elk Herd Optimizer: A Novel Nature-Inspired Metaheuristic Algorithm. Artif. Intell. Rev. 2024, 57, 48. [Google Scholar] [CrossRef]
- Hu, G.; Cheng, M.; Houssein, E.H.; Hussien, A.G.; Abualigah, L. SDO: A Novel Sled Dog-Inspired Optimizer for Solving Engineering Problems. Adv. Eng. Inform. 2024, 62, 102783. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z.; Fan, H.; Zhang, J.; Mirjalili, S.; Khodadadi, N.; Cao, Q. Electric Eel Foraging Optimization: A New Bio-Inspired Optimizer for Engineering Applications. Expert Syst. Appl. 2024, 238, 122200. [Google Scholar] [CrossRef]
- Örnek, B.N.; Aydemir, S.B.; Düzenli, T.; Özak, B. A Novel Version of Slime Mould Algorithm for Global Optimization and Real World Engineering Problems Enhanced Slime Mould Algorithm. Math. Comput. Simul. 2022, 198, 253–288. [Google Scholar] [CrossRef]
- Mostafa, M.; Rezk, H.; Aly, M.; Ahmed, E.M. A New Strategy Based on Slime Mould Algorithm to Extract the Optimal Model Parameters of Solar PV Panel. Sustain. Energy Technol. Assess. 2020, 42, 100849. [Google Scholar] [CrossRef]
- Yu, T.Y.; Pan, J.W.; Qian, Q.; Song, M.; Yin, J.B.; Feng, Y.; Fu, Y.F.; Li, Y.N. Improved Slime Mould Algorithm by Perfecting Bionic-Based Mechanisms. Int. J. Bio-Inspired Comput. 2023, 22, 1–15. [Google Scholar] [CrossRef]
- Chen, H.M.; Wang, Z.; Jia, H.M.; Zhou, X.D.; Abualigah, L. Hybrid Slime Mold and Arithmetic Optimization Algorithm with Random Center Learning and Restart Mutation. Biomimetics 2023, 8, 396. [Google Scholar] [CrossRef]
- Alhashash, K.M.; Samma, H.; Suandi, S.A. MSMA: Merged Slime Mould Algorithm for Solving Problems. Int. J. Adv. Comput. Sci. Appl. 2024, 15, 501–516. [Google Scholar]
- Conteh, I.M.; Njai, G.; Conteh, A.; Du, Q.G. An Optimized Feature Selection Using Triangle Mutation Rule and Restart Strategy in Enhanced Slime Mould Algorithm. Egypt. Inform. J. 2025, 30, 100709. [Google Scholar] [CrossRef]
- Ma, Y.L.; Zhang, Z.R.; Yao, M.; Fan, G.L. A Self-Adaptive Improved Slime Mold Algorithm for Multi-UAV Path Planning. Drones 2025, 9, 219. [Google Scholar] [CrossRef]
- Duan, Z.X.; Qian, X.Z.; Song, W. Multi-Strategy Enhanced Slime Mould Algorithm for Optimization Problems. IEEE Access 2025, 13, 7850–7871. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Li, X.; Lin, Z.; Lv, H.; Yu, L.; Heidari, A.A.; Zhang, Y.; Chen, H.; Liang, G. Advanced Slime Mould Algorithm Incorporating Differential Evolution and Powell Mechanism for Engineering Design. iScience 2023, 26, 107736. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Liu, S. A Multi-Strategy Improved Slime Mould Algorithm for Global Optimization and Engineering Design Problems. Comput. Methods Appl. Mech. Eng. 2023, 404, 115764. [Google Scholar] [CrossRef]
- Naik, M.K.; Panda, R.; Abraham, A. An Entropy Minimization Based Multilevel Colour Thresholding Technique for Analysis of Breast Thermograms Using Equilibrium Slime Mould Algorithm. Appl. Soft Comput. 2021, 113, 107955. [Google Scholar] [CrossRef]
- Naik, M.K.; Panda, R.; Abraham, A. Normalized Square Difference Based Multilevel Thresholding Technique for Multispectral Images Using Leader Slime Mould Algorithm. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 4524–4536. [Google Scholar] [CrossRef]
- Son, P.V.H.; Khoi, L.N.Q. Adaptive Opposition Slime Mold Algorithm for Time–Cost–Quality–Safety Trade-off for Construction Projects. Asian J. Civ. Eng. 2023, 24, 1927–1942. [Google Scholar] [CrossRef]
- Yin, S.; Luo, Q.; Zhou, Y. EOSMA: An Equilibrium Optimizer Slime Mould Algorithm for Engineering Design Problems. Arab. J. Sci. Eng. 2022, 47, 10115–10146. [Google Scholar] [CrossRef]
- Tang, A.-D.; Tang, S.Q.; Han, T.; Zhou, H.; Xie, L. A Modified Slime Mould Algorithm for Global Optimization. Comput. Intell. Neurosci. 2021, 2021, 2298215. [Google Scholar] [CrossRef]
- Yin, S.; Luo, Q.; Du, Y.; Zhou, Y. DTSMA: Dominant Swarm with Adaptive T-Distribution Mutation-Based Slime Mould Algorithm. Math. Biosci. Eng. 2022, 19, 2240–2285. [Google Scholar] [CrossRef]
- Sadiq, A.S.; Dehkordi, A.A.; Mirjalili, S.; Pham, Q.V. Nonlinear Marine Predator Algorithm: A Cost-Effective Optimizer for Fair Power Allocation in NOMA-VLC-B5G Networks. Expert Syst. Appl. 2022, 203, 117395. [Google Scholar] [CrossRef]
- Hu, G.; Yang, R.; Abbas, M.; Wei, G. BEESO: Multi-Strategy Boosted Snake-Inspired Optimizer for Engineering Applications. J. Bionic Eng. 2023, 20, 1791–1827. [Google Scholar] [CrossRef]
- Bakır, H. Dynamic Fitness-Distance Balance-Based Artificial Rabbits Optimization Algorithm to Solve Optimal Power Flow Problem. Expert Syst. Appl. 2024, 240, 122460. [Google Scholar] [CrossRef]
- Yang, C.; Yang, H.; Zhu, D.; Hu, Y.W.; Zhang, Y.; Ma, H.Y.; Zhang, D. A Multi-Mechanism Balanced Advanced Learning Sparrow Search Algorithm for UAV Path Planning. Clust. Comput. 2024, 27, 6623–6666. [Google Scholar] [CrossRef]
- Lou, T.S.; Wang, Y.; Guan, G.S.; Lu, Y.B.; Qi, R.L. A Physically Hybrid Strategy-Based Improved Snow Ablation Optimizer for UAV Trajectory Planning. J. Bionic Eng. 2024, 21, 2985–3003. [Google Scholar] [CrossRef]
- Deng, L.Y.; Liu, S.Y. Advancing Photovoltaic System Design: An Enhanced Social Learning Swarm Optimizer with Guaranteed Stability. Comput. Ind. 2025, 164, 104209. [Google Scholar] [CrossRef]
- Deng, L.Y.; Liu, S.Y. A Sine Cosine Algorithm Guided by Elite Pool Strategy for Global Optimization. Appl. Soft Comput. 2024, 164, 111946. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An Improved Grey Wolf Optimizer for Solving Engineering Problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A Novel Human-Based Metaheuristic Approach. Knowl.-Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Karami, H.; Anaraki, M.V.; Farzin, S.; Mirjalili, S. Flow Direction Algorithm (FDA): A Novel Optimization Approach for Solving Optimization Problems. Comput. Ind. Eng. 2021, 156, 107224. [Google Scholar] [CrossRef]
- Versaci, M.; Laganà, F.; Morabito, F.C.; Palumbo, A.; Angiulli, G. Adaptation of an Eddy Current Model for Characterizing Subsurface Defects in CFRP Plates Using FEM Analysis Based on Energy Functional. Mathematics 2024, 12, 2854. [Google Scholar] [CrossRef]
- Lagana, F.; Pellicano, D.; Arruzzo, M.; Pratticò, D.; Pullano, S.A.; Fiorillo, A.S. FEM-Based Modelling and AI-Enhanced Monitoring System for Upper Limb Rehabilitation. Electronics 2025, 14, 2268. [Google Scholar] [CrossRef]
- Bibbò, L.; Angiulli, G.; Laganà, F.; Pratticò, D.; Cotroneo, F.; La Foresta, F.; Versaci, M. MEMS and IoT in HAR: Effective Monitoring for the Health of Older People. Appl. Sci. 2025, 15, 4306. [Google Scholar] [CrossRef]
- Pratticò, D.; Laganà, F.; Oliva, G.; Fiorillo, A.S.; Pullano, S.A.; Calcagno, S.; De Carlo, D.; La Foresta, F. Integration of LSTM and U-Net Models for Monitoring Electrical Absorption With a System of Sensors and Electronic Circuits. IEEE Trans. Instrum. Meas. 2025, 74, 2533311. [Google Scholar] [CrossRef]
- Laganà, F.; Bibbò, L.; Calcagno, S.; De Carlo, D.; Pullano, S.A.; Pratticò, D.; Angiulli, G. Smart Electronic Device-Based Monitoring of SAR and Temperature Variations in Indoor Human Tissue Interaction. Appl. Sci. 2025, 15, 2439. [Google Scholar] [CrossRef]
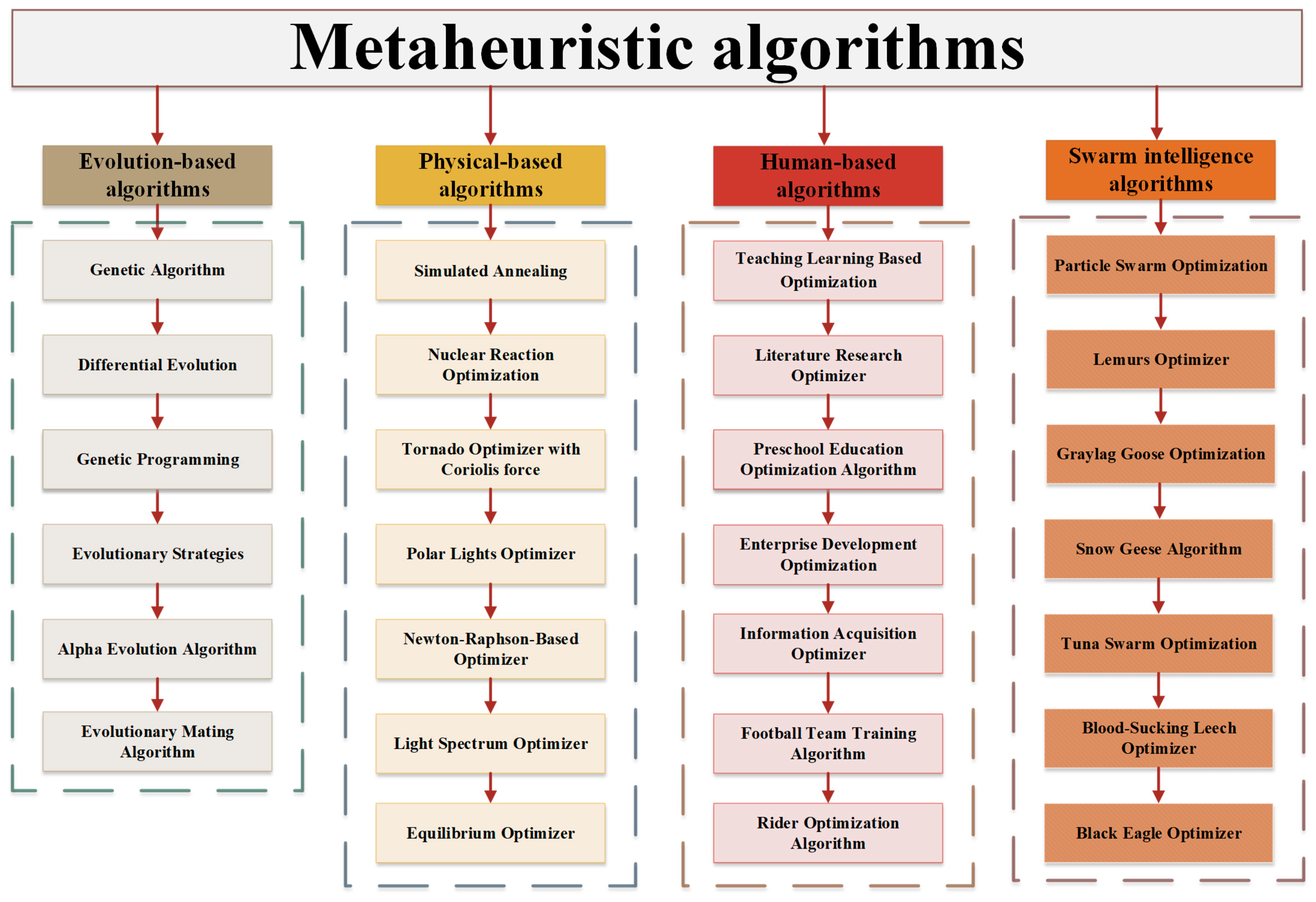

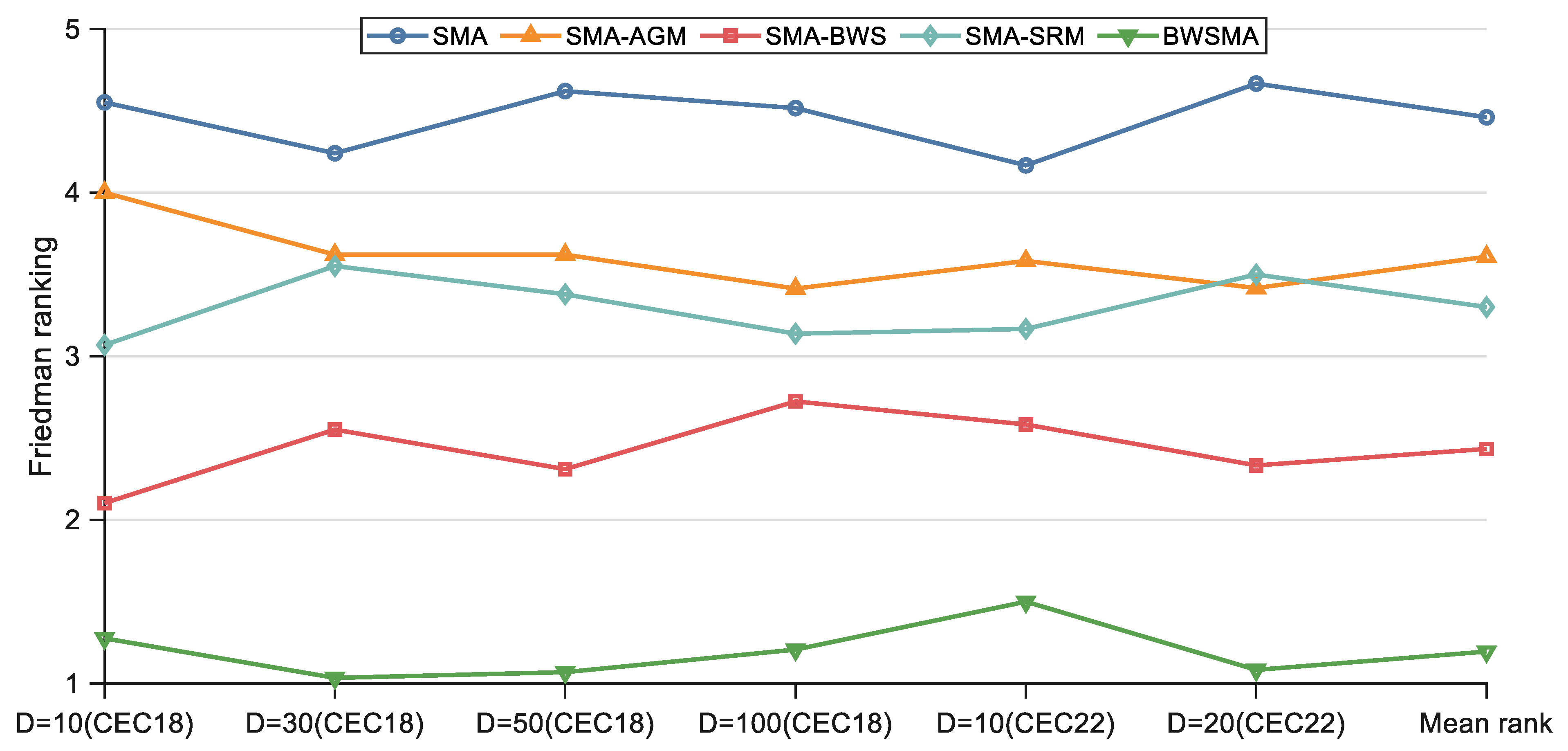






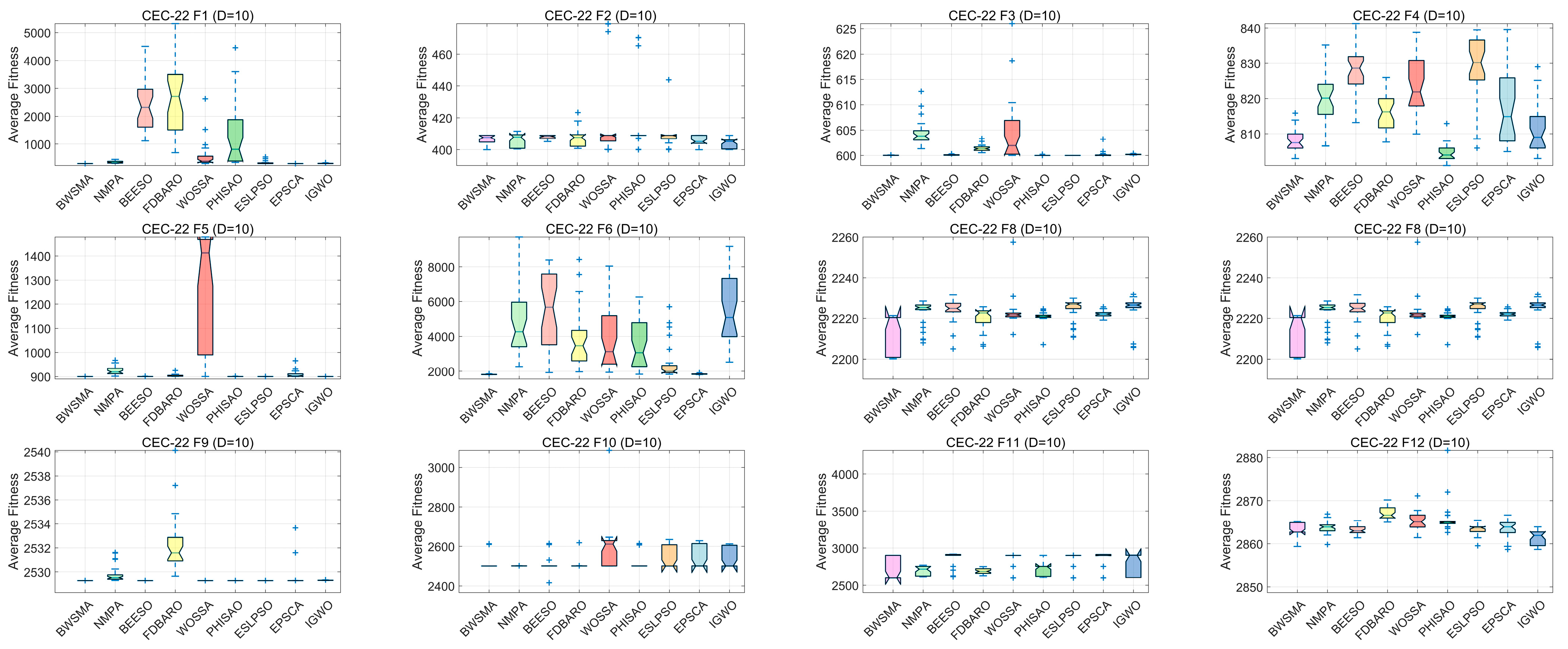
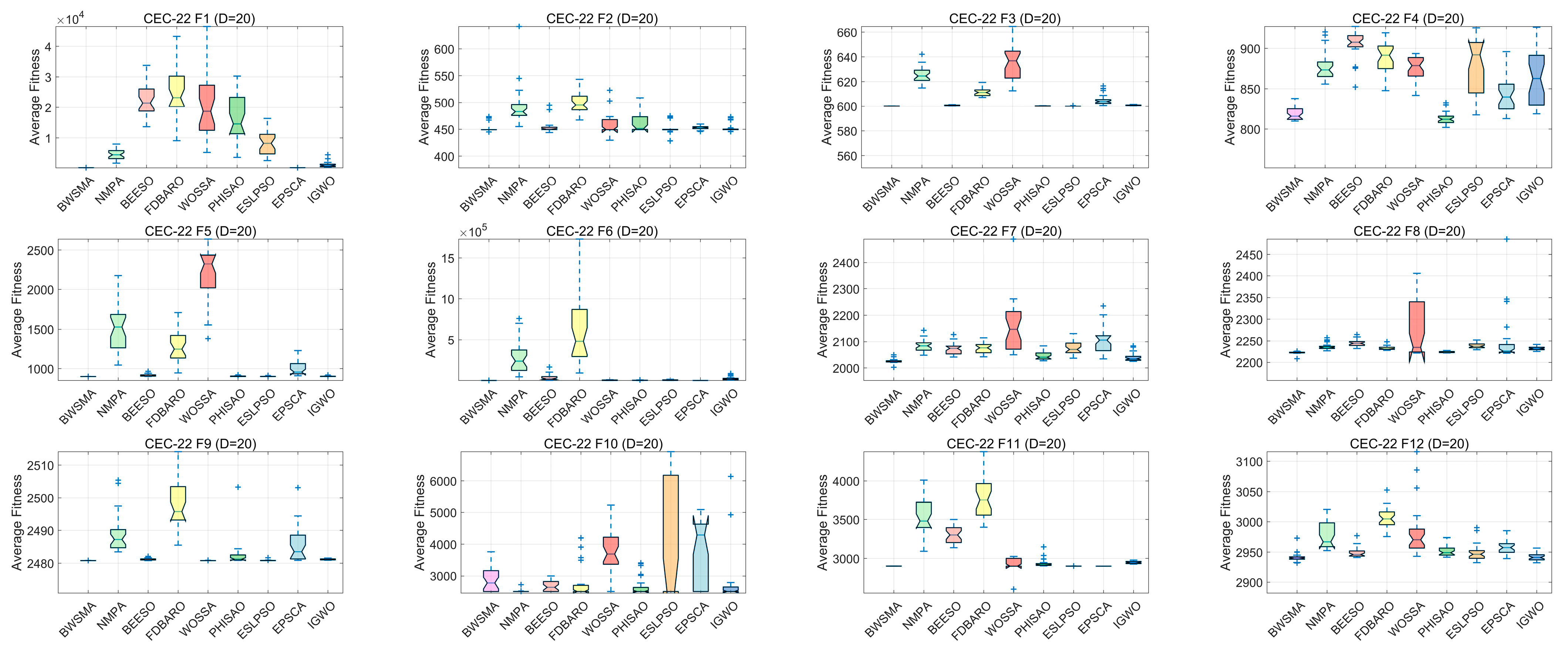
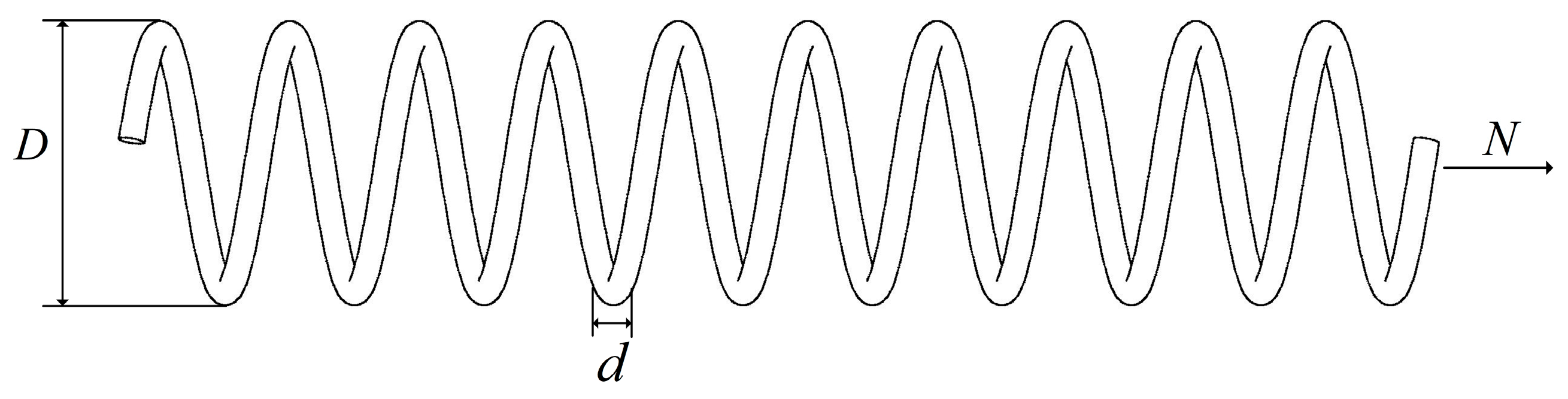
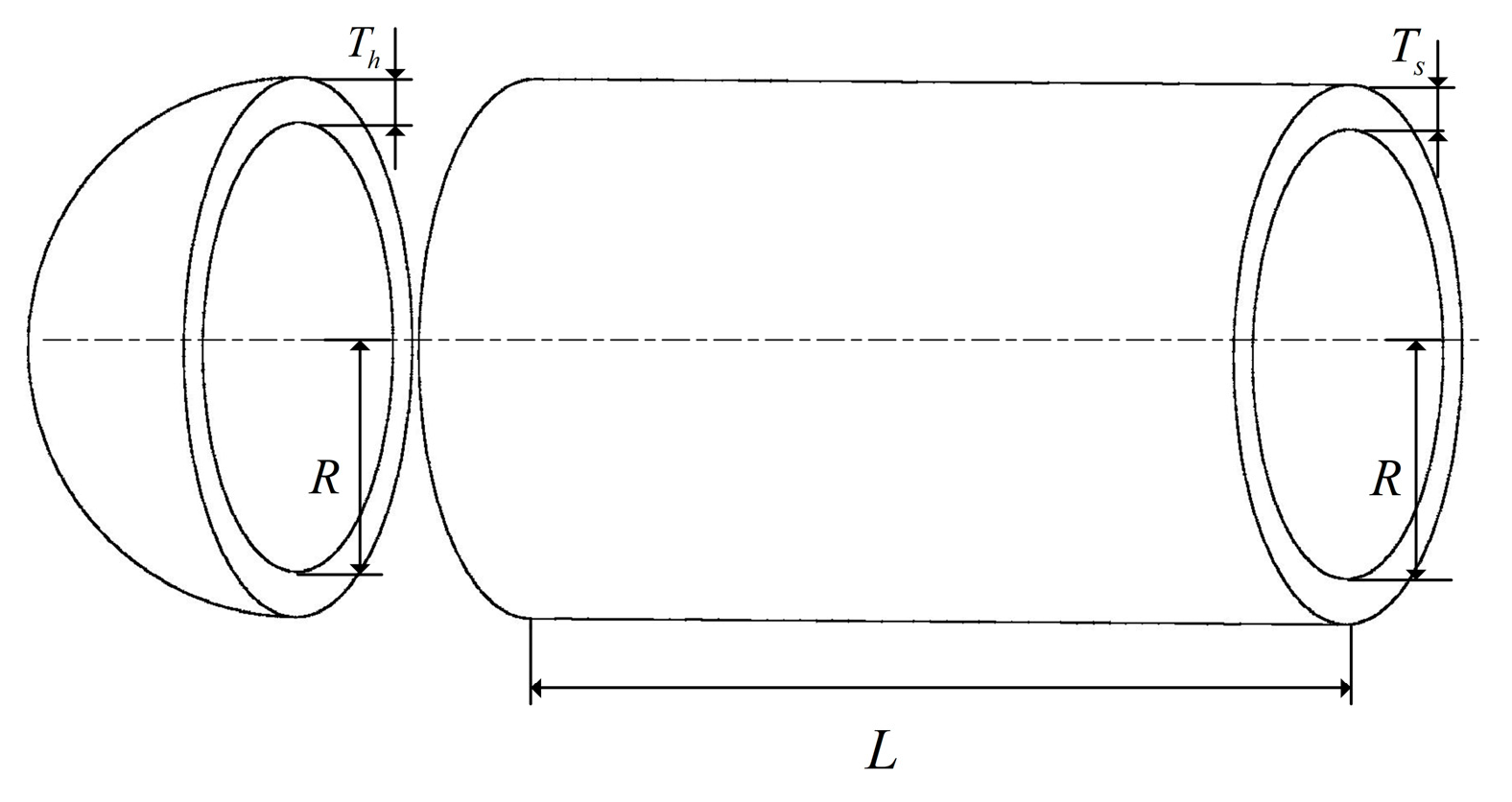
| Test Suite | Dimension | SMA | SMA-AGM | SMA-BWS | SMA-SRM | BWSMA | p-Value |
|---|---|---|---|---|---|---|---|
| CEC2018 | 10 | 4.552 | 4.000 | 2.103 | 3.069 | 1.276 | 3.33E−17 |
| 30 | 4.241 | 3.621 | 2.552 | 3.552 | 1.034 | 5.22E−15 | |
| 50 | 4.621 | 3.621 | 2.310 | 3.379 | 1.069 | 1.26E−17 | |
| 100 | 4.517 | 3.414 | 2.724 | 3.138 | 1.207 | 9.33E−14 | |
| CEC2022 | 10 | 4.167 | 3.583 | 2.583 | 3.167 | 1.500 | 5.15E−04 |
| 20 | 4.667 | 3.417 | 2.333 | 3.500 | 1.083 | 4.36E−07 | |
| Mean rank | 4.461 | 3.609 | 2.434 | 3.301 | 1.195 | N/A | |
| Overall rank | 5 | 4 | 2 | 3 | 1 | N/A | |
| vs. SMA +/=/− | CEC-2018 Test Suite | CEC-2022 Test Suite | ||||
|---|---|---|---|---|---|---|
| 10D | 30D | 50D | 100D | 10D | 20D | |
| SMA-AGM | 9/19/1 | 7/22/0 | 8/21/0 | 21/7/1 | 4/8/0 | 4/8/0 |
| SMA-BWS | 26/2/1 | 19/8/2 | 24/5/0 | 22/7/0 | 9/3/0 | 10/2/0 |
| SMA-SRM | 21/5/3 | 18/6/5 | 18/8/3 | 22/1/6 | 5/4/3 | 4/5/3 |
| BWSMA | 29/0/0 | 29/0/0 | 28/1/0 | 28/1/0 | 11/1/0 | 12/0/0 |
| Algorithm | Parameter Settings |
|---|---|
| BWSMA | |
| PSMADE [71] | |
| MSSMA [72] | |
| ESMA [73] | |
| LSMA [74] | |
| AOSMA [75] | |
| EOSMA [76] | |
| ISMA [77] | |
| DTSMA [78] |
| BWSMA vs. +/=/− | Dimension | PSMADE | MSSMA | ESMA | LSMA | AOSMA | EOSMA | ISMA | DTSMA |
|---|---|---|---|---|---|---|---|---|---|
| CEC-2018 test suite | 10D | 24/5/0 | 29/0/0 | 29/0/0 | 28/0/1 | 29/0/0 | 24/4/1 | 25/2/2 | 28/1/0 |
| 30D | 24/3/2 | 28/1/0 | 28/1/0 | 29/0/0 | 29/0/0 | 28/1/0 | 27/2/0 | 29/0/0 | |
| 50D | 25/2/2 | 27/2/0 | 29/0/0 | 28/1/0 | 29/0/0 | 29/0/0 | 29/0/0 | 29/0/0 | |
| 100D | 19/4/6 | 26/2/1 | 23/6/0 | 29/0/0 | 29/0/0 | 29/0/0 | 29/0/0 | 29/0/0 |
| Algorithm | CEC-2018 Test Suite | |||||
|---|---|---|---|---|---|---|
| 10D | 30D | 50D | 100D | Mean Rank | Overall Rank | |
| BWSMA | 1.414 | 1.138 | 1.069 | 1.414 | 1.259 | 1 |
| PSMADE | 3.793 | 4.586 | 4.207 | 3.379 | 3.991 | 2 |
| MSSMA | 5.897 | 4.862 | 4.586 | 3.862 | 4.802 | 5 |
| ESMA | 6.000 | 3.621 | 3.138 | 3.207 | 3.991 | 2 |
| LSMA | 6.310 | 5.552 | 5.586 | 5.759 | 5.802 | 6 |
| AOSMA | 8.034 | 8.069 | 7.966 | 7.414 | 7.871 | 9 |
| EOSMA | 3.793 | 6.586 | 7.103 | 8.000 | 6.371 | 7 |
| ISMA | 5.759 | 6.552 | 6.655 | 6.586 | 6.388 | 8 |
| DTSMA | 4.000 | 4.034 | 4.690 | 5.379 | 4.526 | 4 |
| p-value | 1.92E−21 | 1.90E−23 | 2.79E−26 | 7.65E−28 | N/A | N/A |
| Algorithm | Parameter Settings |
|---|---|
| NMPA [79] | |
| BEESO [80] | |
| FDBARO [81] | |
| WOSSA [82] | |
| PHISAO [83] | |
| ESLPSO [84] | |
| EPSCA [85] | |
| IGWO [86] | N/A |
| Algorithm | CEC-2022 Test Suite | |||||
|---|---|---|---|---|---|---|
| Friedman Test | Wilcoxon Rank-Sum Test | |||||
| 10D | 20D | Mean Rank | Overall Rank | 10D | 20D | |
| BWSMA | 2.583 | 1.833 | 2.208 | 1 | BWSMA vs. +/=/− | |
| BWSMA | 5.667 | 6.500 | 6.083 | 7 | 9/2/1 | 11/1/0 |
| NMPA | 5.333 | 5.667 | 5.500 | 6 | 8/2/2 | 11/1/0 |
| BEESO | 5.333 | 7.500 | 6.417 | 8 | 9/2/1 | 11/1/0 |
| FDBARO | 7.000 | 6.667 | 6.833 | 9 | 9/2/1 | 10/2/0 |
| WOSSA | 4.333 | 3.917 | 4.125 | 2 | 5/4/3 | 9/2/1 |
| PHISAO | 5.000 | 4.167 | 4.583 | 4 | 7/3/2 | 9/1/2 |
| ESLPSO | 4.917 | 5.000 | 4.958 | 5 | 7/4/1 | 9/1/2 |
| EPSCA | 4.833 | 3.750 | 4.292 | 3 | 9/1/2 | 10/2/0 |
| p-value | 2.46E−02 | 2.83E−06 | N/A | N/A | N/A | N/A |
| Algorithm | Optimal Values for Variable | Optimal Value | Ranking | ||
|---|---|---|---|---|---|
| d | D | N | |||
| BWSMA | 5.171E−02 | 3.559E−01 | 1.132E+01 | 1.268E−02 | 1 |
| SMA | 5.301E−02 | 3.842E−01 | 1.001E+01 | 1.298E−02 | 8 |
| ESMA | 5.171E−02 | 3.573E−01 | 1.128E+01 | 1.272E−02 | 4 |
| PSMADE | 5.163E−02 | 3.549E−01 | 1.141E+01 | 1.269E−02 | 3 |
| DTSMA | 5.191E−02 | 3.630E−01 | 1.101E+01 | 1.270E−02 | 5 |
| PHISAO | 5.142E−02 | 3.500E−01 | 1.171E+01 | 1.273E−02 | 6 |
| EPSCA | 5.231E−02 | 3.722E−01 | 1.050E+01 | 1.271E−02 | 7 |
| WOSSA | 5.159E−02 | 3.550E−01 | 1.141E+01 | 1.271E−02 | 2 |
| Algorithm | Optimal Values for Variable | Optimal Value | Ranking | |||
|---|---|---|---|---|---|---|
| Ts | Th | R | L | |||
| BWSMA | 7.781E−01 | 3.850E−01 | 4.030E+01 | 2.001E+02 | 5.890E+03 | 1 |
| SMA | 7.929E−01 | 4.101E−01 | 4.100E+01 | 1.911E+02 | 6.879E+03 | 8 |
| ESMA | 7.780E−01 | 3.850E−01 | 4.030E+01 | 2.000E+02 | 5.971E+03 | 3 |
| PSMADE | 7.931E−01 | 3.920E−01 | 4.101E+01 | 1.901E+02 | 6.290E+03 | 5 |
| DTSMA | 7.780E−01 | 3.851E−01 | 4.030E+01 | 2.000E+02 | 5.892E+03 | 2 |
| PHISAO | 7.789E−01 | 3.851E−01 | 4.039E+01 | 2.000E+02 | 6.081E+03 | 4 |
| EPSCA | 8.830E−01 | 4.401E−01 | 4.571E+01 | 1.371E+02 | 6.310E+03 | 6 |
| WOSSA | 7.801E−01 | 3.850E−01 | 4.038E+01 | 1.991E+02 | 6.442E+03 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Meng, H.; Wang, D.; Fu, B.; Shao, Y.; Liu, Z. An Enhanced Slime Mould Algorithm Based on Best–Worst Management for Numerical Optimization Problems. Biomimetics 2025, 10, 504. https://doi.org/10.3390/biomimetics10080504
Li T, Meng H, Wang D, Fu B, Shao Y, Liu Z. An Enhanced Slime Mould Algorithm Based on Best–Worst Management for Numerical Optimization Problems. Biomimetics. 2025; 10(8):504. https://doi.org/10.3390/biomimetics10080504
Chicago/Turabian StyleLi, Tongzheng, Hongchi Meng, Dong Wang, Bin Fu, Yuanyuan Shao, and Zhenzhong Liu. 2025. "An Enhanced Slime Mould Algorithm Based on Best–Worst Management for Numerical Optimization Problems" Biomimetics 10, no. 8: 504. https://doi.org/10.3390/biomimetics10080504
APA StyleLi, T., Meng, H., Wang, D., Fu, B., Shao, Y., & Liu, Z. (2025). An Enhanced Slime Mould Algorithm Based on Best–Worst Management for Numerical Optimization Problems. Biomimetics, 10(8), 504. https://doi.org/10.3390/biomimetics10080504






