Abstract
In this work, we present a new partially coherent adjustable anomalous vortex laser beam (PCAAVLB) and introduce it into turbulent biological tissue. The equation of such PCAAVLB in turbulent biological tissue is obtained. By numerical analysis, the evolution of the intensity of such PCAAVLB in turbulent biological tissue is analyzed. It is found that the PCAAVLB in biological tissue can lose its ring shape and become a Gaussian beam, and a PCAAVLB with smaller topological charge or coherence length will evolve into a Gaussian profile faster. The PCAAVLB in turbulent biological tissue with a smaller small-length-scale factor or larger fractal dimension will evolve into a Gaussian profile faster and have a larger intensity as z increases. The results may have potential applications in sensing under biological tissue environments and laser imaging in biology.
1. Introduction
The properties of tissue affect the application of lasers in medicine, and the optical properties of tissue have been investigated [1]. To explore the applications of lasers in biological tissues, the influences of tissue turbulence on optical waves have attracted attention [2], as have the properties (intensity and beam spread et al.) of light in biological tissues. In addition, the intensity of various lasers in turbulent biological tissue has been studied, such as the hollow Gaussian beam [3], partially coherent beam [4], vortex beam [5], Hermite–Gaussian correlated beam [6], rectangular multi-Gaussian beam [7], and Gaussian–Schell model vortex beam [8]. The coherence properties of laser in tissue are still analyzed [9]. Moreover, the coupling efficiency to fiber [10] and adaptive optics correction in tissues [11] are also investigated. From the above references, one sees that different types of laser beams may have potential applications in tissues.
A vortex is a signature of natural systems and is observed in fluids, smoke rings, and tornados [12]. The high speed of the peregrine falcon can be enhanced by the vortices emanating from the frontal and dorsal regions [13]. The trailing-edge vortices have been found in the flight of mosquitoes [14]. Moreover, the vortex has also been introduced into the light, and the double vortex beams have also been investigated [15,16]. The intensity pattern of a laser usually has a Gaussian profile. However, the intensity pattern of light can be modulated, and an anomalous hollow beam can show a unique intensity profile [17]. And the propagation of such AHB has been studied [18,19,20]. Such an AHB has also been extended into a partially coherent beam [21,22,23]. Recently, a new adjustable anomalous vortex beam (AAVB) has been introduced [24]; the properties of such AAVB can be modulated by adjustable parameters. It will be interesting if this adjustable beam is introduced into biological tissue.
The vortex in nature [12], birds [13] and mosquitoes [14], shows unique properties. In this work, the AAVB is extended into a partially coherent beam, and a new partially coherent adjustable anomalous vortex laser beam (PCAAVLB), which can be modulated by the adjustable parameters, is introduced. The intensity of the PCAAVLB can be controlled by adjustable parameters, while the intensity of the multi-Gaussian correlated AHB has the ring symmetry in Reference [23]. This PCAAVLB is introduced into the tissues, and the intensity equation of such PCAAVLB in turbulent biological tissue is derived. Based on the derived equations, the effects of turbulent biological tissue on the intensity of such PCAAVLB are analyzed.
2. Propagation of PCAAVLB in Turbulent Biological Tissue
When the PCAAVLB propagates along the z-axis, the intensity of PCAAVLB in turbulent biological tissue is described by the Huygens–Fresnel integral as follows [3,4,5,6,7,8]:
where represents the intensity; is the cross spectral density (CSD) of laser at ; is the wavenumber with is the wavelength in vacuum; and are position vectors at and , respectively; is imaginary unit; is the phase perturbation of biological tissue.
The Λ is the coherence length of a spherical wave in turbulent biological tissue and which can be written as follows [10]:
where denotes the strength coefficient of biological tissues; denotes the fractal dimension; denotes the characteristic length of heterogeneity; denotes small length-scale factor; denotes the gamma function; denotes the confluent hypergeometric function of the second kind.
The electric field of AAVB at is written as follows [24,25]:
where and are the beam width of the Gaussian part; is a topological charge; and , , and are adjustable parameters.
Considering the coherence theory [26], the CSD of a PCAAVLB is written as follows:
where and are the coherence length along x-axis and y-axis. The intensity of PCAAVLB can be modulated by the adjustable parameters in Equation (5), and this beam is newly introduced, which is different from the multi-Gaussian correlated partially coherent anomalous hollow beam in Reference [23].
We next consider the following equations [27]:
By substituting Equation (5) into Equation (1), the intensity of such PCAAVLB in turbulent biological tissue is derived as follows:
with
with
By using Equations (8)–(20), the evolution of intensity of PCAAVLB in turbulent biological tissue can be obtained.
3. Results and Analyses
In this section, the intensity of a PCAAVLB in turbulent biological tissue is analyzed based on the numerical simulations. In the numerical simulation, the following parameter are chosen, such as , , , , , , , and .
First, the intensity of a PCAAVLB with , , and in free space () is illustrated in Figure 1. The intensity of this PCAAVLB in free space shows a ring profile at (Figure 1a). As z increases, the hollow width of ring shape of such a PCAAVLB will gradually lessen (Figure 1b) and disappear (Figure 1c). At last, the intensity of this PCAAVLB will become a spot pattern with a Gaussian-like profile (Figure 1d). Then the adjustable parameters change. Figure 2 shows the intensity of a PCAAVLB with , , and in free space. When , the intensity of this PCAAVLB can show the two-spot pattern at (Figure 2a). The PCAAVLB with has the ring profile (Figure 1a). As z increases, the two-spot pattern of this PCAAVLB will overlap (Figure 2b,c). Lastly, the intensity of this PCAAVLB can become an elliptical profile (Figure 2d) when cx > cy; the intensity of PCAAVLB with , , and in free space is shown in Figure 3. The intensity of such a PCAAVLB will have two spots along x-axis (Figure 3a), while the PCAAVLB with cx < cy shows two spots along the y-axis (Figure 2a). And this PCAAVLB will evolve into an elliptical beam along the x-axis (Figure 3b). Therefore, the intensity of such PCAAVLB can be controlled by adjustable parameters and the circular or elliptical intensity shape can be obtained by setting the different parameters.
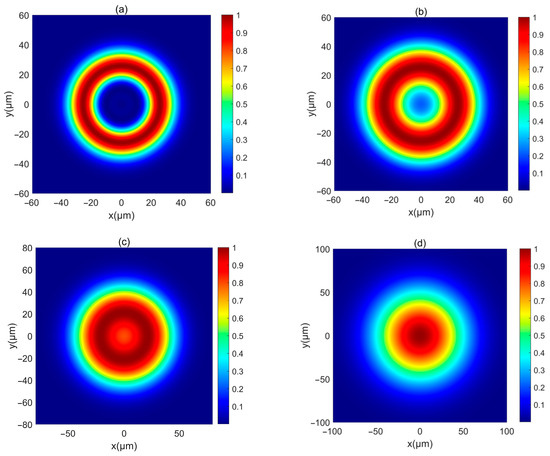
Figure 1.
The normalized intensity of a PCAAVLB with , in free space: (a) z = 20 μm, (b) z = 300 μm, (c) z = 500 μm, and (d) z = 1000 μm.
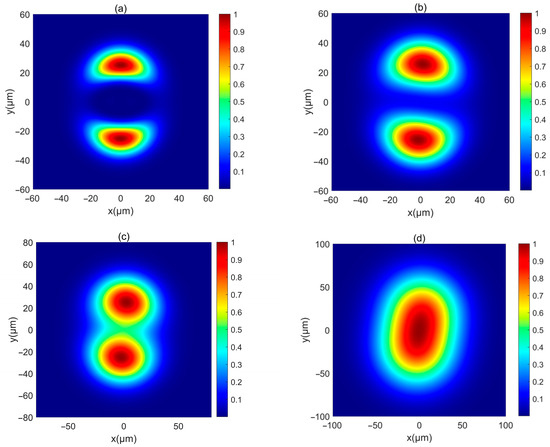
Figure 2.
The normalized intensity of a PCAAVLB with , , and cy = 8 in free space: (a) z = 20 μm, (b) z = 300 μm, (c) z = 500 μm, and (d) z = 1000 μm.
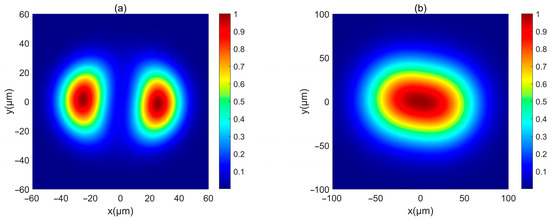
Figure 3.
The normalized intensity of a PCAAVLB with and , and cy = 2 in free space: (a) z = 300 μm, and (b) z = 1000 μm.
Next, the intensity of such PCAAVLB in turbulent biological tissue is studied. Figure 4 illustrates the intensity of a PCAAVLB with a = 2 and cx = cy = 8 in turbulent biological tissue. Intensity shape of this PCAAVLB in turbulent biological tissue at z = 20 μm retains its ring shape (Figure 4a), and the hollow center will gradually disappear at z = 150 μm (Figure 4b), while the PCAAVLB with δ = 5 μm in free space at z = 300 μm just has the ring shape (Figure 1a). Therefore, the biological tissue will accelerate the speed of the PCAAVLB ring shape loss. As z increases, this PCAAVLB in turbulent biological tissue will show a Gaussian-like shape (Figure 4c), and the spot of intensity will spread farther (Figure 4d). When cx ≠ cy, the intensity of PCAAVLB with cx < cy in turbulent biological tissue becomes an elliptical profile with the long axis along the y-axis at z = 300 μm (Figure 5a), while the same PCAAVLB in free space will evolve into a two-spot pattern (Figure 2c). In addition, the intensity of PCAAVLB with cx > cy in turbulent biological tissue will evolve into an elliptical Gaussian profile with the long axis along the x-axis at z = 300 μm (Figure 5b). From Figure 4 and Figure 5, one concludes that the PCAAVLB in turbulent biological tissue will evolve into one spot pattern faster as z increases.
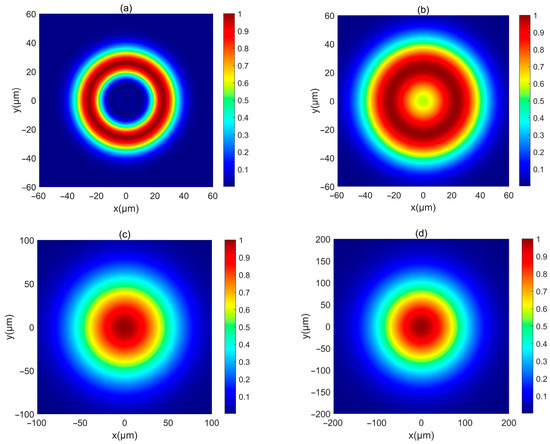
Figure 4.
The normalized intensity of a PCAAVLB with and in biological tissue for the different δ: (a) z = 20 μm, (b) z = 150 μm, (c) z = 300 μm, and (d) z = 500 μm.

Figure 5.
Cross sections of a PCAAVLB with and in biological tissue at z = 300 μm: (a) a = 1, cx = 2, and cy = 8; (b) a = 1, cx = 8, and cy = 2.
To see the beam parameters on the intensity of a PCAAVLB in turbulent biological tissue, Figure 6 shows the intensity of a PCAAVLB with , , and in biological tissue for the different . The intensity of PCAAVLBs with the different in turbulent biological tissue has the same profile at (Figure 6a). As z increases, such PCAAVLB with smaller in turbulent biological tissue will first lose the ring profile (Figure 6a) and gradually become a Gaussian-like profile (Figure 6c). As z increases further, such PCAAVLBs with the different can all have Gaussian-like patterns, such PCAAVLBs with smaller will have a larger width, and the intensity of PCAAVLB with smaller will decrease faster (Figure 6d). Thus, the speed of evolution can be controlled by , and the PCAAVLBs with a smaller will evolve into a Gaussian shape faster and have a smaller intensity.
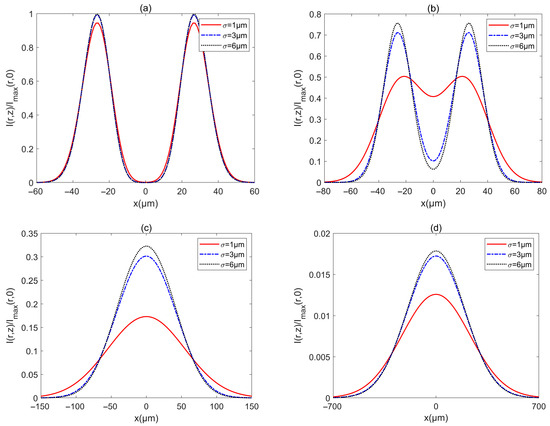
Figure 6.
Cross sections of intensity of a PCAAVLB with and in biological tissue for the different δ: (a) z = 20 μm, (b) z = 100 μm, (c) z = 300 μm, and (d) z = 1000 μm.
The intensity of a PCAAVLB with , , and in turbulent biological tissue for the different is illustrated in Figure 7. The PCAAVLB with a larger has a bigger width at (Figure 7a). As z increases, the PCAAVLB with a smaller in turbulent biological tissue will first lose its ring profile, while the intensity of the PCAAVLB with a larger will have a lower intensity (Figure 7b). As z increases further, the PCAAVLB with a different can gradually become a Gaussian profile (Figure 7c), and such a PCAAVLB with a smaller in turbulent biological tissue will have a larger intensity although all PCAAVLBs have the Gaussian profile (Figure 7d).
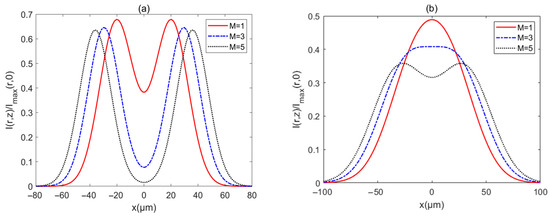
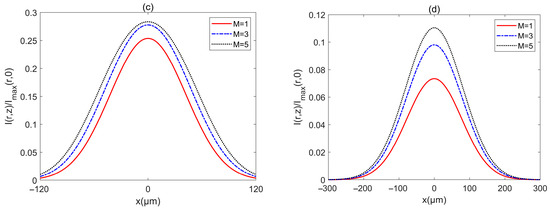
Figure 7.
Cross sections of intensity of a PCAAVLB with and in biological tissue for the different M: (a) z = 100 μm, (b) z = 200 μm, (c) z = 300 μm, and (d) z = 500 μm.
The influences of parameters of turbulent biological tissue on the intensity of PCAAVLB are shown in Figure 8 and Figure 9. The intensity of a PCAAVLB with , , and in turbulent biological tissue for the different is illustrated in Figure 8. The intensity profile of such a PCAAVLB in turbulent biological tissue with different remains the ring profile at (Figure 8a). As z increases, such PCAAVLB in a turbulent biological tissue with a larger will first lose its ring shape (Figure 8b), evolve into a Gaussian profile, and the beam in a turbulent biological tissue with a larger will have a larger intensity. (Figure 8c). The PCAAVLB in a turbulent biological tissue with a larger will have a larger spot at and remain the larger intensity (Figure 8d).
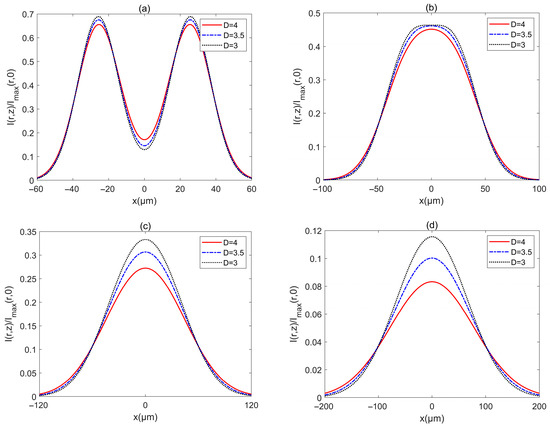
Figure 8.
Cross sections of intensity of a PCAAVLB with and in biological tissue for the different D: (a) z = 100 μm, (b) z = 200 μm, (c) z = 300 μm, and (d) z = 500 μm.
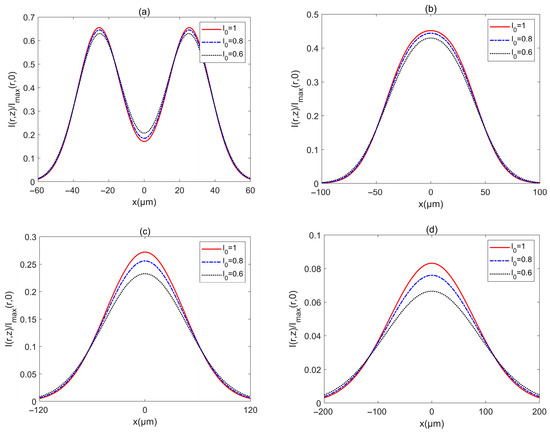
Figure 9.
Cross sections of intensity of a PCAAVLB with and in biological tissue for the different : (a) z = 100 μm, (b) z = 200 μm, (c) z = 300 μm, and (d) z = 500 μm.
Figure 9 shows the intensity of a PCAAVLB with , , and in turbulent biological tissue for different l0. The intensity profile of such a PCAAVLB in turbulent biological tissue with different l0 remains almost similar at z = 100 x3BCm (Figure 9a). As z increases, the PCAAVLB in turbulent biological tissue for the different l0 will have similar evolution properties (Figure 9b,c). At last, the PCAAVLB in turbulent biological tissue with different l0 will have a similar spot and the beam with larger l0 will have a larger intensity. Therefore, one can conclude that the PCAAVLB in turbulent biological tissue with a larger D or a smaller l0 will evolve from a ring profile into a Gaussian-like profile faster, and such a PCAAVLB in turbulent biological tissue with a larger D or a smaller l0 will have a larger intensity.
4. Conclusions
Vortices are ubiquitous in nature, such as in fluids, smoke rings, and tornados, and vortices have also been observed in light. In this work, a new beam carried vortex, which is named PCAAVLB, is introduced, and the intensity of such PCAAVLB in turbulent biological tissue is derived. The intensity shape of such PCAAVLB in free space can have the ring shape or a two-spot pattern, and the intensity profile is controlled by adjustable initial parameters. The intensity of such a PCAAVLB can gradually evolve into a Gaussian-like profile. And the intensity of such a PCAAVLB with a smaller or in turbulent biological tissue will lose its ring shape faster, and the intensity profile of such a PCAAVLB with smaller in turbulent biological tissue will have a larger spot, while the PCAAVLB with different in turbulent biological tissue has almost the same intensity profile at a larger distance. In addition, the PCAAVLB in turbulent biological tissue with larger or smaller will evolve from a ring profile into a Gaussian-like profile faster and have a larger intensity. The obtained results may have potential applications in laser sensing under biological tissue environments and laser imaging in biology.
Author Contributions
Conceptualization, Y.S. and R.D.; software, W.W. and X.D.; data curation, L.S. and Z.Q.; writing—original draft preparation, Y.Z.; writing—review and editing, H.J.; project administration, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program Project ‘Intersatellite Laser Communication Measurement Integrated System Technology’ (2022YFB3902505), the National Natural Science Foundation of China (under Grant 62201307), the 111 Project of China (D21009), and the Major Key Project of PCL (PCL2024A01).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this work are available upon request from the corresponding author.
Conflicts of Interest
Author Wu Wang was employed by the North Navigation Control Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef] [PubMed]
- Gökçe, M.C.; Ata, Y.; Baykal, Y. Tissue turbulence and its effects on optical waves: A review. Opt. Commun. 2023, 546, 129816. [Google Scholar] [CrossRef]
- Saad, F.; Belafhal, A. A theoretical investigation on the propagation properties of Hollow Gaussian beams passing through turbulent biological tissues. Optik 2017, 141, 72–82. [Google Scholar] [CrossRef]
- Wu, Y.Q.; Zhang, Y.X.; Wang, Q.; Hu, Z.D. Average intensity and spreading of partially coherent model beams propagating in a turbulent biological tissue. J. Quant. Spectrosc. Radiat. Transf. 2016, 184, 308–315. [Google Scholar] [CrossRef]
- Liu, D.; Zhong, H.; Wang, Y. Intensity properties of anomalous hollow vortex beam propagating in biological tissues. Optik 2018, 170, 61–69. [Google Scholar] [CrossRef]
- Zhang, H.; Cui, Z.; Han, Y.; Guo, J.; Chang, C. Average Intensity and Beam Quality of Hermite-Gaussian Correlated Schell-Model Beams Propagating in Turbulent Biological Tissue. Front. Phys. 2021, 9, 650537. [Google Scholar] [CrossRef]
- Liu, D.J.; Zhong, H.Y.; Yin, H.M.; Dong, A.Y.; Wang, G.Q.; Wang, Y.C. Spreading and coherence properties of a rectangular multi-Gaussian Schell-model beam propagating in biological tissues. Indian J. Phys. 2021, 95, 571–577. [Google Scholar] [CrossRef]
- Duan, M.; Tian, Y.; Zhang, Y.; Li, J. Influence of biological tissue and spatial correlation on spectral changes of Gaussian-Schell model vortex beam. Opt. Laser. Eng. 2020, 134, 106224. [Google Scholar] [CrossRef]
- Duan, M.L.; Wu, Y.G.; Zhang, Y.M.; Li, J.H. Coherence properties of a random electromagnetic vortex beam propagating in biological tissues. J. Mod. Optic. 2019, 66, 59–66. [Google Scholar] [CrossRef]
- Liang, Q.; Hu, B.; Zhang, Y.; Zhu, Y.; Deng, S.; Yu, L. Coupling efficiency of a partially coherent collimating laser from turbulent biological tissue to fiber. Results Phys. 2019, 13, 102162. [Google Scholar] [CrossRef]
- Baykal, Y. Adaptive optics correction of beam spread in biological tissues. J. Quant. Spectrosc. Radiat. Transf. 2022, 283, 108145. [Google Scholar] [CrossRef]
- Dorrah, A.H.; Palmieri, A.; Li, L.; Capasso, F. Rotatum of light. Sci. Adv. 2025, 11, eadr9092. [Google Scholar] [CrossRef] [PubMed]
- Gowree, E.R.; Jagadeesh, C.; Talboys, E.; Lagemann, C.; Brücker, C. Vortices enable the complex aerobatics of peregrine falcons. Commun. Biol. 2018, 1, 27. [Google Scholar] [CrossRef]
- Bomphrey, R.J.; Nakata, T.; Phillips, N.; Walker, S.M. Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight. Nature 2017, 544, 92–95. [Google Scholar] [CrossRef] [PubMed]
- Guo, M.; Le, W.; Wang, C.; Rui, G.; Zhu, Z.; He, J.; Gu, B. Generation, Topological Charge, and Orbital Angular Momentum of Off-Axis Double Vortex Beams. Photonics 2023, 10, 368. [Google Scholar] [CrossRef]
- Chen, L.; Liu, D.; Gao, H.; Dong, A.; Wang, Y. Research on characteristics of partially coherent radially polarized off-axis double vortex beam in oceanic turbulence. Opt. Laser Technol. 2025, 190, 113264. [Google Scholar] [CrossRef]
- Cai, Y.J. Model for an anomalous hollow beam and its paraxial propagation. Opt. Lett. 2007, 32, 3179–3181. [Google Scholar] [CrossRef]
- Dai, Z.P.; Wang, Y.J.; Wang, Y.C.; Liu, X.J.; Yang, Z.J.; Pang, Z.G. Propagation of adjustable anomalous hollow Gaussian beams in the cascade of left-handed and right-handed media. Optik 2022, 270, 170024. [Google Scholar] [CrossRef]
- Dai, Z.P.; Wang, Y.J.; Wang, Y.C.; Yang, Z.J.; Pang, Z.G. Propagation properties of controllable anomalous hollow beams in strongly nonlocal nonlinear media. Results Phys. 2022, 42, 105951. [Google Scholar] [CrossRef]
- Dai, Z.P.; Yang, Z.J.; Zhang, S.M.; Pang, Z.G.; You, K.M. Transversal reverse transformation of anomalous hollow beams in strongly isotropic nonlocal media. Chin. Phys. B 2014, 23, 074208. [Google Scholar] [CrossRef]
- Wang, K.L.; Zhao, C.H. Propagation properties of a radial phased-locked partially coherent anomalous hollow beam array in turbulent atmosphere. Opt. Laser Technol. 2014, 57, 44–51. [Google Scholar] [CrossRef]
- Tian, H.H.; Xu, Y.G.; Yang, T.; Ma, Z.R.; Wang, S.J.; Dan, Y.Q. Propagation characteristics of partially coherent anomalous elliptical hollow Gaussian beam propagating through atmospheric turbulence along a slant path. J. Mod. Optic. 2017, 64, 422–429. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Zhong, H.; Wang, G.; Yin, H.; Dong, A. Properties of multi-Gaussian correlated partially coherent anomalous hollow beam propagating in underwater oceanic turbulence. Opt. Laser Technol. 2019, 119, 105604. [Google Scholar] [CrossRef]
- Guo, X.; Song, Y.; Dong, K.; Zhang, L. Adjustable anomalous hollow vortex beam and its properties. Microw. Opt. Techn. Let. 2024, 66, e34099. [Google Scholar] [CrossRef]
- Wang, Y.J.; Yang, Z.J.; Shen, S.; Cai, Z.H.; Li, X.L.; Zhang, S.M. Controllable anomalous hollow beam and its propagation properties. Optik 2021, 241, 167054. [Google Scholar] [CrossRef]
- Wolf, E. Unified theory of coherence and polarization of random electromagnetic beams. Phys. Lett. A 2003, 312, 263–267. [Google Scholar] [CrossRef]
- Jeffrey, A. Handbook of Mathematical Formulas and Integrals, 4th ed.; Academic Press Inc.: Cambridge, MA, USA, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).