Feedback-Driven Dynamical Model for Axonal Extension on Parallel Micropatterns
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Model Parameters
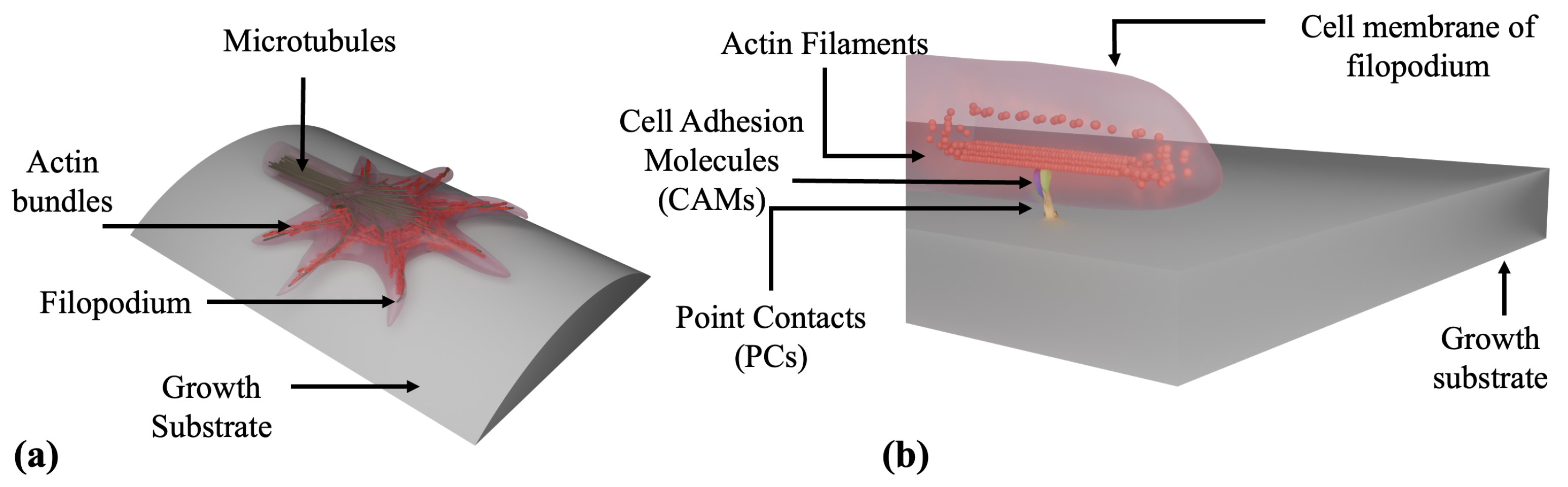
- Biochemical–mechanical state of a single growth cone:
- : polymerized F-actin density;
- : density of active CAM-PC complexes (effective adhesion sites);
- traction force transmitted to the substrate.
- Growth cone repulsion (lateral inhibition):
- : repulsive signal (Netrin, Ephrin) received by a growth cone on micropattern i;
- : repulsive ligand (Semaphorin3A or Slit proteins) emitted by a growth cone on micropattern i.
- Tubulin transport model:
- : tubulin concentration in the soma;
- : tubulin concentration in the growth cone;
- : axonal length.
3.2. Governing Equations
- Generation of traction forces. Growth cones translate extracellular cues into directed motion by coordinating cytoskeletal dynamics and cell–substrate adhesion through a molecular clutch mechanism. Moreover, Traction Force Microscopy (TFM) experiments indicate that the contractile force transmitted to the substrate scales with both actin and PC-CAM density [37,38,39]. Based on this framework we introduce the following mathematical model for actin–adhesion generated traction:
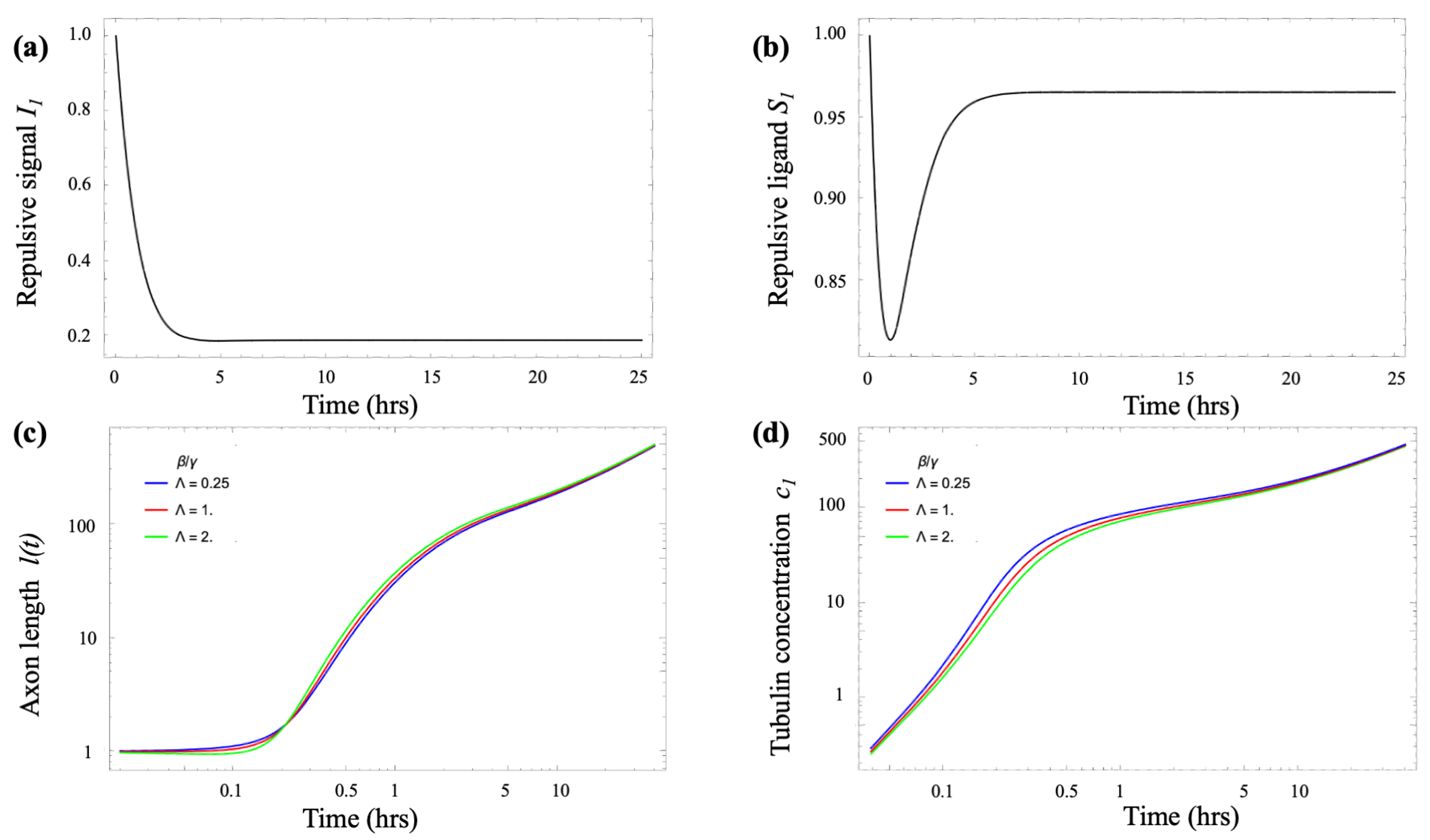
- Growth cone lateral inhibition. To model the near-neighbor axonal inhibition we adapt the “Delta-Notch” lateral-inhibition model of Collier et al. [20], and write the following coupled equations for received inhibition and emitted inhibitory ligand for a growth cone on micropattern i (, where N is the total number of micropatterns):
- Tubulin transport. A key factor in neurite growth is the availability of tubulin, which polymerizes to form microtubules that support axonal extension. During the early stages of axonal development, tubulin and other essential cellular components are synthesized in the soma and must be delivered to the growth cone. This transport occurs through a combination of diffusion and active motor-driven mechanisms along the axonal shaft [4,5,6,7]. A common modeling approach represents the neuron as a small number of compartments, each characterized by specific chemical concentrations [13,21]. These compartments exchange materials via diffusion and active transport driven by molecular motors. Following the model introduced by Oliveri & Goriely [21], we adopt a simplified two-compartment framework in which the compartments are separated by a distance l, representing the axonal length. In dimensionless form, the resulting coupled differential equations describe tubulin transport from the soma to the growth cone as follows [21]:where and are the (scaled) tubulin concentrations in the soma and growth cone, respectively, and ℓ is the axonal length. The parameter represents the tubulin transport rate, the local consumption rate, and the treadmilling offset. A detailed derivation, along with a discussion of the key properties of these equations, is provided in the Appendix B.
3.3. Dynamical–Systems Analysis
3.4. Connecting the Dynamical-Systems Analysis to Axonal Growth
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Steady States of the Biomechanical Equations and Pitchfork Bifurcation
Appendix B. Tubulin Transport
- (axon shortens),
- (axon elongates).
References
- Azevedo, F.A.; Carvalho, L.R.; Grinberg, L.T.; Farfel, J.M.; Ferretti, R.E.; Leite, R.E.; Filho, W.J.; Lent, R.; Herculano-Houzel, S. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J. Comp. Neurol. 2009, 513, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Striedter, G. Neurobiology: A Functional Approach; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Arimura, N.; Kaibuchi, K. Neuronal polarity: From extracellular signals to intracellular mechanisms. Nat. Rev. Neurosci. 2007, 8, 194–205. [Google Scholar] [CrossRef] [PubMed]
- Huber, A.B.; Kolodkin, A.L.; Ginty, D.D.; Cloutier, J.F. Signaling at the growth cone: Ligand-receptor complexes and the control of axon growth and guidance. Annu. Rev. Neurosci. 2003, 26, 509–563. [Google Scholar] [CrossRef] [PubMed]
- Lowery, L.A.; Van Vactor, D. The trip of the tip: Understanding the growth cone machinery. Nat. Rev. Mol. Cell Biol. 2009, 10, 332–343. [Google Scholar] [CrossRef]
- Franze, K.; Guck, J. The biophysics of neuronal growth. Rep. Prog. Phys. 2010, 73, 094601. [Google Scholar] [CrossRef]
- Kiryushko, D.; Berezin, V.; Bock, E. Regulators of Neurite Outgrowth: Role of Cell Adhesion Molecules. Ann. N. Y. Acad. Sci. 2004, 1014, 140–154. [Google Scholar] [CrossRef]
- Goodhill, G.; Urbach, J. Axon Guidance and Gradient Detection by Growth Cones; The MIT Press: Cambridge, MA, USA, 2003; pp. 95–110. [Google Scholar] [CrossRef]
- Franze, K. The mechanical control of nervous system development. Development 2013, 140, 3069–3077. [Google Scholar] [CrossRef]
- Moeendarbary, E.; Harris, A.R. Cell mechanics: Principles, practices, and prospects. Wiley Interdiscip Rev. Syst. Biol. Med. 2014, 6, 371–388. [Google Scholar] [CrossRef]
- Riveline, D.; Zamir, E.; Balaban, N.Q.; Schwarz, U.S.; Ishizaki, T.; Narumiya, S.; Kam, Z.; Geiger, B.; Bershadsky, A.D. Focal contacts as mechanosensors: Externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism. J. Cell Biol. 2001, 153, 1175–1186. [Google Scholar] [CrossRef]
- Fivaz, M.; Bandara, S.; Inoue, T.; Meyer, T. Robust neuronal symmetry breaking by Ras-triggered local positive feedback. Curr. Biol. 2008, 18, 44–50. [Google Scholar] [CrossRef]
- Samuels, D.C.; Hentschel, H.G.; Fine, A. The origin of neuronal polarization: A model of axon formation. Philos Trans. R. Soc. Lond B. Biol. Sci. 1996, 351, 1147–1156. [Google Scholar] [CrossRef] [PubMed]
- Toriyama, M.; Sakumura, Y.; Shimada, T.; Ishii, S.; Inagaki, N. A diffusion-based neurite length-sensing mechanism involved in neuronal symmetry breaking. Mol. Syst. Biol. 2010, 6, 394. [Google Scholar] [CrossRef] [PubMed]
- Franze, K. Integrating Chemistry and Mechanics: The Forces Driving Axon Growth. Annu. Rev. Cell Dev. Biol. 2020, 36, 61–83. [Google Scholar] [CrossRef]
- Alert, R.; Trepat, X. Physical models of collective cell migration. Annu. Rev. Condens. Matter Phys. 2020, 11, 77–101. [Google Scholar] [CrossRef]
- Franze, K.; Gerdelmann, J.; Weick, M.; Betz, T.; Pawlizak, S.; Lakadamyali, M.; Bayer, J.; Rillich, K.; Gögler, M.; Lu, Y.B.; et al. Neurite branch retraction is caused by a threshold-dependent mechanical impact. Biophys. J. 2009, 97, 1883–1890. [Google Scholar] [CrossRef]
- Takano, T.; Funahashi, Y.; Kaibuchi, K. Neuronal Polarity: Positive and Negative Feedback Signals. Front. Cell Dev. Biol. 2019, 7, 69. [Google Scholar] [CrossRef]
- El-Samad, H. Biological feedback control-Respect the loops. Cell Syst. 2021, 12, 477–487. [Google Scholar] [CrossRef]
- Collier, J.R.; Monk, N.A.; Maini, P.K.; Lewis, J.H. Pattern formation by lateral inhibition with feedback: A mathematical model of delta-notch intercellular signalling. J. Theor. Biol. 1996, 183, 429–446. [Google Scholar] [CrossRef]
- Oliveri, H.; Goriely, A. Mathematical models of neuronal growth. Biomech. Model. Mechanobiol. 2022, 21, 89–118. [Google Scholar] [CrossRef]
- Descoteaux, M.; Sunnerberg, J.P.; Brady, D.D.; Staii, C. Feedback-controlled dynamics of neuronal cells on directional surfaces. Biophys. J. 2022, 121, 769–781. [Google Scholar] [CrossRef]
- Recho, P.; Jerusalem, A.; Goriely, A. Growth, collapse, and stalling in a mechanical model for neurite motility. Phys. Rev. E 2016, 93, 032410. [Google Scholar] [CrossRef] [PubMed]
- Maccioni, R.B.; Cambiazo, V. Role of microtubule-associated proteins in the control of microtubule assembly. Physiol. Rev. 1995, 75, 835–864. [Google Scholar] [CrossRef] [PubMed]
- Caviston, J.P.; Holzbaur, E.L. Microtubule motors at the intersection of trafficking and transport. Trends Cell Biol. 2006, 16, 530–537. [Google Scholar] [CrossRef] [PubMed]
- Coles, C.; Bradke, F. Coordinating Neuronal Actin–Microtubule Dynamics. Curr. Biol. 2015, 25, R677–R691. [Google Scholar] [CrossRef]
- Miller, K.E.; Joshi, H.C. Tubulin transport in neurons. J. Cell Biol. 1996, 133, 1355–1366. [Google Scholar] [CrossRef]
- Lim, S.S.; Edson, K.J.; Letourneau, P.C.; Borisy, G.G. A test of microtubule translocation during neurite elongation. J. Cell Biol. 1990, 111, 123–130. [Google Scholar] [CrossRef]
- Okabe, S.; Hirokawa, N. Turnover of fluorescently labelled tubulin and actin in the axon. Nature 1990, 343, 479–482. [Google Scholar] [CrossRef]
- Medeiros, N.A.; Burnette, D.T.; Forscher, P. Myosin II functions in actin-bundle turnover in neuronal growth cones. Nat. Cell Biol. 2006, 8, 215–226. [Google Scholar] [CrossRef]
- McKayed, K.K.; Simpson, J.C. Actin in action: Imaging approaches to study cytoskeleton structure and function. Cells 2013, 2, 715–731. [Google Scholar] [CrossRef]
- Lilja, J.; Ivaska, J. Integrin activity in neuronal connectivity. J. Cell Sci. 2018, 131, jcs212803. [Google Scholar] [CrossRef]
- Polackwich, R.J.; Koch, D.; McAllister, R.; Geller, H.M.; Urbach, J.S. Traction force and tension fluctuations in growing axons. Front. Cell Neurosci. 2015, 9, 417. [Google Scholar] [CrossRef] [PubMed]
- Pouwels, J.; Nevo, J.; Pellinen, T.; Ylänne, J.; Ivaska, J. Negative regulators of integrin activity. J. Cell Sci. 2012, 125, 3271–3280. [Google Scholar] [CrossRef] [PubMed]
- Jurchenko, C.; Salaita, K.S. Lighting Up the Force: Investigating Mechanisms of Mechanotransduction Using Fluorescent Tension Probes. Mol. Cell Biol. 2015, 35, 2570–2782. [Google Scholar] [CrossRef] [PubMed]
- Buskermolen, A.B.C.; Ristori, T.; Mostert, D.; van Turnhout, M.C.; Shishvan, S.S.; Loerakker, S.; Kurniawan, N.A.; Deshpande, V.S.; Bouten, C.V.C. Cellular Contact Guidance Emerges from Gap Avoidance. Cell Rep. Phys. Sci. 2020, 1, 100055. [Google Scholar] [CrossRef]
- Hyland, C.; Mertz, A.F.; Forscher, P.; Dufresne, E. Dynamic peripheral traction forces balance stable neurite tension in regenerating Aplysia bag cell neurons. Sci. Rep. 2014, 4, 4961. [Google Scholar] [CrossRef]
- Koch, D.; Rosoff, W.J.; Jiang, J.; Geller, H.M.; Urbach, J.S. Strength in the periphery: Growth cone biomechanics and substrate rigidity response in peripheral and central nervous system neurons. Biophys. J. 2012, 102, 452–460. [Google Scholar] [CrossRef]
- Kumarasinghe, U.; Fox, L.N.; Staii, C. Combined Traction Force-Atomic Force Microscopy Measurements of Neuronal Cells. Biomimetics 2022, 7, 157. [Google Scholar] [CrossRef]
- Purohit, P.K.; Smith, D.H. A model for stretch growth of neurons. J. Biomech. 2016, 49, 3934–3942. [Google Scholar] [CrossRef]
- O’Toole, M.; Lamoureux, P.; Miller, K. Measurement of Subcellular Force Generation in Neurons. Biophys. J. 2015, 108, 1027–1037. [Google Scholar] [CrossRef]
- Lin, J.; Li, X.; Yin, J.; Qian, J. Effect of Cyclic Stretch on Neuron Reorientation and Axon Outgrowth. Front. Bioeng. Biotechnol. 2020, 8, 597867. [Google Scholar] [CrossRef]
- Anthonisen, M.; Grutter, P. Growth and Elasticity of Mechanically-Created Neurites. arXiv 2019, arXiv:1912.05735. [Google Scholar] [CrossRef]
- Wang, L.M.; Kuhl, E. Viscoelasticity of the axon limits stretch-mediated growth. Comput. Mech. 2020, 65, 587–595. [Google Scholar] [CrossRef]
- Oliveri, H.; Franze, K.; Goriely, A. Theory for Durotactic Axon Guidance. Phys. Rev. Lett. 2021, 126, 118101. [Google Scholar] [CrossRef] [PubMed]
- Rizzo, D.J.; White, J.D.; Spedden, E.; Wiens, M.R.; Kaplan, D.L.; Atherton, T.J.; Staii, C. Neuronal growth as diffusion in an effective potential. Phys. Rev. E 2013, 88, 042707. [Google Scholar] [CrossRef]
- Spedden, E.; White, J.D.; Naumova, E.N.; Kaplan, D.L.; Staii, C. Elasticity Maps of Living Neurons Measured by Combined Fluorescence and Atomic Force Microscopy. Biophys. J. 2012, 103, 868–877. [Google Scholar] [CrossRef]
- Basso, J.M.V.; Yurchenko, I.; Wiens, M.R.; Staii, C. Neuron dynamics on directional surfaces. Soft. Matter 2019, 15, 9931–9941. [Google Scholar] [CrossRef]
- Staii, C. Biased Random Walk Model of Neuronal Dynamics on Substrates with Periodic Geometrical Patterns. Biomimetics 2023, 8, 267. [Google Scholar] [CrossRef]
- Staii, C. Nonlinear Growth Dynamics of Neuronal Cells Cultured on Directional Surfaces. Biomimetics 2024, 9, 203. [Google Scholar] [CrossRef]
- Yurchenko, I.; Farwell, M.; Brady, D.D.; Staii, C. Neuronal Growth and Formation of Neuron Networks on Directional Surfaces. Biomimetics 2021, 6, 41. [Google Scholar] [CrossRef]
- Yurchenko, I.; Vensi Basso, J.M.; Syrotenko, V.S.; Staii, C. Anomalous diffusion for neuronal growth on surfaces with controlled geometries. PLoS ONE 2019, 14, e0216181. [Google Scholar] [CrossRef]
- Vensi Basso, J.M.; Yurchenko, I.; Simon, M.; Rizzo, D.J.; Staii, C. Role of geometrical cues in neuronal growth. Phys. Rev. E 2019, 99, 022408. [Google Scholar] [CrossRef] [PubMed]
- Athamneh, A.I.; Suter, D.M. Quantifying mechanical force in axonal growth and guidance. Front. Cell. Neurosci. 2015, 9, 359. [Google Scholar] [CrossRef] [PubMed]
- Athamneh, A.I.M.; He, Y.; Lamoureux, P.; Fix, L.; Suter, D.M.; Miller, K.E. Neurite elongation is highly correlated with bulk forward translocation of microtubules. Sci. Rep. 2017, 7, 7292. [Google Scholar] [CrossRef] [PubMed]
- Roy, S. Finding order in slow axonal transport. Curr. Opin. Neurobiol. 2020, 63, 87–94. [Google Scholar] [CrossRef]
- Jakobs, M.A.; Franze, K.; Zemel, A. Mechanical Regulation of Neurite Polarization and Growth: A Computational Study. Biophys. J. 2020, 118, 1914–1920. [Google Scholar] [CrossRef]
- Pfister, B.J.; Gordon, T.; Loverde, J.R.; Kochar, A.S.; Mackinnon, S.E.; Cullen, D.K. Biomedical engineering strategies for peripheral nerve repair: Surgical applications, state of the art, and future challenges. Crit. Rev. Biomed. Eng. 2011, 39, 81–124. [Google Scholar] [CrossRef]
- Holland, M.A.; Miller, K.E.; Kuhl, E. Emerging Brain Morphologies from Axonal Elongation. Ann. Biomed. Eng. 2015, 43, 1640–1653. [Google Scholar] [CrossRef]
- Bayly, P.; Taber, L.; Kroenke, C. Mechanical forces in cerebral cortical folding: A review of measurements and models. J. Mech. Behav. Biomed. Mater. 2014, 29, 568–581. [Google Scholar] [CrossRef]
- de Rooij, R.; Kuhl, E. Microtubule Polymerization and Cross-Link Dynamics Explain Axonal Stiffness and Damage. Biophys. J. 2018, 114, 201–212. [Google Scholar] [CrossRef]
- de Rooij, R.; Kuhl, E. Physical Biology of Axonal Damage. Front. Cell. Neurosci. 2018, 12, 144. [Google Scholar] [CrossRef]
- Mahar, M.; Cavalli, V. Intrinsic mechanisms of neuronal axon regeneration. Nat. Rev. Neurosci. 2018, 19, 323–337. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, M.I.; Amaral, M.H.; Costa, P.C.; Lopes, C.M.; Lamprou, D.A. Recent Developments in Microfluidic Technologies for Central Nervous System Targeted Studies. Pharmaceutics 2020, 12, 542. [Google Scholar] [CrossRef] [PubMed]
- Ahmadzadeh, H.; Smith, D.H.; Shenoy, V. Mechanical Effects of Dynamic Binding between Tau Proteins on Microtubules during Axonal Injury. Biophys. J. 2015, 109, 2328–2337. [Google Scholar] [CrossRef] [PubMed]
- Montanino, A.; Kleiven, S. Utilizing a Structural Mechanics Approach to Assess the Primary Effects of Injury Loads Onto the Axon and Its Components. Front. Neurol. 2018, 9, 643. [Google Scholar] [CrossRef]
- Gladkov, A.; Pigareva, Y.; Kutyina, D.; Kolpakov, V.; Bukatin, A.; Mukhina, I.; Kazantsev, V.; Pimashkin, A. Design of Cultured Neuron Networks in vitro with Predefined Connectivity Using Asymmetric Microfluidic Channels. Sci. Rep. 2017, 7, 15625. [Google Scholar] [CrossRef]
- Ishihara, M.; Mochizuki-Oda, N.; Iwatsuki, K.; Kishima, H.; Iwamoto, Y.; Ohnishi, Y.; Umegaki, M.; Yoshimine, T. A new three-dimensional axonal outgrowth assay for central nervous system regeneration. J. Neurosci. Methods 2011, 198, 181–186. [Google Scholar] [CrossRef]
- Kundu, A.; Micholt, L.; Friedrich, S.; Rand, D.R.; Bartic, C.; Braeken, D.; Levchenko, A. Superimposed topographic and chemical cues synergistically guide neurite outgrowth. Lab. Chip 2013, 13, 3070–3081. [Google Scholar] [CrossRef]
- Xu, G.; Knutsen, A.K.; Dikranian, K.; Kroenke, C.D.; Bayly, P.V.; Taber, L.A. Axons Pull on the Brain, But Tension Does Not Drive Cortical Folding. J. Biomech. Eng. 2010, 132, 071013. [Google Scholar] [CrossRef]
- Beighley, R.; Spedden, E.; Sekeroglu, K.; Atherton, T.; Demirel, M.C.; Staii, C. Neuronal alignment on asymmetric textured surfaces. Appl. Phys. Lett. 2012, 101, 143701. [Google Scholar] [CrossRef]
- Spedden, E.; Wiens, M.R.; Demirel, M.C.; Staii, C. Effects of Surface Asymmetry on Neuronal Growth. PLoS ONE 2014, 9, e106709. [Google Scholar] [CrossRef]
- Pearson, Y.E.; Castronovo, E.; Lindsley, T.A.; Drew, D.A. Mathematical modeling of axonal formation. Part I: Geometry. Bull. Math. Biol. 2011, 73, 2837–2864. [Google Scholar] [CrossRef] [PubMed]
- Amselem, G.; Theves, M.; Bae, A.; Bodenschatz, E.; Beta, C. A stochastic description of Dictyostelium chemotaxis. PLoS ONE 2012, 7, e37213. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Cox, E.C.; Flyvbjerg, H. ‘Dicty dynamics’: Dictyostelium motility as persistent random motion. Phys. Biol. 2011, 8, 046006. [Google Scholar] [CrossRef] [PubMed]
- de Gennes, P.G. Collective neuronal growth and self organization of axons. Proc. Natl. Acad. Sci. USA 2007, 104, 4904–4906. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology, 2nd ed.; Springer: Berlin, Germany, 2013. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Boulder, CO, USA, 2015. [Google Scholar]
- Castro-Domínguez, C.; Lozano-Picazo, P.; Álvarez López, A.; Garrote-Junco, J.; Panetsos, F.; Guinea, G.; Elices, M.; Rojo, F.; González-Nieto, D.; Colchero, L.; et al. Axonal Guidance Using Biofunctionalized Straining Flow Spinning Regenerated Silk Fibroin Fibers as Scaffold. Biomimetics 2023, 8, 65. [Google Scholar] [CrossRef]



| Symbol | Meaning |
|---|---|
| Actin and adhesion turnover ratios | |
| k | Force constant in |
| a | Ratio between pattern spatial period d and growth cone dimension |
| Ligand/receiver lifetime ratio | |
| Coupling strength between traction and ligand export | |
| Orientation-torque coefficient and stiffness anisotropy | |
| Parameters of the tubulin model (see governing equations) | |
| Angular diffusion coefficient (orientation-noise strength) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, K.; Kumarasinghe, U.; Staii, C. Feedback-Driven Dynamical Model for Axonal Extension on Parallel Micropatterns. Biomimetics 2025, 10, 456. https://doi.org/10.3390/biomimetics10070456
Cheng K, Kumarasinghe U, Staii C. Feedback-Driven Dynamical Model for Axonal Extension on Parallel Micropatterns. Biomimetics. 2025; 10(7):456. https://doi.org/10.3390/biomimetics10070456
Chicago/Turabian StyleCheng, Kyle, Udathari Kumarasinghe, and Cristian Staii. 2025. "Feedback-Driven Dynamical Model for Axonal Extension on Parallel Micropatterns" Biomimetics 10, no. 7: 456. https://doi.org/10.3390/biomimetics10070456
APA StyleCheng, K., Kumarasinghe, U., & Staii, C. (2025). Feedback-Driven Dynamical Model for Axonal Extension on Parallel Micropatterns. Biomimetics, 10(7), 456. https://doi.org/10.3390/biomimetics10070456









