Design of a Modular Wall-Climbing Robot with Multi-Plane Transition and Cleaning Capabilities
Abstract
1. Introduction
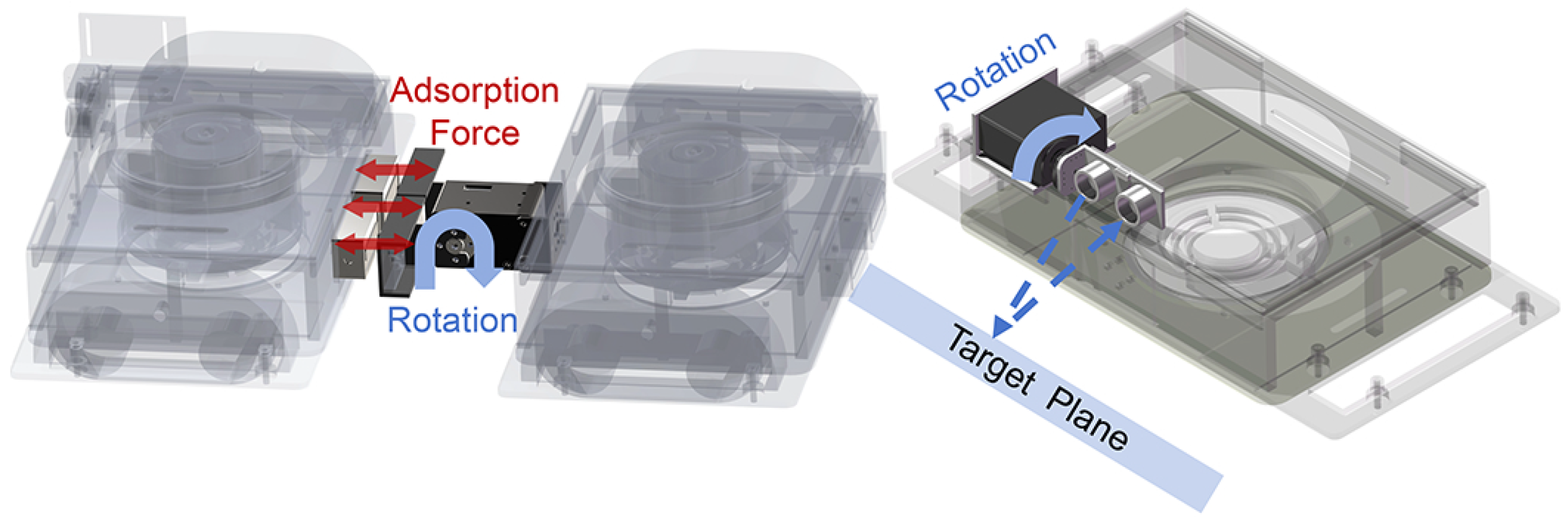
- A modular design is realized with multiple modules connected by servo motors and magnets. Each module has the same structure and composition, and they can be connected in series with each other and realize mutual lifting. The modules can be quickly assembled and disassembled, enhancing flexibility and simplifying maintenance work.
- The combination of servo motors and ultrasonic sensors is introduced for wall-angle measurement, allowing the robot to autonomously adapt to different wall planes. This new detection method is computationally fast and has a simple detection structure, which makes it suitable for low-cost confined-space use.
- The mechanical theory analysis of the robot was carried out under a variety of attachment conditions to calculate the required minimum suction force, which is verified by experiments.
2. Design of the MC-1 Robot
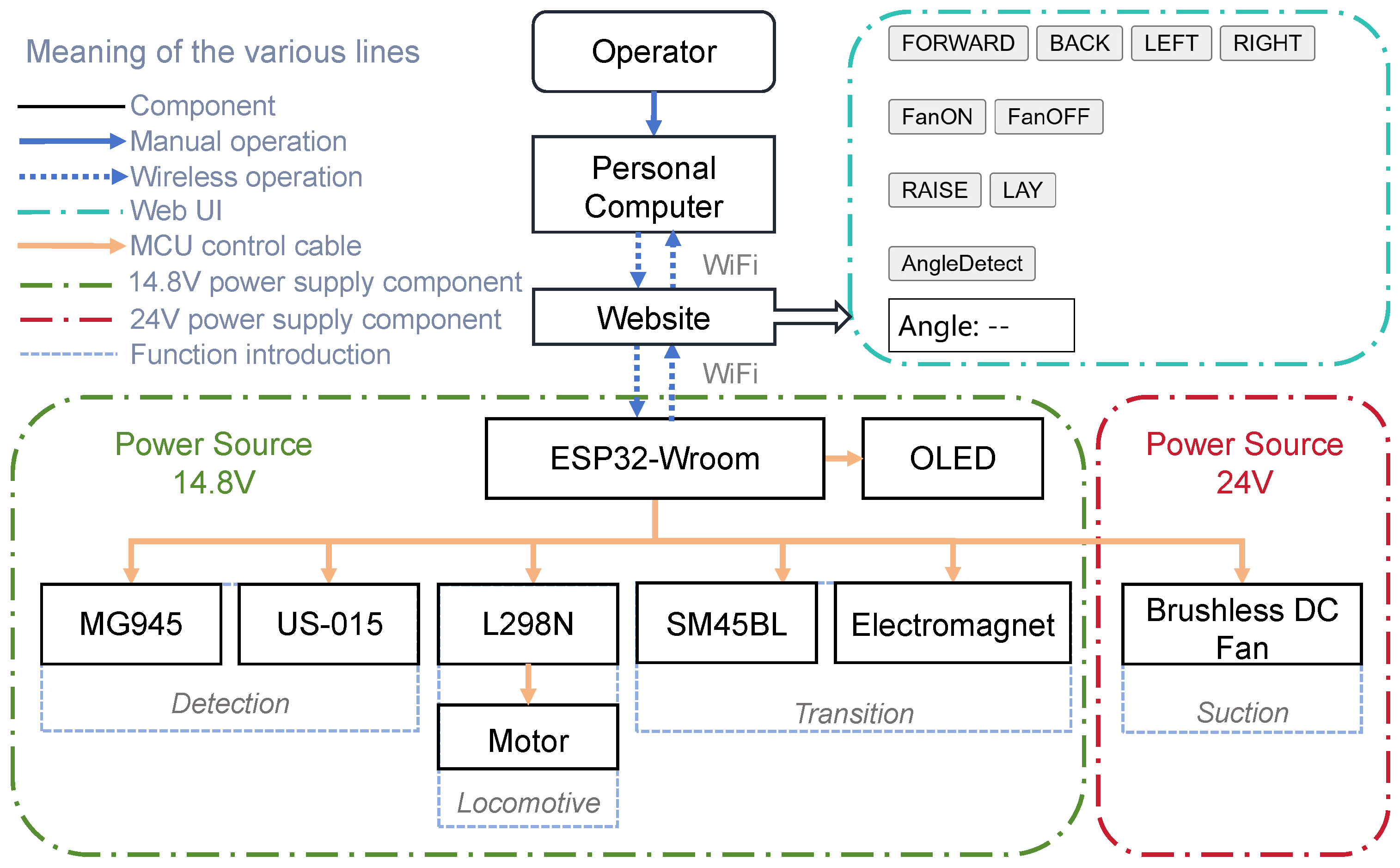
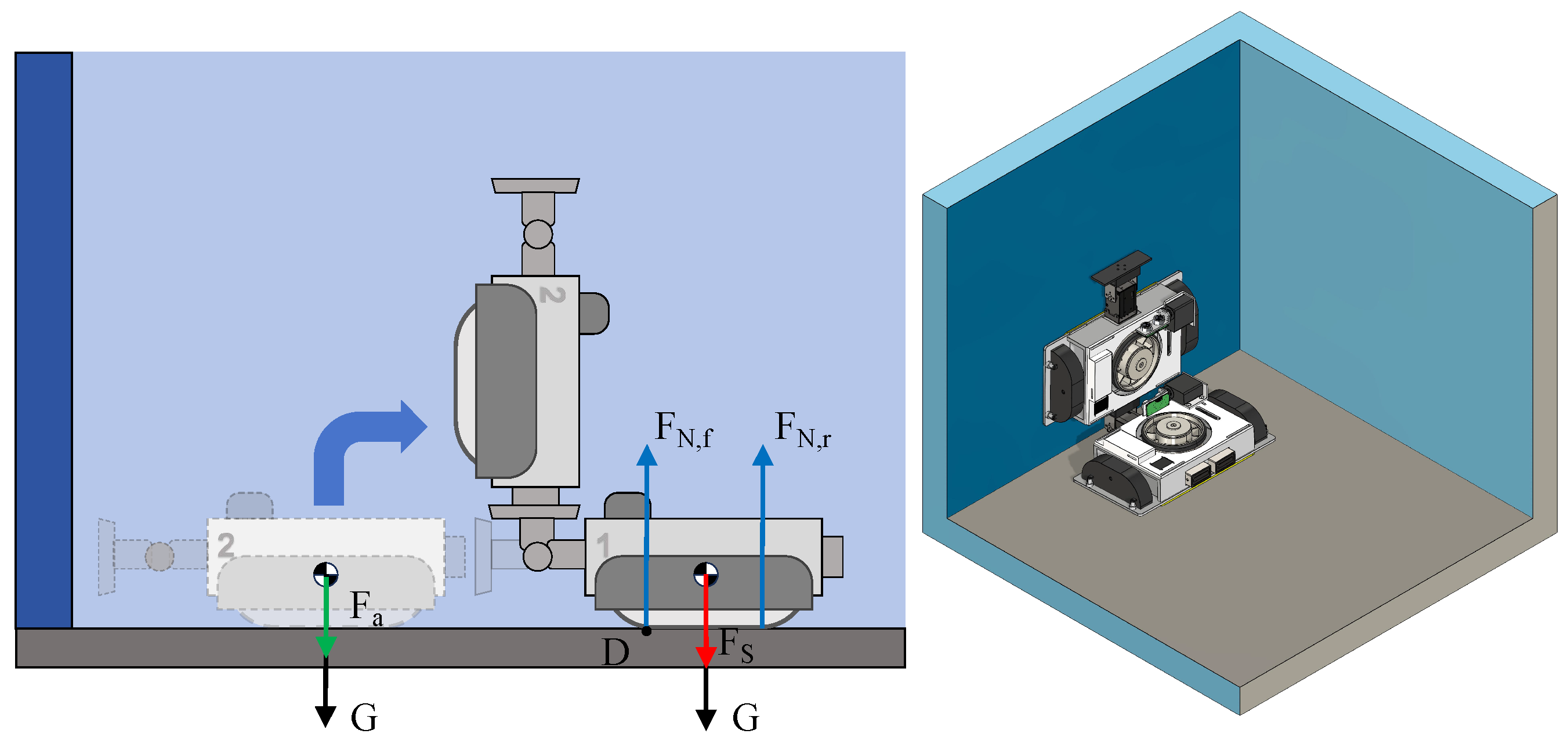
2.1. Components and Electrical System Architecture
2.2. Main Mechanisms of MC-1
3. Working Principle and Analysis of MC-1 Robot
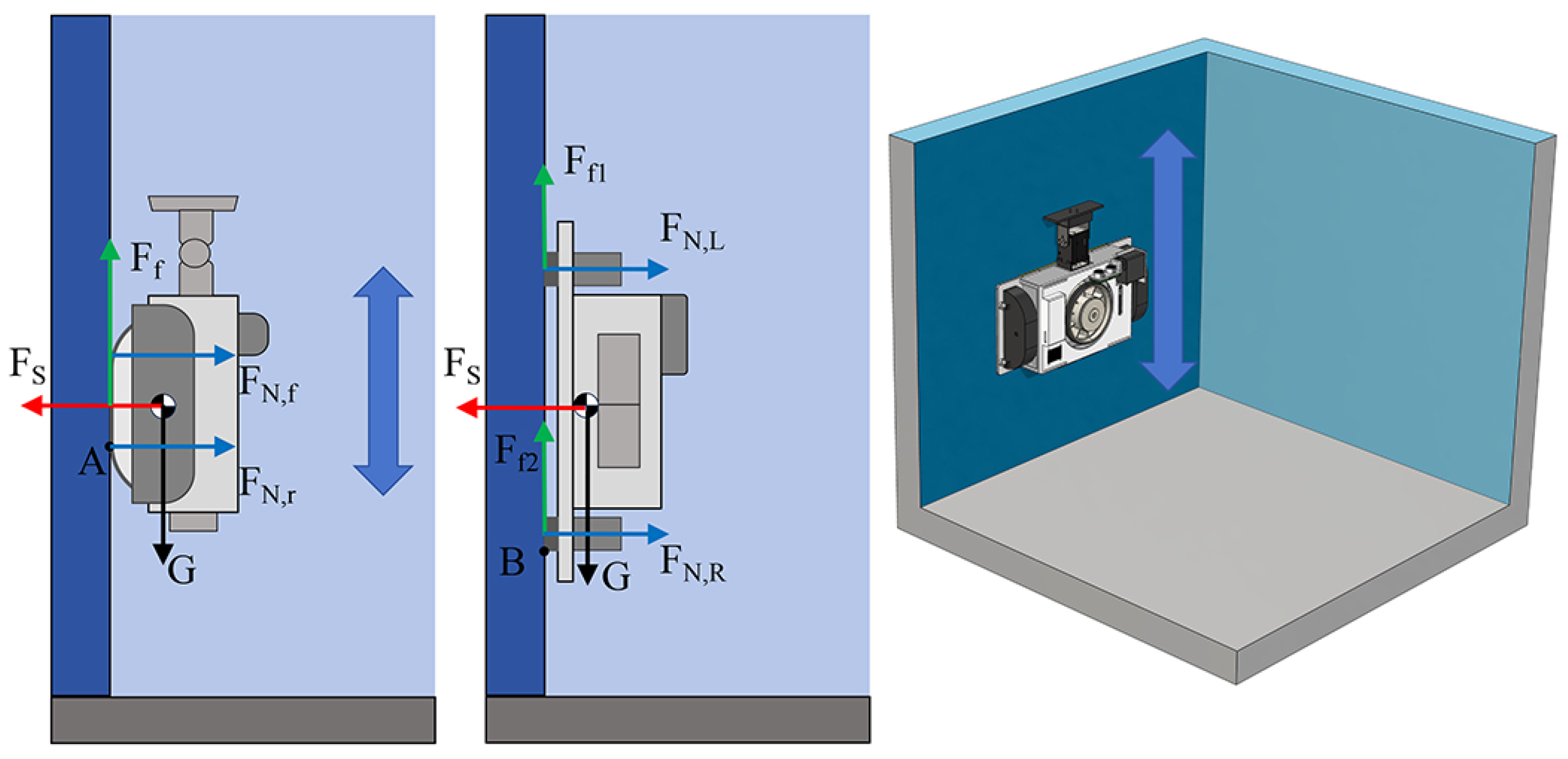
3.1. Static Mechanical Analysis
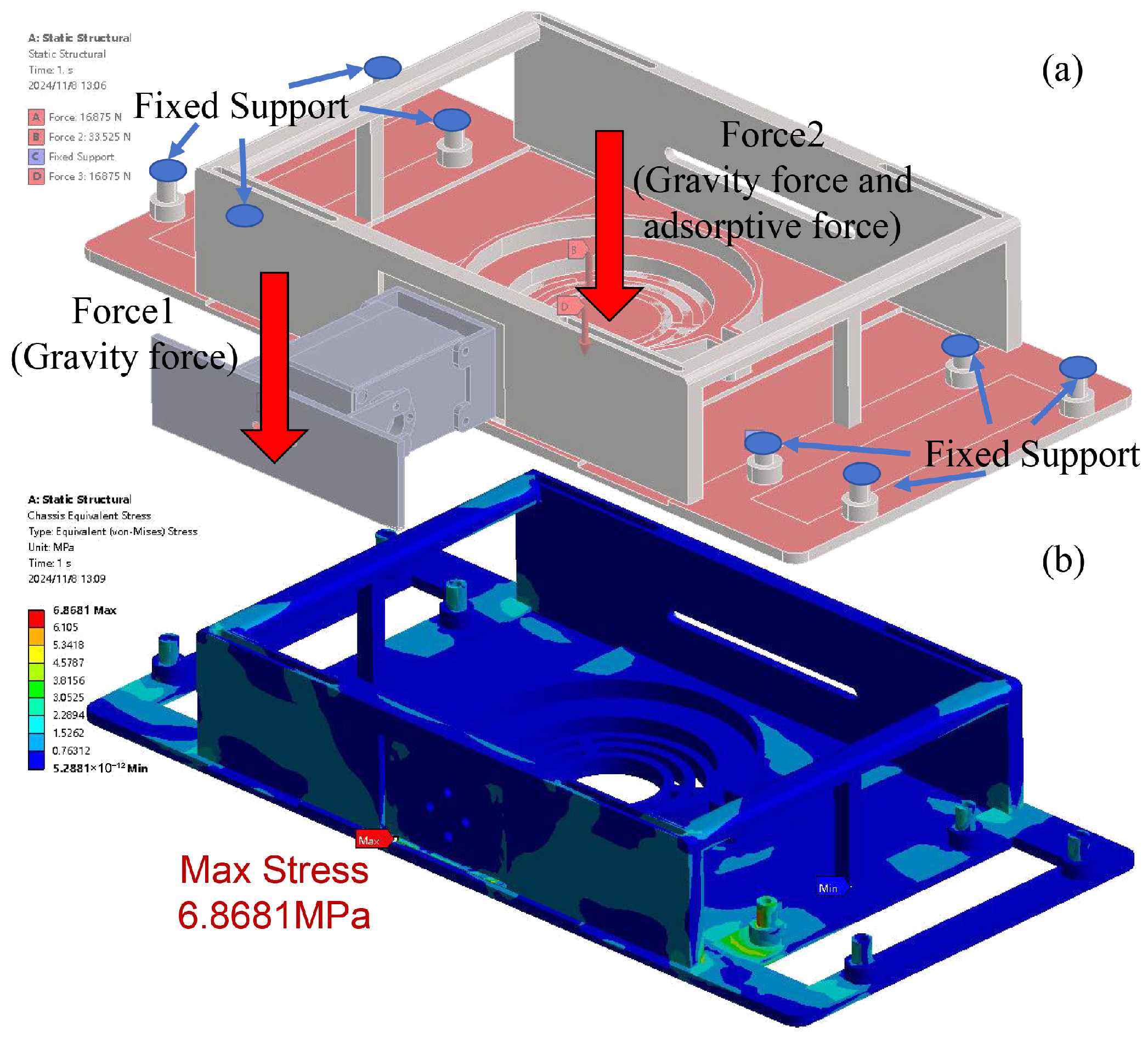
3.2. FEA Simulation Study
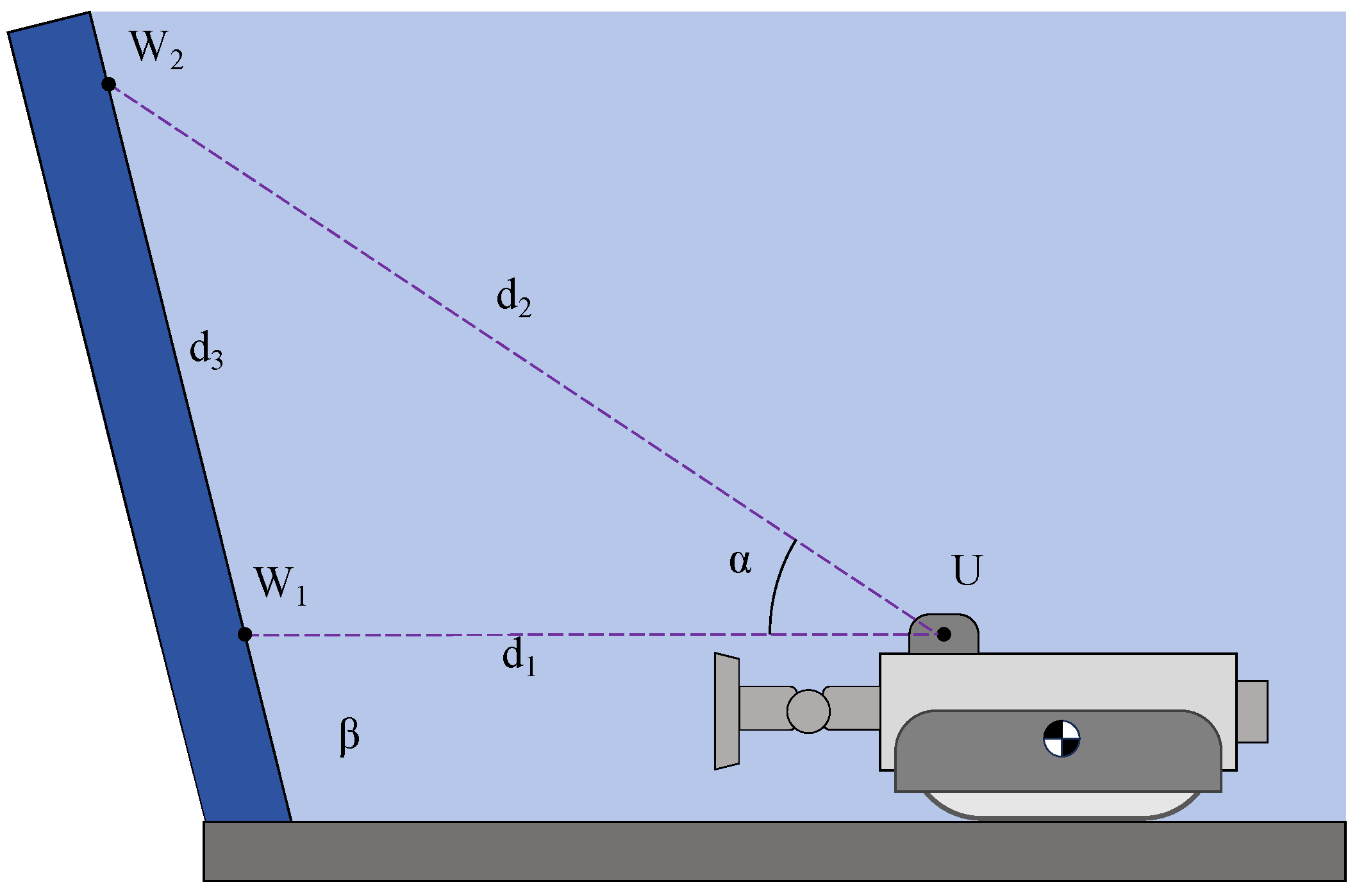
3.3. Detection of Wall Inclination Angle
4. Experimental Results
4.1. Testing Result of Suction Force
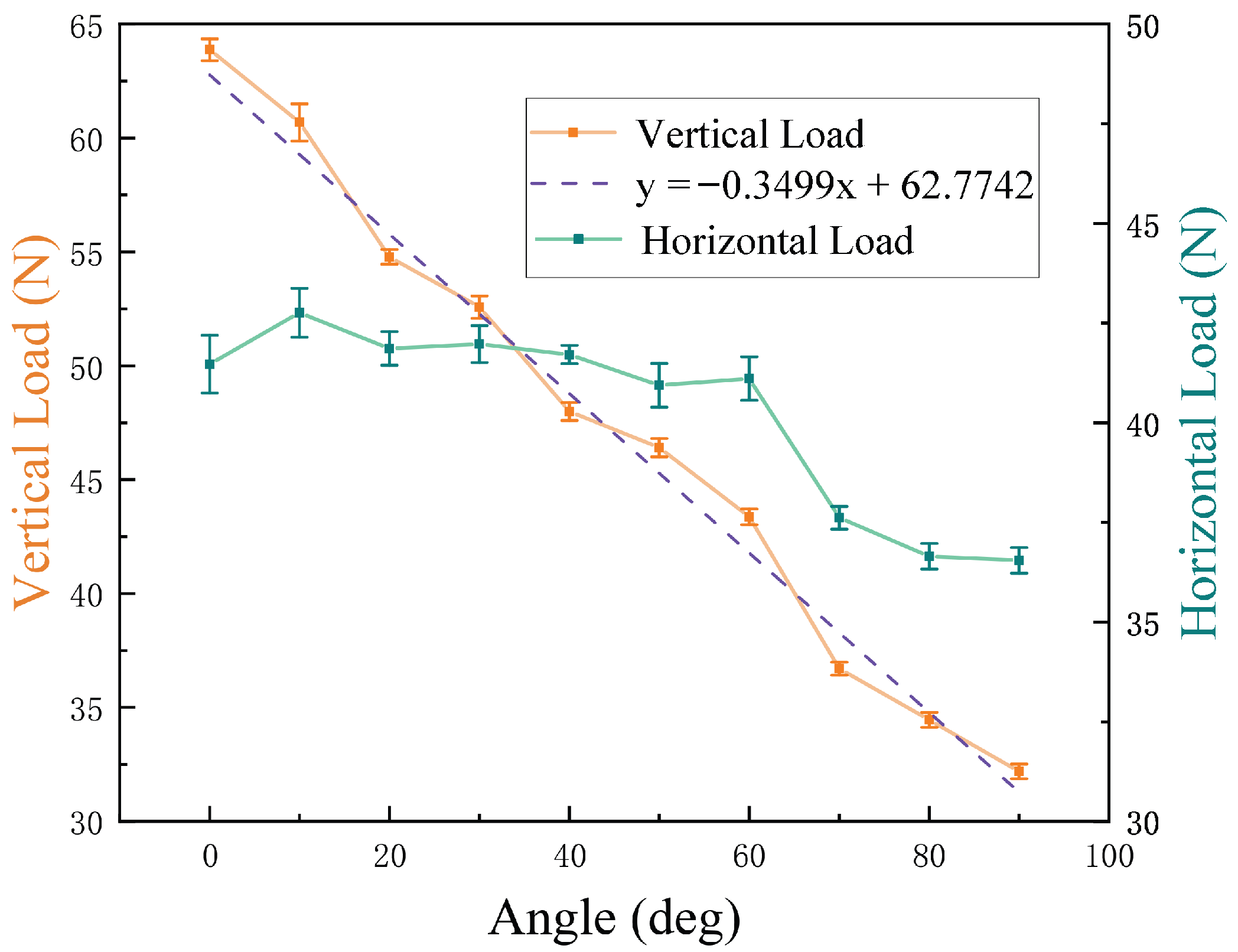
4.2. Testing Result of Loading Capacity
4.3. Testing Result of Wall-Climbing Speed
4.4. Testing Result of Plane-Transition Speed
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Fang, G.; Cheng, J. Advances in Climbing Robots for Vertical Structures in the Past Decade: A Review. Biomimetics 2023, 8, 47. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Xu, Q.; Tam, L.M. A Survey on Techniques and Applications of Window-Cleaning Robots. IEEE Access 2021, 9, 111518–111532. [Google Scholar] [CrossRef]
- Prados, C.; Hernando, M.; Gambao, E.; Brunete, A. A Review and Evaluation of Control Architectures for Modular Legged and Climbing Robots. Biomimetics 2024, 9, 319. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Wang, S.; Bi, Q.; Cui, D.; Yan, C. Design and technical development of wall-climbing robots: A review. J. Bionic Eng. 2022, 19, 877–901. [Google Scholar] [CrossRef]
- Nansai, S.; Mohan, R.E. A survey of wall climbing robots: Recent advances and challenges. Robotics 2016, 5, 14. [Google Scholar] [CrossRef]
- Ishihara, H. Basic study on wall climbing root with magnetic passive wheels. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 1964–1969. [Google Scholar]
- Gao, S.; Hou, R.; Li, J.; Pan, Y.; He, S.; Li, H. Magnetic field analysis and structure design of a new magnetic wheel for wall-climbing robot. J. Supercond. Nov. Magn. 2022, 35, 529–537. [Google Scholar] [CrossRef]
- Muthugala, M.V.J.; Vega-Heredia, M.; Mohan, R.E.; Vishaal, S.R. Design and control of a wall cleaning robot with adhesion-awareness. Symmetry 2020, 12, 122. [Google Scholar] [CrossRef]
- Cao, K.; Qin, G.; Zhou, J.; Xu, J.; Xu, L.; Ji, A. Design and experimental research of a rolling-adsorption wall-climbing robot. Ind. Robot. Int. J. Robot. Res. Appl. 2024, 51, 258–268. [Google Scholar] [CrossRef]
- Shen, W.; Gu, J.; Shen, Y. Permanent magnetic system design for the wall-climbing robot. In Proceedings of the 2005 IEEE International Conference Mechatronics and Automation, Niagara Falls, ON, Canada, 20 July–1 August 2005; pp. 2078–2083. [Google Scholar]
- Fang, S.; Shi, S.; Wu, X.; Wang, X. A walking and climbing quadruped robot capable of ground-wall transition: Design, mobility analysis and gait planning. Intell. Serv. Robot. 2023, 16, 431–451. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Wang, X.; Huang, Y.; Li, J.; Tam, L.M.; Xu, Q. Design and Development of a New Biped Robotic System for Exoskeleton-Structure Window Cleaning. IEEE Trans. Autom. Sci. Eng. 2024, 22, 3160–3171. [Google Scholar] [CrossRef]
- Li, X.; Dong, L. Development and analysis of an electrically activated sucker for handling workpieces with rough and uneven surfaces. IEEE/ASME Trans. Mechatron. 2015, 21, 1024–1034. [Google Scholar] [CrossRef]
- Lin, T.H.; Chiang, P.C.; Putranto, A. Multispecies hybrid bioinspired climbing robot for wall tile inspection. Autom. Constr. 2024, 164, 105446. [Google Scholar] [CrossRef]
- Park, C.; Bae, J.; Ryu, S.; Lee, J.; Seo, T. R-track: Separable modular climbing robot design for wall-to-wall transition. IEEE Robot. Autom. Lett. 2020, 6, 1036–1042. [Google Scholar] [CrossRef]
- Gao, X.; Yan, L.; Wang, G.; Chen, I.M. Modeling and analysis of magnetic adhesion module for wall-climbing robot. IEEE Trans. Instrum. Meas. 2022, 72, 1–9. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Wang, B.; Yuan, Q.; Weng, Z.; Dai, Z. Reversible Adhesive Bio-Toe with Hierarchical Structure Inspired by Gecko. Biomimetics 2023, 8, 40. [Google Scholar] [CrossRef] [PubMed]
- Bian, S.; Xu, F.; Wei, Y.; Kong, D. A novel type of wall-climbing robot with a gear transmission system arm and adhere mechanism inspired by Cicada and Gecko. Appl. Sci. 2021, 11, 4137. [Google Scholar] [CrossRef]
- Chen, R.; Liu, R.; Shen, H. Design of a double-tracked wall climbing robot based on electrostatic adhesion mechanism. In Proceedings of the 2013 IEEE Workshop on Advanced Robotics and Its Social Impacts, Tokyo, Japan, 7–9 November 2013; pp. 212–217. [Google Scholar]
- Qin, L.; Jin, Z.; Suo, S.; Zhang, C.; Qiao, K.; Liu, J. Design and research of a wall climbing robot with ducted fan for aircraft appearance inspection. In Proceedings of the 2022 International Conference on Sensing, Measurement & Data Analytics in the Era of Artificial Intelligence (ICSMD), Harbin, China, 22–24 December 2022; pp. 1–6. [Google Scholar]
- Wang, K.; Wang, Z.; Zhang, H. Development of modular wall-climbing robot inspired by natural caterpillar. In Proceedings of the 2011 IEEE 2nd International Conference on Computing, Control and Industrial Engineering, Wuhan, China, 20–21 August 2011; pp. 293–297. [Google Scholar]
- Vega-Heredia, M.; Mohan, R.E.; Wen, T.Y.; Siti’Aisyah, J.; Vengadesh, A.; Ghanta, S.; Vinu, S. Design and modelling of a modular window cleaning robot. Autom. Constr. 2019, 103, 268–278. [Google Scholar] [CrossRef]
- Seo, T.; Sitti, M. Tank-like module-based climbing robot using passive compliant joints. IEEE/ASME Trans. Mechatron. 2012, 18, 397–408. [Google Scholar] [CrossRef]
- Hernando, M.; Gambao, E.; Prados, C.; Brito, D.; Brunete, A. ROMERIN: A new concept of a modular autonomous climbing robot. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221123416. [Google Scholar] [CrossRef]


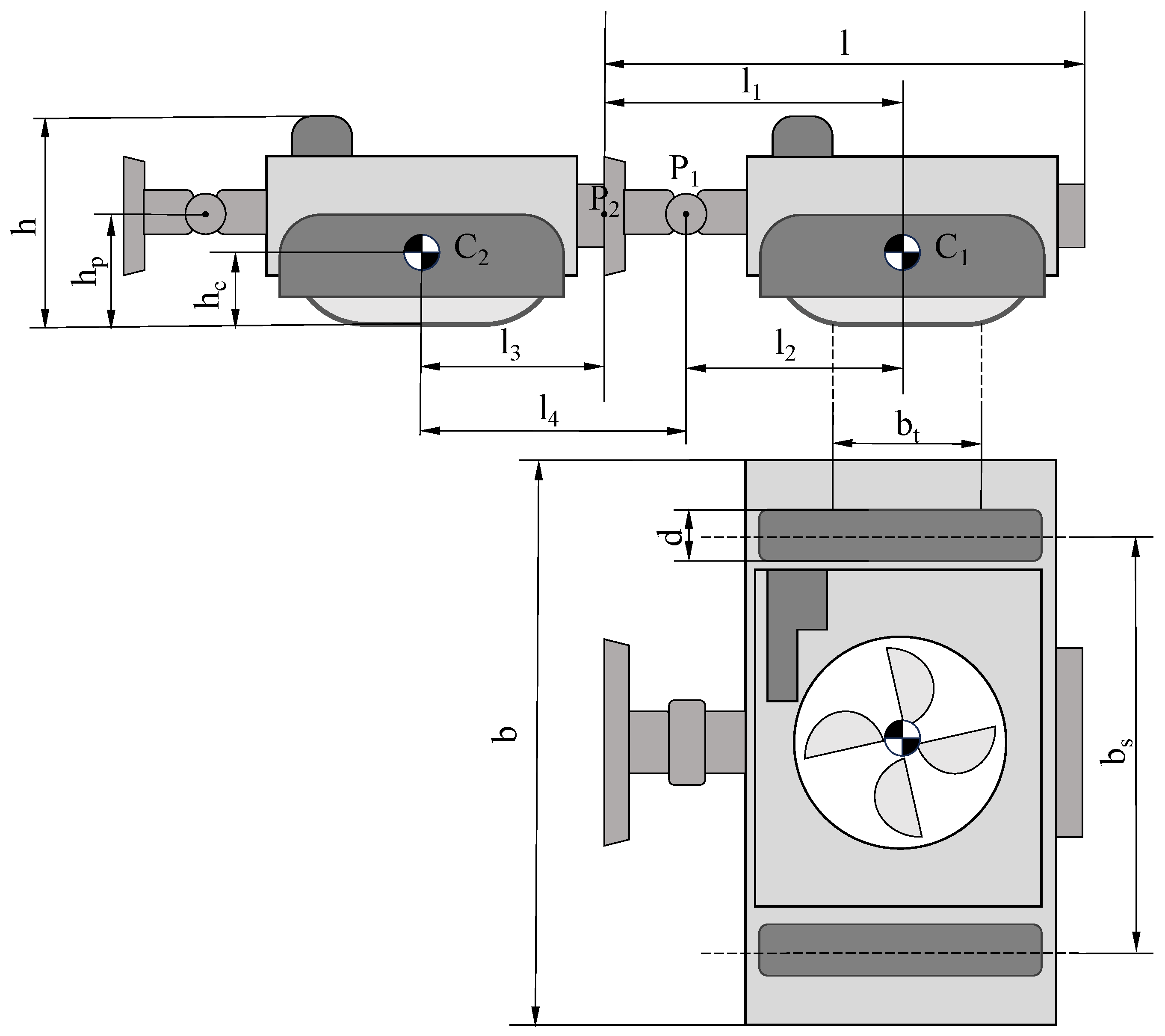





| l | h | ||||
| 221 mm | 141 mm | 110 mm | 80 mm | 111 mm | 73.5 mm |
| b | d | ||||
| 27.1 mm | 280 mm | 234.4 mm | 74 mm | 20 mm | 20 mm |
| Angle (°) | Mean (N) | Standard Deviation | Maximum (N) | Minimum (N) |
|---|---|---|---|---|
| 0 | 37.01 | 0.37 | 37.63 | 36.47 |
| 90 | 34.11 | 0.28 | 34.52 | 33.65 |
| Angle (°) | 0 | 10 | 20 | 30 | 40 |
| Vertical (N) | |||||
| Horizontal (N) | |||||
| Angle (°) | 50 | 60 | 70 | 80 | 90 |
| Vertical (N) | |||||
| Horizontal (N) |
| Angle (°) | 0 | 15 | 30 | 45 |
| Speed (cm/s) | ||||
| Angle (°) | 60 | 75 | 90 | – |
| Speed (cm/s) | – |
| Angle (°) | 0 | 15 | 30 | 45 | 60 | 75 | 90 |
| Transition time (s) | 0 | ||||||
| Coefficient of Variation (%) | 0 | 2.8 | 3.0 | 2.4 | 3.6 | 4.6 | 2.0 |
| Specifications | This Work (MC-1) | R-Track [15] | Modular Robot [21] | Mantis [22] | Tank-Like Robot [23] | ROMERIN [24] |
|---|---|---|---|---|---|---|
| Adhesion | Negative pressure | Magnetic adhesion | Negative pressure | Negative pressure | Flat elastomer | Negative pressure |
| Locomotion | Rubber track | Magnetic track | Legged | Rubber track | Rubber track | Legged |
| Mass (g) | 1350 | 2750 | 47 | 8000 | 180 | 2026 |
| Modular | Yes | Yes | Yes | Yes | Yes | Yes |
| Wall-transition Speed (cm/s) | 2.020 | – | 0.056 | – | 6 | – |
| Loading (N) | 32.24 | – | 15 | – | 5 | 77.4 |
| Plane types | Smooth planes | Magnetism surfaces | Smooth planes | Smooth planes | Dry surfaces | Smooth planes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zhang, W.; Luo, J.; Xu, Q. Design of a Modular Wall-Climbing Robot with Multi-Plane Transition and Cleaning Capabilities. Biomimetics 2025, 10, 450. https://doi.org/10.3390/biomimetics10070450
Wang B, Zhang W, Luo J, Xu Q. Design of a Modular Wall-Climbing Robot with Multi-Plane Transition and Cleaning Capabilities. Biomimetics. 2025; 10(7):450. https://doi.org/10.3390/biomimetics10070450
Chicago/Turabian StyleWang, Boyu, Weijian Zhang, Jianghan Luo, and Qingsong Xu. 2025. "Design of a Modular Wall-Climbing Robot with Multi-Plane Transition and Cleaning Capabilities" Biomimetics 10, no. 7: 450. https://doi.org/10.3390/biomimetics10070450
APA StyleWang, B., Zhang, W., Luo, J., & Xu, Q. (2025). Design of a Modular Wall-Climbing Robot with Multi-Plane Transition and Cleaning Capabilities. Biomimetics, 10(7), 450. https://doi.org/10.3390/biomimetics10070450







