A Vector-Based Motion Retargeting Approach for Exoskeletons with Shoulder Girdle Mechanism
Abstract
1. Introduction
- A vector-based analytical motion retargeting approach is proposed for exoskeletons with shoulder girdle mechanism, mapping the vectors of the upper limb segments to the joint space through a vector-based method with high computational efficiency and precision.
- The approach can accommodate four motion representation methods: (a) joint positions; (b) the end-effector (wrist) pose; (c) shoulder girdle angles, swivel angle, and wrist position (SGASAWP); and (d) polynomial descriptions of the SHR, swivel angle, and wrist position (SHRSAWP).
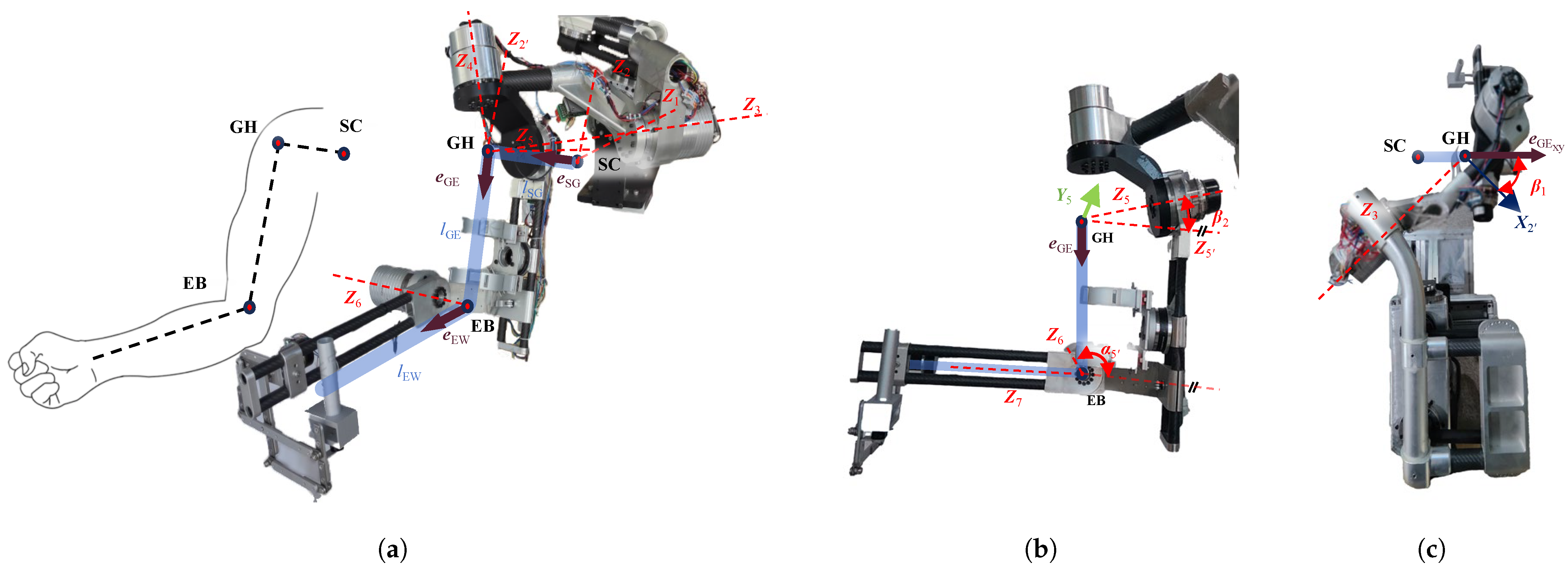
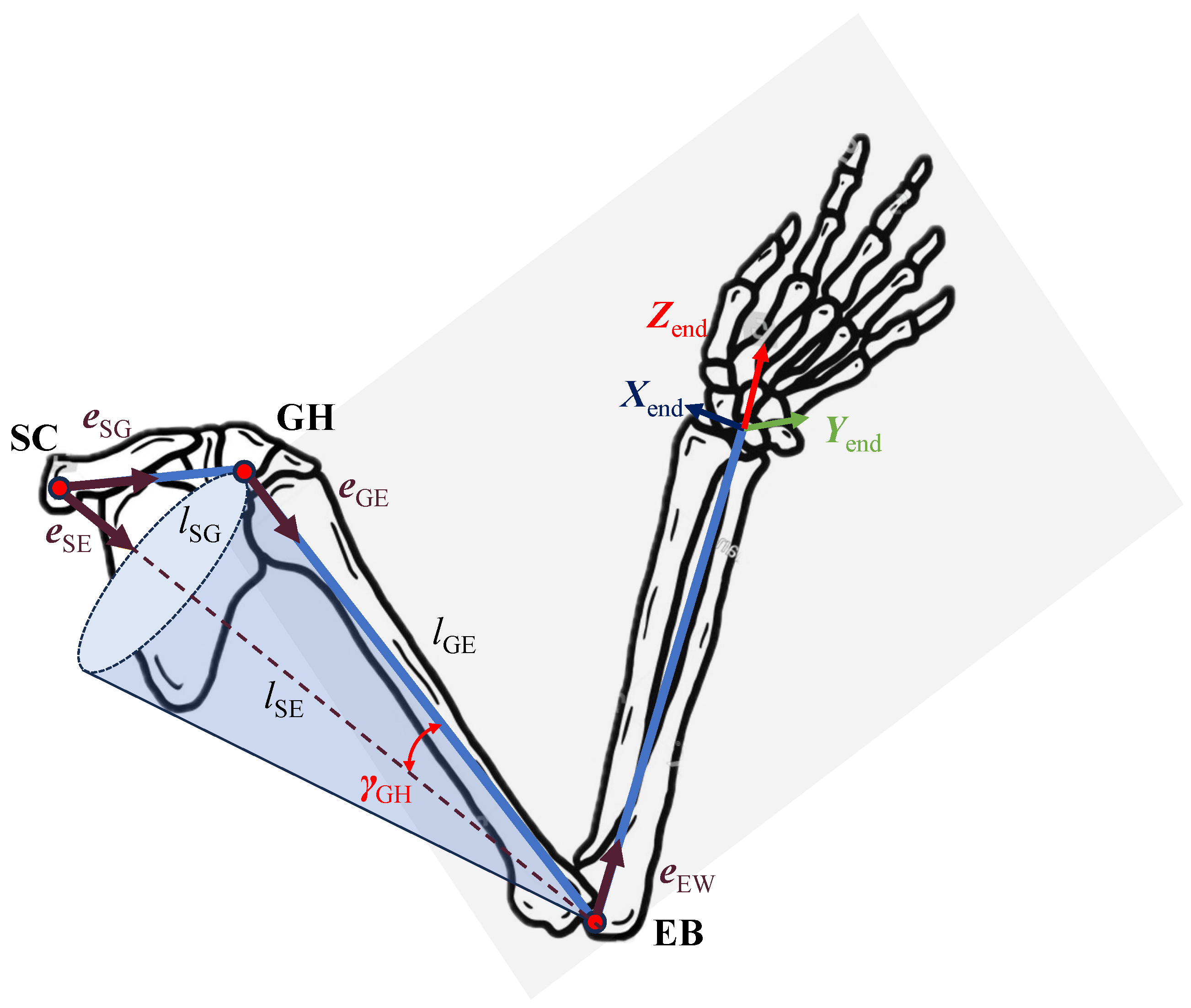
2. The Kinematic Structure of the Upper Limb Exoskeleton
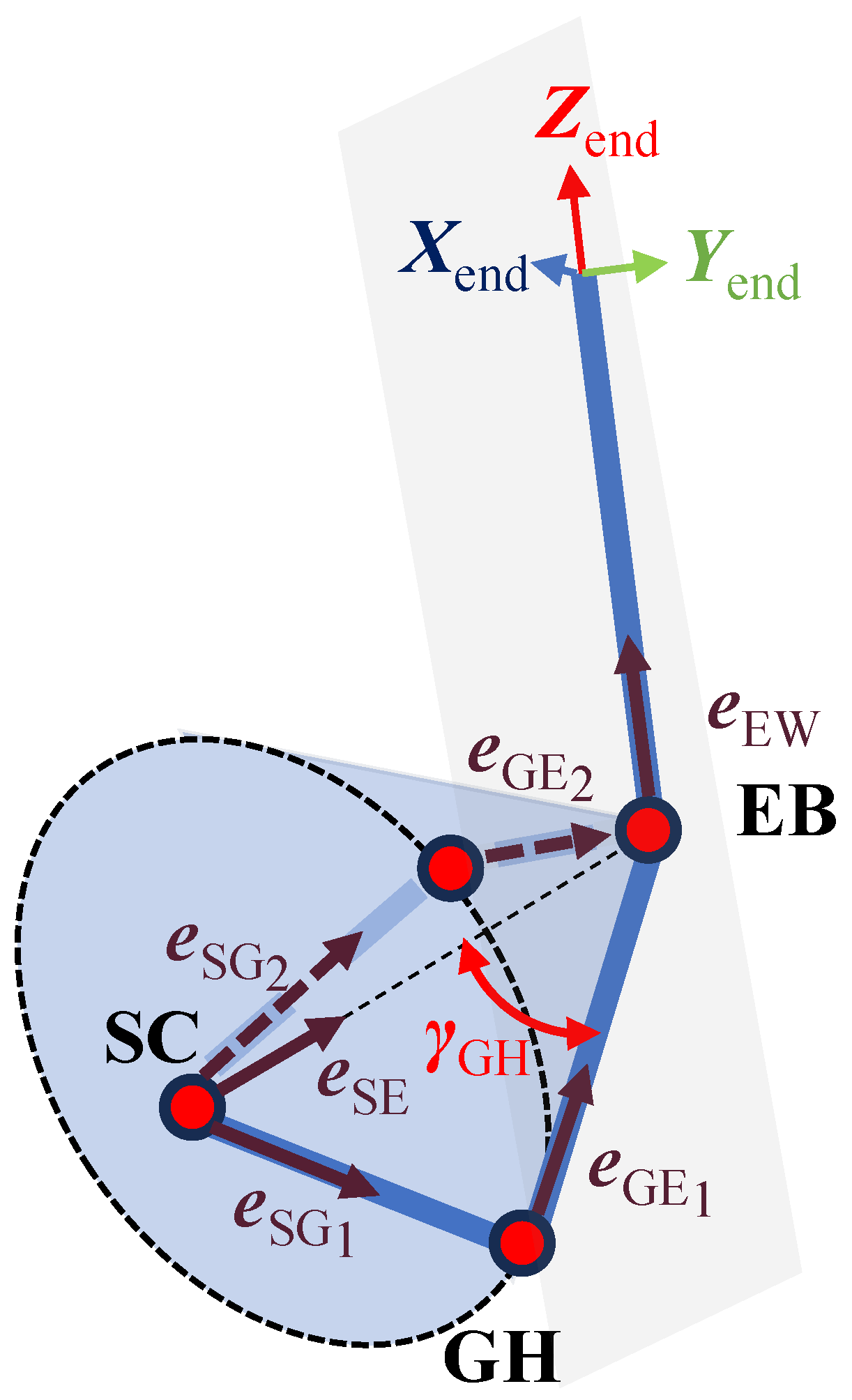
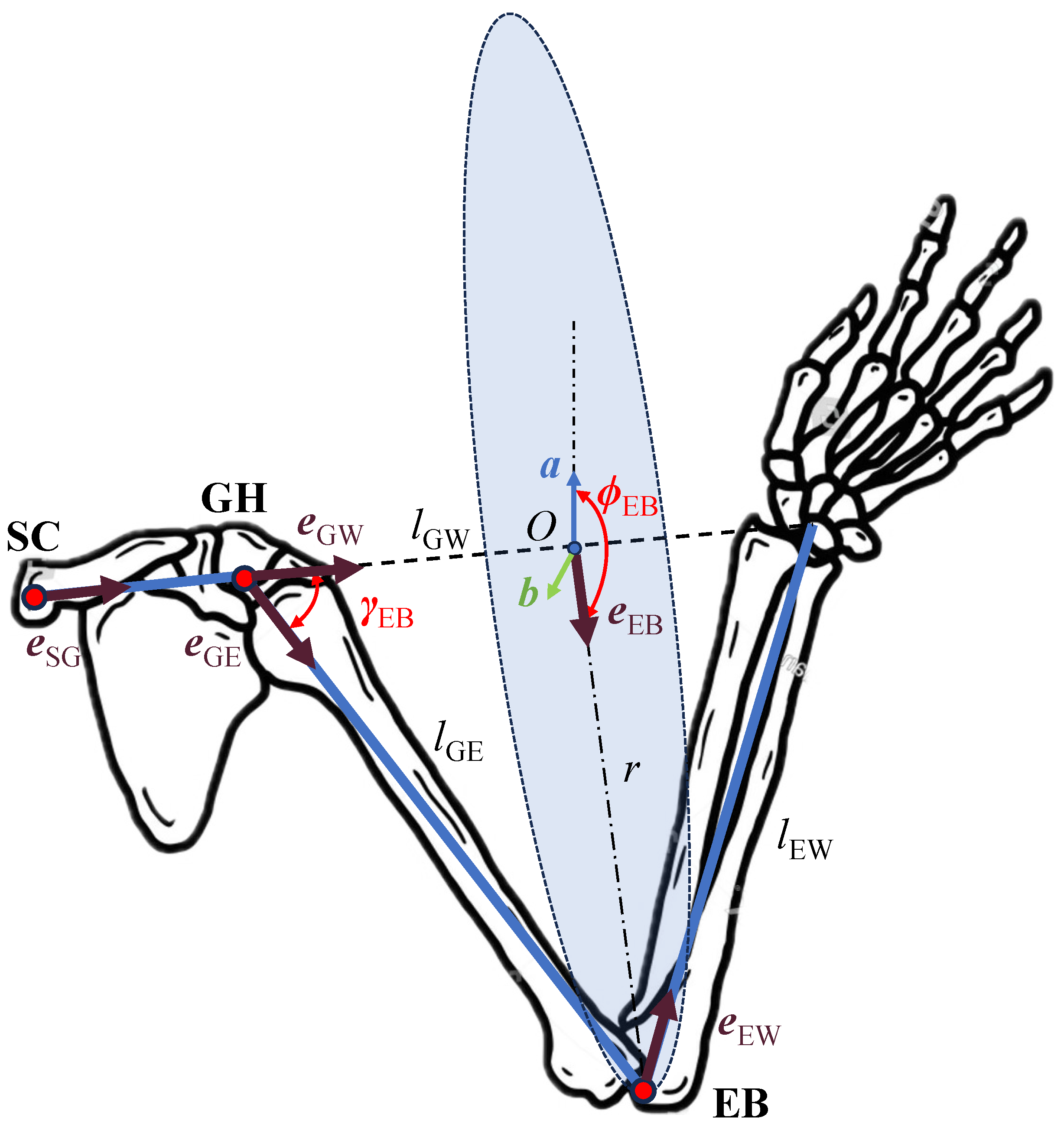
3. The Vector-Based Analytical Motion Retargeting Approach
4. Mapping Different Motion Representation Methods into the Joint Space Using the Approach
4.1. Joint Positions
4.2. End-Effector Pose
4.3. SGASAWP
4.4. SHRSAWP
5. Numerical Simulation
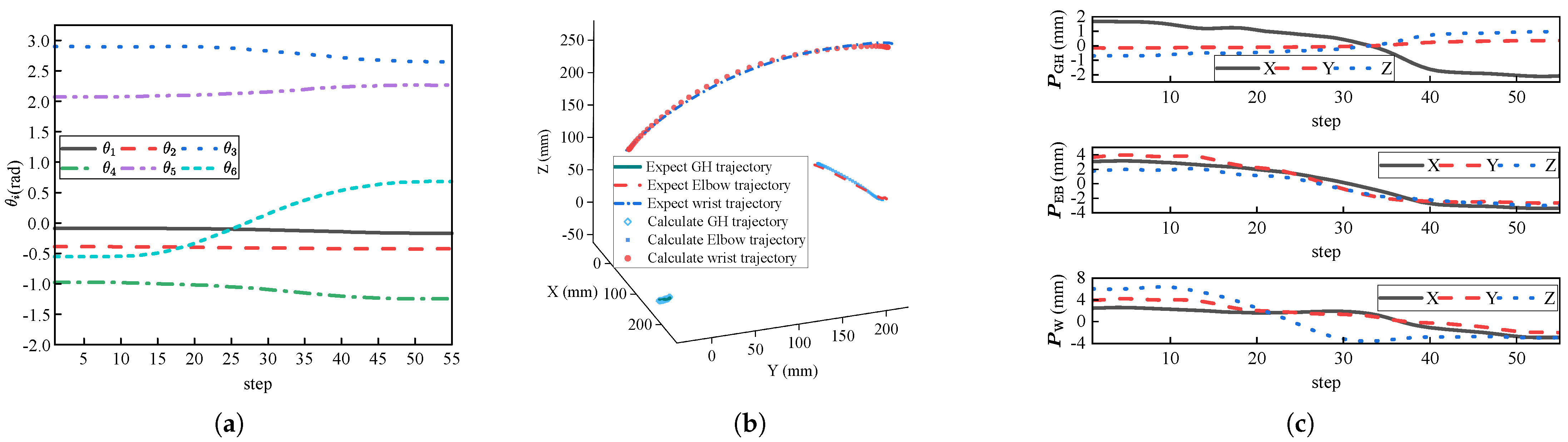
5.1. Joint Positions
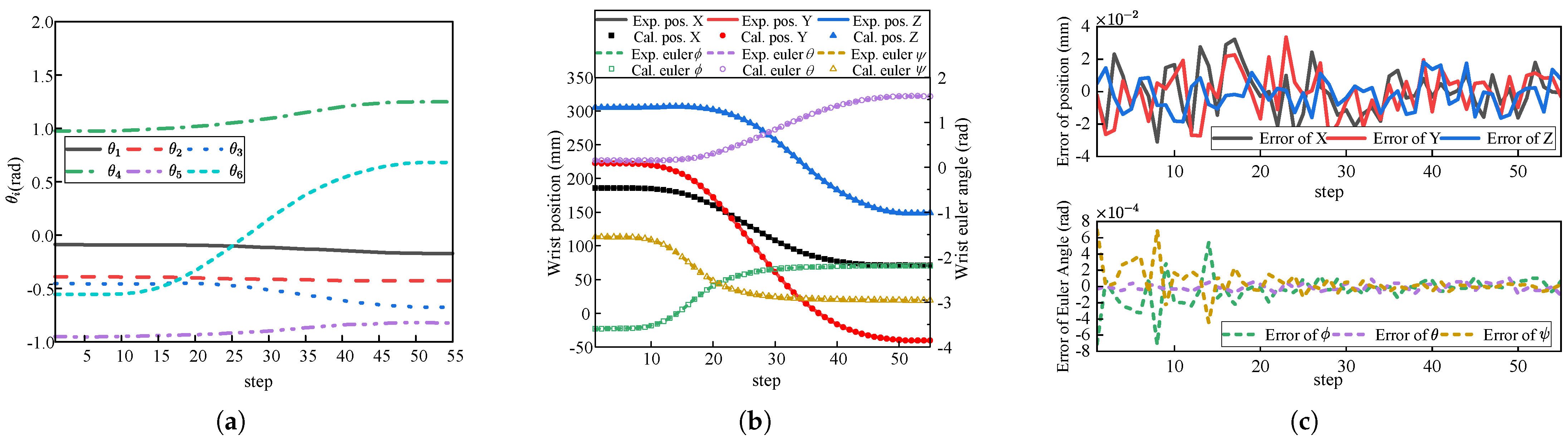
5.2. End-Effector Pose
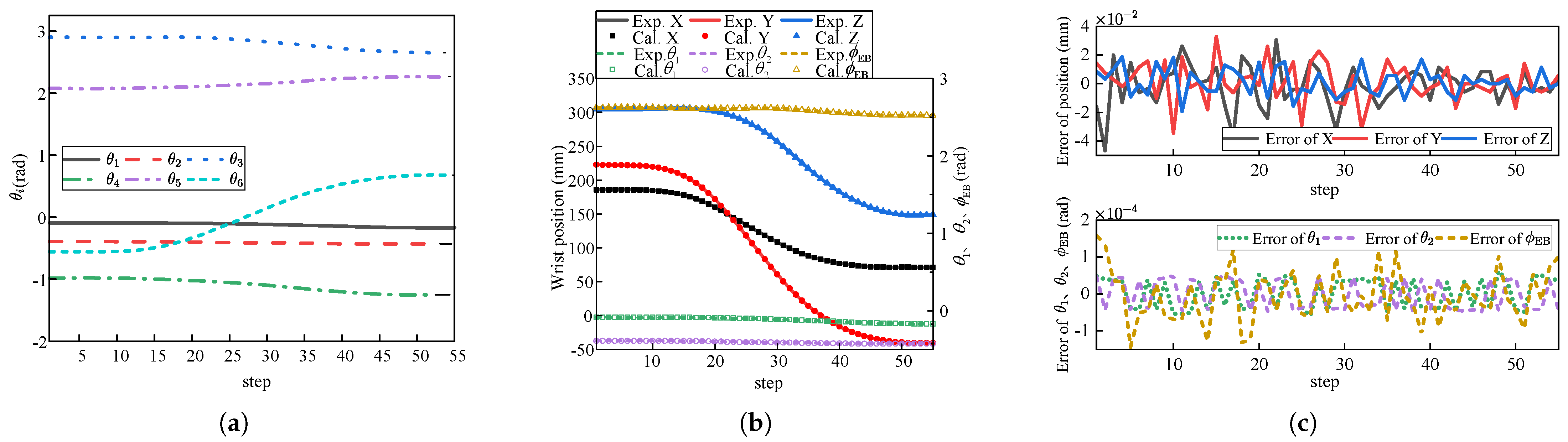
5.3. SGASAWP
5.4. SHRSAWP
5.5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mancisidor, A.; Zubizarreta, A.; Cabanes, I.; Bengoa, P.; Jung, J.H. Kinematical and dynamical modeling of a multipurpose upper limbs rehabilitation robot. Robot.-Comput.-Integr. Manuf. 2018, 49, 374–387. [Google Scholar] [CrossRef]
- Kim, B.; Deshpande, A.D. An upper-body rehabilitation exoskeleton Harmony with an anatomical shoulder mechanism: Design, modeling, control, and performance evaluation. Int. J. Robot. Res. 2017, 36, 414–435. [Google Scholar] [CrossRef]
- Zimmermann, Y.; Sommerhalder, M.; Wolf, P.; Riener, R.; Hutter, M. ANYexo 2.0: A Fully Actuated Upper-Limb Exoskeleton for Manipulation and Joint-Oriented Training in All Stages of Rehabilitation. IEEE Trans. Robot. 2023, 39, 2131–2150. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, P.; Wu, C. Variable tensile stiffness pneumatic actuators with adjustable stick-slip friction of soft-tooth structures. Mater. Des. 2025, 253, 113860. [Google Scholar] [CrossRef]
- He, T.; Luo, Z.; Xiao, W.; Zhang, C.; Kitani, K.; Liu, C.; Shi, G. Learning Human-to-Humanoid Real-Time Whole-Body Teleoperation. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 8944–8951. [Google Scholar] [CrossRef]
- Toedtheide, A.; Chen, X.; Sadeghian, H.; Naceri, A.; Haddadin, S. A Force-Sensitive Exoskeleton for Teleoperation: An Application in Elderly Care Robotics. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 12624–12630. [Google Scholar] [CrossRef]
- Jo, I.; Park, Y.; Bae, J. A teleoperation system with an exoskeleton interface. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013; pp. 1649–1654. [Google Scholar] [CrossRef]
- Cheng, C.; Dai, W.; Wu, T.; Chen, X.; Wu, M.; Yu, J.; Jiang, J.; Lu, H. Efficient and Precise Homo-Hetero Teleoperation Based on an Optimized Upper Limb Exoskeleton. IEEE/ASME Trans. Mechatronics 2024. [Google Scholar] [CrossRef]
- Kim, Y.G.; Little, K.; Noronha, B.; Xiloyannis, M.; Masia, L.; Accoto, D. A voice activated bi-articular exosuit for upper limb assistance during lifting tasks. Robot.-Comput.-Integr. Manuf. 2020, 66, 101995. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Liu, G.; Xu, W. Variable motion mapping to enhance stiffness discrimination and identification in robot hand teleoperation. Robot.-Comput.-Integr. Manuf. 2018, 51, 202–208. [Google Scholar] [CrossRef]
- Walsh, C.J.; Paluska, D.; Pasch, K.; Grand, W.; Herr, H.M. Development of a lightweight, underactuated exoskeleton for load-carrying augmentation. In Proceedings of the IEEE International Conference on Robotics & Automation, Orlando, FL, USA, 15–19 May 2006. [Google Scholar]
- Riley, M.; Ude, A.; Wade, K.; Atkeson, C. Enabling real-time full-body imitation: A natural way of transferring human movement to humanoids. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Taipei, Taiwan, 14–19 September 2003; Volume 2, pp. 2368–2374. [Google Scholar] [CrossRef]
- Dariush, B.; Gienger, M.; Arumbakkam, A.; Goerick, C.; Zhu, Y.; Fujimura, K. Online and markerless motion retargeting with kinematic constraints. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 191–198. [Google Scholar] [CrossRef]
- Asfour, T.; Dillmann, R. Human-like motion of a humanoid robot arm based on a closed-form solution of the inverse kinematics problem. In Proceedings of the Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), Las Vegas, NV, USA, 27 October–1 November 2003; Volume 2, pp. 1407–1412. [Google Scholar] [CrossRef]
- Shimizu, M.; Kakuya, H.; Yoon, W.K.; Kitagaki, K.; Kosuge, K. Analytical Inverse Kinematic Computation for 7-DOF Redundant Manipulators With Joint Limits and Its Application to Redundancy Resolution. IEEE Trans. Robot. 2008, 24, 1131–1142. [Google Scholar] [CrossRef]
- Liu, W.; Chen, D.; Steil, J. Analytical inverse kinematics solver for anthropomorphic 7-DOF redundant manipulators with human-like configuration constraints. J. Intell. Robot. Syst. 2017, 86, 63–79. [Google Scholar] [CrossRef]
- Yang, Z.; Bien, S.; Nertinger, S.; Naceri, A.; Haddadin, S. An Optimization-based Scheme for Real-time Transfer of Human Arm Motion to Robot Arm. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 12220–12225. [Google Scholar] [CrossRef]
- Suleiman, W.; Yoshida, E.; Kanehiro, F.; Laumond, J.P.; Monin, A. On human motion imitation by humanoid robot. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2697–2704. [Google Scholar] [CrossRef]
- Yamane, K.; Ariki, Y.; Hodgins, J. Animating non-humanoid characters with human motion data. In Proceedings of the Proceedings of the 2010 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Madrid, Spain, 2–4 July 2010; pp. 169–178. [Google Scholar] [CrossRef]
- Lawrence, N. Gaussian process latent variable models for visualisation of high dimensional data. Adv. Neural Inf. Process. Syst. 2003, 16. Available online: https://proceedings.neurips.cc/paper/2003/hash/9657c1fffd38824e5ab0472e022e577e-Abstract.html (accessed on 9 May 2024).
- Shon, A.; Grochow, K.; Hertzmann, A.; Rao, R.P. Learning shared latent structure for image synthesis and robotic imitation. Adv. Neural Inf. Process. Syst. 2005, 18. Available online: https://papers.nips.cc/paper_files/paper/2005/hash/030e65da2b1c944090548d36b244b28d-Abstract.html (accessed on 9 May 2024).
- Chen, Q.; Wang, T.; Yang, Z.; Li, H.; Lu, R.; Sun, Y.; Zheng, B.; Yan, C. SDPL: Shifting-Dense Partition Learning for UAV-view Geo-localization. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 11810–11824. [Google Scholar] [CrossRef]
- Yin, H.; Melo, F.; Billard, A.; Paiva, A. Associate latent encodings in learning from demonstrations. In Proceedings of the Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar] [CrossRef]
- Choi, S.; Kim, J. Cross-domain motion transfer via safety-aware shared latent space modeling. IEEE Robot. Autom. Lett. 2020, 5, 2634–2641. [Google Scholar] [CrossRef]
- Jarrassé, N.; Crocher, V.; Morel, G. A Method for measuring the upper limb motion and computing a compatible exoskeleton trajectory. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 3461–3466. [Google Scholar]
- Zarrin, R.S.; Zeiaee, A.; Langari, R.; Buchanan, J.J.; Robson, N. Towards autonomous ergonomic upper-limb exoskeletons: A computational approach for planning a human-like path. Robot. Auton. Syst. 2021, 145, 103843. [Google Scholar] [CrossRef]
- Miniato, M.A.; Anand, P.; Varacallo, M. Anatomy, shoulder and upper limb, shoulder. In StatPearls; StatPearls Publishing: St. Petersburg, FL, USA, 2021. [Google Scholar]
- Zimmermann, Y.; Forino, A.; Riener, R.; Hutter, M. ANYexo: A Versatile and Dynamic Upper-Limb Rehabilitation Robot. IEEE Robot. Autom. Lett. 2019, 4, 3649–3656. [Google Scholar] [CrossRef]
- Pei, S.; Wang, J.; Yang, Y.; Dong, A.; Guo, B.; Guo, J.; Yao, Y. A Human-Centered Kinematics Design Optimization of Upper Limb Rehabilitation Exoskeleton Based on Configuration Manifold. IEEE Open J. Comput. Soc. 2025, 6, 282–293. [Google Scholar] [CrossRef]
- Denavit, J.; Hartenberg, R.S. A kinematic notation for lower-pair mechanisms based on matrices. J. Appl. Mech. 1955, 22, 215–221. [Google Scholar] [CrossRef]
- Siciliano, B. Robotics: Modelling, Planning and Control (G.-L. Zhang Trans.); Xi’an Jiaotong University Press: Xi’an, China, 2016. [Google Scholar]


| i | ||||
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | |
| 2 | 90 | 0 | 0 | |
| 2′ | 0 | 0 | ||
| 3 | 86.47 | 0 | 0 | |
| 4 | −90 | 0 | 0 | |
| 5 | 85 | 0 | 0 | |
| 5′ | Rotation with respect to by | |||
| 6 | −95 | 0 | ||
| End | −90 | 0 | 0 | |
| Method | Mean Error of PGH (mm) | Mean Error of PEB (mm) | Mean Error of PW (mm) | Time (ms) |
|---|---|---|---|---|
| Vector method | 1.44 | 3.94 | 4.73 | 0.0145 |
| CLIK [13] | 3.86 | 4.49 | 6.90 | 0.1891 |
| Method | Mean Position Error (mm) | Mean Euler Angle Error (rad) | Calculation Time (ms) |
|---|---|---|---|
| Vector method | 0.018 | 0.0236 | |
| Jacobian-based method [31] | 0.022 | 1.3 |
| Method | Mean Position Error (mm) | Mean Error of θ1 (rad) | Mean Error of θ2 (rad) | Calculation Time (ms) |
|---|---|---|---|---|
| Vector method | 0.018 | 13.5 | ||
| GEAA [26] | 0.021 | 0.039 | 27.5 |
| Representation Method | Joint Positions | End-Effector Pose | SGASAWP | SHRSAWP |
|---|---|---|---|---|
| m-file (ms) | 0.0145 | 0.0236 | 0.0127 | 13.5 |
| C++ (ms) | 0.0015 | 0.0030 | 0.0014 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Pei, S.; Guo, J.; Bao, M.; Yao, Y. A Vector-Based Motion Retargeting Approach for Exoskeletons with Shoulder Girdle Mechanism. Biomimetics 2025, 10, 312. https://doi.org/10.3390/biomimetics10050312
Wang J, Pei S, Guo J, Bao M, Yao Y. A Vector-Based Motion Retargeting Approach for Exoskeletons with Shoulder Girdle Mechanism. Biomimetics. 2025; 10(5):312. https://doi.org/10.3390/biomimetics10050312
Chicago/Turabian StyleWang, Jiajia, Shuo Pei, Junlong Guo, Mingsong Bao, and Yufeng Yao. 2025. "A Vector-Based Motion Retargeting Approach for Exoskeletons with Shoulder Girdle Mechanism" Biomimetics 10, no. 5: 312. https://doi.org/10.3390/biomimetics10050312
APA StyleWang, J., Pei, S., Guo, J., Bao, M., & Yao, Y. (2025). A Vector-Based Motion Retargeting Approach for Exoskeletons with Shoulder Girdle Mechanism. Biomimetics, 10(5), 312. https://doi.org/10.3390/biomimetics10050312






