Research on Assembly Sequence Planning of Large Cruise Ship Cabins Based on Improved Genetic Algorithm
Abstract
1. Introduction
2. Problem Description and Model Construction
2.1. Problem Description
2.2. Model Construction
- ➀
- Number of Direction Changes
- ➁
- Number of Tool Replacements
- ➂
- Connection Relationships Among Parts
- ➃
- Selection of Reference Part
- ➄
- Sequential Relationship of Assembly Parts
- ➅
- Geometric Relationships Between Assembly Parts
2.3. Establishment of Fitness Function
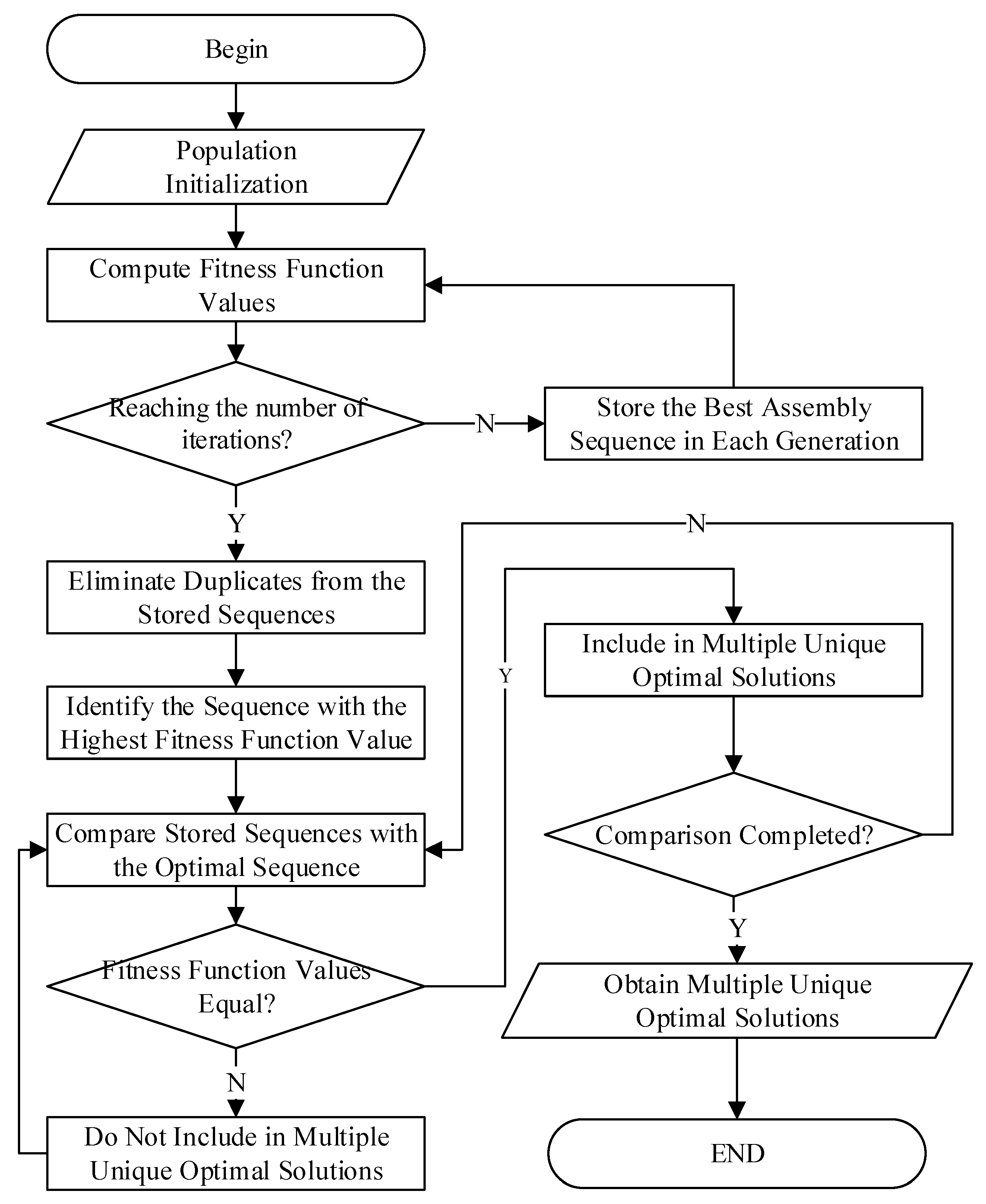
3. Design of a Genetic Greedy Algorithm
3.1. Algorithm Steps
3.2. Greedy Criterion
- Initially, select an assembly sequence that meets the sequence constraints, such that equals 0.
- On the basis of the first criterion, select an assembly sequence that satisfies geometric constraints, also ensuring that equals 0.
- Continuing from the prior criteria, select an assembly sequence that begins with the reference part, hence equals 1.
- Among the sequences satisfying the first three criteria, select the sequence with fewer direction changes in assembly, aiming for a smaller value. A threshold can be set based on the actual conditions of the assembly, and selection occurs if is below a certain number of direction changes.
- From the sequences meeting the first four criteria, choose the sequence with fewer tool replacements, aiming for a smaller value. Again, a threshold may be set based on the assembly’s specifics, and selection is made if is below a certain number of tool replacements.
- Among the sequences fulfilling the first five criteria, choose the assembly sequence with the most stable contact relationships, where a greater is preferable. A threshold should be set according to the specific conditions of the assembly, with selection occurring if exceeds a certain level.
- The optimal assembly sequence identified so far is added to the new generation’s population to ensure that the best individual obtained remains unlost and undamaged by crossover or mutation.
- The optimal assembly sequence serves as a parent for generating two-thirds of the new population through crossover and mutation, significantly increasing the likelihood of evolving towards superior sequences and augmenting the quantity of high-quality solutions in the new generation.
- The remaining individuals are generated randomly to expand the search space for the optimal solution, thereby enhancing the probability of escaping local optima.
3.3. Multiple Unique Optimal Solutions
4. Genetic Greedy Combination Algorithm: An Overview
4.1. Genome-Based Encoding Method
4.1.1. Crossover
| Parent A = | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Parent B = | 3 | 2 | 4 | 1 | 9 | 14 | 11 | 15 | 5 | 10 | 7 | 12 | 13 | 6 | 8 |
| Parent A = | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9 | 14 | 11 | 15 | 5 | 10 | 11 | 12 | 13 | 14 | 15 |
| Parent B = | 3 | 2 | 4 | 1 | 9 | 14 | 11 | 15 | 5 | 5 | 6 | 7 | 8 | 9 | 10 | 7 | 12 | 13 | 6 | 8 |
| Offspring C = | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 14 | 11 | 15 | 10 | 12 | 13 |
| Offspring D = | 3 | 2 | 4 | 1 | 9 | 14 | 11 | 15 | 5 | 6 | 7 | 8 | 10 | 12 | 13 |
4.1.2. Mutation
| Parent A = | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Parent B = | 3 | 2 | 4 | 1 | 9 | 14 | 11 | 15 | 5 | 10 | 7 | 12 | 13 | 6 | 8 |
| Offspring C = | 1 | 2 | 3 | 9 | 8 | 7 | 6 | 5 | 4 | 10 | 11 | 12 | 13 | 14 | 15 |
| Offspring D = | 3 | 2 | 4 | 5 | 15 | 11 | 14 | 9 | 1 | 10 | 7 | 12 | 13 | 6 | 8 |
4.2. Establishment of Multiple Unique Optimal Solutions
5. Case Study Validation
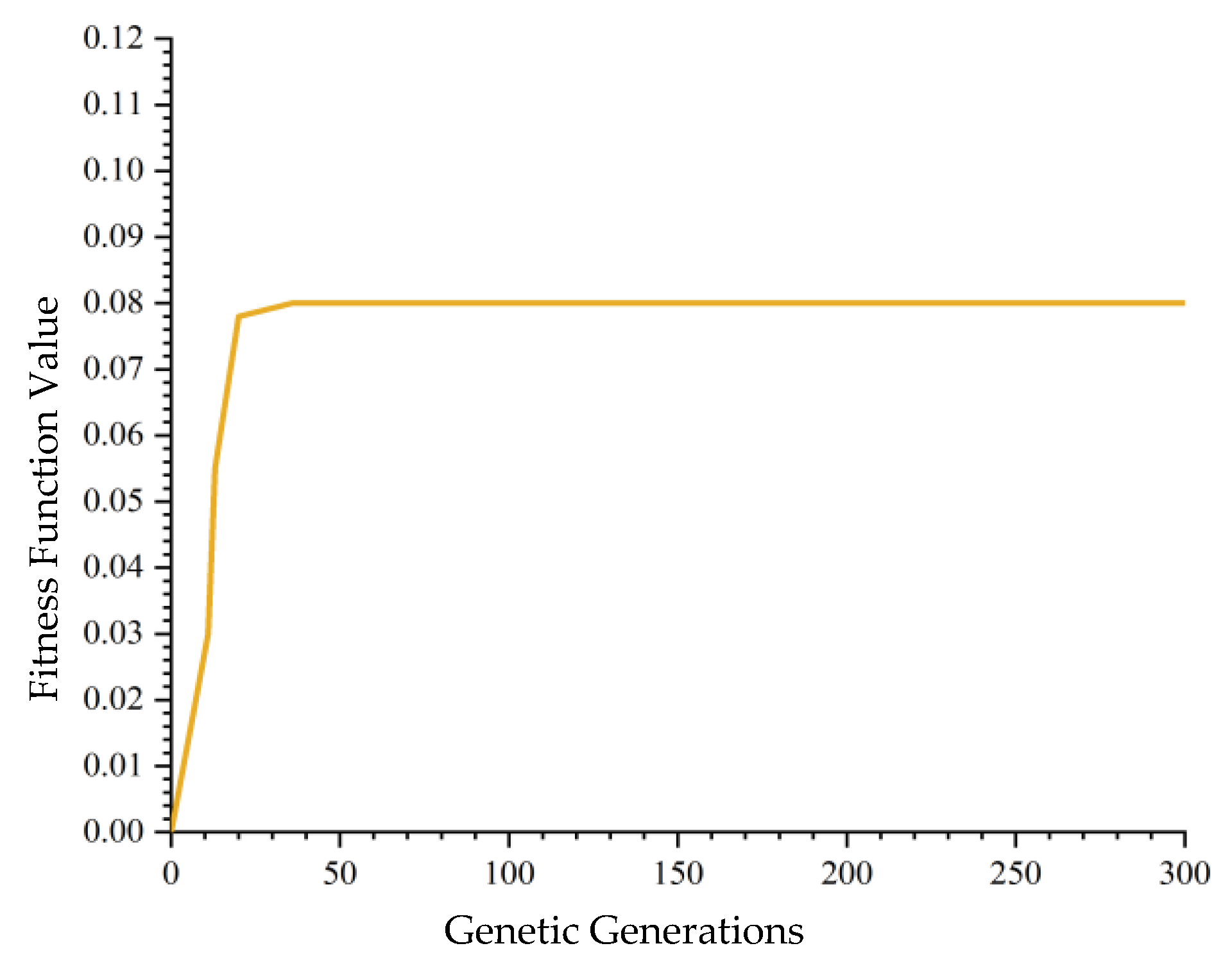
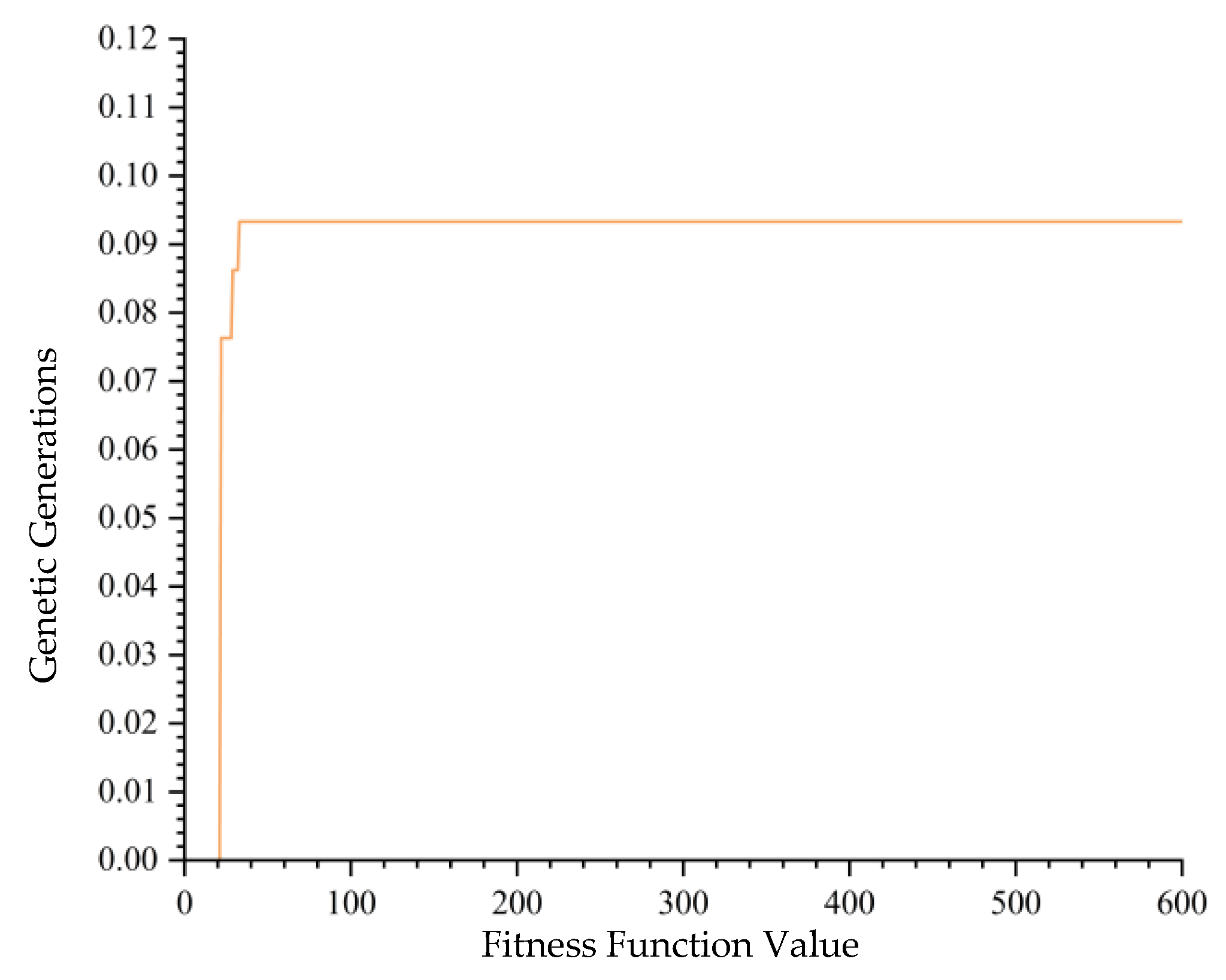
5.1. Case Verification
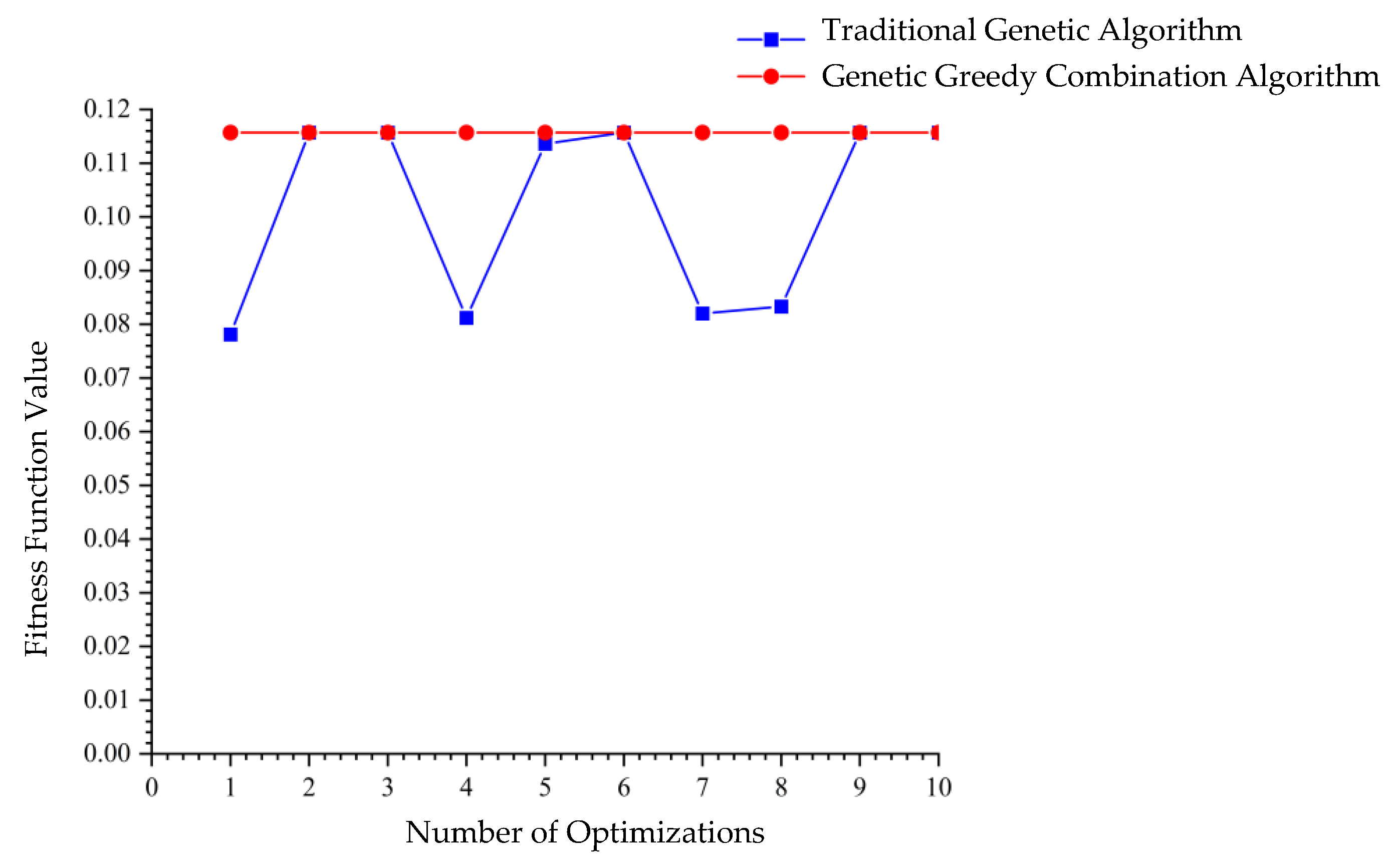
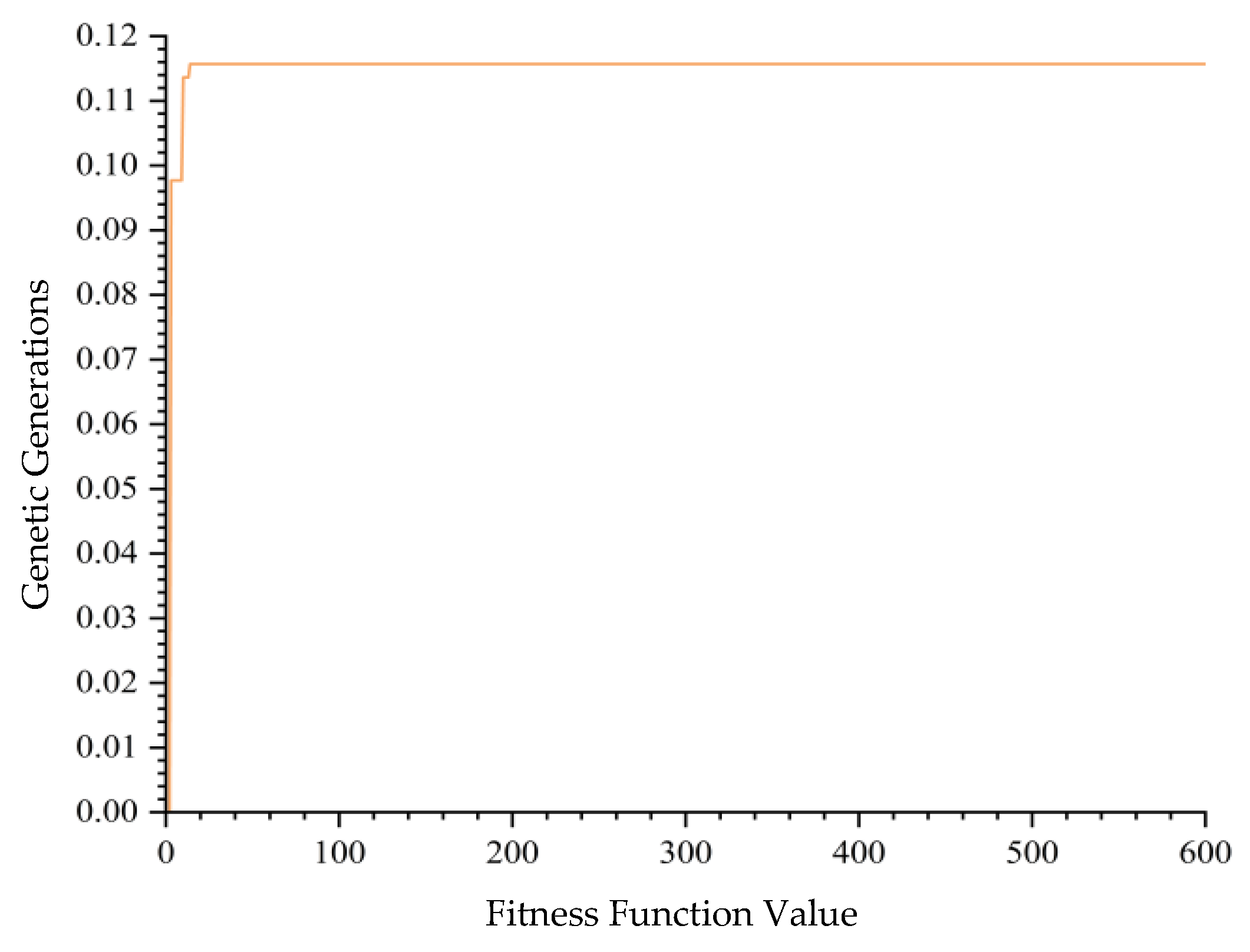
5.2. Analysis and Comparison of Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Su, Y.; Mao, H.; Tang, X. Algorithms for solving assembly sequence planning problems. Neural Comput. Appl. 2020, 33, 525–534. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Lu, C. An integrated job shop scheduling and assembly sequence planning approach for discrete manufacturing. J. Manuf. Syst. 2021, 61, 27–44. [Google Scholar] [CrossRef]
- Kang, M.; Seo, J.; Chung, H. Ship block assembly sequence planning considering productivity and welding deformation. Int. J. Nav. Archit. Ocean. Eng. 2018, 10, 450–457. [Google Scholar] [CrossRef]
- Deng, M.; Tang, Q.; Lei, Z. A novel approach for assembly sequence planning based on ant colony algorithm. Eng. J. Wuhan Univ. 2013, 46, 246–251. (In Chinese) [Google Scholar]
- Jang, C.; Xi, J. Multi-project Scheduling in ETO Assembly Process Based on Hybrid Algorithm. Modul. Mach. Tool Autom. Manuf. Tech. Manuf. Technol. 2020, 1, 164–168. (In Chinese) [Google Scholar] [CrossRef]
- Hamdi, H.; Regaya, C.B.; Zaafouri, A. Real-time study of a photovoltaic system with boost converter using the PSO-RBF neural network algorithms in a MyRio controller. Sol. Energy 2019, 183, 1–16. [Google Scholar] [CrossRef]
- Osman, S.E.; Zarog, M. Optimized v-shaped beam micro-electrothermal actuator using particle swarm optimization (PSO) technique. Micro Nanosyst. 2019, 11, 62–67. [Google Scholar] [CrossRef]
- He, X.; Yang, Y. Optimization of Assembly Sequences Using a Genetic Algorithm with Multi-objective Constraints. Int. J. Comput. Integr. Manuf. 2015, 28, 770–782. [Google Scholar]
- Ghosh, S.; Shankar, R. A Genetic Algorithm-Based Approach for Efficient Assembly Sequence Planning. Procedia CIRP 2018, 67, 324–329. [Google Scholar]
- Jiang, C.; Wu, B.; Li, M.Y.; Zhao, Y.L.; Wang, X.C. Product Assembly Sequence Planning Based on Genetic Algorithm. Mach. Electron. 2012, 4, 7–11. (In Chinese) [Google Scholar]
- Xu, Z.; Ni, W.; Ji, Y. Rotation forest based on multimodal genetic algorithm. J. Cent. South Univ. 2021, 28, 1747–1764. [Google Scholar] [CrossRef]
- Perea, F.; De Waard, H.W. Greedy and K-Greedy Algorithms for Multidimensional Data Association. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1915–1925. [Google Scholar] [CrossRef]
- Berasategui, M.; Lassalle, S. Weak greedy algorithms and the equivalence between semi-greedy and almost greedy Markushevich bases. J. Fourier Anal. Appl. 2023, 29, 20. [Google Scholar] [CrossRef]
- Wen, G.J.; Dai, L.K.; Liu, W. Raman spectroscopic quantitative analysis based on genetic algorithm and linear superposition principle. Chin. J. Anal. Chem. 2021, 49, 85–94. [Google Scholar]
- Boukhalfa, G.; Belkacem, S.; Chikhi, A.; Bouhentala, M. Fuzzy-second order sliding mode control optimized by genetic algorithm applied in direct torque control of dual star induction motor. J. Cent. South Univ. 2022, 29, 3974–3985. [Google Scholar] [CrossRef]
- Kou, X.; Cao, Y.; Qiao, H. A method for intelligently optimizing hierarchical assembly structure sequences by assembly hybrid G-diagram. Int. J. Adv. Manuf. Technol. 2022, 122, 27–39. [Google Scholar] [CrossRef]
- Yang, H.; Chen, J.; Wang, C.; Cui, J.; Wei, W. Intelligent planning of product assembly sequences based on spatio-temporal semantic knowledge. Assem. Autom. 2020, 40, 755–768. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, X.; Han, F.; Wang, Y.-L. Cobalt crust recognition based on kernel Fisher discriminant analysis and genetic algorithm in reverberation environment. J. Cent. South Univ. 2021, 28, 179–193. [Google Scholar] [CrossRef]
- Zhang, J.; Lee, J. Hybrid Genetic Algorithm for Assembly Sequence Planning: Combining Genetic Algorithms and Simulated Annealing. J. Manuf. Sci. Eng. 2020, 142, 071003. [Google Scholar]




| Symbol | Definition |
|---|---|
| Number of parts in the product | |
| Assembly sequence for the cabin | |
| The -th assembly part in the assembly sequence | |
| Setup time for part in the assembly sequence | |
| Operation time for part in the assembly sequence | |
| Number of changes in assembly direction for part | |
| Additional work time due to a change in assembly direction for part | |
| Number of tool changes during the assembly of part | |
| Additional work time due to a tool change for part | |
| Connection relationship between parts and | |
| Whether part in the assembly sequence is a reference part | |
| Whether parts and satisfy geometric constraints | |
| Whether parts and satisfy sequence constraints |
| Component Name | ID | Connection Method | Installation Tool/ID | Assembly Direction | Reference Component | Sequential Constraint |
|---|---|---|---|---|---|---|
| Cabin Base Groove | 1 | Welding | Welding Machine T1 | X | Yes | None |
| Sanitary Unit | 2 | Welding | Welding Machine T1 | X | No | 1–2 |
| Cabin Wall Panel | 3 | Self-tapping Screws | Electric Drill T2 | Y | No | 2–3 |
| Fireproof Door Frame | 4 | Welded Bolt Connection | Welding Machine T1 | X | No | None |
| Cabin Ceiling | 5 | Anchor Connection | Screwdriver T3 | Y | Yes | 3–5 |
| Temporary Reinforcement | 6 | Bolts | Electric Drill T2 | −X | No | None |
| Furniture | 7 | Bolts | Electric Drill T2 | −X | No | None |
| Ceiling Trim Strip | 8 | Bolts | Electric Drill T2 | −Y | No | None |
| Permanent Reinforcement | 9 | Bolts | Electric Drill T2 | Y | No | None |
| Water Pipes and Sprinkler Heads | 10 | Bolts | Electric Drill T2 | Y | No | 5–10 |
| Electrical Equipment | 11 | Bolts | Electric Drill T2 | Y | No | None |
| Switches and Sockets | 12 | Bolts | Electric Drill T2 | Z | No | 11–12 |
| Fireproof Door | 13 | Bolts | Electric Drill T2 | Z | No | 4–13 |
| Cabin Unit Protection | 14 | Bolts | Electric Drill T2 | −Z | No | None |
| Cable | 15 | Anchor Connection | Screwdriver T3 | −Z | No | 3–15 |
| Iterations | Optimal Assembly Sequence | Fitness Function Value | Number of Part Direction Changes | Number of Tool Changes | Connection Stability | as Reference Component | Satisfies Sequence Constraints | Satisfies Geometric Constraints |
|---|---|---|---|---|---|---|---|---|
| 1 | 1,6,4,13,2,3,8,14,15,5,9,11,10,12,7 | 0.0781 | 10 | 7 | 7 | Yes | Yes | Yes |
| 2 | 1,4,2,8,11,9,3,5,15,14,7,6,12,13,10 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 3 | 1,4,2,3,5,11,10,9,8,13,12,7,6,14,15 | 0.1157 | 5 | 4 | 13 | Yes | Yes | Yes |
| 4 | 1,11,14,2,3,5,4,9,10,8,7,6,12,13,15 | 0.0812 | 10 | 7 | 8 | Yes | Yes | Yes |
| 5 | 1,2,4,9,3,15,5,11,10,8,6,7,12,13,14 | 0.1136 | 7 | 3 | 13 | Yes | Yes | Yes |
| 6 | 1,4,2,8,3,5,11,10,9,7,6,13,12,14,15 | 0.1157 | 5 | 4 | 13 | Yes | Yes | Yes |
| 7 | 9,1,2,4,14,11,8,3,5,10,6,7,13,12,15 | 0.0820 | 8 | 5 | 12 | No | Yes | Yes |
| 8 | 11,8,12,1,4,2,9,3,5,10,13,7,6,14,15 | 0.0833 | 7 | 5 | 12 | No | Yes | Yes |
| 9 | 1,4,2,8,7,6,3,9,11,5,10,13,12,14,15 | 0.1157 | 5 | 4 | 13 | Yes | Yes | Yes |
| 10 | 1,4,2,8,3,5,15,14,6,7,9,11,10,12,13 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| Iterations | Optimal Assembly Sequence | Fitness Function Value | Number of Part Direction Changes | Number of Tool Changes | Connection Stability | as Reference Component | Satisfies Sequence Constraints | Satisfies Geometric Constraints |
|---|---|---|---|---|---|---|---|---|
| 1 | 1,4,2,3,5,15,14,9,10,11,8,13,12,7,6 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 2 | 1,2,4,9,3,5,10,11,8,12,13,6,7,14,15 | 0.1157 | 5 | 4 | 13 | Yes | Yes | Yes |
| 3 | 1,4,2,3,9,11,12,13,7,6,8,14,15,5,10 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 4 | 1,4,2,3,5,15,14,11,9,10,8,6,7,13,12 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 5 | 1,2,4,7,6,3,5,15,14,8,11,9,10,13,12 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 6 | 1,4,2,7,6,8,3,14,15,5,9,11,10,13,12 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 7 | 1,2,4,8,7,6,3,9,5,15,14,11,10,12,13 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 8 | 1,2,4,8,3,14,15,5,9,10,11,6,7,13,12 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 9 | 1,4,2,7,6,11,9,3,8,14,15,5,10,12,13 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 10 | 1,2,4,8,6,7,11,9,3,5,10,12,13,14,15 | 0.1157 | 5 | 4 | 13 | Yes | Yes | Yes |
| Iterations | Optimal Assembly Sequence | Fitness Function Value | Number of Part Direction Changes | Number of Tool Changes | Connection Stability | as Reference Component | Satisfies Sequence Constraints | Satisfies Geometric Constraints |
|---|---|---|---|---|---|---|---|---|
| 1 | 1,11,8,4,2,3,5,15,14,13,12,9,10,6,7 | 0.0933 | 8 | 5 | 10 | Yes | Yes | Yes |
| 2 | 1,2,7,3,5,4,8,9,11,10,13,12,6,14,15 | 0.0977 | 8 | 5 | 11 | Yes | Yes | Yes |
| 3 | 11,6,1,4,2,12,13,9,3,7,8,14,15,5,10 | 0.0833 | 8 | 4 | 12 | No | Yes | Yes |
| 4 | 1,2,4,8,6,7,3,5,15,14,10,9,11,12,13 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 5 | 4,1,2,14,11,13,12,7,6,8,9,3,5,15,10 | 0.0893 | 7 | 3 | 13 | No | Yes | Yes |
| 6 | 1,2,3,8,14,15,5,4,9,10,11,7,6,13,12 | 0.0992 | 8 | 4 | 11 | Yes | Yes | Yes |
| 7 | 8,1,2,4,7,6,3,9,5,15,14,10,11,12,13 | 0.0862 | 6 | 4 | 12 | No | Yes | Yes |
| 8 | 1,2,4,7,6,3,5,11,10,9,8,12,13,14,15 | 0.1157 | 5 | 4 | 13 | Yes | Yes | Yes |
| 9 | 11,14,4,1,2,8,6,7,3,13,12,15,5,10,9 | 0.0833 | 8 | 4 | 12 | No | Yes | Yes |
| 10 | 1,2,4,8,3,9,11,5,15,14,10,13,12,7,6 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| Iterations | Optimal Assembly Sequence | Fitness Function Value | Number of Part Direction Changes | Number of Tool Changes | Connection Stability | as Reference Component | Satisfies Sequence Constraints | Satisfies Geometric Constraints |
|---|---|---|---|---|---|---|---|---|
| 1 | 1,2,4,8,3,5,11,10,9,13,12,6,7,14,15 | 0.1157 | 5 | 4 | 13 | Yes | Yes | Yes |
| 2 | 1,4,2,8,9,3,5,15,14,7,6,11,10,12,13 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 3 | 1,4,2,3,5,11,10,9,12,13,6,7,8,14,15 | 0.1157 | 5 | 4 | 13 | Yes | Yes | Yes |
| 4 | 1,2,4,6,7,8,9,3,5,15,14,10,11,13,12 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 5 | 1,4,2,6,7,3,9,11,5,15,14,8,10,12,13 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 6 | 1,4,2,8,6,7,3,9,11,14,15,5,10,13,12 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 7 | 1,4,2,8,3,5,15,14,11,9,10,7,6,13,12 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 8 | 1,2,4,6,7,11,9,3,14,15,5,10,8,13,12 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 9 | 1,2,4,9,3,5,15,14,6,7,11,10,8,12,13 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 10 | 1,4,2,3,5,11,10,9,6,7,8,13,12,14,15 | 0.1157 | 5 | 4 | 13 | Yes | Yes | Yes |
| 11 | 1,2,4,7,6,8,9,3,5,15,14,11,10,13,12 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 12 | 1,2,4,8,11,9,3,5,15,14,6,7,10,12,13 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 13 | 1,4,2,3,14,15,5,11,9,10,12,13,8,7,6 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 14 | 1,4,2,7,6,8,3,5,15,14,10,9,11,13,12 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 15 | 1,4,2,3,9,14,15,5,11,10,12,13,8,6,7 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
| 16 | 1,2,4,7,6,3,5,15,14,10,9,11,13,12,8 | 0.1157 | 6 | 3 | 13 | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, L.; Wu, X.; Zhao, Y.; Liu, J.; Liu, K. Research on Assembly Sequence Planning of Large Cruise Ship Cabins Based on Improved Genetic Algorithm. Biomimetics 2025, 10, 237. https://doi.org/10.3390/biomimetics10040237
Ju L, Wu X, Zhao Y, Liu J, Liu K. Research on Assembly Sequence Planning of Large Cruise Ship Cabins Based on Improved Genetic Algorithm. Biomimetics. 2025; 10(4):237. https://doi.org/10.3390/biomimetics10040237
Chicago/Turabian StyleJu, Liyang, Xiaoyuan Wu, Yixi Zhao, Jianfeng Liu, and Kun Liu. 2025. "Research on Assembly Sequence Planning of Large Cruise Ship Cabins Based on Improved Genetic Algorithm" Biomimetics 10, no. 4: 237. https://doi.org/10.3390/biomimetics10040237
APA StyleJu, L., Wu, X., Zhao, Y., Liu, J., & Liu, K. (2025). Research on Assembly Sequence Planning of Large Cruise Ship Cabins Based on Improved Genetic Algorithm. Biomimetics, 10(4), 237. https://doi.org/10.3390/biomimetics10040237






