Model Parametrization-Based Genetic Algorithms Using Velocity Signal and Steady State of the Dynamic Response of a Motor
Abstract
1. Introduction
- Using a single signal for parameterization of the dynamic model of an motor.
- Leveraging stationary relationships for single-signal parametric estimation.
- Adaptability to any metaheuristic algorithm.
2. Materials and Methods
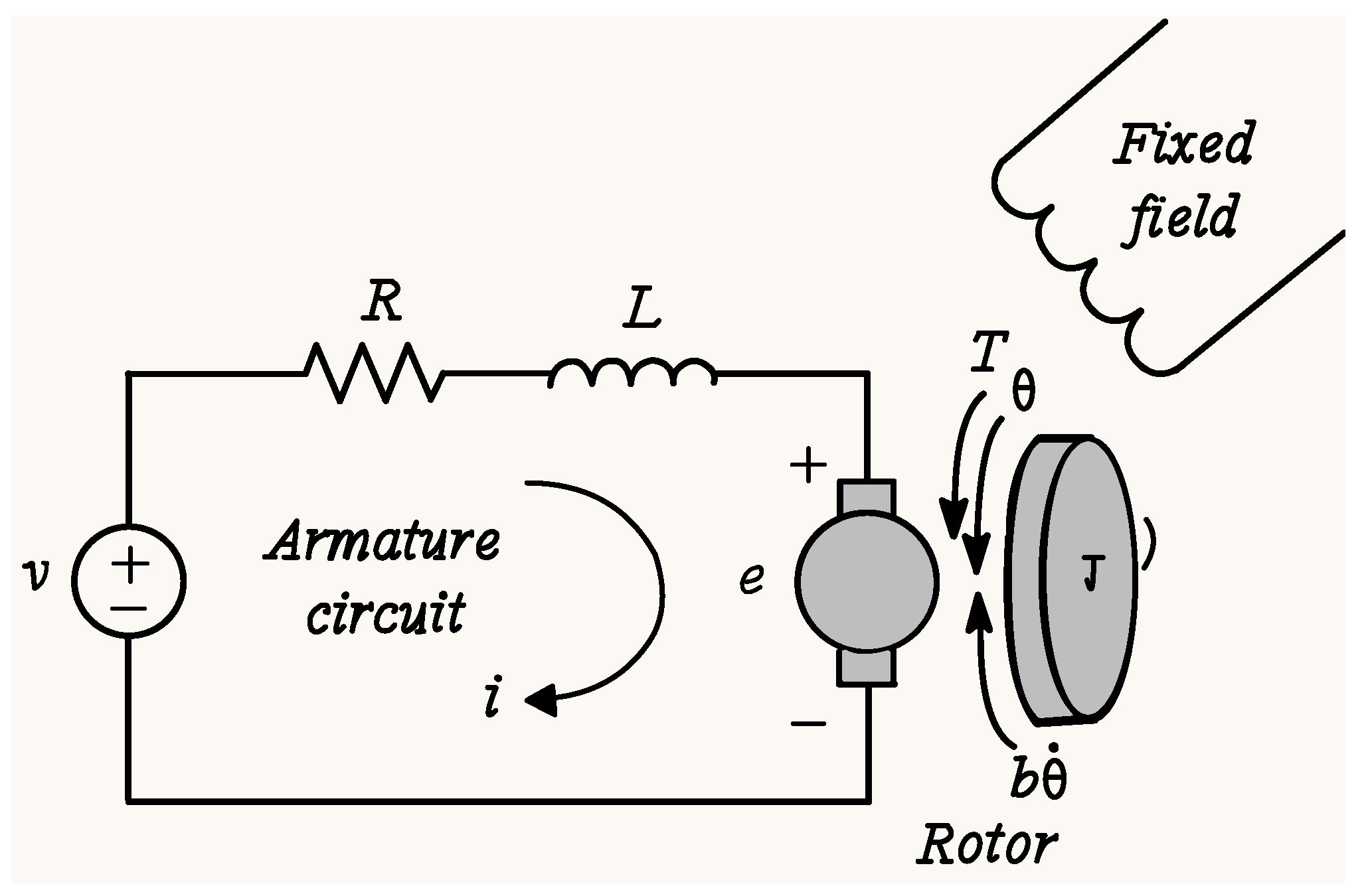
2.1. Dynamic Description of a Direct Current Motor
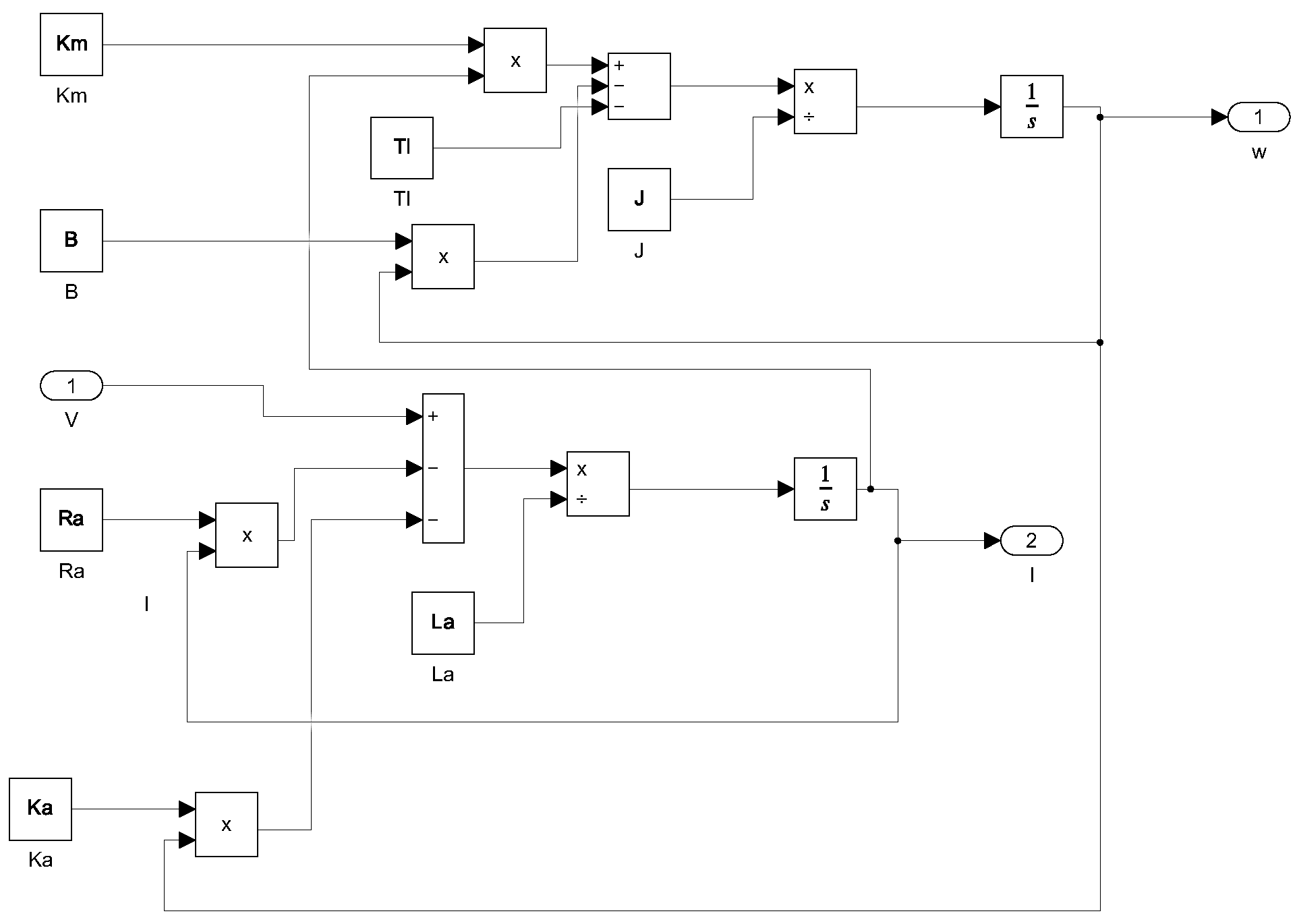
2.2. Simulation of the Dynamic Model of the DC Motor
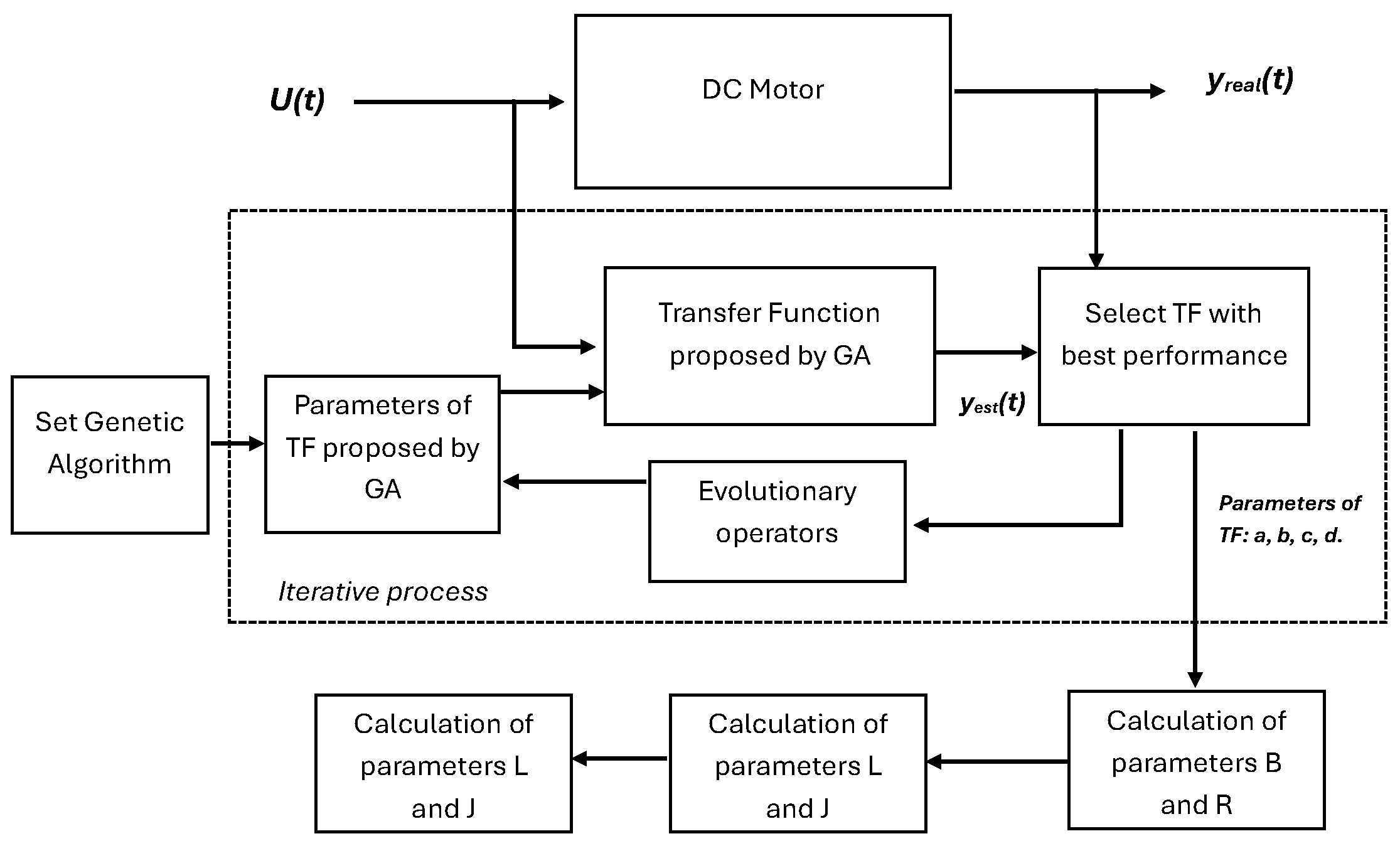
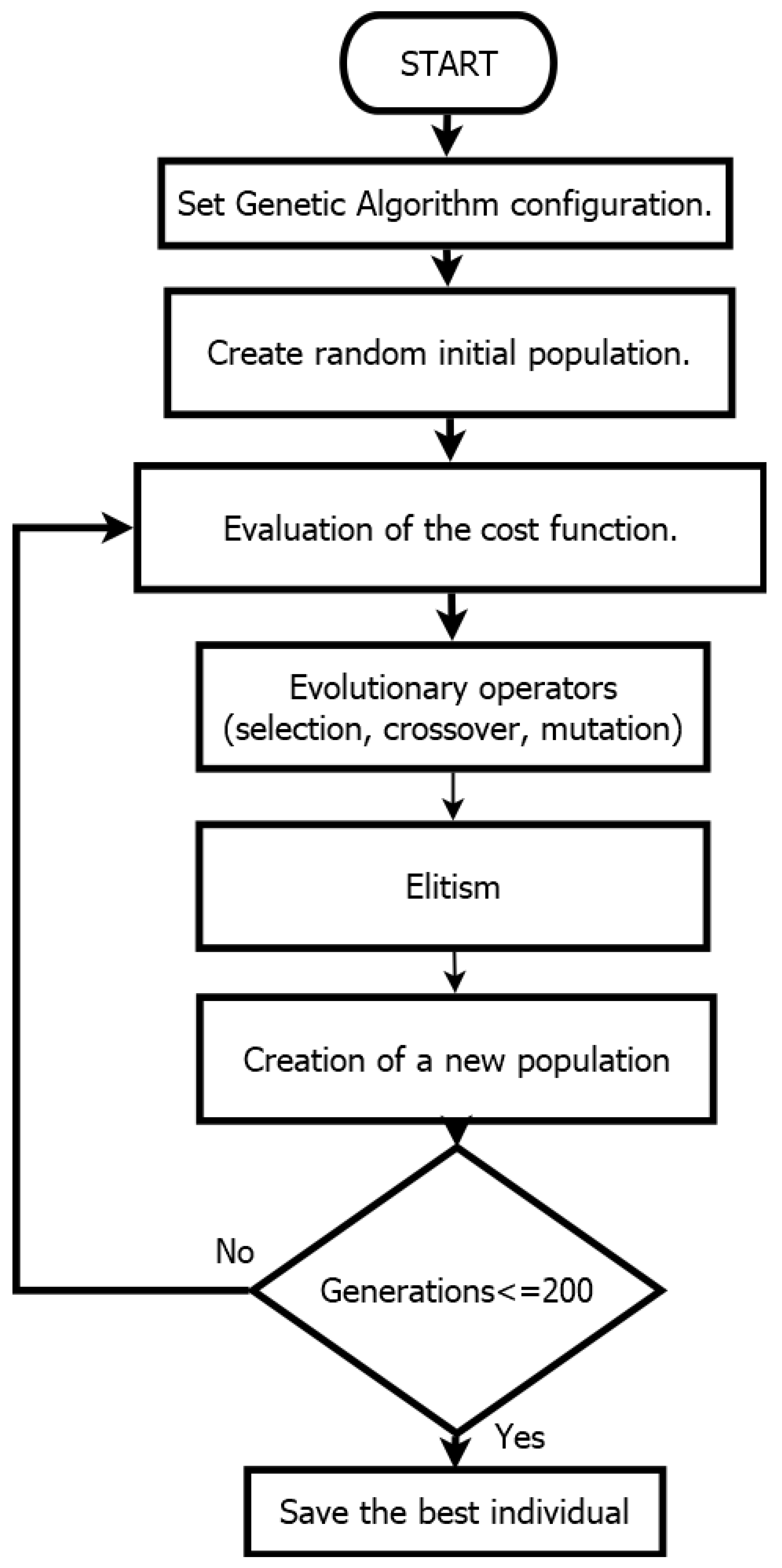
2.3. Genetic Algorithms as a Parametric Estimator in Transfer Functions
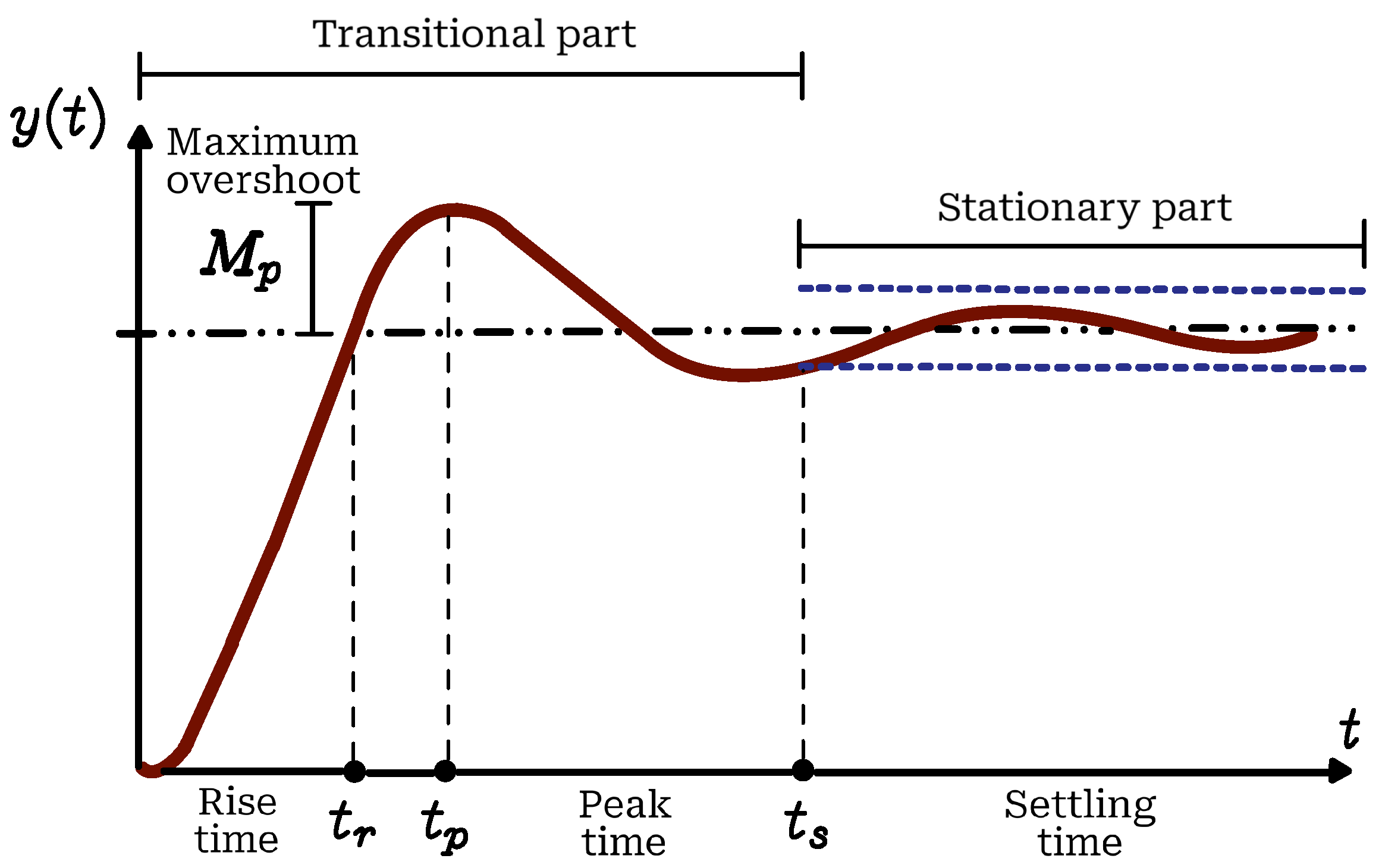
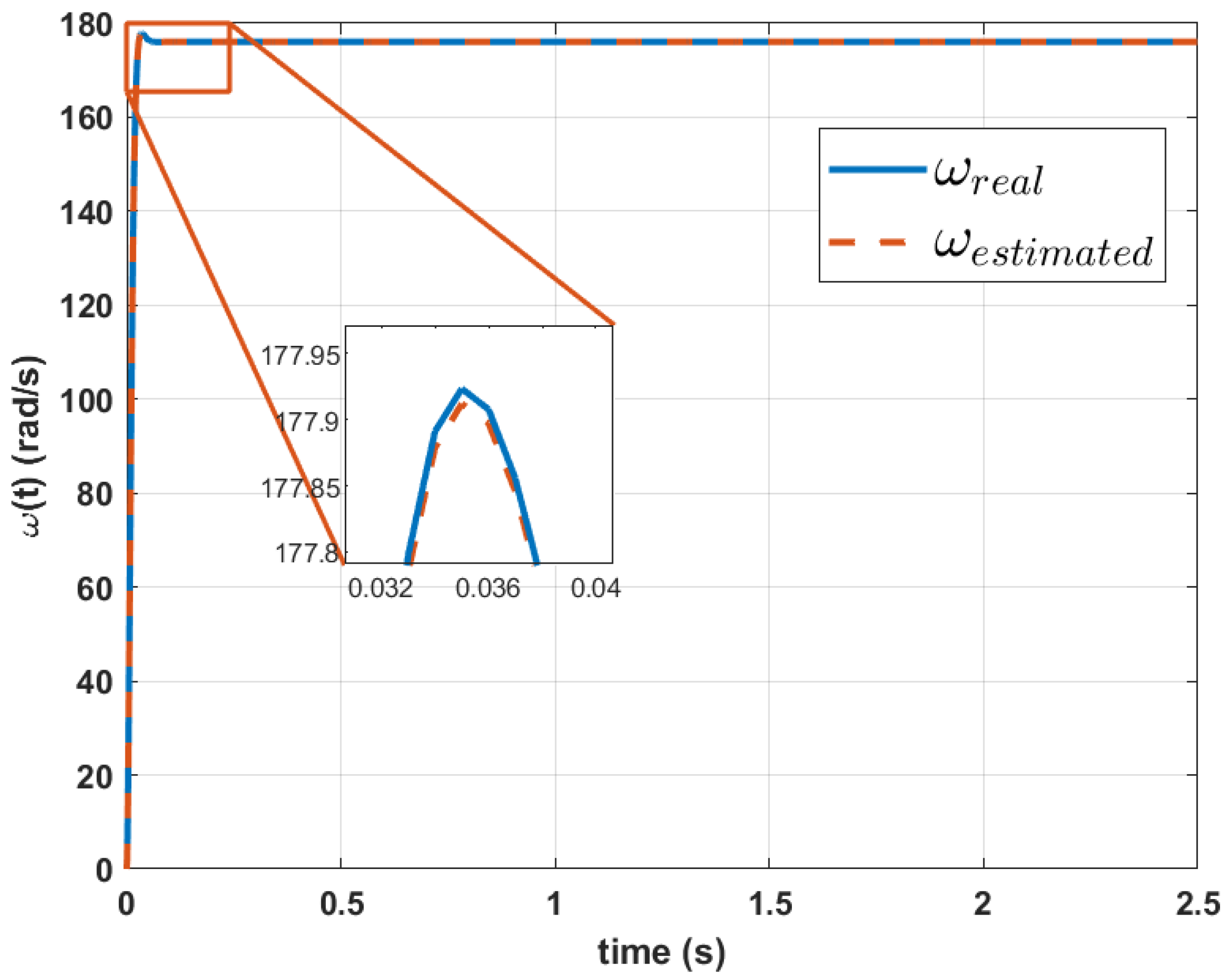
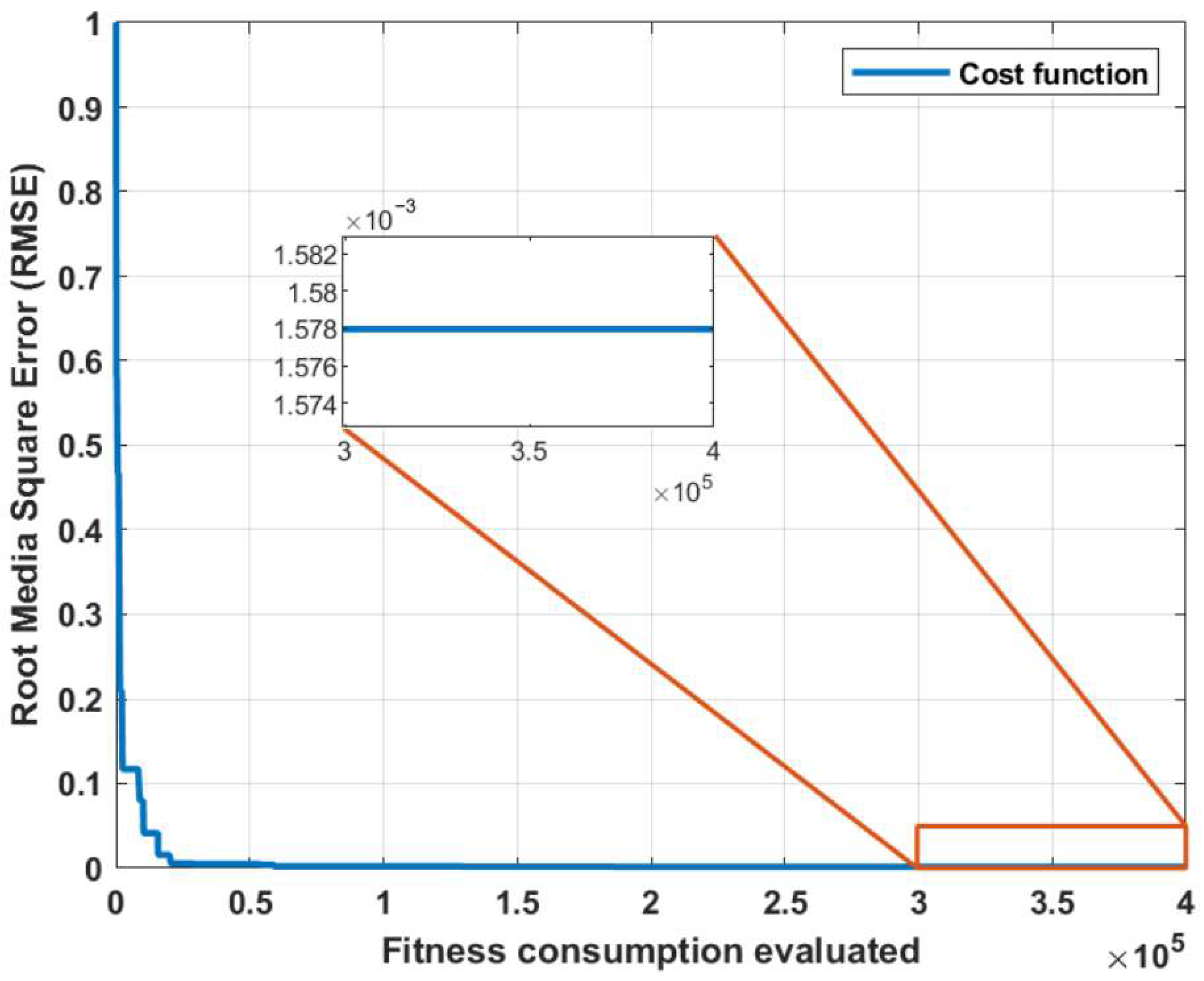
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DC | Direct Current |
| GA | Genetic Algorithm |
| TF | Transfer Function |
| Angular velocity | |
| a | Numerator coefficient in velocity transfer function |
| b | Denominator coefficient in quadratic term for the velocity transfer function |
| c | Denominator coefficient in lineal term for the velocity transfer function |
| d | Denominator coefficient in independent term for the velocity transfer function |
| K | Value of the mechanical and electrical constant of the DC motor. |
| B | Motor friction coefficient value. |
| R | DC motor winding resistance value |
| J | Rotor moment of inertia |
| L | Motor winding inductance |
References
- Aguilar-Mejia, O.; Zuñiga-Peña, N.S.; Hernández-Romero, N.; Seck-Touh-Mora, J.C.; Medina-Marín, J. Optimization of a PI speed control for a permanent magnet motor using metaheuristic algorithms. Pän Sci. Bull. Basic Sci. Eng. ICBI 2024, 12, 156–164. [Google Scholar]
- Almawla, A.M.; Hussein, M.J.; Abdullah, A.T. A Comparative Study of DC Motor Speed Control Techniques Using Fuzzy, SMC and PID. J. Eur. Des Syst. Autom. 2024, 57, 397–406. [Google Scholar] [CrossRef]
- Miquelanti, M.G.; Pugliese, L.F.; Silva, W.W.; Braga, R.A.; Monte-Mor, J.A. Comparison between an Adaptive Gain Scheduling Control Strategy and a Fuzzy Multimodel Intelligent Control Applied to the Speed Control of Non-Holonomic Robots. Appl. Sci. 2024, 14, 6675. [Google Scholar] [CrossRef]
- Sundaram, M.; Chelladurai, J.; Anand, M.; Kumari, M.S.; Sharma, S.; Assad, M.E.H. A novel approach to energy-optimized variable-speed sensorless-based brushless DC motors (BLDC) control for automotive wiper applications. Arab. J. Sci. Eng. 2024, 49, 1491–1504. [Google Scholar] [CrossRef]
- Alcázar-García, D.; Martínez, J.L.R. Model-based design validation and optimization of drive systems in electric, hybrid, plug-in hybrid and fuel cell vehicles. Energy 2022, 254, 123719. [Google Scholar] [CrossRef]
- Amanuel, T.; Ghirmay, A.; Ghebremeskel, H.; Ghebrehiwet, R.; Bahlibi, W. Design of Vibration Frequency Method with Fine-Tuned Factor for Fault Detection of Three Phase Induction Motor. J. Innov. Image Process. (JIIP) 2021, 3, 52–65. [Google Scholar] [CrossRef]
- Fabio, A.; Mario, C.; Liliana, L.; Marianna, R.; Gaetano, T.F. Predictive maintenance in the automotive sector: A literature review. Math. Comput. Appl. 2021, 27, 2. [Google Scholar] [CrossRef]
- Fazdi, M.F.; Hsueh, P.W. Parameters identification of a permanent magnet dc motor: A review. Electronics 2023, 12, 2559. [Google Scholar] [CrossRef]
- Abdullah, Q.; Farah, N.; Ahmed, M.S.; Shah, N.S.M.; Aydoğdu, Ö.; Talib, M.H.N.; Al-Moliki, Y.M.; Uğurenver, A.; Al-Mekhalfi, M.A.; Aihsan, M.Z.; et al. Sensorless Speed Control of Induction Motor Drives Using Reinforcement Learning and Self-Tuning Simplified Fuzzy Logic Controller. IEEE Access 2024, 12, 136485–136501. [Google Scholar] [CrossRef]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.; HosseinNia, S.H.; Petlenkov, E. FOPID controllers and their industrial applications: A survey of recent results. IFAC-PapersOnLine 2018, 51, 25–30. [Google Scholar] [CrossRef]
- Arifin, B.; Nugroho, A.A.; Budisusila, E.N.; Khosyi’in, M. System Identification and Control Strategy on Electric Power Steering DC Motor. J. Robot. Control (JRC) 2024, 5, 655–666. [Google Scholar]
- Ahmadirad, Z. Evaluating the Influence of AI on Market Values in Finance: Distinguishing Between Authentic Growth and Speculative Hype. Int. J. Adv. Res. Humanit. Law 2024, 1, 50–57. [Google Scholar] [CrossRef]
- Hassoun, S.; Jefferson, F.; Shi, X.; Stucky, B.; Wang, J.; Rosa Epaminondas, J. Artificial Intelligence for Biology. Integr. Comp. Biol. 2021, 61, 2267–2275. [Google Scholar] [CrossRef]
- Sheida, K.; Seyedi, M.; Afridi, M.A.; Ferdowsi, F.; Khattak, M.J.; Gopu, V.K.; Rupnow, T. Resilient Reinforcement Learning for Voltage Control in an Islanded DC Microgrid Integrating Data-Driven Piezoelectric. Machines 2024, 12, 694. [Google Scholar] [CrossRef]
- Emiroglu, S.; Uyaroglu, Y. Genetic algorithm (GA)–based delay feedback control of chaotic behavior in the voltage mode controlled direct current (DC) drive system. Z. Für Naturforschung A 2021, 76, 13–21. [Google Scholar] [CrossRef]
- Brito, W.; Chamba, M.; Echeverría, D.; Torre, A.; Panchi, D. Parametric Identification, Validation and Tuning Tool for Speed Regulators Using Heuristic Optimization Algorithms. Rev. Técnica Energía 2024, 20, 21–33. [Google Scholar] [CrossRef]
- Munciño, D.M.; Damian-Ramírez, E.A.; Cruz-Fernández, M.; Montoya-Santiyanes, L.A.; Rodríguez-Reséndiz, J. Metaheuristic and Heuristic Algorithms-Based Identification Parameters of a Direct Current Motor. Algorithms 2024, 17, 209. [Google Scholar] [CrossRef]
- Jesenik, M.; Hamler, A.; Trbušić, M.; Trlep, M. The use of evolutionary methods for the determination of a DC motor and drive parameters based on the current and angular speed response. Mathematics 2020, 8, 1269. [Google Scholar] [CrossRef]
- Nouaoui, T.; Dendouga, A.; Bendaikha, A. Speed control of PMSM using a fuzzy logic controller with deformed MFS tuned by a novel hybrid meta-heuristic algorithm. Electr. Eng. 2024, 106, 6927–6939. [Google Scholar] [CrossRef]
- El Mansouri, F.E.; Mosaad, M.I.; Kadi, L.; Ouannou, A.; Oubouaddi, H.; Brouri, A. Application of Frequency Response Analysis for Parameters Estimation of Switched Reluctance Motors. J. Electr. Eng. Technol. 2024, 19, 3851–3871. [Google Scholar] [CrossRef]
- Udomsuk, S.; Areerak, K.; Areerak, T.; Areerak, K. Online Estimation of Three-Phase Induction Motor Parameters Using an Extended Kalman Filter for Energy Saving. Energies 2024, 17, 2115. [Google Scholar] [CrossRef]
- Kuczmann, M. Reviewof DC Motor Modeling and Linear Control: Theory with Laboratory Tests. Electronics 2024, 13, 2225. [Google Scholar] [CrossRef]
- Rahayu, E.S.; Ma’arif, A.; Çakan, A. Particle Swarm Optimization (PSO) Tuning of PID Control on DC Motor. Int. J. Robot. Control Syst. 2022, 2, 435–447. [Google Scholar] [CrossRef]
- Vanchinathan, K.; Selvaganesan, N. Adaptive fractional order PID controller tuning for brushless DC motor using Artificial Bee Colony algorithm. Results Control Optim. 2021, 4, 100032. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; EL Ouanjli, N.; EL Mahfoud, M.; Taoussi, M. A New Strategy-Based PID Controller Optimized by Genetic Algorithm for DTC of the Doubly Fed Induction Motor. Systems 2021, 9, 37. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; El Ouanjli, N.; Mossa, M.A.; Motahhir, S.; El Mahfoud, M.; Al-Sumaiti, A.S. Comparative Study between Cost Functions of Genetic Algorithm Used in Direct Torque Control of a Doubly Fed Induction Motor. Appl. Sci. 2022, 12, 8717. [Google Scholar] [CrossRef]
- Alasali, F.; Sweidan, T.O.; Abuashour, M.I.; Holderbaum, W. Advanced Modelling and Performance Analysis of a Separately Excited Direct-Current Motor Powered by Photovoltaic Generators Using Maximum Power Point Tracking Techniques. J. Low Power Electron. Appl. 2024, 14, 56. [Google Scholar] [CrossRef]
- Venkatesh, J.; Nkengne, S.T.; Kingni, S.T.; Fotsin, H.B.; Sekhar, D.C.; Rajagopal, K. Dynamics, Controls of the Nonsmooth-Air-Gap Brushless Direct Current Motor Under the Influence of Temperature and Embedded in a Microcontroller. J. Control Autom. Electr. Syst. 2024, 35, 1121–1134. [Google Scholar] [CrossRef]
- Patrascoiu, N. Modeling and simulation of the DC motor using Matlab and LabVIEW. Int. J. Eng. Educ. 2005, 21, 49–54. [Google Scholar]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; Velásquez, F.A.C.; Ortiz Verdin, A.A.; Garcia-Guendulain, J.M.; Garduño-Aparicio, M. Estimation of Transfer Function Coefficients for Second-Order Systems via Metaheuristic Algorithms. Sensors 2021, 21, 4529. [Google Scholar] [CrossRef] [PubMed]
- Amini-Valashani, M.; Mirzakuchaki, S. Performance Evaluation of Latest Meta-Heuristic Algorithms in Finding Optimum Value of Mathematical Functions and Problems. Arab. J. Sci. Eng. 2024, 1–41. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Hernandez-Paredes, J.M.; Rangel, A.F.; Fuentes-Silva, C.; Velásquez, F.A.C. Parameter Identification of Motors by Cuckoo Search Using Steady-State Relations. IEEE Access 2021, 9, 72017–72024. [Google Scholar] [CrossRef]
- Miguel, H.P.J.; Benigno, M.B.; Omar, R.A. Sistema de identificación paramétrica para motores de corriente directa. Mecatrónica México 2019, 8, 115–130. [Google Scholar]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; Álvarez Alvarado, J.M.; García-Cerezo, A. Metaheuristic Parameter Identification of Motors Using Dynamic Response Relations. Sensors 2022, 22, 4050. [Google Scholar] [CrossRef] [PubMed]
- Desale, S.; Rasool, A.; Andhale, S.; Rane, P. Heuristic and meta-heuristic algorithms and their relevance to the real world: A survey. Int. J. Comput. Eng. Res. Trends 2015, 351, 2349–7084. [Google Scholar]
- Alhijawi, B.; Awajan, A. Genetic algorithms: Theory, genetic operators, solutions, and applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Liang, D.; Liu, K. Online Parameter Estimation for Permanent Magnet Synchronous Machines: An Overview. IEEE Access 2021, 9, 59059–59084. [Google Scholar] [CrossRef]
- Amiri, M.S.; Ibrahim, M.F.; Ramli, R. Optimal parameter estimation for a DC motor using genetic algorithm. Int. J. Power Electron. Drive Syst 2020, 11, 1047–1054. [Google Scholar] [CrossRef]
- Ghasri, M. File Exchange Matlab. 2023. Available online: https://la.mathworks.com/matlabcentral/fileexchange/124565-real-genetic-algorithm (accessed on 1 June 2024).
- Yang, X.S.; Deb, S. Engineering Optimisation by Cuckoo Search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
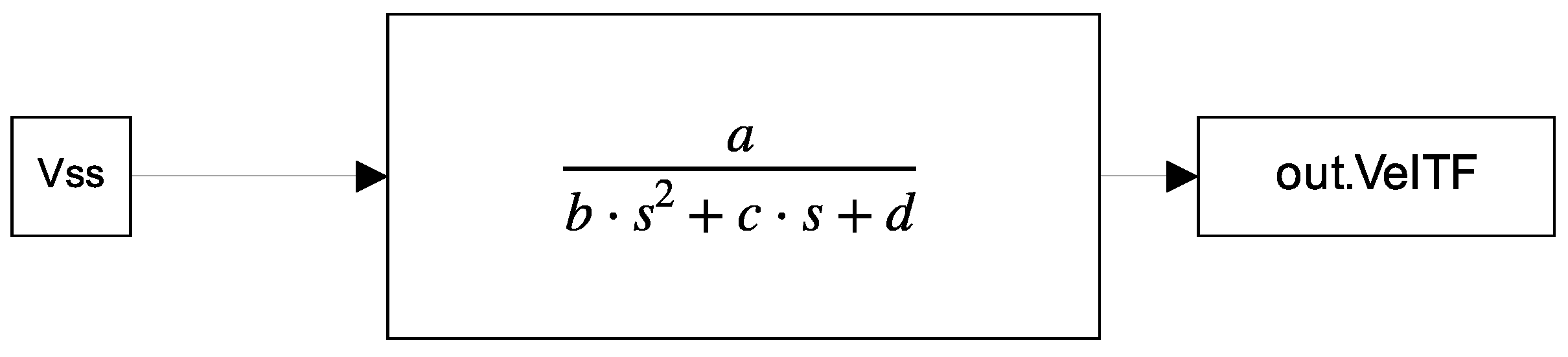
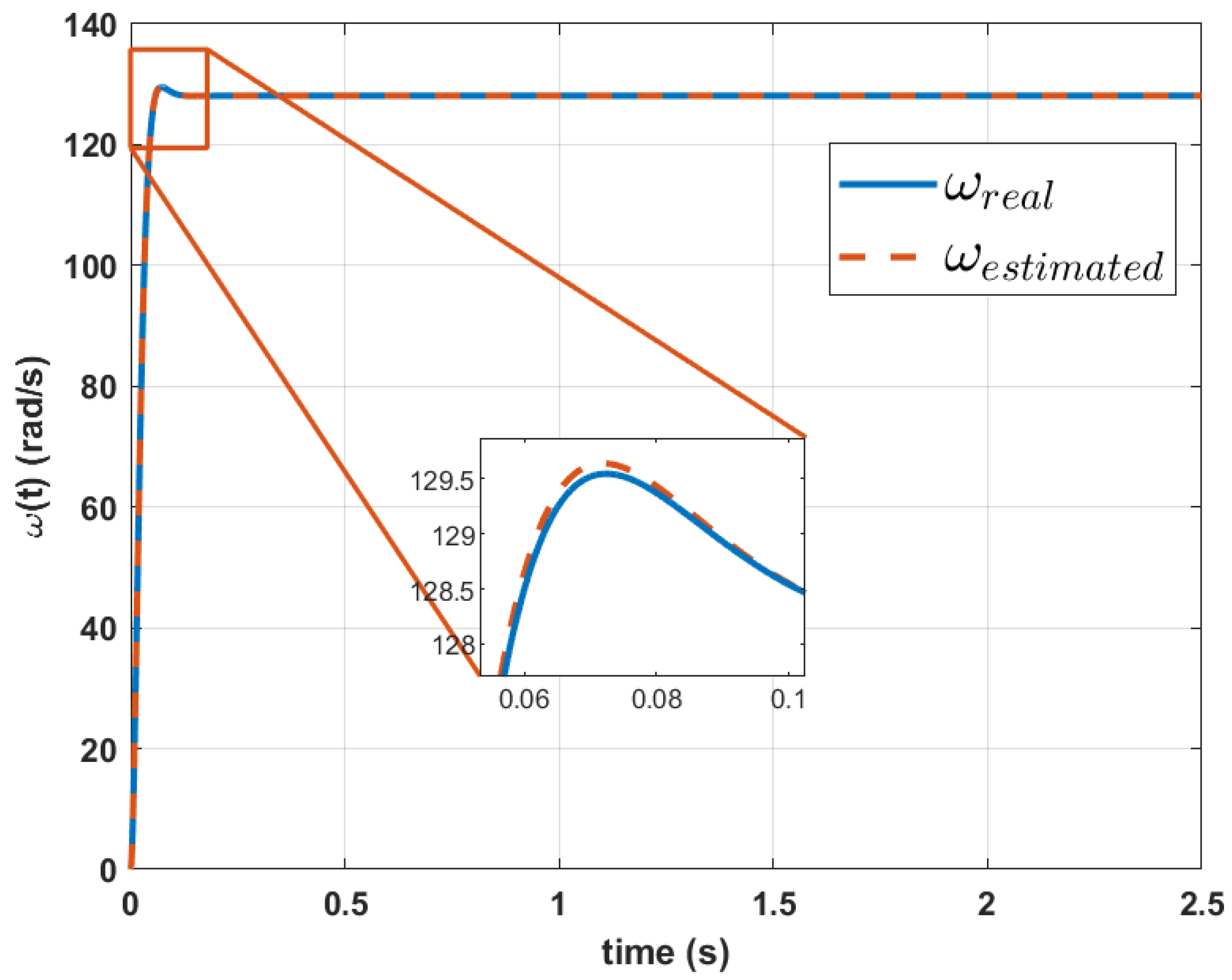
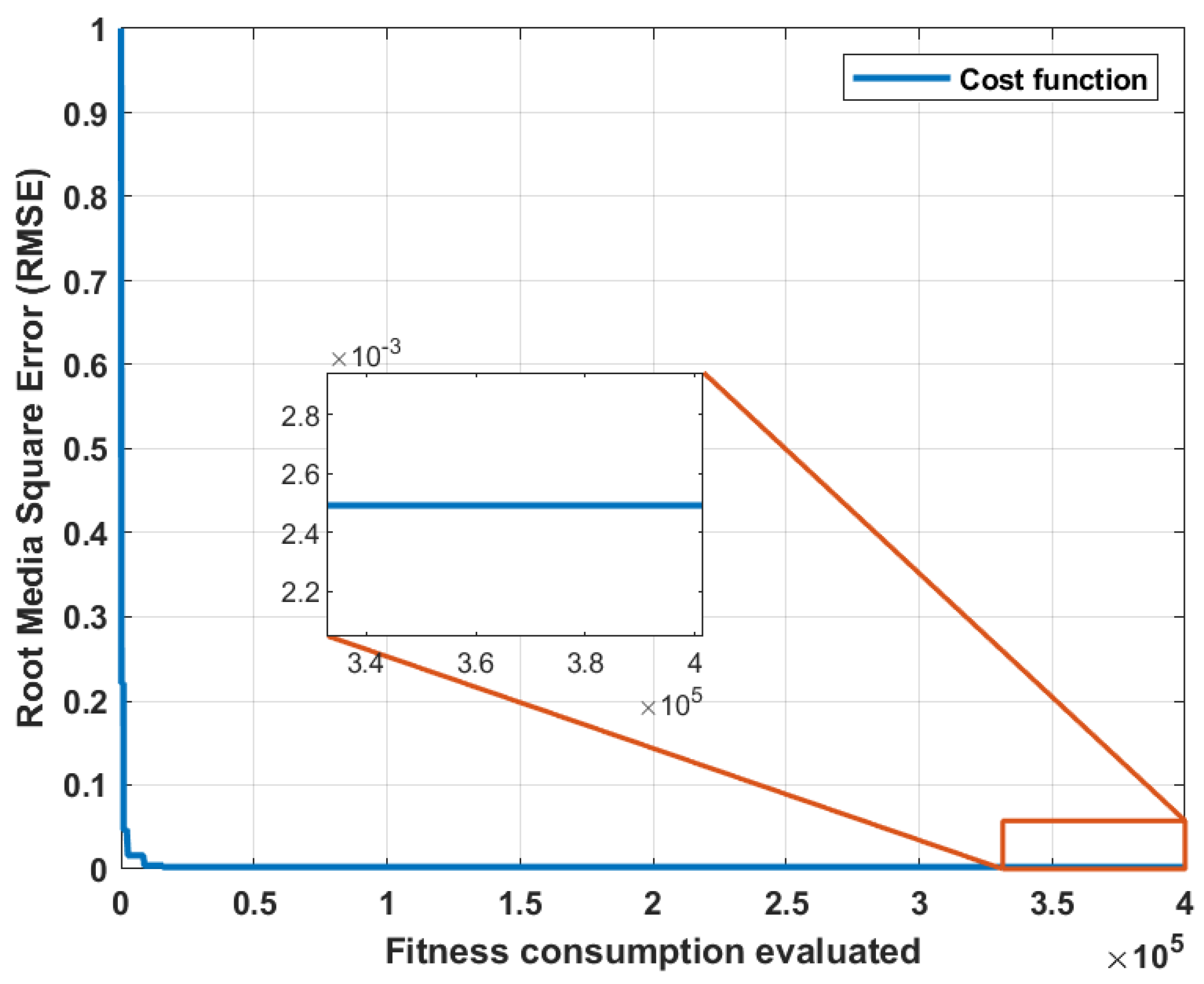
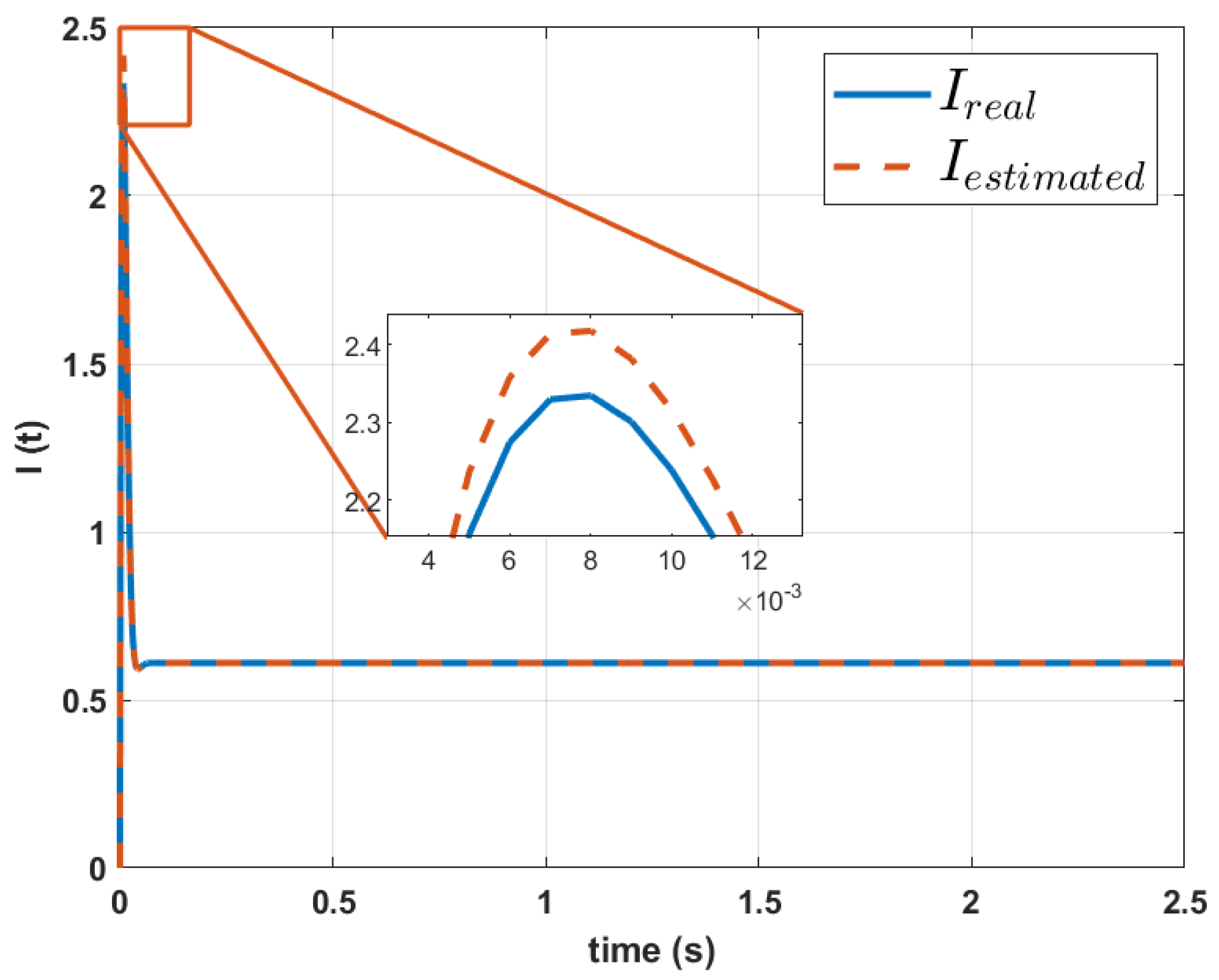
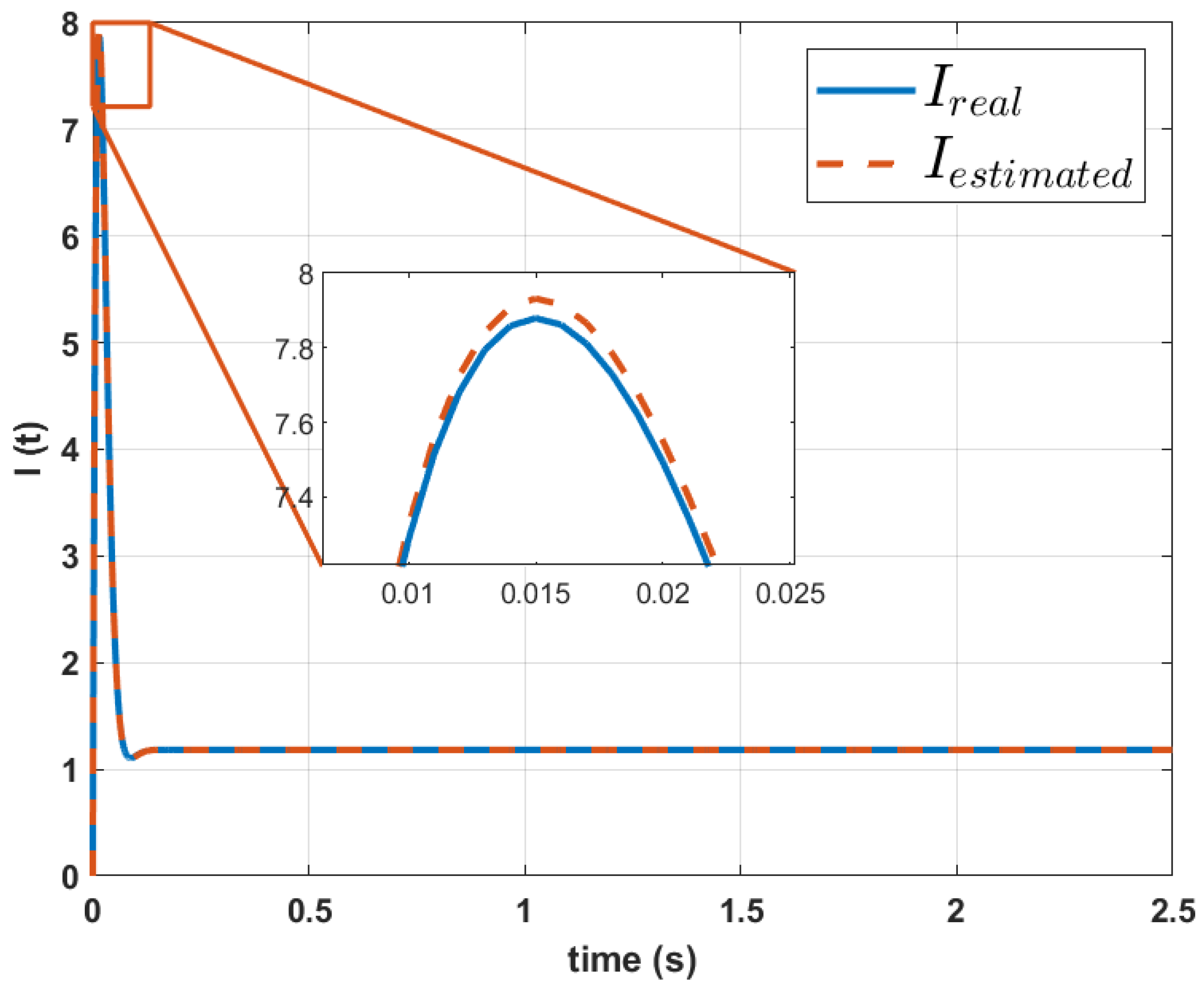
| Work | Applied Method | Problem | Advantages | Limitations | Results |
|---|---|---|---|---|---|
| This work | Genetic Algorithms. | Parameterization of motor dynamic models using only speed signals. | Does not require multiple signals; less than 1% error in reconstruction; innovative and efficient approach. | Dependent on accurate input data; limited validation for specific systems. | Reconstruction of dynamic equations with RMSE < 1% for speed and current signals. |
| [23] | Particle Swarm Optimization (PSO) Algorithm. | Optimization of control parameters in robotic systems involving motors. | High precision in optimization; easy implementation. | Dependence on initial configuration; sensitivity to overfitting. | Parameter optimization with a 15% improvement in precision compared to traditional methods. |
| [24] | Deep Neural Networks (DNN) | Fault prediction in electrical systems, including motor components. | Advanced prediction capabilities; adaptable to non-linear data. | High computational cost; requires large datasets. | 94% accuracy in predicting electrical faults. |
| [25] | GA | Parameter identification in mechanical systems, particularly motors. | Precise results for complex models; robust to noise. | Slow for large-scale problems; requires parameter tuning. | Accurate parameter identification with an average error below 2%. |
| [26] | Dynamic Modeling and Statistical Analysis. | Analysis of dynamic behavior in industrial systems, including motor dynamics. | Detailed modeling; enables precise analysis of complex dynamics. | Limited generalizability to other systems. | Dynamic models with a 90% accuracy rate in simulations. |
| Parameter (Units) | CML050 Nominal Value | RMCS2004 Nominal Value |
|---|---|---|
| K | 0.048774 | 0.073472 |
| B () | 0.000169 | 0.000678 |
| R () | 3.1363 | 0.921042 |
| L (H) | 0.01307 | 0.000136 |
| J (Nm) | 0.000009 | 0.000678 |
| GA Hyperparameters | Value | Details |
|---|---|---|
| Population | 2000 | Numbers of vectors with random coefficients for a, b, c and d. |
| Upper search limit | [ 1 1 ] | Maximum value in the search for parameters. |
| Lower search limit | [ 1 1 ] | Minimum value in the search for parameters. |
| Fitness function | Function for evaluate the performance of each individual (Root Media Square Error) | |
| Stop condition | genetration <= 200 | Iterations that must be reached to stop the genetic algorithm |
| Elitism | 1% | Percentage of the best individuals with guaranteed reproduction |
| Biological pressure | 70% | Percentage of individuals that can reproduce |
| Mutation | 30% | Probability of each individual suffering a mutation |
| Parameter | CML050 Nominal Value | CML050 GA Value | RMCS2004 Nominal Value | RMCS2004 GA Value |
|---|---|---|---|---|
| a | 4.8774 | 4.92 | 7.3472 | 7.354 |
| b | 1.1763 | 1.1893 | 1.0552 | 1.0609 |
| c | 3.0436 | 3.0777 | 1.3052 | 1.3032 |
| d | 2.908 | 2.949 | 6.022 | 6.028 |
| Parameter (Units) | CML050 Nominal Value | CML050 GA Value | RMCS2004 Nominal Value | RMCS2004 GA Value |
|---|---|---|---|---|
| K | 0.048774 | 0.0492 | 0.073472 | 0.0735 |
| B () | 1.69 | 1.7031 | 6.78 | 6.7868 |
| R () | 3.1363 | 3.0278 | 0.921042 | 0.9131 |
| L (H) | 0.01307 | 0.0126 | 0.007759 | 0.007745 |
| J (Nm) | 9.0 | 9.4573 | 1.36 | 1.3697 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz-Fernández, M.; López-Maldonado, J.T.; Rodriguez-Abreo, O.; Ortiz Verdín, A.A.; Amezcua Tinajero, J.I.; Macías-Socarrás, I.; Rodríguez-Reséndiz, J. Model Parametrization-Based Genetic Algorithms Using Velocity Signal and Steady State of the Dynamic Response of a Motor. Biomimetics 2025, 10, 146. https://doi.org/10.3390/biomimetics10030146
Cruz-Fernández M, López-Maldonado JT, Rodriguez-Abreo O, Ortiz Verdín AA, Amezcua Tinajero JI, Macías-Socarrás I, Rodríguez-Reséndiz J. Model Parametrization-Based Genetic Algorithms Using Velocity Signal and Steady State of the Dynamic Response of a Motor. Biomimetics. 2025; 10(3):146. https://doi.org/10.3390/biomimetics10030146
Chicago/Turabian StyleCruz-Fernández, Mayra, J. T. López-Maldonado, Omar Rodriguez-Abreo, Alondra Anahí Ortiz Verdín, J. Iván Amezcua Tinajero, Idalberto Macías-Socarrás, and Juvenal Rodríguez-Reséndiz. 2025. "Model Parametrization-Based Genetic Algorithms Using Velocity Signal and Steady State of the Dynamic Response of a Motor" Biomimetics 10, no. 3: 146. https://doi.org/10.3390/biomimetics10030146
APA StyleCruz-Fernández, M., López-Maldonado, J. T., Rodriguez-Abreo, O., Ortiz Verdín, A. A., Amezcua Tinajero, J. I., Macías-Socarrás, I., & Rodríguez-Reséndiz, J. (2025). Model Parametrization-Based Genetic Algorithms Using Velocity Signal and Steady State of the Dynamic Response of a Motor. Biomimetics, 10(3), 146. https://doi.org/10.3390/biomimetics10030146











