Enhancing Human–Robot Compatibility in Shoulder Exoskeletons: Passive Joint Optimization of PPRRRP vs. RRRUP Configurations
Abstract
1. Introduction
2. Configuration of the Compatible Mechanisms for Shoulder Rehabilitation
2.1. Kinematic Modeling of the Shoulder Complex
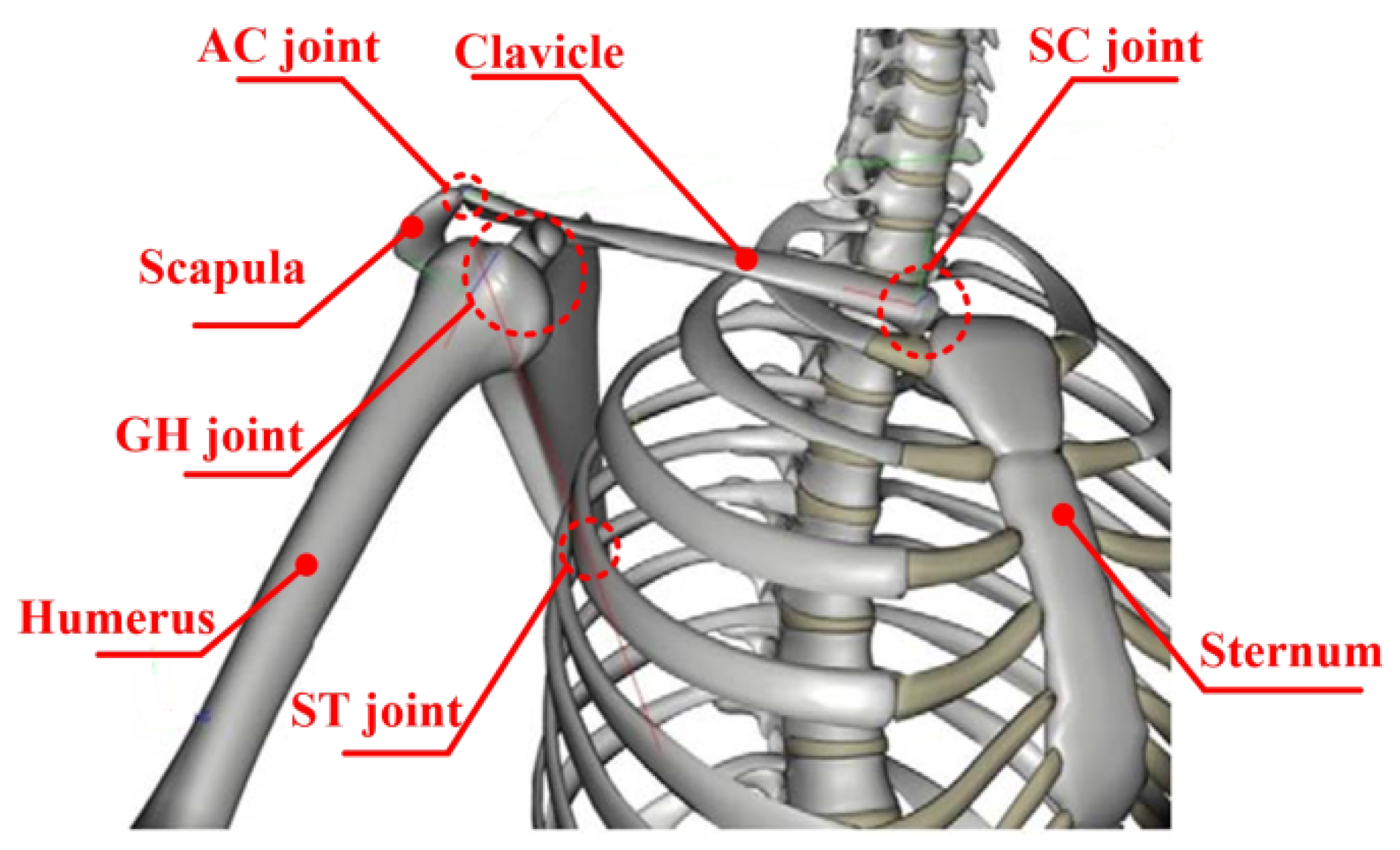
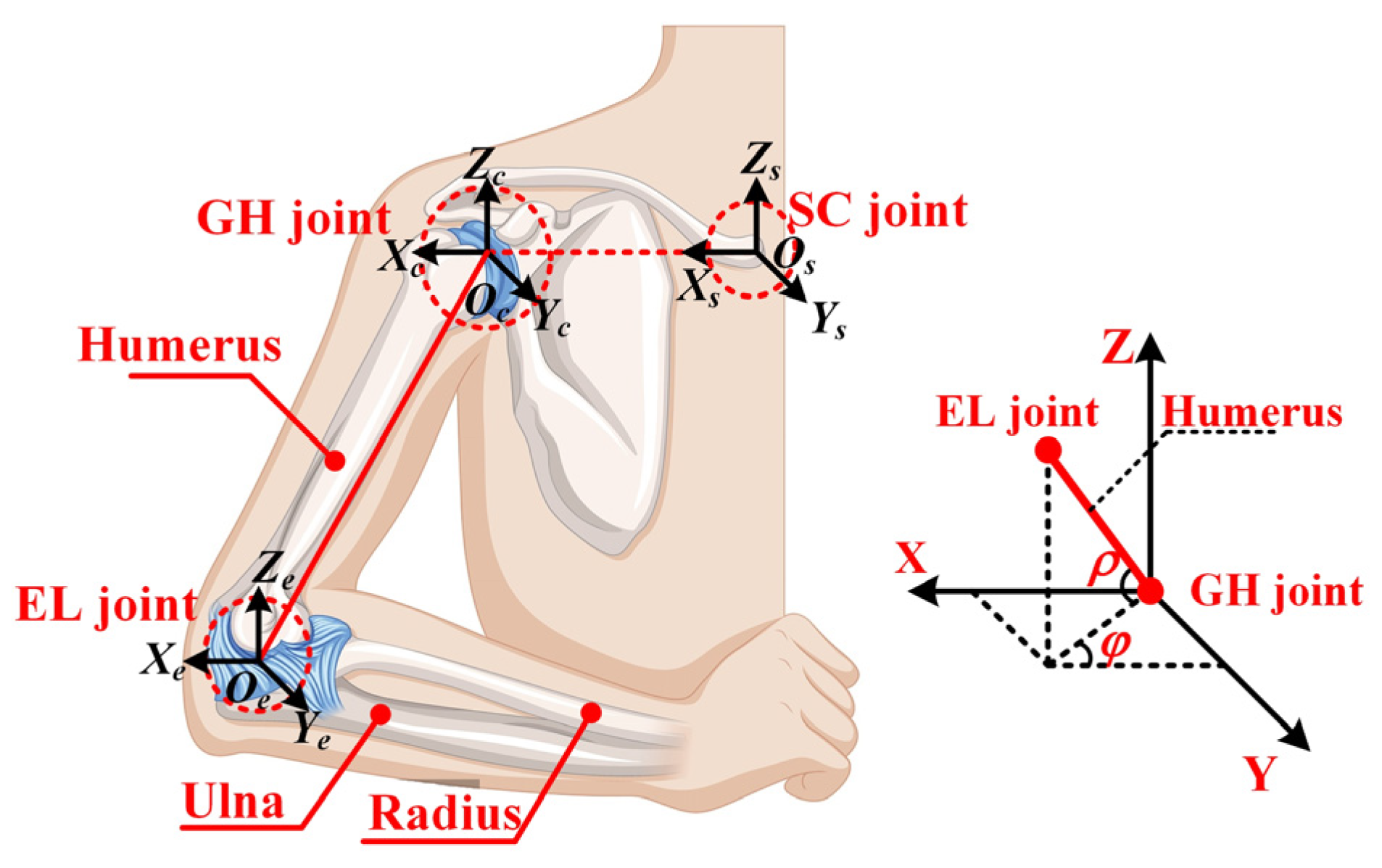
2.2. Typically Presentation of Shoulder Mechanism Configurations
- Prismatic Joint Necessity: The GH joint’s floating center exhibits 79 mm (Z-axis) and 35 mm (X/Y-axis) displacements [22], mandating ≥1 prismatic joint. This excludes 3Ra3R, 3Ra1R1U, and 3Ra1S configurations.
- Manufacturability: Multi-DOF joints (spherical/cylindrical) were discarded due to fabrication complexity and limited motion ranges, eliminating 3Ra1P1C, 3Ra1R1C, and 3Ra1S.
- Passive Chain Optimization: Configurations with elongated sub-chains (e.g., 3Ra2R1P) were rejected in favor of compact designs.
3. Positional Solutions of the Mechanisms for Shoulder Rehabilitation
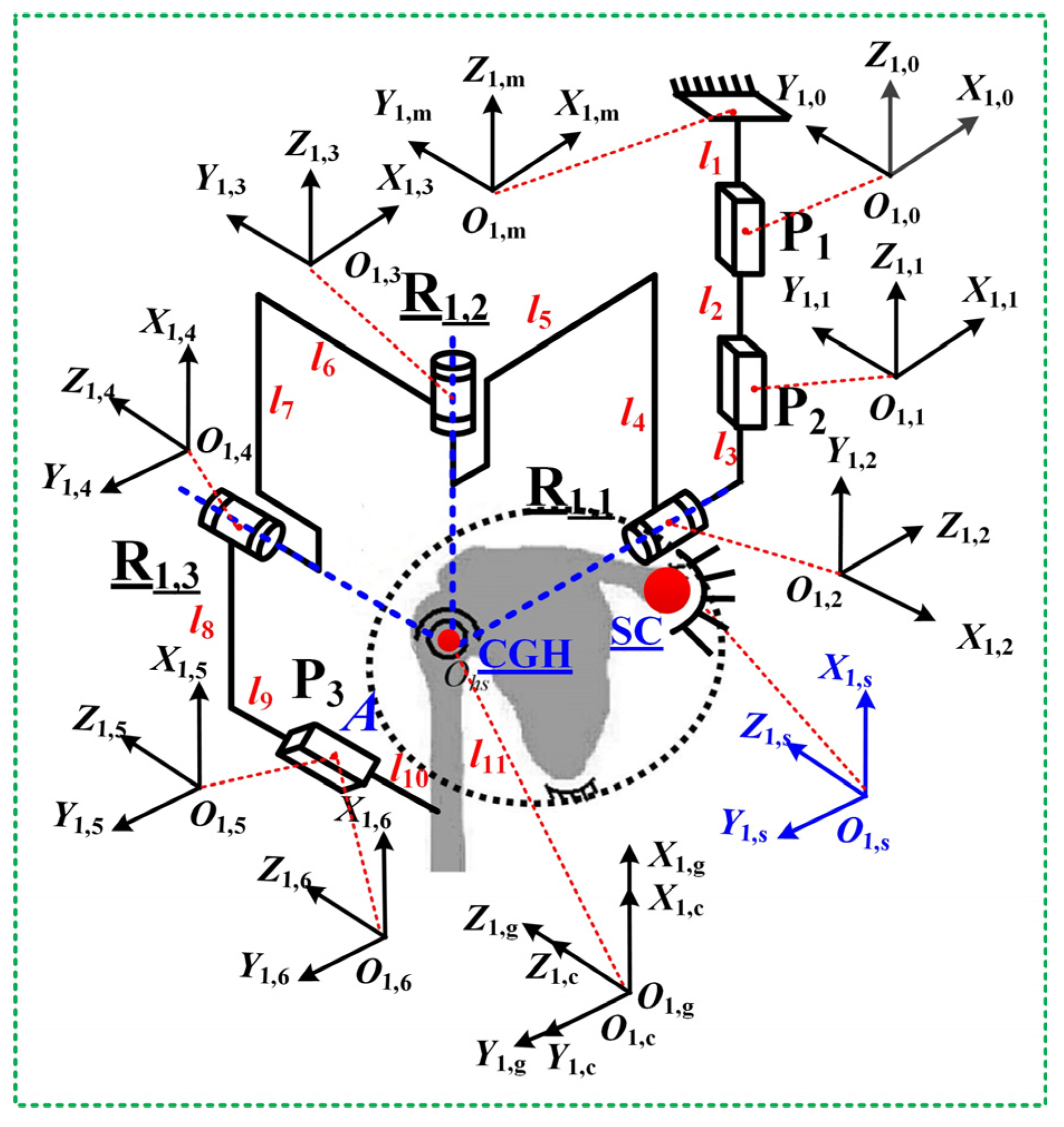
3.1. Jacobian Matrix of Mechanism Configuration PPRRRP
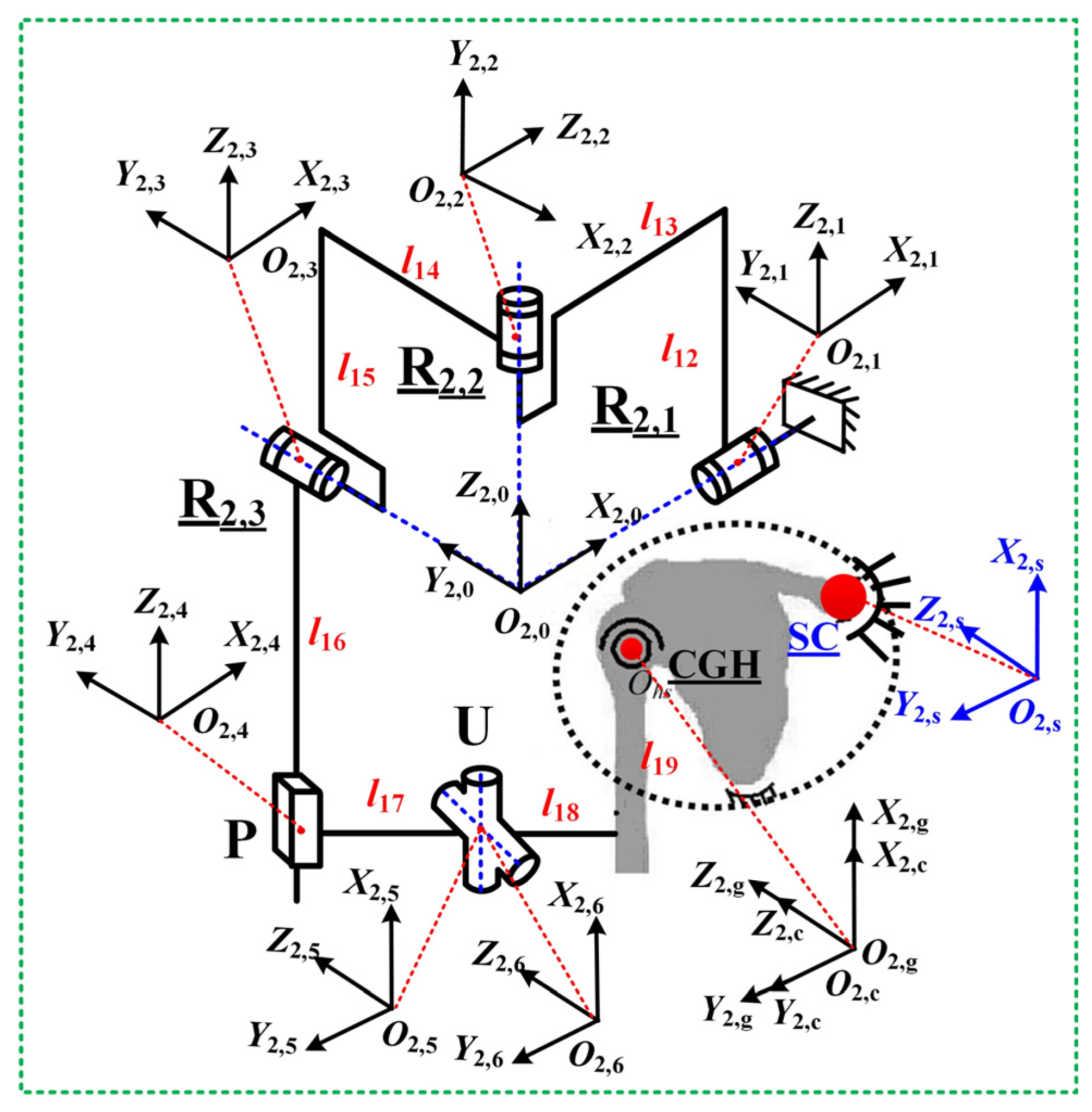
3.2. Jacobian Matrix of Mechanism Configuration RRRUP
4. Kinematic Performance Evaluation of Shoulder Rehabilitation Mechanisms
4.1. Dexterity
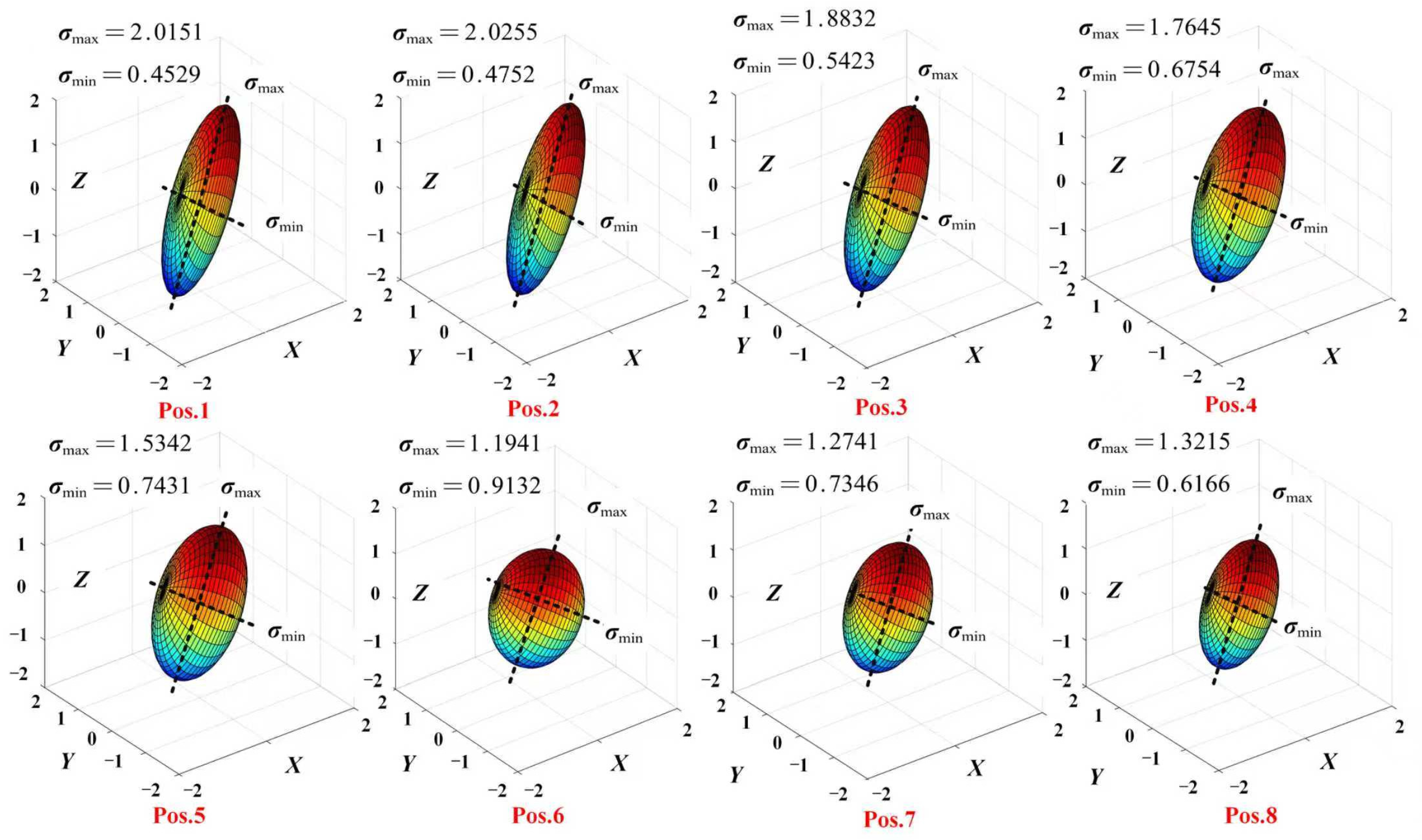
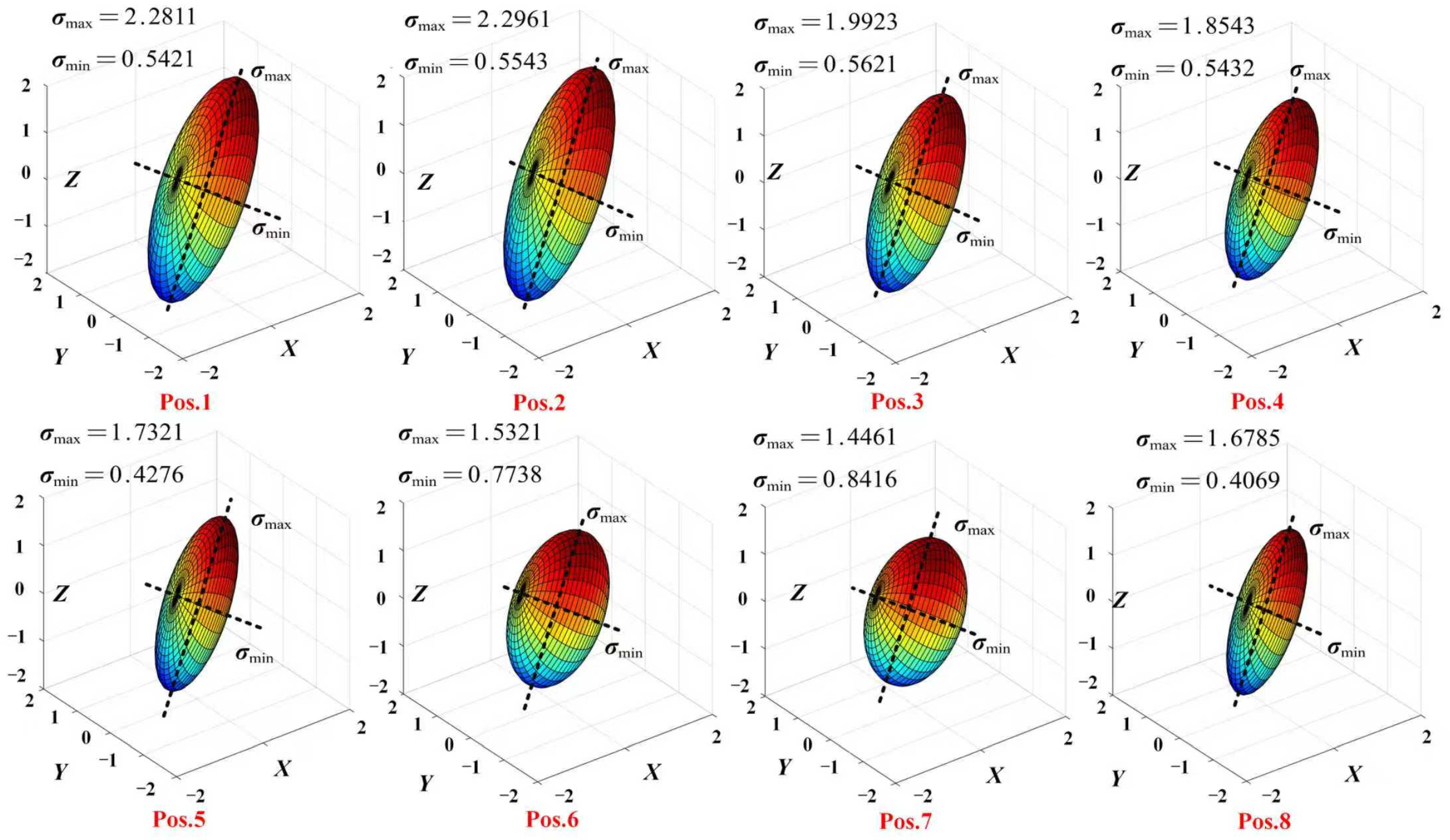
4.2. Manipulability Ellipsoid
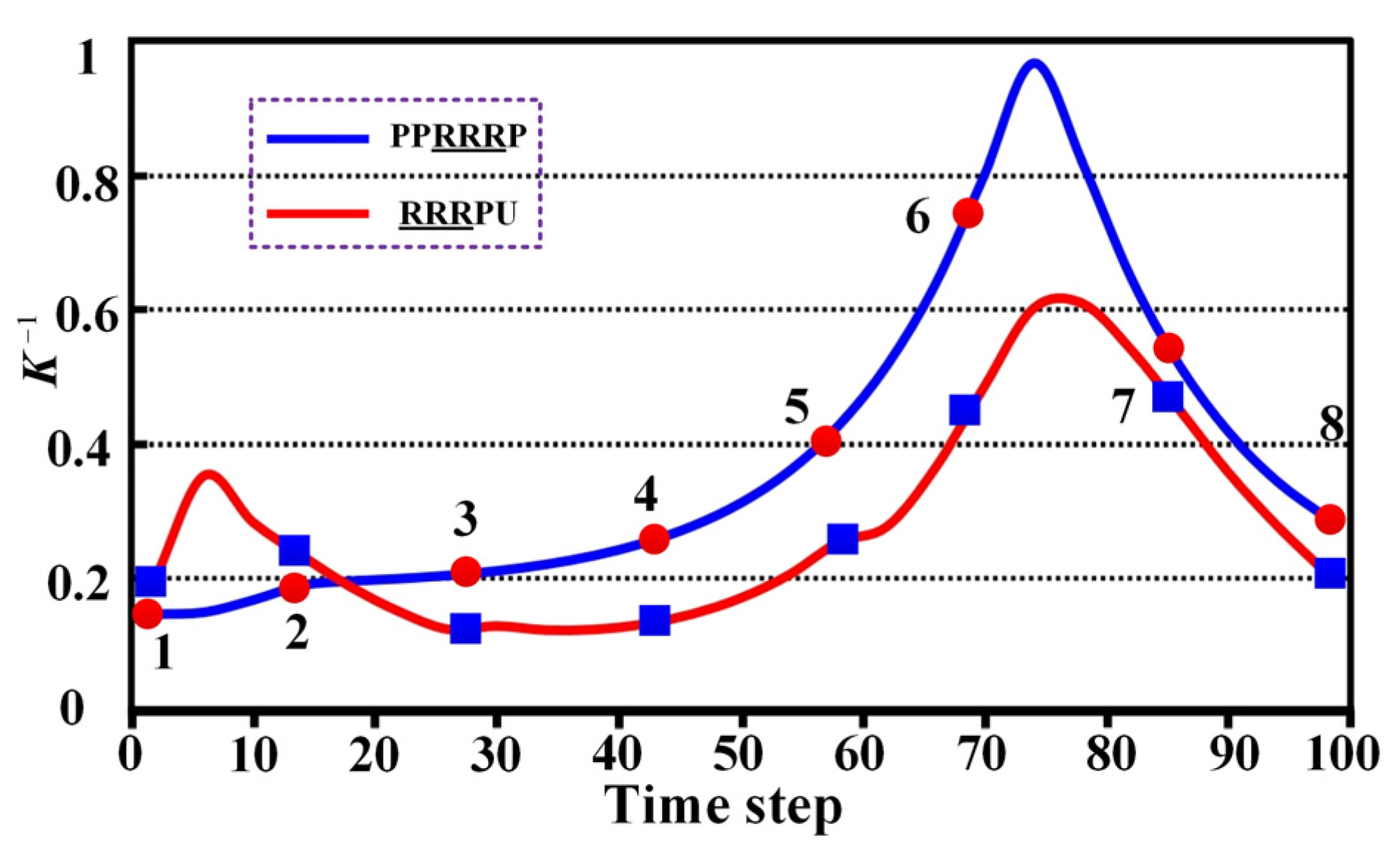
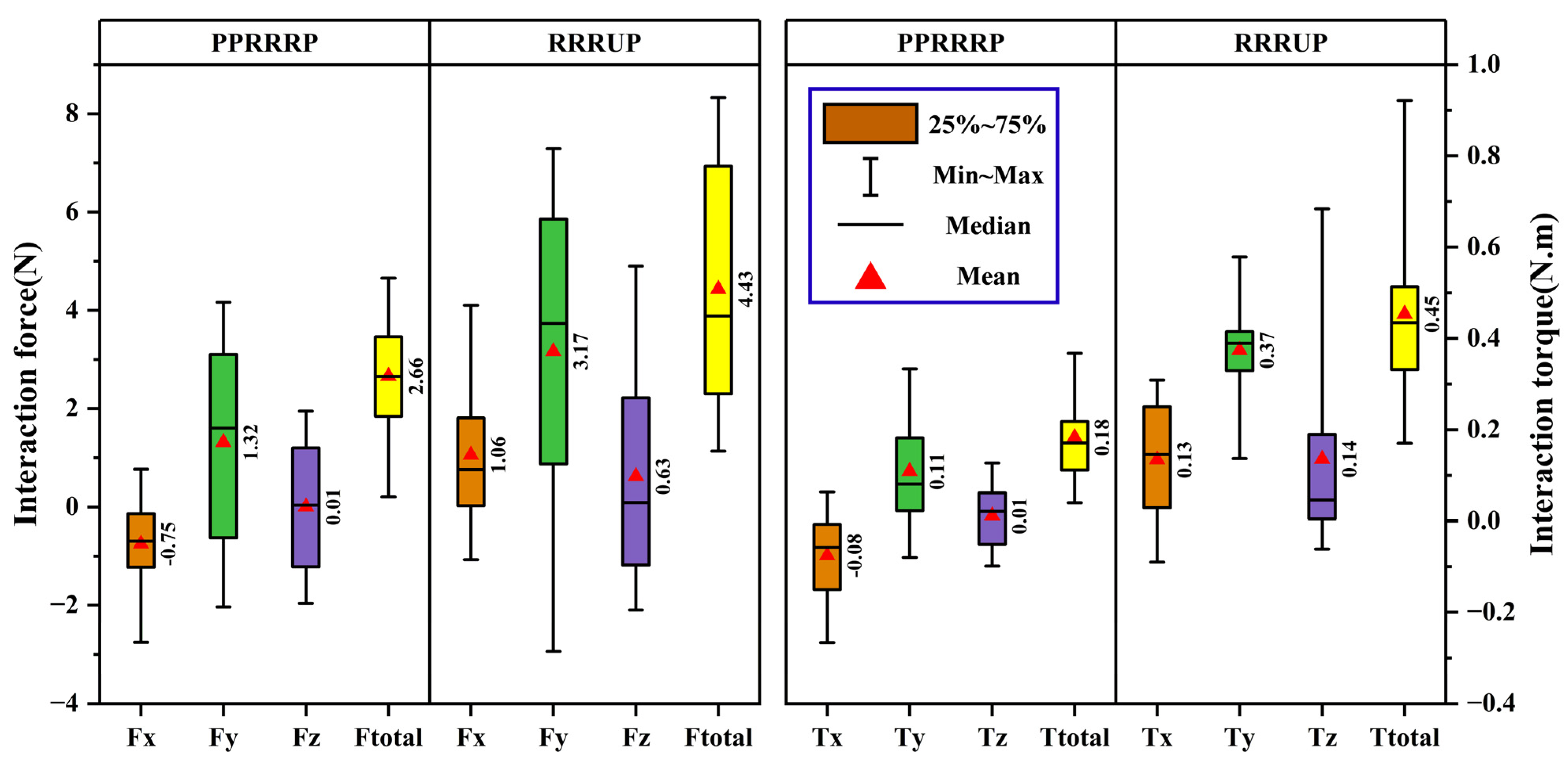
4.3. Compatibility
4.4. Description of the Prototype Shoulder Robot
- Passive joint integration: A kinematically constrained shoulder system with multiple passive joints enhances compatibility, enabling natural interaction during rehabilitation.
- Gravity compensation: A passive mechanism nullifies gravitational joint torques, reducing actuator loads and user exertion while improving comfort.
4.5. Experimental Procedure for Compatibility Analysis
5. Analysis and Results
5.1. Dexterity Analysis
5.2. Manipulability Ellipsoid Analysis
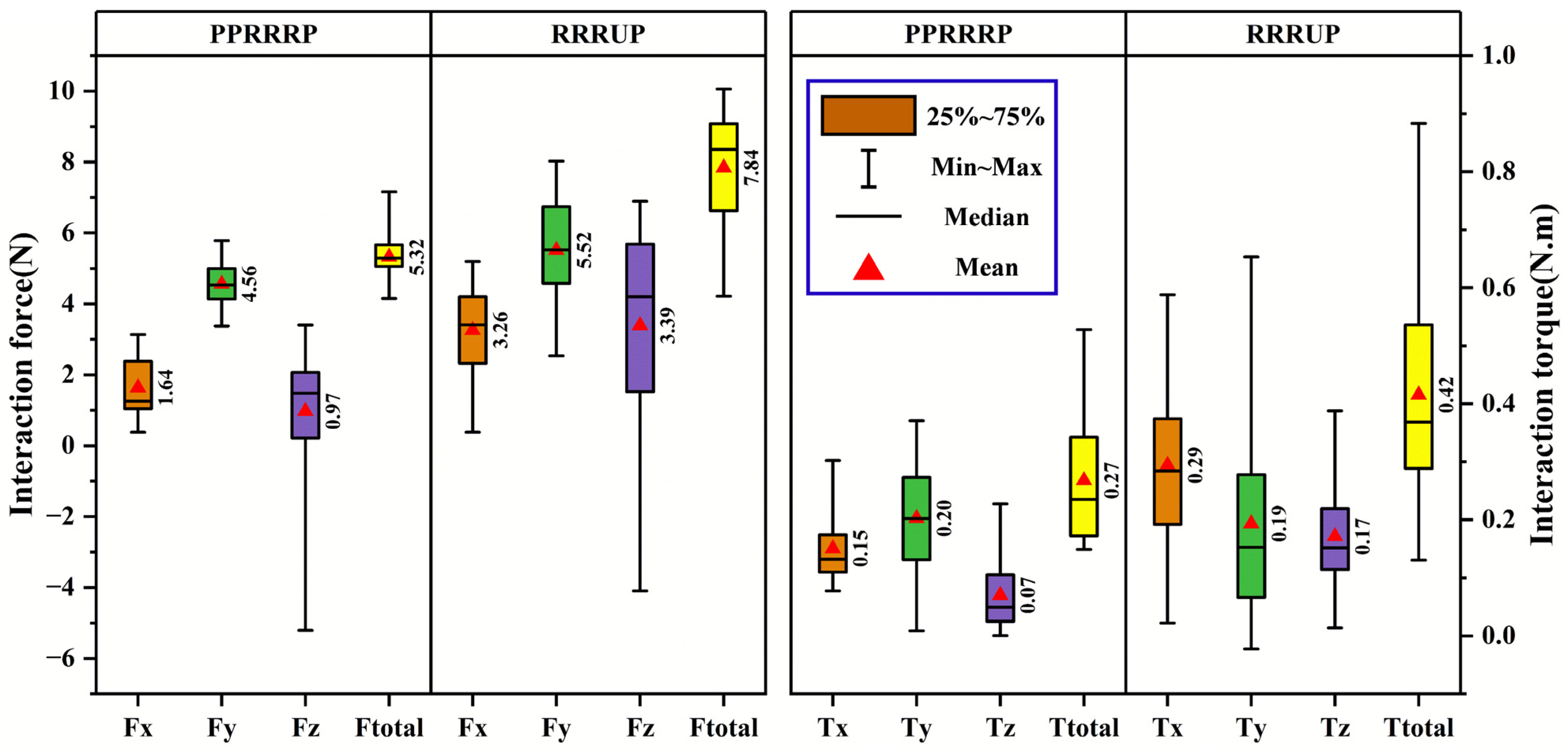
5.3. Comparative Analysis of Compatibility
6. Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- 1.
- PPRRRP configuration
- 2.
- RRRUP configuration
References
- Ito, D.; Fukuda, M.; Hosoi, Y.; Hirose, R.; Teramae, T.; Kamimoto, T.; Yamada, Y.; Tsuji, T.; Noda, T.; Kawakami, M. Optimizing shoulder elevation assist rate in exoskeletal rehabilitation based on muscular activity indices: A clinical feasibility study. BMC Neurol. 2024, 24, 144. [Google Scholar] [CrossRef] [PubMed]
- Mousley, J.J.; Gill, S.D.; Page, R.S. Rehabilitation for total shoulder replacement: An Australian perspective. ANZ J. Surg. 2023, 93, 1471–1473. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.F.; Lohre, R.; Elhassan, B.T. Muscular retraining and rehabilitation after shoulder muscle tendon transfer. Phys. Med. Rehabil. Clin. N. Am. 2023, 34, 481–488. [Google Scholar] [CrossRef] [PubMed]
- Ryul, L.J.; Min, C.Y. Robot-assisted orthopedic surgeries around shoulder joint: Where we are? Biomed. Eng. Lett. 2023, 13, 553–559. [Google Scholar] [CrossRef]
- Zeldin, E.R.; Boyette, D.M.; Norbury, J.W. Shoulder pain after influenza vaccine administration. Am. J. Phys. Med. Rehabil. 2023, 102, e141–e143. [Google Scholar] [CrossRef]
- Chao, Z.T.; Guo, H.R. Reliability and validity of quick disabilities of the arm, shoulder, and hand questionnaire in Taiwan. Arch. Phys. Med. Rehabil. 2023, 104, e49. [Google Scholar] [CrossRef]
- Laura, L.; Cheryl, H.; Kolber, M.J.; McClure, P. Application of the staged approach for rehabilitation classification system and associated improvements in patient-reported outcomes following rehabilitation for shoulder pain. Phys. Ther. 2023, 104, pzae029. [Google Scholar]
- Miyauchi, H.; Iwasaki, W.; Kaneko, S.; Nihei, Y.; Sawano, Y.; Takahashi, K.; Takahashi, N. Comparison between radial pressure wave therapy and stretching on shoulder range of motion of horizontal flexion and internal rotation. Sci. Res. Phys. Ther. 2023, 14, 14_41–14_46. [Google Scholar]
- Hussain, S.; Xie, S.Q.; Jamwal, P.K.; Parsons, J. An intrinsically compliant robotic orthosis for treadmill training. Med. Eng. Phys. 2012, 34, 1448–1453. [Google Scholar] [CrossRef]
- Wu, M.; Hornby, T.G.; Landry, J.M.; Roth, H.; Schmit, B.D. A cable-driven locomotor training system for restoration of gait in human SCI. Gait Posture 2011, 33, 256–260. [Google Scholar] [CrossRef]
- Stegall, P.; Winfree, K.; Zanotto, D.; Agrawal, S.K. Rehabilitation exoskeleton design: Exploring the effect of the anterior lunge degree of freedom. IEEE Trans. Robot. 2013, 29, 825–830. [Google Scholar] [CrossRef]
- Ren, Y.; Kang, S.H.; Park, H.-S.; Wu, Y.-N.; Zhang, L.-Q. Developing a multi-joint upper limb exoskeleton robot for diagnosis, therapy, and outcome evaluation in neurorehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 21, 490–499. [Google Scholar] [CrossRef] [PubMed]
- Kooij, V.D. LIMPACT: A hydraulically powered self-aligning upper limb exoskeleton. IEEE/ASME Trans. Mechatron. 2015, 20, 2285–2298. [Google Scholar]
- Park, H.S.; Ren, Y.; Zhang, L.Q. IntelliArm: An exoskeleton for diagnosis and treatment of patients with neurological impairments. In Proceedings of the 2008 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008; pp. 109–114. [Google Scholar]
- Al-Halimi, R.; Moussa, M. Performing complex tasks by users with upper-extremity disability using a 6-dof robotic arm: A study. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 686–693. [Google Scholar] [CrossRef] [PubMed]
- Florian, G.; Georgios, N.; Alireza, G. Compensation or restoration: Closed-loop feedback of movement quality for assisted reach-to-grasp exercises with a multi-joint arm exoskeleton. Front. Neurosci. 2016, 10, 280. [Google Scholar]
- Mishra, S.; Narayan, J.; Nikum, A.K.; Singh, R. Design and modeling of a novel exoskeleton suit for load-bearing augmentation. In Revolutions in Product Design for Healthcare; Springer: Singapore, 2022. [Google Scholar]
- Jarrasse, N.; Morel, G. Connecting a human limb to an exoskeleton. IEEE Trans. Robot. 2013, 28, 697–709. [Google Scholar] [CrossRef]
- Li, J.F.; Zhang, Z.Q.; Tao, C.J.; Ji, R. A number synthesis method of the self-adapting upper-limb rehabilitation exoskeletons. Int. J. Adv. Robot. Syst. 2017, 14, 172988141771079. [Google Scholar] [CrossRef]
- Jianfeng, L.; Shicai, L.; LeiYu, Z.; Chunjing, T.; Run, J. Position solution and kinematic interference analysis of a novel parallel hip -assistive mechanism. Mech. Mach. Theory 2018, 120, 265–287. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, M.; Li, J.; Cao, Q. A Modified kinematic model of shoulder complex based on vicon motion capturing system: Generalized GH joint with floating centre. Sensors 2020, 20, 3713. [Google Scholar] [CrossRef]
- Klopcar, N.; Lenarcic, J. Bilateral and unilateral shoulder girdle kinematics during humeral elevation. Int. J. Clin. Biomech. 2006, 21, 20–26. [Google Scholar] [CrossRef]
- Newkirk, J.T.; Tomšič, M.; Crowell, C.R.; Villano, M.A.; Stanišić, M.M. Measurement and quantification of the human shoulder girdle motion. Appl. Bionics Biomech. 2013, 10, 159–173. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C.; Dong, M.; Cao, Q. A kinematic model of the shoulder complex obtained from a wearable detection system. Appl. Sci. 2020, 10, 3696. [Google Scholar] [CrossRef]
- Nef, T.; Guidali, M.; Riener, R. ARMin III—Arm therapy exoskeleton with an ergonomic shoulder actuation. Appl. Bionics Biomech. 2009, 6, 127–142. [Google Scholar] [CrossRef]
- Calabrò, R.S.; Russo, M.; Naro, A.; Milardi, D.; Balletta, T.; Leo, A.; Filoni, S.; Bramanti, P. Who may benefit from armeo power treatment? a neurophysiological approach to predict neurorehabilitation outcomes. PMR J. Inj. Funct. Rehabil. 2016, 8, 971–978. [Google Scholar] [CrossRef]
- Salisbury, J.K.; Craig, J.J. Articulated hands: Force control and kinematic issues. Int. J. Robot. Res. 1982, 1, 4–17. [Google Scholar] [CrossRef]
- Yoshikawa, T. Manipulability of robotic mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Klamroth-Marganska, V.; Blanco, J.; Campen, K.; Curt, A.; Dietz, V.; Ettlin, T.; Felder, M.; Fellinghauer, B.; Guidali, M.; Kollmar, A.; et al. Three-dimensional, task-specific robot therapy of the arm after stroke: A multicentre, parallel-group randomised trial. Lancet Neurol. 2014, 13, 159–166. [Google Scholar] [CrossRef]
- Xie, B.Y.; Zhao, J. Directional manipulability constrained by the condition number. J. Mech. Eng. 2010, 23, 8–15. [Google Scholar] [CrossRef]
- Li, J.; Cao, Q.; Dong, M.; Zhang, C. Compatibility evaluation of a 4-DOF ergonomic exoskeleton for upper limb rehabilitation. Mech. Mach. Theory 2020, 156, 104146. [Google Scholar] [CrossRef]
- Niu, L.; Guo, S.; Song, M.; Wu, Y.; Qu, H. Design and Analysis of a Novel Shoulder Exoskeleton Based on a Parallel Mechanism. Chin. J. Mech. Eng. 2023, 36, 65. [Google Scholar] [CrossRef]
- Cempini, M.; De Rossi, S.M.M.; Lenzi, T.; Vitiello, N.; Carrozza, M.C. Self-alignment mechanisms for assistive wearable robots: A kinetostatic compatibility method. IEEE Trans. Robot. 2013, 29, 236–250. [Google Scholar] [CrossRef]
- Li, J.; Cao, Q.; Zhang, C.; Tao, C.; Ji, R. Position solution of a novel four-DOFs self-aligning exoskeleton mechanism for upper limb rehabilitation. Mech. Mach. Theory 2019, 141, 14–39. [Google Scholar] [CrossRef]
- GB/T 10000-1988; National Standard of the People’s Republic of China: Chinese Adult Human Dimensions. Standardization Administration of the People’s Republic of China: Beijing, China, 1988.
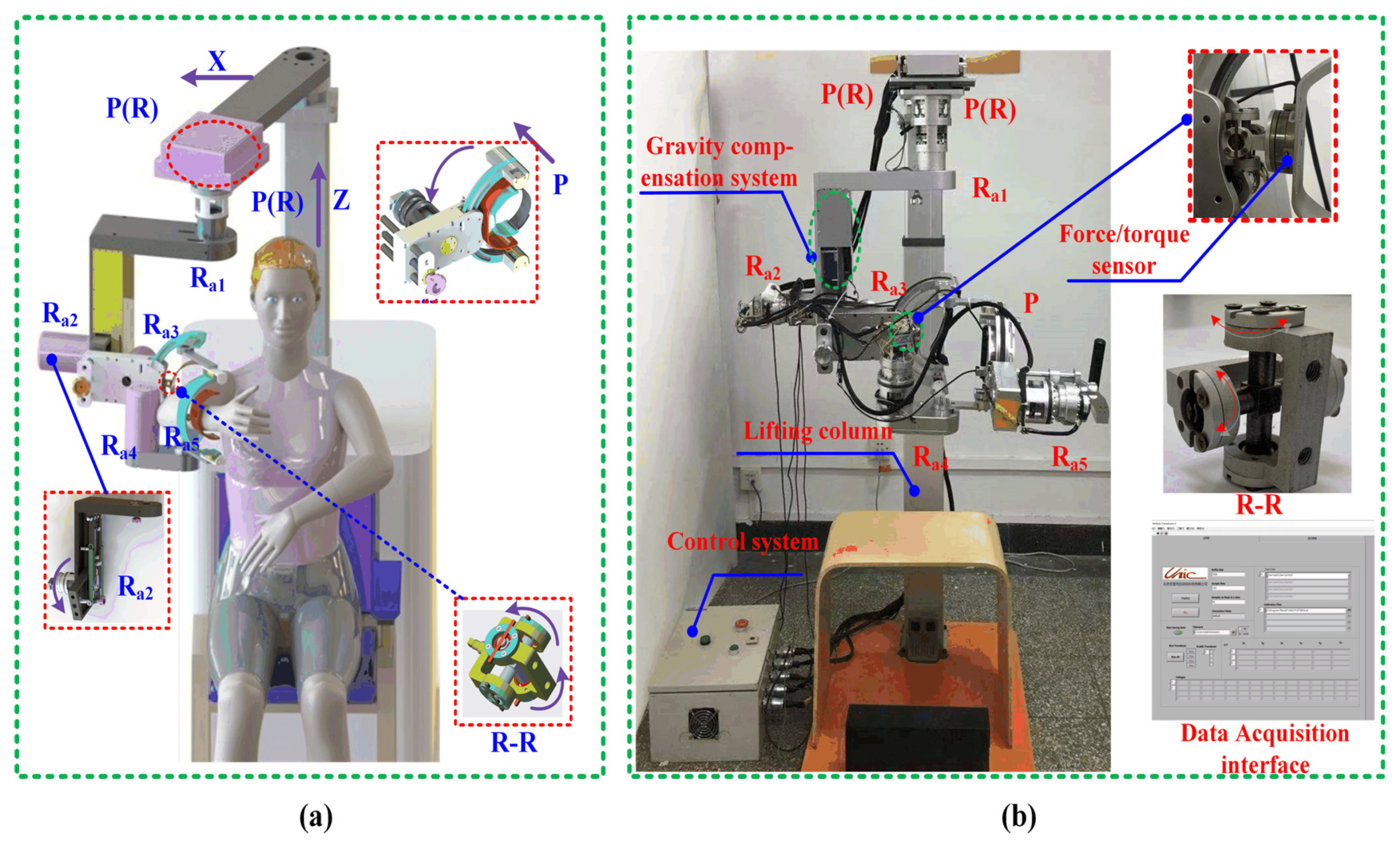
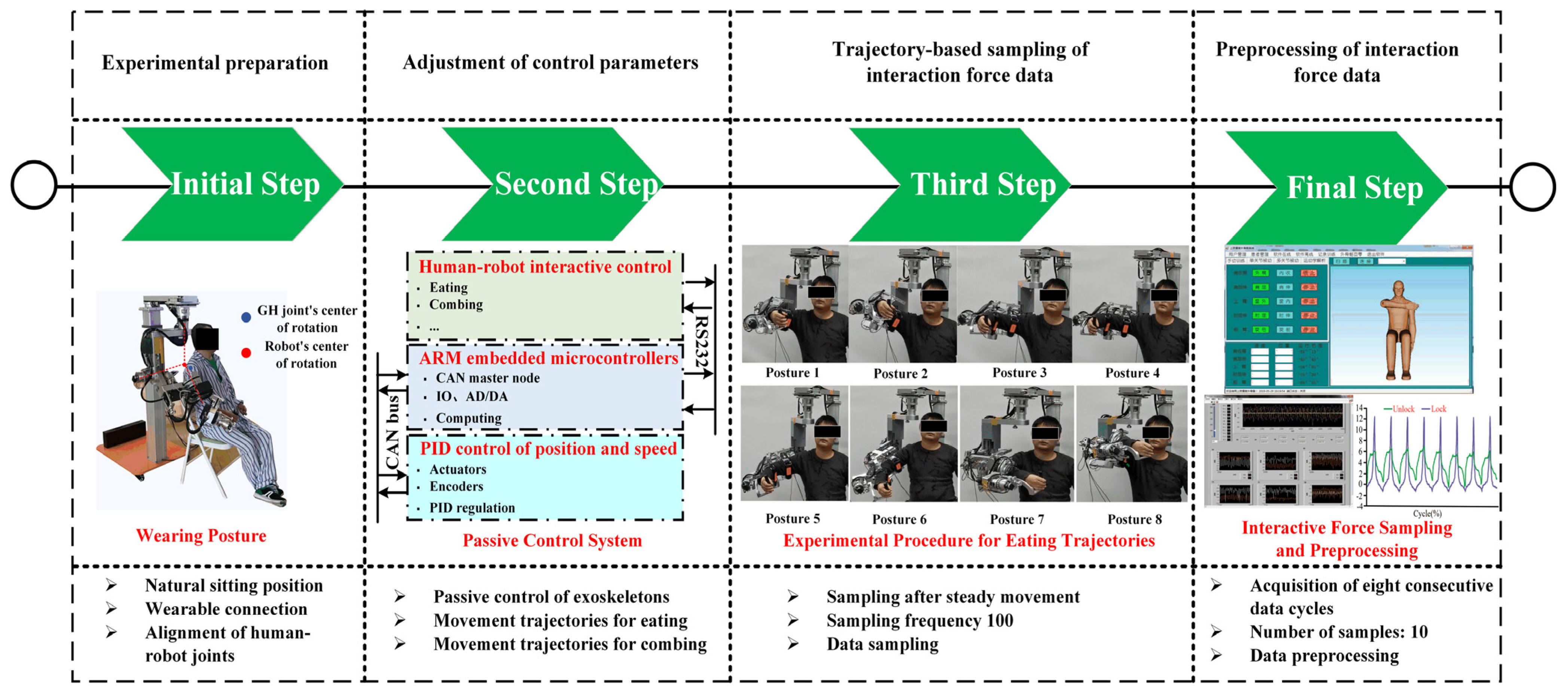
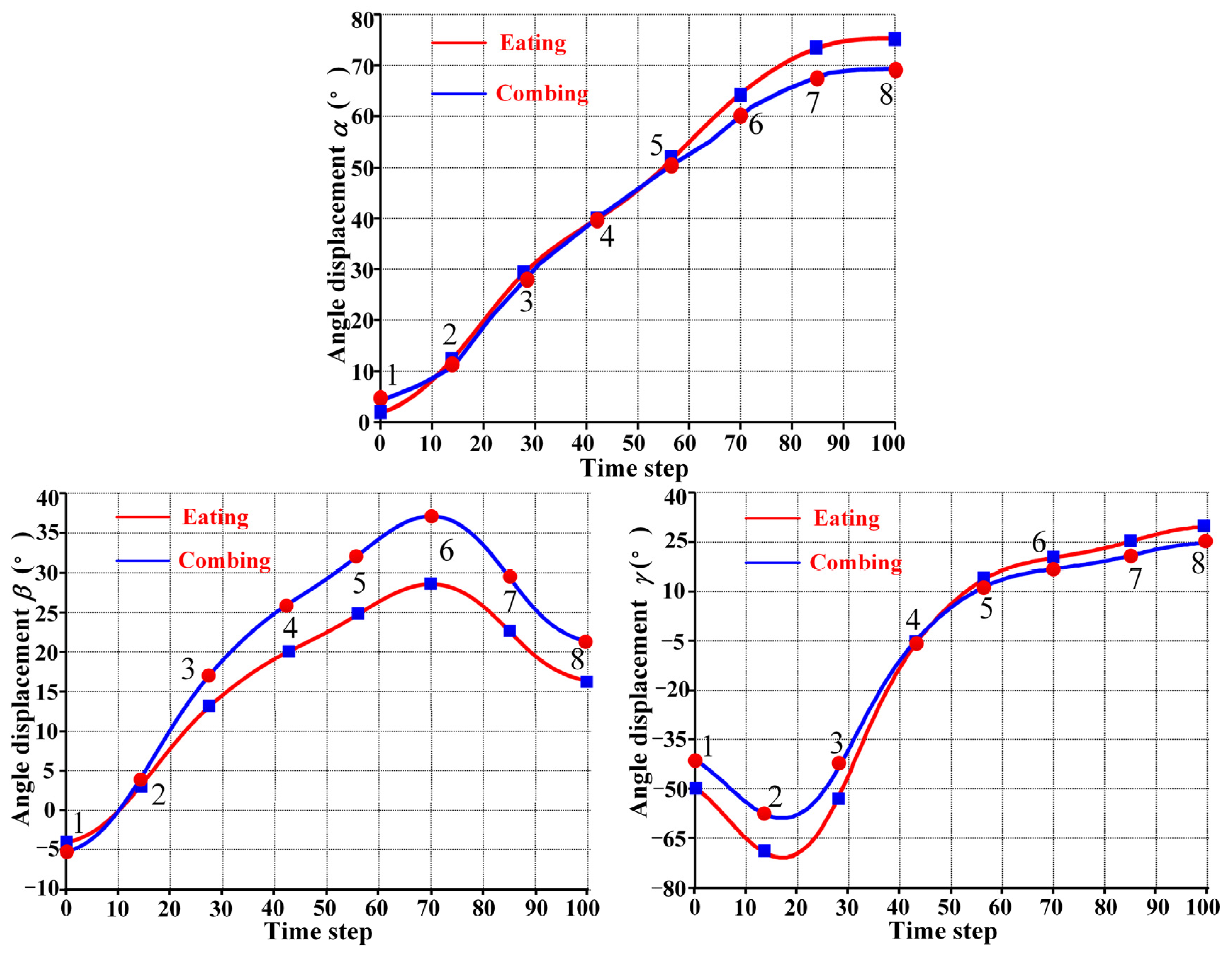

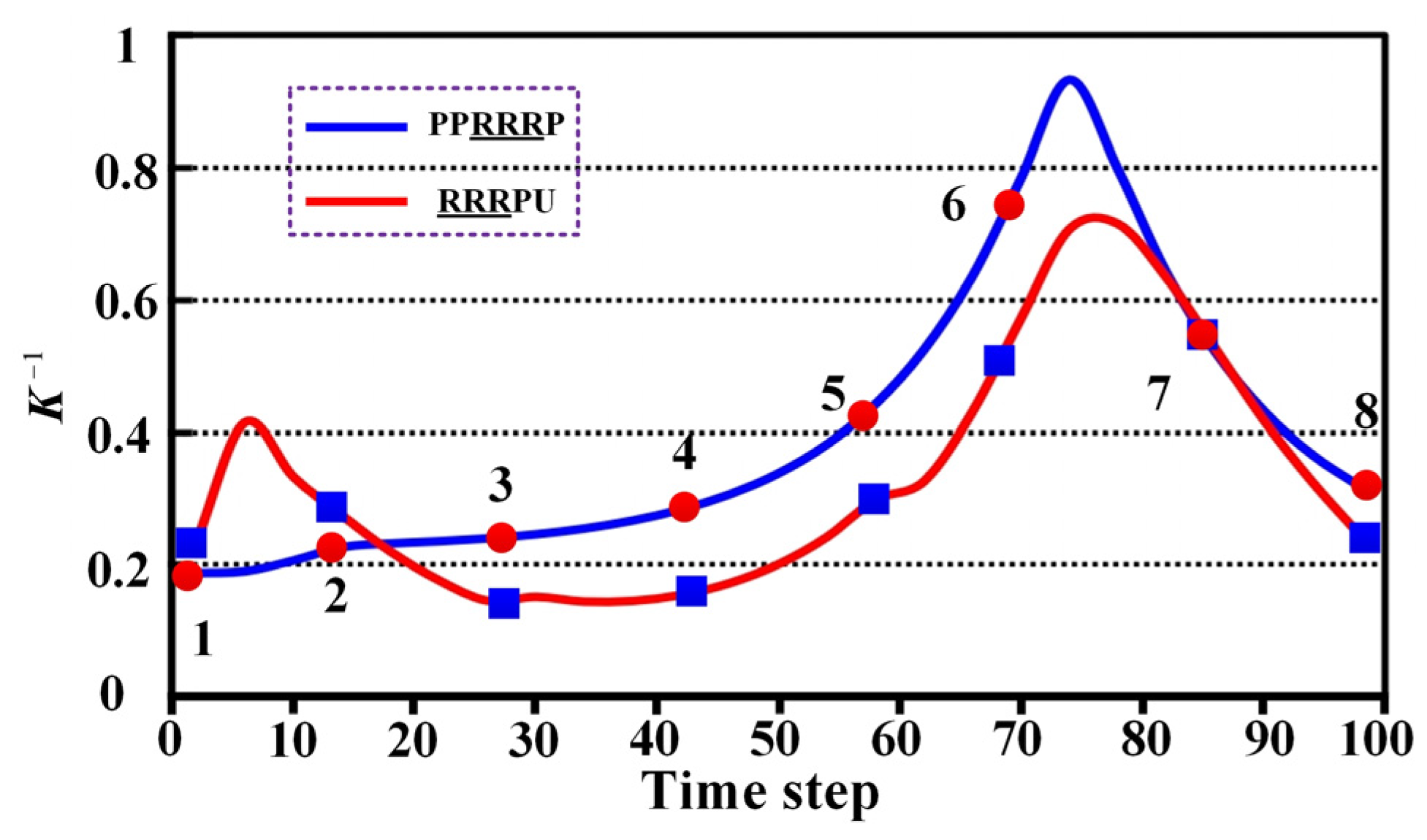
| Amount of Active Joints | Amount of Passive Joints | Configurations of Sub-Chains |
|---|---|---|
| 3 | 3 | 3Ra3R, 3Ra3P, 3Ra2P1R, 3Ra2R1P |
| 3 | 2 | 3Ra1P1U, 3Ra1R1U, 3Ra1P1C, 3Ra1R1C |
| 3 | 1 | 3Ra1S |
| Torque Sensor | Data Acquisition | ||
|---|---|---|---|
| Specification | Details | Specification | Details |
| Model | Mini45-SI-145-5 | Model | ATI Net F/T DAQ System |
| Measurement Range | Fx,Fy (± 145N); Fz (±290 N); Tx,Ty,Tz (±5 Nm) | Sampling Rate | 7000 samples/second per channel |
| Uncertainty | ±0.5% of full scale | Uncertainty | ±0.01% of reading |
| Bandwidth | 1000 Hz | Resolution | 16-bit |
| Resolution | 0.01 N; 0.001 Nm | Input Range | ±10 V |
| Nonlinearity | <±0.2% of full scale | Communication Interface | Ethernet, USB, Serial |
| Name | l1 | l2 | l3 | l4 | l5 | l6 | l7 | l8 | l9 | l10 | l11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Numeric (mm) | 40 | 100 | 100 | 400 | 300 | 260 | 400 | 400 | 280 | 120 | 254 |
| Name | l12 | l13 | l14 | l15 | l16 | l17 | l18 | l19 | x0 | y0 | z0 |
| Numeric (mm) | 400 | 300 | 260 | 400 | 400 | 160 | 80 | 254 | 156 | 136 | 36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Q.; Shan, W.; Liu, Y.; Yuan, Y. Enhancing Human–Robot Compatibility in Shoulder Exoskeletons: Passive Joint Optimization of PPRRRP vs. RRRUP Configurations. Biomimetics 2025, 10, 795. https://doi.org/10.3390/biomimetics10120795
Cao Q, Shan W, Liu Y, Yuan Y. Enhancing Human–Robot Compatibility in Shoulder Exoskeletons: Passive Joint Optimization of PPRRRP vs. RRRUP Configurations. Biomimetics. 2025; 10(12):795. https://doi.org/10.3390/biomimetics10120795
Chicago/Turabian StyleCao, Qiang, Wenhao Shan, Yue Liu, and Yongqi Yuan. 2025. "Enhancing Human–Robot Compatibility in Shoulder Exoskeletons: Passive Joint Optimization of PPRRRP vs. RRRUP Configurations" Biomimetics 10, no. 12: 795. https://doi.org/10.3390/biomimetics10120795
APA StyleCao, Q., Shan, W., Liu, Y., & Yuan, Y. (2025). Enhancing Human–Robot Compatibility in Shoulder Exoskeletons: Passive Joint Optimization of PPRRRP vs. RRRUP Configurations. Biomimetics, 10(12), 795. https://doi.org/10.3390/biomimetics10120795





