The Vibrational Signature of Alzheimer’s Disease: A Computational Approach Based on Sonification, Laser Projection, and Computer Vision Analysis
Abstract
1. Introduction
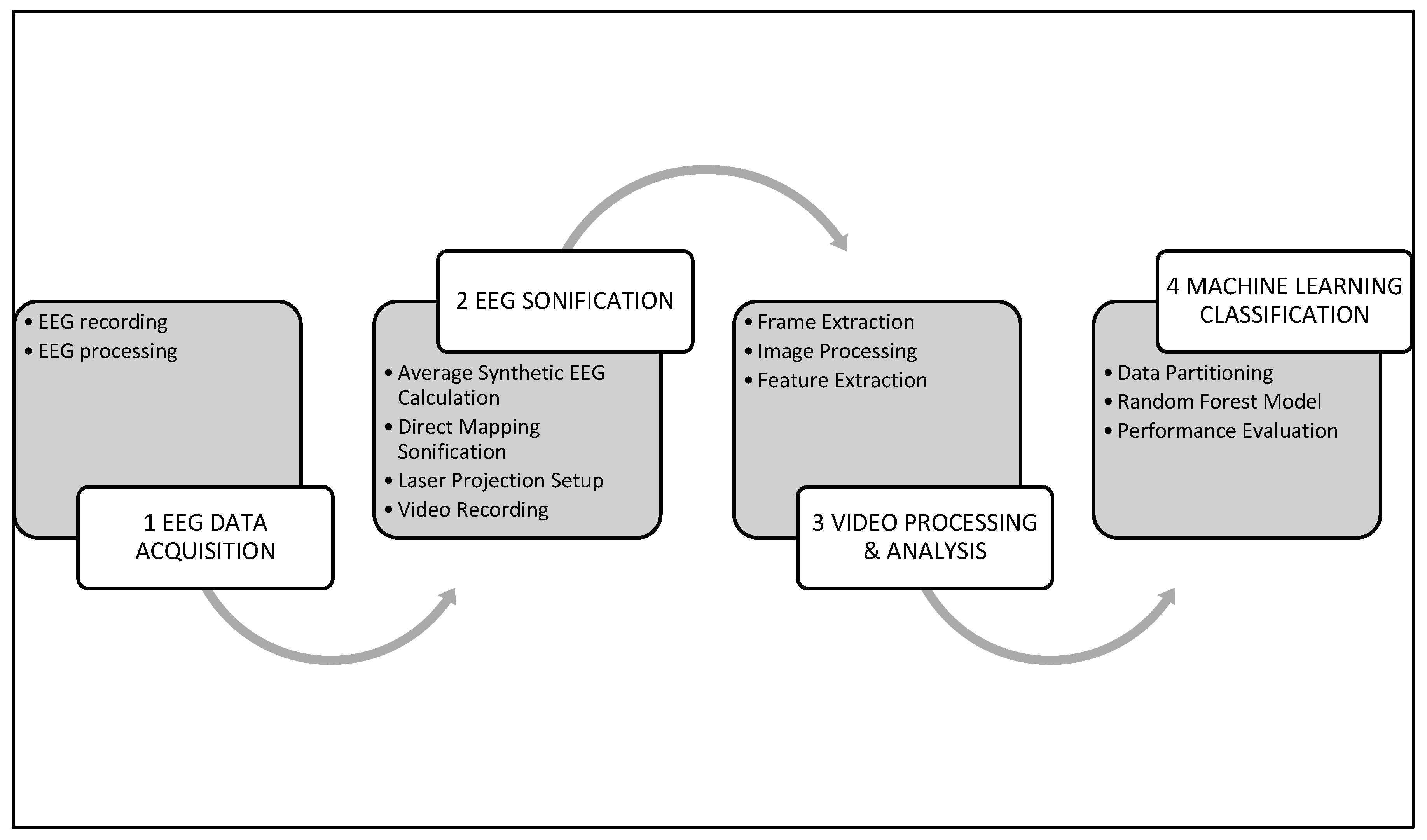
2. Materials and Methods
2.1. Subjects
Features of the Participants
2.2. Procedure
2.2.1. EEG Recording Procedures
2.2.2. EEG Processing
2.2.3. EEG Sonification
Average Synthetic EEG Calculation
Conversion of EEG Signal to Sound File
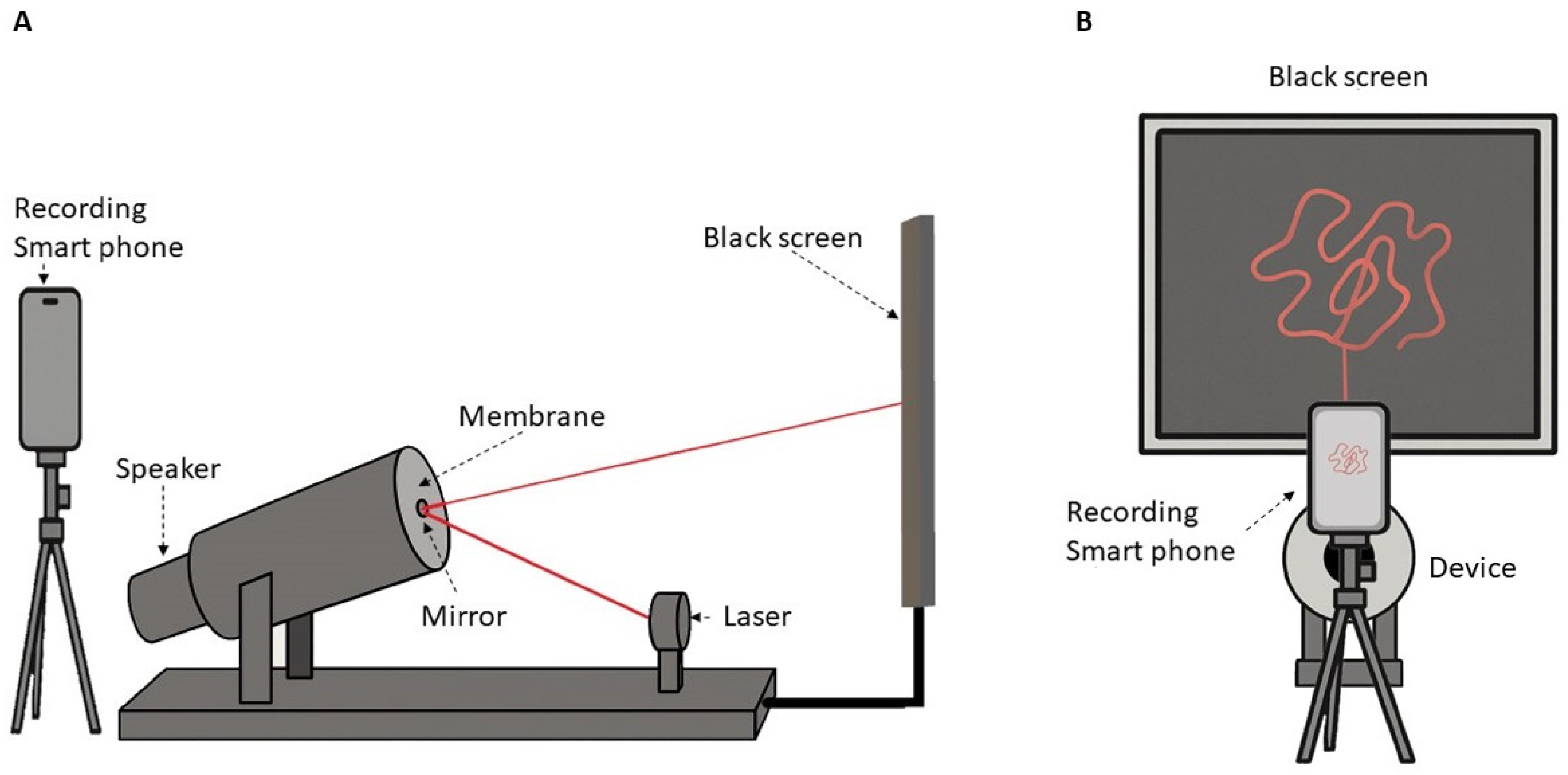
Vibration-Modulated Laser Projection and Visual Capture
2.2.4. Computational Pipeline for Video Frame Preprocessing and Visual Pattern Isolation
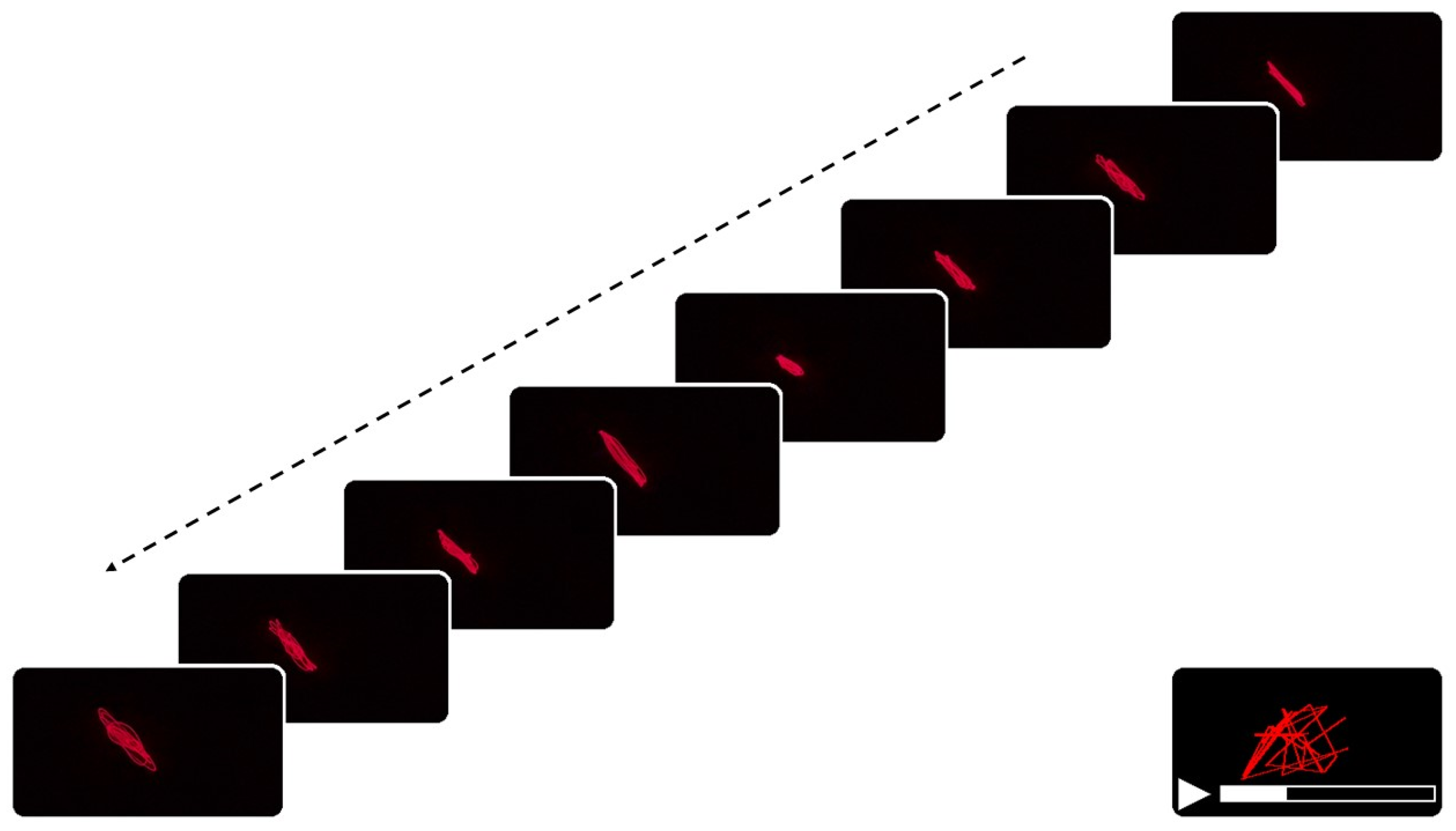
Frame Extraction
Image Binarization and Structural Optimization for Quantitative Extraction
2.2.5. Quantitative Extraction of Spatial and Dynamical Features from Laser Projection Patterns
2.2.6. Machine Learning Classification Analysis
Data Partitioning Strategy
Model Robustness Validation
Classification Algorithm and Evaluation Metrics
Performance Analysis
2.2.7. Statistical Analysis Framework
3. Results
3.1. Stratified Cross-Validation
3.2. Evaluation in Independent Test Set
3.3. Performance Metrics
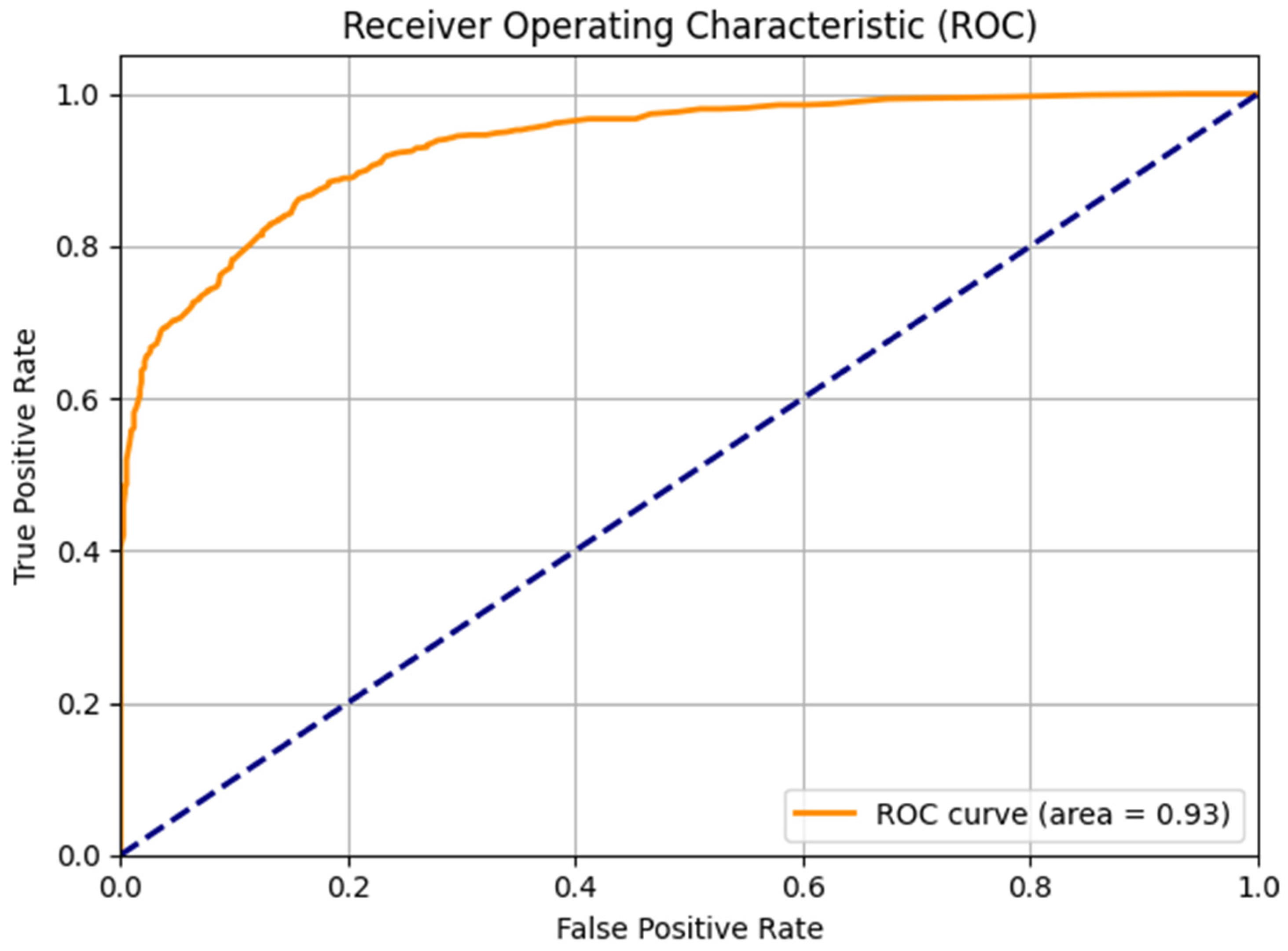
3.4. ROC Curve Analysis
Model Robustness Evaluation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Note
Abbreviations
| AD | Alzheimer’s Disease |
| EEG | Electroencephalogram |
| PET | Positron Emission Tomography |
References
- Lanctôt, K.L.; Hviid Hahn-Pedersen, J.; Eichinger, C.S.; Freeman, C.; Clark, A.; Tarazona, L.R.S.; Cummings, J. Burden of Illness in People with Alzheimer’s Disease: A Systematic Review of Epidemiology, Comorbidities and Mortality. J. Prev. Alzheimers Dis. 2024, 11, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Chimthanawala, N.M.A.; Haria, A.; Sathaye, S. Non-Invasive Biomarkers for Early Detection of Alzheimer’s Disease: A New-Age Perspective. Mol. Neurobiol. 2024, 61, 212–223. [Google Scholar] [CrossRef] [PubMed]
- Atri, A.; Dickerson, B.C.; Clevenger, C.; Karlawish, J.; Knopman, D.; Lin, P.; Norman, M.; Onyike, C.; Sano, M.; Scanland, S.; et al. The Alzheimer’s Association Clinical Practice Guideline for the Diagnostic Evaluation, Testing, Counseling, and Disclosure of Suspected Alzheimer’s Disease and Related Disorders (DETeCD-ADRD): Validated Clinical Assessment Instruments. Alzheimers Dement. 2025, 21, e14335. [Google Scholar] [CrossRef]
- Alzola, P.; Carnero, C.; Bermejo-Pareja, F.; Sánchez-Benavides, G.; Peña-Casanova, J.; Puertas-Martín, V.; Fernández-Calvo, B.; Contador, I. Neuropsychological Assessment for Early Detection and Diagnosis of Dementia: Current Knowledge and New Insights. J. Clin. Med. 2024, 13, 3442. [Google Scholar] [CrossRef]
- Oltra-Cucarella, J.; Sánchez-SanSegundo, M.; Lipnicki, D.M.; Sachdev, P.S.; Crawford, J.D.; Pérez-Vicente, J.A.; Cabello-Rodríguez, L.; Ferrer-Cascales, R. For the Alzheimer’s Disease Neuroimaging Initiative Using Base Rate of Low Scores to Identify Progression from Amnestic Mild Cognitive Impairment to Alzheimer’s Disease. J. Am. Geriatr. Soc. 2018, 66, 1360–1366. [Google Scholar] [CrossRef]
- Shaughnessy, L.W.; Weintraub, S. The Role of Neuropsychological Assessment in the Evaluation of Patients with Cognitive-behavioral Change Due to Suspected Alzheimer’s Disease and Other Causes of Cognitive Impairment and Dementia. Alzheimers Dement. 2025, 21, e14363. [Google Scholar] [CrossRef]
- Johnson, K.A.; Fox, N.C.; Sperling, R.A.; Klunk, W.E. Brain Imaging in Alzheimer Disease. Cold Spring Harb. Perspect. Med. 2012, 2, a006213. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Du, X.; Chen, W.; Zhang, T.; Xu, Z. Advances in Diagnosing Mild Cognitive Impairment and Alzheimer’s Disease Using 11C-PIB- PET/CT and Common Neuropsychological Tests. Front. Neurosci. 2023, 17, 1216215. [Google Scholar] [CrossRef]
- Rapaka, D.; Saniotis, A.; Mohammadi, K.; Galassi, F.M.; Kumar, P.O.; Bitra, V.R. From Ambiguity to Accuracy: A Review of Alzheimer’s Disease Diagnostic Errors and the Need for Non-Invasive Biomarkers. J. Neurosci. Rural Pract. 2025, 16, 14–21. [Google Scholar] [CrossRef]
- Chetty, C.A.; Bhardwaj, H.; Kumar, G.P.; Devanand, T.; Sekhar, C.S.A.; Aktürk, T.; Kiyi, I.; Yener, G.; Güntekin, B.; Joseph, J.; et al. EEG Biomarkers in Alzheimer’s and Prodromal Alzheimer’s: A Comprehensive Analysis of Spectral and Connectivity Features. Alzheimers Res. Ther. 2024, 16, 236. [Google Scholar] [CrossRef]
- Yamauchi, K.; Chaleunxay, B.; Lin, K.; Vallo, N.; Bow-Keola, J.; Read, M.; Nakahira, S.; Borrello, K.; Nakamura, R.; Cheung, A.; et al. Utility of the P300 EEG Biomarker in the Early Identification of Alzheimer’s Disease: A Systematic Review (P1-3.005). Neurology 2025, 104, 4485. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhao, Y. The Role of Quantitative EEG Biomarkers in Alzheimer’s Disease and Mild Cognitive Impairment: Applications and Insights. Front. Aging Neurosci. 2025, 17, 1522552. [Google Scholar] [CrossRef]
- Babiloni, C.; Arakaki, X.; Azami, H.; Bennys, K.; Blinowska, K.; Bonanni, L.; Bujan, A.; Carrillo, M.C.; Cichocki, A.; De Frutos-Lucas, J.; et al. Measures of Resting State EEG Rhythms for Clinical Trials in Alzheimer’s Disease: Recommendations of an Expert Panel. Alzheimers Dement. 2021, 17, 1528–1553. [Google Scholar] [CrossRef]
- Moretti, D. Individual Analysis of EEG Frequency and Band Power in Mild Alzheimer’s Disease. Clin. Neurophysiol. 2004, 115, 299–308. [Google Scholar] [CrossRef] [PubMed]
- Al-Nuaimi, A.H.; Jammeh, E.; Sun, L.; Ifeachor, E. Complexity Measures for Quantifying Changes in Electroencephalogram in Alzheimers Disease. Complexity 2022, 2018, 8915079. [Google Scholar] [CrossRef]
- Şeker, M.; Özbek, Y.; Yener, G.; Özerdem, M.S. Complexity of EEG Dynamics for Early Diagnosis of Alzheimer’s Disease Using Permutation Entropy Neuromarker. Comput. Methods Programs Biomed. 2021, 206, 106116. [Google Scholar] [CrossRef] [PubMed]
- Paitel, E.R.; Otteman, C.B.D.; Polking, M.C.; Licht, H.J.; Nielson, K.A. Functional and Effective EEG Connectivity Patterns in Alzheimer’s Disease and Mild Cognitive Impairment: A Systematic Review. Front. Aging Neurosci. 2025, 17, 1496235. [Google Scholar] [CrossRef]
- Aslan, U.; Akşahin, M.F. Detection of Alzheimer and Mild Cognitive Impairment Patients by Poincare and Entropy Methods Based on Electroencephalography Signals. Biomed. Eng. OnLine 2025, 24, 47. [Google Scholar] [CrossRef]
- Gaubert, S.; Raimondo, F.; Houot, M.; Corsi, M.-C.; Naccache, L.; Diego Sitt, J.; Hermann, B.; Oudiette, D.; Gagliardi, G.; Habert, M.-O.; et al. EEG Evidence of Compensatory Mechanisms in Preclinical Alzheimer’s Disease. Brain 2019, 142, 2096–2112. [Google Scholar] [CrossRef]
- Choi, J.; Ku, B.; Doan, D.N.T.; Park, J.; Cha, W.; Kim, J.U.; Lee, K.H. Prefrontal EEG Slowing, Synchronization, and ERP Peak Latency in Association with Predementia Stages of Alzheimer’s Disease. Front. Aging Neurosci. 2023, 15, 1131857. [Google Scholar] [CrossRef]
- Grubov, V.V.; Kuc, A.K.; Kurkin, S.A.; Andrikov, D.A.; Utyashev, N.; Maksimenko, V.A.; Karpov, O.E.; Hramov, A.E. Harnessing Long-Range Temporal Correlations for Advanced Epilepsy Classification. PRX Life 2025, 3, 013005. [Google Scholar] [CrossRef]
- Chaddad, A.; Wu, Y.; Kateb, R.; Bouridane, A. Electroencephalography Signal Processing: A Comprehensive Review and Analysis of Methods and Techniques. Sensors 2023, 23, 6434. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, Q.-Q.; Chen, H.; Hu, X.-Q.; Li, W.-G.; Bai, Y.; Han, J.-X.; Wang, Y.; Liang, Z.-H.; Chen, D.; et al. The Applied Principles of EEG Analysis Methods in Neuroscience and Clinical Neurology. Mil. Med. Res. 2023, 10, 67. [Google Scholar] [CrossRef]
- Finnis, R.; Mehmood, A.; Holle, H.; Iqbal, J. Exploring Imagined Movement for Brain–Computer Interface Control: An fNIRS and EEG Review. Brain Sci. 2025, 15, 1013. [Google Scholar] [CrossRef]
- Hermann, T.; Meinicke, P.; Ritter, H.; Müller, H.M.; Weiss, S. Sonifications for EEG Data Analysis. In Proceedings of the 2002 International Conference on Auditory Display, Kyoto, Japan, 2–5 July 2002. [Google Scholar]
- Vialatte, F.B.; Dauwels, J.; Musha, T.; Cichocki, A. Audio Representations of Multi-Channel EEG: A New Tool for Diagnosis of Brain Disorders. Am. J. Neurodegener. Dis. 2012, 1, 292–304. [Google Scholar]
- Kramer, G.; Walker, B.; Bargar, R. Sonification Report: Status of the Field and Research Agenda; International Community for Auditory Display: Lincoln, RI, USA, 1999; ISBN 978-0-9670904-0-5. [Google Scholar]
- Miranda, E.; Brouse, A. Toward Direct Brain-Computer Musical Interfaces. In Proceedings of the 2005 Conference on New Interfaces for Musical Expression, Vancouver, BC, Canada, 26–28 May 2005. [Google Scholar] [CrossRef]
- Inoue, H. Music Generation by Direct Sonification and Musification Using EEG Data. Int. J. Music Sci. Technol. Art 2023, 5, 69. [Google Scholar] [CrossRef]
- Sanyal, S.; Nag, S.; Banerjee, A.; Sengupta, R.; Ghosh, D. Music of Brain and Music on Brain: A Novel EEG Sonification Approach. Cogn. Neurodyn. 2019, 13, 13–31. [Google Scholar] [CrossRef]
- Miltiadous, A.; Tzimourta, K.D.; Afrantou, T.; Ioannidis, P.; Grigoriadis, N.; Tsalikakis, D.G.; Angelidis, P.; Tsipouras, M.G.; Glavas, E.; Giannakeas, N.; et al. A Dataset of Scalp EEG Recordings of Alzheimer’s Disease, Frontotemporal Dementia and Healthy Subjects from Routine EEG. Data 2023, 8, 95. [Google Scholar] [CrossRef]
- Buzsáki, G. Rhythms of the Brain; Oxford University Press: Oxford, UK, 2006; ISBN 978-0-19-530106-9. [Google Scholar]
- Jeong, J. EEG Dynamics in Patients with Alzheimer’s Disease. Clin. Neurophysiol. 2004, 115, 1490–1505. [Google Scholar] [CrossRef] [PubMed]
- Nunez, P.L.; Srinivasan, R. Electric Fields of the Brain: The Neurophysics of EEG, 2nd ed.; Oxford University Press: Oxford, UK, 2006; ISBN 978-0-19-986567-3. [Google Scholar]
- Chang, C.-Y.; Hsu, S.-H.; Pion-Tonachini, L.; Jung, T.-P. Evaluation of Artifact Subspace Reconstruction for Automatic Artifact Components Removal in Multi-Channel EEG Recordings. IEEE Trans. Biomed. Eng. 2020, 67, 1114–1121. [Google Scholar] [CrossRef] [PubMed]
- Bradsky, G. The OpenCV Library. Dr Dobb’s J. Softw. Tools 2000, 120, 122–125. [Google Scholar]
- Yoon, J.; Choi, M.-K. Exploring Video Frame Redundancies for Efficient Data Sampling and Annotation in Instance Segmentation. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Vancouver, BC, Canada, 17–24 June 2023; IEEE: Vancouver, BC, Canada, 2023; pp. 3308–3317. [Google Scholar]
- Bradley, D.; Roth, G. Adaptive Thresholding Using the Integral Image. J. Graph. Tools 2007, 12, 13–21. [Google Scholar] [CrossRef]
- Jamil, N.; Sembok, T.M.T.; Bakar, Z.A. Noise Removal and Enhancement of Binary Images Using Morphological Operations. In Proceedings of the 2008 International Symposium on Information Technology, Kuala Lumpur, Malaysia, 26–29 August 2008; IEEE: Kuala Lumpur, Malaysia, 2008; pp. 1–6. [Google Scholar]
- Bhutada, S.; Yashwanth, N.; Dheeraj, P.; Shekar, K. Opening and Closing in Morphological Image Processing. World J. Adv. Res. Rev. 2022, 14, 687–695. [Google Scholar] [CrossRef]
- Rama Bai, M.; Venkata Krishna, V.; SreeDevi, J. International Journal of Computer Science Issues; SoftwareFirst, Ltd.: Lenexa, KS, USA, 2010; pp. 187–190. [Google Scholar]
- Sivasakthi, S. A Study on Morphological Image Processing and Its Operations. 2018. Available online: https://www.researchgate.net/publication/354598374_A_STUDY_ON_MORPHOLOGICAL_IMAGE_PROCESSING_AND_ITS_OPERATIONS (accessed on 14 November 2025).
- Chang, J.; Gao, X.; Wang, N. Object-Oriented Building Contour Optimization Methodology for Image Classification Results via Generalized Gradient Vector Flow Snake Model. Remote Sens. 2021, 13, 2406. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Park, M.-H.; Lee, C.; Hur, J.-J.; Lee, W.-J. Prediction of Fuel Consumption and Shaft Torque Using Machine Learning and Analysis of Engine Curve Diagrams. Measurement 2025, 248, 116984. [Google Scholar] [CrossRef]
- Karim, A.; Ryu, S.; Jeong, I.C. Ensemble Learning for Biomedical Signal Classification: A High-Accuracy Framework Using Spectrograms from Percussion and Palpation. Sci. Rep. 2025, 15, 21592. [Google Scholar] [CrossRef]
- Khan, A.A.; Chaudhari, O.; Chandra, R. A Review of Ensemble Learning and Data Augmentation Models for Class Imbalanced Problems: Combination, Implementation and Evaluation. Expert Syst. Appl. 2024, 244, 122778. [Google Scholar] [CrossRef]
- Ramezan, C.A.; Warner, T.A.; Maxwell, A.E. Evaluation of Sampling and Cross-Validation Tuning Strategies for Regional-Scale Machine Learning Classification. Remote Sens. 2019, 11, 185. [Google Scholar] [CrossRef]
- Szeghalmy, S.; Fazekas, A. A Comparative Study of the Use of Stratified Cross-Validation and Distribution-Balanced Stratified Cross-Validation in Imbalanced Learning. Sensors 2023, 23, 2333. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Sirak Rakin, A.; Deliang, F. Parametric Noise Injection: Trainable Randomness to Improve Deep Neural Network Robustness Against Adversarial Attack. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 588–597. [Google Scholar]
- Zur, R.M.; Jiang, Y.; Pesce, L.L.; Drukker, K. Noise Injection for Training Artificial Neural Networks: A Comparison with Weight Decay and Early Stopping. Med. Phys. 2009, 36, 4810–4818. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A Systematic Analysis of Performance Measures for Classification Tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The Advantages of the Matthews Correlation Coefficient (MCC) over F1 Score and Accuracy in Binary Classification Evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Fiscon, G.; Weitschek, E.; Cialini, A.; Felici, G.; Bertolazzi, P.; De Salvo, S.; Bramanti, A.; Bramanti, P.; De Cola, M.C. Combining EEG Signal Processing with Supervised Methods for Alzheimer’s Patients Classification. BMC Med. Inform. Decis. Mak. 2018, 18, 35. [Google Scholar] [CrossRef]
- AlSharabi, K.; Salamah, Y.B.; Aljalal, M.; Abdurraqeeb, A.M.; Alturki, F.A. EEG-Based Clinical Decision Support System for Alzheimer’s Disorders Diagnosis Using EMD and Deep Learning Techniques. Front. Hum. Neurosci. 2023, 17, 1190203. [Google Scholar] [CrossRef] [PubMed]
- Vicchietti, M.L.; Ramos, F.M.; Betting, L.E.; Campanharo, A.S.L.O. Computational Methods of EEG Signals Analysis for Alzheimer’s Disease Classification. Sci. Rep. 2023, 13, 8184. [Google Scholar] [CrossRef]
- Wu, D.; Li, C.-Y.; Yao, D.-Z. Scale-Free Music of the Brain. PLoS ONE 2009, 4, e5915. [Google Scholar] [CrossRef]
- Buzi, G.; Fornari, C.; Perinelli, A.; Mazza, V. Functional Connectivity Changes in Mild Cognitive Impairment: A Meta-Analysis of M/EEG Studies. Clin. Neurophysiol. 2023, 156, 183–195. [Google Scholar] [CrossRef]
- Fischer, M.H.F.; Zibrandtsen, I.C.; Høgh, P.; Musaeus, C.S. Systematic Review of EEG Coherence in Alzheimer’s Disease. J. Alzheimers Dis. 2023, 91, 1261–1272. [Google Scholar] [CrossRef]
- Lizio, R.; Vecchio, F.; Frisoni, G.B.; Ferri, R.; Rodriguez, G.; Babiloni, C. Electroencephalographic Rhythms in Alzheimer’s Disease. Int. J. Alzheimers Dis. 2011, 2011, 927573. [Google Scholar] [CrossRef]
- Stylianou, O.; Racz, F.S.; Kim, K.; Kaposzta, Z.; Czoch, A.; Yabluchanskiy, A.; Eke, A.; Mukli, P. Multifractal Functional Connectivity Analysis of Electroencephalogram Reveals Reorganization of Brain Networks in a Visual Pattern Recognition Paradigm. Front. Hum. Neurosci. 2021, 15, 740225. [Google Scholar] [CrossRef]
- Taylor, R.P.; Spehar, B. Fractal Fluency: An Intimate Relationship Between the Brain and Processing of Fractal Stimuli. In The Fractal Geometry of the Brain; Di Ieva, A., Ed.; Springer Series in Computational Neuroscience; Springer: New York, NY, USA, 2016; pp. 485–496. ISBN 978-1-4939-3993-0. [Google Scholar]
- Stam, C.J. Nonlinear Dynamical Analysis of EEG and MEG: Review of an Emerging Field. Clin. Neurophysiol. 2005, 116, 2266–2301. [Google Scholar] [CrossRef]
- Abásolo, D.; Hornero, R.; Espino, P.; Álvarez, D.; Poza, J. Entropy Analysis of the EEG Background Activity in Alzheimer’s Disease Patients. Physiol. Meas. 2006, 27, 241–253. [Google Scholar] [CrossRef]
- Abásolo, D.; Hornero, R.; Gómez, C.; García, M.; López, M. Analysis of EEG Background Activity in Alzheimer’s Disease Patients with Lempel–Ziv Complexity and Central Tendency Measure. Med. Eng. Phys. 2006, 28, 315–322. [Google Scholar] [CrossRef]
- Koenig, T.; Prichep, L.; Dierks, T.; Hubl, D.; Wahlund, L.O.; John, E.R.; Jelic, V. Decreased EEG Synchronization in Alzheimer’s Disease and Mild Cognitive Impairment. Neurobiol. Aging 2005, 26, 165–171. [Google Scholar] [CrossRef] [PubMed]
- Varoquaux, G. Cross-Validation Failure: Small Sample Sizes Lead to Large Error Bars. NeuroImage 2018, 180, 68–77. [Google Scholar] [CrossRef] [PubMed]
- Poldrack, R.A.; Baker, C.I.; Durnez, J.; Gorgolewski, K.J.; Matthews, P.M.; Munafò, M.R.; Nichols, T.E.; Poline, J.-B.; Vul, E.; Yarkoni, T. Scanning the Horizon: Towards Transparent and Reproducible Neuroimaging Research. Nat. Rev. Neurosci. 2017, 18, 115–126. [Google Scholar] [CrossRef]
- Yarkoni, T. The Generalizability Crisis. Behav. Brain Sci. 2022, 45, e1. [Google Scholar] [CrossRef] [PubMed]

| Category | Parameter | Value |
|---|---|---|
| Random Forest Classifier | n_estimators | 100 |
| random_state | 42 | |
| max_depth | None | |
| criterion | ‘gini’ | |
| min_samples_split | 2 | |
| min_samples_leaf | 1 | |
| bootstrap | True | |
| max_features | ‘sqrt’ |
| Metrics | Mean | Standard Deviation | Confidence Interval (95%) |
|---|---|---|---|
| Accuracy | 0.8400 | 0.0120 | 0.8280–0.8520 |
| Real Class | Predicted Class | Total | |
|---|---|---|---|
| Control | Alzheimer | ||
| Control | 645 | 108 | 753 |
| Alzheimer’s | 122 | 637 | 759 |
| Total | 767 | 745 | 1512 |
| Class | Accuracy | Recall | F1-Score | Specificity |
|---|---|---|---|---|
| Control | 0.84 | 0.86 | 0.85 | 0.84 |
| Alzheimer’s | 0.86 | 0.84 | 0.85 | 0.86 |
| Average | 0.85 | 0.85 | 0.85 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Elvira, R.; Oltra-Cucarella, J.; Agudo Juan, M.; Polo-Ferrero, L.; Juárez-Vela, R.; Bosch-Bayard, J.; Quintana Díaz, M.; de la Cruz, J.; Salgado Ruíz, A. The Vibrational Signature of Alzheimer’s Disease: A Computational Approach Based on Sonification, Laser Projection, and Computer Vision Analysis. Biomimetics 2025, 10, 792. https://doi.org/10.3390/biomimetics10120792
Pérez-Elvira R, Oltra-Cucarella J, Agudo Juan M, Polo-Ferrero L, Juárez-Vela R, Bosch-Bayard J, Quintana Díaz M, de la Cruz J, Salgado Ruíz A. The Vibrational Signature of Alzheimer’s Disease: A Computational Approach Based on Sonification, Laser Projection, and Computer Vision Analysis. Biomimetics. 2025; 10(12):792. https://doi.org/10.3390/biomimetics10120792
Chicago/Turabian StylePérez-Elvira, Rubén, Javier Oltra-Cucarella, María Agudo Juan, Luis Polo-Ferrero, Raúl Juárez-Vela, Jorge Bosch-Bayard, Manuel Quintana Díaz, Jorge de la Cruz, and Alfonso Salgado Ruíz. 2025. "The Vibrational Signature of Alzheimer’s Disease: A Computational Approach Based on Sonification, Laser Projection, and Computer Vision Analysis" Biomimetics 10, no. 12: 792. https://doi.org/10.3390/biomimetics10120792
APA StylePérez-Elvira, R., Oltra-Cucarella, J., Agudo Juan, M., Polo-Ferrero, L., Juárez-Vela, R., Bosch-Bayard, J., Quintana Díaz, M., de la Cruz, J., & Salgado Ruíz, A. (2025). The Vibrational Signature of Alzheimer’s Disease: A Computational Approach Based on Sonification, Laser Projection, and Computer Vision Analysis. Biomimetics, 10(12), 792. https://doi.org/10.3390/biomimetics10120792









