Research on the Optimization of Uncertain Multi-Stage Production Integrated Decisions Based on an Improved Grey Wolf Optimizer
Abstract
1. Introduction
- Development of an Integrated Multi-stage Production Optimization Model: The MsPIO model systematically unifies a two-stage sampling inspection mechanism—designed for defect-rate estimation and criterion-based decision-making—with multi-process, multi-component production planning. This integrated framework provides a coherent structure for addressing uncertainty and variability in complex production systems, aligning with systemic approaches to operational decision-making.
- Design of an Enhanced Metaheuristic Solution Strategy: An Improved Grey Wolf Optimizer (IGWO) is introduced, incorporating Latin hypercube sampling to ensure uniform initialization of the population. The algorithm further integrates an evolutionary factor mechanism based on simulated binary crossover (SBX) and three leadership-guided parents (Alpha, Beta, Delta) to strengthen global exploration. A greedy mutation-based opposition learning strategy is applied to the lowest-performing quarter of the population, enabling effective local refinement and accelerating convergence toward high-quality solutions.
- Comprehensive Experimental Validation and Sensitivity Analysis: Extensive experiments validate the model’s effectiveness and robustness under both cost-minimization and profit-maximization objectives. Results demonstrate that the proposed IGWO-based method not only identifies cost-optimal strategies across multiple single-stage production configurations but also achieves a total profit of 43,800 in a multi-stage production scenario. Through systematic sensitivity analysis, the study elucidates how key parameters—such as estimated defect rates (modulated by confidence levels), finished product price fluctuations, and replacement losses—influence optimal decisions. These insights offer valuable guidance for intelligent production management in environments shaped by mass customization and operational uncertainty.
2. Related Work
3. Methodologies
3.1. Model Assumptions
- It is assumed that the qualification of each sample is independent.
- It is assumed that the enterprise’s quality inspection system is accurate and error-free.
- It is assumed that all finished products entering the market will be successfully sold.
3.2. Two-Stage Sampling Inspection Model
3.2.1. Simulation of Product Sequence
3.2.2. Stage Two: Acceptance Test
- 1.
- If the number of defectives in the first-stage sample is , the lot is immediately rejected.
- 2.
- If , the lot moves to the second stage for further inspection.
3.2.3. Stage One: Quick Rejection Test
- 1.
- If , the lot is accepted.
- 2.
- If , the lot is rejected.
3.2.4. Estimation and Confidence Prediction Under Uncertain Defective Rate
- Lower confidence bound pL
- Upper confidence bound pU
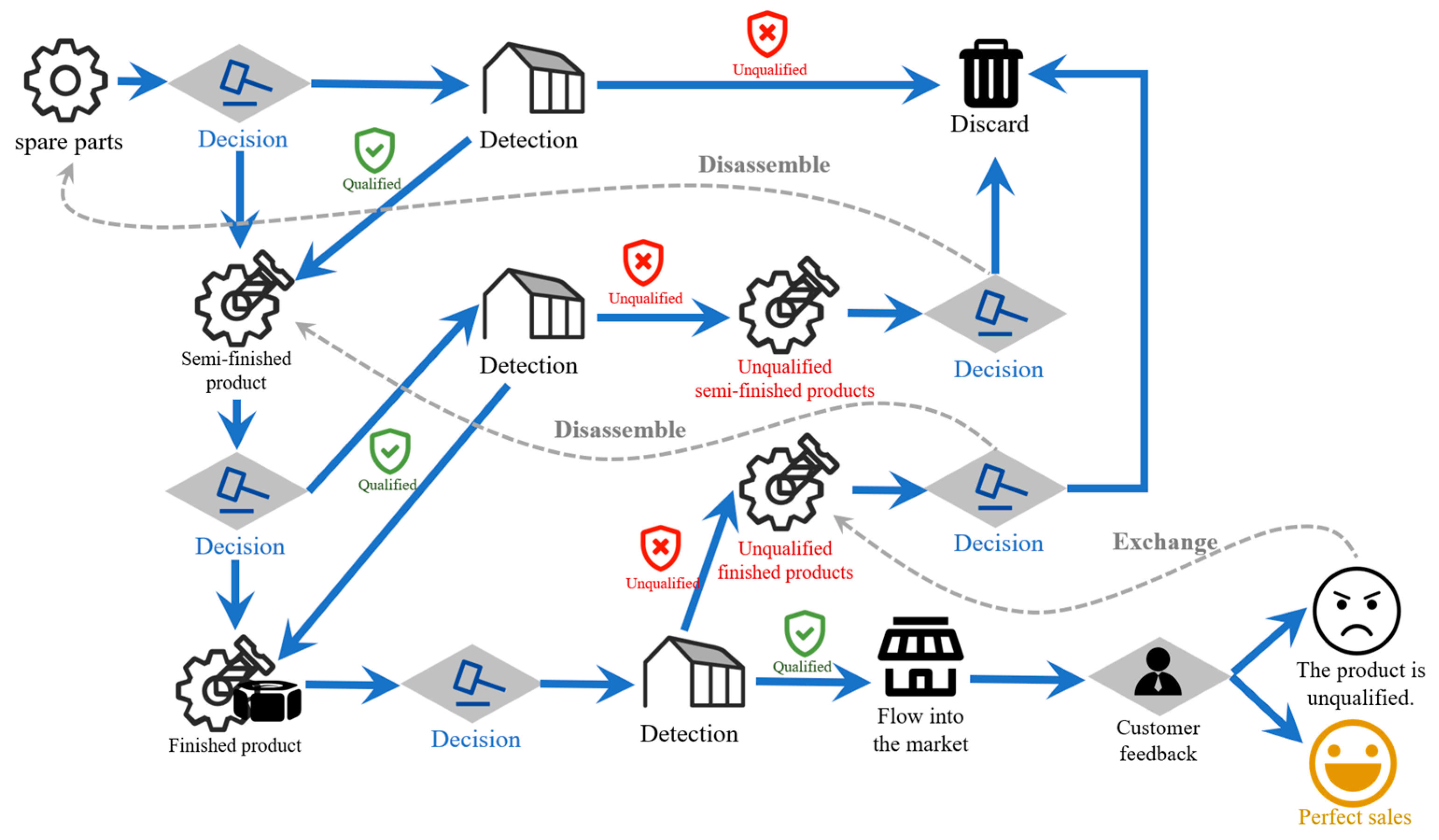
3.3. Decision-Making Model for Multiple Processes and Multiple Parts
3.3.1. Decision Variables
3.3.2. Objective Function
- Spare Parts Inspection Stage
- Finished Product Inspection Stage
- Defective Finished Product Disassembly Stage
- Replacement Stage for Sold Defective Products
- Semi-Finished Product Inspection Stage
- Defective Semi-Finished Product Disassembly Stage
- Total Cost
3.4. Improved Grey Wolf Optimizer (IGWO)
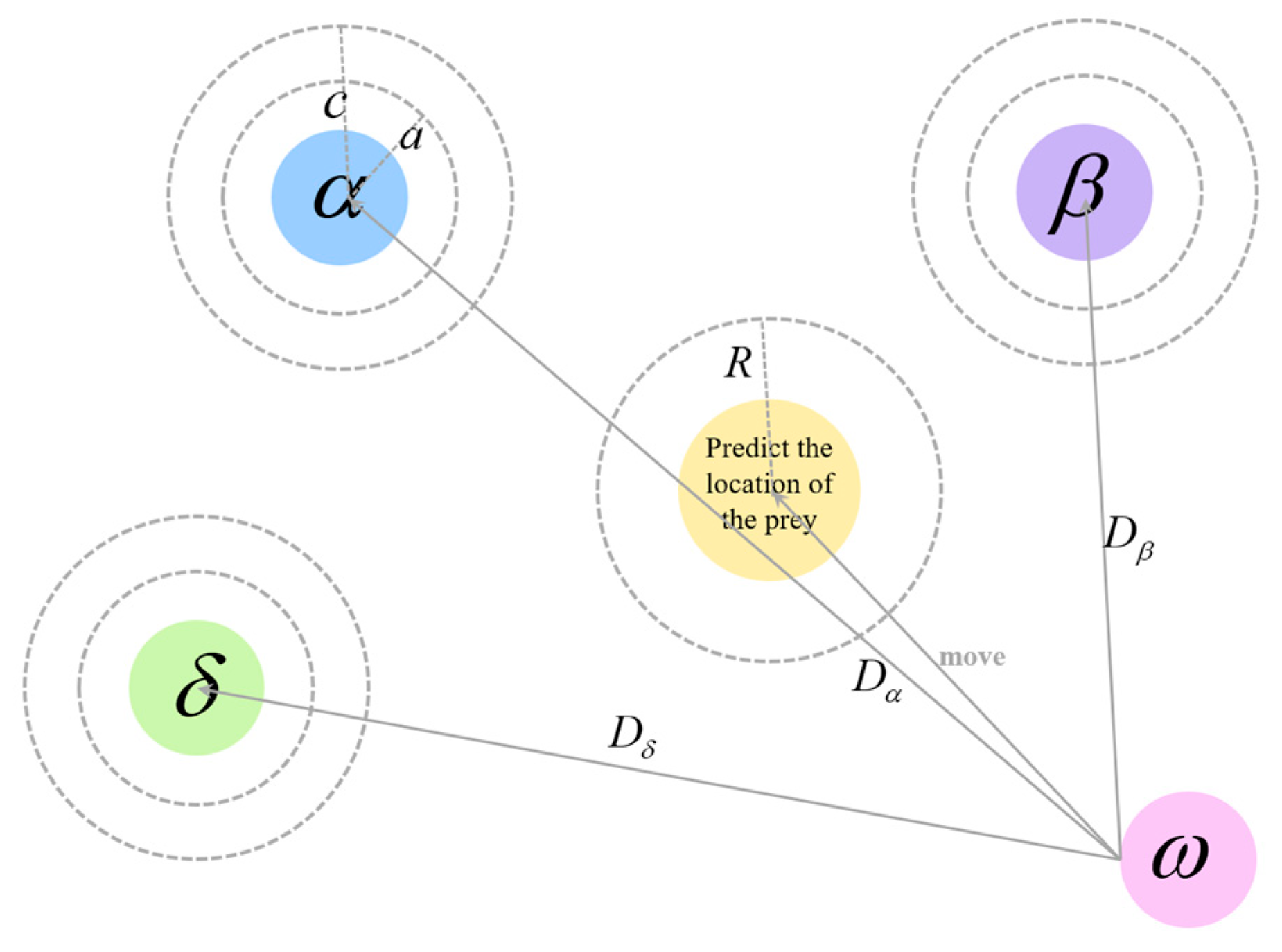
3.4.1. GWO Original Position Update Steps
- 1.
- Encircling the Prey
- 2.
- Hunting the Prey
- 3.
- Besieging the Prey
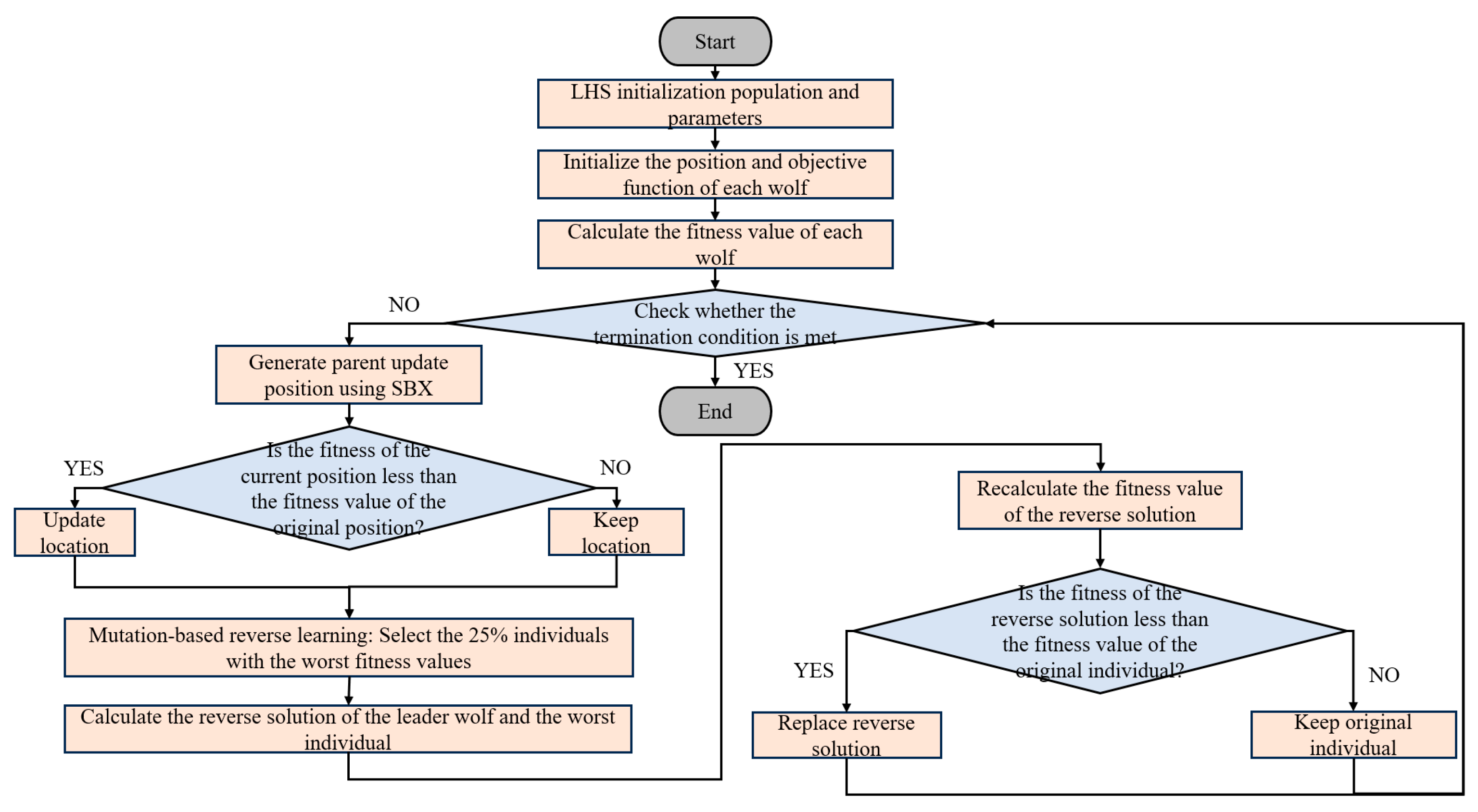
3.4.2. Improvement Strategies
- 1.
- LHS Initialization
- 2.
- Evolutionary Parent Roundup
- 3.
- Mutation Reverse Learning Strategy
4. Experimental Analysis
4.1. A Case Study
4.2. Inspection Results
4.3. Experimental Results Analysis
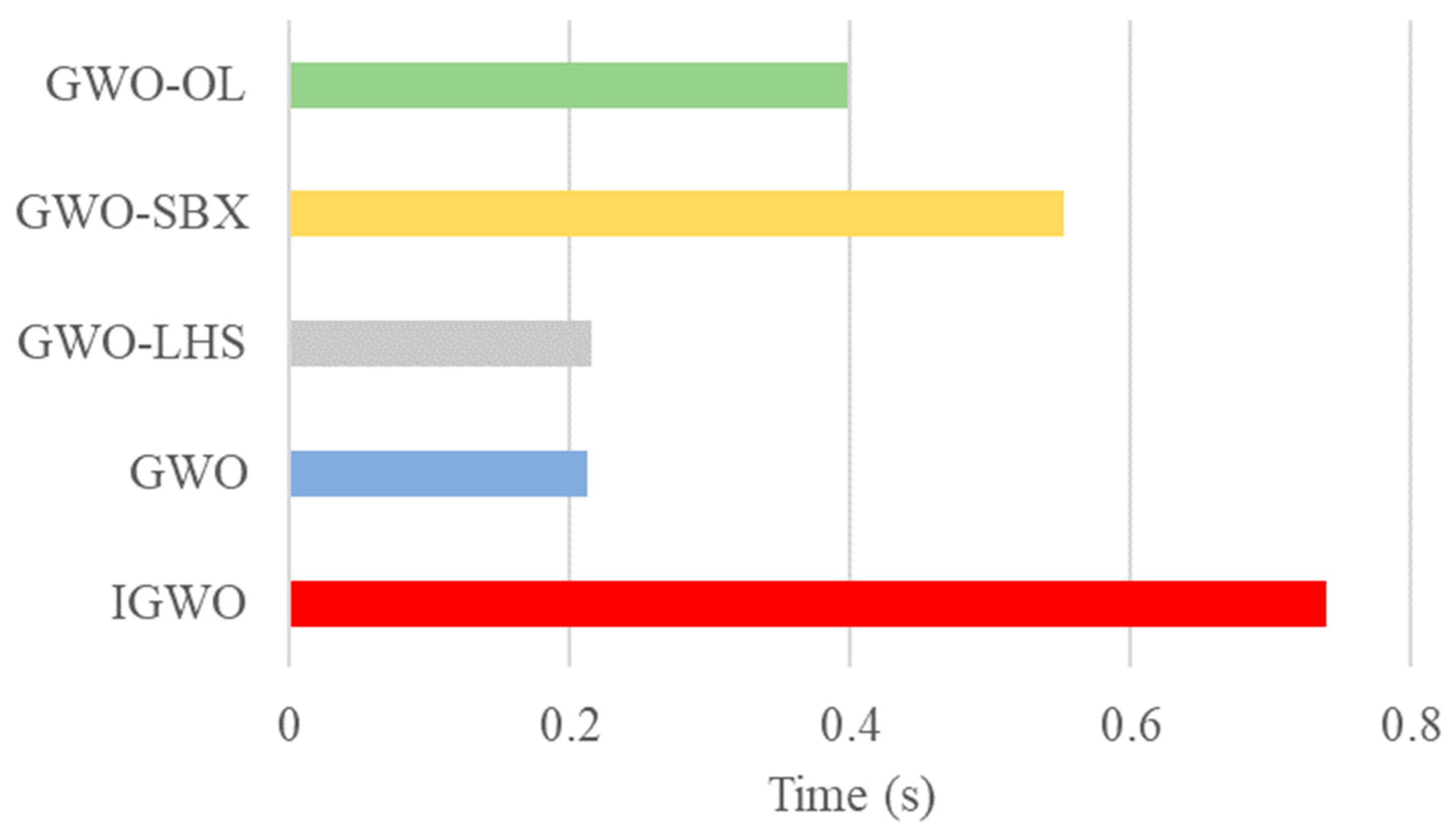
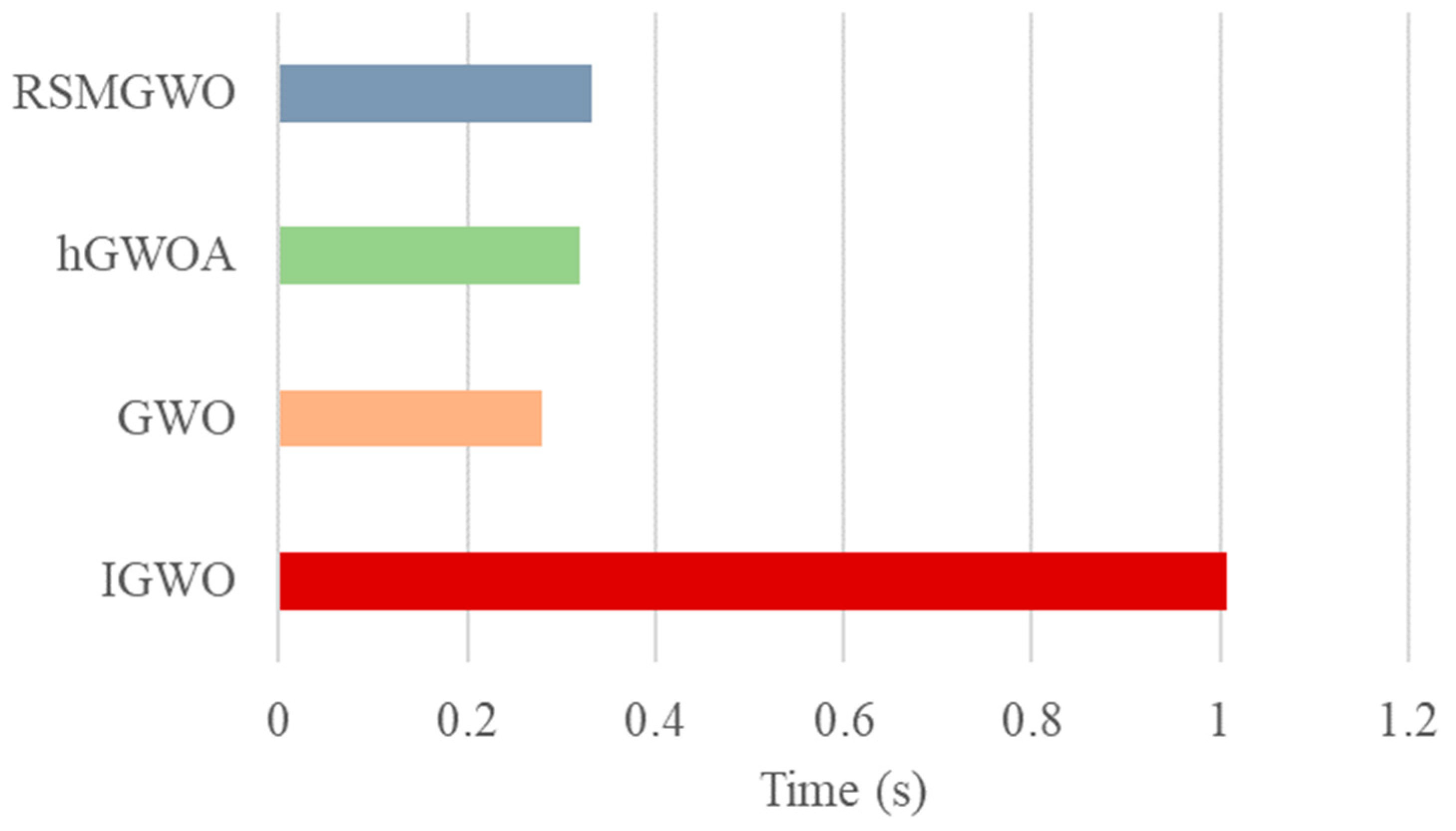
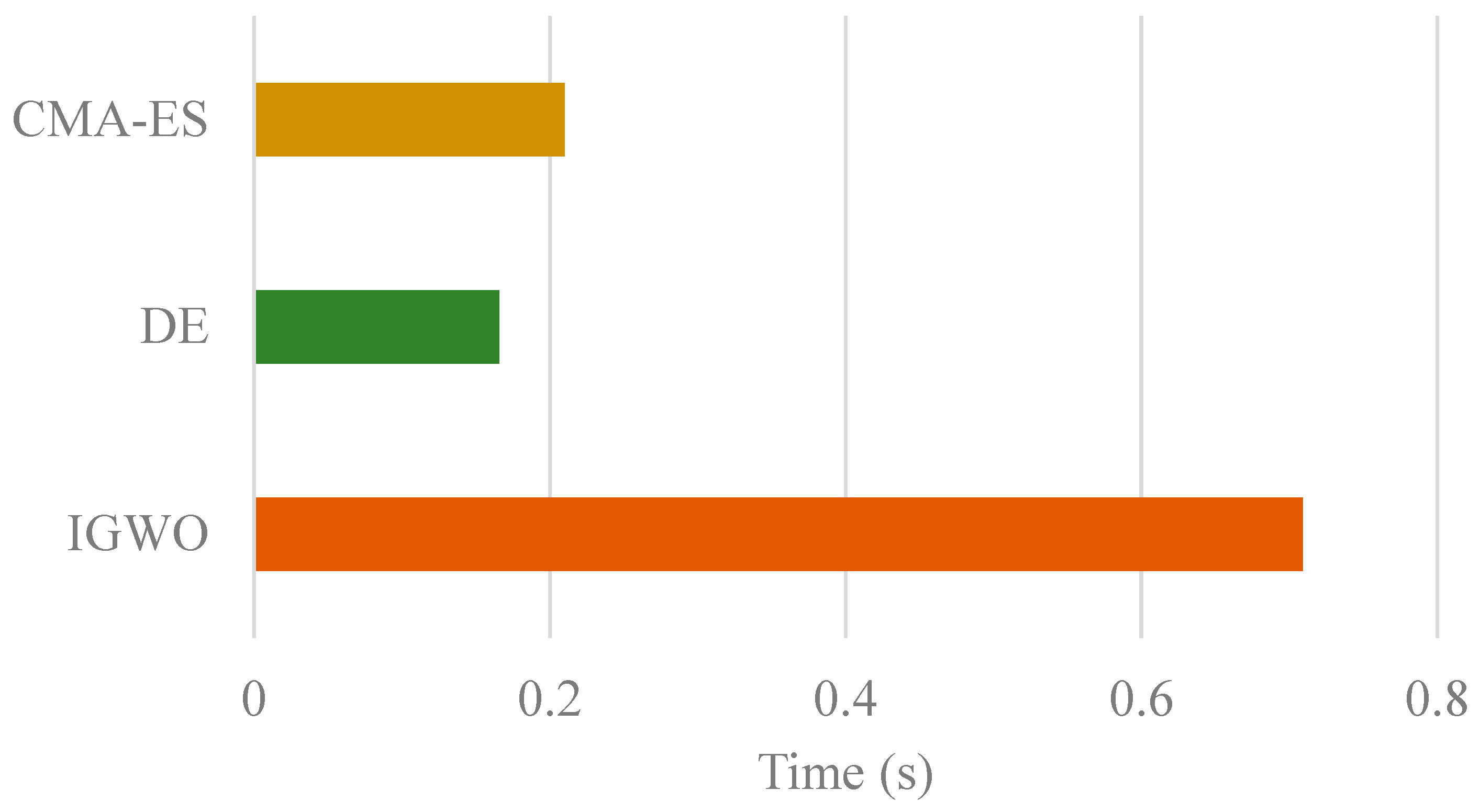
4.3.1. Performance Testing
4.3.2. Single-Process Test
4.3.3. Multi-Process Test
4.3.4. Confidence Level Analysis
4.3.5. Finished Product Selling Price Analysis
4.3.6. Exchange Loss Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Scenario | Spare Part 1 | Spare Part 2 | Finished Product | Defective Finished Product | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Defect Rate | Purchase Unit Price | Inspection Cost | Defect Rate | Purchase Unit Price | Inspection Cost | Defect Rate | Assembly Cost | Inspection Cost | Market Price | Exchange Cost | Disassembly Cost | |
| 1 | 10% | 4 | 2 | 10% | 18 | 3 | 10% | 6 | 3 | 56 | 6 | 5 |
| 2 | 20% | 4 | 2 | 20% | 18 | 3 | 20% | 6 | 3 | 56 | 6 | 5 |
| 3 | 10% | 4 | 2 | 10% | 18 | 3 | 10% | 6 | 3 | 56 | 30 | 5 |
| 4 | 20% | 4 | 1 | 20% | 18 | 1 | 20% | 6 | 2 | 56 | 30 | 5 |
| 5 | 10% | 4 | 8 | 20% | 18 | 1 | 10% | 6 | 2 | 56 | 10 | 5 |
| 6 | 5% | 4 | 2 | 5% | 18 | 3 | 5% | 6 | 3 | 56 | 10 | 40 |
| Spare Part | Defect Rate | Purchase Unit Price | Inspection Cost | Semi-Finished Product | Defect Rate | Assembly Cost | Inspection Cost | Disassembly Cost |
|---|---|---|---|---|---|---|---|---|
| 1 | 10% | 2 | 1 | 1 | 10% | 8 | 4 | 6 |
| 2 | 10% | 8 | 1 | 2 | 10% | 8 | 4 | 6 |
| 3 | 10% | 12 | 2 | 3 | 10% | 8 | 4 | 6 |
| 4 | 10% | 2 | 1 | |||||
| 5 | 10% | 8 | 1 | Finished product | 10% | 8 | 6 | 10 |
| 6 | 10% | 12 | 2 | |||||
| 7 | 10% | 8 | 1 | Market price | Exchange cost | |||
| 8 | 10% | 12 | 2 | Finished product | 200 | 40 | ||
References
- Schwab, K. The Fourth Industrial Revolution: What it means, how to respond1. In Handbook of Research on Strategic Leadership in the Fourth Industrial Revolution; Edward Elgar Publishing: Cheltenham, UK, 2024; pp. 29–34. [Google Scholar]
- Soori, M.; Jough, F.K.G.; Dastres, R.; Arezoo, B. AI-based decision support systems in Industry 4.0, A review. J. Econ. Technol. 2024, 4, 206–225. [Google Scholar] [CrossRef]
- Ghasemi, A.; Farajzadeh, F.; Heavey, C.; Fowler, J.; Papadopoulos, C.T. Simulation optimization applied to production scheduling in the era of industry 4.0: A review and future roadmap. J. Ind. Inf. Integr. 2024, 39, 100599. [Google Scholar] [CrossRef]
- Missbauer, H.; Uzsoy, R. Optimization models of production planning problems. In Planning Production and Inventories in the Extended Enterprise: A State of the Art Handbook; Springer Science & Business Media: Berlin/Heidelberg, Germany; Volume 1, pp. 437–507.
- Tseng, M.L.; Ha, H.M.; Tran, T.P.T.; Bui, T.D.; Chen, C.C.; Lin, C.W. Building a data-driven circular supply chain hierarchical structure: Resource recovery implementation drives circular business strategy. Bus. Strategy Environ. 2022, 31, 2082–2106. [Google Scholar] [CrossRef]
- Khan, S.A.R.; Yu, Z.; Farooq, K. Green capabilities, green purchasing, and triple bottom line performance: Leading toward environmental sustainability. Bus. Strategy Environ. 2023, 32, 2022–2034. [Google Scholar] [CrossRef]
- Tambe, P.P.; Kulkarni, M.S. A reliability based integrated model of maintenance planning with quality control and production decision for improving operational performance. Reliab. Eng. Syst. Saf. 2022, 226, 108681. [Google Scholar] [CrossRef]
- Alvandi, S.; Li, W.; Kara, S. An integrated simulation optimisation decision support tool for multi-product production systems. Mod. Appl. Sci. 2025, 11, 56. [Google Scholar] [CrossRef]
- Meng, Y.; Yang, Y.; Chung, H.; Lee, P.H.; Shao, C. Enhancing sustainability and energy efficiency in smart factories: A review. Sustainability 2018, 10, 4779. [Google Scholar] [CrossRef]
- Lee, J.; Chua, P.C.; Liu, B.; Moon, S.K.; Lopez, M. A hybrid data-driven optimization and decision-making approach for a digital twin environment: Towards customizing production platforms. Int. J. Prod. Econ. 2025, 279, 109447. [Google Scholar] [CrossRef]
- Frank, A.G.; Dalenogare, L.S.; Ayala, N.F. Industry 4.0 technologies: Implementation patterns in manufacturing companies. Int. J. Prod. Econ. 2019, 210, 15–26. [Google Scholar] [CrossRef]
- Xu, L.D.; Xu, E.L.; Li, L. Industry 4.0: State of the art and future trends. Int. J. Prod. Res. 2018, 56, 2941–2962. [Google Scholar] [CrossRef]
- Chauhan, D.; Singh, A.P.; Chauhan, A.; Arora, R. Sustainable supply chain: An optimization and resource efficiency in additive manufacturing for automotive spare part. Sustain. Futures 2025, 9, 100563. [Google Scholar] [CrossRef]
- Stanković, K.; Jelić, D.; Tomašević, N.; Krstić, A. Manufacturing process optimization for real-time quality control in multi-regime conditions: Tire tread production use case. J. Manuf. Syst. 2024, 76, 293–313. [Google Scholar] [CrossRef]
- Paraschos, P.D.; Koulouriotis, D.E. Learning-based production, maintenance, and quality optimization in smart manufacturing systems: A literature review and trends. Comput. Ind. Eng. 2024, 198, 110656. [Google Scholar] [CrossRef]
- Vidakovic, B.; Vidakovic, B. Point and Interval Estimators. In Statistics for Bioengineering Sciences: With MATLAB and WinBUGS Support; Springer: New York, NY, USA, 2011; pp. 229–277. [Google Scholar]
- Sarhan, M.A.; Rasheed, M.; Mahmood, R.S.; Rashid, T.; Maalej, O. Evaluating the Effectiveness of Continuity Correction in Discrete Probability Distributions. J. Posit. Sci. 2024, 4, 4. [Google Scholar]
- Trouvé, R.; Arthur, A.D.; Robinson, A.P. Assessing the quality of offshore Binomial sampling biosecurity inspections using onshore inspections. Ecol. Appl. 2022, 32, e2595. [Google Scholar] [CrossRef]
- Mannu, R.; Olivieri, M.; Francesconi, A.H.D.; Lentini, A. Monitoring of Larinus spp. (Coleoptera Curculionidae) infesting cardoon and development of a binomial sampling plan for the estimation of Larinus cynarae infestation level in Mediterranean conditions. Crop Prot. 2025, 187, 106955. [Google Scholar] [CrossRef]
- Kemp, C.D.; Kemp, A.W. Generalized hypergeometric distributions. J. R. Stat. Soc. Ser. B Stat. Methodol. 1956, 18, 202–211. [Google Scholar] [CrossRef]
- Schilling, M.F.; Stanley, A. A new approach to precise interval estimation for the parameters of the hypergeometric distribution. Commun. Stat.-Theory Methods 2022, 51, 29–50. [Google Scholar] [CrossRef]
- Hafid, A.; Hafid, A.S.; Samih, M. A novel methodology-based joint hypergeometric distribution to analyze the security of sharded blockchains. IEEE Access 2020, 8, 179389–179399. [Google Scholar] [CrossRef]
- Puza, B.; O’neill, T. Generalised Clopper–Pearson confidence intervals for the binomial proportion. J. Stat. Comput. Simul. 2006, 76, 489–508. [Google Scholar] [CrossRef]
- Bu, H.; Sun, M. Clopper-Pearson algorithms for efficient statistical model checking estimation. IEEE Trans. Softw. Eng. 2024, 50, 1726–1746. [Google Scholar] [CrossRef]
- Skėrė, S.; Žvironienė, A.; Juzėnas, K.; Petraitienė, S. Optimization experiment of production processes using a dynamic decision support method: A solution to complex problems in industrial manufacturing for small and medium-sized enterprises. Sensors 2023, 23, 4498. [Google Scholar] [CrossRef]
- Zhang, K.; Yuan, F.; Jiang, Y.; Mao, Z.; Zuo, Z.; Peng, Y. A Particle Swarm Optimization-Guided Ivy Algorithm for Global Optimization Problems. Biomimetics 2025, 10, 342. [Google Scholar] [CrossRef]
- Hussein, N.K.; Qaraad, M.; El Najjar, A.M.; Farag, M.A.; Elhosseini, M.A.; Mirjalili, S.; Guinovart, D. Schrödinger optimizer: A quantum duality-driven metaheuristic for stochastic optimization and engineering challenges. Knowl.-Based Syst. 2025, 328, 114273. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Farag, M.A.; Mirjalili, S.; Elhosseini, M.A. Quadratic interpolation and a new local search approach to improve particle swarm optimization: Solar photovoltaic parameter estimation. Expert Syst. Appl. 2024, 236, 121417. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Badawy, M.; Mirjalili, S.; Elhosseini, M.A. Photovoltaic parameter estimation using improved moth flame algorithms with local escape operators. Comput. Electr. Eng. 2023, 106, 108603. [Google Scholar] [CrossRef]
- Mahmood, B.S.; Hussein, N.K.; Aljohani, M.; Qaraad, M. A modified gradient search rule based on the quasi-newton method and a new local search technique to improve the gradient-based algorithm: Solar photovoltaic parameter extraction. Mathematics 2023, 11, 4200. [Google Scholar] [CrossRef]
- Tao, S.; Liu, S.; Zhou, H.; Mao, X. Research on inventory sustainable development strategy for maximizing cost-effectiveness in supply chain. Sustainability 2024, 16, 4442. [Google Scholar] [CrossRef]
- Silva, C.; Ribeiro, R.; Gomes, P. Algorithmic Optimization Techniques for Operations Research Problems. In Data Analytics in System Engineering, Proceedings of the Computational Methods in Systems and Software, Szczecin, Poland, 12–14 October 2023; Springer Nature: Cham, Switzerland, 2023; pp. 331–339. [Google Scholar]
- Liu, S.; Jin, Z.; Lin, H.; Lu, H. An improve crested porcupine algorithm for UAV delivery path planning in challenging environments. Sci. Rep. 2024, 14, 20445. [Google Scholar] [CrossRef]
- Zhang, K.; Li, X.; Zhang, S.; Zhang, S. A Bio-Inspired Adaptive Probability IVYPSO Algorithm with Adaptive Strategy for Backpropagation Neural Network Optimization in Predicting High-Performance Concrete Strength. Biomimetics 2025, 10, 515. [Google Scholar] [CrossRef]
- Qiu, Y.; Yang, X.; Chen, S. An improved gray wolf optimization algorithm solving to functional optimization and engineering design problems. Sci. Rep. 2024, 14, 14190. [Google Scholar] [CrossRef]
- Sujono, S.; Musafa, A. Load-Shedding Optimization Using Hybrid Grey Wolf-Whale Algorithm to Improve the Isolated Distribution Networks. J. INFOTEL 2025, 17, 377–393. [Google Scholar] [CrossRef]
- Fauzan, M.N.; Munadi, R.; Sumaryo, S.; Nuha, H.H. Enhanced Grey Wolf Optimization for Efficient Transmission Power Optimization in Wireless Sensor Network. Appl. Syst. Innov. 2025, 8, 36. [Google Scholar] [CrossRef]
- Musshoff, O.; Hirschauer, N. Optimizing production decisions using a hybrid simulation–genetic algorithm approach. Can. J. Agric. Econ./Rev. Can. D’agroeconomie 2009, 57, 35–54. [Google Scholar] [CrossRef]
- Pan, C.; Si, Z.; Du, X.; Lv, Y. A four-step decision-making grey wolf optimization algorithm. Soft Comput. 2021, 25, 1841–1855. [Google Scholar] [CrossRef]
- Cochran, W.G. Sampling Techniques, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Zareie, A.; Sheikhahmadi, A.; Jalili, M. Identification of influential users in social network using gray wolf optimization algorithm. Expert Syst. Appl. 2020, 142, 112971. [Google Scholar] [CrossRef]
- Escobar-Cuevas, H.; Cuevas, E.; Avila, K.; Avalos, O. An advanced initialization technique for metaheuristic optimization: A fusion of Latin hypercube sampling and evolutionary behaviors. Comput. Appl. Math. 2024, 43, 234. [Google Scholar] [CrossRef]
- Xiong, Q.; Dong, L.; Chen, H.; Zhu, X.; Zhao, X.; Gao, X. Enhanced NSGA-II algorithm based on novel hybrid crossover operator to optimise water supply and ecology of Fenhe reservoir operation. Sci. Rep. 2024, 14, 31621. [Google Scholar] [CrossRef]
- Dong, W.; Kang, L.; Zhang, W. Opposition-based particle swarm optimization with adaptive mutation strategy. Soft Comput. 2017, 21, 5081–5090. [Google Scholar] [CrossRef]
- Pham, V.H.S.; Nguyen, V.N.; Nguyen Dang, N.T. Hybrid whale optimization algorithm for enhanced routing of limited capacity vehicles in supply chain management. Sci. Rep. 2024, 14, 793. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Chen, H.; Wang, D.; Fu, Z. Improved GWO for large-scale function optimization and MLP optimization in cancer identification. Neural Comput. Appl. 2020, 32, 1305–1325. [Google Scholar] [CrossRef]
- Siddiqui, L.; Mani, A.; Singh, J. Investigating Quantum-Inspired Evolutionary Algorithm with Restarts for Solving IEEE CEC 2022 Benchmark Problems. In Proceedings of the International Conference on Recent Developments in Control, Automation & Power Engineering, Penghu, Taiwan, 26–29 October 2023; Springer Nature: Singapore, 2023; pp. 219–230. [Google Scholar]



| Variable | Definition |
|---|---|
| 0-1 variable, used to determine whether to test spare parts or whether to test and disassemble finished products | |
| Purchase cost of spare parts | |
| Quantity of the i-th spare part | |
| Purchase unit price of the i-th spare part | |
| Inspection cost of spare parts | |
| Inspection cost of the i-th spare part | |
| Assembly cost of finished products | |
| Sales revenue of finished products | |
| Quantity of finished products | |
| Assembly cost per finished product | |
| Market price per finished product | |
| Inspection cost of finished products | |
| Inspection cost per finished product | |
| Defect rate of finished products | |
| Disassembly cost of defective finished products | |
| Disassembly cost per defective finished product | |
| Exchange cost of finished products | |
| Return cost of finished products | |
| Exchange cost per finished product | |
| Return cost per finished product | |
| Assembly cost of semi-finished products | |
| Quantity of the b-th semi-finished product | |
| Assembly cost of the b-th semi-finished product | |
| Inspection cost of semi-finished products | |
| Inspection cost of the b-th semi-finished product | |
| Disassembly cost of defective semi-finished products | |
| Defect rate of the b-th defective semi-finished product | |
| Disassembly cost of the b-th defective semi-finished product | |
| Total cost |
| Defect Rate Interval of Semi-Finished Product 1 | Defect Rate Interval of Semi-Finished Product 2 | Defect Rate Interval of Semi-Finished Product 3 | Defect Rate Interval of Finished Product | |
|---|---|---|---|---|
| Production scenario1 | × | × | × | [0.1, 0.356] |
| Production scenario 2 | × | × | × | [0.2, 0.390] |
| Production scenario 3 | × | × | × | [0.1, 0.356] |
| Production scenario 4 | × | × | × | [0.2, 0.390] |
| Production scenario 5 | × | × | × | [0.1, 0.356] |
| Production scenario 6 | × | × | × | [0.05, 0.320] |
| Multi-process production inspection scenario | [0, 0.455] | [0, 0.455] | [0, 0.356] | [0, 0.828] |
| No. | Functions | ||
|---|---|---|---|
| Unimodal function | 1 | Shifted and Fully Rotated Zakharov Function | 300 |
| Basic functions | 2 | Shifted and Fully Rotated Rosenbrock’s Function | 400 |
| 3 | Shifted and Fully Rotated Expanded Schaffer’s Function | 600 | |
| 4 | Shifted and Fully Rotated Non-Continuous Rastrigin’s Function | 800 | |
| 5 | Shifted and Fully Rotated Levy Function | 900 | |
| Hybrid functions | 6 | Hybrid Function 1 (N = 3) | 1800 |
| 7 | Hybrid Function 2 (N = 6) | 2000 | |
| 8 | Hybrid Function 3 (N = 5) | 2200 | |
| Composition functions | 9 | Composition Function 1 (N = 5) | 2300 |
| 10 | Composition Function 2 (N = 4) | 2400 | |
| 11 | Composition Function 3 (N = 5) | 2600 | |
| 12 | Composition Function 4 (N = 6) | 2700 | |
| Search range: | |||
| Algorithms | Parameter |
|---|---|
| IGWO | |
| GWO | No fixed initial parameters |
| hGWOA | No fixed initial parameters |
| RSMGWO | |
| DE | |
| CMA-ES | No fixed initial parameters |
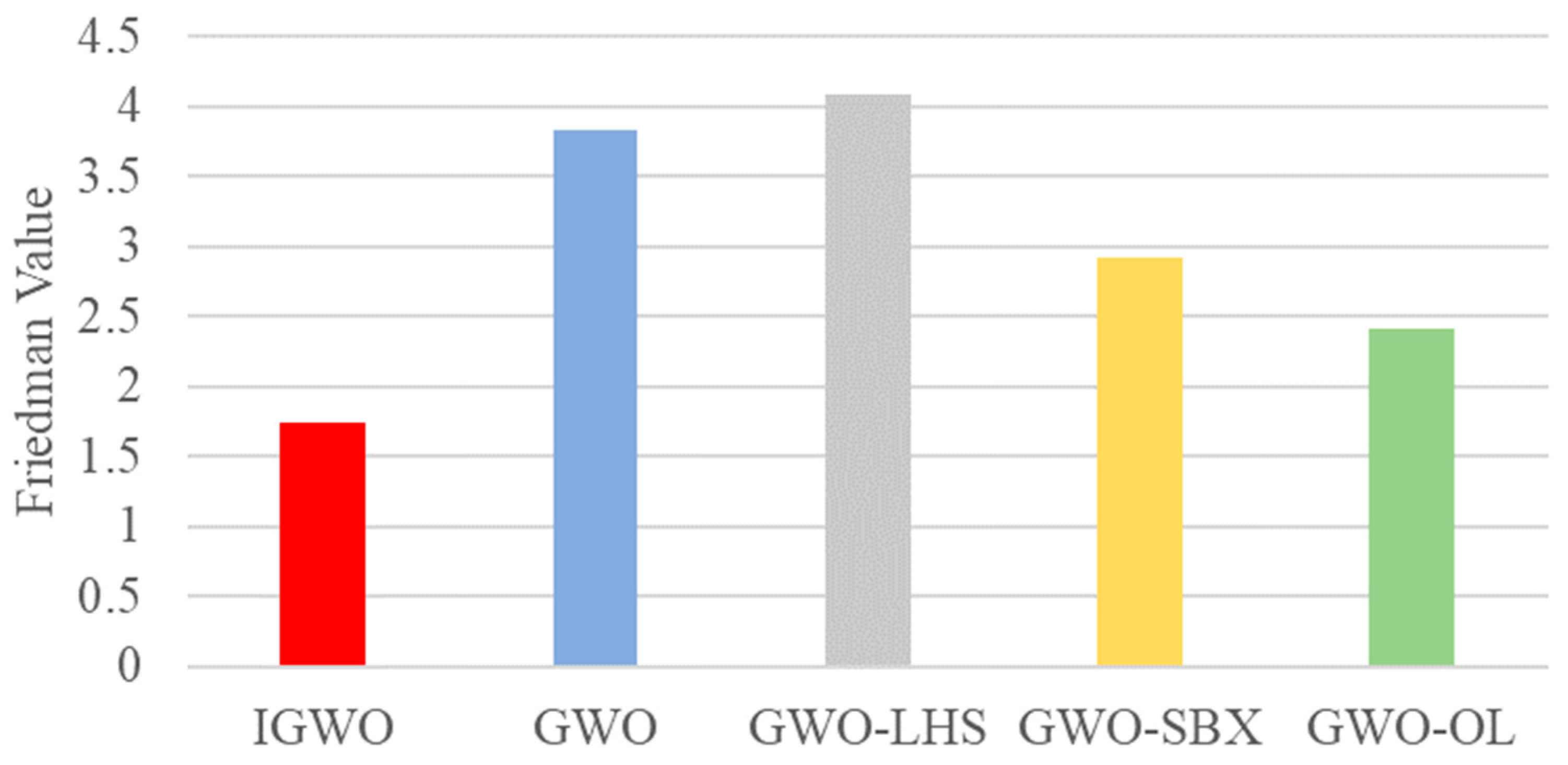
| Function | IGWO | GWO | GWO-LHS | GWO-SBX | GWO-OL | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Avg | Std | Best | Avg | Std | Best | Avg | Std | Best | Avg | Std | Best | Avg | Std | |
| F1 | 3.01 × 102 | 3.40 × 102 | 35.1 | 4.12 × 102 | 1.68 × 103 | 1.64 × 103 | 3.77 × 102 | 1.69 × 103 | 1.74 × 103 | 3.00 × 102 | 3.54 × 102 | 31.7 | 3.72 × 102 | 4.17 × 102 | 33.3 |
| F2 | 4.00 × 102 | 4.10 × 102 | 14.2 | 4.03 × 102 | 4.20 × 102 | 19.2 | 4.00 × 102 | 4.18 × 102 | 23.7 | 4.07 × 102 | 4.29 × 102 | 32.7 | 4.05 × 102 | 4.24 × 102 | 24.6 |
| F3 | 6.00 × 102 | 6.00 × 102 | 0.142 | 6.00 × 102 | 6.00 × 102 | 0.305 | 6.00 × 102 | 6.01 × 102 | 1.51 | 6.00 × 102 | 6.00 × 102 | 0.475 | 6.00 × 102 | 6.00 × 102 | 0.351 |
| F4 | 8.02 × 102 | 8.09 × 102 | 4.36 | 8.06 × 102 | 8.13 × 102 | 6.42 | 8.06 × 102 | 8.15 × 102 | 8.16 | 8.06 × 102 | 8.16 × 102 | 9.81 | 8.04 × 102 | 8.14 × 102 | 9.76 |
| F5 | 9.00 × 102 | 9.08 × 102 | 14.0 | 9.00 × 102 | 9.06 × 102 | 8.36 | 9.00 × 102 | 9.01 × 102 | 0.648 | 9.00 × 102 | 9.01 × 102 | 0.720 | 9.00 × 102 | 9.03 × 102 | 6.01 |
| F6 | 2.22 × 103 | 5.35 × 103 | 2.33 × 103 | 2.24 × 103 | 5.39 × 103 | 2.62 × 103 | 2.57 × 103 | 6.62 × 103 | 2.08 × 103 | 2.14 × 103 | 5.61 × 103 | 2.78 × 103 | 2.10 × 103 | 4.48 × 103 | 2.75 × 103 |
| F7 | 2.02 × 103 | 2.03 × 103 | 7.96 | 2.02 × 103 | 2.04 × 103 | 11.8 | 2.02 × 103 | 2.04 × 103 | 14.2 | 2.00 × 103 | 2.02 × 103 | 10.8 | 2.01 × 103 | 2.03 × 103 | 10.4 |
| F8 | 2.20 × 103 | 2.22 × 103 | 8.77 | 2.22 × 103 | 2.23 × 103 | 2.07 | 2.20 × 103 | 2.22 × 103 | 10.1 | 2.22 × 103 | 2.23 × 103 | 1.87 | 2.22 × 103 | 2.22 × 103 | 2.94 |
| F9 | 2.53 × 103 | 2.53 × 103 | 12.8 | 2.53 × 103 | 2.56 × 103 | 26.3 | 2.53 × 103 | 2.55 × 103 | 27.3 | 2.53 × 103 | 2.54 × 103 | 46.4 | 2.53 × 103 | 2.53 × 103 | 12.7 |
| F10 | 2.50 × 103 | 2.53 × 103 | 54.8 | 2.50 × 103 | 2.57 × 103 | 58.6 | 2.50 × 103 | 2.59 × 103 | 49.9 | 2.50 × 103 | 2.56 × 103 | 58.4 | 2.50 × 103 | 2.51 × 103 | 15.0 |
| F11 | 2.60 × 103 | 2.70 × 103 | 1.46 × 102 | 2.73 × 103 | 2.92 × 103 | 1.55 × 102 | 2.60 × 103 | 2.95 × 103 | 1.69 × 102 | 2.60 × 103 | 2.86 × 103 | 1.09 × 102 | 2.60 × 103 | 2.75 × 103 | 1.57 × 102 |
| F12 | 2.86 × 103 | 2.86 × 103 | 0.916 | 2.86 × 103 | 2.87 × 103 | 5.06 | 2.86 × 103 | 2.87 × 103 | 6.56 | 2.86 × 103 | 2.86 × 103 | 1.82 | 2.86 × 103 | 2.86 × 103 | 0.616 |
| IGWO | GWO | GWO-LHS | GWO-SBX | GWO-OL | |
|---|---|---|---|---|---|
| IGWO | 2.44 × 10−3 | 4.88 × 10−3 | 2.69 × 10−2 | 0.470 | |
| GWO | 2.44 × 10−3 | 0.470 | 0.176 | 1.22 × 10−2 | |
| GWO-LHS | 4.88 × 10−3 | 0.470 | 6.40 × 10−2 | 6.40 × 10−2 | |
| GWO-SBX | 2.69 × 10−2 | 0.176 | 6.40 × 10−2 | 0.301 | |
| GWO-OL | 0.470 | 1.22 × 10−2 | 6.40 × 10−2 | 0.301 |
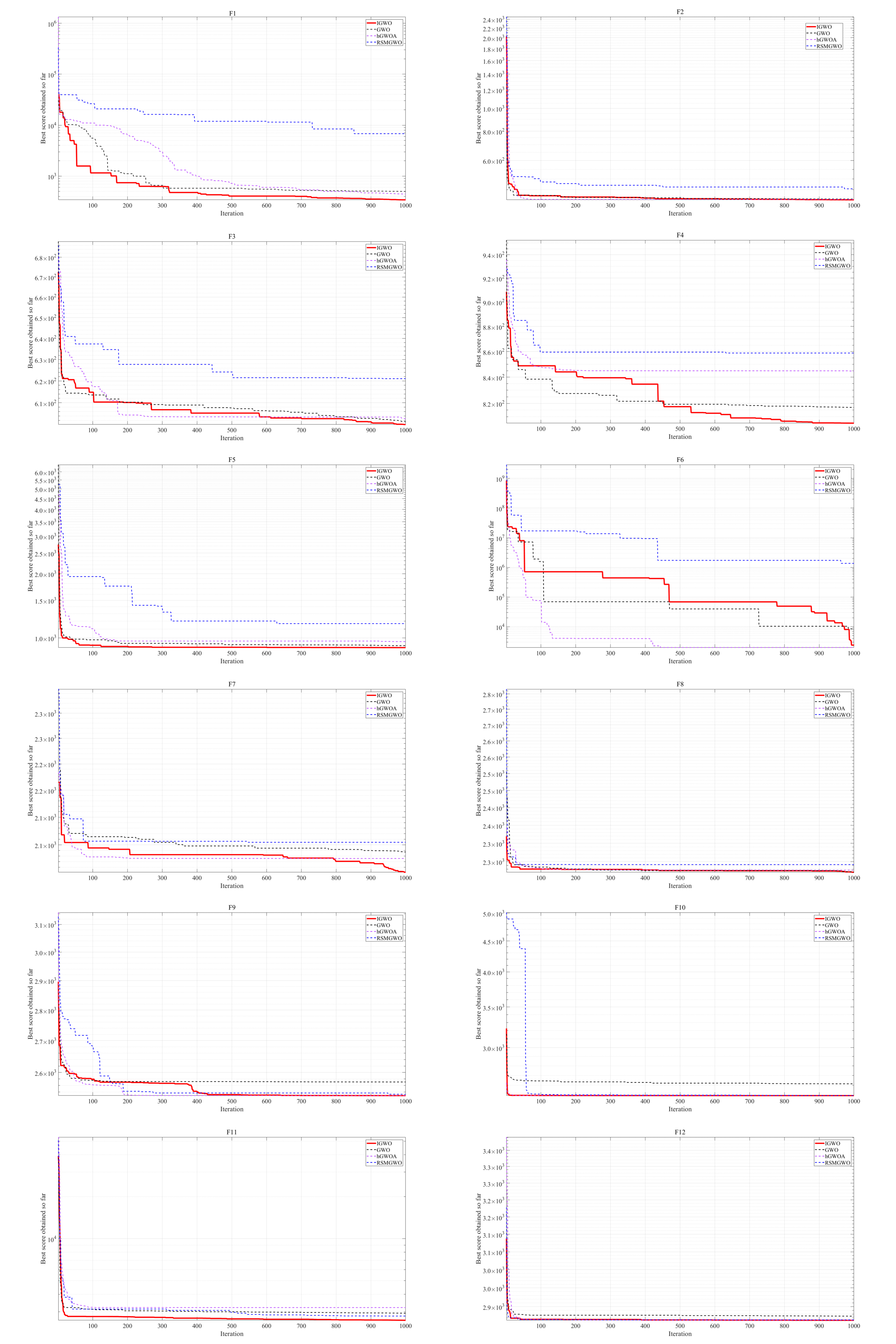
| Function | IGWO | GWO | hGWOA | RSMGWO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Avg | Std | Best | Avg | Std | Best | Avg | Std | Best | Avg | Std | |
| F1 | 3.13 × 102 | 3.48 × 102 | 36.0 | 4.03 × 102 | 1.22 × 103 | 1.24 × 103 | 3.02 × 102 | 8.37 × 102 | 8.72 × 102 | 1.84 × 103 | 4.91 × 103 | 2.12 × 103 |
| F2 | 4.06 × 102 | 4.09 × 102 | 1.82 | 4.02 × 102 | 4.24 × 102 | 25.2 | 4.00 × 102 | 4.27 × 102 | 36.6 | 4.17 × 102 | 4.26 × 102 | 9.90 |
| F3 | 6.00 × 102 | 6.00 × 102 | 0.208 | 6.00 × 102 | 6.01 × 102 | 1.20 | 6.00 × 102 | 6.02 × 102 | 3.44 | 6.10 × 102 | 6.16 × 102 | 5.20 |
| F4 | 8.04 × 102 | 8.13 × 102 | 8.01 | 8.06 × 102 | 8.10 × 102 | 3.12 | 8.14 × 102 | 8.33 × 102 | 12.1 | 8.45 × 102 | 8.61 × 102 | 13.7 |
| F5 | 9.00 × 102 | 9.01 × 102 | 0.727 | 9.00 × 102 | 9.05 × 102 | 13.1 | 9.01 × 102 | 1.01 × 103 | 1.20 × 102 | 9.60 × 102 | 1.08 × 103 | 1.81 × 102 |
| F6 | 2.00 × 103 | 4.73 × 103 | 2.96 × 103 | 3.39 × 103 | 6.43 × 103 | 2.12 × 103 | 2.21 × 103 | 4.60 × 103 | 2.16 × 103 | 2.79 × 104 | 4.85 × 105 | 4.05 × 105 |
| F7 | 2.00 × 103 | 2.02 × 103 | 7.42 | 2.02 × 103 | 2.03 × 103 | 7.94 | 2.02 × 103 | 2.03 × 103 | 8.80 | 2.04 × 103 | 2.05 × 103 | 10.8 |
| F8 | 2.20 × 103 | 2.22 × 103 | 10.6 | 2.22 × 103 | 2.23 × 103 | 2.09 | 2.22 × 103 | 2.22 × 103 | 1.85 | 2.23 × 103 | 2.23 × 103 | 2.14 |
| F9 | 2.53 × 103 | 2.53 × 103 | 0.389 | 2.53 × 103 | 2.55 × 103 | 24.6 | 2.53 × 103 | 2.54 × 103 | 20.2 | 2.53 × 103 | 2.55 × 103 | 27.8 |
| F10 | 2.50 × 103 | 2.52 × 103 | 46.4 | 2.50 × 103 | 2.57 × 103 | 58.3 | 2.50 × 103 | 2.56 × 103 | 63.4 | 2.50 × 103 | 2.52 × 103 | 54.6 |
| F11 | 2.60 × 103 | 2.69 × 103 | 1.25 × 102 | 2.91 × 103 | 2.97 × 103 | 92.2 | 2.60 × 103 | 2.74 × 103 | 1.48 × 102 | 2.76 × 103 | 2.80 × 103 | 18.0 |
| F12 | 2.86 × 103 | 2.86 × 103 | 1.42 | 2.86 × 103 | 2.86 × 103 | 0.981 | 2.86 × 103 | 2.88 × 103 | 21.7 | 2.86 × 103 | 2.86 × 103 | 0.888 |
| IGWO | GWO | hGWOA | RSMGWO | |
|---|---|---|---|---|
| IGWO | 2.44 × 10−3 | 2.69 × 10−2 | 1.47 × 10−3 | |
| GWO | 2.44 × 10−3 | 0.677 | 0.110 | |
| hGWOA | 2.69 × 10−2 | 0.677 | 4.25 × 10−2 | |
| RSMGWO | 1.47 × 10−3 | 0.110 | 4.25 × 10−2 |
| Function | IGWO | DE | CMA-ES | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Best | Avg | Std | Best | Avg | Std | Best | Avg | Std | |
| F1 | 3.01 × 102 | 3.40 × 102 | 35.1 | 7.63 × 102 | 1.59 × 103 | 4.76 × 102 | 3.00 × 102 | 9.50 × 102 | 8.42 × 102 |
| F2 | 4.00 × 102 | 4.10 × 102 | 14.2 | 4.00 × 102 | 4.04 × 102 | 3.14 | 4.00 × 102 | 4.11 × 102 | 7.21 |
| F3 | 6.00 × 102 | 6.00 × 102 | 0.142 | 6.00 × 102 | 6.00 × 102 | 7.12× 10−2 | 6.00 × 102 | 6.00 × 102 | 1.27 × 10−4 |
| F4 | 8.02 × 102 | 8.09 × 102 | 4.36 | 8.11 × 102 | 8.13 × 102 | 2.86 | 8.01 × 102 | 8.03 × 102 | 1.75 |
| F5 | 9.00 × 102 | 9.08 × 102 | 14.0 | 9.00 × 102 | 9.00 × 102 | 0.344 | 9.00 × 102 | 9.00 × 102 | 0.00 |
| F6 | 2.22 × 103 | 5.35 × 103 | 2.33 × 103 | 1.81 × 103 | 2.17 × 103 | 5.04 × 102 | 1.87 × 103 | 3.72 × 103 | 1.91 × 103 |
| F7 | 2.02 × 103 | 2.03 × 103 | 7.96 | 2.00 × 103 | 2.00 × 103 | 2.50 | 2.02 × 103 | 2.04 × 103 | 45.1 |
| F8 | 2.20 × 103 | 2.22 × 103 | 8.77 | 2.21 × 103 | 2.22 × 103 | 5.74 | 2.22 × 103 | 2.24 × 103 | 37.1 |
| F9 | 2.53 × 103 | 2.53 × 103 | 12.8 | 2.53 × 103 | 2.53 × 103 | 1.68 | 2.54 × 103 | 2.57 × 103 | 38.3 |
| F10 | 2.50 × 103 | 2.53 × 103 | 54.8 | 2.40 × 103 | 2.41 × 103 | 24.6 | 2.50 × 103 | 2.55 × 103 | 55.4 |
| F11 | 2.60 × 103 | 2.70 × 103 | 1.46 × 102 | 2.90 × 103 | 3.11 × 103 | 1.79 × 102 | 2.60 × 103 | 2.87 × 103 | 94.9 |
| F12 | 2.86 × 103 | 2.86 × 103 | 0.916 | 2.86 × 103 | 2.87 × 103 | 0.936 | 2.86 × 103 | 2.87 × 103 | 0.942 |
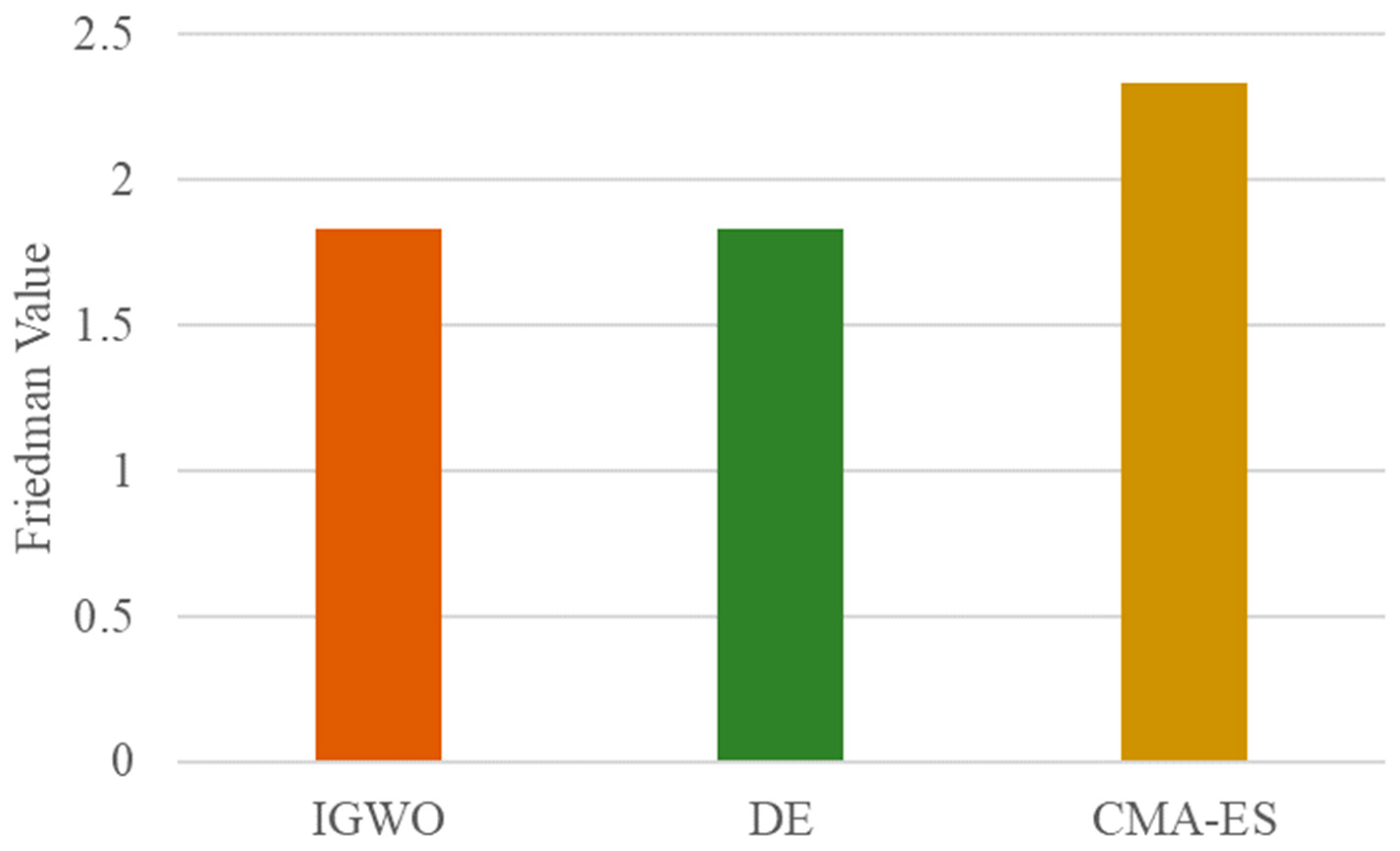
| IGWO | DE | CMA-ES | |
|---|---|---|---|
| IGWO | 0.424 | 0.151 | |
| DE | 0.424 | 0.470 | |
| CMA-ES | 0.151 | 0.470 |
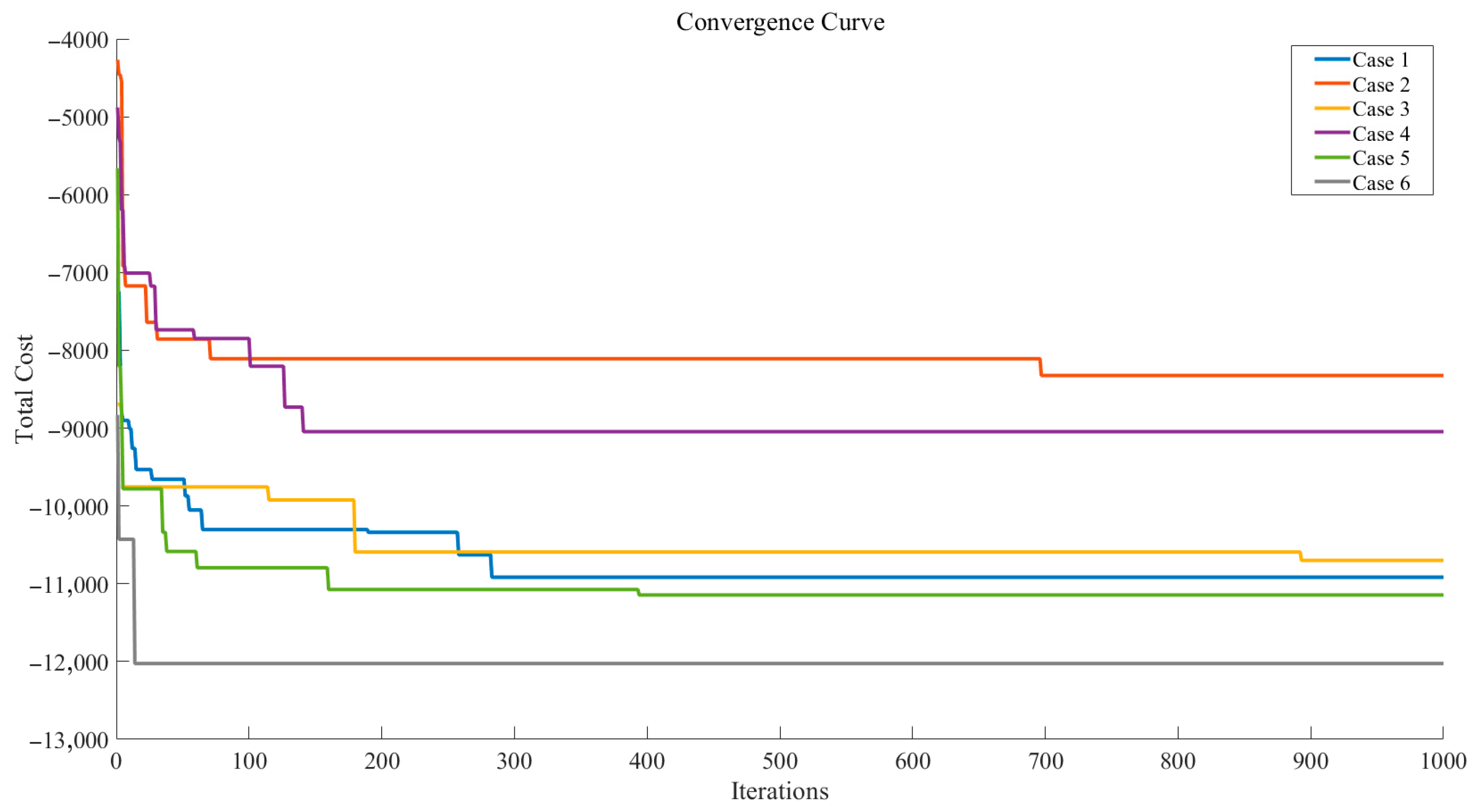
| Inspecting Spare Parts 1 | Inspecting Spare Parts 2 | Inspecting Finished Products | Disassembling Unqualified Finished Products | Total Profit (The Opposite of Total Cost) | |
|---|---|---|---|---|---|
| Case 1 | 0.16% | 14.84% | 100.00% | 100.00% | 10,916 |
| Case 2 | 19.71% | 1.10% | 100.00% | 100.00% | 8324 |
| Case 3 | 30.52% | 0.07% | 100.00% | 100.00% | 10,700 |
| Case 4 | 4.95% | 37.22% | 100.00% | 100.00% | 9045 |
| Case 5 | 3.70% | 6.14% | 100.00% | 100.00% | 11,145 |
| Case 6 | 22.90% | 79.66% | 12.16% | 18.52% | 12,026 |
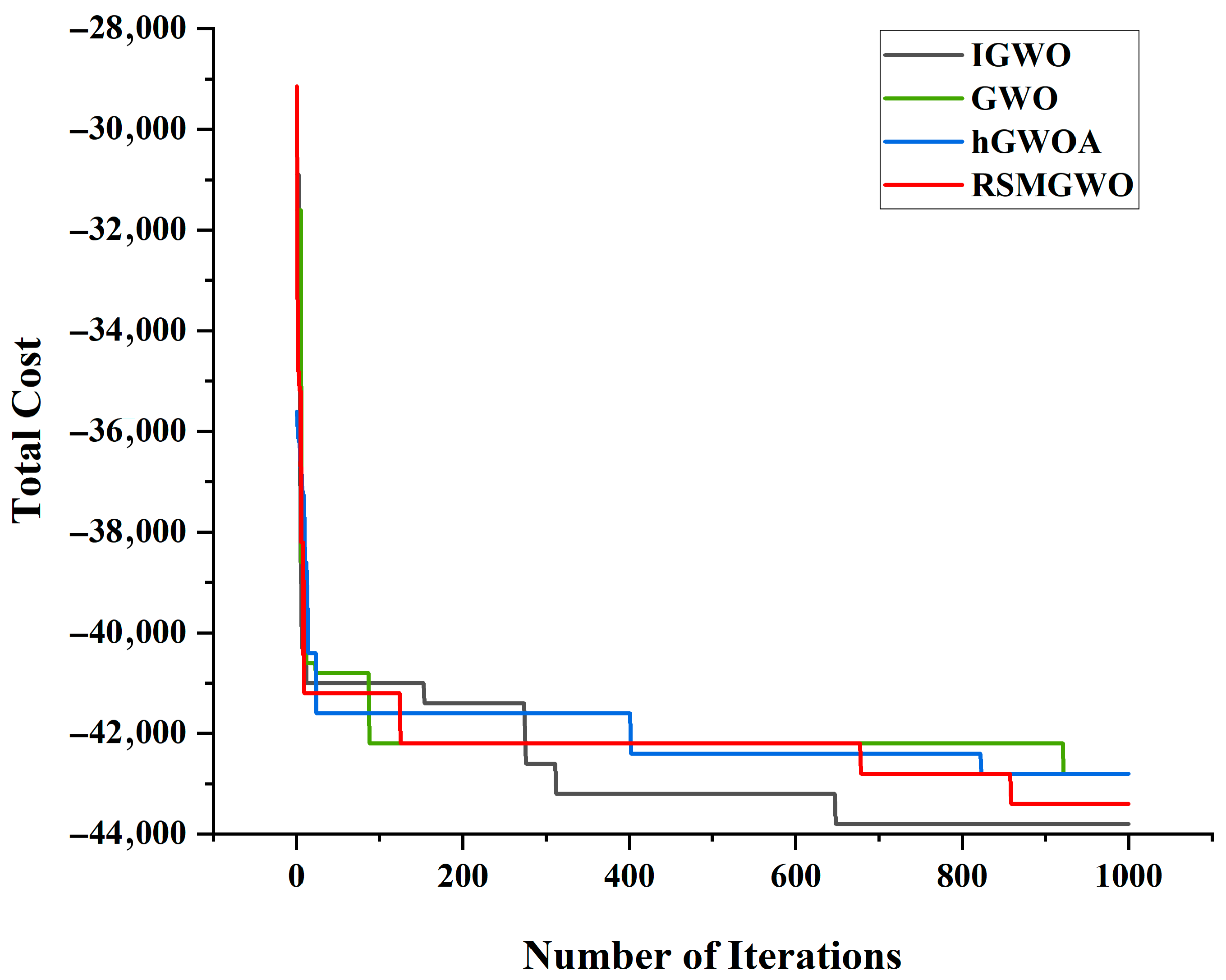
| IGWO | GWO | hGWOA | RSMGWO | |
|---|---|---|---|---|
| Inspecting spare parts 1 | 39.94% | 58.13% | 47.00% | 55.80% |
| Inspecting spare parts 2 | 21.16% | 30.53% | 70.03% | 3.06% |
| Inspecting spare parts 3 | 27.00% | 14.67% | 60.98% | 39.60% |
| Inspecting spare parts 4 | 48.57% | 6.13% | 67.83% | 2.44% |
| Inspecting spare parts 5 | 22.59% | 11.01% | 26.16% | 63.23% |
| Inspecting spare parts 6 | 5.13% | 80.00% | 91.08% | 22.03% |
| Inspecting spare parts 7 | 22.12% | 17.70% | 74.66% | 45.08% |
| Inspecting spare parts 8 | 34.64% | 9.27% | 10.47% | 81.59% |
| Inspecting semi-finished products 1 | 40.72% | 6.73% | 89.79% | 33.46% |
| Inspecting semi-finished products 2 | 28.53% | 54.90% | 38.25% | 15.25% |
| Inspecting semi-finished products 3 | 27.37% | 12.63% | 53.49% | 49.28% |
| Dismantling semi-finished products 1 | 16.09% | 50.90% | 47.25% | 0.45% |
| Dismantling semi-finished products 2 | 1.19% | 11.85% | 61.62% | 87.11% |
| Dismantling semi-finished products 3 | 65.60% | 79.23% | 79.91% | 9.90% |
| Inspecting finished products | 100.00% | 100.00% | 100.00% | 100.00% |
| Dismantling of unqualified finished products | 62.65% | 70.13% | 88.61% | 56.66% |
| Total profit (The opposite of total cost) | 43,800 | 42,800 | 42,800 | 43,400 |
| Confidence Level | 15% | 35% | 55% | 75% |
|---|---|---|---|---|
| Part 1 | [0.000, 0.038] | [0.000, 0.050] | [0.000, 0.066] | [0.000, 0.090] |
| Part 2 | [0.000, 0.038] | [0.000, 0.050] | [0.000, 0.066] | [0.000, 0.090] |
| Part 3 | [0.000, 0.038] | [0.000, 0.050] | [0.000, 0.066] | [0.000, 0.090] |
| Part 4 | [0.000, 0.038] | [0.000, 0.050] | [0.000, 0.066] | [0.000, 0.090] |
| Part 5 | [0.000, 0.038] | [0.000, 0.050] | [0.000, 0.066] | [0.000, 0.090] |
| Part 6 | [0.000, 0.038] | [0.000, 0.050] | [0.000, 0.066] | [0.000, 0.090] |
| Part 7 | [0.000, 0.038] | [0.000, 0.050] | [0.000, 0.066] | [0.000, 0.090] |
| Part 8 | [0.000, 0.038] | [0.000, 0.050] | [0.000, 0.066] | [0.000, 0.090] |
| Semi-finished product 1 | [0.100, 0.199] | [0.100, 0.228] | [0.100, 0.267] | [0.100, 0.322] |
| Semi-finished product 2 | [0.100, 0.199] | [0.100, 0.228] | [0.100, 0.267] | [0.100, 0.322] |
| Semi-finished product 3 | [0.100, 0.167] | [0.100, 0.188] | [0.100, 0.215] | [0.100, 0.255] |
| Finished Product | [0.100, 0.519] | [0.100, 0.564] | [0.100, 0.620] | [0.100, 0.692] |
| Confidence Level | 15% | 35% | 55% | 75% |
|---|---|---|---|---|
| Inspecting spare parts 1 | 59.43% | 13.61% | 25.20% | 22.16% |
| Inspecting spare parts 2 | 62.92% | 52.89% | 15.08% | 15.04% |
| Inspecting spare parts 3 | 55.71% | 7.48% | 59.86% | 39.56% |
| Inspecting spare parts 4 | 34.29% | 25.45% | 67.40% | 2.89% |
| Inspecting spare parts 5 | 55.82% | 25.27% | 65.29% | 16.39% |
| Inspecting spare parts 6 | 88.68% | 30.75% | 81.28% | 15.60% |
| Inspecting spare parts 7 | 74.23% | 33.93% | 34.52% | 31.65% |
| Inspecting spare parts 8 | 96.22% | 39.92% | 30.52% | 15.25% |
| Inspecting semi-finished products 1 | 8.58% | 13.90% | 20.93% | 83.82% |
| Inspecting semi-finished products 2 | 14.73% | 42.25% | 28.72% | 5.22% |
| Inspecting semi-finished products 3 | 4.56% | 76.79% | 20.49% | 4.52% |
| Dismantling semi-finished products 1 | 30.07% | 10.35% | 60.80% | 37.94% |
| Dismantling semi-finished products 2 | 46.45% | 43.32% | 57.60% | 62.97% |
| Dismantling semi-finished products 3 | 21.13% | 1.48% | 60.16% | 48.44% |
| Inspecting finished products | 100.00% | 100.00% | 100.00% | 100.00% |
| Dismantling of unqualified finished products | 97.46% | 71.98% | 48.19% | 35.39% |
| Total profit (The opposite of total cost) | 43,400 | 41,600 | 41,200 | 43,600 |
| Finished Product Price | −40% | −20% | 0% | 20% | 40% |
|---|---|---|---|---|---|
| Inspecting spare parts 1 | 44.27% | 33.77% | 39.94% | 36.15% | 59.86% |
| Inspecting spare parts 2 | 30.81% | 19.91% | 21.16% | 11.93% | 36.28% |
| Inspecting spare parts 3 | 46.46% | 73.99% | 27.00% | 42.43% | 66.98% |
| Inspecting spare parts 4 | 76.88% | 13.91% | 48.57% | 45.34% | 34.99% |
| Inspecting spare parts 5 | 56.89% | 41.53% | 22.59% | 54.54% | 43.67% |
| Inspecting spare parts 6 | 19.30% | 45.74% | 5.13% | 24.29% | 60.02% |
| Inspecting spare parts 7 | 22.13% | 61.12% | 22.12% | 35.46% | 2.36% |
| Inspecting spare parts 8 | 76.96% | 73.98% | 34.64% | 63.71% | 97.83% |
| Inspecting semi-finished products 1 | 36.67% | 82.37% | 40.72% | 0.00% | 4.35% |
| Inspecting semi-finished products 2 | 55.19% | 34.79% | 28.53% | 20.05% | 0.00% |
| Inspecting semi-finished products 3 | 22.41% | 16.57% | 27.37% | 53.53% | 13.64% |
| Dismantling semi-finished products 1 | 22.02% | 12.13% | 16.09% | 35.62% | 34.83% |
| Dismantling semi-finished products 2 | 4.07% | 31.73% | 1.19% | 84.45% | 96.11% |
| Dismantling semi-finished products 3 | 64.97% | 50.49% | 65.60% | 94.79% | 52.10% |
| Inspecting finished products | 100.00% | 100.00% | 100.00% | 100.00% | 100.00% |
| Dismantling of unqualified finished products | 61.13% | 59.66% | 62.65% | 7.30% | 0.00% |
| Total profit (The opposite of total cost) | 7920 | 24,600 | 43,800 | 59,640 | 78,480 |
| Swap Losses | −20% | −10% | 0% | 10% | 20% |
|---|---|---|---|---|---|
| Inspecting spare parts 1 | 78.75% | 47.15% | 39.94% | 40.38% | 59.43% |
| Inspecting spare parts 2 | 3.31% | 55.16% | 21.16% | 63.62% | 62.92% |
| Inspecting spare parts 3 | 38.68% | 74.12% | 27.00% | 18.60% | 55.71% |
| Inspecting spare parts 4 | 88.42% | 67.84% | 48.57% | 6.96% | 34.29% |
| Inspecting spare parts 5 | 12.65% | 66.59% | 22.59% | 70.70% | 55.82% |
| Inspecting spare parts 6 | 14.57% | 69.37% | 5.13% | 19.51% | 88.68% |
| Inspecting spare parts 7 | 12.89% | 56.46% | 22.12% | 22.46% | 74.23% |
| Inspecting spare parts 8 | 84.60% | 36.44% | 34.64% | 55.62% | 96.22% |
| Inspecting semi-finished products 1 | 7.49% | 23.91% | 40.72% | 0.31% | 8.58% |
| Inspecting semi-finished products 2 | 5.26% | 20.02% | 28.53% | 11.85% | 14.73% |
| Inspecting semi-finished products 3 | 3.26% | 36.58% | 27.37% | 7.54% | 4.56% |
| Dismantling semi-finished products 1 | 81.99% | 32.15% | 16.09% | 62.91% | 30.07% |
| Dismantling semi-finished products 2 | 53.18% | 32.48% | 1.19% | 17.30% | 46.45% |
| Dismantling semi-finished products 3 | 50.22% | 8.19% | 65.60% | 29.49% | 21.13% |
| Inspecting finished products | 100.00% | 100.00% | 100.00% | 100.00% | 100.00% |
| Dismantling of unqualified finished products | 14.04% | 19.61% | 62.65% | 41.70% | 97.46% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, W.; Zhou, X.; Wu, W.; Xu, C.-A. Research on the Optimization of Uncertain Multi-Stage Production Integrated Decisions Based on an Improved Grey Wolf Optimizer. Biomimetics 2025, 10, 775. https://doi.org/10.3390/biomimetics10110775
Gan W, Zhou X, Wu W, Xu C-A. Research on the Optimization of Uncertain Multi-Stage Production Integrated Decisions Based on an Improved Grey Wolf Optimizer. Biomimetics. 2025; 10(11):775. https://doi.org/10.3390/biomimetics10110775
Chicago/Turabian StyleGan, Weifei, Xin Zhou, Wangyu Wu, and Chang-An Xu. 2025. "Research on the Optimization of Uncertain Multi-Stage Production Integrated Decisions Based on an Improved Grey Wolf Optimizer" Biomimetics 10, no. 11: 775. https://doi.org/10.3390/biomimetics10110775
APA StyleGan, W., Zhou, X., Wu, W., & Xu, C.-A. (2025). Research on the Optimization of Uncertain Multi-Stage Production Integrated Decisions Based on an Improved Grey Wolf Optimizer. Biomimetics, 10(11), 775. https://doi.org/10.3390/biomimetics10110775






