Optimal Scheduling of Microgrids Based on a Two-Population Cooperative Search Mechanism
Abstract
1. Introduction
1.1. Related Work
1.2. Contributions
1.2.1. Algorithmic Innovation and Hybrid Framework Development
- Novel Hybrid Multi-Objective Algorithm: This paper introduces IMOHHOGWO, which innovatively combines the dynamic raid strategy of HHO with the social hierarchy mechanism of the GWO. This hybrid approach leverages the complementary strengths of both algorithms—HHO’s superior global exploration capabilities through stochastic raid strategies and the GWO’s efficient local exploitation through α/β/δ wolf leadership guidance.
- Advanced Adaptive Parameter Mechanisms: The algorithm incorporates several cutting-edge improvements, including (1) a nonlinear convergence factor that replaces traditional linear approaches with exponential forms for enhanced convergence speed; (2) a diversity perception energy factor that dynamically adjusts based on population standard deviation to balance exploration and exploitation; and (3) adaptive energy factor control that responds to solution set distribution density.
- Enhanced Global–Local Search Balance: The fusion strategy successfully addresses the fundamental challenge of balancing global exploration and local exploitation in multi-objective optimization through dynamic strategy switching controlled by escape energy factors and leadership hierarchy guidance.
- Lévy Flight Integration: Incorporates Lévy flight mechanics during exploitation phases to enable strategic long-distance jumps, significantly improving the algorithm’s ability to escape local optima and explore promising solution regions in high-dimensional search spaces.
- Simulated Annealing Integration: A temperature decay perturbation mechanism is strategically integrated during the exploitation phase with 0.3 probability, significantly enhancing the algorithm’s ability to escape local optima and improve solution quality in complex constraint environments.
1.2.2. Mathematical Modeling and Problem Formulation Excellence
- Comprehensive Microgrid Mathematical Framework: This establishes detailed mathematical models for all distributed generation units, including wind turbines, photovoltaic systems, micro-gas turbines, diesel generators, and energy storage batteries, incorporating realistic operational constraints, efficiency factors, and environmental parameters that accurately reflect real-world microgrid operations.
- Dual-Objective Optimization Model: This develops a sophisticated multi-objective mathematical model that simultaneously optimizes economic operating costs and carbon emission costs, addressing the critical trade-off between economic efficiency and environmental sustainability in microgrid operations. The model incorporates fuel costs, depreciation costs, maintenance costs, and comprehensive pollutant treatment costs (CO2, SO2, and NO2).
- Advanced Constraint Handling: Implements comprehensive constraint management, including power balance constraints, distributed generation output limits, energy storage SOC constraints, and grid interaction limits, ensuring the practical feasibility of optimization solutions.
1.2.3. Superior Performance Validation and Comparative Analysis
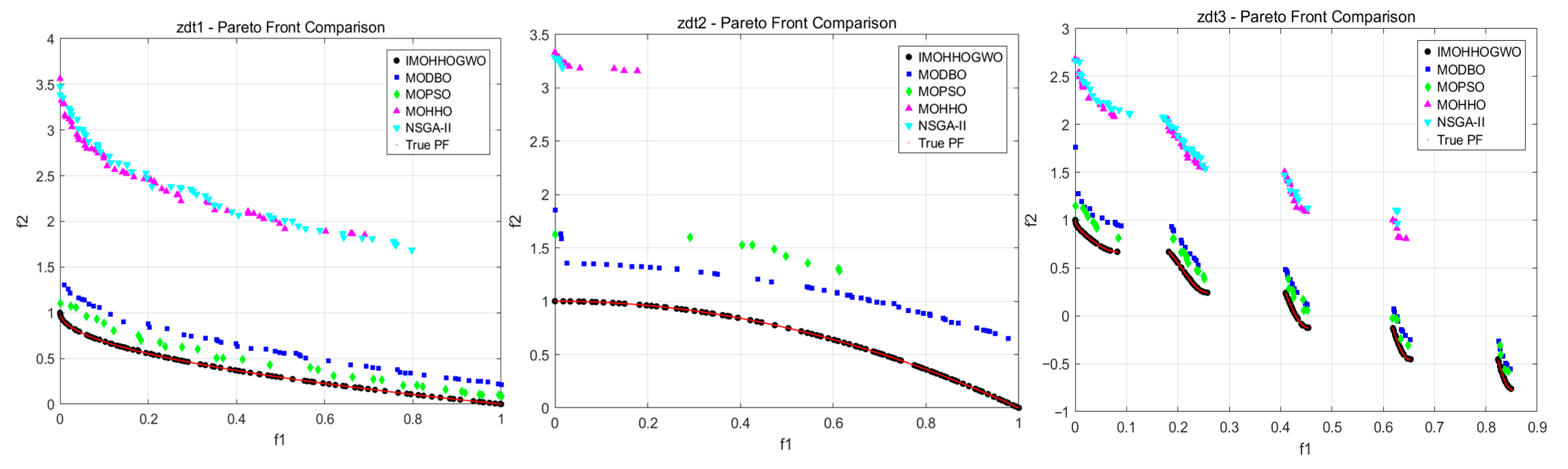
- Exceptional Multi-Objective Test Performance: Comprehensive evaluation using standard ZDT1, ZDT2, and ZDT3 test functions demonstrates IMOHHOGWO’s superiority across all metrics. IMOHHOGWO consistently obtained the best GD values and achieved the highest hypervolume (HV) values among all compared algorithms while maintaining competitive solution distribution uniformity.
- Robust Algorithm Comparison: Systematic comparison with four state-of-the-art algorithms (MODBO, MOPSO, MOHHO, and NSGA-II) across multiple performance metrics validates the consistent superiority of the proposed approach in terms of convergence accuracy, solution quality, and computational efficiency.
1.2.4. Application Impact and Innovation
- Practical Microgrid Implementation: This successfully validates the algorithm using real microgrid data with 24 h load profiles, actual equipment parameters, real-time electricity pricing, and authentic operational constraints, demonstrating annual operating cost savings of RMB 37,669.6 and carbon emission reduction of 0.449 tons.
- Multi-Scenario Optimization Capability: This provides comprehensive analysis across three optimization scenarios (economic dispatch, environmental dispatch, and multi-objective scheduling), offering decision-makers flexible tools to balance economic and environmental objectives based on specific operational requirements and policy constraints.
- Advanced Energy Management Strategy: The algorithm enables sophisticated energy management through optimal scheduling of diverse distributed generation sources, intelligent energy storage utilization, and strategic grid interaction, significantly improving overall microgrid efficiency and sustainability.
2. Microgrid Power Systems with Renewable Energy
2.1. Modelling of Distributed Power for Microgrids
2.1.1. Wind Turbine Model (WT)
2.1.2. Photovoltaic Power Generation (PV)
2.1.3. Diesel Electric Generator (DE)
2.1.4. Micro-Gas Turbine (MT)
2.1.5. Energy Storage Battery (BESS)
2.2. Multi-Objective Mathematical Model for Optimal Microgrid Scheduling
2.2.1. Operating Costs
Power Generation Cost
Depreciation Expenses
Maintenance Cost
2.2.2. Cost of Carbon Emissions
2.2.3. Constraints
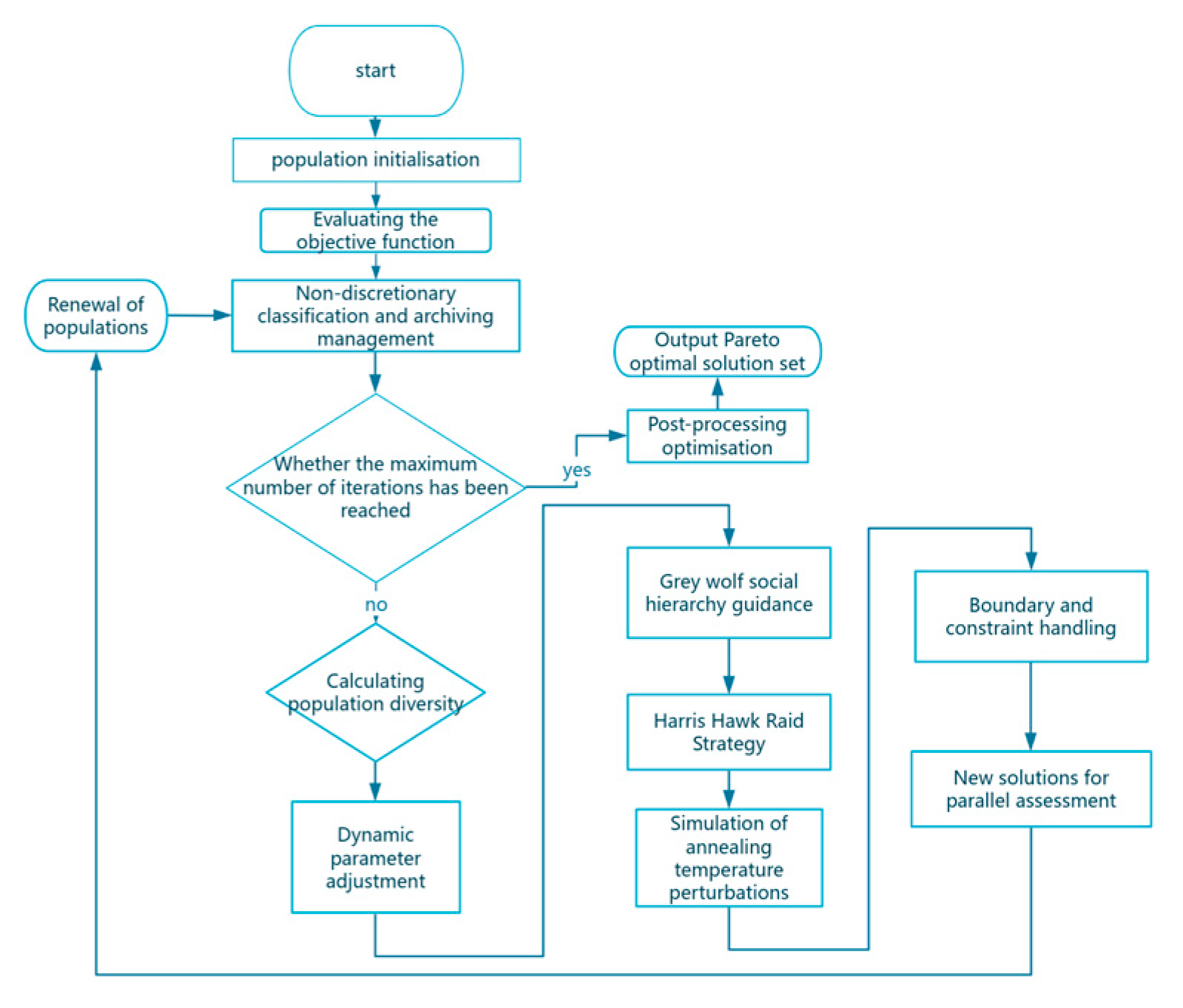
3. IMOHHO-GWO
3.1. Convergence Strategy of HHO and GWO
- a.
- Social hierarchy to guide the search direction: Using GWO’s α, β, and δ wolves to define the leadership and guide the population to move toward the potential optimal area.
- b.
- Dynamic hunting strategy to enhance exploitation: Under the control of HHO’s escape energy (E), the GWO’s position update mechanism is introduced to optimize the local exploitation accuracy.
- c.
- Hybrid exploration mechanism: Combining the random raid strategy of HHO with the group collaboration of GWO in the global search phase to enhance diversity.
3.2. Improved Algorithm
3.2.1. Nonlinear Factor
3.2.2. Diversity Perception Energy Factor
3.2.3. Grey Wolf Social Hierarchy Guidance + Harris Hawk Raids
| Algorithm 1. GWO social hierarchy guidance. |
| Input: Current individual position X, alpha, beta, delta positions 1: Calculate coefficient a = 2 × exp(−3 × iter/maxIter) 2: For each leader (alpha, beta, delta) do 3: | Generate random vectors A and C 4: | Calculate distance D = |C × leader.position—X| 5: | Update position component X_leader = leader.position—A × D 6: end For 7: Output GWOPosition = (X_alpha + X_beta + X_delta)/3 |
| Algorithm 2. Harris hawk exploration behavior. |
| Input: current position X, alpha position, population mean 1: Generate random value q 2: if q ≥ 0.5 3: | Apply random escape pattern 4: | newPosition = alpha.position - rand × |alpha.position - 2 × rand × X| 5: else 6: | Apply perching strategy 7: | newPosition = (alpha.position - mean(population)) + rand × (varMax - varMin) 8: Output newPosition |
| Algorithm 3. Harris hawk exploitation with progressive rapid dives. |
| Input: current position X, GWOPosition, energy E 1: Generate random value r 2: if r ≥ 0.5 and |E| < 0.5 3: | Apply soft besiege 4: | newPosition = GWOPosition - E × |GWOPosition - X| 5: else 6: | Apply hard besiege with progressive rapid dives 7: | newPosition = GWOPosition - E × |GWOPosition - X| + 0.01 × LevyFlight(D) 8: Output newPosition |
| Algorithm 4. Lévy flight. |
| Input: dimension nVar 1: Set Lévy exponent β = 1.5//typical value for Lévy flight 2: Calculate sigma parameter: 3: | numerator = Γ(1 + β) × sin(π × β/2) 4: | denominator = Γ((1 + β)/2) × β × 2^((β-1)/2) 5: | σ = (numerator/denominator)^(1/β)//Lévy distribution parameter 6: Generate random variables: 7: | u = randn(1, nVar) × σ//numerator random variable 8: | v = randn(1, nVar)//denominator random variable 9: Calculate Levy flight step: 10: | For i = 1 to nVar do 11: | | step[i] = u[i]/|v[i]|^(1/β)//Lévy flight formula 12: | end for 13: Output step |
3.2.4. Simulated Annealing Perturbations
| Algorithm 5. Simulated annealing perturbation mechanism. |
| Input: current position position, current iteration iter, maximum iterations maxIter, variable bounds varMin and varMax, dimension nVar 1: Calculate temperature factor T = 1 - iter/maxIter//linear cooling schedule 2: Generate Gaussian noise noise = randn(nVar)//standard normal distribution 3: Calculate perturbation magnitude magnitude = T × (varMax - varMin) 4: Apply perturbation perturbedPosition = position + magnitude × noise 5: For i = 1 to nVar do//boundary handling 6: | If perturbedPosition[i] < varMin then 7: | | perturbedPosition[i] = varMin 8: | If perturbedPosition[i] > varMax then 9: | | perturbedPosition[i] = varMax 10: end for 11: Output perturbedPosition |
3.2.5. ZDT1-3 Test Functions
4. Background
5. Results and Discussion
5.1. Simulation Analysis
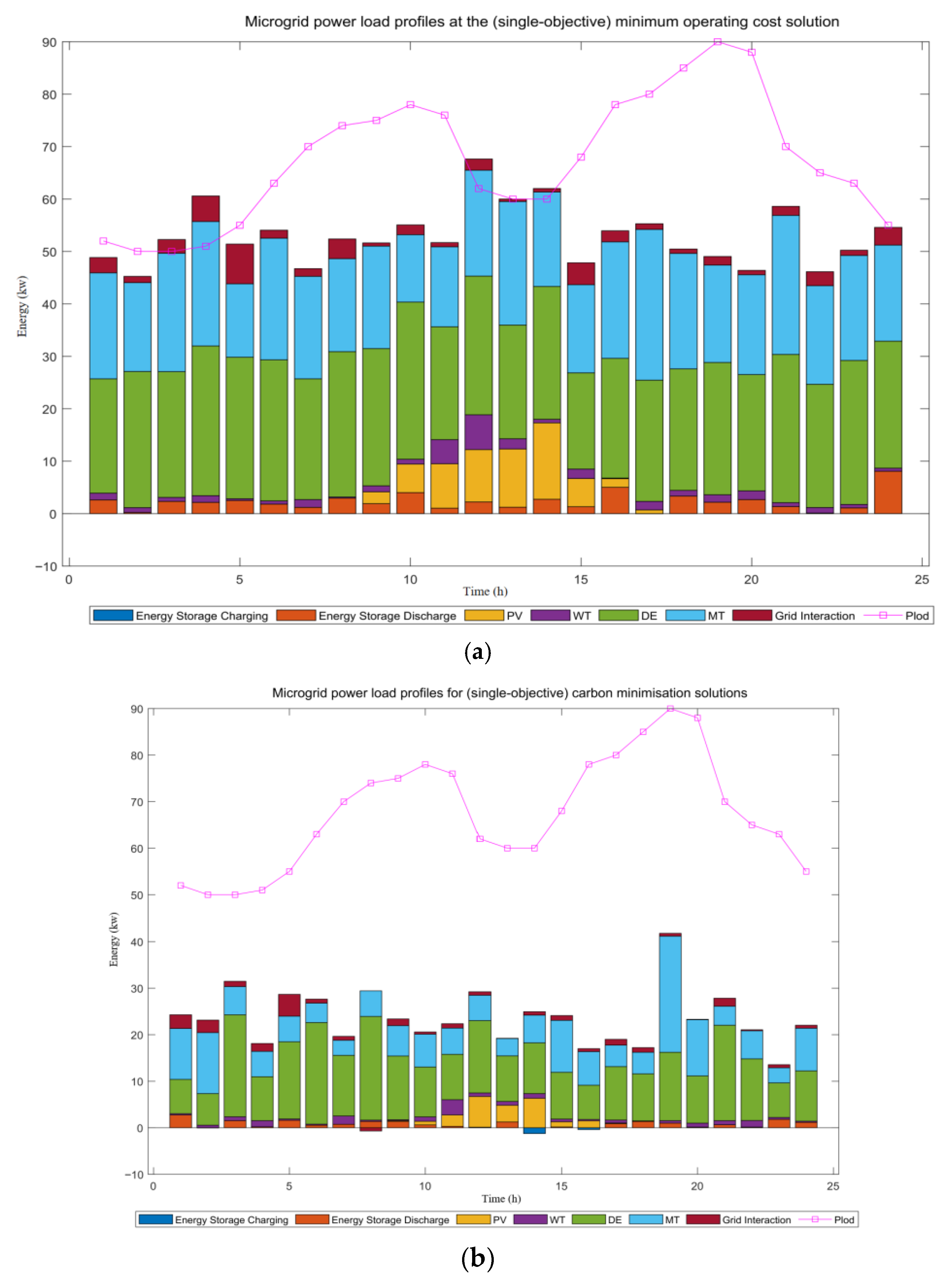
5.2. Single-Objective Optimization
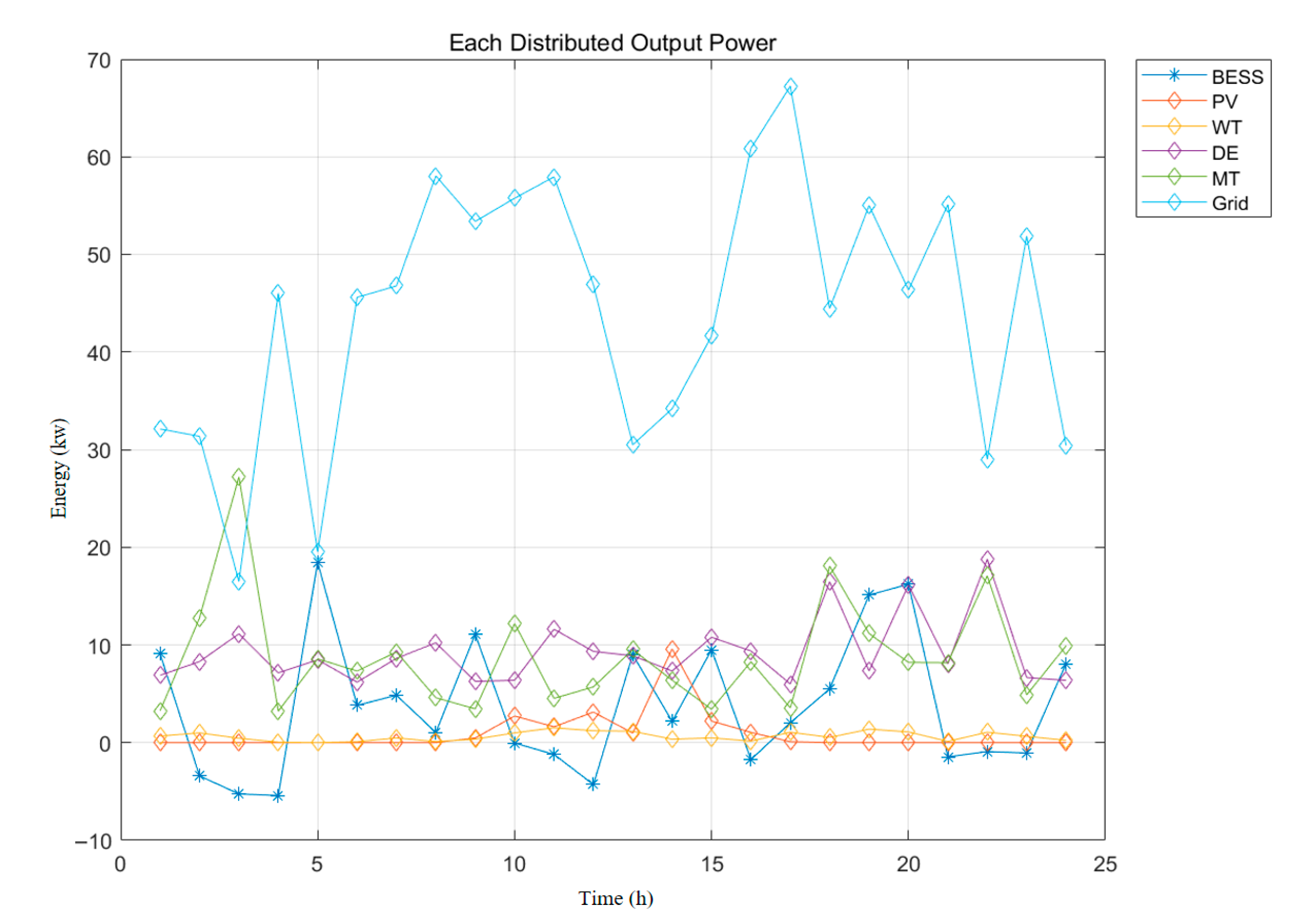
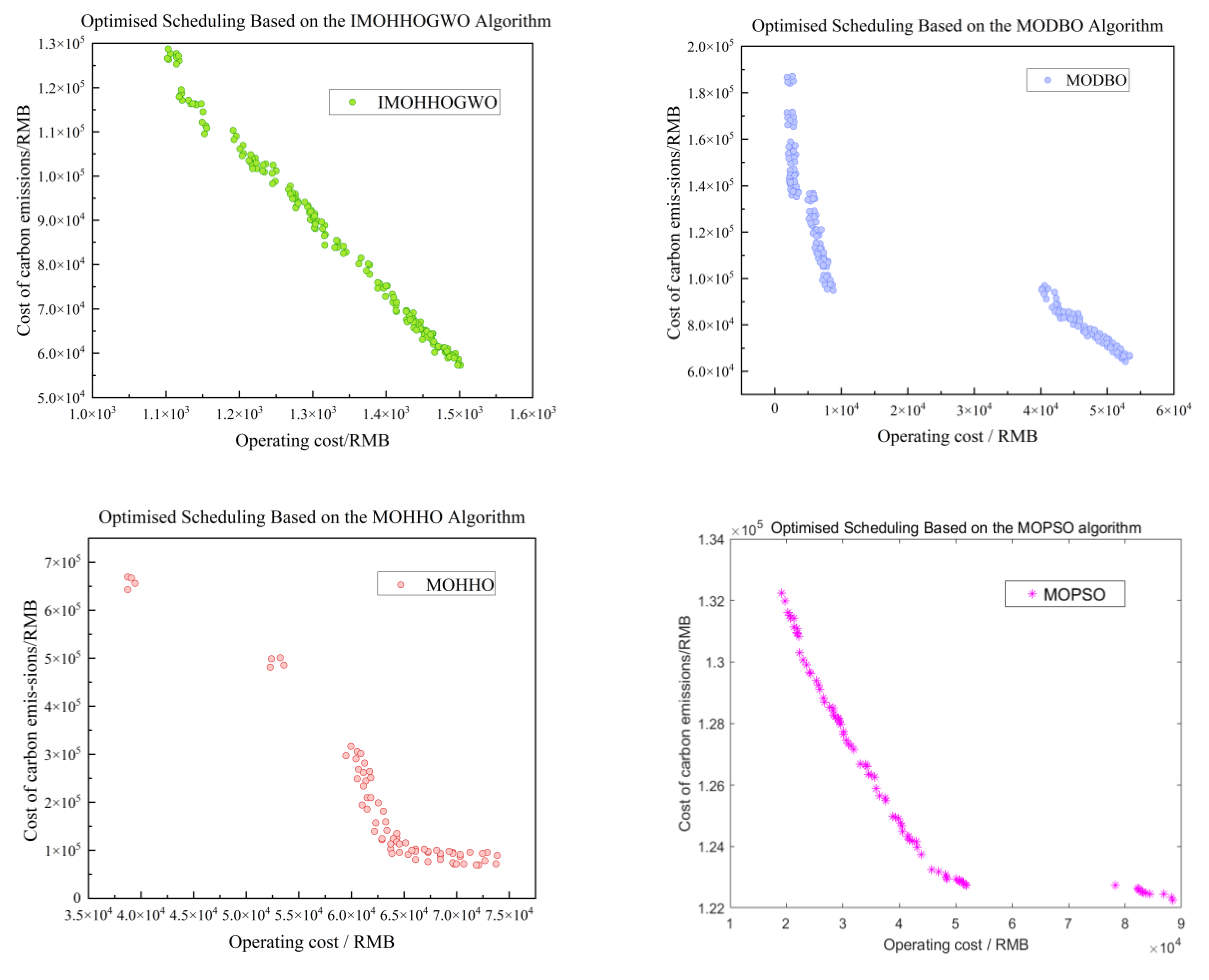
5.3. Multi-Objective Optimization Scheduling vs. Single-Objective Optimization Scheduling
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, X.; Qi, S.; Wang, Z.; Duan, C.; Wang, X.; Li, F. Optimal scheduling for microgrids with hydrogen fueling stations considering uncertainty using data-driven approach. Appl. Energy 2019, 253, 113568. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Yang, Z. Optimal scheduling of isolated microgrids using automated reinforcement learning-based multi-period forecasting. IEEE Trans. Sustain. Energy 2021, 13, 159–169. [Google Scholar] [CrossRef]
- Gbadega, P.A.; Sun, Y.; Balogun, O.A. Advanced control technique for optimal power management of a prosumer-centric residential microgrid. IEEE Access 2024, 12, 163819–163855. [Google Scholar] [CrossRef]
- Aguilar, D.; Quinones, J.J.; Pineda, L.R.; Ostanek, J.; Castillo, L. Optimal scheduling of renewable energy microgrids: A robust multi-objective approach with machine learning-based probabilistic forecasting. Appl. Energy 2024, 369, 123548. [Google Scholar] [CrossRef]
- Gbadega, P.A.; Sun, Y.X. JAYA algorithm-based energy management for a grid-connected micro-grid with PV-wind-microturbine-storage energy system. Int. J. Eng. Res. Afr. 2023, 63, 159–184. [Google Scholar] [CrossRef]
- Chen, H.; Yang, S.; Chen, J.; Wang, X.; Li, Y.; Shui, S.; Yu, H. Low-carbon environment-friendly economic optimal scheduling of multi-energy microgrid with integrated demand response considering waste heat utilization. J. Clean. Prod. 2024, 450, 141415. [Google Scholar] [CrossRef]
- Gbadega, P.A.; Sun, Y.; Balogun, O.A. A Unified Optimization Framework for Cost-Effective and Voltage-Stable Operation of Renewable Energy-Based Microgrids Using Mixed-Integer Nonlinear Programming. e-Prime-Advances in Electrical Engineering. Electron. Energy 2025, 12, 101010. [Google Scholar]
- Gbadega, P.A.; Balogun, O.A. Transactive energy management for efficient scheduling and storage utilization in a grid-connected renewable energy-based microgrid. e-Prime-Advances in Electrical Engineering. Electron. Energy 2025, 11, 100914. [Google Scholar]
- Li, C.; Li, C.; Song, L.; Zhang, N.; Lin, D. Multi-Objective Optimal Scheduling of Microgrids Based on Improved Particle Swarm Optimization Algorithm. In Proceedings of the 2024 IEEE 7th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 20–22 September 2024; Volume 7, pp. 1081–1086. [Google Scholar]
- Zhang, X.; Yang, Y.; Zhao, H.; Luo, Y.; Xu, X. Two-stage optimal scheduling of an islanded microgrid considering uncertainties of renewable energy. Int. J. Electr. Power Energy Syst. 2024, 162, 110324. [Google Scholar] [CrossRef]
- Liu, C. An improved Harris hawks optimizer for job-shop scheduling problem. J. Supercomput. 2021, 77, 14090–14129. [Google Scholar] [CrossRef]
- Kumar, V.M.; Chokkalingam, B.; Mihet-Popa, L. Mitigation of complexity in charging station allocation for EVs using chaotic harris hawks optimization charge scheduling algorithm. IEEE Access 2023, 11, 130466–130482. [Google Scholar] [CrossRef]
- Shaker, Y.O.; Yousri, D.; Osama, A.; Al-Gindy, A.; Tag-Eldin, E.; Allam, D. Optimal charging/discharging decision of energy storage community in grid-connected microgrid using multi-objective hunger game search optimizer. IEEE Access 2021, 9, 120774–120794. [Google Scholar] [CrossRef]
- Al-Shamma’a, A.A.; Hussein Farh, H.M.; Noman, A.M.; Al-Shaalan, A.M.; Alkuhayli, A. Optimal Sizing of a Hybrid Renewable Photovoltaic-Wind System-Based Microgrid Using Harris Hawk Optimizer. Int. J. Photoenergy 2022, 2022, 4825411. [Google Scholar] [CrossRef]
- Choo, Y.H.; Cai, Z.; Le, V.; Johnstone, M.; Chan, W.K.; Creighton, D. Multi-objective flexible job-shop scheduling with an ensemble optimisation model. In Proceedings of the 2022 IEEE Industrial Electronics and Applications Conference (IEACon), Kuala Lumpur, Malaysia, 3–4 October 2022; pp. 229–234. [Google Scholar]
- Rajagopalan, A.; Nagarajan, K.; Montoya, O.D.; Dhanasekaran, S.; Kareem, I.A.; Perumal, A.S.; Lakshmaiya, N.; Paramasivam, P. Multi-objective optimal scheduling of a microgrid using oppositional gradient-based grey wolf optimizer. Energies 2022, 15, 9024. [Google Scholar] [CrossRef]
- Tang, B.; Shiting, C.; Wang, X.; Yuan, C.; Zhu, R. Optimized operation strategy for energy storage charging piles based on multi-strategy hybrid improved Harris hawk algorithm. Heliyon 2024, 10, e31525. [Google Scholar] [CrossRef] [PubMed]
- Makhadmeh, S.N.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Abasi, A.K.; Alyasseri, Z.A.A. A novel hybrid grey wolf optimizer with min-conflict algorithm for power scheduling problem in a smart home. Swarm Evol. Comput. 2021, 60, 100793. [Google Scholar] [CrossRef]
- Yue, Y.; Ren, H.; Liu, D.; Zhang, L. Optimal Scheduling of Microgrids Based on an Improved Dung Beetle Optimization Algorithm. Appl. Sci. 2025, 15, 975. [Google Scholar] [CrossRef]
- Yang, M.; Cui, Y.; Wang, J. Multi-Objective optimal scheduling of island microgrids considering the uncertainty of renewable energy output. Int. J. Electr. Power Energy Syst. 2023, 144, 108619. [Google Scholar] [CrossRef]
- Bidgoli, M.A.; Ahmadian, A. Multi-stage optimal scheduling of multi-microgrids using deep-learning artificial neural network and cooperative game approach. Energy 2022, 239, 122036. [Google Scholar] [CrossRef]
- Dey, B.; Raj, S.; Mahapatra, S.; Márquez, F.P.G. Optimal scheduling of distributed energy resources in microgrid systems based on electricity market pricing strategies by a novel hybrid optimization technique. Int. J. Electr. Power Energy Syst. 2022, 134, 107419. [Google Scholar] [CrossRef]
- Mianaei, P.K.; Aliahmadi, M.; Faghri, S.; Ensaf, M.; Ghasemi, A.; Abdoos, A.A. Chance-constrained programming for optimal scheduling of combined cooling, heating, and power-based microgrid coupled with flexible technologies. Sustain. Cities Soc. 2022, 77, 103502. [Google Scholar] [CrossRef]
- Basak, S.; Bhattacharyya, B. Optimal scheduling in demand-side management based grid-connected microgrid system by hybrid optimization approach considering diverse wind profiles. ISA Trans. 2023, 139, 357–375. [Google Scholar] [CrossRef] [PubMed]
- Bian, Z.; Zhang, Q. Combined compromise solution and blockchain-based structure for optimal scheduling of renewable-based microgrids: Stochastic information approach. Sustain. Cities Soc. 2022, 76, 103441. [Google Scholar] [CrossRef]
- Singh, B.; Sharma, A.K. Benefit maximization and optimal scheduling of renewable energy sources integrated system considering the impact of energy storage device and Plug-in Electric vehicle load demand. J. Energy Storage 2022, 54, 105245. [Google Scholar] [CrossRef]
- ÇetınbaŞ, İ.; Tamyürek, B.; Demırtaş, M. The hybrid harris hawks optimizer-arithmetic optimization algorithm: A new hybrid algorithm for sizing optimization and design of microgrids. IEEE Access 2022, 10, 19254–19283. [Google Scholar] [CrossRef]
- Sahoo, G.; Sahu, R.K.; Panda, S.; Samal, N.R.; Arya, Y. Modified Harris Hawks optimization-based fractional-order fuzzy PID controller for frequency regulation of multi-micro-grid. Arab. J. Sci. Eng. 2023, 48, 14381–14405. [Google Scholar] [CrossRef]
- Jasim, A.M.; Jasim, B.H.; Bureš, V. A novel grid-connected microgrid energy management system with optimal sizing using hybrid grey wolf and cuckoo search optimization algorithm. Front. Energy Res. 2022, 10, 960141. [Google Scholar] [CrossRef]
- Javidsharifi, M.; Niknam, T.; Aghaei, J.; Mokryani, G.; Papadopoulos, P. Multi-objective day-ahead scheduling of microgrids using modified grey wolf optimizer algorithm. J. Intell. Fuzzy Syst. 2019, 36, 2857–2870. [Google Scholar] [CrossRef]
- Teo, T.T.; Logenthiran, T.; Woo, W.L.; Abidi, K.; John, T.; Wade, N.S. Optimization of fuzzy energy-management system for grid-connected microgrid using NSGA-II. IEEE Trans. Cybern. 2020, 51, 5375–5386. [Google Scholar] [CrossRef]
- Ren, Z.; Qu, X.; Wang, M.; Zou, C. Multi-objective optimization for DC microgrid using combination of NSGA-II algorithm and linear search method. IEEE J. Emerg. Sel. Top. Circuits Syst. 2023, 13, 789–796. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, W.; Wang, H.; Wu, J.; Wang, J. An improved beetle swarm algorithm based on social learning for a game model of multiobjective distribution network reconfiguration. IEEE Access 2020, 8, 200932–200952. [Google Scholar] [CrossRef]
- Anh, H.P.H.; Kien, C.V. Optimal energy management of microgrid using advanced multi-objective particle swarm optimization. Eng. Comput. 2020, 37, 2085–2110. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Qin, Z.; Lu, K.D.; Li, L.M. CMOPEO-OP: Constrained multi-objective population extremal optimization-based optimal planning of standalone microgrids. Swarm Evol. Comput. 2025, 92, 101787. [Google Scholar] [CrossRef]
- Phommixay, S.; Doumbia, M.L.; Lupien St-Pierre, D. Review on the cost optimization of microgrids via particle swarm optimization. Int. J. Energy Environ. Eng. 2020, 11, 73–89. [Google Scholar] [CrossRef]



| Test Function | f1 | f2 |
|---|---|---|
| ZDT1 | ||
| ZDT2 | ||
| ZDT3 |
| ZDT Test Function | Algorithm | IGD | GD | HV | Spacing |
|---|---|---|---|---|---|
| ZDT1 | IMOHHOGWO | 0.005457483 | 0.000160994 | 0.718245734 | 0.010915841 |
| MODBO | 0.105478098 | 0.0134272 | 0.586794498 | 0.01778148 | |
| MOPSO | 0.015991113 | 0.001027113 | 0.701984641 | 0.019467523 | |
| MOHHO | 0.971229064 | 0.149448205 | 0 | 0.072009007 | |
| NSGA-II | 1.030093286 | 0.136262293 | 0 | 0.023899979 | |
| ZDT2 | IMOHHOGWO | 0.005366116 | 4.77685E−05 | 0.443433903 | 0.010412705 |
| MODBO | 0.351724216 | 0.050378461 | 0.109103142 | 0.033920912 | |
| MOPSO | 0.708313239 | 0.190107182 | 0 | 0.099084718 | |
| MOHHO | 2.526116922 | 0.59851304 | 0 | 0.016399538 | |
| NSGA-II | 2.582003529 | 0.917594038 | 0 | 0.00900713 | |
| ZDT3 | IMOHHOGWO | 0.006075159 | 0.000242328 | 0.601626492 | 0.00919141 |
| MODBO | 0.126822825 | 0.022813843 | 0.523296438 | 0.068080756 | |
| MOPSO | 0.084408876 | 0.011523584 | 0.562794384 | 0.030188536 | |
| MOHHO | 0.772131651 | 0.115864593 | 0.090405316 | 0.017544413 | |
| NSGA-II | 0.872717681 | 0.137291279 | 0.040347006 | 0.0244188 |
| Typology | Management Costs (RMB/KW h) | Service Life/Year |
|---|---|---|
| PV | 0.0096 | 20 |
| WT | 0.0296 | 10 |
| MT | 0.0401 | 10 |
| DE | 0.0859 | 10 |
| Type of Pollutant | Pollutant Emission Factor (g/KW h) | Cost of Governance (RMB/KG) | |
|---|---|---|---|
| DE | MT | ||
| 1.400 | 1.600 | 0.092 | |
| 21.800 | 0.440 | 27.540 | |
| 0.454 | 0.008 | 6.490 | |
| Typology | Parametric | Numerical Value | Parametric | Numerical Value |
|---|---|---|---|---|
| BESS | Maximum capacity/KW h | 150 | Initial capacity/KW h | 50 |
| Minimum capacity/KW h | 5 | Maximum output power/KW | 50 | |
| Maximum Input Power/KW | 30 | Charge and Discharge Rate | 0.9 |
| Electrical Loads (MW) | PV (MW) | WT (MW) | Purchase Price of Electricity from the Grid (KW h) | Price of Electricity Sold to the Grid (KW h) |
|---|---|---|---|---|
| 52 | 0 | 2 | 0.38 | 0.36 |
| 50 | 0 | 2 | 0.38 | 0.36 |
| 50 | 0 | 2 | 0.38 | 0.36 |
| 51 | 0 | 2 | 0.38 | 0.36 |
| 55 | 0 | 2 | 0.38 | 0.36 |
| 63 | 0 | 1 | 0.38 | 0.36 |
| 70 | 0 | 2 | 0.82 | 0.36 |
| 74 | 0 | 1 | 0.82 | 0.36 |
| 75 | 4 | 2 | 0.82 | 0.36 |
| 78 | 6 | 3 | 1.35 | 0.36 |
| 76 | 10 | 8 | 1.35 | 0.36 |
| 62 | 12 | 10 | 1.35 | 0.36 |
| 60 | 23 | 4 | 1.35 | 0.36 |
| 60 | 20 | 3 | 1.35 | 0.36 |
| 68 | 6 | 2 | 0.82 | 0.36 |
| 78 | 4 | 1 | 0.82 | 0.36 |
| 80 | 1 | 2 | 0.82 | 0.36 |
| 85 | 0 | 2 | 1.35 | 0.36 |
| 90 | 0 | 2 | 1.35 | 0.36 |
| 88 | 0 | 3 | 1.35 | 0.36 |
| 70 | 0 | 2.5 | 1.35 | 0.36 |
| 65 | 0 | 2.5 | 1.35 | 0.36 |
| 63 | 0 | 2 | 0.38 | 0.36 |
| 55 | 0 | 1 | 0.38 | 0.36 |
| Equipment Name | Parameters |
|---|---|
| DE | 6–30 KW |
| MT | 3–30 KW |
| Grid | −60–60 KW |
| Algorithm | Dispatch Type | Operating Costs/RMB | Cost of Carbon Emissions/RMB |
|---|---|---|---|
| IMOHHOGWO | Economic Dispatch | 1114.1 | 124,809.2 |
| Environmental Scheduling | 1500.6 | 57,027.2 | |
| Multi-target scheduling | [1114.1, 1500.6] | [57,027.2, 124,809.2] | |
| MODBO | Economic dispatch | 2570.1 | 155,121.9 |
| Environmental scheduling | 5406.2 | 96,022.5 | |
| Multi-target scheduling | [2570.1, 5406.2] | [69,411.8, 155,121.9] | |
| MOHHO | Economic dispatch | 38,726.4 | 669,346.4 |
| Environmental scheduling | 73,867.9 | 69,411.8 | |
| Multi-target scheduling | [38,726.4, 73,867.9] | [96,022.5, 669,346.4] | |
| MOPSO | Economic dispatch | 119,135 | 132,227 |
| Environmental scheduling | 88,187.5 | 122,340 | |
| Multi-target scheduling | [119,135, 88,187.5] | [122,340, 132,227] |
| Algorithm | Time Reduction | Improved Convergence Speed | Increased Pareto Density | Reduced Operating Cost | Reduced Carbon Emission Costs |
|---|---|---|---|---|---|
| MODBO | 12% | 15% | 20% | 56.7% | 19.5% |
| MOHHO | 15% | 18% | 22% | 97.1% | 91.4% |
| MOPSO | 20% | 25% | 15% | 99.1% | 14.5% |
| Feature | Multi-Objective Optimization | Single-Objective (Economic) | Single-Objective (Carbon Emissions) |
|---|---|---|---|
| Energy Storage Utilization | Balanced (charging and discharging) | Primarily discharge, with limited charging | Balanced but higher emphasis on discharge |
| Renewable Energy Usage (PV/WT) | Maximized when available | Limited by economic factors | Maximized to reduce emissions |
| Grid Interaction | Optimized (minimized during peak) | Increased during peak | Increased during low renewable output |
| Backup Generation (DE/MT) | Minimally used | Relatively high during low renewables | Used minimally to reduce emissions |
| Cost Efficiency | Balanced with environmental goals | High, but not environmentally optimized | Higher due to reliance on renewables |
| Carbon Emissions | Reduced due to efficient renewable use | Higher, especially during low renewables | Minimizing emissions is the priority |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, L.; Zhong, H. Optimal Scheduling of Microgrids Based on a Two-Population Cooperative Search Mechanism. Biomimetics 2025, 10, 665. https://doi.org/10.3390/biomimetics10100665
Wei L, Zhong H. Optimal Scheduling of Microgrids Based on a Two-Population Cooperative Search Mechanism. Biomimetics. 2025; 10(10):665. https://doi.org/10.3390/biomimetics10100665
Chicago/Turabian StyleWei, Liming, and Heng Zhong. 2025. "Optimal Scheduling of Microgrids Based on a Two-Population Cooperative Search Mechanism" Biomimetics 10, no. 10: 665. https://doi.org/10.3390/biomimetics10100665
APA StyleWei, L., & Zhong, H. (2025). Optimal Scheduling of Microgrids Based on a Two-Population Cooperative Search Mechanism. Biomimetics, 10(10), 665. https://doi.org/10.3390/biomimetics10100665






