Walking Pattern Generation Through Step-by-Step Quadratic Programming for Biped Robots
Abstract
1. Introduction
- (1)
- We propose a novel step period that includes both single and double support phases, and generate walking trajectories in units of a step by imposing terminal constraints. This approach allows us to shorten the optimization horizon while still generating natural walking trajectories.
- (2)
- We impose boundary constraints on the vertical state of the COM, ensuring the linearity of the optimization problem while allowing for variable COM height.
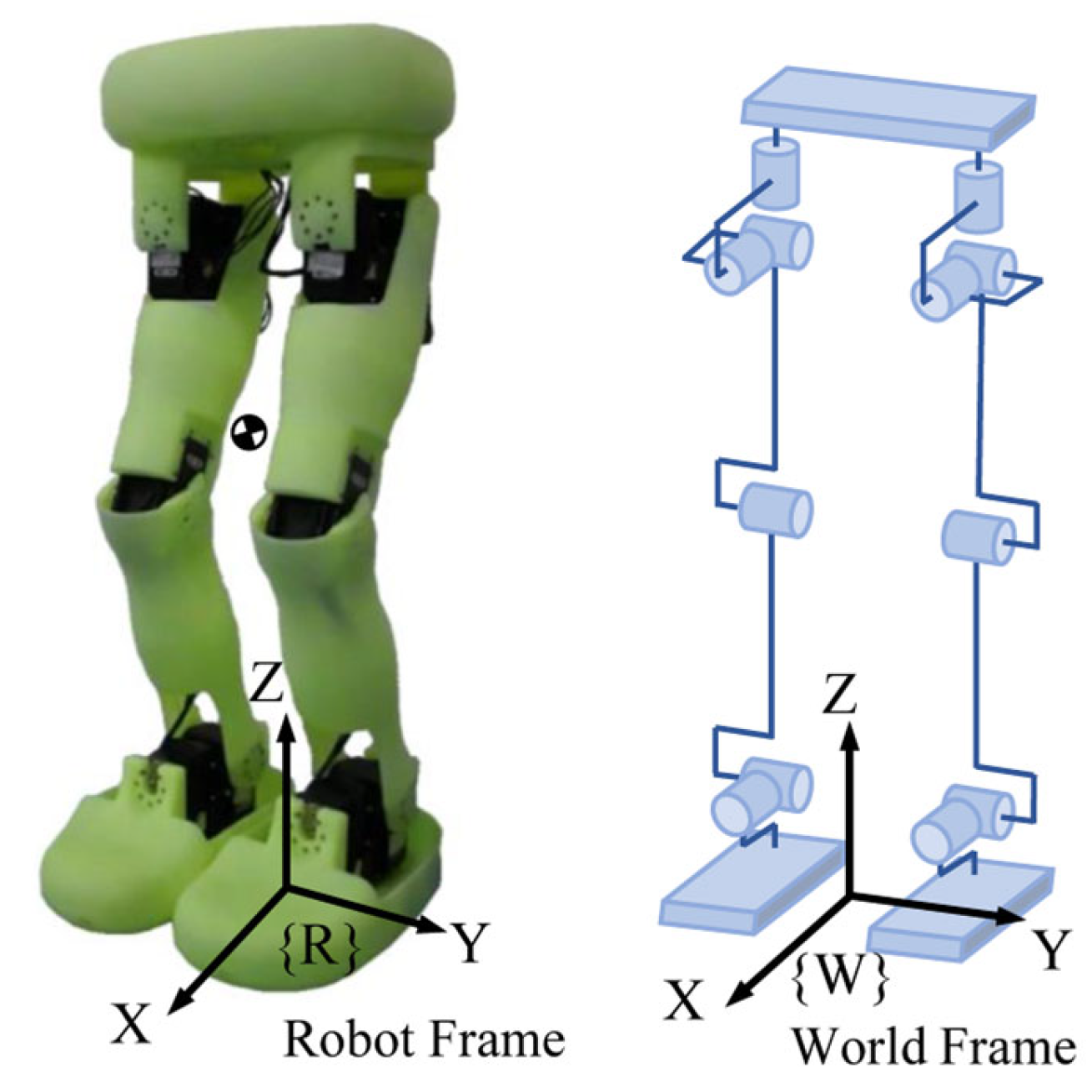
2. Preliminaries
2.1. Motion Model and Constraints
2.2. A Step Period with Double Support
3. Walking Pattern Generation for a Step
3.1. Quadratic Programming Within a Step
3.2. Foot Placement
4. Walking Pattern Generation with Height Variation
4.1. Constraints on the ZMP with Variable COM Height
4.2. Quadratic Programming with Height Variation
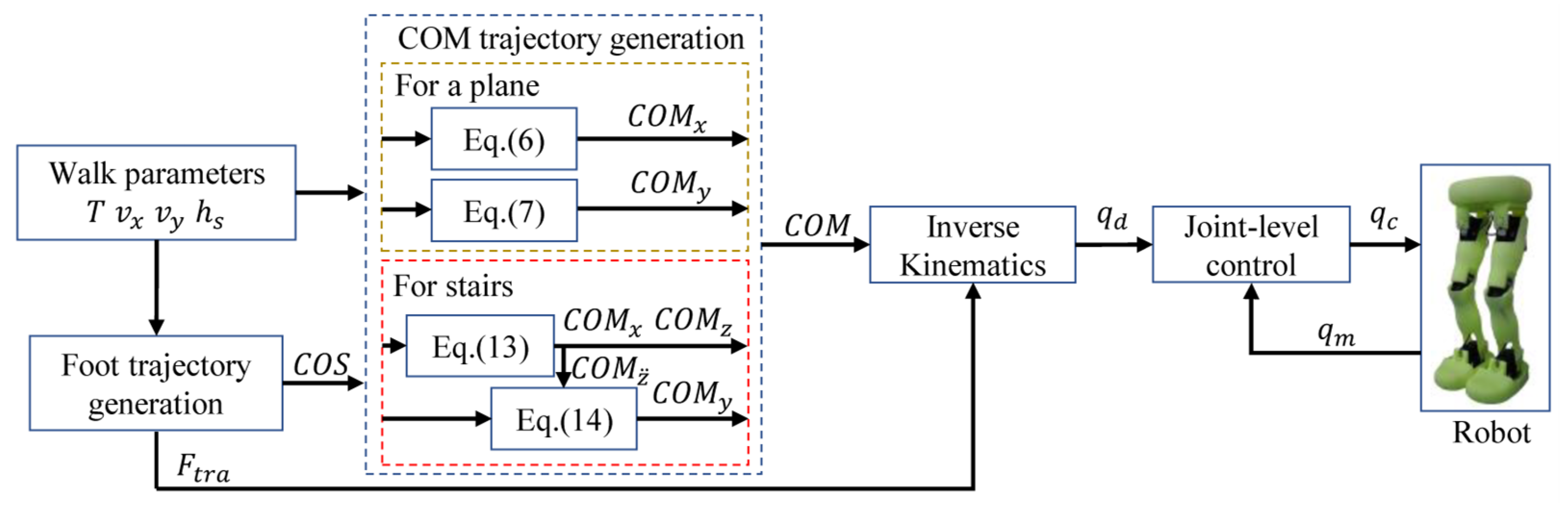
5. Overview of the Control Framework
6. Method Demonstrations
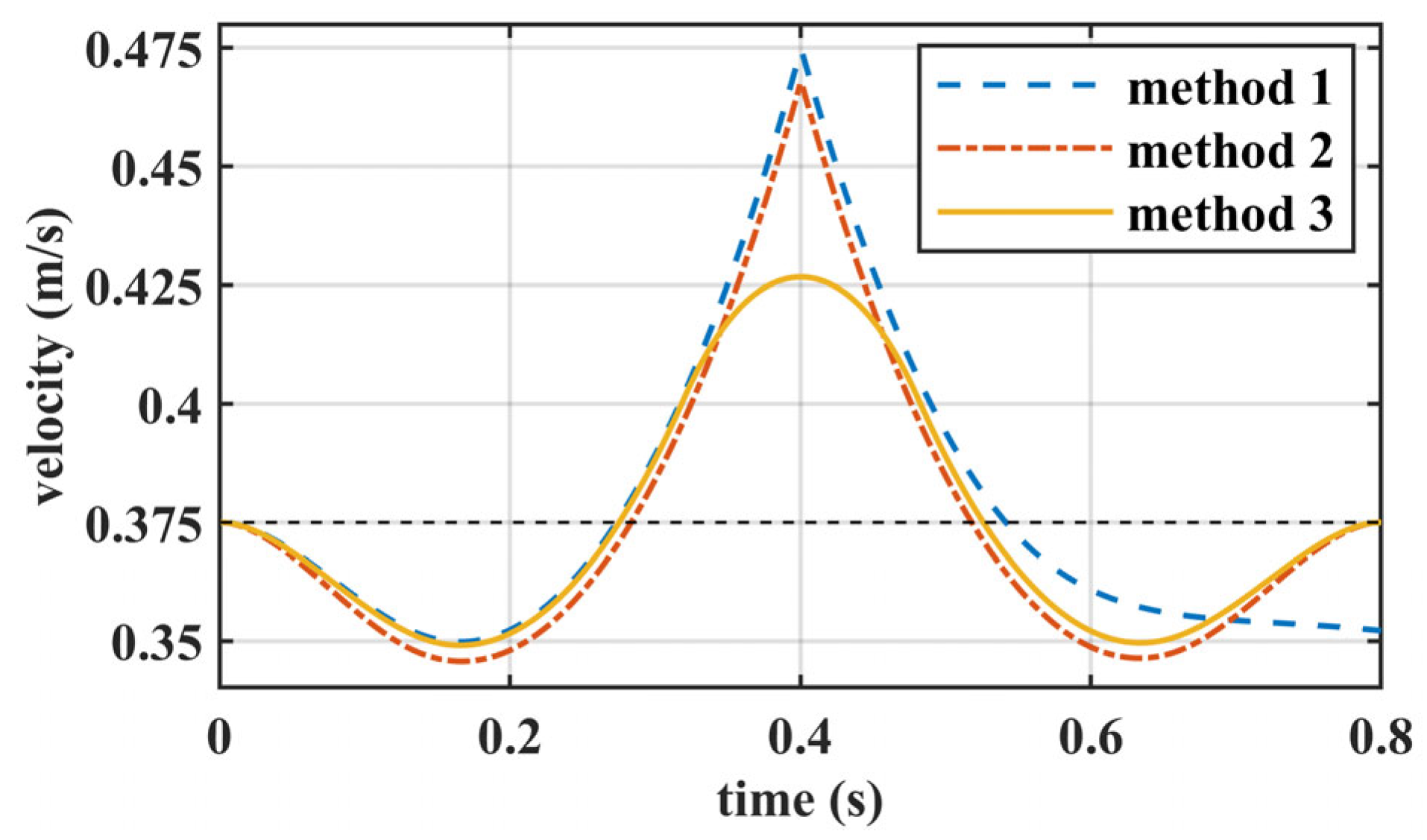
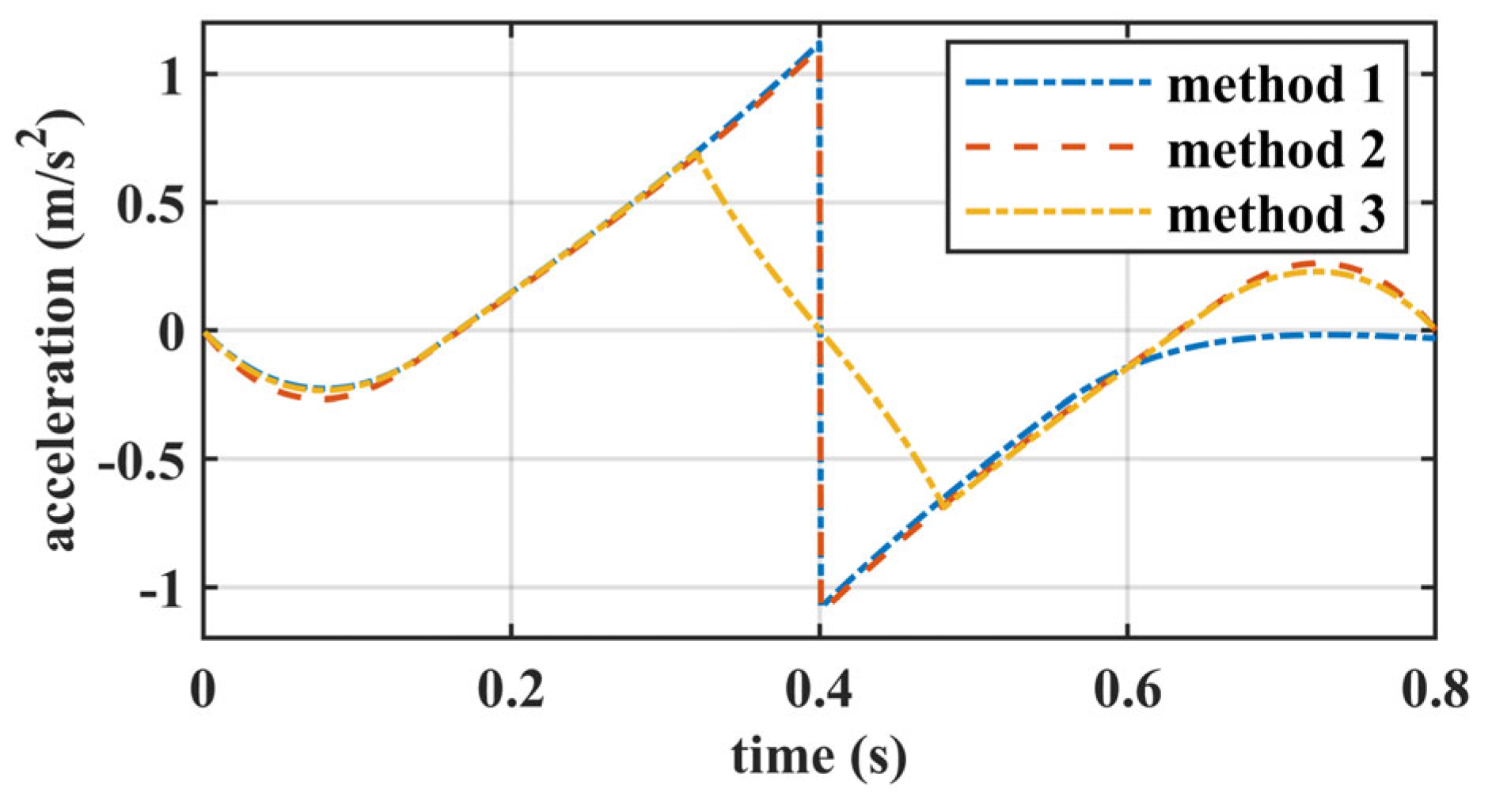
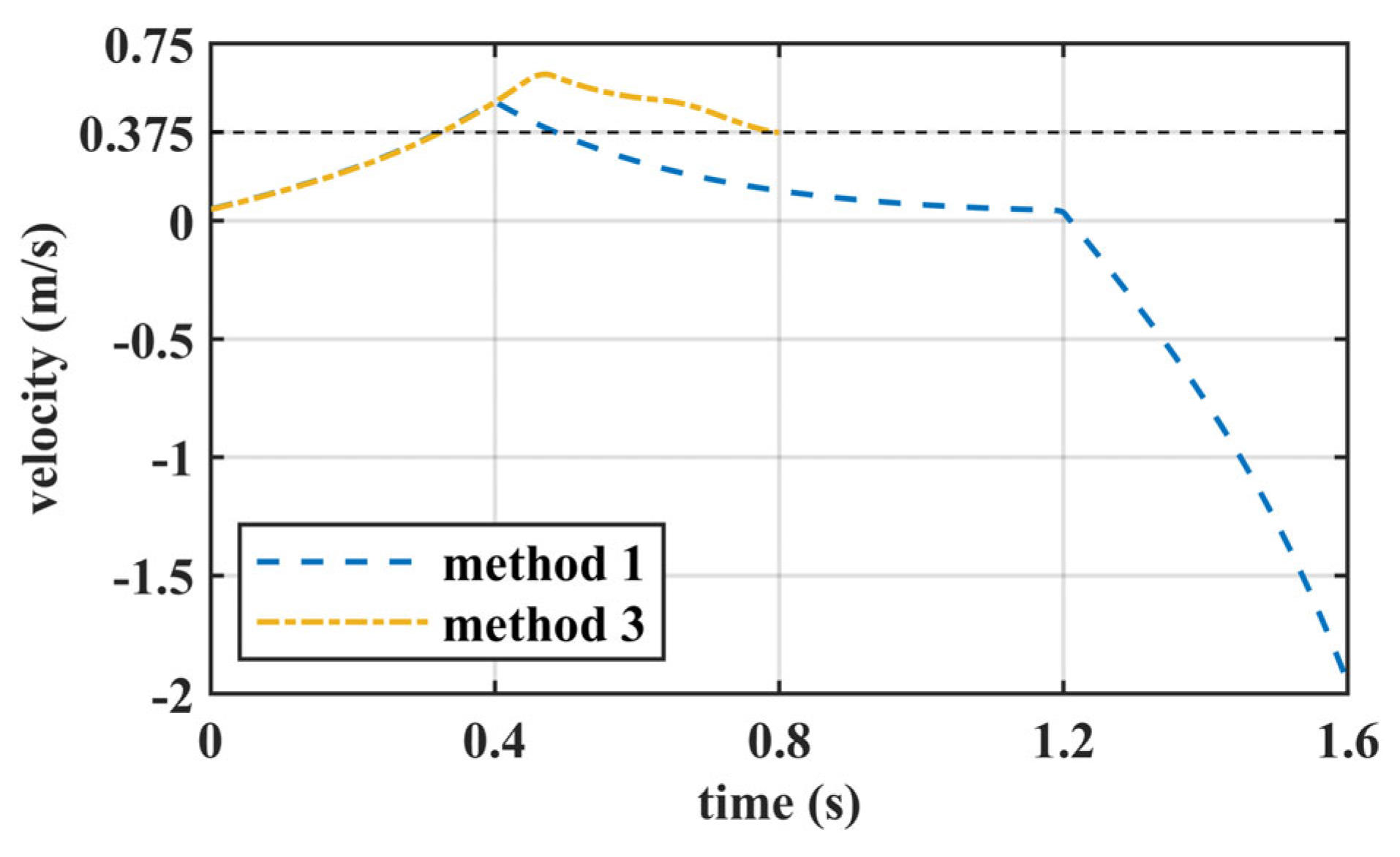
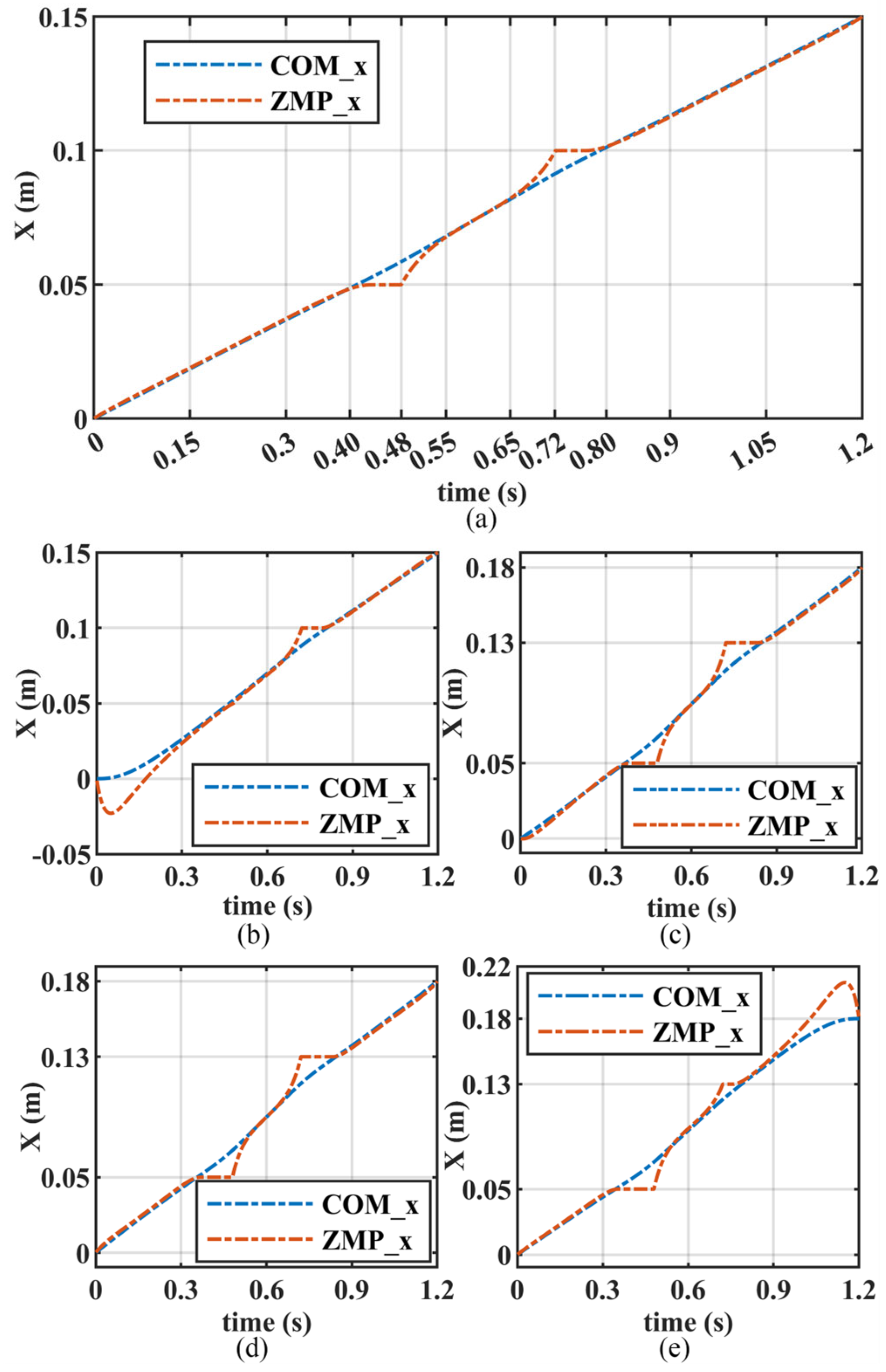
6.1. Numerical Comparison
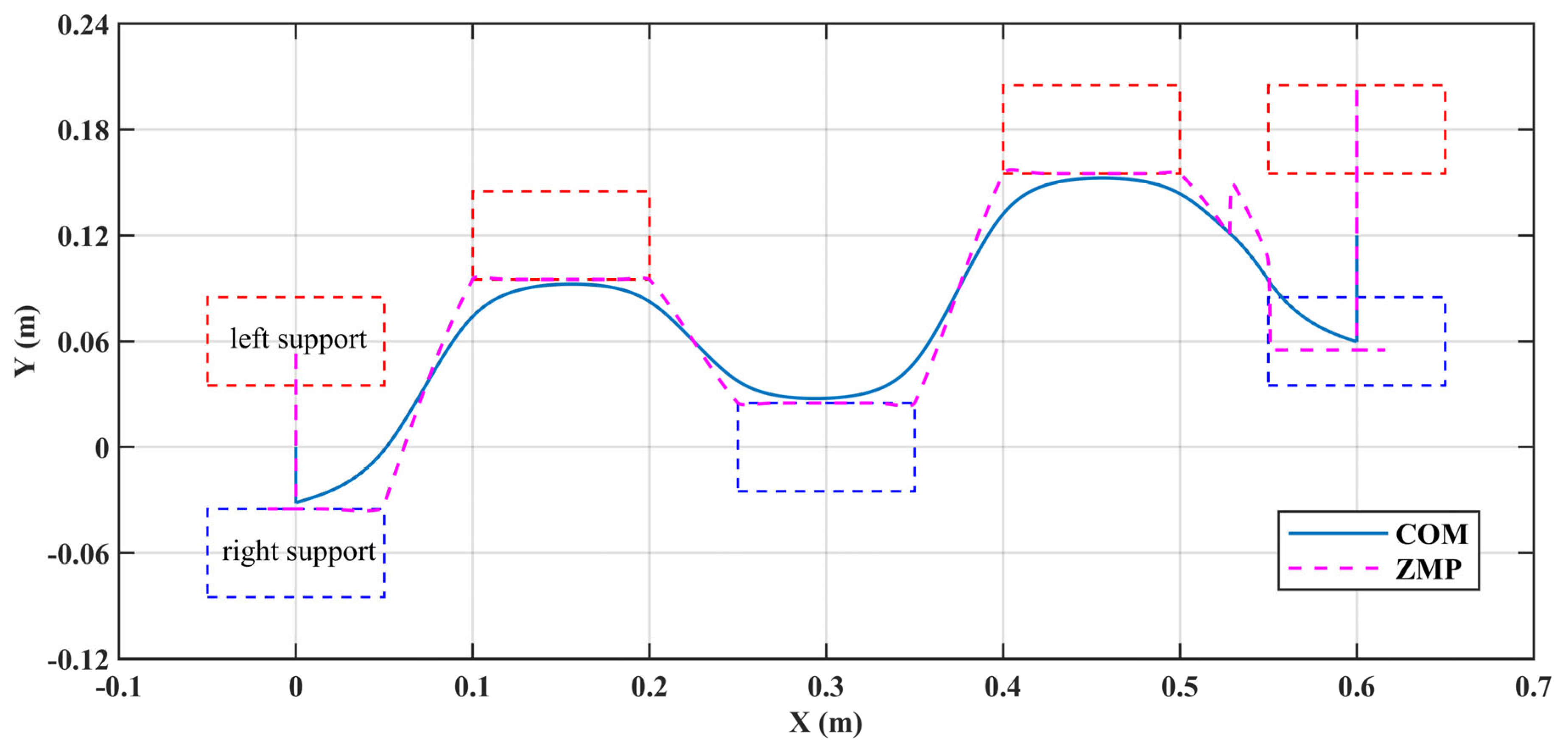
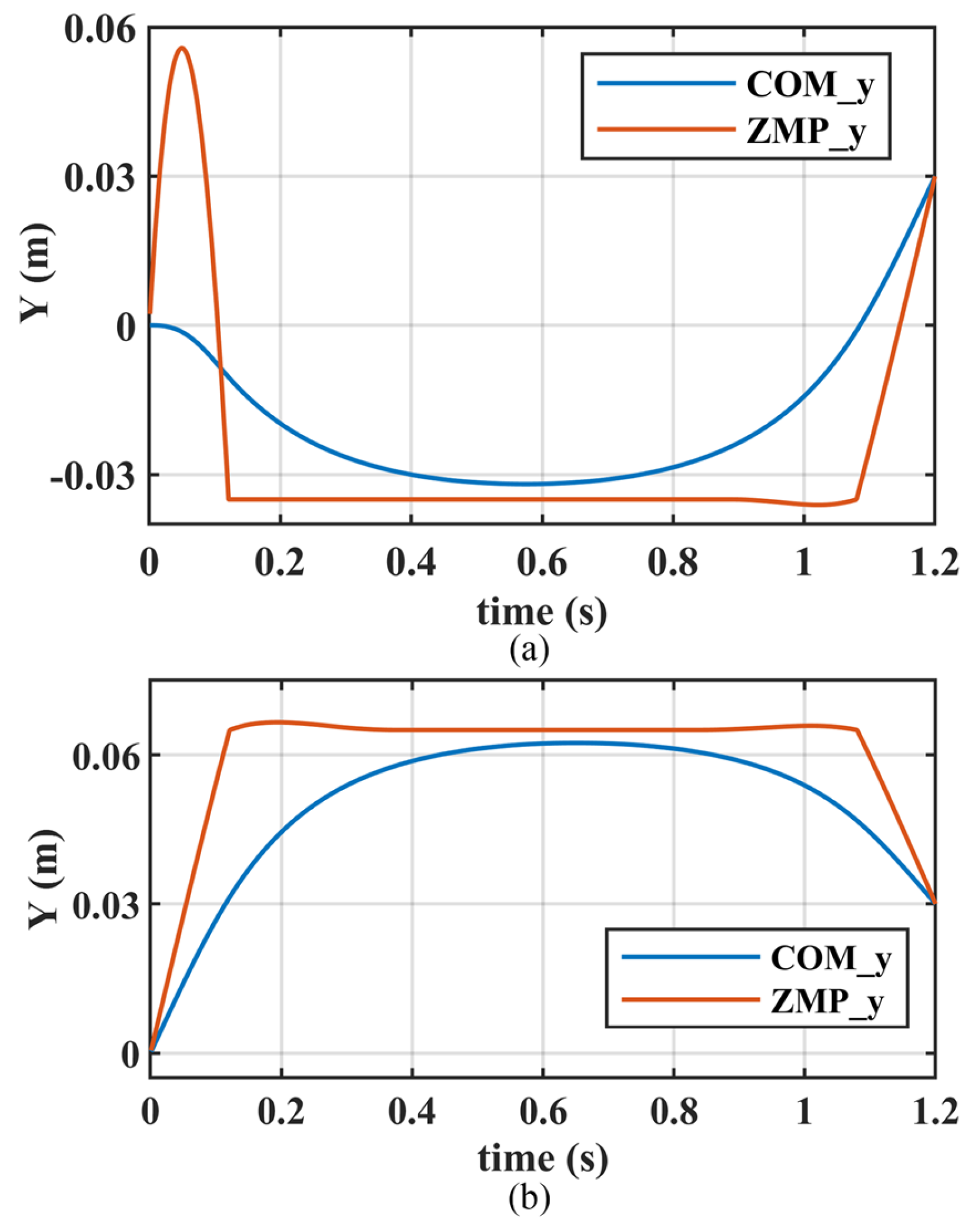
6.2. Walk Simulation on Flat Ground
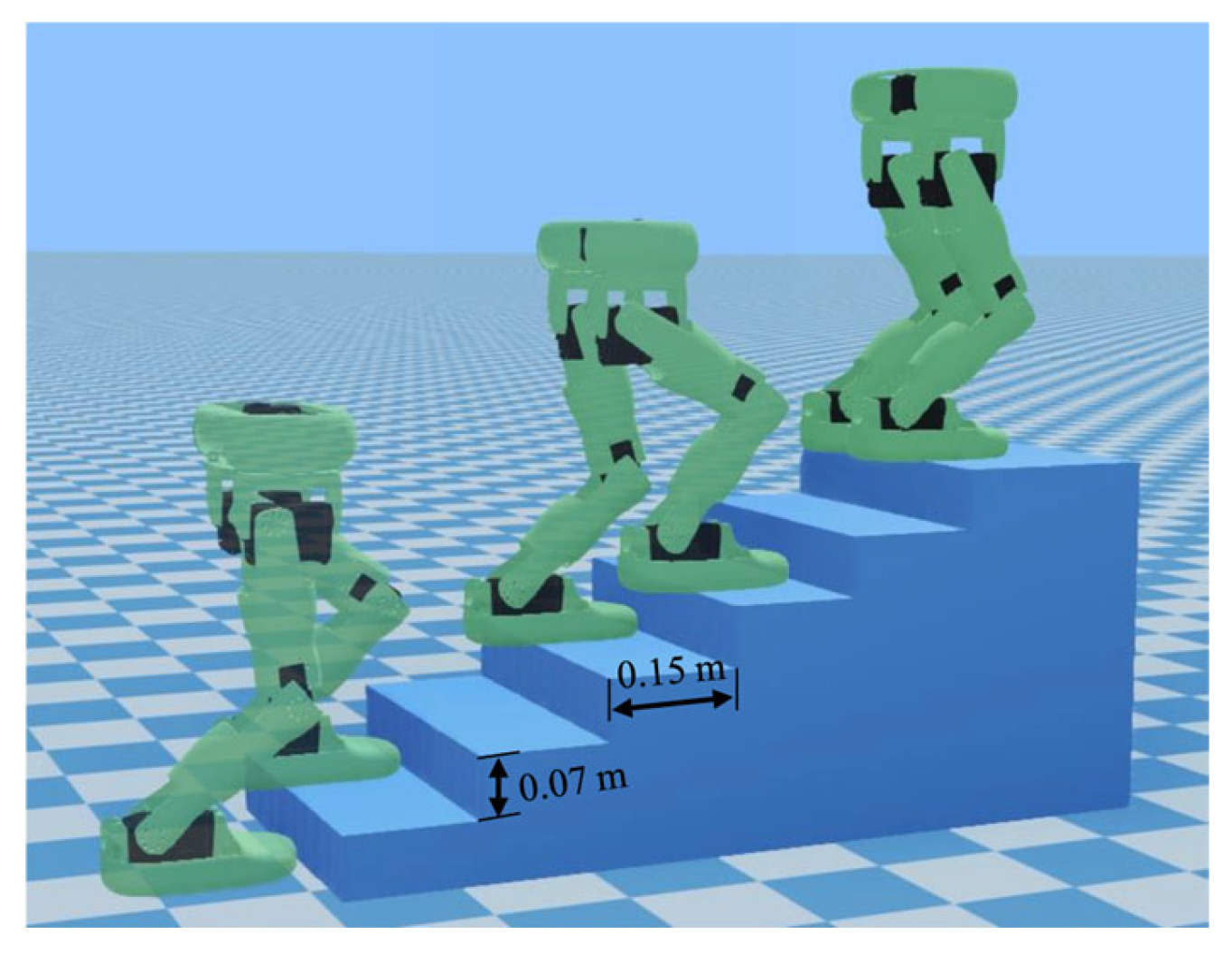
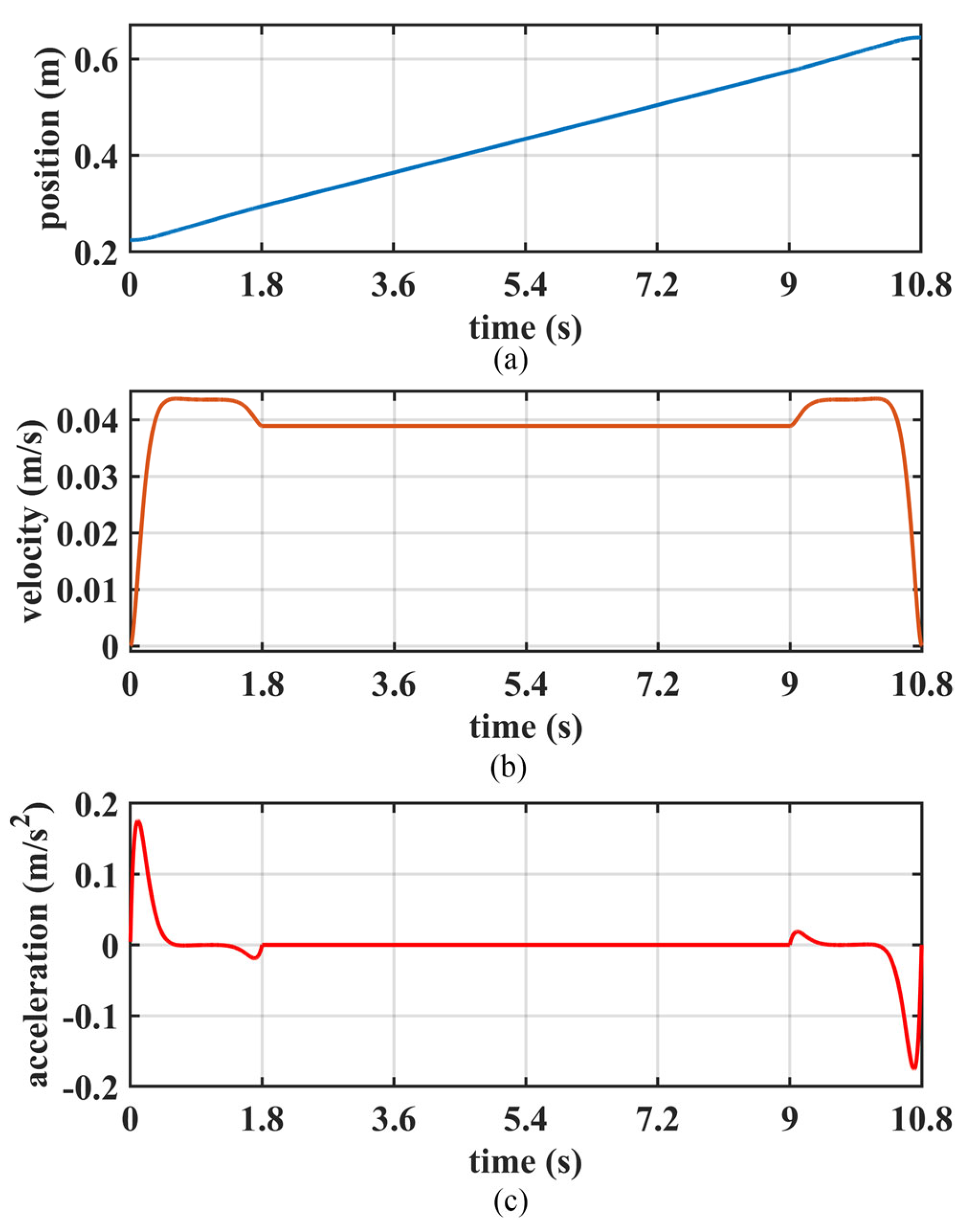
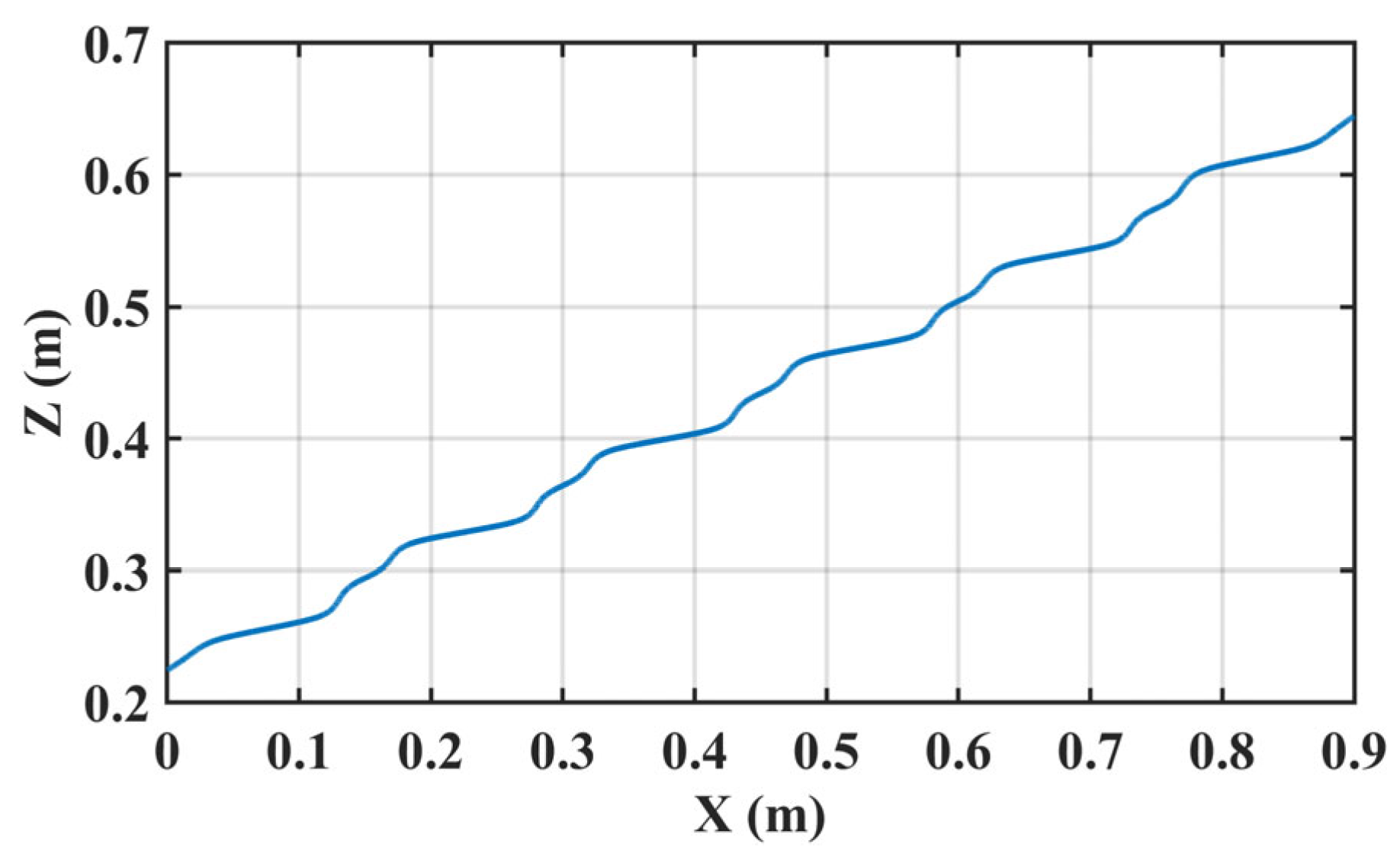
6.3. Walking Simulation on Stairs
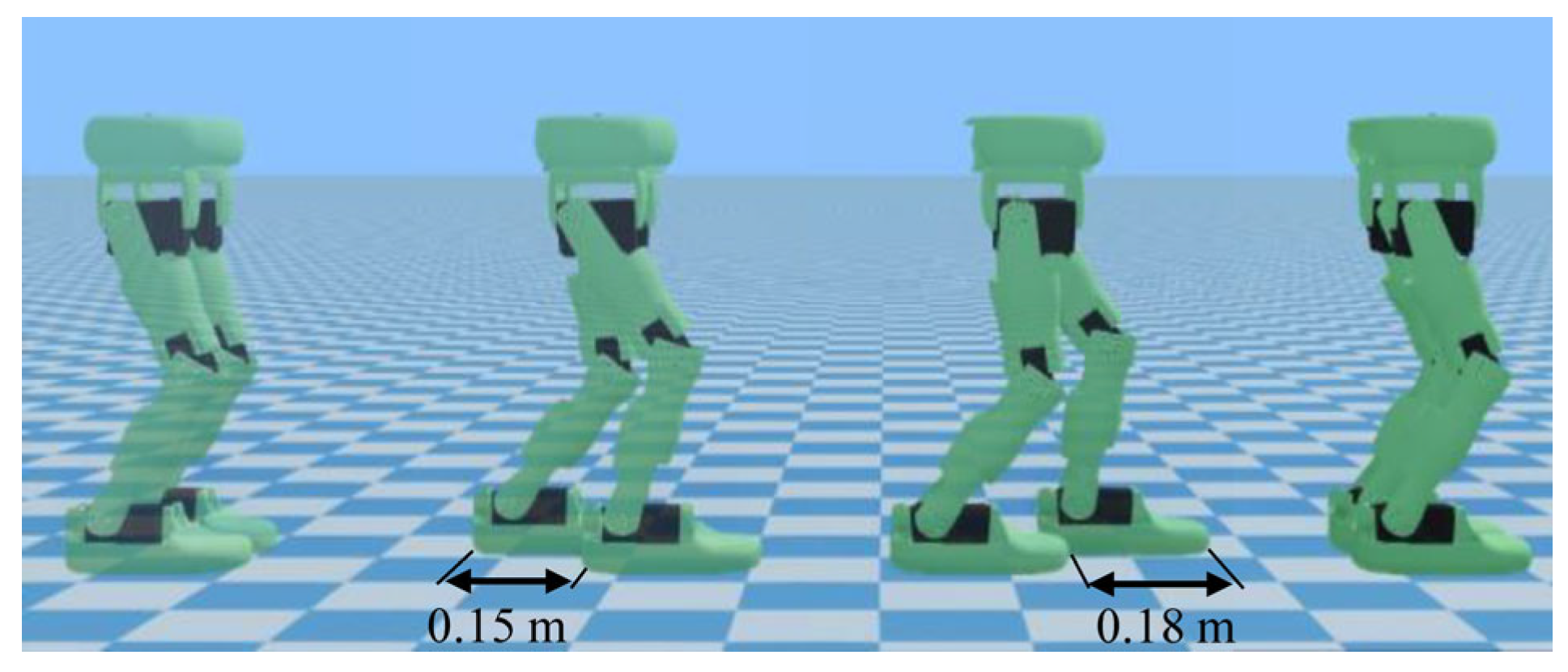
6.4. Walking Experiments
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Erbatur, K.; Kurt, O. Natural ZMP trajectories for biped robot reference generation. IEEE Trans. Ind. Electron. 2009, 56, 835–845. [Google Scholar] [CrossRef]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Biped walking pattern generation by using preview control of zero-moment point. In Proceedings of the IEEE International Conference on Robotics and Automation 2003, Taipei, Taiwan, 14–19 September 2003; Volume 2, pp. 1620–1626. [Google Scholar]
- Wieber, P.-B. Trajectory free linear model predictive control for stable walking in the presence of strong perturbations. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; pp. 137–142. [Google Scholar]
- Diedam, H.; Dimitrov, D.; Wieber, P.-B.; Mombaur, K.; Diehl, M. Online walking gait generation with adaptive foot positioning through linear model predictive control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 1121–1126. [Google Scholar]
- Herdt, A.; Diedam, H.; Wieber, P.-B.; Dimitrov, D.; Mombaur, K.; Diehl, M. Online walking motion generation with automatic footstep placement. Adv. Robot. 2010, 24, 719–737. [Google Scholar] [CrossRef]
- Khadiv, M.; Herzog, A.; Moosavian, S.A.A.; Righetti, L. Walking control based on step timing adaptation. IEEE Trans. Robot. 2020, 36, 629–643. [Google Scholar] [CrossRef]
- Buschmann, T.; Lohmeier, S.; Bachmayer, M.; Ulbrich, H.; Pfeiffer, F. A collocation method for real-time walking pattern generation. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots (Humanoids), Pittsburgh, PA, USA, 29 November–1 December 2007; pp. 1–6. [Google Scholar]
- Takenaka, T.; Matsumoto, T.; Yoshiike, T. Real time motion generation and control for biped robot-1st report: Walking gait pattern generation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 1084–1091. [Google Scholar]
- Tajima, D.; Honda, R.; Suga, K. Fast running experiments involving a humanoid robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Kobe, Japan, 12–17 May 2009; pp. 1571–1576. [Google Scholar]
- Nishiwaki, K.; Kagami, S. Online walking control system for humanoids with short cycle pattern generation. Int. J. Robot. Res. 2009, 28, 729–742. [Google Scholar] [CrossRef]
- Park, J.; Youm, Y. General ZMP preview control for bipedal walking. In Proceedings of the IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 2682–2687. [Google Scholar]
- Englsberger, J.; Koolen, T.; Bertrand, S.; Pratt, J.; Ott, C.; AlbuSchaffer, A. Trajectory generation for continuous leg forces during double support and heel-to-toe shift based on divergent component of motion. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4022–4029. [Google Scholar]
- Yi, S.J.; Lee, D.D. Dynamic heel-strike toe-off walking controller for full-size modular humanoid robots. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Cancun, Mexico, 15–17 November 2016; pp. 395–400. [Google Scholar]
- Hanasaki, S.; Tazaki, Y.; Nagano, H.; Yokokohji, Y. Running trajectory generation including gait transition between walking based on the time-varying linear inverted pendulum mode. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Ginowan, Japan, 28–30 November 2022; pp. 851–857. [Google Scholar]
- Faraji, S.; Pouya, S.; Atkeson, C.G.; Ijspeert, A.J. Versatile and robust 3D walking with a simulated humanoid robot (Atlas): A model predictive control approach. In Proceedings of the IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 1943–1950. [Google Scholar]
- Ding, J.; Zhou, C.; Xin, S.; Xiao, X.; Tsagarakis, N.G. Nonlinear model predictive control for robust bipedal locomotion: Exploring angular momentum and com height changes. Adv. Robot. 2021, 35, 1079–1097. [Google Scholar] [CrossRef]
- Katayama, S.; Murooka, M.; Tazaki, Y. Model predictive control of legged and humanoid robots: Models and algorithms. Adv. Robot. 2023, 37, 298–315. [Google Scholar] [CrossRef]
- Van Heerden, K. Planning COM trajectory with variable height and foot position with reactive stepping for humanoid robots. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6275–6280. [Google Scholar]
- Van, K. Heerden Real-time variable center of mass height trajectory planning for humanoids robots. IEEE Robot. Autom. Lett. 2017, 2, 135–142. [Google Scholar]
- Xie, Z.; Wang, Y.; Luo, X.; Arpenti, P.; Ruggiero, F.; Siciliano, B. Three-dimensional variable center of mass height biped walking using a new model and nonlinear model predictive control. Mech. Mach. Theory 2024, 197, 105651. [Google Scholar] [CrossRef]
- Ryu, K.; Yoo, J.; Back, J.; Park, I.-W. Preview control-based online walking pattern generation for biped robots with vertical center-of-mass motion. Int. J. Precis. Eng. Manuf. 2020, 21, 1653–1661. [Google Scholar] [CrossRef]
- Brasseur, C.; Sherikov, A.; Collette, C.; Dimitrov, D.; Wieber, P.-B. A robust linear MPC approach to online generation of 3D biped walking motion. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Seoul, Republic of Korea, 3–5 November 2015; pp. 595–601. [Google Scholar]
- Ho, Y.-F.; Li, T.-H.S.; Kuo, P.-H.; Ye, Y.-T. Parameterized gait pattern generator based on linear inverted pendulum model with natural ZMP references. Knowl. Eng. Rev. 2016, 32, e3. [Google Scholar] [CrossRef]
- Yu, H.; Gao, H.; Deng, Z. Toward a unified approximate analytical representation for spatially running spring-loaded inverted pendulum model. IEEE Trans. Robot. 2021, 37, 691–698. [Google Scholar] [CrossRef]
- Grant, A.D. Gait analysis: Normal and pathological function. JAMA 2010, 304, 907. [Google Scholar] [CrossRef]
- Sato, T.; Sakaino, S.; Ohashi, E.; Ohnishi, K. Walking trajectory planning on stairs using virtual slope for biped robots. IEEE Trans. Ind. Electron. 2011, 58, 1385–1396. [Google Scholar] [CrossRef]
- Englsberger, J.; Ott, C.; Albu-Schäffer, A. Three-Dimensional Bipedal Walking Control Based on Divergent Component of Motion. IEEE Trans. Robot. 2015, 31, 355–368. [Google Scholar] [CrossRef]
- Joe, H.-M.; Oh, J.-H. A Robust Balance-Control Framework for the Terrain-Blind Bipedal Walking of a Humanoid Robot on Unknown and Uneven Terrain. Sensors 2019, 19, 4194. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Piao, S.; Leng, X.; Wu, Y. Uneven Terrain Walking with Linear and Angular Momentum Allocation. Sensors 2023, 23, 2027. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.-J.; Lim, D.; Park, G.; Lee, K.; Park, J. A Model Predictive Capture Point Control Framework for Robust Humanoid Balancing Via Ankle, Hip, and Stepping Strategies. IEEE Trans. Robot. 2025, 41, 3297–3316. [Google Scholar] [CrossRef]
- Jeong, H.; Lee, I.; Oh, J.; Lee, K.K.; Oh, J.-H. A Robust Walking Controller Based on Online Optimization of Ankle, Hip, and Stepping Strategies. IEEE Trans. Robot. 2019, 35, 1367–1386. [Google Scholar] [CrossRef]
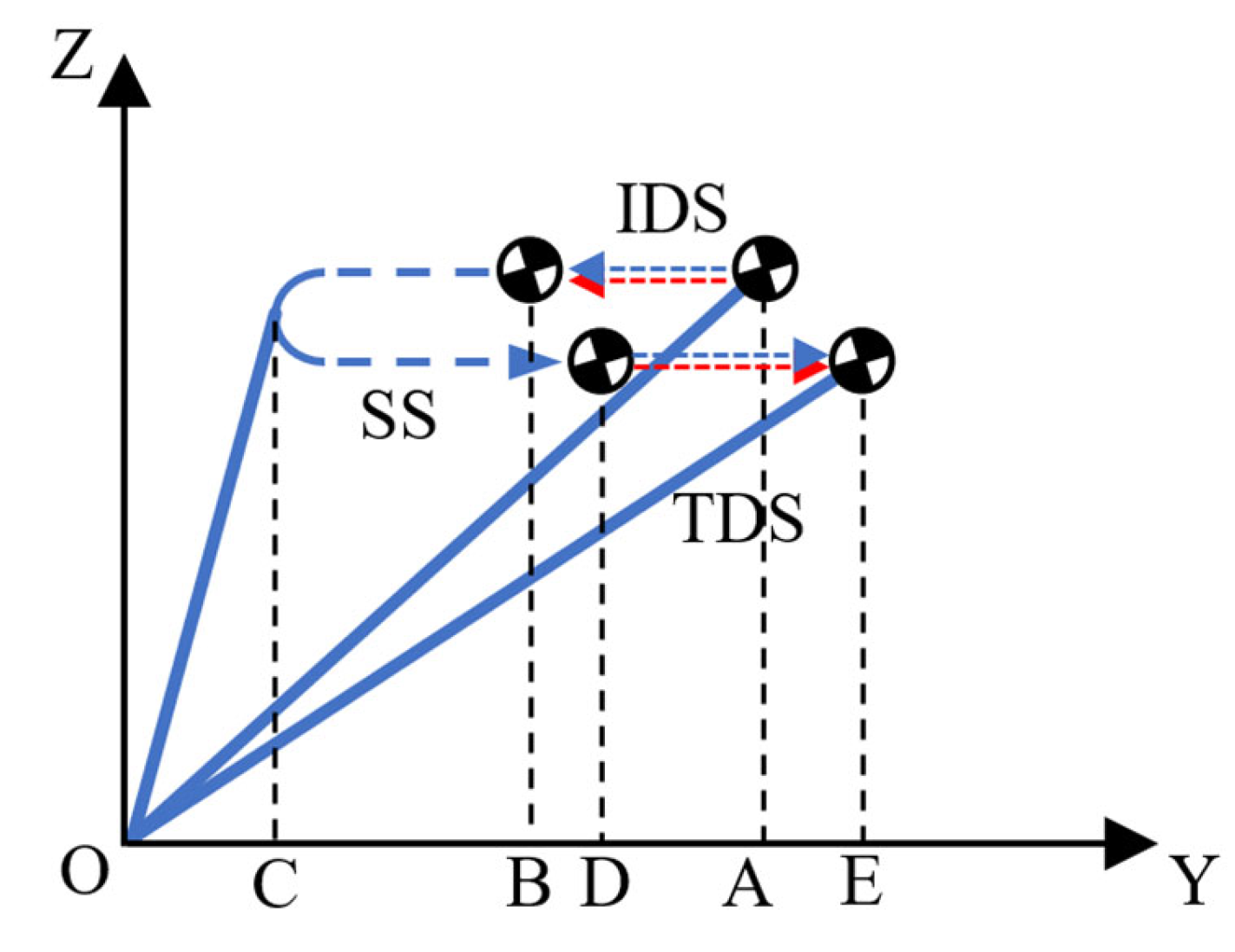
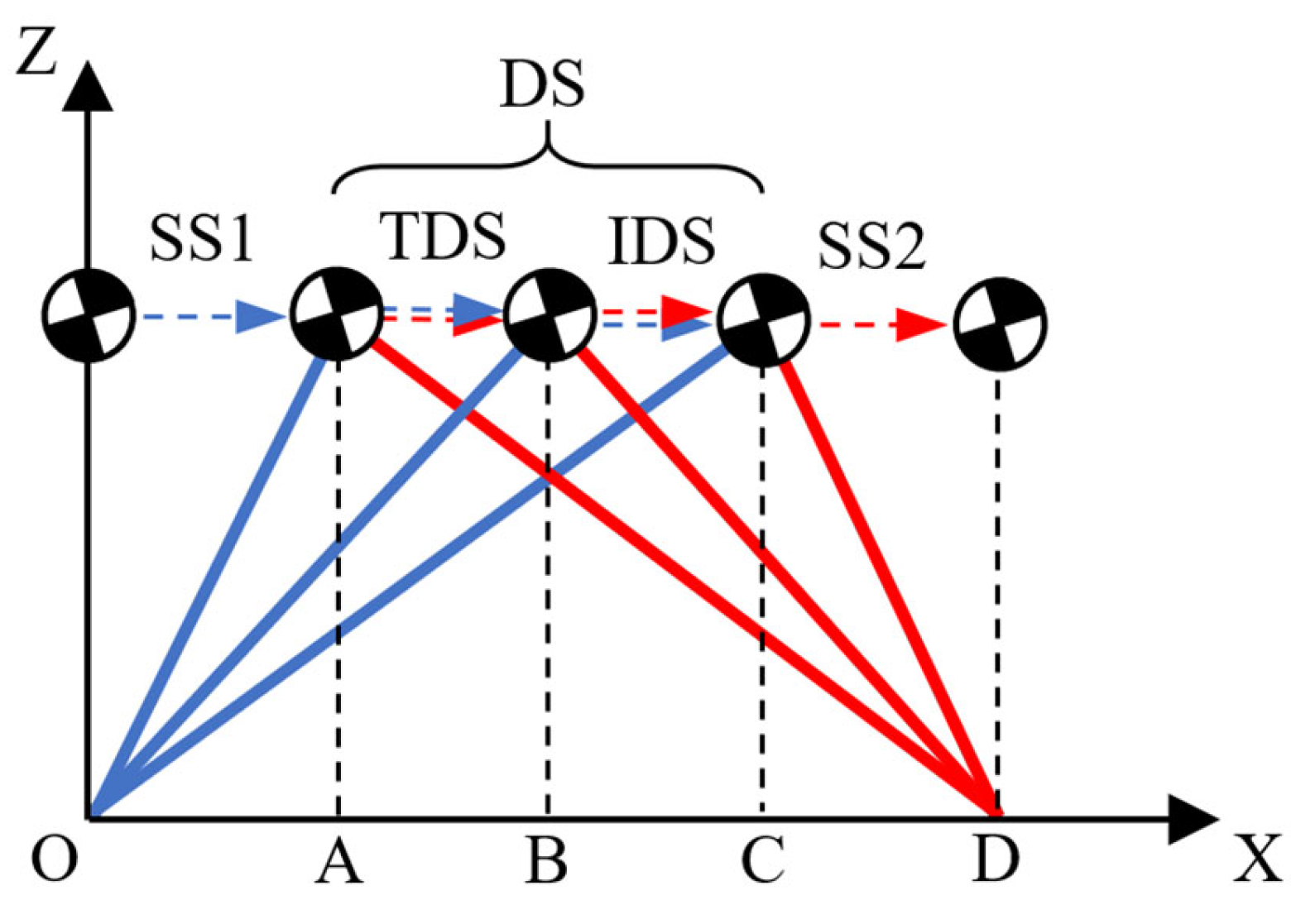


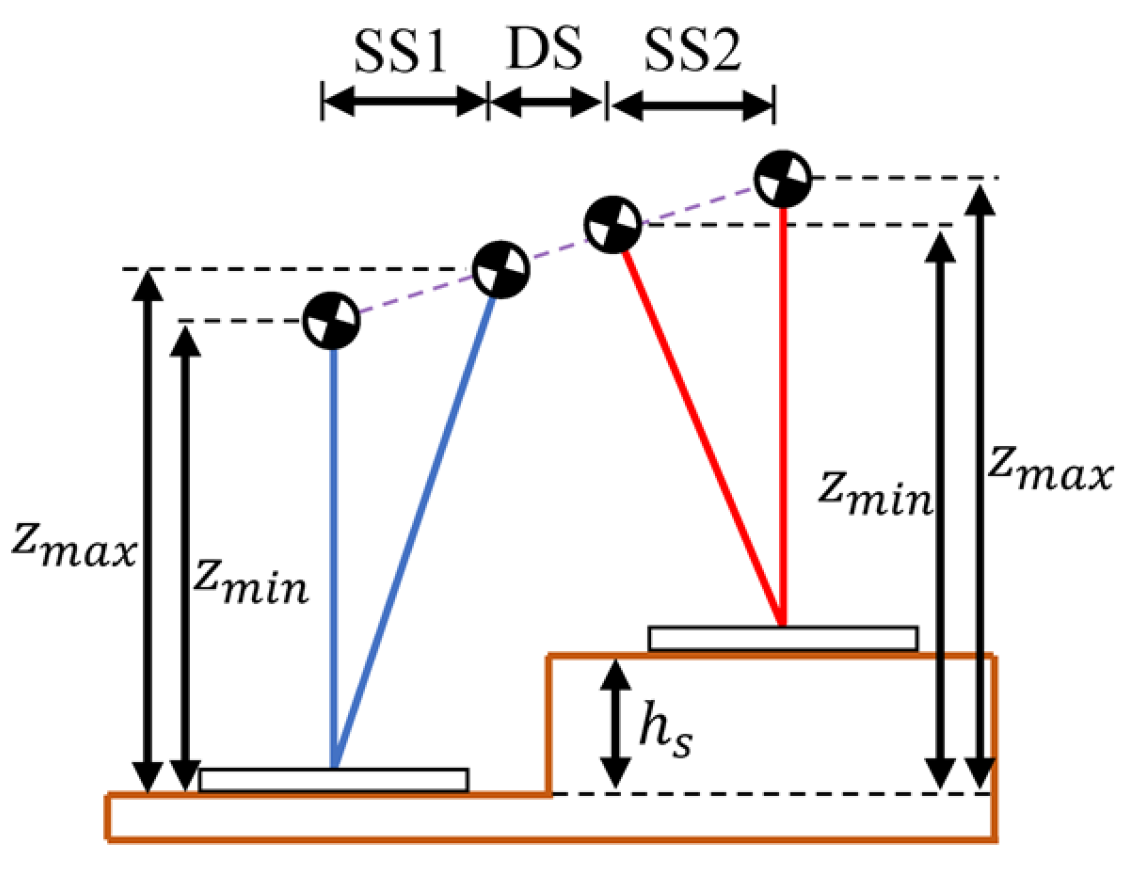



| Stance | 60% | |
| Initial double stance | 10% | |
| Single limb support | 40% | |
| Terminal double stance | 10% | |
| Swing | 40% |
| Step Period | Step Length | COM Height | Support Range | Without Double Support | With Double Support | |||
|---|---|---|---|---|---|---|---|---|
| 0.8 s | 0.3 m | 0.8 s | 0.1 m | 0.4 s | 0.4 s | 0.32 s | 0.16 s | 0.32 s |
| Step Period | Step Length | COM Height | Support Range | SS1 | DS | SS2 |
|---|---|---|---|---|---|---|
| 1.2 s | 0.15 and 0.18 m | 0.27 m | 0.1 m | 0.48 s | 0.24 s | 0.48 s |
| Step Period | COM Height | Support Range | SS1 | DS | SS2 | ||
|---|---|---|---|---|---|---|---|
| 1.2 s | 0.125 m/s | 0.025 m/s | 0.27 m | 0.1 0.05 m | 0.48 s | 0.24 s | 0.48 s |
| Step period | 1.8 s | |
| COM normal height | 0.27 m | |
| Step height | 0.07 m | |
| Support range | 0.2 0.2 m | |
| Acceleration limit | 0.1 9.8 | |
| SS1 | Duration | 0.4 |
| 0 | ||
| DS | Duration | 0.2 |
| SS2 | Duration | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Lu, Z.; Zhang, H.; Liu, Z. Walking Pattern Generation Through Step-by-Step Quadratic Programming for Biped Robots. Biomimetics 2025, 10, 654. https://doi.org/10.3390/biomimetics10100654
Liu G, Lu Z, Zhang H, Liu Z. Walking Pattern Generation Through Step-by-Step Quadratic Programming for Biped Robots. Biomimetics. 2025; 10(10):654. https://doi.org/10.3390/biomimetics10100654
Chicago/Turabian StyleLiu, Guoshuai, Zhiguo Lu, Hang Zhang, and Zeyang Liu. 2025. "Walking Pattern Generation Through Step-by-Step Quadratic Programming for Biped Robots" Biomimetics 10, no. 10: 654. https://doi.org/10.3390/biomimetics10100654
APA StyleLiu, G., Lu, Z., Zhang, H., & Liu, Z. (2025). Walking Pattern Generation Through Step-by-Step Quadratic Programming for Biped Robots. Biomimetics, 10(10), 654. https://doi.org/10.3390/biomimetics10100654






