Q-Learning-Driven Butterfly Optimization Algorithm for Green Vehicle Routing Problem Considering Customer Preference
Abstract
1. Introduction
2. Hybrid Mechanism Butterfly Optimization Algorithm
2.1. Butterfly Optimization Algorithm
| Algorithm 1 BOA |
| Initialize parameters and generate the initial population of N butterflies. |
| Calculate the fitness and choose the best solution. |
| While stopping criteria are not met, do |
| For each butterfly in the population, do |
| Generate fragrance using Equation (1). |
| End for |
| Calculate the fitness and choose the best individual. |
| For each butterfly in the population, do |
| Set r in [0, 1] randomly. |
| If r < p, then |
| Update position using Equation (2) |
| Else |
| Update position using Equation (3). |
| End if |
| End for |
| End while |
| Output the best solution. |
2.2. Q-Learning
2.3. The Adaptive Gaussian Mutation Mechanism
3. Butterfly Optimization Algorithm with Q-Learning (QLBOA)
3.1. Move Formulation Incorporating Gaussian Mutation
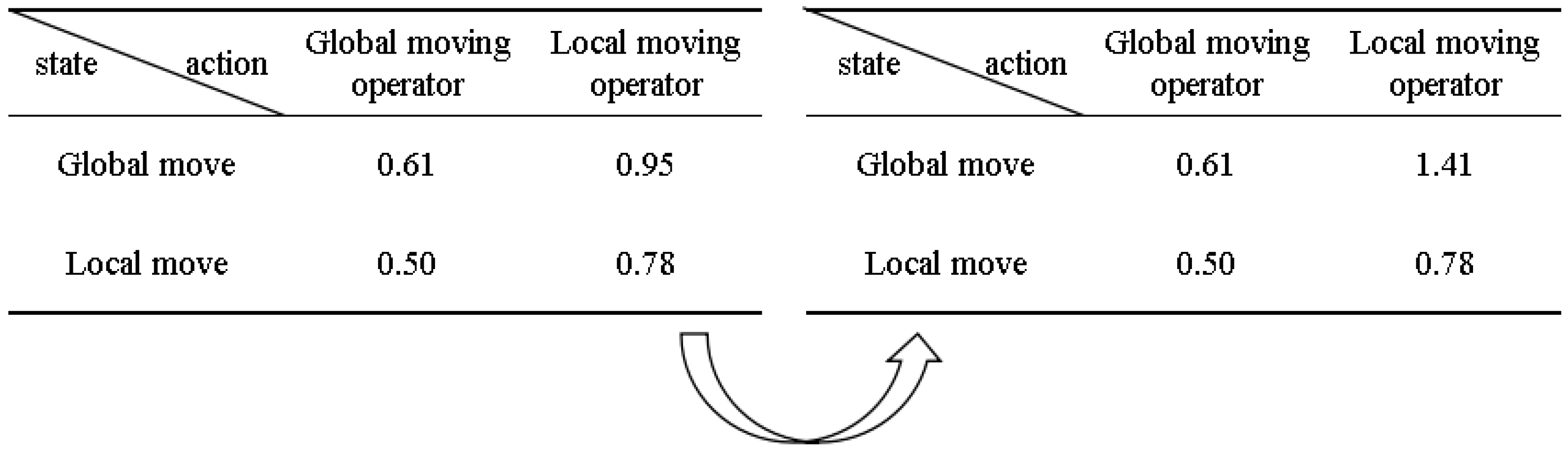
3.2. Update Strategy of Reinforcement Learning
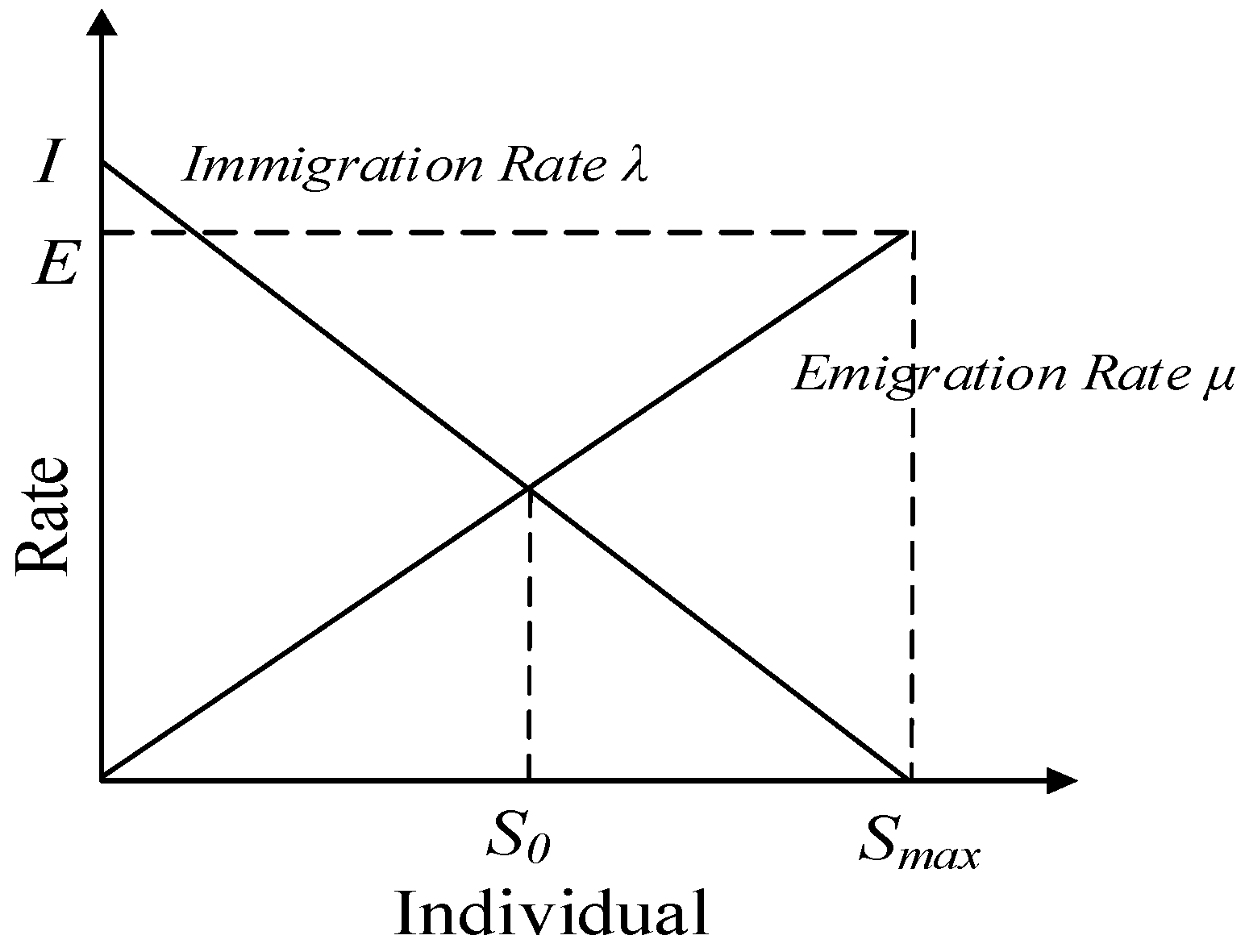
3.3. Migration and Mutation Mechanisms
| Algorithm 2 QLBOA | |
| Generate the initial population of N butterflies. | |
| Calculate the fitness of each search agent. | |
| Sort the fitness and choose the best solution. | |
| While t < 80% of the maximum number of iterations, do | |
| For each butterfly in the population, do | |
| Calculate fragrance | |
| set Q(st, at) = 0 | |
| End for | |
| For each butterfly in the population, do | |
| Select action and state randomly. | |
| Select the best action at from the Q-table. | |
| If action == global search mechanism. then | |
| Update position using Equation (6) | |
| Else | |
| Update position using Equation (7) | |
| End if | |
| Evaluate the butterfly individual and update | |
| End for | |
| End while | |
| While 80% of the maximum number of iterations <= t < maximum number of iterations, do | |
| For each butterfly in the population, do | |
| Calculate the fitness value and choose the elites. | |
| Perform migration and mutation operations. | |
| End for | |
| Calculate the fitness of each search agent. | |
| Sort the fitness and choose the best solution. | |
| End while | |
| Output the best solution. | |
4. Simulation Experiments
4.1. Experimental Setup
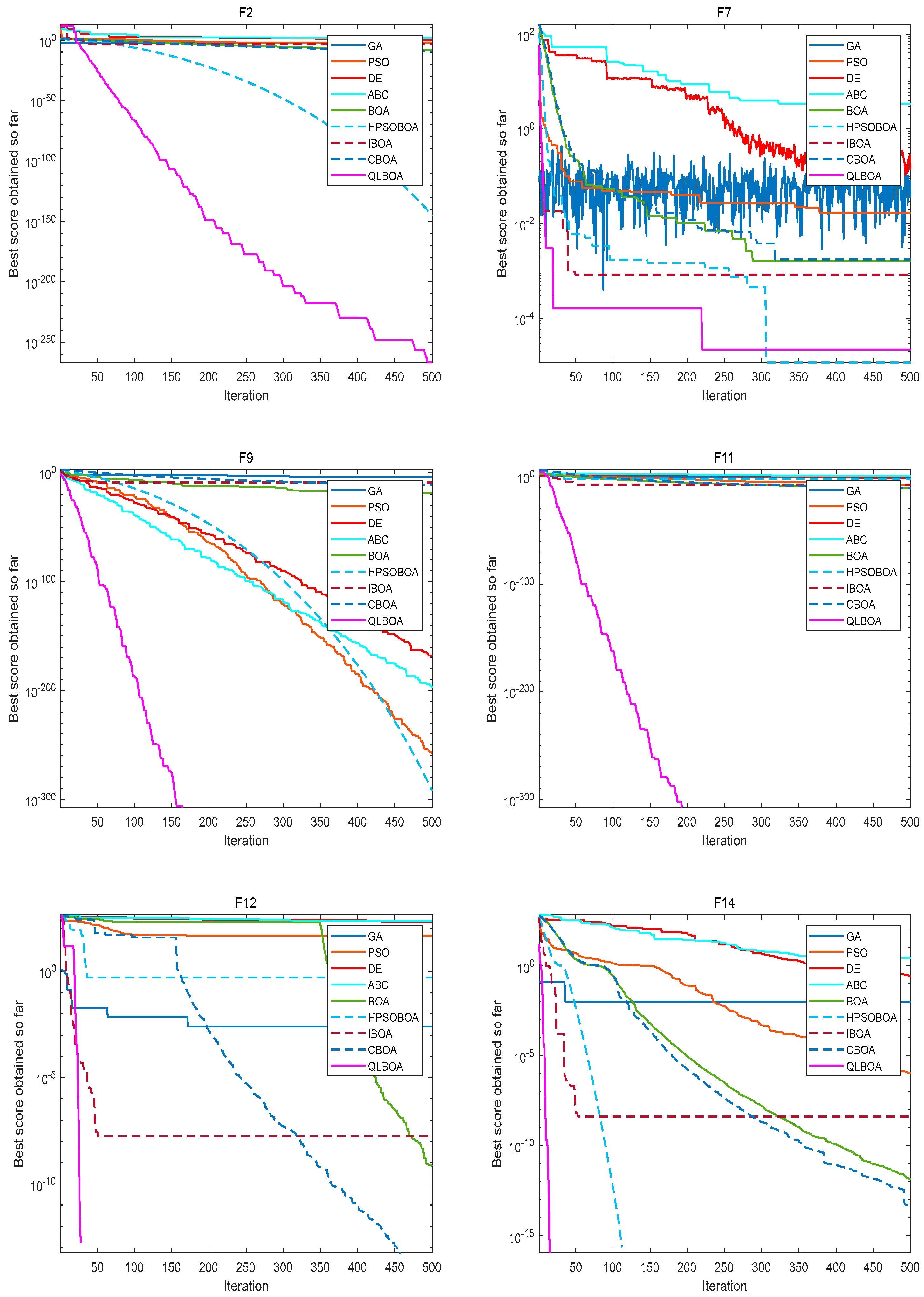
4.2. Analysis and Discussion of 18 Benchmark Functions’ Outcomes
4.3. Analysis and Discussion of CEC2022 Outcomes
4.4. Computational Complexity of BOA and QLBOA
5. The QLBOA Solves the Green Vehicle Routing Problem Considering Customer Preferences
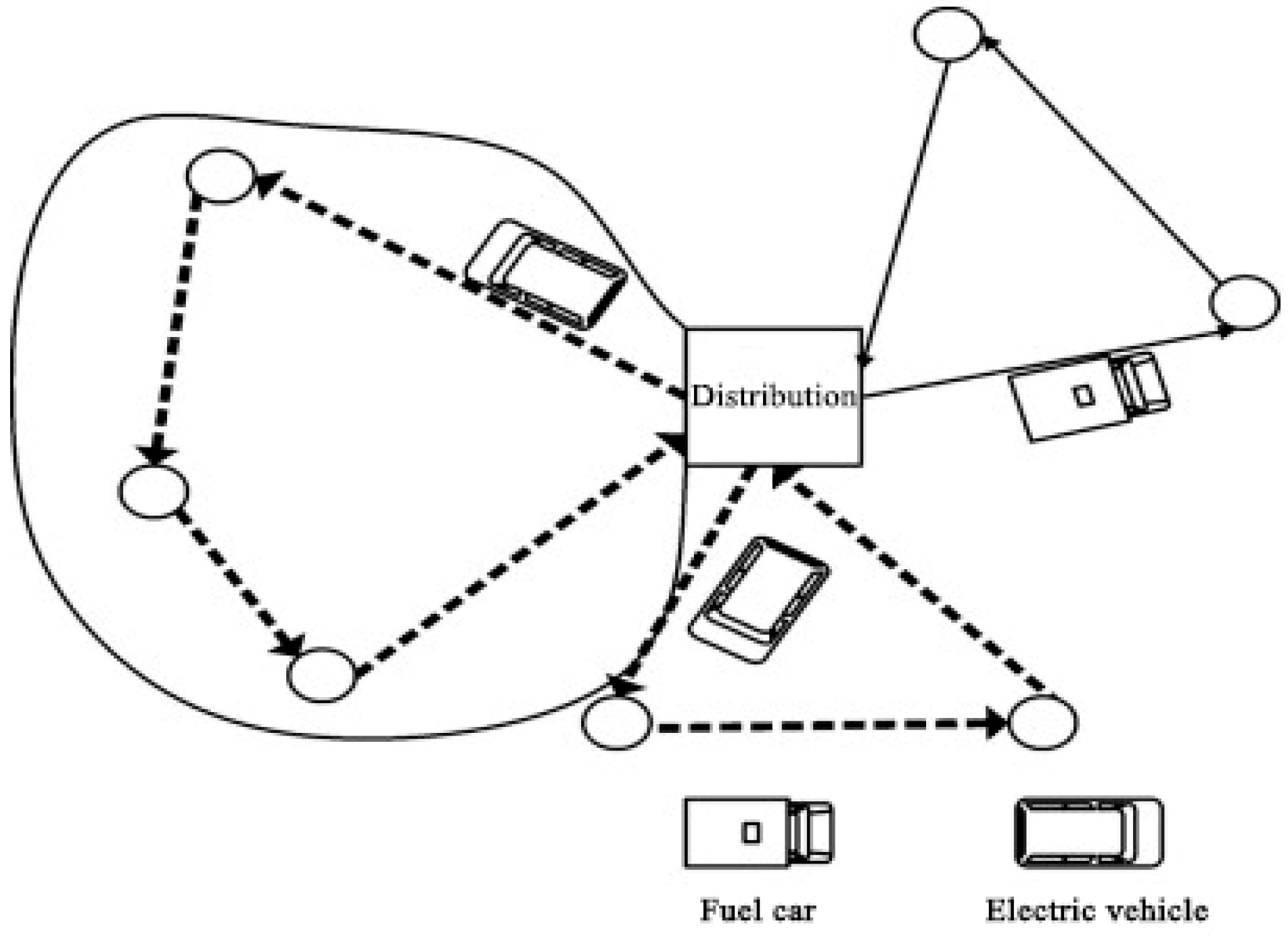
5.1. Description of the Vehicle Routing Problem
- (1)
- Customer requirements are independent of each other, and they will be updated only after the vehicle arrives at the customer point;
- (2)
- Vehicles depart from and return to the distribution center;
- (3)
- Vehicle use has a transportation cost, fuel cost, and penalty cost;
- (4)
- The quantity of goods delivered can meet the predicted demand and actual demand of customers.
5.2. Problem Model
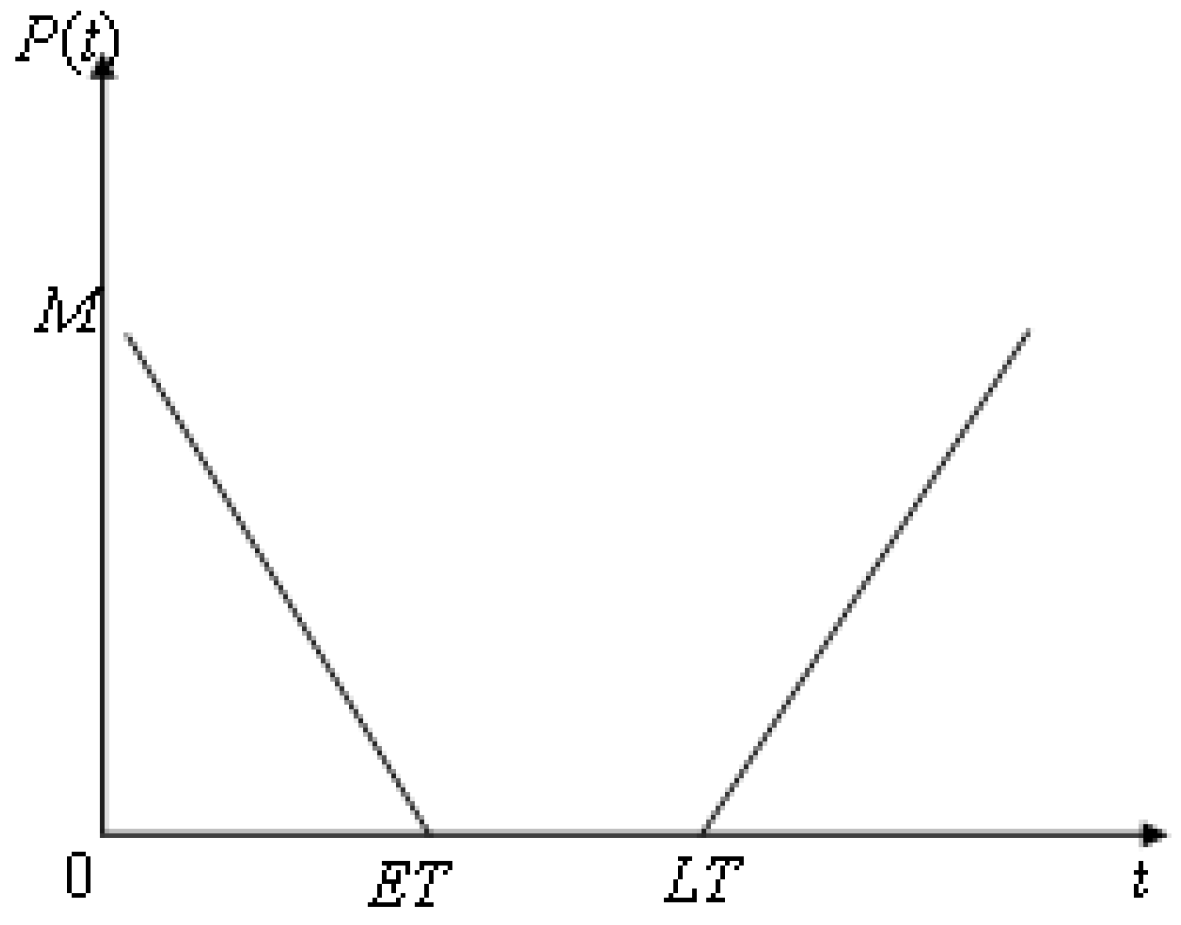
5.2.1. Soft Time Window
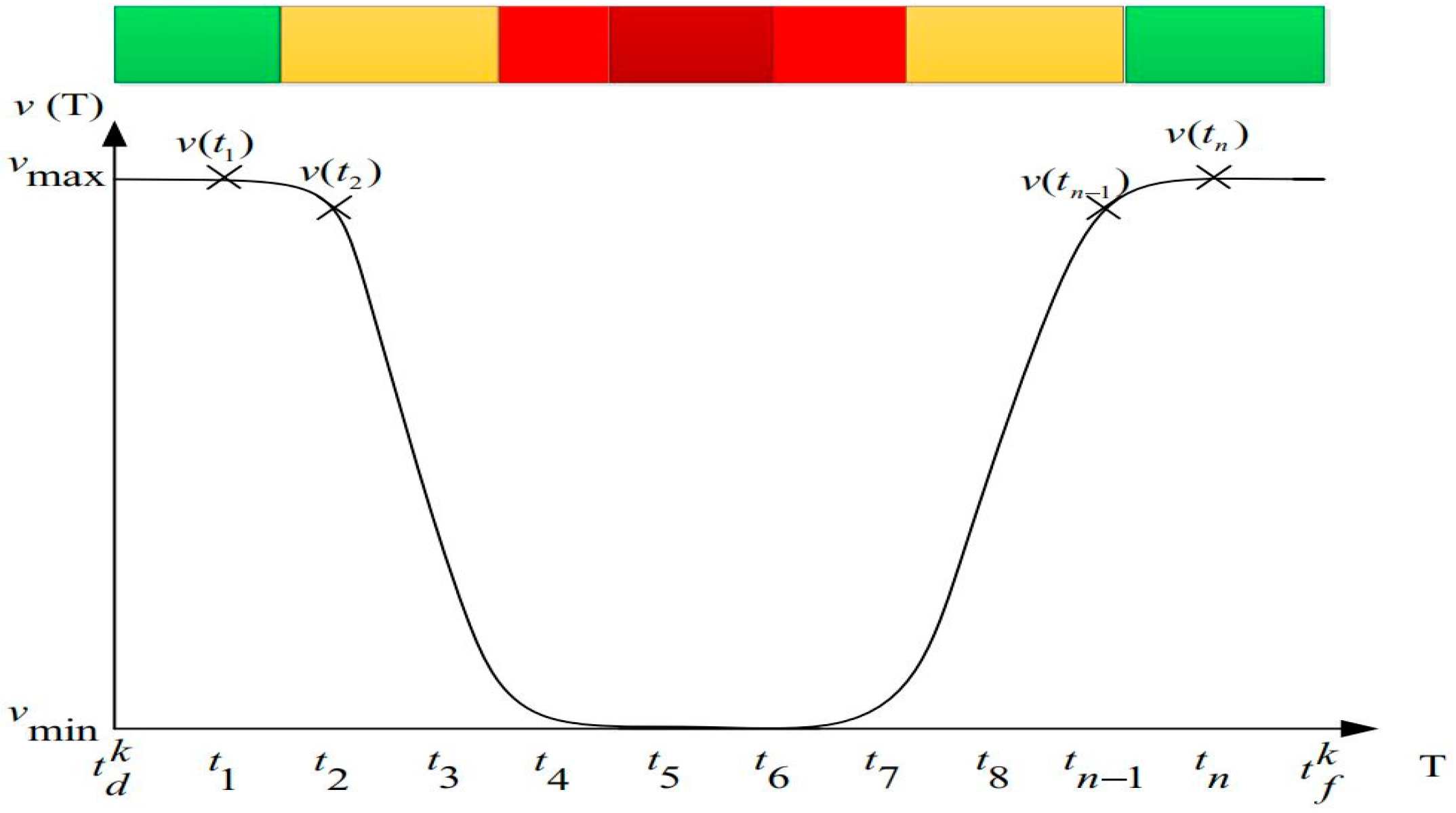
5.2.2. Vehicle Speed
5.2.3. Fuel Consumption
5.2.4. Penalty Costs
5.3. Objective Function
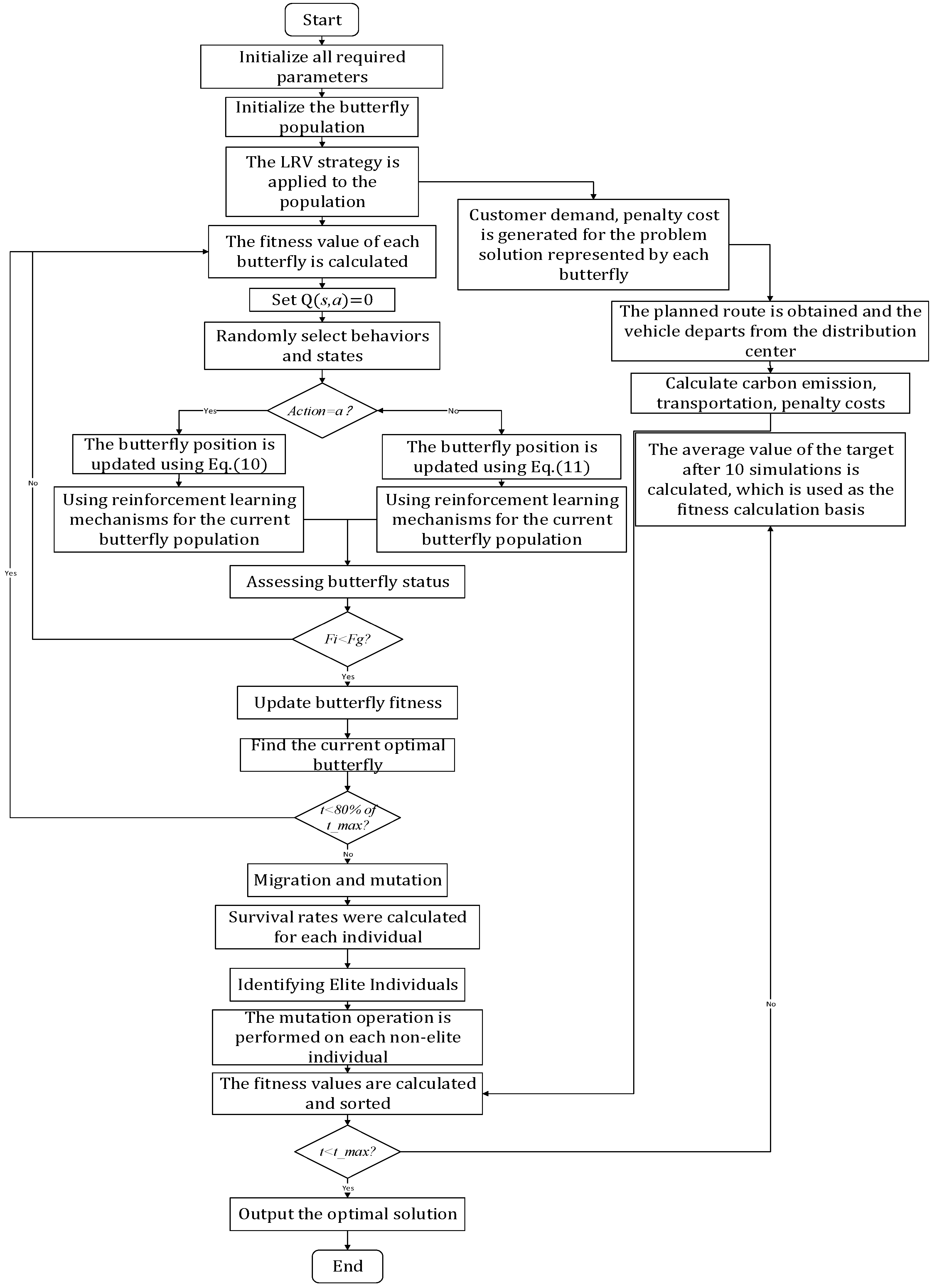
5.4. The Flow of the QLBOA to Solve the Problem
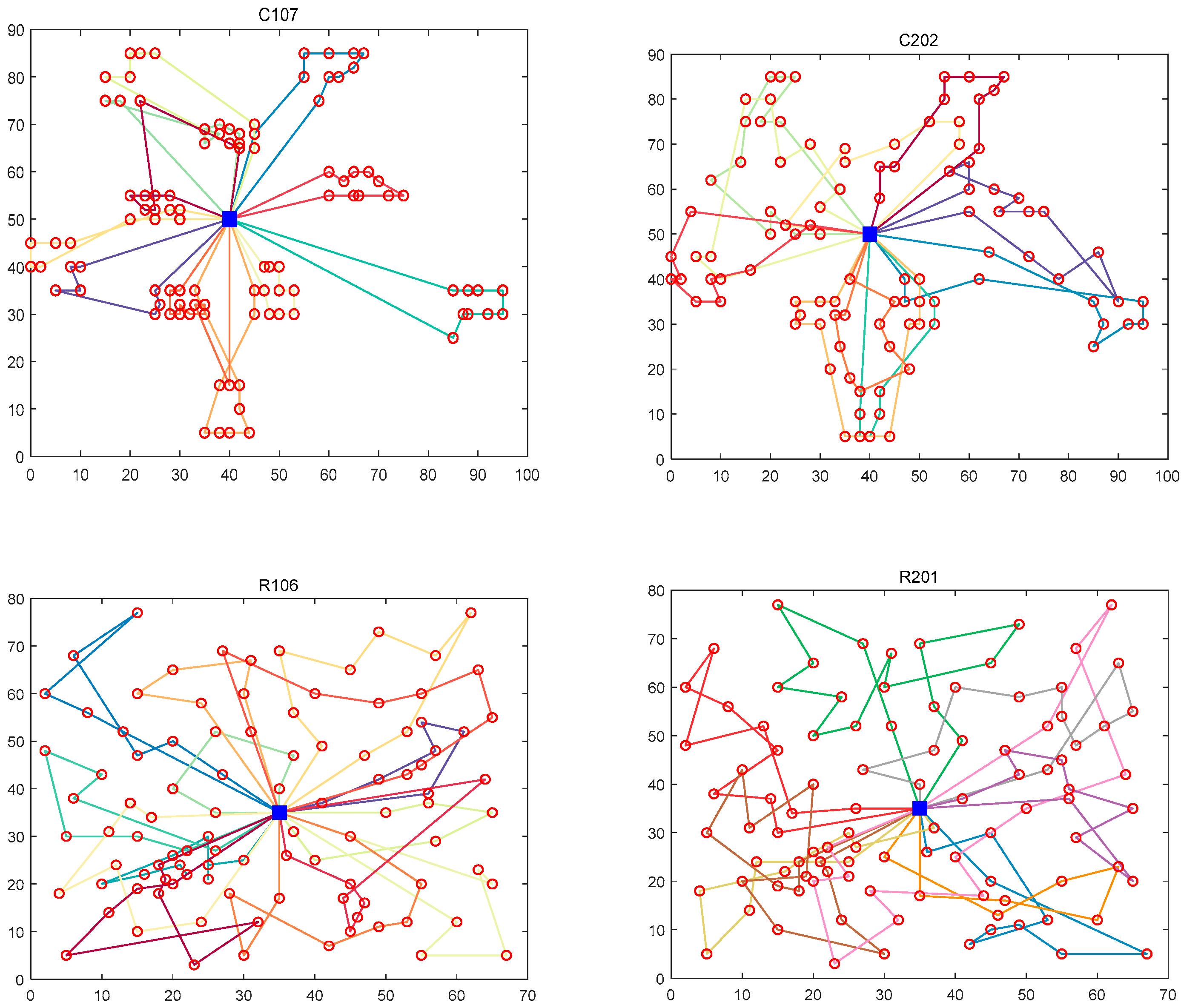
5.5. Datasets and Parameter Settings
5.6. Response Analysis
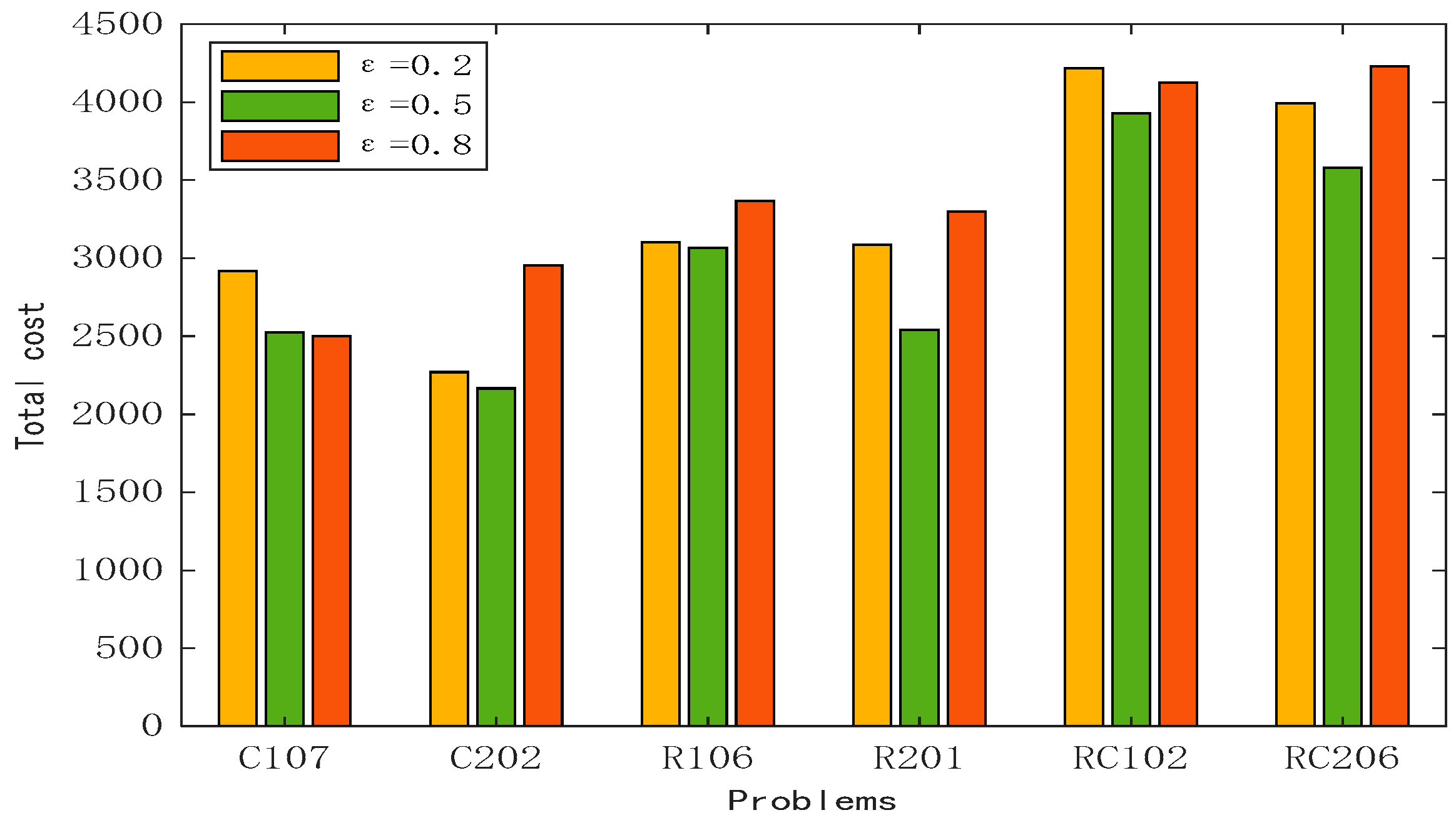
5.6.1. Analysis of the Influence of Decision Makers’ Subjective Preferences on Goals
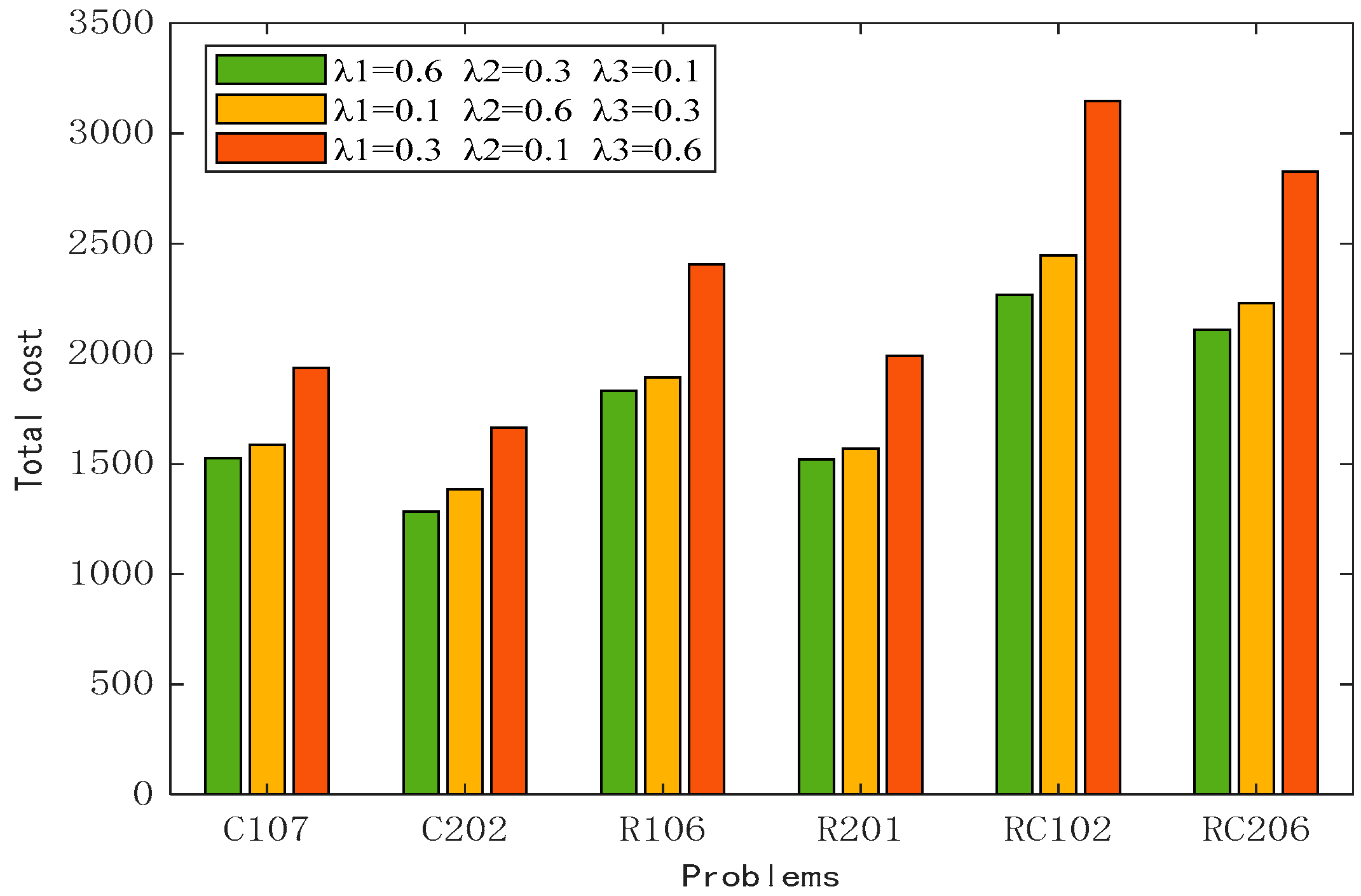
5.6.2. Analysis of the Impact of Weight Factors on the Target
5.6.3. Comparison with Other Algorithms
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Pepin, A.-S.; Desaulniers, G.; Hertz, A.; Huisman, D. A comparison of five heuristics for the multiple depot vehicle scheduling problem. J. Sched. 2009, 12, 17–30. [Google Scholar] [CrossRef]
- Ye, C.; He, W.; Chen, H. Electric vehicle routing models and solution algorithms in logistics distribution: A systematic review. Environ. Sci. Pollut. Res. 2022, 29, 57067–57090. [Google Scholar] [CrossRef]
- Bektaş, T.; Laporte, G. The pollution-routing problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Barth, M.; Boriboonsomsin, K. Real-World Carbon Dioxide Impacts of Traffic Congestion. Transp. Res. Rec. J. Transp. Res. Board 2008, 2058, 163–171. [Google Scholar] [CrossRef]
- Demir, E.; Bektaş, T.; Laporte, G. A comparative analysis of several vehicle emission models for road freight transportation. Transp. Res. Part D Transp. Environ. 2011, 16, 347–357. [Google Scholar] [CrossRef]
- Demir, E.; Bektaş, T.; Laporte, G. An adaptive large neighborhood search heuristic for the Pollution-Routing Problem. Eur. J. Oper. Res. 2012, 223, 346–359. [Google Scholar] [CrossRef]
- Mehlawat, M.K.; Gupta, P.; Khaitan, A.; Pedrycz, W. A hybrid intelligent approach to integrated fuzzy multiple depot capacitated green vehicle routing problem with split delivery and vehicle selection. IEEE Trans. Fuzzy Syst. 2019, 28, 1155–1166. [Google Scholar] [CrossRef]
- Franceschetti, A.; Honhon, D.; Van Woensel, T.; Bektaş, T.; Laporte, G. The time-dependent pollution-routing problem. Transp. Res. Part B Methodol. 2013, 56, 265–293. [Google Scholar] [CrossRef]
- Çimen, M.; Soysal, M. Time-dependent green vehicle routing problem with stochastic vehicle speeds: An approximate dynamic programming algorithm. Transp. Res. Part D Transp. Environ. 2017, 54, 82–98. [Google Scholar] [CrossRef]
- Kazemian, I.; Rabbani, M.; Farrokhi-Asl, H. A way to optimally solve a green time-dependent vehicle routing problem with time windows. Comput. Appl. Math. 2018, 37, 2766–2783. [Google Scholar] [CrossRef]
- Qi, R.; Li, J.Q.; Wang, J.; Jin, H.; Han, Y.Y. QMOEA: A Q-learning-based multiobjective evolutionary algorithm for solving time-dependent green vehicle routing problems with time windows. Inf. Sci. 2022, 608, 178–201. [Google Scholar] [CrossRef]
- Prakash, R.; Pushkar, S. Green vehicle routing problem: Metaheuristic solution with time window. Expert Syst. 2022, 41, 13007. [Google Scholar] [CrossRef]
- Wang, Y.; Assogba, K.; Fan, J.; Xu, M.; Liu, Y.; Wang, H. Multi-depot green vehicle routing problem with shared transportation resource: Integration of time-dependent speed and piecewise penalty cost. J. Clean. Prod. 2019, 232, 12–29. [Google Scholar] [CrossRef]
- Wu, D.; Wu, C. Research on the Time-Dependent Split Delivery Green Vehicle Routing Problem for Fresh Agricultural Products with Multiple Time Windows. Agriculture 2022, 12, 793. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, Z.; Luo, R.; Zhao, R.; Xiao, Y.; Xu, Y. A low-carbon, fixed-tour scheduling problem with time win-dows in a time-dependent traffic environment. Int. J. Prod. Res. 2023, 61, 6177–6196. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Sharma, S.; Saha, A.K.; Nama, S. An enhanced butterfly optimization algorithm for function optimization. In Soft Computing: Theories and Applications: Proceedings of SoCTA 2019; Springer: Singapore, 2020; pp. 593–603. [Google Scholar]
- Fathy, A. Butterfly optimization algorithm based methodology for enhancing the shaded photovoltaic array extracted power via reconfiguration process. Energy Convers. Manag. 2020, 220, 113115. [Google Scholar] [CrossRef]
- El-Hasnony, I.M.; Elhoseny, M.; Tarek, Z. A hybrid feature selection model based on butterfly optimization algorithm: COVID-19 as a case study. Expert Syst. 2022, 39, e12786. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, Q.; Zhou, Y. Hybrid metaheuristic algorithm using butterfly and flower pollination base on mutual-ism mechanism for global optimization problems. Eng. Comput. 2021, 37, 3665–3698. [Google Scholar] [CrossRef]
- Shahbandegan, A.; Naderi, M. A binary butterfly optimization algorithm for the multidimensional knapsack problem. In Proceedings of the 2020 6th Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS), Mashhad, Iran, 23–24 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Mazaheri, H.; Goli, S.; Nourollah, A. Path planning in three-dimensional space based on butterfly optimization algorithm. Sci. Rep. 2024, 14, 2332. [Google Scholar] [CrossRef]
- Chatterjee, S.; Debnath, R.; Biswas, S.; Bairagi, A.K. Prediction of RNA Secondary Structure Using Butterfly Optimization Algorithm. Hum.-Centric Intell. Syst. 2024, 4, 220–240. [Google Scholar] [CrossRef]
- Bhanja, S.; Das, A. An air quality forecasting method using fuzzy time series with butterfly optimization algorithm. Microsyst. Technol. 2024, 30, 613–623. [Google Scholar] [CrossRef]
- Alhassan, A.M. Thresholding Chaotic Butterfly Optimization Algorithm with Gaussian Kernel (TCBOGK) based seg-mentation and DeTrac deep convolutional neural network for COVID-19 X-ray images. Multimed. Tools Appl. 2024, 1–24. [Google Scholar]
- Gade, V.S.R.; Manickam, S. Speaker recognition using Improved Butterfly Optimization Algorithm with hybrid Long Short Term Memory network. Multimed. Tools Appl. 2024, 83, 73817–73839. [Google Scholar] [CrossRef]
- Sharma, S.; Saha, A.K. m-MBOA: A novel butterfly optimization algorithm enhanced with mutualism scheme. Soft Comput. 2020, 24, 4809–4827. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.; Liang, X.; Wu, T.; Xu, M.; Cai, S. Pinhole-imaging-based learning butterfly optimization algorithm for global optimization and feature selection. Appl. Soft Comput. 2021, 103, 107146. [Google Scholar] [CrossRef]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Sinha, D.; Chakrabarty, S.P. A review of efficient Multilevel Monte Carlo algorithms for derivative pricing and risk management. MethodsX 2023, 10, 102078. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L.; Alharbi, S.K.; Khalifa, H.A.E.-W. Efficient Initialization Methods for Population-Based Metaheuristic Algorithms: A Comparative Study. Arch. Comput. Methods Eng. 2023, 30, 1727–1787. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.Q.; Wang, H.Y.; Khodaei, H. Improved Butterfly Optimization Algorithm for CCHP driven by PEMFC. Appl. Therm. Eng. 2020, 173, 114766. [Google Scholar]
- Zhang, M.; Long, D.; Qin, T.; Yang, J. A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems. Symmetry 2020, 12, 1800. [Google Scholar] [CrossRef]
- Biedrzycki, R.; Arabas, J.; Warchulski, E. A Version of NL-SHADE-RSP Algorithm with Midpoint for CEC 2022 Single Objective Bound Constrained Problems. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Vesterstrom, J.; Thomsen, R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No. 04TH8753), Portland, OR, USA, 19–23 June 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 2, pp. 1980–1987. [Google Scholar]
- Lim, S.P.; Haron, H. Performance comparison of Genetic Algorithm, Differential Evolution and Particle Swarm Optimization towards benchmark functions. In Proceedings of the 2013 IEEE Conference on Open Systems (ICOS), Kuching, Malaysia, 2–4 December 2013; pp. 41–46. [Google Scholar]
- Li, X.; Yang, G. Artificial bee colony algorithm with memory. Appl. Soft Comput. 2016, 41, 362–372. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Wang, G.-G. Hierarchical learning particle swarm optimization using fuzzy logic. Expert Syst. Appl. 2023, 232, 120759. [Google Scholar] [CrossRef]
- Abdelrazek, M.; Elaziz, M.A.; El-Baz, A.H. CDMO: Chaotic Dwarf Mongoose Optimization Algorithm for feature selection. Sci. Rep. 2024, 14, 701. [Google Scholar] [CrossRef]
- Zhang, Q.; Bu, X.; Gao, H.; Li, T.; Zhang, H. A hierarchical learning based artificial bee colony algorithm for numerical global optimization and its applications. Appl. Intell. 2024, 54, 169–200. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Niu, Y.; He, K.; Wang, Y. T Cell Immune Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. IEEE Access 2023, 11, 95545–95566. [Google Scholar] [CrossRef]
- He, K.; Zhang, Y.; Wang, Y.K.; Zhou, R.H.; Zhang, H.Z. EABOA: Enhanced adaptive butterfly optimization algorithm for numerical optimization and engineering design problems. Alex. Eng. J. 2024, 87, 543–573. [Google Scholar] [CrossRef]
- Jie, K.W.; Liu, S.Y.; Sun, X.J. A hybrid algorithm for time-dependent vehicle routing problem with soft time windows and stochastic factors. Eng. Appl. Artif. Intell. 2022, 109, 104606. [Google Scholar] [CrossRef]
- Utama, D.M.; Widodo, D.S.; Ibrahim, M.F.; Hidayat, K.; Baroto, T.; Yurifah, A. The hybrid whale optimization algorithm: A new metaheuristic algorithm for energy-efficient on flow shop with dependent sequence setup. J. Physics Conf. Ser. 2020, 1569, 022094. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]

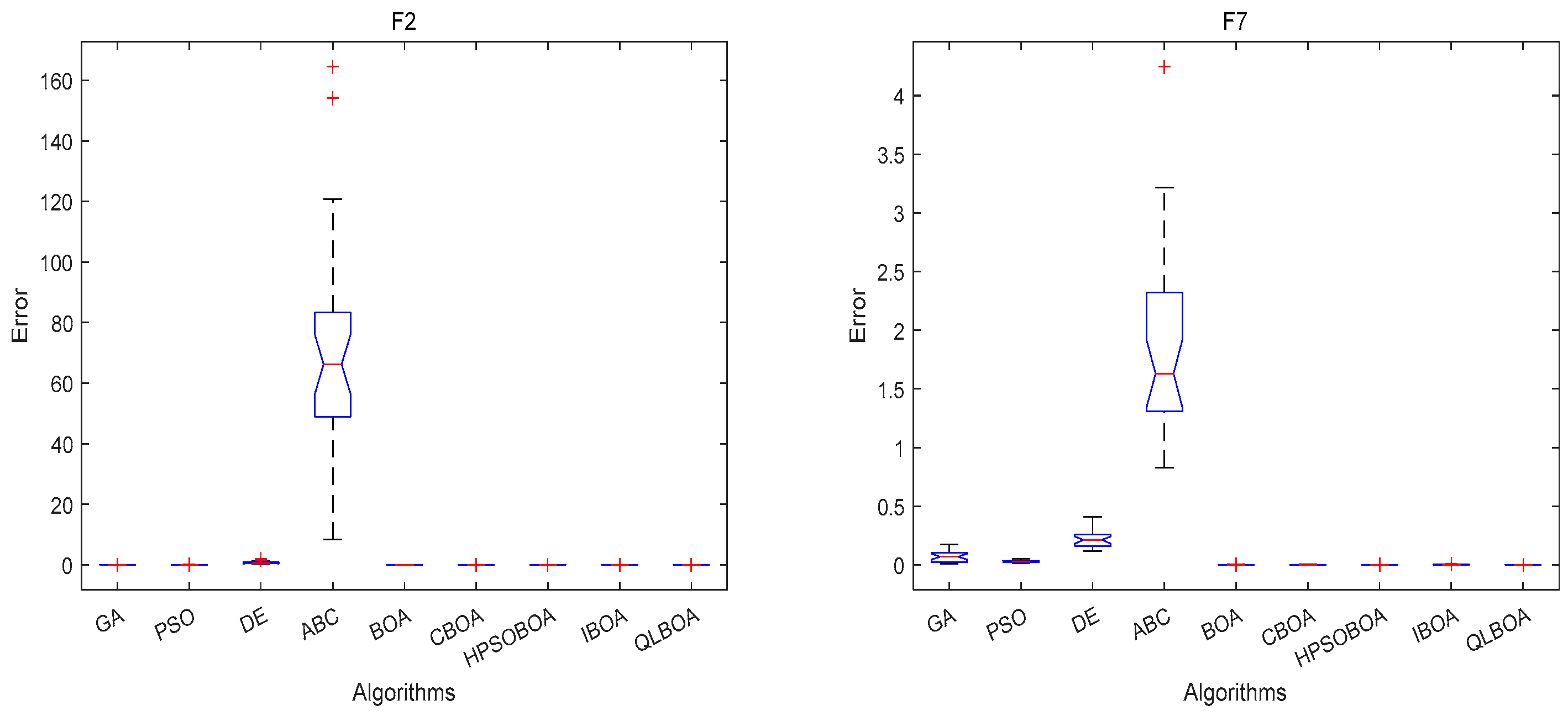
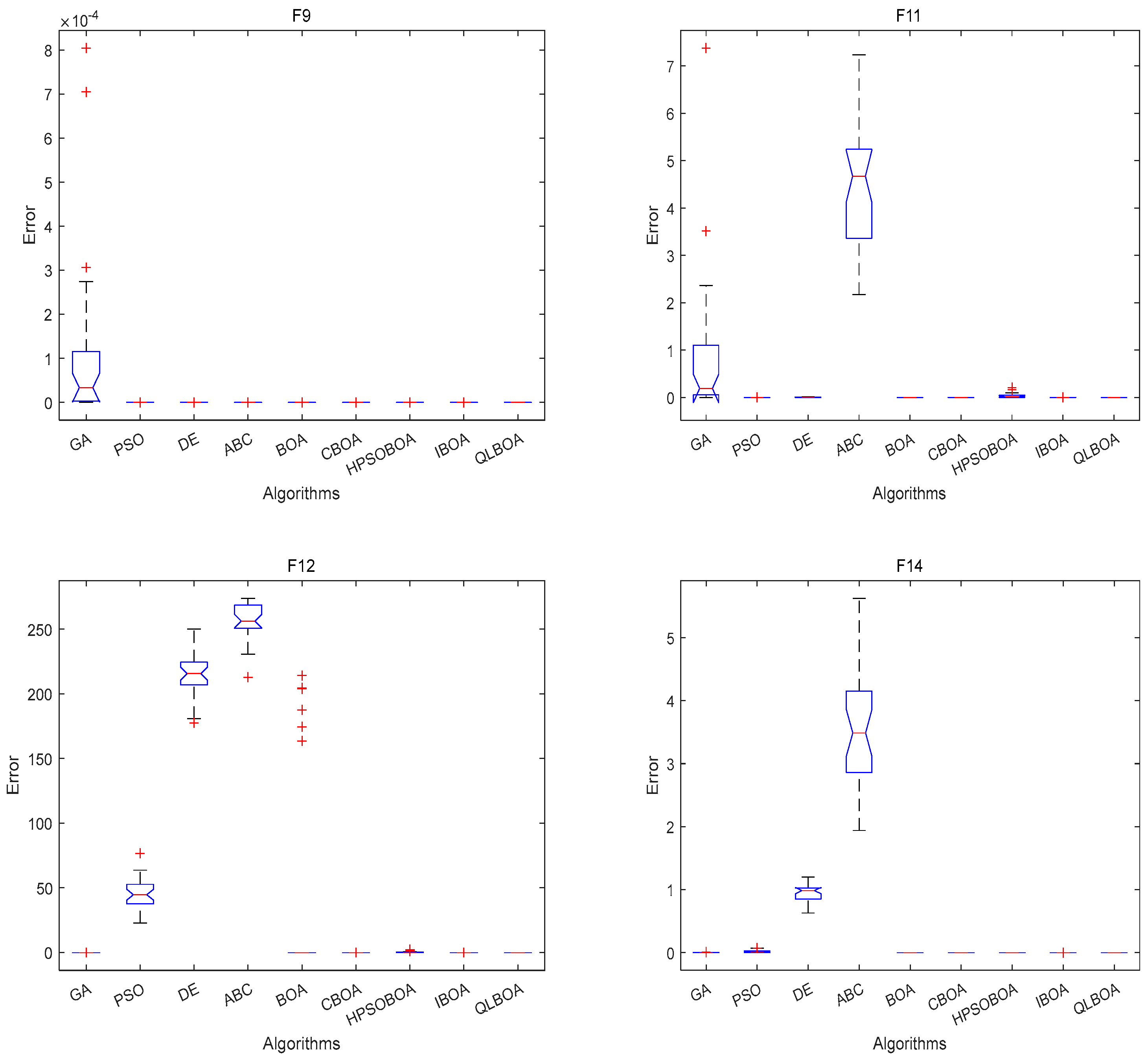
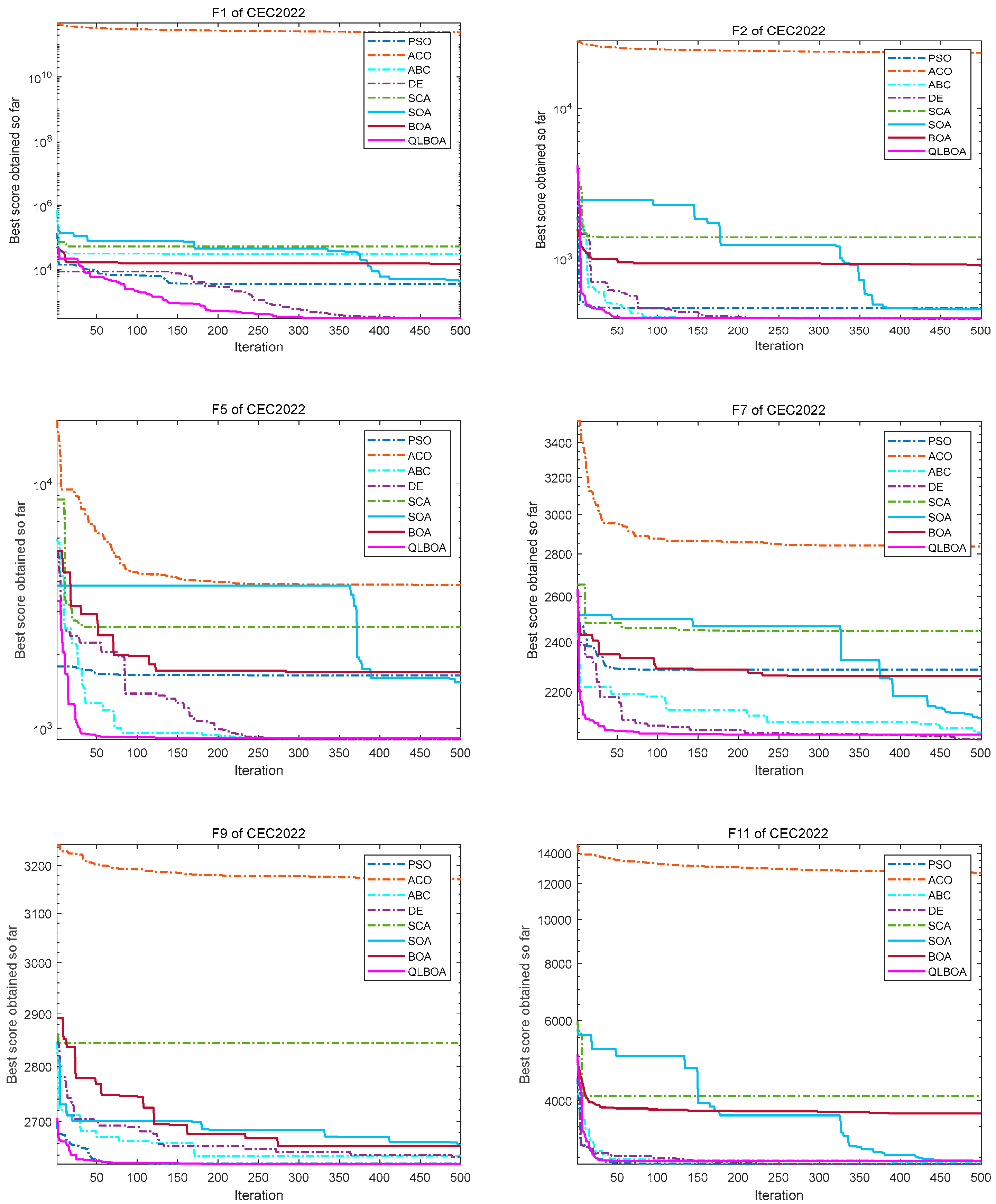
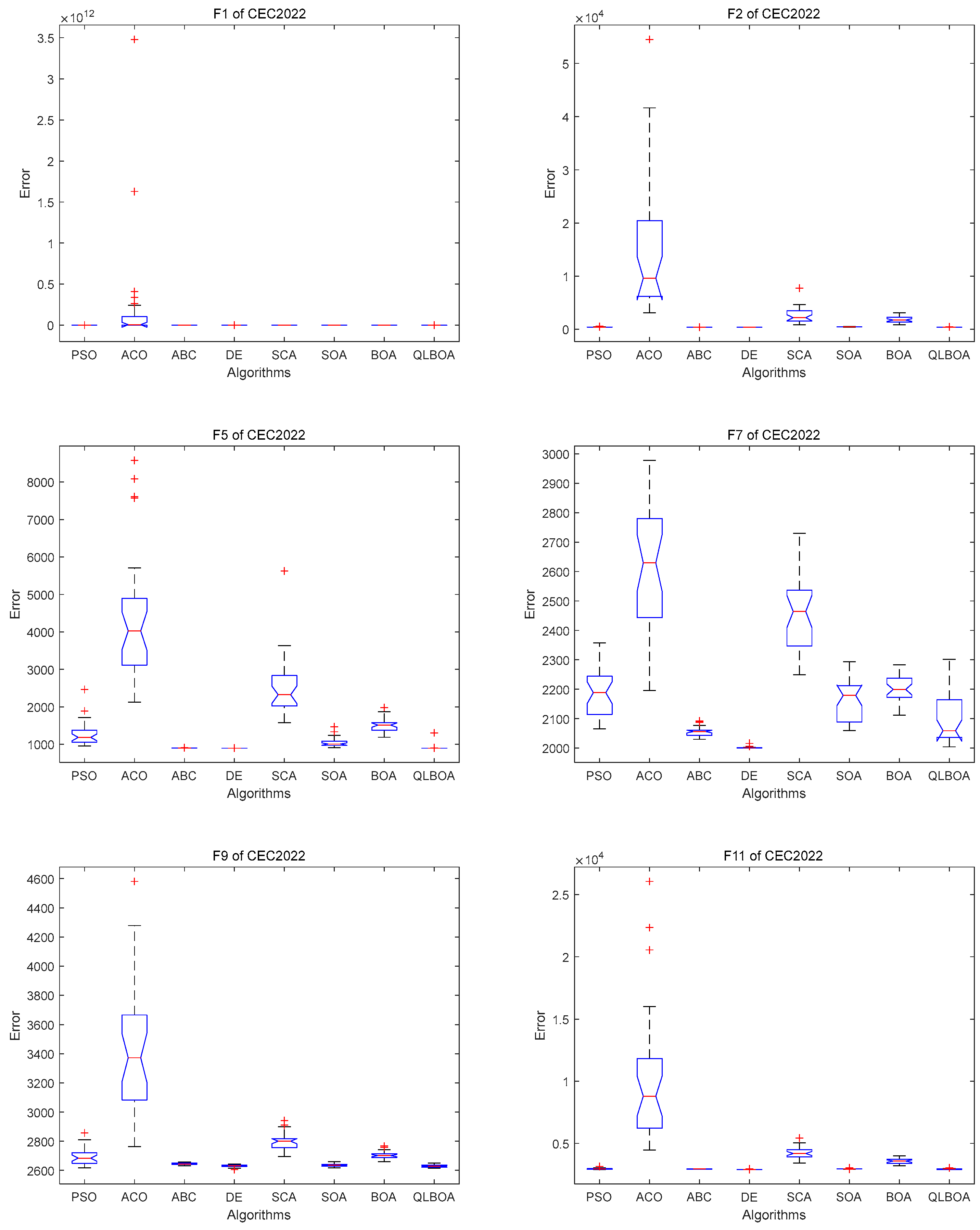
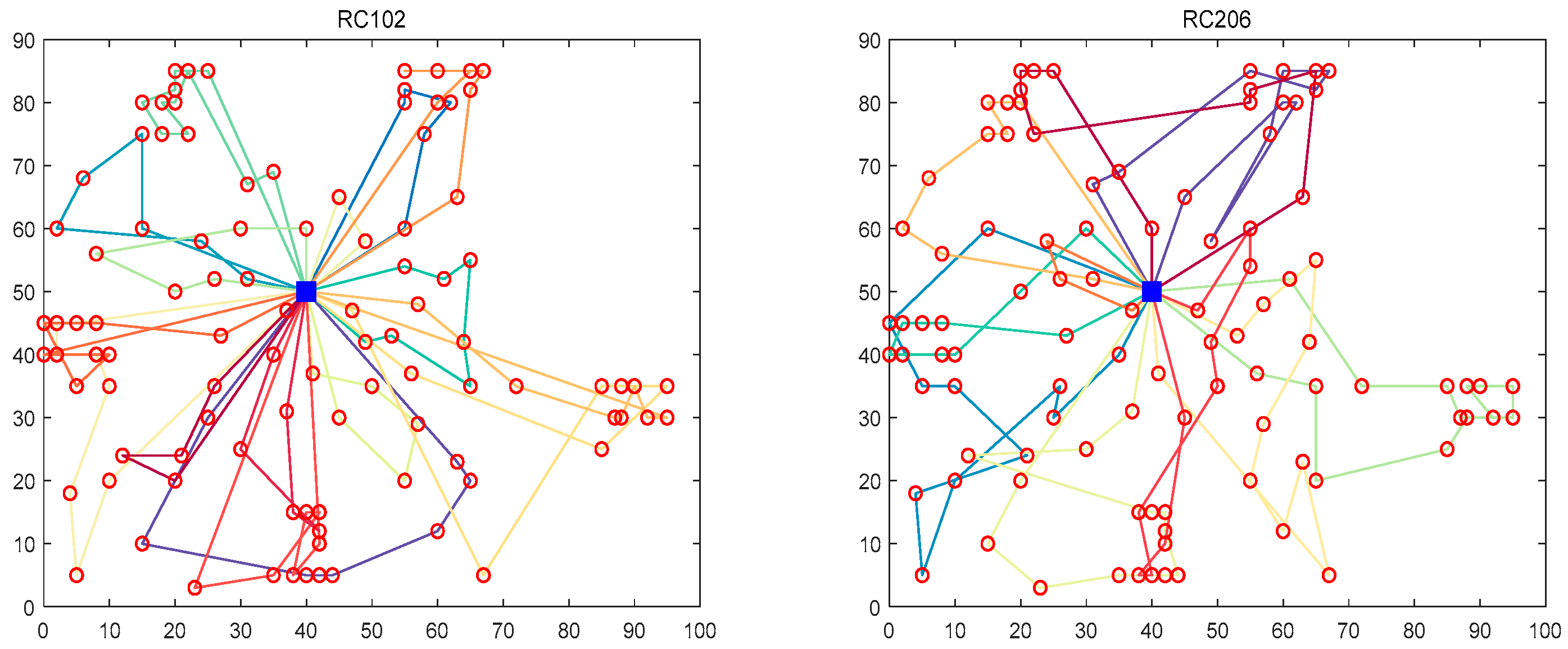
| Algorithms | Name | Parameter Settings |
|---|---|---|
| PSO | Particle Swarm Optimization | a = 0.3, b = 1, c = 1 |
| ABC | Artificial Bee Colony Algorithm | m = 0.2 |
| ACO | Ant Colony Optimization | c = 10−6, Q = 20, m = 1, |
| GA | Genetic Algorithm | Qc = 1, Qm = 0.01 |
| DE | Differential Evolution Algorithm | q = 0.2, α1 = 0.8, α2 = 0.2 |
| SCA | Sine Cosine Algorithm | α = 2, c1 = b − t × (b/T), |
| SOA | Seagull Optimization Algorithm | c = 1 |
| BOA | Butterfly Optimization Algorithm | p = 0.8, α = 0.1, c = 0.01 |
| CBOA | Optimization Algorithm with Cubic Map | a1 = 0.1, a2 = 0.3, c = 0.01, p = 0.6, m = 0.315, P = 0.295 |
| HPSOBOA | Hybrid PSO with BOA and Cubic Map | a1 = 0.1, a2 = 0.3, c = 0.01, p = 0.6, x = 0.315, P = 0.295, c1 = c2 = 0.5 |
| IBOA | Improved BOA | a = 0.1, c = 0.01, P = 0.6, x = 0.33, w = 4 |
| QLBOA | BOA with Q-learning | p = [0.1, 0.8], α = 0.1, c = 0.01, m = 0.1, e = 0.4 |
| Type | No. | Functions | Search Ranges | Fmin |
|---|---|---|---|---|
| High-dimensional unimodal | F1 | Schwefel’s Problem 1.2 | [−100, 100] | 0 |
| F2 | Generalized Rosenbrock’s Function | [−10, 10] | 0 | |
| F3 | Sphere Function | [−100, 100] | 0 | |
| F4 | Schwefel’s Problem 2.21 | [−100, 100] | 0 | |
| F5 | Schwefel’s Problem 2.22 | [−10, 10] | 0 | |
| F6 | Sum-of-Different-Powers Function | [−100, 100] | 0 | |
| F7 | Quartic Function, i.e., Noise | [−1.28, 1.28] | 0 | |
| F8 | Bent Cigar Function | [−10, 10] | 0 | |
| F9 | Step Function | [−100, 100] | 0 | |
| F10 | Zakharov Function | [−5, 10] | 0 | |
| F11 | Discus Function | [−5, 5] | 0 | |
| High-dimensional multimodal | F12 | Generalized Rastrigin’s Function | [−5.12, 5.12] | 0 |
| F13 | Ackley’s Function | [−32, 32] | 0 | |
| F14 | Generalized Griewank’s Function | [−600, 600] | 0 | |
| F15 | HappyCat Function | [−50, 50] | 0 | |
| F16 | Lévy Function | [−10, 10] | 0 | |
| F17 | Katsuura Function | [−50, 50] | 0 | |
| F18 | HGBat Function | [−20, 20] | 0 |
| Type | NO. | Functions | Fmin |
|---|---|---|---|
| Unimodal Functions | 1 | Shifted and full Rotated Zakharov Function | 300 |
| Multimodal Functions | 2 | Shifted and full Rotated Rosenbrock’s Function | 400 |
| 3 | Shifted and full Rotated Rastrigin’s Function | 600 | |
| 4 | Shifted and full Rotated Non-Continuous Rastrigin’s Function | 800 | |
| 5 | Shifted and full Rotated Lévy Function | 900 | |
| Hybrid Functions | 6 | Hybrid Function 1 (N = 3) | 1800 |
| 7 | HF 2 (N = 6) | 2000 | |
| 8 | HF 3 (N = 5) | 2200 | |
| Composition Functions | 9 | Composition Function 1 (N = 5) | 2300 |
| 10 | CF 2 (N = 4) | 2400 | |
| 11 | CF 3 (N = 5) | 2600 | |
| 12 | CF 4 (N = 6) | 2700 |
| Function | GA [36] | DE [37] | PSO [37] | ABC [38] | BOA [28] | QLBOA | |
|---|---|---|---|---|---|---|---|
| F1 | Mean | 1.4181 × 10+03 | 3.8513 × 10−03 | 6.8100 × 10−13 | 2.6770 × 10−16 | 2.5100 × 10−11 | 8.0212 × 10−231 |
| Std | 5.9444 × 10+02 | 1.0000 × 10−02 | 5.3000 × 10−13 | 6.4934 × 10−17 | 1.9300 × 10−12 | 0.0000 × 10+00 | |
| F2 | Mean | 2.4766 × 10+01 | −2.0602 × 10−00 | 2.0892 × 10−02 | 3.1462 × 10−09 | 2.3900 × 10−11 | 0.0000 × 10+00 |
| Std | 5.2444 × 10+00 | 9.2312 × 10−08 | 1.4800 × 10−01 | 5.3864 × 10−09 | 2.2800 × 10−12 | 0.0000 × 10+00 | |
| F3 | Mean | 2.2230 × 10+04 | −1.0000 × 10−00 | 1.4184 × 10−05 | 9.3412 × 10−10 | 2.2400 × 10−11 | 0.0000 × 10+00 |
| Std | 4.4852 × 10+03 | 3.1712 × 10−06 | 5.9800 × 10+02 | 8.9224 × 10−03 | 1.8800 × 10−12 | 0.0000 × 10+00 | |
| F4 | Mean | 5.1304 × 10+01 | −2.8732 × 10−00 | 1.4184 × 10−05 | 5.9962 × 10−10 | 1.1900 × 10−08 | 1.3380 × 10−249 |
| Std | 6.4693 × 10+00 | 1.5538 × 10−12 | 8.2700 × 10−06 | 2.3114 × 10−12 | 8.3500 × 10−10 | 0.0000 × 10+00 | |
| F5 | Mean | 6.9558 × 10+03 | 1.7400 × 10−01 | 3.5600 × 10+02 | 2.9732 × 10−10 | 2.8900 × 10+01 | 4.7112 × 10−02 |
| Std | 9.7903 × 10+03 | 2.1200 × 10−01 | 2.1500 × 10+03 | 3.5514 × 10+01 | 9.5400 × 10−02 | 5.2924 × 10−02 | |
| F6 | Mean | 9.5971 × 10+02 | −4.1413 × 10−00 | 4.0300 × 10−02 | 4.9872 × 10−17 | 5.1700 × 10+00 | 3.6750 × 10−03 |
| Std | 2.5531 × 10+02 | 1.6542 × 10−02 | 3.9800 × 10−01 | 4.6481 × 10−14 | 6.3900 × 10−01 | 3.3326 × 10−03 | |
| F7 | Mean | 3.5458 × 10−01 | 1.1500 × 10−00 | 1.4082 × 10−04 | 7.3670 × 10−14 | 4.0300 × 10−03 | 1.1574 × 10−04 |
| Std | 7.3510 × 10−02 | 0.2300 × 10−00 | 1.1400 × 10−03 | 5.3882 × 10−09 | 8.7000 × 10−04 | 1.1050 × 10−04 | |
| F8 | Mean | 2.8900 × 10+01 | 1.5000 × 10−02 | 7.3800 × 10−61 | 6.0962 × 10−03 | 6.5100 × 10−17 | 5.5810 × 10−02 |
| Std | 2.5400 × 10−02 | 4.0414 × 10−02 | 3.8102 × 10−60 | 7.3131 × 10−03 | 1.3900 × 10−16 | 2.8200 × 10−01 | |
| F9 | Mean | 1.5721 × 10+01 | 2.0000 × 10−08 | 1.3712 × 10−14 | 1.8780 × 10−14 | 6.3300 × 10−14 | 0.0000 × 10+00 |
| Std | 5.1484 × 10+00 | 5.3312 × 10−08 | 4.6430 × 10−14 | 2.4251 × 10−13 | 3.4000 × 10−14 | 0.0000 × 10+00 | |
| F10 | Mean | 1.4434 × 10+01 | −1.8732 × 10+02 | 9.0222 × 10−05 | 6.5802 × 10−05 | 6.7200 × 10−11 | 0.0000 × 10+00 |
| Std | 8.4536 × 10−01 | 3.3950 × 10−04 | 1.0544 × 10−04 | 1.4841 × 10−05 | 6.9000 × 10−12 | 0.0000 × 10+00 | |
| F11 | Mean | 1.5250 × 10+01 | 4.3300 × 10−03 | 9.0221 × 10−05 | 7.8280 × 10−04 | 6.7200 × 10−11 | 0.0000 × 10+00 |
| Std | 7.3036 × 10+00 | 1.9000 × 10−02 | 1.0504 × 10−04 | 2.2000 × 10−04 | 6.9000 × 10−12 | 0.0000 × 10+00 | |
| F12 | Mean | 3.0789 × 10+00 | 3.1300 × 10−03 | 8.5598 × 10−03 | 3.2000 × 10−08 | 2.5100 × 10+01 | 0.0000 × 10+00 |
| Std | 1.8282 × 10+00 | 9.5412 × 10−03 | 4.7900 × 10−02 | 2.2112 × 10−08 | 6.5200 × 10+01 | 0.0000 × 10+00 | |
| F13 | Mean | 8.7058 × 10+00 | 2.5170 × 10+76 | 5.3300 × 10−03 | 5.4671 × 10−05 | 7.6400 × 10−12 | 8.8824 × 10−16 |
| Std | 1.2778 × 10+00 | 1.1750 × 10+77 | 7.4800 × 10−03 | 2.6163 × 10−05 | 6.9400 × 10−12 | 0.0000 × 10+00 | |
| F14 | Mean | 9.9800 × 10−01 | 6.3350 × 10−01 | 1.1512 × 10−03 | 9.1182 × 10−11 | 1.9000 × 10−10 | 0.0000 × 10+00 |
| Std | 5.6000 × 10−16 | 8.6912 × 10−01 | 9.3600 × 10−04 | 7.6752 × 10−11 | 4.3400 × 10−10 | 0.0000 × 10+00 | |
| F15 | Mean | 6.1300 × 10−03 | 4.8452 × 10−04 | 4.5600 × 10+01 | 5.5400 × 10−16 | 2.5100 × 10+01 | 0.0000 × 10+00 |
| Std | 5.3700 × 10−03 | 6.6000 × 10−04 | 1.1100 × 10+01 | 1.5300 × 10−16 | 6.5200 × 10+01 | 0.0000 × 10+00 | |
| F16 | Mean | 7.7620 × 10−01 | −1.9400 × 10−00 | 4.7700 × 10−02 | 1.0210 × 10+01 | 1.1700 × 10+01 | 1.3780 × 10−05 |
| Std | 2.0844 × 10−01 | 5.4200 × 10−07 | 6.5800 × 10−02 | 7.3521 × 10+00 | 2.6600 × 10+00 | 1.4504 × 10−02 | |
| F17 | Mean | 4.6481 × 10+01 | 1.8713 × 10+03 | 1.6900 × 10+06 | 6.7600 × 10+08 | 1.0900 × 10+09 | 3.2042 × 10+04 |
| Std | 6.7914 × 10+02 | 8.0654 × 10+05 | 1.3200 × 10+06 | 2.6100 × 10+05 | 8.1600 × 10+10 | 2.3582 × 10+03 | |
| F18 | Mean | 3.0000 × 10+00 | 7.1000 × 10+05 | 5.3300 × 10+05 | 2.7110 × 10−01 | 7.6400 × 10+12 | 2.0000 × 10−01 |
| Std | 0.0000 × 10+00 | 8.6942 × 10−05 | 7.4800 × 10+05 | 1.5000 × 10−01 | 6.9400 × 10+12 | 2.0940 × 10−07 |
| Function | IBOA [33] | HPSO-BOA [34] | CBOA [34] | QLBOA | |
|---|---|---|---|---|---|
| F1 | Mean | 1.6100 × 10−30 | 3.7400 × 10−104 | 1.0100 × 10−13 | 0.0000 × 10+00 |
| Std | 3.9000 × 10−30 | 2.0500 × 10−103 | 2.1100 × 10−13 | 0.0000 × 10+00 | |
| F2 | Mean | 5.1100 × 10−19 | 2.6300 × 10−22 | 1.2500 × 10−14 | 8.0212 × 10−231 |
| Std | 1.7300 × 10−18 | 1.4400 × 10−21 | 2.1500 × 10−14 | 0.0000 × 10+00 | |
| F3 | Mean | 6.1500 × 10−31 | 3.0400 × 10−71 | 6.3000 × 10−13 | 0.0000 × 10+00 |
| Std | 1.1600 × 10−30 | 1.6700 × 10−70 | 1.3700 × 10−12 | 0.0000 × 10+00 | |
| F4 | Mean | 1.3600 × 10−19 | 3.6100 × 10−46 | 2.7700 × 10−10 | 1.3380 × 10−249 |
| Std | 1.9700 × 10−19 | 1.9700 × 10−45 | 2.9600 × 10−10 | 0.0000 × 10+00 | |
| F5 | Mean | 2.8900 × 10+01 | 2.9000 × 10+01 | 2.8700 × 10+01 | 4.7112 × 10−02 |
| Std | 3.4000 × 10−02 | 8.1800 × 10−02 | 1.3900 × 10−05 | 5.2924 × 10−02 | |
| F6 | Mean | 4.4400 × 10+00 | 4.1700 × 10−02 | 8.5000 × 10−06 | 3.6750 × 10−03 |
| Std | 8.7000 × 10−01 | 6.4000 × 10−02 | 1.0600 × 10−05 | 3.0320 × 10−03 | |
| F7 | Mean | 1.2200 × 10−04 | 2.5500 × 10−04 | 2.0000 × 10−03 | 1.1774 × 10−04 |
| Std | 8.0600 × 10−05 | 4.0000 × 10−04 | 7.8900 × 10−04 | 1.1000 × 10−04 | |
| F8 | Mean | 8.4500 × 10−31 | 7.1500 × 10−15 | 2.2400 × 10−23 | 5.5810 × 10−02 |
| Std | 2.5200 × 10−30 | 3.9200 × 10−14 | 7.5100 × 10−23 | 2.8200 × 10−01 | |
| F9 | Mean | 1.3200 × 10−36 | 3.1900 × 10−118 | 6.5800 × 10−15 | 0.0000 × 10+00 |
| Std | 4.5900 × 10−36 | 1.6800 × 10−117 | 1.1900 × 10−14 | 0.0000 × 10+00 | |
| F10 | Mean | 1.1000 × 10−30 | 3.6400 × 10−78 | 2.3700 × 10−14 | 0.0000 × 10+00 |
| Std | 2.9000 × 10−30 | 1.9900 × 10−77 | 4.2400 × 10−14 | 0.0000 × 10+00 | |
| F11 | Mean | 0.0000 × 10+00 | 1.3200 × 10−136 | 1.5400 × 10−18 | 0.0000 × 10+00 |
| Std | 0.0000 × 10+00 | 6.8400 × 10−135 | 2.8500 × 10−18 | 0.0000 × 10+00 | |
| F12 | Mean | 0.0000 × 10+00 | 0.0000 × 10+00 | 0.0000 × 10+00 | 0.0000 × 10+00 |
| Std | 0.0000 × 10+00 | 0.0000 × 10+00 | 0.0000 × 10+00 | 0.0000 × 10+00 | |
| F13 | Mean | 8.2400 × 10−12 | 8.6900 × 10−11 | 1.8400 × 10−09 | 8.8824 × 10−16 |
| Std | 0.0000 × 10+00 | 4.7300 × 10−10 | 1.7600 × 10−09 | 0.0000 × 10+00 | |
| F14 | Mean | 0.0000 × 10+00 | 0.0000 × 10+00 | 1.7000 × 10−14 | 0.0000 × 10+00 |
| Std | 0.0000 × 10+00 | 0.0000 × 10+00 | 1.8200 × 10−14 | 0.0000 × 10+00 | |
| F15 | Mean | 0.0000 × 10+00 | 0.0000 × 10+00 | 2.5700 × 10−22 | 0.0000 × 10+00 |
| Std | 0.0000 × 10+00 | 0.0000 × 10+00 | 2.2300 × 10−24 | 0.0000 × 10+00 | |
| F16 | Mean | 9.8300 × 10+00 | 7.2800 × 10−02 | 4.3500 × 10−04 | 1.3780 × 10−05 |
| Std | 2.4700 × 10+00 | 1.8700 × 10−01 | 4.6600 × 10−04 | 1.0504 × 10−02 | |
| F17 | Mean | 5.8500 × 10+06 | 5.8500 × 10+04 | 2.4500 × 10+07 | 3.2042 × 10+04 |
| Std | 3.2400 × 10+05 | 7.6200 × 10+03 | 3.2400 × 10+05 | 2.3582 × 10+03 | |
| F18 | Mean | 6.1000 × 10+04 | 4.5300 × 10+02 | 3.6800 × 10+03 | 2.0000 × 10−01 |
| Std | 5.2000 × 10+03 | 3.1200 × 10+01 | 4.2700 × 10+03 | 2.3640 × 10−07 |
| No. | PSO | GA | DE | ABC | BOA | CBOA | IBOA | HPSOBOA |
|---|---|---|---|---|---|---|---|---|
| F1 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 3.0345 × 10−11 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F2 | 3.0199 × 10−11 | 2.9802 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F3 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 2.1449 × 10−13 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F4 | 3.0199 × 10−11 | 3.0212 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F5 | 3.4742 × 10−10 | 3.9935 × 10−04 | 3.9881 × 10−04 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.1559 × 10−01 | 8.1527 × 10−11 | 8.5641 × 10−04 |
| F6 | 5.9673 × 10−09 | 2.8745 × 10−10 | 3.0199 × 10−11 | 1.3685 × 10−05 | 3.0199 × 10−11 | 3.3384 × 10−11 | 1.3289 × 10−10 | 3.0199 × 10−11 |
| F7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.0139 × 10−10 | 1.9963 × 10−05 | 3.0199 × 10−11 |
| F8 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 7.6083 × 10−13 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F9 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 2.3371 × 10−01 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F10 | 1.2118 × 10−12 | 3.0199 × 10−11 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 3.3735 × 10−02 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F11 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 5.6493 × 10−13 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F12 | 1.9324 × 10−09 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 4.5336 × 10−12 | 3.9229 × 10−05 | 2.2574 × 10−04 |
| F13 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 3.0199 × 10−11 | 1.2118 × 10−12 |
| F14 | 1.2118 × 10−12 | 3.0199 × 10−11 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 4.3492 × 10−12 | 2.5474 × 10−04 | 1.2118 × 10−12 |
| F15 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F16 | 6.7869 × 10−02 | 3.0199 × 10−11 | 1.8577 × 10−01 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.1589 × 10−10 | 1.3252 × 10−06 | 3.0199 × 10−11 |
| F17 | 1.5369 × 10−03 | 3.0199 × 10−11 | 1.366 × 10−02 | 3.5350 × 10−09 | 5.6900 × 10−08 | 1.1549 × 10−12 | 1.4333 × 10−05 | 2.0149 × 10−03 |
| F18 | 1.6490 × 10−03 | 3.0199 × 10−11 | 2.5455 × 10−05 | 4.3230 × 10−01 | 1.2118 × 10−12 | 1.2118 × 10−12 | 3.8406 × 10−03 | 1.2118 × 10−12 |
| Function | PSO [39] | ACO [40] | ABC [41] | DE [39] | SCA [42] | SOA [42] | BOA [43] | QLBOA | |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 1.9400 × 10+03 | 1.7000 × 10+03 | 1.3900 × 10+03 | 2.4164 × 10+03 | 1.2745 × 10+03 | 1.1900 × 10+03 | 7.9116 × 10+03 | 3.1289 × 10+02 |
| Std | 7.0900 × 10+02 | 5.7400 × 10+02 | 2.7200 × 10+02 | 2.7820 × 10+02 | 6.4150 × 10+02 | 1.8300 × 10+02 | 3.2110 × 10+03 | 5.8670 × 10+01 | |
| F2 | Mean | 9.8800 × 10+02 | 5.4900 × 10+02 | 4.2200 × 10+02 | 2.5130 × 10+02 | 4.6409 × 10+02 | 4.0000 × 10+03 | 4.3443 × 10+03 | 4.1452 × 10+02 |
| Std | 1.6800 × 10+02 | 3.9700 × 10+02 | 1.4700 × 10+02 | 7.0540 × 10+00 | 2.4199 × 10+01 | 1.4800 × 10+03 | 4.6354 × 10+02 | 2.5278 × 10+01 | |
| F3 | Mean | 1.5300 × 10 +03 | 1.3400 × 10+03 | 7.2100 × 10+02 | 7.3080 × 10+02 | 6.1885 × 10+03 | 9.3100 × 10+02 | 1.3365 × 10+03 | 7.1135 × 10+02 |
| Std | 4.5200 × 10 +01 | 5.0100 × 10+01 | 1.0300 × 10+01 | 7.6000 × 10+01 | 4.9100 × 10+01 | 4.9900 × 10+01 | 7.9134 × 10+01 | 4.6948 × 10+01 | |
| F4 | Mean | 1.8200 × 10+03 | 1.6500 × 10+03 | 1.0300 × 10+03 | 2.6500 × 10+03 | 1.6540 × 10+03 | 1.2400 × 10+03 | 1.6562 × 10+03 | 1.0012 × 10+03 |
| Std | 6.4400 × 10+01 | 5.5400 × 10+01 | 1.2300 × 10+01 | 4.3370 × 10+00 | 4.3850 × 10+01 | 4.9700 × 10+01 | 4.6885 × 10+01 | 4.8552 × 10+01 | |
| F5 | Mean | 7.7600 × 10 +03 | 4.7900 × 10+03 | 1.5000 × 10+02 | 7.4620 × 10−02 | 4.4750 × 10+04 | 2.0700 × 10+03 | 4.3724 × 10+03 | 9.1416 × 10+02 |
| Std | 1.2200 × 10 +02 | 3.6200 × 10 +03 | 3.0100 × 10+02 | 8.9320 × 10−02 | 8.6800 × 10+01 | 4.5200 × 10+02 | 4.9864 × 10+03 | 7.4438 × 10+01 | |
| F6 | Mean | 2.5700 × 10+03 | 2.4900 × 10 +03 | 2.2500 × 10+03 | 2.9460 × 10+03 | 2.5000 × 10+04 | 6.5800 × 10+03 | 2.5074 × 10+04 | 2.0000 × 10+03 |
| Std | 4.6200 × 10+02 | 2.8900 × 10+03 | 5.1100 × 10+02 | 5.7010 × 10+02 | 2.1400 × 10+03 | 2.6000 × 10+03 | 4.8867 × 10+03 | 2.7954 × 10+02 | |
| F7 | Mean | 4.6900 × 10+03 | 4.1700 × 10+03 | 3.0800 × 10+03 | 1.1360 × 10+03 | 2.7405 × 10+03 | 1.0100 × 10+04 | 4.7423 × 10+03 | 2.0962 × 10+03 |
| Std | 1.8700 × 10+02 | 1.4600 × 10+02 | 1.0500 × 10+02 | 5.5810 × 10+02 | 6.2500 × 10+02 | 4.1500 × 10+03 | 4.2523 × 10+02 | 8.0452 × 10+01 | |
| F8 | Mean | 3.6400 × 10 +03 | 3.1800 × 10+03 | 2.3300 × 10+03 | 7.7570 × 10+03 | 2.6505 × 10+03 | 2.2000 × 10+02 | 3.3674 × 10+03 | 2.6948 × 10+03 |
| Std | 1.2600 × 10+02 | 3.2300 × 10+01 | 1.0600 × 10+01 | 5.1360 × 10+01 | 9.3450 × 10+01 | 3.9300 × 10+03 | 9.3323 × 10+01 | 1.0420 × 10+01 | |
| F9 | Mean | 5.4300 × 10 +03 | 4.2400 × 10 +03 | 2.8400 × 10+03 | 2.1240 × 10+03 | 5.1550 × 10+03 | 3.4100 × 10+02 | 5.1562 × 10+03 | 2.6297 × 10+03 |
| Std | 3.7800 × 10 +02 | 9.4900 × 10+01 | 1.4000 × 10+01 | 2.9450 × 10−02 | 1.4700 × 10+01 | 3.5800 × 10+03 | 2.4776 × 10+02 | 9.9538 × 10+00 | |
| F10 | Mean | 6.8700 × 10+03 | 4.6700 × 10 +03 | 3.0600 × 10+03 | 3.2000 × 10+03 | 3.7804 × 10+03 | 6.3400 × 10+03 | 5.7883 × 10+03 | 3.0014 × 10+03 |
| Std | 2.9500 × 10+02 | 9.6300 × 10 +01 | 1.0300 × 10+01 | 1.2870 × 10+01 | 4.3100 × 10+02 | 6.8000 × 10+03 | 4.3124 × 10+02 | 1.4200 × 10+02 | |
| F11 | Mean | 3.0600 × 10+04 | 1.7100 × 10+04 | 6.6400 × 10+05 | 3.9200 × 10+02 | 1.6450 × 10+04 | 3.2900 × 10+02 | 1.6478 × 10+04 | 2.9350 × 10+03 |
| Std | 2.9300 × 10+03 | 1.7400 × 10+03 | 1.8300 × 10+05 | 7.9870 × 10+01 | 3.4607 × 10+01 | 4.3600 × 10+03 | 1.0234 × 10+03 | 3.0226 × 10+01 | |
| F12 | Mean | 2.8100 × 10+04 | 1.5500 × 10+04 | 5.5700 × 10+03 | 1.0350 × 10+00 | 1.8400 × 10+04 | 1.6300 × 10+03 | 1.8402 × 10+04 | 7.6228 × 10+03 |
| Std | 1.9200 × 10+03 | 8.3500 × 10+02 | 9.4400 × 10+01 | 1.8570 × 10−02 | 5.5370 × 10+02 | 1.1300 × 10+04 | 6.5305 × 10+02 | 1.7782 × 10+03 |
| No. | PSO | ACO | ABC | DE | SCA | SOA | BOA |
|---|---|---|---|---|---|---|---|
| F1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.5105 × 10−08 | 3.0199 × 10−11 | 3.5384 × 10−11 | 3.0199 × 10−11 |
| F2 | 8.6634 × 10−05 | 3.0199 × 10−11 | 2.3168 × 10−06 | 1.1058 × 10−04 | 3.0199 × 10−11 | 2.7829 × 10−07 | 3.0199 × 10−11 |
| F3 | 3.8347 × 10−05 | 3.0199 × 10−11 | 6.4878 × 10−09 | 5.3874 × 10−02 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.8507 × 10−05 |
| F4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.4645 × 10−08 | 3.4384 × 10−11 | 5.4541 × 10−11 | 3.0199 × 10−11 |
| F5 | 2.3715 × 10−10 | 3.0199 × 10−11 | 3.5201 × 10−07 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.6159 × 10−10 | 4.0772 × 10−11 |
| F6 | 3.4642 × 10−10 | 4.3374 × 10−02 | 2.6947 × 10−09 | 2.5771 × 10−07 | 8.6334 × 10−05 | 3.4542 × 10−10 | 3.0199 × 10−11 |
| F7 | 3.5923 × 10−05 | 5.4941 × 10−11 | 3.4029 × 10−01 | 4.0772 × 10−11 | 6.0658 × 10−11 | 1.6813 × 10−04 | 2.3168 × 10−06 |
| F8 | 3.0199 × 10−11 | 8.1714 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.7941 × 10−11 | 3.6597 × 10−11 | 3.0199 × 10−11 |
| F9 | 4.4440 × 10−07 | 3.0199 × 10−11 | 8.1975 × 10−07 | 2.3399 × 10−01 | 3.0199 × 10−11 | 1.9883 × 10−02 | 3.0199 × 10−11 |
| F10 | 1.4743 × 10−10 | 1.6480 × 10−08 | 7.3391 × 10−11 | 3.3374 × 10−11 | 8.4348 × 10−09 | 1.4810 × 10−09 | 1.4643 × 10−10 |
| F11 | 1.9527 × 10−03 | 3.0199 × 10−11 | 4.5530 × 10−01 | 2.7829 × 10−07 | 3.0199 × 10−11 | 3.4783 × 10−01 | 3.0199 × 10−11 |
| F12 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| Symbol | Meaning |
|---|---|
| N | Set of nodes, N = {0, 1, …, n} |
| N’ | Customer collection |
| K | Set k of distribution vehicles, k ∈ K |
| Q | Maximum vehicle loading capacity |
| ti | Customer delivery time i ∈ N |
| qijk | Load of vehicle k from customer i to customer j |
| [ETi, DTi, LTi] | The service time window at customer point i |
| δe | Waiting penalty for early arrival of customer i |
| δli | Tardiness penalty for late arrival of customer i |
| dij | The distance from customer point i to j |
| fijk | Fuel consumption rate of vehicle k on road segment (i, j) (kg/km) |
| Cv | Unit fuel consumption cost (CNY/L) |
| eijk | Carbon emission rate of vehicle k on road segment (i, j) (kg/km) |
| Ck | Unit transportation cost (CNY/km) |
| tijk | Travel time of vehicle k on road segment (i, j) |
| Cf | Charge per unit of carbon emissions (CNY/kg) |
| Ce | Vehicle fixed cost (CNY/car) |
| vk | The traveling speed of vehicle k |
| ε | Customer personal preference value |
| M | Total vehicle weight (kg) |
| g | Constant of gravity (9.81 m/s2) |
| ζ | Speed of engine |
| V | Displacement of engine |
| ξ | Diesel fuel calorific value |
| xijk | 0–1 variable, which is 1 if vehicle k is driving on road (i, j) and 0 otherwise |
| yik | 0–1 variable, 1 when customer point i is served by vehicle k and 0 otherwise |
| zk | 0–1 variable, 1 when vehicle k is used and 0 otherwise |
| Symbol | Meaning |
|---|---|
| K | 25 |
| Coefficient of penalty δ | 100 |
| Unit transportation cost Ck (CNY/km) | 1 |
| Unit fuel consumption cost Cv (CNY/L) | 7.5 |
| Charge per unit of carbon emissions Cf (CNY/kg) | 0.0528 |
| Vehicle fixed cost Ce (CNY/car) | 100 |
| ω0, ω1, ω2, ω3, ω4, ω5, ω6 | 110, 0, −0.0011, −0.00235, 0, 0 |
| χ0, χ1, χ2, χ3, χ4, χ5, χ6, χ7 | 1.27, 0.0614, 0, −0.0011, −0.00235, 0, 0, −1.33 |
| Datasets | ε | Transportation Cost | Fuel Cost | Penalty Cost | Number of Vehicles |
|---|---|---|---|---|---|
| C107 | 0.2 | 972.85 | 1687.28 | 256.42 | 8 |
| 0.6 | 987.59 | 1258.63 | 278.36 | 11 | |
| 0.8 | 1008.35 | 1381.44 | 112.05 | 13 | |
| C202 | 0.2 | 916.14 | 1118.112 | 236.12 | 7 |
| 0.6 | 909.76 | 1048.52 | 208.14 | 10 | |
| 0.8 | 1193.26 | 1634.77 | 125.02 | 11 | |
| R106 | 0.2 | 1185.45 | 1607.34 | 308.25 | 11 |
| 0.6 | 1199.10 | 1642.16 | 225.03 | 14 | |
| 0.8 | 1346.10 | 1844.26 | 175.74 | 15 | |
| R201 | 0.2 | 1206.68 | 1652.32 | 227.64 | 6 |
| 0.6 | 988.85 | 1353.29 | 198.76 | 9 | |
| 0.8 | 1326.53 | 1817.48 | 155.31 | 11 | |
| RC102 | 0.2 | 1695.36 | 2322.64 | 198.52 | 14 |
| 0.6 | 1685.74 | 2135.84 | 108.43 | 16 | |
| 0.8 | 1702.84 | 2331.78 | 89.35 | 17 | |
| RC206 | 0.2 | 1589.37 | 2176.93 | 225.35 | 6 |
| 0.6 | 1466.67 | 1906.07 | 208.93 | 10 | |
| 0.8 | 1697.85 | 2324.8 | 205.35 | 12 |
| Datasets | Weighting Factor (λ) | Transportation Cost | Fuel Cost | Penalty Cost | Number of Vehicles |
|---|---|---|---|---|---|
| C107 | λ1 = 0.6, λ2 = 0.3, λ3 = 0.1 | 395.04 | 881.04 | 250.52 | 8 |
| λ1 = 0.1, λ2 = 0.6, λ3 = 0.3 | 888.83 | 503.45 | 194.85 | 11 | |
| λ1 = 0.3, λ2 = 0.1, λ3 = 0.6 | 691.31 | 1132.77 | 111.34 | 13 | |
| C202 | λ1 = 0.6, λ2 = 0.3, λ3 = 0.1 | 363.90 | 733.96 | 187.33 | 8 |
| λ1 = 0.1, λ2 = 0.6, λ3 = 0.3 | 818.78 | 419.41 | 145.70 | 10 | |
| λ1 = 0.3, λ2 = 0.1, λ3 = 0.6 | 636.83 | 943.67 | 83.26 | 12 | |
| R106 | λ1 = 0.6, λ2 = 0.3, λ3 = 0.1 | 479.64 | 1149.51 | 202.53 | 12 |
| λ1 = 0.1, λ2 = 0.6, λ3 = 0.3 | 1079.19 | 656.86 | 157.52 | 14 | |
| λ1 = 0.3, λ2 = 0.1, λ3 = 0.6 | 839.37 | 1477.94 | 90.01 | 15 | |
| R201 | λ1 = 0.6, λ2 = 0.3, λ3 = 0.1 | 395.54 | 947.30 | 178.88 | 6 |
| λ1 = 0.1, λ2 = 0.6, λ3 = 0.3 | 889.97 | 541.32 | 139.13 | 9 | |
| λ1 = 0.3, λ2 = 0.1, λ3 = 0.6 | 692.20 | 1217.96 | 79.50 | 12 | |
| RC102 | λ1 = 0.6, λ2 = 0.3, λ3 = 0.1 | 674.30 | 1495.09 | 97.59 | 11 |
| λ1 = 0.1, λ2 = 0.6, λ3 = 0.3 | 1517.17 | 854.34 | 75.90 | 13 | |
| λ1 = 0.3, λ2 = 0.1, λ3 = 0.6 | 1180.02 | 1922.26 | 43.37 | 17 | |
| RC206 | λ1 = 0.6, λ2 = 0.3, λ3 = 0.1 | 586.66 | 1334.25 | 188.04 | 6 |
| λ1 = 0.1, λ2 = 0.6, λ3 = 0.3 | 1319.99 | 762.43 | 146.25 | 10 | |
| λ1 = 0.3, λ2 = 0.1, λ3 = 0.6 | 1026.66 | 1715.46 | 83.57 | 12 |
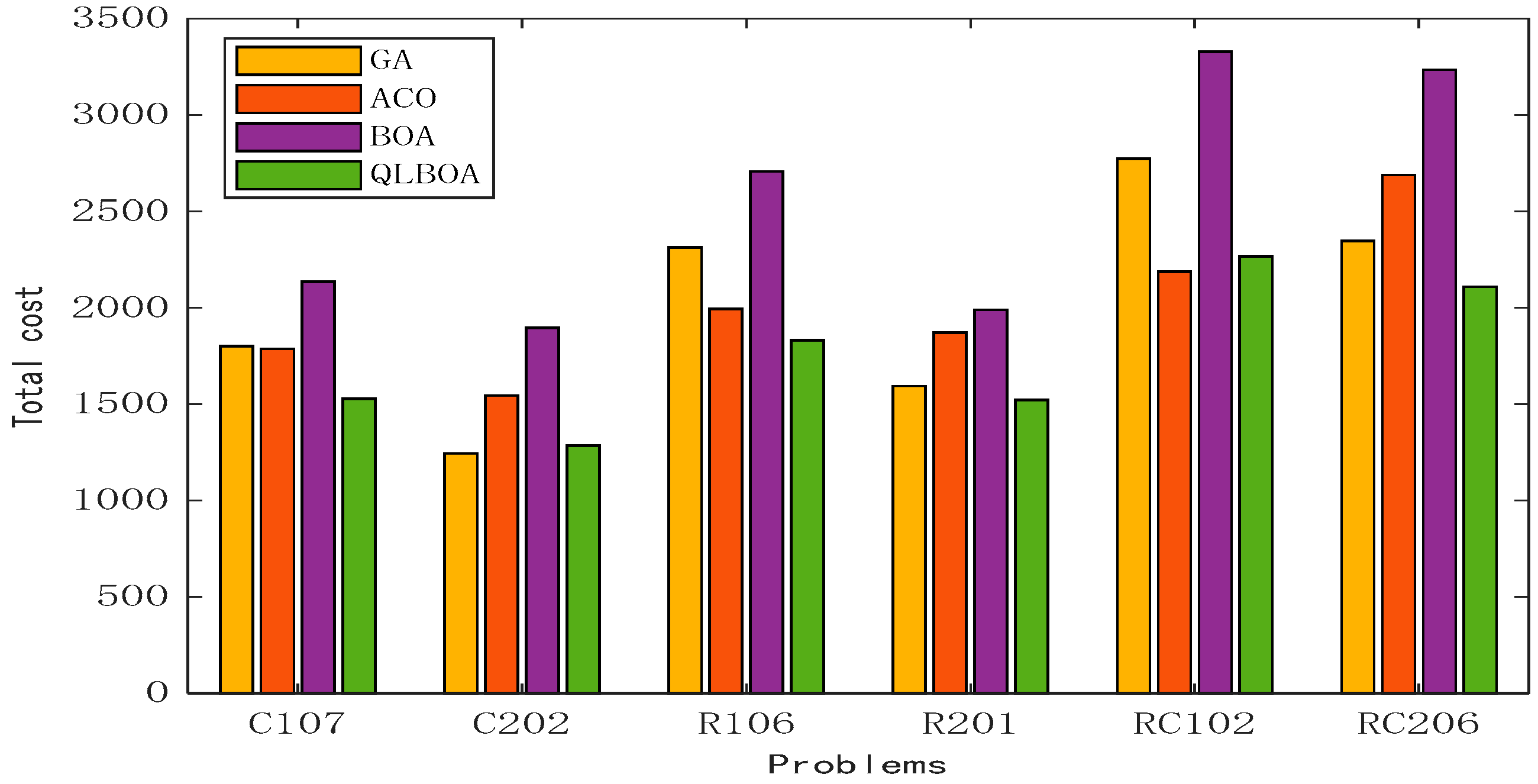
| Datasets | Algorithms | Transportation Cost | Fuel Cost | Penalty Cost |
|---|---|---|---|---|
| C107 | GA | 449.04 | 1081.05 | 270.53 |
| ACO | 435.87 | 1103.47 | 247.95 | |
| BOA | 691.31 | 1132.77 | 311.34 | |
| QLBOA | 395.04 | 881.04 | 250.52 | |
| C202 | GA | 347.68 | 678.78 | 217.63 |
| ACO | 818.78 | 579.46 | 145.70 | |
| BOA | 635.83 | 973.68 | 285.76 | |
| QLBOA | 363.90 | 733.96 | 187.33 | |
| R106 | GA | 426.57 | 1648.75 | 237.47 |
| ACO | 1079.19 | 656.86 | 257.52 | |
| BOA | 839.37 | 1477.94 | 390.01 | |
| QLBOA | 479.64 | 1149.51 | 202.53 | |
| R201 | GA | 405.55 | 997.39 | 190.08 |
| ACO | 889.97 | 841.32 | 139.13 | |
| BOA | 692.20 | 1217.96 | 79.50 | |
| QLBOA | 395.54 | 947.30 | 178.88 | |
| RC102 | GA | 1078.38 | 1585.89 | 108.96 |
| ACO | 1017.17 | 1064.04 | 105.90 | |
| BOA | 1180.02 | 1906.27 | 243.37 | |
| QLBOA | 674.30 | 1495.09 | 97.59 | |
| RC206 | GA | 1088.67 | 1054.25 | 204.33 |
| ACO | 1386.34 | 1056.49 | 246.25 | |
| BOA | 1056.47 | 1895.44 | 283.57 | |
| QLBOA | 586.66 | 1334.25 | 188.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, W.; He, Y.; Zhou, Y. Q-Learning-Driven Butterfly Optimization Algorithm for Green Vehicle Routing Problem Considering Customer Preference. Biomimetics 2025, 10, 57. https://doi.org/10.3390/biomimetics10010057
Meng W, He Y, Zhou Y. Q-Learning-Driven Butterfly Optimization Algorithm for Green Vehicle Routing Problem Considering Customer Preference. Biomimetics. 2025; 10(1):57. https://doi.org/10.3390/biomimetics10010057
Chicago/Turabian StyleMeng, Weiping, Yang He, and Yongquan Zhou. 2025. "Q-Learning-Driven Butterfly Optimization Algorithm for Green Vehicle Routing Problem Considering Customer Preference" Biomimetics 10, no. 1: 57. https://doi.org/10.3390/biomimetics10010057
APA StyleMeng, W., He, Y., & Zhou, Y. (2025). Q-Learning-Driven Butterfly Optimization Algorithm for Green Vehicle Routing Problem Considering Customer Preference. Biomimetics, 10(1), 57. https://doi.org/10.3390/biomimetics10010057






