Aerodynamic and Inertial Loading Effects of Insect-Inspired Appendages in Small Unmanned Aerial Vehicles
Abstract
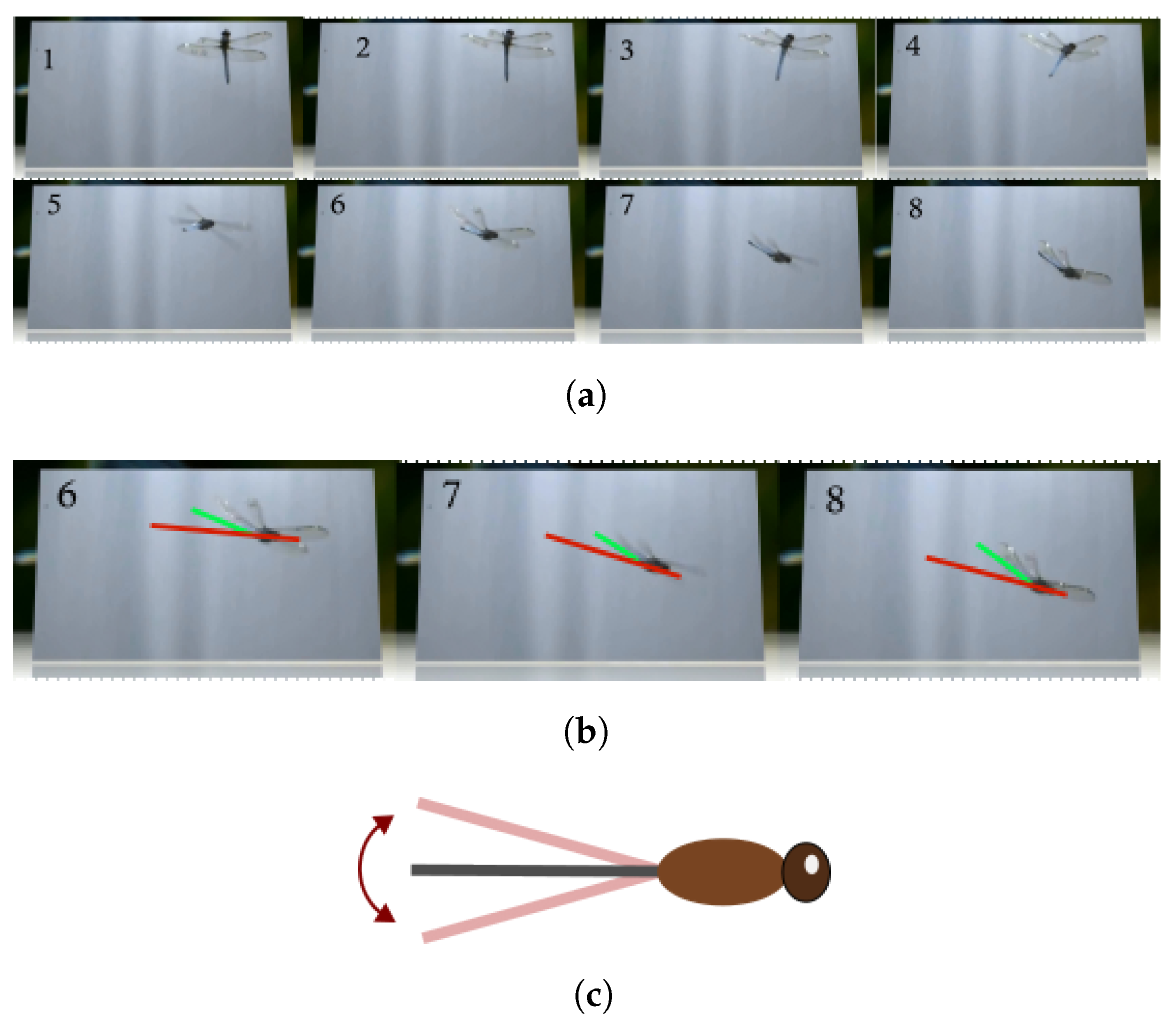
1. Introduction
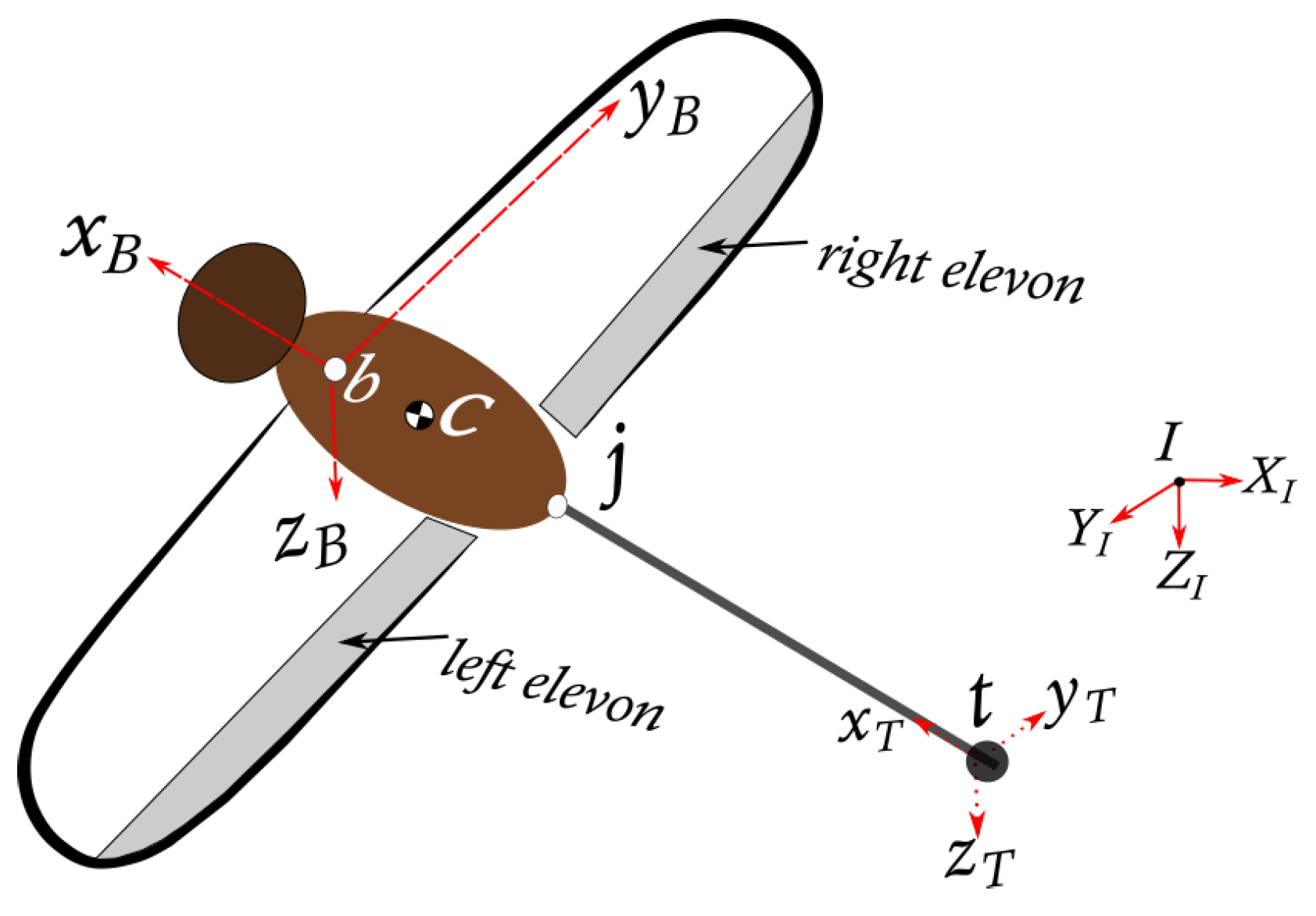
2. Multibody Equations of Motion
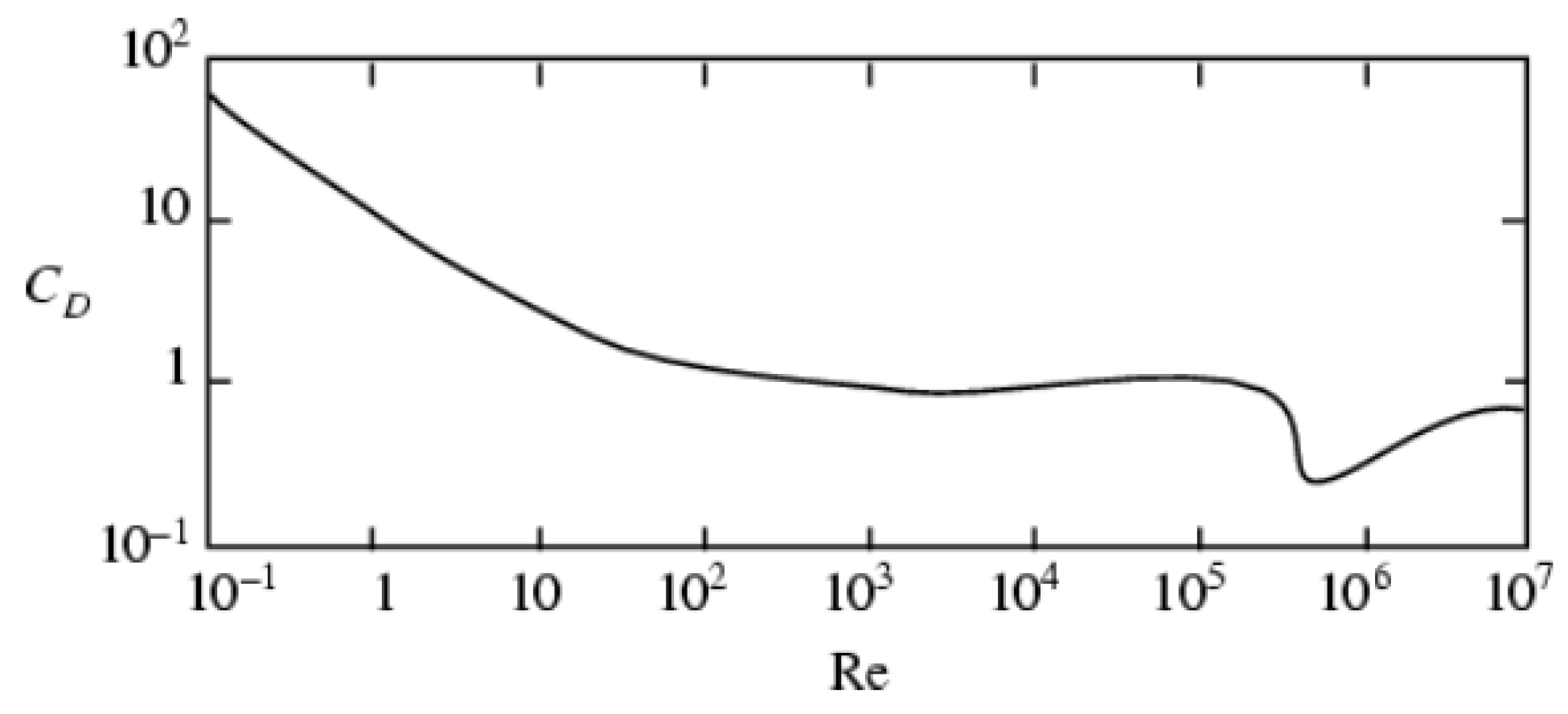
3. Aerodynamic Loading of the Abdomen
4. Aircraft Specification
5. Performance Effects of Appendages
5.1. Steady Cruise Flight
5.2. Quasi-Steady Pull Up Manoeuvre
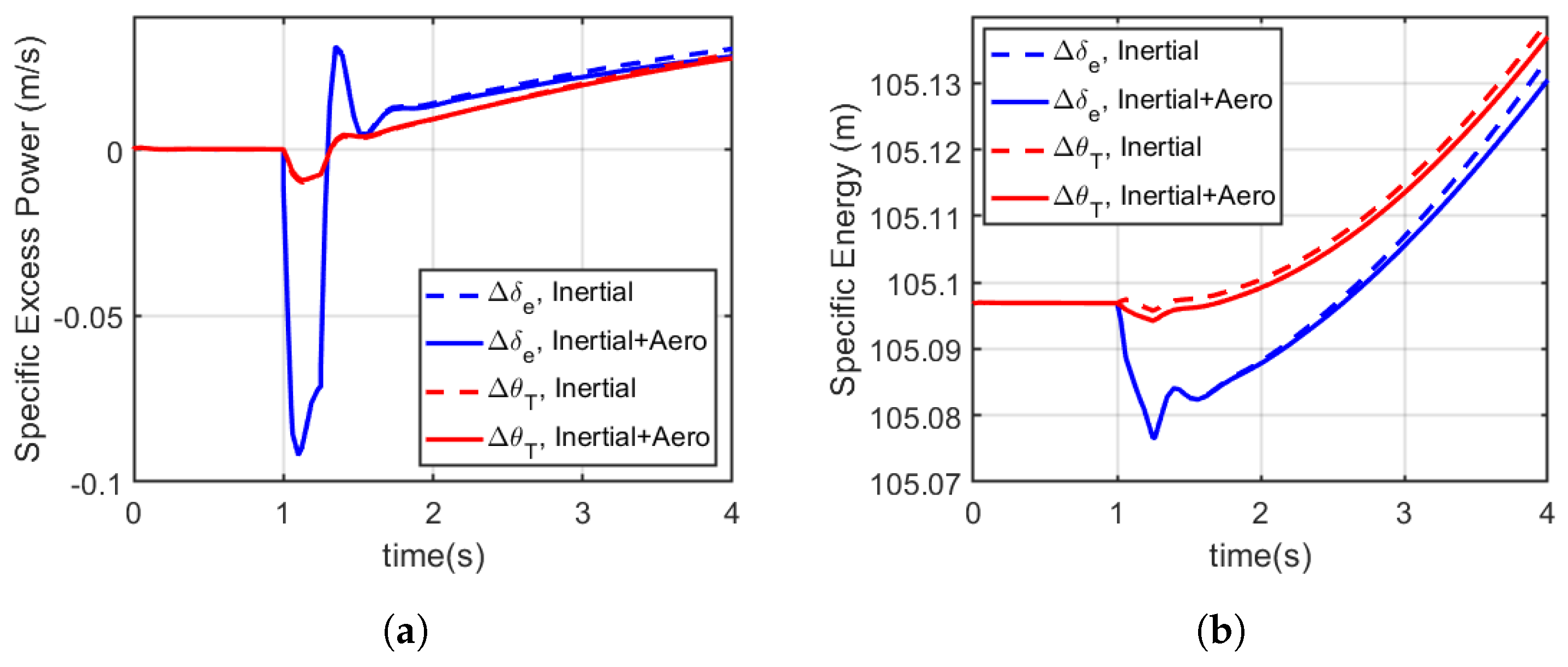
5.3. Discussion of Performance Effects of Appendage
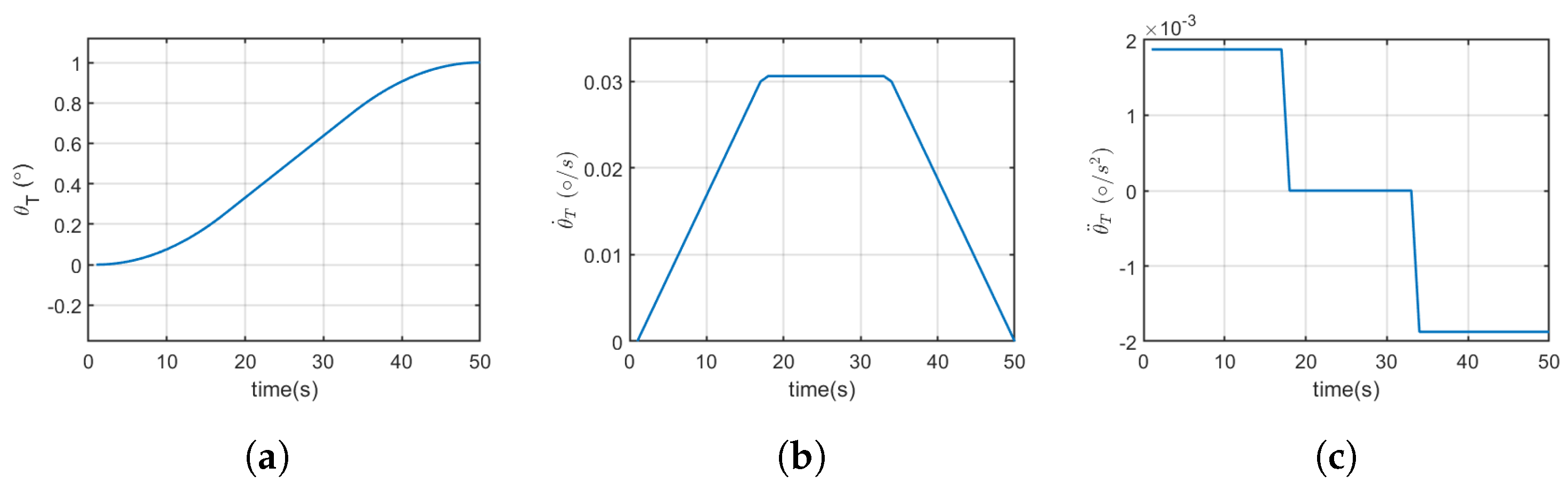
6. Manoeuvring Using Abdominal Deflection
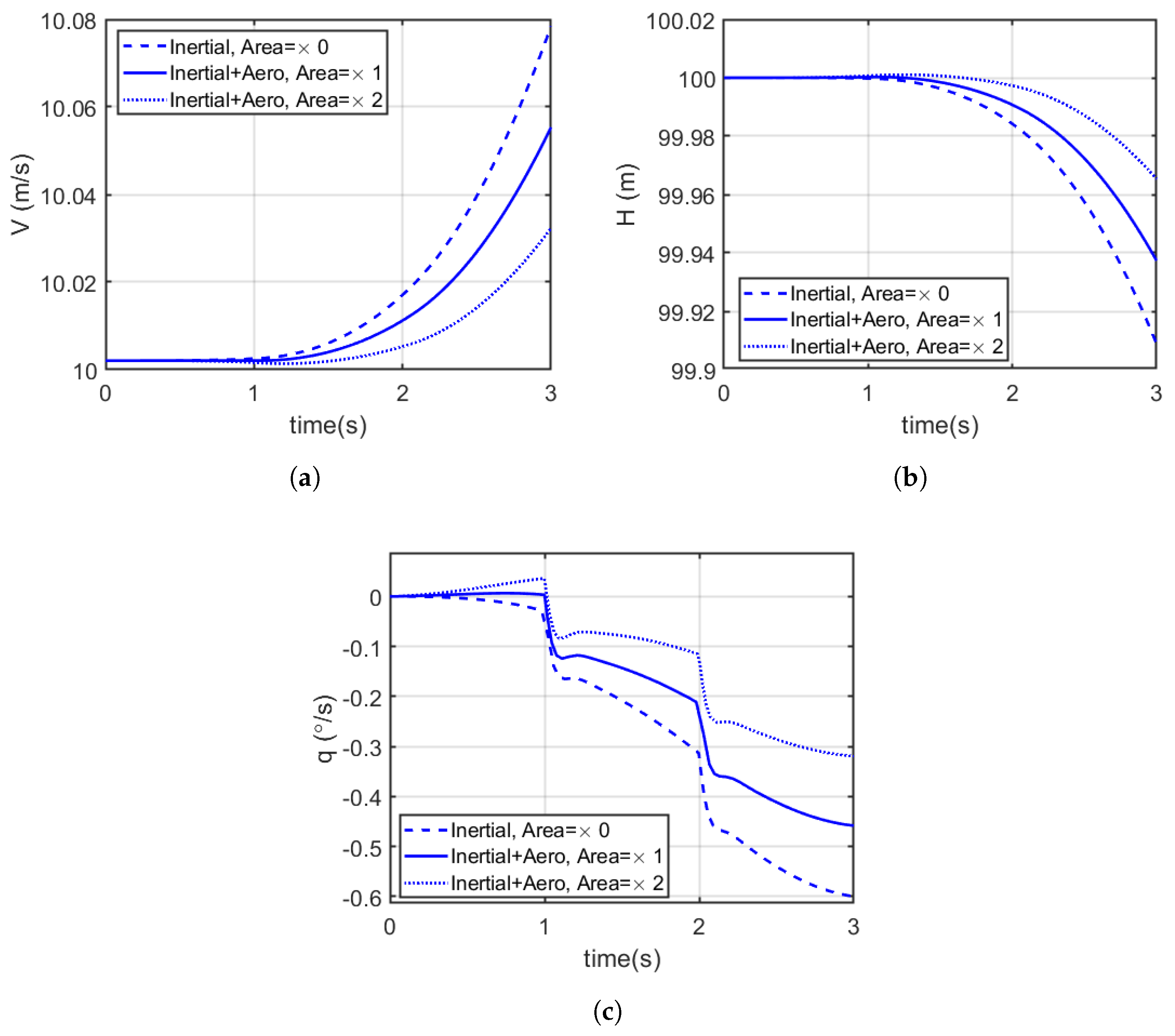
6.1. Effect of Increased Abdominal Area on Longitudinal Manoeuvring
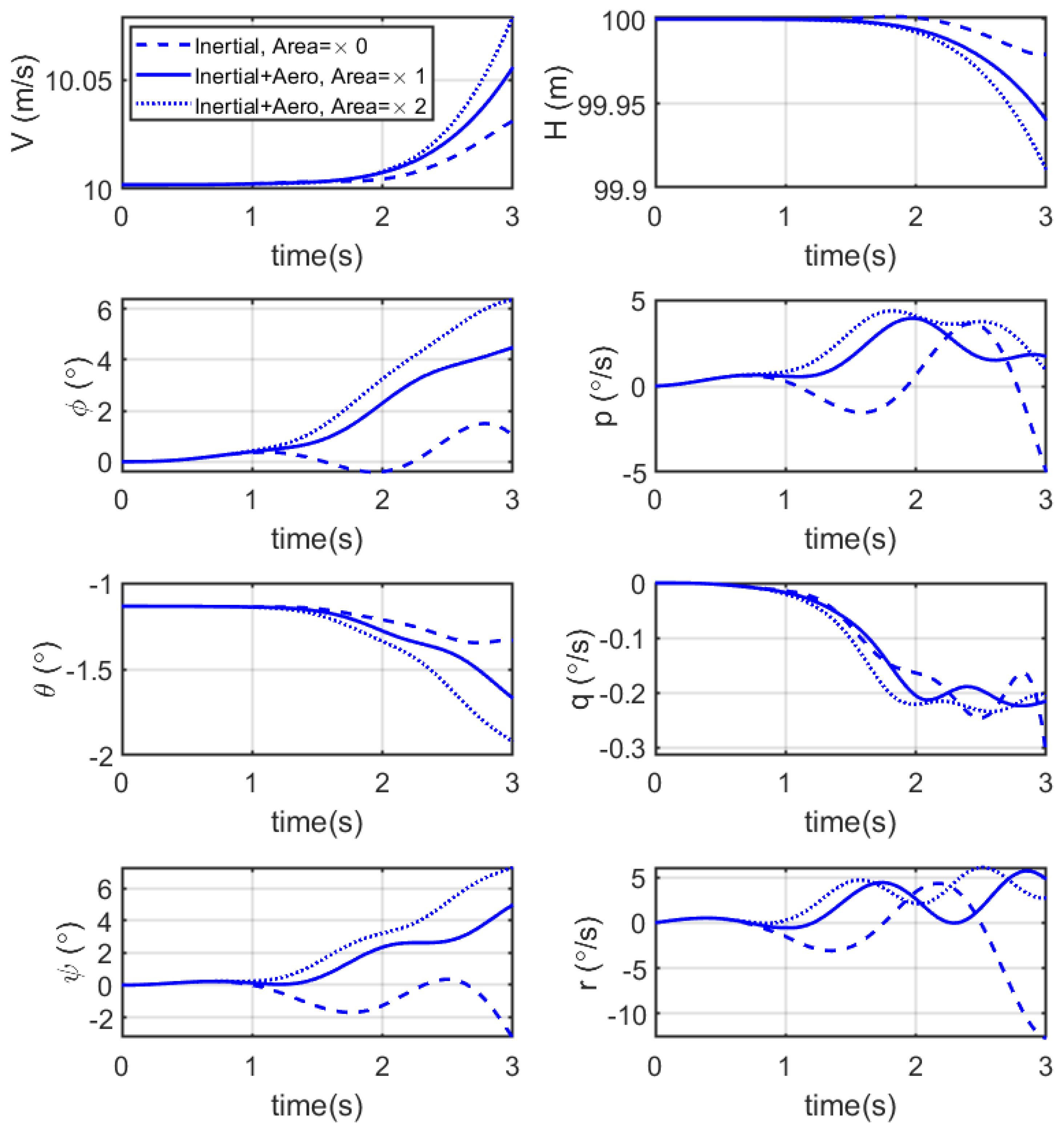
6.2. Effect of Increased Abdominal Area on Lateral Manoeuvring
6.3. Discussion of Manoeuvring Using Abdominal Deflection
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| * (model, vector or tensor) expressed in arbitrary reference frame A (Inertial (I), central body (B) and abdominal (T) reference frames in text) | |
| A | Arbitrary Rigid body A (Central body (B), abdomen (T) or whole aircraft (C) in text) |
| The rotation matrix from reference frame A to B | |
| b, t, j, c | Locations of the centre of mass of the central body, tail, tail joint and whole aircraft, respectively |
| Displacement, skew-symmetric matrix of displacement of point a relative to point b (m) | |
| Velocity of point A relative to point B () | |
| Mass of rigid body , total mass of the aircraft, respectively () | |
| Inertia tensor of rigid body A about point a () | |
| Angular velocity, skew symmetric matrix of angular velocity of frame A relative to frame B, respectively () | |
| F | External force vector (N) |
| M | External moment vector (N m) |
| Superscripts | |
| First-order time derivative | |
| Second-order time derivative |
Appendix A. Athena Vortex Lattice File for Aerodynamic Data

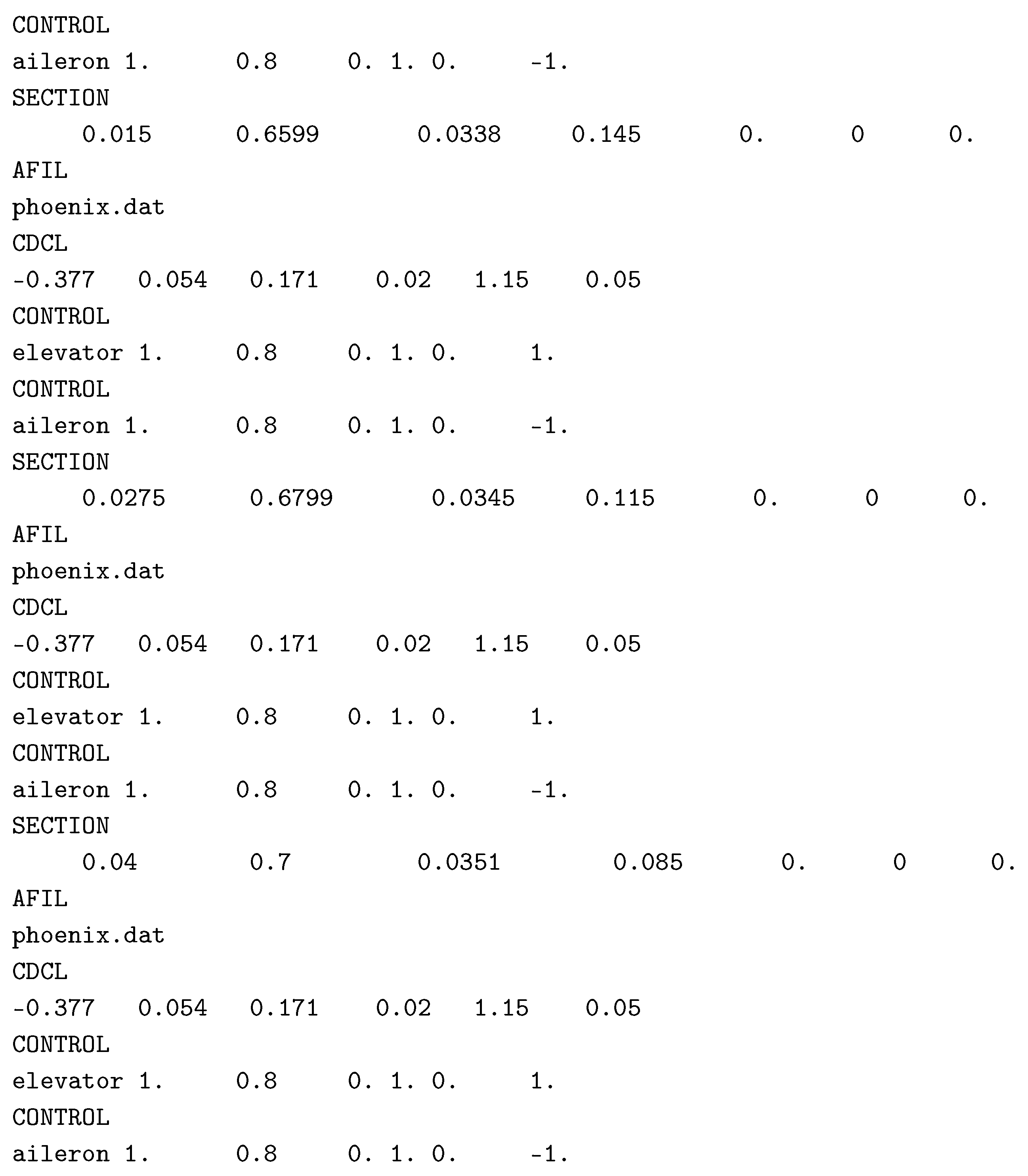
Appendix B. Model Validation: Single-Body vs. Multibody
| (m/s) | (m) | (°) | Model Type | (°) | (°) | (N) | (Nm) |
|---|---|---|---|---|---|---|---|
| 10 | 100 | 0 | Single-body | −11.35 | 0.228 | 0.679 | - |
| Multibody | −11.35 | 0.228 | 0.679 | −0.235 | |||
| −10 | Single-body | −10.66 | 0.0707 | 0.683 | - | ||
| Multibody | −10.66 | 0.0707 | 0.683 | −0.232 | |||
| −30 | Single-body | −6.02 | −0.96 | 0.708 | - | ||
| Multibody | −6.02 | −0.96 | 0.708 | −0.204 |
References
- Alexander, R.M. Principles of Animal Locomotion; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Laouris, Y.; Kalli-Laouri, J.; Schwartze, P. The postnatal development of the air-righting reaction in albino rats. Quantitative analysis of normal development and the effect of preventing neck-torso and torso-pelvis rotations. Behav. Brain Res. 1990, 37, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Jusufi, A.; Zeng, Y.; Full, R.J.; Dudley, R. Aerial righting reflexes in flightless animals. Integr. Comp. Biol. 2011, 51, 937–943. [Google Scholar] [CrossRef] [PubMed]
- Jusufi, A.; Goldman, D.I.; Revzen, S.; Full, R.J. Active tails enhance arboreal acrobatics in geckos. Proc. Natl. Acad. Sci. USA 2008, 105, 4215–4219. [Google Scholar] [CrossRef] [PubMed]
- Libby, T.; Moore, T.Y.; Chang-Siu, E.; Li, D.; Cohen, D.J.; Jusufi, A.; Full, R.J. Tail-assisted pitch control in lizards, robots and dinosaurs. Nature 2012, 481, 181. [Google Scholar] [CrossRef] [PubMed]
- Pennycuick, C.J. A wind-tunnel study of gliding flight in the pigeon Columba livia. J. Exp. Biol. 1968, 49, 509–526. [Google Scholar] [CrossRef]
- Pennycuick, C.J. Control of gliding angle in Ruppell’s griffon vulture Gyps ruppellii. J. Exp. Biol. 1971, 55, 39–46. [Google Scholar] [CrossRef]
- Cook, M.; Spottiswoode, M. Modelling the flight dynamics of the hang glider. Aeronaut. J. 2005, 109, I–XX. [Google Scholar] [CrossRef]
- Ellington, C.P. The aerodynamics of hovering insect flight. IV. Aerodynamic mechanisms. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1984, 305, 79–113. [Google Scholar]
- Jankauski, M.; Daniel, T.L.; Shen, I. Asymmetries in wing inertial and aerodynamic torques contribute to steering in flying insects. Bioinspiration Biomimetics 2017, 12, 046001. [Google Scholar] [CrossRef] [PubMed]
- Hedrick, T.L.; Daniel, T.L. Flight control in the hawkmoth Manduca sexta: The inverse problem of hovering. J. Exp. Biol. 2006, 209, 3114–3130. [Google Scholar] [CrossRef] [PubMed]
- Fabian, S.T.; Zhou, R.; Lin, H.T. Dragondrop: A novel passive mechanism for aerial righting in the dragonfly. Proc. R. Soc. B 2021, 288, 20202676. [Google Scholar] [CrossRef]
- Gotz, K.G.; Hengstenberg, B.; Biesinger, R. Optomotor control of wing beat and body posture in Drosophila. Biol. Cybern. 1979, 35, 101–112. [Google Scholar] [CrossRef]
- Zanker, J.M. How does lateral abdomen deflection contribute to flight control of Drosophila melanogaster? J. Comp. Physiol. A 1988, 162, 581–588. [Google Scholar] [CrossRef]
- Zanker, J. On the mechanism of speed and altitude control in Drosophila melanogaster. Physiol. Entomol. 1988, 13, 351–361. [Google Scholar] [CrossRef]
- Zanker, J.M.; Egelhaaf, M.; Warzecha, A.K. On the coordination of motor output during visual flight control of flies. J. Comp. Physiol. A 1991, 169, 127–134. [Google Scholar] [CrossRef]
- Dyhr, J.P.; Morgansen, K.A.; Daniel, T.L.; Cowan, N.J. Flexible strategies for flight control: An active role for the abdomen. J. Exp. Biol. 2013, 216, 1523–1536. [Google Scholar] [CrossRef] [PubMed]
- Hinterwirth, A.J.; Daniel, T.L. Antennae in the hawkmoth Manduca sexta (Lepidoptera, Sphingidae) mediate abdominal flexion in response to mechanical stimuli. J. Comp. Physiol. A 2010, 196, 947–956. [Google Scholar] [CrossRef]
- Frye, M.A. Effects of stretch receptor ablation on the optomotor control of lift in the hawkmoth Manduca sexta. J. Exp. Biol. 2001, 204, 3683–3691. [Google Scholar] [CrossRef]
- Cheng, B.; Deng, X.; Hedrick, T.L. The mechanics and control of pitching manoeuvres in a freely flying hawkmoth (Manduca sexta). J. Exp. Biol. 2011, 214, 4092–4106. [Google Scholar] [CrossRef] [PubMed]
- Arbas, E.A. Control of hindlimb posture by wind-sensitive hairs and antennae during locust flight. J. Comp. Physiol. A 1986, 159, 849–857. [Google Scholar] [CrossRef] [PubMed]
- Yanoviak, S.P.; Kaspari, M.; Dudley, R. Gliding hexapods and the origins of insect aerial behaviour. Biol. Lett. 2009, 5, 510–512. [Google Scholar] [CrossRef] [PubMed]
- Yanoviak, S.P.; Munk, Y.; Kaspari, M.; Dudley, R. Aerial manoeuvrability in wingless gliding ants (Cephalotes atratus). Proc. R. Soc. B Biol. Sci. 2010, 277, 2199–2204. [Google Scholar] [CrossRef]
- Agrawal, S.; Madangopal, R.; Khan, Z. Biologically inspired design of small flapping wing air vehicles using four-bar mechanisms and quasi-steady aerodynamics. J. Mech. Des. 2005, 127, 809. [Google Scholar]
- Deng, X. Flapping flight for biomimetic robotic insects: Part I-system modeling’. IEEE Trans. Robot. 2006, 22, 776–788. [Google Scholar] [CrossRef]
- Deng, X.; Schenato, L.; Sastry, S.S. Flapping flight for biomimetic robotic insects: Part II-flight control design. IEEE Trans. Robot. 2006, 22, 789–803. [Google Scholar] [CrossRef]
- Liang, B.; Sun, M. Aerodynamic interactions between wing and body of a model insect in forward flight and maneuvers. J. Bionic Eng. 2013, 10, 19–27. [Google Scholar] [CrossRef]
- Lasek, M.; Sibilski, K. Modelling and simulation of flapping wing control for a micromechanical flying insect (entomopter). In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4973. [Google Scholar]
- Jackson, J.; Bhattacharya, R.; Strganac, T. Modelling and suboptimal trajectory generation for a symmetric flapping wing vehicle. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6465. [Google Scholar]
- Bolender, M. Rigid multi-body equations-of-motion for flapping wing mavs using kane’s equations. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 6158. [Google Scholar]
- Gebert, G.; Gallmeier, P.; Evers, J. Equations of motion for flapping flight. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4872. [Google Scholar]
- Paranjape, A.A.; Chung, S.J.; Selig, M.S. Flight mechanics of a tailless articulated wing aircraft. Bioinspiration Biomimetics 2011, 6, 026005. [Google Scholar] [CrossRef]
- Sakhaei, A. Dynamic Modelling And Predictive Control For Insect-Like Flapping Wing Aerial Micro Robots. Ph.D. Thesis, Ryerson University, Toronto, ON, Canada, 2010. [Google Scholar]
- Orlowski, C.T. Flapping Wing Micro Air Vehicles: An Analysis of the Importance of the Mass of the Wings to Flight Dynamics, Stability, and Control. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2011. [Google Scholar]
- Hassan, A.M.; Taha, H.E. Aerodynamic-dynamic interactions and multi-body formulation of flapping wing dynamics: Part I modeling. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017; p. 1274. [Google Scholar]
- Du, C.; Xu, J.; Zheng, Y. Modeling and control of a dragonfly-like micro aerial vehicle. Adv. Robot. Autom. S 2015, 2, 2. [Google Scholar]
- Tejaswi, K.; Kang, C.K.; Lee, T. Dynamics and control of a flapping wing uav with abdomen undulation inspired by monarch butterfly. In Proceedings of the IEEE 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 66–71. [Google Scholar]
- Tejaswi, K.; Sridhar, M.K.; Kang, C.k.; Lee, T. Effects of abdomen undulation in energy consumption and stability for monarch butterfly. Bioinspiration Biomimetics 2021, 16, 046003. [Google Scholar] [CrossRef]
- Huber, J.; Noyes, J. A new genus and species of fairyfly, Tinkerbella nana (Hymenoptera, Mymaridae), with comments on its sister genus Kikiki, and discussion on small size limits in arthropods. J. Hymenopt. Res. 2013, 32, 17–44. [Google Scholar] [CrossRef]
- Grimaldi, D.; Engel, M.S.; Engel, M.S. Evolution of the Insects; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Ogunwa, T.; McIvor, B.; Jumat, N.A.; Abdullah, E.; Chahl, J. Longitudinal Actuated Abdomen Control for Energy Efficient Flight of Insects. Energies 2020, 13, 5480. [Google Scholar] [CrossRef]
- Ogunwa, T.; Abdullah, E.; Chahl, J. Modeling and Control of an Articulated Multibody Aircraft. Appl. Sci. 2022, 12, 1162. [Google Scholar] [CrossRef]
- Times, T.N.Y. ScienceTake: How a Dragonfly Hunts—The New York Times. Available online: https://www.nytimes.com/video/science/100000002459273/sciencetake-how-a-dragonfly-hunts.html?smid=url-share (accessed on 8 February 2024).
- Mischiati, M.; Lin, H.T.; Herold, P.; Imler, E.; Olberg, R.; Leonardo, A. Internal models direct dragonfly interception steering. Nature 2015, 517, 333–338. [Google Scholar] [CrossRef] [PubMed]
- Ellington, C. Aerodynamics and the origin of insect flight. Adv. Insect Physiol. 1991, 23, 171–210. [Google Scholar]
- Anderson, J.D., Jr. Fundamentals of Aerodynamics; Tata McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Zhu, Z. Nonlinear Elastodynamic Analysis of Low Tension Cable Using a New Beam Element. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2004. [Google Scholar]
- Nelson, R.C. Flight Stability and Automatic Control; WCB/McGraw Hill: New York, NY, USA, 1998. [Google Scholar]
- Hoerner, S.F. Fluid-Dynamic Drag: Theoretical, Experimental and Statistical Information. Hoerner Fluid Dynamics 1965. Available online: https://www.amazon.com/Fluid-Dynamic-Drag-Theoretical-experimental-statistical/dp/B000E6W72O (accessed on 2 February 2024).
- Drela, M.; Youngren, H. AVL Overview. Online Product Brochure. 2014. Available online: http://web.mit.edu/drela/Public/web/avl/ (accessed on 12 June 2020).
- Drela, M.; Youngren, H. XFOIL manual, 2001. Available online: https://web.mit.edu/drela/Public/web/xfoil/ (accessed on 12 June 2022).
- Deperrois, A. XFLR5 Analysis of foils and wings operating at low Reynolds numbers. Available online: https://sourceforge.net/projects/xflr5/ (accessed on 2 March 2020).
- Sims, T.A. Design and Control Considerations for a Skid-to-Turn Unmanned Aerial Vehicle; California Polytechnic State University: San Luis Obispo, CA, USA, 2009. [Google Scholar]
- Budziak, K. Aerodynamic Analysis with Athena Vortex Lattice (AVL); Aircraft Design and Systems Group (AERO), Department of Automotive: Hamburg, Germany, 2015. [Google Scholar]
- Dantsker, O.; Vahora, M. Comparison of Aerodynamic Characterization Methods for Design of Unmanned Aerial Vehicles. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 0272. [Google Scholar]
- Deperrois, A. XFLR5. Available online: http://www.xflr5.tech/xflr5.htm (accessed on 3 August 2020).
- Corke, P. Robotics toolbox. Obtained from Peter O. Corke Site. 2002. Available online: https://petercorke.com/toolboxes/robotics-toolbox/ (accessed on 4 August 2023).
- Bacon, B.; Gregory, I. General equations of motion for a damaged asymmetric aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; p. 6306. [Google Scholar]


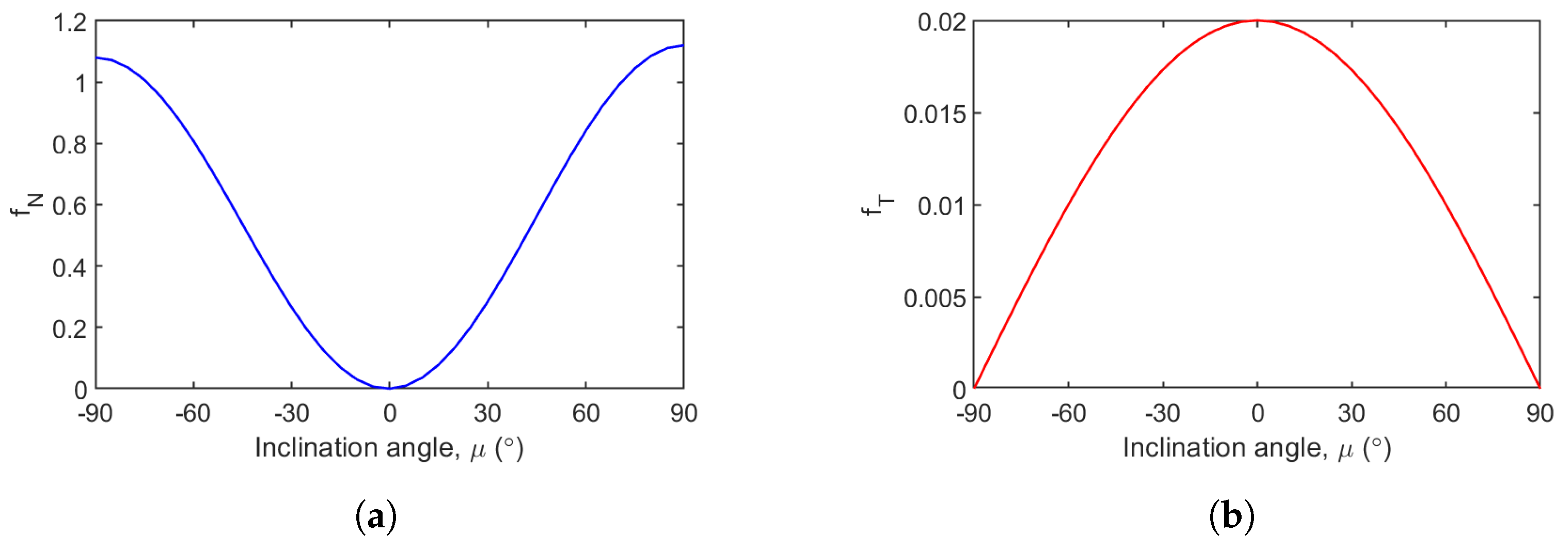

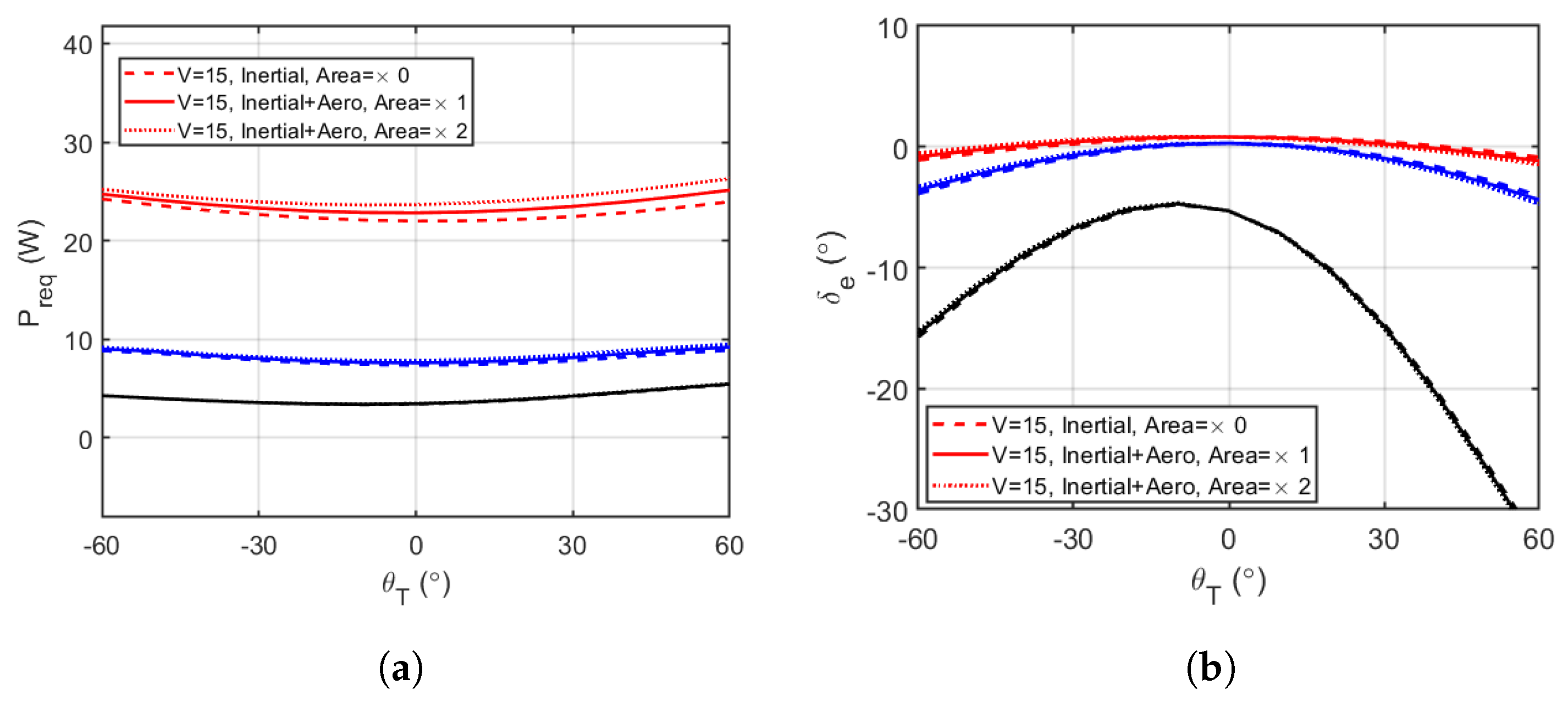
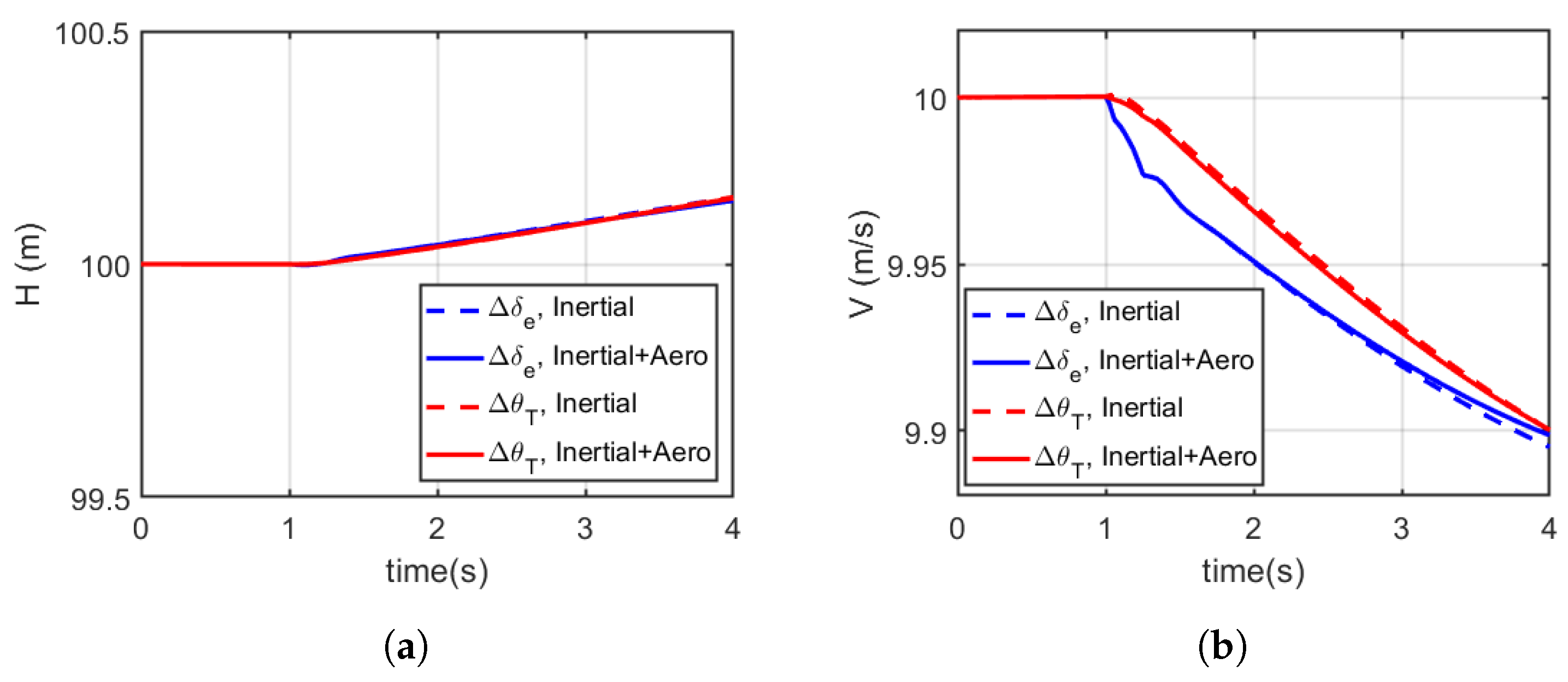
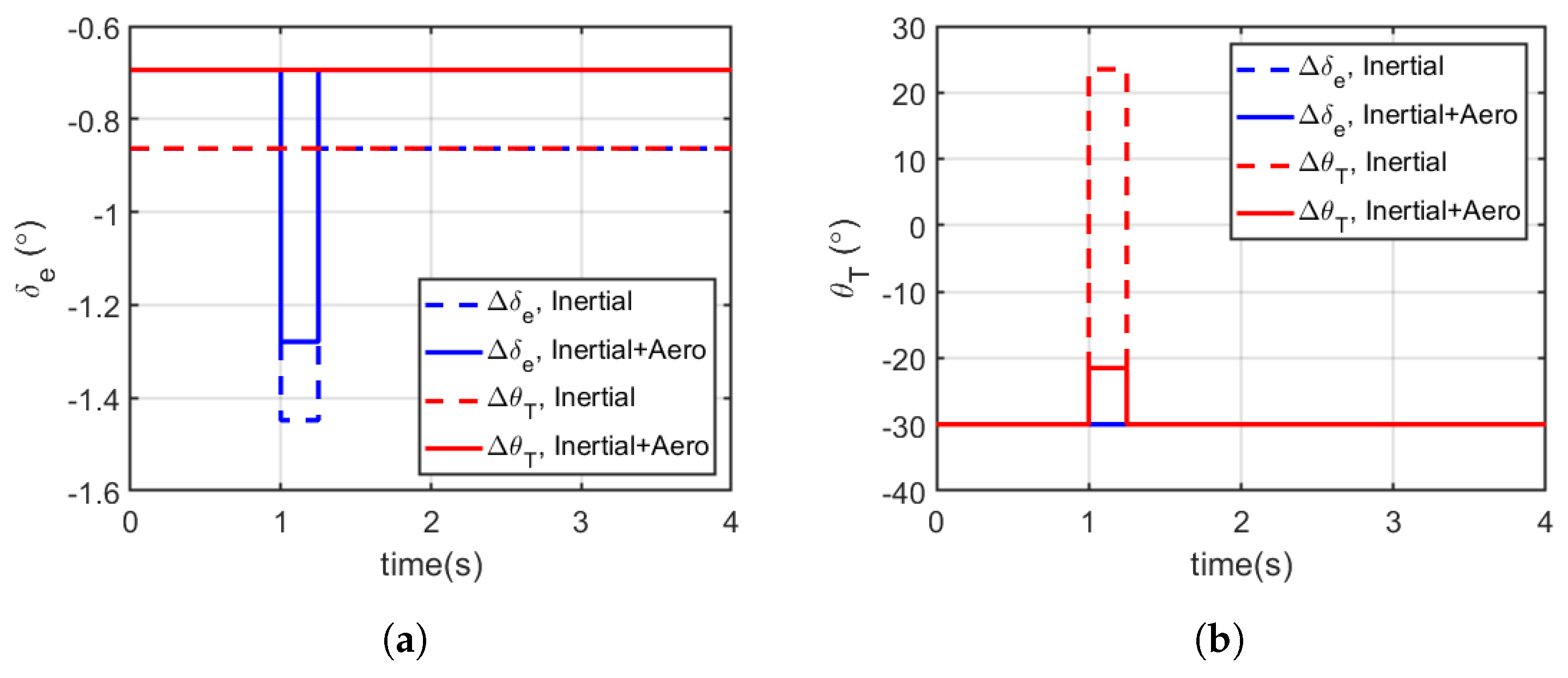
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.325 | 0.06 | ||
| Body length, | 0.3 | Tail length, | 0.4 |
| Max. body diameter, | 0.14 | Tail diameter, | 0.05 |
| 0.00187 | 1.4 | ||
| 0.01117 | 0.19434 | ||
| 0.00934 | 0.26865 | ||
| [−0.064; 0; 0.003] | [0.025; 0; 0] |
| V (m/s) | Percentage Average Variation (%) | |||
| Power Required | Elevator Deflection | |||
| 5 | 0.7667 | 1.5317 | 0.1656 | 0.3290 |
| 10 | 3.0853 | 6.1339 | 0.5732 | 1.2012 |
| 15 | 3.6385 | 7.2757 | −3.2011 | −6.9674 |
| Control Effector and Model Used | Average Specific Energy (m) | Average Specific Excess Power (m/s) |
|---|---|---|
| , Inertial | 105.093 | −0.014 |
| , Inertial | 105.103 | 0.0043 |
| , Inertial + Aero | 105.0927 | −0.0138 |
| , Inertial + Aero | 105.1015 | 0.0042 |
| Modified Model | Percentage Average Variation (%) | ||
| Velocity | Height | Pitch Rate | |
| Area × 1 | |||
| Area × 2 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogunwa, T.; Chahl, J. Aerodynamic and Inertial Loading Effects of Insect-Inspired Appendages in Small Unmanned Aerial Vehicles. Biomimetics 2025, 10, 22. https://doi.org/10.3390/biomimetics10010022
Ogunwa T, Chahl J. Aerodynamic and Inertial Loading Effects of Insect-Inspired Appendages in Small Unmanned Aerial Vehicles. Biomimetics. 2025; 10(1):22. https://doi.org/10.3390/biomimetics10010022
Chicago/Turabian StyleOgunwa, Titilayo, and Javaan Chahl. 2025. "Aerodynamic and Inertial Loading Effects of Insect-Inspired Appendages in Small Unmanned Aerial Vehicles" Biomimetics 10, no. 1: 22. https://doi.org/10.3390/biomimetics10010022
APA StyleOgunwa, T., & Chahl, J. (2025). Aerodynamic and Inertial Loading Effects of Insect-Inspired Appendages in Small Unmanned Aerial Vehicles. Biomimetics, 10(1), 22. https://doi.org/10.3390/biomimetics10010022






