A Crash Data Analysis through a Comparative Application of Regression and Neural Network Models
Abstract
1. Introduction
- To study crash data collected between 2014 and 2017 through a comparison of modelling methodologies, in terms of their performance and results, using four paradigms, namely, artificial neural networks (ANNs), generalized linear mixed-effects (GLME), multinomial regression (MNR), and general nonlinear regression (NLM);
- To find the analytical formulation that better describes the relationship between input and output;
- To analyze common variables of the models.
2. Methodology
- Analysis of data;
- Pre-processing and normalization of data;
- Model building;
- Check of model performance (if not satisfactory, we went back to step 3 for model building);
- Analysis of results and discussion.
3. The Data Set
3.1. Database Information
- Crash type, with three categories, including between circulating vehicles, pedestrian hit, and isolated vehicle crash;
- Crash effects, with two categories, including injuries and fatalities.
3.2. Data Set Variables
- Variables referring to the road conditions;
- Variable referring to the infrastructure;
- Variables referring to the crash characteristics;
- Variables for vehicle characteristics;
- Variables for driver’s description.
- 6.1.
- Crash effects, indicating the severity of the crash;
- 6.2.
- Type of crash, indicating the dynamic of the crash.
3.3. Data Oversampling and Normalization
4. Models and Their Performance
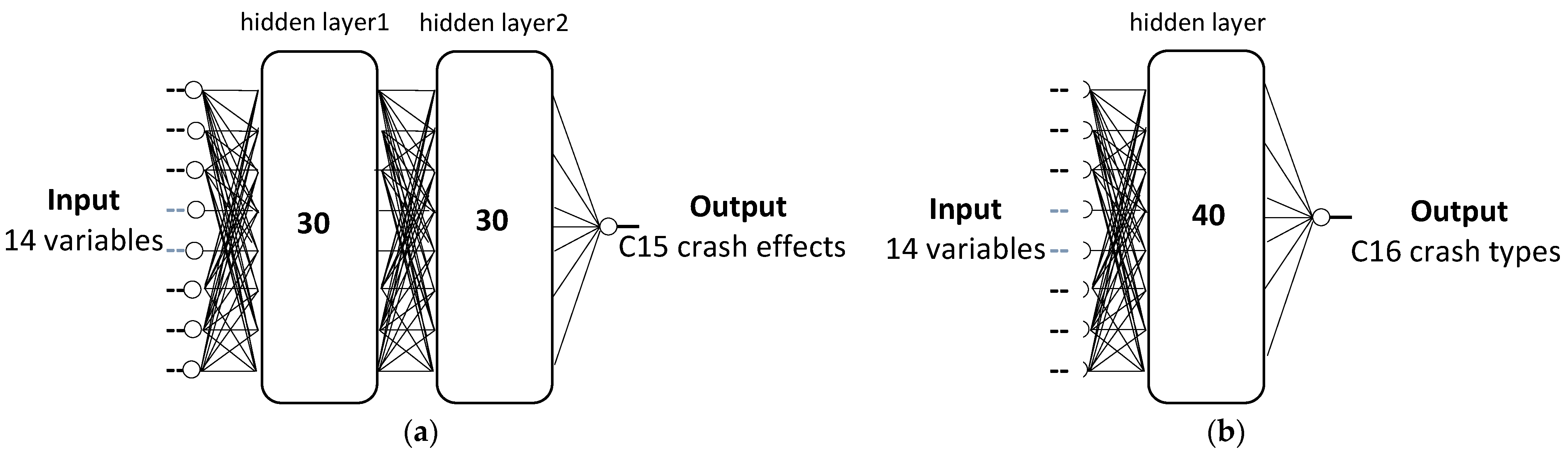
4.1. Back Propagation Artificial Neural Network
4.2. Generalized Linear Mixed Effects (GLME)
4.3. Multinomial Regression (MNR)
4.4. General Nonlinear Regression (NLM)
- Errors are independent;
- Errors have mean zero and constant variance;
- Errors are normally distributed.
+(β711 ∗ C7 ∗ C11) + (β913 ∗ C9 ∗ C13) + (β12 ∗ C12) + (β13 ∗ C13)
+ (exp (β99 ∗ C9) + exp (β11 ∗ C11))/(1 + β90 ∗ C9)
5. Analyses and Results
5.1. Database Information Content
5.2. Sensitivity Analysis
5.3. Marginal Effects Analysis
5.4. Model Comparison
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Predicted Values | ||||||
|---|---|---|---|---|---|---|
| Class | −1 | 0 | 1 | Total | PR | |
| Real values | 0 | 230 | 33,325 | 1432 | 34,987 | 4.8% |
| <1% | 95.2% | 4.8% | 100% | |||
| 1 | 0 | 0 | 35,100 | 35,100 | 0.0% | |
| 0.0% | 0.0% | 100% | 100% | |||
| Total PO | 230 | 33,325 | 36,532 | 70,087 | Accuracy 97.6% | |
| 100% | 0.0% | 3.9% | ||||
| Predicted Values | |||||
|---|---|---|---|---|---|
| Class | 0 | 1 | Total | PR | |
| Real values | 0 | 24,533 | 10,454 | 34,987 | 29.9% |
| 70.1% | 29.9% | 100% | |||
| 1 | 12,420 | 22,680 | 35,100 | 35.4% | |
| 35.4% | 64.6% | 100% | |||
| Total PO | 36,953 | 33,134 | 70,087 | Accuracy 67.3% | |
| 33.6% | 31.6% | ||||
| Predicted Values | |||||
|---|---|---|---|---|---|
| Class | 0 | 1 | Total | PR | |
| Real values | 0 | 23,592 | 11,395 | 34,987 | 32.6% |
| 67.4% | 32.6% | 100% | |||
| 1 | 12,960 | 22,140 | 35,100 | 36.9% | |
| 36.9% | 63.1% | 100% | |||
| Total | 36,552 | 33,535 | 70,087 | Accuracy 65.2% | |
| PO | 35.5% | 34.0% | |||
| Predicted Values | |||||
|---|---|---|---|---|---|
| Class | 0 | 1 | Total | PR | |
| Real values | 0 | 22,695 | 12,292 | 34,987 | 35.1% |
| 64.9% | 35.1% | 100% | |||
| 1 | 10,080 | 25,020 | 35,100 | 28.7% | |
| 28.7% | 71.3% | 100% | |||
| Total | 32,775 | 37,312 | 70,087 | Accuracy 68.0% | |
| PO | 30.8% | 32.9% | |||
| Predicted Values | PR | |||||
|---|---|---|---|---|---|---|
| Class | 1 | 2 | 3 | Total | ||
| Real values | 1 | 23,398 | 0 | 0 | 23,398 | 0.0% |
| 100% | 0.0% | 0.0% | 100% | |||
| 2 | 0 | 3898 | 1477 | 5375 | 27.5% | |
| 0.0% | 72.5% | 27.5% | 100% | |||
| 3 | 0 | 837 | 5572 | 6409 | 13.1% | |
| 0.0% | 13.1% | 86.9% | 100% | |||
| Total | 23,398 | 4735 | 7049 | 35,182 | Accuracy 93.4% | |
| PO | 0% | 17.7% | 21.0% | |||
| Predicted Values | ||||||
|---|---|---|---|---|---|---|
| Class | 1 | 2 | 3 | Total | PR | |
| Real values | 1 | 23,398 | 0 | 0 | 23,398 | 0.0% |
| 100% | 0.0% | 0.0% | 100% | |||
| 2 | 0 | 3797 | 1578 | 5375 | 29.4% | |
| 0.0% | 70.6% | 29.4% | 100% | |||
| 3 | 0 | 901 | 5508 | 6409 | 14.1% | |
| 0.0% | 14.1% | 85.9% | 100% | |||
| Total | 23,398 | 4698 | 7086 | 35,182 | Accuracy 93.0% | |
| PO | 0.0% | 19.2% | 22.3% | |||
| Predicted Values | ||||||
|---|---|---|---|---|---|---|
| Class | 1 | 2 | 3 | Total | PR | |
| Real values | 1 | 23,398 | 0 | 0 | 23,398 | 0.0% |
| 100% | 0.0% | 0.0% | 100% | |||
| 2 | 0 | 3768 | 1607 | 5375 | 29.9% | |
| 0.0% | 70.1% | 29.9% | 100% | |||
| 3 | 0 | 1322 | 5087 | 6409 | 20.6% | |
| 0.0% | 20.6% | 79.4% | 100% | |||
| Total | 23,398 | 5090 | 6694 | 35,182 | Accuracy | |
| PO | 0.0% | 26.0% | 24.0% | 91.7% | ||
| Predicted Values | PR | |||||
|---|---|---|---|---|---|---|
| Class | 1 | 2 | 3 | Total | ||
| Real values | 1 | 23,398 | 0 | 0 | 23,398 | 0.0% |
| 100% | 0.0% | 0.0% | 100% | |||
| 2 | 0 | 3640 | 1735 | 5375 | 32.3% | |
| 0.0% | 67.7% | 32.3% | 100% | |||
| 3 | 0 | 1180 | 5229 | 6409 | 18.4% | |
| 0.0% | 18.4% | 81.6% | 100% | |||
| Total | 23,398 | 5090 | 6694 | 35,182 | Accuracy 91.7% | |
| PO | 0.0% | 28.5% | 21.9% | |||
References
- WHO (2022) World Health Organization. Global Status Report on Road Safety 2018; World Health Organization: Geneva, Switzerland, 2018; Available online: https://www.who.int/news-room/fact-sheets/detail/road-traffic-injuries (accessed on 12 March 2023).
- Williams, A.F.; Carsten, O. Driver age and crash involvement. Am. J. Public Health 1989, 79, 326–327. [Google Scholar] [CrossRef] [PubMed]
- Hu, P.S.; Young, J.R.; Lu, A. Highway Crash Rates and Age-Related Driver Limitations: Literature Review and Evaluation of Data Bases; United States: Washington, DC, USA, 1993. [Google Scholar] [CrossRef]
- Massie, D.L.; Green, P.E.; Campbell, K.L. Crash involvement rates by driver gender and the role of average annual mileage. Accid. Anal. Prev. 1997, 29, 675–685. [Google Scholar] [CrossRef]
- Bergel-Hayat, R.; Debbarh, M.; Antoniou, C.; Yannis, G. Explaining the road accident risk: Weather effects. Accid. Anal. Prev. 2013, 60, 456–465. [Google Scholar] [CrossRef] [PubMed]
- Brodsky, H.; Hakkert, A.S. Risk of a road accident in rainy weather. Accid. Anal. Prev. 1988, 20, 161–176. [Google Scholar] [CrossRef] [PubMed]
- Ulfarsson, G.F.; Mannering, F.L. Differences in male and female injury severities in sport-utility vehicle, minivan, pickup and passenger car accidents. Accid. Anal. Prev. 2004, 36, 135–147. [Google Scholar] [CrossRef] [PubMed]
- Noland, R.B.; Oh, L. The effect of infrastructure and demographic change on traffic-related fatalities and crashes: A case study of Illinois County-level data. Accid. Anal. Prev. 2004, 36, 525–532. [Google Scholar] [CrossRef]
- Abdulhafedh, A. Road Traffic Crash Data: An Over-view on Sources, Problems, and Collection Methods. J. Transp. Technol. 2017, 7, 206–219. [Google Scholar] [CrossRef]
- Amoros, E.E.; Martin, J.L.; Laumon, B. Under-reporting of road crash casualties in France. Accid. Anal. Prev. 2006, 38, 627–635. [Google Scholar] [CrossRef]
- Abay, K.A. Investigating the nature and impact of reporting bias in road crash data. Transp. Res. A 2015, 71, 31–45. [Google Scholar] [CrossRef]
- Watson, A.; Watson, B.; Vallmuur, K. Estimating under-reporting of road crash injuries to police using multiple linked data collections. Accid. Anal. Prev. 2015, 83, 18–25. [Google Scholar] [CrossRef]
- Imprialou, M.; Quddus, M. Crash data quality for road safety research: Current state and future directions. Accid. Anal. Prev. 2019, 130, 84–90. [Google Scholar] [CrossRef]
- Mehdizadeh, A.; Miao Cai Hu, Q.; Alamdar Yazdi, M.A.; Mohabbati-Kalejahi, N.; Vinel, A.; Rigdon, S.E.; Davis, K.C.; Megahed, F.M. A Review of Data Analytic Applications inRoad Traffic Safety. Part 1: Descriptive and Predictive Modeling. Sensors 2020, 20, 1107. [Google Scholar] [CrossRef]
- Dimitrijevic, B.; Khales, S.D.; Asadi, R.; Lee, J. Short-term segment-level crash risk prediction using advanced data modeling with proactive and reactive crash data. Appl. Sci. 2022, 12, 856. [Google Scholar] [CrossRef]
- Fausett, L.V. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Mccullagh, P.; Nelder, J.A. Generalized Linear Models; Chapman & Hall: London, UK; New York, NY, USA, 1985. [Google Scholar]
- Hosmer, D.W.; Jovanovic, B.; Lemeshow, S. Best subsets logistic regression. Biometrics 1989, 45, 1265–1270. [Google Scholar] [CrossRef]
- Molenberghs, G.; Renard, D.; Verbeke, G. A review of generalized linear mixed models. J. Société Française Stat. 2002, 143, 53–78. Available online: https://www.numdam.org/item?id=jsfs_2002__143_1-2_53_0.pdf (accessed on 30 March 2023).
- Iranitalaba, A.; Khattakb, A. Comparison of four statistical and machine learning methods for crash severity prediction. Accid. Anal. Prev. 2017, 108, 27–36. [Google Scholar] [CrossRef]
- Mussone, L.; Kim, K. The analysis of motor vehicle crash clusters using the vector quantization technique. J. Adv. Transp. 2010, 44, 162–175. [Google Scholar] [CrossRef]
- Goldenbeld, C.; de Craen, S. The comparison of road safety survey answers between web-panel and face-to-face; Dutch results of SARTRE-4 survey. J. Saf. Res. 2013, 46, 13–20. [Google Scholar] [CrossRef]
- Espinoza Molina, F.E.; Arenas Ramirez, B.D.V.; Aparicio Izquierdo, F.; Zúñiga Ortega, D.C. Road Safety Perception Questionnaire (RSPQ) in Latin America: A development and validation study. Int. J. Environ. Res. Public Health 2021, 18, 2433. [Google Scholar] [CrossRef]
- AAAM-Association for Advancement of Automotive Medicine. Available online: https://www.aaam.org/ (accessed on 20 September 2022).
- Ling, C.; Ling, C.X.; Li, C. Data mining for direct marketing: Problems and solutions. In Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining (KDD-98), New York, NY, USA, 27–31 August 1998; pp. 73–79. [Google Scholar]
- Dutka, A.F. Fundamentals of Data Normalization; Addison Wesley Publishing Company: Boston, MA, USA, 1988. [Google Scholar]
- Mussone, L.; Ferrari, A.; Oneta, M. An analysis of urban collisions using an artificial intelligence model. Accid. Anal. Prev. 1999, 31, 705–718. [Google Scholar] [CrossRef]
- Chakraborty, A.; Mukherjee, D.; Mitra, S. Development of pedestrian crash prediction model for a developing country using artificial neural network. Int. J. Inj. Control Saf. Promot. 2019, 26, 283–293. [Google Scholar] [CrossRef]
- Ali, G.A.; Tayfour, A. Characteristics and prediction of traffic accident casualties in Sudan using statistical modeling and artificial neural networks. Int. J. Transp. Sci. Technol. 2012, 1, 305–317. [Google Scholar] [CrossRef]
- Mussone, L.; Bassani, M.; Masci, P. Analysis of Factors Affecting the Severity of Crashes in Urban Road Intersections. Acc. Anal. Prev. 2017, 103, 112–122. [Google Scholar] [CrossRef]
- Huang, H.; Zeng, Q.; Pei, X.; Wong, S.C.; Xu, P. Predicting crash frequency using an optimised radial basis function neural network model. Transp. A 2016, 12, 330–345. [Google Scholar] [CrossRef]
- Kumaraswamy, B. Neural networks for data classification. In Artificial Intelligence in Data Mining; Binu, D., Rajakumar, B.R., Eds.; Academic Press: Middlesex County, MA, USA, 2021; pp. 109–131. [Google Scholar] [CrossRef]
- Wu, L. Mixed Effects Models for Complex Data; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Lebart, L.; Tabard, N.; Morineau, A. Techniques de la Description Statistique: Méthodes et Logiciels Pour l’Analyse Des Grands Tableaux; Dunod: Paris, France, 1986. [Google Scholar]
- Powers, D.M.W. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar]
- Slikboer, R.; Muir, S.D.; Silva, S.S.M.; Meyer, D. A systematic review of statistical models and outcomes of predicting fatal and serious injury crashes from driver crash and offense history data. Syst. Rev. 2020, 9, 220. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Pu, Z.; Xu, C. Comparing Prediction Performance for Crash Injury Severity Among Various Machine Learning and Statistical Methods. IEEE Access 2018, 6, 60079–60087. [Google Scholar] [CrossRef]


| Var. | Name | Type | Min | Median | Max | Label | Description | Frequency | Percentage |
|---|---|---|---|---|---|---|---|---|---|
| C1 | Day of week | C | 1 | 4 | 7 | 1 | Sunday | 3421 | 10% |
| 2 | Monday | 5153 | 14% | ||||||
| 3 | Tuesday | 5585 | 16% | ||||||
| 4 | Wednesday | 5642 | 16% | ||||||
| 5 | Thursday | 5537 | 16% | ||||||
| 6 | Friday | 5617 | 16% | ||||||
| 7 | Saturday | 4227 | 12% | ||||||
| C2 | Hour (daytime/night-time) | B | 0 | 0 | 1 | 0 | Day time | 24,503 | 70% |
| 1 | Night-time | 10,679 | 30% | ||||||
| C3 | Road typology | C | 1 | 2 | 4 | 1 | One-way carriag. | 6719 | 19% |
| 2 | Two-way carriag. | 14,117 | 40% | ||||||
| 3 | Two carriageways | 8297 | 24% | ||||||
| 4 | >two carriageways | 6049 | 17% | ||||||
| C4 | Type of road infrastructure | B | 0 | 1 | 1 | 0 | Intersection | 16,906 | 48% |
| 1 | Section | 18,276 | 52% | ||||||
| C5 | Road conditions | C | 1 | 1 | 3 | 1 | Dry | 28,690 | 81.50% |
| 2 | Wet | 6231 | 17.71% | ||||||
| 3 | Slippery/Icy/Frozen | 261 | 0.74% | ||||||
| C6 | Meteorological conditions | C | 1 | 1 | 4 | 1 | Serene | 30,582 | 87.00% |
| 2 | Wind | 25 | 0.07% | ||||||
| 3 | Fog | 284 | 0.81% | ||||||
| 4 | Rain/Snow/Hail | 4291 | 12.00% | ||||||
| C7 | Type of vehicle A | C | 1 | 2 | 3 | 1 | Two-wheeled | 14,355 | 41% |
| 2 | Passenger car | 18,375 | 52% | ||||||
| 3 | Other-heavy veh. | 2452 | 7% | ||||||
| C8 | Age A [years] | N | 4 | 41 (mean = 42, std = 15) | 96 | 0 | Unknown/not present | 1359 | 4% |
| [1–99] | years | 33,823 | 96% | ||||||
| C9 | Gender A | C | 0 | 1 | 2 | 0 | Unknown | 916 | 2% |
| 1 | Male | 26,576 | 76% | ||||||
| 2 | Female | 7690 | 22% | ||||||
| C10 | Years of driving license A | N | 0 | 4 (mean = 9, std = 10) | 58 | 0 | Unknown/not present | 7511 | 21% |
| [1–99] | years | 27,793 | 79% | ||||||
| C11 | Type of vehicle B | C | 0 | 1 | 3 | 0 | Unknown | 11,784 | 34% |
| 1 | Two-wheeled | 6844 | 19% | ||||||
| 2 | Passenger car | 14,998 | 43% | ||||||
| 3 | Other-heavy veh. | 1556 | 4% | ||||||
| C12 | Age B [years] | N | 4 | 42 (mean = 42, std = 14) | 93 | 0 | Unknown/not present | 12,326 | 35% |
| [1–99] | years | 22,356 | 65% | ||||||
| C13 | Gender B | C | 0 | 1 | 2 | 0 | Unknown | 12,050 | 34% |
| 1 | Male | 17,154 | 49% | ||||||
| 2 | Female | 5978 | 17% | ||||||
| C14 | Years of driving license B | N | 0 | 5 (mean = 9, std = 11) | 58 | 0 | Unknown/not present | 16,789 | 48% |
| [1–99] | years | 18,393 | 52% | ||||||
| C15 | Crash effects | B | 0 | 0 | 1 | 0 | Injuries | 34,987 | 99.5% |
| 1 | Fatalities | 195 | 0.5% | ||||||
| C16 | Crash types | C | 1 | 2 | 3 | 1 | Between circulating vehicles | 23,398 | 67% |
| 2 | Pedestrian hit | 5375 | 15% | ||||||
| 3 | Isolated vehicle crash | 6509 | 18% | ||||||
| Total observations | 35,182 | 100% |
| AIC | Likelihood | ||||
|---|---|---|---|---|---|
| 89,319 | −44,652 | ||||
| Name | Estimate | p Value | SE | Lower Limit | Upper Limit |
| C8 | 0.29417 | <10−3 | 0.018389 | 0.25812 | 0.33021 |
| C9 | 10.769 | <10−3 | 1.5483 | 7.7595 | 13.833 |
| C42 | −0.09477 | <10−3 | 0.0067284 | −0.10797 | −0.08159 |
| C92 | −8.0156 | <10−3 | 1.0326 | −10.041 | −5.9904 |
| Group variables | Estimate | ||||
| Intercept | 4.2363 | ||||
| C2 (Intercept) | −0.92965 | ||||
| C2 (Intercept) | 0.26753 | ||||
| AIC | Likelihood | ||||
|---|---|---|---|---|---|
| 81,010 | −40,497 | ||||
| Name | Estimate | p Value | SE | Lower Limit | Upper Limit |
| C4 | −0.0445 | <10−3 | 0.0088324 | −0.0618 | −0.02729 |
| C5 | 0.05081 | 0.01044 | 0.0198400 | 0.0119 | 0.08969 |
| C7 | −0.1832 | <10−3 | 0.0150050 | −0.2126 | −0.15379 |
| C9 | 0.5606 | <10−3 | 0.0866160 | 0.3908 | 0.73038 |
| C92 | −0.3508 | <10−3 | 0.0621540 | −0.4726 | −0.22903 |
| Group variables | Estimate | ||||
| Intercept | 0.40461 | ||||
| C2 (Intercept) | 1 | ||||
| C2 (Intercept) | 0.021654 | ||||
| Name | Estimate | SE | p Value |
|---|---|---|---|
| α | −0.635 | 0.040 | <10−3 |
| β11 | 0.518 | 0.026 | <10−3 |
| β12 | −0.743 | 0.018 | 0 |
| β13 | −0.457 | 0.025 | <10−3 |
| β14 | 0.422 | 0.017 | <10−3 |
| β15 | 1.614 | 0.065 | <10−3 |
| β16 | −0.310 | 0.038 | <10−3 |
| β17 | −0.680 | 0.026 | <10−3 |
| β18 | −1.864 | 0.051 | <10−3 |
| β19 | 1.921 | 0.046 | 0 |
| β110 | 0.740 | 0.050 | <10−3 |
| β111 | 0.045 | 0.044 | 0.306 |
| β112 | −1.174 | 0.054 | <10−3 |
| β113 | 1.944 | 0.046 | 0 |
| β114 | 1.664 | 0.068 | <10−3 |
| Name | Estimate | SE | p Value | Name | Estimate | SE | p Value |
|---|---|---|---|---|---|---|---|
| α1 | −31.400 | 0.482 | 0 | α2 | −0.348 | 0.0912 | 0.0001 |
| β11 | −0.127 | 0.362 | 0.723 | β21 | 0.145 | 0.0700 | 0.0370 |
| β12 | −1.739 | 0.244 | <10−3 | β22 | −0.724 | 0.0487 | <10−3 |
| β13 | 0.809 | 0.339 | 0.017 | β23 | 0.163 | 0.0690 | 0.0170 |
| β14 | −0.455 | 0.224 | 0.042 | β24 | 1.045 | 0.0453 | <10−3 |
| β15 | 1.348 | 0.797 | 0.091 | β25 | −1.641 | 0.1480 | <10−3 |
| β16 | −0.027 | 0.494 | 0.955 | β26 | 0.630 | 0.0880 | <10−3 |
| β17 | −14.595 | 0.424 | <10−3 | β27 | 3.897 | 0.0890 | 0.0000 |
| β18 | 0.118 | 0.662 | 0.857 | β28 | −0.129 | 0.1310 | 0.3240 |
| β19 | −0.866 | 0.468 | 0.064 | β29 | −1.977 | 0.0980 | <10−3 |
| β110 | 0.010 | 0.644 | 0.987 | β210 | 0.776 | 0.1280 | <10−3 |
| β111 | 226.185 | 1.115 | 0 | β211 | −2.699 | 1.3720 | 0.0490 |
| β112 | 31.872 | 1.625 | <10−3 | β212 | 2.290 | 2.4240 | 0.3440 |
| β113 | 2.755 | 1.053 | 0.009 | β213 | 1.837 | 1.5880 | 0.2470 |
| β114 | 2.303 | 1.447 | 0.111 | β214 | 0.022 | 2.1290 | 0.9910 |
| Name | Estimate | SE | p Value |
|---|---|---|---|
| β4 | 0.81083 | 0.0061205 | 0 |
| β5 | 0.17332 | 0.0056368 | <10−3 |
| β6 | −0.29411 | 0.010835 | <10−3 |
| β7 | −0.19772 | 0.016101 | <10−3 |
| β9 | −0.14945 | 0.019974 | <10−3 |
| β12 | −0.40295 | 0.0094004 | 0 |
| β13 | −0.23681 | 0.016157 | <10−3 |
| β44 | 0.13937 | 0.010201 | <10−3 |
| β411 | −0.14607 | 0.016511 | <10−3 |
| β711 | −0.25411 | 0.026614 | <10−3 |
| β913 | 0.54439 | 0.040193 | <10−3 |
| Name | Estimate | SE | p Value |
|---|---|---|---|
| β2 | 0.16018 | 0.0097000 | <10−3 |
| β4 | −0.31900 | 0.0049883 | 0 |
| β5 | −0.67276 | 0.0075298 | 0 |
| β7 | 0.15286 | 0.0070069 | <10−3 |
| β8 | 0.14588 | 0.0328520 | <10−3 |
| β11 | −0.20741 | 0.0056216 | <10−3 |
| β44 | −0.43761 | 0.0222610 | <10−3 |
| β90 | 7.13780 | 0.0892520 | 0 |
| β99 | 2.00000 | 0.0146530 | 0 |
| β913 | 0.64146 | 0.0622290 | <<10−3 |
| Model | Evaluation Method | Output C15 (Crash Severity) | Output C16 (Crash Type) | ||
|---|---|---|---|---|---|
| Relevant Variables | Accuracy [PR1,2] [PO1,2] | Relevant Variables | Accuracy [PR1,2,3 [PO1,2,3] | ||
| ANN | Sensitivity analysis | C8: Driver A age C3: Road typology C2: Hour of crash C13: Gender B | 97.6% [4.8, 0.0]% [0.0, 3.9]% | C8: Driver A age C7: Type of vehicle A C4: Type of road infrastructure C11: Type of vehicle B | 93.4% [0.0,27.5,13.1]% [0.0,17.7,21.0]% |
| GLME | Marginal Effects | C8: Driver A age C9: Gender A C4: Type of road infrastructure | 67.3% [29.9, 35.4]% [33.6, 31.6]% | C5: Road conditions C9: Gender A C4: Type of road infrastructure C7: Type of vehicle A | 93.0% [0.0,29.4,14.1]% [0.0,19.2,22.3]% |
| NLM | Model coefficients | C4: Type of road infrastructure C6: Meteorological conditions C12: Drive B age C13: Gender B | 65.2% [32.6, 36.9]% [35.5, 34.0]% | C5: Road Conditions C4: Type of road infrastructure C11: Type of vehicle B C9: Gender A | 91.7% [0.0,29.9,20.6]% [0.0,26.0,24.0]% |
| MNR | Model coefficients | C13: Gender B C9: Gender A C14: Years of driving license B C8: Driver A age | 68.0% [35.1, 28.7]% [30.8, 32.9]% | C12: Driver B age C11: Type of vehicle B C7: Type of vehicle A C13: Gender B | 91.7% [0.0,32.3,18.4]% [0.0,28.5,21.9]% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mussone, L.; Alizadeh Meinagh, M. A Crash Data Analysis through a Comparative Application of Regression and Neural Network Models. Safety 2023, 9, 20. https://doi.org/10.3390/safety9020020
Mussone L, Alizadeh Meinagh M. A Crash Data Analysis through a Comparative Application of Regression and Neural Network Models. Safety. 2023; 9(2):20. https://doi.org/10.3390/safety9020020
Chicago/Turabian StyleMussone, Lorenzo, and Mohammadamin Alizadeh Meinagh. 2023. "A Crash Data Analysis through a Comparative Application of Regression and Neural Network Models" Safety 9, no. 2: 20. https://doi.org/10.3390/safety9020020
APA StyleMussone, L., & Alizadeh Meinagh, M. (2023). A Crash Data Analysis through a Comparative Application of Regression and Neural Network Models. Safety, 9(2), 20. https://doi.org/10.3390/safety9020020





