Using Different Types of Artificial Neural Networks to Classify 2D Matrix Codes and Their Rotations—A Comparative Study
Abstract
:1. Introduction
Related Work
2. Materials and Methods
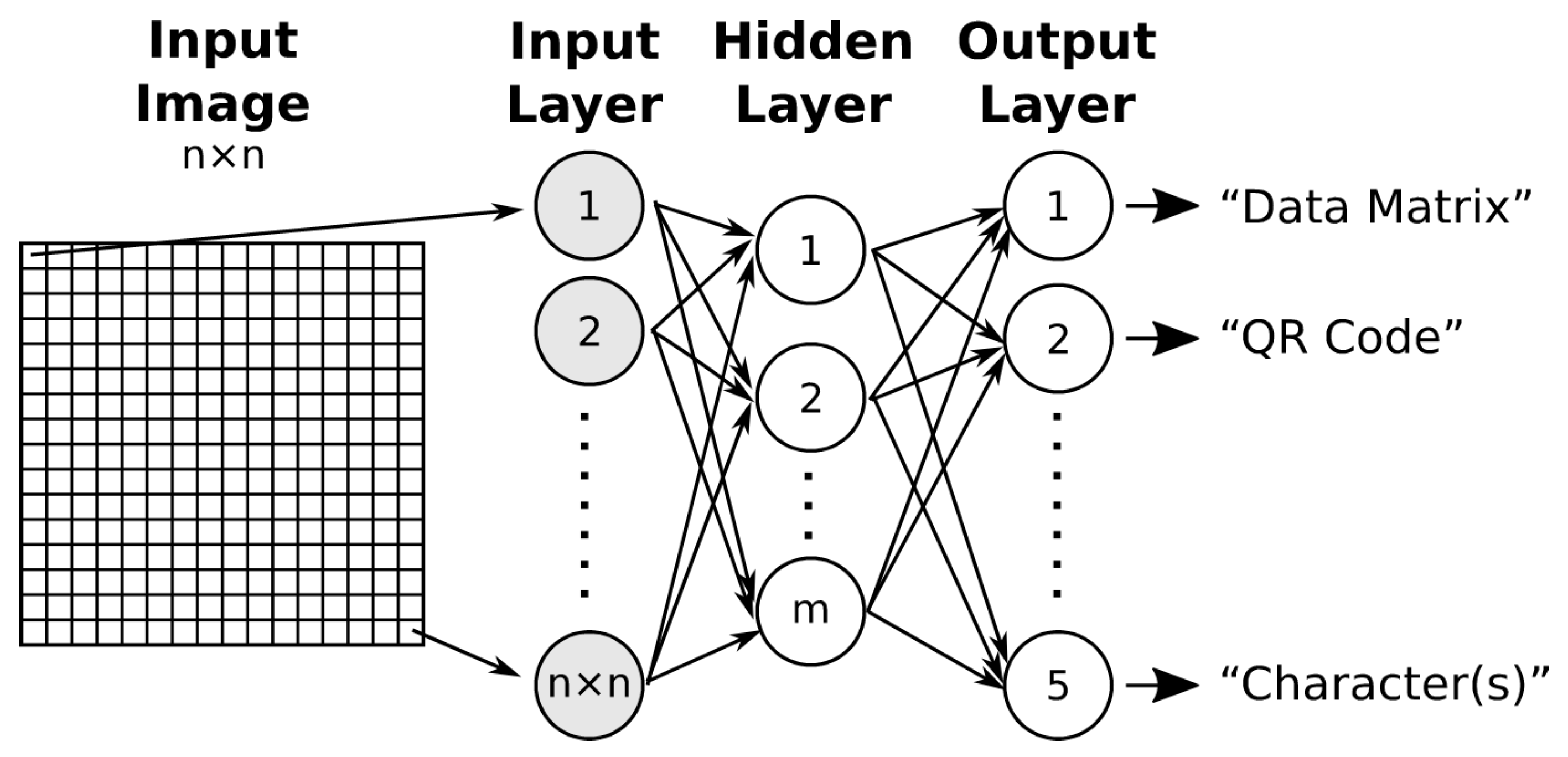
2.1. Multilayer Perceptron (MLP)
2.2. Probabilistic Neural Network (PNN)
- common to all pattern layer neurons (a cross-validation (between training and validation datasets) method that minimises network error can be used);
- common to pattern layer neurons belonging to the same class (the σ values can be calculated as half the average distance between the training samples in the same class or, for each training sample, it can be half the distance from that sample to the nearest other sample vector [18]);
- determined for individual features of the feature vector (standard deviation of training samples for each feature);
- determined for each class and feature of the feature vector.
2.3. Radial Basis Function Network (RBF NN)
- One-phase learning: central vectors are randomly selected from a set of input vectors (or all data points are used as central vectors), and typically a single predefined value for β is used. Then, only the weights of the output layer are adjusted by some method of supervised learning, e.g., minimizing the square of the differences between the network output and the desired output value;
- Two-phase learning: the hidden and output layers of the RBF network are trained separately. First, the centre’s µi and the scaling parameter’s βi are determined. Then, the weights of the output layer are adjusted. A clustering algorithm such as K-Means can be used to select the centre’s µi, while βi is calculated as , where σi is the average distance of the samples belonging to cluster i from the centre µi;
- Three-phase learning: First, the RBF network is initialised using two-phase learning. Then, the entire network architecture is turned using another optimisation procedure.
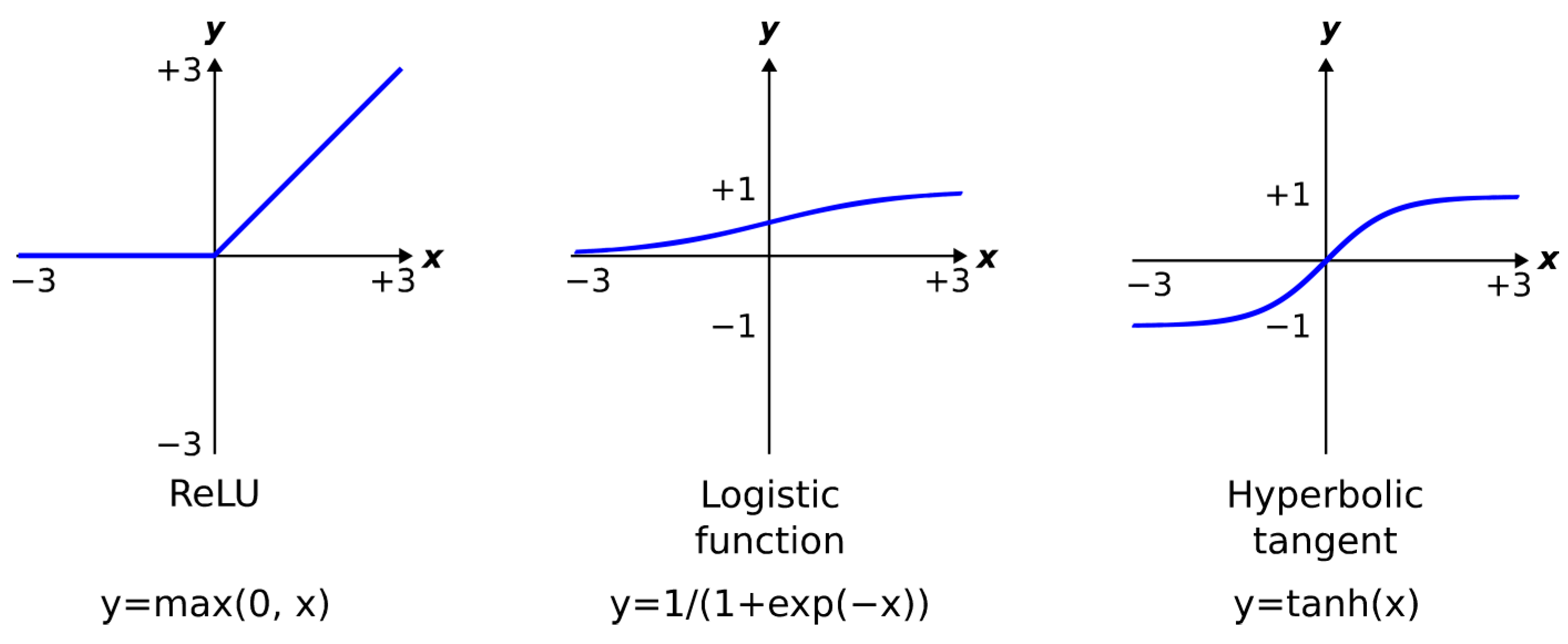
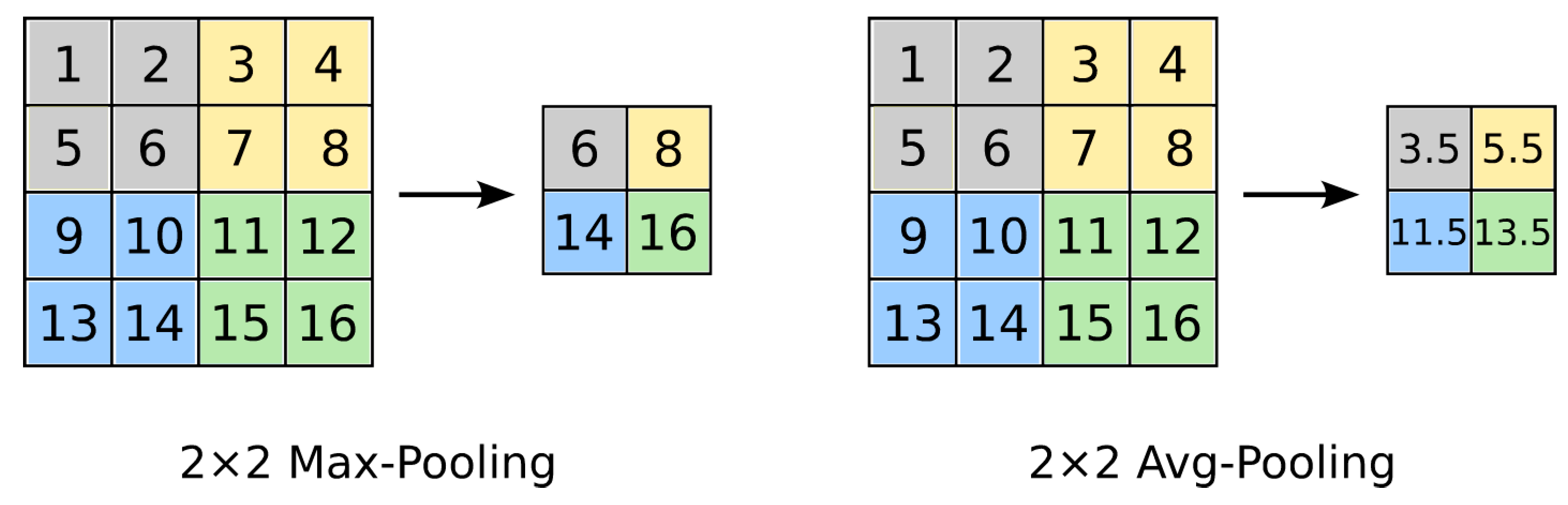
2.4. Convolutional Neural Network (CNN or ConvNet)
- I → C + ReLU → F.
- I → [C + ReLU → S] × 2 → F + ReLU → F.
- I → [[C + ReLU] × 2 → S] × 3 → [F + ReLU] × 2 → F.(two convolutional layers (C) stacked before every pooling layer (S))
2.5. k-Nearest Neighbors (k-NN)
3. Results
3.1. Multilayer Perceptron (MLP)
3.2. Probabilistic Neural Network (PNN)
3.3. Radial Basis Function Network (RBF NN)
3.4. Convolutional Neural Network (CNN)
- If the size of the training dataset of samples is large enough to cover a large number of variations in samples from the test dataset and/or the diversity between the training and test datasets is low, the classifier itself does not play an important role;
- Classification accuracy is not only influenced by the type of ANN, but also by correct configuration and parameterization (such as the number of layers, the number of feature maps, the number of neurons in the layers, the sigma parameter);
- The convolutional neural network achieved the best results because it is not only a classifier but also a feature extractor and is designed to work directly with images.
- The number of training samples must be large enough to train the classifiers satisfactorily (the number of samples must increase as the number of output classes increases);
- A convolutional neural network with two stacked convolutional layers performed slightly better than traditional neural networks (RBF neural network and multilayer perceptron) when trained on a larger number of samples (900). However, when trained on fewer samples (90), traditional neural networks (the RBF neural network and the multilayer perceptron) outperformed convolutional networks.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karrach, L.; Pivarčiová, E. Location and Recognition of Data Matrix and QR Codes in Images; RAM-Verlag: Lüdenscheid, Germany, 2022; ISBN 978-3-96595-022-1. [Google Scholar]
- Karrach, L.; Pivarčiová, E.; Božek, P. Identification of QR Code Perspective Distortion Based on Edge Directions and Edge Projections Analysis. J. Imaging 2020, 6, 67. [Google Scholar] [CrossRef]
- Bodnár, P.; Nyúl, L.G. Improved QR Code Localization Using Boosted Cascade of Weak Classifiers. Acta Cybern. 2015, 22, 21–33. [Google Scholar] [CrossRef]
- Gaur, P.; Tiwari, S. 2D QR Barcode Recognition Using Texture Features and Neural Network. Int. J. Res. Advent Technol. 2014, 2, 433–437. [Google Scholar]
- Grosz, T.; Bodnar, P.; Toth, L.; Nyul, L.G. QR code localization using deep neural networks. In Proceedings of the 2014 IEEE International Workshop on Machine Learning for Signal Processing (MLSP), Reims, France, 21–24 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Hansen, D.K.; Nasrollahi, K.; Rasmusen, C.B.; Moeslund, T.B. Real-Time Barcode Detection and Classification using Deep Learning. In Proceedings of the 9th International Joint Conference on Computational Intelligence 2017, Funchal, Portugal, 1–3 November 2017; pp. 321–327. [Google Scholar] [CrossRef]
- Almeida, T.; Santos, V.; Mozos, O.M.; Lourenço, B. Comparative Analysis of Deep Neural Networks for the Detection and Decoding of Data Matrix Landmarks in Cluttered Indoor Environments. J. Intell. Robot. Syst. 2021, 103, 13. [Google Scholar] [CrossRef]
- Che, Z.; Zhai, G.; Liu, J.; Gu, K.; Le Callet, P.; Zhou, J.; Liu, X. A Blind Quality Measure for Industrial 2D Matrix Symbols Using Shallow Convolutional Neural Network. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 2481–2485. [Google Scholar] [CrossRef]
- Chou, T.-H.; Ho, C.-S.; Kuo, Y.-F. QR code detection using convolutional neural networks. In Proceedings of the 2015 International Conference on Advanced Robotics and Intelligent Systems (ARIS), Taipei, Taiwan, 29–31 May 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Huo, L.; Zhu, J.; Singh, P.K.; Pavlovich, P.A. Research on QR image code recognition system based on artificial intelligence algorithm. J. Intell. Syst. 2020, 30, 855–867. [Google Scholar] [CrossRef]
- Waziry, S.; Wardak, A.B.; Rasheed, J.; Shubair, R.M.; Rajab, K.; Shaikh, A. Performance comparison of machine learning driven approaches for classification of complex noises in quick response code images. Heliyon 2023, 9, e15108. [Google Scholar] [CrossRef]
- Jain, A.; Mao, J.; Mohiuddin, K. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Werbos, P.J. Applications of advances in nonlinear sensitivity analysis. In System Modeling and Optimization; Lecture Notes in Control and Information Sciences; Springer: Berlin, Heidelberg, 2005; Volume 38, pp. 762–770. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Heaton, J. The Number of Hidden Layers. 2017. Available online: https://www.heatonresearch.com/2017/06/01/hidden-layers.html (accessed on 5 May 2023).
- Specht, D.F. Probabilistic neural networks. Neural Networks 1990, 3, 109–118. [Google Scholar] [CrossRef]
- Looney, C.G. Probabilistic Neural Network Tutorial. 2008. Available online: https://www.cse.unr.edu/~looney/cs773b/PNNtutorial.pdf (accessed on 20 May 2023).
- Bors, A. Introduction of the Radial Basis Function (RBF) Networks. Online Symp. Electron. Eng. 2001, 1, 1–7. [Google Scholar]
- Schwenker, F.; Kestler, H.A.; Palm, G. Three learning phases for radial-basis-function networks. Neural Netw. 2001, 14, 439–458. [Google Scholar] [CrossRef] [PubMed]
- Benoudjit, N.; Verleysen, M. On the Kernel Widths in Radial-Basis Function Networks. Neural Process. Lett. 2003, 18, 139–154. [Google Scholar] [CrossRef]
- Kafunah, J. Backpropagation in Convolutional Neural Networks. 2016. Available online: https://www.jefkine.com/general/2016/09/05/backpropagation-in-convolutional-neural-networks/ (accessed on 20 May 2023).
- Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D.; Laboratories, H.Y.L.B.; Zhu, Z.; Cheng, J.; Zhao, Y.; et al. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. arXiv 2013, arXiv:1311.2901. Available online: https://arxiv.org/pdf/1311.2901v3.pdf (accessed on 20 May 2023).
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. Available online: https://arxiv.org/pdf/1409.1556> (accessed on 20 May 2023).
- Standford.edu. CS231n: Convolutional Neural Networks for Visual Recognition. 2023. Available online: https://cs231n.github.io/convolutional-networks/ (accessed on 20 May 2023).
- Solai, P. Convolutions and Backpropagations. 2018. Available online: https://pavisj.medium.com/convolutions-and-backpropagations-46026a8f5d2c (accessed on 20 May 2023).
- Bozek, P.; Karavaev, Y.L.; A Ardentov, A.; Yefremov, K.S. Neural network control of a wheeled mobile robot based on optimal trajectories. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420916077. [Google Scholar] [CrossRef]
- Pecháč, P.; Sága, M. Memetic Algorithm with Normalized RBF ANN for Approximation of Objective Function and Secondary RBF ANN for Error Mapping. Procedia Eng. 2017, 177, 540–547. [Google Scholar] [CrossRef]
- Wiecek, D.; Burduk, A.; Kuric, I. The use of ANN in improving efficiency and ensuring the stability of the copper ore mining process. Acta Montan. Slovaca 2019, 24, 1–14. [Google Scholar]






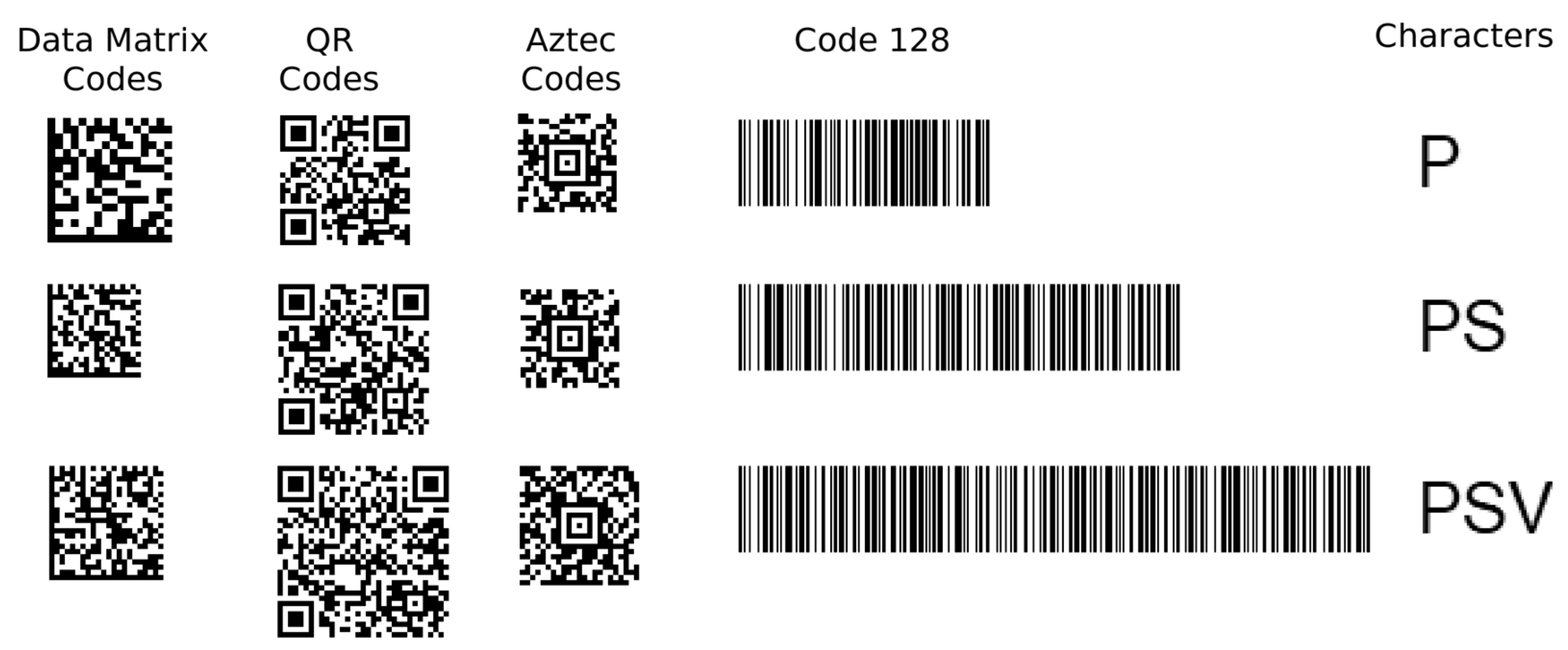

| Data Encoded by 2D and 1D Codes | Image Classes and Sizes | ||||
|---|---|---|---|---|---|
| Data Matrix Codes | QR Codes | Aztec Codes | 1D Barcode (Code 128) | Characters (A–Z) | |
| 10 alpha-numeric characters, 3 px module size | 16 × 16 modules (48 × 48 px) | 25 × 25 modules (75 × 75 px) | 19 × 19 modules (57 × 57 px) | 290 × 100 px | 1 char (w1 × 32 px) |
| 20 alpha-numeric characters, 2 px module size | 18 × 18 modules (36 × 36 px) | 29 × 29 modules (58 × 58 px) | 19 × 19 modules (38 × 38 px) | 510 × 100 px | 2 chars (w2 × 32 px) |
| 30 alpha-numeric characters, 2 px module size | 22 × 22 modules (44 × 44 px) | 33 × 33 modules (66 × 66 px) | 23 × 23 modules (46 × 46 px) | 730 × 100 px | 3 chars (w3 × 32 px) |
| Classifier | Configuration: Number of Neurons in the Hidden Layer(s) | Number of Training Samples | |
|---|---|---|---|
| 1500 | 150 | ||
| Multilayer Perceptron (one hidden layer, sigmoid activation function) | 20 | 97.3% | 93.9–95.5% |
| 60 | 97.7% | 94.3–95.6% | |
| 120 | 97.3% | 94.4–95.7% | |
| 720 | 93.4% | 93.2–96.2% | |
| Multilayer Perceptron (two hidden layers, sigmoid activation function) | 20, 18 | 67.8% * | – |
| 60, 45 | 96.5% | – | |
| 120, 85 | 74.9% | – | |
| 720, 485 | 76.3% * | – | |
| Classifier | Configuration: Parameter Sigma | Number of Training Samples | |
|---|---|---|---|
| 1500 | 150 | ||
| Probabilistic Neural Network | sigma per sample * | 64.6% | – |
| sigma per class ** | 51.7% | – | |
| sigma = 3 | 82.7% | – | |
| sigma = 4 | 94.6% | 91.7–93.7% | |
| sigma = 5 | 94.4% | 91.5–92.9% | |
| sigma = 6 | 91.1% | – | |
| sigma = 7 | 86.0% | – | |
| sigma = 8 | 82.5% | – | |
| sigma = 15 *** | 58.1% | – | |
| Classifier | Configuration: Parameter Sigma | Number of Training Samples | |
|---|---|---|---|
| 1500 | 150 | ||
| RBF Neural Network, one-phase learning, all unique samples (hidden neurons = 1470) | σ1 = 0.9 | 94.2% | 92.2–93.0% |
| σ2 = 66.8 | 20.0% * | – | |
| σ2/2 = 33.4 | 25.9% * | – | |
| σ2/4 = 16.7 | 22.1% * | – | |
| σ = 11 | 98.3% | 95.4–96.2% | |
| RBF Neural Network, two-phase learning, clustering = 5 (hidden neurons = 285) | σ = 8 | 97.9% | – |
| σ = 9 | 99.7% | 95.9–98.1% | |
| σ = 10 | 99.4% | – | |
| σ = 11 | 97.6% | – | |
| σ3 | 21.1% * | – | |
| σ4 | 87.9% | – | |
| RBF Neural Network, two-phase learning, clustering = 10 (hidden neurons = 148) | σ = 8 | 96.9% | – |
| σ = 9 | 98.7% | – | |
| σ = 10 | 99.3% | 94.1–97.7% | |
| σ = 11 | 98.9% | – | |
| σ3 | 25.1% * | – | |
| σ4 | 89.7% | – | |
| RBF Neural Network, two-phase learning, clustering = 15 (hidden neurons = 100) | σ = 8 | 96.8% | – |
| σ = 9 | 98.1% | – | |
| σ = 10 | 99.0% | 92.7–94.7% | |
| σ = 11 | 95.0% | – | |
| σ3 | 20.0% | – | |
| σ4 | 97.1% | – | |
| Classifier | Configuration: Number of Feature Maps | Number of Training Samples | |
|---|---|---|---|
| 1500 | 150 | ||
| CNN-1: C1, S2, F3-4 | 4 | 96.9% | 95.3–97.3% |
| 8 | 98.1% | 95.7–97.4% | |
| 16 | 99.3% | 96.3–98.4% | |
| 32 | 99.4% | 97.7–98.8% | |
| CNN-2: C1, S2, C3, S4, F5-6 | 4, 8 | 99.0% | 93.9–99.2% |
| 8, 16 | 99.4% | 96.3–99.3% | |
| 16, 16 | 60.5% | 98.1–99.1% | |
| 16, 32 | 95.7% | 98.7–99.7% | |
| 32, 32 | 100% | 98.8–99.7% | |
| 32, 64 | 100% | 99.4–99.8% | |
| CNN-3: C1, S2, C3, S4, C5, S6, F7-8 | 4, 8, 16 | 99.5% | 91.0–98.7% |
| 8, 16, 32 | 97.3% | 91.7–99.9% | |
| 16, 16, 16 | 99.3% | 93.5–98.3% | |
| 16, 32, 64 | 97.9% | 98.1–99.6% | |
| 32, 32, 32 | 99.7% | 97.4–99.2% | |
| 32, 64, 128 | 98.8% | 97.9–99.9% | |
| CNN-4: C1, S2, C3, S4, C5, S6, C7, S8, F9-10 | Adding an additional convolutional layer (C7) and a pooling layer (S8) reduced the classification rate. | ||
| Classifier | Configuration | Number of Training Samples | |
|---|---|---|---|
| 1500 | 150 (Average of Five Runs) | ||
| CNN-2: C1, S2, C3, S4, F5-6 | 32, 32 32, 64 | 100% | 99.3% 99.6% |
| CNN-3: C1, S2, C3, S4, C5, S6, F7-8 | 32, 32, 32 | 99.7% | 98.6% |
| RBF Neural Network | clustering = 5, σ = 9 | 99.7% | 96.8% |
| Multilayer Perceptron | hidden = 60 | 97.7% | 95.1% |
| Probabilistic Neural Network | sigma = 4 | 94.6% | 92.7% |
| k-NN | k = 1 k = 3 k = 5 | 94.2% 93.6% 93.9% | 92.4% 92.2% 85.4% |
| Classifier | Configuration | Number of Training Samples | |
|---|---|---|---|
| 900 | 90 | ||
| CNN-1: C1, C2, S3, F4-5 | C1, C2: 16 feature maps C1, C2: 8 feature maps | 99.3% 99.0% | 72.3% 71.8% |
| RBF Neural Network, two-phase learning, clustering = 5 | σ = 8–10 | 98.9% | 77.7% |
| Multilayer Perceptron | 40 neurons in hidden layer | 98.4% | 82.5% |
| CNN-1: C1, S2, F3-4 | C1: 8 feature maps | 98.1% | 74.8% |
| CNN-2: C1, S2, C3, S4, F5-6 | C1: 16, C3: 32 feature maps | 96.3% | 69.2% |
| Probabilistic Neural Network | sigma = 4–6 | 94.0% | 76.8% |
| RBF Neural Network, one-phase learning, all unique samples | σ1=1.0 | 91.0% | 75.2% |
| k-NN | k = 1 k = 3 k = 5 | 90.8% 92.7% 92.6% | 74.5% 56.3% 57.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karrach, L.; Pivarčiová, E. Using Different Types of Artificial Neural Networks to Classify 2D Matrix Codes and Their Rotations—A Comparative Study. J. Imaging 2023, 9, 188. https://doi.org/10.3390/jimaging9090188
Karrach L, Pivarčiová E. Using Different Types of Artificial Neural Networks to Classify 2D Matrix Codes and Their Rotations—A Comparative Study. Journal of Imaging. 2023; 9(9):188. https://doi.org/10.3390/jimaging9090188
Chicago/Turabian StyleKarrach, Ladislav, and Elena Pivarčiová. 2023. "Using Different Types of Artificial Neural Networks to Classify 2D Matrix Codes and Their Rotations—A Comparative Study" Journal of Imaging 9, no. 9: 188. https://doi.org/10.3390/jimaging9090188
APA StyleKarrach, L., & Pivarčiová, E. (2023). Using Different Types of Artificial Neural Networks to Classify 2D Matrix Codes and Their Rotations—A Comparative Study. Journal of Imaging, 9(9), 188. https://doi.org/10.3390/jimaging9090188







