Initial Steps towards a Multilevel Functional Principal Components Analysis Model of Dynamical Shape Changes
Abstract
1. Introduction
2. Materials and Methods
2.1. Sine Wave Dataset
2.2. Blink Dataset
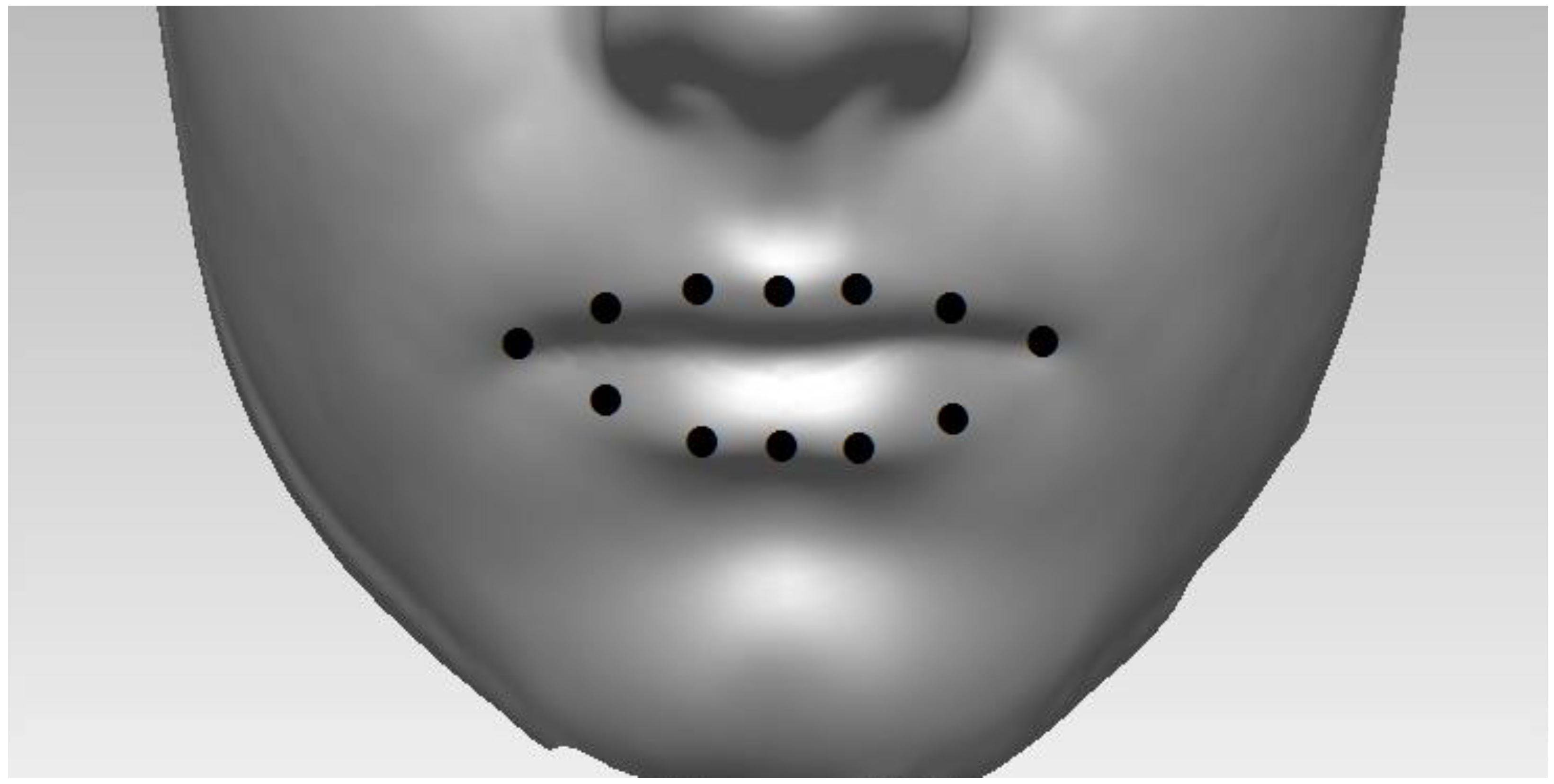
2.3. Smile Dataset
2.4. Functional Principal Components Analysis (FPCA)
2.5. Multilevel Functional Principal Components Analysis (mPCA)
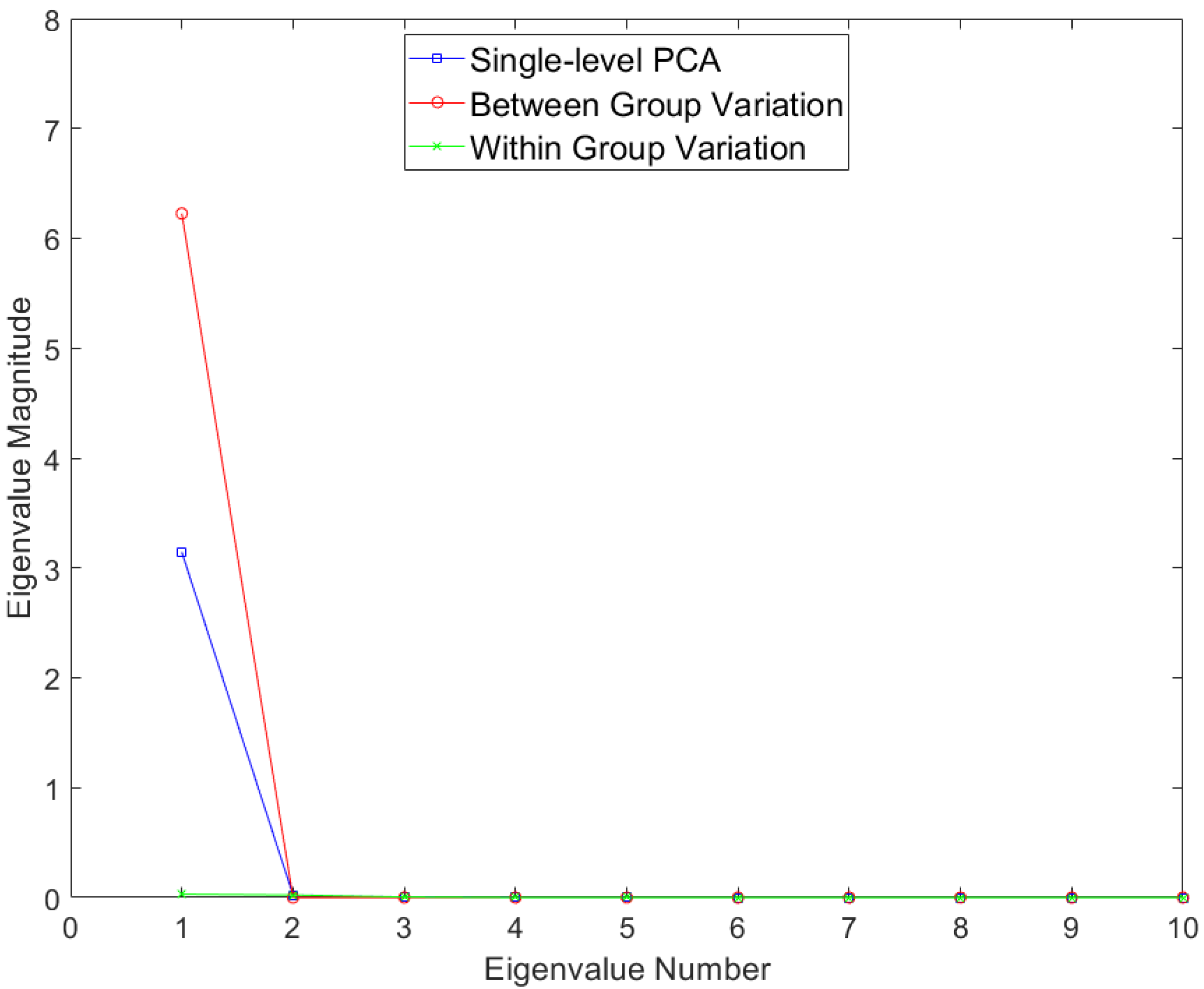
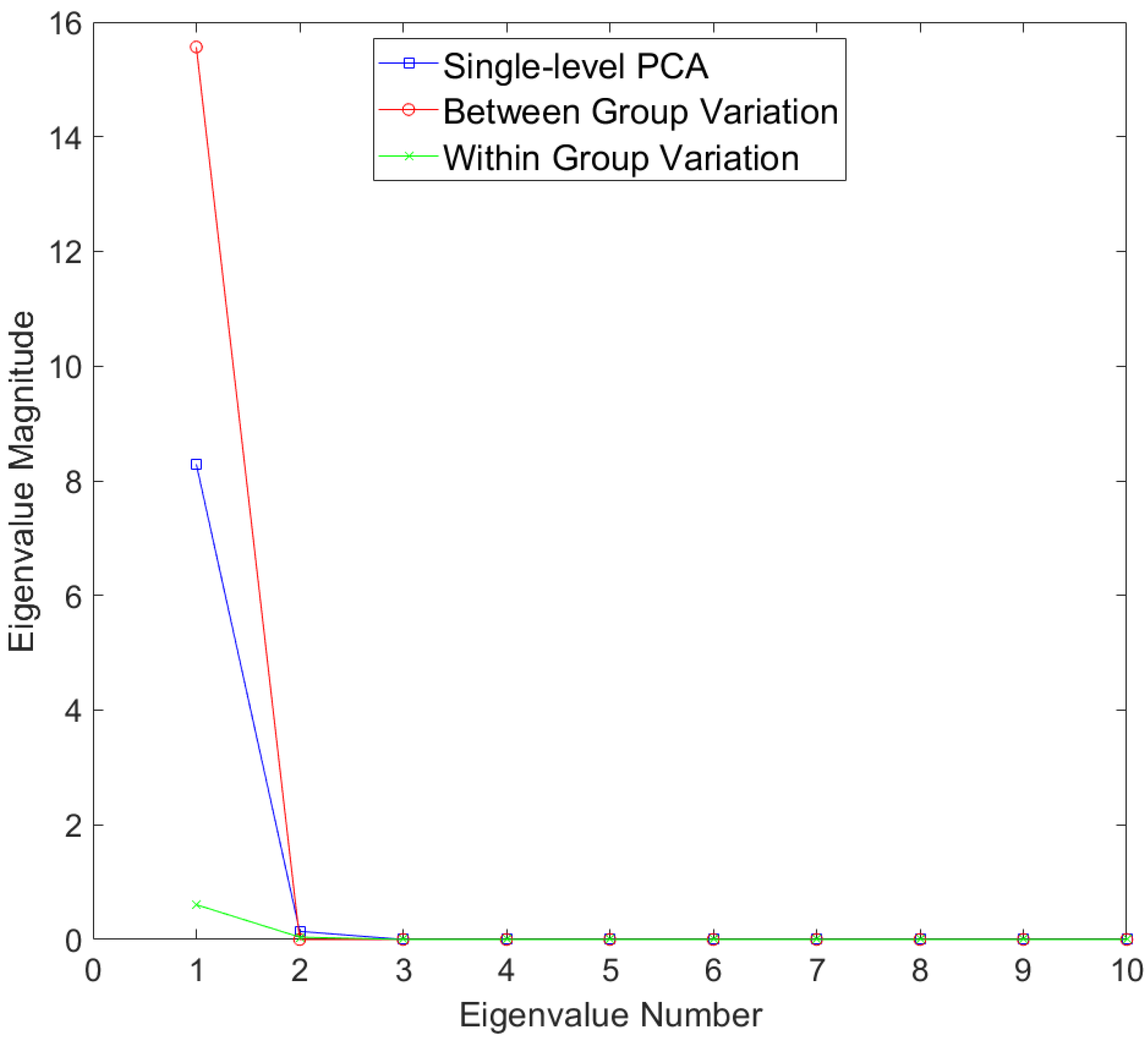
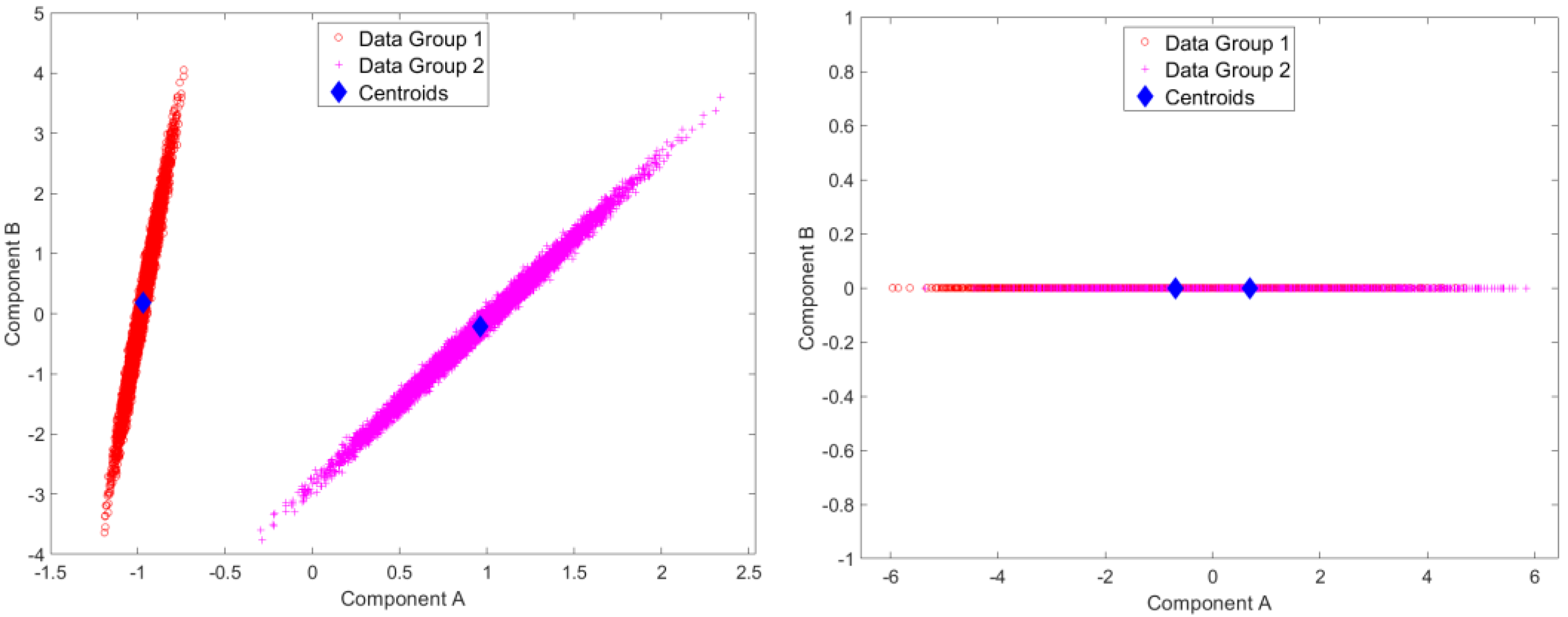
3. Results
3.1. Sine Wave Dataset
3.2. Blink Dataset
3.3. Smile Dataset
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
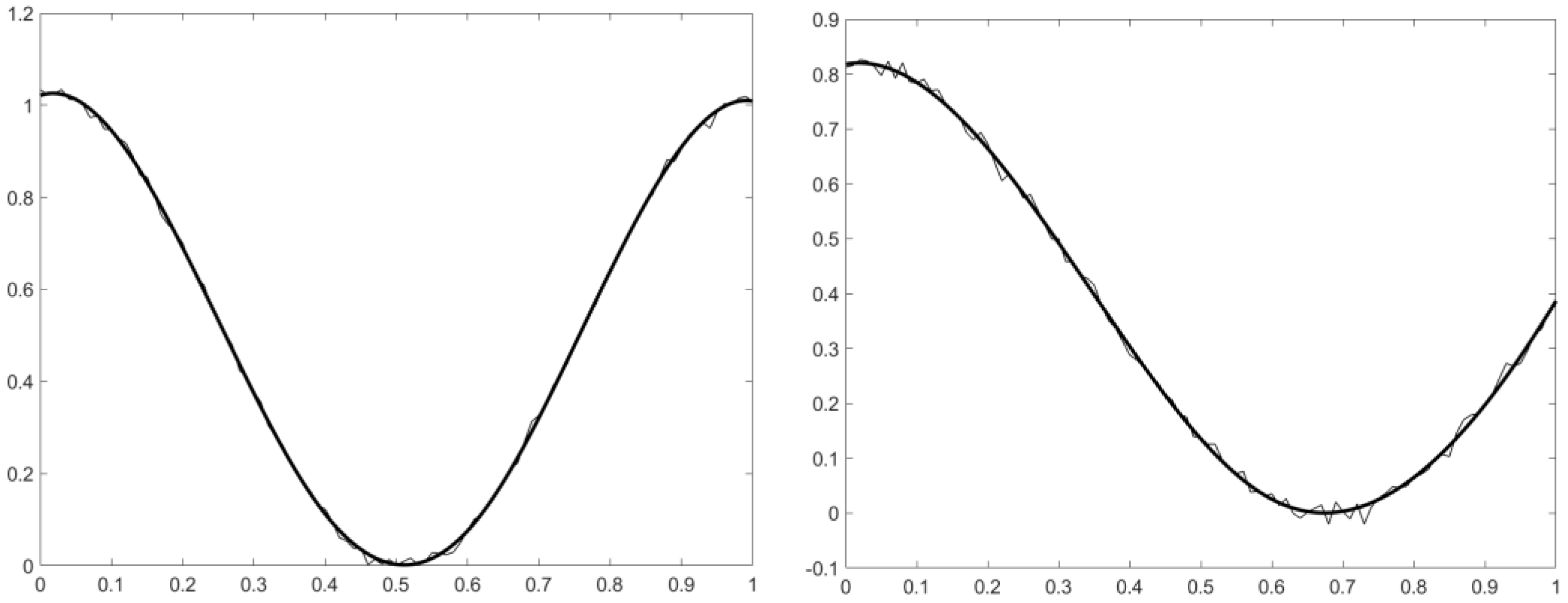

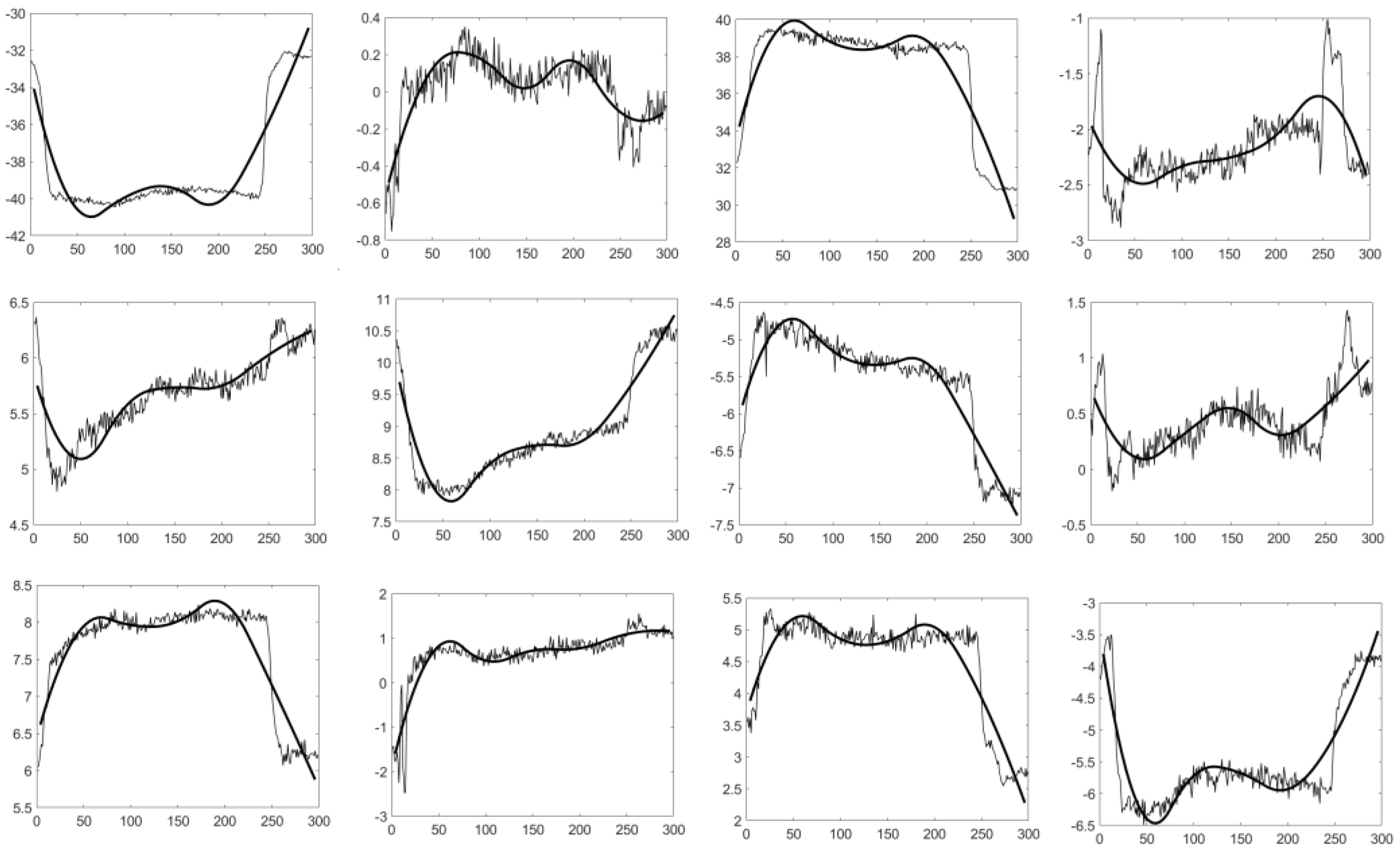
Appendix B
References
- Deutsch, C.K.; Shell, A.R.; Francis, R.W.; Bird, B.D. The Farkas system of craniofacial anthropometry: Methodology and normative databases. In Handbook of Anthropome-Try: Physical Measures of Human Form in Health and Disease; Springer: Berlin/Heidelberg, Germany, 2012; pp. 561–573. [Google Scholar]
- Zelditch, M.L.; Swiderski, D.L.; Sheets, H.D. Geometric Morphometrics for Biologists: A Primer; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Botton-Divet, L.; Houssaye, A.; Herrel, A.; Fabre, A.-C.; Cornette, R. Tools for quantitative form description; an evaluation of different software packages for semi-landmark analysis. PeerJ 2015, 3, e1417. [Google Scholar] [CrossRef] [PubMed]
- Bookstein, F.L. Pathologies of Between-Groups Principal Components Analysis in Geometric Morphometrics. Evol. Biol. 2019, 46, 271–302. [Google Scholar] [CrossRef]
- Cardini, A.; O’higgins, P.; Rohlf, F.J. Seeing Distinct Groups Where There are None: Spurious Patterns from Between-Group PCA. Evol. Biol. 2019, 46, 303–316. [Google Scholar] [CrossRef]
- Farnell, D.; Popat, H.; Richmond, S. Multilevel principal component analysis (mPCA) in shape analysis: A feasibility study in medical and dental imaging. Comput. Methods Programs Biomed. 2016, 129, 149–159. [Google Scholar] [CrossRef]
- Farnell, D.J.J.; Galloway, J.; Zhurov, A.; Richmond, S.; Perttiniemi, P.; Katic, V. Initial results of multilevel principal components analysis of facial shape. Commun. Comput. Inf. Sci. 2017, 723, 674–685. [Google Scholar]
- Farnell, D.J.J.; Galloway, J.; Zhurov, A.I.; Richmond, S. Multilevel Models of Age-Related Changes in Facial Shape in Adolescents. Commun. Comput. Inf. Sci. 2020, 1065, 101–113. [Google Scholar]
- Farnell, D.J.J.; Richmond, S.; Galloway, J.; Zhurov, A.I.; Pirttiniemi, P.; Heikkinen, T.; Harila, V.; Matthews, H.; Claes, P. Multilevel Principal Components Analy-sis of Three-Dimensional Facial Growth in Adolescents. Comput. Methods Programs Biomed. 2019, 188, 105272. [Google Scholar] [CrossRef]
- Galloway, J.; Farnell, D.J.; Richmond, S.; Zhurov, A.I. Multilevel Analysis of the Influence of Maternal Smoking and Alcohol Consumption on the Facial Shape of English Adolescents. J. Imaging 2020, 6, 34. [Google Scholar] [CrossRef]
- Farnell, D.J.J.; Galloway, J.; Zhurov, A.I.; Richmond, S.; Perttiniemi, P.; Lähdesmäki, R. What’s in a Smile? Initial Results of Multilevel Principal Compo-nents Analysis of Facial Shape and Image Texture. Commun. Comput. Inf. Sci. 2018, 894, 177–188. [Google Scholar]
- Farnell, D.J.J.; Galloway, J.; Zhurov, A.I.; Richmond, S.; Marshall, D.; Rosin, P.L.; Al-Meyah, K.; Perttiniemi, P.; Lähdesmäki, R. What’s in a Smile? Initial Analyses of Dynamic Changes in Facial Shape and Appearance. J. Imaging 2019, 5, 2. [Google Scholar] [CrossRef]
- Farnell, D.J.J. An Exploration of Pathologies of Multilevel Principal Components Analysis in Statistical Models of Shape. J. Imaging 2022, 8, 63. [Google Scholar] [CrossRef]
- Warmenhoven, J.; Bargary, N.; Liebl, D.; Harrison, A.; Robinson, M.A.; Gunning, E.; Hooker, G. PCA of waveforms and functional PCA: A primer for biomechanics. J. Biomech. 2021, 116, 110106. [Google Scholar] [CrossRef]
- Hall, P.; Hosseini-Nasab, M. On properties of functional principal components analysis. J. R. Stat. Soc. Ser. B Stat. Methodol. 2006, 68, 109–126. [Google Scholar] [CrossRef]
- Shang, H.L. A survey of functional principal component analysis. AStA Adv. Stat. Anal. 2014, 98, 121–142. [Google Scholar] [CrossRef]
- Di, C.-Z.; Crainiceanu, C.M.; Caffo, B.S.; Punjabi, N.M. Multilevel functional principal component analysis. Ann. Appl. Stat. 2009, 3, 458–488. [Google Scholar] [CrossRef]
- Zipunnikov, V.; Caffo, B.; Yousem, D.M.; Davatzikos, C.; Schwartz, B.S.; Crainiceanu, C. Multilevel Functional Principal Component Analysis for High-Dimensional Data. J. Comput. Graph. Stat. 2011, 20, 852–873. [Google Scholar] [CrossRef]
- Tissainayagam, P.; Suter, D. Object tracking in image sequences using point features. Pattern Recognit. 2005, 38, 105–113. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Fischer, P.; Ilg, E.; Hausser, P.; Hazirbas, C.; Golkov, V.; Van Der Smagt, P.; Cremers, D.; Brox, T. Flownet: Learning optical flow with convolu-tional networks. In Proceedings of the IEEE International Conference on Computer Vision 2015, Las Condes, Chile, 7–13 December 2015; pp. 2758–2766. [Google Scholar]
- Barron, J.L.; Thacker, N.A. Tutorial: Computing 2D and 3D Optical Flow. Imaging Science and Biomedical Engineering Division, Medical School; University of Manchester: Manchester, UK, 2005; p. 1. [Google Scholar]
- Debayle, J.; Hatami, N.; Gavet, Y. Classification of time-series images using deep convolutional neural networks. In Proceedings of the Tenth International Conference on Machine Vision, 2017, Vienna, Austria, 13 April 2018; pp. 242–249. [Google Scholar] [CrossRef]
- Matthews, H.; de Jong, G.; Maal, T.; Claes, P. Static and Motion Facial Analysis for Craniofacial Assessment and Diagnosing Diseases. Annu. Rev. Biomed. Data Sci. 2022, 5, 111413. [Google Scholar] [CrossRef]
- Rohlf, F.J. Why Clusters and Other Patterns Can Seem to be Found in Analyses of High-Dimensional Data. Evolutionary Biology 2021, 48, 1–16. [Google Scholar] [CrossRef]
- Cardini, A.; Polly, P.D. Cross-validated Between Group PCA Scatterplots: A Solution to Spu-rious Group Separation? Evol. Biol. 2020, 47, 85–95. [Google Scholar] [CrossRef]
- Thioulouse, J.; Renaud, S.; Dufour, A.-B.; Dray, S. Overcoming the Spurious Groups Problem in Between-Group PCA. Evol. Biol. 2021, 48, 458–471. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis Analysis; Springer: New York, NY, USA, 2005. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farnell, D.J.J.; Claes, P. Initial Steps towards a Multilevel Functional Principal Components Analysis Model of Dynamical Shape Changes. J. Imaging 2023, 9, 86. https://doi.org/10.3390/jimaging9040086
Farnell DJJ, Claes P. Initial Steps towards a Multilevel Functional Principal Components Analysis Model of Dynamical Shape Changes. Journal of Imaging. 2023; 9(4):86. https://doi.org/10.3390/jimaging9040086
Chicago/Turabian StyleFarnell, Damian J. J., and Peter Claes. 2023. "Initial Steps towards a Multilevel Functional Principal Components Analysis Model of Dynamical Shape Changes" Journal of Imaging 9, no. 4: 86. https://doi.org/10.3390/jimaging9040086
APA StyleFarnell, D. J. J., & Claes, P. (2023). Initial Steps towards a Multilevel Functional Principal Components Analysis Model of Dynamical Shape Changes. Journal of Imaging, 9(4), 86. https://doi.org/10.3390/jimaging9040086





