Digital Filtering Techniques Using Fuzzy-Rules Based Logic Control
Abstract
:1. Introduction
2. General Filtering Framework for a Color Image
2.1. Impulse Noise Models
- (I)
- Salt and pepper noise (fixed-valued noise):
- (a)
- Let with model the original pixel before being vitiated by the noise processing. And the picture elements are subsequently distorted as per the scheme below:where are independent and equal to 0 or 255, p is the sample corruption probability with and are corruption possibilities regarding every color channel, so that . In such circumstances, the contamination of color image components is still non-correlated [7,27,28,30].
- (b)
- In this kind of noise model, the RGB channels are corrupted due to the impulse noise (0 or 255) and possibility p like in (a), while the contamination process is correlated. This case is called the extended noise model and has been discussed extensively in [27,30,31,32]. Its main characteristic is that , . This implies that one of the image channels will probably be corrupted since an additional channel has been corrupted already.
- (II)
- Impulsive uniform or randomly valued noise: In such a case, the average value is equal to the real one. Let with probability p, where the value of a noisy pixel from each color channel is modelled as a random process, being identically distributed and independent, with an arbitrary potential probability density function. The contamination of the color image components is uncorrelated.
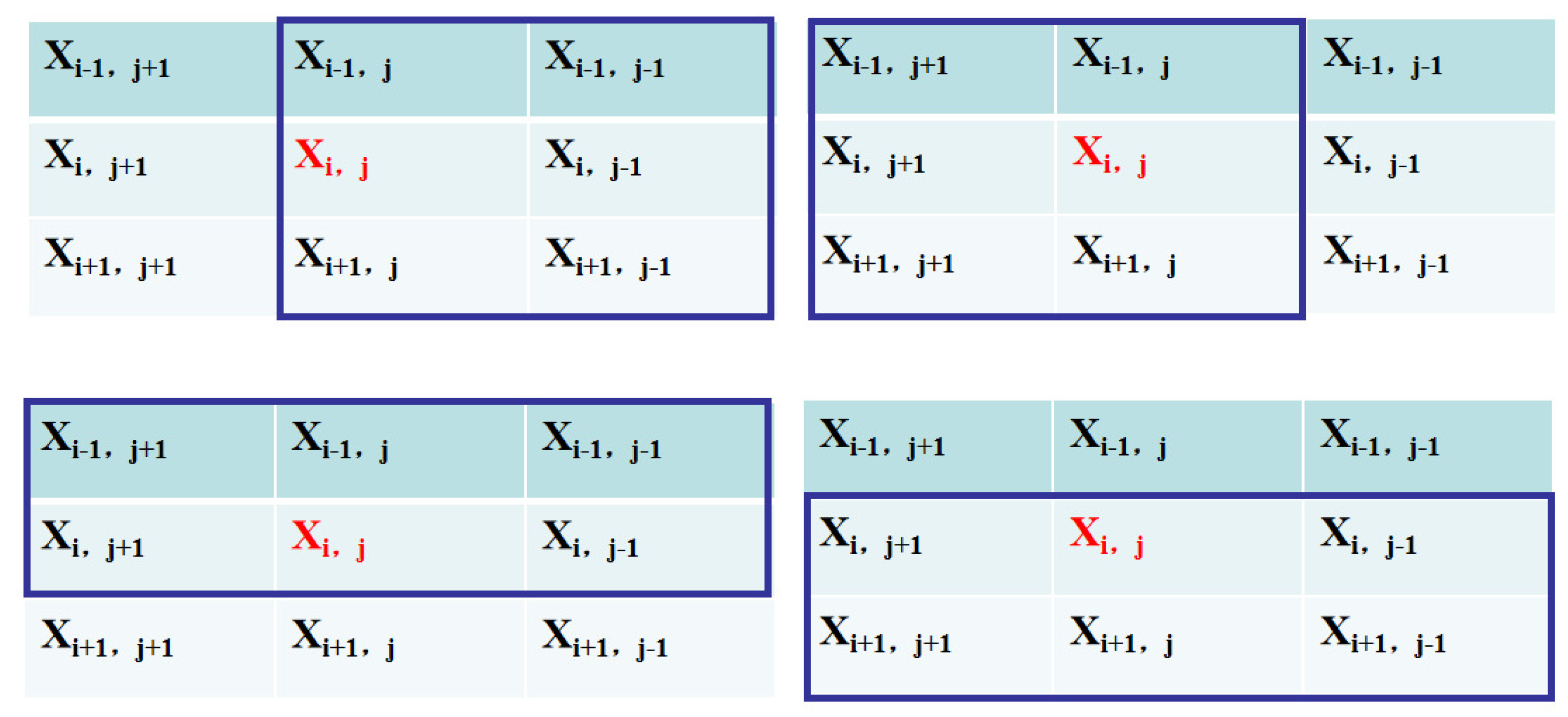
2.2. Window-Based Filtering for Fuzzy Inference System
3. Basic Concepts of Vector Filters
3.1. Ranking Vector-Valued Data
3.2. Vector Directional Filters
3.2.1. Directional-Distance Filters
3.2.2. Hybrid Multichannel Filters
3.2.3. Center-Weighted Vector Median Filters (CWVMFs)
3.2.4. Peer Group Techniques
4. Fuzzy Vector Filters
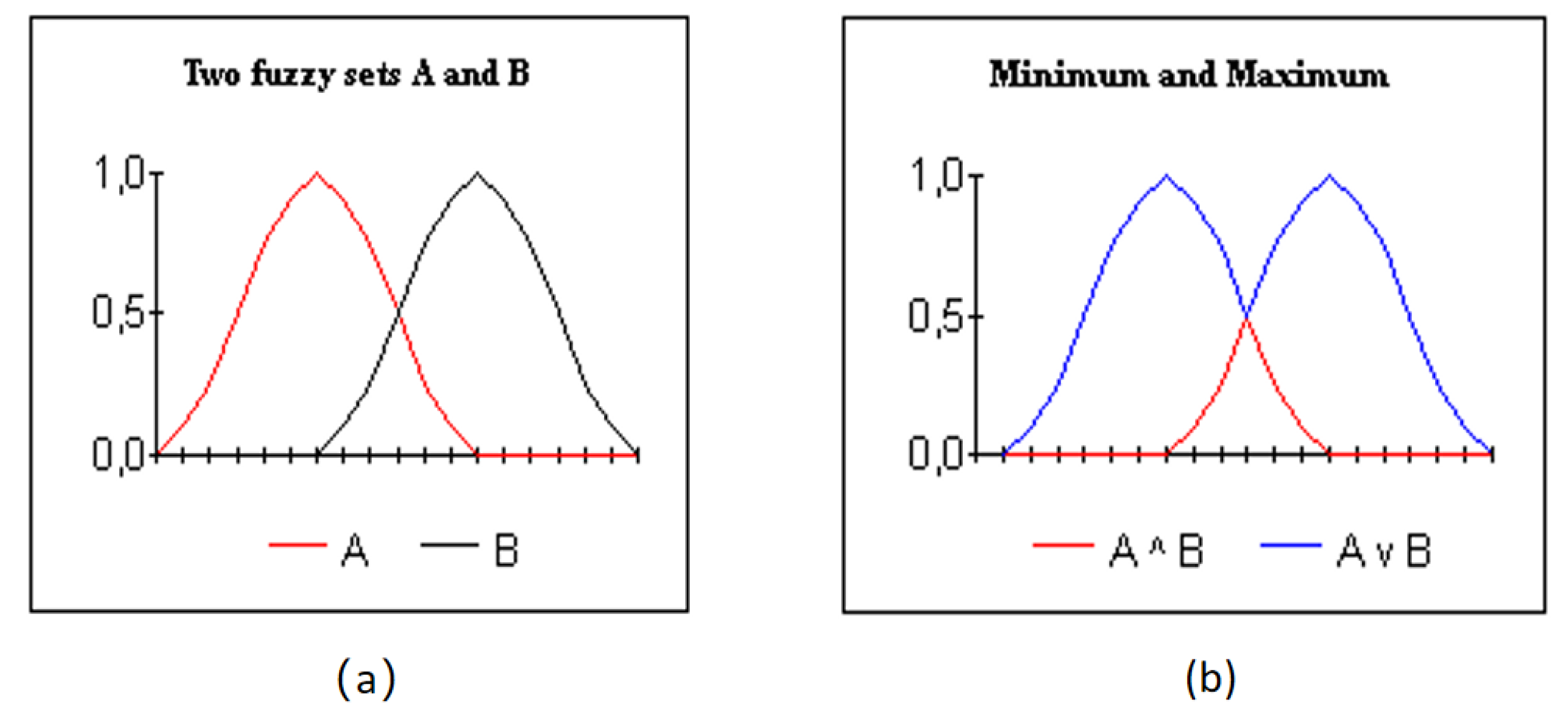
4.1. Standard Operations of Fuzzy Set
4.2. Fuzzy Approaches for Noise Identification
- (a)
- it resembles certain neighbour values
- (b)
- the local differences compared with neighbours resemble the local differences in certain other chromatic components
- (c)
- the resemblance levels of the other RGB component values compared with the neighbour values are high. It is crucial not to introduce a probably noisy component as reference when calculating the similarity between the local differences.
4.2.1. Fixed Valued Impulse Noise
4.2.2. Random Valued Impulse Noise
4.3. Fuzzy Vector Partition
5. Fuzzy Filters Design and Implication
5.1. Fuzzy Cellular Automata for Noise Removal
5.2. An Optimized Fuzzy System for Edge Detection
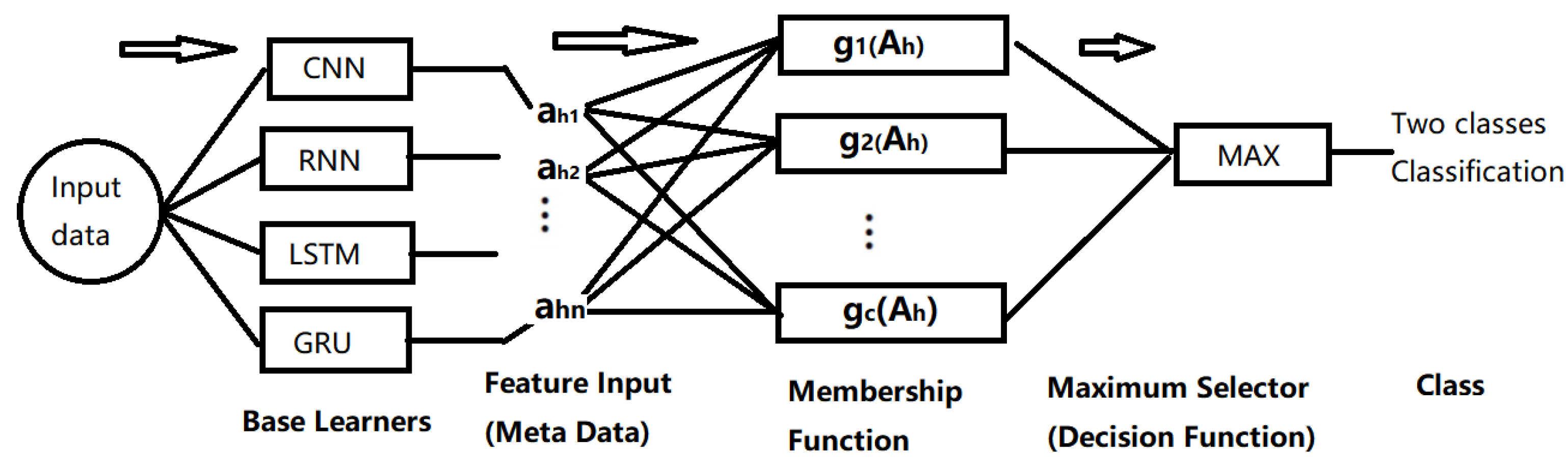
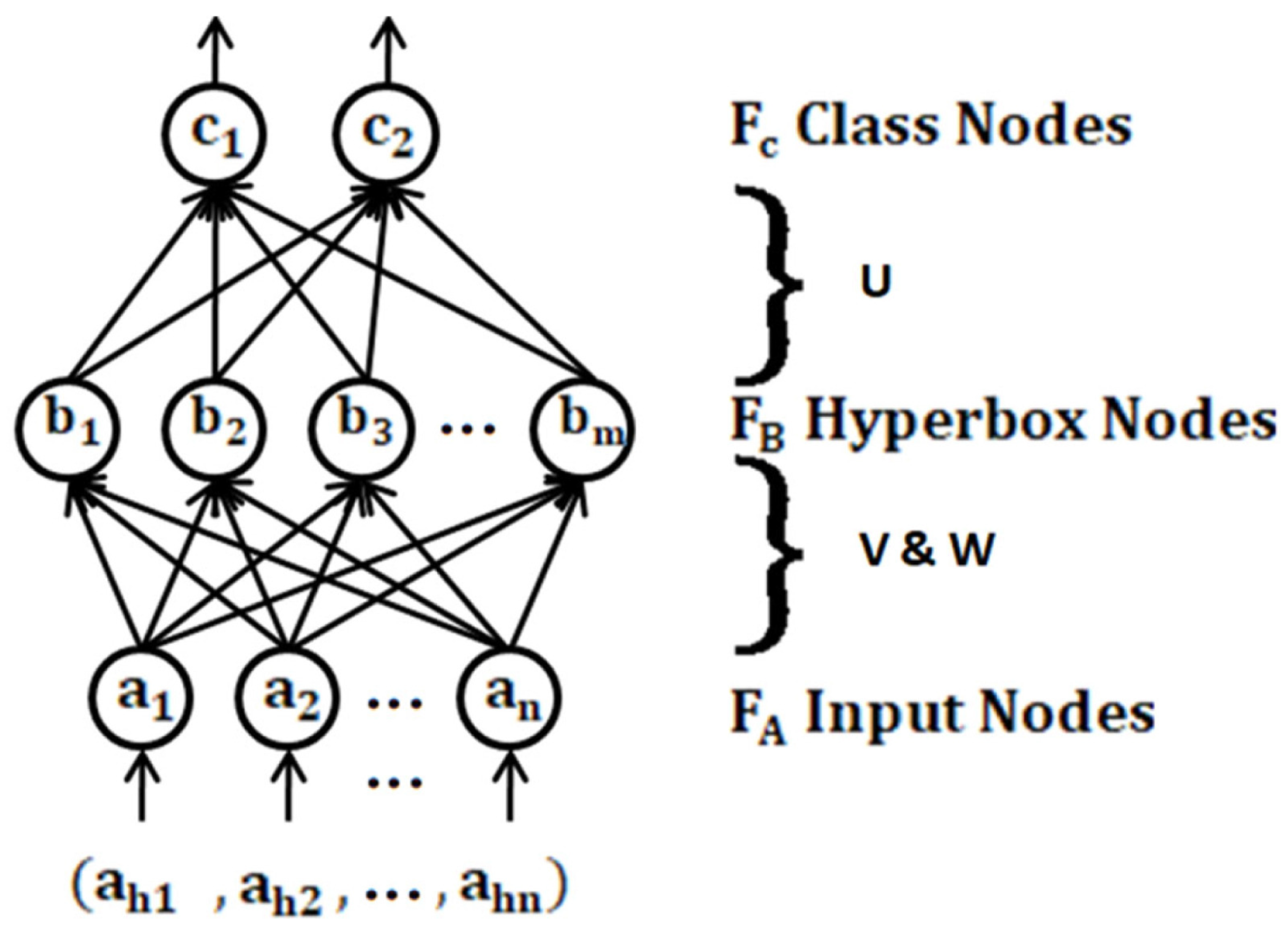
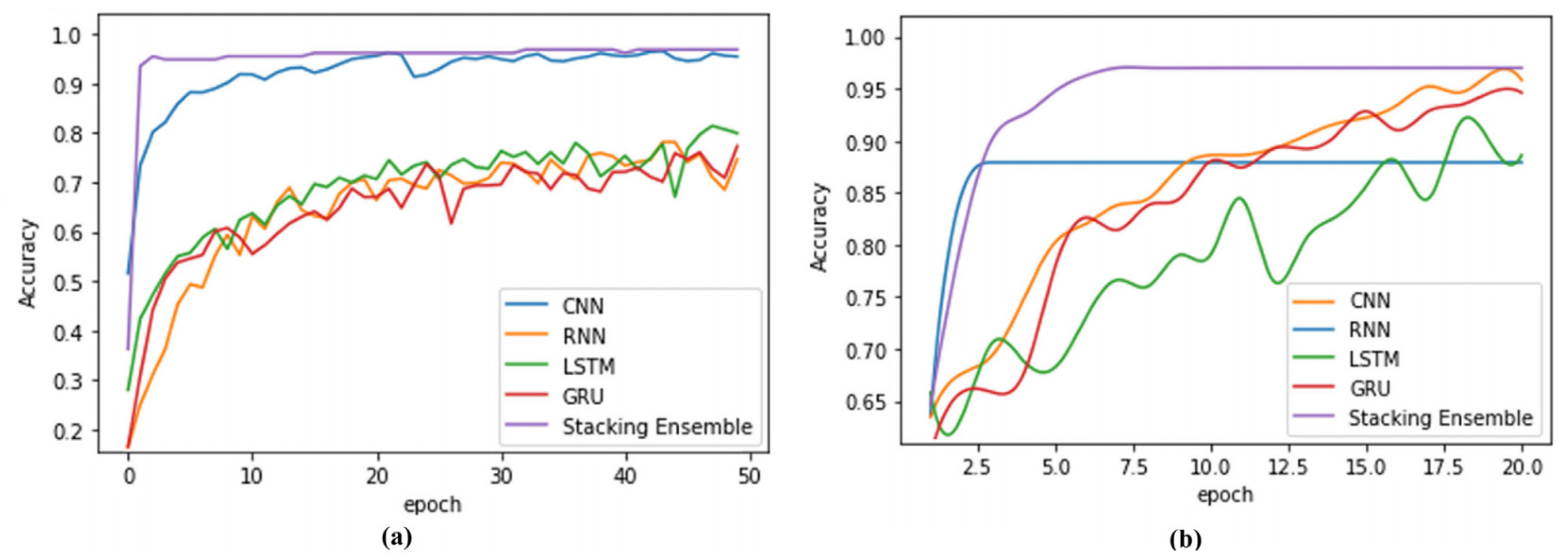
5.3. Fuzzy Deep Ensemble Classifier
5.4. Fuzzy Non Local Mean Filter
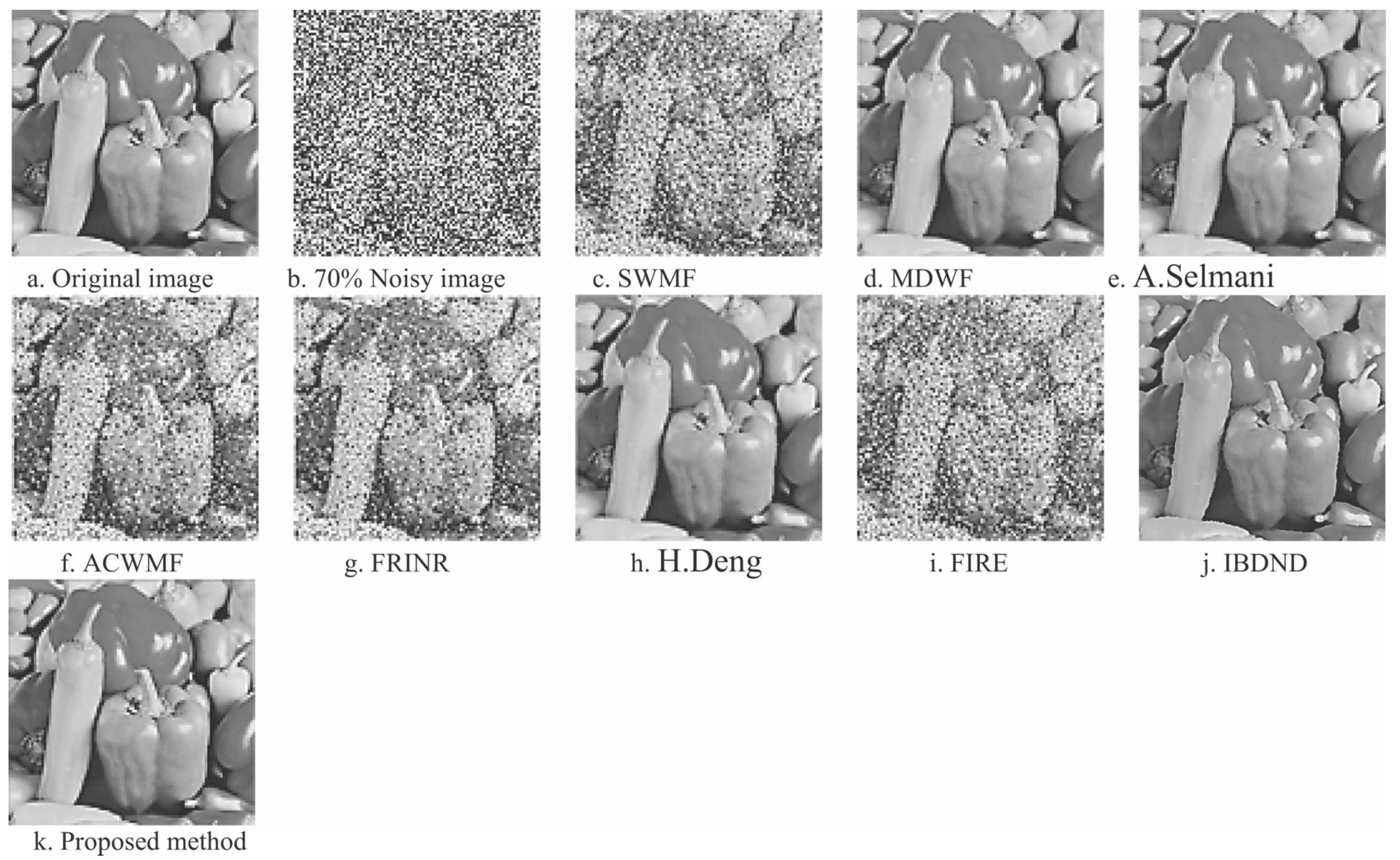
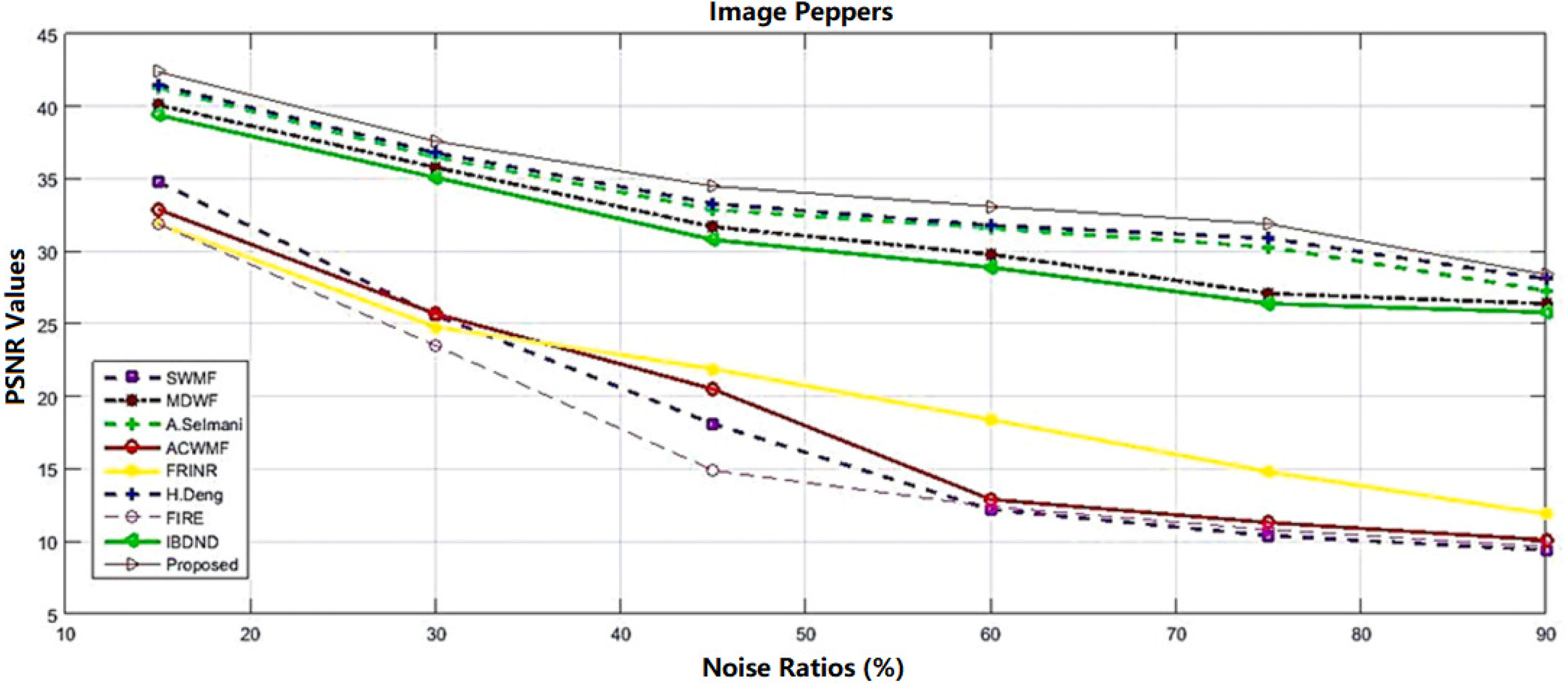
5.5. Resultant Experiments and Comparison
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| a two-dimensional (2-D) image | |
| a two-dimensional (2-D) image matrix | |
| H | the number of rows of an image matrix |
| W | the number of columns of an image matrix |
| a pixel addressed by 2-D sequence | |
| a pixel addressed by 1-D sequence | |
| L | individual channel of a color image |
| red, green, blue color components | |
| model the original pixel | |
| contamination component | |
| p | the sample corruption probability |
| a support window | |
| N | commonly used filter window size |
| c | center pixel position under a window |
| l | gray levels |
| the output color vector | |
| norm parameter | |
| norm of Block distance | |
| norm of Euclidean distance | |
| norm of Max distance | |
| an aggregated distance of a specific pixel | |
| an aggregated distance of VMF | |
| an aggregated distance of VDF | |
| an aggregated distance of DDF | |
| accumulated similarity of peer group | |
| distance function | |
| output of vector median filters | |
| output of vector directional filters | |
| output of basic vector directional filter | |
| output of hybrid multichannel filter | |
| output of identification filter | |
| modified L filter output | |
| output of fuzzy peer group | |
| , | coefficients of hybrid multichannel filter |
| center weighted aggregated vector distance | |
| w | a positive integer central weight |
| output of a CWVM filter | |
| center pixel reference distance | |
| ℏ | a group of preset thresholds |
| threshold value | |
| switch-based center weight vector median | |
| peer group | |
| T | triangular norm |
| S | triangular conorm |
| membership function | |
| certainty | |
| number i partition cell | |
| fuzzy matrix | |
| sample spread | |
| Laplacian mask | |
| basic gradient value | |
| related gradient values | |
| related gradient values | |
| D | gradient direction within a sliding window |
| SVM | support vector machine |
| DDMM | Distinct distance measure metrics |
| BVDF | Basic vector directional filter |
| GVDF | Generalised vector directional filter |
| DDF | A directional distance filter |
| FPGA | Field programmable gate array |
| AVDDF | Adaptive vector directional distance filter |
| HMF | Hybrid multichannel filter |
| CWVMFs | Center weighted vector median filters |
| PRT | Peer group filter |
| FPGF | Fast peer group filter |
| ACWMF | Adaptive center weighted median filters |
| SWMF | Switching median filtering |
| MDWF | Modified directional weighted filter |
| FRINR | Fuzzy stochastic stimulus related noise removal method |
| FIRE | Fuzzy inference rule by the else-action filter |
| BDND | Boundary discriminative noise detection |
| FMM | Fuzzy min max |
| CNN | Convolutional Neural Networks |
| RNN | Recurrent Neural Network |
| LSTM | Long Short Term Memory neural network |
| GRU | Gated Recurrent Unit |
| NLM | Non local Means |
| NAFSM | Noise adaptive fuzzy switching median filtered image |
| MSE | Mean Square Error |
| PSNR | Peak Signal to Noise Ratio |
| SNR | Signal to Noise Ratio |
| AFT2F | Adaptive fuzzy type 2 filter |
| VDF | Vector directional filter |
| SSIM | Structured Similarity Index |
| QFT | Quaternion Fourier Transform |
| DDF | Directional-distance filters |
| NCD | Normalized color difference |
| HMF | Hybrid multichannel filter |
| HMAMF | Hybrid marginal arithmetic mean filter |
| HVMF | Hybrid Vector mean Filters |
| AVMF | Adaptive vector median filter |
| PGSVMF | Peer group switching vector median filter |
| PRF | Peer region filter |
| PGSAMF | Peer group switching arithmetic mean filter |
| FMPGSAMF | Fuzzy modified peer group switching arithmetic mean filter |
| WVDFs | Weighted vector directional filters |
| HVFs | Vector directional hybrid filters |
| DPGF | Directional weighted peer group |
| FWMF | Fuzzy based Weighted Mean Filter |
| FSIM | Feature similarity index |
| MWMF | Modified Weighted Mean Filter |
| FINR | Fuzzy based impulse noise reduction method |
| PGSF | Peer group switching filter |
| FISF | Fuzzy inference system filter |
| HAF | Histogram adaptive fuzzy filter |
| FIDRM | Fuzzy impulse noise detection and reduction method |
| QSAF | Quadrant based spatially adaptive fuzzy filter |
| FRVP | Fuzzy-rank vector partition |
| FCA | Fuzzy cellular automata |
| ADCWM | Adaptive impulse detection via center weighted median filters |
| SWF | Switching median filter |
| FARTMAP | Fuzzy adaptive resonance theory mapping |
| FANLM | Fuzzy Cmeans and adaptive non-local means |
| UNLM | Unbiased NLM filter |
| AT2F | Adaptive Type-2 Fuzzy Approach |
References
- Jiang, J.; Yang, K.; Xu, X.; Cui, Y. A serial attention module based deep convolutional neural network for mixed gaussian-impulse removal. IET Image Process. 2023, 17, 1837–1851. [Google Scholar] [CrossRef]
- Majlesein, B.; Asghar, G.; Zabih, G. Investigation of the scattering noise in underwater optical wireless communications. Sciences 2021, 3, 27. [Google Scholar] [CrossRef]
- Nadeem, M.; Hussain, A.; Munir, A.; Habib, M.; Naseem, M.T. Removal of random valued impulse noise from grayscale images using quadrant based spatially adaptive fuzzy filter. Signal Process. 2020, 169, 107403. [Google Scholar] [CrossRef]
- Yin, X.-X.; Ng, B.W.-H.; Abbott, D. Pattern Recognition and Tomographic Reconstruction of Terahertz Signals: Applications in Biomedical Engineering; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Yin, X.-X.; Hadjiloucas, S.; Chen, J.H.; Zhang, J.-L.W.Y.; Su, M.-Y. Tensor based multichannel reconstruction for breast tumours identified from DCE-MRIs. PLoS ONE 2017, 12, e0172111. [Google Scholar]
- Yin, X.-X.; Zhang, Y.; Cao, J.; Wu, J.-L.; Hadjiloucas, S. Exploring the complementarity of THz pulse imaging and DCE-MRIs: Towards a unified multi-channel classification & a deep learning framework. Comput. Methods Programs Biomed. 2016, 137, 87–114. [Google Scholar] [PubMed]
- Schulte, S.; Nachtegael, M.; De Witte, V.; van der Weken, D.; Kerre, E. A fuzzy impulse noise detection and reduction method. IEEE Trans. Image Process. 2006, 15, 1153–1162. [Google Scholar] [CrossRef]
- Nikias, C.L.; Shao, M. Signal Processing with Alpha-Stable Distributions and Applications; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Plataniotis, K.N.; Androutsos, D.; Venetsanopoulos, A.N. Adaptive fuzzy systems for multichannel signal processing. Proc. IEEE 1999, 87, 1601–1622. [Google Scholar] [CrossRef]
- Yildirim, M.; Basturk, A.; Yuksel, M. Impulse noise removal from digital images by a detail-preserving filter based on type-2 fuzzy logic. IEEE Trans. Fuzzy Syst. 2008, 16, 920–928. [Google Scholar] [CrossRef]
- Toh, K.; Isa, N. Noise adaptive fuzzy switching median filter for salt-and-pepper noise reduction. IEEE Signal Process. Lett. 2010, 17, 281–284. [Google Scholar] [CrossRef]
- Chou, H.-H.; Hsu, L.-Y.; Hu, H.-T. Turbulent-pso-based fuzzy image filter with no-reference measures for high-density impulse noise. IEEE Trans. Cybern. 2013, 43, 296–307. [Google Scholar] [CrossRef]
- Roy, A.; Singha, J.; Devi, S.S.; Laskar, R.H. Impulse noise removal using svm classification based fuzzy filter from gray scale images. Signal Process. 2016, 128, 262–273. [Google Scholar] [CrossRef]
- Senthil Selvi, A.; Kumar, K.P.M.; Dhanasekeran, S.; Maheswari, P.U.; Ramesh, S.; Pandi, S.S. De-noising of images from salt and pepper noise using hybrid filter, fuzzy logic noise detector and genetic optimization algorithm (hfgoa). Multimed. Tools Appl. 2020, 79, 4115–4131. [Google Scholar] [CrossRef]
- Hemalatha, C.; Periasamy, A.; Muruganand, S. A hybrid approach for efficient removal of impulse, Gaussian and mixed noise from highly corrupted images using adaptive neuro fuzzy inference system (ANFIS). Int. J. Comput. Appl. 2012, 45, 15–21. [Google Scholar]
- Wen, J.; Heng, J.; Hu, J.; Zhao, W. Deterministic and probabilistic wind speed forecasting with de-noising-reconstruction strategy and quantile regression based algorithm. Renew. Energy 2020, 162, 1208–1226. [Google Scholar]
- Tian, C.; Fei, L.; Zuo, W.; Tian, C.; Zheng, W.; Xu, Y.; Zuo, W.; Lin, C.-W. Deep learning on image denoising: An overview. Neural Netw. 2020, 131, 251–275. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, F.; Fan, H.; Zhang, C. Brief review of image denoising techniques, Visual Computing for Industry. Biomed. Art 2019, 2, 1–12. [Google Scholar]
- Ma, Z.; Wu, H.R.; Feng, D. Fuzzy vector partition filtering technique for color image restoration. Comput. Vis. Image Underst. 2007, 107, 26–37. [Google Scholar] [CrossRef]
- Lv, Z.; Xue, F.; Qian, W. Edges and hues keeping denoising algorithm for color images. In AOPC 2022: Optical Sensing, Imaging, and Display Technology; SPIE: Bellingham, WA, USA, 2023; Volume 12557, pp. 425–430. [Google Scholar]
- Chen, D.B.; Zhao, C.X. Data-driven fuzzy clustering based on maximum entropy principle and PSO. Expert Syst. Appl. 2019, 36, 625–633. [Google Scholar] [CrossRef]
- Zhou, H.; Li, Y.; Xu, H.; Su, Y.; Zhang, Q. Soft-sensing of effluent total phosphorus using adaptive recurrent fuzzy neural network with gustafson-kessel clustering. Expert Syst. Appl. 2022, 203, 117589. [Google Scholar]
- Guo, S.M.; Lee, C.S.; Hsu, C.Y. An intelligentimage agent based on soft-computing techniquesfor color image processing. Expert Syst. Appl. 2005, 28, 483–494. [Google Scholar] [CrossRef]
- Hu, Y.; Xia Zhao, C. A novel lbp based methods for pavement crack detection. J. Pattern Recognit. Res. 2010, 5, 140–147. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Keller, J.; Krisnapuram, R.; Pal, N.R. Fuzzy Models and Algorithms for Pattern Recognition and Image Processing (The Handbooks of Fuzzy Sets); Springer: New York, NY, USA, 2005. [Google Scholar]
- Chanu, T.R.; Singh, T.; Singh, K. A new algorithm for removing salt and pepper noise from color medical images. Multimed. Tools Appl. 2023, 82, 24991–25013. [Google Scholar] [CrossRef]
- Smolka, B.; Lukac, R.; Chydzinski, A.; Plataniotis, K.N.; Wojciechowski, W. Fast adaptive similarity based impulsive noise reduction filter. Real-Time Imaging 2003, 9, 261–276. [Google Scholar] [CrossRef]
- Schulte, S.; de Witte, V.; Nachtegael, M.; van der Weken, D.; Kerre, E.E. Fuzzy random impulse noise reduction method. Fuzzy Sets Syst. 2007, 158, 270–283. [Google Scholar] [CrossRef]
- Li, Q.; Li, J.; Ma, B.; Xia, Z.; Luo, T. Light-field image watermarking based on geranion polar harmonic fourier moments. Eng. Appl. Artif. Intell. 2022, 113, 104970. [Google Scholar]
- Plataniotis, K.N.; Venetsanopoulos, A.N. Color Image Processing and Applications; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Lukac, R. Adaptive vector median filtering. Pattern Recognit. Lett. 2003, 24, 1889–1899. [Google Scholar] [CrossRef]
- Vardavoulia, M.I.; Andreadis, I.; Tsalides, P. A new vector median filter for color image processing. Pattern Recognit. Lett. 2001, 22, 675–689. [Google Scholar] [CrossRef]
- Mafi, M.; Martin, H.; Cabrerizo, M.; Andrian, J.; Barreto, A.; Adjouadi, M. A comprehensive survey on impulse and gaussian denoising filters for digital images. Signal Process. 2019, 157, 236–260. [Google Scholar] [CrossRef]
- Lukac, R.; Smolka, B.; Martin, K.; Plataniotis, K.N.; Venetsanopoulos, A.N. Vector filtering for color imaging. IEEE Signal Process. Mag. 2005, 22, 74–86. [Google Scholar] [CrossRef]
- Russo, F. FIRE operators for image processing. Fuzzy Sets Syst. 1999, 103, 265–275. [Google Scholar] [CrossRef]
- Russo, F.; Ramponi, G. A fuzzy filter for images corrupted by impulse noise. IEEE Signal Process. Lett. 1996, 3, 168–170. [Google Scholar] [CrossRef]
- Tsai, H.H.; Yu, P.T. Adaptive fuzzy hybrid multichannel filters for removal of impulsive noise from color images. Signal Process. 1999, 74, 127–151. [Google Scholar] [CrossRef]
- Barnett, V. The ordering of multivariate data. J. R. Stat. Soc. Ser. A 1976, 139, 318–343. [Google Scholar] [CrossRef]
- Battula, V.; Ambati, S. Evaluation of images using various distance metrics. Int. J. Engi. Res. Appl. 2018, 8, 29–34. [Google Scholar]
- Trahanias, P.E.; Karakos, D.; Venetsanopoulos, A.N. Directional processing of color images: Theory and experimental results. IEEE Trans. Image Process. 1996, 5, 868–880. [Google Scholar] [CrossRef] [PubMed]
- Smolka, B.; Plataniotis, K.N.; Chydzinski, A.; Szczepanski, M.; Venetsanopoulosb, A.N.; Wojciechowskia, K. Self-adaptive algorithm of impulsive noise reduction in color images. Pattern Recognit. 2002, 35, 1771–1784. [Google Scholar] [CrossRef]
- Bhatti, U.A.; Zhou, M.-Q.; Huo, Q.-S.; Ali, S.; Hussain, A.; Yan, Y.; Yu, Z.; Yuan, L.; Nawaz, S.A. Advanced color edge detection using clifford algebra in satellite images. IEEE Photonics J. 2021, 13, 1–20. [Google Scholar] [CrossRef]
- Karakos, D.G.; Trahanias, P.E. Generalized multichannel image-filtering structure. IEEE Trans. Image Process. 1997, 6, 1038–1045. [Google Scholar] [CrossRef]
- Atitallah, A.B. A new adaptive filter to remove impulsive noise in color images. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 1048–1053. [Google Scholar] [CrossRef]
- Lukac, R. Adaptive color image filtering based on center-weighted vector directional filters. Multidimens. Syst. Signal Process. 2004, 15, 169–196. [Google Scholar] [CrossRef]
- Ma, Z.; Feng, D.; Wu, H.R. A neighborhood evaluated adaptive vector filter for suppression of impulsive noise in color images. Real-Time Imaging 2005, 11, 403–416. [Google Scholar] [CrossRef]
- Zhong, L.; Ibrahim, M.T.; Zhang, Y.; Guan, L. Hybrid vector filters based on marginal ordering for impulsive noise suppression in color images. J. Signal Process. Syst. 2017, 89, 379–394. [Google Scholar] [CrossRef]
- Lukac, R.; Smolka, B.; Plataniotis, K.N.; Venetsanopoulos, A.N. Selection weighted vector directional filter. Comput. Vis. Image Underst. 2004, 94, 140–167. [Google Scholar] [CrossRef]
- Lucat, L.; Siohan, P.; Barba, D. Adaptive and global optimization methods for weighted vector median filters. Signal Process. Image Commun. 2002, 17, 509–524. [Google Scholar] [CrossRef]
- Ma, Z.H.; Wu, H.R.; Feng, D. Partition-based vector filtering technique for suppression of noise in digital color images. IEEE Trans. Image Process. 2006, 15, 2324–2342. [Google Scholar] [PubMed]
- Kenney, C.; Deng, Y.; Manjunath, B.; Hewer, G. Peer group image enhancement. IEEE Trans. Image Process. 2001, 10, 326–334. [Google Scholar] [CrossRef]
- Camarena, J.G.; Gregori, V.; Morillas, S.; Sapena, A. Fast detection and removal of impulsive noise using peer groups and fuzzy metrics. J. Vis. Commun. Image Represent. 2008, 19, 20–29. [Google Scholar] [CrossRef]
- Morillas, S.; Gregori, V.; Peris-Fajarnes, G. Isolating impulsive noise pixels in color images by peer group techniques. Comput. Vis. Image Underst. 2008, 110, 102–116. [Google Scholar] [CrossRef]
- Smolka, B.; Chydzinski, A. Fast detection and impulsive noise removal in colorimages. Real-Time Imag. 2005, 11, 389–402. [Google Scholar] [CrossRef]
- Ho, J.Y.F. Peer region determination based impulsive noise detection. Proc. Int. Conf. Acoust. Signal Process. 2003, 3, 713–716. [Google Scholar]
- Hsu, L.-Y.; Chia, S.-T.; Chou, H.-H. Fpga implementation of directional peer-group image filter. Adv. Nat. Comput. Fuzzy Syst. Knowl. Discov. 2019, 1075, 720–727. [Google Scholar]
- David, H.A. Order Statistics; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Huber, P.S. Robust Statistics; John Wiley and Sons: New York, NY, USA, 1981. [Google Scholar]
- Ponomaryov, V.I. Real-time 2D-3D filtering using order statistics based algorithms. J. Real-Time Image Process. 2007, 1, 173–194. [Google Scholar] [CrossRef]
- Jin, L.H.; Li, D.H. A switching vector median filter based on the cielab color space for color image restoration. Signal Process. 2007, 87, 1345–1354. [Google Scholar] [CrossRef]
- Elmoataz, A.; Lezoray, O.; Bougleux, S. Non-local discrete regularization on weighted graphs: A framework for image and manifold processing. IEEE Trans. Image Process. 2008, 17, 1047–1060. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Xu, S. A new directional weighted median filter for removal of random-valued impulse noise. IEEE Signal Process. Lett. 2007, 14, 193–196. [Google Scholar] [CrossRef]
- Wang, J.-S.; Chiang, J.-C.; Yang, Y.-T. Support vector clustering with outlier detection. Commun. Comput. Inf. Sci. 2007, 2, 423–431. [Google Scholar]
- Zeng, G.P.; Zhao, R.Z. Image denoising using least squares wavelet support vector machines. Chin. Opt. Lett. 2007, 5, 632–635. [Google Scholar]
- Lukac, R.; Plataniotis, K.N.; Venetsanopoulos, A.N.; Smolka, B. A statistically-switched adaptive vector median filter. J. Intell. Robot. Syst. 2005, 42, 361–391. [Google Scholar] [CrossRef]
- Allende, H.; Galbiati, J. A non-parametric filter for image restoration using cluster analysis. Pattern Recognit. Lett. 2004, 25, 841–847. [Google Scholar] [CrossRef]
- Khriji, L.; Gabbouj, M. Adaptive fuzzy order statistics-rational hybrid filters for color image processing. Fuzzy Sets Syst. 2002, 128, 35–46. [Google Scholar] [CrossRef]
- Scheunders, P. Wavelet thresholding of multivalued images. IEEE Trans. Image Process. 2004, 13, 475–483. [Google Scholar] [CrossRef] [PubMed]
- Sendur, L.; Selesnick, I.W. Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency. IEEE Trans. Signal Process. 2002, 50, 2744–2756. [Google Scholar] [CrossRef]
- Balster, E.J.; Zheng, Y.F.; Ewing, R.L. Featurebased wavelet shrinkage algorithm for image denoising. IEEE Trans. Image Process. 2005, 14, 2024–2039. [Google Scholar] [CrossRef]
- Zhang, B.; Fadili, J.M.; Starck, J.L. Wavelets, ridgelets, and curvelets for poisson noise removal. IEEE Trans. Image Process. 2008, 17, 1093–1108. [Google Scholar] [CrossRef] [PubMed]
- Civicioglu, P. Using uncorrupted neighborhoods of the pixels for impulsive noise suppression with ANFIS. Fuzzy Sets Syst. 2007, 158, 759–773. [Google Scholar] [CrossRef]
- Qin, H.; Yang, S.X. Adaptive neuro-fuzzy inference systems based approach to nonlinear noise cancellation for images. Fuzzy Sets Syst. 2007, 158, 1036–1063. [Google Scholar] [CrossRef]
- Yuksel, M.E. A hybrid neuro-fuzzy for edge preserving restoration of images corrupted by impulse nois. IEEE Trans. Image Process. 2006, 15, 928–936. [Google Scholar] [CrossRef]
- Hanmandlu, M.; Jha, D.; Sharma, R. Color image enhancement by fuzzy intensification. Pattern Recognit. Lett. 2003, 24, 81–87. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Goguen, J.A. The logic of inexact concepts. Synthesis 1969, 19, 325–373. [Google Scholar] [CrossRef]
- Bloch, I. Fuzzy spatial relationships for image processing and interpretation: A review. Image Vis. Comput. 2005, 23, 89–110. [Google Scholar] [CrossRef]
- Mendel, J.M. Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Dubois, D.; Prade, H. Fundamentals of Fuzzy Sets; Kluwer Academic Publishers: Boston, MA, USA, 2000. [Google Scholar]
- Hore, E.S.; Qiu, B.; Wu, H.R. Improved vector filtering for color images using fuzzy noise detection. Opt. Eng. 2003, 42, 1656–1664. [Google Scholar] [CrossRef]
- Hota, N.R.; Pattanaik, S.P.; Padhy, R. Removal of random valued impulse noise with modified weighted mean filter by using denoising algorithm: Emerging opportunities of image processing application. Int. J. Res. Appl. Sci. Eng. Technol. 2018, 6, 812–832. [Google Scholar] [CrossRef]
- Schulte, S.; Morillas, S.; Gregori, V.; Kerre, E.E. A new fuzzy color correlated impulse noise reduction method. IEEE Trans. Image Process. 2007, 16, 2565–2575. [Google Scholar] [CrossRef]
- Schulte, S.; de Witte, V.; Nachtegael, M.; van der Weken, D.; Kerre, E.E. Fuzzy two-step filter for impulse noise reduction from color images. IEEE Trans. Image Process. 2006, 15, 3567–3578. [Google Scholar] [CrossRef]
- Zlokolica, V.; Philips, W. Motion and detail adaptive denoising of video. IS T/SPIE Symp. Electron. Imaging 2004, 5298, 403–412. [Google Scholar]
- Lin, T.C.; Yu, P.T. Partition fuzzy median filter based on fuzzy rules for image restoration. Fuzzy Sets Syst. 2004, 147, 75–97. [Google Scholar] [CrossRef]
- Sayood, K. Introduction to Data Compression, 2nd ed.; Morgan Kaufmann: Los Altos, CA, USA, 2000. [Google Scholar]
- Shao, M.; Barner, K.E. Optimization of partition based weighted sum filters and their application to image denoising. IEEE Trans. Image Process. 2006, 15, 1900–1915. [Google Scholar] [CrossRef]
- Flaig, A.; Barner, K.E.; Arce, G.R. Fuzzy ranking: Theory and applications. Signal Process. 2000, 80, 1017–1036. [Google Scholar] [CrossRef]
- Barner, K.E.; Nie, Y.; An, W. Fuzzy ordering theory and its use in filter generalization. EURASIP J. Appl. Signal Process. 2001, 2001, 206–218. [Google Scholar] [CrossRef]
- Alparone, L.; Barni, M.; Bartolini, F.; Caldelli, R. Regularization of optic flow estimates by means of weighted vector median filtering. IEEE Trans. Image Process. 1999, 8, 1462–1467. [Google Scholar] [CrossRef] [PubMed]
- Viero, T.; Oistamo, K.; Neuvo, Y. Three dimensional median-related filters for color image sequence filtering. IEEE Trans. Circuits Syst. 1994, 4, 129–142. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Dey, N.; Ashour, A.S.; Sifaki-Pistolla, D.; Balas-Timar, D.; Balas, V.E.; Tavares, J.M.R.S. Effect of fuzzy partitioning in crohn’s disease classification: A neuro-fuzzy-based approach. Med. Biol. Eng. Comput. 2017, 55, 101–115. [Google Scholar] [CrossRef] [PubMed]
- Piroozmandan, M.M.; Farokhi, F.; Kangarloo, K.; Jahanshahi, M. Removing the impulse noise from images based on fuzzy cellular automata by using a two-phase innovative method. Optik 2007, 255, 168713. [Google Scholar] [CrossRef]
- Cattaneo, G.; Flocchini, P.; Mauri, G.; Vogliotti, C.; Santoro, N. Cellular automata in fuzzy backgrounds. Phys. D Nonlinear Phenom. 1997, 105, 105–120. [Google Scholar] [CrossRef]
- Komić, J. Harmonic Mean; Springer: Berlin/Heidelberg, Germany, 2011; pp. 622–624. [Google Scholar] [CrossRef]
- Chen, T.; Wu, H. Adaptive impulse detection using center weighted median filters. IEEE Signal Process. Lett. 2001, 8, 1–3. [Google Scholar] [CrossRef]
- Zhang, S.; Karim, M. A new impulse detector for switching median filter. IEEE Signal Process. Lett. 2002, 9, 360–363. [Google Scholar] [CrossRef]
- Li, Z.; Liu, G.; Xu, Y.; Cheng, Y. Modified directional weighted filter for removal of salt and pepper noise. Pattern Recognit. Lett. 2014, 40, 113–120. [Google Scholar] [CrossRef]
- Selmani, A.; Seddik, H. Anisotropic smart shape-adapted image smoothing without conductance function efficient for impulse noise removal. Digit. Signal Process 2018, 75, 83–95. [Google Scholar] [CrossRef]
- Deng, H.; Zhang, Q.; Song, X.; Tao, J. A decision-based modified total variation diffusion method for impulse noise removal. Hindawi Comput. Intell. Neurosci. 2017, 2017, 2024396. [Google Scholar] [CrossRef]
- Jafar, I.; AlNamneh, R. Efficient improvements on the bdnd filtering algorithm for the removal of high-density impulse noise. IEEE Trans. Image Process 2013, 22, 1223–1232. [Google Scholar] [CrossRef]
- Azimirad, E. Design of an optimized fuzzy system for edge detection in images. J. Intell. Fuzzy Syst. 2022, 43, 1–11. [Google Scholar] [CrossRef]
- Deepak, B.; Atulkar, M. Detection of edges using fuzzy inference system. Int. J. Innov. Res. Comput. Commun. Eng. 2013, 1, 1–6. [Google Scholar]
- Das, A.; Mohapatra, S.K.; Mohanty, M.N. Design of deep ensemble classifier with fuzzy decision method for biomedical image classification. Appl. Soft Comput. 2022, 115, 108178. [Google Scholar] [CrossRef]
- Simpson, P. Fuzzy min-max neural networks-part 1: Classification. IEEE Trans. Neural Netw. 1992, 5, 776–786. [Google Scholar] [CrossRef]
- Singh, D.; Kaur, A. Fuzzy based fast non local mean filter to denoise rician noise. Mater. Today Proc. 2021, 46, 6445–6452. [Google Scholar] [CrossRef]
- Unni, V.S.; Ghosh, S.; Chaudhury, K.N. Chaudhury, Linearized admm and fast nonlocal denoising for efficient plug-and-play restoration. In Proceedings of the IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018; pp. 11–15. [Google Scholar]
- Jeon, G.; Kang, S.; Lee, J.-K. A robust fuzzy-bilateral filtering method and its application to video deinterlacing. J. Real-Time Image Process. 2016, 11, 223–233. [Google Scholar] [CrossRef]
- Ghosh, S.; Gavaskar, R.G.; Panda, D.; Chaudhury, K.N. Fast scale-adaptive bilateral texture smoothing. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2015–2026. [Google Scholar] [CrossRef]
- Singh, V.; Dev, R.; Dhar, N.K.; Agrawal, P.; Verma, N.K. Adaptive type-2 fuzzy approach for filtering salt and pepper noise in grayscale images. IEEE Trans. Fuzzy Syst. 2018, 26, 3170–3176. [Google Scholar] [CrossRef]
- Suganya, C.; Umamaheswari, O. Image restoration using noise adaptive fuzzy switching weighted median filter for the removal of impulse noise. In Proceedings of the 2011 Defense Science Research Conference and Expo (DSR), Singapore, 3–5 August 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Xu, J.; Wang, L.; Shi, Z. A switching weighted vector median filter based on edge detection. Signal Process. 2014, 98, 359–369. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, G.; Peng, H.; Wang, D. Adaptive fuzzy switching filter for images corrupted by impulse noise. Pattern Recognit. Lett. 2004, 25, 1657–1663. [Google Scholar] [CrossRef]
- Wang, J.H.; Liu, W.J.; Lin, L.D. Histogram-based fuzzy filter for image restoration. IEEE Trans. Syst. Man Cybern. B Cybern. 2002, 32, 230–238. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.-X.; Ng, B.W.-H.; He, J.; Zhang, Y.; Abbott, D. Accurate image analysis of the retina using hessian matrix and binarisation of thresholded entropy with application of texture mapping. PLoS ONE 2014, 9, e95943. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; He, J.; Yin, X.-X.; Zhang, Y.; Chen, J.-H.; Kron, T.; Su, M.-Y. An image segmentation framework for etrating tumours from breast Magnetic Resonance Images. J. Innov. Opt. Health Sci. 2018, 11, 1850014. [Google Scholar] [CrossRef]
- Yin, X.-X.; Hadjiloucas, S.; Sun, L.; Bowen, J.W.; Zhang, Y. A review on the rule-based filtering structure with applications on computational biomedical images. J. Healthc. Eng. 2022, 2022, 2599256. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Wang, Y.; Qu, Z.; Xiong, N.N. Beatclass: A sustainable ecg classification system in iot-based ehealth. IEEE Internet Things J. 2021, 9, 7178–7195. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, L.; Subramani, S. Cab: Classifying arrhythmias based on imbalanced sensor data. KSII Trans. Internet Inf. Syst. 2021, 15, 2304–2320. [Google Scholar]
- Yin, X.-X.; Hadjiloucas, S.; Zhang, Y. Pattern Classification of Medical Images: Computer Aided Diagnosis; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]



| Input | Output | |||
|---|---|---|---|---|
| PI1 | PI2 | PI3 | PI4 | Out |
| Wh | Bl | Bl | Bl | En |
| Bl | Wh | Bl | Bl | En |
| Bl | Bl | Wh | Bl | En |
| Bl | Bl | Bl | Wh | En |
| Bl | Bl | Bl | Bl | En |
| Bl | Wh | Wh | Wh | En |
| Wh | Bl | Wh | Wh | En |
| Wh | Wh | Bl | Wh | En |
| Wh | Wh | Wh | Bl | En |
| Wh | Wh | Wh | Wh | Wh |
| Bl | Bl | Wh | Wh | En |
| Bl | Wh | Bl | Wh | En |
| Bl | Wh | Wh | Bl | En |
| Wh | Bl | Wh | Bl | En |
| Wh | Wh | Bl | Bl | En |
| Wh | Bl | Bl | Wh | En |
| Fuzzy Filters | Fuzzy Smoothing | Wavelet Fuzzy Filter | AFT2F | NAFSM |
|---|---|---|---|---|
| MSE | 189.35 | 107.18 | 5.9392 | 2.3532 |
| PSNR | 15.3587 | 17.8798 | 40.3935 | 44.4141 |
| SNR | 10.7782 | 12.9507 | 16.3254 | 20.3461 |
| Filter | Image | NT | ND | MAE | MSE | NCD | PSNR | SSIM | FSIM | Sens | Spec | Accu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VMF | Lena | NM2 | 10% | 3.69 | 56.5 | 4.29 | ||||||
| BVDFs | Lena | NM2 | 10% | 4.10 | 67.6 | 4.32 | ||||||
| DDFs | Lena | NM2 | 10% | 3.73 | 57.3 | 4.24 | ||||||
| AVDF | Lena | NM2 | 10% | 4.54 | 59.5 | 5.0 | 3 | |||||
| HMAMF | Lena | NM2 | 10% | 5.67 | 91.98 | |||||||
| HVMF | Lena | NM2 | 10% | 3.59 | 39.16 | |||||||
| CWTVM | Lena | NM2 | 10% | 21.80 | ||||||||
| CWVM | Lena | NM2 | 10% | 25.9 | ||||||||
| SCWVMF [113] | Boats | NM2 | 10% | 3.89 | 112.54 | 27.62 | ||||||
| PRF [53] | Peppers | NM4 | 10% | 8.54 | 8.44 | 25.44 | ||||||
| AVMF | Peppers | NM4 | 10% | 7.93 | 8.04 | 26.59 | ||||||
| PGSVMF | Peppers | NM4 | 10% | 8.17 | 9.01 | 26.36 | ||||||
| PGSAMF | Peppers | NM4 | 10% | 8.36 | 8.25 | 27.28 | ||||||
| FMPGSAMF | Peppers | NM4 | 10% | 8.33 | 8.48 | 26.23 | ||||||
| FRVP | Parrot | NM2 | 10% | 0.90 | 24.4 | 0.57 | ||||||
| ACWVDF | Parrot | NM2 | 10% | 0.72 | 37.4 | 0.37 | ||||||
| DPGF [56] | Lena | NM2 | 20% | 32.2 | ||||||||
| DWM [62] | Lena | NM2 | 20% | 33.6 | ||||||||
| AVDDF [44] | Lena | NM4 | FPGA | 1.00 | 33.34 | |||||||
| CA+QFT [42] | SI | SIN | 25.24 | 2.77 | 0.38 | |||||||
| FWMF [82] | Lena | NM2 | 20% | 39.5 | 0.98 | 0.997 | ||||||
| FINR [83] | Parrot | NM2 | 20% | 2.37 | 32.92 | |||||||
| AFSF [114] | Parrot | NM2 | 20% | 2.86 | 30.53 | |||||||
| HAF | Parrot | NM2 | 20% | 9.28 | 25.84 | |||||||
| PGSF [54] | Parrot | NM2 | 20% | 4.18 | 28.48 | |||||||
| FISF | Parrot | NM2 | 20% | 3.01 | 29.23 | |||||||
| QSAF | Parrot | NM2 | 40% | 35.33 | 0.939 | 0.972 | ||||||
| FIDRM [115] | Parrot | NM2 | 40% | 35.13 | 0.88 | 0.97 | ||||||
| FCA [94] | Lena | NM2 | 15% | 34.7 | 0.98 | |||||||
| SWF | Pepper | NM1 | 30% | 18.1 | 0.79 | |||||||
| ACWMF | Pepper | NM1 | 30% | 20.5 | 0.87 | |||||||
| FCA | Pepper | NM1 | 30% | 42.5 | 0.999 | |||||||
| FANLM [107] | BMRI | Rician | 9% | 30.5 | 81.5 | |||||||
| NLM [107] | BMRI | Rician | 9% | 28.1 | 73.2 | |||||||
| AT2F [111] | Lena | NM2 | 20% | 40.79 | ||||||||
| FARTMAP [105] | BH | 0.99 | 0.98 | 98.7 | ||||||||
| RNN | BH | 0.90 | 0.79 | 87.2 | ||||||||
| LSTM | BH | 0.92 | 0.86 | 90.38 | ||||||||
| GRU | BH | 0.92 | 0.83 | 89.7 | ||||||||
| NFP [93] | GD | 96.07 | 100 | 97.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, X.-X.; Hadjiloucas, S. Digital Filtering Techniques Using Fuzzy-Rules Based Logic Control. J. Imaging 2023, 9, 208. https://doi.org/10.3390/jimaging9100208
Yin X-X, Hadjiloucas S. Digital Filtering Techniques Using Fuzzy-Rules Based Logic Control. Journal of Imaging. 2023; 9(10):208. https://doi.org/10.3390/jimaging9100208
Chicago/Turabian StyleYin, Xiao-Xia, and Sillas Hadjiloucas. 2023. "Digital Filtering Techniques Using Fuzzy-Rules Based Logic Control" Journal of Imaging 9, no. 10: 208. https://doi.org/10.3390/jimaging9100208
APA StyleYin, X.-X., & Hadjiloucas, S. (2023). Digital Filtering Techniques Using Fuzzy-Rules Based Logic Control. Journal of Imaging, 9(10), 208. https://doi.org/10.3390/jimaging9100208






